Models at the Single Cell Level

Abstract

Many cellular behaviors cannot be completely captured or appropriately described at the cell population level. Noise induced by stochastic chemical reactions, spatially polarized signaling networks and heterogeneous cell-cell communication are among the many phenomena that require fine-grained analysis. Accordingly, the mathematical models used to describe such systems must be capable of single cell or subcellular resolution. Here, we review techniques for modeling single cells, including models of stochastic chemical kinetics, spatially heterogeneous intracellular signaling, and spatial stochastic systems. We also briefly discuss applications of each type of model.

The past few decades have seen an explosion of interest in the study of the functioning of individual cells, whether belonging to a unicellular species or to specific functional units of a multicellular organism. This focus has been fueled by two complementary developments. The first deals with the technological advances that have allowed more detailed and precise observation and manipulation of living cells, both on the individual cell and population levels. Molecular biology techniques have not only allowed us to perturb cellular function at the genetic or post-transcriptional level, but also tagging of individual proteins with fluorescent markers [1, 2] and development of a myriad of protein, DNA, or cellular compartment-specific dyes [3–5]. Genomic and proteomic studies have provided previously undreamt-of amounts of high-throughput data that have enhanced our general understanding of genetic and signaling networks [6, 7]. Imaging techniques now allow one not only to follow individual cells over long periods of time using phase-contrast and fluorescent imaging [8–10], but have also permitted researchers to delve into the sub-cellular level through the use of techniques like electron microscopy, TIRF, FRAP, etc. [11, 12]. Flow cytometry and fluorescence-activated cell sorting (FACS) have provided tools to study the variance in population responses in a high-throughput manner [13, 14]. The ability to modulate immediate cell surroundings using chemical, mechanical, or electrical stimuli, as well as creating specific extracellular matrix based inputs, has been advanced with the development of micro- and nano-fabrication technologies [15–21]. Microfluidics, microelectromechanical systems (MEMS) and nanofabricated structures now allow specific stimulation or modulation of cellular responses at the individual cell resolution. The second reason for the interest in individual cell function has arguably been a paradigm shift caused by the emergence of the myriad of data obtained from the above-mentioned technological advances. It is now not only widely accepted that individual cell response can be remarkably variable even in an isogenic population [22–24], but we also realize that understanding this diversity of response is crucial to understanding the basic mechanisms of biology.

The huge amounts of experimental data and the realization of the increasingly interconnected nature of biological networks have fueled the need for mathematical and computational descriptions of particular intracellular biological processes, extending to the cell as a whole. The modeling has to incorporate the realization that the same set of cells can respond with widely differing gene expression and physiological responses depending on the spatial and temporal aspects of their activation [25–28]. Indeed, the same signaling pathways, say MAPK pathways, show widely different behaviors, e.g. oscillations, bistability, and abrupt switching, under different conditions [29–31]. Traditional modeling techniques have most often involved sets of coupled ordinary differential equations (ODEs), using mass action kinetics to model the biochemical reactions, and this approach has been exceptionally fruitful in furthering our understanding of biological networks. These modeling techniques combine biologically specific formulations, such as enzyme kinetics descriptions with positive and negative feedback regulation, and the various methodologies as well as their biological significance have been thoroughly addressed in a host of excellent reviews [28, 32–37]. In this review, we have chosen to focus on some of the developing methodologies for modeling single cells that complement or extend the ODE-based efforts. Specifically, we address two critical assumptions of most ODE models, i.e., that there are sufficiently large numbers of molecules to justify the use of the notion of concentration as a continuous variable and that the system is well-mixed and spatially homogeneous. Individual cells often have small numbers of signaling molecules that critically regulate their response, and hence the assumption of a concentration as continuous and continuously differentiable function in the ODE models is not always accurate. We begin by reviewing techniques used for stochastic modeling of signaling pathways. The variation in the numbers of molecules between different cells as well as the inherent non-linearity of biological systems produces significant heterogeneity of response in a cell population. This makes it important to differentiate between average population measurements and individual cell measurements (Fig. 1). We also address the importance of spatial heterogeneity in the individual cell response, and discuss several spatial modeling techniques, both deterministic involving the use of coupled partial differential equations (PDEs) as well as stochastic spatial models. Finally, we note the application of individual cell models in cell-cell communication, and the factors that are likely to underlie the development and functioning of colonies of unicellular organisms or tissues in multicellular organisms.

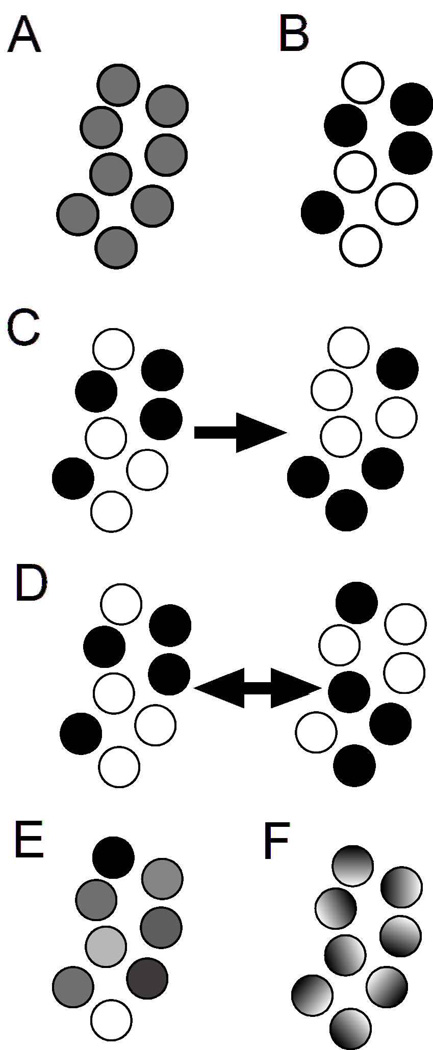
Figure 1. Examples of single cell behaviors that produce the same average population behavior.

Individual cells are shown as circles with each cell’s signaling activity denoted by its color; black denotes 100% signaling and white denotes 0% signaling. The population average for each panel is 50%. In panel A, each cell signals at 50%. In panel B, half of the cells are in the 100% state and half of the cells are in the 0% state. In panel C, cells are as in panel B, but individual cells may switch states in time without affecting the population average. The switching may occur stochastically, or result from oscillatory signaling activity whose phase and frequency vary from cell to cell. In panel D, cell signaling is distributed between 0 and 100%. In panel E, signaling within a cell is spatially heterogeneous such that the average signaling within each cell is 50%.

Models of single cell behavior arising from stochastic effects

Stochastic modeling

Many mathematical models of signaling networks are based on ordinary differential equations. An implicit assumption underlying the use of ODEs is that there are enough molecules of the modeled species to justify the usage of the concept of concentration as a smooth, differentiable function, rather than accounting for individual molecules. This assumption is often inaccurate for signaling in single cells. Due to a cell’s small volume (down to a few femtoliters for bacterial cells) and typically low biomolecular concentrations, the absolute number of molecules of a given signaling species in a cell may be quite small (typically on the order of 100 to 103). At such low numbers of reacting molecules, the reactions are heavily influenced by chance events, such as the chance encounter of reactant molecules. As such, the system as a whole diverges substantially from deterministic behavior, helping to explain why simplistic ODE models may sometimes fail to display the rich diversity of responses seen in biological systems [38]. Signaling within an individual cell often behaves probabilistically and requires stochastic modeling techniques.

A formal way to represent a stochastic system is through a chemical master equation. The master equation, fundamentally, is a differential equation that governs how the probability that the system contains a certain number of molecules of each modeled species evolves over time [39]. Solving the master equation represents a complete understanding of the stochastic behavior of the system, and would allow one to compute any desired statistical quantity, which could then be compared to experimental values. Unfortunately, master equations are typically analytically intractable for all but the simplest processes. In one notable exception, the analytical distribution can be obtained for a generic model of gene expression, consisting of first-order rates of transcription, translation, and mRNA transcript and protein degradation, given that the protein lifetime is much longer than the mRNA lifetime [40].

Approximate methods can be used instead of a direct attempt to solve a master equation, such as through the Langevin approach. In this approach, the chemical master equation is simplified into deterministic ODEs that are augmented with Gaussian white noise terms. For some simple systems, the resulting Langevin equation can be solved analytically to yield a time-evolution of the system’s probability density. Alternately, it may be possible to derive statistics for the probability density, such as the mean and variance, without fully solving the Langevin equation. This strategy has been used to predict how fluctuations in gene expression, about a steady state, depend on the rates of transcription and translation, and the qualitative dependence was then experimentally confirmed [23]. An advantage of the Langevin equations is that they are tractable for many simple systems, especially about steady state points, but a full solution may require some understanding of the noise characteristics which may not be known a priori.

Another alternative to solving the master equation is to apply a linear noise approximation [41]. The idea in this approximation is to apply a so-called Ω-expansion (analogous to a Taylor expansion) to the master equation. The first order term of the Ω-expansion yields the deterministic rate equations corresponding to the master equation. The second order term gives the linear noise approximation, an equation which can be solved to give estimates of variances of the system’s state variables. Because this method relies on an expansion about stationary points of the master equation, the variance estimates are only accurate for small fluctuations about steady states. Despite this limitation, this method has been quite successful in understanding the origin and propagation of noise, and their constituent components, in a variety of genetic networks [42].

If neither the master equation nor approximate methods are mathematically tractable, then simulation methods must be used. The Gillespie algorithm is a popular method for numerical simulations of coupled stochastic chemical reactions [43]. The idea behind the algorithm is that, under some basic assumptions, the waiting time to the next instance of each reaction is exponentially distributed with a time constant that can be computed from the numbers of each molecular species and macroscopic reaction rates. Furthermore, the propensity (probability) that a specific reaction will occur next, before any of the other reactions, is a simple function of these time constants. The Gillespie algorithm simulates this process by randomly choosing a waiting time and randomly choosing a particular reaction to occur according to these probabilities. In this way, the algorithm iteratively simulates the time course of the system one reaction at a time, giving a trajectory that is a faithful realization of the stochastic master equation. Running the Gillespie algorithm multiple times from the same initial condition gives an ensemble of solutions representing how the probability density of the system evolves over time.

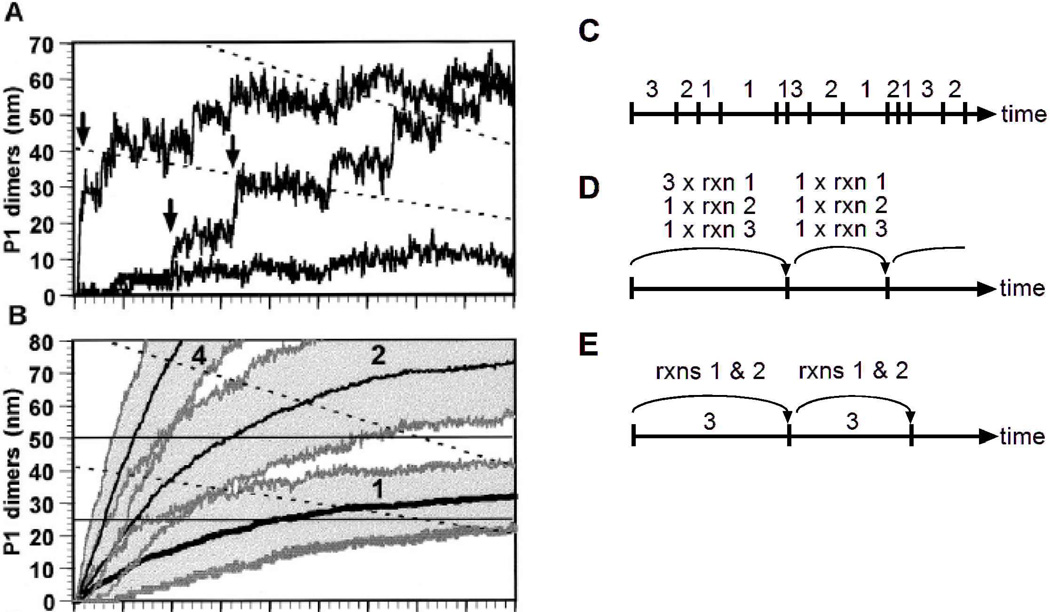
A key strength of the Gillespie algorithm is that it is an exact numerical simulation of the master equation that is easy to implement. Among the early applications of the algorithm to biological systems was a classic study by McAdams and Arkin on gene expression by λ phage [44]. They showed that a key viral transcriptional inhibitor ought to be produced in random bursts (Fig. 2A, arrows), and as a result, the lysis-lysogeny decision made by the λ phage should be stochastic. Viewing the process as being deterministic is highly misleading because the presence of the bursts is masked (Fig. 2B). The algorithm is especially well suited to such a system because the numbers of molecules of each of the chemical species in each cell is small, and therefore stochastic effects are expected to be prominent. For these reasons, the algorithm has since gained wide popularity in the systems biology community for modeling the behavior of single cells.

Figure 2. Schematic showing the Gillespie algorithm and its variations.

Panels A and B show examples of the Gillespie algorithm applied to the λ phage system, as described in the text (reprinted with permission from [44], copyright 1997 National Academy of Sciences, U.S.A.). Panels C-E, show schematics of different implementations of the Gillespie algorithm. In this schematic, the chemical system is composed of 3 different reactions. In each diagram, the axis represents time, tick marks represent iterations of the algorithm, and the labels represent the reaction(s) that occur during each iteration. Panel C illustrates the direct method in which one reaction (rxn) occurs per iteration. Panel D illustrates the tau-leaping method, in which multiple instances of multiple reactions may occur per iteration. Panel E illustrates a hybrid method, in which one instance of the slow reaction (reaction 3) occurs per iteration, while the other reactions are updated by some other technique. In each method, the period of time corresponding to each iteration is chosen stochastically, with tau-leaping and hybrid methods using generally larger time steps than the direct method.

The original formulation of the Gillespie algorithm, called the “Direct Method”, however, carries the disadvantage that it scales poorly (Fig. 2C). Since the method simulates each instance of each reaction, it becomes proportionately slower if the number of reactions increases or if the number of molecules increases, thereby increasing the instances of the corresponding reactions. To deal with this problem, many variations on the Gillespie algorithm have been developed to increase its efficiency [45]. One well-regarded reformulation of the algorithm, termed the Next Reaction Method, provides equivalent results as the direct method but scales logarithmically instead of linearly [46].

If an approximation to exactness can be tolerated, additional Gillespie-like algorithms are available with significant increases in speed. The tau-leaping method is one such algorithm, recently developed by Gillespie himself [47]. For each iteration of this method, a time interval τ is chosen during which multiple reactions may occur, hence “leaping” over what the direct method would take several iterations to perform (Fig. 2D). If the propensity of each reaction does not significantly change during this time interval, then the deviation from exactness will be small. Further improvements in speed can be obtained through hybrid algorithms that combine continuous and stochastic simulations, though at further expense to exactness. Hybrid methods are especially useful for systems in which some reactions occur rapidly and others occur slowly. In non-hybrid methods, the fast reactions dominate most iterations, and thereby determine the overall speed of the algorithm. If the fast reactions do not display strongly stochastic behavior on the time scale of the slow reactions, then it may be appropriate to focus the stochastic algorithm on the slow reactions to increase speed. Thus, during each iteration of a hybrid method, the slow reactions are updated in a Gillespie-type manner, whereas changes to the fast reactions are approximated using a Langevin, deterministic, or other approximate equation [48] (Fig. 2E). Hybrid methods, available for example in the KinetiKit software, have been particularly effective in modeling several interacting signaling pathways in a single cell [49].

Single cell versus population responses

Cellular response heterogeneity despite isogenicity is a common feature that has been observed across cell types from bacterial [22, 23] to mammalian cells [24]. One reason a population of cells may display response heterogeneity is due to “extrinsic” and “intrinsic” noise sources. Extrinsic noise results from differences in the concentrations, states, and locations of the several molecules, such as regulatory proteins and RNA polymerases, involved in gene expression [22]. One of the many examples of a process that can introduce such variation is unequal distribution of the cytoplasm, and hence, cellular components between the two daughter cells during cell division. Intrinsic sources of noise are a result of the discrete nature of the biochemical process of gene expression, which lends itself to significant randomness in terms of the order and timing of events, even in a (hypothetical) case of a population of cells which have the same genetic code as well as identical concentrations of cellular components [22]. In addition to gene expression, cellular response variability can also result from stochastic differences in post-translational modifications and in the concentrations, activities and localization of different states of proteins involved in signaling networks inside cells.

Several techniques have been employed to study gene and protein expression in single cells. Protein or promoter fusions with the green fluorescent protein (GFP) or its variants occupying other frequency spectra [1, 50] have been used to study individual cell responses using live-cell microscopy (which also allows temporal tracking of individual cell responses) as well as flow cytometry. Two distinguishable fluorescent probes (e.g. CFP and YFP) expressed simultaneously in single cells have been used to measure the contribution of intrinsic and extrinsic noise sources to cell-cell variability [22], and three simultaneous probes (e.g. CFP, YFP, and RFP) have been used to investigate noise transmission in gene expression cascades [51]. This technique has revolutionized the kind of information that can be obtained from individual cells, and compares well to predictions made by stochastic mathematical models. A complementary approach involves using immunostaining followed by individual cell analysis to obtain data that displays the variability in the population response, which can be used to constrain dynamical mathematical models of signaling pathways [52]. This approach can be important when fluorescent protein tagging of the native protein alters its functional response or when a plasmid-induced change in the expression of key proteins can affect the signaling pathway response [53]. Despite these recent advances, there are still several limitations in the quantitative characterization of proteins, especially those corresponding to weakly transcribed genes. Approaches like gene amplifier circuits [54] or single molecule detection techniques [55, 56] as well as techniques that allow direct observation of mRNA production and diffusion [57–59] will likely permit quantitative measurements that can be tested against mathematical models of single cells. Extensive reviews have further addressed this subject [38, 60–63].

Despite the proliferation of several single cell measurement techniques, a large majority of biological measurements involve population-wide average measurements. These include Western blots (or immuno-blots) assaying the total protein levels or the protein activity, Northern and Southern blots reporting on mRNA and DNA levels respectively, DNA and protein microarray measurements, liquid chromatography- mass spectrometry data, etc. Accordingly, there is a need to develop ways to reconcile data obtained at the single cell and population levels.

Population level measurements may not only average out the variation in the response, thereby masking the underlying response heterogeneity; but may also camouflage important biological phenomena, and hence need to be considered with care (Fig. 1). As an example, one can consider the presence of bistability or multistability in several natural and engineered biological systems, usually the result of one or more positive feedbacks [64–68]. In the region of bistability (or multistability), say a specific ligand input range, a deterministic system should display only one of the stable steady states and yield a unimodal response histogram (dependent on the initial conditions). However, the combination of bistability (multistability) with sufficient large inherent stochastic noise can help some cells switch from one stable steady state to another, thereby leading to a bimodal (multimodal) response histogram [30, 65]. However, a purely population-based measurement would most likely miss these details and only present the average response. Thus, what may actually be a bistable response on the single cell level may appear to be a graded response at the level of the population average. In a similar manner, several biological systems display oscillatory gene expression or pathway activity [69–73]. Individual cells are often asynchronous in their oscillatory responses or may have variable oscillatory time-periods, either due to asynchronous cell cycles or differences in concentration of cellular components. A population averaged measurement may smooth out and lose or severely dampen the appearance of oscillations.

Models of single cells exhibiting spatially heterogeneous signaling

Spatial modeling in the single cell

ODE-based models, as well as the stochastic models described above, assume that the system is well-mixed and the modeled species are distributed in a spatially homogeneous manner. This assumption may be inaccurate depending on the particular signaling network being modeled, as the intracellular environment displays several features which make it important to consider the spatial aspects of models. Receptor stimulation leads to the recruitment of cytosolic adaptors and enzymes to the plasma membrane. Subsequent activation steps can lead to the formation of signaling complexes through interactions with receptors, G-proteins, cytoskeletal elements or specialized proteins like scaffolds that bind to multiple proteins thereby facilitating formation of a “signalosome”. In particular, scaffold proteins functionally regulate signaling as well as signal specificity in MAPK pathways from yeast cells to mammalian cells [74, 75]. Membrane recruitment has been postulated to increase the local concentrations of proteins by several orders of magnitudes in some instances, thus pointing to the need for spatial modeling to correctly model the cell as a whole [76]. The targeting of proteins to internal membranes of cell structures like endosomes or in specialized membrane regions like lipid rafts is another way to exert spatial control of signaling [28]. Additionally, spatial segregation of opposing reactions, e.g. kinase- and phosphatase-mediated reactions, can lead to intracellular gradients of protein activity, depending on the substrate diffusivity and the activities of the enzymes involved. Such gradients have been implicated in regulation of microtubule polymerization and positioning during the mitotic spindle assembly step of cell division [77, 78]. Other important spatially distributed regulatory mechanisms in eukaryotic cells include endocytosis and directed secretion of proteins. Endocytosis not only can downregulate membrane protein concentrations in a part of or the whole cell, but also redirect some of these proteins to other parts of the cell using the directed secretory mechanisms. Cytoskeletal elements like actin cables or microtubules play an important role in directed secretion [79]. Indeed, a combination of endocytosis, membrane diffusion and directed secretion has been shown to generate spontaneous polarization in yeast cells [80].

Deterministic solutions to spatial simulations can be obtained by solving a set of coupled partial differential equations. In general, the spatiotemporal dynamics of signaling species can be modeled using reaction-diffusion equations, PDEs which relate the change in time of the concentration of the species due to diffusion, convection and chemical reaction. In the absence of any convective flow, the diffusible range of the signaling species is determined by the diffusion coefficient alone [81], and we obtain a reaction-diffusion equation. In general, analytic solutions are difficult to obtain for a set of coupled PDEs, and even numerical simulations are non-trivial considering the fact that biological systems often have large sets of coupled non-linear PDEs.

Reaction-diffusion (RD) equations have been used to study pattern formation in general, and biological pattern formation in particular. The pioneering study in this field was done by Alan Turing in 1952 [82]. He showed that a two-component system of reaction diffusion equations (on a bounded domain with no-flux boundary conditions) that has a stable spatially homogenous steady state solution under spatially homogeneous conditions (in the absence of diffusion), can be de-stabilized and can generate a spatially heterogeneous pattern in the presence of sufficiently different diffusivities of the two components [82] (Fig. 3A). Detailed studies of various formulations of the reaction terms of the two component system have given rise to the classical Gierer-Meinhardt model [83], the Gray-Scott model [84], the Brusselator model [85] and the Fitzhugh-Nagumo [86] model among many others. Various modeling efforts in biology and chemistry involving RD systems [87, 88], including patterning in biological morphogenesis [89, 90], have been extensively reviewed. Some of the directions of research pursued have included the introduction of non-dimensional variables in order to simplify the analysis of these systems under extreme variations of the critical non-dimensional parameter(s), as well as work on bifurcation theory in order to study the stability of solution branches in a small neighborhood around the bifurcation point [88].

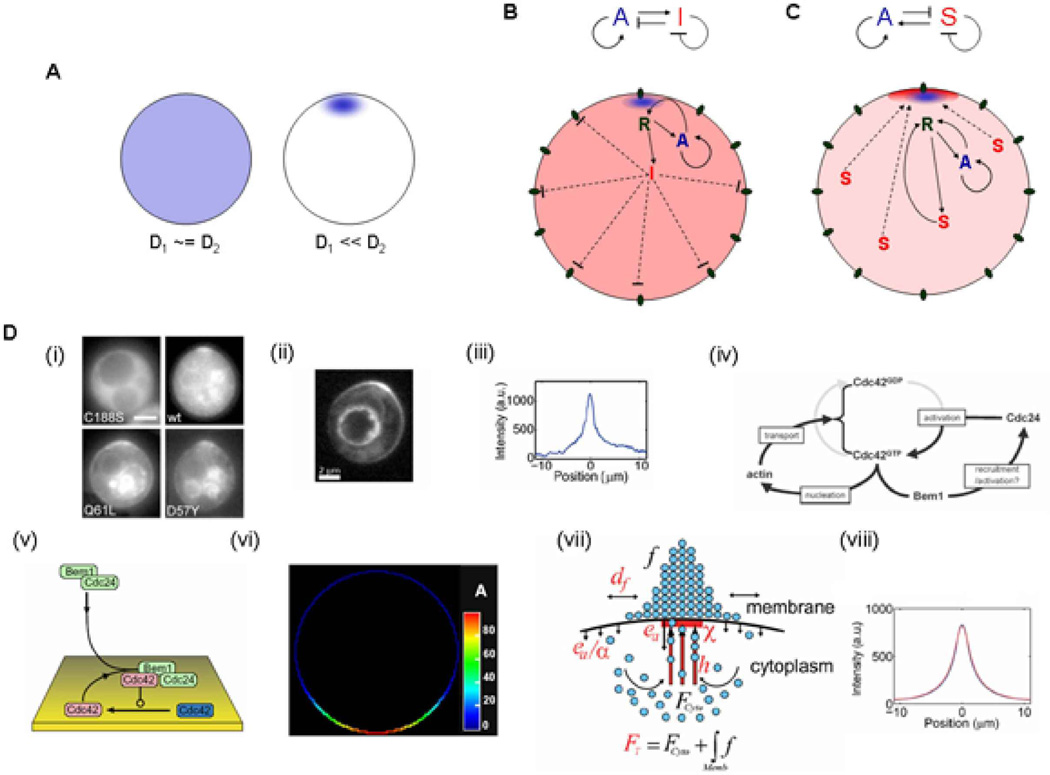
Figure 3. Pattern generation through Turing-like mechanisms.

The Turing mechanism shows that a two component system can generate a spatially heterogeneous pattern when the diffusion coefficients are significantly different, as shown in (A). The two basic mechanisms of pattern formation in a two component system are the activator-inhibitor mechanism (B) and the substrate-depletion mechanism (C), as described in the text. Both panels show the connection diagrams for the respective mechanism above and a possible biological implementation below. (D) The yeast bud-site selection and polarization mechanism offers a unique example of parallel Turing mechanisms in biology. As shown in panel (i), the WT GTPase Cdc42 displays a polarized response corresponding to the presumptive bud site, as do the two mutant versions of Cdcd42 i.e. Q61L (constitutively GTP bound form) and D57Y (constitutively GDP bound form) [146]. The membrane bound polarized profile of a cell with the Cdc42-Q61L mutation (ii) is plotted in (iii) [80]. The formation of the incipient bud can be divided into two parallel phases (iv). The initial symmetry-breaking phase involves the formation of a cluster of activated Cdc42, which can occur without the presence of actin or microtubule machinery, and requires a positive feedback mechanism involving Cdc42, its GEF Cdc24 and the scaffold protein Bem1 (which binds both Cdc24 and Cdc42GTP). In particular, this polarization depends on the cycling of Cdc42 between the GDP and GTP bound forms. The second phase involves an actin mediated positive feedback involving polarized secretion of vesicles (containing proteins like Cdc42 or Cdc24) along actin cables leads to an ensuing phase of growth and protrusion. This mechanism does not depend on Bem1 and Cdc24 and leads to the polarized distribution of the Q61L and D57Y mutants. Mathematical models of each of these phases display polarization through inherently Turing-based mechanisms. Panel (v) shows a model of the initial actin-independent phase which leads to a polarized Cdc42 distribution as shown in (vi) [147]. Mathematical modeling shows that a combination of lateral diffusion of Cdc42, its endocytosis and its polarized secretion as part of a positive feedback (increased presence of Cdc42 leads to increased probability of actin cable formation and decreased actin cable detachment) as shown in panel (vii) can lead to a polarized distribution of Cdc42 as shown in panel (viii) [80]. (Panels (i) and (iv) reprinted with permission from [146], copyright Wedlich-Soldner et al., 2004, originally published in The Journal of Cell Biology, doi:10.1083/jcb.200405061. Panels (ii), (iii), (vii), (viii) reprinted from [80] with permission from Elsevier. Panels (v) and (vi) reprinted with permission from [147].)

In general, two component systems that display Turing-like diffusive instability and pattern formation can be classified into two categories: activator-inhibitor mechanisms and substrate-depletion mechanisms (Fig. 3B,C) [91]. Fig. 3B displays one of the possible biological implementations of an activator-inhibitor (AI) mechanism. The stimulus (as represented by receptors R, which are preferentially activated at the top in the schematic, say, due to an external ligand gradient) activates both an activator (blue, slow diffusing) and an inhibitor (red, fast diffusing). The fast diffusing inhibitor inhibits activation in the cell as a whole, whereas the preferential activation at the top is amplified through a positive feedback mechanism. Fig. 3C shows a possible biological implementation of a substrate-depletion (SD) mechanism, wherein the substrate S (red) is fast diffusing, while the activator A (blue) is slow diffusing and may be membrane-bound. The input signal, the receptor R activated preferentially at the top in the schematic, activates (or produces) the activator species A. The activator A (possibly in conjunction with the receptor R) then recruits the cytoplasmic substrate S to the membrane, thereby reducing its diffusion and depleting its availability to the rest of the cell. The bound complex involving S then leads to further activation (or production) of A through the receptor R, which leads to a positive feedback mechanism. The central mechanism in SD systems involves depletion of substrate S from a common pool available to the rest of the cell, in contrast to an AI system where the inhibitor I inhibits the rest of the cell. Several models of biological pattern formation have been based on these mechanisms. One such system involves cell polarization (eventually leading to budding) despite the absence of a pre-existing spatial cue in the budding yeast. This polarization has been experimentally shown to display two phases, an initial symmetry breaking phase involving polarization of the GTPase Cdc42 independent of actin, and a second actin-dependent phase of polarization (Fig. 3D (i–iv)). Both of these mechanisms have been mathematically simulated by models that have Turing-like mechanisms (Fig. 3D (v–viii)).

Mathematical models of gradient sensing in single cells from Dictyostelium to neutrophils have often involved different variations along the common theme of local positive feedback (activation) and global negative feedback (inhibition) [92–95]. These models have had to balance a trade-off between high gradient signal amplification (i.e., conversion of a shallow external ligand gradient to a sharp internal signaling gradient), and avoidance of simple positive feedback loops leading to “self-locking”. The positive feedback can lock cells into a robust, polarized response that may not be sensitive to changes in gradient shape or direction [96], contrary to observed data. Thus, models that rely on positive-feedback mediated bistability in the response tend to display high amplification, but also self-locking, and often need a second inhibitor or another negative feedback mechanism to poison the previous polarized site to allow for gradient sensing over time [93–95]. Positive feedback-dependent yet monstable mechanisms can display more sensitivity to the external gradient shape and direction, though with less amplification [92]. Similar models have been proposed for several other polarized mechanisms, including selection of a projection formation site during the mating response [97, 98] and budding site selection during vegetative growth in yeast [99, 100]. In general, more realistic spatial models, especially those tailored to gradient sensing, will likely require better representation of the intricate interactions between the signaling machinery consisting of the receptors and downstream cascades, and the morphogenetic machinery involving the actin cytoskeleton and related proteins [101–103]. Additionally, these models would need to move beyond static spatial geometries in order to accurately reflect the changing cell shape during gradient sensing or morphogenesis [104–106].

Spatial stochastic models

Biological systems are often characterized by complex spatial structure, low numbers of molecules and low diffusion rates leading to stochastic differences in the molecular concentrations in a local environment, which then combine with the non-linear amplification observed in several biological pathways to increase the effects of noise. Thus, stochastic models in both the spatial and temporal domain are essential to accurately model the system, whereby diffusion is modeled as Brownian random walks of individual molecules and chemical kinetics is simulated as stochastic reaction events [107]. These spatial models are often of variable spatial resolution, with the most highly resolved ones represented by lattice and off-lattice particle based methods [108]. Lattice based methods consist of Monte Carlo simulations involving two or three dimensional lattices populated with particles of different molecular species, which undergo chemical reactions based on a certain probability and diffusion from one lattice point to another. Off-lattice simulations consist of the simulation space discretized such that each particle has a reaction bin size that corresponds to the diffusion coefficient of the particle. Particles within the same bin may react chemically with some probability. Chemcell [109] and M-Cell [110, 111] are some examples of software programs tailored towards highly resolved stochastic spatial simulations. Another implementation of stochastic spatial models involves a modification of the original Gillespie algorithm [43] to create the ‘next subvolume method’ (NSM), where the total system volume is divided into subvolumes that are small enough to be considered homogenous for diffusion over the time scale of the reaction [112]. The binomial tau-leaping modification can be applied to the NSM to provide spatially accurate chemical kinetics in reduced simulation times [108]. However, it is often not necessary, or is indeed counter-productive, to model individual molecules of every species, especially ones that are available in large concentrations, or variables such as the cell membrane shape or cytoskeletal motion. Accordingly, there are hybrid methods being created for stochastic spatial simulations, wherein the discrete reaction dynamics of some molecular components is simulated stochastically and is coupled to continuous fields of others that vary according to partial differential equations [113, 114].

There is a large body of mathematical modeling studies that have used analysis or numerical simulations to model spatial effects in their specific biological system of interest, and is beyond the scope of this review. However, certain software packages have been developed in recent years that allow the spatiotemporal study of a wider and more general range of biological systems. These include but are not limited to packages like StochSim, M-Cell and Virtual Cell [107]. StochSim as the name suggests, has developed a stochastic simulation framework based on a modification of the Gillespie algorithm, by shifting its focus from the reactions towards the individual molecules, which are treated as individual automata [115, 116]. The program allows one to simulate systems where molecules can exist in multiple states more efficiently than by using the Gillespie algorithm, and also allows the tracking of individual molecules over the time duration. Recent versions have included the implementation of simple two-dimensional spatial structures, where nearest neighbor interactions of molecules and the corresponding modulation of individual reactivities can now be modeled. The combination of spatial heterogeneity with stochastic simulations using StochSim was used to show that the extensive sensitivity and dynamic range of bacterial chemotaxis is attained through adaptive receptor clustering. [116, 117]. This is in contrast to many models of bacterial chemotaxis, that have traditionally focused on ODE based formulations of receptor and downstream signaling molecules to model the robust adaptation of the response [118–120]. (A more detailed review of the largely successful modeling and experimental approaches to understand the mechanisms of bacterial chemotaxis, can be read here [121].

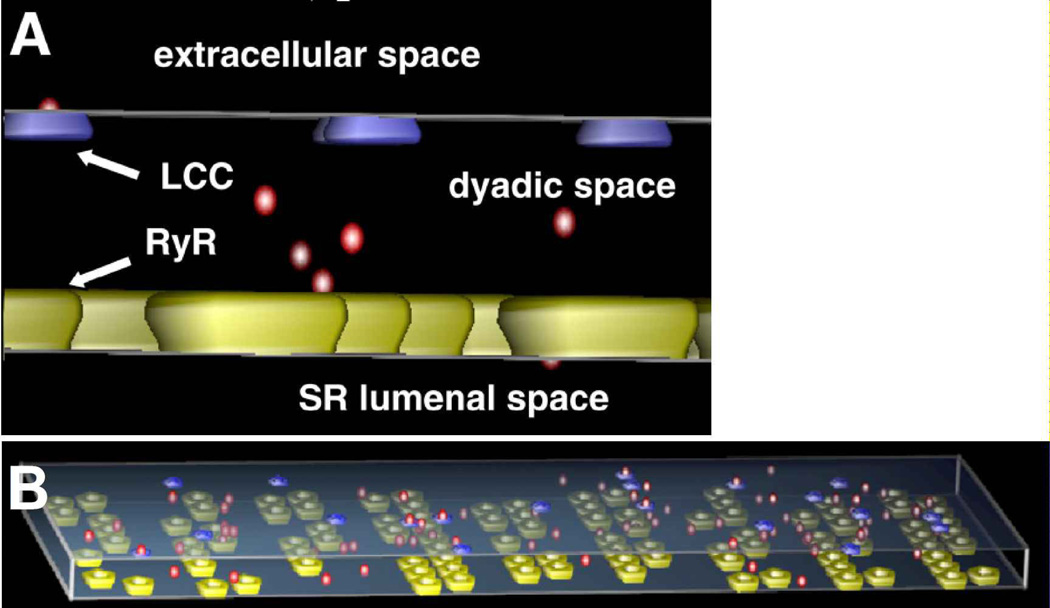
M-Cell, a Monte Carlo simulator of cellular microphysiology, provides a 3D modeling environment for realistic and detailed stochastic models of cellular signaling in and around the cell. Ligands, receptors, and other effector molecules, as well as reaction mechanisms and specific initial distributions are described in a user-defined 3D environment using a Model Description Language (MDL) that is accessible to biologists. These commands are then converted into simulation objects that are then simulated using highly optimized Monte Carlo algorithms to track the diffusion and reaction of molecules in space and time. M-Cell provides an ideal framework for studying biological phenomena, especially signaling that occurs in very small spatial domains. For example, MCell has been used to examine calcium signaling in dyadic clefts, the space formed by the apposition of the cell membrane and the sarcoplasmic reticulum in cardiomyocytes [122] (Fig. 4). In this example, the modeling revealed the role geometry played in signaling, especially through its effects on the concentration of the signaling species and the degree of coupling between receptors on the two membranes. MCell has also been used to great effect to studying signaling in the microdomains at synaptic junctions and at neuromuscular junctions [110, 123].

Figure 4. Example of spatial stochastic modeling.

Panel A shows a schematic of an M-Cell model used to model cardiac myocyte dyadic clefts (the narrow space between the cell membrane and sarcoplasmic reticulum). Calcium ions are shown in red, L-type calcium channels in blue, and ryanodine receptors in yellow. Panel B shows an example of an M-Cell simulation showing calcium signaling in the dyadic cleft. M-Cell tracks the location, random movement, and identity of each molecule within the system volume, thereby providing a spatial stochastic simulation. (Reprinted with permission from Fig. 1 of Reference [122]).

Virtual Cell is a general and widely flexible modeling framework that combines the capacity to run deterministic simulations in compartmental (ODE-based) as well as spatial (PDE-based) domains. Recent versions have also introduced stochastic simulation capabilities to this program. It provides two user workspaces, one tailored to scientists who prefer a graphical user interface or are not comfortable with a programming interface (BioModel workspace) as well as a MathModel workspace that allows model definition using a mathematics description language (VCMDL) [107, 124]. The BioModel workspace offers an intuitive graphical user interface allowing the specification of model topology and reacting species as well as reaction mechanisms, membrane fluxes and kinetic constants. For spatial simulations, the program allows user-defined 1D, 2D, and 3D analytical geometries, along with the potential to import arbitrary geometries from, say, imaging experiments. The latter is particularly useful for reproducing the exact spatial constraints for a mathematical model, allowing for direct comparison of model predictions and experimental observations. Systems of ODEs are solved numerically using a number of solvers including variable time-step stiff solvers [107]. Systems of PDEs are solved using a finite volume method, which is similar to finite difference methods, but allows for better control over boundary conditions and geometrical profile assumptions. The program allows for single or multi-parameter variations during the simulations, and appropriate interfaces for displaying and exporting simulation results. The package has been used to model a wide variety of spatial models from gradient sensing in Dictyostelium cells [125], the analysis of G-actin transport in motile cells [126], compartment-specific activation of Ras [127] and RNA trafficking from the nucleus outwards [128].

Cell-cell communication

Individualized cell responses within a population may be obtained as a result of external directed cues that are distributed in a spatially heterogeneous manner, thus promoting localized responses that depend on a cell’s location. In the immunological response, for example, leukocytes and macrophages sense gradients of cytokines secreted by other cells (e.g. activated endothelial cells) leading them to an injury site. In the nervous system, neuronal axons grow towards or away from chemoattractants or chemorepellants, which may often be the same molecule playing an opposite role in different contexts [129]. Directed chemical or extracellular matrix (ECM) cues lead to chemotaxis (dissolved chemical gradient cues), haptotaxis (substrate bound chemical gradient cues) [130] or durotaxis (substrate rigidity gradient cues) responses [131]. During development, external ligand gradients, such as those produced by mother cells, can determine spatial patterning in tissues either by selectively inducing differentiated phenotypes of cells along the gradient, or by inducing movement of cells to requisite positions. Cancer cells are believed to use chemical cues during their metastatic spread [132, 133]. Generally speaking, models of spatially heterogeneous cell-cell communication must take into account certain factors: (1) the physical nature of the intercellular signal (e.g. contact-mediated, diffusible ligand, etc.), (2) the spatial distribution of the signal and the cells, and (3) how the signal received by an individual cell influences its behavior, and whether this causes the cell to alter the signal in its local environment. In this section, we will illustrate these principles with various specific examples.

Models of cell-cell communication at the single cell level arise frequently in developmental biology, especially with regards to pattern formation. One example is the remarkable property in many organisms with hair (or similar fibers) to have the direction of each hair to be closely aligned with that of its neighbors. Communication between the individual hair-producing cells (or hair follicles) is required to produce such a pattern. In particular, the wing cells of the Drosophila melanogaster fruit fly produce an actin-rich hair on their distal end that points distally. The location and direction of the hair produced by each cell is determined by physical contact with neighboring cells, as several membrane bound ligands and receptors (e.g. Frizzled, Van Gogh) have been implicated in the process [134]. The bound receptors trigger spatially heterogeneous intracellular signaling, and feedback within the signaling network in turn helps to determine the ligands and receptors that the cell ultimately presents to each of its neighbors and also determine the position and direction of the hair. One model to describe the hair specification process took these features into account by approximating the wing as a 2-dimensional hexagonal lattice of wing cells, with each cell governed by a system of partial differential reaction-diffusion equations, and with the equations of neighboring cells coupled together via ligand-receptor interactions [134]. This model is able to recapitulate and explain hair patterns in wildtype Drosophila wings, as well as the patterns resulting from a wide variety of genetic mutations. In mice, fur hair is likewise locally aligned, and mutation of Frizzled6, a mammalian homolog of Frizzled, results in randomly oriented hair. A simplified method was used to model this system. Instead of modeling each cell with detailed differential equations, the response of each cell was recast as a simple update rule (specifically, at the next time step, a cell’s response is set to the consensus of its neighbors). This cellular automata-type model was used to explain hair patterns in mice lacking Frizzled6 [135].

Since multicellular models based on differential equations may scale poorly with cell number, cellular automata models are particularly useful in describing systems consisting of a large number of locally interacting cells. This is especially true for systems mediated by contact-mediated interactions, such as in pattern formation due to Delta-Notch lateral inhibition [136, 137], myxobacterial aggregation [138], and proliferation of contact-inhibited cells [139]. In such systems, it is important that interactions between pairs of cells are sufficiently well-understood that they can be summarized in cellular automata rules. Microfluidic devices may be used to capture and experiment on pairs of cells in isolation to determine the rules and predict multicellular behavior, as done recently with endothelial and stromal cells to predict patterns of angiogenesis [140].

Paracrine signaling is another general category of cell-cell communication phenomena that has been the focus of many extensive modeling efforts. Specifically, paracrine signals, such as receptor ligands, are secreted by some cells and diffuse to affect other cells some distance away. When a small set of cells secretes a paracrine signal into a larger field of cells, diffusion causes the concentration of the signal to drop as a function of distance from the secreting cells. So, cells receiving the paracrine signal can use its concentration to determine position relative to the paracrine source [141]. This property of paracrine signaling can be used to tailor an immune response based on the distance from “danger” (infection) [142], to limit the extent of EGF-induced tissue remodeling [143], and to pattern developing tissue [144]. Models of these types of systems are often composed of two generally decoupled parts. The first part focuses on simulating the extracellular distribution of the paracrine signal. This is typically achieved through reaction-diffusion equations, where boundary conditions are used to model the production of signal from one area and absorption of the signal at other areas [145]. The second part focuses on simulating the response of individual cells, given the particular signal each cell receives. In this way, cells that in principle have the same signaling machinery can adopt different behaviors, leading to individualized behavior.

Conclusion

The stochastic, spatial, and stochastic spatial modeling techniques described above help recapitulate single cell signaling in a greater detail. One of the challenges facing modelers is to choose the technique with enough spatiotemporal resolution and numerical speed to describe the cellular behavior of interest, but not so greatly resolved as to make the model prohibitive to implement or difficult to interpret. One key consideration is the source of cell-to-cell variability. Differences due to intrinsic noise have proven to be amenable to stochastic chemical kinetics models, whereas differences due to extrinsic noise likely require a different mathematical description. Another consideration is whether cell-cell communication is a determinant of the cells’ responses. Spatial models are appropriate if a cell’s response depends on its location, such as its position within a gradient of stimulus or whether a cell borders particular types of other cells. On the other hand, if the responses of a population of cells are strongly coupled due to intercellular signaling, as might be the case in some paracrine signaling and quorum sensing systems, then the differences between individual cells may not be important to model in detail. The modeler should be guided by the biology of the system of interest. As such, we expect models at the single cell level to be increasingly useful, as the ability to experimentally probe single cells and single molecules, and hence the ability to test these models, reaches ever higher.