Separate enrichment analysis of pathways for up- and downregulated genes

Abstract

Two strategies are often adopted for enrichment analysis of pathways: the analysis of all differentially expressed (DE) genes together or the analysis of up- and downregulated genes separately. However, few studies have examined the rationales of these enrichment analysis strategies. Using both microarray and RNA-seq data, we show that gene pairs with functional links in pathways tended to have positively correlated expression levels, which could result in an imbalance between the up- and downregulated genes in particular pathways. We then show that the imbalance could greatly reduce the statistical power for finding disease-associated pathways through the analysis of all-DE genes. Further, using gene expression profiles from five types of tumours, we illustrate that the separate analysis of up- and downregulated genes could identify more pathways that are really pertinent to phenotypic difference. In conclusion, analysing up- and downregulated genes separately is more powerful than analysing all of the DE genes together.

1. Introduction

The enrichment analysis of pathways is a basic task for biologically interpreting a list of interesting genes extracted from various ‘omics’ data generated by microarray, next-generation RNA sequencing (RNA-seq) or other high-throughput biotechnologies [1,2]. A vast number of enrichment analysis tools have been developed. The most popular type is singular enrichment analysis and tools of this type include GO-function [3], DAVID [4], GoMiner [5], Onto-express [6], BINGO [7], GOseq [8] and many others [1]. These tools are quite similar as they all calculate the enrichment p-values of pathways for a user-preselected list of interesting genes using slightly different statistical methods, including Fisher's exact test, the χ²-test, the hypergeometric and binomial distribution tests and others [1–3,9]. Fisher's exact test [10] is appropriate for analysing pathways containing a small number of genes and the χ²-test is adequate when the number of genes is greater than five [11]. Similar to Fisher's exact test, the hypergeometric distribution [12] is used for sampling from a small number of genes but approximates to the binomial distribution when the number of genes is large [13]. The binomial is more suitable when a large number of genes are considered, while the other three are applicable for analysis with a small number of genes. When identifying significant pathways, the differences among these statistical methods will not be dramatic [9,14]. In studies comparing gene expression profiles of two phenotypes, researchers usually consider the differentially expressed (DE) genes detected between the two phenotypes as genes of interest and apply a selected enrichment analysis tool to identify the pathways associated with the phenotypic difference. Currently, there are two different strategies to apply to an existing singular enrichment analysis tool. The often-used strategy of applying a singular enrichment analysis tool is to analyse all of the DE genes together (referred to as the all-DE strategy for short) [15–17]. The alternative strategy is to analyse the up- and downregulated genes separately (referred to as the separate-DE strategy for short) [18–20]. However, the rationales of these two strategies have not been strictly scrutinized or compared.

Based on the Kyoto Encyclopaedia of Genes and Genomes (KEGG) pathways [21], which provides different types of functional links among genes or their corresponding proteins, some studies report that the numbers of the up- and downregulated genes in disease when compared with normal controls could be highly imbalanced in biological pathways [22,23]. Some pathways are even found to comprise only up- or downregulated genes in a particular disease [22,24]. However, to our knowledge, no study has systemically examined the imbalance of up- and downregulated gene numbers in pathways that are disturbed in a disease and, more importantly, how this imbalance influences the singular enrichment analysis of pathways.

In this report, using both microarray and RNA-seq datasets of gene expression profiles of five types of tumours, we first show that gene pairs with functional links defined in the KEGG database tended to exhibit positively correlated expression levels. We then show that this tendency could lead to the imbalance between the numbers of up- and downregulated genes in disease-associated pathways. We further illustrate numerically that, owing to this imbalance, analysing all of the DE genes together could greatly reduce the power of disease-associated pathway detection. Finally, we validate this conclusion for the singular enrichment analysis of pathways based on Gene Ontology (GO) [25]. Another five singular enrichment tools were also compared to support our conclusion.

2. Material and methods

2.1. Datasets

We collected three microarray datasets from the Gene Expression Omnibus database [26] and two RNA-seq datasets from The Cancer Genome Atlas database [27] for five types of tumours (table 1). All of the microarray datasets were generated using the Affymetrix HG-U133 Plus 2.0 platform. The raw data were preprocessed using the Robust Multi-array Analysis algorithm [28] and the SOURCE database [29] (March 2011) was used to annotate the CloneIDs to GeneIDs. All of the RNA-seq datasets were generated using the Illumina HiSeq platform. The raw data were TMM normalized [30] using the edgeR BioConductor package [31].

Table 1.

Datasets analysed in this study. T denotes the number of tumour samples; N denotes the number of normal samples. Abbreviations are same as in figure 2.

cancer	T : N	data source
BC	42 : 143	GSE10780
CRA	32 : 32	GSE8671
GC	38 : 31	GSE13911
KIRC	465 : 68	TCGA
LUAD	125 : 37	TCGA

2.2. Kyoto Encyclopaedia of Genes and Genomes pathways

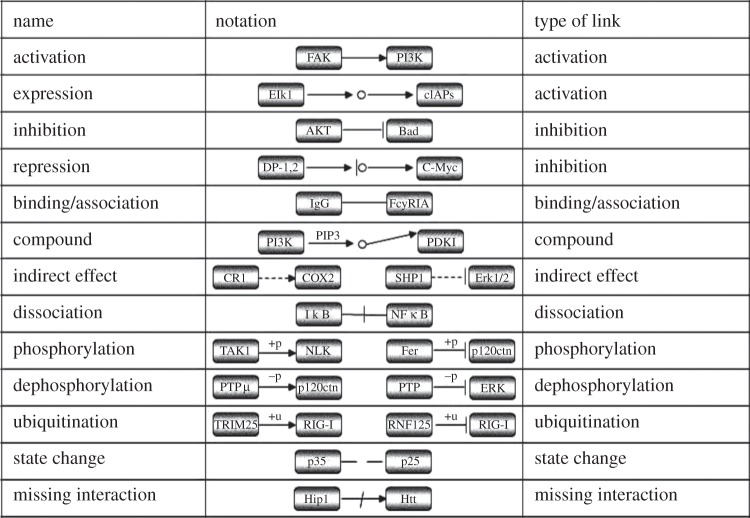
In the KEGG database, biological pathways are described in KEGG Markup Language (KGML) files, including nodes (genes or compounds) and edges (functional links) [21]. The KGML data files were obtained manually from the KEGG website on 16 January 2012. A total of 216 pathways were analysed after excluding the pathways without functional links between genes. Totally, these 216 pathways included 30 263 functional links comprising 4171 genes measured in the microarray datasets and 33 367 functional links comprising 4548 genes measured in the RNA-seq datasets. If a functional link was included in multiple pathways, we counted it only once. A total of 11 types of functional links were analysed (figure 1).

Figure 1.

Different types of functional links between genes in the KEGG database.

2.3. Correlation analyses of expression of functionally linked genes

For a dataset, suppose there were totally m samples including both the tumour and normal samples. For each gene pair, let the expression levels of gene X and gene Y be given by 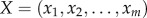and 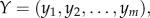respectively. Then the Pearson correlation coefficient of their expressions, denoted by R, was calculated as

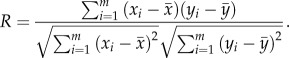2.1

The hypotheses tested by Pearson's test are

where ρ represents Pearson's population correlation coefficient. A positive correlation coefficient indicates that expression levels of the two genes increase or decrease together, whereas a negative correlation coefficient indicates that increased expression of one gene correlates with decreased expression of the other. After the multiple testing was corrected with a false discovery rate (FDR) [32] of less than 5%, a significantly positively (or negatively) correlated gene pair was referred to as a positively (or negatively) associated gene pair.

For a given dataset, all of the measured genes annotated in the KEGG pathways were considered as the background genes. Then, using the binomial distribution model, we tested whether the gene pairs with functional links in the KEGG pathways were more likely to have positively (or negatively) correlated expression levels than background gene pairs that were randomly extracted from the background genes. The number of the background gene pairs (N) was calculated by using the following formula:

2.2

where n represents the number of the background genes. If the null hypothesis that the frequency of positively (or negatively) associated gene pairs among the gene pairs with functional links of a particular type equals to the background frequency was true, then the probability of observing at least M₁ positively (or negatively) associated pairs by chance from M gene pairs with functional links of a particular type could be calculated by the following cumulative binomial distribution model:

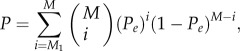2.3

where 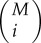is calculated as

2.4

and P_e represents the background frequency of positively associated gene pairs (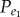) (or negatively associated gene pairs (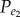)). Let N₁ represent the number of positively (or negatively) associated gene pairs among the N background gene pairs, then 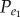(or 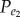) was calculated as

2.5

If the p-value < 0.05, we rejected the null hypothesis and accepted the alternative hypothesis that the frequency of positively (or negatively) associated gene pairs among the gene pairs with functional links of a particular type is higher than the background frequency.

2.4. Imbalance between the up- and downregulated genes in pathways

For microarray data, the significance analysis of microarrays (SAM) method [33] was used to identify DE genes with an FDR [32] less than 5%. In a dataset, a DE gene was considered upregulated if its d(i) value outputted by SAM, representing its relative difference of expression between the tumour and normal samples, was larger than zero. A DE gene was considered downregulated if its d(i) value was smaller than zero. For RNA-seq data, differential expression of a gene was assessed by the exactTest method of the edgeR package [31] with an FDR [32] less than 5%. A DE gene was considered upregulated if its logFC value outputted by exactTest, representing the log fold change of expression in tumour versus normal samples, was larger than zero. A DE gene was considered downregulated if its logFC value was smaller than zero. A DE gene was either upregulated (henceforth termed an upregulated gene) or downregulated (henceforth termed a downregulated gene).

For a pathway, the degree of imbalance between the up- and downregulated genes was defined as the absolute difference between the numbers of the up- and downregulated genes divided by the number of all of the DE genes in this pathway. Let x_i represent the degree of imbalance between the up- and downregulated genes in the ith pathway, which was calculated as

2.6

where 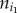and 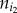represent the numbers of up- and downregulated genes in the ith pathway, respectively. Let y_i represent the frequency of positively associated gene pairs among all of the significant gene pairs in the ith pathway, which was calculated by

2.7

where 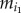represents the number of positively associated gene pairs and N_i represents the number of all significantly correlated gene pairs in the ith pathway. Then, using the Spearman rank correlation test, we analysed the correlation between the frequencies of positively associated gene pairs among all of the significant gene pairs in the pathways and the degrees of imbalance between the up- and downregulated genes for the pathways. Suppose there were p pathways. Then the degrees of imbalance for all of the p pathways could be represented by 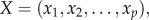and the frequencies of positively associated gene pairs in all of the p pathways could be represented by 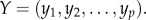Converting the p raw values x_i, y_i to ranks X_i, Y_i, the Spearman's coefficient of rank correlation, denoted by R_s, was calculated as

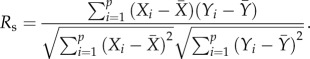2.8

Let 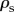represent Spearman's population correlation coefficient, then the hypotheses tested by the Spearman rank test are

This is a one-sided test testing whether a high frequency of the positively associated gene pairs could lead to a high degree of imbalance between the up- and downregulated genes. A p-value < 0.05 was considered significant.

Fisher's exact test was used to assess the significance of the imbalance between the up- and downregulated genes in a pathway by evaluating whether the ratio of the number of upregulated genes to the number of downregulated genes in the pathway was significantly different from that in the background. To do this, we tested the null hypothesis that the ratios of numbers of the up- to downregulated genes in a particular pathway and in the background are equal, against the alternative hypothesis that the two ratios are unequal. Considering that the DE genes in many cancer types might not have balanced upward and downward expression level changes [23,34], the ratio of numbers of the up- to downregulated genes in the background was used instead of 0.5 which indicates that the numbers of up- and downregulated genes are approximately equal in a disease. The imbalance between the up- and downregulated genes in a pathway was considered significant if the Fisher's exact p-value < 0.05.

2.5. Enrichment analyses based on Kyoto Encyclopaedia of Genes and Genomes

For each dataset, three interesting gene lists were generated, namely the all-DE gene list including both up- and downregulated genes, up-DE gene list including upregulated genes and down-DE gene list including downregulated genes. If k genes are identified as interesting genes from n genes in a dataset and x of them are annotated in a pathway with m genes, then the probability of observing at least x genes in this pathway by chance can be appropriately modelled by the cumulative hypergeometric distribution model as follows:

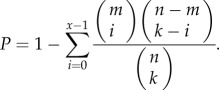2.9

The hypergeometric distribution tested the null hypothesis that the frequency of interesting genes in a pathway is equal to the frequency of interesting genes in the background genes against the alternative hypothesis that the frequency is higher in the pathway than in the background. Thus, we used the one-sided test. The significant pathways were identified after multiple testing adjustments with an FDR [35] less than 5%.

For each dataset, to test whether the increased number of the significant pathways detected by analysing the up- and downregulated genes separately could be observed by random chance, we did random experiments by randomly assigning all-DE genes into the up- and downregulated gene lists for the enrichment analysis of pathways. First, for each dataset, all-DE genes were randomly divided into sublist1 with the same length as the up-DE gene list and sublist2 with the same length as the down-DE gene list. Then, we used these two randomized sublists to perform enrichment analysis separately and counted the total number of the detected significant pathways. This procedure was repeated 10 000 times. The p-value was defined as the percentage of the random experiments in each of which the total number of detected pathways was not less than the observed number of pathways detected by the all-DE strategy (or the separate-DE strategy) in the 10 000 random experiments.

Multiple datasets were used to assess the reproducibility of a significant pathway detected from one dataset. As we previously defined [36], the probability of observing the enrichment p-values of a pathway smaller than 0.05 in at least k of n datasets by chance could be modelled by the cumulative binomial distribution model as follows:

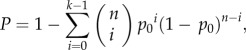2.10

where p₀ was estimated using the cumulative uniform distribution model, based on the assumption that the enrichment p-values follow a uniform distribution, i.e. every enrichment p-value has an equal probability to occur between zero and one. A pathway was defined as a non-randomly reproducible pathway across different studies if p-value < 0.05 [36].

2.6. Enrichment analyses based on Gene Ontology

We used the GO-function algorithm [3], which is based on the cumulative hypergeometric distribution model, to detect GO terms that were significantly enriched for the genes of interest from each dataset. The significant GO terms were identified after multiple testing adjustments with an FDR [35] less than 5%.

We also compared the two strategies of the singular enrichment analysis of pathways using another five commonly applied singular enrichment tools including DAVID, GoMiner, Onto-express, BINGO and GOseq, which calculate the enrichment p-values using slightly different statistical models as described in the electronic supplementary material file S1, table S1. As only DAVID and GOseq are applicable to KEGG, we analysed them based on both GO and KEGG. The other tools were analysed based only on GO. The adjusted p-values were calculated by using multiple testing adjustments with an FDR < 5%.

3. Results

3.1. Positively correlated expression of functionally linked genes

First, we analysed the correlated expression patterns of gene pairs with functional links in KEGG pathways without distinguishing which type of functional links they possessed. In all five datasets, we observed more positively associated gene pairs than negatively associated gene pairs among all gene pairs with functional links in the KEGG pathways (table 2). Using the binomial distribution model (see Material and methods), we found that it was unlikely to observe by chance the number of positive correlations among the gene pairs with functional links, whereas the number of negative correlations could be expected by chance for gene pairs randomly extracted from the background (table 2). For example, in the breast cancer (BC) dataset, among the 15 227 gene pairs with functional links in the KEGG pathways that showed significantly correlated expression levels (FDR adjusted p-value < 0.05, Pearson's correlation test), 64.7% (9854) were positively associated gene pairs, significantly more than what could be expected by chance (p-value < 2.2 × 10⁻¹⁶, binomial test); whereas 35.3% (5373) were negatively associated gene pairs, the number of which could be purely expected by chance (p-value = 1, binomial test). The frequencies (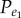 and 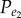) for positively and negatively associated gene pairs in the background were listed in the electronic supplementary material file S1, table S2.

Table 2.

Correlated expression patterns of gene pairs with various types of functional links. Abbreviations are same as in figure 2.

dataset	link	positiveb	negativec	P1d	P2e
BC	all (30263)a	9854	5373	<2.2 × 10−16	1
	activation (10125)	3370	1759	<2.2 × 10−16	1
	binding/association (4078)	1521	634	<2.2 × 10−16	1
	compound (12911)	3919	2255	<2.2 × 10−16	1
CRA	all (30263)	7138	4042	<2.2 × 10−16	1
	activation (10125)	2369	1327	<2.2 × 10−16	1
	binding/association (4078)	1189	420	<2.2 × 10−16	1
	compound (12911)	2888	1780	<2.2 × 10−16	1
GC	all (30263)	6735	3311	<2.2 × 10−16	1
	activation (10125)	2149	1142	<2.2 × 10−16	0.99
	binding/association (4078)	1148	353	<2.2 × 10−16	1
	compound (12911)	2717	1409	<2.2 × 10−16	0.99
KIRC	all (33367)	21 979	1010	<2.2 × 10−16	0.99
	activation (10835)	7163	297	<2.2 × 10−16	0.99
	binding/association (4373)	3163	103	<2.2 × 10−16	0.99
	compound (14563)	9152	507	<2.2 × 10−16	0.78
LUAD	all (33367)	19 305	182	<2.2 × 10−16	0.99
	activation (10835)	6197	39	<2.2 × 10−16	0.99
	binding/association (4373)	2731	25	<2.2 × 10−16	0.88
	compound (14563)	8250	93	<2.2 × 10−16	0.86

^aThe number of the specific link.

^bThe number of positively associated gene pairs.

^cThe number of negatively associated gene pairs.

^dThe binomial p-value for positively associated gene pairs.

^eThe binomial p-value for negatively associated gene pairs.

We then examined the expression correlations of gene pairs with functional links of each particular type. As expected, in all five datasets, the gene pairs with activation links were more likely to exhibit positively correlated than negatively correlated expression levels (table 2). Similarly, the gene pairs with compound links and binding/association links were also more likely to have positively correlated than negatively correlated expression levels, respectively (table 2). These three types of functional links covered the majority (89%) of the gene pairs with functional links in the KEGG pathways. Similar results were found for the gene pairs with the other eight types of functional links (see electronic supplementary material file S1, table S3). Notably, our results showed that the gene pairs with inhibition links also tended to exhibit positively correlated expression levels (see electronic supplementary material file S1, table S3), raising doubt on the existing assumption that inhibition links tend to cause negatively correlated expression levels [37,38].

3.2. Imbalance between the up- and downregulated genes in disease-associated pathways

As described above, gene pairs with functional links in KEGG pathways tended to exhibit positively correlated gene expression levels. As a pathway is a collection of genes closely connected by functional links, it tends to include more positively associated than negatively associated gene pairs. As the positive correlation of expression between two genes in all the tumour and normal samples indicates that their expressions tend to increase or decrease simultaneously [39], the genes in a pathway tend to show similar expression changes (up- or downregulation), potentially leading to an imbalance between the up- and downregulated genes in the pathway disturbed in a disease. To test this inference, we calculated the correlation between the frequencies of the positively associated gene pairs and the degrees of imbalance between the up- and downregulated genes in the pathways for each dataset. In the BC dataset, the degrees of imbalance increased as the frequencies of positively associated gene pairs increased (p-value < 4.32 × 10⁻⁹, Spearman's rank correlation test); a similar tendency was observed for the colorectal adenomas (CRA), gastric cancer (GC), lung adenocarcinoma (LUAD) and kidney renal clear cell carcinoma (KIRC) datasets, respectively (p-value < 0.05, Spearman's rank correlation test; see electronic supplementary material file S1, table S4).

The imbalance between the up- and downregulated genes in the pathways disturbed in a disease could influence the power of the singular enrichment analysis of pathways. For a dataset, suppose that the n background genes include n₁ upregulated genes and n₂ downregulated genes. Then the expected frequencies of the up- and downregulated genes observed in a pathway by chance could be estimated by the background frequency as q₁ = n₁/n and q₂ = n₂/n, respectively. The expected frequency of all of the DE genes observed in this pathway by chance could be estimated by the background frequency as q = (n₁ + n₂)/n = q₁ + q₂. For a pathway, the observed frequency (f) of all of the DE genes could also be divided into two parts, f = f₁ + f₂, where f₁ and f₂ represent the observed frequencies of the up- and downregulated genes, respectively. When f₁ is considerably larger (or smaller) than q₁, the observed frequency (f) of all-DE genes might not be significantly different from q when f₂ is smaller (or larger) than q₂. In this situation, this pathway might not be detected as significant in an analysis that considered all of the DE genes together. This suggests that the power to detect significant pathways could be reduced in the presence of the imbalance between the up- and downregulated genes in pathways. Below, we numerically showed that the number of detecting significant pathways could be greatly reduced through the all-DE strategy.

3.3. Significant Kyoto Encyclopaedia of Genes and Genomes pathways and Gene Ontology terms detected with different gene lists

For each dataset, three interesting gene lists, namely the all-DE gene list, up-DE gene list and down-DE gene list, were analysed for the detection of significant KEGG pathways by employing the cumulative hypergeometric distribution test [9]. In all of the microarray datasets, at the same FDR control level of 5%, the separate-DE strategy produced much more significant pathways than the all-DE strategy (figure 2a). Extremely, in the BC dataset, only one pathway was detected with an FDR < 5% by the all-DE strategy, while a total of 20 pathways were detected by the separate-DE strategy at the same FDR control level. Similar results were observed for the RNA-seq datasets. As shown in figure 2b, in the LUAD dataset, at the same FDR control level of 5%, separately analysing up- and downregulated genes detected 18 and 26 significant pathways, respectively, in contrast to four significant pathways detected by analysing all of the DE genes together. In the KIRC dataset, 30, 27 and 24 pathways were detected by analysing up-DE, down-DE and all-DE gene lists, respectively. The significant KEGG pathways detected by analysing all-DE, up-DE and down-DE gene lists for the five datasets were listed in the electronic supplementary material, file S2.

Figure 2.

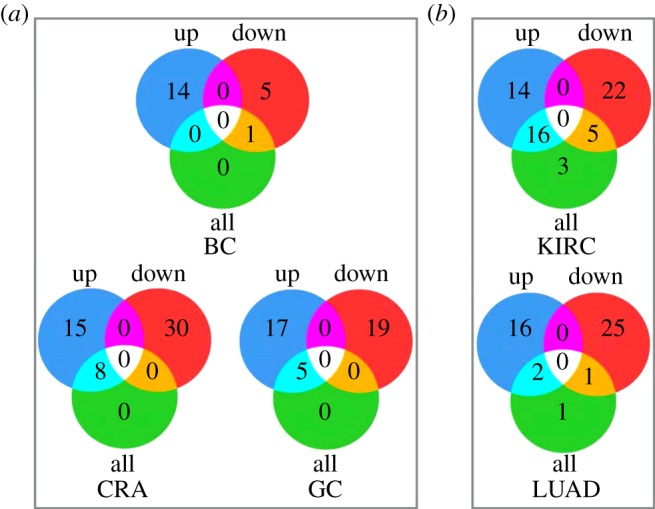
Number of significant KEGG pathways for five tumour datasets. (a) Venn diagrams for the number of significant KEGG pathways detected by analysing the all-DE, up-DE and down-DE gene lists from the three microarray datasets. (b) Venn diagrams for the number of significant KEGG pathways detected by analysing the all-DE, up-DE and down-DE gene lists from the two RNA-seq datasets. BC denotes breast cancer; CRA denotes colorectal adenomas; GC denotes gastric cancer; KIRC denotes kidney renal clear cell carcinoma; LUAD denotes lung adenocarcinoma. (Online version in colour.)

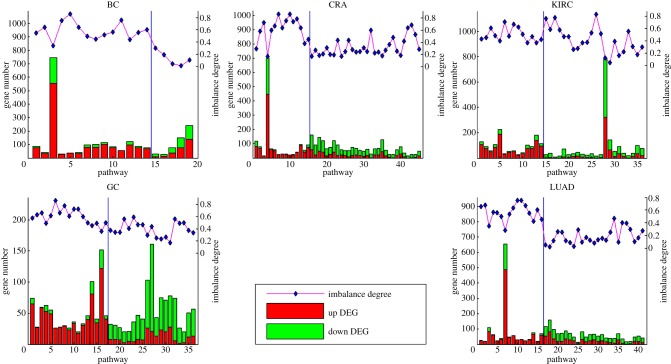
Then, we examined whether the numbers of up- and downregulated genes in the significant pathways detected by the separate-DE strategy but missed by the all-DE strategy were imbalanced. As shown in figure 3, in all five datasets, the numbers of up- and downregulated genes in all of the significant pathways detected by the separate-DE strategy but missed by the all-DE strategy were significantly imbalanced (all p-value < 0.05, Fisher's exact test), and many of these pathways contained only up- or downregulated genes. To test whether the increased number of the significant pathways detected by the separate-DE strategy could be observed by random chance, we conducted experiments by randomly assigning all-DE genes into the up- and downregulated gene lists for the enrichment analysis of pathways (see Material and methods). Results of the random experiments for each dataset showed that, without the imbalance between the up- and downregulated genes in pathways, the total number of significant pathways detected by separately analysing two randomly divided DE gene sublists was not more but significantly fewer than that by applying the all-DE strategy (p-value < 0.05, electronic supplementary material file S1, table S5) in all datasets except the BC and much fewer than that by applying the separate-DE strategy (all p-value < 0.05, electronic supplementary material file S1, table S5) in all datasets. The p-value in the BC dataset was not significant but tended to be significant (p-value = 0.0961, electronic supplementary material file S1, table S5), probably because the number of significant pathways detected by the all-DE strategy observed in the real data was only one. These results indicated that the increased number of significant pathways identified by the separate-DE strategy resulted from the imbalance between the up- and downregulated genes in pathways.

Figure 3.

Number of up- and downregulated genes in significant KEGG pathways. Only pathways that are detected as significant by analysing the up- or downregulated genes but missed by analysing all of the DE genes together are plotted on the x-axis. For each dataset, the bar plot shows the gene number in each pathway in the left y-axis. The corresponding imbalance degree of each pathway represented by filled diamond is shown in the right y-axis. The pathways detected by analysis of the upregulated genes are shown on the left of the vertical line, and the pathways detected by analysis of the downregulated genes are shown on the right of the vertical line. Abbreviations are same as in figure 2. (Online version in colour.)

One way to evaluate whether the significant pathways detected from one dataset are really relevant to the phenotype is to assess their reproducibility in multiple datasets [36]. As an example, we evaluated the reproducibility of the significant pathways detected in the BC dataset using another five datasets collected from GEO (see electronic supplementary material file S1, table S6). According to the binomial test (see Material and methods), the probability of observing the enrichment p-values of a pathway smaller than 0.05 by chance in at least two of five datasets is 2.26 × 10⁻², and thus it can be defined as a non-randomly reproducible pathway across different studies. In the BC dataset, 19 significant pathways were detected by the separate-DE strategy but missed by the all-DE strategy, among which 16 had the enrichment p-values smaller than 0.05 in at least two of the additional five datasets. The only one pathway detected by the all-DE strategy was also non-randomly reproducible in the additional five datasets. This pathway was also detected in the BC dataset and non-randomly reproducible in the additional five datasets by the separate-DE strategy. As another example, in the GC dataset, 32 out of the 36 significant pathways detected by the separate-DE strategy but missed by the all-DE strategy had the enrichment p-values smaller than 0.05 in at least two of another five datasets (see electronic supplementary material file S1, table S6). For the five significant pathways detected by the all-DE strategy, four were non-randomly reproducible across the additional five datasets. These five pathways were also detected by the separate-DE strategy in the GC dataset and all of them were non-randomly reproducible in the additional five datasets. As a non-randomly reproducible pathway is more likely to be really disturbed by some conditions relevant to the phenotype, these results suggested that the separate-DE strategy could detect more phenotype-related pathways than the all-DE strategy could.

We were able to find evidence of biological relevance for some of the pathways that were detected by the separate-DE but missed by the all-DE strategy. For example, in the CRA dataset, the focal adhesion pathway was significantly enriched for downregulated genes (FDR adjusted p-value = 1.47 × 10⁻³); the observed frequency of the downregulated genes in focal adhesion was 0.41, whereas the frequency in the background was 0.27. However, this pathway was not detected as significant when analysing all-DE genes together (FDR adjusted p-value > 0.05), because the observed frequency of all of the DE genes in this pathway was 0.61 compared with the background frequency of 0.63. The focal adhesion pathway is a canonical oncogenic pathway that is involved in cell–extracellular matrix contact and plays an essential role in cell attachment, motility, proliferation, differentiation, survival and the regulation of gene expression [40]. As another example, in the GC dataset, the p53 signalling pathway was found to be enriched for upregulated genes (FDR adjusted p-value = 1.78 × 10⁻²); the observed frequency of the upregulated genes in this pathway was 0.59, while the frequency in the background was only 0.37. However, this pathway was not detected as significant when all of the DE genes were analysed together (FDR adjusted p-value > 0.05), as the observed frequency of all-DE genes in this pathway was 0.68 and the background frequency was 0.62. It is well known that the activation of the p53 pathway can initiate DNA repair, cell cycle arrest, cellular senescence or apoptosis, which is related to the suppression of tumour formation and response to many types of cancer therapy [41]. As the third example, in the LUAD dataset, the JAK/STAT signalling pathway was found to be enriched for downregulated genes (FDR adjusted p-value = 3.22 × 10⁻²), as the observed frequency of the downregulated genes in this pathway was 0.31 and the frequency in the background was 0.20. When analysing all of the DE genes together, it was not detected as significant (FDR adjusted p-value > 0.05), as the observed frequency of all-DE genes in this pathway was 0.52 and the background frequency was 0.55. The dysregulation of the JAK/STAT signalling pathway has been implicated in malignant progression, including lung cancer [42]. The background frequency and the observed frequency for each significant KEGG pathway can be found in the electronic supplementary material, file S2.

Similar enrichment results were observed using GO-function based on GO biological process terms for all five datasets (table 3). For example, in the BC dataset, with an FDR < 5%, only 22 significant GO terms were detected by the all-DE strategy, whereas a total of 86 GO terms were detected as significant when the up- and downregulated genes were analysed separately, consistent with the tendency observed in the analysis based on the KEGG pathways. The significantly enriched GO terms detected by analysing all-DE, up-DE and down-DE gene lists for the five datasets were listed in the electronic supplementary material, file S3.

Table 3.

Numbers of significant GO terms detected by using the separate-DE strategy and all-DE strategy. Abbreviations are same as in figure 2.

tumour type	up-DEa	down-DEb	all-DEc	FDRd	p-value1e	p-value2f
BC	44	42	22	11	63	22
CRA	101	48	54	35	111	54
GC	86	31	38	24	77	38
KIRC	53	29	62	16	67	62
LUAD	29	79	39	14	77	39

^aThe number of GO terms detected by analysing the upregulated genes.

^bThe number of GO terms detected by analysing the downregulated genes.

^cThe number of GO terms detected by analysing all-DE genes.

^dThe number of overlapping GO terms detected by both the separate-DE strategy and all-DE strategy at the same FDR level.

^eThe number of GO terms detected by the separate-DE strategy with an FDR < 0.05 that were also detected by the all-DE strategy with a p-value < 0.05.

^fThe number of GO terms detected by the all-DE strategy with an FDR < 0.05 that were also detected by the separate-DE strategy with a p-value < 0.05.

Notably, we found that, when performing the enrichment analysis based on KEGG pathways, with the same FDR control, all significant pathways detected by the all-DE strategy were also found by the separate-DE strategy in each of the microarray datasets (figure 2a). However, in the RNA-seq datasets, not all pathways detected by analysing all of the DE genes together were found by analysing the up- or downregulated genes separately at the same FDR level (figure 2b). Nevertheless, all of them could be detected by analysing the up- or downregulated genes with an un-adjusted p-value < 0.05. Similarly, the enrichment analysis based on GO showed that some of the GO terms detected by the all-DE strategy were also not found by the separate-DE strategy at the same FDR level but could be detected with an un-adjusted p-value < 0.05 (table 3). This result was probably owing to the loss of power in the procedure of multiple test adjustments. By contrast, not all of the KEGG pathways and GO terms detected by the separate-DE strategy could be found by the all-DE strategy even with an un-adjusted p-value < 0.05. Only 12, 22, 16, 38 and 19 pathways detected by the separate-DE strategy were detected by the all-DE strategy with an un-adjusted p-value < 0.05 for BC, CRA, GC, KIRC and LUAD dataset, respectively. For GO terms, the numbers were 63, 111, 77, 67 and 77, respectively (table 3).

Five other commonly applied enrichment tools, with their default parameter settings, were also analysed. The results showed that the separate-DE strategy also produced much more significant KEGG pathways/GO terms than the all-DE strategy with an FDR of 5% in all five datasets (table 4).

Table 4.

Number of significant pathways/GO terms detected by using the separate-DE and all-DE strategies for five other enrichment tools. Abbreviations are same as in figure 2.

enrichment tool name	annotations	disease type	up-DEa	down-DEb	all-DEc
DAVID	GO	BC	50	38	11
		CRA	130	55	56
		GC	124	34	45
		KIRC	94	31	65
		LUAD	28	85	29
	KEGG	BC	4	2	1
		CRA	14	7	3
		GC	10	6	3
		KIRC	13	10	4
		LUAD	6	4	1
GoMiner	GO	BC	196	372	156
		CRA	392	455	270
		GC	356	111	111
		KIRC	460	119	408
		LUAD	121	450	250
Onto-Express	GO	BC	269	289	238
		CRA	559	364	336
		GC	425	315	115
		KIRC	491	277	340
		LUAD	202	468	268
BINGO	GO	BC	86	226	48
		CRA	220	195	97
		GC	257	66	65
		KIRC	141	79	36
		LUAD	43	353	33
GOseq	GO	KIRC	219	164	219
		LUAD	114	350	220
	KEGG	KIRC	26	27	23
		LUAD	12	13	1

^aThe number of pathways/GO terms detected by analysing the upregulated genes.

^bThe number of pathways/GO terms detected by analysing the downregulated genes.

^cThe number of pathways/GO terms detected by analysing all-DE genes.

4. Discussion

Our results revealed that gene pairs with various types of functional links defined in KEGG pathways tend to have positively correlated expression levels; thus, the genes in a pathway that is disturbed in tumour cells tend to be up- or downregulated similarly owing to their close functional links. This analysis provided the biological foundation for the separation of the up- and downregulated genes in the singular enrichment analysis of pathways. Then, we revealed that the imbalance between the up- and downregulated genes in pathways could greatly reduce the power to detect significant pathways by analysing all of the DE genes together, as demonstrated by the results of five tumour datasets. Therefore, singular enrichment analysis of pathways through the separate-DE strategy is both reasonable and powerful, even though currently the all-DE strategy is still widely applied.

Notably, many researchers often refer to the KEGG pathways that are enriched for up- or downregulated genes as activating or inhibiting pathways [19,43]. However, considering a KEGG pathway as an activating or inhibiting pathway based only on its enrichment for up- or downregulated genes may be inappropriate [44]. For example, though the focal adhesion pathway was significantly enriched for downregulated genes, it also involved many upregulated genes, and may be activated in tumour cells to facilitate the invasion and migration of tumour cells [45]. Further, as the posttranslational modifications could inhibit or activate the functions of proteins [21,38,44,46], they should be considered in determining the activation or inhibition of a perturbed pathway. Thus, interpreting the biological meaning of an identified pathway requires domain-dependent knowledge and further experimental data.

Generally, we should keep in mind the limitation of the enrichment analysis of pathways: a statistically ‘significant’ pathway only indicates that this pathway is disturbed non-randomly. In fact, a pathway is deemed statistically significant if an event observed for this pathway, such as the frequency of interesting genes in this pathway as observed in the singular enrichment analysis [3] or an enrichment score for this pathway as observed in the Gene Set Enrichment Analysis (GSEA) [47], could not be expected to occur just by chance. As for the biological event(s) that may lead to the occurrence of this non-random statistical observation, there are various possibilities such as the dysfunction of one or several specific regulator genes of the pathway by methylation or mutation changes or the deregulation of one or several microRNAs targeting genes in this pathway. In other words, a pathway found to be statistically significant does not directly indicate what biological event(s) has led to its statistical significance and the underlying specific biological implications require generation of biological hypotheses for wet laboratory experiment validation. Thus, there are no any predefined ‘gold standards’ for biological validation of the pathways found to be statistically significant in real data. As the statistical significance of a pathway detected by an enrichment analysis tool is self-proved at a predefined FDR level, the more significant pathways an enrichment tool can find, the higher power it has. In addition, to demonstrate that the significant pathways detected by the separate-DE strategy are phenotype related, we first illustrated that the increased number of significant pathways detected by the separate-DE strategy could not be observed by random chance using a randomization technique. Then, using multiple datasets for breast and gastric tumours respectively, as examples, we showed that most of the significant pathways were non-randomly reproducible across different studies. Finally, for some of the pathways that were detected by applying the separate-DE strategy but missed by applying the all-DE strategy, we found evidences from the published literature to support that they could be related to the corresponding phenotype. Though simulation studies could be applied to evaluate the performance of enrichment analysis tools by setting which pathways are disturbed in what ways in advance [48], simulation results are usually heavily dependent on the models for generating the simulated data, risking bias in producing data preferentially favourable to a specific hypothesis of the data distribution [3]. Therefore, in this work, we did not present the result of a simulation experiment that numerically demonstrated that the separate-DE strategy is more powerful than the all-DE strategy when imbalance between the up- and downregulated genes exists in the disturbed pathways.

We suggested that singular enrichment analysis of pathways through a separate-DE strategy is more powerful for finding significant functional pathways documented in the KEGG or GO database. The same suggestion should be applicable to other gene sets if genes in them tend to exhibit positively correlated expression by any transcriptional or non-transcriptional mechanisms, which could introduce the imbalance between the up- and downregulated genes between different phenotypes. For example, the MSigDB database [49] provides gene sets besides the KEGG pathways (C2 gene sets) and GO terms (C5 gene sets), including sets of target genes corresponding to different microRNAs or transcription factors (C3 gene sets), sets of co-expressed genes (C4 gene sets), sets of genes representing signatures of cellular pathways that are often deregulated in cancer (C6 gene set), and sets of genes representing immunologic signatures under specific conditions (C7 gene sets). These kinds of gene sets are already known to be co-regulated under specific conditions, and thus could have positively correlated expression. For the C1 gene sets containing genes located in the same chromosome or cytogenetic band, genes in them could also tend to be simultaneously upregulated (or downregulated) by chromosomal amplifications (or deletions) or by epigenetic mechanisms. These five types of gene sets are all likely to have imbalanced numbers of up- and downregulated genes under a specific condition, as numerically demonstrated in our analysis using the five tumour datasets (see electronic supplementary material file S1, table S7). Briefly, in all datasets, the separate-DE strategy detected more significant gene sets than the all-DE strategy and at least 88.89% of the significant gene sets detected by the separate-DE strategy but missed by the all-DE strategy exhibited significantly imbalanced numbers of up- and downregulated genes according to the same evaluation for KEGG pathway analysis (p-value < 0.05, Fisher's exact test, electronic supplementary material file S1, table S7).

The singular enrichment analysis requires a list of user-preselected interesting genes. Therefore, enrichment tools of this class are also called the threshold-dependent tools [50]. By contrast, another class of tools such as GSEA are threshold-free, which take all genes from a microarray experiment without a cut-off for defining DE genes. They are efficient in finding categories containing high frequencies of lowly DE genes, while the singular enrichment tools can be more powerful in detecting categories containing low frequencies of highly DE genes [51]. For example, in the GC dataset, based on KEGG pathways, the singular enrichment analysis of pathways using hypergeometric distribution detected 28 pathways by the separate-DE strategy, among which 19 pathways were not found by using GSEA. By contrast, five out of 14 pathways detected by GSEA were missed by the hypergeometric distribution test. This result validated that these two main streams of enrichment analysis methods would be mutually complementary [50].

Finally, we note that a similar problem also exists for the singular enrichment analysis of pathways using other types of ‘omics’ data. For example, for genome-wide methylation data, our previous study revealed that the genes differentially hypermethylated or hypomethylated between the cancer samples and normal controls tended to be enriched in distinct functions and that many functional categories were significantly enriched for hypermethylated (or hypomethylated) genes and simultaneously significantly depleted of hypomethylated (or hypermethylated) genes [52]. Thus, the hypermethylated and hypomethylated genes in cancer genomes should also be separately analysed for the singular enrichment analysis of pathways. We propose that efficient pathway analyses should consider more details of the biological properties of the interesting genes under study because of their fundamental importance in determining which functional categories will be identified.

Funding statement

This work was supported in part by the National Natural Science Foundation of China (grant nos. 30970668, 81071646, 91029717, 81201702).