Abstract
Internal friction arising from local steric hindrance and/or the excluded volume effect plays an important role in controlling not only the dynamics of protein folding but also conformational transitions occurring within the native state potential well. However, experimental assessment of such local friction is difficult because it does not manifest itself as an independent experimental observable. Herein, we demonstrate, using the miniprotein trp-cage as a testbed, that it is possible to selectively increase the local mass density in a protein and hence the magnitude of local friction, thus making its effect directly measureable via folding kinetic studies. Specifically, we show that when a helix cross-linker, m-xylene, is placed near the most congested region of the trp-cage it leads to a significant decrease in both the folding rate (by a factor of 3.8) and unfolding rate (by a factor of 2.5 at 35 °C), but has little effect on protein stability. Thus, these results, in conjunction with those obtained with another cross-linked trp-cage and two uncross-linked variants, demonstrate the feasibility of using a non-perturbing cross-linker to help quantify the effect of internal friction. In addition, we estimate that an m-xylene cross-linker could lead to an increase in the roughness of the folding energy landscape by as much as 0.4-1.0kBT.
Keywords: Protein folding, Cross-linker, Temperature-jump, Infrared, Relaxation kinetics
1. Introduction
Since the native state of proteins is stabilized by many weak forces and consists of well packed and ordered structural elements, the process of folding is expected to contain a certain degree of energetic and/or steric/topological frustrations.1-8 For energy landscapes that give rise to a single free energy bottleneck (i.e., two-state folding), such frustrations, which could arise from various local motions and interactions, typically manifest themselves as an internal frictional force or drag acting on the conformational motion along the folding coordinate.9-12 Theory and simulations have provided us with useful insights regarding how internal friction affects protein conformational dynamics.13-24 While the frictional force exerted by the solvent can be experimentally evaluated by altering the bulk viscosity,13,25-30 quantifying the effect of various sources of internal friction on protein folding is nevertheless more challenging. For example, when two chains (e.g., two α-helices) become sufficiently close during folding, one expects that the further motion of one chain will be affected by the other, due to various local attractive and/or repulsive interactions between them, as well as the steric effect. This type of internal friction, which is prevalent in protein folding and may also play an important role in controlling the dynamics of conformational transitions occurring in or near the native potential well, has not, to the best of our knowledge, been studied systematically. This is due, at least in part, to the fact that for any naturally occurring proteins it is almost impossible to isolate and independently assess the contribution of a specific structural element to the overall internal frictional effect. Herein, we show that the local frictional effect arising from a nearby chain in proteins could be estimated by using an external structural linker.
The most commonly used experimental method to determine or infer the effect of internal friction on protein folding and conformational dynamics is to measure how the rate of the dynamic event of interest varies with solvent viscosity.31-34 If the rate does not show a linear dependence on the reciprocal of viscosity, as expected for a barrier crossing process in solution, then the discrepancy is attributed to an additional friction term arising from the protein itself. For example, Eaton and coworkers31 have utilized this strategy to show that the conformational reconfiguration rate of myoglobin, in response to photodissociation of the CO ligand, is subject to internal friction. Similarly, by assessing polymer chain dynamics in solvents containing denaturant or different viscosities via either FRET or fluorescence quenching measurements,32,35-38 Buscaglia et al.35 have shown that even loop formation in simple polypeptides is affected by internal friction, and, Schuler and coworkers37 have shown that it is possible to determine the relative amount of internal friction at different points along the folding coordinate of two α-spectrin domains (i.e., R16 and R17). Specifically, they found that the effect of internal friction is highly localized in the early transition state, suggesting that there are particular interactions stemming from local frustrations that contribute to the rate-limiting step of folding.37 In addition, by measuring and analyzing the viscoelastic response of a single protein molecule, several groups have demonstrated that force spectroscopy can also be used to characterize the internal friction associated with the unfolding of several proteins.39-42 While these previous studies provided significant insights into the effect of internal friction on the folding dynamics of the protein systems studied, they were unable to disentangle the relative contributions of various sources of friction, such as those stemming from a single chain element. Herein, we attempt to use a structural cross-linker to help estimate how local friction, resulting simply from local crowding or the excluded volume effect, affects the dynamics of protein folding. Specifically, we employ the miniprotein trp-cage43,44 and a helix cross-linker to demonstrate the feasibility of this method.
The use of a cross-linker to constrain the structural integrity of a specific fold and/or to investigate protein folding mechanism is not new. For instance, disulfide45,46 and dichloroacetone47 cross-linkers have been used, in conjunction with Φ-value analysis, to characterize the folding transition state ensemble of proteins of interest. In addition, photoresponsive cross-linkers, such as those based on an azobenzene48 or a tetrazine49 moiety, have been used to initiate a targeted folding or unfolding process.48-52 In this regard, the study of Hamm and coworkers50-52 on helix-coil transition kinetics is particularly relevant to the present work, as it demonstrates that an azobenene cross-linker could increase the internal friction along the α-helix folding coordinate, due to interactions between bulky side chains and the linker. Recently, Jo et al.53 have shown that m-xylene is one of the most efficient helix staples for short peptides. Because of the structural rigidity of m-xylene, which will minimize its entropic effect on the folding dynamics of interest, herein we chose to use it as a chain surrogate.
The miniprotein trp-cage was chosen for the following reasons: (1) the study of Qiu and Hagen54 indicates that, despite its small size, the folding kinetics of this miniprotein are subject to the influence of internal friction, (2) trp-cage contains only one α-helix, spanning residues 1 to 9, which simplifies the choice of location for cross-linker incorporation, and (3) more importantly, a number of experimental55-57 and computational58-78 studies have shown that this α-helix is formed in the folding transition state, thus making trp-cage an ideal candidate to interrogate the effect of local friction through the incorporation of an appropriate helix cross-linker. Our hypothesis is that when the cross-linker is placed near the hydrophobic core region of the trp-cage, its frictional effect will become large enough to be observed in kinetic experiments. In particular, if the cross-linker is further designed to point away from the interior of the protein, we expect that its interaction with the non-helical part of the trp-cage will be minimized and, as a result, the incorporation of the cross-linker will not induce a significant change in trp-cage stability, but will lead to a significant decrease in the folding/unfolding rate, due to an increased frictional force.
2. Experimental Section
2.1 Peptide Synthesis and Cross-Linking
All peptides were prepared by standard 9-fluorenylmethoxy-carbonyl (Fmoc) solid phase peptide synthesis methods and purified by reverse-phase high-performance liquid chromatography (HPLC). The detail of the cross-linking method has been described elsewhere.53 Briefly, a solution of the targeted trp-cage cysteine mutant (10 mg, 4.8 μmol) in 50 mM ammonium bicarbonate buffer (20 mL, pH 8) was mixed with a freshly prepared 0.1 M solution of m-dibromoxylene in DMF (100 μL) and stirred for 2 hours at room temperature. The reaction was then quenched by addition of 1 M HCl (1 mL), followed by lyophilization. The cross-linked peptide product was further purified and characterized (see details in Supporting Information). Residual trifluoroacetic acid (TFA) from the synthesis was removed via three rounds of lyophilization against a 0.1 M DCl solution.
2.2 Peptide Cyanylation
Lyophilized peptide was first dissolved in 2 mM tris(2-carboxyethyl)phosphine (TCEP), 4 M guanidine hydrochloride, 100 mM phosphate buffer (pH 7) with a final peptide concentration of 200 μM. This peptide solution was then mixed with a 45 mM 2-nitro-5-thiocyanatobenzoic acid (NTCB) solution prepared in 100 mM phosphate buffer (pH 7) with a final NTCB (Sigma Aldrich) to peptide concentration ratio of 6:1. The mixture was incubated at room temperature for 30 minutes, allowing for cysteine cyanylation. The targeted peptide product was purified by HPLC and verified by mass spectrometry.
2.3. Static and Time-Resolved Spectroscopic Measurements
Circular dichroism (CD) CD measurements were carried out on an Aviv 62A DS spectropolarimeter (Aviv Associates, NJ) with a 1 mm cuvette. The peptide concentration was approximately 40-60 μM in 20 mM phosphate buffer solution (pH 7). Infrared spectra at a resolution of 1 cm-1 were collected on a Magna-IR 860 spectrometer (Nicolet, WI) using a home built CaF2 sample cell with an optical path length of 52 μm.79 For both static and time-resolved IR measurements, all peptide solutions had a concentration of approximately 4 mM, prepared in 20 mM phosphate D2O buffer (pH 7). Time-resolved experiments were carried out on a home built laser-induced temperature jump (T-jump) apparatus79,80 using a quantum cascade laser (Daylight Solutions, CA) as the IR probe. For the T-jump kinetics reported, the probing frequency was either 1665 cm-1 or 1620 cm-1, and the T-jump amplitude was in the range of 10-15 °C.
2.3. Molecular Dynamics (MD) Simulation
MD simulations were carried out using the NAnoscale Molecular Dynamics (NAMD) program (version 2.7)81 and the CHARM36 or CHARM22 force field. The peptide of interested was immersed in 1692 TIP3P water molecules in a 40 Å cubic box.82 For simulation of the cross-linked trp-cage variants, the force field parameters of the xylene cross-linker were generated from those of phenylalanine and cysteine. For each simulation, the temperature was gradually increased from 0 to 368 K with an increment of 20 K every 500 timesteps. The temperature was then held constant once it reached its final value, 368 K. After energy minimization of the entire system, a production run of 10 ns was performed. Full electrostatics were calculated every second step using the particle-mesh Ewald (PME) method. A 2 fs time step was used to integrate the equations of motion and the structural coordinates were saved every 1 ps for further analysis. During the simulation, the pressure was maintained at 1 atm using the Nosé-Hoover Langevin piston method and the temperature was controlled by Langevin dynamics. In addition, periodic boundary conditions were used to reduce edge effects and a cutoff of 12 Å was used for nonbonded interactions.
3. Results and Discussion
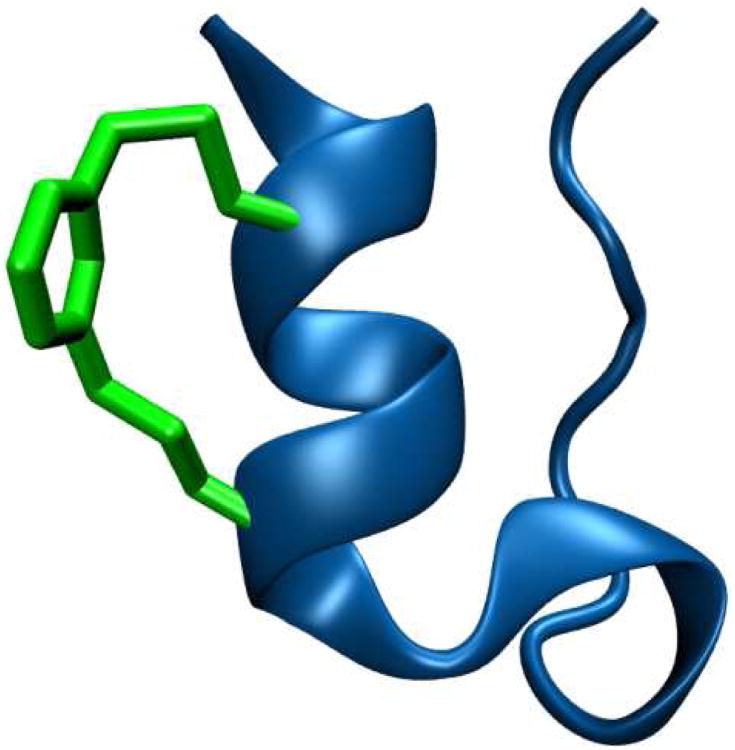
We chose the 10b variant (sequence: DAYAQWLKDGGPSSGRPPPS) of the trp-cage miniprotein44 as our model system because its folding kinetics and mechanism have been studied previously.55,83 To introduce the m-xylene cross-linker via cysteine alkylation,53 we first synthesized two 10b cysteine variants, the first containing double cysteine mutations at positions 4 and 8, with the second having double cysteine mutations at positions 1 and 5. Incorporation of the m-xylene moiety into these peptides yielded two cross-linked 10b variants (hereafter referred to as 4-8-CL-Trp-cage and 1-5-CL-Trp-cage, respectively). The reason that we chose these positions is because, as shown (Figure 1), the m-xylene cross-linker in both cases is expected to point away from the interior of the protein and, thus, should not directly interact with the hydrophobic core and the key Asp9-Arg16 salt bridge in the folded state. MD simulations indeed confirm this point (Figure S1, Supporting Information). However, since the N-terminal Asp1 residue, which has been shown to be critical to the α-helix stability in trp-cage,44 is altered in 1-5-CL-Trp-cage, we expect that its stability will decrease. In contrast, we expect that the stability of 4-8-CL-Trp-cage will be similar to that of the wild type. Furthermore, because the m-xylene moiety in 4-8-CL-Trp-cage encloses two residues (i.e., Trp6 and Leu7) that are part of the hydrophobic core, we expect that in this case the cross-linker will lead to an additional frictional force along the folding coordinate, thus slowing down both the folding and unfolding rates. On the other hand, for 1-5-CL-Trp-cage, because the cross-linker is moved away from the most congested region of the protein, we expect that the frictional effect induced by the cross-linker will be significantly reduced.
Figure 1.
Cartoon representation of the 4-8-CL-Trp-cage.
Effect of the m-xylene cross-linker on folding thermodynamics
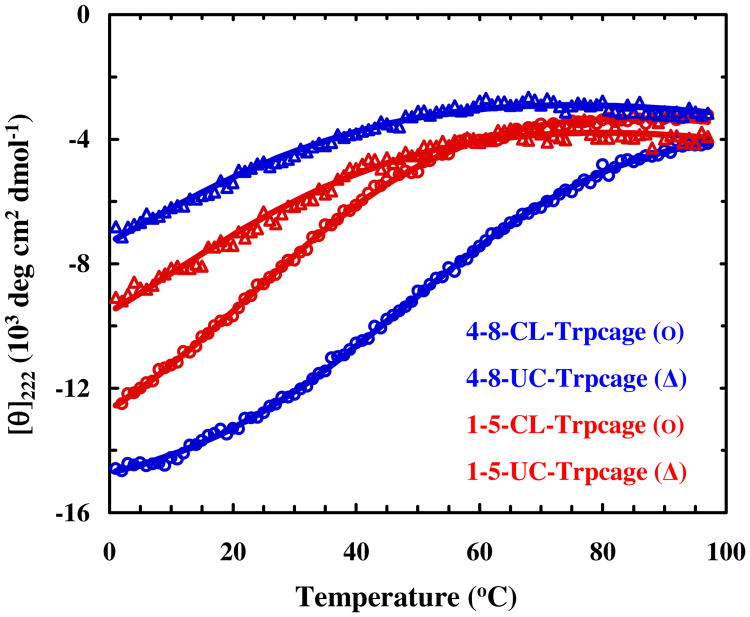
The folding thermodynamics of 4-8-CL-Trp-cage and 1-5-CL-Trp-cage, as well as their uncross-linked counterparts (hereafter referred to as 4-8-UC-Trp-cage and 1-5-UC-Trp-cage), were examined by CD spectroscopy. For 1-5-UC-Trp-cage, we directly used the mutated sequence for experiments, whereas for 4-8-UC-Trp-cage, to prevent any potential interaction between the free cysteines and Asp9, we further modified the peptide by cyanylating the cysteines as has been described previously.84 As shown (Figure S2, Supporting Information), the far-UV CD spectra of 4-8-CL-Trp-cage and 1-5-CL-Trp-cage are consistent with that of the wild type,44,55,85 indicating that these peptides are folded at low temperatures. Further CD thermal unfolding measurements monitored at 222 nm confirm the role of the cross-linker, which effectively increases the thermal stability of the trp-cage structure in comparison to the uncross-linked variants (Figure 2). To better quantify the thermal stabilities of these trp-cage peptides, we globally fit their CD unfolding curves to the following two-state model:
Figure 2.
CD T-melts of the cross-linked and uncross-linked trp-cage variants, as indicated. The solid lines are global fits of these data to a two-state model discussed in text.
| (1) |
| (2) |
| (3) |
where θ(i,T) is the temperature-dependent mean residue elipticity of peptide i, Keq(i,T) is the corresponding equilibrium constant for unfolding, Tm = ΔHm(i)/ΔSm(i) is the thermal melting temperature, ΔHm(i) and ΔSm(i) are the enthalpy and entropy changes at Tm, and ΔCp is the heat capacity change, which has been assumed to be the same as that (i.e., 176 J K-1 mol-1) determined for 10b.55 In addition, the folded and unfolded CD baselines, θF(i,T) and θU(i,T), respectively, are assumed to be linear functions of temperature, as follows:
| (4) |
| (5) |
where b, c, and d were treated as global fitting parameters and ai was peptide dependent and treated as a local fitting parameter.
As shown (Figure 2), this model fits the data satisfactorily. In addition, the resultant thermodynamic quantities for unfolding meet our expectations (Table 1). For example, in both cases the Tm of the cross-linked peptide is much higher than that of the uncross-linked variant, validating the role of m-xylene as a stabilizing α-helix cross-linker.53 To verify that the cross-linker does not alter the trp-cage fold, we have performed MD simulations on both cross-linked 10b variants for a length of 10 ns and at an elevated temperature of 368 K. These simulation conditions were chosen to allow for the observation of any significant structural changes in the folded state, arising from the cross-linker. As indicated (Figure S1, Supporting Information), the overall structures of these cross-linked trp-cage variants are comparable to that of the wild type.
Table 1.
Summary of the unfolding thermodynamic parameters obtained from global fitting of the CD thermal melting data of the four peptides. Also listed are the folding and unfolding times of these peptide determined at 35 °C.
| 10b* | 4-8-CL-Trp-cage | 4-8-UC-Trp-cage | 1-5-CL-Trp-cage | 1-5-UC-Trp-cage | |
|---|---|---|---|---|---|
| ΔHm (kJ mol-1) | 58.0 | 44.5 ± 4.2 | 19.6 ± 5.9 | 38.9 ± 4.3 | 25.4 ± 5.1 |
| ΔSm (J K-1 mol-1) | 177 | 133 ± 12.5 | 72 ± 21 | 129 ± 14 | 89 ± 18 |
| ΔCp (J K-1 mol-1) | 176 | 176 | 176 | 176 | 176 |
| Tm (°C) | 55.0 | 54.1 ± 4.9 | -0.9 ± 3.0 | 27.8 ± 3.1 | 12.0 ± 2.9 |
| τf (μs) | 1.3 | 5.0 ± 0.6 | 6.9 ± 1.4 | 6.9 ± 1.2 | 13.8 ± 0.6 |
| τu (μs) | 5.1 | 12.9 ± 1.5 | 2.5 ± 0.6 | 4.8 ± 0.6 | 5.8 ± 0.3 |
The thermodynamic and kinetic parameters of 10b were obtained from ref 55.
More importantly, the Tm (∼54 °C) of 4-8-CL-Trp-cage is almost identical to that (∼55 °C) of the wild type,44,55 which is not only consistent with our hypothesis but also indicates that 4-8-CL-Trp-cage is an ideal candidate to characterize the effect of local internal friction on the conformational relaxation dynamics due to the added cross-linker. Specifically, this result suggests that the thermodynamic role of the cross-linker is merely to compensate the loss of stability due to the cysteine mutations and that any static interactions between the linker and non- helical residues of the protein, if any, are minimal. Thus, changes in the conformational kinetics, especially unfolding kinetics, between the wild type and 4-8-CL-Trp-cage, can be attributed to changes in local friction. In addition, the finding that the 1-5-CL-Trp-cage exhibits a lower Tm (26.1 °C) compared to 4-8-CL-Trp-cage is consistent with the fact that the N-terminus α-helical cap, Asp1, is critical to the thermal stability of the trp-cage fold44 and also demonstrates that a helix cross-linker beginning at the N-terminus of a peptide is less effective in stabilizing its α-helical structure. In support of this notion, our MD simulations also show that the α-helix in 1-5-CL-Trp-cage becomes more extended in comparison to that of the wild type (Figure S3, Supporting Information).
Effect of the cross-linker on the folding and unfolding kinetics
To determine the effect of the m-xylene cross-linker on the folding and unfolding rates of trp-cage, we measured the conformational relaxation kinetics of all four peptides (i.e., two cross-linked and two uncross-linked variants) using a T-jump IR technique.80 Our previous T-jump study55 on the 10b trp-cage indicated that the 310-helix is populated only at relatively low temperatures (i.e., below Tm) and its T-jump induced relaxation is detectable at a probing frequency of 1668 cm-1. As shown (Figure S4, Supporting Information), the T-jump induced relaxation kinetics of 4-8-CL-Trp-cage, probed at 1668 cm-1, also indicate that the unfolding of the 310-helix occurs independently from the rest of the molecule. Thus, this result further confirms that the incorporation of the m-xylene cross-linker in 4-8-CL-Trp-cage does not change the folding mechanism of the trp-cage fold and therefore it serves as a good mimic of a nearby chain that could lead to local crowding or friction, due to its close proximity to the most congested region of the protein. Because the 310- helix unfolds independently,55,65,86-88 below we only discuss the effect of the cross-linker on the global folding/unfolding kinetics of the cage structure.
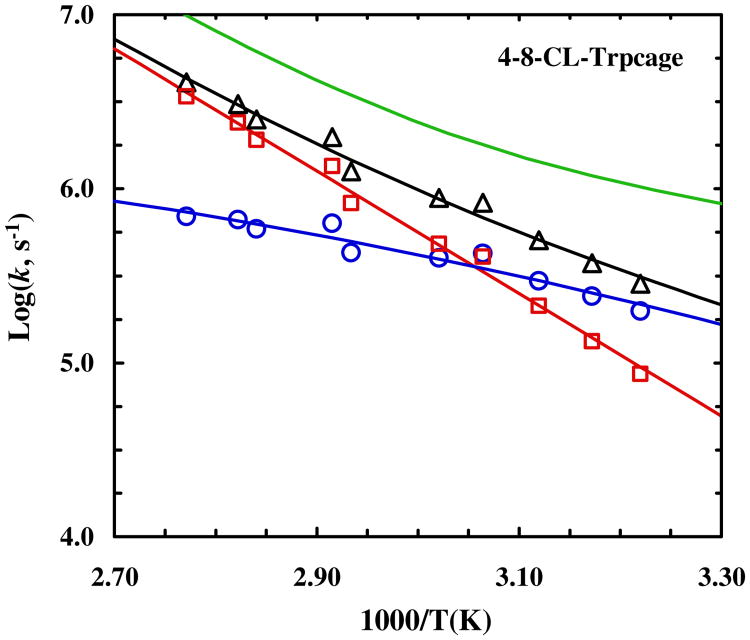
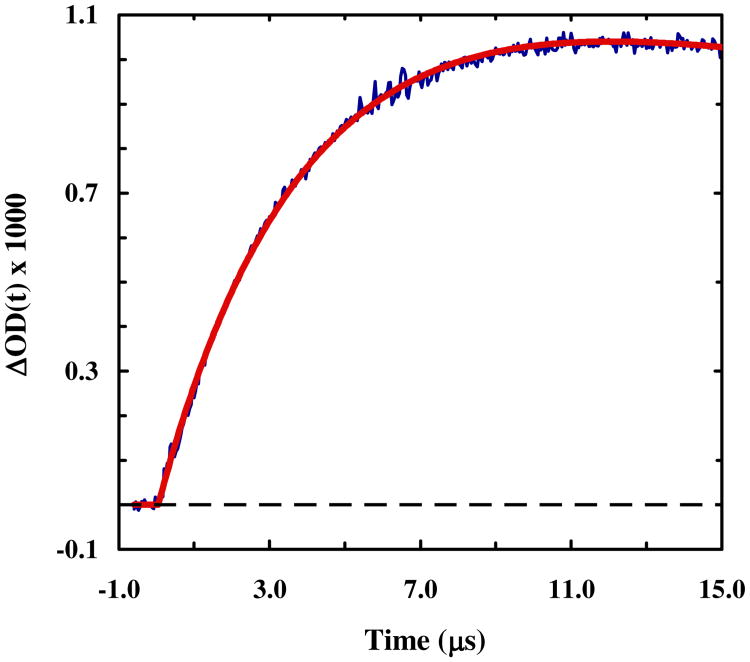
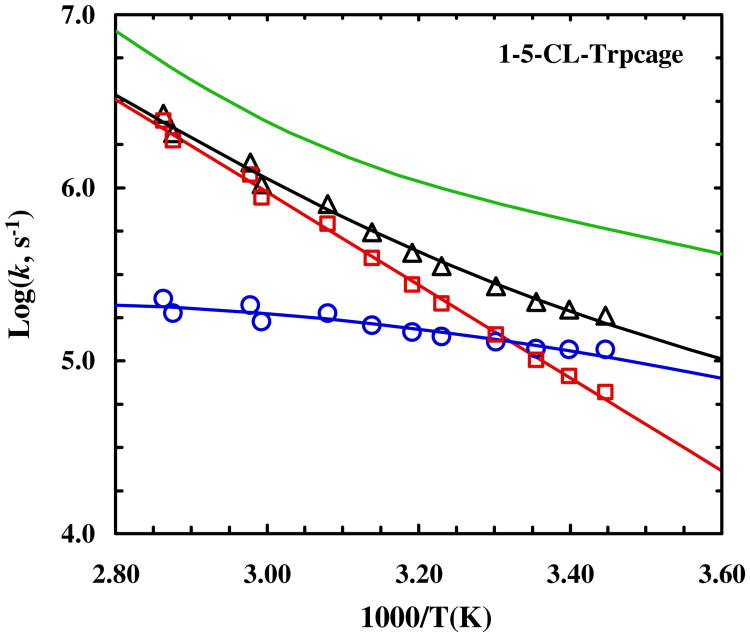
As shown (Figure 3), the T-jump induced relaxation kinetics of 4-8-CL-Trp-cage, probed at both 1668 cm-1 and 1620 cm-1 (Figure S5, Supporting Information) and at a final temperature of higher than 30 °C, can be fit well by a single-exponential function. However, as shown (Figure 4), the conformational relaxation rates obtained in the temperature range of interest are distinctively slower than that of the wild type (i.e., 10b). In fact, both the folding and unfolding rates of 4-8-CL-Trp-cage become slower than those of 10b (Figure 4). More specifically, for example, at 35 °C the folding rate of 4-8-CL-Trp-cage is decreased by a factor of 3.8, whereas its unfolding rate slows down by a factor of 2.5 (Table 1). Since the stability of the 4-8-CL-Trp-cage is almost identical to that of 10b, we believe that these rate changes reflect at least partially, if not entirely, an increase in the frictional force along the folding coordinate.89 This argument is based on the fact that a simple adjustment of the transition state position in the current case cannot account for the different degrees of decrease in the folding and unfolding rates. To further verify this assessment, we have also measured the T-jump induced relaxation kinetics of 1-5-CL-Trp-cage wherein the cross-linker is placed at the N-terminus of the peptide. In this case, as discussed above, we expect that the linker-induced frictional effect will become less pronounced or even diminished as the cross-linker is surrounding a less obstructed region of the protein. In other words, if our hypothesis is correct, we expect that 1-5-CL-Trp-cage will exhibit a slower folding rate, due to its lower stability, but a comparable unfolding rate, in comparison to 10b. As shown (Figures 5 and 6), the T-jump induced relaxation process of 1-5-CL-Trp-cage also follows first-order kinetics and is slower than that of the wild type. A further analysis indicates, for example at 35 °C, that its folding rate is decreased by a factor of 5.3, whereas its unfolding rate is, within our experimental uncertainties, identical to that of 10b (Table 1). Thus, these results provide further compelling evidence in support of the above claim that the cross-linker in 4-8-CL-Trp-cage induces an additional frictional force along the folding-unfolding coordinate, due to its close proximity to several side chains that undergo relatively large-amplitude motions upon folding or unfolding.
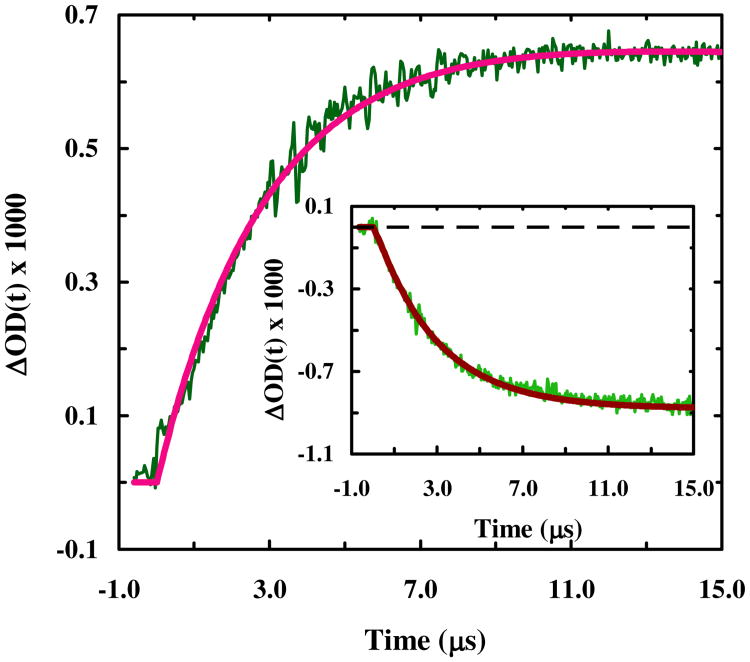
Figure 3.
Relaxation kinetics of 4-8-CL-Trp-cage in response to a T-jump from 29.3 to 42.1 °C, probed at 1668 cm-1. The smooth line represents the best fit of this curve to a single exponential function with a relaxation time constant of 2.7 μs. Shown in the inset are the relaxation kinetics of the same peptide obtained with a probing frequency of 1620 cm-1 in response to a T-jump of 29.1 to 43.4 °C. Fitting this relaxation curve to a single exponential function yielded a relaxation time constant of 2.9 μs.
Figure 4.
Temperature dependence of the relaxation rate constant (triangle), folding rate constant (circle) and unfolding rate constant (square) of 4-8-CL-Trp-cage. The green smooth line represents the relaxation rate constant of the wild type 10b trp-cage.55
Figure 5.
Relaxation kinetics of 1-5-CL-Trp-cage in response to a T-jump from 20.5 to 36.4 °C, probed at 1668 cm-1. The smooth line represents the best fit of this curve to a single exponential function with a relaxation time constant of 2.8 μs.
Figure 6.
Temperature dependence of the relaxation rate constant (triangle), folding rate constant (circle) and unfolding rate constant (square) of 1-5-CL-Trp-cage. The green line represents the relaxation rate constant of the wild type 10b trp-cage.55
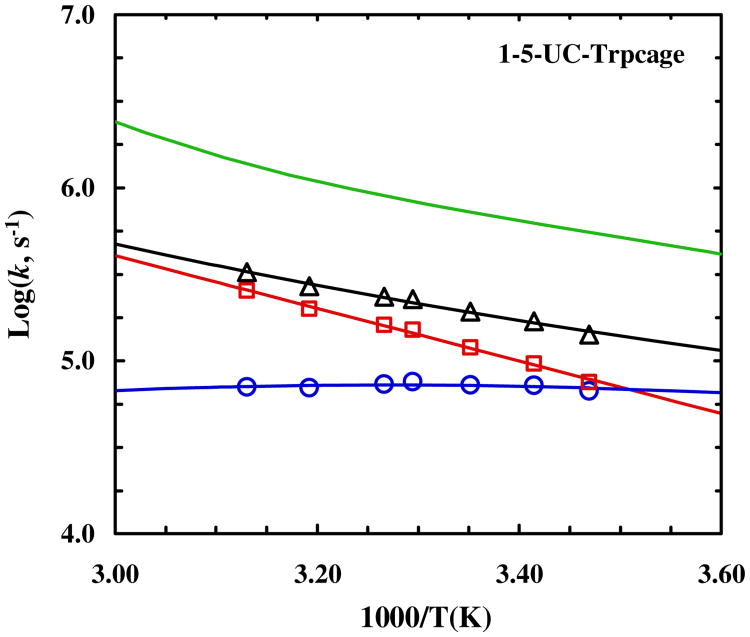
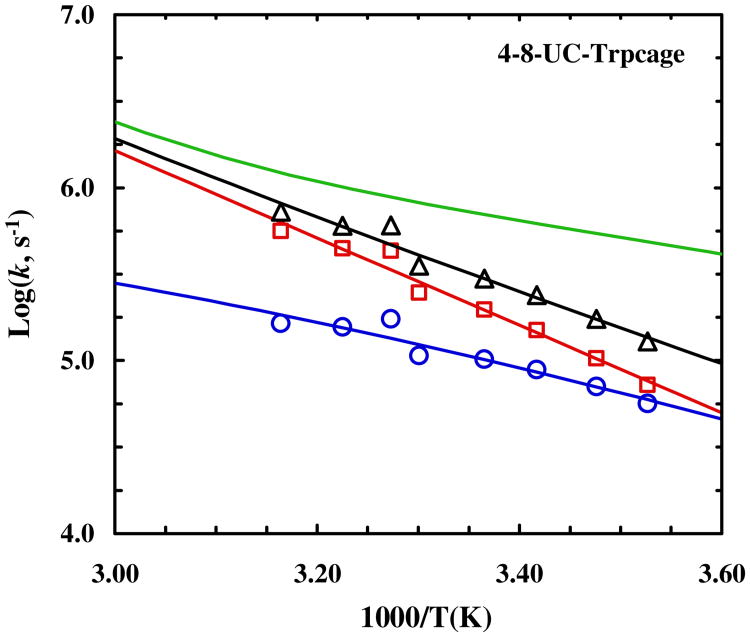
It is well known that mutations can change the unfolding rate. Therefore, to ensure that the slower unfolding rate of 4-8-CL-Trp-cage does not simply stem from the cysteine mutations, we also measured the conformational relaxation kinetics of the two uncross-linked trp-cage variants (i.e., 1-5-UC-Trp-cage and 4-8-UC-Trp-cage). In addition, the results of these measurements will help further substantiate our previous study, which depicts a trp-cage folding mechanism wherein the α-helix is either partially or completely formed in the transition state.55 As shown (Figures 7 and 8), both peptides exhibit a slower conformational relaxation rate than the wild type. However, as indicated (Table 1), this decrease in the relaxation rate originates almost exclusively from a decrease in the folding rate for peptides. Thus, taken together, these results not only corroborate our early conclusion55 that helix formation is the rate limiting step in trp-cage folding, but also confirm that the slower unfolding rate of 4-8-CL-Trp-cage arises explicitly from the cross-linker. Furthermore, it is interesting to note that the unfolding rate of 4-8-UC-Trp-cage at 35 °C shows a measureable increase from that of 10b. Because 1-5-UC-Trp-cage does not show any appreciable change in its unfolding rate in comparison to that of 10b, this increase most likely arises from the mutation at position 8. This notion is consistent with our previous study,90 which showed that the native interactions involving the C-terminal region of the helix are developed at the downhill side of the free energy barrier.
Figure 7.
Temperature dependence of the relaxation rate constant (triangle), folding rate constant (circle) and unfolding rate constant (square) of 1-5-UC-Trp-cage. The green line represents the relaxation rate constant of the wild type 10b trp-cage.55
Figure 8.
Temperature dependence of the relaxation rate constant (triangle), folding rate constant (circle) and unfolding rate constant (square) of 4-8-UC-Trp-cage. The green line represents the relaxation rate constant of the wild type 10b trp-cage.55
Quantifying the magnitude of internal friction and its effect on protein folding and conformational dynamics has been the subject of a number of theoretical and computational studies,1,2,4,91-95 and in particular, several studies have attempted to make a direct connection between internal friction and the roughness of the underlying energy landscape. For example, Zwanzig showed that the conformational diffusion coefficient of a protein on a barrierless one dimensional free energy surface is a direct measure of the roughness of this surface.91 Upon expanding this theoretical model, Thirumalai, Straub and coworkers92 further demonstrated that for a barrier-crossing process the roughness (U†) could be assessed via the following relationship:
| (6) |
where γint represents the friction exerted by the solvent, whereas γ is the internal friction. Below we apply this equation to provide an estimate of how much the helix cross-linker in 4-8-CL-Trp-cage increases the roughness of the trp-cage folding energy landscape, assuming that the deviations of its folding and unfolding rates from those of 10b are due entirely to increased internal friction, and that the value of γint can be approximated by that of 10b. Using the rate equation of transition state theory and these assumptions, we can easily show,
| (7) |
where kU(WT) and kU(CL) represent the unfolding rates of 10b and 4-8-CL-Trp-cage, respectively. Using equations (6) and (7) and the rates at 35 °C for 10b and 4-8-CL-Trp-cage (Table 1), we estimate the values of U† to be ∼0.4 kBT and ∼1.0 kBT for unfolding and folding, respectively. The order of magnitude of these values is reasonable given that the energetic roughness of a much larger protein, the α-spectrin domain R17, was estimated to be ∼2.0kBT.
The above analysis suggests that the friction along the free energy surface is asymmetric, which is expected if we take into account the sequence of events in the trp-cage folding mechanism. Given that the unfolded side of the free energy barrier involves side chain interactions in close proximity leading to helix formation, we would expect more local interactions with the cross-linker, resulting in a larger degree of internal friction. Indeed, Hamm and coworkers have shown that a photo-switchable cross-linker on a monomeric α-helix slows down its folding,50-52 due to the increased friction between the cross-linker and side chains from a combination of steric and non-native interaction effects. In addition, several simulations73,96 have suggested the presence of compact molten globule intermediates in the unfolded ensemble, which can act as a kinetic trap and may be stabilized by non-native hydrophobic interactions. Thus, it is also possible that the cross-linker increases the friction of folding by decreasing the rate out of such kinetic traps. Conversely, the folded side of the potential has a greater influence from intrinsic steric effects as the polypeptide chain becomes more compact upon folding, and is presumably less affected by the added frictional force of the cross-linker.
In summary, we employed an external linker to help assess the extent to which a local structural element increases the friction along the folding coordinate of trp-cage. While the current study only yielded a global view regarding this effect, future studies employing linkers of different lengths and structures may help provide a more detailed picture regarding the source of interactions that affect the folding-unfolding kinetics. In addition, we believe that the current method is also a useful addition to the toolbox for mechanistic study of protein folding and conformational dynamics. For example, it is possible to use a specific cross-linker to manipulate the folding free energy barrier and to selectively increase/decrease the flux of a particular folding pathway.
4. Conclusions
Because of chain connectivity and also the compactness of the native state, protein folding is subject to a frictional force due to, for example, local steric effects. However, assessing the frictional force arising from an individual structural element is difficult, if not impossible, as conventional kinetics studies do not provide independent information regarding the individual contributions to the overall effect of internal friction. To circumvent this difficulty, herein we use a cross-linker to selectively increase the local mass density, and thus the local friction, of a particular region of the protein of interest and to make the internal friction thus induced detectable via kinetic measurements. We apply this strategy to a well studied miniprotein, trp-cage, and find that a helix cross-linker (m-xylene) appended between residues 4 and 8 on its α-helix can induce a significant decrease in both the folding and unfolding rates, which is consistent with the notion that the cross-linker will result in an increase in local crowding or internal friction. Using a simple theoretical model, we further show that the cross-linker used, which could be thought as an individual chain segment in proteins, could increase the roughness of the folding energy surface by as much as 0.4-1.0kBT.
Supplementary Material
Acknowledgments
We gratefully acknowledge financial support from the National Institutes of Health (GM-065978 to FG and GM-054616 to WFD).
Footnotes
Supporting Information: Peptide characterization, MD simulation results, CD spectra, FTIR difference spectra, and T-jump relaxation kinetics. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Bryngelson JD, Onuchic JN, Socci ND, Wolynes PG. Funnels, Pathways, and the Energy Landscape of Protein Folding: a Synthesis. Proteins: Struct, Funct, Bioinf. 1995;21:167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
- 2.Socci ND, Onuchic JN, Wolynes PG. Diffusive Dynamics of the Reaction Coordinate for Protein Folding Funnels. J Chem Phys. 1996;104:5860–5868. [Google Scholar]
- 3.Dill KA, Chan HS. From Levinthal to Pathways to Funnels. Nat Struct Biol. 1997;4:10–19. doi: 10.1038/nsb0197-10. [DOI] [PubMed] [Google Scholar]
- 4.Onuchic JN, Luthey-Schulten Z, Wolynes PG. Theory of Protein Folding: the Energy Landscape Perspective. Annu Rev Phys Chem. 1997;48:545–600. doi: 10.1146/annurev.physchem.48.1.545. [DOI] [PubMed] [Google Scholar]
- 5.Shea JE, Onuchic JN, Brooks CL. Exploring the Origins of Topological Frustration: Design of a Minimally Frustrated Model of Fragment B of Protein A. Proc Natl Acad Sci U S A. 1999;96:12512–12517. doi: 10.1073/pnas.96.22.12512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ferreiro DU, Hegler JA, Komives EA, Wolynes PG. Localizing Frustration in Native Proteins and Protein Assemblies. Proc Natl Acad Sci U S A. 2007;104:19819–19824. doi: 10.1073/pnas.0709915104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Hills RD, Kathuria SV, Wallace LA, Day IJ, Brooks CL, Matthews CR. Topological Frustration in Beta Alpha-Repeat Proteins: Sequence Diversity Modulates the Conserved Folding Mechanisms of Alpha/Beta/Alpha Sandwich Proteins. J Mol Biol. 2010;398:332–350. doi: 10.1016/j.jmb.2010.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Wolynes PG, Eaton WA, Fersht AR. Chemical Physics of Protein Folding. Proc Natl Acad Sci U S A. 2012;109:17770–17771. doi: 10.1073/pnas.1215733109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Jacob M, Geeves M, Holtermann G, Schmid FX. Diffusional Barrier Crossing in a Two-State Protein Folding Reaction. Nat Struct Biol. 1999;6:923–926. doi: 10.1038/13289. [DOI] [PubMed] [Google Scholar]
- 10.Qiu L, Hagen SJ. A Limiting Speed for Protein Folding at Low Solvent Viscosity. J Am Chem Soc. 2004;126:3398–3399. doi: 10.1021/ja049966r. [DOI] [PubMed] [Google Scholar]
- 11.Hagen SJ, Qiu LL, Pabit SA. Diffusional Limits to the Speed of Protein Folding: Fact or Friction? J Phys: Condens Matter. 2005;17:S1503–S1514. [Google Scholar]
- 12.Frauenfelder H, Fenimore PW, Chen G, McMahon BH. Protein Folding is Slaved to Solvent Motions. Proc Natl Acad Sci U S A. 2006;103:15469–15472. doi: 10.1073/pnas.0607168103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Plaxco KW, Baker D. Limited Internal Friction in the Rate-Limiting Step of a Two-State Protein Folding Reaction. Proc Natl Acad Sci U S A. 1998;95:13591–13596. doi: 10.1073/pnas.95.23.13591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wagner C, Kiefhaber T. Intermediates can Accelerate Protein Folding. Proc Natl Acad Sci U S A. 1999;96:6716–6721. doi: 10.1073/pnas.96.12.6716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Hinsen K, Petrescu AJ, Dellerue S, Bellissent-Funel MC, Kneller GR. Harmonicity in Slow Protein Dynamics. Chem Phys. 2000;261:25–37. [Google Scholar]
- 16.Shea JE, Onuchic JN, Brooks CL. Energetic Frustration and the Nature of the Transition State in Protein Folding. J Chem Phys. 2000;113:7663–7671. [Google Scholar]
- 17.Portman JJ, Takada S, Wolynes PG. Microscopic Theory of Protein Folding Rates. II. Local Reaction Coordinates and Chain Dynamics. J Chem Phys. 2001;114:5082–5096. [Google Scholar]
- 18.Kaya H, Chan HS. Solvation Effects and Driving Forces for Protein Thermodynamic and Kinetic Cooperativity: How Adequate is Native-Centric Topological Modeling? J Mol Biol. 2003;326:911–931. doi: 10.1016/s0022-2836(02)01434-1. [DOI] [PubMed] [Google Scholar]
- 19.Zagrovic B, Pande V. Solvent Viscosity Dependence of the Folding Rate of a Small Protein: Distributed Computing Study. J Comput Chem. 2003;24:1432–1436. doi: 10.1002/jcc.10297. [DOI] [PubMed] [Google Scholar]
- 20.Ellison PA, Cavagnero S. Role of Unfolded State Heterogeneity and En-Route Ruggedness in Protein Folding Kinetics. Protein Sci. 2006;15:564–582. doi: 10.1110/ps.051758206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Chahine J, Oliveira RJ, Leite VBP, Wang J. Configuration-Dependent Diffusion can Shift the Kinetic Transition State and Barrier Height of Protein Folding. Proc Natl Acad Sci U S A. 2007;104:14646–14651. doi: 10.1073/pnas.0606506104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Alexander-Katz A, Wada H, Netz RR. Internal Friction and Nonequilibrium Unfolding of Polymeric Globules. Phys Rev Lett. 2009;103:028102. doi: 10.1103/PhysRevLett.103.028102. [DOI] [PubMed] [Google Scholar]
- 23.Best RB. How well does a Funneled Energy Landscape Capture the Folding Mechanism of Spectrin Domains? J Phys Chem B. 2013;117:13235–13244. doi: 10.1021/jp403305a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Schulz JC, Schmidt L, Best RB, Dzubiella J, Netz RR. Peptide Chain Dynamics in Light and Heavy Water: Zooming in on Internal Friction. J Am Chem Soc. 2012;134:6273–6279. doi: 10.1021/ja211494h. [DOI] [PubMed] [Google Scholar]
- 25.Jas GS, Eaton WA, Hofrichter J. Effect of Viscosity on the Kinetics of Alpha-Helix and Beta-Hairpin Formation. J Phys Chem B. 2001;105:261–272. [Google Scholar]
- 26.Liu F, Nakaema M, Gruebele M. The Transition State Transit Time of WW Domain Folding is Controlled by Energy Landscape Roughness. J Chem Phys. 2009;131:195101. doi: 10.1063/1.3262489. [DOI] [PubMed] [Google Scholar]
- 27.Hagen SJ. Solvent Viscosity and Friction in Protein Folding Dynamics. Curr Protein Pept Sci. 2010;11:385–395. doi: 10.2174/138920310791330596. [DOI] [PubMed] [Google Scholar]
- 28.Wensley BG, Batey S, Bone FA, Chan ZM, Tumelty NR, Steward A, Kwa LG, Borgia A, Clarke J. Experimental Evidence for a Frustrated Energy Landscape in a Three-Helix-Bundle Protein Family. Nature. 2010;463:685–688. doi: 10.1038/nature08743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Wensley BG, Kwa LG, Shammas SL, Rogers JM, Browning S, Yang ZQ, Clarke J. Separating the Effects of Internal Friction and Transition State Energy to Explain the Slow, Frustrated Folding of Spectrin Domains. Proc Natl Acad Sci U S A. 2012;109:17795–17799. doi: 10.1073/pnas.1201793109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sekhar A, Vallurupalli P, Kay LE. Defining a Length Scale for Millisecond-Timescale Protein Conformational Exchange. Proc Natl Acad Sci U S A. 2013;110:11391–11396. doi: 10.1073/pnas.1303273110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Ansari A, Jones CM, Henry ER, Hofrichter J, Eaton WA. The Role of Solvent Viscosity in the Dynamics of Protein Conformational Changes. Science. 1992;256:1796–1798. doi: 10.1126/science.1615323. [DOI] [PubMed] [Google Scholar]
- 32.Lapidus LJ, Eaton WA, Hofrichter J. Measuring the Rate of Intramolecular Contact Formation in Polypeptides. Proc Natl Acad Sci U S A. 2000;97:7220–7225. doi: 10.1073/pnas.97.13.7220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Pabit SA, Roder H, Hagen SJ. Internal Friction Controls the Speed of Protein Folding from a Compact Configuration. Biochemistry. 2004;43:12532–12538. doi: 10.1021/bi048822m. [DOI] [PubMed] [Google Scholar]
- 34.Cellmer T, Henry ER, Hofrichter J, Eaton WA. Measuring Internal Friction of an Ultrafast-Folding Protein. Proc Natl Acad Sci U S A. 2008;105:18320–18325. doi: 10.1073/pnas.0806154105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Buscaglia M, Lapidus LJ, Eaton WA, Hofrichter J. Effects of Denaturants on the Dynamics of Loop Formation in Polypeptides. Biophys J. 2006;91:276–288. doi: 10.1529/biophysj.105.071167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Waldauer SA, Bakajin O, Lapidus LJ. Extremely Slow Intramolecular Diffusion in Unfolded Protein L. Proc Natl Acad Sci U S A. 2010;107:13713–13717. doi: 10.1073/pnas.1005415107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Borgia A, Wensley BG, Soranno A, Nettels D, Borgia MB, Hoffmann A, Pfeil SH, Lipman EA, Clarke J, Schuler B. Localizing Internal Friction Along the Reaction Coordinate of Protein Folding by Combining Ensemble and Single-Molecule Fluorescence Spectroscopy. Nat Commun. 2012;3:1–9. doi: 10.1038/ncomms2204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Soranno A, Buchli B, Nettels D, Cheng RR, Muller-Spath S, Pfeil SH, Hoffmann A, Lipman EA, Makarov DE, Schuler B. Quantifying Internal Friction in Unfolded and Intrinsically Disordered Proteins with Single-Molecule Spectroscopy. Proc Natl Acad Sci U S A. 2012;109:17800–17806. doi: 10.1073/pnas.1117368109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Kawakami M, Byrne K, Brockwell DJ, Radford SE, Smith DA. Viscoelastic Study of the Mechanical Unfolding of a Protein by AFM. Biophys J. 2006;91:L16–L18. doi: 10.1529/biophysj.106.085019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Khatri BS, Byrne K, Kawakami M, Brockwell DJ, Smith DA, Radford SE, McLeish TCB. Internal Friction of Single Polypeptide Chains at High Stretch. Faraday Discuss. 2008;139:35–51. doi: 10.1039/b716418c. [DOI] [PubMed] [Google Scholar]
- 41.Hinczewski M, von Hansen Y, Netz RR. Deconvolution of Dynamic Mechanical Networks. Proc Natl Acad Sci U S A. 2010;107:21493–21498. doi: 10.1073/pnas.1010476107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Lannon H, Haghpanah JS, Montclare JK, Vanden-Eijnden E, Brujic J. Force-Clamp Experiments Reveal the Free-Energy Profile and Diffusion Coefficient of the Collapse of Protein Molecules. Phys Rev Lett. 2013;110:128301. doi: 10.1103/PhysRevLett.110.128301. [DOI] [PubMed] [Google Scholar]
- 43.Neidigh JW, Fesinmeyer RM, Andersen NH. Designing a 20-Residue Protein. Nat Struct Biol. 2002;9:425–430. doi: 10.1038/nsb798. [DOI] [PubMed] [Google Scholar]
- 44.Barua B, Lin JC, Williams VD, Kummler P, Neidigh JW, Andersen NH. The Trp-Cage: Optimizing the Stability of a Globular Miniprotein. Protein Eng, Des Sel. 2008;21:171–185. doi: 10.1093/protein/gzm082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Abkevich VI, Shakhnovich EI. What can Disulfide Bonds tell us about Protein Energetics, Function and Folding: Simulations and Bioinformatics Analysis. J Mol Biol. 2000;300:975–985. doi: 10.1006/jmbi.2000.3893. [DOI] [PubMed] [Google Scholar]
- 46.Grantcharova VP, Riddle DS, Baker D. Long-Range Order in the Src SH3 Folding Transition State. Proc Natl Acad Sci U S A. 2000;97:7084–7089. doi: 10.1073/pnas.97.13.7084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Shandiz AT, Capraro BR, Sosnick TR. Intramolecular Cross-Linking Evaluated as a Structural Probe of the Protein Folding Transition State. Biochemistry. 2007;46:13711–13719. doi: 10.1021/bi701042e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Chen EF, Kumita JR, Woolley GA, Kliger DS. The Kinetics of Helix Unfolding of an Azobenzene Cross-Linked Peptide Probed by Nanosecond Time-Resolved Optical Rotatory Dispersion. J Am Chem Soc. 2003;125:12443–12449. doi: 10.1021/ja030277+. [DOI] [PubMed] [Google Scholar]
- 49.Tucker MJ, Courter JR, Chen JX, Atasoylu O, Smith AB, Hochstrasser RM. Tetrazine Phototriggers: Probes for Peptide Dynamics. Angew Chem, Int Edit. 2010;49:3612–3616. doi: 10.1002/anie.201000500. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Ihalainen JA, Paoli B, Muff S, Backus EHG, Bredenbeck J, Woolley GA, Caflisch A, Hamm P. α-Helix Folding in the Presence of Structural Constraints. Proc Natl Acad Sci U S A. 2008;105:9588–9593. doi: 10.1073/pnas.0712099105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Paoli B, Seeber M, Backus EHG, Ihalainen JA, Hamm P, Caflisch A. Bulky Side Chains and Non-Native Salt Bridges Slow Down the Folding of a Cross-Linked Helical Peptide: a Combined Molecular Dynamics and Time-Resolved Infrared Spectroscopy Study. J Phys Chem B. 2009;113:4435–4442. doi: 10.1021/jp810431s. [DOI] [PubMed] [Google Scholar]
- 52.Paoli B, Pellarin R, Caflisch A. Slow Folding of Cross-Linked Alpha-Helical Peptides due to Steric Hindrance. J Phys Chem B. 2010;114:2023–2027. doi: 10.1021/jp910216j. [DOI] [PubMed] [Google Scholar]
- 53.Jo H, Meinhardt N, Wu YB, Kulkarni S, Hu XZ, Low KE, Davies PL, DeGrado WF, Greenbaum DC. Development of Alpha-Helical Calpain Probes by Mimicking a Natural Protein-Protein Interaction. J Am Chem Soc. 2012;134:17704–17713. doi: 10.1021/ja307599z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Qiu LL, Hagen SJ. Internal Friction in the Ultrafast Folding of the Tryptophan Cage. Chem Phys. 2004;307:243–249. [Google Scholar]
- 55.Culik RM, Serrano AL, Bunagan MR, Gai F. Achieving Secondary Structural Resolution in Kinetic Measurements of Protein Folding: a Case Study of the Folding Mechanism of Trp-Cage. Angew Chem, Int Edit. 2011;50:10884–10887. doi: 10.1002/anie.201104085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Halabis A, Zmudzinska W, Liwo A, Oldziej S. Conformational Dynamics of the Trp-Cage Miniprotein at its Folding Temperature. J Phys Chem B. 2012;116:6898–6907. doi: 10.1021/jp212630y. [DOI] [PubMed] [Google Scholar]
- 57.Meuzelaar H, Marino KA, Huerta-Viga A, Panman MR, Smeenk LEJ, Kettelarij AJ, van Maarseveen JH, Timmerman P, Bolhuis PG, Woutersen S. Folding Dynamics of the Trp-Cage Miniprotein: Evidence for a Native-like Intermediate from Combined Time-Resolved Vibrational Spectroscopy and Molecular Dynamics Simulations. J Phys Chem B. 2013;117:11490–11501. doi: 10.1021/jp404714c. [DOI] [PubMed] [Google Scholar]
- 58.Snow CD, Zagrovic B, Pande VS. The Trp Cage: Folding Kinetics and Unfolded State Topology via Molecular Dynamics Simulations. J Am Chem Soc. 2002;124:14548–14549. doi: 10.1021/ja028604l. [DOI] [PubMed] [Google Scholar]
- 59.Chowdhury S, Lee MC, Xiong GM, Duan Y. Ab initio Folding Simulation of the Trp-Cage Mini-Protein Approaches NMR Resolution. J Mol Biol. 2003;327:711–717. doi: 10.1016/s0022-2836(03)00177-3. [DOI] [PubMed] [Google Scholar]
- 60.Nikiforovich GV, Andersen NH, Fesinmeyer RM, Frieden C. Possible Locally Driven Folding Pathways of TC5b, a 20-Residue Protein. Proteins: Struct, Funct, Genet. 2003;52:292–302. doi: 10.1002/prot.10409. [DOI] [PubMed] [Google Scholar]
- 61.Ding F, Buldyrev SV, Dokholyan NV. Folding Trp-Cage to NMR Resolution Native Structure using a Coarse-Grained Protein Model. Biophys J. 2005;88:147–155. doi: 10.1529/biophysj.104.046375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Linhananta A, Boer J, MacKay I. The Equilibrium Properties and Folding Kinetics of an All-Atom Gō Model of the Trp-Cage. J Chem Phys. 2005;122:114901. doi: 10.1063/1.1874812. [DOI] [PubMed] [Google Scholar]
- 63.Chen JH, Im WP, Brooks CL. Balancing Solvation and Intramolecular Interactions: Toward a Consistent Generalized Born Force Field. J Am Chem Soc. 2006;128:3728–3736. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kentsis A, Gindin T, Mezei M, Osman R. Calculation of the Free Energy and Cooperativity of Protein Folding. PLoS One. 2007;2:1–10. doi: 10.1371/journal.pone.0000446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Paschek D, Nymeyer H, Garcia AE. Replica Exchange Simulation of Reversible Folding/Unfolding of the Trp-Cage Miniprotein in Explicit Solvent: On the Structure and Possible Role of Internal Water. J Struct Biol. 2007;157:524–533. doi: 10.1016/j.jsb.2006.10.031. [DOI] [PubMed] [Google Scholar]
- 66.Piana S, Laio A. A Bias-Exchange Approach to Protein Folding. J Phys Chem B. 2007;111:4553–4559. doi: 10.1021/jp067873l. [DOI] [PubMed] [Google Scholar]
- 67.Yang LJ, Grubb MP, Gao YQ. Application of the Accelerated Molecular Dynamics Simulations to the Folding of a Small Protein. J Chem Phys. 2007;126:125102. doi: 10.1063/1.2709639. [DOI] [PubMed] [Google Scholar]
- 68.Juraszek J, Bolhuis PG. Rate Constant and Reaction Coordinate of Trp-Cage Folding in Explicit Water. Biophys J. 2008;95:4246–4257. doi: 10.1529/biophysj.108.136267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Paschek D, Hempel S, Garcia AE. Computing the Stability Diagram of the Trp-Cage Miniprotein. Proc Natl Acad Sci U S A. 2008;105:17754–17759. doi: 10.1073/pnas.0804775105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Xu WX, Mu YG. Ab Initio Folding Simulation of Trpcage by Replica Exchange with Hybrid Hamiltonian. Biophys Chem. 2008;137:116–125. doi: 10.1016/j.bpc.2008.08.002. [DOI] [PubMed] [Google Scholar]
- 71.Cerny J, Vondrasek J, Hobza P. Loss of Dispersion Energy Changes the Stability and Folding/Unfolding Equilibrium of the Trp-Cage Protein. J Phys Chem B. 2009;113:5657–5660. doi: 10.1021/jp9004746. [DOI] [PubMed] [Google Scholar]
- 72.Kannan S, Zacharias M. Folding Simulations of Trp-Cage Mini Protein in Explicit Solvent using Biasing Potential Replica-Exchange Molecular Dynamics Simulations. Proteins: Struct, Funct, Bioinf. 2009;76:448–460. doi: 10.1002/prot.22359. [DOI] [PubMed] [Google Scholar]
- 73.Marinelli F, Pietrucci F, Laio A, Piana S. A Kinetic Model of Trp-Cage Folding from Multiple Biased Molecular Dynamics Simulations. Plos Comput Biol. 2009;5:1–18. doi: 10.1371/journal.pcbi.1000452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Best RB, Mittal J. Balance Between Alpha and Beta Structures in Ab Initio Protein Folding. J Phys Chem B. 2010;114:8790–8798. doi: 10.1021/jp102575b. [DOI] [PubMed] [Google Scholar]
- 75.Shao Q, Shi JY, Zhu WL. Enhanced Sampling Molecular Dynamics Simulation Captures Eperimentally Suggested Intermediate and Unfolded States in the Folding Pathway of Trp-Cage Miniprotein. J Chem Phys. 2012;137:125103. doi: 10.1063/1.4754656. [DOI] [PubMed] [Google Scholar]
- 76.Juraszek J, Saladino G, van Erp TS, Gervasio FL. Efficient Numerical Reconstruction of Protein Folding Kinetics with Partial Path Sampling and Pathlike Variables. Phys Rev Lett. 2013;110:108106. doi: 10.1103/PhysRevLett.110.108106. [DOI] [PubMed] [Google Scholar]
- 77.Lee IH, Kim SY. Dynamic Folding Pathway Models of the Trp-Cage Protein. Biomed Res Int. 2013;2013:1–9. doi: 10.1155/2013/973867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Marinelli F. Following Easy Slope Paths on a Free Energy Landscape: the Case Study of the Trp-Cage Folding Mechanism. Biophys J. 2013;105:1236–1247. doi: 10.1016/j.bpj.2013.07.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Huang CY, Getahun Z, Zhu Y, Klemke JW, DeGrado WF, Gai F. Helix Formation via Conformation Diffusion Search. Proc Natl Acad Sci U S A. 2002;99:2788–2793. doi: 10.1073/pnas.052700099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Huang CY, Klemke JW, Getahun Z, DeGrado WF, Gai F. Temperature-Dependent Helix-Coil Transition of an Alanine Based Peptide. J Am Chem Soc. 2001;123:9235–9238. doi: 10.1021/ja0158814. [DOI] [PubMed] [Google Scholar]
- 81.Kalé L, Skeel R, Bhandarkar M, Brunner R, Gursoy A, Krawetz N, Phillips J, Shinozaki A, Varadarajan K, Schulten K. NAMD2: Greater Scalability for Parallel Molecular Dynamics. J Comput Phys. 1999;151:283–312. [Google Scholar]
- 82.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of Simple Potential Functions for Simulating Liquid Water. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 83.Williams DV, Byrne A, Stewart J, Andersen NH. Optimal Salt Bridge for Trp-Cage Stabilization. Biochemistry. 2011;50:1143–1152. doi: 10.1021/bi101555y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Patchornik A, Degani Y, Neumann H. Selective Cyanylation of Sulfhydryl Groups. J Am Chem Soc. 1970;92:6969–6971. doi: 10.1021/ja00726a043. [DOI] [PubMed] [Google Scholar]
- 85.Streicher WW, Makhatadze GI. Unfolding Thermodynamics of Trp-Cage, a 20 residue Miniprotein, studied by Differential Scanning Calorimetry and Circular Dichroism Spectroscopy. Biochemistry. 2007;46:2876–2880. doi: 10.1021/bi602424x. [DOI] [PubMed] [Google Scholar]
- 86.Ahmed Z, Beta IA, Mikhonin AV, Asher SA. UV-Resonance Raman Thermal Unfolding Study of Trp-Cage shows that it is not a Simple Two-State Miniprotein. J Am Chem Soc. 2005;127:10943–10950. doi: 10.1021/ja050664e. [DOI] [PubMed] [Google Scholar]
- 87.Hu Z, Tang Y, Wang H, Zhang X, Lei M. Dynamics and Cooperativity of Trp-Cage Folding. Arch Biochem Biophys. 2008;475:140–147. doi: 10.1016/j.abb.2008.04.024. [DOI] [PubMed] [Google Scholar]
- 88.Day R, Paschek D, Garcia AE. Microsecond Simulations of the Folding/Unfolding Thermodynamics of the Trp-Cage Miniprotein. Proteins: Struct, Funct, Bioinf. 2010;78:1889–1899. doi: 10.1002/prot.22702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Mukherjee S, Waegele MM, Chowdhury P, Guo L, Gai F. Effect of Macromolecular Crowding on Protein Folding Dynamics at the Secondary Structure Level. J Mol Biol. 2009;393:227–236. doi: 10.1016/j.jmb.2009.08.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Culik RM, Annavarapu S, Nanda V, Gai F. Using D-Amino Acids to Delineate the Mechanism of Protein Folding: Application to Trp-Cage. Chem Phys. 2013;422:131–134. doi: 10.1016/j.chemphys.2013.01.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Zwanzig R. Diffusion in a Rough Potential. Proc Natl Acad Sci U S A. 1988;85:2029–2030. doi: 10.1073/pnas.85.7.2029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Sagnella DE, Straub JE, Thirumalai D. Time Scales and Pathways for Kinetic Energy Relaxation in Solvated Proteins: Application to Carbonmonoxy Myoglobin. J Chem Phys. 2000;113:7702–7711. [Google Scholar]
- 93.Hyeon CB, Thirumalai D. Can Energy Landscape Roughness of Proteins and RNA be Measured by using Mechanical Unfolding Experiments? Proc Natl Acad Sci U S A. 2003;100:10249–10253. doi: 10.1073/pnas.1833310100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Best RB, Hummer G. Diffusion Models of Protein Folding. Phys Chem Chem Phys. 2011;13:16902–16911. doi: 10.1039/c1cp21541h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Erbaş A, Netz RolandR. Confinement-Dependent Friction in Peptide Bundles. Biophys J. 2013;104:1285–1295. doi: 10.1016/j.bpj.2013.02.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Juraszek J, Bolhuis PG. Sampling the Multiple Folding Mechanisms of Trp-Cage in Explicit solvent. Proc Natl Acad Sci U S A. 2006;103:15859–15864. doi: 10.1073/pnas.0606692103. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.