Cutting the Wires: Modularization of Cellular Networks for Experimental Design

Abstract

Understanding naturally evolved cellular networks requires the consecutive identification and revision of the interactions between relevant molecular species. In this process, initially often simplified and incomplete networks are extended by integrating new reactions or whole subnetworks to increase consistency between model predictions and new measurement data. However, increased consistency with experimental data alone is not sufficient to show the existence of biomolecular interactions, because the interplay of different potential extensions might lead to overall similar dynamics. Here, we present a graph-based modularization approach to facilitate the design of experiments targeted at independently validating the existence of several potential network extensions. Our method is based on selecting the outputs to measure during an experiment, such that each potential network extension becomes virtually insulated from all others during data analysis. Each output defines a module that only depends on one hypothetical network extension, and all other outputs act as virtual inputs to achieve insulation. Given appropriate experimental time-series measurements of the outputs, our modules can be analyzed, simulated, and compared to the experimental data separately. Our approach exemplifies the close relationship between structural systems identification and modularization, an interplay that promises development of related approaches in the future.

Introduction

Our knowledge of the species and their interactions in most cellular networks is incomplete. For many networks, a consensus already exists about a set of core species and high-confidence reactions, but this cannot yet explain all experimental data. To close the gap between model predictions and experimental results, one might extend the network with hypothetical, low-confidence reactions. However, if several (sets of) competing model extensions exist that are consistent with already available data, new experiments have to be designed to either confirm or discard the individual extensions. The corresponding tasks of model discrimination and experimental design for model structure identification pose substantial theoretical and computational challenges.

In model discrimination (see Kirk et al. (1) for a recent review), each possible combination of low-confidence reactions defines a so-called candidate model M_i, i ∈ 1,…, m, typically with unknown parameterization (2–6). The goal is to identify the most probable model $\hat{M}$, respective to estimating the posterior probabilities p(M_i|D) in Bayesian approaches, given the experimental data D. However, the number of candidate models typically increases exponentially with the number of low-confidence reactions, and each model has to be evaluated in potentially high-dimensional parameter spaces. In our opinion, the computational complexity resulting from these two effects constitutes one of the most important challenges in constructing larger biomolecular models. Consequently, model discrimination has focused on networks with typically only up to 20 or 30 parameters, and with only a small number of mutually compatible hypothetical reactions (5) or candidate models (2,6).

These approaches assume that the existence of a given low-confidence reaction cannot be detected directly, but only through its influence on the dynamics of measurable species in the network. The decision of which species to measure is thereby often not given a priori, but rather as the subject of experimental design (5,7). For large, highly interconnected networks including several—often only poorly understood—low-confidence reactions, it becomes challenging to identify which species concentrations should be measured such that the experimentally observable dynamics can be explained only by the existence or nonexistence of specific low-confidence reactions, and not by a combination of other hypothetical reactions.

Here, we propose to solve this problem of experimental design for model discrimination by modularization: with an adequate definition of modularization, a module—which is interpretable as a subnetwork—and the low-confidence reactions therein can be (structurally) identified separately from the rest of the network in a divide-and-conquer strategy (see below for a discussion of identifiability issues).

Modularity has been hypothesized early to be a key feature of biological network organization (8). Albeit modularization is an important tool for analyzing large-scale networks, surprisingly few conceptually different modularization methods exist (9,10). Most approaches determine highly connected cliques or communities of species, subnetworks with relatively few connections to other modules, or a combination thereof (11–15). Depending on the specific definitions of the terms “highly connected” and “modularity”, they utilize various automatic or semiautomatic approaches including hierarchical clustering (11,16), graph cuts based on the number of shortest paths through network edges (i.e., “betweenness”; see Girvan and Newman (14)), aggregation of smaller elementary modules based on size (12), greedy algorithms (17), or hybrid approaches based on eigenvectors of a modularity matrix combined with fine-tuning by local optimization (13). A recent approach punishes only bidirectional connections between modules to eliminate minimal, nontrivial feedback loops that establish retroactivity (18,19). These and similar approaches are especially valuable when trying to initially understand larger networks because the elements in a given module typically have common—sometimes surprising—properties that might help to explain the structure of the network (14).

Other module definitions aim at facilitating the analysis of specific network properties (20). Pioneering work on monotone network decompositions (21,22), however, appears to have limited practical applicability because analytical simplicity gained by monotone modules is often compensated for by complex interfaces between modules. For metabolic (mass-balanced) networks, elementary flux modes are (minimal) sets of reactions that can operate at steady state (23). This and similar concepts (24,25) can be seen as modules describing functionally related sets of reactions in steady state. Network motifs (26)—that is, small subnetworks with a wiring that appears statistically more often in networks than expected—constitute another approach; their practical value lies in coarse-graining and identification of small functional units, rather than in the modularization of large networks.

Nearly all available modularization approaches have in common what we consider an inherent design problem (pathway-based methods such as from Stelling et al. (23) are an exception): they will (nearly) always return at least one network modularization. Therefore, the absolute significance of a given modularization typically cannot be quantified because scores and similar metrics provide relative assessments only. Note that this holds also for approaches like those of Newman (13) and Clauset et al. (17), which might return a single module containing the whole network, but for which only slightly worse performing modularizations with more than one module might exist. Often, this inherent design problem results from weakly defined goals of modularization approaches beyond visualization, data mining, and similar.

Here, we propose that modularization methods should provide experimental designs for structural systems identification, and succeed if and only if a given type of experimental design is possible. Our graph-based modularization approach, called insulating modularization, aims at identifying groups of outputs that should be measured simultaneously such that each output defines a module with exactly one low-confidence reaction, and such that the models of each module can be simulated and analyzed separately, specifically without knowledge on the existence of all other low-confidence reactions.

It is an intuitive idea to define modules such that (at least parts of) the interactions in a given module can be analyzed in isolation from the other modules. However, this idea is rarely considered as part of the definition of a module. As mentioned explicitly in Bowsher (12), the isolated identification of most of the parameters in a module should be feasible by measuring all (and probably also a subset of) the species in that module. Different to Bowsher (12), we do not consider parameter identification but model selection, based on a minimal numbers of species to be measured for a specific model selection task. Thus, our proposed method is conceptually different to other modularization approaches in that we consider modularity of a specific question on a (biological) network, rather than modularity of the network as such (27,28). Consequently, the modularizations proposed by our method can change completely with the (biological) question; similarities between modularizations proposed by our method and by other methods would be rather coincidental.

Our method has the main advantage of attenuating the combinatorial explosion both in the number of competing model structures and in the required number of parameter samples (because of lower-dimensional parameter spaces for each module). Other experimental design methods are typically concerned with determining dynamic trajectories of input signals, sampling times, suitable gene knockouts, and similar (29–33) to improve model identification or selection. Albeit some methods (33) can also identify (optimal) sets of outputs, the majority of these approaches are complementary to our method: for a given modularization, they can further specify the experimental design, for example, by determining (optimal) dynamic trajectories for external inputs.

Results

Overview

We analyze relatively well-known networks in which the number of high-confidence reactions is (significantly) higher than the number of hypothetical, low-confidence reactions. Furthermore, albeit not strictly necessary, we assume that at least a few reactions are irreversible. The goal of an insulating modularization is to separate the network into the same number of subnetworks (modules) as the number of low-confidence reactions. Each module contains exactly one low-confidence reaction, and it is insulated from the rest of the network by choosing an adequate set of outputs such that the dynamics of all species in the interface of a module to the rest of the network are experimentally measured. Each output is furthermore defined such that it can be used for the evaluation of models of exactly one module, that is, for testing whether the associated low-confidence reaction exists (Fig. 1).

Figure 1.

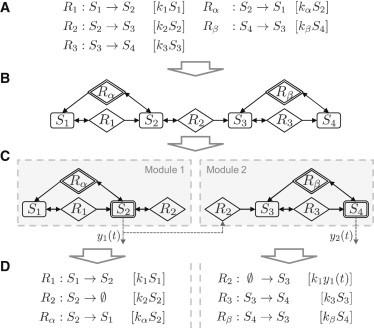
Workflow of our modularization approach. (A) Mass-action kinetics model with four species (S₁–S₄), three high-confidence reactions (R₁–R₃), and two low-confidence reactions R_α and R_β that should be experimentally verified or discarded. (B) Species-reaction graph of the network, where box-shaped vertices represent species, diamond-shaped ones reactions, and low-confidence reaction vertices are marked by two borders. A directed edge is drawn from a species to a reaction if the respective reaction rate depends on the species’ concentration, and a directed edge from a reaction to a species if turnover of the reaction changes the concentration of the species. (C) By measuring S₂ and S₄, the network can be split into two modules, with each module including exactly one low-confidence reaction. The time series data y₁ of species S₂, the output of the first module, serves as a virtual input for the second module. (D) Models of the two identified modules can be extracted, simulated separately given the experimental time-series data y₁(t) and y₂(t), and used to assess the existence of each low-confidence reaction independently.

We achieve the insulation between the modules by utilizing that the representation of applied input signals and measured output signals is essentially identical for the mathematical analysis; both are typically given as a set of time-value pairs. Thus, when measuring the sets of outputs proposed by our method, one can use the measurement data of the output of one module (respectively a spline fitted to the data) as a virtual input for the simulation of all others (compare Fig. 1 D).

For strict modularizations, two alternative models of each module (with and without the respective low-confidence reaction) can be created. The strictness property guarantees that both models only depend on measured outputs and high-confidence reactions (see the Supporting Material), such that their agreement with the experimental results can be directly compared using, for instance, Bayesian inference (5). Specifically, if the strict modules do not overlap, the probability for the existence of one low-confidence reaction becomes conditionally independent of the existence of all other low-confidence reactions, given the experimental measurements of the proposed outputs (see the Supporting Material). Overlapping modules, as in Fig. 1 C, may contain reactions assigned to more than one module (here: R₂). If the corresponding reaction rates depend on parameters that are adjusted by a model discrimination algorithm, independent adjustments in different modules may lead to incompatibilities. Thus, for overlapping modularizations, one should check at least a posteriori if such a case appeared. Such cases should be taken seriously, the more so as they may indicate certain flaws in the structure of the original model. We will not discuss details because corrections depend on the specific modeling technique and the specific model discrimination method (e.g., including fixing of parameter values or coupled discrimination approaches), and because in our experience these overlaps occur rarely in real-world modularizations problems, might not occur in all possible modularizations, and are commonly small in size (concerning only a few reactions; see examples in sections Example Network and JAK2/STAT5 signaling).

For simple modularizations, only models of the modules representing the network without the respective low-confidence reactions are guaranteed to be independent of all other low-confidence reactions. Thus, models pertaining to one module cannot necessarily be directly compared without knowledge on the existence of other low-confidence reactions. However, following the principle of parsimony, which also underlies Bayesian inference (35), one should favor the network without the hypothetical reaction if it is in sufficient agreement with all data. If details on the interactions of the species in the low-confidence reactions are unknown, one might, for example, merge whole subnetworks into one black-box, low-confidence reaction to represent the hypothesis that some species might influence—by a yet unknown mechanism—the concentrations of some other species.

It is important to note that our algorithm only guarantees—given adequate measurement data with sufficient temporal and quantitative resolution—that the modules can be virtually insulated from each other. More specifically, our method guarantees that there exists a directed path between the low-confidence reaction and the corresponding output in a given module. This is necessary but not sufficient for identification of the low-confidence reaction using its corresponding output. Symmetries in the network might, for example, lead to structural nonidentifiability of a low-confidence reaction given the outputs of a modularization. In addition, practical identifiability can be prevented, for example, by a low sensitivity of the output of a module to the respective low-confidence reaction, or by high model uncertainties. We therefore recommend the application of an adequate method (e.g., Sedoglavic (36) for deterministic models consisting of ordinary differential equations) to check identifiability of the low-confidence reactions for a given modularization, and potentially to choose a different modularization. Measurements of additional species in the modules corresponding to the nonidentifiable low-confidence reactions may alleviate these problems.

Insulating modularizations

In this section, we provide the mathematic definitions and theorems used by our modularization approach. We illustrate each definition by discussing the small example given in Fig. 1. We recommend that readers not interested in all details of our method focus on Definitions 1–4, given below, and the respective examples. In the following, we assume that standard graph-theoretical notations are known to the reader (see, e.g., Cormen et al. (37)).

Definition 1 (binary-labeled species-reaction graph)

A species-reaction (SR) graph is a directed bipartite graph G_SR = (V_S, V_R, E). The vertices in V_S = {S₁,…,S_n} and in V_R = {R₁,…,R_r} represent the species and the reactions of a biomolecular network, respectively. The directed edges of the network are defined as (S_i,R_j) ∈ E if the reaction rate of R_j depends on the concentration of S_i, and (R_j,S_i) ∈ E if turnover of reaction R_j changes the concentration of species S_i.

An SR graph is binary-labeled (BLSR graph) if each of its vertices has a binary label (weight) of 0 or 1. These labels are assigned in the following manner: (low-confidence reaction label function) η_R(R_j) is 1 (0), if R_j is in the low-confidence (high-confidence) set of reactions, and (output label function) η_S(S_i) is 1 (0), if the concentration of S_i is measured (not measured).

For notational convenience, let V_R,η = {R_j ∈ V_R:η_R(R_j) = 1} and V_S,η = {S_i ∈ V_S:η_S(S_i) = 1} be the set of low-confidence reactions and the set of measured outputs, respectively.

Fig. 1 A shows a small example of a mass-action reaction network with three high-confidence (R₁–R₃) and two low-confidence reactions (R_α and R_β), and Fig. 1 B its corresponding BLSR graph. In this example, none of the species S₁–S₄ is measured yet, but measuring any combination of species would also correspond to a BLSR graph. Note that the definition is not limited to mass-action models, and that it is compatible with reactions that involve more than two species and with reaction rates of (nearly) arbitrary form.

Definition 2 (reachability cost of a BLSR graph)

The reachability cost (length) ω(p) of a directed path p in a given BLSR graph is the sum of labels of the vertices in the path. The reachability cost ω_min(u,v) is the minimal reachability cost of all directed paths from vertex u to another vertex v ≠ u, or +∞ if no path from u to v exists. For u = v, the reachability cost equals the label of the vertex.

In our example network (Fig. 1 B), the reachability costs from S₁ to R₁ and from S₁ to S₄ are zero because directed paths exist that do not contain R_α or R_β. On the other hand, the reachability cost from S₂ to S₁ is 1, because the only simple directed path contains R_α. Without a directed path between S₄ and S₁, the corresponding reachability cost is +∞. Finally, by definition the reachability cost from S₁ to itself is 0 (S₁ is not measured), and from the low-confidence reaction R_α to itself it is 1.

Definition 3 (insulating modularization)

A BLSR graph is a simple insulating modularization, if and only if the number of low-confidence reactions is equal to the number of measured species, and there exists a unique, bijective function μ mapping low-confidence reactions to measured outputs, such that the reachability cost from a low-confidence reaction R_η to a measured output S_η is 2 if and only if μ(R_η) = S_η.

A BLSR graph is a strict insulating modularization, if and only if it is a simple insulating modularization, and the reachability cost between two distinct low-confidence reactions is larger than 2.

Intuitively, in a simple insulating modularization, for every low-confidence reaction there exists exactly one measured species, such that the corresponding two vertices are connected by a directed path that does not contain any other measured species or low-confidence reactions. A strict insulating modularization additionally requires that every path between two different low-confidence reactions contains at least one measured species.

In our example network (Fig. 1 B), we obtain an insulating modularization if we decide to measure species S₂ and S₄ (that is, change the corresponding labels to 1). In this case, the reachability costs from R_α to S₂ and from R_β to S₄ are 2, whereas the reachability cost from R_α to S₄ is 3 (the shortest path contains S₂), and the reachability cost from R_β to S₂ is +∞ (no directed path exists). This insulating modularization is strict: the shortest path from R_α to R_β has reachability cost 3, and there exists no directed path from R_β to R_α (reachability cost +∞). Alternatively, we could also decide to measure S₂ and S₃, which leads to another strict insulating modularization. However, we would not obtain an insulating modularization by measuring S₁ and S₃ because the reachability costs from R_β to S₃ and from R_α to S₃ would be 2, indicating that S₁ fails to insulate S₃ from the influence of R_α.

Definition 4 (module)

A module M(S_η) in a simple insulating modularization is the set of all vertices that have a reachability cost of 1 to a given measured output S_η:

$$M\left(S_{\eta }\right)=\left\{V_i\in V_S\cup V_R:{\omega }_{min}\left(V_i,S_{\eta }\right)=1\right\}.$$ (1)

The interface I(S_η) of a module is the set of all vertices for which a directed edge to a vertex in the corresponding module exists:

$$I\left(S_{\eta }\right)=\left\{V_i\in V_S\cup V_R:{\omega }_{\text{min}}\left(V_i,S_{\eta }\right)=2\wedge \exists V_M\in M\left(S_{\eta }\right):\left(V_i,V_M\right)\in E\right\}.$$ (2)

Fig. 1 C shows the two resulting modules when choosing to measure S₂ and S₄ in our example network (Fig. 1 B). The first module contains species S₁ and S₂ as well as reactions R₁ and R₂; its interface consists only of the low-confidence reaction R_α. The second module encompasses S₃ and S₄ as well as R₂ and R₃; the interface is constituted by the low-confidence reaction R_β and the measured output of S₂ (y₁(t)) of the first module. Note that in this example the two modules overlap because reaction R₂ pertains to both modules.

Lemma 5

A module in a simple insulating modularization contains exactly one measured species, and no low-confidence reaction:

$$M\left(S_{\eta }\right)\cap V_{S,\eta }=\left\{S_{\eta }\right\},$$ (3a)

$$M\left(S_{\eta }\right)\cap V_{R,\eta }=\text{Ø}\text{.}$$ (3b)

The interface of a module only contains vertices that correspond to measured species, and exactly one vertex corresponding to a low-confidence reaction:

$$I\left(S_{\eta }\right)\subseteq V_{S,\eta }\cup V_{R,\eta },$$ (4a)

$$I\left(S_{\eta }\right)\cap V_{R,\eta }=\left\{R_{\eta }\right\},\text{with}\mu \left(R_{\eta }\right)=S_{\eta }.$$ (4b)

Proof

A module M(S_η) is defined by the set of all vertices for which a path to S_η with a reachability cost of one exists. S_η is part of M(S_η) because ω_min(S_η, S_η) = η_S(S_η) = 1. No other vertex V_i ∈ V_S,η ∪ V_R,η, V_i ≠ S_η, being an output species or low-confidence-reaction, can be in the module M(S_η), because every path from it to S_η at least contains itself and S_η (ω_min(V_i, S_η) ≥ η(V_i) + η_S (S_η) = 2), or else no path exists between them at all (ω_min(V_i, S_η) = ∞).

That R_η, μ(R_η) = S_η, is the only element of V_R,η, which is part of the interface I(S_η), follows directly from the definition of a simple insulating modularization.

The shortest path between any element in the interface and S_η has, by definition, a reachability cost of 2 (∀V_i ∈ I(S_η) ∃p = (V_i,V_j,…,S_η):V_j ∈ M(S_η) ∧ ω(p) = 2). Because, by definition, V_j is part of the module, it is true that ω_min(V_j, S_η) = 1, and ω(p) = η(V_i) + ω_min(V_j, S_η) ⇒ η(V_i) = 1, that is, V_i is a measured species or a low-confidence reaction.

Lemma 6 (branching)

The BLSR graph that results from removing a low-confidence reaction vertex R_η (and all edges from and to this vertex) from a simple insulating modularization and from setting the label of the corresponding measured species S_η = μ(R_η) to 0 is a simple insulating modularization.

In our example network (Fig. 1 B), we could, for example, completely remove the low-confidence reaction vertex R_β and obtain an insulating modularization by measuring S₂ because measuring S₂ and S₄ would result in an insulating modularization of the original network. In this case, the first module remains unchanged, while the second module disappears (S₃, S₄, and R₃ would be part of no module). On the other hand, if we would remove the low-confidence reaction R_α and only measure S₄, we would obtain a single module with all vertices.

Proof

Assume μ(R_η) = S_η, R_η ∈ V_Rη, and S_η ∈ V_Sη. Furthermore, assume M(S′_η) being a different module (S^′_η ≠ S_η) with S_η ∈ I(S^′_η). Then, removing the low-confidence reaction R_η and the measured species label from S_η, there will be a new module $\tilde{M}\left(S_{\eta }^{\prime }\right)=M\left(S_{\eta }\right)\cup M\left(S_{\eta }^{\prime }\right)$ with interface $\tilde{I}\left(S_{\eta }^{\prime }\right)=\left(I\left(S_{\eta }^{\prime }\right)\mathrm{\setminus }\left\{S_{\eta }\right\}\right)\cup \left(I\left(S_{\eta }\right)\mathrm{\setminus }\left\{R_{\eta }\right\}\right)$. If $S_{\eta }\notin I\left(S_{\eta }^{″}\right)$, $S_{\eta }^{″}\ne S_{\eta }$: $\tilde{M}\left(S_{\eta }^{″}\right)=M\left(S_{\eta }^{″}\right)$, and $\tilde{I}\left(S_{\eta }^{″}\right)=I\left(S_{\eta }^{″}\right)$.

Lemma 7 (strictness)

The BLSR graph resulting from simultaneously setting the label of a low-confidence reaction vertex R_η and its corresponding measured species vertex S_η = μ(R_η) of a strict insulating modularization to 0 is a strict insulating modularization.

Note that the difference between Lemmas 6 and 7 is that for a strict insulating modularization the respective vertex of a low-confidence reaction R_η is not removed from the BLSR-graph together with the label of the corresponding measured species, but only its low-confidence label. The proof is according to Lemma 6.

Because measuring species S₂ and S₄ in our example (Fig. 1 B) results in a strict insulating modularization, we could—instead of removing a low-confidence reaction vertex as before—simply change its label such that it becomes a high-confidence reaction. Removing the label of R_α and measuring only S₄, or removing the label of R_β and measuring only S₂, would then also result in a strict insulating modularization.

Definition 8

Let the bijective function l_S:{1,…,n} → V_S, and respectively, l_R:{1,…,r} → V_R, induce an order on the elements of V_S, respectively V_R, of a BLSR graph. Without loss of generality, let ∀j∈ {1,…,|V_R,η|}:l_R(j) ∈ V_R,η, and ∀i∈ {1,…,|V_S,η|}:l_S(i) ∈ V_S,η.

Then there exists a unique (n + r) × (n + r) 0-1 biadjacency matrix

$${\mathbf{A}}_{\mathbf{E}}=\left(\begin{array}{cc}\mathbf{0}& {\mathbf{A}}_{\mathbf{RS}}\\ {\mathbf{A}}_{\mathbf{SR}}& \mathbf{0}\end{array}\right),$$ (5)

with the element a_ij ∈ {0,1} of the n × r 0-1 matrix A_RS = (A_RS,η, A_RS,) equal to 1 if (R_j, S_i) ∈ E, and 0 otherwise. Likewise, the element b_ji ∈ {0,1} of the r × n 0-1 matrix A_SR = ($A_{SR,\eta }^T,A_{SR,}^T$)^T is equal to 1 if (S_j, R_i) ∈ E, and 0 otherwise.

Theorem 9 (main result)

Let G_BLSR be a binary-labeled species reaction graph, and $\mathcal{C}$ be the set of all 0-1 matrices $C={\left[c_{ij}\right]}_{\left|V_{R,\eta }\right|\times \left|V_S\right|}$, with

$$\forall i\in \left\{1,\dots ,\left|V_{R,\eta }\right|\right\}:{\sum }_{j=1}^{\left|V_S\right|}{c}_{ij}=1.$$

For a given C ∈ $\mathcal{C}$, let D_Σ,0 be defined as

$$D_{\text{Σ},0}\left(E\right)=E{e}^{AF}{A}_{RS,\eta }$$ (6)

with F = (I – C^TC), and A = A_RS, A_SR,.

Then, G_BLSR is a simple insulating modularization, if |V_S,η| = |V_R,η| ∧∃!C ∈ $\mathcal{C}$, c_ij = 1 ⇒S_j ∈V_S,η, such that D_Σ,0(C) = diag(d_i), d_i > 0, with diag(d_i) = [d_ij] as a diagonal matrix with d_ij = d_i if i = j and d_ij = 0 otherwise.

The matrix C defines the mapping between the low-confidence reactions and their associated measured output species:

$$c_{ij}=1\iff \mu \left(l_R\left(i\right)\right)=l_S\left(j\right).$$ (7)

Furthermore, G_BLSR is a strict insulating modularization, if G_BLSR is a simple insulating modularization and D_Σ,0 (A_SR,ηF) = diag(δ_i), δ_i ≥ 0.

Note that for a strict insulating modularization, D_Σ,0(A_SR,ηF) has to be a diagonal matrix with diagonal elements ≥0, whereas the diagonal elements of D_Σ,0(C) have to be strictly >0.

For the proof of this theorem and alternative formulations, see the Supporting Material.

Lemma 10

Let G_IM be a simple insulating modularization (IM) with the matrices C, A, F, and A_RS, as described above. Then, species j belongs to module i if element m_s,ij of M_S = Ce^AF is unequal to 0, and reaction k belongs to the module if element m_r,ik of M_R = Ce^AF A_RS, is unequal to 0.

The proof for this lemma follows the proof for Theorem 9.

Finding insulating modularizations

An algorithm for computing all insulating modularizations has to solve the modularization problem defined by the following.

Problem 11 (modularization problem)

Input. An SR-graph G_SR = (V_S, V_R, E) and a low-confidence reaction label function η_R:V_R → {0,1}.

Output. The unique set L_Σ = {η_S,1···η_S,k} of all output label functions η_S,i, such that ∀ i ∈ 1,…, k:G_IM = (V_S, V_R, E, η_s,i, η_R) is a simple insulating modularization.

In the example discussed in the previous section (Fig. 1 B), there are, in principle, $\left(\begin{array}{c}4\\ 2\end{array}\right)=6$ possibilities to choose two measured species out of a total of four species. It is easy to check that an algorithm to solve this modularization problem should have as an output that only two of these possibilities, namely either to measure S₂ and S₃, or S₂ and S₄, correspond to a simple insulating modularization. While in this small example it is feasible to check all possibilities by hand, it is desirable to have an efficient algorithm to solve larger modularization problems.

An exhaustive search to find all insulating modularizations for a given modularization problem with |η_R| ≪ |V_S| has computational cost that is exponential in |η_R| (see the Supporting Material for details). Thus, the problem becomes computationally intractable for larger values of |η_R|. However, for a fixed |η_R|, we have polynomial complexity in |V_S|. Hence, networks with many vertices but few low-confidence reactions can be modularized by exhaustive search.

In fact, the following theorem shows that it is unlikely that a polynomial-time algorithm to solve Problem 11 exists:

Theorem 12 (NP-hardness)

The modularization problem is nondeterministic polynomial-time (NP)-hard. The proof of this theorem, which is based on showing that the problem of deciding if at least one simple insulating modularization exists is NP-complete, is given in the Supporting Material.

However, superpolynomial runtime in the number of low-confidence reactions as indicated by Theorem 12 is a worst-case scenario. The structure of many practically relevant modularization problems allows one to determine all possible simple insulating modularizations in reasonable time using a recursive branch-and-bound algorithm (see the Supporting Material for details) based on Lemma 6. It exploits that the first k, k < |η_R|, measured outputs of a final modularization also define an insulating modularization for a reduced modularization problem with only the first k low-confidence reactions. Thus, if the solution for the respective modularization problem defined by the first |η_R|−1 low-confidence reactions is already known, finding the solution to the original problem requires only testing all concatenations of the subsolutions to the remaining, not yet-labeled, species. The complexity of each of the |η_R| recursion steps depends on the number of solutions found in the previous step and |V_S|, but not on |η_R|. In practice, we experienced significantly higher efficiency compared to an exhaustive search, making it possible to modularize networks with many species and several low-confidence reactions in reasonable time (see the Supporting Material for details).

Example network

To demonstrate our modularization approach, we considered the small species-reaction network depicted in Fig. 2 consisting of nine species, ten high-confidence, and two low-confidence reactions. Our branch-and-bound algorithm identified the six distinct insulating modularizations shown in the network representations in Fig. 3.

Figure 2.

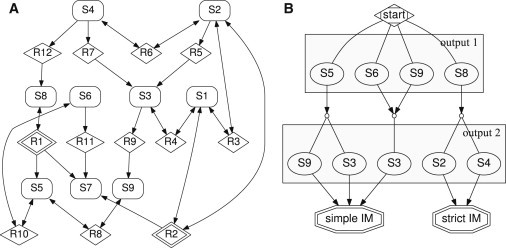
Example of modularization problem. (A) Network representation. (Box-shaped vertices) Species; (diamond-shaped vertices) reactions. Low-confidence reaction vertices are marked by two borders. (B) Reduced ordered multiple-valued decision diagram depicting the choices of species to measure in the example network to obtain an insulating modularization (IM). Conveniently, only decisions leading either to a strict or a simple modularization are shown. All graphs were drawn with GRAPHVIZ (43).

Figure 3.

Distinct insulating modularizations of the example network. (Box-shaped vertices) Species; (diamond-shaped vertices) reactions. (Yellow vertices) Part of Module 1; (brown vertices) part of Module 2; (gray vertices) parts of both modules; and (white vertices) no module. Vertices representing the measured species of a module and the corresponding low-confidence reactions are filled differently (slightly darker color than their corresponding modules) and they have two borders (note that, by definition, low-confidence reactions do not belong to the respective module, but to its interface). All graphs were drawn with GRAPHVIZ (43). To see this figure in color, go online.

For more complex problems, one may obtain combinatorially many possible insulating modularizations, typically when the measured-output labels for several modules can be chosen (partly) independently. Albeit being able to choose between different sets of outputs is an advantage when it comes to (feasible) experimental designs, a more compact and intuitive representation of the different possibilities than an unsorted list seems favorable. Each element of L_Σ can be interpreted as |η_R| subsequent (ordered) choices of outputs leading to an insulating modularization, and each sequence of choices not represented by an element in L_Σ as not leading to a modularization. Similar to binary functions represented by a truth table, our multivariate function defining whether a given output-labeling function leads to an insulating modularization can be compactly represented by a so-called reduced ordered multiple-valued decision diagram (ROMDD, see Srinivasan et al. (38) and Miller (39)), a rooted directed acyclic graph with a minimal number of vertices for a given order of variables (see Fig. 2). The diagram is traveled from the root to the leaves. In our case, the outgoing edges represent all possible choices that a given output label, represented by the current non-leaf vertex, can be assigned to. Finally, the leaves of an ROMDD depict whether a given labeling function, represented by the directed path from the root to the respective leaf, leads to a case of strict, simple, or no modularization. For our purposes, we adjusted the algorithm for the construction and modification of ROMDD presented in Miller and Drechsler (40) to handle decisions with more than four-valued variables.

The ROMD diagram of the example network (Fig. 2) and the six corresponding modularizations (Fig. 3) illustrate several important properties of our modularization approach:

• 1.The choice of an output for one module depends on the choice of all others, e.g., measuring species S₆ requires measuring species S₃, too.
• 2.Not all species and reactions belong to a module, such as species S₇ and reaction R₁₁.
• 3.Modules might overlap; species S₄ and reaction R₆, for example, can belong to more than one module.
• 4.The same species might be measured in different modularizations to identify the existence of distinct low-confidence reaction such as, for example, species S₉.
• 5.Our modularization approach can work for highly connected networks with a substantial number of bidirectional interactions.

JAK2/STAT5 signaling

In a recent study, Bachmann et al. (7) analyzed the possibility for the existence of a dual feedback mechanism in JAK2/STAT5 signaling, and its implications for the dynamic response to external Epo stimulation. Based on their results, they proposed an ordinary differential equation model composed of 26 states and 36 reactions. With several well-designed experiments, Bachmann et al. (7) could show the existence of the feedbacks, and identify most of their model’s parameters. Here, we put ourselves in the position of a researcher having developed a hypothetical network structure represented by the model (7), but who is unaware of the experiments that were performed to validate this structure. In this thought-experiment, we use our modularization approach to propose experimental designs to prove or disprove the existence of the (assumed) low-confidence dual feedback mechanism.

We imported the Systems Biology Markup Language (SBML) description of the JAK2/STAT5 signaling model (7) from the BioModels Database (41) and automatically generated its respective species-reaction graph (Fig. 4). Subsequently, we labeled the reactions corresponding to the dual feedback loop as being of low confidence. Specifically, this labeling includes the following interactions:

• 1.CIS and SOCS3 production rates are under transcriptional control of activated and nuclear localized STAT5 (reactions R₁₇ and R₂₇);
• 2.SOCS3 and CIS inhibit STAT5 activation by the Epo receptor complex (R₁₄); and
• 3.Phosphatase activity of SHP-1 requires prior binding to an Epo receptor with phosphorylated residue Tyr⁴²⁹ (R₁₁).

The last hypothesis (see also Klingmüller et al. (42)) was included although it is not essential for the dual feedback mechanism. Reactions R₁₁, R₁₄, R₁₇, and R₂₇ also represent other molecular interactions and dependencies than the stated ones. Consequently, nonexistence of a described interaction would only imply modification, but not a complete removal of the respective low-confidence reaction. A strict insulating modularization guarantees that the measured outputs are insulated from all other low-confidence reactions except their corresponding ones for all models with arbitrarily reduced complexity of the low-confidence reactions (see Lemma 7). However, to preserve integrity, we also include simple modularizations in the following analysis.

Figure 4.

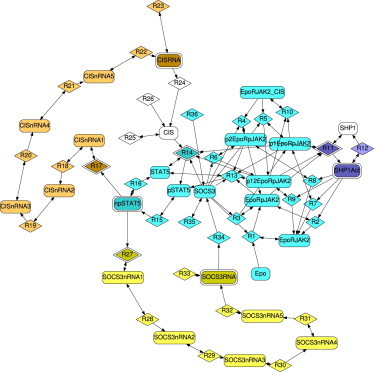
Example insulating modularization for the JAK2/STAT5 signaling network. The graphical notation corresponds to Fig. 3 (open for no module). Graph drawn with GRAPHVIZ (43). To see this figure in color, go online.

Using a nonoptimized MATLAB (The MathWorks, Natick, MA) implementation of our branch-and-bound algorithm (see the Supporting Material) to solve this modularization problem (26 states and 36 reactions, of which 4 were marked to be low-confidence) resulted in a total of 147 possible insulating modularizations, of which 98 are strict, in reasonable computational time (<4 s on an Intel Core 2 Duo, 3.16 GHz, 4 GB RAM). In contrast to the example network above, the ROMDD (Fig. 5) shows that all measured outputs can be chosen independently. Only measuring phosphorylated nuclear or cytosolic STAT5 concentrations leads to strict modularizations; measuring nonphosphorylated STAT5 concentrations results in simple modularizations. This is because conservation of the total STAT5 concentration is only implicitly modeled (7) and, thus, not considered by our algorithm. Furthermore, to simplify analysis, Bachmann et al. (7) used artificial intermediate mRNA species (SOCS3nRNA1–5 and CISnRNA1–5) to emulate transcriptional delays. Again, our algorithm is agnostic of the specific modeling approach and it consequently proposes to measure the artificial species. However, it is straightforward to exclude these artifacts before or after applying our modularization algorithm, and several other insulating modularizations remain.

Figure 5.

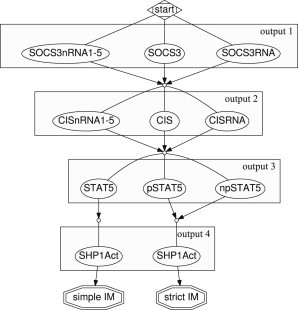
Reduced ordered multiple-valued decision diagram representing possible choices of tuples of suitable outputs to identify the low-confidence reactions in the JAK2/STAT5 pathway example. Conveniently, decisions representing the intermediate artificial mRNA species (SOCS3nRNA1–5 and CISnRNA1–5, respectively) were combined. Graph drawn with GRAPHVIZ (43).

Remarkably, the strict insulating modularization shown in Fig. 4 requires us to measure SOCS3 and CIS mRNA concentrations, phosphorylated nuclear STAT5, and activated SHP-1. In Bachmann et al. (7), the authors measured CIS and SOCS3 expression profiles as well as the phosphorylation state of STAT5 over time, noting that several parameters in their model were not identifiable due to missing quantifications of (relative) SHP-1 activation levels. Thus, except for the SHP-1 module, their experiments were sufficient to modularize the JAK2/STAT5 signaling network using our approach, and to validate the different reactions comprising the proposed dual feedback mechanism separately. We believe that this shows that the freedom of choice our modularization approach offers by not only returning one, but several solutions in an easily comprehensible visual way, is essential to make an otherwise purely theoretical approach experimentally feasible.

Discussion

Our modularization approach to split a biomolecular network into several, smaller modules differs in four main aspects from previous approaches:

• 1.Our modules have a practical meaning: a modularization directly instructs on which species should be experimentally measured to confirm or reject hypothetical reactions in a cellular network. Our approach thus shows a close relationship between modularization and experimental design, whereas most other modularization methods serve mainly to sort and visualize already available information.
• 2.Our modules can overlap each other and the union of all modules is not required to reconstitute the original network. The opposite requirements of other approaches seem intuitively reasonable, but they often lead to rather complex interfaces and so-called leftover or “scraggy” modules. Reactions and species unassigned to modules by our algorithm do not help in experimental design; requiring modules to contain unnecessary vertices would pose additional constraints on how the necessary vertices can be distributed.
• 3.Our approach can fail (return an empty set of possible modularizations) or give more than one solution. We believe that being able to fail is advantageous. Other methods returning modules for any given network structure leave the experimenter with the question of whether to trust the result, and relative quality indicators do not help in this regard. In contrast, representing all possible modularizations in a condensed and intuitive way as by the ROMDDs leaves the experimenter the freedom to select a set of outputs to implement.
• 4.Our approach is compatible with any modeling technique that describes which species influence each other (such that an adjacency matrix can be defined for a species-reaction graph). This applies to practically all contemporary modeling techniques that aim to represent real-world biomolecular networks, such as ordinary differential equations, stochastic representations, Boolean networks, and graphical models.

Note that we assume that outputs can be measured with sufficient precision and temporal resolution. In reality, all measurement methods are noisy and have limited temporal resolution. Thus, when using measured outputs as virtual inputs for our modules, the respective models will necessarily experience different input signals than the real-world networks. We expect that methods that quantify the agreement between a model and a real-world system, and which are able to deal with reasonable amounts of input noise, will also cope with measurement noise in our virtual inputs.

Future research might extend and adjust our approach, for instance, by increasing the amount of information used during the modularization—at the cost of restrictions to certain modeling techniques. One could use stoichiometric information, or tightly combine our approach with Bayesian analysis to further specify the experimental design in terms of type and the parameters of hypothetical reactions. We intentionally did not pursue these avenues here, to preserve the general applicability of our method. Furthermore, one could relax the requirement that each low-confidence reaction should be identifiable completely independently. In this case, Eq. 6 should result in lower triangular matrices (for a given order of low-confidence reactions) instead of diagonal matrices with nonzero diagonal elements. The existence of the first low-confidence reaction could then still be identified independently, and one could iterate over the remaining low-confidence reactions using this information. However, this modification would be prone to error propagation.

Finally, measuring a higher number of outputs than the number of low-confidence reactions in the network would help to ensure identifiability, verify the conclusions obtained by the outputs defining the modules, and—even more importantly—insulate the modules from each other. Thus, even when modularization as presented here fails, the principal idea of the approach could still be employed. Conversely, it would be possible to extend our approach to allow for more than one low-confidence reactions in each module. Thus, by accepting a certain small (exponential) increase in the number of candidate models per module, the number of outputs that are necessary to be implemented experimentally could be significantly decreased.