Statistical Methods for Integrating Multiple Types of High-Throughput Data

Abstract

Large-scale sequencing, copy number, mRNA, and protein data have given great promise to the biomedical research, while posing great challenges to data management and data analysis. Integrating different types of high-throughput data from diverse sources can increase the statistical power of data analysis and provide deeper biological understanding. This chapter uses two biomedical research examples to illustrate why there is an urgent need to develop reliable and robust methods for integrating the heterogeneous data. We then introduce and review some recently developed statistical methods for integrative analysis for both statistical inference and classification purposes. Finally, we present some useful public access databases and program code to facilitate the integrative analysis in practice.

1. Introduction

With the unprecedented amount of information from high-throughput experiments, such as gene expression microarrays, protein–protein interactions, large-scale sequencing, genome-wide copy number information, and genome–wide DNA–protein binding maps, there is an urgent need to develop reliable and robust methods for integrating these heterogeneous data to generate systematic biological insights into states of cells, mechanisms of disease, and treatments. Integrating diverse sources of data can not only increase statistical power of data analysis, but also provide deeper biological understanding. Concrete efforts have been made to study the best ways to collect, store, and distribute these data. This chapter will focus on the statistical methods to improve the power of identifying meaningful biological findings by integrating different types of data efficiently. We will introduce the problem by giving two examples and then discuss several statistical methods.

2. Examples

2.1. Gene Expression Regulation

Gene expression is a process of “the full use of the information in a gene via transcription and translation leading to production of a protein and hence the appearance of the phenotype determined by that gene” (1). The gene expression process determines the intra-cellular concentration of proteins, which play an important role in many biological systems. On the other hand, the gene expression procedure is controlled by certain proteins (regulators) in an organized way. Transcriptional control is a critical step in regulation of gene expression. Understanding such a control on a genomic level involves deciphering the mechanisms and structures of regulatory programs and networks, which will facilitate understanding the ways organisms function and respond to environmental signals. Answers to these questions will facilitate basic biology and medical research, leading to applications in clinical diagnosis and finding new treatments for diseases.

Gene regulation is a complicated biology process, and we will describe some basic steps of the process. First, cells get input signals from their environment. Second, through many signaling pathways, some transcription factors (TFs) are activated. Third, the TFs bind to the target genes’ cis-regulatory DNA sequence. Finally, the binding of TFs and their cis-regulatory DNA sequence control the expression level of the target genes. A critical element of understanding the gene regulation is to identify which genes are target genes of a specific TF. There are two ways to answer this question: (1) A direct way is to investigate which DNA sequences that a TF is binding to. A chromatin immunoprecipitation microarray experiment (CHIP-chip or genome-wide location experiment) (2, 3) could be used to detect the genome-wide target DNA sequences that are bound by specific proteins. (2) An indirect way is to investigate which genes express differently under the condition of with and without the appearance of TFs. Global expression profiles by microarray experiments could be used for this purpose. DNA sequence information is also very important to identify the target genes.

All of global expression profiles (indirect way), genome-wide location data (direct way), and DNA sequence data play important roles in constructing regulatory networks, but none of them can accurately get the whole picture alone. Using expression profiles alone cannot discriminate direct targets of the transcription factors from indirect downstream effects, all of which are observed if expression profiles alone are analyzed (4). On the other hand, using genome-wide location data, we can identify the binding sites of a (TF), suggesting the transcription factor may have regulatory effects on the gene, but it is possible that the (TF) does not fully or even partially regulate the gene at the time (5). Also, DNA sequence data can provide information about potential binding affinities of each gene to the TF, but potential binding does not necessarily mean that sequence will be bound and regulated by TF in vivo. More importantly, because of the high noise–signal ratio nature of the high-throughput data, there is limited statistical power to identify the TF binding targets using only one source of data alone. Thus, integrating these heterogeneous and independently obtained data can improve the detection power and is a key step to understand the complete mechanism of transcriptional regulation and the form of regulatory networks (2-6).

On the other hand, how to integrate diverse types of genomic data in an efficient way is still a challenge problem in the current bioinformatics research. In this chapter, we will review some existing methods to address this question.

2.2. Cancer Prognosis

Cancer prognosis predicts the course and outcome of cancer, that is, the chance that a patient will recover or have a recurrence (return of the cancer). Traditionally, cancer prognosis largely depends on clinical information such as the type and location of the cancer, the stage and grade of the disease, the patient’s age and general health. Recently, patient’s molecular profiles have been increasingly used to predict cancer prognosis. Shedden et al. (7) showed that genome-wide expression profile can improve the prediction of lung cancer recurrence compared to clinical prognostic factors. The molecular profiles used for cancer prognosis will be extended to protein expression profiling, miRNA profiling, DNA copy number profiling, potentially large-scale tumor genomic sequencing such as for specific oncogene mutations. This information will be coupled with germ line DNA polymorphism analysis which now can evaluate about 106 polymorphisms at one time, some of which identify inter-individual variation that could provide prognostic information as well as response to therapy and toxicity prediction. Also some groups are using serum proteomic and antibody profiles for early cancer detection, prognosis, and predicting response to specific therapies. Xie and Minna (8) described how to use molecular profiles to facilitate the prediction for lung cancer patients. With such large amounts of high-throughput data, there is an urgent need for statistical methods to integrate these information for cancer prognosis.

3. Integrative Approach for Statistical Inference

3.1. Using Shrinkage Approach to Incorporate Prior Information

Shrinkage methods have been widely used in classification and prediction (9-11). The motivation is more from the point of a better bias-variance trade-off. It serves as a “de-noising” procedure that reduces the variance (with a possible increase of bias) and therefore results in the improved prediction performance. Besides the good empirical performance, shrinkage methods can be also justified from a Bayesian point of view (12, 13). Xie et al. (14) considered a use of shrinkage in the context of hypothesis testing, such as detecting differential gene expression for expression data or DNA–protein binding sites for genome-wide location data. An advantage of the method is that we can incorporate prior biological knowledge, for example, in detecting differential gene expression for thousands of genes, in many applications we know a priori that most of the genes will be equally expressed (EE); use of this prior knowledge can be accomplished by shrinking the test statistics of those genes believed a priori to be EE toward their null values (i.e., expected values under the null hypothesis of EE). Furthermore, we can also take advantage of the existence of other sources of data.

To illustrate the shrinkage method, Xie et al. (14) used a SAM-t (statistical analysis of microarray) statistic to analyze microarray data (15, 16), but other more elaborate statistical methods, such as the nonparametric empirical Bayes method (17), SAM (18), and the mixture model method (16), can be also implemented. A statistical analysis method can be similarly applied to either genome-wide location data or gene expression data. A difference is that we are only interested in the enriched spots in location data whereas both up and down expressed genes are of interest in gene expression data. Hence, we will use a one-sided test for genome-wide location data, rather than a two-sided test commonly taken for gene expression data. Specifically, for any given d > 0, we claim any gene i satisfying Z_i > d to be significant, and we estimate the total positive (TP) numbers as

$$\widehat{\mathrm{TP}}(\mathrm{d})=\#\{i:Z_i>d\}.$$

If there are total G₁ genes with true positives, the sensitivity and specificity are

$$\mathrm{sens}(d)=\mathrm{TP}(d)/G_1,\mathrm{spec}(d)=1-\mathrm{FP}(d)/(G-G_1),$$

where TP and FP are the numbers of total positives and true false positives, respectively.

The true/observed false discovery rate (FDR) (19, 20) and its estimate are

$$\mathrm{FDR}(d)=\mathrm{FP}(d)/\widehat{\mathrm{TP}}(d),\widehat{\mathrm{FDR}}(d)=\widehat{\mathrm{FP}}(d)/\widehat{\mathrm{TP}}(d),$$

where $\widehat{\mathrm{FP}}(d)$ is the estimated false positive number. A standard way to estimate FP is

$$\widehat{\mathit{FP}}(d)=\sum _{b=1}^B\#\{i:z_i^{(b)}>d\}/B,$$

where $z_i^{(b)}$ is the test statistic calculated from the bth permutated data set and B is the total number of permutations. This standard method may overestimate FP (16), and furthermore, the magnitude of induced bias may depend on the test statistic being used (21). Hence, it is not appropriate to use the resulting FDR estimates to evaluate different statistics. In this chapter, we will use a modified method proposed by Xie et al. (21) to estimate FP. The idea is quite simple: the overestimation of the standard method is mainly caused by the existence of target genes; if we use only the predicted non-target genes to estimate the null distribution, it will reduce the impact of target genes and improve the estimation of FP. Specifically, we use only non-significant genes to estimate FP:

$$\widehat{\mathrm{FP}}(\mathrm{d})=\sum _{b=1}^B\#\{i:z_i^{(b)}>d\&Z_i>d\}/B.$$

Xie et al. (21) gave more detailed descriptions and justifications for this method. In testing a null hypothesis, a false rejection occurs because just by chance the test statistic value (or its absolute value) is too large. Hence, if we know a priori that the null hypothesis is likely to be true, we can shrink the test statistic (or its absolute value) toward zero, which will reduce the chance of making a false positive. In the current context, among all the genes, suppose that based on some prior information we can specify a list of genes for which the null hypothesis is likely to hold, thus their test and null statistics are to be shrunken. If gene i is in the list, then for a given threshold value s, its test and null statistics are shrunken:

$$Z_i(s)=\mathrm{sign}(Z_i){(|Z_i|-s)}_{+},z_i^{(b)}(s)=\mathrm{sign}(z_i^{(b)}){(|z_i^{(b)}|-s)}_{+},$$

where f₊ = f if f > 0 and f₊ = 0 if f ≤ 0. On the other hand, if gene i is not in the list, then Z_i(s) = Z_i and $z_i^{(b)}(s)=z_i^{(b)}$.

We proceed as before to draw statistical inference using Z_i(s) and $z_i^{(b)}(s)$. The shrinkage method we use is called soft thresholding (22, 23), in contrast to the usual hard thresholding. In the hard thresholding, when |Z_i| is larger than s, the new statistic will remain unchanged, rather than be shrunken toward zero by the amount of s as the soft thresholding does. This property makes the statistics generated by the hard thresholding “jumpy,” since as the threshold s increases, the statistics of some genes may suddenly jump from zero to their original values.

How many genes to shrink and how much to shrink are important parameters to be determined in data analysis. Xie et al. (14) proposed taking multiple trials using various parameter values and then using estimated FDR as a criterion to choose the optimal parameter values. It has been shown to work well. In practice, we suggest to use area under curve (AUC) as a measurement to compare estimated FDRs and tune the parameter. Specifically, we try different s values, for example, s = 0, 0.2, 0.4, and 0.6. For each s value, we estimate FDRs for different number of total positive genes and then make a plot of FDR vs. the number of total positive genes. So we can get one curve for each s value, and then calculate AUC for each curve. We will choose s value with lowest AUC as the optimal parameter value.

The idea of using shrinkage to combine two data sets is simple: in the example with gene expression data and DNA–protein binding data, first, we use the expression data to generate a prior gene list where the genes are more likely to be “non-target” of the protein; and then we shrink the statistics of these genes toward null values in the binding data analysis. We treat all the genes in the gene list equally; this simplicity makes the shrinkage method flexible and thus applicable to combining various types of data or prior knowledge. For example, if we can generate a list of genes for which the null hypothesis is more likely to hold based on a literature review or some relevant databases, such as Gene Ontology (GO), then we can incorporate this prior information into the following analysis by using our proposed shrinkage method. An alternative way of a combined analysis is to make the amount of shrinkage for each gene depend on the probability of that gene in the gene list (or equivalently, on the amount of statistical evidence of rejecting the null hypothesis for the gene based on prior information): the higher probability, the more we will shrink it toward zero. This method can possibly use the prior information more efficiently, but it also requires a stronger link and association between the two sources of data; otherwise, it may not perform well.

Xie et al. (14) illustrated that the quality of the prior gene list influenced the amount of shrinkage we should have and the final performance of the shrinkage method. The more the gene list agrees with the truth, the larger amount of shrinkage should be taken, and the better the shrinkage method performs. On the other hand, when the gene list is very unreliable, any shrinking does not help. This phenomenon is consistent with the general Bayesian logic: how much information we should use from the prior knowledge (i.e., the gene list here) depends on the quality of the prior knowledge; if the prior knowledge is very vague, then we should use flat prior (here s = 0) so that the posterior information comes largely or only from the data itself.

3.2. Incorporate Gene Pathway and Network Information for Statistical Inference

Gene functional groups and pathways, such as the Kyoto Encyclopedia of Genes and Genomes (KEGG) pathways (24), play critical roles in biomedical research. Recently, genome-wide gene networks, represented by undirected graphs with genes as nodes and gene–gene interactions as edges, have been constructed using high-throughput data. Lee et al. (25) constructed functional networks for the yeast genome using a probabilistic approach. Franke et al. (26) constructed a human protein–protein interaction network. It is reasonable to assume that the neighboring genes in a network are more likely to share biological functions and thus to participate in the same biological processes, therefore, their expression levels are more likely to be similar to each other. Some recent work has attempted to incorporate genome-wide gene network information into statistical analysis of microarray data to increase the analysis power. Wei and Li (27) proposed integrating KEGG pathways or other gene networks into analysis of differential gene expression via a Markov random field (MRF) model. In their model, the state of each gene was directly modeled via a MRF.

Spatial statistical models have been increasingly used to incorporate other information into microarray data analysis. Xiao et al. (28) applied a hidden Markov model to incorporate gene chromosome location information into gene expression data analysis. Broet et al. (29) applied a spatial mixture mode to introduce gene-specific prior probabilities to analyze comparative genomic hybridization (CGH) data. Wei and Pan (30) extended the work of Broet et al. from incorporating one-dimensional chromosome locations to two-dimensional gene network. They utilized existing biological knowledge databases, such as KEGG pathways, or computationally predicted gene networks from integrated analysis (25), to construct gene functional neighborhoods and incorporating them into a spatially correlated normal mixture model. The basic rationale for their model is that functionally linked genes tend to be co-regulated and co-expressed, which is thus incorporated into analysis. This is an efficient way to incorporate network information into statistical inference and we will introduce their method in this section.

3.2.1. Standard Normal Mixture Model

We want to identify binding targets or differentially expressed genes in this analysis. We will use latent variable T_i to indicate whether gene i is true binding target (or differently expressed) gene. Suppose that the distribution functions of the data (e.g., Z-score) for the genes with T_i = 1 and T_i = 0 are f₁ and f₀, respectively. Assuming that a priori all the genes are independently and identically distributed (iid), we have a marginal distribution of Z_i as a standard mixture model:

$$f(z_i)={\pi }_0{f}_0(z_i)+(1-{\pi }_0)f_1(z_i),$$ [1]

where π₀ is the prior probability that H_0,i (null hypothesis) holds. It is worth noting that the prior probabilities are the same for all genes. The standard mixture model has been widely used in microarray data analysis (17, 31-33).

The null and non-null distributions f₀ and f₁ can be approximated by finite normal mixtures: $f_0={\sum }_{k_0=1}^{K_0}{\pi }_{0k_0}\varphi ({\mu }_{k_0},{\sigma }_{k_0}^2)$ and $f_1={\sum }_{k_1=1}^{K_1}{\pi }_{1k_1}\varphi ({\mu }_{k_1},{\sigma }_{k_1}^2)$, where ϕ(μ, σ²) is the density function for a Normal distribution with mean μ and variance σ². For Z-score, using K_j = 1 often suffices (33). Wei and Pan (30) demonstrated that K₀ = 2 and K₁ = 1 worked well in most cases. The standard mixture model can be fitted via maximum likelihood with the Expectation-Maximization (EM) algorithm (34). Once the parameter estimates are obtained, statistical inference is based on the posterior probability that H_1,i (alternative hypothesis) holds: Pr(T_i = 1∣z_i) = π₁f₁(z_i)/f(z_i).

3.2.2. Spatial Normal Mixture Model

In a spatial normal mixture model, Wei and Pan (30) introduced gene-specific prior probabilities π_i,j = Pr(T_i = j) for i = 1,…, G and j = 0, 1. The marginal distribution of z_i is

$$f(z_i)={\pi }_{i,0}{f}_0(z_i)+{\pi }_{i,1}{f}_1(z_i),$$ [2]

where f₀(z_i) and f₁ (z_i) represent density distributions under null and alternative hypotheses, respectively. Note that the prior probability specification in a stratified mixture model (35, 36) is a special case of Equation [2]: a group of the genes with the same function share a common prior probability while different groups have possibly varying prior probabilities; in fact, a partition of the genes by their functions can be regarded as a special gene network.

Based on a gene network, the prior probabilities π_i,j are related to two latent Markov random fields x_j = {x_i,j;i = 1,…, G} by a logistic transformation:

$${\pi }_{i,j}=\exp (x_{i,j})/[\exp (x_{i,0})+\exp (x_{i,1})].$$

Each of the G-dimensional latent vectors x_j is distributed according to an intrinsic Gaussian conditional autoregression model (ICAR) (37). One key feature of ICAR is the Markovian interpretation of the latent variables’ conditional distributions: the distribution of each spatial latent variable x_i,j, conditional on x_(−i),j = {x_k,j;k ≠ i}, depends only on its direct neighbors. More specifically, we have

$$x_{i,j}\mid x_{(-i),j}~N\left(\frac{1}{m_i}\sum _{l\in {\delta }_i}{x}_{l,j},\frac{{\sigma }_{C_j}^2}{m_i}\right),$$

where δ_i is the set of indices for the neighbors of gene i, and m_i is the corresponding number of neighbors. To allow identifiability, they imposed Σ_i x_ij = 0 for j = 0, 1. In this model, the parameter ${\sigma }_{Cj}^2$ acts as a smoothing prior for the spatial field and consequently controls the degree of dependency among the prior probabilities of the genes across the genome: the smaller ${\sigma }_{Cj}^2$ induces more similar π_i,j’s for those genes that are neighbors in the network.

3.3. Joint Modeling Approaches for Statistical Inference

Now we will discuss a joint modeling approach to integrate different sources of data. The benefit of joint modeling is that it can potentially improve the statistical power to detect target genes. For example, a gene may be supported in each source of data with some but not overwhelming evidence to be a target gene; in other words, this gene will not be identified as statistically significant based on either source of data, however, by integrating different sources of data in a joint model, the gene may be found to be significant. Pan et al. (38) proposed a nonparametric empirical Bayes approach to joint modeling of DNA–Protein binding data and gene expression data. The simulated data shows the improved performance of the proposed joint modeling approach over that of other approaches, including using binding data or expression data alone, taking an intersection of the results from the two separate analyses and a sequential Bayesian method that inputs the results of analyzing expression data as priors for the subsequent analysis of binding data. Application to a real data example shows the effects of the joint modeling. The nonparametric empirical Bayes approach is attractive due to its flexibility. Xie (39) proposed a parametric Bayesian approach to jointly modeling DNA–protein binding data (ChIP-chip data), gene expression data and DNA sequence data to identify the binding target genes of a transcription factor. We will focus on this method here.

3.3.1. Analyzing Binding Data Alone

We use a Bayesian mixture model (40) to analyze binding data. Specifically, suppose X_ij is the log ratio of the intensities of test and control samples in ChIP-chip experiment for gene i (i = 1, …, G) and replicate j (j = 1, …, K). We specify the model as following:

$$\begin{array}{ccc}\hfill X_{\mathit{ij}}\mid {\mu }_{\mathit{ix}}& \stackrel{\mathit{iid}}{~}& N({\mu }_{\mathit{ix}},{\sigma }_{\mathit{ix}}^2),\hfill \\ \hfill {\mu }_{\mathit{ix}}\mid I_{\mathit{ix}}=0& \stackrel{\mathit{iid}}{~}& N(0,{\tau }_{0x}^2),\hfill \\ \hfill {\mu }_{\mathit{ix}}\mid I_{\mathit{ix}}=1& \stackrel{\mathit{iid}}{~}& N({\mathrm{\lambda }}_x,{\tau }_{1x}^2),\hfill \\ \hfill I_{\mathit{ix}}\mid p_x& \stackrel{\mathit{iid}}{~}& \mathrm{Ber}(p_x),\hfill \end{array}$$

where μ_ix is the mean of log ratio for gene i; I_ix is an indicator variable: I_ix = 0 means the gene i being non-binding target gene and I_ix = 1 means gene i being binding target gene. We assume that the mean log ratios of non-target genes concentrate around 0 with small variance ( ${\tau }_{0x}^2$), while the expected mean log ratios of target genes follow a normal distribution with a positive mean. The prior distribution for indicator I_ix is a Bernoulli distribution with probability p_x. The advantage of this hierarchical mixture model is that we can borrow information across genes to estimate the expected mean intensity, and we can use the posterior probability of being a binding target gene directly to do inference.

3.3.2. Joint Modeling

Similar to binding data, we used mixture models to fit expression data ϒ_ij and sequence data z_i. For expression data

$$\begin{array}{ccc}\hfill {\Upsilon }_{\mathit{ij}}\mid {\mu }_{\mathit{iy}}& \stackrel{\mathit{iid}}{~}& N({\mu }_{\mathit{iy}},{\sigma }_{\mathit{iy}}^2),\hfill \\ \hfill {\mu }_{\mathit{iy}}\mid I_{\mathit{iy}}=0& \stackrel{\mathit{iid}}{~}& N(0,{\tau }_{0y}^2),\hfill \\ \hfill {\mu }_{\mathit{iy}}\mid I_{\mathit{iy}}=1& \stackrel{\mathit{iid}}{~}& N({\mathrm{\lambda }}_y,{\tau }_{1y}^2),\hfill \\ \hfill {\mu }_{\mathit{iy}}\mid I_{\mathit{iy}}=2& \stackrel{\mathit{iid}}{~}& N(-{\mathrm{\lambda }}_y,{\tau }_{1y}^2),\hfill \\ \hfill I_{\mathit{iy}}\mid I_{\mathit{ix}}=0& \stackrel{\mathit{iid}}{~}& \mathrm{Multinomial}(p_{y00},p_{y10},p_{y20}),\hfill \\ \hfill I_{\mathit{iy}}\mid I_{\mathit{ix}}=1& \stackrel{\mathit{iid}}{~}& \mathrm{Multinomial}(p_{y01},p_{y11},p_{y21}),\hfill \end{array}$$

where I_iy is a three-level categorical variable: I_iy = 0 indicates an equally expressed gene, I_ij = 1 represents an up-regulated gene, and I_ij = 2 means a down-regulated gene. Here we used conditional probabilities to connect the binding data and the expression data. Intuitively, the probability of being equally expressed for a non-binding target gene, p_y00, should be higher than the probability of being equally expressed for a binding target gene, p_y01. The difference between the conditional probabilities measures the correlation between the binding data and the expression data. If the two data sets are independent, the two sets of conditional probabilities will be the same. Therefore, this model is flexible to accommodate the correlations between data.

Similarly, we model the sequence data as

$$\begin{array}{l}{z}_i\mid I_{\mathit{iz}}=0\stackrel{\mathit{iid}}{~}N({\mathrm{\lambda }}_{z1},{\tau }_{1z}^2),\\ z_i\mid I_{\mathit{iz}}=1\stackrel{\mathit{iid}}{~}N({\mathrm{\lambda }}_{z2},{\tau }_{2z}^2),\\ I_{\mathit{iz}}\mid I_{\mathit{ix}}=0\stackrel{\mathit{iid}}{~}\mathrm{Ber}(p_{z0}),\\ I_{\mathit{iz}}\mid I_{\mathit{ix}}=1\stackrel{\mathit{iid}}{~}\mathrm{Ber}(p_{z1}),\end{array}$$

where I_iz = 1 indicates gene i being potential target gene based on sequence data, we will call it a potential gene; and I_iz = 0 means gene i being a non-potential gene.

Figure 19.1 gives a graphical overview of this model. In summary, the model combines expression data and sequence data with binding data through the indicator variables. This model can automatically account for heterogeneity and different specificities of multiple sources of data. The posterior distribution of being a binding target can be used to explain how this model integrates different data together. For example, if we combine binding and expression data, the posterior distribution of being a binding target gene I_ix is

$$\begin{array}{ccc}\hfill I_{\mathit{ix}}\mid ·& ~& \mathit{Ber}(p_{\mathit{ix}}),\hfill \\ \hfill p_{\mathit{ix}}& =& \frac{A}{A+B},\hfill \\ A& =& p_x{({\tau }_{1x}^2)}^{-\frac{1}{2}}\exp \left(-\frac{{({\mu }_{\mathit{ix}}-{\mathrm{\lambda }}_x)}^2}{2{\tau }_{1x}^2}\right)p_{y01}^{I_{\mathit{i\Upsilon }}=0}{p}_{y11}^{I_{\mathit{i\Upsilon }}=1}{p}_{y21}^{I_{\mathit{i\Upsilon }}=2}\hfill \\ B& =& (1-p_x){({\tau }_{0x}^2)}^{-\frac{1}{2}}\exp \left(-\frac{{\mu }_{\mathit{ix}}^2}{2{\tau }_{0x}^2}\right)p_{y00}^{I_{\mathit{i\Upsilon }}=0}{p}_{y10}^{I_{\mathit{i\Upsilon }}=1}{p}_{y20}^{I_{\mathit{i\Upsilon }}=2}.\hfill \end{array}$$

where I_ix∣· represents the posterior distribution of I_ix condition on all other parameters in the model and the data. We define $\overrightarrow{p_{y0}}=(p_{y00},p_{y10},p_{y20})$ and $\overrightarrow{p_{y1}}=(p_{y01},p_{y11},p_{y21})$. If the expression data do not contain information about binding, then $\overrightarrow{p_{y0}}=\overrightarrow{p_{y1}}$, which makes all the terms containing ϒ in the formula canceled out. In this case, only information contained in binding data X is used to do inference. On the other hand, the difference between $\overrightarrow{p_{y0}}$ and $\overrightarrow{p_{y1}}$ will be big when expression data contain information about binding. In this case, the information in expression data I_iϒ will also be used to make inference.

Fig. 19.1.

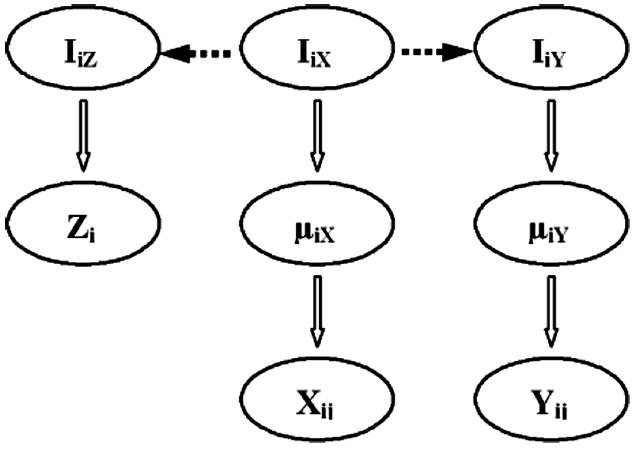
The graphical overview of the hierarical structure of the joint model.

3.3.3. Statistical Inference

Assuming that the binding, expression, and sequence data are conditionally independent (condition on the indicator I_ix), we can get the joint likelihood for the model. Based on the joint likelihood, we can obtain the closed form of full conditional posterior distribution for most of the parameters (except λ_x, λ_y, and d_z). Gibbs sampler was used to do Markov Chain Monte Carlo simulations for the parameters having the closed form. For λ_x, λ_y, and d_z, Metropolis–Hastings algorithm was applied to draw the simulation samples. The iterations after burn-in samples were used as posterior simulation samples and were used for statistical inferences.

3.3.4. The Effects of Joint Modeling

Xie (39) illustrated that when using the binding data alone, the estimated posterior probabilities were positively associated with the mean binding intensities from binding data. In this model, the posterior probability does not depend on the expression data or sequence data. On the other hand, after doing the joint modeling, the posterior probabilities of the genes with high expression values have been increased compared to using binding data alone, but the sequence score did not have much influence on the inference for this data. In summary, this model can automatically account for heterogeneity and different specificity of multiple sources of data. Even if an addition data type does not contain any information about binding, the model can be approximated to that of using binding data alone.

4. Integrative Analysis for Classification Problem

Statistical classification methods, such as support vector machine (SVM) (41), random forest (42) and Prediction Analysis for Microarrays (PAM) (9), have been widely used for diagnosis and prognosis of breast cancer (10, 43), prostate cancer (44, 45), lung cancer (7, 46), and leukemia (47). Meanwhile, biological functions and relationships of genes have been explored intensively by the biological research community, and those information has been stored in databases, such as those with the Gene Ontology annotations (48) and the Kyoto Encyclopedia of Genes and Genomes (24). In addition, as mentioned before, prior experiments with similar biological objectives may have generated data that are relevant to the current study. Hence, integrating information from prior data or biological knowledge has potential to increase the classification and prediction performance.

The standard classification methods treat all the genes equally a priori in the process of model building, ignoring biological knowledge of gene functions, which may result in a loss of their effectiveness. For example, some genes have been identified or hypothesized to be related to cancer by previous studies; others may be known to have the same function of or be involved in a pathway with some known/putative cancer-related genes, hence we may want to treat these genes differently from other genes a priori when choosing genes to predict cancer-related outcomes.

Some recent research has taken advantages of the prior information for classification problem. Lottaz and Spang (49) proposed a structured analysis of microarray data (StAM), which utilized the GO hierarchical structure. Biological functions of genes in GO hierarchal structure are organized as a directed acyclic graph: each node in the graph represents a biological function, and a child node has a more specific function while its parent node has a more general one. StAM first built classifiers for every leaf node based on an existing method, such as PAM, then propagated their classification results by a weighted sum to their parent nodes. The weights in StAM are related to the performance of the classifiers and a shrinkage scheme is used to shrink the weights toward zero so that a sparse representation is possible. This process is repeated until the results are propagated to the root node. Because the final classifier is built based on the GO tree, StAM greatly facilitates the interpretation of a final result in terms of identifying biological processes that are related to the outcome. StAM uses only genes that are annotated in the leaf nodes (i.e., with most detailed biological functions) as predictors, so it may miss some important predictive genes. Wei and Li (27) proposed a modified boosting method, non-parametric pathway-based regression (NPR), to incorporate gene pathway information into classification model. NPR assumed that the genes can be first partitioned into several groups or pathways, and only pathway-specific new classifiers (i.e., using only the genes in each of the pathways) were built for boosting procedure. More recently, Tai and Pan (50) proposed a flexible statistical method to incorporate prior knowledge of genes into prediction models. They adopted group-specific penalty terms in a penalized method allowing genes from different groups to have different prior distributions (e.g., different prior probabilities of being related to the cancer). Their model is similar to NPR with regard to grouping genes, but they apply to any penalized method through the use of group-specific penalty terms while NPR only applies to boosting. Garrett-Mayer et al. (51) proposed using meta-analytic approaches to combine several studies using pooled estimates of effect sizes.

5. Useful Databases and Program Code

5.1. Databases

In order to meet the urgent need of integrated analysis of high-throughput data, the National Institutes of Health (NIH) and the European Molecular Biology Laboratory (EMBL) have made concrete effort to build and maintain several large-scale and public-accessible databases. These databases are very valuable for both biomedical research and methodology development. We will introduce several of them briefly.

5.1.1. Array Express

Founded by EMBL, ArrayExpress is a public repository for transcriptomics data. It stores gene-indexed expression profiles from a curated subset of experiments in the repository. Public data in ArrayExpress are made available for browsing and querying on experiment properties, submitter, species, etc. Queries return summaries of experiments, and complete data or subsets can be retrieved. A subset of the public data is re-annotated to update the array design annotation and curated for consistency. These data are stored in the ArrayExpress Warehouse and can be queried on gene, sample, and experiment attributes. Results return graphed gene expression profiles, one graph per experiment.

Complete information about ArrayExpress can be found from the web site http://www.ebi.ac.uk/Databases/.

5.1.2. Gene Expression Omnibus (GEO)

Founded by National Center for Biotechnology Information (NCBI), GEO is a gene expression/molecular abundance repository supporting Minimum Information About a Microarray Experiment (MIAME) compliant data submissions and a curated, online resource for gene expression data browsing, query, and retrieval. Currently it has 2,61,425 data including 4,931 platforms 2,47,016 samples and 9,478 series. All data are accessible through the web site http://www.ncbi.nlm.nih.gov/geo/.

5.1.3. Oncomine

Founded by Drs. Arul Chinnaiyan and Dan Rhodes at the University of Michigan and currently maintained by Compendia Bioscience Company, the Oncomine Research Platform is a suite of products for online cancer gene expression analysis dedicated to the academic and non-profit research community.

Oncomine combines a rapidly growing compendium of 20,000+ cancer transcriptome profiles with an analysis engine and a web application for data mining and visualization. It currently includes over 687 million data points, 25,447 microarrays, 360 studies, and 40 cancer types. Oncomine access is available through the Oncomine Research Edition and the Oncomine Research Premium Edition. Information is available via the web site http://www.oncomine.org/main/index.jsp.

5.1.4. The Cancer Genome Atlas (TCGA)

Joint effort by the National Cancer Institute (NCI) and the National Human Genome Research Institute (NHGRI) of the NIH, TCGA is a comprehensive and coordinated effort to accelerate our understanding of the molecular basis of cancer through the application of genome analysis technologies, including large-scale genome sequencing. TCGA Data Portal provides a platform for researchers to search, download, and analyze data sets generated by TCGA. This portal contains all TCGA data pertaining to clinical information associated with cancer tumors and human subjects, genomic characterization, and high-throughput sequencing analysis of the tumor genomes. In addition, the Cancer Molecular Analysis Portal provides the ability for researchers to use analytical tools designed to integrate, visualize, and explore genome characterization from TCGA data. The following web site will lead to download TCGA data http://tcga-data.nci.nih.gov/tcga/.

5.2. WinBUGS Codes for Incorporating Gene Network Information into Statistical Inference

5.2.1. For a Three-Component Standard Normal Mixture Model

model
{
for (i in 1:N){
Z[i] ~dnorm(muR[i], tauR[i]) # z-scores
muR[i] <- mu[T[i]]
tauR[i] <- tau[T[i]]
T[i] ~dcat(pi[ ]) # latent variable (zero/negative/# postive components)
T1[i] <-equals(T[i], 1) ;T2[i] <-equals(T[i],2);
T3[i] <-equals(T[i],3);
}
# prior for mixing proportions
pi[1:3] ~ddirch(alpha[])
# priors (means of normal mixture components)
mu[1] <- 0 # zero component
mu[2] ~dnorm(0, 1.0E-6)I(a,0.0) # negative component
mu[3] ~dnorm(0, 1.0E-6)I(0.0,b) # positive component
# priors (precision/variance of normal mixture # components)
tau[1] ~dgamma(0.1, 0.1)
tau[2] ~dgamma(0.1, 0.1)
tau[3] ~dgamma(0.1, 0.1)
sigma2[1] <-1/tau[1]
sigma2[2] <-1/tau[2]
sigma2[3] <-1/tau[3]
}

5.2.2. For a Three-Component Spatial Normal Mixture Model

model
{
for(i in 1:N) {
Z[i] ~dnorm(muR[i], tauR[i]) # z-scores
muR[i] <- mu[T[i]]
tauR[i] <- tau[T[i]]
# logistic transformation
pi[i,1] <-1/(1+exp(x2[i]-x1[i])+exp(x3[i]-x1[i]))
pi[i,2] <-1/(1+exp(x1[i]-x2[i])+exp(x3[i]-x2[i]))
pi[i,3] <-1/(1+exp(x1[i]-x3[i])+exp(x2[i]-x3[i]))
T[i] ~dcat(pi[i,1:3]) # latent variable (zero/
# negative/postive components)
T1[i] <-equals(T[i],1) ;T2[i] <-equals(T[i],2);
T3[i] <-equals(T[i],3)
}
# Random Fields specification
x1[1:N] ~car.normal(adj[], weights[], num[], tauC[1])
x2[1:N] ~car.normal(adj[], weights[], num[], tauC[2])
x3[1:N] ~car.normal(adj[], weights[], num[], tauC[3])
# weights specification
for(k in 1:sumNumNeigh) { weights[k] <- 1 }
# priors (precision/variance for MRF)
tauC[1] ~dgamma(0.01, 0.01)I(0.0001,)
tauC[2] ~dgamma(0.01, 0.01)I(0.0001,)
tauC[3] ~dgamma(0.01, 0.01)I(0.0001,)
sigma2C[1] <- 1/tauC[1]
sigma2C[2] <- 1/tauC[2]
sigma2C[3] <- 1/tauC[3]
# priors (means of normal mixture components)
mu[1] <- 0 # zero component
mu[2] ~dnorm(0, 1.0E-6)I(a,0.0) # negative component
mu[3] ~dnorm(0, 1.0E-6)I(0.0,b) # positive component
# priors (precision/variance of normal mixture
# components)
tau[1]~dgamma(0.1, 0.1)
tau[2]~dgamma(0.1, 0.1)
tau[3]~dgamma(0.1, 0.1)
sigma2[1] <- 1/tau[1]
sigma2[2] <- 1/tau[2]
sigma2[3] <- 1/tau[3]
}