A Decision-Theory Approach to Interpretable Set Analysis for High-Dimensional Data

Summary

A key problem in high-dimensional significance analysis is to find pre-defined sets that show enrichment for a statistical signal of interest; the classic example is the enrichment of gene sets for differentially expressed genes. Here, we propose a new decision-theory approach to the analysis of gene sets which focuses on estimating the fraction of non-null variables in a set. We introduce the idea of “atoms,” non-overlapping sets based on the original pre-defined set annotations. Our approach focuses on finding the union of atoms that minimizes a weighted average of the number of false discoveries and missed discoveries. We introduce a new false discovery rate for sets, called the atomic false discovery rate (afdr), and prove that the optimal estimator in our decision theory framework is to threshold the afdr. These results provide a coherent and interpretable framework for the analysis of sets that addresses the key issues of overlapping annotations and difficulty in interpreting p-values in both competitive and self-contained tests. We illustrate our method and compare it to a popular existing method using simulated examples, as well as gene-set and brain ROI data analyses.

1. Introduction

Many modern scientific studies measure many variables on each sample. Examples include gene expression measurements on tens of thousands of genes from a microarray (Quackenbush, 2001) or intensities at hundreds of thousands of voxels in a functional magnetic resonance imaging (fMRI) study (Friston et al., 2007). One way of reducing the dimension of these data and simultaneously making results more interpretable is to analyze sets of pre-defined variables together as a unit. A particularly relevant example is gene-set analysis (Tavazoie et al., 1999; Mirnics et al., 2000; Bouton and Pevsner, 2002). In such analyses, sets of genes - known to be biologically related - are analyzed jointly for differential expression in a microarray experiment. Analogously, “region of interest” (ROI) analyses in fMRI analyze sets of voxels together that are known to be physically or functionally related (Maldjian et al., 2003).

In these examples, measurements are obtained for a collection of variables, or features, on multiple samples. The samples could either have recorded outcomes, belong to different experimental conditions, be paired (e.g. tumor-normal), or belong to a single group, which is being compared to some standard. A subset of these variables belong to one of a fixed number of pre-defined sets of variables. Sets may be defined by any known spatial, geographic, functional, or biological relationship between the variables. Many set-level analyses have as a goal finding sets that show “enrichment” for a statistical signal of interest, e.g. sets which have a large fraction of non-null variables. We thus often consider results in reference to the fraction of alternatives for each set. In practice, this quantity is unknown, but may be estimated. Enriched sets may be taken to have a fraction of alternatives higher than either a fixed value with a special meaning in the scientific context, or the overall fraction of alternatives in the entire experiment or study. The precise definition will depend on the specific problem of scientific interest. For example, in the analysis of a microarray experiment the goal may be to find the sets that are enriched for differentially expressed genes (Tavazoie et al., 1999). Set-level analyses are popular for three reasons: (1) they have the power to detect subtle but consistent statistical signal present in related variables (Mootha et al., 2003), (2) true differences may only exist at the set level (Parsons et al., 2008), and (3) findings may be easier to interpret than those pertaining to individual variables.

Despite these appealing characteristics, there are still a number of key difficulties in the statistical analysis of sets. One difficulty is that variables often belong to more than one set, which complicates simultaneous inference on the collection of all pre-defined sets. A second difficulty is that set-analysis is typically a secondary analysis performed based on single-variable analyses. However, the uncertainty in the variable-level analysis is often ignored or underestimated by set-analyses. Thirdly, most statistical methods for the analysis of sets are based on hypothesis testing (Goeman and Buhlmann, 2007; Efron and Tibshirani, 2007). They are divided by Goeman and Buhlmann (2007) into self-contained and competitive tests: The null hypothesis for a self-contained test is that all the variables in the set are from the null distribution, the alternative being that at least one of them is from the alternative distribution. The null hypothesis for a competitive test is that the variables in a given set S are at most as often non-null as the variables in the complement of S. Competitive tests result in a zero-sum problem where more significant variables in one set will conservatively bias the results for the remaining sets. Finally, p-values from hypothesis tests are not direct estimates of the quantity that is often of greatest interest in a set analysis, namely enrichment. This may result in p-values which are not comparable across sets of different sizes and different enrichment fractions. In this paper, we suggest a framework for high-dimensional set analysis which differs in two main ways from the approaches described above: 1) We propose the use of “atoms,” which are non-overlapping sets, and 2) We propose the use of a decision-theoretic framework, coupled with an Empirical Bayes estimation procedure.

Other Bayesian frameworks for set analysis have been proposed. Notably, Bauer et al. (2010) develops a model-based Bayesian network approach. However, to the best of our knowledge, our method is the first decision-theory based approach applied to set analysis.

2. Notation and Preliminaries

We denote the collection of variables on which measurements are obtained by ℳ= {1, 2, …, M}. In a high-dimensional study we often work with: (1) a matrix of high-dimensional data X, where the measurement for the mth variable, where 1 ≤ m ≤ M, on the jth sample corresponds to the (i, j) element of X; and (2) possibly a vector of assignments/outcomes Y for each sample (as the samples could be paired or considered in reference to some standard.)

One common approach in high-dimensional inference in genomics has been to use the two-groups model (Efron et al., 2001; Storey, 2002; Newton et al., 2004) which assumes a summary statistic T_m for each m (such as a t-test) is drawn from a mixture distribution:

$$f(T_m|\mathbf{Y})={\pi }_0{f}_0(T_m|\mathbf{Y})+(1-{\pi }_0)f_1(T_m|\mathbf{Y}),$$ (1)

where π₀ is the prior probability of a randomly selected variable being from the null distribution, f₀ is the null density, and f₁ is the alternative density.

The pre-defined sets of variables are designated by 𝒮 = {S₁, S₂, …, S_K}. We define the set of “interesting” variables as τ ⊂ ℳ. “Interesting” here means having densities from the alternative, as opposed to the null, distribution.

3. Atoms

A major complexity in set analysis is that predefined sets typically share variables. This overlap leads to unusual forms of dependence between sets, that are difficult to model directly. Nearly every set-analysis method proposed so far ignores this potential overlap (Goeman and Buhlmann, 2007; Efron and Tibshirani, 2007). Overlap between sets may also lead to difficulties when interpreting results. A large set may achieve modest significance - simply because a smaller subset within the large set is highly enriched for interesting results. Others have suggested dividing sets to remove the overlap (Jiang and Gentleman, 2007), but this issue has not fully been explored until now.

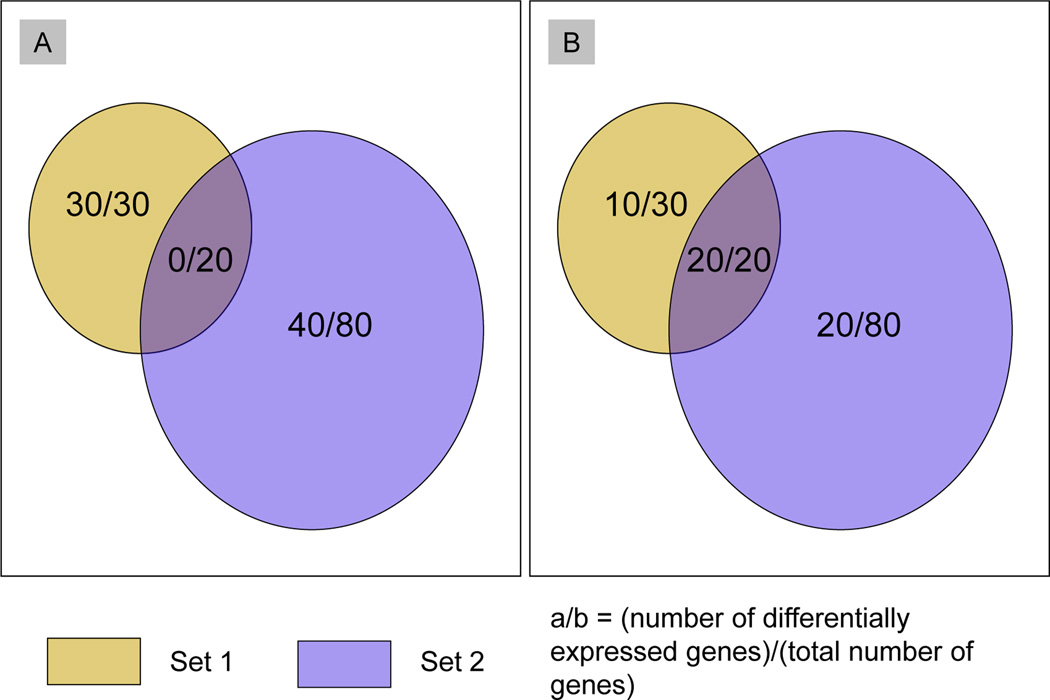
Figure 1 illustrates the difficulties that may arise from overlapping sets with a hypothetical example. Panels (A) and (B) show two potential experimental outcomes for the same two sets. In both cases, set 1 has 50 variables and set 2 has 100 variables, the overlap between the sets is the same 20 variables, and there are 40 non-null variables in set 2. However, in (A), all of the variables in the intersection of the two sets are null, while in (B), they are all non-null. Standard set analysis methods which do not make use of atoms would treat both of these cases identically, but clearly the set annotations give richer information.

Figure 1.

Set 1 has a fraction of alternatives of 0.6 (30/50 variables), set 2 has a fraction of alternatives of 0.4 (40/100 variables). In (A) there are no non-null variables common to sets 1 and 2, and although set 2 has a lower fraction of alternatives compared to set 1, the fraction of alternatives in set 2 but not in set 1 is higher than the fraction of alternatives in set 2 (0.5 compared to 0.4). In (B), the fraction of alternatives in set 2 but not in set 1 (0.25) is lower than the fraction of alternatives in set 2 (0.4). This figure appears in color in the electronic version of this article.

Our solution to this issue is to define non-overlapping sets based on the original set annotation, which we call “atoms,” thus avoiding the difficulties in analysis and interpretation from overlap. One approach to defining atoms is to identify the largest non-overlapping subsets of the original sets S₁, …, S_K, which we call “units.” Thus, a collection A₁, …, A_L contains the units of the collection 𝒮 = {S₁, …, S_K} if it has the following three properties:

1. Any of the original sets S_k can be written as a union of atoms S_k = ∪_ℓ∈𝒜k A_ℓ.

2. For all atoms A_i and A_j with i ≠ j, A_i ∩ A_j = ∅.

3. They form a collection of minimal cardinality among all the collections which satisfy properties 1 and 2.

Note that defining atoms in this way is equivalent to partitioning the set of variables ℳ which belong to one of the pre-defined sets in 𝒮 in such a way that the variables which have the same annotations belong to the same unit. Another way of stating this is that the atoms correspond to the unique rows of the incidence matrix of elements δ_ij = 1(variable i is in set j), where the rows correspond to the variables and the columns to the set annotations. Thus, the units can be seen as equivalence classes.

A fast procedure for inductively obtaining a collection of atoms from the original sets is given in Algorithm 1. The atoms derived in this way can also be shown to represent all the possible set differences and intersections of the original sets, of which there can be at most 2^K (Lemma A1 in Web Appendix A). Theorem A1 in Web Appendix A shows that the atoms obtained from Algorithm 1 uniquely satisfy the properties for units of a collection of sets.

Algorithm 1.

Algorithm to obtain atoms

The examples in Figure 1 highlight the potential utility of focusing on atoms rather than on sets. In both cases, there are three atoms, consisting of the intersection between the two sets, the set difference between set 1 and set 2, and the set difference between set 2 and set 1. In (A), the atom created by the set overlap only consists of null variables, whereas in (B), it consists solely of variables from the alternative distribution.

When the number of sets is large, there may be many units, some of which may correspond to complex intersections of many sets. An alternative approach would be to cluster or otherwise collapse the units into larger atoms, by using the set annotations themselves. In some cases, set annotations are naturally non-overlapping. For example, brain regions of interest in functional imaging do not overlap. In this case, the units are simply the sets.

4. Decision Theory Framework

In any set-analysis, the goal is to find sets that show an enrichment for variables that show a statistical or scientific signal of interest. Using our notation, this goal is translated as finding sets that have a large intersection with τ, the set of “interesting” variables, where large is often defined in terms of statistical significance (Goeman and Buhlmann, 2007). This is in contrast to the usual variable by variable analysis, which tries to find the set τ based on only the data for each individual variable, ignoring the sets.

Here we consider a decision theory framework for set analysis of high-dimensional data. While the concept is general, we detail it here in terms of a loss function that is linear in two components, one relating to false discoveries and the other to missed discoveries (defined below). Within this context we study conditions under which the posterior expected loss can be written in terms of posterior probabilities that individual variables are non-null. The goal is to find a union of atoms, U, from A₁, …, A_L that minimizes a posterior expected loss, where the loss is defined by the overlap between U and τ, the set of non-null variables.

The set of variables that are in our estimator, but are not among the non-null variables (U\τ) can be thought of as false discoveries. The set of variables that are non-null, but not included in our estimator (τ\U) can be thought of as the missed discoveries. With these two quantities in mind, we consider the following general class of loss functions, which depend on a discrepancy function d and a fixed constant w ∈ [0, 1]:

$$L(\tau ,U)=(1-w)\sum _{m\in U\backslash \tau }d(m,\tau )+w\sum _{m\in \tau \backslash U}d(m,U)$$ (2)

for all U ∈ 𝒰. Notice that the loss function is linear in two components, with the first one measuring how close variables which are false discoveries are to the set of non-null variables (τ) and the second one measuring how close variables which are missed discoveries are to the candidate estimator (U).

This loss function is at the level of unions of atoms, which results in a potential computational challenge for finding the Bayes estimator for our general framework. The loss function can be equivalently written in terms of sums over atoms, with the first sum being over all the atoms in U and the second sum over all the atoms not in U:

$$L(\tau ,U)=(1-w)\sum _{A_l\subset U}\sum _{m\in A_l\backslash \tau }d(m,\tau )+w\sum _{A_l\not\subset U}\sum _{m\in \tau \cap A_l}d(m,U).$$ (3)

From here onwards we will always assume that there are no variables for which there are no set annotations when considering the loss functions, although un-annotated variables may be used to estimate the marginal posterior probabilities.

The posterior probability that τ is the real set of non-null variables, conditional on X and Y, is denoted for simplicity by p_τ. Using the loss function L from equation (3), we get the following posterior expected loss:

$$ℒ(U)=\sum _{\tau \in 2^{ℳ}}L(\tau ,U)p_{\tau }=(1-w)\sum _{\tau \in 2^{ℳ}}\sum _{A_l\subset U}\sum _{m\in A_l\backslash \tau }d(m,\tau )p_{\tau }+w\sum _{\tau \in 2^{ℳ}}\sum _{A_l\not\subset U}\sum _{m\in \tau \cap A_l}d(m,U)p_{\tau },$$

where 2^ℳ is the power set of the set of variables, ℳ. This expression fully reflects uncertainty from the variable-level modeling and dependencies between variables. The two components of the loss can be interpreted as the posterior expected value of the sum of distances from each false discovery (A_l ⊂ U, m ∈ A_l\τ) to the set of non-null variables (τ) and the posterior expected value of the sum of distances from each missed discovery (A_l ⊂ U, m ∈ τ\A_l) to the set of all discoveries (U), summed over all possible sets τ ∈ 2^ℳ.

Under this formulation, the posterior expected loss is written in terms of posterior probabilities that each subset of variables is exactly the interesting set τ. To estimate this quantity would require a model over a discrete posterior with support on 2^ℳ points. Since the number of variables in these studies is usually on the order of tens of thousands or more, the modeling and computation quickly become intractable.

In most common high-dimensional applications it is not the distance to a false positive that matters, but whether a variable itself is a false positive. This observation suggests the use of a simpler discrepancy measure: d(m₁, m₂) = 1(m₁ ≠ m₂). This 0–1 function says the discrepancy from a variable to a set is 0 if the variable is in the set and 1 otherwise. The discrepancy between any two sets of variables is then defined via single linkage:

$$d(A,B)=\underset{m_A\in A,m_B\in B}{\text{min}}d(m_A,m_B).$$

In this case, the loss function is reduced to:

$$L(\tau ,U)=(1-w)*|U\backslash \tau |+w*|\tau \backslash U|=(1-w)*\text{Number of false discoveries}+w*\text{Number of missed discoveries}.$$

Using this discrepancy, the posterior expected loss is a function of the posterior expected number of false discoveries for the estimator (EFD(U)) and the posterior expected number of missed discoveries for the estimator (EMD(U)):

$$ℒ(U)=\sum _{\tau \in 2^{ℳ}}L(\tau ,U)p_{\tau }=(1-w)\mathrm{E}\mathrm{F}\mathrm{D}(U)+w\mathrm{E}\mathrm{M}\mathrm{D}(U),$$

where:

$$\mathrm{E}\mathrm{F}\mathrm{D}(U)=E_{\tau |\mathbf{X},\mathbf{Y}}\{\sum _{m\in U\backslash \tau }d(m,\tau )\}=\sum _{\tau \in 2^{ℳ}}\sum _{m\in U\backslash \tau }{p}_{\tau },\mathrm{E}\mathrm{M}\mathrm{D}(U)=E_{\tau |\mathbf{X},\mathbf{Y}}\{\sum _{m\in \tau \backslash U}d(m,U)\}=\sum _{\tau \in 2^{ℳ}}\sum _{m\in \tau \backslash U}{p}_{\tau }.$$

This loss function is similar to the loss functions used by Cai and Sun (2009); Genovese and Wasserman (2002); Storey (2003); Müller et al. (2004), but to our knowledge it has not been used for set analysis, as opposed to marginal variable analysis. Related loss functions are described in Web Appendix C.

Theorem 1 presents the important result that it is not necessary to obtain the posterior probabilities for each set under the common 0–1 discrepancy measure, but that the variable-level posterior probabilities suffice. This is because EFD(U) and EMD(U) can be expressed in terms of the marginal posterior probabilities that each individual variable is non-null, i.e. $p_m^{*}={\sum }_{\tau \in 2^{ℳ},m\in \tau }{p}_{\tau }$.

Theorem 1: Under the 0–1 discrepancy and the single linkage property, EFD(U) and EMD(U) simplify to:

$$EFD(U)=\sum _{m\in U}(1-p_m^{*})=|U|-\sum _{m\in U}{p}_m^{*},EMD(U)=\sum _{m\notin U}{p}_m^{*}.$$

The parametrization in Theorem 1 substantially reduces the modeling and computational burdens, as it simply requires the calculation of the posterior probability that each of the M variables is not null, as opposed to the calculation of a complicated multivariate posterior probability that each of the 2^ℳ sets is τ. Multiple methods for estimating the marginal posterior probabilities exist; we detail one such method in Section 5.2.

Under the mixture model, it is possible to write the EFD(U) and EMD(U) as functions of the local false discovery rate (fdr) as defined in Efron and Tibshirani (2002):

$$\mathrm{f}\mathrm{d}\mathrm{r}(T_m|\mathbf{Y})={\pi }_0{f}_0(T_m|\mathbf{Y})/f(T_m|\mathbf{Y}),$$ (4)

where the fdr for a variable is also the posterior probability that the variable is from the null distribution. Corollary 1 shows that the EFD is a sum of the fdr for each variable in the estimator and the EMD is the sum of one minus the fdr for each variable outside the estimator.

Corollary 1: When considered as functions of the data, EFD(U) and EMD(U) can be written in terms of local false discovery rates:

$$EFD(U)=\sum _{m\in U}fdr(T_m|\mathbf{Y}),EMD(U)=\sum _{m\notin U}[1-fdr(T_m|\mathbf{Y})]$$

For a general discrepancy measure d, the posterior expected loss ℒ(U) cannot be written as an affine function of the marginal-level posterior probabilities, given the single-linkage property. Corollary A1 in Web Appendix A shows that this can only be done if the discrepancy measure does not take into account how far or close variables are to each other, which is equivalent to the 0–1 discrepancy measure case.

5. Computationally Efficient EB Estimator with the Atomic FDR

We first note that the expected fraction of false discoveries for a given atom can be thought of as a false discovery rate (FDR) for atom A_l, which we denote by afdr_l (the atomic false discovery rate). It may be written as: afdr_l = EFD(A_l)/n_l, where EFD(A_l) is the expected number of false discoveries in A_l and n_l = |A_l|, i.e. the number of variables in A_l.

We use a result proven in other scenarios, such as Müller et al. (2004) and Carvalho and Lawrence (2008) to obtain an analytic solution for the Bayes estimate based on the 0–1 discrepancy, which is shown in Theorem 2. We note that Carvalho and Lawrence (2008) prove this result for the case of centroid estimation in discrete high-dimensional spaces, not for the case of set analysis. Eq. (3) and Theorem 1 are necessary to move from the set analysis level to the variable-level case. The algorithm for finding the Bayes estimator corresponds to thresholding the afdr at a fixed level determined by the parameter w. For large values of w the procedure allows more false positives, since the EFD is down-weighted in the loss function, while small values of w more strongly weight the EFD, restricting the afdr:

Theorem 2: For a fixed value of w ∈ [0, 1], the Bayes estimator for the posterior expected loss ℒ is δ_l = 1{afdr_l ≤ w}, where δ_l is the indicator 1(A_l ⊂ U).

5.1 Interpretation of the afdr

The afdr has a convenient interpretation as the posterior expected fraction of null variables in a specific atom. Theorem 2 shows that for the loss function L it is sufficient to consider atoms which have afdr below a threshold w. This loss does not depend directly on the estimates outside of the atom and hence does not constitute a competitive analysis approach.

In applied examples, it may be more intuitive to focus on 1 − afdr, which is the expected fraction of non-null variables, or alternatives, in an atom (or the expected “true discovery rate”). This quantity can be thought of directly as enrichment for interesting variables. An atom is included in the Bayes estimator if $1-{\widehat{afdr}}_l\ge 1-w$, for a fixed weight w, as seen from Theorem 2. In general these quantities will be interpreted in the context of an experiment and the threshold 1 − w may be best determined by the overall fraction of alternatives.

5.2 Empirical Bayes Estimators

Here we propose a simple implementation of our decision theory framework for use in applied examples. We will use this approach in subsequent sections for comparisons with previous approaches and applied data analysis. We create irreducible atoms from sets as described in the Section 3. Then we use the popular empirical Bayes model for estimating posterior probabilities that variables are non-null, following the development of Efron and Tibshirani (2002) and Newton and Kendziorski (2003):

$${\mathrm{p̂}}_m^{*}=1-\widehat{\mathrm{f}\mathrm{d}\mathrm{r}}(T_m|\mathbf{Y})=1-{\mathrm{\pi ̂}}_0\times \widehat{f_0/f}(T_m|\mathbf{Y}),$$ (5)

where the quantities begin estimated are defined in equations (1) and (4). We estimate ${\mathrm{p̂}}_m^{*}$ using the approach proposed by Storey et al. (2005), with the exact steps being described in Algorithm 2 (see also Dabney and Storey, with assistance from Warnes, 2012). For the examples that follow, we set B = 20, use variable-level statistics that are or can be approximated to be normally distributed with known mean and variance under the null (for example, t-tests), and let the number of knots be equal to the total number of variables. The posterior probabilities are then combined into afdr estimates using the result of Corollary 1.

6. Applications

6.1 Simulations

We carried out simulations which compared our method to two representative testing methods which are in the limma package in R (Smyth, 2004): roast (Wu et al., 2010) and romer (Majewski et al., 2010). The roast method performs self-contained testing, while the romer method performs competitive testing; both methods consider linear models and look at contrasts between groups of samples. We use all the default parameter settings in the R functions roast and romer and consider the mixed alternative hypotheses, which state that variables can change in either the up or down direction. The roast method also outputs an “estimated active proportion” for each set. Thus, this is similar to $1-\widehat{afdr}$ and can also be seen as an estimate of the fraction of alternatives.

Algorithm 2.

Algorithm to obtain empirical Bayes estimates of posterior probabilities for individual variables. The variables are indexed 1 ≤ m ≤ M.

We set up the simulations in a such a way as to allow them to be used as input into roast and romer, which require the sample assignments/outcomes Y and the data matrix X. We consider 30 cases and 30 controls, simulating the values for null variables in all samples and for alternative variables in control samples from N(0, 1) and the values for non-null variables in case samples from N(1, 1). Thus, for each null variable, the difference between mean values in cases and controls is N(0, 1/15), while for each non-null variable it is N(1, 1/15). We perform 100 simulations for each scenario.

For each atom l, we calculate the p-values for the roast and romer methods, as well as the corresponding q-values, which are adjusted to control the FDR for independent hypothesis tests (Benjamini and Hochberg, 1995). We additionally give the estimated active proportion from the roast method. We also provide $1-\widehat{afdr}$ from our approach.

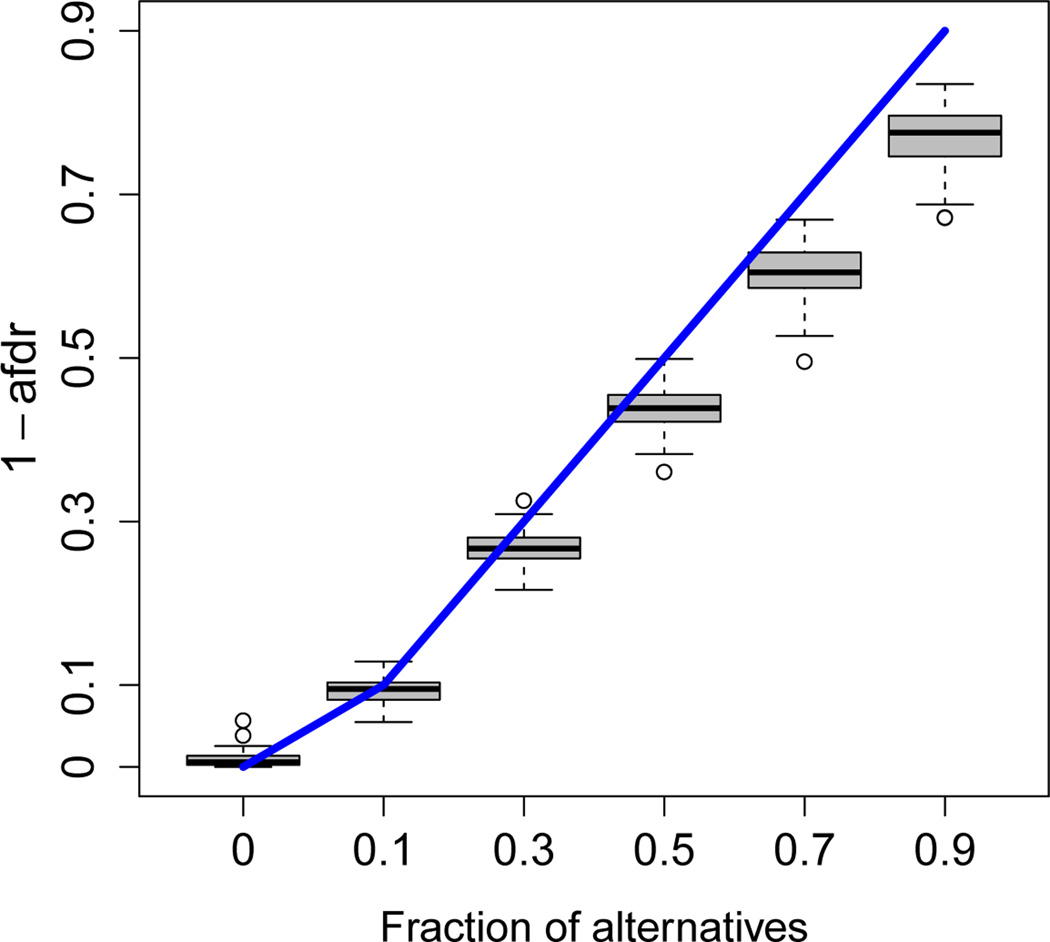
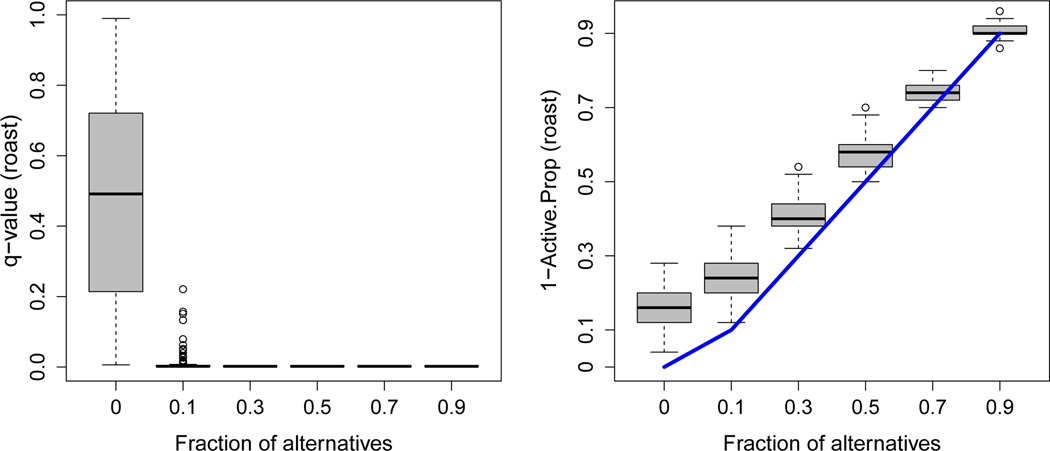
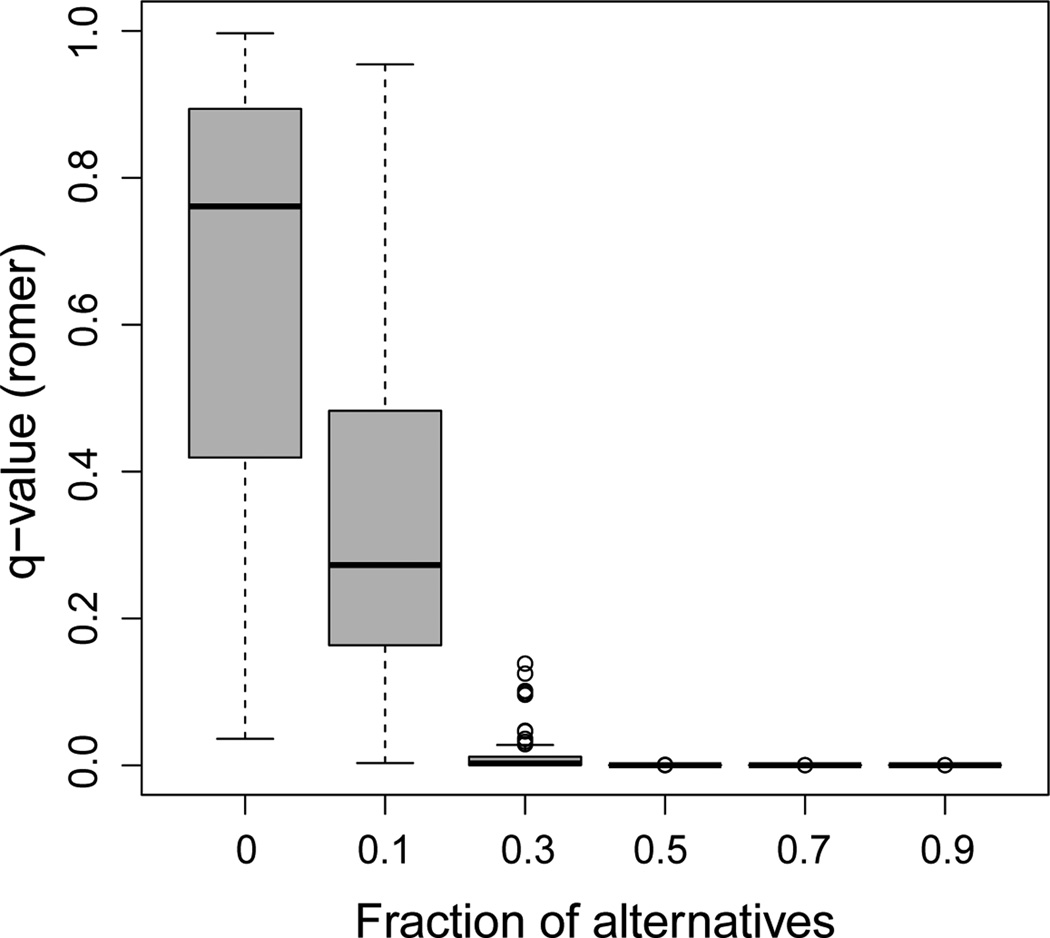
We first compared the methods for the scenario where the atom size is held fixed, but the fraction of alternatives varies. 2, 500 variables, 125 (5%) of which were from the alternative distribution, were considered. 300 of these variables were distributed among 6 atoms, each with a different fraction of alternatives (0.9, 0.7, 0.5, 0.3, 0.1, and 0). The overall estimated fraction of alternatives was 0.052, with a standard deviation (SD) across simulations of 0.003. This was close to the true value of 0.05. Results are presented in Figures 2, 3, and 4. Given that the posterior probabilities are estimated to be between 0 and 1, we observe a slight anti-conservative bias for the sets with low fractions of alternatives and a conservative bias for the sets with high fractions for the decision-theory method (Figure 2). Since we are more likely to be interested in the sets with higher fractions of alternatives, this is unlikely to be a problem. The roast method (Figure 3) gives similar q-values for the sets with fractions of alternatives greater than or equal to 0.3 (means of 0.002 and SD < 0.001 in each case). The estimated active proportion is closer to the true fraction of alternatives than $1-\widehat{afdr}$ for high values, but much more anticonservative for low values: For example, for true fractions of alternatives of 0 and 0.1, the mean estimates for roast are 0.165 and 0.239 (SD of 0.056 and 0.052, respectively), while for the decision-theory approach they are 0.009 and 0.093 (SD of 0.009 and 0.015, respectively). For romer (Figure 4), many of the simulation runs result in the sets with the fraction of alternatives of 0.1 not being declared significant (mean q-value is 0.358, SD is 0.27), despite the fact that these fractions of alternatives are much higher than the overall fraction of 0.05. The results for our estimator for this scenario with different variances 1/N, where 4N can be considered the sample size for the study design considered in this simulation framework, are shown in Table B1 in Web Appendix B.

Figure 2.

Plot of $1-\widehat{afdr}$ versus the true fraction of alternatives. The line segments represent the ideal scenario, where $1-\widehat{afdr}$ perfectly estimates the fraction of alternatives. 100 simulated datasets with 6 atoms of size 50 are considered. The overall fraction of alternatives is 0.05. This figure appears in color in the electronic version of this article.

Figure 3.

Plot of the q-values and the estimated active proportion from the roast method versus the true fraction of alternatives. The line segments represent the ideal scenario, where the estimated active proportion perfectly estimates the fraction of alternatives. 100 simulated datasets with 6 atoms of size 50 are considered. The overall fraction of alternatives is 0.05. This figure appears in color in the electronic version of this article.

Figure 4.

Plot of the q-values from the romer method versus the true fraction of alternatives. 100 simulated datasets with 6 atoms of size 50 are considered. The overall fraction of alternatives is 0.05.

We also explored the effect of a varying the atom size and a fixed fraction of alternatives. We once again considered 2500 variables, 5% of which were from the alternative distribution. In the first scenario, 3 atoms were considered, each having only null variables, but different sizes (10, 50, and 100 variables). The mean values of $1-\widehat{afdr}$ are between 0.010 and 0.012 for the three atoms (SD of 0.026 or smaller). The roast method (Subfigure a) of Figure B1 in Web Appendix B) results in mean p-values between 0.498 and 0.512 (SD between 0.274 to 0.296). The mean estimated active proportions are between 0.157 and 0.158, so, once again, very anti-conservative. The romer method (Subfigure b) of Figure B1) results in p-values which are increasingly skewed towards 1 as the atom size increases.

In the second scenario, the 3 atoms of sizes 10, 50, and 100 had a fraction of alternatives of 0.5. The mean values of $1-\widehat{afdr}$ are similar across the different set sizes (between 0.433 and 0.439, with SD between 0.019 and 0.059). For the roast method, the mean p-values and q-values are 0.001, respectively 0.002 for all three atoms (SD < 0.001). The estimated active proportion is on average between 0.577 and 0.587 (SD between 0.028 and 0.095). For the romer method, the p-values and q-values for the atom of size 10 (means of 0.025 and SD 0.043) are much higher than for the other two (means and SD < 0.001).

In general, our decision theoretic framework returned qualitatively similar results to the roast approach. However, while our method was only slightly anti-conservative for low fractions of alternatives, the roast method was extremely anti-conservative. Our framework also provides a much clearer interpretation when different enrichment fractions or different set sizes are considered compared to the romer method. In both of the scenarios we considered where the atom size was varied, but the fraction of alternatives was fixed, the results from the romer method are not comparable across the different set sizes, due to its competitive nature: As the atom size increases while the fraction of alternatives stays fixed, the fraction of alternatives in the complement of the atom changes, in order to maintain the overall fraction of alternatives (in this case, 0.05). If the fraction of alternatives in the atom is smaller than the overall fraction of alternatives (first scenario), the fraction of alternatives in the complement increases, thus also increasing the p-values, while if it larger than the overall fraction of alternatives (second scenario), the fraction of alternatives in the complement decreases, decreasing the p-values.

6.2 Gene-set data analysis

We perform two data analyses on genomic data, using standard gene-sets. We first present a proof-of-principle analysis of a dataset from Subramanian et al. (2005), which compares mRNA expression from lymphoblastoid cell lines of 15 males and 17 females (additional details are provided in Web Appendix B). The gene-sets used represented 172 nonoverlapping chromosomal regions. We compared the methods in Subramanian et al. (2005) and Irizarry et al. (2009), as well as the roast and romer methods to our method. The results from the top 5 sets using our method are presented in Table B2 in Web Appendix B.

The set which has the highest $1-\widehat{afdr}$ with our method is the only set which had a chromosomal region on the Y chromosome, and it also ranked first in terms of p-values and q-values with the other four methods. The q-values from the roast and romer methods are 0.172, respectively 0.258, while the q-values from the GSEA and t-test method are < 0.001. Thus, whether or not that particular set is discovered depends on which exact hypothesis test is used. We note that our method is much more interpretable than methods which rely on p-values or q-values: The estimate of the fraction of alternatives in the set chrYq11, 0.398, can be directly compared to both the overall estimate, 0.025, and the estimate for the set ranked second, 0.041. Therefore, providing the actual estimate and allowing direct comparisons is much more useful than trying to understand the difference between a q-value of nearly 0, one of 0.2, and one of over 0.9. Once again, the estimated active proportion from the roast method is higher than from $1-\widehat{afdr}$ (0.562). In this case, the true fraction of alternatives should be 1, so both estimation methods are conservative.

We further analyzed a dataset from Sotiriou et al. (2006) (downloaded from http://pierotti.group.ifom-ieo-campus.it/biocdb/data/experiment/ last accessed February 5, 2012), consisting of expression microarrays from breast tumors. We looked at a subset of untreated tumors, considering the differential expression between 10 ER-negative and 53 ER-positive samples, the variable-level statistics being two-sample t-tests. We used KEGG annotations (Kanehisa and Goto, 2000) through the hgu133a.db package version 2.8.0 (Carlson et al., 2011) in Bioconductor for 10 pathways, which resulted in 17 atoms. The strongest signal is found in the atom represented by one of the three-way intersections, namely that of the Wnt signaling pathway, the cell cycle, and the ubiquitination pathway, with $1-\widehat{afdr}$ being 0.54. Results are shown in Table 1. The estimated overall fraction of alternatives was 0.17. As a comparison, the range of the estimated fraction of alternatives (also estimated using the same EB method) for the original sets was 0.15 to 0.33. Thus, we uncovered a higher-level biological interaction than would have been possible to find via an analysis which used the original sets as opposed to the atoms.

Table 1.

Estimated fractions of alternatives ($1-\widehat{afdr}$) for the 17 atoms resulting from 10 KEGG sets, using data from Sotiriou et al. (2006). Each column represents an atom and each row represents a set, with an “X” specifying whether an atom is part of a set. The highest $1-\widehat{afdr}$ is for atom 4, which represents a three-way intersection of the Wnt signaling pathway, the cell cycle, and ubiquitin mediated proteolysis.

		Atoms
		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17
	$1-\widehat{afdr}$	0.22	0.06	0.11	0.54	0.36	0.22	0.16	0.14	0.21	0.23	0.26	0.13	0.23	0.33	0.20	0.33	0.24
	Size	226	23	7	6	174	30	195	20	47	18	11	43	20	11	51	33	43
KEGG sets	Wnt signaling pathway	X	X	X	X
	Cell cycle		X		X	X	X
	Ubiquitin mediated proteolysis			X	X		X	X
	Glycolysis/Gluconeogenesis								X	X	X	X
	Citrate cycle (TCA cycle)											X	X
	Pentose phosphate pathway										X			X
	Fatty acid biosynthesis														X
	Fatty acid metabolism								X							X
	RNA polymerase																X
	Basal transcription factors																	X

6.3 Brain ROI data analysis

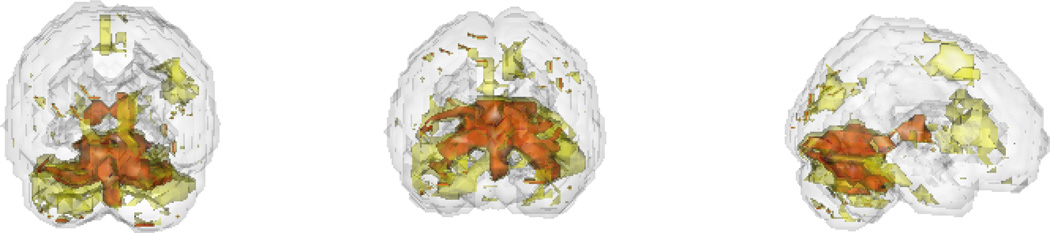
We perform an analysis involving brain imaging data arising from fMRI, where each set is a ROI. In this case, variables corresponded to voxels and the variable-level statistics were one sample t-tests. The experiment consisted in the presentation of famous and non-famous faces to 12 subjects (Henson et al., 2002, additional details in Web Appendix B). The set-level analysis involved a parcellation of the brain, which we obtained by using the anatomical decomposition from Tzourio-Mazoyer et al. (2002). 22 of the 117 brain regions had $1-\widehat{afdr}$ greater than 0.75 and 11 had $1-\widehat{afdr}$ greater than 0.85 (Figure 5). The overall estimated fraction of alternatives was 0.46. The results show differences in the occipital lobe and parts of the frontal and parietal. This is not surprising, as the occipital lobe is associated with vision, and the task is visual, while the cortical group activation likely is associated with processing the visual information. Since the analysis in this case was not amenable to the use of a linear model, we could not use the roast or romer methods. We did, however, compare results from our method to performing Wilcoxon tests which consider each set and its complement, also implemented in the limma package (see Figure B2 in Web Appendix B.) Most the q-values from the Wilcoxon test are either very high (greater than 0.9) or very low (less than 0.1), while the distribution of $1-\widehat{afdr}$ looks similar to a truncated normal.

Figure 5.

Rendered brain images in three orientations with the highlighted regions being those with $1-\widehat{afdr}$ greater than 0.75 (lighter), respectively 0.85 (darker). This figure appears in color in the electronic version of this article.

6.4 Obtaining standard errors via the bootstrap

Standard errors for the estimate $1-\widehat{afdr}$ may be calculated using a bootstrapping approach. In each bootstrap iteration, we calculate new statistics for each variable using a form of data re-sampling. Next, we re-estimate the variable-specific posterior probabilities based on the bootstrap statistics, and hence obtain bootstrapped values of $1-\widehat{afdr}$. One hundred such bootstrap iterations were used with the data from Sotiriou et al. (2006), described in Section 6.2. The bootstrap standard deviations for the 17 atoms described in Table 1 are all between 0.064 and 0.173.

7. Discussion

We introduced a general approach for set-analysis for high-dimensional data, which casts the problem in a decision-theoretic framework and focuses on estimation rather than testing. Set-analysis is an area of increasing interest in many areas of science, because of the necessity of combining data from multiple related variables in high-dimensional studies. Our method introduces atoms as the unit of analysis for set-analyses. These atoms can be used to both improve statistical inference and interpretability of the results of a set-analysis, for instance, by revealing biological interactions that would not have been uncovered if considering overlapping sets. No assumptions are made about dependencies between the variables.

Most methods currently used for set-analysis use a multiple hypothesis testing approach. However, the p-values from these analyses do not propagate the errors from the original variable-by-variable analysis and are not directly interpretable on the scientific scale of interest. Our approach focuses on estimating directly the quantity of interest in a set-analysis: enrichment for interesting variables.

We show that the loss function defined as the weighted sum of false discoveries and missed discoveries for any union of atoms, can be reduced to a form which depends only on the marginal variable-level posterior probabilities. These probabilities can easily be estimated using existing Empirical Bayes methods. This approach compares favorably with the current state of the art for gene set analysis. We have also shown this framework may have some utility in region of interest analysis in functional neuroimaging. The decision-theory framework also allows possible extensions to other loss functions, such as those presented in Web Appendix C, which may be useful in different scenarios.

We note that the main difficulty with implementing our method will generally lay with obtaining atoms. Breaking the set annotations up into units via Algorithm 1 could potentially result in a very large number of atoms, with many of those atoms containing just 1 or 2 variables, in which case there would not be much difference between implementing a set-level analysis and a variable-level analysis. There are, of course, many cases where the annotations naturally lead to atoms or where the set of atoms obtained is manageable. For very large collections of set annotations, a clustering approach may be necessary to obtain atoms, and we acknowledge that this is not without its own controversies.

The estimates resulting from our method are the result of a single rigorous, unified decision-theory framework for set analysis, which is, to the best of our knowledge, the first of its kind. They have clearly defined optimality properties, and are scientifically interpretable based on the new atomic false discovery rate. We use a popular EB estimation procedure for the probability that a given variable is not null, but we note that this can be replaced by any other EB or fully Bayes procedure. Additionally, it is possible to incorporate prior information obtained from previous studies or from additional assumptions on the variables annotated to the sets being analyzed.