Predicting the spatiotemporal dynamics of hair follicle patterns in the developing mouse

Significance

The establishment of orderly patterns in living systems is fascinating. While the Turing class of reaction–diffusion models defines a paradigm for the emergence of primary patterns, we propose here a much simpler expansion–induction (EI) model for the formation of secondary patterns. The EI model is derived from a simple geometric rule revealed by quantitative analysis of the patterns of secondary hair follicles in the developing mouse. It is driven by the physical growth of the embryo and is able to predict the formation of secondary follicles spatially and temporally, given only the locations of primary follicles. The robustness of the EI model provides an important advance by allowing comparison to real biological patterns beyond the qualitative, visual level.

Abstract

Reaction–diffusion models have been used as a paradigm for describing the de novo emergence of biological patterns such as stripes and spots. In many organisms, these initial patterns are typically refined and elaborated over the subsequent course of development. Here we study the formation of secondary hair follicle patterns in the skin of developing mouse embryos. We used the expression of sex-determining region Y box 2 to identify and distinguish the primary and secondary hair follicles and to infer the spatiotemporal dynamics of the follicle formation process. Quantitative analysis of the specific follicle patterns observed reveals a simple geometrical rule governing the formation of secondary follicles, and motivates an expansion–induction (EI) model in which new follicle formation is driven by the physical growth of the embryo. The EI model requires only one diffusible morphogen and provides quantitative, accurate predictions on the relative positions and timing of secondary follicle formation, using only the observed configuration of primary follicles as input. The same model accurately describes the positions of additional follicles that emerge from skin explants treated with an activator. Thus, the EI model provides a simple and robust mechanism for predicting secondary space-filling patterns in growing embryos.

In mouse skin development, well defined waves of induction during embryogenesis give rise to several major hair types. The first wave, starting around embryonic day 13 (E13), generates the future guard hair. This primary hair is the longest and is surrounded by Merkel cells (1, 2). The second wave (around E14.5–E16.5) generates two types of secondary hair: awls and auchenes. The third wave (around E17) generates the “Z” shape zigzag tertiary hair. During the formation of these hair types, smaller secondary follicles appear in the interstitial space of the larger primary follicles (1, 3). Unlike the feather buds in chick, which are organized in a highly ordered hexagonal array (4–6), mouse hair follicles are distributed in characteristic but less orderly space-filling patterns, the specifics of which have not been quantitatively characterized (Fig. 1A), and without which a quantitative assessment of pattern integrity in mutants cannot be made.

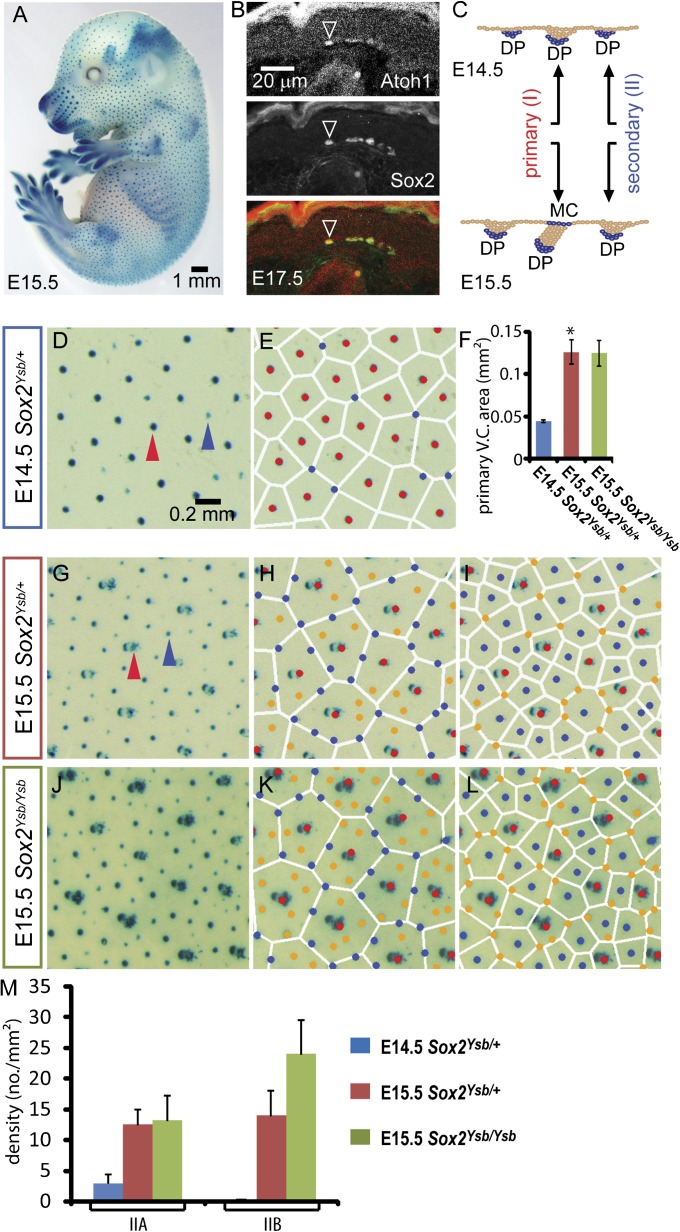
Fig. 1.

Spatial regularity in hair follicle patterns as revealed by Voronoi analysis. (A) Whole-mount X-gal staining of an E15.5 Sox2^Ysb/+ mouse embryo. (B) Sox2 is coexpressed with Merkel cell marker Atoh1 in E17.5 skin. (C) Schematic diagram of LacZ expression in primary and secondary follicles during hair morphogenesis in Sox2^Ysb/+ embryos. At E14.5, the primary and secondary follicles, marked by LacZ (X-gal staining) expressed from the dermal papillae (DP), can be distinguished by their relative sizes because secondary follicles (fainter) are just beginning to emerge (blue arrowhead, D). (E) A Voronoi diagram is generated according to the positions of the primary hair follicles (red dots) in E14.5 skin. All secondary follicles (blue dots) are located near the vertices of the Voronoi cells (white polygons). (F) The average area of the Voronoi cells generated by the primary hair follicles. The E15.5 Voronoi cells are ∼2.8-fold larger than (*P < 0.05) the E14.5 Voronoi cells, indicating expansion of the epithelium during this time. At E15.5, primary follicles are distinguished by the characteristic associated presence of Merkel cells (MC), which also express LacZ (red arrowhead in G). (H) The same Voronoi diagram as (E) is generated for E15.5 skin. Two groups of secondary follicles are seen: IIA (blue dots) located close to the Voronoi boundaries, and IIB (orange dots) located in the interior of the Voronoi cells; see Supplemental Methods. (I) A Voronoi diagram generated according to the positions of the primary and IIA follicles. (J) In the Sox2^Ysb/Ysb E15.5 skin, the X-gal signal is stronger, hence more juvenile IIB hair follicles could be observed (M). (K and L) IIA (blue) and IIB (orange) follicles are distinguished by the Voronoi diagrams as shown in H. (L) Similar to the Sox2^Ysb/+ E15.5 skin, the IIB follicles fall on the vertices of the Voronoi diagrams generated by the primary and IIB follicles.

Turing’s analysis of the reaction–diffusion (RD) model, involving the diffusion of two types of morphogens (“activator” and “inhibitor”) whose interaction regulates their own synthesis, has been regarded as a paradigm to explain the de novo emergence of approximately periodic patterns of epidermal appendages (reviewed in refs. 1, 3, and 7–11; SI Appendix, Note 1). The Turing class of RD models were postulated long ago to explain the initiation of skin appendage patterns (8, 12–15), the secondary follicle patterns (16), the coat pattern (17), and skin pigmentation (7, 18, 19). Sick et al. (3) provided molecular evidence for regulators necessary in the formation of hair follicles patterns. They further extended the Turing model developed by Nagorcka and Mooney (8) to describe the patterning of the wave of secondary follicles in between preexisting primary follicles. However, direct assessment of the applicability of Turing-class models to an observed pattern is difficult due to the lack of quantitative information including the biophysical properties and the initial distribution of the morphogens, all of which can significantly affect quantitative predictions by these models (20).

Equally importantly, the physical growth of the embryo is often not taken into account in typical applications of Turing models. In a number of cases where physical growth was considered, the models were found to generate peak doubling via either tip-splitting bifurcations or tip insertion depending on model parameters and the specifics of the growth kinetics (17, 21–23). Because tip-splitting processes have never been observed in hair follicle development, even qualitative assessment of the applicability of Turing-type RD models to follicle development requires quantitative knowledge of the model parameters, which is difficult. Moreover, existing studies of Turing models with growth have been done in one spatial dimension (24, 25), or on the effective 1D problem of stripe formation in two dimensions (26, 27), but not on the geometrically more complex case of spot formation in 2D.

Here we describe an alternative approach to characterize the formation of secondary hair follicle patterns in the developing mouse, after the establishment of the primary follicles (13). We show quantitative spatiotemporal data for the formation and placement of newly generated hair follicles. These data motivate a simple mathematical model that predicts the timing and location of newly formed follicles without knowledge of the morphogen profiles or the growth dynamics.

Results

Sox2 Expression Marks the Positions of Primary and Secondary Hair Follicles.

Primary and secondary follicles are characterized and distinguished by expression of Sox2 in the dermal papillae and Merkel cells (28) (Fig. 1B). We used the Sox2 regulatory mutant Yellow submarine (Ysb) (29), in which the endogenous regulatory elements of Sox2 that drive its expression in the inner ear and hair follicles control expression of a LacZ transgene (29, 30). Thus, LacZ expression allows the identification of both the primary and secondary follicles by X-gal staining (Fig. 1 A–C), enabling the ensuing analysis of the spatial patterns of the primary (red arrows) and secondary (blue arrows) hair follicles formed at different stages of embryo development (E14.5 in Fig. 1D and E15.5 in Fig. 1G).

Voronoi Analysis Reveals Hidden Regularity in the Spatial Distribution of Hair Follicle Positions.

A cursory inspection of the pattern of follicle positions reveals that it is globally disordered, but locally ordered. Therefore, to characterize the spatial arrangement of the secondary follicles relative to the primary follicles in detail, we applied the Voronoi analysis (SI Appendix, Fig. S1), which is widely used in characterizing local ordering and has been particularly important in the study of liquids (31). We constructed Voronoi diagrams based on the locations of the primary follicles formed by the Sox2^Ysb/+ embryo at E14.5 (red dots in Fig. 1E), shown as polygons (white lines) surrounding the primary follicles. Each polygon defines the boundaries of a “Voronoi cell,” which partitions the interstitial space into regions located closest to each primary follicle (SI Appendix, Fig. S1). Only a small number of secondary follicles (blue dots) were detected at this stage; significantly, all were located close to the vertices of the Voronoi cells.

Next, we analyzed the follicle patterns formed at E15.5 (Fig. 1H), by which time most of the secondary hair follicles were detectable. The same Voronoi analysis based on the positions of the primary follicles (red dots) for 10 such embryos revealed a portion (46 ± 8.4%, SD) of secondary follicles located on the Voronoi boundaries (vertices and edges). These boundary-located secondary follicles appeared larger than the remainder (54 ± 8.4%, SD) located in the interior (SI Appendix, Fig. S2), suggesting that they had formed earlier (32). We refer to these follicles as IIA follicles and the ones in the interior as IIB follicles (Fig. 1H, blue and orange dots, respectively). Strikingly, if a new Voronoi diagram is constructed based on the locations of both the primary and IIA follicles (Fig. 1I), all of the IIB follicles reside close to the vertices of the new Voronoi cells. A difference between the follicles at E14.5 and E15.5 that will be crucial for the subsequent analysis is that the average areas of the Voronoi cells of the primary follicles increased by nearly threefold (Fig. 1F), indicating increased separation of the follicles due to the physical growth of the embryo. In Sox2^Ysb/Ysb embryos, there are two copies of the LacZ transgene, which show stronger X-gal staining than heterozygotes (Fig. 1J). For the same stage, the enhancement of the signal reveals more juvenile IIB follicles (Fig. 1M), which exhibit a similar pattern as the IIB follicles in Sox2^Ysb/+ embryos; in other words, they reside close to the boundaries of the Voronoi cells formed by the primary and IIA follicles (Fig. 1 K and L).

Generation of Secondary Follicles by the Expansion–Induction Model.

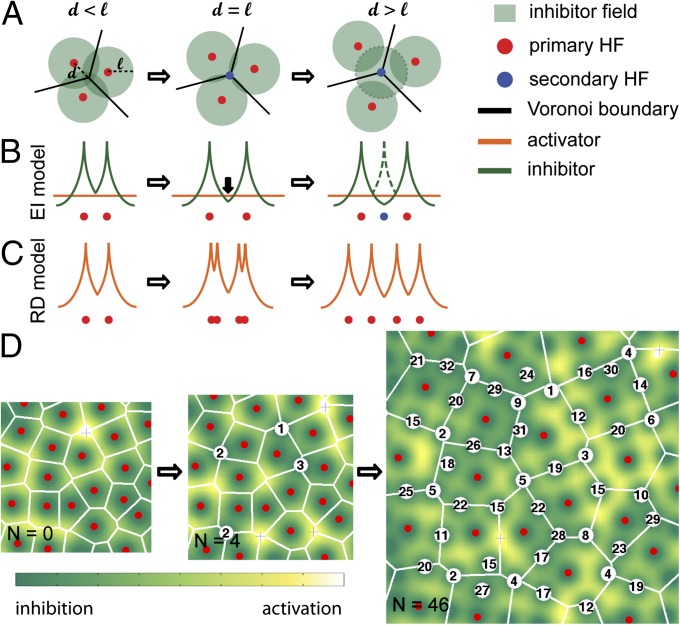
As illustrated in SI Appendix, Fig. S1, vertices of the Voronoi cells are located furthest away from the follicles generating the Voronoi cells. Thus, one possible reason for the initial formation of secondary follicles at the Voronoi vertices (rather than in the much larger interior space) is a tendency for the secondary follicles to form far from the preexisting primary follicles. This pattern could occur if each primary follicle produces morphogen molecules that diffuse to the surrounding space and inhibit the formation of secondary follicles. Turnover of the morphogen would ensure that the inhibitory effect is confined to a finite distance ℓ from the primary follicles, given by the distance the morphogen can diffuse before turning over (SI Appendix, Note 1). To explain why secondary follicles form initially right at the Voronoi vertices (Fig. 1E), we propose a dynamic mechanism driven by the expansion of the skin (Fig. 2). This expansion process is marked by a gradual increase in the distances between the primary follicles (Fig. 1F), or the distance d between a Voronoi vertex and the surrounding primary follicles (Fig. 2A). Initially, d < ℓ for all vertices; the inhibitory zones (green circles) overlap and no secondary follicles could form. As expansion proceeds, there comes a time when the Voronoi vertex becomes no closer than ℓ from any primary follicles, allowing a new follicle to form at the Voronoi vertex. Vertices with successively smaller d will reach the scale ℓ later in the expansion process. We expect the newly formed follicles to have the same inhibitory zone radius, ℓ. This expectation is based on the fact that IIB follicles are located at the vertices of Voronoi cells generated by the primary and IIA follicles (Fig. 1I), which suggests that the primary and IIA follicles exert comparable inhibitory effects on the formation of the IIB follicles. We also expect that once the hair follicle is formed, it becomes insensitive to both activator and inhibitor (3).

Fig. 2.

Generation of secondary follicles by the EI model. (A) Illustration of new follicle induction as a result of epithelial expansion: The three primary follicles (red dots) each synthesize an inhibitor which diffuses to a distance ℓ (green circles). The lines are the edges of the Voronoi cells constructed from the three primary follicles. The vertex (where the three edges meet) is at an equal distance (d) from the three follicles. As the skin expands and the three follicles move away from each other, the vertex is the first location to escape from inhibition (when d = ℓ) and a new follicle (blue dot) is generated. The inhibitor synthesized by the new follicle (zone indicated by the dashed circle) suppresses the formation of additional follicles in the immediate vicinity as expansion proceeds further. (B) A 1D illustration in terms of the diffusible inhibitor’s concentration (green curves) localized to each follicle. In the EI model, a new follicle is created at a location where the local inhibitor concentration falls below a certain level (orange line) and basal activation sets in. Upon formation of the new follicle (blue dot), a new inhibitor field (dashed green line) is immediately established. (C) Turing-type RD model in a continuously expanding domain. Although different types of behaviors are possible depending on the parameter choices, a dominant class of behaviors has the activator concentration (red curve) first bifurcating into two peaks, followed by migration to new quasiequilibrium locations (21). (D) Simulation of new hair follicle formation during expansion according to the EI model. n = 0: The initial condition taken from the arrangement of primary follicles. n = 4: Shortly after the system started expanding, four new follicles were generated (white circles), each marked by a number indicating its birth time. n = 46: The simulation is stopped at a later time when the number of new follicles is 46.

The above cartoon scenario can be formulated into a quantitative mathematical model (SI Appendix, Note 2), assuming that (i) each existing follicle (primary and secondary) synthesizes inhibitory morphogens, which diffuse and turnover in the interstitial space in the same way; (ii) the follicles are embedded in space which expands uniformly at a constant rate, much slower than the rate of morphogen diffusion and turnover; and (iii) a new follicle is formed at the location where the inhibitory morphogen drops to a certain level below which basal activation takes over. We refer to this model as the expansion–induction (EI) model, as it features the irreversible induction of hair follicle formation when the inhibitor level is lowered due to the physical expansion process (Fig. 2B). Unlike Turing models, which use a “short-range activation and long-range inhibition” strategy to generate space-filling patterns, diffusible activators are not required in the EI model as long as there exists a basal level of activity to drive the formation of new follicles for sufficiently low inhibitor levels. [However, the EI model can also accommodate a diffusible activator synthesized from the follicles as long as the activator is longer ranged than the inhibitor; see SI Appendix, Note 2 and below.] Furthermore, we note that, in the Turing model implementation by Sick et al. (3) using a one-step expansion, the follicles are formed in a single burst rather than sequentially, and their positions do not align well with the Voronoi boundaries as do the observed follicles (SI Appendix, Fig. S3). Moreover, previous studies of Turing models on continuously expanding spatial domains found a variety of peak-doubling mechanisms depending on model parameters (21, 22), including tip-splitting bifurcation followed by follicle migration toward the new equilibrium positions (Fig. 2C); neither of these processes are consistent with current understanding of hair follicle development. Although peak insertion processes similar to those found for hair follicles can also be generated by Turing models on growing domains (23), the parameter dependence of these models substantially weakens their predictive power compared with that of the EI model described below.

Simulation of New Hair Follicles Formation During Expansion According to the EI Model.

Starting with a configuration of primary follicles observed on the E15.5 skin as the initial condition, the EI model inserts secondary follicles sequentially into the interstitial space (Fig. 2D; numbers indicate the “birth time” of the corresponding secondary follicles). As expected, the insertion sites were at the Voronoi vertices of the primary follicles at early times, but took up interior positions at later times, after the vertex positions were mostly occupied (SI Appendix, Fig. S4 and Movie S1). Therefore, the EI model provides a simple explanation for the geometric rule exhibited by the IIA and IIB follicles (Fig. 1 E, H, and I), independent of the activation mechanism or model parameters.

The EI Model Predicts the Position and Timing of Appearance of Secondary Follicles.

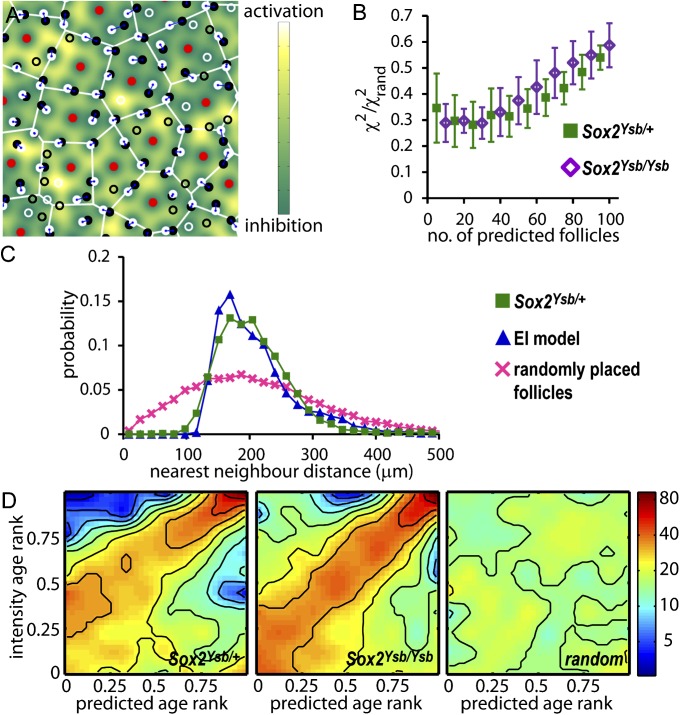
So far, the comparison between the model output (Fig. 2D) and the observed patterns (Fig. 1) is at a static, geometrical level. Next, we describe experiments to test quantitatively various predictions of the EI model, regarding both the location and timing of the new follicles. The analysis was done for the hair follicle pattern from the E15.5 flat-mounted X-gal–stained Sox2^Ysb/+ and Sox2^Ysb/Ysb skin. In Fig. 3A, the observed primary and secondary follicles are shown as the red dots and black circles, respectively. New follicles generated by EI (starting with the red dots as the initial follicle pattern) are shown as the white circles. In Fig. 3B, we assess the accuracy of follicle placement in the EI model by first pairing each of the predicted follicles with their nearest neighbor among the observed secondary follicles. The positional error is determined by χ², the root mean squared distance between the observed–predicted pair for the 10 combined samples of the Sox2^Ysb/+ E15.5 skin (green squares) and the Sox2^Ysb/Ysb E15.5 skin (purple diamonds). We normalized the χ² values and show a greater than threefold improvement of follicle prediction over the random distribution. χ² gradually increases as more follicles are placed, due to the compounded effect of small errors in early follicle placement.

Fig. 3.

The EI model predicts the position and timing of appearance of secondary follicles. (A) The locations of the primary follicles (red) are used by the EI model to predict the location of secondary follicles (shown as white circles); the observed secondary follicles are labeled as black circles. If the predicted follicle can be paired with an observed follicle nearby, both follicles are indicated as filled circles and are linked by a line. Unpaired follicles are indicated as open circles. Two follicles are paired if the follicle newly created by the EI model is a mutual nearest neighbor with an unpaired observed follicle, and if the mutual distance is smaller than a specified threshold; see SI Appendix, SI Materials and Methods. (B) The root mean square distance, χ², between the predicted follicles and their nearest neighbors among the observed follicles, versus the number of follicles predicted for the Sox2^Ysb/+ E15.5 skin (solid green squares), and the Sox2^Ysb/Ysb E15.5 skin (open purple diamonds). χ² is normalized by the limiting value for randomly placed follicles, χ²_rand such that a completely random placement would reach χ² value of 1. χ² is plotted versus the number of follicles predicted, in the order they appear in the EI model. (C) The probability distribution of the distance between nearest neighbors in the experimental (green squares), predicted (blue triangles), and the random follicle patterns (pink crosses). (D) The age of an observed follicle is estimated as the linear dimension of the follicle size (SI Appendix, Fig. S2) and correlates clearly with the birth time of the EI-predicted follicles. Panels show the density of points in the rank ordering of the observed versus predicted follicle ages for the 10 samples of E15.5 skin from Sox2^Ysb/+ (Left) and Sox2^Ysb/Ysb (Center) (SI Appendix, Fig. S6 and main text). (Right) The distribution for randomly placed predicted follicles on the Sox2^Ysb/+ E15.5 skins. The correlation can be seen in the broad maximum in density (reddish color) along the diagonal for the observed and predicted follicles, whereas the density is uniform for randomly placed follicles (Right).

The most significant feature of the follicle pattern is the extremely regular distances between neighboring follicles. In Fig. 3C, we plot the combined distribution of nearest neighbor follicle distances for the complete pattern of primary plus secondary follicles in the 10 Sox2^Ysb/+ E15.5 skin samples (green squares). This distribution is sharply peaked at 170 µm, and there are essentially no neighbors at an interfollicle distance of less than 100 μm, which may be interpreted as the minimum inhibitory distance, ℓ. The EI model reproduces the interfollicle distance distribution extremely well (blue triangles), whereas a random distribution of follicle positions gives a much wider distribution (pink crosses), with significantly more follicles that are very close together. For the complete patterns of all neighbor distances for the observed, predicted, and random follicles, see SI Appendix, Fig. S5.

Finally, the EI model not only predicts the final pattern of follicle locations, but also the temporal evolution of the pattern. To examine the timing of secondary follicle formation, we hypothesize that the size and intensity of a follicle reflects its age. Next, we pair each predicted follicle with its closest observed follicle (within some reasonable range that excluded <10% of the follicles). The age of each observed and predicted pair is plotted as a point in a correlation plot, with the age taken as a rank ordering; the youngest follicle is assigned an age of one, the next is two, and so on (SI Appendix, Fig. S6). The rank-ordered age has the advantage that sample images with different average follicle intensities may be combined together on the same plot. The collage of all of the correlation plots can be quantified as a density plot as shown in Fig. 3D for data obtained from 10 samples each of Sox2^Ysb/+ and Sox2^Ysb/Ysb E15.5 skin. In both cases, despite background arising from a stochastic component to the follicle intensities (SI Appendix, Fig. S7), there is clearly a correlation between the predicted and observed ages, as indicated by a maximum in the distribution along the diagonal. In contrast, there is no correlation between the observed follicle age and predicted follicles placed randomly (Fig. 3D, Right). Thus, the EI model is able to predict simultaneously the position and timing of follicle formation, given only the information of the positions of the primary follicles. Similar results are obtained using a diffusible activator instead of basal activation (SI Appendix, Fig. S8).

The EI Model Predicts the Position of Additional Follicles Formed in Explant Skins.

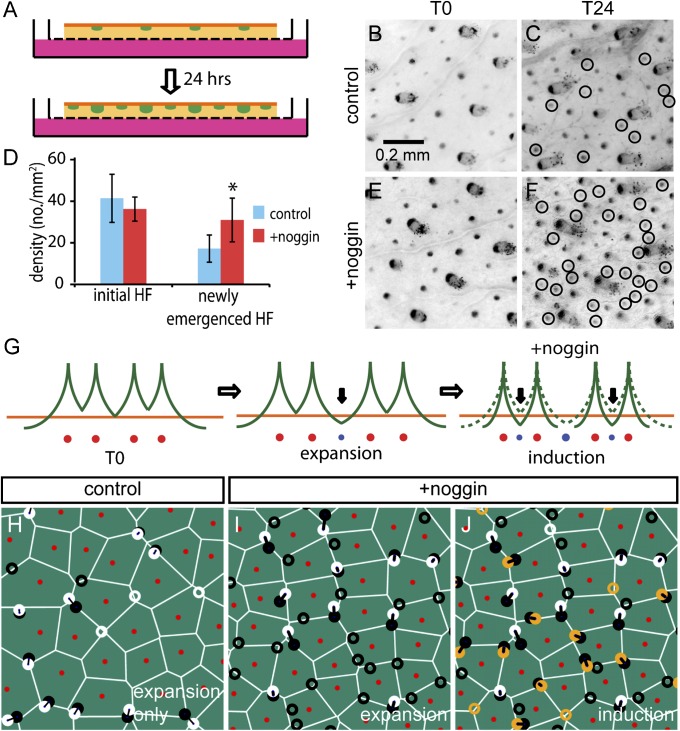
In the EI model, formation of new hair follicles is driven by the physical expansion of the embryo, which changes the spatial activator/repressor ratio (Fig. 2 A and B). However, the model does not require physical expansion if the activator/repressor ratio can be altered independently. To examine the follicle patterns resulting from the latter process, we followed the emergence of new follicles in skin explants from Sox2^Egfp/+ knock-in reporter mice (13, 33) (Fig. 4A), in which physical expansion is expected to be minimal but the activator/repressor ratio can be manipulated. In these mice, EGFP reports transcription from the Sox2 locus, allowing us to follow the temporal emergence of these follicles by repeatedly imaging the location of the primary and secondary hair follicles. For E15.25 Sox2^Egfp/+ back skin, newly emerged follicles can be readily identified after 24 h of culture (T24) by comparisons with the image of the same skin at the beginning of culture (T0) (Fig. 4 B and C). On average, ∼40 EGFP-expressing follicles per mm² could be identified at T0, and ∼16 more emerged at T24 (blue bars, Fig. 4D). During the incubation period, the growth of the hair follicles is clearly seen in the vertical direction (SI Appendix, Fig. S9), indicating the viability of the tissue; but there is little or no lateral expansion of the skin in the explant cultures (SI Appendix, Fig. S10), as expected (34). Because there is no lateral expansion, many of these newly emerged follicles were likely already prespecified, but not yet observable, when the fetuses were dissected. The identity of endogeneous follicle activator/repressor is still unknown (35). However, exogenous treatment by the BMP antagonist noggin can increase the density of hair follicles in vitro (13, 36, 37) and should effectively increase the activator/repressor ratio if applied in the explant system. We examined whether the flexibility of the EI model and the pattern simulation were able to accommodate the perturbation of the hair follicle density seen in response to exogenous noggin. Noggin treatment resulted in an average of ∼15 new follicles at 24 h compared with the untreated skin (Fig. 4B red bars, and Fig. 4 D–F). To simulate noggin treatment, we applied the EI model using the observed location of the follicles at T0 as input. As illustrated in Fig. 4G, we first applied expansion to generate the ∼40% increase in follicle density as observed in the control sample (Fig. 4 C and D), assuming that all those newly emerged follicles were prespecified before embryo dissection when physical expansion occurred. Then, we simulated the effect of noggin treatment (“induction” step in Fig. 4G) by reducing the lateral range of the inhibitors (SI Appendix, Fig. S1 and SI Methods). Additional follicles emerged when the inhibitor level in between follicles dropped below that needed to prevent activation (compare the solid and dashed green lines in Fig. 4G). The positions of the simulated follicles obtained from this procedure agree with the observed new follicles to χ²/χ²_rand = 0.4 ± 0.05, which is comparable to the degree of agreement between simulation and observation found for the generation of new follicles during normal growth in vivo (Fig. 3B). In fact, the pattern of follicles produced by noggin treatment is remarkably similar to that produced by expansion, a direct result of the form of the EI equations (SI Appendix, Fig. S11) as explained in SI Appendix, Note 2.

Fig. 4.

Modulation of the inhibitor level in explant skins. (A) Schematic diagram of the explant culture. E15.25 Sox2^Egfp/+ skin was flat-mounted on a filter and cultured for 24 h. For noggin-treated samples, 500 ng/mL noggin was added to the medium. (B and C) Hair follicles of the skin explant at the beginning of the culture (T0) and after 24 h (T24). Circles mark all the newly emerged follicles at T24. For noggin-treated samples (E and F), more newly emerged follicles were found after 24 h of culture. (D) Number of the newly emerged follicles at T24 are significantly more in noggin-treated samples (*P < 0.05). (G) Schematic diagram of the two-step EI model to simulate follicle formation in noggin-treated samples. Some follicles were first generated by expansion to match the newly emerged follicles in the control, and the remainder are induced by repression of inhibitor levels by noggin, implemented through a reduction in the lateral diffusion range of the inhibitor; see (SI Appendix, Note 3). (H) Comparison of the positions of newly generated follicles (black) and predicted follicles (white circles) in control sample. In noggin-treated samples, predicted follicles were generated by expansion (I, white circles from the first stage of expansion) and induction (J, orange circles from reduced lateral diffusion).

Discussion

The skin and its appendages can form complex patterns to meet diverse physiological needs. However, the mechanisms and principles of pattern formation, especially for placement of hair follicles are poorly understood. Previous studies have demonstrated that the balance of activator/repressor levels (3, 13, 37, 38) and genes involved in planar cell polarity (39–42) may participate in patterning. However, for quantitative understanding of the patterning process, one significant hurdle has been the lack of a precise geometrical characterization of the specific patterns formed.

In this study, we establish a simple geometric approach to characterizing the patterns of secondary hair follicles. By analyzing specific patterns on the skin of individual embryos, we reveal a strikingly simple geometrical rule governing the development of secondary follicles in the mouse embryo. This rule is quantified by the proposed EI model, which can predict accurately both the timing and positions of the newly formed secondary follicles in 2D domains in the growing embryo without requiring quantitative knowledge of the physical and biochemical parameters. In addition, the EI model can predict the patterns arising from altered morphogen levels that change follicle density in the absence of physical growth.

Turing’s RD models have been postulated to govern the generation of many biological patterns including those formed by hair follicles. However, the specific patterns generated by these are sensitive to initial conditions, noise, boundary effects, local growth (expansion) rates, and so forth (43). Despite 50+ years of work on the application of these models to biological patterns, success in accounting for the formation of a specific pattern in any individual animal are limited (24, 25, 44, 45). In contrast, the EI model proposed here was able to account for the spatiotemporal development of specific patterns in a nearly parameter-free manner (SI Appendix, Figs. S12 and S13) without the need for sensitive knowledge of initial concentrations, reaction, diffusion rates, and initiation thresholds, all of which are difficult to obtain. Furthermore, the EI model requires only a single diffusing morphogen (an inhibitor) together with a basal activation mechanism, whereas Turing’s RD models require at least two morphogens.

Turing models are designed to address the de novo formation of patterns and are derived from “diffusion-driven instabilities” (9). In contrast, EI does not attempt to address the self-organization of patterns de novo, but may describe a wide range of space-filling patterns in developmental processes after an initial pattern is laid down. Physical expansion of the patterning domain is a critical element of pattern formation in the EI model. Some Turing models have been shown to accommodate growth, in that in some parameter regime the models can also give rise to peak insertion in between existing peaks in growing 1D or quasi-1D domains (24–27). We are currently not aware of reports of spot insertion generated by Turing-type RD models in continuously growing 2D domains; however, one can imagine that an analogous system in 2D will have many more types of behaviors.

An inhibitor-based model was proposed previously in the context of new teeth formation in reptiles (46). However, there, spatial patterning was determined mainly by the teeth movement with respect to the growth zone in a one-dimensional geometry. The EI model also shares some common features with the model of lateral inhibition proposed to explain the formation of microchaetae and bristles in Drosophila melanogaster (47, 48). However, that model uses a different mechanism (contact inhibition), and has a different instability mechanism: competition rather than growth-driven. Indeed, lateral inhibition is commonly discussed in a fixed domain. Like Turing-type RD models, it is used to account for the de novo generation of patterns, not the maintenance of patterns in a growing domain. The EI model directs the embryo to generate new follicles when the local follicle density becomes too low due to physical growth. The EI model provides a simple mechanism to implement an automated “need-based” strategy, which gives the animal a desired density of hair follicles. Moreover, the target hair density can be easily adjusted by changing the basal activation rate or the rate of inhibitor synthesis, thereby providing evolutionary flexibility as physiological demand changes. EI thus provides a robust and yet flexible means of hair density specification after the primary hair follicle pattern is laid down.

Materials and Methods

Sox2^Ysb/+ and Sox2^Egfp/+ mouse strains were previously described (29, 30, 33). Mice were maintained within the animal facilities at the University of Hong Kong. All experiments were authorized by licenses from the Hong Kong Government Department of Health, University of Hong Kong Committee on the Use of Live Animals in Teaching and Research. For a detailed description of the whole-mount X-Gal staining, skin organ culture, and computational analysis, see SI Appendix, SI Materials and Methods.