Macroeconomic effects on mortality revealed by panel analysis with nonlinear trends

Abstract

Many investigations have used panel methods to study the relationships between fluctuations in economic activity and mortality. A broad consensus has emerged on the overall procyclical nature of mortality: perhaps counter-intuitively, mortality typically rises above its trend during expansions. This consensus has been tarnished by inconsistent reports on the specific age groups and mortality causes involved. We show that these inconsistencies result, in part, from the trend specifications used in previous panel models. Standard econometric panel analysis involves fitting regression models using ordinary least squares, employing standard errors which are robust to temporal autocorrelation. The model specifications include a fixed effect, and possibly a linear trend, for each time series in the panel. We propose alternative methodology based on nonlinear detrending. Applying our methodology on data for the 50 US states from 1980 to 2006, we obtain more precise and consistent results than previous studies. We find procyclical mortality in all age groups. We find clear procyclical mortality due to respiratory disease and traffic injuries. Predominantly procyclical cardiovascular disease mortality and countercyclical suicide are subject to substantial state-to-state variation. Neither cancer nor homicide have significant macroeconomic association.

1 Introduction

The impact of fluctuations in economic activity on mortality has been a long-running debate. Early evidence for procyclical mortality (i.e., increased mortality during economic booms) was presented by Ogburn and Thomas (1922). Subsequently, Harvey Brenner made determined efforts to support the hypothesis of counter-cyclical mortality (e.g., Brenner, 1979), although his controversial statistical methods were eventually discredited (Gravelle et al., 1981; Wagstaff, 1985). There is now evidence for procyclical mortality in many developed and developing countries (reviewed by Tapia Granados and Ionides, 2011). Mortality is the most clear-cut measure of population health, but may be the tip of an iceberg of procyclical morbidity. Indeed, corresponding patterns have been found for other health-related outcomes (Ruhm, 2003, 2005b), though these are complicated both by the scope of available data and by the possibility of macroeconomic influences on data collection.

Cyclical mortality is distinct from the debated relationship between long-term economic development and long-term improvements in public health. Nevertheless, the two debates are related: inasmuch as cyclical mortality is observed for macroeconomic fluctuations at all time scales, it plays a role in determining the long time scale variations which are identified as trends. Certainly, many factors other than macroeconomic considerations contribute to population mortality levels (Cutler et al., 2006).

Population level associations are distinct from the health consequences of economic fluctuations on specific vulnerable groups, such as those who become unemployed. Adverse health outcomes are certainly associated with unemployment, with evidence for causation in both directions (McDonough and Amick, 2001). The present investigation concerns aggregate effects, which may include both beneficial and harmful consequences for different subpopulations.

A landmark in the investigation of cyclical mortality was the application of panel methods by Ruhm (2000), allowing the consideration of extensive spatiotemporal data. Ruhm (2000) analyzed annual statistics for 50 US states over 20 years and found predominantly procyclical mortality. This conclusion has been largely confirmed by subsequent panel investigations (Ruhm, 2003, 2006, 2007; Neumayer, 2004; Tapia Granados, 2005b; Gerdtham and Ruhm, 2006; Buchmueller et al., 2007; Miller et al., 2009; Gonzalez and Quast, 2010, 2011). The spatial units in these studies vary (states, countries, regions, French departments) but we will consistently refer to them as states. These panel studies were typically carried out in the spirit of difference-in-difference analysis (Bertrand et al., 2004). In this paradigm, temporal variations in mortality are controlled by taking a difference between state mortality and national mortality, interpreted in regression models as a fixed year effect; spatial variations in mortality are controlled by including state-specific mortality effects. The resulting relationships identified between macroeconomic variables and mortality are therefore resistant to bias from either strictly spatial or strictly temporal additive omitted variables. By removing national mortality effects, difference-in-difference panel analysis is complementary to time series analysis (Ruhm, 2005a), though the two approaches have led to broadly consistent results (Tapia Granados, 2005a). Individual-level data have also revealed predominantly procyclical effects (Edwards, 2008). Sample size issues limit the scope of individual-level analyses; macroeconomic impact on mortality is an effect of small size (for any given individual) which nevertheless has a considerable overall effect on entire populations.

A critical question for the proper understanding of procyclical aggregate mortality is to what extent different age groups and mortality causes are involved in the procyclical phenomenon. Problematically, different analyses have previously led to different answers. We argue that these inconsistencies can be explained by the use of misspecified state-specific trend models. Previous analyses have typically employed linear or constant state-specific trends, and have performed statistical regression techniques which are inefficient or biased for the data under consideration. The methodological limitations of these analyses have had severe consequences for investigating age and cause specific mortality, without being large enough to interfere with the results for total mortality. To support our argument, we will show how removal of nonlinear trends allows appropriate statistical analysis using standard regression methods.

In this investigation, we study data from the US states in the years 1980–2006. Thus, our data updates the 1972-1991 analysis of Ruhm (2000) and overlaps the 1978-2004 analysis of Miller et al. (2009). Whereas Miller et al. (2009) extended Ruhm (2000) by breaking down the data more extensively by age and mortality cause, here we focus instead on the specification of the model and its consequences for the conclusions reached. We find that some estimates of interest are fragile to changes in the specification. Results which are sensitive to the model specification should be treated with additional caution, and also raise the question of which specification is most appropriate. To resolve existing ambiguities, and to make further progress, there is a need for objective evaluation of the strengths and weaknesses of alternative analyses. Assessing the model specification via analysis of the regression residuals can provide such a tool. The constant or linear state-specific trend specifications used in previous work, including Ruhm (2000) and Miller et al. (2009), entail substantial violations of the standard assumptions that justify the use of ordinary least squares (OLS). Combining OLS point estimates with state-clustered standard errors is a standard econometric technique in this situation (Bertrand et al., 2004; Petersen, 2009), however this only partially alleviates the adverse consequences of the model violations. Our methodological remedy is to apply nonlinear detrending methods in this spatiotemporal setting. We show that our method has many of the advantages of feasible generalized least squares (FGLS) while avoiding some of the difficulties inherent in using data to estimate a large covariance matrix (Hausman and Kuersteiner, 2008).

Our results confirm the finding of Ruhm (2000) that general mortality fluctuates procyclically and this procylical phenomenon is stronger in young adults (ages 20-44) though it is present also in mid-age adults (45-64) and individuals at retirement ages (65+). The conclusion of Miller et al. (2009) that mid-age adults are not subject to procyclical mortality may be a consequence of model misspecification. Since Miller et al. (2009) and Ruhm (2000) used similar model formulations, it is fortuitous that many of the results of Ruhm (2000) happen to agree with the conclusions from a more statistically principled analysis of recent data. We find that the procyclical oscillation of general mortality is mainly mediated by increases in respiratory disease mortality, cardiovascular disease mortality, and traffic mortality, all of which oscillate procyclically. Suicide differs by being countercyclical; we find cancer and homicide to be acyclical.

The remainder of this paper is organized as follows. Section 2 describes the data. Section 3 introduces the panel models under consideration. Section 4 discusses the methodological issues involved in fitting these models. Section 5 carries out a data analysis, focusing on issues of methodological relevance. Section 6 investigates goodness of fit for the models under consideration. Section 7 discusses these results in the context of the current understanding of cyclical mortality.

2 Data

We analyzed annual data from the 50 US states over the years 1980–2006. Crude, age-specific, sex-specific, and cause-specific mortality rates were computed using data publicly available from the US Centers for Disease Control and Prevention (wonder.cdc.gov). Data on annual unemployment rates were obtained from the US Bureau of Labor Statistics (www.bls.gov). Age-specific mortality rates were calculated for three age groups: 20–44, 45–64 and 65+. We analyzed cause-specific mortality rates for eight major causes of death, defined via (ICD9; ICD10) codes as follows: cardiovascular disease (390–459; I00–I99), ischemic heart disease (410–414; I20–I25), cancer (140–165, 170–175, 179–203; C00–C97), respiratory disease (460–519; J00–J98), other infectious disease (001–139; A00–B99), traffic injuries (E810–E819; V01–V79), suicide (E950–E959; X60–X84), homicide (E960–E969; X85–Y09).

Inspection of the plotted series of mortality rates for the 50 states revealed a jump in the series for ischemic heart disease and cancer mortality between the years 1998 and 1999 (results not shown) which corresponds to the transition in disease coding from the 9th to the 10th edition of the International Classification of Diseases (i.e., from ICD9 to ICD10). The annual change in ischemic heart disease mortality took its largest value at this time for 48 states. For cancer, the largest annual change occurred at this time for 20 states, with the times of the biggest jump being scattered for the other states. To correct for the potential error introduced by a change in mortality codes for these two categories, we replaced the log mortality increment for 1998-1999 by the average value of the remaining increments (a simple way to remove the effect of the jump while keeping the temporal structure of the time series intact). This data correction made no qualitative difference to our conclusions.

3 Models

We consider panel model specifications extending the choices of Ruhm (2000). Our general model is

$$M_{\mathit{it}}=\alpha U_{\mathit{it}}+\beta N_t+\gamma A_{\mathit{it}}+{\delta }_t+{\varphi }_i+{\psi }_{i}t+{\epsilon }_{\mathit{it}},$$ (1)

where M_it is a measure of mortality for state i in year t; U_it is a measure of state-level unemployment; N_t is a measure of national unemployment; A_it is a column vector representing population age-structure,¹ with γ being a row vector of corresponding size; δ_t are year-specific state-invariant effects; ϕ_i are state-specific time-invariant effects; the term Ψ_it corresponds to state-specific linear trends; ε_it is an error term. The mortality rate measure, M_it may correspond to total mortality, age-specific mortality, or cause-specific mortality. When M_it is an age-specific mortality measure, we do not include the term γA_it.

To define our mortality and unemployment measures, we introduce notation for the raw data. The mortality rate data are denoted by m_it, state-specific unemployment rate by u_it and national unemployment rate by n_t. A vector with population proportions of children under 5 and of persons over 65 is written as a_it. We consider four types of model, corresponding to four different ways to work with state-specific levels and trends.

• (B)The Basic model is the foundation for the analysis of Ruhm (2000). It has dependent variable M_it = log m_it and fits a constant level effect for each state (i.e., it has a constraint ψ_i = 0). The remaining variables are untransformed (U_it = u_it, N_t = n_t, A_it = a_it).
• (L)The Linear model includes linear state-specific trends. The linear model differs from the basic model only by the inclusion of the term ψ_it.
• (D)The Differenced model includes all time-dependent variables in first temporal differences. Specifically, M_it = Δ log m_it = m_it+1 − m_it, U_it = Δu_it, N_t = Δn_t, and A_it = Δa_it.
• (HP_λ)The Hodrick-Prescott model includes the time-dependent variables after subtracting trends computed via a Hodrick-Prescott filter with smoothing parameter λ. In this case, we write M_it = H_λ (log m_it), U_it = H_λ(u_it), N_t = H_λ(n_t), and A_it = H_λ(a_it). Here, H_λ(x_t) denotes the residual component of the time series x_t after removing a trend computed by the method of Hodrick and Prescott (1997). As discussed in Section 4, and at greater length by Ionides et al. (2012), λ can be chosen to approximately prewhiten the mortality measure rather than aiming specifically to isolate business cycle fluctuations. The choice λ = 100 satisfies this requirement (Ionides et al., 2012, Figure S-2).

The model types are summarized in Table 1(a). All regression models were weighted by the square root of the state population to account for heteroskedasticity; this has become a standard formulation (Ruhm, 2000; Tapia Granados, 2005b; Miller et al., 2009; Gonzalez and Quast, 2011). State-specific fixed effects and linear trends are removed by the Hodrick-Prescott filter and so are not included in models of type HP_λ. The linear trends in models of type L correspond to fixed effects after temporal differencing; we therefore include state-specific fixed effects in models of type D.

Table 1.

Models under consideration, written as special cases of equation (1). (a) The mortality variable and time-dependent explanatory variables for the different model types. (b) Model subtypes, including differing subsets of the explanatory variables.

(a)	Model type	Mortality measure (Mit)	State economy (Uit)	National economy (Nt)	Age structure (Ait)	Fixed effect (ϕi)	Linear trend (ψit)
	B (Basic)	log mit	uit	nt	ait	yes	no
	L (Linear)	log mit	uit	nt	ait	yes	yes
	D (Difference)	Δ log mit	Δuit	Δnt	Δait	no	no
	HPλ (HP-detrended)	Hλ (log mit)	Hλ(uit)	Hλ(nt)	Hλ(ait)	no	no

(b)	Model subtype	State economy	National economy	Year effects
	1	yes	no	yes
	2	yes	no	no
	3	no	yes	no
	4	yes	yes	no

We consider four subtypes of each model type, corresponding to the inclusion of differing sets of covariates. The national economy covariate, N_t, can be expressed as a linear combination of the year effects, {δ_t}, and so we never include both in the model simultaneously. Model B1 has β = 0, excluding an explicit role for the national economy; model B2 excludes both national unemployment and year effects (β = δ_t = 0); model B3 excludes state unemployment and year effects (α = δ_t = 0); model B4 excludes year effects (δ_t = 0). These model subtypes were considered by Ruhm (2000), with the goal of disentangling the effects of state-level unemployment and national-level unemployment on mortality. Subtypes of the other model types are defined in an identical way, as summarized in Table 1(b).

4 Methodology

In a panel study such as ours, many variables are measured at many geographical locations across many time points. This wealth of data leads to challenges in building graphical representations. Nevertheless, plotting the data or regression residuals in various ways can play an important role in model development and diagnostics. We demonstrate this in Sections 5 and 6. By contrast, previous panel studies relating mortality to macroeconomics have not shown any graphical representations of the data below national levels of aggregation.

A classical approach to regression analysis is to present estimates and standard errors based on OLS methodology, after checking that thorough investigation of the residuals does not reveal any major violations of the corresponding model assumptions. When serious violations are discovered one seeks to remove them by respecifying the model, for example by using transformations of variables or appropriately weighting the error terms. An alternative approach to inference is to employ nonparametric error models which operate under weaker assumptions, as discussed in the context of panel analysis by Bertrand et al. (2004) and Petersen (2009). A hidden cost of nonparametric error models is that the finite-sample properties can be undesirable despite demonstrably good asymptotic properties (Kauermann and Carroll, 2001). In numerical experiments, a sample size of 50 independent time series has sometimes been found sufficient to validate the asymptotic justification of robust standard errors for panel models (Bertrand et al., 2004; Petersen, 2009). However, the numerical validation is dependent on the data and models under consideration and so should be rechecked on a case-by-case basis. If a relatively simple respecification justifies standard OLS techniques, the additional complexities of employing and validating nonparametric error models can be avoided.

In the context of time series analysis, regression with autocorrelated errors can be handled by a procedure called prewhitening (Shumway and Stoffer, 2006). One looks for a transformation which provides approximately uncorrelated residuals when the transformed dependent time series is regressed on the transformed independent series. If the transformation has a linearity property, then the resulting OLS estimates of the regression coefficients remain unbiased. The linearity property of transformations is distinct from the use of the word linear to describe the term β_it in equation (1). Transformations having this linearity property include temporal differencing, detrending by computing the residuals from fitting an auto-regressive moving-average model, and detrending using the Hodrick-Prescott filter. If application of the Hodrick-Prescott filter with a particular choice of smoothing parameter leads to effective prewhitening, this gives a data-driven justification of the resulting analysis. Thus, the extensive literature on the value of the smoothing parameter appropriate to study business cycle fluctuations in annual data (Ravn and Uhlig, 2002) is not directly relevant to our methodology. Additional material on the interpretation and consequences of the choice of smoothing parameter is given in the supplement (Ionides et al., 2012).

Much of the development of econometric panel analysis (both in theory and practice) has focused on the standard errors. OLS standard errors can considerably underestimate the actual variability of the parameter estimates, leading to great potential for the “discovery” of spurious effects (Bertrand et al., 2004). A variety of methods, including clustered error estimates and bootstrap methodology, have been proposed to amend this problem (Petersen, 2009). Even once the standard errors are appropriately corrected, there is a remaining difficulty that OLS point estimates can also be unreliable in these situations. Feasible generalized least squares (FGLS) aims to improve OLS by using an estimated covariance matrix for the error terms (Hansen, 2007). However, the use of FGLS in panel analysis is rare, amounting to just 3% of the panel analyses surveyed by Petersen (2009) and 1% of those surveyed by Bertrand et al. (2004). Applying FGLS using simple models for the covariance structure can be ineffective (Bertrand et al., 2004). Difficulties arise in complex, flexible models of the covariance structure due to the potentially large number of parameters to be estimated (Hansen, 2007; Hausman and Kuersteiner, 2008). Our method of applying a detrending linear transform to both sides of the regression equation (1) is formally similar to the application of FGLS, with detrending playing the role of covariance estimation. From this perspective, nonlinear detrending is a variant of FGLS which is readily interpretable and has favorable numerical properties.

Granger and Newbold (1974) encouraged analyzing temporal differences as a practical resolution to the difficulties of jointly estimating regression coefficients and autocovariance structures in the presence of substantial long-range autocorrelation. However, a relationship between differences does not readily imply a relationship between trends: in practice, fluctuations around a trend can have entirely different relationships to those of the trends themselves (Hodrick and Prescott, 1997). Temporal differencing was the only linear data transformation explored by Bertrand et al. (2004). This transformation performed excellently in their numerical experiment (Table IIA, line 8 of Bertrand et al., 2004). However, the authors commented that differencing was seldom used in their survey of current practice, and gave the method no further consideration. A concern with differencing is that it can result in substantial negative autocorrelation of residuals (and it does so for our data). In this case, differencing is not ideal as a prewhitening filter; it over-enthusiastically removes the positive autocorrelation. The typical consequences of the negative autocorrelation are inefficient OLS effect estimates and conservative standard errors.

If trends are considered as fixed effects, rather than zero mean random effects, then OLS and FGLS models which fail to account for these trends incur bias. Panel model implementations of FGLS typically assume that the error terms are independent between states, so that only temporal autocorrelations are substantial. Nonlinear trends which show similarities between states are not appropriately modeled under this assumption. By contrast, inasmuch as these phenomena are effectively removed by a detrending operation, the corresponding prewhitened regression is protected from bias. The statistical evidence in the data (Sections 5 and 6) suggests that there are unmodeled sources of spatiotemporal dependence which can largely be removed by employing national year effects in combination with nonlinear detrending.

Interpreting the results of observational studies requires care because of the possible consequences of omitted variables. Another hazard is the possibility that an association between two variables which is interpreted as causal in one direction in fact has a causal mechanism in the opposite direction. In the context of cyclical mortality, two uncontroversial assertions can assist the causal interpretation of observed associations:

• (A1)It has been generally accepted that mortality fluctuations could not plausibly be a substantial cause of recent US booms and busts.
• (A2)There is a lack of plausible non-economic phenomena which could simultaneously have substantial effects on civilian mortality and macroeconomic fluctuations in recent years in the US. Perhaps the best candidates are wars, natural disasters, climate variation, or epidemic diseases; none of these have been previously considered as plausible omitted variables to explain procyclical mortality.

An alternative to (A2) is to employ a broad definition of macroeconomic phenomena, including macroeconomic effects of variables external to the economy as well as interacting variables within the economy, by assuming the following:

• (A3)Any phenomenon with macroeconomic consequences is itself a macroeconomic phenomenon.

If there is adequate statistical evidence for an association, then either (A1,A2) or (A1,A3) implies that the association can be interpreted as a causal effect of macroeconomic fluctuations on mortality. This follows directly from a basic principle of inductive reasoning, that an association between two variables must be explained by either a direct causal effect or by each variable responding to some third variable (Mill, 1853). From (A2) or (A3) one can deduce that any such third variable is itself a macroeconomic variable. This argument does not allow us to infer a specific causal mechanism. In particular, we cannot infer that unemployment operates causally to produce an observed association; its role in our analysis is as a proxy for the multitude of economic variables (measurable and non-measurable) which fluctuate synchronously.

5 Results

Figure 1 displays national annual series of total mortality rates and the unemployment rate. The national death rate declined dramatically during the recessions of the early 1980s, and then increased throughout much of the expansion of the mid 1980s. In general, the evolution of mortality tends to mirror the evolution of the unemployment rate, suggesting an inverse relation between unemployment and mortality. The long-run behavior of the crude mortality rate (unadjusted for age, as shown in Figure 1) is affected by changes in the age-structure of the population; it is much less likely, however, that changes in the age-structure cause short term oscillations of the mortality rate. When attempting to interpret the data in Figure 1, the strength of the statistical evidence for the association is more critical than the issues of causal direction and omitted variable bias. Assumptions (A1–A3) can jusify interpreting statistically significant associations as macroeconomic effects on mortality, without being able to pin down specific mechanisms. Securing the statistical evidence in sub-categories, broken down by demographic group and cause of mortality, then gives a foundation for the discussion of causal mechanisms consistent with the resulting pattern of associations. Unfortunately, the association at the 27 annual time points in Figure 1 does not give statistically conclusive evidence. Disaggregating mortality and unemployment rates from the national level to the state level has potential to reinforce the evidence, as long as the states show sufficient variation from the national pattern. Figure 2 plots mortality rates and unemployment rates for four states, revealing quite different patterns in different states. Some of these time series, such as mortality in Alaska, are clearly not well modeled by variation around a linear trend.

Figure 1.

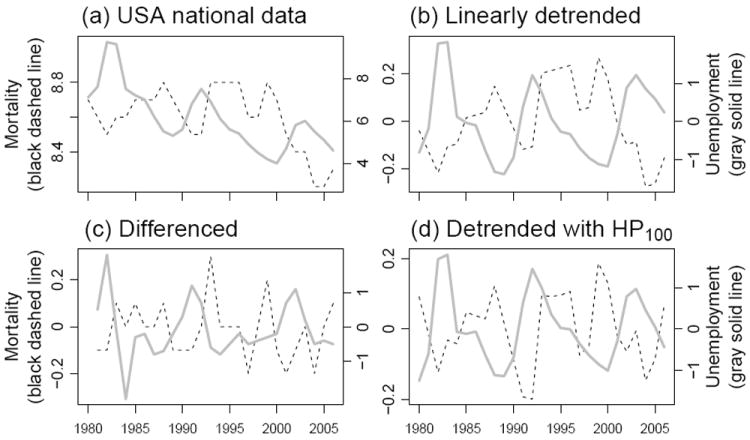
National mortality and unemployment. (a) Mortality per 1,000 per year, shown as a dashed line corresponding to the left axis scale; unemployment rate, shown as a solid line corresponding to the right axis scale. (b,c,d) The data in (a) detrended using a linear trend, first difference and Hodrick-Prescott filter (λ = 100) respectively.

Figure 2.

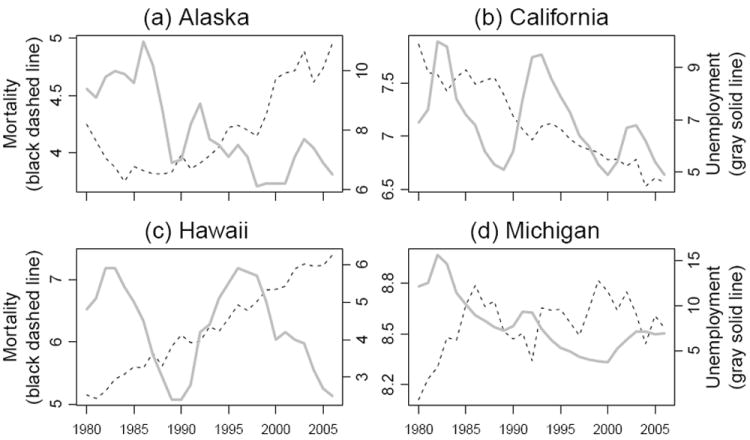
Mortality and unemployment for four states. Mortality per 1,000 per year is shown as a dashed line corresponding to the lefts axis scale. The unemployment rate is shown as a solid gray line corresponding to the right axis scale.

Table 2 summarizes our results in models that have been repeatedly used, following Ruhm (2000), to estimate the effect of macroeconomic fluctuations on mortality. The models with linear trends (L1–L4) give similar results to the corresponding results for 1972-1991 (Ruhm, 2000, Table I). In addition, inspection of the Akaike information criterion (AIC) values in Table 2 shows that L1–L4 provide a considerably superior statistical explanation of the data over B1–B4. AIC is only one of many possible measures for quantitative model comparison (Burnham and Anderson, 2002). However, the differences between the AIC values in Table 2 are entirely unambiguous. Differences of order 1 unit of AIC are considered small, and so alternative methodologies might be expected to disagree; differences of order 100 or 1000 units of AIC are compelling evidence. The comparisons provided by these AIC values are therefore, presumably, insensitive to the measure of model comparison used. Differences in AIC are useful for detecting issues of model misspecification, but they cannot, by themselves, explain how and why this misspecification manifests itself.

Table 2.

Fixed-effects panel regressions with state mortality modeled as a function of economic conditions for the 50 US states.

	Basic model				Linear state-specific trends
	B1	B2	B3	B4	L1	L2	L3	L4
State unemployment	-0.52*** (0.07)	0.12† (0.07)		-0.67*** (0.09)	-0.31*** (0.05)	-0.41*** (0.04)		-0.30*** (0.06)
National unemployment			0.78*** (0.08)	1.36*** (0.11)			-0.46*** (0.05)	-0.20** (0.07)
Year effects	Yes	No	No	No	Yes	No	No	No
AIC	-5818.3	-5027.5	-5114.7	-5165.0	-7569.6	-6938.5	-6917.7	-6945.0

The model specifications are as described in equation (1) and Table 1, and were estimated using least squares, with states weighted by the square root of the state population. The state unemployment effect is reported as the estimate of 100α, the percentage increase in mortality due to a unit increase in unemployment. Similarly, the national unemployment effect is given as the estimate of 100β. Corresponding OLS standard errors (as used by Ruhm, 2000) are in parentheses.

^***P < 0.001,

^**P < 0.01,

^*P < 0.05,

^†P < 0.1.

Ruhm (2000) found that B1–B4 provided qualitatively similar results to L1–L4 and therefore proceeded to use the simpler basic specification for subsequent analysis. For our analysis, B1 is qualitatively consistent with L1–L4, and indeed the effect estimate for this model (-0.52) happens to be identical to the estimate of Ruhm (2000). Problematically, B2–B4 suggest conclusions which are inconsistent both with Ruhm (2000) and with the other specifications in Table 2. Since B2–B4 also provide poor fits to the data (as judged by AIC, and diagnostic plots) this could be explained by model misspecification bias. Model subtypes 2–4 aim to investigate the contextual role of unemployment, addressing whether national macroeconomic conditions continue to play a role given state-level variables. However, our objective here is not to interpret the results from fitting B2–B4 or L2–L4, but to observe how standard methodology can lead to apparent contradictions. The AIC values in Table 2 suggest that year effects play a statistically important role. We therefore focus henceforth on models of subtype 1.

Table 3 shows that the results for age-specific mortality are also sensitive to model specification. Model B1 demonstrates considerable consistency with the 1972-1991 results of Ruhm (2000, Table III), indicating strong procyclical mortality in all age groups and especially in young adults and middle age adults. Our model L1, which corresponds to a supplementary model for Ruhm (2000) and the primary model structure for Miller et al. (2009), is in close agreement with the 1978-2004 results of Miller et al. (2009). In particular, L1 suggests that procyclical mortality is weak or nonexistent in young adults and middle age adults, and is therefore in conflict with the conclusions suggested by B1. Model D1 suggests effect estimates which are relatively small, while being broadly indicative of procyclical mortality across age groups. Model HP1₁₀₀ suggests consistent procyclical mortality across age groups, with smaller effect sizes than B1. Ionides et al. (2012) show that a Hodrick-Prescott smoothing parameter of λ = 100 has superior prewhitening properties to λ = 6.25, and the corresponding regression therefore has more statistical power to identify cyclical effects.

Table 3.

Percentage increase in mortality associated with a unit increase in the state unemployment rate, using different model specifications.

Model	B1		L1		D1		HP16.25		HP1100
Total	-0.52	***	-0.31	***	-0.16	*	-0.24	***	-0.33	***
		**		***		*		***		***
		**		**				*		***
20-44	-1.15	***	0.14		-0.54	*	-0.73	***	-0.47	**
		**				*		**		*
		*				+		*
45-64	-0.72	***	-0.01		-0.13		-0.14		-0.22	**
		**								*
		*								*
65+	-0.43	***	-0.16	***	-0.03		-0.16	*	-0.25	***
		**		+				+		***
		*								*
Cardiovascular disease	-0.38	***	-0.20	**	-0.06		-0.14		-0.24	***
				+						**
				+						*
Ischemic heart disease	-0.33	+	-0.35	**	-0.14		-0.28	+	-0.58	***
				+				+		**
										*
Cancer	-0.20	*	0.21	***	0.13		0.05		0.04
				*
				*
Respiratory disease	-1.04	***	-0.39	**	-0.37		-0.69	**	-0.71	***
		***		**				**		***
		**		*				*		**
Other infectious disease	-0.35		0.37		-1.14	*	-1.72	***	-0.89	*
						*		**		+
						*		**
Traffic injury	-3.76	***	-3.48	***	-1.48	***	-1.44	***	-2.11	***
		***		***		***		***		***
		***		***		***		***		***
Suicide	0.25		1.06	***	0.94	*	0.80	*	0.77	**
				*		+		+		+
				*		*		+		+
Homicide	-1.71	***	-1.20	*	-1.02		-0.74		-0.41
		*		+
		*		+

Columns represent models, as described in equation (1) and Table 1. Rows represent mortality categories. Table entries are estimates of 100α, using OLS with states weighted by the square root of the state population. Statistical significance is shown using standard OLS errors (black symbols, top row), error estimates clustered by state (gray symbols, middle row) and error estimates of Cameron et al. (2011, Section 2.2) with two-way clustering by state and year (gray symbols, bottom row; red in electronic version).

^***P < 0.001,

^**P < 0.01,

^*P < 0.05,

⁺P < 0.1.

From a methodological perspective, the cause-specific mortality results in Table 3 tell a similar story to the age category results. Traffic fatalities, typically the most clearly procyclical mortality cause, are highly statistically significant in all analyses. Procyclical cardiovascular mortality is identified by all models, but is insignificant for D1 and HP1_6.25. Model D1 typically estimates small effect sizes, relative to the other models in Table 3 and relative to previous reports in the literature: we propose an explanation for this later. For cancer, models B1 and L1 detect a cyclical effect, with opposite signs! Model B1 also fails to find a cyclical pattern for suicide, which has been considered countercyclical in the US (Luo et al., 2011; Eyer, 1977; Ruhm, 2000; Tapia Granados, 2005a). When methodologies disagree on detection of accepted relationships, they do not provide a firm foundation for investigating new phenomena. For example, the cyclical behavior of respiratory disease mortality has previously received relatively little attention, perhaps because it is somewhat unexpected. Table 3 agrees with other studies (such as Miller et al., 2009) in detecting a clear procyclical pattern of mortality due to respiratory disease.

The state clustered standard errors in Table 3 generally produce similar conclusions to the OLS standard errors, with some important exceptions. For models D1, HP_16.25 and HP1₁₀₀, state clustered standard errors are generally similar in magnitude to OLS standard errors (results not shown). This is to be expected when residual autocorrelation is small, and in this case state clustered standard errors may be less reliable than the usual OLS standard errors (Kauermann and Carroll, 2001). For models B1 and L1, many large effect sizes remain significant despite substantially inflated clustered standard errors. Conclusions about the effects on suicide and cardiovascular disease are noticeably sensitive to the use of state clustered standard errors. These two mortality categories are also identified in Section 6 as having inconsistent effects between states. Inconsistency between states leads to relatively large state clustered standard errors, since these error estimates assess uncertainty by quantifying variability between states rather than between time points.

The five models in Table 3 emphasize relationships at different ranges of frequencies. The synchronous fluctuations of many macroeconomic variables around their trends, known as business cycles, are of irregular duration and have a power spectrum spread broadly over a wide range of frequencies (Canova, 1998). It need not be the case that all frequencies of macroeconomic fluctuations are equally associated with population health. The range of frequencies at which the statistical evidence for cyclical associations is greatest could, potentially, differ from the range at which the public health consequences are greatest. One way to study these issues is through spectral analysis (Tapia Granados and Ionides, 2008) but here we simply interpret the frequency-domain behavior of the specified regression models (Ionides et al., 2012, Section S3). Model B1 performs the least detrending and therefore places the most emphasis on low frequency associations. This leads to some large effect estimates, matched with increased uncertainty (which can be viewed as larger standard errors, or unknown biases). Model HP1_6.25 emphasizes a range of frequencies intermediate between D1 and HP1₁₀₀, and the results for HP1_6.25 are generally intermediate between these two analyses. Model D1 emphasizes the highest frequencies, to such an extent that some cyclical relationship becomes obscured. Macroeconomic fluctuations involve complex relationships between many variables (Canova, 1998) and so it may be unreasonable to expect any single economic measure to capture reliably, at high frequencies, the relationship to health outcomes. Traffic injuries might be expected to have a relatively clean high-frequency relationship to economic activity (proxied by unemployment in our models) as there is an obvious and immediate causal mechanism. However, even for traffic mortality, the parameter estimates for models D1 and HP1_6.25 are smaller than for the other models.

Inasmuch as equation (1) is valid, all the estimation methods result in unbiased effect estimates: the weighting of frequencies in the estimation procedure affects the variability of the OLS estimate but not its bias. However, in practice, one cannot expect any model to be equally appropriate over all time scales. Investigating the time scales at which the model applies is therefore an integral part of data analysis. Model HP1₁₀₀ emphasizes an intermediate range of frequencies, and is seen to provide the clearest statistical evidence for cyclical mortality.

If cyclical mortality were to exist only in the context of fluctuations around a trend then it would have no long term consequences, since above-trend and below-trend fluctuations necessarily cancel out in the long run. Alternatively, if cyclical mortality were present in macroeconomic fluctuations occurring over a decade or longer, one should consider the cyclical effects at least partly responsible for observed health trends on these time scales. The indications from model B1 that procyclical mortality may be even stronger at low frequencies support this second interpretation.

6 Diagnostic Analysis

The spatiotemporal dependence of the regression residuals affects the appropriate choice of model specification, the suitability of parameter estimation methodologies, and the evaluation of uncertainty in the resulting estimates. Figure 3 shows the temporal autocorrelation of the residuals for each state at each lag. We see that there is strong positive autocorrelation for model B1, at short lags. This positive autocorrelation is reduced, but still substantial, for model L1. The autocorrelation for model D1 becomes significantly negative at lag 1, as might be expected from applying a differencing operation. There is some indication of mild negative autocorrelation after lag 1 for model HP1₁₀₀, but this model shows relatively minor deviation from the expected behavior of uncorrelated residuals.

Figure 3.

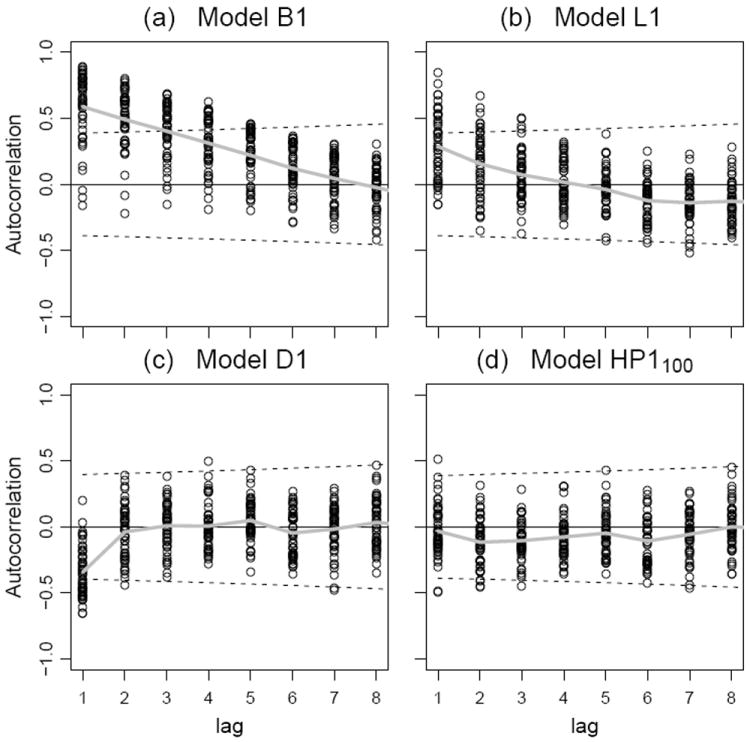
Autocorrelation of the residual in four models for total mortality. Points show the sample autocorrelation for each state at each lag. The dashed lines are at $\pm t_{n-2}{\left\{n-2+t_{n-2}^2\right\}}^{-1/2}$ where t_n−2 is the 97.5 percentile of the t distribution on n − 2 degrees of freedom, and n is the number of pairs of time points available to compute the sample autocorrelation at each lag. If the residual series were temporally uncorrelated, approximately 95% of the points should lie between the dashed lines (Moore and McCabe, 1999, Section 10.2). The gray solid line graphs the mean sample autocorrelation at each lag.

Similar patterns emerge when investigating spatial correlation. Figure 4 shows the sample correlations between the time series of residuals for all 1225(= 50 × 49/2) pairs of states. Models B1 and L1 show considerably more variability in the sample correlation that is consistent with spatiotemporally uncorrelated residuals. The sample autocorrelations of the residuals are necessarily centered near zero, due to the inclusion of year effects. The lack of a substantial spatial pattern suggests that dependence between neighboring states is not a major concern. The increased spread is another indication of temporal correlation: independent sequences which each have positive marginal temporal autocorrelation typically have sample crosscorrelation with mean zero but greater variability than temporally uncorrelated sequences. Models D1 and HP1₁₀₀ have a spread of sample cross-correlations which is approximately consistent with spatiotemporally uncorrelated residuals. The lower variability for models D1 and HP1₁₀₀ reveals a small pattern of positive correlations between residuals of states in close proximity. It would be surprising if no such phenomenon existed, but we see here that the effect is rather weak. Most of the crosscorrelation of fluctuations in mortality between states is removed by the inclusion of the national year effect δ_t. If these year effects are not included (i.e., in models of subtype 2, 3 or 4), a plot analogous to Figure 4 shows consistently positive crosscorrelations across all geographic distances (results not shown).

Figure 4.

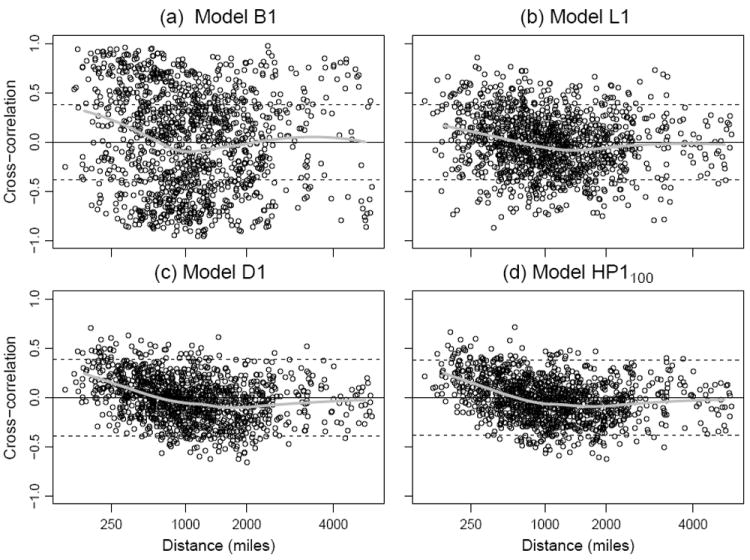
The crosscorrelation between residuals for each pair of states, plotted against distance between population-weighted state centers (from the 2000 census) in four models for total mortality. The dashed lines are at $\pm t_{n-2}{\left\{n-2+t_{n-2}^2\right\}}^{-1/2}$ where t_n−2 is the 97.5 percentile of the t distribution on n − 2 degrees of freedom, and n = 27 (for B1, L1, HP1₁₀₀) or n = 26 (for D1). If the residual series were spatiotemporally uncorrelated, approximately 95% of the points should lie between the dashed lines (Moore and McCabe, 1999, Section 10.2). The actual percentages for models B1, L1, D1 and HP1₁₀₀ are 46.1%, 79.3%, 90.9% and 91.3% respectively. The gray solid line shows a local linear regression fit to these crosscorrelations, implemented using the loess function in R2.15.0, with the default parameter settings.

Residuals can also be investigated by examination of the time plots for each state. Some representative time plots are shown in Figure 5. This figure reinforces the conclusion that OLS estimation of the basic model is a questionable practice, since the underpinning model assumptions are violated for almost all states. The linear trend model is sometimes adequate (e.g., Hawaii and Oklahoma) and sometimes not (e.g., Maine and Ohio). Both differencing and HP detrending remove systematic trends from the time series of residuals.

Figure 5.

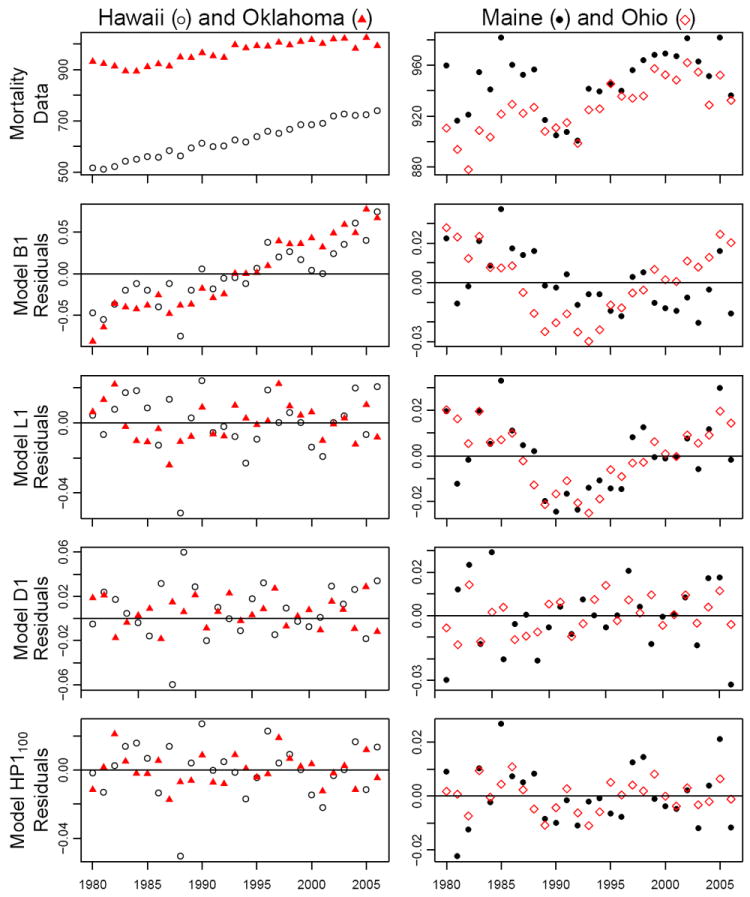
Residual time plots for four states. The top row graphs total state mortality, and subsequent rows graph residuals for each of four models.

The conclusion from these diagnostic investigations is that, among these alternatives, model HP1₁₀₀ unambiguously comes closest to satisfying the model assumptions for a standard linear model analysis. As another criterion to compare model specifications, we compared the consistency of the estimated cyclical mortality effects between states. A robust relationship between macroeconomic fluctuations and mortality might be expected to demonstrate consistent results in separate state-by-state time series analyses. We explored the stability of the panel model effect estimates across states by estimating the unemployment effect on mortality using data for one state only, i.e., the model in equation (1) for a single fixed value of the state label i. For a state-by-state analysis, one cannot estimate fixed year effects but one can still estimate models of subtypes 2–4. The results for subtype 2 are plotted in Figure 6, from which we observe that HP2₁₀₀ provides the greatest consistency between states, closely followed by D2. For example, the standard error of the 50 state-specific estimates of 100α for total mortality is 0.53 for L2, 0.45 for D2, and 0.43 for HP2₁₀₀. National fluctuations in mortality unrelated to the economy, perhaps due to infectious disease or climate, are not controlled for in model subtype 2. Some mortality categories nevertheless demonstrate consistent state-by-state effects, especially for the larger states. As might be expected, there is typically greater variation in the estimated effects for smaller states. From Figure 6, we see that the effects for total mortality, respiratory disease, traffic injuries and ages 65+ have consistent signs in all (or almost all) of the larger states. Perhaps surprisingly, suicide and cardiovascular disease show only weak patterns in the state-by-state analysis despite the evidence for overall cyclical behavior from the full panel analysis (Table 3, column HP1₁₀₀).

Figure 6.

State-specific effects of unemployment on mortality. Columns correspond to models, as specified in Table 1 and equation (1). Rows correspond to mortality categories. The estimate of 100α from fitting the model to a single state is plotted against the population of the state. Each state is represented either by its two letter abbreviation or by an open circle.

7 Conclusions

We have seen that the choice of model can have considerable influence on panel analysis of the associations between fluctuations in mortality and macroeconomic variables. These influences are simultaneously a concern, a challenge and an opportunity. The concern is that, unless a methodological consensus is found, scientific claims which are sensitive to choice of methodology must remain unresolved. The challenge is to establish statistical procedures which objectively assess the strengths and weaknesses of different analyses, and so disambiguate the conclusions. Overcoming this challenge will give an opportunity to improve understanding of the phenomenon of procyclical mortality. A historical precedent for methodological introspection in this research area is the examination and eventual rejection of the methods employed by Harvey Brenner. Indeed, panel analyses have played an important role in clarifying the evidence for overall procyclical mortality. However, we have shown that previous panel approaches have limited capability to identify more subtle components of the cyclical effect.

It is well known that positive temporal autocorrelation (Bertrand et al., 2004) and positive spatial crosscorrelation (Layne, 2007) typically cause OLS standard errors for panel models to be anti-conservative (i.e., inappropriately small). Under-estimated standard errors lead to overestimated statistical significance and hence the detection of spurious relationships. Clustering standard errors by state helps to resolve this issue, but these robust standard errors fail to correct for dependence between states. Clustering standard errors by state and year gains additional robustness, with the cost being increased variability in the standard error estimates. In addition, the OLS regression coefficient estimates remain inefficient (if unmodeled trends are considered random variables) or biased (if unmodeled trends are considered as fixed effects). We have shown that nonlinear detrending can be employed to fix these methodological shortcomings in the context of investigating cyclical mortality.

The study of cyclical mortality fluctuations is sensitive to these methodological issues because relatively small effects, which are hard to unravel from other background sources of variability, can nevertheless have substantial consequences at the population level. The larger and clearer the effect, the less sensitive its detection should be to the details of the statistical methodology used to investigate it. However, understanding the overall pattern requires investigating which subpopulations and mortality causes are involved. Inevitably, one seeks to press to the limits of the available data and statistical methodology.

We have proposed a resolution to the differing accounts of age-dependency for procyclical mortality. Our preferred specification (Table 3, column HP1₁₀₀) suggests that the effect is relatively uniform across ages, which has attractive conceptual simplicity. There may be no reason a priori to expect age uniformity. In particular, individuals in the 65+ age category are predominantly out of the workforce: they are therefore largely unaffected by some potential mechanisms such as extra hours of work, or fewer hours of sleep, during economic expansions. The 20-44 age category has the largest estimated effect for model HP1₁₀₀, yet, according to the spatiotemporal clustered errors, this age group is the only one in which the association is statistically insignificant. Other lines of reasoning, including the spatiotemporal clustered errors for other choices of the Hodrick-Prescott smoothing parameter, and other choices of standard error for model HP1₁₀₀, suggest adequate statistical evidence for this association.

Our results for cause-specific mortality (Table 3, column HP1₁₀₀) give a single set of figures consistent with previous analyses but without the occasional peculiarities that are a hallmark of misspecified models. For example, the models B1 and L1 suggest macroeconomic associations for cancer with differing signs. The statistical significance of cancer for model B1 disappears when using clustered standard errors; for L1, the countercyclical association remains significant. Miller et al. (2009) found a countercyclical association with cancer (with unspecified statistical significance) consistent with the similarity of their model specification to L1. Tapia Granados (2005a) found a procyclical association in the US for 1945-1970, but not in other time intervals. The long lag times involved in the chronic development of cancer are hard to reconcile with an unlagged cyclical relationship. However, it is entirely possible that external factors could be associated with acute complications resulting in death of cancer patients. This possibility is self-evident for cardiovascular disease, where acute cardiovascular failures are associated both with chronic disease development and external stress.

Cardiovascular disease and cancer are the two foremost causes of death in developed countries, and the cyclical behavior of cardiovascular mortality has therefore attracted considerable attention (Ruhm, 2007). Cardiovascular disease mortality has a relatively small procyclical signature over the 23 developed countries in the Organization for Economic Cooperation and Development (OECD) studied by Gerdtham and Ruhm (2006). In some countries, such as Japan (Tapia Granados, 2008), the procyclical signature of cardiovascular disease mortality seems to be strong; in others, such as Germany (Neumayer, 2004), it seems to be negligible. In Sweden there is some evidence for a countercyclical effect (Svensson, 2008; Tapia Granados and Ionides, 2011). In the US, Table 3 reconfirms the conclusions of Ruhm (2000) and Miller et al. (2009) that the dominant behavior of cardiovascular disease is procyclical. However, we found in Figure 6 that this result is not strongly consistent at the level of individual states.

The unambiguous evidence for procyclical respiratory mortality requires further investigation. This phenomenon has been noted in other studies of developed countries (Eyer, 1977; Ruhm, 2000; Neumayer, 2004; Tapia Granados, 2005b; Gerdtham and Ruhm, 2006; Miller et al., 2009), but it has become further clarified by the statistical methods we have employed. Specifically, we have shown the strong consistency between individual states, and we have employed methods that minimize the risk of identifying spurious relationships. Our data cannot readily reveal how mechanisms such as air quality (pollution) and weakened immune status (increased infectious disease transmission) may combine to produce this procyclical effect. Respiratory disease, as categorized in ICD9/10, is not necessarily infectious but does include influenza and pneumonia which are responsible for substantial mortality in old age. Infectious diseases provide a potential avenue by which those outside the workforce suffer procylical mortality, since collective resistance plays a substantial role in controlling disease spread (an effect known as herd immunity in epidemiology; Bonita et al., 2006). Overwork and a reduction in healthy behaviors during economic booms could lead to a population with weaker overall health and therefore greater transmission of pathogens. Increased travel, associated with increased economic activity, provides another potential mechanism for increased transmission of pathogens.

Previous studies (Ruhm, 2000; Miller et al., 2009) have found that homicides oscillate pro-cyclically. This result may appear counter-intuitive, and to our knowledge it has not been fully explored. According to our specification HP1₁₀₀ (and also D1 and HP1_6.25) in Table 3 there is no clear evidence that homicides are correlated with the business cycle. Inasmuch as the data support procyclical homicide, this is based on the models B1 and L1 which place more emphasis than HP1₁₀₀ on longer-term variation.

Our analyses provide weak support for an overall countercyclical nature of suicide in the US, consistent with the conclusions of Luo et al. (2011). A cyclical effect on suicide might be intuitively unsurprising, but the direction of the effect is not consistent between countries. For example, suicide in Japan is strongly countercyclical (Tapia Granados, 2008) whereas in Germany and Finland there is evidence for procyclical suicide (Neumayer, 2004; Hintikka et al., 1999). No dominant pattern was found in a study of OECD data (Gerdtham and Ruhm, 2006). Figure 6 suggests that the cyclical behavior of suicide is inconsistent between states. This conclusion is supported by the the diminished significance of the overall countercyclical effect once the standard errors are clustered by state.

Debate about individual components of cyclical mortality, and remaining uncertainty about specific causal mechanisms, should not obscure the main achievement of recent research in this area. There is now overwhelming evidence that downturns in economic activity have not had overall adverse health consequences at the population level, in the recent past of developed countries with market economies. Groups of individuals adversely affected by phenomena associated with economic booms and busts deserve assistance. At earlier stages of socioeconomic development, economic growth may have substantial health benefits above and beyond other factors such as public health programs and education (Pritchett and Summers, 1996). However, the government’s responsibility to consider the net public health consequences of its actions (Childress et al., 2002) cannot be used as a moral argument for pro-growth economic policies in the US and similar countries. Other moral obligations relevant to macroeconomic policy include the protection of individual liberties, environmental stewardship, and homeland security. Future public policies will require trade-off between economic growth and other objectives, and evidence based assessment of the positive and negative consequences of economic growth should inform this debate.