Structural and Energetic Basis of Allostery

Abstract

Allostery is a biological phenomenon of fundamental importance in regulation and signaling, and efforts to understand this process have led to the development of numerous models. In spite of individual successes in understanding the structural determinants of allostery in well-documented systems, much less success has been achieved in identifying a set of quantitative and transferable ground rules that provide an understanding of how allostery works. Are there organizing principles that allow us to relate structurally different proteins, or are the determinants of allostery unique to each system? Using an ensemble-based model, we show that allosteric phenomena can be formulated in terms of conformational free energies of the cooperative elements in a protein and the coupling interactions between them. Interestingly, the resulting allosteric ground rules provide a framework to reconcile observations that challenge purely structural models of site-to-site coupling, including (a) allostery in the absence of pathways of structural distortions, (b) allostery in the absence of any structural change, and (c) the ability of allosteric ligands to act as agonists under some circumstances and antagonists under others. The ensemble view of allostery that emerges provides insights into the energetic prerequisites of site-to-site coupling and thus into how allostery works.

ALLOSTERY IN PROTEINS: HISTORICAL OBSERVATION, BIOLOGICAL IMPORTANCE, AND PHENOMENOLOGICAL MODELING

The fields of protein allostery and structural biology matured in tandem, with developments in one field informing the other (13). The phenomenon of allostery was formally described more than 50 years ago by Monod & Jacob (5, 39), with the first protein crystal structures of myoglobin and hemoglobin reported only a few years earlier (28, 47). The dramatic appearance of protein structural pictures and rigid physical space-filling models greatly influenced scientific thinking about the molecular basis of biological function, although from the beginning structural information revealed more questions than answers about functional mechanism. Indeed, the first paragraph of the 1965 landmark paper by Monod, Wyman, and Changeux (40) remarked that “The elucidation of the structure of haemoglobin has, if anything, made this problem more challenging ….”

From a vantage point decades after the quotation was written, it is clear that the challenging problem was the development of a quantitative explanatory and predictive understanding of the allosteric mechanism, as well as a means of comparing and characterizing allosteric mechanisms from different proteins. The defining aspect of allostery is the change in binding affinity [e.g., the increase in binding affinity of oxygen by hemoglobin (17) or end-product inhibition of l-Thr deaminase (4)] due to the effect of binding a second ligand at a distinct effector site. The problem of quantitative understanding arises because allostery is action-at-a-distance: The effector site can be many angstroms away from the regulated activity site (45).

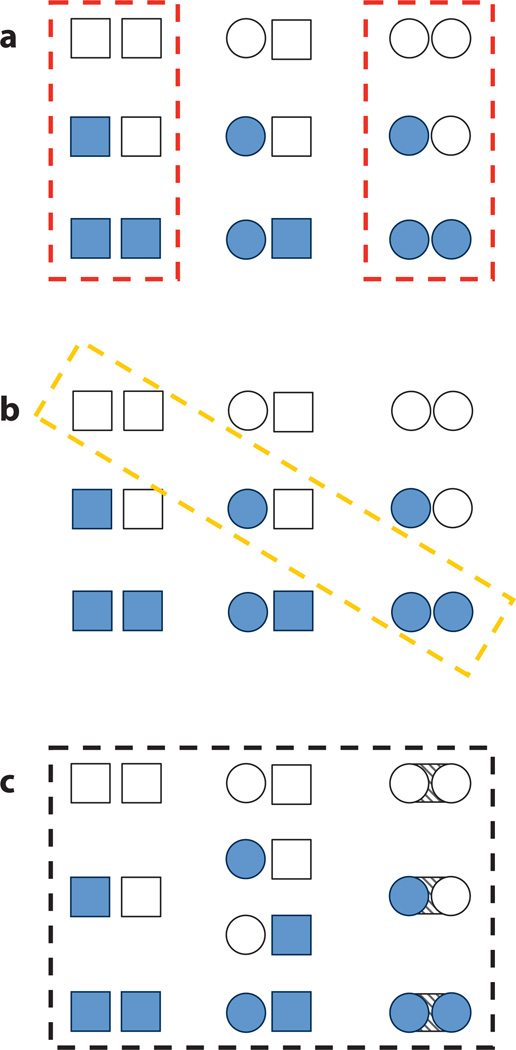
Largely in the contextual absence of structural information, initial proposals for explaining protein allostery centered around two philosophically different models, the sequential, or KNF, model of Koshland, Nemethy, and Filmer (30), and the concerted, or MWC, model of Monod, Wyman, and Changeux (40). Both models explained and predicted some experimentally observed aspects of allostery, and excellent detailed summaries of these historically important models are available (6, 9). Figure 1 emphasizes schematically the similarities and differences between the models for a two-domain allosteric protein by depicting the protein as an ensemble of conformational and liganded states (Figure 1a refers to MWC and Figure 1b refers to KNF). The models are similar in that both employ two major conformational states of the allosteric protein, a low-affinity form and a high-affinity form. Another similarity is that allosteric conformational change is favored when ligand binds. However, conformational change in the sequential model affects ligand affinity presumably through direct alteration of the binding sites, whereas conformational change in the concerted model need only affect the equilibrium between the low- and high-affinity states. The sequential model predicts that conformational changes should be directly proportional to the amount of bound ligand (Figure 1b), while in the concerted model conformational change is also multiplicatively proportional to the equilibrium between low- and high-affinity states (Figure 1a). A third difference between the models is that in the concerted model, the active and inactive conformations preexist at equilibrium, even in the absence of ligand, whereas the sequential model postulates induced fit (29) so that the active conformation is only adopted in the presence of ligand. Notably, the concerted model is considered more restrictive in that symmetric oligomers are required and negative cooperativity cannot be treated (at least in the original formulation). Biochemical and simulation data on many diverse allosteric systems support interpretation by both models (50, 58, 59, 63, 64). Regarding the archetypal allosteric protein, tetrameric hemoglobin, decades of investigation have concluded that the concerted model provides a reasonable description of its observed biological behavior (9, 17). Indeed, after almost 50 years, the ability of the MWC and KNF models to explain allosteric phenomena in a multitude of molecular systems is without question. However, in spite of the ability of these models to capture the quantitative relationship between the affinity of ligand at distinct sites, neither model provides insight into how allostery works. Are there structural and energetic requirements for each binding site? Do the allosteric effects of binding propagate from one site to the other as an obligatory series of structural distortions connecting the sites? Is there a unifying framework that can be applied to all allosteric systems?

Figure 1.

Three schematic models of protein allostery. Each panel depicts all possible microstates of the ensemble of a two-domain allosteric protein, perhaps dimeric invertebrate hemoglobin. Each subunit of the protein can adopt two distinct conformations, tensed (squares) or relaxed (circles), and two distinct modes of ligand binding, unbound (open shapes) or bound (filled shapes). Dashed boxes indicate the possible microstates allowed under the postulates of each model. (a) Model of Monod, Wyman, Changeux (MWC). (b) Model of Koshland, Nemethy, Filmer (KNF). (c) The ensemble allosteric model (EAM) presented in this work. Note that the EAM permits a greater number and diversity of allowed microstates and incorporates a finite subunit interaction energy (diagonal-striped area between circular subunits). The authors believe that these differences endow the EAM with a superior ability to explain, unify, and predict protein allostery. The enumerations of the partition functions corresponding to each of these models are given in Figure 5, and additional details are listed in Table 1.

THE CURRENT APPROACH TO UNDERSTANDING ALLOSTERY IN TERMS OF STRUCTURE IS FUNCTION

The low-resolution structure of tetrameric hemoglobin, among the first protein structures to have been determined, revealed its internal symmetry as a striking confirmation of the predictions of the concerted model of allostery (42, 47). Also in accord with the model, higher-resolution structures of the bound and unbound forms demonstrated two distinct structures of each monomer, an unbound tensed (T) form and a bound relaxed (R) form (46). Perutz (46) thus proposed an influential structural model for hemoglobin allostery, in which a small number of individual salt bridges mediate the equilibrium between ligand binding and tertiary and quaternary structural change. This general model, elaborated and refined by many investigators (9, 16, 17, 20, 23, 34), has explained most experimental data, including cooperativity of ligand binding, the alkaline Bohr effect, and the effect of 2,3-bisphosphoglycerate on ligand affinity, and thus can be viewed as a success story for structure- and computation-based analysis of allosteric systems.

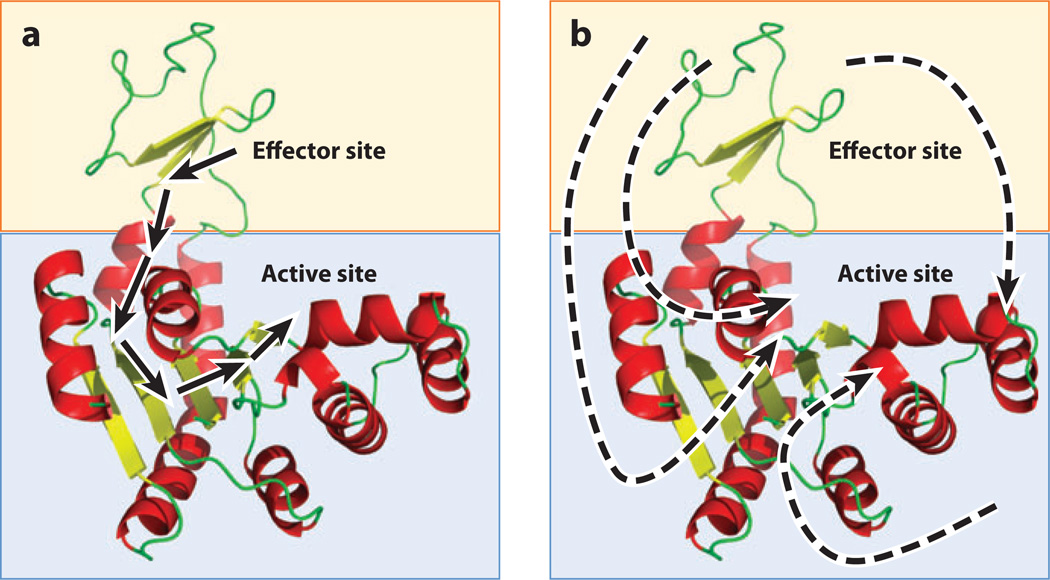
The apparent success of the structural model in describing hemoglobin perhaps suggests that the allosteric phenomenology of any protein can be quantitatively understood by monitoring the presence or absence of individual bonds in a picture of its folded structure. When the MWC requirement for symmetric oligomerization is removed, additional allosteric systems can be rationalized in terms of X-ray crystal structures, increasing the generality of interpretation. Since those original studies, this structural view of allostery has been the reigning paradigm owing to its simplicity and visual appeal. Extreme manifestations of this structural view even propose allosteric pathways spanning a folded protein, in which individual noncovalent bonds between evolutionarily conserved residues are presumably sequentially formed, strained, and broken to transmit energy from an effector site to a binding site (11, 37, 52) (Figure 2a).

Figure 2.

The structure-based and non-structure-based views of allostery. (a) A hypothetical two-domain protein (blue and orange boxes) contains effector and active sites. The structure-based view of allostery posits that one or a small number of unique pathways of structural deformations (arrows) propagate energy between the sites, thus enabling the allosteric mechanism. Such a view tacitly assumes that the free energy of the allosteric mechanism is proportional to the enthalpy of the noncovalent bonds made and broken along this pathway. (b) A hypothetical two-domain protein (blue and orange boxes) contains effector and active sites. The non-structure-based view of allostery posits that regional changes in dynamics, protein, and/or solvent conformational entropy, or population shifts, are the dominant contributors to the free energy of the allosteric mechanism. Unique energetic pathways are difficult or impossible to place on a single molecular structure of the protein because the free energy is potentially a combination of enthalpic and entropic contributions from many sources.

Is this conclusion realistic? In other words, what does a structural view of allostery get right? Apparent pathways of structural distortion in some proteins are verifiable through point-mutation and thermodynamic cycle experiments (37, 52). Many individual allosteric proteins, as well as a recent survey of multiple known allosteric proteins, demonstrate that substantial structural changes occur upon ligand binding (10, 22, 32, 56, 64). In addition, allosteric changes appear to be predictable through the analysis of structural characteristics (19) and in some cases can be simulated with structural knowledge of the unbound and bound forms (18). Taken together, such results suggest that structural change can be a major contributor to the energetics of allostery and that molecular simulation can provide access to these changes. However, an important question remains: Do these demonstrated structural changes in isolated systems provide an understanding of the underlying ground rules for allosteric coupling?

CONFLICTING OBSERVABLES AND CONCEPTUAL LIMITATIONS ARISING FROM THE STRUCTURE-BASED APPROACH

Emerging theory and accumulating experimental examples suggest that the reigning structural paradigm (i.e., that energetic changes can be rationalized by changes in the bonds that are made or broken in the context of the initial and final structures) does not quantitatively explain all the available data. Although this failure is described in more detail below, a fundamental limitation of structural interpretations is the assumption that the macroscopic T and R states obtained from the thermodynamic analysis of the experimental data are adequately represented in the high-resolution structures of the different forms. In essence, the assumption is that the various functional states of the protein (i.e., the T and R states) contain no significant conformational heterogeneity.

How does this affect the structural view of allostery? Cooper & Dryden (8) described in a classic paper almost 30 years ago the possibility of allostery being manifested without structural change, resulting instead from entropy changes that effectively change the width of a conformational distribution, without changing the average position of the atoms. The practical implication is that an understanding of the determinants of allostery need not reside in an inspection of the bonds that are made and lost in the average structure (Figure 2b). Indeed, since that pioneering work, numerous examples have emerged that, if anything, raise more questions about the determinants of allostery than they answer. For example, direct confirmation of allostery without a conformational change (49), allostery in the absence of a structural pathway (12, 48, 60), negative cooperativity (51), allosteric changes from surface mutations that do not affect structure (53, 54), and allosteric communication facilitated by disordered segments (51) are all examples of allosteric phenomena that are difficult, if not impossible, to rationalize in the context of structural changes alone. Perhaps most puzzling of all are examples of allosteric ligands that bind to the same site and elicit agonistic effects under some circumstances and antagonistic effects under others (26, 27).

How can these observations be explained in the context of efforts to relate phenomenological models of allostery (i.e., MWC or KNF) to structural changes? The answer, of course, is that they cannot. No less an authority than one of the creators of the MWC model has noted that, “The simplicity of the theory [MWC] facilitates its experimental test. However, both the theory and the available technology have reached their limits. This is an important area for future research” (6). Here we hope to demonstrate that the limitations to purely structural or phenomenological models of allostery can be overcome by reformulation of the phenomenon of allostery as a property of the energy landscape or ensemble of conformations for a protein (14, 15, 24, 25, 38, 43).

RECONCILING AND UNIFYING EXPERIMENT IN THE CONTEXT OF AN ENSEMBLE MODEL OF ALLOSTERY

To investigate allostery, we take as the starting point the fact that proteins are ensembles of states. Of course, this is not to say that considering proteins as ensembles represents a new view of allostery. Indeed, as rightfully pointed out (9), the authors of the MWC were well aware of the ensemble nature of proteins and the MWC model itself represents an explicit treatment of the ensemble and the effect of ligand on that ensemble. However, also noted by the authors of these early thermodynamic treatments is that the underlying molecular basis for the allostery is not described by the model. How then can we develop a general understanding of allostery that acknowledges the ensemble nature of the process but also provides insights into the structural basis underlying the observed effects? To address this issue, we develop and describe allostery in terms of a general ensemble model, which we refer to as the ensemble allosteric model (EAM).

The hallmark feature of this model is that the allostery is treated as a macroscopic effect that results from the ligand-driven stabilization of cooperative elements, which themselves interact, a notion that has historical roots in both structure-based allostery (24, 43) and more general descriptions of allostery (14, 15, 38, 25). This is described in some detail below, but the end result is that, unlike the KNF model, in which coupling arises as a result of the binding of ligand, and unlike the MWC model, in which coupling between regions is obligatory, the EAM can be used to investigate the effect of thermodynamic architecture of a protein on how energy changes (i.e., binding allosteric ligands, or mutation) in one part of a protein will be manifested at other sites. In other words, the observed binding of ligand and the change in affinity that results from the binding of ligands are seen as effects of both the energy landscape and how the conformational equilibria in the different regions of the protein are poised prior to ligand binding. In essence, the EAM allows us to ask, what role does the energy landscape play in facilitating allostery? Are there unifying principles or ground rules that dictate the requirements for allostery? Can structurally and/or functionally dissimilar proteins share common thermodynamic architecture?

Theory of the Two-Domain EAM

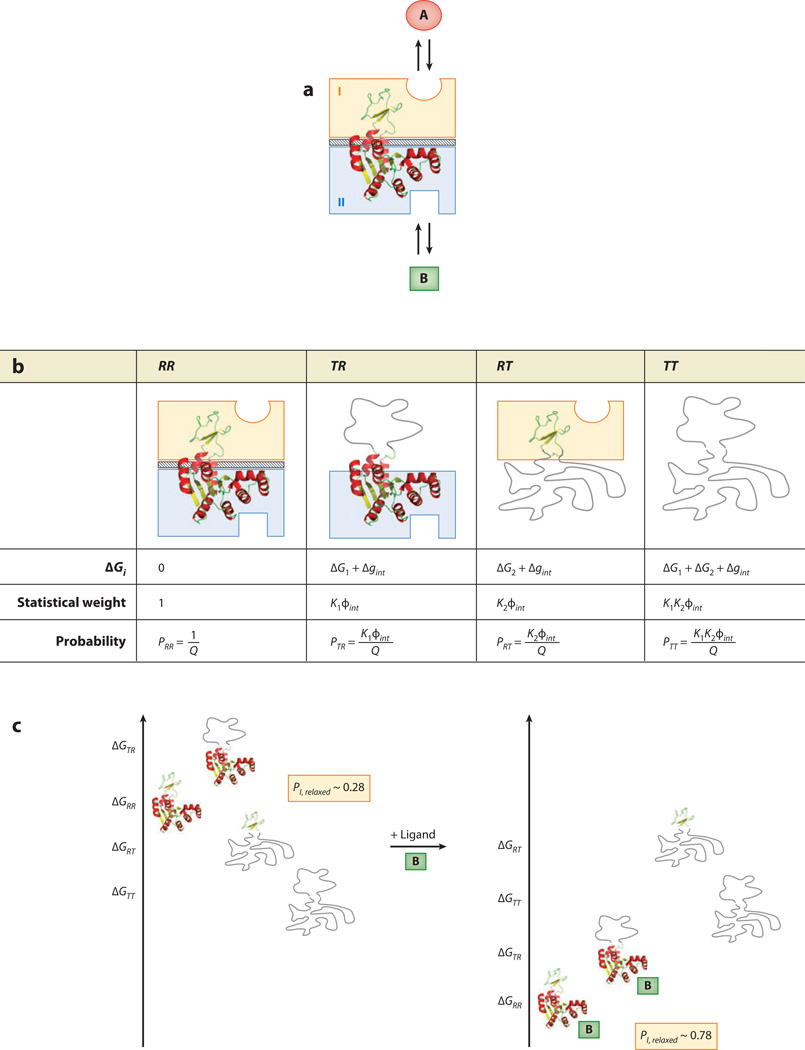
It is well established that proteins have modular structure and that multidomain regulatory proteins often segregate the binding sites for each ligand into different structural domains (2, 3, 31). Thus, as a first approximation, we represent an allosteric protein as two domains that are allowed to interact (Figure 1c). In the general case, depicted in Figure 3a, one domain is considered the allosteric regulatory binding site and the other domain the functional binding site. To explore the energetic basis of allostery, each domain is allowed to independently sample distinct conformations with defined free energies—the simplest of which is a two-state model. Following the lead of the pioneering MWC model, the EAM treats each domain as being in a low-affinity T state or a high-affinity R state as described above (Figure 3b). This results in four distinct microstates i each having a free energy contribution from transitions between the R and T states (ΔG_C,i) and change in interaction energy (Δg_int,i) if one or both of the domains adopt the low-affinity state:

$$\mathrm{\Delta }{G}_i=\mathrm{\Delta }{G}_{C,i}+\mathrm{\Delta }{g}_{\mathit{\text{int,i}}}.$$ 1.

Equation 1 highlights the feature that distinguishes the EAM from structure-based models: Allostery is viewed, without regard to structure, in terms of ensembles whose populations are dictated by the free energy of conformational change within each domain and the magnitude of coupling between domains. As such, the EAM can be applied equally well to the study of allostery in any system exhibiting conformational change (e.g., intrinsically disordered proteins, folded proteins, or combinations thereof).

Figure 3.

The ensemble allosteric model (EAM) applied to a two-domain allosteric protein. (a) Schematic representation of a hypothetical two-domain allosteric protein. Domain I (orange box) binds ligand A, and domain II (blue box) binds ligand B. The diagonal-striped area depicts a specific interaction between the two folded domains (i.e., R states) with a free energy Δg_int. Note that this system is conceptually identical to the protein ensemble depicted in Figure 1c. (b) Boltzmann-weighted populations of each microstate in the ensemble. R, relaxed, or high-affinity, state; T, tense, or low-affinity, state. Although the cartoons for T domains appear unstructured, all equations apply equally well to the case in which both T and R states are structured but exhibit a difference in binding affinity. (c) A specific case demonstrating allosteric coupling: Stabilizing domain II with ligand B also stabilizes domain I owing to the favorable interaction energy. Site-to-site coupling is evaluated through the addition of ligand B. Because addition of ligand B stabilizes those states that bind ligand B, the ensemble probabilities are redistributed. Binding of ligand at site B is thus coupled to the transition of domain I from a T state to a R state (possibly but not necessarily folding of domain I) as described in the text. The biologically reasonable values used for this example are ΔG₁ = −0.7 kcal mol⁻¹, ΔG₂ = −2.3 kcal mol⁻¹, Δg_int = +1.6 kcal mol⁻¹, Δg_Lig,B = −3.0 kcal mol⁻¹.

Boltzmann weighting each conformation’s free energy yields statistical weights, S_i:

$$S_i=e^{-\frac{\mathrm{\Delta }{G}_i}{RT}}.$$ 2.

Summing all weights gives the partition function, Q, that thermodynamically describes the ensemble:

$$Q=\sum _i{S}_i.$$ 3.

The probability of any particular state j can be expressed as

$$P_j=\frac{S_j}{Q}=\frac{S_j}{{\sum }_i{S}_i}=\frac{e^{-\frac{\mathrm{\Delta }{G}_j}{RT}}}{{\sum }_i{e}^{-\frac{\mathrm{\Delta }{G}_i}{RT}}}=\frac{e^{-\frac{\mathrm{\Delta }{G}_{C,j}+\mathrm{\Delta }{g}_{\mathit{\text{int,j}}}}{RT}}}{{\sum }_i{e}^{-\frac{\mathrm{\Delta }{G}_{C,i}+\mathrm{\Delta }{g}_{\mathit{\text{int,i}}}}{RT}}}.$$ 4.

The importance of the interaction energy Δg_int in the allosteric response becomes clear in this context. For instance, in the states wherein one domain undergoes a conformational transition, the interaction energy either increases or decreases the probability of the state in which the other domain is low affinity (T). This is the means by which domains sense each other in the EAM.

It is worth elaborating on the physical meaning of Δg_int to add clarity to the model. The domains are coupled to one another, i.e., the domains can allosterically sense one another, when Δg_int ≠ 0. When Δg_int > 0, the statistical weights of states associated with the broken interaction are reduced. Such a situation can arise, for example, when two domains share a complementary hydrophobic surface. The most energetically favorable arrangement would be for both domains to interact with one another, as opposed to exposing hydrophobic side chains to solvent. A contrasting situation can arise in which Δg_int < 0 when it is energetically more favorable to expose the interaction surfaces to solvent. Such a situation might exist for the same hydrophobic surfaces described above, but at low temperatures (1). An important aspect of the model that allows it to capture general thermodynamic ground rules for allostery is that the structural basis for the coupling is irrelevant: Only the magnitude and sign of the energy matter. This is important because, in principle, it provides a means of describing two completely different allosteric proteins in terms of the same thermodynamic rules. This point is discussed in more detail below.

To ascertain the allosteric response of our ensemble, a perturbation can be introduced. This can arise from any source contributing to a change in the free energy of a domain, including but not limited to ligand binding, amino acid substitution, a change in ionic strength, osmolyte/denaturant concentration, and covalent modification (e.g., phosphorylation and methylation). The perturbation is depicted here as ligand binding; i.e., ligand A can bind to domain I and ligand B can bind to domain II (Figure 3a). How does the binding of ligand B to domain II influence the ability of domain I to bind ligand A?

Mass action dictates that the addition of ligand to a system stabilizes the state with the higher affinity for ligand. To generally represent all allosteric proteins, whether structured or disordered, the EAM is depicted here as having an R state that is more structured and a T state to which binding is neglected; i.e., ligand A can bind only to microstates that have domain I in the R state, and ligand B can bind only to microstates that have domain II in the R state (Figure 3a). Accordingly, the native state (RR) can bind both ligands, microstate 1 (TR) can bind only ligand B, microstate 2 (RT) can bind only ligand A, and the TT microstate can bind neither (Figure 3b).

To address the posed question, ligand B is introduced and assumed to bind only macrostates that have domain II in the R state. The free energy of binding will stabilize the R states for domain II (i.e., states 1 and N), which redistributes the ensemble and has the following effect on the partition function:

$$Q_{B>0}=Z_{\mathit{\text{Lig,B}}}\left(\sum _{\mathit{\text{i,II Relaxed}}}{S}_i\right)+\sum _{\mathit{\text{j,II Tensed}}}{S}_j,$$ 5.

where Z_Lig,B = 1 + K_a,B[B], such that K_a,B is the intrinsic association constant of domain II for ligand B. The redistribution of the ensemble becomes clear in the context of Equation 5 because states that have domain II in the R state have an additional term in their statistical weight (i.e., Z_Lig,B). We can thus evaluate allostery by determining the probability of domain I to be in the R state both with and without ligand B.

Without ligand B, the probability of having a domain I in the R state is

$$P_{\mathit{\text{I,Relaxed}}}(B=0)=\frac{{\sum }_{\mathit{\text{I,Relaxed}}}{S}_i}{Q}=\frac{1+S_{RT}}{1+S_{TR}+S_{RT}+S_{TT}}.$$ 6.

In the presence of ligand B, this probability becomes

$$P_{\mathit{\text{I,Relaxed}}}(B>0)=\frac{{\sum }_{\mathit{\text{I,Relaxed}}}{S}_i}{Q}=\frac{Z_{\mathit{\text{Lig,B}}}+S_{RT}}{Z_{\mathit{\text{Lig,B}}}(1+S_{TR})+S_{RT}+S_{TT}}.$$ 7.

As Equation 7 indicates, the impact of ligand B will depend on the intrinsic stabilities, interaction energy, and free energy of ligand binding. An example of such a system is depicted in Figure 3c, which demonstrates the nature of the allosteric response of the system. In the absence of ligand B, domain I is only modestly populating (~30%) the R state (i.e., states RR and RT). Upon addition of ligand B, each microstate with domain II in the R state is stabilized by

$$\mathrm{\Delta }{g}_{\mathit{\text{Lig,B}}}=-RT\text{ln}(Z_{\mathit{\text{Lig,B}}})=-RT(1+K_{a,B}[B]).$$ 8.

Because the two domains can sense each other through the interaction energy, stabilizing the R states of domain II also stabilizes the R states of domain I through the redistribution. This leads to domain I populating the R state ~80% of the time in the presence of ligand B (Figure 3c). As described below, despite the relative simplicity of the two-domain model, it provides unique mechanistic insight into the thermodynamic basis of allosteric activation.

Results from the Two-Domain EAM: The Connection Between Structure and Allostery Is not Straightforward

To quantify allostery, we introduced the coupling response (CR) between the two ligand binding sites (25), which provides a measure of the change in probability of domain I being in the R state, normalized to a value proportional to the free energy introduced into the system (at the effector site):

$$CR\equiv \frac{|\mathrm{\Delta }{P}_{\mathit{\text{I,Relaxed}}}|}{\mathrm{\Delta }\text{ln}(Z_{\mathit{\text{Lig,B}}})}=\frac{|P_{\mathit{\text{I,Relaxed}}}(B>0)-P_{\mathit{\text{I,Relaxed}}}(B=0)|}{\text{ln}(Z_{\mathit{\text{Lig,B}}})}.$$ 9.

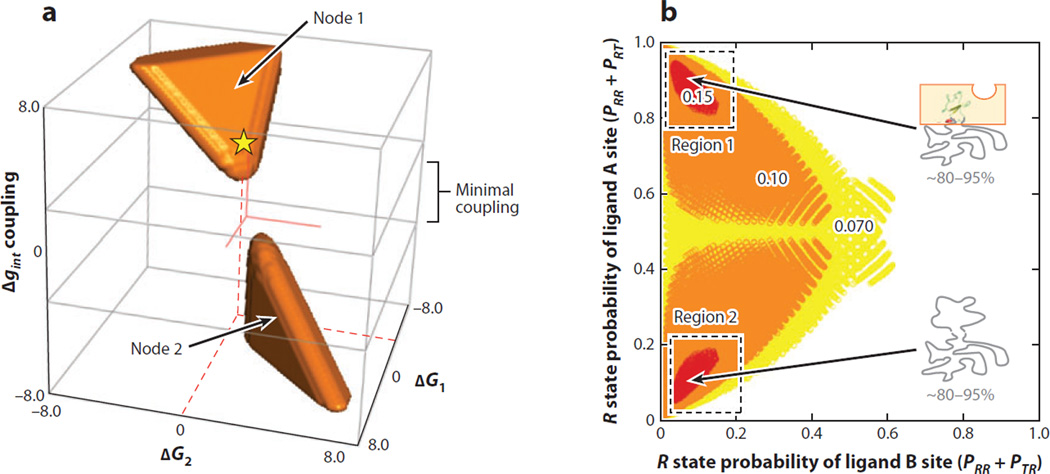
In other words, CR is a metric that reports on the degree of allosteric response by domain I when ligand B is introduced. By performing an exhaustive search of parameter space, we can determine unambiguously what thermodynamic architectures result in the highest CR (Figure 4).

Figure 4.

Coupling response (CR) in the ensemble allosteric model EAM: Disorder maximizes allostery. (a) An exhaustive search of parameter space reveals two nodes (orange regions) where coupling is most substantial (CR > 0.10). Node 1 exhibits agonistic behavior, and Node 2 exhibits antagonistic behavior. Red solid lines indicate the origin of the coordinate system, and the yellow star with red dashed lines indicates the approximate parameter combination used to generate the data in Figure 3c. (b) Plot of the probability of R state (high-affinity) domain I ligand A site versus R state (high-affinity) probability of domain II ligand B site. Colors indicate the relative CR upon addition of ligand B (red is strongest response, white is weakest response). Allosteric coupling is maximized if one or both of the domains are substantially disordered, as indicated. Note that Region 1 corresponds to probabilities calculated from the energetic parameters of Node 2 and vice versa.

Structural models of allostery might view coupling as a phenomenon that results from a direct energetic pathway linking the two sites, i.e., a network of interactions that can be viewed in a crystal structure (11, 37, 52). Were this to be true, it would generally be expected that coupling would be maximized in cases in which a stable, well-folded structure connects two domains. Paradoxically, such a conclusion is not borne out of the current analysis. In particular, an inverse relationship between allosteric coupling and stability within the molecule is seen (Figure 4). The importance of this result can be appreciated when the different models for conformational change are considered. In the case where both the T and R states correspond to folded structures, the ligand-induced shift from T to R can easily be conceptually recast in terms of the ligand inducing a structural change that propagates from the binding site to the active site. Such a mechanical interpretation is challenged, however, when the T state instead corresponds to an intrinsically disordered (or unfolded) state. In such a case, the unfolded domain would undergo cooperative folding upon ligand binding. In the absence of ligand, the unfolded domain would presumably occupy a multitude of conformations. The coupled folding and binding would result in the formation of numerous bonds within the domain, between the two domains, and between the domain and solvent. In the limit that the folding reaction is cooperative, all bonds would be formed in a more or less all-or-none fashion, regardless of whether they correspond to the interior or exterior of domain II. In effect, such a scenario would suggest that a defined structural pathway through the protein is not a prerequisite for allostery. If a structural pathway is not the determinant of the allosteric effects, what is?

To address this question, we can examine what parameter combinations for the stabilities and interaction energy produce maximum allosteric coupling (Figure 4a). Inspection of the data reveals several features. First, two separate groups of parameter combinations facilitate coupling, although within each group, significant degeneracy in parameters is observed (i.e., a unique set of values for ΔG₁, ΔG₂, Δg_int is not required). Second, despite the significant degeneracy of parameter combinations, all such combinations invariably involve either significant positive or negative interaction energy Δg_int (Figure 4a).

More detailed insight can be gained by recasting the parameter combinations in Figure 4a in terms of the probabilities of microstates for domains I and II to be in the R state in the absence of ligand (Figure 4b). Shown are the parameter combinations that produce the most significant CR values (i.e., CR values greater than 0.07, 0.10, or 0.15 in Figure 4b). Several features of the data are evident. First, despite the highly degenerate energies, the common feature shared by all parameter sets is that optimum coupling is observed when one or both of the domains are populating the T state (i.e., 1 – P_R) a significant fraction of time in the absence of ligand. In essence, the allosteric coupling is greatest when the ensemble is poised to respond to the addition of ligand B by switching from T to the R state. Second, the two nodes in Figure 4a correspond to antagonistic (i.e., ΔP_I,Relaxed > 0) or agonistic (i.e., ΔP_I,Relaxed < 0) responses elicited by ligand B, indicating that even in the context of the most simple two-domain model portrayed in Figure 3, both positive and negative coupling can, in principle, be captured. Finally, it should be noted that the results shown in Figure 4 are not an artifact of the simplicity of the two-domain model. To the contrary, increasing the complexity to include multiple domains results in the same conclusion. Namely, coupling is maximized when at least one domain is significantly biased toward the T state (25).

So what is happening that results in a bimodal maximum in CR? As noted above, each node in Figure 4 corresponds to either significant positive (i.e., agonistic) or significant negative (i.e., antagonistic) response to ligand B. Agonism occurs when the TT microstate dominates the ensemble, and the two domains are positively coupled. In this case, adding ligand B stabilizes domain II, which in turn stabilizes domain I. Antagonism occurs when only domain II is in the T state, but the interaction between domains is negative. In this case, addition of ligand B stabilizes the R state of domain II, which destabilizes the R state of domain I. Although the effects are opposite, both agonism and antagonism result from the same factors. If the energetic balance in the protein is such that the ensemble is poised with domain II populating the T state, a significant fraction of the time the ligand-induced redistribution of the ensemble to high-affinity states for ligand B (i.e., the R state) will induce a shift to the high- or low-affinity state of domain I, resulting in agonism or antagonism, respectively.

Returning to our question, if structural pathways are not responsible for allosteric coupling, what is? The results presented here reveal allostery to be a consequence of conformational stabilities of domains as well as the interactions between domains. Inasmuch as individual bonds within a domain play a role in stabilizing one conformation relative to another, they obviously play a role in coupling. However, extending this logic to support the argument that the intervening residues correspond to a pathway or a network of interactions belies the physical principles underlying the observed effects. For example, surface-exposed mutations destabilize a domain without changing its structure, yet nonetheless result in long-range effects (53, 54), demonstrating that the stability of the cooperative element of the different substructures plays a role in coupling. Thus, changes in the protein that affect the stability of a particular substructure, whether or not they affect the interactions within (or path through) the protein, can affect allosteric coupling. Indeed, inspection of the parameter combinations in Figure 4 suggests that changes in the stability of any one domain or interaction energy in response to a perturbation can be compensated by changes in other domains, regardless of the nature of the perturbations. In short, in the context of the ground rules revealed here, allostery can be both ablated and restored without any consideration of the structural origins of the effects. Although lacking the visual appeal of a conserved structural pathway traversing a protein core, the view of allostery that emerges from this model allows us to reconcile the puzzling observations of allostery without a pathway of structural distortion or without any structural change at all (7, 21, 49).

The Relationship Between EAM and Classic Models of Allostery

The framework of the EAM is unique in that it views allostery in terms of ensembles that are dictated by the intrinsic stabilities of conformations for each cooperative substructure (i.e., domain) in the protein and the interactions between domains, a construction that contrasts sharply with the MWC and KNF models (62). The defining characteristic of MWC is that there is an intrinsic equilibrium between two macroscopic states that bind ligand. The transition from all R to all T states is assumed to be completely cooperative, i.e., implicitly there is infinite coupling between domains that suppresses any conformational intermediates. In addition, MWC has two intrinsic binding affinities built into it: one for the T state and one for the R state. This apparent difference in binding affinity leads to the cooperative nature of the oxygen binding curve. This is different from KNF, which assumes a transition between states upon ligand binding that has been sometimes referred to as induced fit (29).Of course, KNF need not obligatorily propagate through induced fit, as KNF is a purely thermodynamic model. Conformational selection is also formally compatible with KNF depending on which of the two processes dominates in the ensemble-mediated allosteric response. KNF also assumes the binding affinity of the T state to be negligible compared to that of the R state. The qualitative differences between the various models of allostery can best be understood by a detailed comparison of the partition functions of each model.

The MWC model has the following partition function:

$$Q_{MWC}={(1+c{K}_{R,MWC}x)}^2+L^{-1}{(1+K_{R,MWC}x)}^2.$$ 10.

In Equation 10, L is the intrinsic equilibrium between the dimer unbound T₀ and R₀ states (i.e., L = T₀/R₀) (Figure 5).

Figure 5.

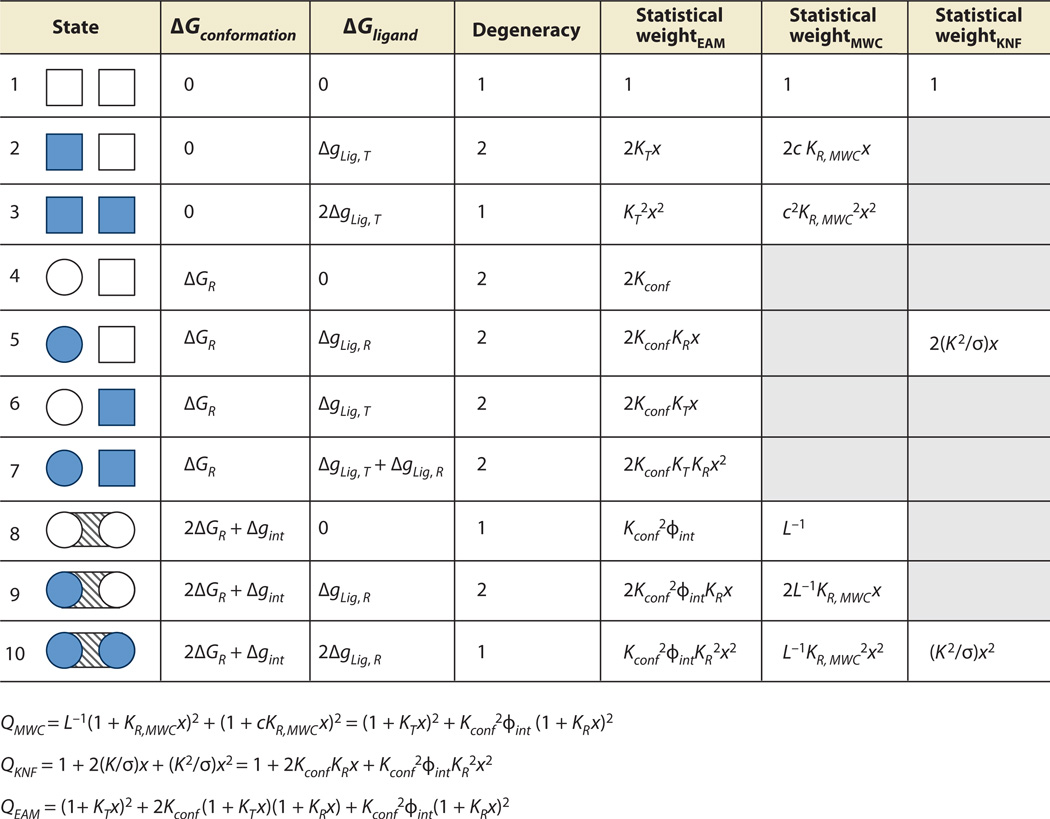
Allowed microstates and partition functions for three models of allostery. The two-domain protein depicted can be thought of as dimeric hemoglobin, binding the ligand oxygen (x = [O₂]). Columns MWC, KNF, and EAM specify which microstates are allowed in each model, based on the ensembles of Figure 1. L is the MWC equilibrium between unbound tense (T) and relaxed (R) states, c = K_T,MWC/K_R,MWC is the MWC coupling parameter, and K_T,MWC and K_R,MWC are the MWC affinities of the T and R states, respectively, for oxygen. K is the KNF affinity of the R state for oxygen and −RTlnσ represents the KNF-Pauling perturbed interaction energy. K_conf is the EAM equilibrium between unbound T and R states, ϕ_int is the EAM interaction statistical weight, Δg_Lig,T = −RTln(K_Tx), and Δg_Lig,R = −RTln(K_Rx), where K_T and K_R are the intrinsic association constants for the T and R states, respectively. The mathematical expansions described in the main text result in the three partition functions listed at the bottom of the figure. Each partition function is expressed in terms of the variables of the EAM to facilitate direct comparison of each term (Table 1). Note that the EAM permits the maximum degree of freedom in this allosteric system. Abbreviations: EAM, ensemble allosteric model; MWC, Monod-Wyman-Changeux; KNF, Koshland-Nemethy-Filmer.

Similar expressions can be developed for the Pauling-KNF model. The Pauling-KNF model is slightly different than the KNF model as follows. Pauling-KNF states that there is an interaction energy endowed to the system when two adjacent hemoglobin subunits bind oxygen, whereas KNF posits that only one subunit binding results in the breaking of the interaction (44) (Figure 5). We consider the KNF model, which has the following partition function:

$$Q_{KNF}=1+2\left(\frac{K}{\sigma }\right)x+\left(\frac{K^2}{\sigma }\right)x^2.$$ 11.

In Equation 11, K is the intrinsic binding affinity of the R state (which assumes that the binding affinity to the T state is negligible), and −RTln(σ) is the free energy of the perturbed interaction.

Finally, a similar logic permits development of an expression for the partition function for the EAM (Figure 5). In this case, the full spectrum of possible states are included in the partition:

$$Q_{EAM}={(1+K_{T}x)}^2+2K_{\mathit{\text{conf}}}(1+K_{T}x)(1+K_{R}x)+K_{\mathit{\text{conf}}}^2{\mathrm{\varphi }}_{\text{int}}{(1+K_{R}x)}^2.$$ 12.

In Equations 11 and 12, K_R and K_T represent the intrinsic association constants for each state, ϕ_int is the interaction energy statistical weight [i.e., ϕ_int = exp(−Δg_int/RT)], and K_conf is the conformational equilibrium between T and R states for each monomer, which is different from the L term in the MWC model, as noted below.

The expressions in Figure 5 provide an appreciation for the difficulty in deducing mechanism from the MWC and KNF formulations. By consideration of only the EAM terms that have a corresponding term in either the MWC or KNF models, the physical origins of the fitted parameters for the KNF and MWC models in the context of the EAM can be demonstrated (Table 1). It is clear from the table that all models for allostery divide the same total system energy differently. For instance, in the MWC model, the L⁻¹ term (i.e., the conformational equilibrium of T/R) is analogous in the EAM to a nonlinear combination of the intrinsic conformational equilibrium of the monomers (K_conf) and the additional energetic penalty of breaking the interaction between two domains (ϕ_int). Furthermore, the binding affinities of the so-called T and R states are in fact a convolution of the intrinsic affinities of each state, the conformational equilibrium, and the energy of interaction. Similarly, the KNF model has the intrinsic binding affinity of a R state mixed with the conformational equilibrium and the interaction energy.

Table 1.

Partition function coefficients for several models of allostery where Q = c + bx + ax²

Modela	Coefficient a	Coefficient b	Coefficient c
EAM(MWC)b	(1 + Kconf2 ϕint)	(KT + Kconf2 ϕint KR)	(KT2 + Kconf2 ϕint KR2)
MWC	1 + L−1	KR,MWC(L−1 + c)	KR,MWC2 (L−1 + c2)
EAM(KNF)c	1	Kconf KR	Kconf2 ϕint KR2
KNF	1	K/σ	K2/σ

^aThe EAM coefficients a, b, and c of the quadratic forms of the three partition functions listed in Figure 5 can be directly compared to the corresponding coefficients of either the KNF model or the MWC model using Table 1. Each pair of rows represents a comparable set of coefficients between two allosteric models.

^bEAM_(MWC) terms include contributions from to states 1, 2, 3, 8, 9, and 10 from Figure 5.

^cEAM_(KNF) terms include contributions from to states 1, 5, and 10 from Figure 5.

Abbreviations: EAM, ensemble allosteric model; MWC, Monod-Wyman-Changeux; KNF, Koshland-Nemethy-Filmer.

The importance of the differences contained within Figure 5 and Table 1 with regard to interpreting mechanisms cannot be overstated. These relationships reveal that quantitatively similar results in apparent coupling between sites (in the context of MWC and KNF models) can be obtained from numerous combinations of parameters and thus a multitude of possible mechanisms. It is these differences, however, that provide a framework for understanding the energetic determinants of allostery.

Biological Insights Provided by the Two-Domain EAM

A significant advantage conferred by the EAM is that it provides organizing principles for understanding allostery, in terms of transferable principles that apply to different systems without restrictions of symmetry, oligomerization state, or even presence of structure. Because the EAM has been developed in terms of experimentally accessible quantities (i.e., stability of individual domains can be measured and interaction energies can be inferred by the degree of additivity of multidomain constructs), the model in principle provides a venue for obtaining a quantitative understanding of allostery. Furthermore, because this description is based purely on thermodynamics, it does not require that the observed effects be rationalized in terms of individual bonds being broken or made in the context of a static structure of the molecule. In addition to the generality of the model, EAM also provides a vehicle for understanding phenomena that have been neglected for decades, including, but not limited to, the effects of distal or surface-exposed mutations on activity, how the same ligand in different tissues can act as agonist or antagonist (see below), and allosteric changes that are not manifested as changes in structure. Finally, the EAM explains why reciprocity is not a necessity in allosteric systems; i.e., the effect of a perturbation to domain A on domain B is not equivalent to the effect of a perturbation to domain B on domain A. As Figure 3 and Figure 4 reveal, the interaction surfaces and thus coupling energies are likely to be different in each case, and thus the observed coupling will be different. The biological implications of this last point are intriguing, as it explains why structurally similar domains can exhibit different regulatory properties when their sequential order is changed in a multidomain protein (3). In our view, these conceptual differences permit the EAM to pose additional questions amenable neither to classical allosteric models nor to purely structural interpretations of allostery.

THE THREE-DOMAIN EAM CAN EXPLAIN AGONISM-ANTAGONISM SWITCHING

Because the EAM can be used to explore the range of parameter spaces that can facilitate allosteric coupling between two sites, it can, in principle, provide a means of identifying parameter combinations that will be optimally poised to respond to two different ligands. This potential is especially relevant in considering transcription factor (TF) function. Gene regulation by TFs is of critical importance for multicellular organisms, allowing for differentiation and specialization of cell types within tissues (33). Most TFs have a modular structure that generally includes a regulatory domain that allosterically activates or represses gene expression in response to ligand binding. Classically, ligands that bind to transcription factors have been classified by their mode of action: Agonists enhance gene expression, and antagonists depress gene expression (33). However, several examples, including but not limited to human steroid hormone receptors, challenge this paradigm by acting as agonists under one set of conditions and as antagonists under another (26, 27). This phenomenon is of medical interest as well. For instance, tamoxifen was developed as an antagonist for breast cancer tissue but had an unanticipated agonistic effect in bone and uterus tissue (26, 27). This phenomenon has qualitatively been explained in terms of differing sets of binding proteins, although a quantitative model describing these effects is lacking. This observation is challenging to address within the context of existing allosteric models. In the following section, we demonstrate that agonism and antagonism from the same ligand is a possible consequence of interdomain coupling behavior within the EAM (41).

The Three-Domain EAM

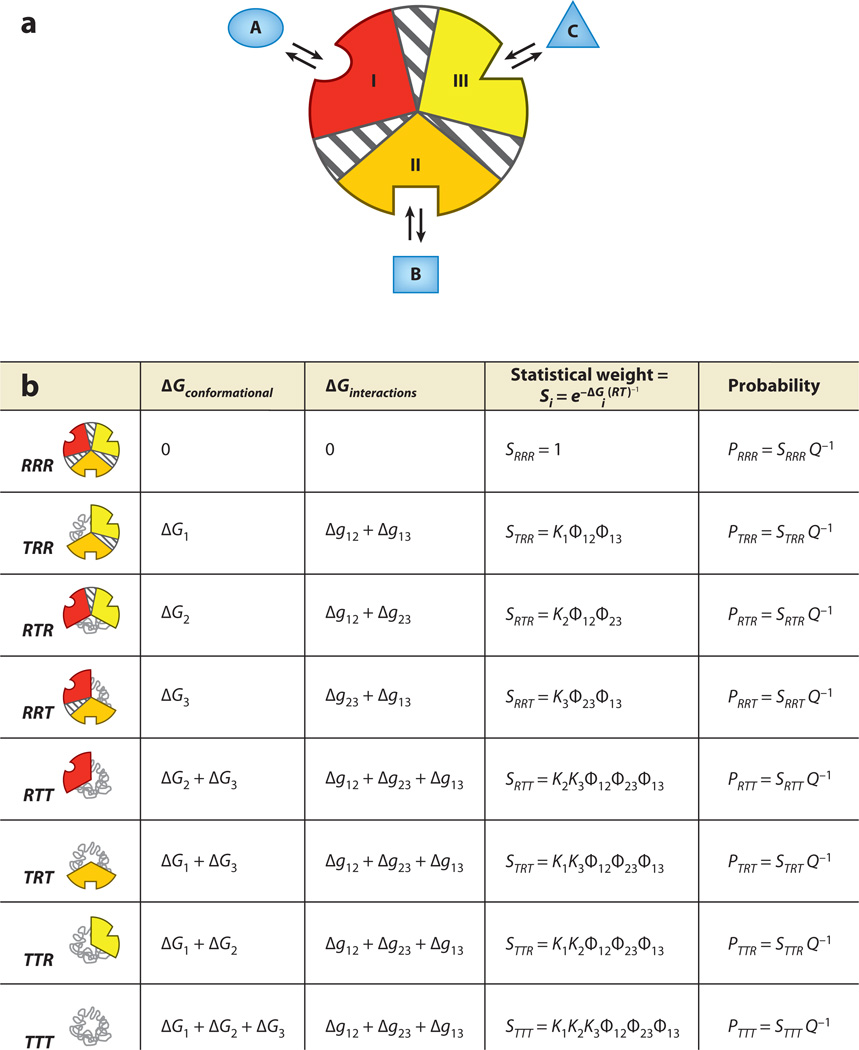
Agonism-antagonism switching can be investigated by a simple extension of the EAM to three domains (41). The construction is similar to that described above, with each domain having an intrinsic stability and an interaction energy with its adjacent domains (Figure 6a). We consider, for the time being, heterotropic allostery by allowing domains 1, 2, and 3 to bind to ligands A, B, and C, respectively (Figure 6a). Allowing each domain to be tensed (T) or relaxed (R) independently results in eight possible microstates in the ensemble (Figure 6b). As before, each state has a free energy contribution both from conformational change and from their interaction energies.

Figure 6.

The ensemble allosteric model applied to a three-domain allosteric protein. (a) Three domains (possibly subdomains) within a single hypothetical molecule. Each domain is specific to a separate ligand, and each subdomain contains an energetic interaction between the two remaining subdomains. As for the two-domain model, each conformational state may be thought of as tense (low affinity) or relaxed (high affinity), which may possibly be related to the folded state of the domain. Thus, microstate 1, where domain I is low affinity and domains II and III are high affinity, is abbreviated TRR. (b) Free energies and Boltzmann-weighted populations of each microstate in the ensemble. Note that this three-domain model is a simple mathematical extension of that developed above.

For the purposes of investigating agonism and antagonism, domain III is considered to be the functional site (i.e., being in the R state confers activity), and domains I and II are the allosteric regulation sites. This analysis is independent of the choice of functional site because of the internal symmetry of the model. To explore the extent of allosteric response, we introduce into the system a perturbation in the form of ligand binding.

First, the change in probability of domain III remaining in the R state upon the addition of ligand A is considered:

$$\mathrm{\Delta }{P}_{\mathit{\text{III,Relaxed}}}(B=0)=P_{\mathit{\text{III,Relaxed}}}(A>0|B=0)-P_{\mathit{\text{III,Relaxed}}}(A=0|B=0).$$ 13.

An agonistic effect is defined as being positive (Equation 13), and an antagonistic effect as being negative (Equation 13). If ligand B is considered to be another effector that binds domain II, then the impact of ligand B on the previously described coupling can be expressed as

$$\mathrm{\Delta }{P}_{\mathit{\text{III,Relaxed}}}(B>0)=P_{\mathit{\text{III,Relaxed}}}(A>0|B=0)-P_{\mathit{\text{III,Relaxed}}}(A=0|B>0).$$ 14.

Is there a thermodynamic architecture that allows ligand A to have an antagonistic or agonistic effect by itself, but an opposite effect in the presence of ligand B? In other words can ligand A switch between being an agonist to an antagonist (or vice versa) simply by adding another ligand that binds to a separate domain?

To determine whether and what parameters create such thermodynamic architecture within the framework of the EAM, an unbiased search of parameter space was performed to explore all possible combinations that elicit the desired response (41). Remarkably, the answer is yes, and the resultant thermodynamic architectures have simple selection rules that are dictated by the signs of the interaction parameters.

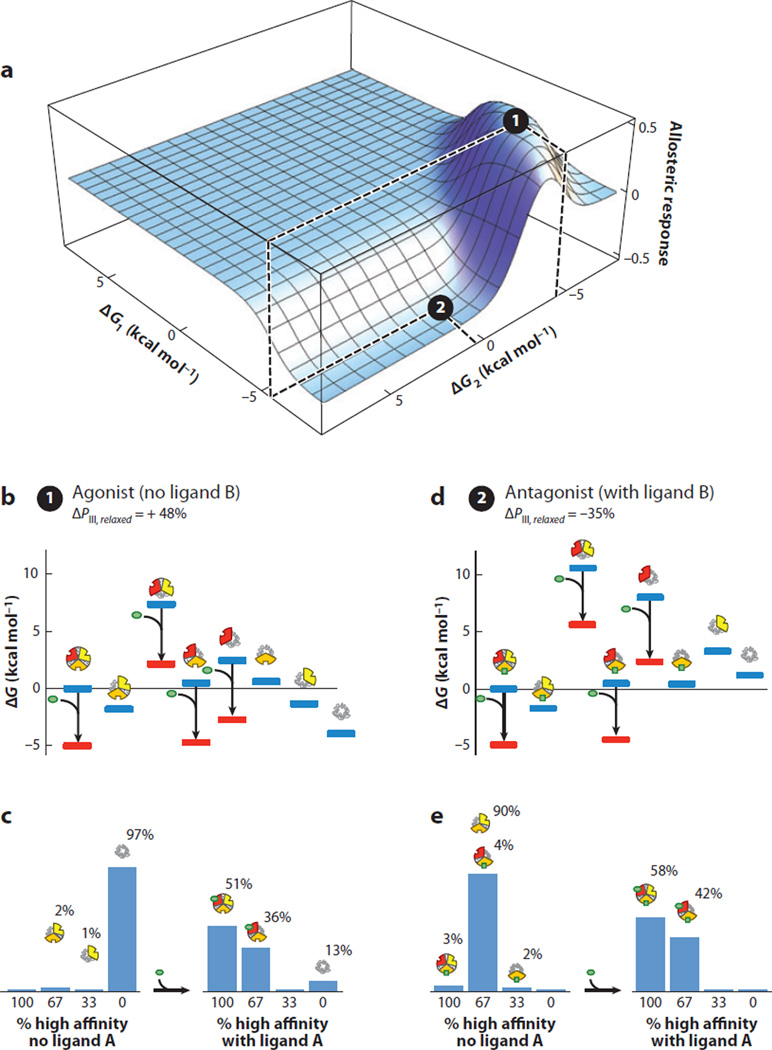
Shown in Figure 7 is an example of an architecture eliciting both agonistic and antagonistic responses. In the example, the energy landscape of the molecule without ligand B present is depicted in Figure 7b. The ensemble is dominated by the TTT microstate prior to the addition of ligand A (Figure 7b), and the energy of any state containing domain III in the R state is such that no significant population of these species exists. In essence, despite the low population of domain III in its R state, the ensemble is energetically poised to respond to addition of ligand A. Upon addition of ligand A, the ensemble is redistributed by the stabilization of states with high affinity for ligand A (i.e., domain I in the R state) (Figure 7b). Redistribution by ligand A shifts the population such that the fully R microstate (i.e., RRR) is now the dominant species (Figure 7b,c). This results in a macroscopically agonistic response to ligand A (ΔP_III,Relaxed = 51%–3% = +48%, Figure 7b,c).

Figure 7.

A specific combination of parameters for the three-domain ensemble allosteric model (EAM) reveals agonist and antagonist properties co-occurring in the same molecule. (a) A specific combination of parameters consistent with agonism-antagonism is indicated by the black circles: Δg₁₂ = 6.8, Δg₂₃ = 4.8, Δg₁₃ = −1.9, ΔG₁ = −6.75, ΔG₂(2) = 0.6, ΔG₂(1) = −4.4, and ΔG₃ = −2.7 (all values in kcal mol⁻¹). The allosteric response is the change in probability of domain III being in the high-affinity R state upon addition of ligand A. Position 1 (black circle at local maximum) exhibits agonistic response to ligand A in the absence of ligand B. Position 2 (black circle at local minimum) exhibits antagonistic response to ligand A in the presence of ligand B. (b) Ensemble microstate energies of the agonistic example, evaluated using Figure 6b and the parameters listed above. Blue bars indicate energy levels in the absence of ligand A (green ovals), and red bars indicate energy levels in the presence of ligand A. (c) Populations of folded domains for the agonistic model in the absence (left) and presence (right) of ligand A. The population of folded domain III rises from 3% to 51%, as indicated. (d) Ensemble microstate energies of the antagonistic example, evaluated using Figure 6b and the parameters listed above. Blue bars indicate energy levels in the absence of ligand A (green ovals), and red bars indicate energy levels in the presence of ligand A. (e) Populations of folded domains for the antagonistic model in the absence (left) and presence (right) of ligand A. The population of high-affinity domain III decreases from 93% to 58%, as indicated.

In contrast, Figure 7d represents the energy landscape of the ensemble if ligand B were present. The states that have domain II in the R state are now lower in energy, rendering them more populated as a result of the binding to ligand B. Under these conditions the ensemble is poised to respond in a different manner: It is dominated by the state that has both domains II and III in the R state. Addition of ligand A changes the energy landscape (Figure 7d), redistributing every state and now eliciting an antagonistic response to the regulatory domain (ΔP_III,Relaxed = 58%–93% = −35%; Figure 7d,e). This example demonstrates how identical thermodynamic architecture can position the ensemble to respond in a “functionally pluripotent” (41) manner. In other words, identical domains with identical intrinsic stabilities and interaction energies can be tuned to elicit two opposite biological effects; the only difference is the presence of a ligand that can bind to a third regulatory site and redistribute the ensemble (Figure 7a). Is this result general?

Exhaustive Search of Thermodynamic Parameter Space Reveals Diversity of Allosteric Responses in Multidomain Architectures

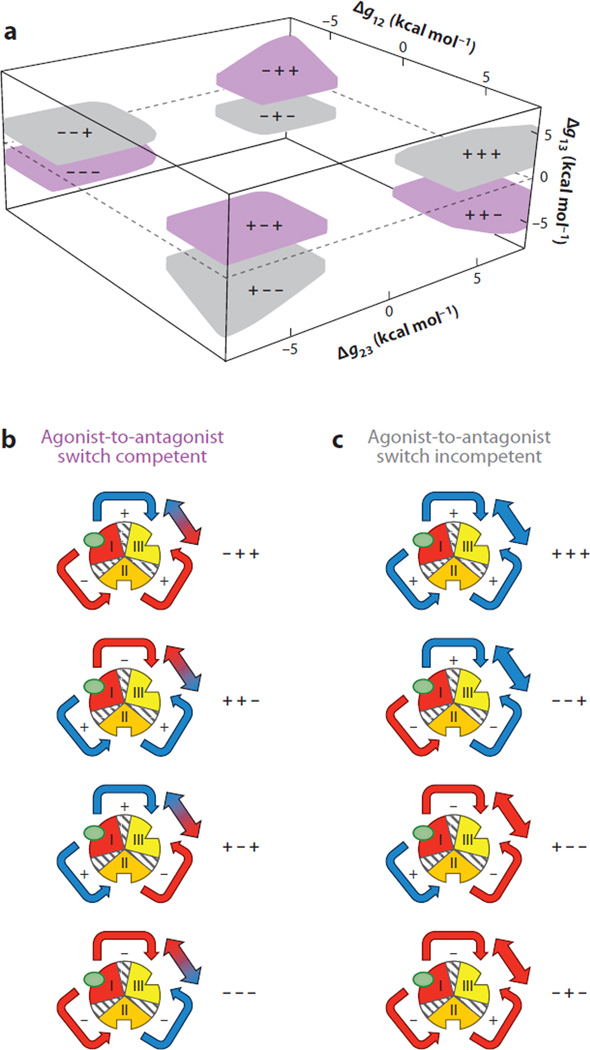
To determine the generality of the agonism-antagonism result, a systematic search of parameter space was conducted to identify the parameter combinations that elicited similar results. Initial inspection of the interaction parameter space that maximizes the desired response shows four discrete nodes capable of agonist-to-antagonist (or antagonistic-to-agonistic) switch behavior (Figure 8a). Surprisingly, this reveals that the ground rules for agonism/antagonism switching within the three-domain EAM have two simple architectures: Either one or all three interaction energies are negative. The reason these architectures produce switching is that they produce opposing energetic effects at domain III. For instance, in the case in which domains I and III are negatively coupled (Figure 8a), addition of ligand A stabilizes domain I and antagonistically affects the functional domain. Thus, the direct impact of ligand A on domain III is negative (Figure 8b). However, because the remaining domains are positively coupled, the redistribution also stabilizes domain II, which in turn agonistically affects domain III. Thus, in contrast to the direct impact, the indirect impact of ligand A (i.e., the effect that is mediated through domain II) is agonistic (Figure 8b). Indeed, the hallmark feature of switch-competent architectures is that the direct and indirect effects of ligand A are opposite in sign. By addition of ligand A, the relative contribution of the indirect effect is modulated in analog fashion (41).

Figure 8.

Exhaustive search of parameter space of the three-domain ensemble allosteric model (EAM) demonstrates four nodes of parameter combinations that exhibit agonism-antagonism. (a) Interaction parameters that exhibit significant agonistic (>35%) and antagonistic (<−35%) responses are depicted in purple. The axes correspond to values of interaction parameters between coupled domains. In contrast, parameters that were sampled and did not exhibit such behavior are depicted in gray. Each of the colored nodes is represented with +/− signs corresponding to the values of Δg₁₂, Δg₂₃, and Δg₁₃; for instance, ++− corresponds to Δg₁₂ > 0, Δg₂₃ > 0, and Δg₁₃ < 0. This result demonstrates that agonism-antagonism in allosteric systems may be a general thermodynamic phenomenon, i.e., stabilities of individual domains and coupling energies between domains need not be biologically rare combinations of values. (b) All possible interaction architectures that lead to allosteric response competitions between coupled domains are depicted. Red indicates an antagonistic redistribution as a result of interaction, and blue indicates an agonistic redistribution. Note: the color of the arrows connecting domains II and III refers to the overall impact of domain III from stabilization of domain I. For example, in the node denoted −−−, stabilization of domain I destabilizes domain II (making the arrow red). However, that destabilization of domain II (because of negative coupling to domain III) has the effect of stabilizing domain III (making the arrow to domain III blue). (c) All possible interaction architectures that do not elicit allosteric response competitions are depicted. The coloring scheme is similar to that in panel b and demonstrates that certain architectures are limited to agonistic responses (+++, −−+) and antagonistic responses (+−−, −+−). As discussed in the text, the case where domains I and III are negatively coupled is contained in the ++− region in panel a.

In contrast to switching-competent architectures, the sign of the direct and indirect effects for switching-incompetent architectures is the same (Figure 8). As a result, addition of ligand B simply reinforces the energetic relationship that existed in the absence of ligand B. Thus, in the case of switch-incompetent architectures, ligands are either committed agonists or committed antagonists (Figure 8c).

SUMMARY AND OUTLOOK: IS A UNIFIED QUANTITATIVE AND TRANSFERABLE UNDERSTANDING OF HOW ALLOSTERY WORKS POSSIBLE?

The groundbreaking investigations into protein allostery initiated by Monod-Wyman-Changeux and Koshland-Nemethy-Filmer have resulted in advances in our understanding of the role of structure in allosteric mechanisms. Nonetheless, a quantitative understanding of how allostery works has proven more elusive. This is made more evident by, and perhaps is even rooted in, the well-documented observations that allostery (a) can occur without structural change (49, 57), (b) is found in the absence of pathways of structural or dynamic perturbations (43, 48), (c) can be manifested as a result of surface-exposed, structure-preserving mutations (53, 54), (d) is sometimes correlated to stability changes in the protein (35, 51, 55), and (e), perhaps most interesting, can be manifested either as agonism or antagonism, depending on context (27). An ensemble-based representation of allostery provides a means of accounting for these disparate and puzzling observations, while also providing insight into the energetic prerequisites for the observation of coupling in a particular molecular system. Because the energetics within the protein determines the probability of states, and the probabilities and properties of those states determine not only the allosteric coupling, but whether different regions of the protein will appear as structurally heterogeneous before and after activation, the EAM provides a framework for quantitatively reconciling changes in energy, conformational dynamics, and function.

The most important aspect of the EAM is that it has provided a framework to investigate the energetic determinants of allostery, from which we have been able to identify thermodynamic ground rules that govern the ability of perturbations at one site to propagate to other sites. We have found that allostery is consistent with only a subset of the possible thermodynamic architectures available to proteins. Inasmuch as these architectures are facilitated by structure, structure is of course important. However, a significant strength of the EAM is that it can, in principle, be used to identify common thermodynamic architecture, even among structurally dissimilar proteins. In fact, perhaps one of the most intriguing results of the EAM is that it appears to undermine the importance of specific obligatory allosteric pathways in a protein. The EAM does not preclude that pathways of structural distortions may exist. Yet the apparent lack of a requirement for allosteric pathways certainly calls into question the utility of a quantitative description of allostery that is based on such pathways (Figure 2). Whether a pathway-based framework can provide organizing principles that can be used to make predictions and possibly even compare different allosteric proteins is nonetheless an open question.

The benefit of the EAM or any alternative approach to understanding allostery is its ability to generate a new line of questioning. Because the EAM formulates allostery in terms of the thermodynamic interdependence of cooperatively behaving structural elements, questions regarding mechanism would rightfully focus on the determinants of T-to-R energy differences for each cooperative element as well as the origins of the positive or negative coupling between elements. That the genetic record indicates new regulatory proteins evolved through the mixing and matching of different cooperative domains (36) suggests that the organizing principles outlined here are not incompatible with the genetic origins of allosteric proteins. Domains with multiple conformations (which presumably will have different affinities for ligand) will combine so that the high affinities for one ligand will be negatively or positively coupled with high affinities for other ligands. Our results demonstrate that this framework provides a broad repertoire of potential regulatory schemes, schemes that even allow for agonism and antagonism from the same energy landscape (41).

Finally, taken as a whole, the results presented here have important evolutionary implications as well. If allosteric signalling is not only quantitatively, but qualitatively, dependent on the conformational ensemble of the protein, it must be the case that protein sequences code not just for the high-resolution structure of the protein, but also for its entire energy landscape. Because the sign of the signal (i.e., activation or repression) can be changed by modulating the stability of just one domain, even without a structural change, the notion that structure codes for function, or more precisely that function can be inferred from structure, must be critically revisited.

SUMMARY POINTS.

1. A general ensemble-based model of allostery is developed in terms of free energies of, and coupling interactions between, cooperative elements within a protein.

2. The EAM can rationalize many puzzling experimental observations, such as dynamically driven allostery, that are difficult to reconcile using classical models.

3. The EAM can explain the biological phenomenon of a ligand acting as agonist under some circumstances and as antagonist under others.

Glossary

Allostery

the biological phenomenon where ligand binding or energetic perturbation at one molecular site results in structure or activity change at a second distinct site

KNF

Koshland, Nemethy, and Filmer

MWC

Monod, Wyman, and Changeux

Ensemble

a theoretical device constructed according to the laws of statistical mechanics that considers a large number of possible states of a system

Sequential model

one important model of allostery stating that ligand binding results in subunit conformational change to high-affinity (or R) conformation

Concerted model

one important model of allostery stating that ligand binding is possible to subunits only in completely low-affinity (T) or high-affinity (R) conformations

T

tensed, i.e., low affinity for ligand or biologically inactive

R

relaxed, i.e., high affinity for ligand or biologically active

Agonist

a ligand that enhances biological activity of an allosteric system

Antagonist

a ligand that represses activity of an allosteric system

EAM

ensemble allosteric model

Partition function

a mathematical device that describes sum of the statistical weights of the states in an ensemble

Law of mass action

a principle of chemistry stating that the concentration quotient of products and reactants (i.e., the equilibrium constant) does not change at equilibrium

CR

coupling response