Abstract
Principal surrogate (PS) endpoints are relatively inexpensive and easy to measure study outcomes that can be used to reliably predict treatment effects on clinical endpoints of interest. Few statistical methods for assessing the validity of potential PSs utilize time-to-event clinical endpoint information and to our knowledge none allow for the characterization of time-varying treatment effects. We introduce the time-dependent and surrogate-dependent treatment efficacy curve, 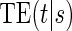 , and a new augmented trial design for assessing the quality of a biomarker as a PS. We propose a novel Weibull model and an estimated maximum likelihood method for estimation of the
, and a new augmented trial design for assessing the quality of a biomarker as a PS. We propose a novel Weibull model and an estimated maximum likelihood method for estimation of the 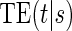 curve. We describe the operating characteristics of our methods via simulations. We analyze data from the Diabetes Control and Complications Trial, in which we find evidence of a biomarker with value as a PS.
curve. We describe the operating characteristics of our methods via simulations. We analyze data from the Diabetes Control and Complications Trial, in which we find evidence of a biomarker with value as a PS.
Keywords: Case–control study, Causal inference, Clinical trials, Principal stratification, Survival analysis, Treatment efficacy curve, Weibull model
1. Introduction
A valid principal surrogate (PS) endpoint can be used as a primary outcome for evaluating and comparing treatments in phase I–II trials, and for predicting phase III treatment effects without requiring large efficacy trials to directly assess clinical treatment effects. Frangakis and Rubin (2002) introduced the principal stratification framework and a definition of a PS. Since then, alternative definitions of and criteria for assessing a PS have been suggested and several methods for evaluation have been developed (e.g., Taylor and others, 2005; Follmann, 2006; Gilbert and Hudgens, 2008; Li and others, 2010; Wolfson and Gilbert, 2010; Huang and Gilbert, 2011; Zigler and Belin, 2012; Huang and others, 2013).
There are two distinct strategies for assessing the value of a biomarker as a PS. Both strategies quantify the prediction of the treatment effect on the clinical outcome; however, one bases the prediction on the treatment effect on the candidate PS and the other on the candidate PS under active treatment. The strength of either predictive association can be displayed via the causal effect predictiveness (CEP) function, which is a surface if treatment effect on the surrogate is considered or a marginal curve if the surrogate under active treatment is considered. An example of a marginal CEP curve is the surrogate-dependent treatment efficacy curve, TE(s) (Gilbert and Hudgens, 2008). We will focus on the active treatment PS strategy for our methods, but we will discuss both strategies in detail outlining when they are equivalent.
To our knowledge, only one method of PS evaluation under any strategy allows for time-to-event clinical endpoints subject to right censoring (Qin and others, 2008); however, time-constancy of treatment effects was assumed via a proportional hazards model. Time-varying treatment efficacy occurs in many trials, for example, Duerr and others (2012). We propose to accommodate both the use of time-to-event data and the potential for time-varying treatment efficacy by introducing the time-dependent and surrogate-dependent marginal treatment efficacy curve, 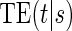 . We propose an estimated maximum likelihood (EML) method for estimating the
. We propose an estimated maximum likelihood (EML) method for estimating the 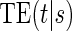 curve via a novel parameterization of the conditional Weibull distribution.
curve via a novel parameterization of the conditional Weibull distribution.
In Section 2, we outline our notation, introduce the time-dependent risk estimands, and give some assumptions that are helpful for identifying these estimands. In Section 3, we outline the strategies for classifying the value of a biomarker as a PS and discuss when they are equivalent. In Section 4, we outline previously suggested augmented trial designs and introduce a new augmentation to aid in evaluation. In Section 5, we introduce a Weibull model for the risk estimands and outline our suggested procedure for its use in evaluating time-varying treatment efficacy. In Section 6, we outline the results of a simulation study of the methods; in Section 7, we give the results of an analysis of the Diabetes Control and Complications Trial (DCCT) using our proposed methods. In Section 8, we discuss some potential limitations of our methods and make suggestions for future research. A table of acronyms can be found in Appendix B of the supplementary material available at Biostatistics online.
2. Notation and time-dependent risk estimands
2.1. Notation
Let Z be the treatment indicator, 0 for control/placebo and 1 for treatment. Let W be a baseline measurement taken prior to randomization. In the principal stratification framework of Frangakis and Rubin (2002), we use potential outcomes, where all post-randomization measures are considered under either treatment arm for each individual. Let 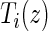 be the potential time from randomization to clinical event for individual i had s/he received treatment
be the potential time from randomization to clinical event for individual i had s/he received treatment 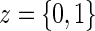 . Let
. Let 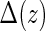 be the indicator of
be the indicator of 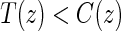 , where
, where 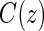 is the potential censoring time. Let
is the potential censoring time. Let 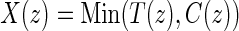 . Let
. Let 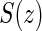 be the candidate surrogate under treatment arm
be the candidate surrogate under treatment arm 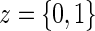 .
.
The candidate surrogate S is measured at a fixed time point 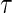 after randomization. If
after randomization. If 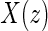 is less than or equal to
is less than or equal to 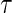 ,
, 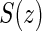 is undefined. Subjects with
is undefined. Subjects with 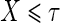 are excluded from the analysis cohort. Let R be the indicator that
are excluded from the analysis cohort. Let R be the indicator that 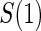 is observed. We assume that the observed and potential outcomes
is observed. We assume that the observed and potential outcomes 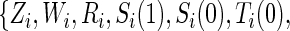 ¡inlinegif¿Ti(1),Ci(0),Ci(1),Δi(0),Δi(1)}¡/inlinegif¿,
¡inlinegif¿Ti(1),Ci(0),Ci(1),Δi(0),Δi(1)}¡/inlinegif¿, 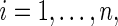 are independently and identically distributed. Let
are independently and identically distributed. Let  and
and 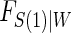 be the joint cumulative distribution function (CDF) of
be the joint cumulative distribution function (CDF) of 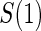 and W and the conditional cdf of
and W and the conditional cdf of 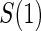 given W, respectively. Let
given W, respectively. Let 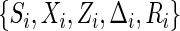 denote the observed variables for subject i.
denote the observed variables for subject i.
2.2. Time-dependent risk estimands
In the time-to-event setting there are many ways to define risk. One could define the marginal potential time-dependent and surrogate-dependent risks using the conditional cdf for T, 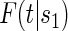 , by
, by
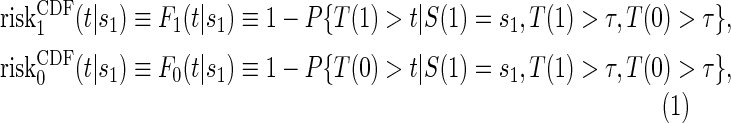 |
(2.1) |
where the subscript of a function indicates the level of 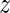 for the potential outcomes. Contrasts in these conditional risks measure a causal effect of treatment assignment on failure time in subgroups defined by
for the potential outcomes. Contrasts in these conditional risks measure a causal effect of treatment assignment on failure time in subgroups defined by 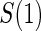 . We define one such contrast
. We define one such contrast 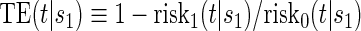 . This form of
. This form of 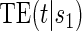 directly extends the surrogate-dependent treatment efficacy curve of Gilbert and Hudgens (2008),
directly extends the surrogate-dependent treatment efficacy curve of Gilbert and Hudgens (2008), 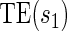 , to the time-dependent setting. One could also define the risks based on the hazard function,
, to the time-dependent setting. One could also define the risks based on the hazard function, 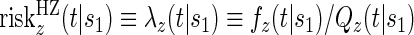 , where
, where 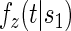 is the conditional probability density function (pdf) of T, assuming it exists.
is the conditional probability density function (pdf) of T, assuming it exists.
Comparisons of 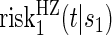 and
and 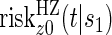 are non-causal, as outlined in Hernán (2010), because the hazard-based risk estimand in the treatment arm is conditional on a different potential set,
are non-causal, as outlined in Hernán (2010), because the hazard-based risk estimand in the treatment arm is conditional on a different potential set, 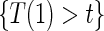 , than is the hazard-based risk estimand in the control arm,
, than is the hazard-based risk estimand in the control arm, 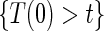 . Comparisons based on the hazards are still of interest in this setting as they are comparisons over subgroups defined by levels of
. Comparisons based on the hazards are still of interest in this setting as they are comparisons over subgroups defined by levels of 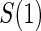 (Qin and others, 2008). There are also some settings, such as rare events, when
(Qin and others, 2008). There are also some settings, such as rare events, when  and
and 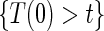 do not differ greatly, making this much less of a concern. We use both the hazard-based TE curve,
do not differ greatly, making this much less of a concern. We use both the hazard-based TE curve, 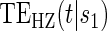 , and the CDF-based TE curve,
, and the CDF-based TE curve, 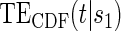 , to illustrate our purposed methods. The flexible parameterization of the Weibull model, given in Assumption A8, allows for the characterization of a variety of time-varying TE when risk is hazard-based; the CDF-based TE curve is always time-dependent and does not illustrate the nuances of time-dependent risk as well as the hazard-based TE. The CDF-based TE curve is useful for definitive evaluation of a biomarker as a PS because it is a causal contrast of risks over the treatment arms. Figure 1 illustrates the difference between the
, to illustrate our purposed methods. The flexible parameterization of the Weibull model, given in Assumption A8, allows for the characterization of a variety of time-varying TE when risk is hazard-based; the CDF-based TE curve is always time-dependent and does not illustrate the nuances of time-dependent risk as well as the hazard-based TE. The CDF-based TE curve is useful for definitive evaluation of a biomarker as a PS because it is a causal contrast of risks over the treatment arms. Figure 1 illustrates the difference between the 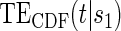 and
and 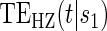 curves.
curves.
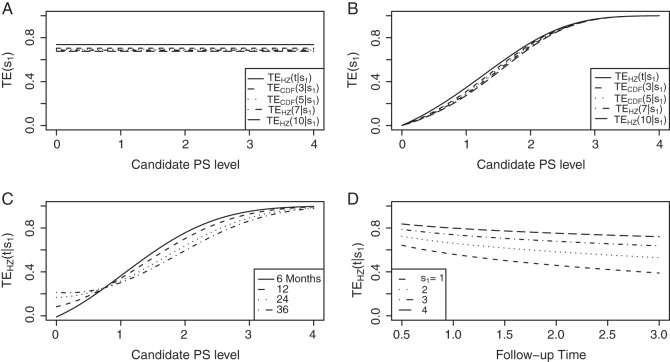
Figure 1.
(A) Displays the 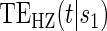 curve which is constant over all time-points t and the
curve which is constant over all time-points t and the 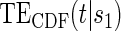 curve for several time points for a useless surrogate in the time-independent hazard Weibull setting. (B) Displays the
curve for several time points for a useless surrogate in the time-independent hazard Weibull setting. (B) Displays the 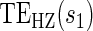 curve for a high-quality surrogate in the time-independent hazard setting and several
curve for a high-quality surrogate in the time-independent hazard setting and several 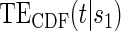 curves for different time points t for this same surrogate scenario. (C) Displays
curves for different time points t for this same surrogate scenario. (C) Displays 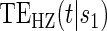 curves for given amounts of follow-up time after
curves for given amounts of follow-up time after 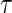 and over the range of
and over the range of 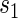 for a high-quality surrogate. These curves illustrate time variation in TE that is both associated with the candidate surrogate and exists when
for a high-quality surrogate. These curves illustrate time variation in TE that is both associated with the candidate surrogate and exists when 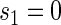 ; the figure depicts a candidate surrogate that declines in value over time while the average TE is remaining approximately the same over time. (D) Displays
; the figure depicts a candidate surrogate that declines in value over time while the average TE is remaining approximately the same over time. (D) Displays 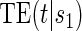 curves for given levels of
curves for given levels of 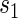 over a range of follow-up times (
over a range of follow-up times (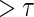 ) in years for a medium-quality surrogate. These curves illustrate time variation in TE that is approximately equal over all levels of the candidate surrogate; the figure depicts a candidate surrogate that retains some value as a PS over time but for declining TE.
) in years for a medium-quality surrogate. These curves illustrate time variation in TE that is approximately equal over all levels of the candidate surrogate; the figure depicts a candidate surrogate that retains some value as a PS over time but for declining TE.
Following Qin and others (2008), Assumptions A1–A4 reduce the number of missing potential outcomes and help identify the risk estimands from the observed data.
A1: Stable Unit Treatment Value Assumption (SUTVA) and Consistency.
A2: Ignorable Treatment Assignment.
A3: Equal individual clinical risk up to time
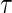 :
: 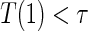 if and only if
if and only if 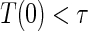 .
.A4: Random censoring:
 for
for 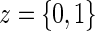 .
.
Assumptions A1–A3 have been used and discussed previously in the literature (Gilbert and Hudgens, 2008; Gilbert and others, 2008; Qin and others, 2008). A relaxed version of Assumption A4, independence of 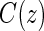 and
and 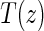 conditional on
conditional on 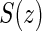 , is sufficient for identification of the risk estimands. However, Assumption A4 as stated is needed to account for censoring in the manner we have prescribed in our model, given as Assumption A8. Assumption A3 is not fully testable and will be violated in some trials. We continue to make A3 here because it is plausible for our motivating example, in which there are no failure events prior to
, is sufficient for identification of the risk estimands. However, Assumption A4 as stated is needed to account for censoring in the manner we have prescribed in our model, given as Assumption A8. Assumption A3 is not fully testable and will be violated in some trials. We continue to make A3 here because it is plausible for our motivating example, in which there are no failure events prior to 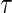 . Assumptions A1–A4 imply that the conditional distribution of
. Assumptions A1–A4 imply that the conditional distribution of 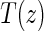 , given
, given 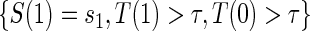 , equals that for T given
, equals that for T given 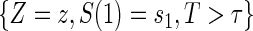 for
for 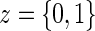 .
.
3. Definition of a PS
A PS was first defined in Frangakis and Rubin (2002) as a biomarker S such that causal treatment effects on the clinical outcome only exist when causal treatment effects exist for S. Building on Frangakis and Rubin (2002), Joffe and Greene (2009) characterized a PS as an intermediate endpoint such that treatment effect on the surrogate can be used to reliably predict treatment effect on the clinical endpoint. Joffe and Greene (2009) and Frangakis and Rubin (2002) stated criteria that can be used to assess biomarkers as PS using the joint risk estimands, 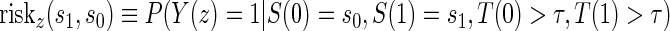 (Gilbert and Hudgens, 2008), where
(Gilbert and Hudgens, 2008), where 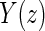 is the clinical event indicator. Frangakis and Rubin (2002) give the criterion that a biomarker is a PS if
is the clinical event indicator. Frangakis and Rubin (2002) give the criterion that a biomarker is a PS if  for all
for all  , which Gilbert and Hudgens (2008) called average causal necessity (ACN). Subsequent work added a second criterion that a good PS should have a risk contrast over the arms of the trial that varies widely in
, which Gilbert and Hudgens (2008) called average causal necessity (ACN). Subsequent work added a second criterion that a good PS should have a risk contrast over the arms of the trial that varies widely in 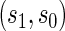 . Together these criteria satisfy the Joffe and Greene (2009) definition of a PS.
. Together these criteria satisfy the Joffe and Greene (2009) definition of a PS.
Gilbert and Hudgens (2008) and Wolfson and Gilbert (2010) note that for a biomarker to be useful as a surrogate it need only help group subjects by TE levels. This led to a utility-driven alternative strategy for assessing biomarkers as PS, such that a biomarker has value as a PS if the potential treatment effect on the biomarker under active treatment assignment can be used to reliably predict the treatment effect on the clinical endpoint. A biomarker can be assessed under active treatment based on the marginal risks defined given in Equation (2.1).
To assess a biomarker under the active treatment, only a marginal version of the second criterion is needed to establish that a biomarker has value as a PS. The marginal risk criterion is that 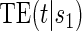 varies widely in
varies widely in 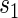 . Biomarkers satisfying this criterion are useful for evaluating future treatments, with the objective to move more treatment recipients to the
. Biomarkers satisfying this criterion are useful for evaluating future treatments, with the objective to move more treatment recipients to the 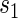 range where treatment is highly effective. As noted in Gilbert and Hudgens (2008), in the special case where all of the
range where treatment is highly effective. As noted in Gilbert and Hudgens (2008), in the special case where all of the 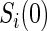 equal some constant c, termed constant biomarker (CB), the joint second criterion and the marginal second criterion are equivalent and ACN can be evaluated based on
equal some constant c, termed constant biomarker (CB), the joint second criterion and the marginal second criterion are equivalent and ACN can be evaluated based on 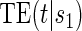 . Our methods are based on the marginal risk estimands, and thus can be used to assess biomarkers under active treatment in all cases and under both arms when CB holds. For either evaluation strategy greater variation in the TE function over the range of
. Our methods are based on the marginal risk estimands, and thus can be used to assess biomarkers under active treatment in all cases and under both arms when CB holds. For either evaluation strategy greater variation in the TE function over the range of 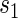 or
or 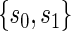 , marginal or joint, suggests increasing value as a PS.
, marginal or joint, suggests increasing value as a PS.
4. Augmented trial design
The marginal risk estimands condition on 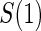 , which is missing for all placebo recipients in a standard clinical trial. Follmann (2006) outlined two vaccine trial design augmentations for inferring
, which is missing for all placebo recipients in a standard clinical trial. Follmann (2006) outlined two vaccine trial design augmentations for inferring 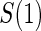 for placebo recipients, baseline immunogenicity predictor (BIP), as coined in Gilbert and Hudgens (2008), and closeout placebo vaccination (CPV). A useful BIP, which we will call W, is highly correlated with
for placebo recipients, baseline immunogenicity predictor (BIP), as coined in Gilbert and Hudgens (2008), and closeout placebo vaccination (CPV). A useful BIP, which we will call W, is highly correlated with 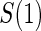 and is easily measurable at baseline. Under CPV, placebo recipients uninfected and uncensored at the end of the follow-up period for infection,
and is easily measurable at baseline. Under CPV, placebo recipients uninfected and uncensored at the end of the follow-up period for infection, 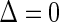 , are vaccinated, and their immune response biomarker,
, are vaccinated, and their immune response biomarker, 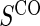 , is measured at time
, is measured at time 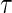 after vaccination. BIP and CPV trial augmentation can be used in combination or separately.
after vaccination. BIP and CPV trial augmentation can be used in combination or separately.
Although the BIP and CPV trial design augmentations were originally proposed in terms of vaccine trials, they can easily be generalized to the clinical trial setting. The concept of a BIP is easily extended to be any baseline measurement(s) that are predictive of the candidate PS. A BIP under this definition is not a priori considered irrelevant to the clinical outcome and therefore should be considered for inclusion in the model for outcome on a case by case basis. Similarly, the concept of CPV can be extended such that non-active treatment arm subjects who are not censored and do not have an observed clinical event prior to closeout, 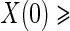 closeout, are given treatment and then followed until trial closeout plus
closeout, are given treatment and then followed until trial closeout plus 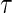 , when the candidate surrogate is measured. In order to replace missing
, when the candidate surrogate is measured. In order to replace missing 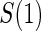 values with the closeout measurement
values with the closeout measurement 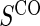 , we adapt the assumptions made by Qin and others (2008).
, we adapt the assumptions made by Qin and others (2008).
A5: Time constancy of the true immune response at time
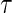 ,
, 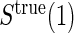 : for placebo recipients with
: for placebo recipients with 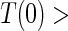 closeout and
closeout and 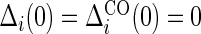 ,
,  , and
, and 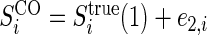 , where
, where 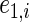 and
and 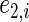 are iid random errors with mean zero;
are iid random errors with mean zero;A6: No infections during the close-out period,
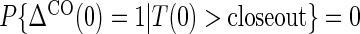 ,
,
where 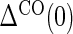 is the indicator of the clinical event during the close-out period of duration
is the indicator of the clinical event during the close-out period of duration 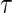 . Assumption A5 is not fully testable, but may be plausible when the follow-up time is not long relative to the age of the subjects and when environmental factors are unlikely to change
. Assumption A5 is not fully testable, but may be plausible when the follow-up time is not long relative to the age of the subjects and when environmental factors are unlikely to change 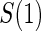 . An obvious testable implication of A6 is that no subjects undergoing CPV should be observed to have an event before
. An obvious testable implication of A6 is that no subjects undergoing CPV should be observed to have an event before 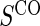 is measured. Some deviations from A5 and A6 may be acceptable and sensitivity analysis can be performed to evaluate the influence of such deviations.
is measured. Some deviations from A5 and A6 may be acceptable and sensitivity analysis can be performed to evaluate the influence of such deviations.
We propose an additional trial augmentation; we will refer to this augmentation as the baseline surrogate measure (BSM). The BSM augmentation is defined simply as measuring the biomarker of interest at baseline; this can be useful for multiple purposes. Under Assumption A7, given below, the BSM measurement 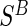 can replace missing
can replace missing 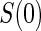 values and the difference biomarker
values and the difference biomarker 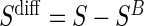 satisfies Case CB
satisfies Case CB 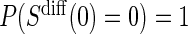 . Even when A7 does not hold, the BSM is useful as a potentially highly correlated BIP. Assumption A7 is no change in the biomarker from baseline to
. Even when A7 does not hold, the BSM is useful as a potentially highly correlated BIP. Assumption A7 is no change in the biomarker from baseline to  in a non-active treatment arm. This is stated formally as follows:
in a non-active treatment arm. This is stated formally as follows:
A7:
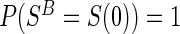 .
.
Assumption A7 has testable hypotheses that the distribution of 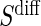 in the control arm has point mass at zero; violations of this assumption are easily observable. When a measurement error is present, the measurements of
in the control arm has point mass at zero; violations of this assumption are easily observable. When a measurement error is present, the measurements of 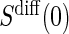 may differ from zero for many subjects and A7 still holds. If it is believed that a measurement error is present and non-systematic, one can test for evidence against A7 by testing the null
may differ from zero for many subjects and A7 still holds. If it is believed that a measurement error is present and non-systematic, one can test for evidence against A7 by testing the null 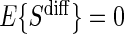 . Both tests allow for some quantification of the plausibility of A7; however, subject-matter knowledge is just as important when determining if A7 is plausible. This augmentation is available in our motivating data set and greater discussion of Assumption A7 and its implications for candidate PS evaluation can be found in Section 7.
. Both tests allow for some quantification of the plausibility of A7; however, subject-matter knowledge is just as important when determining if A7 is plausible. This augmentation is available in our motivating data set and greater discussion of Assumption A7 and its implications for candidate PS evaluation can be found in Section 7.
5. Weibull structural risk model
We assume a Weibull model for the conditional pdf 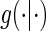 of T given Z,
of T given Z,  which parameterizes both the scale,
which parameterizes both the scale, 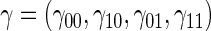 , and shape,
, and shape, 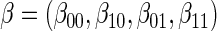 , components of the Weibull model with treatment Z and potential surrogate
, components of the Weibull model with treatment Z and potential surrogate 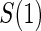 . Specifically, our Weibull assumption A8 states that
. Specifically, our Weibull assumption A8 states that
A8:
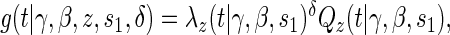
where 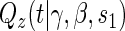 is the parameterized conditional Weibull survivor function for the treatment arm
is the parameterized conditional Weibull survivor function for the treatment arm 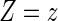 , and the conditional hazard function is given by
, and the conditional hazard function is given by
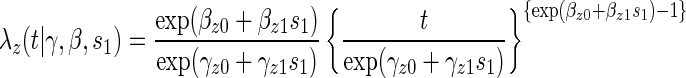 |
(5.1) |
for 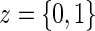 . Given A8, the conditional likelihood of the observed data can be written as
. Given A8, the conditional likelihood of the observed data can be written as
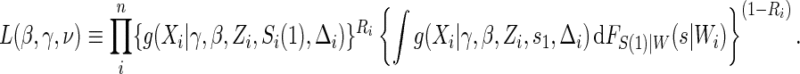 |
(5.2) |
We use a parametric form for the joint cdf of 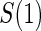 and W in our simulations,
and W in our simulations, 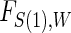 , which implies a form for
, which implies a form for 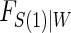 , and we estimate
, and we estimate 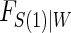 using maximum likelihood. The choice of the estimated form of
using maximum likelihood. The choice of the estimated form of 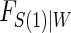 should be based on the trial data and can be tailored to the particular type of
should be based on the trial data and can be tailored to the particular type of 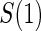 and W data observed. The
and W data observed. The 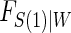 model can be of any form which integration is feasible. Huang and Gilbert (2011) use a semiparametric model for
model can be of any form which integration is feasible. Huang and Gilbert (2011) use a semiparametric model for 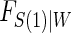 and this can also be used with the Weibull model, as we demonstrate in the DCCT example. Regardless of the choice of model for
and this can also be used with the Weibull model, as we demonstrate in the DCCT example. Regardless of the choice of model for 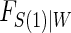 , Monte-Carlo integration is suggested over numerical integration to reduce computational burden. Once an estimate for
, Monte-Carlo integration is suggested over numerical integration to reduce computational burden. Once an estimate for 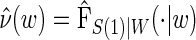 is obtained, we can use it in the likelihood above to obtain an estimated likelihood
is obtained, we can use it in the likelihood above to obtain an estimated likelihood 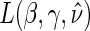 over
over 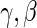 . We can then maximize for estimates of
. We can then maximize for estimates of 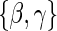 . This general approach of EML was introduced by Pepe and Fleming (1991) and used by Follmann (2006) and Gilbert and Hudgens (2008) among others.
. This general approach of EML was introduced by Pepe and Fleming (1991) and used by Follmann (2006) and Gilbert and Hudgens (2008) among others.
We state a result for the identifiability of 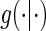 in Appendix A of the supplementary material available at Biostatistics online. Using the identifiability result for
in Appendix A of the supplementary material available at Biostatistics online. Using the identifiability result for  and following the proof in Gilbert and Hudgens (2008), it can be shown that the observed estimated likelihood
and following the proof in Gilbert and Hudgens (2008), it can be shown that the observed estimated likelihood 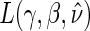 has a unique maximum given the data from a BIP-augmented trial, provided that there are observed failures. This result also holds in a CPV augmented trial design, following the proof of Proposition 3 in Wolfson (2009). Given that the appropriate assumptions hold, A1–A4 and A8 for BIP and A1–A6 and A8 for CPV, as well as implicit conditioning on
has a unique maximum given the data from a BIP-augmented trial, provided that there are observed failures. This result also holds in a CPV augmented trial design, following the proof of Proposition 3 in Wolfson (2009). Given that the appropriate assumptions hold, A1–A4 and A8 for BIP and A1–A6 and A8 for CPV, as well as implicit conditioning on 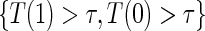 , the unique solutions to the EML imply identification of the causal estimands of interest. Given the identifiability of
, the unique solutions to the EML imply identification of the causal estimands of interest. Given the identifiability of 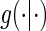 and data augmentations, the EML estimators are also consistent for
and data augmentations, the EML estimators are also consistent for 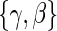 for consistent
for consistent 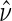 (Pepe and Fleming, 1991). However, the asymptotic distributional results of Pepe and Fleming (1991) for general EML estimators do not carry over to our setting, due to the zero probability of observing
(Pepe and Fleming, 1991). However, the asymptotic distributional results of Pepe and Fleming (1991) for general EML estimators do not carry over to our setting, due to the zero probability of observing 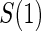 in infected placebo recipients. We suggest using the bootstrap for variance estimation and inference.
in infected placebo recipients. We suggest using the bootstrap for variance estimation and inference.
We refer to model A8 as the time-dependent hazard TE Weibull model. The conditional risks, 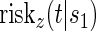 , can be expressed as functions of the coefficients
, can be expressed as functions of the coefficients 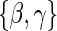 for any of the conditional risk forms of interest (i.e. based on a hazard, cumulative hazard or cdf). Although the model is depicted without the inclusion of additional baseline that variables, baseline variables such as the BIP, W, can be included in the scale term if it is believed they may be associated with outcome. Figure 1 depicts some example
for any of the conditional risk forms of interest (i.e. based on a hazard, cumulative hazard or cdf). Although the model is depicted without the inclusion of additional baseline that variables, baseline variables such as the BIP, W, can be included in the scale term if it is believed they may be associated with outcome. Figure 1 depicts some example 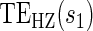 ,
,  , and
, and 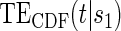 curves.
curves.
5.1. Evaluating surrogate value under the Weibull model
We propose a three-step process for evaluating a potential PS using the above estimation method.
Step 1: Fit the time-dependent-hazard TE Weibull model via EML; determine the EML estimates by maximizing
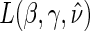 , where
, where 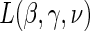 is defined in Equation (5.2).
is defined in Equation (5.2).Step 2: Test for time-varying conditional hazard-based treatment efficacy,
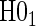 :
: 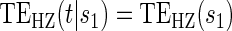 , by testing
, by testing 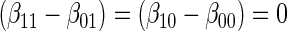 .
.Step 3: If the data support
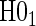 , fit the time-independent hazard TE Weibull model, outlined below and in Appendix A of supplementary material available at Biostatistics online. Use estimates from this model for figures and inference on surrogate quality. If the data support rejection of
, fit the time-independent hazard TE Weibull model, outlined below and in Appendix A of supplementary material available at Biostatistics online. Use estimates from this model for figures and inference on surrogate quality. If the data support rejection of 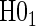 , use the time-dependent-hazard TE model estimates for figures and inference on surrogate quality.
, use the time-dependent-hazard TE model estimates for figures and inference on surrogate quality.
The testable null hypotheses of interest are as follows:
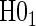 :
: 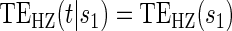 , Null equivalent
, Null equivalent 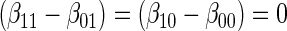 ;
;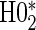 :
: 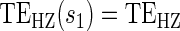 , Null equivalent
, Null equivalent 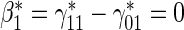 ;
;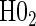 :
: 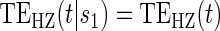 , Null equivalent
, Null equivalent 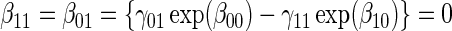 ;
;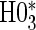 :
: 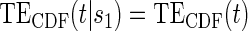 , Null equivalent
, Null equivalent 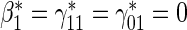 ;
;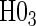 :
: 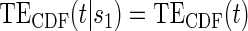 , Null equivalent
, Null equivalent 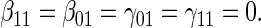
We suggest Wald tests for all nulls. If we fail to reject 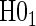 , we use a simpler model for inference that fully characterizes the scale component
, we use a simpler model for inference that fully characterizes the scale component 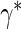 and only allows for terms in the shape component
and only allows for terms in the shape component 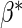 that will affect hazard-based risk equally for the two treatment groups (parameterization outlined in Appendix A of supplementary material available at Biostatistics online). We refer to this model as the time-independent hazard TE Weibull model and place stars on the
that will affect hazard-based risk equally for the two treatment groups (parameterization outlined in Appendix A of supplementary material available at Biostatistics online). We refer to this model as the time-independent hazard TE Weibull model and place stars on the 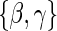 model coefficients to distinguish them from their time-dependent hazard TE counterparts. This model can again be fit via EML and can also accommodate the inclusion of baseline variables in the scale parameter.
model coefficients to distinguish them from their time-dependent hazard TE counterparts. This model can again be fit via EML and can also accommodate the inclusion of baseline variables in the scale parameter.
The justifications for the coefficient equivalents of 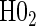 and
and 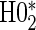 are not conceptually difficult but require some algebra and are given in Appendix A of supplementary material available at Biostatistics online. The CDF-based TE is always time-dependent and nulls based on it are always a subset of the null space of the hazard-based TE tests for the same model. For this reason, we suggested testing both the hazard-based TE null and the CDF-based TE null, accounting for multiple testing, to evaluate a biomarker as having any value as a PS. Sequential testing is also suggested; if the data do not support rejection of
are not conceptually difficult but require some algebra and are given in Appendix A of supplementary material available at Biostatistics online. The CDF-based TE is always time-dependent and nulls based on it are always a subset of the null space of the hazard-based TE tests for the same model. For this reason, we suggested testing both the hazard-based TE null and the CDF-based TE null, accounting for multiple testing, to evaluate a biomarker as having any value as a PS. Sequential testing is also suggested; if the data do not support rejection of 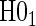 , the appropriate tests for any surrogate value are
, the appropriate tests for any surrogate value are 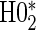 and
and 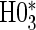 . Similarly, when data do support rejection of
. Similarly, when data do support rejection of 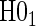 , the appropriate tests for any surrogate value are
, the appropriate tests for any surrogate value are 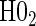 and
and 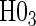 .
.
If case CB holds for S or 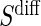 , via BSM and Assumption A7, then assessment of ACN can be made using the marginal risk estimands as parameterized by the Weibull models; tight confidence intervals about
, via BSM and Assumption A7, then assessment of ACN can be made using the marginal risk estimands as parameterized by the Weibull models; tight confidence intervals about 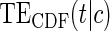 that include c for all t of interest are support for ACN. Further discussion of the different strategies of PS evaluation can be found in the discussion section and above in Section 3.
that include c for all t of interest are support for ACN. Further discussion of the different strategies of PS evaluation can be found in the discussion section and above in Section 3.
The time-dependent hazard model allows for time variation of 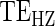 in many forms, as illustrated in Figure 1. If the data support rejection of the null hypothesis
in many forms, as illustrated in Figure 1. If the data support rejection of the null hypothesis 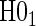 , the most comprehensive way to evaluate the time variation is to plot the estimated
, the most comprehensive way to evaluate the time variation is to plot the estimated 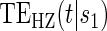 for a range of
for a range of  values for several different time points of interest. In addition, one can plot the estimated
values for several different time points of interest. In addition, one can plot the estimated 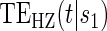 for a range of time points
for a range of time points 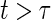 and less than the longest follow-up time, for several different
and less than the longest follow-up time, for several different 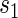 values. These plots provide a clear visual indication of the surrogate value of S as well as the meaning of any significant time variation; an example of this type of plot can be seen Figure S1 in Appendix B of the supplementary material available at Biostatistics online. Hypothesis tests can be used to provide inference about the nature of the time dependence depicted by the
values. These plots provide a clear visual indication of the surrogate value of S as well as the meaning of any significant time variation; an example of this type of plot can be seen Figure S1 in Appendix B of the supplementary material available at Biostatistics online. Hypothesis tests can be used to provide inference about the nature of the time dependence depicted by the 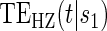 curve. Some suggested coefficient-based hypothesis tests are outlined in Appendix A of supplementary material available at Biostatistics online.
curve. Some suggested coefficient-based hypothesis tests are outlined in Appendix A of supplementary material available at Biostatistics online.
6. Simulation
Simulated data follow a 1:1 randomized, two-arm trial with 2000 subjects per treatment arm using the various case–control sampling designs for CPV and BIP. Suppose that the conditional cdf of T, given 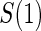 and Z, follows a Weibull model and that
and Z, follows a Weibull model and that 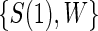 follows a bivariate normal model with correlation
follows a bivariate normal model with correlation 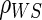 . Information lost to drop-out occurs completely at random, and occurs at a rate of 5% per year. Event times are censored at 3 years post
. Information lost to drop-out occurs completely at random, and occurs at a rate of 5% per year. Event times are censored at 3 years post  , at which time the trials have 50% TE on average, with an average of 104 treatment group infections and 208 placebo group infections over the 1000 simulated trials. This follows the HIV vaccine trial design proposed in Gilbert and others (2011).
, at which time the trials have 50% TE on average, with an average of 104 treatment group infections and 208 placebo group infections over the 1000 simulated trials. This follows the HIV vaccine trial design proposed in Gilbert and others (2011).
We investigate Weibull models for T given 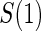 and Z under 7 different scenarios. We investigate three different PS quality levels which characterize time-independent hazard-based TE curves: a high quality surrogate, a marginal quality surrogate, and a useless surrogate. We call these the time independent scenarios. We also consider four scenarios with differing amounts of time dependence in
and Z under 7 different scenarios. We investigate three different PS quality levels which characterize time-independent hazard-based TE curves: a high quality surrogate, a marginal quality surrogate, and a useless surrogate. We call these the time independent scenarios. We also consider four scenarios with differing amounts of time dependence in 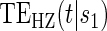 . We investigate a high-quality surrogate and a marginal-quality surrogate with time dependence in
. We investigate a high-quality surrogate and a marginal-quality surrogate with time dependence in 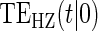 alone and a high-quality surrogate and a marginal-quality surrogate under time-dependence that is both associated with the surrogate quality and with
alone and a high-quality surrogate and a marginal-quality surrogate under time-dependence that is both associated with the surrogate quality and with 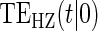 . We refer to this as the multiple time-dependent scenario, labeled as “Multi Time-dep” in Tables 1, 2 and 3, and all four settings with time-dependence as the time-dependent scenarios.
. We refer to this as the multiple time-dependent scenario, labeled as “Multi Time-dep” in Tables 1, 2 and 3, and all four settings with time-dependence as the time-dependent scenarios.
Table 1.
Percent Bias: two-arm trial for given sampling of 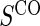 and
and 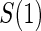 ; for W and
; for W and 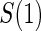 correlation (0.8)
correlation (0.8)
| Time Indep. |
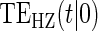 Time-dep. Time-dep. |
Multi Time-dep. |
Time Indep. |
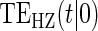 Time-dep. Time-dep. |
Multi Time-dep. |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Estimand | No Val. | Some Val. | High Val. | Some | High | Some | High | No | Some | High | Some | High | Some | High |
Full sampling 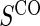 and and 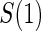
|
1:5 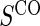 and full and full 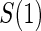
|
|||||||||||||
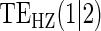 |
 0.50 0.50 |
 1.10 1.10 |
 0.90 0.90 |
0.20 | 0.00 | 0.20 | 0.70 |
 0.40 0.40 |
 1.10 1.10 |
 0.80 0.80 |
0.10 | 0.20 | 0.10 | 0.60 |
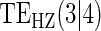 |
0.10 |
 0.40 0.40 |
 0.10 0.10 |
 1.50 1.50 |
 0.10 0.10 |
 1.40 1.40 |
0.10 | 0.10 |
 0.40 0.40 |
 0.10 0.10 |
 1.60 1.60 |
0.00 |
 1.70 1.70 |
0.10 |
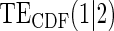 |
 0.50 0.50 |
 1.10 1.10 |
 0.90 0.90 |
0.40 | 0.30 | 0.40 | 0.40 |
 0.50 0.50 |
 1.10 1.10 |
 0.80 0.80 |
0.20 |
 0.00 0.00 |
0.80 | 0.60 |
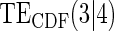 |
 0.40 0.40 |
 0.40 0.40 |
 0.10 0.10 |
 1.40 1.40 |
0.00 | 0.00 | 0.20 | 0.10 |
 0.40 0.40 |
 0.10 0.10 |
 1.50 1.50 |
 0.30 0.30 |
 0.40 0.40 |
 0.00 0.00 |
No 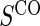 and full and full 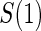
|
full 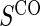 and 1:5 and 1:5 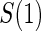
|
|||||||||||||
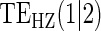 |
 0.70 0.70 |
 1.20 1.20 |
 0.70 0.70 |
 0.20 0.20 |
0.40 | 0.50 | 0.70 |
 0.70 0.70 |
 1.20 1.20 |
 0.70 0.70 |
 0.20 0.20 |
0.40 | 0.50 | 0.70 |
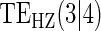 |
1.00 |
 0.50 0.50 |
0.10 |
 1.90 1.90 |
 0.30 0.30 |
 1.20 1.20 |
 0.10 0.10 |
1.00 |
 0.50 0.50 |
0.10 |
 1.90 1.90 |
 0.30 0.30 |
 1.20 1.20 |
 0.10 0.10 |
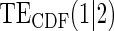 |
 0.60 0.60 |
 1.10 1.10 |
 0.70 0.70 |
0.30 | 0.50 | 0.40 | 0.30 |
 0.60 0.60 |
 1.10 1.10 |
 0.70 0.70 |
0.30 | 0.50 | 0.40 | 0.30 |
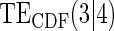 |
0.80 |
 0.40 0.40 |
0.00 |
 0.80 0.80 |
0.40 |
 0.10 0.10 |
0.20 | 0.80 |
 0.40 0.40 |
0.00 |
 0.80 0.80 |
0.40 |
 0.10 0.10 |
0.20 |
1:5 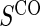 and and 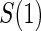
|
no 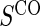 and 1:5 and 1:5 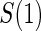
|
|||||||||||||
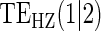 |
 0.70 0.70 |
 1.10 1.10 |
 0.70 0.70 |
 0.10 0.10 |
0.30 | 0.50 | 0.70 |
 0.50 0.50 |
 1.10 1.10 |
 0.60 0.60 |
0.00 | 0.10 | 0.30 | 0.60 |
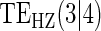 |
0.10 |
 0.50 0.50 |
0.00 |
 1.60 1.60 |
 0.20 0.20 |
 1.60 1.60 |
 0.10 0.10 |
0.10 |
 0.30 0.30 |
 0.10 0.10 |
 1.40 1.40 |
 0.20 0.20 |
 1.30 1.30 |
 0.10 0.10 |
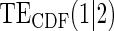 |
 0.60 0.60 |
 1.10 1.10 |
 0.70 0.70 |
0.30 | 0.50 | 0.40 | 0.30 |
 0.60 0.60 |
 1.10 1.10 |
 0.60 0.60 |
0.40 | 0.50 | 0.30 | 0.30 |
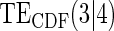 |
0.00 |
 0.50 0.50 |
0.00 |
 1.30 1.30 |
0.20 |
 0.40 0.40 |
0.10 | 0.00 |
 0.30 0.30 |
 0.10 0.10 |
 1.20 1.20 |
0.00 |
 0.30 0.30 |
0.10 |
Average bias over the 1000 simulations less than 1 Monte Carlo standard error in all cases.
Table 2.
Proportion of Rejections: two-arm trial when 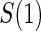 is measured on all treated subjects and given sampling of
is measured on all treated subjects and given sampling of 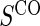 ; W,
; W,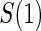 correlation (0.8)
correlation (0.8)
| Time indep. |
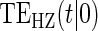 Time-dep. Time-dep. |
Multi time-dep. 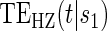 |
|||||
|---|---|---|---|---|---|---|---|
| Null | No val. | Some val. | High val. | Some | High | Some | High |
Full sampling 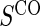
|
|||||||
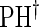 |
0.05 | 0.04 | 0.05 | 0.37 | 0.42 | 0.59 | 0.53 |
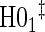 |
0.04 | 0.05 | 0.09 | 0.41 | 0.50 | 0.84 | 0.74 |
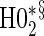 |
0.05 | 0.45 | 1.00 | 0.34 | 0.90 | 0.43 | 0.92 |
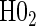 ¶ ¶
|
0.06 | 0.30 | 1.00 | 0.26 | 0.88 | 0.48 | 0.94 |
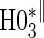 |
0.06 | 0.90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
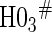 |
0.05 | 0.86 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
1:5 case:control sampling 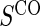
|
|||||||
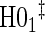 |
0.08 | 0.05 | 0.10 | 0.40 | 0.48 | 0.83 | 0.73 |
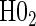 §¶ §¶
|
0.06 | 0.43 | 1.00 | 0.25 | 0.81 | 0.43 | 0.90 |
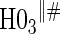 |
0.07 | 0.90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
No sampling 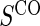
|
|||||||
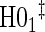 |
0.08 | 0.08 | 0.09 | 0.40 | 0.49 | 0.84 | 0.75 |
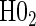 §¶ §¶
|
0.06 | 0.45 | 1.00 | 0.26 | 0.86 | 0.45 | 0.90 |
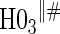 |
0.06 | 0.90 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
 Proportional hazards test based on the Cox model.
Proportional hazards test based on the Cox model.  Test of
Test of 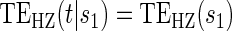 based on a joint Wald test of
based on a joint Wald test of 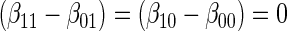 .
.  Test of
Test of 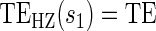 based on a Wald test of
based on a Wald test of 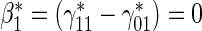 . ¶ Test of
. ¶ Test of 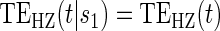 based on a Wald test
based on a Wald test 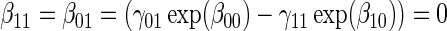 . §¶ The model-specific test of surrogate value based on the hazard, test §in the time-independent case and test ¶ in the time-dependent.
. §¶ The model-specific test of surrogate value based on the hazard, test §in the time-independent case and test ¶ in the time-dependent. Test
Test 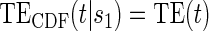 based on a Wald test of
based on a Wald test of 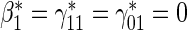 .
.  Test
Test 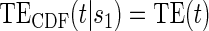 based on a Wald test of
based on a Wald test of 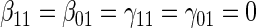 .
.  The model-specific test of surrogate value based on the CDF, test
The model-specific test of surrogate value based on the CDF, test  in the time-independent case and test # in the time-dependent.
in the time-independent case and test # in the time-dependent.
Table 3.
Proportion of Rejections: two-arm trial for 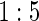 case–control subsampling
case–control subsampling 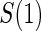 and given sampling of
and given sampling of 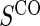 ; W,
; W,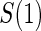 correlation (0.8)
correlation (0.8)
| Time indep. |
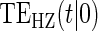 Time-dep. Time-dep. |
Multi time-dep. 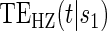 |
|||||
|---|---|---|---|---|---|---|---|
| Null | No val. | Some val. | High val. | Some | High | Some | High |
Full sampling 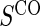
|
|||||||
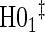 |
0.08 | 0.05 | 0.09 | 0.39 | 0.47 | 0.82 | 0.73 |
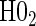 §¶ §¶
|
0.05 | 0.39 | 0.99 | 0.21 | 0.78 | 0.35 | 0.88 |
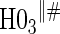 |
0.06 | 0.87 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
1:5 case:control sampling 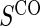
|
|||||||
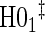 |
0.07 | 0.05 | 0.08 | 0.38 | 0.46 | 0.82 | 0.72 |
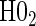 §¶ §¶
|
0.05 | 0.42 | 1.00 | 0.22 | 0.79 | 0.37 | 0.86 |
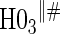 |
0.06 | 0.86 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
No sampling 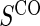
|
|||||||
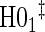 |
0.08 | 0.05 | 0.09 | 0.39 | 0.47 | 0.83 | 0.72 |
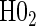 §¶ §¶
|
0.05 | 0.43 | 1.00 | 0.21 | 0.78 | 0.36 | 0.85 |
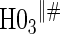 |
0.06 | 0.87 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
 Test of
Test of 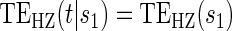 based on a joint Wald test of
based on a joint Wald test of  =
=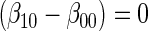 . § Test of
. § Test of 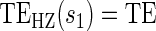 based on a Wald test of
based on a Wald test of 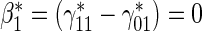 . ¶ Test of
. ¶ Test of 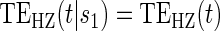 based on a Wald test
based on a Wald test 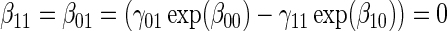 . §¶ The model-specific test of surrogate value based on the hazard, test §in the time-independent case and test ¶ in the time-dependent.
. §¶ The model-specific test of surrogate value based on the hazard, test §in the time-independent case and test ¶ in the time-dependent. Test
Test 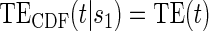 based on a Wald test of
based on a Wald test of 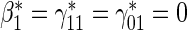 .
.  Test
Test 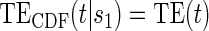 based on a Wald test of
based on a Wald test of 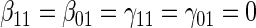 .
.  The model-specific test of surrogate value based on the CDF, test
The model-specific test of surrogate value based on the CDF, test  in the time-independent case and test # in the time-dependent.
in the time-independent case and test # in the time-dependent.
We also consider six different types of case–control sampling of 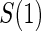 /
/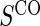 all for
all for 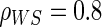 . The six case–control sampling scenarios considered are broken into two groups of three to consider the issues of case–control sampling of
. The six case–control sampling scenarios considered are broken into two groups of three to consider the issues of case–control sampling of 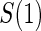 and
and 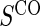 separately. First, we consider case–control sampling of
separately. First, we consider case–control sampling of 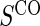 , measuring
, measuring 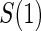 for all treated subjects. Case–control sampling of
for all treated subjects. Case–control sampling of 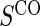 refers to obtaining
refers to obtaining 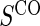 measurements from a random sample of non-active treatment subjects for whom
measurements from a random sample of non-active treatment subjects for whom 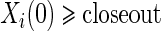 . We consider 1:5 case–control sampling of
. We consider 1:5 case–control sampling of  , no sampling of
, no sampling of 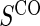 , and sampling of all non-active treatment subjects with
, and sampling of all non-active treatment subjects with 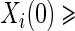 closeout. We then investigate the effects of subsampling of
closeout. We then investigate the effects of subsampling of 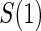 , by holding case–control sampling of
, by holding case–control sampling of 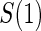 at 1:5 and again varying sampling of
at 1:5 and again varying sampling of 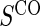 between 1:5 case–control, no sampling, and all non-active treatment subjects with
between 1:5 case–control, no sampling, and all non-active treatment subjects with 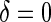 . Case–control sampling of
. Case–control sampling of 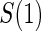 is the same as that for
is the same as that for 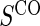 , with the addition of obtaining
, with the addition of obtaining 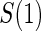 measurements for all treated subjects with observed events at closeout,
measurements for all treated subjects with observed events at closeout, 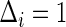 .
.
Table 1 displays the percent bias for various points on the 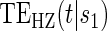 and
and 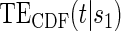 curves for each of the seven surrogate types and 6 sampling scenarios. We find that the Weibull EML estimation method has satisfactory performance in terms of minimal percent bias for points on both the
curves for each of the seven surrogate types and 6 sampling scenarios. We find that the Weibull EML estimation method has satisfactory performance in terms of minimal percent bias for points on both the 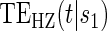 and
and 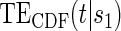 curves and with average bias less than one Monte Carlo standard error in all cases. In addition, all model coefficient estimates have minimal bias, with all estimates of mean bias well within one Monte Carlo standard error (results not shown).
curves and with average bias less than one Monte Carlo standard error in all cases. In addition, all model coefficient estimates have minimal bias, with all estimates of mean bias well within one Monte Carlo standard error (results not shown).
We display in Tables 2 and 3 the results from Wald tests of 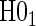 –
–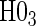 and
and 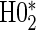 –
–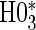 for each of the seven surrogate scenarios and 6 sampling scenarios; Monte Carlo standard errors are used in the Wald tests due to the computational burden of the bootstrap. We also display the power of a test of proportional hazards (PH),
for each of the seven surrogate scenarios and 6 sampling scenarios; Monte Carlo standard errors are used in the Wald tests due to the computational burden of the bootstrap. We also display the power of a test of proportional hazards (PH), 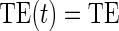 , using a Cox model containing treatment alone based on the Schoenfeld residuals (Grambsch and Therneau, 1994). We find that with full sampling the Cox-based PH test has lower power to reject
, using a Cox model containing treatment alone based on the Schoenfeld residuals (Grambsch and Therneau, 1994). We find that with full sampling the Cox-based PH test has lower power to reject 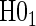 than the Weibull model-based test. We find that the test of
than the Weibull model-based test. We find that the test of 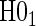 has power ranging from 0.37 to 0.84 and nearly correct type 1 error.
has power ranging from 0.37 to 0.84 and nearly correct type 1 error.
We also display in Table 2 the results for the tests of the nulls 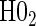 and
and 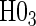 , for all of the surrogate scenarios and two of the sampling scenarios based on the time-dependent hazard Weibull model. We find that both tests have adequate power and correct size in the time-independent hazard scenarios. Tests of the nulls
, for all of the surrogate scenarios and two of the sampling scenarios based on the time-dependent hazard Weibull model. We find that both tests have adequate power and correct size in the time-independent hazard scenarios. Tests of the nulls 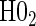 and
and 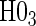 have noticeably less power than the tests of
have noticeably less power than the tests of 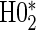 and
and 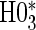 in the truly time-independent hazards scenarios; this justifies reverting to the simpler model when there is no evidence of time-dependent hazards. In the time-dependent hazard setting, the tests of
in the truly time-independent hazards scenarios; this justifies reverting to the simpler model when there is no evidence of time-dependent hazards. In the time-dependent hazard setting, the tests of 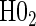 and
and 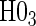 have power ranging from (0.21–1.00). The CDF-based TE test of any surrogate value, testing null
have power ranging from (0.21–1.00). The CDF-based TE test of any surrogate value, testing null 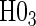 , has markedly better power than
, has markedly better power than 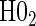 is all cases. This is also true in the time-independent hazard scenarios, where
is all cases. This is also true in the time-independent hazard scenarios, where 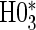 has markedly better power than
has markedly better power than 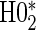 is all cases.
is all cases.
The non-hierarchical power and type 1 error rate of testing 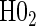 and
and 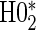 over the various sampling scenarios can be seen in Tables 2 and 3. To evaluate type 1 error and power, the entire suggested hierarchical testing procedure for assessing surrogate value was followed for all full sample simulations. Under this procedure we found that correct type 1 error and power was approximately the same as a power-of-
over the various sampling scenarios can be seen in Tables 2 and 3. To evaluate type 1 error and power, the entire suggested hierarchical testing procedure for assessing surrogate value was followed for all full sample simulations. Under this procedure we found that correct type 1 error and power was approximately the same as a power-of-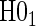 -weighted average of
-weighted average of 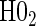 and
and 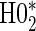 . For example, the power for the hierarchical procedure for the high-quality surrogate with multiple types of time dependence is 0.935, which is almost exactly
. For example, the power for the hierarchical procedure for the high-quality surrogate with multiple types of time dependence is 0.935, which is almost exactly 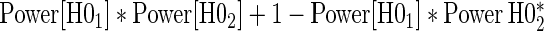 for that scenario. This was similarly found for null hypotheses
for that scenario. This was similarly found for null hypotheses 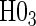 and
and 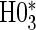 , suggesting that the hierarchical procedure maintains the correct size in all scenarios.
, suggesting that the hierarchical procedure maintains the correct size in all scenarios.
Power to reject all nulls declines from full sampling to case–control sampling of  . This decline is much more noticeable in the tests of surrogate quality; this is not surprising given that the coefficients involved in testing are associated with
. This decline is much more noticeable in the tests of surrogate quality; this is not surprising given that the coefficients involved in testing are associated with 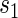 . It is clear from a comparison of Tables 2 and 3 that subsampling of
. It is clear from a comparison of Tables 2 and 3 that subsampling of 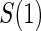 has a greater impact on power than subsampling of
has a greater impact on power than subsampling of 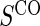 . In some of our simulation scenarios there exists a paradox of reduced power with increased sampling of
. In some of our simulation scenarios there exists a paradox of reduced power with increased sampling of 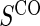 for a fixed level of
for a fixed level of 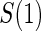 sampling; this paradox was first observed in Gilbert and others (2011). The paradox is a characteristic of the EML estimator as explained in Huang and others (2013). For weaker BIP, adding
sampling; this paradox was first observed in Gilbert and others (2011). The paradox is a characteristic of the EML estimator as explained in Huang and others (2013). For weaker BIP, adding 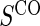 has been shown in previous works to improve power compared with BIP alone (Gilbert and others, 2011).
has been shown in previous works to improve power compared with BIP alone (Gilbert and others, 2011).
The simulations for full sampling were repeated for lower-quality BIPs with 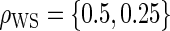 (Table S1 in Appendix B of supplementary material available at Biostatistics online). As expected, power decreases rapidly and bias increases slowly as
(Table S1 in Appendix B of supplementary material available at Biostatistics online). As expected, power decreases rapidly and bias increases slowly as 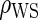 decreases. Hence, highly predictive BIPs are essential for accurate and reasonably precise PS evaluation for EML-based methods; this was also found to be true in previous works (Follmann, 2006; Gilbert and Hudgens, 2008; Huang and Gilbert, 2011). Based on our simulation results, the 0.701 correlation in our motivating example is adequate for unbiased and reasonably precise estimation via the Weibull EML method.
decreases. Hence, highly predictive BIPs are essential for accurate and reasonably precise PS evaluation for EML-based methods; this was also found to be true in previous works (Follmann, 2006; Gilbert and Hudgens, 2008; Huang and Gilbert, 2011). Based on our simulation results, the 0.701 correlation in our motivating example is adequate for unbiased and reasonably precise estimation via the Weibull EML method.
07. DCCT example
The DCCT enrolled 1441 persons with type 1 diabetes from 1983 to 1989 to determine the effects of intensive diabetes therapy on long-term complications of diabetes. Participants in DCCT were randomly assigned to intensive diabetes therapy aimed at lowering glucose concentrations as close as safely possible to the normal range or to conventional therapy aimed at preventing hyperglycemic symptoms. One of the outcomes of the DCCT, nephropathy (damage to the kidneys), is the leading cause of death and dialysis in the young with type 1 diabetes, particularly those with poorly controlled glucose levels. Nephropathy is often defined by a high albumin excretion rate, as micro-albuminuria (defined as an albumin excretion rate 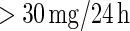 ) is the best non-invasive indicator of kidney damage. The trial ended early in 1993 due to overwhelming evidence of treatment efficacy, with an average of 6.5 years of follow-up; the estimated adjusted mean risk of micro-albuminuria was reduced by 56%, P-value 0.01 (DCCT/EDIC Research, 2011).
) is the best non-invasive indicator of kidney damage. The trial ended early in 1993 due to overwhelming evidence of treatment efficacy, with an average of 6.5 years of follow-up; the estimated adjusted mean risk of micro-albuminuria was reduced by 56%, P-value 0.01 (DCCT/EDIC Research, 2011).
The current study includes all participants who were free from micro-albuminuria at baseline (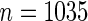 ); baseline micro-albuminuria was balanced over the arms of the trial. The difference in log-transformed hemoglobin A1C (HBA1C) measurements from baseline to year 1 is the candidate PS. The event of interest is the onset of persistent micro-albuminuria, which is defined as having two consecutive albumin excretion rate measurements
); baseline micro-albuminuria was balanced over the arms of the trial. The difference in log-transformed hemoglobin A1C (HBA1C) measurements from baseline to year 1 is the candidate PS. The event of interest is the onset of persistent micro-albuminuria, which is defined as having two consecutive albumin excretion rate measurements 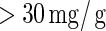 . Right censoring occurs due to drop-out or due to the end of the trial in 1993. No subject had an event prior to
. Right censoring occurs due to drop-out or due to the end of the trial in 1993. No subject had an event prior to  year post-randomization. All subjects had the BIP measured, which was defined as a linear combination of the BSM measurement, age, BMI and smoking status fit via linear regression to change in HBA1C using the Akaike information criterion. The estimated Spearman correlation between the BIP and the candidate PS is (0.7). We use a linear combination of baseline variables here to demonstrate that a set of weaker BIPs can be combined to form a higher-quality BIP; when fitting a linear combination, care should be taken to only include variables that truly improve predictive power and to avoid overfitting.
year post-randomization. All subjects had the BIP measured, which was defined as a linear combination of the BSM measurement, age, BMI and smoking status fit via linear regression to change in HBA1C using the Akaike information criterion. The estimated Spearman correlation between the BIP and the candidate PS is (0.7). We use a linear combination of baseline variables here to demonstrate that a set of weaker BIPs can be combined to form a higher-quality BIP; when fitting a linear combination, care should be taken to only include variables that truly improve predictive power and to avoid overfitting.
We fit the time-dependent hazard Weibull model to these data assuming a semiparametric location-scale model for 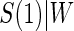 and assuming a parametric normal model. We found that the results were nearly identical, but the parametric model was more efficient. We found only marginal evidence of time dependence (P-values
and assuming a parametric normal model. We found that the results were nearly identical, but the parametric model was more efficient. We found only marginal evidence of time dependence (P-values 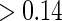 ), and for parsimony we use the time-independent hazard model as the main model for analysis. Figure S1 in Appendix B of the supplementary material (available at Biostatistics online) depicts the time-dependent hazard model for the parametric analysis. Under the time-independent hazard Weibull model we find evidence to support that 1-year change in HBA1C is a high-quality surrogate as the P-values for testing both
), and for parsimony we use the time-independent hazard model as the main model for analysis. Figure S1 in Appendix B of the supplementary material (available at Biostatistics online) depicts the time-dependent hazard model for the parametric analysis. Under the time-independent hazard Weibull model we find evidence to support that 1-year change in HBA1C is a high-quality surrogate as the P-values for testing both 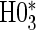 and
and 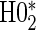 are
are  for both the semiparametric and the parametric analysis. Figure 2 illustrates the estimated
for both the semiparametric and the parametric analysis. Figure 2 illustrates the estimated  and
and 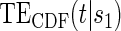 curves for the time-independent hazard model, assuming a location-scale model for
curves for the time-independent hazard model, assuming a location-scale model for 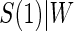 . Figure 2 in Appendix B of the supplementary material (available at Biostatistics online) depicts these same results for the parametric analysis. We also ran the analysis adjusting for the BIP. The adjusted models were very similar to the unadjusted, with all P-values within the same range as the unadjusted analysis and very similar TE curves.
. Figure 2 in Appendix B of the supplementary material (available at Biostatistics online) depicts these same results for the parametric analysis. We also ran the analysis adjusting for the BIP. The adjusted models were very similar to the unadjusted, with all P-values within the same range as the unadjusted analysis and very similar TE curves.
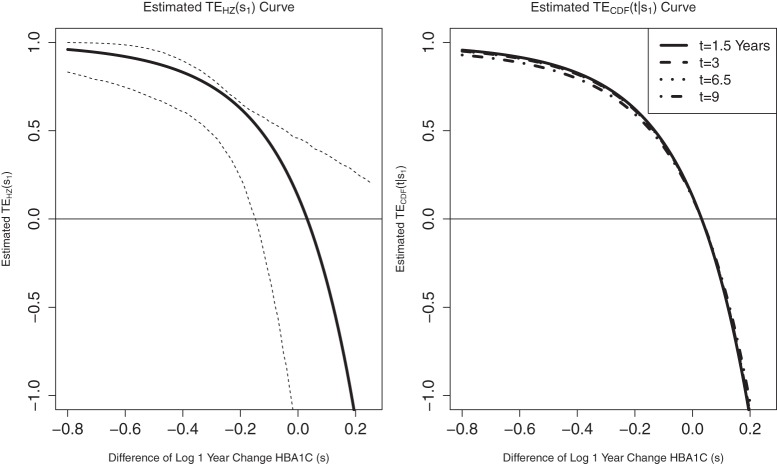
Figure 2.
Time-independent hazard Weibull EML analysis assuming a location-scale model 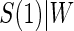 using the DCCT trial data with the difference of log baseline and log 1 year hemoglobin A1C as the candidate PS. The left panel depicts the estimated
using the DCCT trial data with the difference of log baseline and log 1 year hemoglobin A1C as the candidate PS. The left panel depicts the estimated 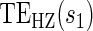 for the DCCT data and illustrates a highly variable curve over the range of the difference of log baseline and log 1 year hemoglobin A1C, suggesting a biomarker that is valuable as a target in future trials. The right panel depicts the estimated
for the DCCT data and illustrates a highly variable curve over the range of the difference of log baseline and log 1 year hemoglobin A1C, suggesting a biomarker that is valuable as a target in future trials. The right panel depicts the estimated 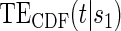 for the DCCT data and again suggests a highly variable curve. The
for the DCCT data and again suggests a highly variable curve. The 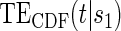 curves are displayed for time points
curves are displayed for time points 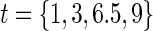 to illustrate differences over a range of follow-up times observed in the trial; little to no difference can be seen in the CDF-based curves over time.
to illustrate differences over a range of follow-up times observed in the trial; little to no difference can be seen in the CDF-based curves over time.
There is evidence to suggest that Assumption A7 does not hold if there is no measurement error. As there is information to suggest the presence of measurement error in these measurements of HBA1C, we also test the null 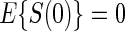 and find that this suggests no evidence against A7; (P-value 0.863). Figure 3 in Appendix B of the supplementary material (available at Biostatistics online) depicts the observed association between one year change in HBA1C and the clinical outcome separately by treatment arm. The estimated
and find that this suggests no evidence against A7; (P-value 0.863). Figure 3 in Appendix B of the supplementary material (available at Biostatistics online) depicts the observed association between one year change in HBA1C and the clinical outcome separately by treatment arm. The estimated 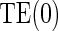 is 0.13 (95% CI
is 0.13 (95% CI  1.27, 0.458) for the semiparametric analysis; the P-value for
1.27, 0.458) for the semiparametric analysis; the P-value for 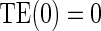 is 0.228. This is consistent with but not supportive of ACN. This is not surprising as treatment continued for 9 years after the candidate surrogate was measured. However, 1-year change in HBA1C under active treatment still strongly modifies the
is 0.228. This is consistent with but not supportive of ACN. This is not surprising as treatment continued for 9 years after the candidate surrogate was measured. However, 1-year change in HBA1C under active treatment still strongly modifies the 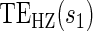 and
and 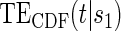 curves. Therefore, HBA1C reduction at year 1 is a good target for treatments in this setting.
curves. Therefore, HBA1C reduction at year 1 is a good target for treatments in this setting.
8. Discussion
PSs are important endpoints for Phase I and II trials. Few PS evaluation methods allow for a time-to-event clinical endpoint with right-censoring and, to our knowledge, none allow for or characterize the time-dependent effects of the treatment. There is evidence of time-varying treatment effects in many treatment and vaccine efficacy trials. Methods of PS evaluation that do not allow for or characterize time-varying effects may classify potential PS as high-quality ignoring their lack of durability or dismiss high-quality surrogates in trials that have rapidly waning TE.
The time-dependent hazard TE Weibull model allows for the characterization of the time-varying treatment effects in the time-to-event setting. The EML method is an adequate means to estimate the parameters of the time-dependent hazard TE Weibull model, allowing for flexible modeling of the PS given BIP distribution. The EML estimators perform well when there is a highly predictive BIP, but the need for a highly correlated BIP is a limitation of EML estimation. When a highly correlated BIP is available, EML is consistent and relatively efficient without requiring  as was recently suggested by Zigler and Belin (2012).
as was recently suggested by Zigler and Belin (2012).
The CPV argumentation does not seem to materially improve power with EML estimation. This suggests that full likelihood should be considered as an alternative to EML when CPV is available, (Follmann, 2006). Huang and others (2013) develop a pseudoscore method for PS evaluation that improves efficiency over EML methods when CPV is available. However, in cases where CPV is not available, EML methods and pseudoscore methods perform similarly and an extension of the pseudoscore method to time-to-event has yet to be developed.
There are two concepts of what makes a biomarker useful as a PS. For one, the quality of a biomarker as a PS can be measured by the degree of variation in the marginal treatment efficacy curve 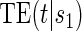 over the biomarker under the active treatment and for the other evaluation of the biomarker under both trial arms is required. When the CB holds, these concepts are equivalent. We have proposed a BSM trial augmentation plus assumption, A7, that increases the number of trials where CB is likely to hold for some candidate PS. The suggested BSM augmentation is likely feasible when the candidate surrogate of interest is not difficult to measure at baseline. In trials with adequate augmentation, our methods can be useful for evaluating biomarkers under active treatment as surrogates for time-to-event clinical endpoints regardless of the validity of assumption CB and under both concepts of principal surrogacy when the CB holds.
over the biomarker under the active treatment and for the other evaluation of the biomarker under both trial arms is required. When the CB holds, these concepts are equivalent. We have proposed a BSM trial augmentation plus assumption, A7, that increases the number of trials where CB is likely to hold for some candidate PS. The suggested BSM augmentation is likely feasible when the candidate surrogate of interest is not difficult to measure at baseline. In trials with adequate augmentation, our methods can be useful for evaluating biomarkers under active treatment as surrogates for time-to-event clinical endpoints regardless of the validity of assumption CB and under both concepts of principal surrogacy when the CB holds.
Supplementary Material
supplementary Material is available at http://biostatistics.oxfordjournals.org.
Funding
The research of Dr E.E.G. was partially supported by the National Institute Of Allergy And Infectious Diseases (NIAID) of the National Institutes of Health (NIH) under award numbers R37AI054165 and R37AI032042. The research of Dr P.B.G. was partially supported under NIAID NIH grant number R37AI054165. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
Supplementary Material
Acknowledgements
The authors are grateful to the DCCT Research Group for releasing their data to the public domain. Conflict of Interest: None declared.
References
- DCCT/EDIC Research, Group. Intensive diabetes therapy and glomerular filtration rate in type 1 diabetes. The New England Journal of Medicine. 2011;365(25):2366–2376. doi: 10.1056/NEJMoa1111732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duerr A., Huang Y., Buchbinder S., Coombs R. W., Sanchez J., del Rio C., Casapia M., Santiago S., Gilbert P. B., Corey L. Extended follow-up confirms early vaccine-enhanced risk of HIV acquisition and demonstrates waning effect over time among participants in a randomized trial of recombinant adenovirus HIV vaccine (Step study) Journal of Infectious Diseases. 2012;206(2):258–266. doi: 10.1093/infdis/jis342. and others. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Follmann D. Augmented designs to assess immune response in vaccine trials. Biometrics. 2006;62(4):1161–1169. doi: 10.1111/j.1541-0420.2006.00569.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frangakis C. E., Rubin D. B. Principal stratification in causal inference. Biometrics. 2002;58(1):21–29. doi: 10.1111/j.0006-341x.2002.00021.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P. B., Grove D., Gabriel E. E., Huang Y., Gray G., Hammer S. M., Buchbinder S. P., Kublin J., Corey L., Self S. G. A sequential phase 2b trial design for evaluating vaccine efficacy and immune correlates for multiple HIV vaccine regimens. Statistical Communications in Infectious Diseases. 2011;3(1) doi: 10.2202/1948-4690.1037. [Epub ahead of print] [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P. B., Hudgens M. G. Evaluating candidate principal surrogate endpoints. Biometrics. 2008;64(4):1146–1154. doi: 10.1111/j.1541-0420.2008.01014.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gilbert P. B., Qin L., Self S. G. Evaluating a surrogate endpoint at three levels, with application to vaccine development. Statistics in Medicine. 2008;27(23):4758–4778. doi: 10.1002/sim.3122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grambsch P. M., Therneau T. M. Proportional hazards tests and diagnostics based on weighted residuals. Biometrika. 1994;81(3):515–526. [Google Scholar]
- Hernán M. The hazards of hazard ratios. Epidemiology. 2010;21(1):13–15. doi: 10.1097/EDE.0b013e3181c1ea43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y., Gilbert P. B. Comparing biomarkers as principal surrogate endpoints. Biometrics. 2011;67(4):1442–1451. doi: 10.1111/j.1541-0420.2011.01603.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y., Gilbert P. B., Wolfson J. Design and estimation for evaluating principal surrogate markers in vaccine trials. Biometrics. 2013;69(2):301–309. doi: 10.1111/biom.12014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joffe M. M., Greene T. Related causal frameworks for surrogate outcomes. Biometrics. 2009;65(2):530–538. doi: 10.1111/j.1541-0420.2008.01106.x. [DOI] [PubMed] [Google Scholar]
- Li Y., Taylor J. M. G., Elliott M. R. A Bayesian approach to surrogacy assessment using principal stratification in clinical trials. Biometrics. 2010;66(2):523–531. doi: 10.1111/j.1541-0420.2009.01303.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pepe M. S., Fleming T. R. A nonparametric method for dealing with mismeasured covariate data. Journal of the American Statistical Association. 1991;86(413):108–113. [Google Scholar]
- Qin L., Gilbert P. B., Follmann D., Dongfeng L. Assessing surrogate endpoints in vaccine trials with case-cohort sampling and the Cox model. Annals of Applied Statistics. 2008;2(1):386–407. doi: 10.1214/07-AOAS132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor J. M. G., Wang Y., Thibaut R. Counterfactual links to the proportion of treatment effect explained by a surrogate marker. Biometrics. 2005;61(4):1102–1111. doi: 10.1111/j.1541-0420.2005.00380.x. [DOI] [PubMed] [Google Scholar]
- Wolfson J. Statistical methods for identifying surrogate endpoints in vaccine trials [Doctor of Philosophy Dissertation] 2009 University of Washington, Department of Biostatistics. [Google Scholar]
- Wolfson J., Gilbert P. B. Statistical identifiability and the surrogate endpoint problem, with application to vaccine trials. Biometrics. 2010;66(4):1153–1161. doi: 10.1111/j.1541-0420.2009.01380.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zigler C. M., Belin T. R. A Bayesian approach to improved estimation of causal effect predictiveness for a principal surrogate endpoint. Biometrics. 2012;68:922–932. doi: 10.1111/j.1541-0420.2011.01736.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.