Determinants of Fluidlike Behavior and Effective Viscosity in Cross-Linked Actin Networks

Abstract

The actin cortex has a well-documented ability to rapidly remodel and flow while maintaining long-range connectivity, but how this is achieved remains poorly understood. Here, we use computer simulations to explore how stress relaxation in cross-linked actin networks subjected to extensional stress depends on the interplay between network architecture and turnover. We characterize a regime in which a network response is nonaffine and stress relaxation is governed by the continuous dissipation of elastic energy via cyclic formation, elongation, and turnover of tension-bearing elements. Within this regime, for a wide range of network parameters, we observe a constant deformation (creep) rate that is linearly proportional to the rate of filament turnover, leading to a constant effective viscosity that is inversely proportional to turnover rate. Significantly, we observe a biphasic dependence of the creep rate on applied stress: below a critical stress threshold, the creep rate increases linearly with applied stress; above that threshold, the creep rate becomes independent of applied stress. We show that this biphasic stress dependence can be understood in terms of the nonlinear force-extension behavior of individual force-transmitting network elements. These results have important implications for understanding the origins and control of viscous flows both in the cortex of living cells and in other polymer networks.

Introduction

The ability of the cell cortex to undergo large and irreversible deformations while maintaining structural integrity is essential for numerous developmental and physiological processes including cell motility, polarization, division, and tissue morphogenesis (1,2). The cell cortex is a network of short actin filaments interconnected by actin cross-linking proteins (ACPs) that is enriched just beneath the plasma membrane (3). On short timescales (<2–3 s), the cortex shows viscoelastic resistance to deformation, whereas on longer timescales, it can undergo viscous deformations and flow (4,5). These mechanical responses are likely to depend both on 1), network architecture, e.g., the length, density, and connectivity of actin filaments and ACPs; and 2), network turnover via ACP binding/unbinding (6) and the dynamic control of actin polymerization/depolymerization (7–11). However, how different modes of cortex deformation and flow depend on the interplay of architecture and turnover remains poorly understood.

Previous studies of stress relaxation in solution and networks of semiflexible polymers considered networks of stable filaments and focused predominately on the role of polymer motions and ACP dynamics (12,13). In entangled solutions of F-actin, translational diffusion or reptation of filaments facilitates stress relaxation at a rate proportional to the filament length (14,15). Large stresses enhance polymer mobility and result in stress thinning or fluidization under applied stress. Reptation is constrained in cross-linked actin networks, but stress relaxation can occur via ACP unbinding (12,16,17). The extent to which filament turnover might impact these different modes of stress relaxation is unknown. Moreover, previous theoretical analyses of stress relaxation assumed highly cross-linked networks and affine deformations, such that response at the single-filament level reflects the network response. However, nonaffine deformations have been shown to dominate within certain regimes of elastic response (18), with consequences for stress relaxation that remain to be explored.

Here, we use computer simulations to investigate the fluidlike response of a cross-linked network of dynamically treadmilling, semiflexible actin filaments to extensional stress. A key advantage of this approach is that it allows us to relate network mechanical response to network architecture as well as to the microscopic dynamics of filaments and ACPs. Our simulations predict a simple creep response characterized by an approximately constant creep rate and thus a relatively constant effective viscosity that are tunable by varying the density, turnover rate, and length of actin filaments. For a wide range of these parameters, we observe a biphasic dependence of a creep rate on the level of applied stress. At low levels of applied stress, we observe a linear dependence of creep rate on applied stress; at higher levels, we observe a sharp transition to a nonlinear response regime in which the creep rate is independent of applied stress. Comparing microscale dynamics of the full simulations with the predictions of a simpler toy model, we show that the existence of these two regimes and the transition between them can be explained in terms of the interplay of network architecture/turnover and the elastic resistance of network subelements to applied stress. At each moment, the elastic resistance is sustained by a small fraction of the network filaments that are interconnected to form network-spanning elements; the elastic contribution to effective viscosity is governed by the continuous dissipation of elastic energy via cyclic turnover of these tension-bearing elements. The transition between linear and nonlinear response regimes for creep originates from the nonlinear force-extension response of the tension-bearing elements where resistance builds rapidly above a critical level of strain. We discuss the broader implications of this work for both materials design and the physiological control of cellular deformation and flow.

Methods

We used a Brownian dynamics approach to simulate the response of a thin cortical network, formed by dynamically treadmilling semiflexible actin filaments and elastic ACPs, to applied stress. The approach and software implementation are direct extensions of our previous works on cross-linked actin networks (17,19). We modeled actin filaments as a series of cylindrical segments connected by elastic hinges to form semiflexible rods. In a similar way, we modeled ACPs as pairs of rigid rods connected to one another and to actin filaments by elastic hinges. Each actin filament has a fixed polarity with fast-growing (barbed) and slow-growing (pointed) ends.

The forces that arise along each cylindrical segment due to filament-filament, ACP-ACP, or filament-ACP interactions are referred to endpoints of the cylinders, whose displacements are governed by a Langevin equation with inertia neglected:

$${\mathbf{F}}_i-{\zeta }_i\frac{\text{d}{\mathbf{r}}_i}{\text{d}t}+{\mathbf{F}}_i^{\text{B}}=0,$$ (1)

where ${\mathbf{r}}_i$ is the location of ith segment endpoint (actin or ACP), ζ_i is an effective drag coefficient (see below), t is time, ${\mathbf{F}}_i^{\text{B}}$ is a stochastic force satisfying the fluctuation-dissipation theorem, and ${\mathbf{F}}_i$ is a net deterministic force. The positions of all segments are updated using the Euler integration scheme:

$${\mathbf{r}}_i(t+\Delta t)={\mathbf{r}}_i\left(t\right)+\frac{\text{d}{\mathbf{r}}_i}{\text{d}t}\Delta t={\mathbf{r}}_i\left(t\right)+\frac{1}{{\zeta }_i}\left({\mathbf{F}}_i^{\text{B}}+{\mathbf{F}}_i\right)\Delta t,$$ (2)

where Δt = 2.3 × 10⁻⁶ s is the time step.

Mechanics of actin filaments and ACPs

We fixed the length and diameter of filament segments (r_0,A and r_c,A) to be 140 nm and 7 nm, respectively. This level of coarse-graining is appropriate since 140 nm is still much shorter than the persistence length of an actin filament, 9 μm (20). The length and diameter of two cylindrical arms for ACPs (r_0,ACP and r_c,ACP) are 35 nm and 10 nm, respectively, which mimics the geometry of α-actinin (21).

Harmonic interaction potentials describe extension and bending of actins and ACPs with stiffness κ_s and κ_b, respectively (Table S1):

$$U_{\text{s}}=\frac{1}{2}{\kappa }_{\text{s}}{(r-r_0)}^2\mathrm{and}{U}_{\text{b}}=\frac{1}{2}{\kappa }_{\text{b}}{\left(\theta -{\theta }_0\right)}^2,$$ (3)

where r is the distance between the two endpoints of a segment, θ is the bending angle, and the subscript 0 denotes the equilibrium value. We assigned extensional (${\kappa }_{\text{s,A}}$) and bending stiffnesses (${\kappa }_{\text{b,A}}$) for actin filaments based on experimental measurements (20,22), which yields a persistence length of 9 μm in the presence of stochastic forces. Given the lack of data, we set parameter values for ACPs (${\theta }_{0,\text{ACP}1}$, ${\theta }_{0,\text{ACP}2}$, ${\kappa }_{\text{s,ACP}}$, ${\kappa }_{\text{b},\text{ACP}1}$, ${\kappa }_{\text{b},\text{ACP}2}$) to reasonable values, as in our previous work (19), where ${\theta }_{0,\text{ACP}1}$ is the equilibrium angle between two arms of ACP, and ${\theta }_{0,\text{ACP}2}$ is the angle formed by an arm of ACP and the axis of the actin filament to which the ACP is bound. ${\kappa }_{\text{s,ACP}}$, ${\kappa }_{\text{b},\text{ACP}1}$, and ${\kappa }_{\text{b},\text{ACP}2}$ are stiffness constants related to r_0,ACP, ${\theta }_{0,\text{ACP}1}$, and ${\theta }_{0,\text{ACP}2}$, respectively. We computed repulsive forces using a harmonic potential that depends on the minimum distance between pairs of actin segments, as described in our previous work (19).

Effects of the surrounding medium

We defined the effective drag coefficient for each cylindrical segment to be (23):

$${\zeta }_i=3\pi {\eta }_{\text{m}}{r}_{\text{c,}i}\frac{3+2r_{0,i}/r_{\text{c,}i}}{5},$$ (4)

where η_m is the medium viscosity. We assumed constant ζ_i regardless of the length of the filament to which a segment belongs. Likewise, we neglected hydrodynamic interactions between filaments, since the volume fraction of actin is very low (<1%), and the actin filaments have a very high aspect ratio (24). Because we focus in this article on a regime in which relaxation of elastic stress through network turnover dominates the effects of fluid drag on individual filaments (see below), these assumptions have minimal effects on the results we report.

Dynamics of actin filaments and ACPs

For most simulations, we modeled filament turnover as a simple steady-state treadmilling reaction similar to what occurs in vitro under appropriate conditions, in which actin filaments undergo net elongation at one end (the barbed end) and net shrinkage at the other (the pointed end), such that average length of each filament remains constant. Although filament turnover in cells is more complex, we chose treadmilling because it is easy to implement and provides a simple and transparent way to tune filament turnover rates while keeping other network parameters (e.g., filament length and density) constant. We obtained very similar creep responses for other modes of filament turnover (e.g., severing (25) or bursting disassembly (26)) if we constrained the per-monomer turnover rate and the average length and density of filaments to have similar values (data not shown).

For the treadmilling reaction, we assume distinct force-independent rates for stochastic addition (+) and removal (–) of monomers at barbed (B) and pointed (P) ends ($k_{\text{B}}^{+}$, $k_{\text{P}}^{+}$, $k_{\text{B}}^{-}$, $k_{\text{P}}^{-}$) (27), and we introduced scale factor n to tune overall filament turnover rates while maintaining an approximately fixed amount of filamentous actin:

$$k_{\text{B}}^{+}\mathrm{=}6n\left[\mu {\mathrm{M}}^{\mathrm{-}1}{\mathrm{s}}^{\mathrm{-}1}\right],k_{\text{P}}^{+}\mathrm{=0}.6n\left[\mu {\mathrm{M}}^{\mathrm{-}1}{\mathrm{s}}^{\mathrm{-}1}\right],k_{\text{B}}^{\mathrm{-}}\mathrm{=0}.6n\left[{\mathrm{s}}^{\mathrm{-}1}\right],k_{\text{P}}^{\mathrm{-}}\mathrm{=}6n\left[{\mathrm{s}}^{\mathrm{-}1}\right]$$ (5)

These parameters yield a treadmilling rate of 5.4n s⁻¹ at a dynamic steady state. To balance the occasional loss of filaments due to stochastic polymerization/depolymerization reactions, we introduced simple nucleation at a rate adjusted to maintain a constant number of filaments throughout each simulation.

We assume a bulk pool of free ACPs that bind single actin filaments and in turn bind nearby filaments to form functional cross-links. ACPs cross-link pairs of filaments without preference for angle of contact. In most simulations, we allowed ACPs to unbind only when the actin segments that contain them depolymerize, and to simplify the analysis, we ignored any possible force dependence of ACP unbinding. However, in a few simulations conducted to compare actin turnover with pure ACP unbinding, we modeled the unbinding rate ($k_{\text{ub}}$) of ACPs using Bell’s equation, as in our previous work (17):

$$k_{\text{ub}}=k_{\text{ub}}^0\exp \left(\frac{{\lambda }_{\text{ub}}{F}_{\text{s}}}{k_{\text{B}}T}\right),$$

where $k_{\text{ub}}^0$ is the zero-force unbinding rate coefficient, λ_ub is the mechanical compliance, F_s is a force, and k_BT is a thermal energy. The reference values of $k_{\text{ub}}^0$ = 0.115 s⁻¹ and λ_ub = 1.04 × 10⁻¹⁰ m in these simulations were taken from a single-molecule experiment (28).

Network preassembly

As in previous studies (17,19), we allowed actin monomers and ACPs to self-assemble into a network within a thin three-dimensional rectangular domain with periodic boundary conditions in x and y directions, reaching a dynamic steady state when the concentration of free actin monomers falls to ∼1 μM with treadmilling. Unless specified, we used the following reference parameter values: actin concentration (C_A) is 20 μM, molar ratio of ACPs (R) is 0.02, and the initial widths of the rectangular domain in the x, y, and z directions are 5 × 5 × 1 μm. These parameters yield a network composed of ∼1200 actin filaments with average filament length (<L_f>) ∼0.9 μm and cross-linking distance ∼0.4 μm.

Creep test and measurements of elastic/viscous stresses and effective viscosity

After allowing a network to form, we severed all actin filaments that cross the network boundaries at ±x, then clamped the filament ends at ±x and deactivated periodic boundary conditions in the x direction. To simulate a standard uniaxial creep test, we kept the −x boundary fixed, imposed a constant stress (σ = 10 Pa unless specified) in the +x direction on the +x boundary, and then monitored the time evolution of normal strain, $\epsilon \left(t\right)$ (Fig. 1 A). Assuming that ±x boundaries are rigid plates, we calculated the axial stress at each point in time by dividing the sum of forces acting on the filaments clamped on the +x boundary by its area. We used proportional and derivative feedback to dynamically adjust the location of the +x boundary so as to maintain constant stress. We calculated the effective viscosity (η_eff) from the observed creep response as η_eff = σ/$\dot{\epsilon }$, where $\dot{\epsilon }$ is the average slope of $\epsilon$ over the range of response times for which the slope is relatively constant. We computed the viscous stress (σ_v) as the sum of all viscous forces acting on the portion of the network connected to the +x boundary, divided by the area (Fig. S1) and the elastic stress (σ_e) as the difference between σ and σ_v.

Figure 1.

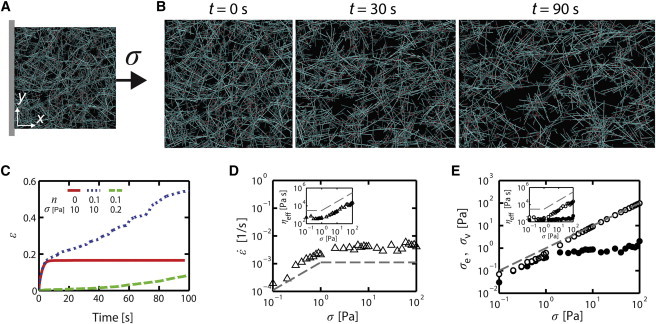
Creep response to uniaxial applied stress. (A) A schematic view of the simulated stress test. A cross-linked actin network is pinned at the –x boundary, and a stress (σ) is applied to the free +x boundary. (B) Snapshots of the deforming network at t = 0, 30, and 90 s with a relative filament turnover rate (n) = 0.1 and σ = 10 Pa. (C) Time evolution of network strain ($\epsilon$) as a function of time for n = 0.1 and σ = 0.2 Pa (green dashed line); n = 0.1 and σ = 10 Pa (blue dotted line); and n = 0 and σ = 10 Pa (red solid line). (D) A strain rate ($\dot{\epsilon }$) as a function of σ for n = 0.1. (Inset) Effective viscosity (η_eff) as a function of σ. (E) Elastic (σ_e, open symbols) and viscous stress (σ_v, solid symbols) depending on σ at n = 0.1. (Inset) η_eff originating from σ_e (= σ_e/$\dot{\epsilon }$, open symbols) and σ_v (= σ_v/$\dot{\epsilon }$, solid symbols), respectively. Dashed lines in D and E indicate either ∼σ¹ or ∼σ⁰. To see this figure in color, go online.

Results

We subjected preassembled networks to uniaxial stress (σ) and monitored network deformation for 100 s in the presence of continuous filament turnover. In initial simulations, we implemented several different forms of filament turnover (treadmilling, severing, and bursting), and observed very similar responses so long as we constrained average filament length, density, and per-monomer turnover rate to have similar values (data not shown). We therefore chose to focus on an idealized form of treadmilling, because it allowed us to tune the per-monomer turnover rates independent of average filament length and density through a single scale factor, n (see Methods). With σ = 0.2 Pa and n = 0.1, we observed continuous deformation (creep) over 100 s with a slow and approximately constant strain rate ($\dot{\epsilon }$) (Fig. 1 C). When we increased σ to 10 Pa, we observed a significant elastic deformation at short times, followed by faster creep over 100 s. A significant finding was that $\dot{\epsilon }$ remained relatively constant for 100 s despite large changes in network density and filament alignment (Fig. 1 B). These creep responses are qualitatively similar to those measured both in vitro (16,29–31) and in vivo (5,32). Significantly, setting n = 0 eliminated the longer-term creep response, but not the initial elastic deformation, indicating that the creep response requires filament (thus cross-link) turnover. Moreover, measurements of linear frequency-dependent viscoelastic moduli E′(f) and E″(f) for f = 0.001–10 Hz revealed a characteristic fall off at low frequencies, as expected for dissipation of elastic stress due to cross-link turnover (Fig. S2).

To further characterize stress dependence of the creep response, we calculated $\dot{\epsilon }$ and effective viscosity, η_eff = σ/$\dot{\epsilon }$, over a wide range of applied stress from 0.1 to 100 Pa (Fig. 1, D and E). At low σ, $\dot{\epsilon }$ increased in proportion to σ (Fig. 1 D), implying a constant η_eff (Fig. 1 D, inset). However, above a critical stress, σ_th, $\dot{\epsilon }$ remained constant over nearly two orders of magnitude, and thus, η_eff increased in proportion to σ. Thus, we observe two distinct regimes of creep-rate dependence on applied stress: a linear regime below σ_th in which creep rate is proportional to σ, and a nonlinear regime above σ_th in which creep rate is constant, independent of σ.

The creep responses that we observed must arise from a combination of viscous dissipation and internal stress relaxation due to rearrangement or turnover of elastic elements within the network. To clarify the relative contributions of these two mechanisms at different levels of σ, we decomposed network forces balancing σ into a viscous component, σ_v, due to the drag of network elements against the surrounding fluid, and an elastic component, σ_e, due to strain on network-spanning elements (Fig. S1). In the linear regime, both σ_e and σ_v increased linearly with σ (Fig. 1 E). In the nonlinear regime (above σ_th), σ_v remained constant, whereas σ_e continued to rise. Accordingly, the viscous contribution to effective viscosity (σ_v/$\dot{\epsilon }$) remained constant across both regimes, whereas the elastic contribution (σ_e/$\dot{\epsilon }$) was constant in the linear regime and increased in proportion to σ in the nonlinear regime (Fig. 1 E, inset). We conclude that elastic stress relaxation and its dependence on σ dominate the creep response to large stress and govern the transition between the linear and nonlinear regimes.

To gain insights into how filament turnover regulates stress relaxation and effective viscosity, we explored how $\dot{\epsilon }$ varies for a fixed level of σ (10 Pa) when n is varied from 0.01 to 1 (Fig. 2 A). We observed qualitatively similar behaviors for all sampled values of n, characterized by roughly constant $\dot{\epsilon }$ over long times. For n ≤ 0.1, the elastic contribution dominated η_eff (Fig. 2 B), and η_eff was inversely proportional to n (Fig. 2 C). For n > 0.1, the viscous contribution to balancing σ (and thus to η_eff) began to increase, and η_eff showed stronger dependence on n. For all values of n ≤ 0.3, we observed a similar transition from linear to nonlinear regimes with increasing σ, and the linear dependence of $\dot{\epsilon }$ on n remained constant over the entire range of σ (Figs. 2 D and S3 A). Within this range of sampled values for n and σ, the data collapsed onto a single master curve defined by the equation

$${\eta }_{\text{eff}}\times n={\eta }_{\text{eff}}^0\frac{\max (\sigma ,{\sigma }_{\text{th}})}{{\sigma }_{\text{th}}},$$ (6)

where ${\eta }_{\text{eff}}^0$ is ∼35 Pa·s and σ_th is ∼1 Pa (Fig. S3 B).

Figure 2.

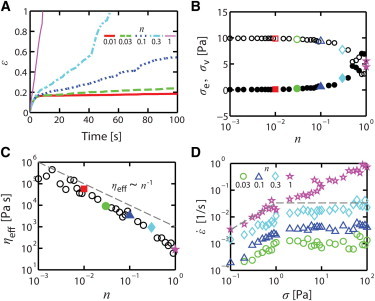
Dependence of creep response on n. (A) $\epsilon$ versus time for σ = 10 Pa and n = 0.01 (red solid line), 0.03 (green dashed line), 0.1 (blue dashed line), 0.3 (cyan dash-dotted line), and 1 (magenta thin solid line). (B) Relative magnitudes of σ_e (open symbols) and σ_v (solid symbols) as a function of n for σ = 10 Pa. (C) η_eff versus n with σ = 10 Pa for n = 0.001 to 1. A dashed line indicates η_eff ∼ n⁻¹ for reference. In B and C, colored symbols correspond to the colored traces in A. (D) $\dot{\epsilon }$ as a function of σ for n = 0.03 (green circles), 0.1 (blue triangles), 0.3 (cyan diamonds), and 1 (magenta stars). For n≤ 0.3, the data are fit well by a single master equation (see Eq. 6). Dashed lines represent either ∼σ¹ or ∼σ⁰. To see this figure in color, go online.

The foregoing analysis was conducted with reference values for C_A, R, and <L_f>. To explore the generality of these results, we varied each of these parameters about their reference values and measured $\dot{\epsilon }$ and η_eff versus σ and n as above. Significantly, we observed the transition between the linear and nonlinear stress dependence and the linear dependence of $\dot{\epsilon }$ on n over a wide range of values for C_A, R, and <L_f> (Fig. 3, A–C). Increases in each of these parameter values lead to sharp decreases in $\dot{\epsilon }$ and thus sharp increases in η_eff, but these could be offset by increases in n (Fig. 3 D). Thus, biphasic dependence of $\dot{\epsilon }$ on increasing stress and a linear dependence of $\dot{\epsilon }$ on n appear to be general characteristics of the response to extensional stress in cross-linked networks with dynamic filaments.

Figure 3.

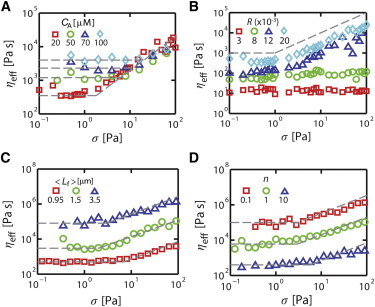
Transition between linear and nonlinear dependence on σ persists over a range of actin concentrations (C_A), cross-linking densities (R), and average filament lengths (<L_f>). (A) η_eff versus σ for n = 0.1 and σ = 10 Pa with C_A = 20 (red squares), 50 (green circles), 70 (blue triangles), and 100 μM (cyan diamonds). (B) η_eff versus σ for R = 0.003 (red squares), 0.008 (green circles), 0.012 (blue triangles), and 0.02 (cyan diamonds). (C) η_eff versus σ for <L_f> = 0.95 (red squares), 1.5 (green circles), and 3.5 μm (blue triangles). (D) η_eff versus σ for n = 0.1 (red squares), 1 (green circles), and 10 (blue triangles) with <L_f> = 3.5 μm. Note that larger networks (10 × 10 × 1 μm) were used for C and D to avoid possible artifacts. Dashed lines in figure indicate either ∼σ¹ or ∼σ⁰. To see this figure in color, go online.

In the above simulations, periodic boundary conditions prevented networks from deforming perpendicular to the axis of applied stress. This approximates the conditions that accompany unidirectional cortical flow in many cells, e.g., motile cells or the C. elegans zygote during polarization (33). To test how this assumption might impact our results, we simulated creep tests with and without periodic boundary conditions in the y direction. Not surprisingly, the initial elastic deformation was larger in the latter case. However, the long-time creep behavior and its biphasic dependence on applied stress were very similar for both cases (Fig. S4).

We also assumed that filament turnover drives cross-link detachment, and we ignored the possible effects of force-dependent cross-link unbinding (28) that could soften networks at higher applied stresses. To evaluate the consequences from these assumptions, we first compared creep responses for treadmilling as above with pure cross-link unbinding (without filament turnover), holding the effective cross-link detachment rate and all other network parameters constant. We observed a very similar biphasic response to σ in both cases (Fig. S5): η_eff was fourfold lower for the case with filament turnover because actin depolymerization both detaches the cross-link and removes its binding partner to prevent immediate rebinding (data not shown). However, the critical stress at which the response becomes nonlinear was nearly the same in both cases. Next, we compared the creep behaviors of networks driven solely by unbinding of cross-linkers with or without force dependence. We introduced force dependence using Bell’s equation, as in previous work (17), with parameters chosen to mimic the force dependence of Filamin A (28), and used reference values for all other parameters. As shown in Fig. S5, we observed nearly identical dependence of $\dot{\epsilon }$ on σ up to σ ∼ 10 Pa for the force-dependent and force-independent cases, and a slight softening of the response above σ = 10 Pa with force-dependent unbinding.

To explore further how elastic stress is supported and dissipated within networks during simulated creep with filament turnover, we examined the distribution of forces on individual filaments over time, F(t). We found that for all values of n within the elasticity-dominated creep regime (i.e., σ_e >> σ_v), at any moment in time, the majority of σ was supported by a relatively small number of highly strained filaments, belonging to percolating pathways that spanned the network from one boundary to the other (Fig. 4 A and Movie S1). The fraction of the filaments that sustain tension slightly varies, depending on n. For n = 0.1 and reference values for other network parameters, ∼5% of filaments sustain 99% of the tension (Fig. 4 B). Likewise, examining the distribution of changes in tension on filament segments (ΔF) over time during simulated creep revealed that in the elasticity-dominated regime, most filaments experience little change in tension, whereas a small fraction of filaments build or release significant tension (Fig. 4 C).

Figure 4.

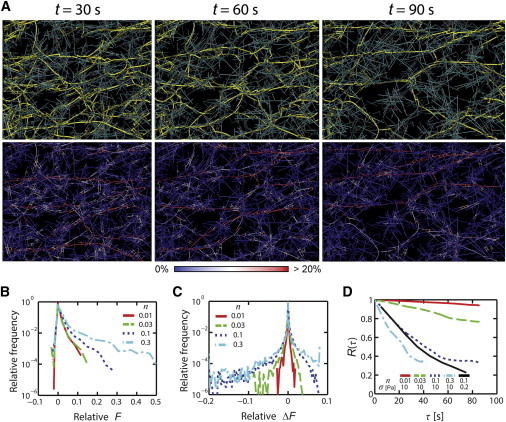
Dissipation of stress through buildup and turnover of forces on network-spanning pathways. (A) Snapshots of a network with n = 0.1 and σ = 10 Pa at t = 30, 60, and 90 s during the creep response. The top row shows network spanning (or percolating) pathways (yellow) in the network comprising actins (cyan) and ACPs (red). The bottom row shows the distribution of tensions with the color scale. (B–D) Analysis of force distribution and turnover across network filaments for simulations with n = 0.01 (red solid line), 0.03 (green dashed line), 0.1 (blue dotted line), and 0.3 (cyan dash-dotted line). (B) Distribution of relative tension across all filaments at one time point, defined as per-filament tension, F, divided by 50 pN, where 50 pN corresponds to a network-level stress of 10 Pa applied to one end of the reference computational domain. Large tensions are exerted by a very small fraction of the filaments. (C) Distribution of changes in relative F (ΔF/50 pN) occurring every 5 s, i.e., ΔF(t) = F(t) − F(t − 5). (D) Autocorrelation function of F, R(τ) versus τ, defined in Eq. 7. The black solid line corresponds to a case with σ = 0.2 Pa and n = 0.1. To see this figure in color, go online.

We hypothesized that changes in $\dot{\epsilon }$ due to variations in n originate from different lifetimes of tension-bearing segments. To test this, we examined the autocorrelation of F(t):

$$R\left(\tau \right)=\frac{\langle \left(F\left(t\right)-\mu \right)\left(F(t+\tau )-\mu \right)\rangle }{std\left(F\right)},$$ (7)

where μ and std(F) are the mean and standard deviation of F(t), respectively (Fig. 4 D). Significantly, we observed faster decay of R(τ) as n increased, with the slope of R(τ) proportional to n (Fig. S6). Thus, the faster creep rate at higher n originates from similar force distributions, but faster turnover of tension-bearing segments. Together, these data imply that the origins of creep and the linear dependence of $\dot{\epsilon }$ on n (Fig. 2 C) lie in the buildup and release of elastic stress on network-spanning elements as they form, become strained, and turn over.

To gain qualitative insight into the origins of elasticity-dominated creep and the transition between linear and nonlinear dependence of creep rate on stress, we analyzed a very simple model network (Fig. 5, and see the Supporting Material for details) in which a parallel array of network-spanning elements form at a constant rate k⁺, elongate, and then turn over at a constant rate k^– such that the total number of elements, n_L = k⁺/k⁻, is constant. As in our simulations, we assumed that the network is pinned at one end, with the other end subjected to a constant stress (σ), and we assumed that the elastic resistance to network deformation dominates the viscous resistance. We considered two kinds of force-extension behaviors for individual elements: 1), linear force-extension (Fig. 5, A–C), with $F\left(\epsilon \right)=K\epsilon$, where K is a constant stiffness; and 2), nonlinear force-extension (Fig. 5, D–F), with

$$F\left(\epsilon \right)=\{\begin{array}{c}K\epsilon \text{if}\epsilon <{\epsilon }_{\text{c}}\\ \infty \text{if}\epsilon \ge {\epsilon }_{\text{c}}\end{array}.$$ (8)

For both cases, we analyzed the steady-state creep rate ($\dot{\epsilon }$) as a function of σ and k⁻ (see the Supporting Material). For linear force-extension (Fig. 5, A and B), the simple model predicts $\dot{\epsilon }$ ∼ k^–σ/E₀, where E₀ = n_LK is the linear elastic modulus of the system of springs (Fig. 5 C). By contrast, for nonlinear force-extension (Fig. 5, D and E), the model predicts a transition from linear to nonlinear dependence of $\dot{\epsilon }$ on σ at a critical stress ${\sigma }_{\text{th}}$ ∼ $E_0\Delta {\epsilon }_{\text{avg}}$, where $\Delta {\epsilon }_{\text{avg}}$ is the average strain increment required to bring the next element to threshold. For $\sigma$ < ${\sigma }_{\text{th}}$, the response is identical to the linear case: $\dot{\epsilon }$ ∼ k^–σ/E₀. For $\sigma$ > ${\sigma }_{\text{th}}$, the network undergoes a series of deformation cycles, in which it first strains rapidly by an average amount, $\Delta {\epsilon }_{\text{avg}}$, to bring the next element to threshold, and then resists further deformation until that element turns over, whereupon the network is free to deform again. When elastic resistance dominates viscous resistance, the time to strain the next element to threshold is small relative to the lifetime of the strained element, and thus the strain rate is the average deformation per cycle ($\Delta {\epsilon }_{\text{avg}}$) times the turnover rate, k⁻: $\dot{\epsilon }$ = $k^{-}\Delta {\epsilon }_{\text{avg}}$, independent of σ (Fig. 5 F). Thus, in this simple model, a sharp transition between linear and nonlinear dependence of $\dot{\epsilon }$ on σ emerges from the nonlinear force-extension behavior of individual network elements. Note that in both regimes, $\dot{\epsilon }$ is predicted to be proportional to filament turnover rate, k^–, as seen in our simulations. Moreover, even when the viscous and elastic resistances are comparable for low σ (as in Fig. 1 E), the model predicts a sharp transition between linear and nonlinear regimes.

Figure 5.

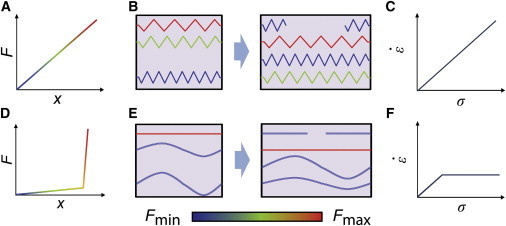
Analysis of two simple toy models reveals the origins of linear and nonlinear creep regimes. (A–C) Model in which network-spanning elements behave as simple linear springs. (A) Force-extension behavior of individual elements. Different colors indicate different force levels shown by the color scale located below. (B) From left to right, a schematic diagram illustrating the appearance, force buildup, and disappearance of individual elements during deformation. (C) Predicted relationship between a strain rate ($\dot{\epsilon }$) and applied stress (σ) for a network of simple linear springs. (D–F) Model in which the force-extension behavior for individual elements is nonlinear. (D) Force-extension behavior with weak linear dependence below a critical extension threshold and rapid increase above the threshold. (E) A schematic diagram during deformation. Only a small subset of highly extended elements support significant force. (F) Predicted dependence of $\dot{\epsilon }$ on σ is linear below a critical stress and constant above it (see Supporting Material for details). To see this figure in color, go online.

The foregoing analysis of a simple toy model suggests how the nonlinear elastic response of individual network elements could give rise to a biphasic creep response at the network level. In particular, it suggests that the transition to a nonlinear creep response occurs at the critical stress that is just sufficient to probe the nonlinear elastic response of the network in the absence of turnover, which will depend on the number and force-extension response of individual network elements. In our simulated networks (and in real actin networks), the network architecture is more complex: The relevant force-transmitting elements are serially connected chains of filaments and ACPs (hereafter subsegments) that are joined at branch points to form network-spanning pathways (Fig. 6, A and B), and the formation and turnover of these subsegments are governed by ACP binding and filament turnover/ACP unbinding. Nevertheless, we found that the creep response (η_eff) in the presence of turnover and the elastic modulus (E = σ/$\epsilon$) in the absence of turnover become nonlinear at the same critical stress, confirming the prediction of the toy model (Fig. S7). To further explore the origins of this threshold in the force-extension behaviors of individual subsegments during simulated network creep, we defined the relative extension of subsegments, L_r, to be the ratio of end-to-end distance to contour length (L_ee/L_c, Fig. 6 B), and we tracked tension versus L_r over time in the linear (σ = 0.2 Pa) and nonlinear (σ = 10 Pa) creep regimes using reference values for the other network parameters. For both cases, individual subsegments paused after formation at an initial L_r, then extended at a fairly constant rate up to a maximum value of L_r, then paused again before undergoing turnover (Fig. 6 C). For σ = 10 Pa, we observed a sharp increase in tension for L_r close to 1 (Fig. 6 D). By contrast, for σ = 0.2 Pa, the average maximal value of L_r was significantly lower than that for σ = 10 Pa (Fig. S8), and there was minimal buildup of force with increasing L_r, i.e., these elements never reach the threshold extension for a nonlinear response. Thus, the same elements can behave as linear or non-linear springs, depending on σ, and consistent with the predictions of our simple model, a transition between the linear and nonlinear regimes for creep occurs when σ is sufficiently large to strain individual elements into the nonlinear extension mode.

Figure 6.

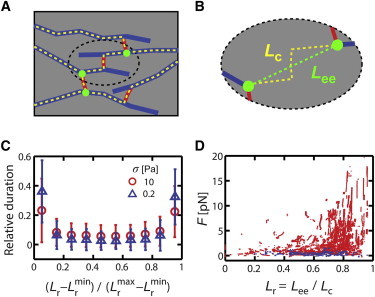
Decomposition and analysis of pathway subsegments reveal linear response under low stress and nonlinear response under high stress. (A and B) A schematic illustration of network decomposition into serially connected pathway subsegments. (A) Blue lines represent semiflexible actin filaments, red are elastic ACPs, yellow dashed lines trace out individual subsegments, and green circles are points where more than two subsegments connect to one another. (B) Magnification of one pathway subsegment, where green and yellow represent the end-to-end distance (L_ee) and contour length (L_c), respectively, of subsegments. (C) Average relative time during which subsegments dwell at a particular L_r at n = 0.1 during network extension under low (σ = 0.2 Pa, blue triangles) and high (σ = 10 Pa, red circles) stress. $L_{\text{r}}^{\min }$ and $L_{\text{r}}^{\max }$ are the minimum and maximum, respectively, of L_r during the lifetime of the subsegment. (D) Distribution of tension (F) over L_r for all subsegments at n = 0.1 in response to either low (σ = 0.2 Pa, blue) or high (σ = 10 Pa, red) stress. The nonlinear response of individual subsegments is probed only under high stress. To see this figure in color, go online.

Discussion

Plastic deformation and viscous flow (creep) are key behaviors of the cell cortex whose underlying mechanisms remain poorly understood. Here, we used detailed computer simulations to explore mechanisms that govern creep in a cross-linked network of dynamically treadmilling semiflexible filaments under extensional stress. We focused our analysis on a range of network architectures and turnover rates that lead to nonaffine deformations and large-scale flow. Under these conditions, we observe a highly nonuniform distribution of stress across the network in which a small fraction of filaments, connected by ACPs into network-spanning pathways, sustain a large fraction of the load. At each instant, these percolating pathways provide a load-bearing and elastic network. However, over time, filament turnover and ACP unbinding allow stress relaxation and network extension. Thus, under these conditions, macroscopic creep is governed by a continuous cycle of pathway formation, force buildup, pathway turnover, and force release. For each choice of network parameters, these pathways turn over with a characteristic timescale, resulting in the fluidlike behavior that can be described in terms of a simple effective viscosity that is inversely proportional to the turnover rate. The mode of creep that we describe here occurs when actin concentration and network connectivity are low enough to allow nonaffine deformations, but high enough that relaxation of elastic stress dominates viscous dissipation due to filament interactions with the surrounding fluid.

A somewhat surprising finding is that the same network can exhibit two distinct regimes of creep response depending on the level of applied stress: at low stresses, we observe a linear response regime in which the creep rate is directly proportional to the magnitude of applied stress; above a critical stress, the creep rate becomes insensitive to further increases in applied stress. By comparing the predictions of a simple model to microscale analysis of simulated creep, we found that the existence of these two regimes and the transition between them can be understood in terms of the nonlinear force-extension behavior of pathway subsegments composed of serially connected chains of semiflexible filaments and ACPs. In the linear regime, the stresses are sufficiently small that only the linear response of the subsegments is probed. Above a critical stress, however, network deformation drives a subset of subsegments into the nonlinear portion of their force-extension curves. In this nonlinear regime, we observe a constant creep rate over a wide range of applied stresses. This insensitivity of creep rate to variation in stress in the nonlinear regime may assist cells to flexibly adapt to rapid changes in their surrounding mechanical environments or to buffer physiological deformations and flows against internal variations in active (e.g., contractile) stress.

We focused here on an idealized form of treadmilling turnover, because it allowed us to vary key network parameters independently of one another. However, we observed a very similar biphasic response to applied stress with other modes of filament turnover (not shown) or with cross-link detachment driven by pure unbinding (regardless of force-dependent kinetics). For the network parameters considered here, in which most of the stress is transmitted by a relatively small number of network subsegments, we found that force-dependent kinetics softens the response, but only at stresses much greater than those required to probe the nonlinear force-extension response of individual network elements. We would expect the force dependence of unbinding to be even less significant at these stresses for more densely connected networks. In addition, recent work suggests that rates of actin assembly and turnover can be modulated by external and internal forces with or without actin accessory proteins (34,35). Exploring how this force dependence shapes the creep response to applied stress will be an interesting topic for future studies.

Our work complements previous studies of stress relaxation in semiflexible networks, which focused on the effects of ACP unbinding in highly cross-linked networks undergoing affine deformation under shear stress (12,13). In these cases, network relaxation is well described by stress relaxations at the filament level, which requires multiple cross-link unbinding events to achieve full relaxation, yielding a broad range of relaxation timescales. By contrast, in the nonaffine regime that we explored, the imposition of constant extensional stress yields a highly nonuniform distribution of stress across individual filaments, and stress relaxation along these filaments is typically achieved through one or a few unbinding events. Under these conditions, the network response appears to be well approximated by a single stress-relaxation timescale, i.e., an effective viscosity, as opposed to the broad spectrum predicted in the affine regime. Although the applied stress is localized to one edge of the network in our simulations, we expect a qualitatively similar mode of stress relaxation in actin networks that flow in response to gradients of active stress, as in the lamella of some motile cells or during polarization in some embryonic cells (1,2).

Conclusion

In this study, we explored how the fluidlike or creep response of cortexlike actin networks to applied stress depends on the interplay of network connectivity, turnover, and the nonlinear force-dependent responses of individual network elements. We found distinct regimes and mechanisms for creep, which are likely to be general for cross-linked networks consisting of dynamic semiflexible polymers, not limited to the actin cortex. We have shown here that the creep can be understood in terms of microscopic force buildup and release on a small subset of network-spanning elements that sustain and transmit most of the applied stress, and we have demonstrated how the nonlinear force response of individual elements allows the network to buffer deformation rates against variation in applied stress.