Abstract
Biological systems often have to measure extremely low concentrations of chemicals with high precision. When dealing with such small numbers of molecules, the inevitable randomness of physical transport processes and binding reactions will limit the precision with which measurements can be made. An important question is what the lower bound on the noise would be in such measurements. Using the theory of diffusion-influenced reactions, we derive an analytical expression for the precision of concentration estimates that are obtained by monitoring the state of a receptor to which a diffusing ligand can bind. The variance in the estimate consists of two terms, one resulting from the intrinsic binding kinetics and the other from the diffusive arrival of ligand at the receptor. The latter term is identical to the fundamental limit derived by Berg and Purcell (Biophys. J., 1977), but disagrees with a more recent expression by Bialek and Setayeshgar. Comparing the theoretical predictions against results from particle-based simulations confirms the accuracy of the resulting expression and reaffirms the fundamental limit established by Berg and Purcell.
Introduction
The evidence is accumulating that sensory systems in biology often operate near the fundamental limit set by the noise of counting signal molecules. Receptors in our visual system can detect single photons (1), some animals can smell single molecules (2), swimming bacteria can respond to the binding and unbinding of only a limited number of molecules (3,4), and eukaryotic cells can respond to a difference in ∼10 molecules between the front and the back of the cell (5). Recent experiments suggest that the precision of the embryonic development of the fruitfly Drosophila is close to the limit set by the available number of regulatory proteins (6–8). This raises the question of what is the fundamental limit to the precision of chemical concentration measurements.
In their classic article, Berg and Purcell (3) considered a scenario in which a cell measures the concentration c of a ligand by monitoring the occupation state of the receptor molecules to which the ligand molecules bind and unbind. A central result is the precision with which the ligand concentration c can be inferred from the time-averaged occupancy of a single receptor. The analysis of Berg and Purcell predicts that in the limit at which the integration time T is much longer than the correlation time of the receptor state, the expected uncertainty in the time-averaged occupancy resulting from the random nature of diffusion is given by
| (1) |
where is the true mean occupancy, σ is the receptor-ligand binding cross section, and D is the diffusion constant of the ligand. The uncertainty or expected error in a corresponding estimate of the concentration is related to the noise in the observed occupancy via the gain ,
| (2) |
yielding Berg and Purcell’s expression for the limit to the precision of concentration measurements by a single receptor (see Eq. 52 in Berg and Purcell (3)):
| (3) |
This result can be understood intuitively by noting that 4Dσc is the flux of ligand molecules arriving at the receptor and is the probability that the receptor is free (3). Therefore, is the effective rate of ligand binding if every collision between ligand and free receptor leads to successful binding. Berg and Purcell (3) argue that their result also holds for reactions that are not deeply in the diffusion-limited regime. After an unsuccessful receptor-ligand encounter, they argue, the ligand will rapidly collide with the receptor again and again until it binds the receptor, and these rounds of encounters can be captured by renormalizing σ.
The argument of Berg and Purcell ignores, however, that after an unsuccessful collision with the receptor the ligand molecule may diffuse back into the bulk, and a different ligand molecule may subsequently bind. Moreover, a ligand molecule that has just dissociated from the receptor may rapidly rebind, or it may diffuse away from the receptor into the bulk. It thus remains unclear to what extent the result of Berg and Purcell applies to binding reactions that are not diffusion-limited.
Bialek and Setayeshgar (9) sought to generalize the result of Berg and Purcell by taking into account ligand-receptor binding dynamics. They considered a model in which the ligand molecules can diffuse, bind the receptor upon contact with an intrinsic association rate ka, and unbind from the receptor with an intrinsic dissociation rate kd. Invoking the fluctuation-dissipation theorem, they linearized the nonlinear reaction-diffusion equation, to obtain the following result for the fractional uncertainty in the estimate for the concentration (Eq. 32 in (9)):
| (4) |
The first term arises from the stochastic arrival of the ligand molecules at the receptor by diffusion, whereas the second term is due to the intrinsic stochasticity of the binding kinetics of the receptor. Indeed, even in the limit that D → ∞, such that the concentration at the receptor is constant, this concentration can still not be measured with infinite precision because the receptor stochastically switches between the bound and unbound states, leading to noise in the estimate of the receptor occupancy. This term is absent in Eq. 3 because Berg and Purcell assume that the binding reaction is fully diffusion-limited, meaning that the intrinsic rates ka and kd go to infinity.
The first term of Eq. 4 should be compared with Eq. 3. This term is considered to be the fundamental limit to the accuracy of measuring chemical concentrations via a single receptor, because it presents a noise floor that is solely due to the physics of diffusion, independent of the binding kinetics (9). Indeed, in the limit that the reaction is diffusion-limited, the second term in Eq. 4 is zero, and both theories should yield the same result. However, it is clear that in addition to the geometrical factor π (which comes from the fact that Berg and Purcell model the receptor as a reactive disk, whereas Bialek and Setayeshgar take the receptor to be a spherical particle), the expressions differ by a factor . This difference can have marked implications. Although the Bialek-Setayeshgar expression predicts that the uncertainty remains bounded even in the limit that , the Berg-Purcell expression suggests that it diverges in this limit.
Here, we rederive the limit to the accuracy of sensing via a single receptor (10), borrowing heavily from the work of Agmon and Szabo (11) on diffusion-influenced reactions. Our expression is identical to that of Berezhkovskii and Szabo (12), who have recently independently derived this limit for an arbitrary number of receptors, when there is one receptor. Like the expression of Bialek and Setayeshgar (Eq. 4), our expression consists of two terms: One term describes the effect of the diffusive transport of the ligand molecules to and from the receptor, and the other describes the effect of the intrinsic binding and unbinding kinetics of the receptor. Although the second term agrees with that of Bialek and Setayeshgar, the first does not agree with their expression but does agree with the expression of Berg and Purcell (again apart from the geometric factor).
We then perform extensive tests of these expressions by performing particle-based simulations using Green’s function reaction dynamics (GFRD), which is an exact scheme for simulating reaction-diffusion systems at the particle level (13–15). The simulation results agree very well with our expression and that of Berezhkovskii and Szabo (12) for the full range of conditions that we considered, which spans the biologically relevant regime. This means that the Berg-Purcell limit is the most accurate expression for the fundamental limit to measuring chemical concentrations.
We end by examining the assumptions of our theory under biologically relevant conditions. This naturally suggests a simple but intuitive model. This model not only explains the origin of the factor in the Berg-Purcell expression, but also shows how their expression can be generalized to reactions that are not diffusion-limited by integrating out the rapid rebindings of dissociated molecules. The model also elucidates that rebindings do not contribute to the accuracy of sensing, because their likelihood does not depend on the concentration.
Methods and Theory
We consider a single receptor A in a volume V that is surrounded by a large number NB of noninteracting ligand molecules B at concentration c = NB/V. We consider the pseudo first-order limit, meaning that NB >> NA = 1 and V → ∞. Without loss of generality, we may assume that the receptor is static and located at the origin, while the ligand molecules diffuse with diffusion constant D. A ligand molecule can bind a free receptor with an intrinsic association rate ka when the two come in contact at the contact distance σ, which is the sum of the radii of the two respective molecules. A bound ligand molecule can dissociate from the receptor with an intrinsic dissociation rate kd. The state of the receptor is denoted by the binary variable n(t), which is one if the receptor is bound to a ligand at time t and zero otherwise. We note that this model is identical to that of Bialek and Setayeshgar (9) for the scenario of a single receptor molecule.
Following Berg and Purcell (3) and Bialek and Setayeshgar (9), we imagine that the cell estimates the concentration c from the receptor occupancy n(t) integrated over an integration time T, . In the limit that the integration time T is much longer than the correlation time of n(t), τn, the variance in our estimate nT of the true mean occupancy is given by
| (5) |
where is the instantaneous variance and Pn(ω) and are, respectively, the power spectrum and the Laplace transform of the correlation function Cn(t) of n(t). The uncertainty in the estimate for the concentration c can then be obtained from Eqs. 2 and 5. In Eq. 2, the gain is , because with KD the receptor-ligand dissociation constant.
The correlation function of any binary switching process is given by
| (6) |
where is the equilibrium probability for the bound state () and is the probability the receptor is bound at t = τ, given it was bound at t = 0. To obtain the correlation function, we thus need . It is convenient to focus on the conjugate probability
| (7) |
which is the probability that the receptor is free at time t given that it was bound at t = 0. Following Agmon and Szabo (11), we use the subscript “rev” to indicate that we consider a reversible reaction, meaning that in between t = 0 and t the receptor may bind and unbind ligand a number of times. The probability that a receptor-ligand pair dissociates between t′ and t′ + dt′ to form an unbound pair at contact is kd[1−(t′|∗)]dt′, whereas the probability that the free receptor with a ligand molecule at contact at time t′ is still unbound at time t > t′ is (t − t′|σ). The subscript “rad” means that we now consider an irreversible reaction (kd = 0), which can be obtained by solving the diffusion equation using a radiation boundary condition (11). Hence, (t|∗) is given by (11)
| (8) |
We emphasize that up to this point no approximation has been made. The question now is what is (t|σ), which is the quantity needed to solve Eq. 8. To address this, we introduce two new quantities:
-
1.
(t|eq), which is the probability that a receptor initially is free and surrounded by an equilibrium distribution of ligand molecules, and it remains free until at least a later time t; and
-
2.
(t|σ), which is the probability that a free receptor initially surrounded by only one single ligand molecule at contact is still unbound at a later time t.
The quantity (t|σ) thus refers to a system consisting of a receptor with only one ligand molecule, which initially is at contact with the receptor, whereas (t|σ) refers to a system of a receptor with NB ≥ 1 ligand molecules, one of which is at contact initially.
In general, it is not possible to obtain an exact analytical expression for (t|σ), the quantity that we need (Eq. 8). To illustrate this, imagine a bound receptor-ligand pair that is surrounded by an equilibrium, i.e., a statistically uniform distribution of ligand particles. When this receptor-ligand pair dissociates to form a receptor-ligand pair at contact surrounded by an equilibrium distribution of ligand molecules, then the probability that the receptor is still unbound at a later time t is given by (11)
| (9) |
Now, the ligand molecule at contact may either rebind the receptor or diffuse away from it. If it rebinds the receptor, then after the next dissociation event, the probability that the receptor will remain free for at least another time t will again be given by Eq. 9. Equation 9 breaks down when the ligand molecule at contact instead diffuses away from the receptor and another ligand molecule binds the receptor before the first ligand has relaxed to equilibrium. Indeed, the process of receptor binding generates nontrivial spatio-temporal correlations between the positions of the ligand molecules, which depend on the history of the association and dissociation events. This impedes an exact solution of the problem. However, if the dissociation rate kd is low then it becomes reasonable to assume that after each dissociation event, the unbound receptor-ligand pair at contact is surrounded by an equilibrium distribution of ligand (11), in which case the survival probability is given by Eq. 9. This is the crucial assumption that we make in our analysis.
With the assumption of Eq. 9, Eq. 8 can now be solved. For a pseudo-first-order irreversible reaction with a static target, (t|eq) of Eq. 9 is given by Rice (16) (see also the Supporting Material) as
| (10) |
where krad(t) is the time-dependent rate coefficient. Here, ckrad(t) is the rate at which ligand molecules will bind a free receptor at time t, given that the ligand distribution at time was the uniform, equilibrium, distribution. As before, the subscript “rad” refers to a radiation boundary condition, meaning that if a ligand molecule and the receptor come into contact, they react with a finite rate ka (11). The quantity (t|σ) in Eq. 9 is via detailed balance (and the backward Smoluchowski equation) related to krad(t): krad(t) = ka(t|σ) (11) (see also the Supporting Material). Together, these relations yield a simple expression for the Laplace transform of (t|σ) in terms of the Laplace transform of (t|eq) (see the Supporting Material). Substituting this in the solution of Eq. 8 in the Laplace domain allows us to obtain the following expression for the Laplace transform of the correlation function in terms of (see the Supporting Material):
| (11) |
where τc = (kac + kd)−1 is the correlation time of the intrinsic receptor switching dynamics, i.e., the correlation time of the receptor occupancy when receptor-ligand association is reaction-limited and the effect of diffusion can be neglected.
To obtain an analytically closed form for the correlation function, we require an expression for . We use
| (12) |
which correctly captures the short- and long-time limit of (t|eq) (11) (see the Supporting Material). We exploit that
(see the Supporting Material), where
is the Laplace transform of the time-dependent diffusion-limited rate constant kabs(t) (16). Here, the subscript “abs” refers to the absorbing boundary condition, meaning that ka → ∞, where each ligand-receptor collision will immediately lead to binding; ckabs(t) is thus the rate at which ligand molecules collide and associate with the receptor at time t, given that they start from the equilibrium (uniform) distribution. Substituting Eq. 12 in Eq. 11 yields (see the Supporting Material)
| (13) |
where τ′c(s) is the intrinsic correlation time τc renormalized by the concentration fluctuations (9),
| (14) |
with the diffusion-limited rate constant kD = kabs(t → ∞) = 4πσD and the molecular timescale τm = σ2/D. The correlation time τn of the receptor is then given by (Eq. 5) as
| (15) |
where kon and koff are the renormalized association and dissociation rates
| (16) |
| (17) |
and Keq = ka/kd = is the equilibrium constant (11). The effective association rate kon is the long-time limit of the time-dependent rate coefficient krad(t): kon = krad(t → ∞); it takes into account the finite rate of diffusion and the finite probability of binding when receptor and ligand are at contact. Similarly, koff is the effective rate at which a ligand dissociates from the receptor and diffuses into the bulk. Our simple coarse-grained model presented below (see Results) gives an intuitive derivation of these effective rate constants.
The uncertainty in the estimate of the concentration can be obtained by combining Eq. 13 with Eqs. 2 and 5, yielding our principal result
| (18) |
The first term describes the uncertainty in the estimate of c that stems from the stochastic diffusive arrival of the ligand molecules, whereas the second term describes variability that results from the intrinsic binding dynamics of the receptor. If the receptor-ligand association reaction is fully reaction-limited, i.e., ka,kd → 0 or D → ∞, then the uncertainty in the concentration estimate is dominated by the latter term. Conversely, if the reaction is diffusion-limited, ka,kd → ∞ or D → 0, then the first term dominates the uncertainty, which is limited by the diffusive arrival and departure of the ligand molecules to and from the receptor.
It is clear that the second term in Eq. 18 is identical to that in the expression of Bialek and Setayeshgar (9), Eq. 4. Yet, the first term, which determines the fundamental limit, is different: the expression of Bialek and Setayeshgar misses a factor . The Berg-Purcell expression does contain this factor, and indeed, apart from a geometrical factor, our expression is identical to theirs in the limit that the reaction is fully diffusion-limited.
Results
Simulation results
To test our theory, we have performed particle-based simulations. A key quantity of our theory is , Eq. 13, because the precision of our concentration estimate directly follows from this quantity and the gain (see Eqs. 2 and 5). We therefore compare the power spectrum,
with given by Eq. 13, to that obtained from simulations. The simulation scheme should not only describe the diffusive transport at large length and timescales, but also capture the (re)binding dynamics at short scales. Moreover, to obtain an accurate estimate for the zero-frequency limit of the power spectrum, which is computationally challenging, the scheme should also be efficient. We have therefore employed Green’s function reaction dynamics (GFRD) (13,15,17). Like Brownian dynamics (overdamped Langevin dynamics), GFRD simulates reaction-diffusion systems at the particle level; in essence, both are numerical procedures for solving the Smoluchowski equation (17). However, while Brownian dynamics uses a fixed time-step to propagate the particles, GFRD is an asynchronous, event-driven kinetic Monte Carlo scheme.
The central idea of GFRD is to decompose the many-body reaction-diffusion problem, which cannot be solved analytically, into sets of one- and two-body problems that can solved analytically using Green’s functions (13,17). In the recent version of GFRD, this decomposition is performed by putting single particles and pairs of particles in mathematical domains (18), for which the reaction-diffusion problem can be solved exactly (15). This yields for each domain an event-type, which is either a reaction or a particle leaving the domain, and an event-time, which is when this event will happen. These events are then executed in chronological order. Importantly, the mathematical domains are nonoverlapping, which means that the stochastic reaction-diffusion processes of the respective domains are independent. This makes GFRD an exact scheme for simulating reaction-diffusion problems at the particle level (15). Because the scheme is event-driven, it is also very fast: at the concentrations considered here, GFRD is up to 4–6 orders-of-magnitude faster than Brownian dynamics (13,15) (for more details, see www.GFRD.org). For this study, we exploited the spherical symmetry of the system and that the ligand molecules only interact with the receptor, but not among themselves.
The computational model is identical to that of our theory, albeit in a finite volume. It consists of a static single receptor in the center of a spherical simulation box with diameter L, surrounded by ligand molecules that diffuse with diffusion constant D. A ligand molecule that is in contact with a free receptor at the contact distance σ can associate with the receptor with an intrinsic association rate ka and then dissociate from it with an intrinsic dissociation rate kd; after dissociation, the ligand molecule is put at contact.
Fig. 1 shows the power spectra as obtained from the simulations (black circles) together with the prediction of our theory (solid red line; Eq. 13), for and c = 0.4 μM. In the Supporting Material, we show results for higher concentrations. The parameters have been chosen such that they are biologically meaningful, yet bring the system in the diffusion-limited regime—this makes it possible to probe the fundamental limit set by diffusion. Specifically, the diffusion constant D = 1 μm2/s is comparable to that of intracellular proteins (19,20).
Figure 1.
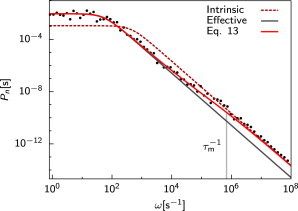
The power spectrum of the receptor state Pn(ω) for c = 0.4 μM. The simulation results (black circles) agree well with the theoretical prediction of Eq. 13 (solid red line). At high frequencies ω > 1/τm = D/σ2, the effect of diffusion is negligible and the receptor dynamics is that of a Markovian switching process with intrinsic rates kac and kd (dashed red line), while at low frequencies it is that of a Markovian switching process with effective rates konc and koff, respectively (solid gray line). The zero-frequency limit determines the precision of the concentration estimate. Parameters: , D = 1 μm2 s−1, σ = 10 nm, L = 1 μm, and ka = 552 μM−1 s−1. To see this figure in color, go online.
Fig. 1 shows that the agreement between theory and simulation is very good over essentially the full frequency range. The high-frequency regime corresponds to the intrinsic switching dynamics of the receptor. In this regime, diffusion hardly plays any role and the receptor dynamics is dominated by the binding of ligand molecules that are essentially in contact with the receptor; consequently, the power spectrum is well approximated by that of a binary switching process with uncorrelated exponentially distributed waiting times with the intrinsic correlation time τc = (kac + kd)−1 (red dashed line). The theory also accurately describes the intermediate frequency regime, which starts at ωm = 1/τm = Dσ2. In this regime a ligand molecule, after dissociation from the receptor, manages to diffuse away from the receptor over a few molecular distances σ, but then rebinds the receptor before another ligand molecule from the bulk does. The low-frequency regime of the power spectrum corresponds to the regime in which, after receptor dissociation, the ligand molecule diffuses into the bulk and, most likely, another molecule from the bulk binds the receptor. In this regime, the spectrum is well approximated by that of a memoryless switching process with the same effective correlation time as that of our theory, τn = τ′c (s = 0) = (konc + koff)−1 (gray solid line).
The most important point of the power spectrum is at zero-frequency, Pn(ω = 0), because this determines the correlation time of the receptor and hence the uncertainty in our estimate of the average receptor occupancy and the concentration c, following Eqs. 2 and 5. Fig. 2 shows Pn(ω = 0) as a function of the average receptor occupancy at a concentration of 0.4 μM. (For higher concentrations, see the Supporting Material.) It is seen that the agreement between the theory and simulations is excellent. Fig. 2 also shows the prediction of Bialek and Setayeshgar for Pn(ω = 0) (9). Although their analysis predicts that Pn(ω = 0) = P1−n(ω = 0), our results show that the dependence of Pn(ω) on n is nonsymmetric, which reflects the fact that if the receptor is free more often, more binding events can be counted, leading to a more accurate estimate of the concentration. Because the Berg-Purcell formula in Eq. 3 directly follows from our expression for , via Eqs. 2, 5, and 13, we conclude that the Berg-Purcell limit provides an accurate upper bound on the precision with which chemical concentrations can be measured.
Figure 2.
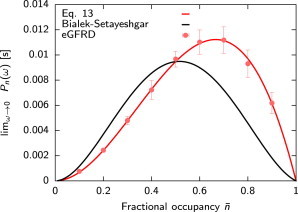
The zero-frequency limit of the power spectrum as a function of the average receptor occupancy for c = 0.4 μM; is varied by changing kd. It is seen that the agreement between the theoretical prediction of Eq. 13 and the simulation results is very good (red line). In contrast, the prediction of Bialek and Setayeshgar (9) (black line) differs markedly from our results. Parameters: see Fig. 1. To see this figure in color, go online.
Validity of assumptions under biological conditions
The central assumption of our theory is Eq. 9, which states that after dissociation the unbound receptor-ligand pair is surrounded by a uniform distribution of ligand molecules. This assumption breaks down when the following conditions apply:
Condition 1
After receptor dissociation, the rebinding of the ligand molecule to the receptor is preempted by the receptor binding of another, second, ligand molecule.
Condition 2
This second ligand molecule dissociates from the receptor before the first has diffused into the bulk.
We argue that under biologically relevant conditions, neither condition arises and, therefore, the key assumption of our analysis holds.
A rebinding trajectory of a ligand molecule that has just dissociated from the receptor is very short on the timescale at which molecules arrive from the bulk at the concentrations considered here (see Fig. S1 in the Supporting Material). Consequently, the likelihood that another molecule interferes with such a rebinding event is negligible (see Fig. S3); a dissociated ligand molecule rebinds the receptor before it diffuses into the bulk as often as when it was the only ligand molecule present in the system. Condition 1 is thus not met and the central assumption, Eq. 9, holds.
Occasionally rebinding interferences will occur, and Condition 1 is met. However, we argue that Eq. 9 is still likely to hold, because Condition 2 is not met: a ligand molecule is typically bound long enough for the previously bound molecules to diffuse into the bulk. Consider a detector that binds a ligand with a cross-section σ = 10 nm, a diffusion constant D = 1 μm2 s−1, and an intrinsic rate ka that equals the diffusion-limited rate kD = 75 μM−1 s−1, yielding an effective association rate kon = 38 μM−1 s−1, consistent with experimentally measured association rates (21). If the ligand is present at a biologically relevant concentration of c = 1 μM, then, for , the time a ligand molecule is bound to the receptor is td = kd−1 ≈ 0.01 s. During this time, the previously bound ligand molecule, on average, has traveled at least a distance
This corresponds to ∼4 times the average distance between the ligand molecules at this concentration, meaning that, effectively, the ligand has diffused into the bulk. For lower concentrations, the dissociation time will be longer at constant , and the previously bound ligand molecule will have penetrated the bulk even deeper by the time that the newly bound ligand molecule dissociates. We thus expect that for concentrations up to micromolar, Condition 2 is not met—meaning that even when rebinding interferences do occasionally arise, and Eq. 9 still holds.
The other approximation of our theory, Eq. 12, ensures that the short- and long-time behavior of (t|eq) is described correctly. Importantly, however, under the biologically relevant concentrations considered here, the receptor-binding rate of ligand molecules starting from a uniform distribution is so low that to a good approximation (t|eq) is given by its long-time behavior, (see Fig. S1). The picture that thus emerges is that after a receptor-ligand dissociation event, the molecules that are not in contact with the receptor truly form a bulk reservoir:
-
1.
They have a uniform distribution (Eq. 9), and
-
2.
They bind the receptor in a memoryless fashion with a constant rate konc.
A simple coarse-grained model
Ultimately, the success of Eq. 9 is due to the fact that the time a ligand molecule spends near the receptor is very short compared to the timescale on which ligand molecules arrive at the receptor from the bulk, (kDc)−1 (see Fig. S1). On this timescale a ligand molecule at contact with the receptor effectively either instantly (re)binds the receptor with splitting probability preb or escapes into the bulk with probability pesc = 1 – preb. This observation naturally suggests the following simple two-state model (17), in which the system switches between a receptor-bound and a receptor-unbound state with effective association and dissociation rates (see Fig. 3).
Figure 3.
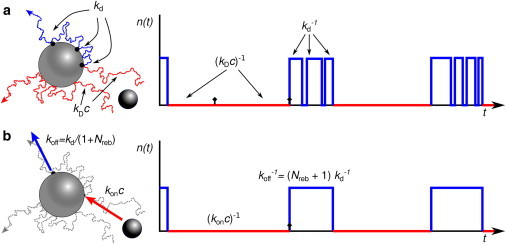
Cartoon of the coarse-grained model. (a) A typical time trace of the receptor state n(t) of the original system. (b) Time trace of the coarse-grained model. (Top-left cartoon; red) a successful and an unsuccessful binding trajectory; (blue) a trajectory in which a ligand molecule undergoes a number of rounds of receptor dissociation and rebinding before it escapes into the bulk. The key observation is that the time a molecule spends near the receptor is very short on the timescale at which molecules arrive from the bulk. This makes it possible to integrate out the receptor rebindings and the unsuccessful arrivals of molecules from the bulk, giving the two-state model of Eq. 19. Fig. S1 in the Supporting Material quantifies the timescale separation. To see this figure in color, go online.
To derive the effective dissociation rate, we note that for a ligand molecule that has just dissociated from the receptor, the probability that it will rebind the receptor rather than diffuse away into the bulk is preb = 1 – Srad(∞|σ) = ka/(ka + kD). The mean number of rounds of rebinding and dissociation before the molecule escapes into the bulk is then
The total time ton the ligand is bound to the receptor before it diffuses away is on average ton = td(1 + Nreb) and the effective dissociation rate is koff = 1/ton = kdkD/(ka + kD), which is precisely the effective dissociation rate of our theory, Eq. 17.
A molecule that arrives at the receptor from the bulk at a rate kD may either bind the receptor or escape back into the bulk. The escape probability is
and the average number of times a molecule from the bulk encounters the receptor before it actually binds is
The effective rate at which a molecule binds from the bulk is then
which is the diffusion-limited rate kD times the probability
that a molecule at contact binds the receptor instead of diffusing back into the bulk. This is the rate as predicted by our theory, Eq. 16. We note that the renormalization of the association and dissociation rates preserves the detailed-balance condition:
The dynamics of this two-state model is given by
| (19) |
which, as Fig. 1 shows, correctly describes the relevant low-frequency dynamics of the receptor state. From Eq. 19, the power spectrum and hence, the uncertainty in our concentration estimate can be obtained straightforwardly:
| (20) |
Three points are worthy of note:
-
1.
Noting that kon is given by Eq. 16, the principal result of this article, Eq. 18, is reproduced.
-
2.
For diffusion-limited reactions kon = kD and the expression of Berg and Purcell, namely, Eq. 3, is recovered.
-
3.
Arguably, however, the most important result is that the Berg-Purcell expression can also be applied to reactions that are not diffusion-limited, by replacing kD with kon.
Point 3 is a nontrivial result, because Eq. 20 takes into account that not every arrival of ligand at a free receptor leads to binding, and also that upon dissociation a ligand molecule may rebind the receptor many times before it escapes into the bulk. This can be seen by exploiting the detailed-balance condition and rewriting Eq. 20 as
| (21) |
This expression has a clear interpretation (see Fig. 3). A receptor-bound molecule that dissociates from the receptor may rebind the receptor, but the probability for this to happen does not depend on the concentration (15). As a result, a rebinding event does not provide information on the concentration and should therefore not be counted as a concentration measurement; it merely increases the receptor correlation time τn by increasing its on-time from kd−1 to . After (1 + Nreb) rounds of dissociation and rebinding, the molecule escapes into the bulk, and then another molecule will arrive at the receptor with a rate kDc. This molecule may return to the bulk or bind the receptor—in either case, possibly after a number of unsuccessful but rapid collisions—such that the net rate at which a molecule from the bulk binds the receptor is konc. Importantly, this binding event occurs in a memoryless fashion and with a rate that depends on the concentration. Consequently, this event does provide an independent measurement of the concentration. The time τw = 1/koff + 1/(konc) is thus the average time between independent concentration measurements, and T/τw is the total number of such measurements in the integration time T.
Discussion
Using results from the theory of diffusion-influenced reactions by Agmon and Szabo (11), we have derived the fundamental limit for the precision of chemical concentration measurements via the reversible binding of ligand to a single receptor, a common motif in cell signaling. We have compared our expression to that of Berg and Purcell (3) and Bialek and Setayeshgar (9) and tested it against particle-based simulations. The premise of our study and that of Berg and Purcell (3) and Bialek and Setayeshgar (9) is that the concentration is estimated from the average receptor occupancy nT over an integration time T set by the downstream network, and inverting the input-output relation (3,9,22–25). Recently, Endres and Wingreen (26) and Mora and Wingreen (27) showed that maximum likelihood estimation can improve this estimate, but it is not clear whether typical networks do this.
Our theoretical analysis, as well as that of Berg and Purcell (3) and Bialek and Setayeshgar (9), assumes that the total number of ligand molecules in the system is fixed; the total concentration c is thus constant. Indeed, the only sources of fluctuations in the receptor state are the diffusion of ligand to and from the receptor, and the stochastic binding and unbinding of ligand to and from the receptor. Moreover, all three analyses assume that the ligand molecules are noninteracting, which is a very reasonable assumption at the low concentrations considered here. The reason that this is nonetheless a nontrival many-body reaction-diffusion problem is due to the interactions of the ligand molecules with the receptor.
As described in the surrounding text for Eq. 9, due to these receptor-ligand interactions, the spatial distribution of ligand molecules, conditioned on the state of the receptor (or the time since the last receptor binding or unbinding event), can deviate from the equilibrium uniform distribution. Only by averaging over the entire ensemble of ligand distributions, taking into account those corresponding to both the bound and unbound states of the receptor, is the uniform equilibrium distribution obtained. The central assumption of our theory is that after each receptor dissociation event, the receptor and ligand molecule at contact are surrounded by a uniform, equilibrium distribution of ligand molecules (see Eq. 9). This assumption makes it possible to reduce the many-body problem to a pair problem, in which the ligand molecules bind the receptor independently of one another.
Also in the analysis of Berg and Purcell (3), the many-body reaction-diffusion problem is reduced to a pair problem. However, the key difference with our analysis is that their analysis strictly holds only for diffusion-limited reactions, but they argue that it also holds for reactions that are not diffusion-limited. In essence, they start from the assumption that the receptor switches between the ligand-bound and unbound states according to a random telegraph process with exponentially distributed waiting times, thus ignoring the rebinding trajectories with algebraic waiting times. The receptor correlation time τn, needed to obtain the fundamental limit (see Eq. 5), is in this Markovian model given by the receptor-ligand association and dissociation rates. Berg and Purcell argue that the association rate kf in the presence of unsuccessful ligand-receptor collisions can be obtained from the diffusion-limited binding rate kD = 4πσD via a rescaling of the cross-section σ, while the dissociation rate kb can then be obtained from the detailed balance relation . However, the validity of this Markovian model with the ad hoc rescaling of kD to get kf remained unclear.
Bialek and Setayeshgar (9) do not assume that the receptor-ligand association rate is diffusion-limited. Indeed, their physical model is identical to ours: ligand molecules are noninteracting; their overall concentration is constant; ligand and receptor associate with a rate ka when at contact, and dissociate with a rate kd when bound. However, they analyze their model by writing down the reaction-diffusion equation, and then solve this equation invoking the fluctuation-dissipation theorem.
Our principal result (Eq. 18) consists of two terms, like the expression of Bialek and Setayeshgar (Eq. 4): one describes the effect of the diffusive transport of ligand to and from the receptor and the other describes the effect of the intrinsic binding kinetics when the ligand is in contact. However, whereas the intrinsic binding term agrees with that of Bialek and Setayeshgar, the diffusive term does not: it contains an additional factor . We believe that this is because, by invoking the fluctuation-dissipation theorem, Bialek and Setayeshgar (9) linearize the reaction-diffusion problem, thereby ignoring correlations between the state of the receptor and the ligand concentration. The expression of Berg and Purcell (Eq. 3) does not feature a term that arises from the intrinsic binding. However, their term agrees with our diffusive term, which is considered to be the fundamental limit. Because both terms in our expression contain the factor , our principal result Eq. 18 can be rewritten as Eq. 20, which shows that the expression of Berg and Purcell (Eq. 3) can be generalized to reactions that are not diffusion-limited by simply replacing kD with kon. Our simple coarse-grained model elucidates why this is possible: is the rate at which molecules independently bind the receptor from the bulk; via detailed balance, this expression not only captures the unsuccessful arrivals of molecules from the bulk, but also the receptor rebindings, which do not provide information about the concentration.
The purpose of sensing is to enable the detection of changes in the ligand concentration. If the concentration varies over only a small range around the dissociation constant KD, then varies in a small interval around , for which the expressions of Berg and Purcell (3) and Bialek and Setayeshgar (9) become equal. However, for most signaling systems it is not known how the ligand concentration varies under physiologically relevant conditions. Yet, information theory tells us that information transmission is maximized when the input distribution spans the full dynamic range of the signaling system, rather than a narrow range around KD (28,29). Or, vice versa, in the case where the input distribution is fixed by the environment, the response curve that maximizes information transmission is one whose dynamic range matches the input distribution. This suggests that can be well above and below —meaning that the difference between the respective expressions can become significant.
A comparison of the power spectrum of the receptor occupancy as predicted by our theory against results from particle-based simulations shows that our theory is very accurate under biologically relevant conditions. As Fig. S6 shows, the theory accurately predicts the zero-frequency limit of the power spectrum for concentrations up to at least 36 μM. Given the complicated algebraic diffusion dynamics of rebinding trajectories, it is perhaps surprising that the error in the concentration estimate is so accurately predicted by a simple expression like Eq. 18 or 20. The success of this expression lies in the fact that biologically relevant concentrations are low, which means that the time a ligand molecule spends near the receptor is very short both on the timescale at which molecules arrive from the bulk and on the timescale a ligand molecule is bound to the receptor. This is the reason why both the rapid rebindings and the unsuccessful bulk arrivals can be integrated out, and the complicated many-body reaction-diffusion problem can be reduced to a pair problem in which ligand molecules interact with the receptor with renormalized association and dissociation rates (see Eq. 19).
Whether this simple approach can also be used when the ligand can bind to multiple receptors that are in close physical proximity remains an open question (3,9,22). Ligand rebinding between neighboring receptors may lead to nontrivial spatio-temporal correlations between the receptor states. Berezhkovskii and Szabo (12) have recently derived an expression for the accuracy of sensing via multiple receptors on a sphere, ignoring these spatio-temporal correlations. In the limit that the number of receptors goes to infinity, their expression for the accuracy of sensing in the diffusion-limited regime reduces to
Paradoxically, by replacing the cross section of the receptor σ with twice the radius of the cell R, this is the result of Bialek and Setayeshgar (9) for a single receptor, Eq. 4: the expression for δc/c does not contain the factor . The absence of this factor can be understood intuitively by noting that in the limit that the number of receptors goes to infinity, there will always be receptors available for binding the ligand. The fact that in this limit the result of Bialek and Setayeshgar (9) for a single receptor is recovered supports the idea that their analysis is essentially a mean-field analysis that ignores receptor-ligand correlations. For a finite number of receptors (including the scenario that there is only one receptor), the occupancy of the receptor will, however, affect the precision of sensing, and these correlations are important. Clearly, it will be of interest to test the accuracy of sensing via multiple receptors, and quantify the importance of spatio-temporal correlations, via simulations. We leave this for future work.
Finally, our observations have implications for the modeling of biochemical networks. They underscore our earlier observation (17) that when the cell does not exhibit concentration gradients on cellular length scales, the effect of diffusion can often be captured in a well-stirred model, which can then be simulated using the Gillespie algorithm (30) instead of a much more computationally demanding particle-based algorithm (15). In such a well-stirred model, the rapid rebindings are integrated out and association and dissociation occur in a memoryless fashion, with exponentially distributed waiting times with mean (konc)−1 and koff−1, respectively. This is a simplification—at short times, the association-time distribution is algebraic due to the rebindings—but it is an accurate one. It not only preserves the equilibria of the association-dissociation reactions, but also the important noise characteristics of the network. Indeed, the high-frequency noise from the rapid rebindings is typically filtered by the network downstream and only the low-frequency noise, obeying exponential statistics, is significantly propagated downstream (17). On the other hand, when rebindings can qualitatively change the macroscopic behavior of the system, as in systems employing multisite protein modification, rebindings cannot simply be integrated out to yield the well-known macroscopic effective rate constants kon and koff (15,31). Yet, Gopich and Szabo (32) have recently shown that, because rebindings remain fast, it is nonetheless possible to arrive at an alternative simplified description for these systems that captures the effect of rebindings.
Acknowledgments
We thank Attila Szabo, Howard Berg, and Bill Bialek for stimulating discussions and Bela Mulder for a critical reading of the manuscript. Calculations were performed on the RIKEN Integrated Cluster of Clusters (RICC) facility in Saitama, Japan.
This work is part of the research program of the Foundation for Fundamental Research on Matter, which is part of the Netherlands Organization for Scientific Research (NOW).
Supporting Material
References
- 1.Rieke F., Baylor D. Single-photon detection by rod cells of the retina. Rev. Mod. Phys. 1998;70:1027–1036. [Google Scholar]
- 2.Boeckh J., Kaissling K.-E., Schneider D. Insect olfactory receptors. Cold Spring Harb. Symp. Quant. Biol. 1965;30:263–280. doi: 10.1101/sqb.1965.030.01.028. [DOI] [PubMed] [Google Scholar]
- 3.Berg H.C., Purcell E.M. Physics of chemoreception. Biophys. J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sourjik V., Berg H.C. Receptor sensitivity in bacterial chemotaxis. Proc. Natl. Acad. Sci. USA. 2002;99:123–127. doi: 10.1073/pnas.011589998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ueda M., Shibata T. Stochastic signal processing and transduction in chemotactic response of eukaryotic cells. Biophys. J. 2007;93:11–20. doi: 10.1529/biophysj.106.100263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gregor T., Tank D.W., Bialek W. Probing the limits to positional information. Cell. 2007;130:153–164. doi: 10.1016/j.cell.2007.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Erdmann T., Howard M., ten Wolde P.R. Role of spatial averaging in the precision of gene expression patterns. Phys. Rev. Lett. 2009;103:258101. doi: 10.1103/PhysRevLett.103.258101. [DOI] [PubMed] [Google Scholar]
- 8.Dubuis J.O., Tkačik G., Bialek W. Positional information, in bits. Proc. Natl. Acad. Sci. USA. 2013;110:16301–16308. doi: 10.1073/pnas.1315642110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bialek W., Setayeshgar S. Physical limits to biochemical signaling. Proc. Natl. Acad. Sci. USA. 2005;102:10040–10045. doi: 10.1073/pnas.0504321102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.De Ronde W.H. FOM Institute AMOLF; Amsterdam, The Netherlands: 2012. PhD thesis, Multiplexing Biochemical Signals. [Google Scholar]
- 11.Agmon N., Szabo A. Theory of reversible diffusion-influenced reactions. J. Chem. Phys. 1990;92:5270–5284. [Google Scholar]
- 12.Berezhkovskii A.M., Szabo A. Effect of ligand diffusion on occupancy fluctuations of cell-surface receptors. J. Chem. Phys. 2013;139:121910. doi: 10.1063/1.4816105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.van Zon J.S., ten Wolde P.R. Simulating biochemical networks at the particle level and in time and space: Green’s function reaction dynamics. Phys. Rev. Lett. 2005;94:128103. doi: 10.1103/PhysRevLett.94.128103. [DOI] [PubMed] [Google Scholar]
- 14.van Zon J.S., ten Wolde P.R. Green’s-function reaction dynamics: a particle-based approach for simulating biochemical networks in time and space. J. Chem. Phys. 2005;123:234910. doi: 10.1063/1.2137716. [DOI] [PubMed] [Google Scholar]
- 15.Takahashi K., Tănase-Nicola S., ten Wolde P.R. Spatio-temporal correlations can drastically change the response of a MAPK pathway. Proc. Natl. Acad. Sci. USA. 2010;107:2473–2478. doi: 10.1073/pnas.0906885107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Rice S.A. Elsevier; Amsterdam, The Netherlands: 1985. Diffusion-Limited Reactions. [Google Scholar]
- 17.van Zon J.S., Morelli M.J., ten Wolde P.R. Diffusion of transcription factors can drastically enhance the noise in gene expression. Biophys. J. 2006;91:4350–4367. doi: 10.1529/biophysj.106.086157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Opplestrup T., Bulatov V.V., Sadigh B. First-passage Monte Carlo algorithm: diffusion without all the hops. Phys. Rev. Lett. 2006;97:230602. doi: 10.1103/PhysRevLett.97.230602. [DOI] [PubMed] [Google Scholar]
- 19.Elowitz M.B., Surette M.G., Leibler S. Protein mobility in the cytoplasm of Escherichia coli. J. Bacteriol. 1999;181:197–203. doi: 10.1128/jb.181.1.197-203.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Elf J., Li G.-W., Xie X.S. Probing transcription factor dynamics at the single-molecule level in a living cell. Science. 2007;316:1191–1194. doi: 10.1126/science.1141967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Northrup S.H., Erickson H.P. Kinetics of protein-protein association explained by Brownian dynamics computer simulation. Proc. Natl. Acad. Sci. USA. 1992;89:3338–3342. doi: 10.1073/pnas.89.8.3338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wang K., Rappel W.-J., Levine H. Quantifying noise levels of intercellular signals. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;75:061905. doi: 10.1103/PhysRevE.75.061905. [DOI] [PubMed] [Google Scholar]
- 23.van Haastert P.J.M. A stochastic model for chemotaxis based on the ordered extension of pseudopods. Biophys. J. 2010;99:3345–3354. doi: 10.1016/j.bpj.2010.09.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hu B., Chen W., Levine H. Physical limits on cellular sensing of spatial gradients. Phys. Rev. Lett. 2010;105:048104. doi: 10.1103/PhysRevLett.105.048104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Govern C.C., ten Wolde P.R. Fundamental limits on sensing chemical concentrations with linear biochemical networks. Phys. Rev. Lett. 2012;109:218103. doi: 10.1103/PhysRevLett.109.218103. [DOI] [PubMed] [Google Scholar]
- 26.Endres R.G., Wingreen N.S. Maximum likelihood and the single receptor. Phys. Rev. Lett. 2009;103:158101. doi: 10.1103/PhysRevLett.103.158101. [DOI] [PubMed] [Google Scholar]
- 27.Mora T., Wingreen N.S. Limits of sensing temporal concentration changes by single cells. Phys. Rev. Lett. 2010;104:248101. doi: 10.1103/PhysRevLett.104.248101. [DOI] [PubMed] [Google Scholar]
- 28.Tkačik G., Callan C.G., Jr., Bialek W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA. 2008;105:12265–12270. doi: 10.1073/pnas.0806077105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Tostevin F., ten Wolde P.R. Mutual information between input and output trajectories of biochemical networks. Phys. Rev. Lett. 2009;102:218101. doi: 10.1103/PhysRevLett.102.218101. [DOI] [PubMed] [Google Scholar]
- 30.Gillespie D.T. Exact stochastic simulation of coupled chemical reactions. J. Phys. Chem. 1977;81:2340–2361. [Google Scholar]
- 31.Mugler A., ten Wolde P.R. The macroscopic effects of microscopic heterogeneity in cell signaling. Adv. Chem. Phys. 2013;153:373–396. [Google Scholar]
- 32.Gopich I.V., Szabo A. Diffusion modifies the connectivity of kinetic schemes for multisite binding and catalysis. Proc. Natl. Acad. Sci. USA. 2013;110:19784–19789. doi: 10.1073/pnas.1319943110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Popov A.V., Agmon N. Three-dimensional simulations of reversible bimolecular reactions: the simple target problem. J. Chem. Phys. 2001;115:8921–8931. [Google Scholar]
- 34.Gopich I.V., Szabo A. Kinetics of reversible diffusion influenced reactions: the self-consistent relaxation time approximation. J. Chem. Phys. 2002;117:507–517. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


