The Relation between Recombination Rate and Patterns of Molecular Evolution and Variation in Drosophila melanogaster

Abstract

Genetic recombination associated with sexual reproduction increases the efficiency of natural selection by reducing the strength of Hill–Robertson interference. Such interference can be caused either by selective sweeps of positively selected alleles or by background selection (BGS) against deleterious mutations. Its consequences can be studied by comparing patterns of molecular evolution and variation in genomic regions with different rates of crossing over. We carried out a comprehensive study of the benefits of recombination in Drosophila melanogaster, both by contrasting five independent genomic regions that lack crossing over with the rest of the genome and by comparing regions with different rates of crossing over, using data on DNA sequence polymorphisms from an African population that is geographically close to the putatively ancestral population for the species, and on sequence divergence from a related species. We observed reductions in sequence diversity in noncrossover (NC) regions that are inconsistent with the effects of hard selective sweeps in the absence of recombination. Overall, the observed patterns suggest that the recombination rate experienced by a gene is positively related to an increase in the efficiency of both positive and purifying selection. The results are consistent with a BGS model with interference among selected sites in NC regions, and joint effects of BGS, selective sweeps, and a past population expansion on variability in regions of the genome that experience crossing over. In such crossover regions, the X chromosome exhibits a higher rate of adaptive protein sequence evolution than the autosomes, implying a Faster-X effect.

Introduction

Levels of variation and rates of evolution in different regions of the genome may be greatly affected by differences in the frequency of recombination, as a result of Hill–Robertson interference (HRI), whereby evolutionary processes at a given site in the genome are influenced by selection acting on closely linked sites (Hill and Robertson 1966; Felsenstein 1974)—see recent reviews by Comeron et al. (2008), Charlesworth et al. (2010), and Cutter and Payseur (2013). HRI can occur through selective sweeps involving favorable mutations that drag closely linked neutral or deleterious variants to fixation (Maynard Smith and Haigh 1974). It may also operate through the effects of the removal by selection of deleterious mutations on variants at linked sites—background selection (BGS; Charlesworth et al. 1993). To a first approximation, selective sweeps and BGS can be viewed as processes that result in a reduction in the effective population size (N_e) at sites linked to those under selection, because of the resulting increased variance in fitness that they experience (Charlesworth et al. 2010). This effect is expected to be maximal in regions with little or no genetic recombination, other things such as gene density being equal, because recombination reduces the intensity of HRI effects.

Reduced N_e associated with HRI effects causes a reduction in the level of variability with respect to neutral or nearly neutral nucleotide variants. It should also cause loci to accumulate more slightly deleterious mutations and fix fewer advantageous ones, provided that these are under sufficiently weak selection. These expectations are consistent with evidence that regions of the Drosophila genome with low levels of genetic recombination often show low levels of genetic diversity (Aguadé et al. 1989; Begun and Aquadro 1992; Betancourt et al. 2009; Arguello et al. 2010). Similar effects have been found in a wide range of species (Frankham 2012; Cutter and Payseur 2013). Low levels of recombination in Drosophila are also often associated with reduced levels of adaptation at the molecular level (Presgraves 2005; Betancourt et al. 2009; Arguello et al. 2010). In addition, species with low levels of genome-wide recombination, such as highly self-fertilizing species, show reduced genetic diversity compared with their outcrossing relatives, although the evidence for reduced molecular sequence adaptation is less clear (Charlesworth 2003; Cutter and Payseur 2013). However, comparisons among species may be confounded by differences in life history and demographic variables such as population size and vulnerability to founder effects (Charlesworth 2003; Cutter and Payseur 2013), so that it is difficult to disentangle the effects of HRI per se. There are therefore considerable advantages in using comparisons among different regions of the genome of the same species.

A major challenge that remains is to determine which of the two nonexclusive causal factors (selective sweeps or BGS) is most important in causing the patterns observed in low recombination genomes or genomic regions (Stephan 2010). One study of the noncrossing over dot chromosome of D. americana has shown that it was hard to account for its reduced diversity by a recent “hard” selective sweep (in which a single newly arisen mutation spreads to fixation) because there were too many intermediate frequency variants in the population (Betancourt et al. 2009). In addition, there appeared to be a lack of evidence for positive selection on nonsynonymous mutations on the dot chromosome, in contrast to the rest of the genome of this species, as was also found for the D. melanogaster dot chromosome (Arguello et al. 2010). However, the classical model of BGS, which assumes that the variants responsible are at equilibrium under mutation–selection balance, predicts a far greater reduction of diversity than is seen in noncrossover (NC) regions of the Drosophila genome (Loewe and Charlesworth 2007). This apparent paradox is resolved by the finding that, in a large genome region without crossing over, HRI among the strongly selected mutations themselves can progressively reduce their effects on linked neutral or weakly selected variants, leading to higher levels of neutral diversity than are predicted by classical BGS (Kaiser and Charlesworth 2009). This modified BGS model is consistent with the level of variation observed on the fourth chromosome of several Drosophila species and on the neo-Y chromosome of D. miranda (Kaiser and Charlesworth 2009).

It is clearly important to extend these types of analyses to other systems, to determine whether the observed patterns can be replicated; this is the purpose of this article, which has the aim of using genome-wide data on polymorphism and divergence to look for the footprints of the processes mentioned earlier. In a previous analysis, we studied the evolutionary effects of highly reduced levels of recombination on the D. melanogaster genome, analyzing more than 200 genes that lack crossing over (Campos et al. 2012). These genes are located in five independent regions that lack crossing over (“noncrossover regions”) of D. melanogaster: the heterochromatic regions of the 2nd, 3rd and X chromosomes, and the 4th (dot) chromosome. All these NC regions exhibited an elevated level of evolutionary divergence from D. yakuba at nonsynonymous sites, as well as lower codon usage bias (CUB), a lower GC content in coding and noncoding regions, and longer introns. These patterns are consistent with a reduction in the efficacy of selection in all regions of the genome of D. melanogaster that lack crossovers, as a result of the effects of enhanced HRI in these regions. However, to rule out the possibility that the higher levels of nonsynonymous divergence are due to positive selection, and to determine whether positive as well as purifying selection is less effective in NC regions, we need to compare levels of divergence and polymorphism (McDonald and Kreitman 1991). In the analyses described here, we use next-generation DNA sequence data from a population that is geographically close to the putatively ancestral population of D. melanogaster, generated in the Drosophila Population Genomics Project (DPGP: Pool et al. 2012), to compare patterns of diversity and divergence across the whole genome, including contrasts between NC and crossover (C) regions, among regions with different nonzero rates of crossing over, and between the X chromosome and the autosomes.

Results

Effects of a Low Recombination Rate on Diversity and Divergence

Table 1 displays the basic diversity and divergence statistics for the two regions with crossing over (X chromosome and autosomes—XC and AC, respectively) and the pooled results for the NC regions. The results for each NC region separately are shown in table 2. The general patterns are similar for the filtered (95% recovered true variants) and the unfiltered data sets (see Materials and Methods), except that the estimates of diversity are lower in the filtered data set, because of the removal of some polymorphic sites. We have therefore reported only the results obtained from the filtered data set; the unfiltered results are given in supplementary tables S1 and S2 of supplementary material S1, Supplementary Material online. Similarly, the data set where no admixture mask was employed produced identical results to the filtered and masked data set (supplementary table S3 of supplementary material S1, Supplementary Material online). Therefore, the removal of these regions has apparently not biased the results.

Table 1.

Summary Statistics for Autosomal Genes in Crossover Regions (AC), X Chromosome Genes in Crossover regions (XC), and All NC Genes.

	AC	XC	NC
N	7,099	1,319	268
SA	45,373	8,868	620
SS	144,370	34,812	777
πA	0.00143 (0.00139, 0.00146)	0.00128 (0.00120, 0.00135)	0.000537 (0.000313, 0.000761)
πS	0.0141 (0.0139, 0.0144)	0.0156 (0.0151, 0.0161)	0.00218 (0.000990, 0.00338)
πA/πS	0.101 (0.098, 0.104)	0.0818 (0.0765, 0.0875)	0.268 (0.215, 0.321)
θA	0.00179 (0.00175, 0.00184)	0.00178 (0.00168, 0.00188)	0.000620 (0.000381, 0.000859)
θS	0.0147 (0.0145, 0.0150)	0.0178 (0.0173, 0.0183)	0.00230 (0.00124, 0.00337)
PsingA	0.514 (0.492, 0.536)	0.610 (0.549, 0.677)	0.439 (0.345, 0.533)
PsingS	0.354 (0.340, 0.369)	0.427 (0.395, 0.465)	0.393 (0.296, 0.491)
DA	−0.666 (−0.685, −0.646)	−0.953 (−0.996, −0.911)	−0.603 (−0.972, −0.234)
DS	−0.173 (−0.190, −0.157)	−0.532 (−0.563, −0.5014)	−0.354 (−0.778, 0.069)
KA	0.0381 (0.0371, 0.0391)	0.0404 (0.0381, 0.0427)	0.0549 (0.0499, 0.0599)
KS	0.262 (0.260, 0.264)	0.258 (0.254, 0.262)	0.273 (0.266, 0.279)
KA/KS	0.145 (0.141, 0.150)	0.156 (0.148, 0.166)	0.204 (0.184, 0.222)
HA	0.000035 (−0.000003, 0.000071)	−0.00004 (−0.00014, 0.00006)	0.000118 (0.000057, 0.000179)
HS	−0.00296 (−0.00319, −0.00274)	−0.00292 (−0.00356, −0.00231)	−0.000089 (−0.000714, 0.000537)

Note.—N, number of genes analyzed; S, number of segregating sites (subscript A: nonsynonymous sites; subscript S: synonymous sites); π, mean number of nucleotide differences per site; θ_w, mean value of Watterson’s theta per gene; D, mean value of Tajima’s D per gene; K, mean value of divergence per nucleotide site from D. yakuba; P_sing, proportion of segregating sites that are singletons; H, mean value of the Fay and Wu statistic. The quantities in parentheses are the 95% CIs of the means; for C regions, these were obtained by bootstrapping across genes and for NC regions by jackknifing across the five independent NC regions.

Table 2.

Summary Statistics for the Five NC Regions.

	N2	N3	N4	NXc	NXt
N	59	99	67	19	23
SA	142	150	191	72	65
SS	222	197	176	104	78
πA	0.000455 (0.000234)	0.000426 (0.000218)	0.000279 (0.000143)	0.000955 (0.000498)	0.00057 (0.000299)
πS	0.00221 (0.00113)	0.00163 (0.000828)	0.000807 (0.000413)	0.004438 (0.002281)	0.001829 (0.000953)
πA/πS	0.206 (0.148)	0.262 (0.190)	0.346 (0.251)	0.215 (0.158)	0.312 (0.230)
θA	0.000564 (0.000215)	0.000431 (0.000164)	0.000384 (0.000146)	0.00107 (0.000418)	0.000651 (0.000256)
θS	0.00254 (0.00096)	0.00160 (0.000606)	0.00102 (0.000387)	0.00422 (0.00162)	0.00215 (0.000838)
PsingA	0.458	0.320	0.597	0.361	0.462
PsingS	0.374	0.279	0.528	0.298	0.487
DA	−0.821	−0.050	−1.173	−0.450	−0.523
DSa	−0.551	0.083	−0.890	0.224	−0.639
KA	0.0603 (0.0496, 0.0698)	0.0549 (0.0452, 0.0635)	0.0556 (0.0467, 0.0643)	0.0597 (0.0374, 0.0799)	0.0349 (0.0258, 0.0445)
KS	0.294 (0.278, 0.310)	0.284 (0.273, 0.296)	0.248 (0.238, 0.259)	0.252 (0.226, 0.277)	0.254 (0.234, 0.274)
KA/KS	0.205 (0.169, 0.244)	0.193 (0.163, 0.226)	0.224 (0.190, 0.258)	0.237 (0.155, 0.336)	0.137 (0.101, 0.175)
HA	0.000105	0.000142	0.0000034	0.000161	0.000177
HS	−0.00111	0.0000632	0.000283	−0.000431	0.000754

Note.—The entries in the columns headed N2–N4 are the mean values for the NC regions of chromosomes 2−4; those under NXc are for the NC region of the X adjacent to the centromere, and those under NXt are for the NC region of the X adjacent to the telomere. The meaning of the other symbols is the same as for table 1, except that the quantities in brackets for the diversity statistics π and θ are the standard errors of the means obtained from the coalescent process formulae with no recombination; the standard errors for the corresponding ratios were obtained by the delta method formula for a ratio (see Materials and Methods).

^aNo D_S was significantly different from 0 when tested by 1,000 coalescent simulations with no recombination.

The main patterns to emerge are as follows. First, consistent with previous studies of the dot chromosome in several species of Drosophila (see Introduction), we found an approximately 7-fold overall reduction in synonymous diversity in the NC regions compared with the C regions. XC had a somewhat higher synonymous diversity level than AC, as was previously found for 4-fold degenerate sites by Campos et al. (2013); the mean π_S values were AC = 0.0141, XC = 0.0156, and NC = 0.00218. The highest reduction in diversity in NC genes was on the fourth chromosome, whereas the NC genes near the X centromere had the highest mean diversity (table 2). The means of the estimates of synonymous divergence from D. yakuba (K_S) were only slightly different among regions (and were somewhat elevated for NC autosomes), so that the greatly reduced diversity in the NC regions cannot be due to a lower mutation rate, in agreement with the conclusions from earlier studies (Begun and Aquadro 1992; Presgraves 2005; Langley et al. 2012; Mackay et al. 2012).

We also found increased values of the ratios π_A/π_S and K_A/K_S in the NC compared with the C regions. The mean π_A/π_S was above 0.2 for all NC regions, but approximately 0.1 for AC and XC. Similarly, mean K_A/K_S was over 0.2 for all NC regions except the telomere of the X chromosome, but about 0.15 for the regions with crossing over, consistent with the results of Campos et al. (2012). A smaller reduction in π_A compared with π_S as N_e decreases is expected if nonsynonymous mutations are subject to stronger purifying selection than synonymous mutations, even with a wide distribution of selection coefficients (Betancourt et al. 2012), so that the fact that π_A/π_S is elevated in the NC regions is consistent with the expected effect of a reduced efficacy of selection in these regions. Nonetheless, it is theoretically possible that, if purifying selection on the majority of nonsynonymous mutations is sufficiently strong that π_A is maintained close to deterministic mutation-selection balance in both the C and NC regions, π_A would not experience a substantial change due to reduced N_e in the NC regions. However, π_A in the NC regions is approximately half the value for the C regions, and the confidence intervals (CIs) for the two regions do not overlap, which contradicts this scenario.

We examined this question further by polarizing segregating variants against two outgroup species, as described in the Materials and Methods. We used the results to calculate the ratios of the numbers of derived nonsynonymous mutations to the numbers of synonymous mutations in different regions (table 3 and fig. 1). The results indicate that there are significant increases in the abundances of derived nonsynonymous mutations relative to synonymous mutations in the NC regions compared with the C regions, even among high-frequency-derived variants. Contrary to what would be expected if nonsynonymous mutations are being held at very low frequencies by strong purifying selection, there is no sign in the NC regions of a very much greater ratio of nonsynonymous to synonymous derived mutations among singletons compared with intermediate or even high-frequency variants. Overall, therefore, the polymorphism data are entirely consistent with a reduced efficacy of selection against slightly deleterious nonsynonymous mutations, and with a wide distribution of selection coefficients around a low mean value, as indicated by previous studies (Kousathanas and Keightley 2013) and as found in our own analyses (see later).

Table 3.

2 × 2 Contingency Tables Comparing the Numbers of Derived Mutations in Different Frequency Categories in C and NC regions for Nonsynonymous (A) and Synonymous (S) Variants.

No. of Derived Mutations	Site	Region		P
		AC	NA
1 (singletons)	A	18,070	135	2 × 10−10
	S	37,810	126
2–7 (intermediate)	A	12,914	127	2 × 10−13
	S	48,427	190
8–16 (high)	A	5,187	49	2 × 10−11
	S	27,010	64
1–16 (all)	A	36,171	311	1 × 10−32
	S	113,247	380
		XC	NX
1 (singletons)	A	3,157	35	0.0023
	S	8,531	46
2–7 (intermediate)	A	1,455	43	5 × 10−11
	S	7769	53
8–16 (high)	A	709	16	0.00017
	S	4097	25
1–16 (all)	A	5321	94	1 × 10−13
	S	20397	124

Note.—AC, autosomal C region; NA, autosomal NC regions; XC, X-chromosome C regions; NX, X chromosome NC regions. P value: Fisher's exact test probability for the corresponding 2 × 2 table.

Fig. 1.

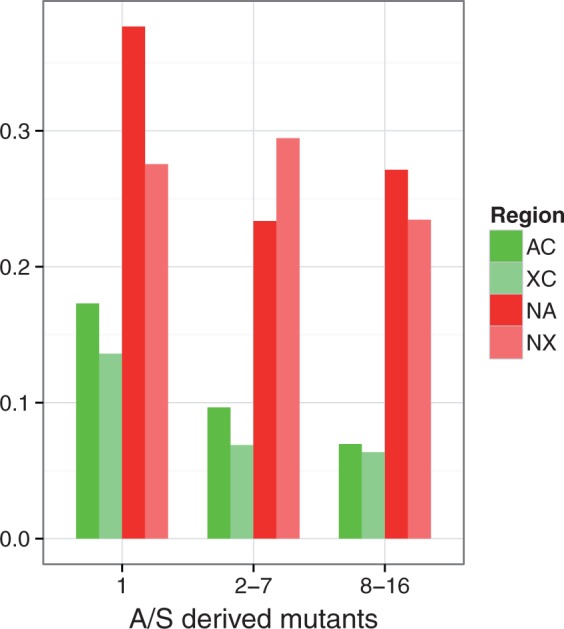
Ratio of the number of derived nonsynonymous mutations per nonsynonymous site to the number of synonymous mutations per synonymous site, for three categories of frequencies of derived variants. AC, autosomal crossover regions; XC, X chromosome crossover regions; NA, autosomal NC regions; NX, X chromosome NC regions.

Is There Positive Selection on Genes in the NC Regions?

The higher K_A/K_S in the NC regions could in principle be due to a faster rate of adaptive evolution on nonsynonymous mutations in the absence of crossing over, although this is theoretically very implausible. We have therefore asked whether the efficacy of positive selection is reduced in the NC regions. This was done using estimates of the proportion, α, of fixed nonsynonymous differences between D. yakuba and D. melanogaster that are due to positive selection, using the method of Fay et al. (2002), as described in the Materials and Methods. This approach was used to avoid possible biases in the distribution of fitness effects (DFE)-alpha method of Eyre-Walker and Keightley (2009), associated with the high level of linkage disequilibrium in the NC regions; similar results are, however, obtained with DFE-alpha, as shown in supplementary table S4 of supplementary material S1, Supplementary Material online.

The results are shown in table 4. We found that α was above 35% for crossover genes but is nonsignificantly different from 0 for the mean over the five NC regions, on the basis of jackknifing over regions (the overall α values were AC = 0.368, XC = 0.569, NC = –0.412). The estimates of the rate of nonsynonymous adaptive substitutions relative to synonymous substitutions per site (ω_α: Gossmann et al. 2010) behaved similarly: the overall ω_α values were AC = 0.053, XC = 0.089, and NC = –0.069. Interestingly, we also observed a higher level of adaptive evolution for nonsynonymous sites on the X chromosome than on the autosomes in the regions with crossing over, suggesting a Faster-X effect (Charlesworth et al. 1987). Evidence for such an effect in D. melanogaster whole-genome resequencing data sets has also been reported by Mackay et al. (2012) and Langley et al. (2012).

Table 4.

Estimates of the Proportions (α) and the Relative Rates (ω_α) of Adaptive Nonsynonymous Substitutions.

	α	ωα
N2	0.016	0.0030
N3	−0.337	−0.0641
N4	−0.449	−0.0998
NXc	−0.039	−0.0085
NXt	−1.253	−0.1762
NC	−0.412 (−0.858, 0.034)	−0.069 (−0.133, −0.0051)
AC	0.368 (0.339, 0.405)	0.053 (0.049, 0.059)
XC	0.569 (0.539, 0.597)	0.089 (0.082, 0.096)
oAC	0.401 (0.382, 0.419)	0.058 (0.054–0.061)
oXC	0.548 (0.496, 0.595)	0.091 (0.079–0.103)

Note.—The quantities in parentheses are the 95% CIs of the values obtained by the method of Fay et al. (2002); for C regions, these are obtained by bootstrapping across genes, and for NC by jackknifing across the five independent NC regions. oAC, overlap autosomal crossover regions; oXC, overlap X crossover region (“overlap” means that the X and autosomal genes in these regions have similar effective rates of recombination—see Materials and Methods for details).

Have There Been Selective Sweeps in the NC Regions?

Although a low positive value of α cannot be ruled out for the NC regions by the results in table 4, the results suggest that the opportunity for selective sweeps is relatively limited (see Discussion). This question can be pursued further, as follows. As described in the Materials and Methods, we also analyzed the NC regions by the method of Betancourt et al. (2009) for testing for the effect of a hard sweep in the absence of recombination. In supplementary material S2, Supplementary Material online, we show the likelihood of the data fitting a selective sweep in each NC region for each combination of θ₀ (the level of neutral variation that would have been present in the absence of a sweep) and T (the time in units of 2N_e generations since the sweep occurred). The coalescent simulations show that a single catastrophic sweep does not fit the observed numbers of segregating sites and k (the average number of pairwise differences between alleles) for any of the five NC regions (supplementary material S2, Supplementary Material online). The data are compatible with a broad range of values of T, but require very low values of θ₀, which are very different from the level of synonymous site variability in the crossover regions. The results are the same when we focus only on genes located in the alpha-heterochromatin (see Materials and Methods), treating each major chromosome separately.

These results were obtained on the assumption that no recombination occurs in the NC regions. However, previous studies of polymorphisms in genes located in the telomere of the X chromosome (Langley et al. 2000; Anderson et al. 2008) and the dot chromosome (Betancourt et al. 2009; Arguello et al. 2010) showed clear evidence for recombination events, as has a recent analysis of the DPGP data (Chan et al. 2012). Consistent with these results, a recent fine-scale single-nucleotide polymorphism (SNP) map of D. melanogaster showed that gene conversion events are occurring in NC regions, at approximately the same rate as elsewhere in the genome (Comeron et al. 2012). To test for recombination events in the NC regions, we used the R_h estimator of the minimum number of recombination events in a sample (Myers and Griffiths 2003).

As can be seen from table 5, there is clear evidence that some recombination has occurred in these regions, almost certainly involving gene conversion and not crossing over. This even applies to genes in the alpha-heterochromatin, which is commonly thought to have little or no recombinational exchange (Ashburner et al. 2005, pp. 462–463); three, six, and nine recombination events were detected in the alpha-heterochromatin of chromosomes X, 2, and 3, respectively. This means that the above test for a selective sweep is not conclusive, because it is conceivable that a low level of recombination between the target of selection and segregating neutral sites could result in a less skewed genealogy than with no recombination, for a given reduction in pairwise diversity. To test whether a recent selective sweep with recombination has occurred in the NC, resulting in some derived variants being dragged to high frequencies but not fixation, we calculated the Fay and Wu (2000) H statistics for each region, as described in the Materials and Methods. These provided no evidence for an excess of derived variants (tables 1 and 2), as expected for a recent sweep with recombination (Fay and Wu 2000).

Table 5.

Minimum Numbers of Recombinants (R_h) Detected in Each NC Region.

	Rh	Rh/Kb
N2	119	1.184
N3	74	0.53
N4	40	0.202
NXc	74	2.709
NXt	27	0.67

Are the Patterns Consistent with BGS?

The lack of support for effects of selective sweeps suggests that the most parsimonious explanation for the reductions in diversity in the NC regions is BGS. Under almost any model of HRI, reductions in diversity and efficacy of selection in an NC region should be positively correlated with the number of sites under selection in the region in question, as explored in detail for the BGS model by Kaiser and Charlesworth (2009). We indeed observed a negative relationship between nucleotide site diversities and the number of coding sequence sites in each NC region, L (Spearman’s rank correlation coefficient ρ: π_A = –1, P < 0.001; π_S = –0.9, P < 0.05; fig. 2) and a positive (but not significant) correlation between π_A/π_S and L (ρ = 0.5, P > 0.05; fig. 2).

Fig. 2.

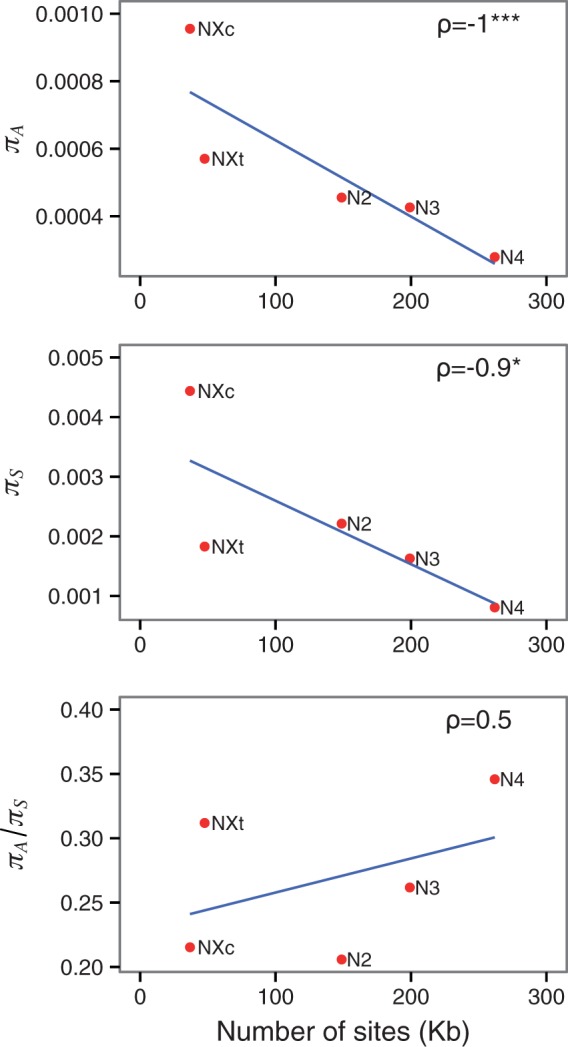
Correlations between diversity statistics and the numbers of sites in coding sequences in the five NC regions for nonsynonymous diversity π_A, synonymous diversity π_S, and the ratio π_A/π_S. ρ, Spearman’s rank correlation coefficient, with significance denoted by asterisks (***<0.001; *<0.05).

Given the overall low level of recombination in these regions, the model of Kaiser and Charlesworth (2009), which takes into account HRI among the deleterious mutations involved in generating effects on linked sites, is probably the most appropriate tool for investigating the question of whether BGS is adequate to explain these results. As described in the Materials and Methods, we quantified the reductions in diversity by means of the statistic B, the ratio of the mean synonymous diversity in an NC region to the mean synonymous diversity for the appropriate crossover region. We compared the observed B values to the predictions of Kaiser and Charlesworth (2009) for a given number of sites under selection (L), based on published estimates of the distribution of mutational effects on fitness, the mutation rate, and the rate of gene conversion. We obtained a reasonably good fit to the observed B values, with a tendency for the model to somewhat overestimate the level of reduction in diversity compared with the data (fig. 3). As noted in the Materials and Methods, such an overestimation may have resulted from the distribution of selection coefficients that were used. The predicted B values are, of course, subject to many uncertainties, because they are sensitive to details of the distribution of mutational effects on fitness and the mutation rate, so the extent of agreement with the data must be interpreted with caution.

Fig. 3.

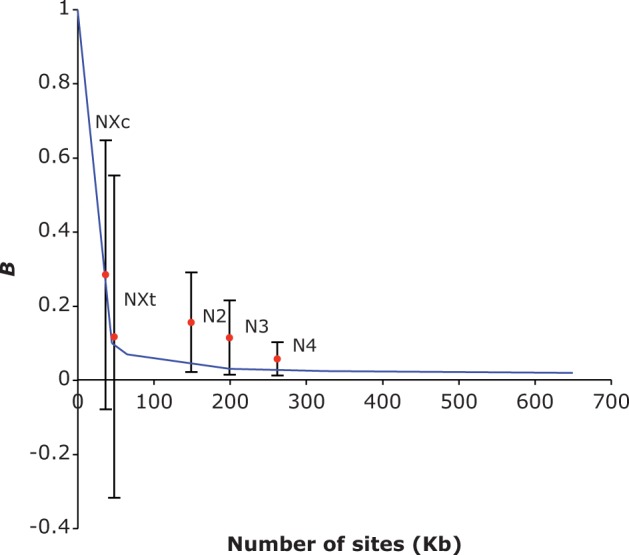
B values for the five NC regions (red dots) against the number of coding sequence sites in each region. The blue line shows the effects of HRI on B due to BGS, predicted by Kaiser and Charlesworth (2009). The error bars are the standard errors of B obtained from the diversity statistics for the NC regions as described for table 2.

With the small number of genes in each NC region in the present case, this BGS model also predicts moderately negative Tajima’s D values at neutral sites compared with standard neutral coalescent expectation, reflecting a skew toward low-frequency variants due to the distortions of gene genealogies by the HRI effects. Furthermore, D for nonsynonymous sites should be close to that for synonymous sites, due to the weakened efficacy of selection. We found a significantly more negative mean synonymous D value for NC than AC regions; however, the skew was less than for the XC genes, which showed a much larger skew than AC genes (synonymous site mean D values per gene were AC = –0.17, XC = –0.53, NC = –0.35). The X centromere genes showed a nonsignificantly positive skew, in line with the evidence from their diversity levels and codon usage (Campos et al. 2012) that they experience smaller HRI effects than the other NC regions. The D values per gene for nonsynonymous sites are highly variable among different NC regions, reflecting the relatively small numbers of segregating sites in each region (table 2). Overall, they are close to the values for synonymous sites; as expected, the CIs of synonymous and nonsynonymous sites overlap in the NC regions, in contrast to the crossover regions (table 1). Broadly similar patterns are also seen for the proportions of singletons, the other measure of skew that we have used here.

Patterns in Genomic Regions with Crossing Over

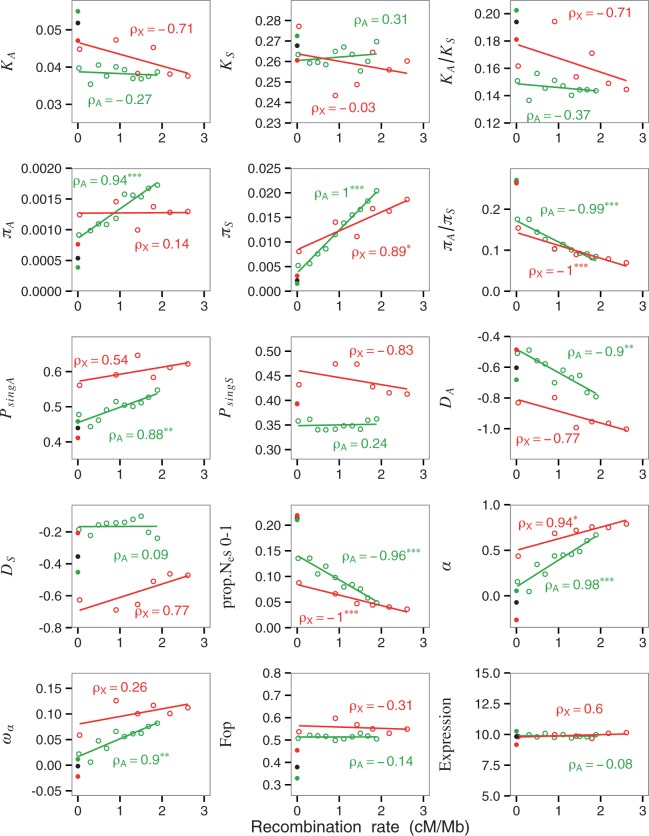
The evidence presented earlier indicates that genomic regions where crossing over is nearly completely absent show strong indications of a reduction in the efficiency of selection on both deleterious and beneficial mutations, as well as a very low silent nucleotide site diversity that implies a reduced effective population size. This raises the question of whether regions of the D. melanogaster genome that have different but nonzero rates of crossing over show similar patterns of effects of the recombination rate, apart from the very well established positive relation between silent site diversity and local rate of crossing over per unit physical distance (Begun and Aquadro 1992; Presgraves 2005; Langley et al. 2012; Mackay et al. 2012).

As described in the Materials and Methods, we have examined this question by assembling DNA sequence polymorphism data from the Gikongoro population, as well as estimates of sequence divergence from D. yakuba, into ten bins with respect to “effective” rates of crossing over per megabase for the autosomes and six for the X chromosome. These effective rates are calculated by multiplying rates of crossing over in female meiosis by one-half for autosomes and two-thirds for the X chromosome, to take into account the amount of time a gene spends in males, which lack crossing over (Campos et al. 2013). The values of potential covariates, such as CUB (estimated as Fop), GC₃, the GC content of short introns, and levels of gene expression, were also determined for these bins; these were estimated as described previously (Campos et al. 2012, 2013).

The assembly into bins was done primarily to enable use of the DFE-alpha program of Eyre-Walker and Keightley (2009) for estimating the parameters of the distribution of the fitness effects of new, deleterious mutations, as well as α, and ω_α for nonsynonymous mutations, because this method is designed to use groups of genes rather than data from individual genes. We used this approach rather than the Fay et al. (2002) method employed for the NC case, because the assumptions of maximum likelihood estimation are likely to be met when there is crossing over, and the Fay et al. (2002) method is known to produce downwardly biased estimates when purifying selection is acting on nonsynonymous variants (Charlesworth and Eyre-Walker 2008; Messer and Petrov 2013). Plots of unbinned values of the other variables are shown in supplementary figure S1 of supplementary material S3, Supplementary Material online; the main conclusions are unaltered.

The resulting parameter estimates and their 95% CIs are shown in supplementary table S5 of supplementary material S1, Supplementary Material online, and tests of significance for correlations with recombination rates are given in supplementary table S6 of supplementary material S1, Supplementary Material online. The major features of the results are displayed in figure 4; in supplementary figure S2 of supplementary material S3, Supplementary Material online, we show similar plots using the recombination rates estimated by Comeron et al. (2012) (see Materials and Methods). Several important points emerge. First, in agreement with previous analyses (Haddrill et al. 2007; Campos et al. 2012; Langley et al. 2012; Mackay et al. 2012), there is little evidence of a systematic relation between recombination rate and the divergence parameters K_A, K_S, or K_A/K_S (fig. 4). Second, as found in all previous studies, the synonymous site diversity estimate, π_S, increases with the recombination rate. Third, there is a much weaker tendency for the nonsynonymous diversity to increase with recombination rate (especially on the X chromosome), so that the ratio π_A/π_S decreases with recombination rate. This is very similar to the pattern that was seen when NC and C regions are contrasted.

Fig. 4.

Relations between the effective recombination rate and the means of several variables for genes in the C regions, after grouping genes into bins defined by rates of crossing over. The x axis gives the mean effective recombination rate (cM/Mb) for each bin. Autosomal genes (A) are shown in green and X-linked (X) genes in red. Values for NC regions are indicated by the filled points at the extreme left of each panel but are not included in the correlation or regression analyses (black: the five NR blocks; green: autosomal NC genes; red: X-linked NC genes). ρ: Spearman’s rank correlation coefficient, with significance denoted by asterisks (***<0.001; **<0.01; *<0.05). The lines are least-squares regressions but should be regarded only as indicative, in view of the binning of the data.

The fact that π_A is lower with lower rates of crossing over implies that a proportion of nonsynonymous mutations are subject to sufficiently weak selection that they are subject to the effects of drift, so the trend in π_A/π_S is not entirely driven by strong selection maintaining nonsynonymous mutations at their mutation-selection equilibrium, combined with a drop in π_S as recombination rates fall. This conclusion is strengthened by the observation that, on the autosomes, the proportion of singletons among nonsynonymous variants increases with increasing recombination, as does nonsynonymous Tajima’s D, whereas there is little systematic change in these variables for synonymous variants for the autosomes (fig. 4; supplementary tables S5 and S6 of supplementary material S1, Supplementary Material online), although there is a nonsignificant negative correlation between the proportion of synonymous singletons and the recombination rate for the X chromosome (this becomes significant when the recombination estimates of Comeron et al. [2012] are used). Similarly, the DFE-alpha estimates of the proportion of nonsynonymous variants that have N_es values in the nearly neutral range 0–1 decrease with increasing recombination rate (fig. 4; supplementary table S5 of supplementary material S1, Supplementary Material online) (the estimates of mean N_es are too noisy to show a clear pattern).

All these results point to an increase in the effectiveness of purifying selection against new nonsynonymous mutations as the local recombination rate increases. The estimates of ω_α and α (fig. 4; supplementary table S5 of supplementary material S1, Supplementary Material online) show a similar pattern for positive selection, with highly significantly positive rank correlations for both variables for autosomal loci, and for α for the X chromosome (fig. 4 and supplementary table S6 of supplementary material S1, Supplementary Material online). In addition, the X chromosome shows consistently higher values of α and ω_α than the autosomes, even for similar effective recombination rates (see Discussion). Similar results were obtained when we used D. simulans instead of D. yakuba as an outgroup, suggesting that possible changes in the recombination landscape since the common ancestor of D. melanogaster and D. yakuba have had only a minor effect on the patterns of sequence evolution (see supplementary fig. S3 of supplementary material S3, Supplementary Material online).

There is no evidence for any strong associations between recombination rate and the potential covariates Fop, GC₃, the GC content of short introns and level of gene expression (see fig. 4 and supplementary tables S5 and S6 of supplementary material S1, Supplementary Material online), so that the major determinant of both the level of synonymous variability and the efficacy of selection appears to be the recombination rate itself.

Discussion

Recombination and the Efficacy of Purifying Selection

Consistent with previous studies of variability in several Drosophila species (Aguadé et al. 1989; Begun and Aquadro 1992; Betancourt et al. 2009; Arguello et al. 2010), we have found an approximately 7-fold reduction in synonymous diversity in NC regions compared with crossover (C) regions of the D. melanogaster genome, but no comparable effect for K_S (tables 1 and 2). This implies a reduction in the effective population size, N_e, for neutral or weakly selected sites, almost certainly because of hitchhiking. In addition, the K_A/K_S ratio is higher in NC than in C regions (Campos et al. 2012; see also tables 1 and 2), consistent with the theoretical expectation of an impairment of the efficacy of selection due to HRI among closely linked sites (Charlesworth et al. 2010; Cutter and Payseur 2013).

Although it is in principle possible that this elevation of K_A/K_S could reflect an increased incidence of hitchhiking due to more frequent positive selection in the NC regions, the polymorphism analyses described earlier, especially the negative relation between the recombination rate and the fraction of nonsynonymous mutations that fall into the nearly neutral category (N_es < 1), as well as the increase in skew at nonsynonymous sites and reduction in skew at synonymous sites on the X chromosome as the recombination rate increases, strongly suggest that the NC regions and the C regions with lower rates of recombination have experienced a reduced efficacy of purifying selection due to HRI (table 3; figs. 1 and 4). There is no reason to expect that NC genes should be less constrained, because they do not differ greatly from C genes in their gene ontology (Smith et al. 2007), or in their expression level (Campos et al. 2012), the major correlate of purifying selection on protein sequences (Drummond and Wilke 2008). Similar remarks apply to the comparisons of C genes in different recombination rate classes (fig. 4; supplementary table S6 of supplementary material S1, Supplementary Material online), so that HRI is the only plausible explanation for these patterns.

Most previous Drosophila studies suggesting that recombination enhances the efficacy of purifying selection on amino acid mutations have used relatively small numbers of loci compared with the results presented here (e.g., Presgraves 2005; Shapiro et al. 2007). The genome-wide study of Mackay et al. (2012) reached a similar conclusion to ours, using data on a sample of 168 haploid genomes from a North Carolina population of D. melanogaster. To estimate the fraction of weakly selected nonsynonymous variants, Mackay et al. (2012) assumed that nonsynonymous variants with a minor allele frequency of less than 5% are either neutral or weakly deleterious and estimated the proportion of neutral variants in this category by comparison with the proportion of 4-fold degenerate site variants (assumed to be neutral) in this frequency class. They estimated the proportion of nonsynonymous variants that are strongly deleterious from the ratio of the fraction of nonsynonymous sites that segregated in their sample to the fraction of 4-fold sites that segregated, on the assumption that strongly selected mutations fail to segregate. Using these criteria, they found a reduction in the estimated proportion of deleterious nonsynonymous variants in autosomal centromeric regions (these extend much further into the regions with detectable rates of crossing over than our NC regions and are more comparable with the lowest recombination bins in our C regions).

These criteria are, however, qualitative rather than quantitative, especially as it cannot be assumed that strongly selected nonsynonymous variants will fail to segregate in a sample, as can be seen as follows. For nonrecessive mutations with N_es >> 1, the expected equilibrium frequency, q*, is close to that under mutation–selection balance; with a sample size n, the probability of segregation is approximately P_seg = nq*. We have q* 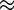π/(4N_es_h), where s_h is the heterozygous selection coefficient against the mutations in question and π is the expected equilibrium neutral diversity (Loewe et al. 2006, eq. 8). These relations imply that P_seg 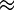nπ/(4N_es_h), so that P_seg increases linearly with the sample size. For large samples, P_seg for selected sites may not be especially small when compared with the neutral equilibrium expectation of πa_n, where a_n is Watterson’s correction factor (the sum of 1/i from i = 1 to n – 1), which increases only logarithmically with the sample size (Charlesworth B and Charlesworth D 2010; p. 29). For example, with n = 168, π = 0.01, and 4N_es_h = 100, P_seg = 0.0168; the corresponding neutral value is 0.01 × 5.70 = 0.0570, giving a ratio of 0.29; that is, the probability of segregation for sites subject to deleterious mutations is only about three times less than for neutral sites. The fraction of strongly deleterious mutations is therefore seriously underestimated by the method of Mackay et al. (2012).

Another source of bias arises from the fact that non-African populations of D. melanogaster, including US populations, show evidence for a bottleneck in population size (Glinka et al. 2003; Haddrill et al. 2005; Thornton and Andolfatto 2006; Langley et al. 2012; Mackay et al. 2012; Pool et al. 2012). Because bottlenecks preferentially eliminate low-frequency variants (Nei et al. 1975), this means that fewer deleterious variants will be present than in a stationary population, which reduces the fraction of nonsynonymous variants that are apparently strongly selected. These two sources of bias mean that the Mackay et al. (2012) estimates of the proportions of nonsynonymous variants in different categories of N_es are subject to considerable uncertainty. It is therefore encouraging that the results obtained by our methods also provide strong support for a reduced efficacy of purifying selection in regions with low rates of recombination.

This conclusion is consistent with previous evidence for greatly reduced CUB in the NC regions (e.g., Campos et al. 2012) but leaves open the question of why there is no positive correlation between CUB and recombination rate in the autosomal and X crossover regions (Singh et al. 2005; Singh et al. 2008; Campos et al. 2013; supplementary table S5 of supplementary material S1, Supplementary Material online). Possible reasons for these patterns were discussed by these workers, the most plausible being that the current recombination landscape in D. melanogaster does not reflect the historical situation when levels of CUB were established, given the very long time required for equilibration of CUB. Although this possibility is consistent with our findings on selection against nonsynonymous segregating variants, where the patterns can be generated on a relatively short timescale, it is perhaps not so easy to reconcile with the evidence for an effect of recombination on the rate of substitution of favorable mutations, discussed in the next section.

Recombination and the Efficacy of Positive Selection

Our analyses of the incidence of positive selection on nonsynonymous variants also demonstrate an enhanced efficacy of positive selection with increasing rates of recombination, with little evidence for positive selection in the NC regions (table 4). There is also a highly significant relation between recombination rate and the proportion of nonsynonymous substitutions fixed by positive selection (α) estimated from the DFE-alpha method (Eyre-Walker and Keightley 2009), for both autosomes and the X chromosome, as well the rate of fixation by positive selection relative to synonymous substitutions (ω_α) for the autosomes (fig. 4 and supplementary table S5 of supplementary material S1, Supplementary Material online). Very similar results were obtained using the recombination rates estimates of Comeron et al. (2012), described in the Materials and Methods (supplementary fig. S2 of supplementary material S3, Supplementary Material online). This suggests that there has been very little adaptive evolution of protein sequences in the low recombination regions of the D. melanogaster genome, although α and ω_α values were substantial (0.43 and 0.06, respectively) in the lowest recombination bin for the crossover regions of the X. Again, similar conclusions were reported in the genome-wide studies of D. melanogaster by Mackay et al. (2012) and Langley et al. (2012), using 168 genomes from N. Carolina and six genomes from Malawi, respectively. Both of these studies, however, used McDonald–Kreitman 2 × 2 table methods of estimating α, similar in their general nature to the Fay et al. (2002) method that we used for the NC regions to avoid potential biases of the DFE-alpha method when crossing over is absent. This method is known to be subject to downward biases that are hard to remove completely, due to the contribution of weakly deleterious mutations to nonsynonymous variability (Charlesworth and Eyre-Walker 2008; Messer and Petrov 2013). For purposes of comparison, we also applied the Fay et al. (2002) method to the groups of genes in the recombination bins presented in figure 4 (supplementary table S5 of supplementary material S1, Supplementary Material online); as expected, it shows consistently lower estimates of α and ω_α than the DFE-alpha method, although the patterns of correlation with recombination rates are similar with both methods.

However, even with the Fay et al. (2002) method, our α values are substantially higher for the C regions of the genome than the estimates of Langley et al. (2012) and Mackay et al. (2012): >0.30 as opposed to 0.13 and 0.24, respectively. We also find much higher rank correlations between recombination rate and α in the crossover regions than those of Langley et al. (2012) (> 0.9 as opposed to around 0.1). The reasons for these discrepancies are not entirely clear, although Langley et al. (2012) relied on individual gene estimates of α to generate their results, which are extremely noisy and thus may reduce the magnitude of the correlation coefficient compared with binned estimates.

There are several sources of bias in estimates of α and ω_α from population and divergence data, especially that arising from selection acting on synonymous sites. The strength of such selection in various species of Drosophila, including the Rwandan population (Campos et al. 2013) has been estimated from polymorphism data; with the exception of the study of Lawrie et al. (2013) on the highly bottlenecked Raleigh population, these suggest 4N_es values of the order of 1.5 for synonymous variants affecting codon usage. As discussed by Haddrill et al. (2010), this intensity of selection is likely to have only minor effects on estimates of α.

Causes of the Reduced N_e in Low Recombination Regions

The main contenders for the causes of the reductions in variability and efficacy of selection with lower recombination rates are selective sweeps of favorable mutations (Maynard Smith and Haigh 1974) and BGS against deleterious mutations (Charlesworth et al. 1993). The relative importance of these in relation to patterns of variability has long been debated (Stephan 2010; Cutter and Payseur 2013). What light do our results shed on this question?

One explanation for the patterns shown in table 2 for the five NC regions is that a selective sweep has occurred recently in each of these regions. There are, however, some reasons for doubting this. Our coalescent simulations showed that a single catastrophic sweep is incompatible with the observed numbers of segregating sites and pairwise diversities in the NC regions (supplementary material S2, Supplementary Material online). This agrees with previous results on the dot chromosome of D. melanogaster and D. simulans (Jensen et al. 2002) and D. americana (Betancourt et al. 2009). A difficulty with this, however, is that four-gamete tests demonstrated recombination in our NC regions (table 5), similar to the results for the dot chromosome reported in the other studies just cited and in Arguello et al. (2010), and for other NC regions by Chan et al. (2012). These are presumably gene conversion events, because the mapping study of Comeron et al. (2012) suggests that these occur at much the same rate in NC regions as elsewhere in the genome, at an effective rate of about 3.2 × 10⁻⁵ per nucleotide site per generation after correcting for the absence of events in males. As shown in supplementary material S4, Supplementary Material online (see Selective sweeps at autosomal loci with gene conversion), this rate of recombination would require a selection coefficient for the sweeping mutations of about 0.0075 to be consistent with the observed reduction in variability in the NC regions, which is much larger than any estimate of s for positively selected mutations in D. melanogaster (Li and Stephan 2006; Andolfatto 2007; Jensen et al. 2008; Sella et al. 2009; Schneider et al. 2011); only the value estimated by Macpherson et al. (2007) for D. simulans is similar in magnitude. Soft sweeps would require even stronger selection (Hermisson and Pennings 2005).

Although this suggests that the sweep model is difficult to reconcile with the data, these arguments are not absolutely watertight. We also used the Fay and Wu (2000) test for the signature of selective sweeps in the presence of recombination; their H statistic measures an excess of high-frequency-derived variants, which should be present if recombination occurs during a sweep. There is no evidence for significantly negative H statistics in the NC regions (tables 1 and 2), whereas the bootstrap CIs for H for synonymous sites in the C regions are consistently negative (table 1; supplementary table S5 of supplementary material S1, Supplementary Material online), suggesting that selective sweeps have influenced patterns of variability in these regions, as argued by Langley et al. (2012). In addition, it is very unlikely that a multiple sweep model alone can account for the apparent severe reduction in the incidence of adaptive nonsynonymous substitutions in the NC regions, as shown in supplementary material S4, Supplementary Material online (see Can there be multiple sweeps in the autosomal NC regions?).

If sweeps are unlikely to explain the patterns of variability and reduced efficacy of selection in the NC regions, we need to ask whether BGS effects are sufficient to explain them. The classic BGS model with parameter values that are reasonable for Drosophila greatly overpredicts the reduction in diversity in NC regions (Loewe and Charlesworth 2007). However, a modification of this model, which includes HRI among the mutations involved (which weakens their effects on linked neutral variants), predicts a reduction in neutral variability on the NC genes that is close to the observed level, as well as strongly distorted neutral variant frequency spectra of the type found here and in other studies (Kaiser and Charlesworth 2009, figs. 1 and 2) (fig. 3).

These considerations leave open; however, the question of whether BGS reducing the fixation probabilities of favorable mutations is sufficient to explain the apparently low rate of adaptive evolution in NC and low crossover regions (table 4; fig. 4; supplementary table S5 of supplementary material S1, Supplementary Material online). Although models of the effects of deleterious mutations on the substitution rates of beneficial mutations in nonrecombining genomic regions have been analyzed previously (Orr and Kim 1998; Johnson and Barton 2002), these have not taken into account the wide distribution of fitness effects of deleterious mutations inferred in Drosophila (e.g., Kousathanas and Keightley 2013; supplementary table S4 of supplementary material S1, Supplementary Material online) and the effects of HRI among these mutations when recombination rates are very low. Further theoretical work is required to determine whether BGS in the NC and low recombination C regions is capable of reducing the level of adaptive evolution to the extent that is observed. In contrast, there seems to be little difficulty in accounting for the virtual absence of selection on CUB in NC regions by BGS, because such selection is known to be much weaker than that on nonsynonymous variants, so that even weakly deleterious nonsynonymous mutations can influence the fates of synonymous mutations that alter CUB (Zeng and Charlesworth 2010).

Differences between X Chromosomes and Autosomes with Respect to Patterns of Variability

There are several differences between the X chromosome and the autosomes in their patterns of variability that require explanation. First, the measures of the degree of distortion of the site frequency spectrum (SFS) at segregating synonymous sites in the C regions (Tajima’s D and the proportion of singletons) are consistently higher for the X than for the autosomes (table 1, fig. 4, and supplementary table S5 of supplementary material S1, Supplementary Material online); this is less clear for the noisier estimates for the NC regions (table 2).

Although there is an apparent difference between the X and A in the strength of selection on synonymous polymorphisms, due to selection on CUB, the analysis shown in table 4 of Campos et al. (2013) implies that this is relatively small (∼10% stronger for the X than A). In itself, this is insufficient to produce the observed difference in level of distortion of the synonymous SFS (supplementary material S4, Supplementary Material online: see Effects of weak selection on site frequency spectra). Similarly, although the GC content of the X chromosome is slightly higher than that of the autosomes (Campos et al. 2013) and could contribute to a difference in mutation rates due to mutational bias in favor of GC to AT mutations (Schrider et al. 2013), the magnitude of the difference is too small to have a major effect on patterns of variability. Furthermore, if synonymous diversity is plotted against GC content, X genes have higher π_S and higher skew (lower D_S and higher P_singS) than A for a given GC content (supplementary fig. S4 of supplementary material S3, Supplementary Material online). This suggests that additional factors are involved.

One possibility is that the greater prevalence of segregating inversions on the autosomes than the X chromosomes in African populations of D. melanogaster may have influenced their relative levels of diversity, because the sweep of a recently derived inversion to an intermediate frequency will tend to reduce diversity on the chromosome that carries it (Andolfatto 2001). The analysis of the DPGP data by Corbett-Detig and Hartl (2012) suggests, however, that the presence of inversions has a relatively small effect on diversity, so that they are unlikely to have much effect on the ratio of X diversity to A diversity. In addition, it is possible that the SFS could be affected by the presence of inversions. The common D. melanogaster inversions all seem to be of relatively recent origin and have had little time to accumulate new mutations (Corbett-Detig and Hartl 2012). This implies that the major effect of the presence of an inversion would have been to take an ancestral haplotype to an intermediate frequency; the inversion is most likely to capture intermediate frequency ancestral variants as opposed to rare variants and will therefore not have much effect in changing singletons to intermediate frequency variants. Singletons from sites that were segregating before the spread of the inversion will mostly be found only in the standard arrangement present in the sample, so the inversion effectively reduces the sample size. The proportion of such singletons would thus be increased by the presence of the inversion, because the expected proportion of singletons decreases with the sample size. It follows that the greater abundance of inversions on A versus X cannot explain the higher incidence of rare variants on the X chromosome.

The two processes that seem most likely to be important are changes in population size and hitchhiking effects. A full analysis of these would require extensive modeling efforts, which are beyond the scope of this article. We will, therefore, simply give a sketch of the possible contributions of these processes to the observed patterns. Our previous analysis of variability at 4-fold degenerate sites suggested a recent population expansion of about 4-fold (Campos et al. 2013, table 4), which is reasonably consistent with the values obtained from the DFE-alpha method (see column N₂ of supplementary table S4 of supplementary material S1, Supplementary Material online). However, as noted by Messer and Petrov (2013) and Zeng (2013), plausible models of hitchhiking effects can also produce distortions of the SFS at neutral or nearly neutral sites within genes that are similar to those produced by demographic changes, so that these estimates should be treated with some caution as indicators of a true effect of demography.

This raises the question of whether a purely demographic model could explain the difference in skew between X and A. It has been pointed out that genomic regions with different effective population sizes will respond differently to changes in population size that induce distortions in gene genealogies and hence in the SFS (Fay and Wu 1999; Hey and Harris 1999; Pool and Nielsen 2008). This effect arises because a genomic region with a longer mean pairwise coalescent time will have external branches that extend further back in time than those for a region with a lower mean coalescent time (which will be reflected in a lower π_S). Depending on the timing of a population expansion or contraction in relation to the present, a region with higher N_e could have either a greater or lesser degree of distortion than a region with a low N_e.

However, a key fact that requires explanation is that the relation between π_S and effective recombination rate for the X is much flatter than for the A, so that π_S for the X is greater than that for the A for recombination rates somewhat below 1 cM/Mb, and smaller when recombination rates are higher (fig. 2 of Campos et al. 2013; fig. 4). Because π_S is a measure of the mean pairwise coalescent time, a purely demographic explanation of the type just outlined is inadequate to explain the fact that P_singS and D_S are consistently higher for the X than for the A across all effective recombination rates. It follows that hitchhiking effects must be involved. Recurrent selective sweeps can produce substantial skews in the SFS, but also reduce neutral diversity by at least as much (e.g., Braverman et al. 1995). It is therefore impossible to explain the X/A difference in skew purely in terms of the higher incidence of adaptive fixations of nonsynonymous mutations on the X (discussed later), given that this occurs even in the low recombination C regions, where (as noted earlier) π_S for X is greater than for A for similar effective recombination rates (i.e., despite α and ω_α being higher on the X, π_S is still higher in the low crossing over regions of X than A).

It therefore seems necessary to invoke both BGS and/or demographic effects, as well as selective sweeps. For a given effective recombination rate, a higher incidence of sweeps on the X associated with its higher α and ω_α values might be expected to reduce π_S below three-quarters of the value for the A, the value expected when there are equal variances in reproductive success of males and females and equal effects of BGS on X and A (Wright 1931). Instead, the X/A ratio for π_S for a given rate of crossing over is either approximately ¾ or greater (Campos et al. 2013, fig. 2). This suggests that a greater variance of male reproductive success (Vicoso and Charlesworth 2009), possibly combined with the overall weaker expected effect of BGS on the X compared with the A (Charlesworth 2012), could counteract the effect on π_S of more sweeps on the X than the A, whereas selective sweeps nevertheless cause a larger skew in the SFS.

In addition, a possible explanation for the rather flat relation between π_S and recombination rate for X compared with A is provided by the difference in gene numbers and densities between the low recombination C regions of the X and A; the two lowest recombination bins for the A contain a mean of 567 genes with an average density of 77.6 genes/Mb, compared with a value of 163 genes with a density of 51.8 for the X. A similar pattern applies to the NC regions (table 2), where the X also shows a much higher value of π_S than the mean for the A. Because BGS effects are expected to be smaller when the number of genes in a low recombination region is lower (Kaiser and Charlesworth 2009), this difference is consistent with the change to an X/A ratio of π_S greater than 1 when the recombination rate is less than 1 cM/Mb and would accordingly make the relation between π_S and recombination rate flatter for the X than for the A. A similar apparent effect of gene density on diversity has been found in Arabidopsis (Kawabe et al. 2008), rice (Flowers et al. 2012) and humans (Gossmann et al. 2011).

Furthermore, the skew in the synonymous SFS is weakly negatively correlated with the recombination rate in the C regions of the X, as would be expected if hitchhiking effects diminish with increasing recombination (see P_singS and D_S in fig. 4), although there is an indication of an upturn at the highest recombination rates (the Loess plots in supplementary fig. S5 of supplementary material S3 and supplementary table S5 of supplementary material S1, Supplementary Material online). For the X, the correlation is significant on a gene by gene analysis using a Spearman’s rank correlation test (P_singS: ρ = – 0.13, P < 0.001 and D_S: ρ = 0.13, P < 0.001; supplementary fig. S5 of supplementary material S3, Supplementary Material online). In contrast, there is a small but significant positive correlation in AC regions for P_singS (ρ = 0.04, P < 0.001), probably reflecting the strong upturn for high AC values in this case (see the Loess plots in supplementary fig. S5 of supplementary material S3, Supplementary Material online; these also show a decline in the skew with recombination rate for AC genes at low to moderate recombination rates).

A demographic effect could contribute to the increase in skew at very high recombination rates, if there had been an increase in population size that ended in the fairly recent past. At the highest recombination rates for both X and A, the larger coalescent time means that a larger proportion of coalescent events occur during the growth phase and the preceding epoch with lower population size, and hence occur more rapidly at this time. This would cause more recent branches of the gene tree to be longer relative to the earlier ones, compared with the constant population size case. However, this effect would be smaller in genomic regions with shorter mean coalescent times, reducing the skew due to this effect, whereas hitchhiking effects become more important. With the appropriate balance of forces, a net increase in skew would occur only at high recombination rates and hence mean coalescent times, as seen in supplementary figure S5 of supplementary material S3, Supplementary Material online (note the upturn at the end of the Loess plots for both AC and XC). When the recombination rate becomes small enough, the increased skew caused by BGS effects at very low recombination rates (Gordo et al. 2002; Kaiser and Charlesworth 2009; Seger et al. 2010) might overcome the reduced effects of both demography and selective sweeps (supplementary fig. S5 of supplementary material S3, Supplementary Material online).

Faster Adaptive Evolution on the X

Our analyses show clear evidence for a faster rate of evolution of protein sequences on the X relative to the A, as measured by K_A, K_A/K_S, α, and ω_α (fig. 4; supplementary table S5 of supplementary material S1, Supplementary Material online). This agrees qualitatively with the conclusions of Mackay et al. (2012) and Langley et al. (2012), using different methods and different populations of D. melanogaster and appears to validate the Faster-X hypothesis that has long been debated (Charlesworth et al. 1987; Meisel and Connallon 2013). This postulates that the exposure of recessive or partially recessive favorable X-linked mutations to selection in hemizygous males causes more rapid evolution, relative to mutations with comparable effects on autosomes.

Another possible cause of a Faster-X effect in D. melanogaster, however, is simply the larger overall effective population size of the X compared with the A—its overall higher effective recombination rate could reduce the intensity of HRI (Charlesworth 2012), allowing a faster rate of adaptive evolution. This possibility can be tested by examining the relevant statistics for the “overlap region” of the two compartments of the genome, where X and A genes have comparable effective recombination rates (supplementary table S7 of supplementary material S1, Supplementary Material online). These have been divided into three bins of recombination rates. In each bin, K_A, K_A/K_S, α, and ω_α are higher for the X than the A; this is also true for α and ω_α when using the overlap region obtained from the recombination estimates of Comeron et al. (2012). This fact appears to exclude a major contribution of recombination and hitchhiking to the Faster-X effect, although the X/A ratio of α decreases from 1.40 to 1.16, and that for ω_α from 1.88 to 1.44, between the low and high recombination bins, suggesting that hitchhiking effects may play some role.

Mackay et al. (2012) and Langley et al. (2012) found overall X/A ratios of α of about 4 and 3.6, respectively, which are much higher than our estimates, even those using the Fay et al. (2002) method that is closer to theirs (supplementary table S5 of supplementary material S1, Supplementary Material online). One possible reason for this difference is that the lowest two recombination bins of the autosomes contribute slightly more to the overall pattern for the A (20% of genes) than the X (17% of genes); they also have zero or negative α values on a McDonald–Kreitman 2 × 2 table approach, presumably reflecting the bias due to the inclusion of deleterious nonsynonymous variants mentioned earlier. Using a weighted average of α over all recombination bins, we get a higher X/A ratio for α using the Fay et al. (2002) method (2.1) than using DFE-alpha (1.6). It seems that not correcting properly for nonsynonymous slightly deleterious mutations affects the autosomes more than the X, due to their lower overall recombination rates. In addition, the Mackay et al. (2012) data come from a heavily bottlenecked population, with greatly reduced variability on the X relative to the A, which may well affect 2 × 2 table estimates of α.

Other factors than the dominance levels of favorable mutations could be involved in causing these X/A differences in α, such as differences in gene content between X and A (Hu et al. 2013). In addition, as pointed out to us by Chuck Langley, the greater prevalence of inversion polymorphisms on the autosomes than the X chromosome could cause a lower overall frequency of recombination on the autosomes, thereby reducing the rate of adaptive sequence evolution; this has not been taken into account in the above analysis of the effects of recombination. It is difficult to assess the importance of this factor, because (as noted earlier) the common polymorphic inversions in D. melanogaster are of relatively recent origin and have therefore had relatively little opportunity to influence the rates of adaptive divergence from its relatives. The same applies to the inversions that differentiate D. melanogaster and D. yakuba, which are predominantly autosomal (Lemeunier and Aulard 1992), and at one time must have been polymorphic in an ancestral population; the time that was available for these to affect rates of adaptive evolution while they were segregating is of course virtually unknowable.

Conclusions

All the evidence presented here on sequence divergence and polymorphism for five NC regions of D. melanogaster, and for crossover regions with different recombination rates, points at hitchhiking being the major cause of the reduction in diversity and efficacy of selection in genomic regions where recombination rates are very low. This supports the view that genetic recombination associated with sexual reproduction increases the efficiency of natural selection. Furthermore, it is hard to account for all features of the data in terms of selective sweeps alone, although they are probably involved in causing the higher degree of distortion of the site frequency spectra at synonymous sites on the X, as a result of its higher rate of adaptive nonsynonymous evolution. The results for very low recombination regions are consistent with a BGS model, where interference among selected sites reduces their overall effects on the behavior of linked variants. A past population expansion probably contributes to the increased patterns of distortion of site frequency spectra at high recombination rates.

Materials and Methods

Assembly and Data Filtering

We downloaded the raw reads of the DPGP2 data set (http://www.dpgp.org/dpgp2/DPGP2.html, last accessed December 25, 2012) for 17 alleles (RG18N, RG19, RG2, RG22, RG24, RG25, RG28, RG3, RG32N, RG33, RG34, RG36, RG38N, RG4N, RG5, RG7, and RG9) from the sample of D. melanogaster collected from Gikongoro, Rwanda (Pool et al. 2012). We selected the samples from the primary core with the lowest estimated levels of admixture from European populations (<3% admixture; see fig. 3B of Pool et al. 2012). We filtered the raw reads by trimming them with the script trim-fastq.pl, from the toolbox PoPoolation (Kofler et al. 2011), using a quality threshold of 20 and a minimum length of 76 nucleotides; we also excluded reads with Ns. The quality of the filtered reads for each allele was examined with FastQC (available at http://www.bioinformatics.babraham.ac.uk/projects/fastqc/, last accessed December 17, 2012).

We aligned and mapped the filtered reads to the reference sequence (r5.34, available on Flybase (http://flybase.org/, last accessed December 20, 2012) with BWA (Li and Durbin 2009), using the setting –n = 0.01 and the other default parameters to generate BAM files (Li et al. 2009) for each sample, as in Campos et al. (2012). We excluded reads with a mapping quality below 20. For comparison with BWA, we also used the Stampy software for mapping short reads from Illumina sequencing (Lunter and Goodson 2011; available at http://www.well.ox.ac.uk/project-stampy, last accessed December 20, 2012), which explicitly takes into account the expected divergence from the reference when calculating mapping qualities. We observed no differences between the results from these two software, so we opted to use BWA for the results described later.

For the rest of the pipeline, we used the Genome Analysis Toolkit (GATK) (DePristo et al. 2011), available at http://www.broadinstitute.org/gatk, last accessed December 20, 2012, to do multisample SNP calling. First, we performed local realignments around indels, because reads that align on the edges of indels often get mapped to mismatching bases that might look like evidence for SNPs. For SNP calling, we used the UnifiedGenotyper for haploid samples (parameter: sample_ploidy 1) and generated a multisample VCF file (Danecek et al. 2011). Subsequently, we performed variant quality score recalibration to separate true variation from machine artifacts (DePristo et al. 2011). The approach taken by variant quality score recalibration is to develop a continuous, covarying estimate of the relationship between SNP call annotations and the probability that an SNP is a true genetic variant versus a sequencing or data processing artifact (DePristo et al. 2011). This model is selected adaptively, using known SNPs provided as training sites, which are normally obtained from a database. Alternatively, it is possible to use high-confidence SNPs as a “known” set; for this purpose, we used biallelic SNPs detected at 4-fold sites at a frequency equal or higher than ten sequenced alleles out of 17. The model was built using the high-quality subset of the input variants and evaluated the model parameters over the full call set. We used as model parameters six SNP call annotations: QD, HaplotypeScore, MQRankSum, ReadPosRankSum, FS, and MQ, as suggested by GATK (see http://www.broadinstitute.org/gatk/; DePristo et al. 2011). The SNPs are allocated to tranches according to the recalibrated score that recovers a given cutoff for the true sites. We retained variants that passed a cutoff of 95%, that is, the variant score limit that recovers 95% of the variants in the true data set.

From the multisample recalibrated VCF file, we made a consensus sequence FASTA file for each individual using a custom Perl script. The variant calls that did not pass the filter were assumed to have the reference base pair at the sites in question. We masked any regions with admixture from European populations, using the coordinates reported by Pool et al. (2012). From the 95% quality filtered data set, we also produced a data set where the admixture regions were not masked to see whether the masking of these regions could bias the results.

Data Sets

Using the coding sequence coordinates of the genes used in Campos et al. (2012), we extracted their sequences and made FASTA alignments using the reference sequence of D. melanogaster and an orthologous outgroup sequence from D. yakuba. Details of the criteria used to obtain orthologous coding sequences are described in Campos et al. (2012). We removed genes that lacked adequate polymorphism data because of sequence masking that meant that we had no information for some alleles in the sample.

We partitioned the genome into two crossover regions, autosomal crossover genes (AC), and X chromosome crossover genes (XC), as well as five independent NC regions. The latter are denoted by N2, second chromosome; N3, 3rd chromosome; N4, 4th (dot) chromosome; NXc, X-chromosome genes located near the centromere; and NXt, X-chromosome genes located near the telomere. For one analysis, we also separated out the genes located in the alpha-heterochromatin, which constitutes the majority of the centromeric heterochromatin and consists mainly of highly repetitive tandem arrays (Miklos and Cotsell 1990). These genes are located in the “scaffold heterochromatin” (denoted in Flybase as: 2LHet, 2RHet, 3LHet, 3RHet, and XHet); they have been cytologically localized to the respective chromosome arms and are located proximal to the centromere relative to the beta-heterochromatin (the region adjacent to the euchromatin), which is highly enriched for transposable element derived sequences (Miklos and Cotsell 1990).

Summary Statistics for Diversity and Divergence

We assumed that segregating polymorphisms are biallelic. If there were more than two variants segregating at a site, we only considered the two most frequent alleles (<2% of polymorphic 4-fold sites had more than two alleles). For all analyses, we excluded sites with missing data (i.e., sites with <17 sequenced alleles), and sites that did not have an outgroup in D. yakuba. For estimating nucleotide site diversity values, we calculated the pairwise diversity measure π (Tajima 1983) and Watterson’s θ_w, which is based on the number of segregating sites (Watterson 1975). To measure the distortion of the SFS, we contrasted π and θ_w for a given class of sites using the D statistic of Tajima (1989). We used DnaSP (Librado and Rozas 2009) to calculate the significance of Tajima’s D at synonymous sites for each NC block by performing 1,000 coalescent simulations with a 0 recombination rate. However, it is likely that the proportion of singletons (P_singS) at synonymous sites is a more reliable measure of distortion than Tajima’s D for the purpose of comparing different genomic regions, because the latter is affected both by the numbers of sites in the sequences being compared and by their levels of variability (Tajima 1989), both of which differ between the X and autosomes, and between regions with different rates of crossing over (fig. 4). Some other difficulties with D and related statistics are discussed by Lohse and Kelleher (2009).

Let the SFS for a given class of sites be the vector {S_i}, where the element S_i (0 ≤ i ≤ n/2) is the fraction of sites with minor allele count i in a sample of n alleles from the population. π and θ_w per nucleotide site were calculated as follows:

(1)

(2)

To assign sites as synonymous and nonsynonymous and to estimate the nonsynonymous divergence and synonymous divergences, K_A and K_S, we used the method of Comeron (1995). We used the ratio of transitions (ts) and transversions (tv) (ts:tv = 0.58:0.42), obtained from the multiallele population genetics model of Zeng (2010, table 3). The method treats 0-fold sites as nonsynonymous, 4-fold sites as synonymous, and 2-fold sites are split into 2S-fold sites (where transitions are synonymous) and 2V-fold sites (where transversions are nonsynonymous). We used the reference genome of Drosophila melanogaster to classify each site. The overall estimates of the ratios π_A/π_S and K_A/ K_S were obtained by taking ratios of the respective mean values.

For each NC region, we estimated the statistic B that measures the ratio of N_e to its value in the absence of HRI (B, Loewe and Charlesworth 2007), using the ratio of the mean NC synonymous diversity for the regions to the mean synonymous diversity in the appropriate crossover genes; for the latter, we used the average π_S for AC for comparisons involving N2, N3, and N4, and the average π_S for XC for NXt and NXc. To test whether B is negatively correlated with the total amount of coding sequence within a NC region (L), we determined the total amount of base pairs in nonoverlapping coding sequence in each of the five NC regions from the reference genome sequence of D. melanogaster.

Confidence Intervals

To obtain 95% CIs for the mean values of our statistics, we analyzed the crossover regions gene by gene, using bootstrapping (the basic bootstrap method as implemented in the function boot.ci of R) across genes. We used also bootstrapping across genes to get the CIs for estimates of divergence in the NC regions. However, for polymorphism data, genes within a NC region cannot be treated as independent of each other, because of high linkage disequilibrium. We therefore concatenated the genes within each of our five independent NC regions and calculated the polymorphism summary statistics for each NC block. We calculated the variance and standard deviation of θ_w and π for each NC region using the (conservative) expressions for nonrecombining sequences given in Charlesworth B and Charlesworth D (2010, p. 212–213). We used the Delta method (Dorfman 1938) to calculate the standard deviation of the ratio statistics π_A/π_S and B (calculated as the ratio of the respective means) for each NC block. We obtained mean values over the five NC blocks and their 95% CIs by jackknifing (Sokal and Rohlf 2003, p. 820–823).

Rates of Adaptive Evolution

We calculated the proportion of nonsynonymous fixed differences between species due to adaptive substitutions (α) using within-species nucleotide polymorphism and between-species divergence data. To avoid potential biases in maximum likelihood estimates resulting from linkage disequilibrium in the NC regions, we used the method of moments estimator of α based on the McDonald–Kreitman test (Fay et al. 2002), implemented in the software MKtest (Welch 2006). We excluded singletons, because the presence of slightly deleterious mutations can bias such estimates of α downward (Charlesworth and Eyre-Walker 2008). We also calculated the rate of adaptive substitutions for nonsynonymous mutations relative to the ostensibly neutral mutations (ω_α) (Gossmann et al. 2010). For each set of genes we analyzed, ω_α was calculated as α × K_A/K_S, using the corresponding mean K_A/K_S. We obtained CIs for ω_α by sampling by bootstrap 1,000 replicates of mean α, K_A and K_S from which we calculated 1,000 ω_α values. We report its CI as the 2.5–97.5 percentiles of the distribution of bootstrapped ω_α values.

Inferring Derived Variants

To estimate the derived SFS (i.e., the unfolded SFS), we used an extension developed by Halligan et al. (2013) of the probabilistic approach of Schneider et al. (2011) for reconstructing the ancestral states of polymorphic sites and distinguishing between derived and ancestral variants (available at http://homepages.ed.ac.uk/eang33/, last accessed February 1, 2013). The method needs two outgroups, so we used D. simulans and D. yakuba.

This information was used as follows to determine the ratios of nonsynonymous to synonymous derived variants in different frequency classes, which provides an index of the extent of selection on nonsynonymous variants (Fay et al. 2002). From the derived SFS, we calculated the ratio of the number of nonsynonymous polymorphisms (per nonsynonymous site) to the number of synonymous polymorphisms (per synonymous site) for each category of the SFS. We reported the results after condensing the SFS into three frequency categories: 1 (singleton), 2–7 (intermediate frequency), and 8–16 (high frequency) derived mutations. We assessed whether there was a significant difference between crossover genes and NC genes from 2 × 2 contingency tables (crossover/NC genes against nonsynonymous/synonymous counts), using a Fisher's exact test for each of the three SFS categories. We controlled for the false discovery rate (FDR) by the method of Benjamini and Hochberg (1995), implemented in the package multtest (Pollard et al. 2005), with an FDR threshold of 0.05. From the derived SFS, we also calculated the Fay and Wu H statistic by calculating the difference between π and θ_H, an estimate of diversity that is weighted toward high-frequency-derived variants (Fay and Wu 2000); this provides a test for the signature of a recent selective sweep.

Recombination Detection

The minimum number of recombination events within each NC block was estimated by the R_h method of Myers and Griffiths (2003), using the RecMin software (http://www.stats.ox.ac.uk/∼myers/RecMin.html, last accessed March 15, 2013). The main objective was to elucidate if any recombination has occurred, not to estimate exact amounts of crossing over and gene conversion, which rely on likelihood methods that need a high amount of nucleotide variation to provide accurate estimates (McVean et al. 2002; Chan et al. 2012). This approach is not suitable for NC regions because they have very low diversity. We did not include nucleotide variation from noncoding regions within the NC parts, because these are enriched in repetitive and transposable elements, which are difficult to sequence and map accurately, so that our data set is limited in size for these regions.

BGS Model

As explained in detail in the supplementary material for Kaiser and Charlesworth (2009), a haploid model was used, where the selection coefficient, s, against a deleterious mutation at a site under selection was drawn from a log-normal distribution with a shape and location parameter of σ_g = 3.022 and µ_g = 0.0368, which correspond to the exponentials of the standard deviation and mean of ln(s), respectively. These were chosen to approximate the estimated mean selection coefficient for mutations that are segregating in a Drosophila population, when the population size is rescaled to 1.3 million from the 1,000 haploid individuals used in the simulations. The majority of selection coefficients with this distribution lie within the range for which BGS formulae are expected to apply, but this is somewhat stronger selection than is indicated by analyses of Drosophila polymorphism data, so that the reduction in intensity of BGS caused by HRI is probably somewhat underestimated (Kaiser and Charlesworth 2009). The mutation rate per site was set to a value that corresponds to 4N_eu = 0.0104 in the absence of BGS. The gene conversion rate was set to correspond to a value of 0.25 × 10⁻⁵ with an effective population size of 1.3 × 10⁶ and a tract length drawn from an exponential distribution with a mean of 352 bp, corresponding to the available information on Drosophila (Comeron et al. 2012).

Fit of a Selective Sweep Model

To investigate the fit of a hard selective sweep to the data, we performed coalescent simulations of a single catastrophic sweep with no recombination for each of the 5 NC regions, following Jensen et al. (2008) and Betancourt et al. (2009). Because the model assumes zero recombination, we also performed the same analysis for the three alpha-heterochromatin regions (chr2Het, chr3Het, and chrXHet) separately, because these genes are the most proximal to the centromere and thus less likely to have experienced any crossing over.

We compared simulated samples of alleles to each of the eight data sets (i.e., N2, N3, N4, NXc, NXt, chr2Het, chr3Het, and chrXHet), by comparing simulated versus observed values of S, the number of segregating sites, and k, the average pairwise differences between alleles. Observed values of synonymous site S and k were obtained from the concatenated data set for each class. To explore possible hitchhiking scenarios, two parameters were varied: 1) the level of neutral variation (θ₀) that would have been present in the absence of a sweep and 2) the time in the past (T, in units of 2N_e generations) since the simulated sweep occurred, with 50,000 replicates performed for each combination of θ₀ and T. Each simulation proceeds neutrally backward in time, according to a standard coalescent process, until time T, at which point all lineages are collapsed into one node, representing the effect of a selective sweep. A combination of θ₀ and T was considered to be compatible with the data if simulated values of the number of segregating sites (S) were equal to the observed S from the concatenated data, and the average number of pairwise differences between alleles (k) was within ±0.1 of the observed value, as in Betancourt et al. (2009). To estimate the amount of neutral variation in the NC regions in the absence of a sweep, we used the average θ_w in AC for N2, N3, N4, chr2Het, and chr3Het, and the average θ_w in XC for NXc, NXt, and chrXHet. Simulations were run using the computer resources of the Edinburgh Compute and Data Facility (http://www.ecdf.ed.ac.uk/, last accessed February 14, 2014).

Recombination Subregions

To test for evidence of associations between our variables of interest and the effective recombination rate, we divided the crossing over regions, AC and XC, into ten and six recombination bins, respectively. The recombination rate was estimated from the recombination rate calculator (Fiston-Lavier et al. 2010), and the effective rates are calculated by multiplying rates of crossing over in female meiosis by one-half for autosomes and two-thirds for the X chromosome, to take account of the amount of time a gene spends in males, which lack crossing over (as in Campos et al. 2013). We also made a similar data set using the recombination data of Comeron et al. (2012). For each gene, we obtained the map positions of its start, mid, and end coordinates. Because we were interested in the overall effects of recombination on the D. melanogaster genome, we fitted a Loess regression to the recombination rates along each chromosome (see supplementary fig. S6 of supplementary material S3, Supplementary Material online). We used this fit to determine the effective recombination rate for each gene from the value for its midco-ordinate.

For each of these regions, we calculated the same summary statistics as for AC and XC and determined the mean and its CI by bootstrapping. We also included Fop (the frequency of optimal codons), GC content in third codon sites (GC₃), GC content of short (<80 bp) introns (GC_I), and levels of gene expression (average log₂ RPKM across all developmental stages of D. melanogaster) in this analysis; for details of how these variables were obtained, see Campos et al. (2012, 2013). For each chromosomal data set type (autosomal and X), we tested whether each variable correlated significantly with the effective recombination rate using Spearman’s rank correlations. We performed the same analysis for the overlap region, the chromosomal regions that have comparable effective recombination rates between A and X (Campos et al. 2013). We divided the overlap region of A and X into three bins of recombination: high (1.75–2 cM/Mb), intermediate (1.40–1.75 cM/Mb), and low (1–1.40 cM/Mb). We did the same using the effective recombination rates of Comeron et al. (2012).

To calculate α, ω_α, and the proportion of nearly neutral mutations for each crossing over bin, we used the software DFE-alpha (available online at http://homepages.ed.ac.uk/eang33/, last accessed April 20, 2013). This program uses the maximum likelihood approach of Eyre-Walker and Keightley (2009) to infer the DFEs of new mutations in a selected class. The method assumes two classes of sites, one neutral (synonymous) and one selected (nonsynonymous) and contrasts SFSs of the two classes. It fits a gamma distribution to the DFE with parameters β (shape) and E(s) (mean), s being the selection coefficient for deleterious mutations in homozygotes. From the DFE distribution, it calculated the proportion of mutations in four ranges of N_es: 0–1 (nearly neutral), 1–10, 10–100, and >100 (strongly deleterious), α and ω_α. We used a demographic model whereby the population at initial size N₁ (set to 100) experiences a step change to N₂, t generations in the past. For each bin, we pooled all genes into a synonymous and nonsynonymous SFS and run several times DFE-alpha to check for convergence of parameters. We obtained CI by bootstrapping across genes (1,000 replicates) and report the CI as the 2.5–97.5 percentiles of the distribution of bootstrapped values.

To see whether the selected outgroup (D. yakuba) affected our estimates of α from the DFE, we used D. simulans as an alternative outgroup, using the same orthologous genes as those in Campos et al. (2012) (supplementary fig. S3 of supplementary material S3). However, we have focused our analyses on D. yakuba because there is less chance of ancestral polymorphism, and the reference genome of D. yakuba is of better quality (Clark et al. 2007).

Supplementary Material

Supplementary materials S1–S4 are available at Molecular Biology and Evolution online (http://www.mbe.oxfordjournals.org/).