Abstract
Studies of macromolecular crowding have shown its important effects on molecular transport and interactions in living cells. Less clear is the effect of crowding when its influence is incorporated into a complex network of interactions. Here, we explore the effects of crowding in the cell nucleus on a model of gene transcription as a network of reactions involving transcription factors, RNA polymerases, and DNA binding sites for these proteins. The novelty of our approach is that we determine the effects of crowding on the rates of these reactions using Brownian dynamics and Monte Carlo simulations, allowing us to integrate molecular-scale information, such as the shapes and sizes of each molecular species, into the rate equations of the model. The steady-state cytoplasmic mRNA concentration shows several regimes with qualitatively different dependences on the volume fraction, ϕ, of crowding agents in the nucleus, including a broad range of parameter values where it depends nonmonotonically on ϕ, with maximum mRNA production occurring at a physiologically relevant value. The extent of this crowding dependence can be modulated by a variety of means, suggesting that the transcriptional output of a gene can be regulated jointly by the local level of macromolecular crowding in the nucleus, together with the local concentrations of polymerases and DNA-binding proteins, as well as other properties of the gene’s physical environment.
Introduction
Systems biology aims to understand cellular processes in terms of networks of interactions among molecules. Ideally, this view of biology would be global and yet still rest on a solid reductionist foundation, since each node of a network would represent a chemical reaction that could be isolated and studied in detail. However, it should be appreciated that this basic framework does not fully capture the complexities of life. The reaction represented by each node in a network may, for example, be influenced by the physical environment of some part of the cell.
One form of such a physical influence has received a great deal of attention from theorists and experimentalists alike: macromolecular crowding (1). The crowded nature of cellular environments exerts an important influence on the thermodynamics and kinetics of reactions. The free energy, as well as the rates (2–4), of a reaction will depend on the overall concentration of molecules; these could then play an important role as crowding agents even if they have no specific role in the reaction. Much work has been done to understand the influence of macromolecular crowding on specific types of processes, such as protein-protein binding (5), protein folding and stability (6), and chromatin compaction (7,8). However, little is known about the global influence of crowding on the scale of networks of interactions. From the theoretical side, an important first step in this direction was taken by Morelli et al. (9), who incorporated the influence of crowding on the rates of reactions into simple gene regulatory networks and found that the level of crowding had an important effect on steady-state protein concentrations.
In this work, we study a more complicated model of gene expression, incorporating the fact that in eukaryotes, RNA polymerase is recruited to a gene promoter via its interactions with transcription factors. We explicitly take into account the movement of DNA-binding proteins by the mechanism of facilitated diffusion (10), whereby molecules undergo free diffusion interspersed with periods of one-dimensional diffusion that occurs while the molecule is nonspecifically bound to DNA. Of most importance, we determine the effects of macromolecular crowding on the reaction rates in the model based on explicit assumptions about molecular shapes and sizes. Specifically, the effects of crowding on the diffusion coefficients of molecules are established using Brownian dynamics (BD)simulations, and the crowding-induced contributions to the binding free energies between molecules are calculated from Monte Carlo simulations. We solve the reaction-rate equations of the model in the steady state, including the dependence of the reaction rates on the volume fraction, ϕ, of crowders as determined from the simulations, and explore the effect of crowding in the cell nucleus on the steady-state concentration of cytoplasmic mRNA (see Fig. 1 for an illustration of our approach). Our incorporation of molecular-scale simulation results into the model allows us to correctly assess the order of magnitude of macromolecular crowding effects.
Figure 1.
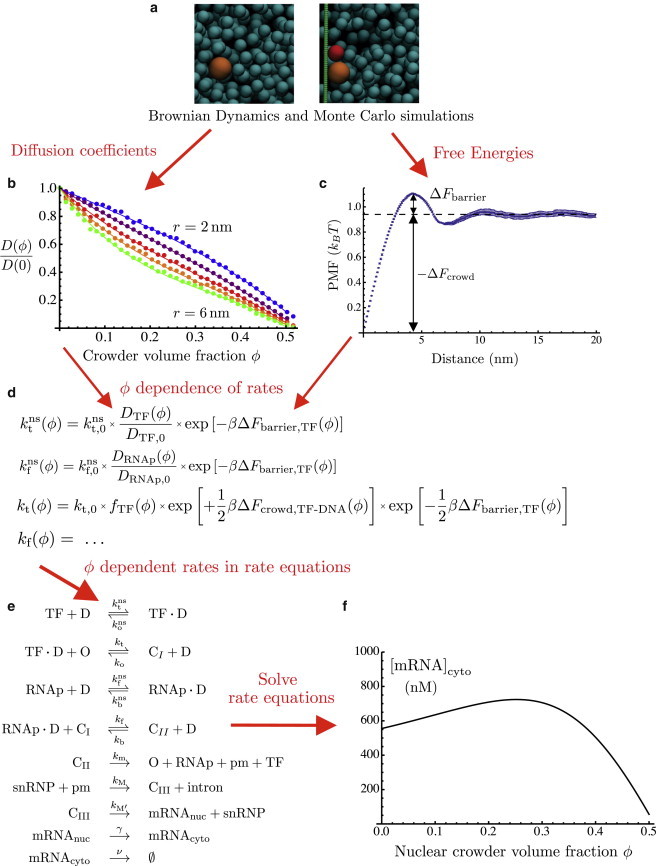
Reaction network model of gene expression incorporating molecular simulation data. (a) Representative snapshots of BD (left) and Monte Carlo (right) simulations used to determine diffusion coefficients and free energies, respectively. TF, RNAp, and DNA are represented in red, orange, and green, respectively. Snapshots were made using VMD (34). (b) Normalized diffusion coefficients calculated from BD simulations. (c) Potential of mean force between TF and DNA, calculated from Monte Carlo simulations at nuclear crowder volume fraction . (d) Representative formulas showing the dependence of reaction rates on the volume fraction, ϕ, of crowders in the nucleus. (e) Reactions in the model of gene expression. (f) Representative plot of nuclear crowder volume fraction dependence of steady-state cytoplasmic mRNA concentration. To see this figure in color, go online.
We show that there are several regimes of nuclear crowding dependence of steady-state cytoplasmic mRNA concentration, depending on the concentrations of the reactants as well as other parameters of the system, such as specific or nonspecific protein-DNA binding affinities. In many cases, we have found that the mRNA levels depend nonmonotonically on the volume fraction, ϕ, of crowders in the nucleus, reaching a maximum at physiologically relevant values near . This dependence may be accentuated by several means, for example, by decreasing the concentrations of the reactants or by increasing the binding affinity of nonspecific protein-DNA binding. The picture that emerges is one in which concentrations of transcription factors, polymerases, and active gene promoters, combined with the overall level of macromolecular crowding, may exert a quantitatively significant and qualitatively nontrivial influence on the level of expression of genes, with potentially important implications for the regulation of gene expression. In particular, the joint dependence of mRNA output on the level of nuclear crowding and the concentrations of transcription factors and RNA polymerases suggests that in the spatially nonuniform cell nucleus, genes in different locations will experience different effects of macromolecular crowding.
Model
The physical modeling of gene regulatory systems as networks of chemical reactions (11) has reached the stage where it is not out of the question to make quantitative comparisons with experiments, at least in the case of bacterial systems (12). As these comparisons become more common it will be increasingly important to incorporate into these models the influence of physical environments occurring in vivo rather than in vitro. In this regard, a key step was taken by Morelli et al. (9) when they considered simple models of gene regulatory networks, taking into account the influence of macromolecular crowding on the reaction rates. Here, we develop a multiscale model of gene expression involving multiple molecular binding events and incorporating microscopic information on the kinetic and thermodynamic effects of crowding. To approach the problem of gene regulation in eukaryotes, where gene regulation involves numerous combinatorial interactions of proteins (13), our model includes both transcription factors and RNA polymerases. The most important element of our approach is our molecular-level treatment of the crowding dependence of the reaction rates. The extent to which crowding slows down diffusion, as well as the way it induces entropic interactions between reactants, is determined from molecular simulations using a simple but consistent choice of shapes and sizes for each molecular species. The overall approach, in which molecular simulations provide the crowding dependence of the parameters in a set of rate equations, is illustrated in Fig. 1.
Rate equations and their steady-state solution
The system of reactions shown in Fig. 1 e summarizes the model considered here. In this section, we set out the steady-state equations for these reactions. Molecular-level formulas for the reaction rates will be given in the next section and will allow us to incorporate the effects of macromolecular crowding in the nucleus.
The first two reactions in Fig. 1 e represent so-called facilitated diffusion (10). Freely diffusing transcription factors (TFs) may bind transiently and nonspecifically to DNA. While a transcription factor is nonspecifically bound, it diffuses along DNA and may encounter its binding site (O) at a gene promoter, forming a complex we will call CI. In a similar way, RNA polymerase (RNAp) binds nonspecifically to DNA and specifically to CI; that is, the TF recruits RNAp to the promoter, forming a transcription-ready complex we call CII. The reactions thus far are all reversible. A transcription-ready complex CII may then undergo transcription initiation with a certain probability, freeing the O, TF, and RNAp and giving rise to a pre-mRNA (pm). The pm undergoes splicing, where it reacts with a small nuclear ribonucleic particle (snRNP) to form Complex III (CIII), and an intron, having been spliced out, is released. Further mRNA processing steps are represented by a reaction in which CIII gives rise to an mRNA molecule in the nucleus (mRNAnuc) as well as the released snRNP. The two final reactions represent the export of mRNA from the nucleus and its degradation in the cytoplasm.
We note that all the steps after the formation of Complex II are modeled as being irreversible. As a consequence, the details of these steps will have no influence on the steady-state level of mRNA production. Indeed, in the steady state,
| (1) |
and if we wish to calculate the steady-state concentration of mRNA in the cytoplasm, we need only find the concentration of CII:
| (2) |
Furthermore, the steady-state flux of mRNA into the cytoplasm is simply
| (3) |
The steady-state concentration of complex CII can be obtained by numerically solving the coupled equations
| (4) |
| (5) |
To do so, however, the quantities [O], [TF · D], and [RNAp · D] must first be given in terms of the concentrations of complexes CI and CII:
The latter two expressions are derived from the steady-state solutions of the reaction-rate equations for the concentrations of and , respectively. They make use of the total concentrations , , and , as well as dissociation constants for nonspecific binding. In deriving them, we have made the assumption that the total concentration of DNA basepairs is very large compared to the concentration of TF, so that we will always have .
To summarize, solving Eqs. 4 and 5 gives us the concentration of transcription-ready complexes CII. We may then use Eq. 2 to compute the concentration of cytoplasmic mRNA or Eq. 3 to compute the rate of mRNA export to the cytoplasm. Having now determined the level of mRNA expression in terms of the reaction rates, our next goal is to use molecular-scale expressions for these rates to incorporate the influence of macromolecular crowding.
Reaction rates: facilitated diffusion
Macromolecular crowding and other molecular-scale physics enter into the model via the reaction rates. In this section, we use the microscopic theory of facilitated diffusion developed by Berg and co-workers (10,14,15) to give expressions for the reaction rates of specific and nonspecific binding processes involving TFs and RNAps. We do not concern ourselves with the rates of the irreversible reactions after pm production, such as splicing and mRNA export, since they do not influence the steady-state results. It is important to keep in mind, however, that they are crucial for determining the dynamics and temporal correlations of the mRNA output (16), which is not a subject of study in this work.
Assuming that nonspecific binding of TF and RNAp to DNA is diffusion-limited, we use for forward rates and the expression (10,14,15)
| (6) |
These rates depend on the diffusion coefficients and of TF and RNAp, as well as on three length scales, l, b, and ξ. These are, respectively, the length along the DNA of one basepair, the radius of the DNA molecule (viewed as an approximate cylinder), and a correlation length giving the characteristic distance between DNA strands.
The nonspecific dissociation rates follow from the dissociation constants for nonspecific binding, called and :
| (7) |
The association rate constants for specific binding of TF and RNAp are given by the expression derived by Berg et al. (10) for specific protein-DNA binding by facilitated diffusion:
| (8) |
Here, and are the one-dimensional diffusion coefficients of TF and RNAp when these are nonspecifically bound to DNA, and L is one-half of the total length of DNA in the nucleus. The factor V, representing the volume of the nucleus, does not appear in the expression of Berg et al. (10). This is due to the fact that in the reaction equations (Eqs. 4 and 5), we take the forward rates to multiply the product of the volume densities (concentrations) of both reagents in such a way that the association rate constants have the usual dimensions of concentration−1 × time−1.
The backward rates for specific binding are determined from (10)
| (9) |
The formulas for the reaction rates given in this section depend on a number of parameters, such as the diffusion coefficients of molecules and their binding affinities, given by dissociation constants. Section 1 of the Supporting Material gives a complete description of all of our choices of the numerical values of these parameters. The resulting numerical values of the reaction rates, which we will use throughout this article unless otherwise mentioned, are given in Table 1. These rates are computed assuming dilute (nuclear crowder volume fraction ) conditions. In the next section, we will see how the level of crowding influences the kinetics and thermodynamics of the reactions in our model.
Table 1.
Numerical values of model parameters.
| Parameter | Description | Value (with ) |
|---|---|---|
| Association rate constant for nonspecific TF-DNA binding | ||
| Association rate constant for nonspecific RNAp-DNA binding | ||
| TF-DNA nonspecific dissociation rate | ||
| RNAp-DNA nonspecific dissociation rate | ||
| Dissociation constant for nonspecific TF-DNA binding | mM | |
| Dissociation constant for nonspecific RNAp-DNA binding | mM | |
| Association rate constant for TF-promoter (O) binding | ||
| Association rate constant for RNAp-Complex I binding | ||
| TF-promoter (O) dissociation rate | ||
| RNAp-Complex I dissociation rate | ||
| Dissociation constant for TF-O (promoter) binding | nM | |
| Dissociation constant for RNAp-O (promoter) binding | nM | |
| Rate of pre-mRNA production | ||
| γ | Nuclear export rate of mRNA | |
| ν | mRNA degradation rate | |
| Total concentration of TF | 30 nM | |
| Total concentration of RNAp | 30 nM | |
| Total concentration of O (promoters) | 30 nM | |
| Total concentration of DNA basepairs | 20 mM |
The values given here correspond to the values used in this article unless otherwise stated. See Supporting Material for all details regarding the choice of values.
Dependence of rates on nuclear crowding level
We now consider the effects of nuclear crowding on the rates of specific and nonspecific binding. It is at this level that microscopic details such as molecular geometries, interactions, and diffusion coefficients enter into our model (see Fig. 1, b–d). Motivated by experimental studies showing dramatic nanostructural differences between the nuclei of cells modeling different stages of carcinogenesis (17), we consider changes in the level of crowding specifically in the cell nucleus.
Consider, for example, the first reaction in Fig. 1 e, namely, the nonspecific binding of a TF to DNA, with forward rate constant and backward rate . Changing the level of crowding affects these rates in several ways (1). First, the reaction rates are reduced because of slower diffusion in a crowded medium. Second, the binding of TF to DNA is enhanced; these two objects have lower excluded volume when in contact than they do when apart, giving rise to an attractive depletion interaction of entropic origin. Finally, the same entropic interaction induces a kinetic barrier (see Fig. 1 c) that must be overcome for association or dissociation to proceed. Each of these effects depends on the geometries of the molecules involved, including the crowders. We model RNAps as spheres of radius 5.4 nm, TFs as spheres of radius 4.0 nm, DNA as a cylinder of radius 1 nm, and the crowding agents (crowders) as spheres of radius 3.0 nm. The crowders represent the proteins found in the nucleus, assuming an average molecular mass of 67.7 kDa (18); together with a typical partial specific volume of 0.73 mL/g, this leads to our choice of radius for the spherical crowders.
The reaction rates are proportional to the diffusion coefficients of the TF or RNAp (see Eq. 6). We performed BD simulations of spherical tracer particles of various sizes diffusing among spherical crowders of radius 3 nm (Fig. 1 a, left). These simulations are described in detail in the Supporting Material (see Fig. 1 b for results). They yield the factor by which the diffusion coefficient of a tracer molecule is reduced by the presence of a volume fraction, ϕ, of crowders:
| (10) |
where r is the radius of the diffusing tracer particle (TF or polymerase). These functions are well fit by cubic polynomials in ϕ, the coefficients of which are given in Table S1 of the Supporting Material.
The influence of crowding on the equilibrium of each binding reaction is determined by the contribution of crowding to the free energy of binding,
| (11) |
The dissociation constant, , of a reaction by definition varies exponentially with the free energy change. Therefore,
| (12) |
We calculate the crowding-induced contribution, , to the binding free energy using Monte Carlo simulations (Fig. 1 a, right; see Supporting Material) in which all the reactants interact via excluded volume. The molecular geometries are as described above, although the DNA (a cylinder of radius 1 nm) is here approximated by a row of overlapping spheres of radius 1 nm, each a distance of 1 nm from the next. From these simulations we obtain the crowder-mediated potential of mean force (PMF) acting between the reactants; an example is shown for TF-DNA binding in Fig. 1 c, which shows how , as well as the crowding-induced free-energy barrier to association, , are obtained from the PMF. It was convenient to perform simulations of dissociation rather than association; the fact that the PMF increases as the TF and DNA are pulled apart is a manifestation of the attractive nature of the depletion interaction. When the molecules are in contact, their excluded-volume regions overlap, so that a larger set of positions is available for the crowders, leading to an entropic attraction between the TF and the DNA. The crowding-induced contribution to the free energy of TF binding to DNA is shown in Fig. S2. Likewise, we have performed simulations to calculate the crowding-induced free energy differences occurring upon RNAp-D binding. From the point of view of excluded volume, there is no difference between binding of a TF to specific or nonspecific DNA. However, there is an interesting effect of crowding in the case of specific binding of RNAp. As nonspecifically bound RNAp slides along DNA and comes into contact with a TF, there is a change in excluded volume, leading to a crowding dependence of the strength of specific binding of RNAp to form complex CII. We have also calculated this free-energy change and the associated free-energy barrier. All crowding-induced free energies, as well as the barriers to association, are well fit by polynomial functions of the volume fraction, ϕ, of crowders (see the Supporting Material).
Based on Eqs. 6 and 10, the full dependence of the rates of nonspecific binding on crowding are now given by
| (13) |
| (14) |
The nonspecific dissociation rates are equal to the association rates multiplied by the appropriate equilibrium dissociation constants (Eq. 7), which themselves depend on ϕ (see Eq. 12).
| (15) |
| (16) |
The microscopic mechanism of facilitated diffusion leads to a complex crowding dependence on the rates of specific association and dissociation. According to Eq. 8, the association rate constants for specific binding depend on ϕ through two sources: the one-dimensional diffusion coefficients, , and the square root of the nonspecific dissociation rates, themselves highly ϕ-dependent, as shown above. We make the plausible assumption that crowding slows one-dimensional diffusion by the same factor as for three-dimensional diffusion. This assumption would be seriously violated if the diffusing objects were much smaller than the crowders; rather, they are larger. Thus,
| (17) |
| (18) |
and
| (19) |
Here we have introduced the aforementioned free-energy barrier that must be overcome as RNAp slides along DNA toward TF (that is, toward a CI complex). Note that the dependence due to the free-energy changes appears under a square root (hence the factors of ), whereas the dependence due to the factors f does not. This is because the f factors influence the overall specific binding rate through both the one-dimensional diffusion coefficient and the nonspecific dissociation rate (see Eq. 8).
The rates of nonspecific dissociation are the last ones whose ϕ dependence we must determine. From Eq. 9,
| (20) |
On the other hand, specific binding of RNAp to Complex I involves bringing RNAp into contact with TF while sliding along the DNA. This brings about a change in excluded volume and therefore a crowding-induced free-energy change, as well as a free-energy barrier.
| (21) |
In view of Eqs. 2 and 3 for steady-state cytoplasmic mRNA concentration and production rate, respectively, it now remains only to determine the ϕ dependence of the transcription rate, , and the mRNA degradation rate, ν. Each of these processes is of course composed of many complicated subprocesses, as well as being driven by energy consumption. We assume that the rates of these processes are independent of the crowder volume fraction, ϕ, occurring in the nucleus:
In particular, since we are interested in understanding the effects of changes in the level of crowding specifically in the nucleus, the lack of ϕ independence of ν reflects the fact that mRNA degradation occurs in the cytoplasm. We now have the complete ϕ dependence of the reaction rates needed to calculate the mRNA production level. These dependences involve the effects of slowed diffusion, which we have determined from BD simulations, as well as the crowding-induced free-energy changes, which we have calculated using Monte Carlo simulations. All of these simulations, as well as their quantitative results, are summarized in the Supporting Material.
Results
Equations 4 and 5 were solved numerically, taking into account the previous section’s ϕ dependences of the reaction rates, as well as the parameter values from Table 1. Equation 2 then gives the steady-state cytoplasmic mRNA concentration (Fig. 2, solid black curve). The cytoplasmic mRNA level shows a distinctly nonmonotonic dependence on the volume fraction, ϕ, of crowders in the nucleus, with a maximum near , a physiologically relevant value. The figure also shows cytoplasmic mRNA concentrations as a function of ϕ for larger values (10 nM and 100 nM) of the dissociation constant for specific binding of RNAp to CI. This corresponds to weaker binding, resulting in a lower overall concentration of complex CII and therefore of mRNA. With weaker RNAp binding, the maximum level mRNA production occurs at higher volume fractions.
Figure 2.
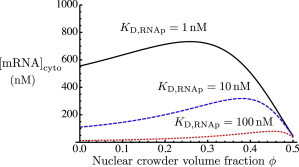
Steady-state mRNA concentration as a function of the crowder volume fraction, ϕ, in the nucleus. This is shown for three different values of the dissociation constant of RNAp binding to CI. To see this figure in color, go online.
As the volume fraction ϕ of crowders is increased, the affinities of protein-DNA and protein-protein interactions are enhanced due to the fact that a bound complex has lower excluded volume than free reactants. Thus, if the states of binding of the proteins (TF and RNAp) were at equilibrium, the concentration of complex CII would increase monotonically with the level of crowding. This is illustrated in Fig. 3, which shows the steady-state cytoplasmic mRNA level as a function of ϕ for small values of the transcription rate . For comparison these quantities are shown normalized by their values at . In the limit of very small transcription rates , we see the monotonic behavior expected at equilibrium, solely due to the enhancement of binding. Only at very high volume fractions, near , where the diffusion coefficients vanish (see Fig. 1 b), does the mRNA production decrease. This highlights the role of the driven, irreversible process of transcription, whose rate is , in keeping the system out of equilibrium and thus allowing the mRNA production level to depend on the kinetics of diffusion, which slows down as a function of ϕ. Thus, the nonmonotonicity of mRNA concentration as a function of crowder volume fraction, ϕ, is a consequence of the competition of enhanced binding (essentially an equilibrium effect) with the slowing down of diffusion.
Figure 3.
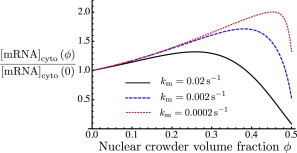
Effect of varying transcription rate . The plot shows the fold change in steady-state mRNA concentration as a function of the crowder volume fraction, ϕ, in the nucleus compared to the mRNA concentration at zero crowding. This quantity is shown for three different values of . To see this figure in color, go online.
The extent of this nonmonotonicity can be modulated by changing various parameters of the system. Fig. 4 shows that the nonmonotonic dependence on ϕ becomes even more pronounced if the reactants (TF, RNAp, and O) are present in smaller concentrations of the order of 3 nM or 0.3 nM, rather than 30 nM. This corresponds to thousands or hundreds of molecules per nucleus, rather than tens of thousands. Fig. 5 shows the effects of lowering the reactant concentrations on the various populations of TFs: free, nonspecifically bound, specifically bound to promoters (CI), and bound in transcription-ready complexes (CII). This is shown for large reactant concentrations (30 nM; Fig. 5, upper) and for lower concentrations (3 nM; Fig. 5, lower). In both cases, free TFs make up a very small fraction of the total; moreover, this fraction decreases as a function of crowding due to the enhancement of binding. However, in the case of high concentrations, the fraction of TFs bound in transcription-ready CII complexes is much larger. For this reason, the decrease in freely diffusing TFs contributes little to the concentration of CII (and hence to the mRNA level). In contrast, in the case of low reactant concentrations (Fig. 5, lower), the concentration of CII is very small, comparable to that of free TFs. As ϕ increases, the decreasing level of free TFs therefore contributes more significantly to the fraction of CII and hence to the cytoplasmic mRNA level.
Figure 4.
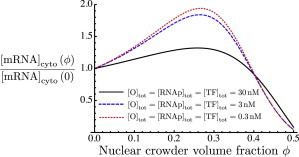
Fold change in steady-state mRNA concentration as a function of the crowder volume fraction, ϕ, in the nucleus, compared to the mRNA concentration at zero crowding. Total concentrations of TF, RNAp, and O are equal to 30 nM (black solid curve), 3 nM (blue dashed curve), and 0.3 nm (red dotted curve). The zero-crowding mRNA concentrations for these three cases are 555.2 nM, 2.9 nM, and 0.004 nM, respectively. To see this figure in color, go online.
Figure 5.
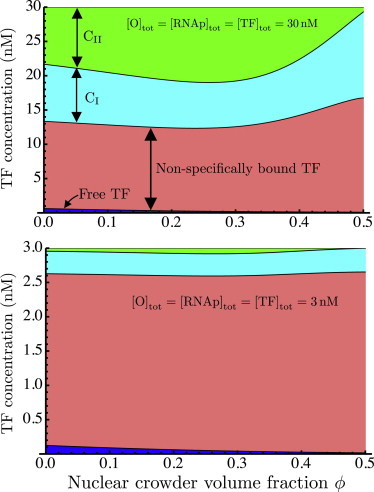
Breakdown of total concentration of transcription factors (TF) into subpopulations of TFs that are free (blue), nonspecifically bound to DNA (pink), specifically bound (complex CI; cyan), and bound in transcription-read complexes CII (green). This is shown for two different sets of reactant concentrations. (Upper) Reactant concentrations of 30 nM. (Lower) Reactant concentrations of 3 nM. Note the different y axis scales in the two plots. To see this figure in color, go online.
Fig. 6 shows another way in which the dependence of mRNA levels on crowding may be modulated, namely, by changing the strength of the nonspecific protein-DNA association. For the sake of comparison, the cytoplasmic mRNA concentration is plotted relative to its value at for values of the nonspecific dissociation constant both larger (10 mM) and smaller (0.1 mM) than that considered previously. Weaker nonspecific binding (a larger dissociation constant) gives rise to a much weaker ϕ dependence of the mRNA output, whereas stronger nonspecific binding (still much weaker than the specific binding) yields a much more prominent maximum in the mRNA level as a function of crowding. Thus, we find that the strength of this ϕ dependence may be modulated by changes in a variety of quantities, such as concentrations and binding affinities. In reality, these might correspond to changes in local physical conditions surrounding a given gene.
Figure 6.
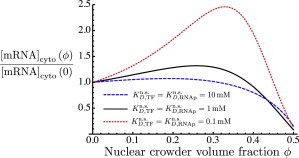
Effect of varying the strength of nonspecific protein-DNA binding is shown in plots of the fold change in steady-state mRNA concentration as a function of the nuclear crowder volume fraction, ϕ, for three different values of the dissociation constant for nonspecific protein-DNA binding. To see this figure in color, go online.
Discussion
In this work, we have used molecular-scale simulations to incorporate the effects of macromolecular crowding into a model of gene transcription as a network of chemical reactions. We made explicit and consistent choices of molecular geometries in determining the effects of crowding on the diffusion coefficients and the binding free energies of all molecular species. The dependence of the diffusion constants on the volume fraction, ϕ, of spherical crowders was determined through BD simulations, whereas the crowding contributions to the free energies of binding were calculated from Monte Carlo simulations. These results were incorporated into expressions for the rates of specific and nonspecific binding involved in the facilitated diffusion of DNA-binding proteins (10). The importance of making a consistent choice of molecular shapes and sizes can be seen from our estimates of , the contribution of crowding to the binding free energy, compared to that used by Morelli et al. (9) in their treatment of crowding effects on TF binding (see Fig. 7). In effect, they assumed that the chemical potentials of all molecular species have the same quantitative dependence on the level of crowding. In a bimolecular association reaction, this corresponds to a very large difference in excluded volume between the free and bound states, equal to the entire excluded volume of a reactant. In contrast, if molecules stick together upon binding, the change in their excluded volume is small compared to the total excluded volume of a molecule. The result is that our crowding-induced free energies are much smaller than those of Morelli et al. (9), showing the importance of a consistent treatment of molecular geometries.
Figure 7.
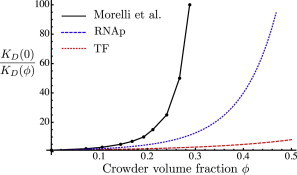
Crowding dependence of the inverse of the dissociation constant. The black solid curve represents data from Morelli et al. (9), relating their parameter Γ to the volume fraction, ϕ, of crowders. For this conversion we took a specific volume of 0.96 mL/g used by Minton (27) to fit the osmotic pressure of hemoglobin solutions (35) to a theoretical model for hard spheres. The blue dotted and red dashed curves give the crowding dependence of inverse dissociation constants for RNAp binding and TF binding, respectively, as determined from our Monte Carlo simulation data and Eq. 12. To see this figure in color, go online.
Our results show that in many conditions, the level of cytoplasmic mRNA shows a markedly nonmonotonic dependence on the volume fraction, ϕ, of crowders in the nucleus, frequently reaching a maximum at values near . This is typical of the levels of crowding typically reported for living cells (19). We have also shown that this crowding dependence may itself be modulated by several means. The location of the maximum in the ϕ dependence may be tuned by changing the binding affinity of RNAp for bound TF (complex CI), whereas the relative amplitude of the ϕ dependence can be greatly accentuated by decreasing the overall concentrations of reactants (Fig. 4) or by increasing the strength of nonspecific protein-DNA binding.
Morelli et al. (9) also found a nonmonotonic dependence of mRNA levels on the level of crowding under certain conditions, especially when taking account of nonspecific binding of polymerase to DNA. Macromolecular crowding has also been found theoretically to exert a nonmonotonic influence on the accessible surface area of chromatin (7), as well as the timescale of loop formation in polymers (20); these are effects of potential relevance to gene expression levels, and suggest the intriguing possibility that the level of crowding could function as a regulatory control mechanism. Several authors have highlighted the dual influence of crowding, which promotes molecular association while slowing diffusion, and the consequent potential existence of an optimal level of macromolecular crowding (21,22). Here, we emphasize the role of the irreversible process of transcription in keeping the system out of equilibrium, allowing its steady-state properties to depend on the diffusion rates.
There is some evidence that the level of macromolecular crowding is conserved across different mammalian cell lines (23). If the level of macromolecular crowding is under evolutionary and homeostatic control, then, conversely, disregulation of crowding may be associated with faulty regulation of gene expression and with related disease states such as cancer. Thus, the link between macromolecular crowding and transcriptional regulation may shed light on previously observed nanoscale structural differences between healthy and precancerous cells (24), since these differences must be associated with variations in local crowding and concentrations, which in turn influence gene expression.
Experiments by Ge et al. (25) have determined the effects of macromolecular crowding in a cell-free protein expression system, using polyethylene glycol as well as Ficoll as the crowding agent. Notably, they found that the level of mRNA produced by cell-free transcription depends nonmonotonically on the concentration of crowding agents.
Recently, Tan et al. (26) studied the crowding dependence of gene expression in a cell-free system using phage T7 components. Using as crowding agents dextran molecules of two different sizes, they showed that in the case of small dextran molecules the gene expression rate is a nonmonotonic function of the density of crowders. Interestingly, they found that at equal weight/volume percent concentrations of crowders, large dextran molecules generate a much larger crowding effect on gene expression than small dextran molecules. Although Tan et al. state that this size effect is consistent with existing theories of crowding, in fact, considerations of excluded volume predict that at equal crowder volume fractions, and therefore equal weight/volume percent, smaller crowders will induce more significant depletion interactions (4,5,27). The size effect found by Tan et al. (26) highlights the currently unknown relationship between theoretical (hard-sphere) and in vitro (dextran, Ficoll, or polyethylene glycol) models of intracellular crowding.
Notwithstanding the numerous theoretical studies of macromolecular crowding, the role of the physical environment of a gene in determining the level of its transcription is still unclear. With respect to the influence of macromolecular crowding, it will be necessary to go beyond the typical treatment of crowders as inert hard spheres. Several steps have been taken in this direction, for example, by considering crowders with interactions or nonspherical shapes (28,29). However, we must take seriously the fact that the role of the crowding agent in the nucleus is played in part by chromatin rather than by independently mobile molecules. Its physical effects on transcription are perhaps intermediate between those of mobile crowders and the confinement effects of fixed obstacles (30,31). Also, the structure of chromatin, which determines the accessibility of DNA binding sites to TFs, is predicted to be influenced by macromolecular crowding in a nonmonotonic way (7). Furthermore, to integrate the physical microenvironments of genes into a systems-level treatment of gene expression, one must take into account the spatial compartmentalization of the nucleus, whose origins may in turn be due to entropic crowding effects (32,33). Finally, it is tempting to speculate on the possibility that chromatin territories within the nucleus regulate gene expression by locally controlling, in additional to specific genes, concentrations of reactants and crowders. This local control could lead to gene upregulation or downregulation, according to our predictions, by the proper choice of environment.
Acknowledgments
The authors acknowledge useful discussions with Luay Almassalha.
This work was supported by the National Science Foundation under grants EFRI CBET-0937987 and EAGER-124931.
Footnotes
Hiroaki Matsuda and Gregory Garbès Putzel contributed equally to this work.
Supporting Material
References
- 1.Zhou H., Rivas G., Minton A. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu. Rev. Biophys. 2008;37:375–397. doi: 10.1146/annurev.biophys.37.032807.125817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Schnell S., Turner T.E. Reaction kinetics in intracellular environments with macromolecular crowding: simulations and rate laws. Prog. Biophys. Mol. Biol. 2004;85:235–260. doi: 10.1016/j.pbiomolbio.2004.01.012. [DOI] [PubMed] [Google Scholar]
- 3.Kim J.S., Yethiraj A. Effect of macromolecular crowding on reaction rates: a computational and theoretical study. Biophys. J. 2009;96:1333–1340. doi: 10.1016/j.bpj.2008.11.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Qin S., Cai L., Zhou H.X. A method for computing association rate constants of atomistically represented proteins under macromolecular crowding. Phys. Biol. 2012;9:066008. doi: 10.1088/1478-3975/9/6/066008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Kim Y.C., Best R.B., Mittal J. Macromolecular crowding effects on protein-protein binding affinity and specificity. J. Chem. Phys. 2010;133:205101. doi: 10.1063/1.3516589. [DOI] [PubMed] [Google Scholar]
- 6.Qin S., Zhou H.X. Atomistic modeling of macromolecular crowding predicts modest increases in protein folding and binding stability. Biophys. J. 2009;97:12–19. doi: 10.1016/j.bpj.2009.03.066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kim J.S., Backman V., Szleifer I. Crowding-induced structural alterations of random-loop chromosome model. Phys. Rev. Lett. 2011;106:168102. doi: 10.1103/PhysRevLett.106.168102. [DOI] [PubMed] [Google Scholar]
- 8.Richter K., Nessling M., Lichter P. Experimental evidence for the influence of molecular crowding on nuclear architecture. J. Cell Sci. 2007;120:1673–1680. doi: 10.1242/jcs.03440. [DOI] [PubMed] [Google Scholar]
- 9.Morelli M.J., Allen R.J., Wolde P.R. Effects of macromolecular crowding on genetic networks. Biophys. J. 2011;101:2882–2891. doi: 10.1016/j.bpj.2011.10.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Berg O.G., Winter R.B., von Hippel P.H. Diffusion-driven mechanisms of protein translocation on nucleic acids. 1. Models and theory. Biochemistry. 1981;20:6929–6948. doi: 10.1021/bi00527a028. [DOI] [PubMed] [Google Scholar]
- 11.Bintu L., Buchler N.E., Phillips R. Transcriptional regulation by the numbers: models. Curr. Opin. Genet. Dev. 2005;15:116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Garcia H.G., Phillips R. Quantitative dissection of the simple repression input-output function. Proc. Natl. Acad. Sci. USA. 2011;108:12173–12178. doi: 10.1073/pnas.1015616108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Coulon A., Chow C.C., Larson D.R. Eukaryotic transcriptional dynamics: from single molecules to cell populations. Nat. Rev. Genet. 2013;14:572–584. doi: 10.1038/nrg3484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Berg O. On diffusion-controlled dissociation. Chem. Phys. 1978;31:47–57. [Google Scholar]
- 15.Li G.-W., Berg O., Elf J. Effects of macromolecular crowding and DNA looping on gene regulation kinetics. Nat. Phys. 2009;5:294–297. [Google Scholar]
- 16.Singh A., Bokes P. Consequences of mRNA transport on stochastic variability in protein levels. Biophys. J. 2012;103:1087–1096. doi: 10.1016/j.bpj.2012.07.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Damania D., Subramanian H., Backman V. Role of cytoskeleton in controlling the disorder strength of cellular nanoscale architecture. Biophys. J. 2010;99:989–996. doi: 10.1016/j.bpj.2010.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bickmore W.A., Sutherland H.G. Addressing protein localization within the nucleus. EMBO J. 2002;21:1248–1254. doi: 10.1093/emboj/21.6.1248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ellis R.J. Macromolecular crowding: an important but neglected aspect of the intracellular environment. Curr. Opin. Struct. Biol. 2001;11:114–119. doi: 10.1016/s0959-440x(00)00172-x. [DOI] [PubMed] [Google Scholar]
- 20.Toan N.M., Marenduzzo D., Micheletti C. Depletion effects and loop formation in self-avoiding polymers. Phys. Rev. Lett. 2006;97:178302. doi: 10.1103/PhysRevLett.97.178302. [DOI] [PubMed] [Google Scholar]
- 21.Vazquez A. Optimal cytoplasmatic density and flux balance model under macromolecular crowding effects. J. Theor. Biol. 2010;264:356–359. doi: 10.1016/j.jtbi.2010.02.024. [DOI] [PubMed] [Google Scholar]
- 22.Dill K.A., Ghosh K., Schmit J.D. Physical limits of cells and proteomes. Proc. Natl. Acad. Sci. USA. 2011;108:17876–17882. doi: 10.1073/pnas.1114477108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Guigas G., Kalla C., Weiss M. The degree of macromolecular crowding in the cytoplasm and nucleoplasm of mammalian cells is conserved. FEBS Lett. 2007;581:5094–5098. doi: 10.1016/j.febslet.2007.09.054. [DOI] [PubMed] [Google Scholar]
- 24.Subramanian H., Pradhan P., Backman V. Optical methodology for detecting histologically unapparent nanoscale consequences of genetic alterations in biological cells. Proc. Natl. Acad. Sci. USA. 2008;105:20118–20123. doi: 10.1073/pnas.0804723105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ge X., Luo D., Xu J. Cell-free protein expression under macromolecular crowding conditions. PLoS ONE. 2011;6:e28707. doi: 10.1371/journal.pone.0028707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tan C., Saurabh S., Leduc P. Molecular crowding shapes gene expression in synthetic cellular nanosystems. Nat. Nanotechnol. 2013;8:602–608. doi: 10.1038/nnano.2013.132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Minton A.P. The effect of volume occupancy upon the thermodynamic activity of proteins: some biochemical consequences. Mol. Cell. Biochem. 1983;55:119–140. doi: 10.1007/BF00673707. [DOI] [PubMed] [Google Scholar]
- 28.Kim J.S., Yethiraj A. Crowding effects on protein association: effect of interactions between crowding agents. J. Phys. Chem. B. 2011;115:347–353. doi: 10.1021/jp107123y. [DOI] [PubMed] [Google Scholar]
- 29.McGuffee S.R., Elcock A.H. Diffusion, crowding & protein stability in a dynamic molecular model of the bacterial cytoplasm. PLOS Comput. Biol. 2010;6:e1000694. doi: 10.1371/journal.pcbi.1000694. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Minton A.P. Confinement as a determinant of macromolecular structure and reactivity. Biophys. J. 1992;63:1090–1100. doi: 10.1016/S0006-3495(92)81663-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Saxton M.J. Anomalous diffusion due to obstacles: a Monte Carlo study. Biophys. J. 1994;66:394–401. doi: 10.1016/s0006-3495(94)80789-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Marenduzzo D., Finan K., Cook P.R. The depletion attraction: an underappreciated force driving cellular organization. J. Cell Biol. 2006;175:681–686. doi: 10.1083/jcb.200609066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Finan K., Cook P.R., Marenduzzo D. Non-specific (entropic) forces as major determinants of the structure of mammalian chromosomes. Chromosome Res. 2011;19:53–61. doi: 10.1007/s10577-010-9150-y. [DOI] [PubMed] [Google Scholar]
- 34.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. 27–28. [DOI] [PubMed] [Google Scholar]
- 35.Adair G. A theory of partial osmotic pressures and membrane equilibria, with special reference to the application of Dalton’s law to haemoglobin solutions in the presence of salts. Proc. R. Soc. Lond. A Math. Phys. Sci. 1928;120:573–603. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


