A Bayesian Semi-parametric Approach for the Differential Analysis of Sequence Counts Data

Summary

Data obtained using modern sequencing technologies are often summarized by recording the frequencies of observed sequences. Examples include the analysis of T cell counts in immunological research and studies of gene expression based on counts of RNA fragments. In both cases the items being counted are sequences, of proteins and base pairs, respectively. The resulting sequence-abundance distribution is usually characterized by overdispersion. We propose a Bayesian semi-parametric approach to implement inference for such data. Besides modeling the overdispersion, the approach takes also into account two related sources of bias that are usually associated with sequence counts data: some sequence types may not be recorded during the experiment and the total count may differ from one experiment to another. We illustrate our methodology with two data sets, one regarding the analysis of CD4+ T cell counts in healthy and diabetic mice and another data set concerning the comparison of mRNA fragments recorded in a Serial Analysis of Gene Expression (SAGE) experiment with gastrointestinal tissue of healthy and cancer patients.

1. Introduction

Many problems in biomedical research require inference for frequencies of some biological entity, such as gene transcripts or molecular receptors. For example, in immunology, investigators may want to compare the number of distinct T cell receptors and their respective abundances in autoimmune patients and healthy individuals (Hsieh et al., 2006; Ferreira et al., 2009). T cell receptors (TCRs) are molecules at the surface of T cells (a white blood cell) that bind to antigens and trigger the immune response itself. Diversity of T cell receptors, i.e., the number of distinct molecules, is an important characteristic of the immune system. In molecular biology, the comparison of different tissue samples may be based on a comparison of counts of different types of messenger RNA (mRNA), an intermediate product in protein synthesis. The abundance of different types of mRNA characterizes gene expression. These two examples serve as the motivating applications in this discussion. In both applications, the data are sequence counts, of proteins and of base pairs, respectively. We will therefore generically refer to the biological entities that are being counted as sequences. Table 1 shows the first few lines of a typical data set. The left table shows the raw data of counts for each unique sequence. The number of rows is the number of unique sequences. The right table shows the summary as frequencies of counts (clonal size distribution or sequence abundance distribution). The corresponding number of rows is the number of different counts in the first table.

Table 1.

Typical data of sequence abundances as counts of unique amino-acid sequences (left table) and summarized as frequencies of counts (right table).

(a) Sequence Counts
unique sequence	count
CAARGGLSGKLTF	40
CAAPRGGLSGKLTF	39
CAARTGGLSGKLTF	39
…	…
CAARGADDNYQLIW	1
CAARGAKDNYQLIW	1

(b) Clonal size distribution
clonal size (count)	frequency
1	22
…	…
39	2
40	1

By the nature of the underlying biological processes or by the way the data are collected or processed, the distribution of the observed data in such studies shows several general characteristics. First, samples may be characterized by a large number of sequences recorded at low frequencies together with just a few sequences recorded very frequently. This leads to overdispersion relative to a Poisson model where variance is tied with the mean (see examples in Bentley et al., 2008; Yoon et al., 2009). In addition, the sequencing experiment may fail to record many rare sequence types of the original population. Therefore, a single sample may not capture all distinct sequences that are present in a population. Zero counts are not included in the count data, i.e., zero counts are censored. As a consequence, the observed frequencies are biased estimates of true abundances. Some correction is needed when analyzing the data (Morris et al., 2003; Sepúlveda et al., 2010).

Several modeling approaches have been proposed to analyse sequence abundance distributions under different inferential assumptions. Common modeling strategies include the zero-inflated Poisson regression model (Nie et al., 2006; Dhavala et al., 2010) and the negative binomial distribution where the variance is modeled explicitly as a function of the mean and an additional dispersion parameter (see Robinson and Smyth, 2007; Hardcastle and Kelly, 2010; Anders and Huber, 2010). Indeed, the negative binomial distribution can be characterized as the marginal distribution in a Poisson-gamma mixture model (see, for example, Cameron and Trivedi, 1998). The method by Robinson and Smyth (2007) is implemented in the widely used EdgeR package and relies on the estimation of a common overdispersion parameter across samples. Other proposals include the Poisson-lognormal distribution (Sepúlveda et al., 2010; Rempala et al., 2011) or the truncated Poisson-gamma (Thygesen and Zwinderman, 2006). Alternatively, finite mixtures of Poisson distributions have been proposed as a way to provide a better description of this type of data, often with an assumed known number of mixing components (Zuyderduyn, 2007).

We build on these approaches and propose Bayesian inference in a semi-parametric mixture of Poissons model to estimate the distribution of the observed counts in the presence of overdispersion and uncertainty on the true number of unique sequences in a population (e.g., tissue or cell type). More specifically, we assume a Dirichlet process prior on the mean of the Poisson components. The Dirichlet process prior has been extensively used as an automatic and adaptive method for density estimation (see, for example Ferguson, 1983; Escobar and West, 1995; Gasparini, 1996). In addition, we explicitly model the experimentally induced censoring of zero counts. Inference includes estimating the underlying population sequence diversity, that is the number of different unique sequences that can be found in the population. We show that for small and moderate size data sets with overdispersed data, such a correction is non-negligible. Reliable estimates of sequence abundances are particularly important if one aims to compare the sequence-abundance distribution under different biological or experimental conditions. An extension of the semi-parametric Poisson mixture model to carry out such comparisons is another contribution of this paper. The proposed inference is valid for both small and large datasets and allows for different degrees of overdispersion across samples.

Recent related nonparametric Bayesian literature includes work by Trippa and Parmigiani (2011) who use semi-parametric Poisson mixture models as a tool to generate realistic simulation scenarios for the evaluation of false discovery procedures, and a sequence of papers by Lijoi et al. (2007a,b, 2008) and Favaro et al. (2009, 2012), where they use nonparametric Bayesian priors for a sampling model on species diversity in experiments similar to the SAGE experiments discussed in this paper. They focus on inference for the expected number of species under a given additional sampling effort. Similar to the use of semi-parametric Poisson mixtures to model overdispersion, Canale and Dunson (2012) develop models with underdispersion, i.e. distributions where variance is less than the mean, by using kernel mixture models with kernels induced through rounding of continuous kernels.

We illustrate our methodology with two applications, one related to the study of T cell receptors in healthy and diabetic mice (Ferreira et al., 2009) and another one measuring gene expression using SAGE (Serial Analysis of Gene Expression) technology. The analysis of the T cell receptor data has two objectives: quantify the receptor diversity and compare the frequencies of the receptors across different T cell populations. In the analysis of the SAGE data, the main objective is to compare the frequency of mRNA transcripts across different libraries of healthy and tumour colon tissues.

The structure of the paper is as follows. Section 2 introduces the model for the single sample analysis. The section includes a simulation study to compare inference with similar parametric models as well as inference for the two motivating applications. Section 3 extends the model to the multivariate case in order to compare several sequence-abundance distributions. Subsections 3.3 and 3.4 discuss related inference in the two motivating applications. Finally, Section 4 finishes with some concluding remarks. Supporting information on the journal website contains implementation details for the posterior simulation.

2. Modeling Relative Sequence Abundances

2.1. A Semi-parametric Model

Sampling model

We start by considering a model for inference with a single sample or library of sequence counts. Let y_i, i = 1, …, k denote the counts of the k distinct sequences in a sample. However, counts y_i = 0 are not observed, leaving only k′ ≤ k observed counts y_i > 0. We refer to k and k′ as the population and the sample diversity, respectively. The balance k₀ = k − k′ is a measure of the sampling error, that is the undercounting of sequences with low copy numbers, due to censoring of zero counts.

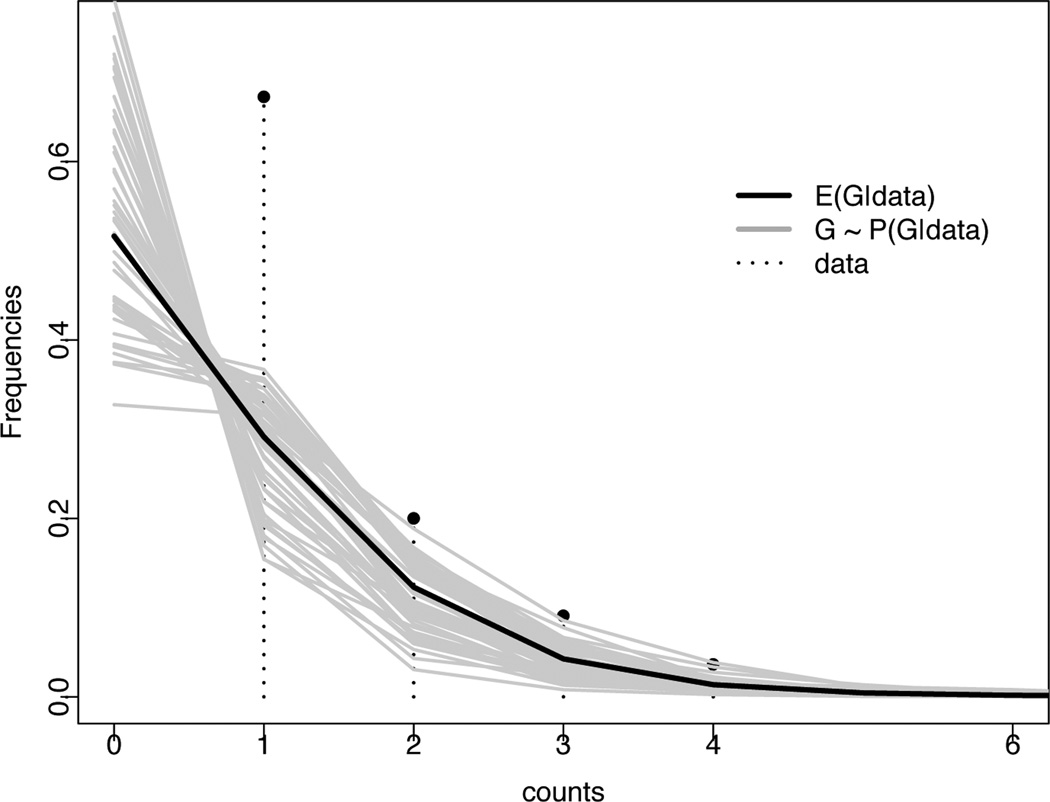
We first summarize the proposed model in words. Let G(y_i) denote the unknown distribution of counts y_i. We estimate G(·) based on the observed data y_i, using a Bayesian non-parametric approach, i.e. with minimal assumptions on the data generating mechanism. In turn, this allows us to make inference about the sample diversity k. Let Ĝ(y) denote the empirical frequency of counts y > 0. Figure 1 shows Ĝ(y) as a pin plot. The frequency of zero counts can be estimated by extrapolating the observed trend of …, Ĝ(3), Ĝ(2), Ĝ(1) to y = 0. This could be done by inferring ad-hoc the behavior of the Ĝ(·) curve at y = 0 and adequately re-normalizing the weights to ensure that the total mass is 1. The proposed model-based approach makes that “eye-balling” more formal and attempts to describe the related uncertainties. In Figure 1 the solid line shows the estimated E(G | y) under the proposed model. The many thin grey dotted lines illustrate uncertainty as draws from the posterior distribution of G, i.e. G ~ p(G | y). Information on G(·) does not yet allow inference about true abundances of the sequences, for lack of any parameter that could be readily interpreted as sequence abundance. We achieve such inference with a simple trick. We represent G(·) as a mixture of Poisson distributions. The mixture naturally introduces a latent variable λ_i that can be interpreted as true abundance of the i-th sequence.

Fig. 1.

The rationale for a model based approach to inference on zero counts for sequence counts data. The pins show the data y_i listed in Table 2, healthy mouse Tconv 2, summarized as empirical frequencies Ĝ(y), y = 1, 2, … Ad-hoc inference for G(0) could be based on extrapolating the trend of Ĝ(y), y ≥ 1, to y = 0. The proposed approach formalizes this extrapolation as model-based inference. The solid line shows the posterior expectation E(G | data) under the proposed semi-parametric mixture of Poissons model. The gray lines show draws from the posterior distribution G ~ p(G | y).

We start the formal model construction with a binomial distribution for the sample diversity k′:

$$p(k\prime |k,G)=(\begin{array}{c}k\hfill \\ k\prime \hfill \end{array}){[G(0)]}^{k-k\prime }{[G(+)]}^{k\prime },$$

where G(0) = Pr(y_i = 0) is the probability of a zero count, and G(+) = Pr(y_i > 0) denotes the complement probability of a non-zero count.

Let y = {y_i, i = 1, …, k′} denote the observed sequence counts. Conditional on the sample diversity k′, the likelihood for G and k is $p(\mathbf{y}|k\prime ,k,G)={\prod }_{i=1}^{k\prime }G(y_i)/G(+)$. Thus,

$$p(\mathbf{y},k\prime |k,G)=(\begin{array}{c}k\hfill \\ k\prime \hfill \end{array})\prod _{i=1}^{k\prime }G(y_i)\prod _{i=k\prime +1}^{k}G(0).$$ (1)

Note that the sampling model (1) includes positive probability for k′ = 0, although by the nature of the experiment at least some tags are always counted, i.e. k′ > 0. This is not a problem for posterior inference, since the observed data always includes k′ > 0.

Nonparametric prior

We continue the model construction with a nonparametric Bayesian prior for G(·). A parametric model would be too restrictive and inappropriately determine the extrapolation to G(0) by the particular assumed parametric form. For example, in a Poisson sampling model the mean determines the Poisson rate, and thus Pr(y_i = 0). From a data analysis perspective this is undesirable. Instead, we assume that the counts y_i are independently sampled from a mixture of Poisson distributions. Let Poi(x; λ) denote a Poisson distribution for the random variable x with expectation λ. In our setting, the parameter λ is a measure of the true abundance of a sequence in the biological sample. We assume

$$G(y_i)=\int \text{Poi}(y_i;{\mathrm{\lambda }}_i)P(d{\mathrm{\lambda }}_i),$$ (2)

i = 1, …, k, independently conditional on P. Besides the increased flexibility in modeling G(·), the introduction of the mixture model is important for the desired inference. One of the inference goals is to estimate the abundance of each sequence. Consider an equivalent expression of (2) as a hierarchical model,

$$y_i|{\mathrm{\lambda }}_i\stackrel{\mathit{\text{ind.}}}{~}\text{Poi}({\mathrm{\lambda }}_i)\text{with}{\mathrm{\lambda }}_i\stackrel{\mathit{\text{iid}}}{~}P.$$ (3)

The variables λ_i can be interpreted as the true abundance of the i−th sequence. Also, since P features in the model as the prior for the latent, unobservable variables λ_i, it suffices to assume a discrete probability measure P. In fact, a discrete mixing measure P has the additional advantage of introducing a clustering of the observed sequences into groups of comparable abundance. We discuss details below.

We specify a prior distribution for the mixture model (2) by assuming a nonparametric prior on the mixing measure P. One of the most commonly used nonparametric Bayes priors is the Dirichlet process prior. The Dirichlet process is characterized by two parameters: the prior mean, G*, and the mass parameter, ν. The mass parameter determines, among other important properties, the variation of the random measure around the prior mean. We write P ~ DP(G*, ν). We refer to Ferguson (1973) and Walker et al. (1999) for a definition and important properties of the Dirichlet process model. The main reasons that motivate us to consider the proposed semi-parametric mixture of Poissons model are the increased robustness of inference with respect to modeling assumptions, the lack of a good biologically justified parametric model and the interpretation of the latent λ_i as sequence abundance. We note that the nonparametric prior can not add information without exploiting additional expert judgment. In general the semi-parametric model will only allow for a more honest description of uncertainties in the extrapolation to G(0). The random G is infinite dimensional, in contrast to, for example, a Poisson model that is determined by a single parameter.

Random partition

Among other implications, the Dirichlet process prior on the mixing measure allows for inference about clustering of observations, in the following sense. A key feature is the a.s. discreteness of P; hence, a sample from P has a positive probability of ties. In (3), let ${\mathrm{\lambda }}_j^{*}$, j = 1, …, L, denote the L ≤ k unique values of λ_i. If we use the ties to define clusters, then mixture of Dirichlet process models such as (2) can be used for detecting clusters of observations (Green and Richardson, 2001; Quintana and Iglesias, 2003). It is often convenient to restate the model in terms of latent cluster indicators s_i, such that s_i = j if and only if observation i belongs to cluster j, that is ${\mathrm{\lambda }}_i={\mathrm{\lambda }}_j^{*}$. Let L denote the number of clusters and let n_j = |{i : s_i = j}| denote the size of the j-th cluster. The prior probability of a given clustering structure, say s = {s₁, …, s_k}, is

$$p(\mathbf{s}|k)=\frac{{\nu }^L\mathrm{\Gamma }(\nu ){\prod }_{j=1}^L\mathrm{\Gamma }(n_j)}{\mathrm{\Gamma }(\nu +k)}.$$ (4)

Assume that the goal is to group sequences with similar frequency patterns, according to the values of the true abundances λ_i. The posterior distribution p(s | y) provides a full probabilistic description of such partitions.

Dirichlet process mixture models like (3) have been extensively studied in the literature. Posterior inference can be implemented by Markov chain Monte Carlo posterior simulation to obtain desired posterior and posterior predictive summaries (Escobar and West, 1995; MacEachern and Müller, 1998; Neal, 2000; Papaspiliopoulos and Roberts, 2008; Dahl, 2003). To achieve faster mixing Markov chains it is possible to analytically integrate out the random probability measure P and the abundances λ_i, leaving a model in s only.

Model (2) is completed with a base measure G* and a prior on k. Using G*(λ) ≡ Ga(α, β), i.e. a gamma distribution with mean α/β, defines a conjugate Dirichlet process mixture. This greatly simplifies posterior simulation. Integrating out the λ_i’s, we are left with a Poisson-gamma random mixture model. In the analysis of the examples in the following section, we considered fixed hyperparameters α and β, chosen so to provide large support to the prior distribution. Furthermore, since E(G) = G* a priori, the implied marginal for one observation, p(y_i) = E(G(y_i)), is a negative binomial. However, the data will inform posterior inference and E(G | data) can be very different a posteriori. Consider, for example, the data for diabetic mouse Treg 1 in Table 2. The data show the skewed distribution that is typical of the datasets that we consider. We can recognize a peak for low counts around 1, and some evidence for a secondary peak for high counts around 36 and 40. Under the negative binomial model, posterior inference has to balance between the very few sequences with high counts and the several sequences with low counts. The resulting posterior shows a single peak around 6. In contrast, the DP mixture model can capture the observed imbalance in the data, allowing for a peak at count 0, and a secondary, much smaller, peak around 38 (not shown).

Table 2.

Clonal size (counts) distributions of regulatory (Treg) and conventional T cells (Tconv) across samples of 3 healthy and 2 diabetic mice. Here, k′ is the total number of distinct sequences (clonotypes) in the samples, whereas n is the total number of TCR sequences per sample. The total number of distinct TCR sequences across all samples is 234 for the healthy mice and 172 for the diabetic mice.

	healthy mice				diabetic mice
	Tconv		Treg		Tconv			Treg
count	Mouse		Mouse		Mouse			Mouse
	1	2	1	2	1	2	3	1	2	3
1	78	37	40	36	46	14	29	8	3	11
2	5	11	5	18	17	6	16	1	0	0
3	1	5	5	3	0	6	4	2	0	0
4	1	2	2	1	0	4	3	0	0	0
5	0	0	3	0	0	4	0	1	0	0
6	0	0	0	0	0	5	0	0	0	0
7	0	0	0	0	0	0	2	0	0	0
8	0	0	0	0	0	0	0	0	1	0
10	0	0	0	0	0	1	0	0	0	0
12	0	0	0	0	0	0	0	0	1	1
16	0	0	0	0	0	0	0	0	1	0
17	0	0	0	0	0	0	0	0	1	1
20	0	0	0	0	0	0	0	0	0	1
23	0	0	0	0	0	0	0	0	1	0
36	0	0	0	0	0	0	0	1	0	0
39	0	0	0	0	0	0	0	0	1	1
40	0	0	0	0	0	0	0	1	0	0
k′	85	55	55	58	63	40	54	14	9	15
n	95	82	88	85	80	120	99	97	118	99

Similar parametric (finite) Poisson mixture models for the analysis of SAGE data have been also considered by Zuyderduyn (2007) as a way to describe the overdispersion typical of these data and identify sets of co-expressed genes. Although similar in motivation, our approach does not require to fix in advance the number of mixture components and it allows for simultaneous estimation of the number of missing sequences.

Finally, the choice of the prior on k requires careful consideration. Inference on k can be very sensitive to the prior choice, and a poor prior may result in an overshrinkage of the frequency estimates of the scarce sequences. The prior should ideally reflect specific expert information. In lack of such information, we suggest to proceed with a conservative approach. For example, a prior centered around the number of observed sequences, k′, provides a reasonable default choice.

Implementing posterior simulation includes a Metropolis transition probability to update k, using a simple discrete proposal (move up/move down). Since the number of parameters of the model is implicitly determined by the nonparametric prior, there is no need for a reversible jump algorithm (Green, 1995). In the online supporting information, we discuss full details of the conditional distributions that are used to define the transition probabilities of a posterior simulation scheme.

2.2. Estimation of TCR Diversity

In Immunology, T cell diversity is a key quantity to understand how an efficient immune system can react to a virtually infinite set of microorganisms without responding against body components at the same time (Nikolich-Zugich et al., 2004). T cell diversity is usually defined as the number of distinct T cell receptors (TCR) collectively presented by this cell type. Distinction between these molecular receptors is often made through the corresponding nucleotide or aminoacid sequence encoding them, as illustrated in Table 1a. These receptors are generated during T cell development in the thymus through a recombination mechanism where different gene segments are randomly assembled. Therefore, TCR diversity might be extremely high in the body and can only be ascertained through sampling. In this scenario, one usually collects a sample of T cells and determines their corresponding TCR sequences. Data are then summarized as sequence counts as shown in Table 1.

We analyze data that report the number of distinct TCR sequences and their respective abundances obtained from 3 NOD and 2 B6 mice as summarized in Table 2 (Ferreira et al., 2009). NOD and B6 are two lab strains that are commonly used in immunology and hereafter referred to as diabetic and healthy mice, respectively, since the former spontaneously develops type I diabetes while the latter maintains stably healthy under strict laboratory conditions. The goal of the analysis is to estimate TCR diversity of two important T cell types, the so-called regulatory and conventional CD4+ T cells, which have been implicated in the pathogenesis of type I diabetes. We fit the semi-parametric hierarchical model (3) to each sample, i.e., the mice in Table 2. Here the index i in (2) denotes the i-th unique sequence and y_i denotes the respective observed abundance. The parameter k is the unknown TCR diversity. We use the following hyperparameters for the nonparametric prior. The mass parameter of the Dirichlet process is fixed at ν = 1. This implies a prior expectation of E(L) = ν log((ν+k′)/ν)) ≈ log(k′) clusters in the population (Antoniak, 1974). The centering measure G* = Ga(1.0, 0.05) (mean=20, σ = 400) was chosen to provide substantial probability for a large range of y_i values, as it is common to observe long-tailed sequence abundance distribution in this type of data. The prior distribution for k, the unknown TCR diversity of each T cell population, is assumed to be a Poisson distribution with mean Ξ = 172 and 234 for sick and healthy mice, respectively, corresponding to the overall number of distinct sequences observed across all samples of the same lab strain. Centering around the observed diversity is a conservative choice to avoid an over-estimation of k by shrinkage to the prior mean. Indeed, we also considered alternative values for Ξ, but found no remarkable variations on the resulting inference over k. Finally, we speed up posterior simulation by analytically integrating out the latent sequence abundance λ_i, leaving us with the marginal model of the cluster membership indicators s_i only. For the Markov chain Monte Carlo implementation we took advantage of the split-merge algorithms proposed in Jain and Neal (2004) and Dahl (2003). See the online supporting information for details.

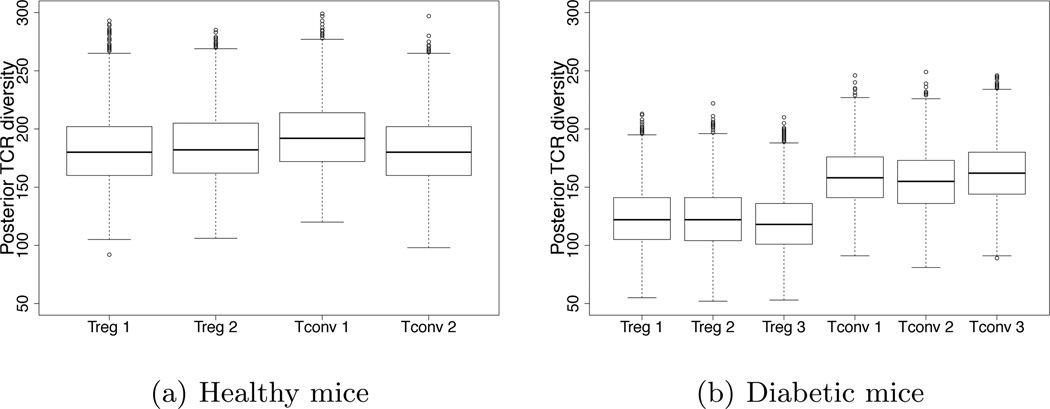
Figure 2(a) shows the boxplots of the posterior distributions for the TCR diversity k. The posterior distributions for TCR diversity are essentially the same across all samples of healthy mice (Figure 2a). In other words, in healthy mice, regulatory and conventional T cells seem equally diverse in terms of TCR diversity. In the case of the diabetic mice data, the posterior distributions for TCR diversity suggest that regulatory T cells are less diverse than conventional T cells (Figure 2b). The result is in agreement with previous findings (Ferreira et al., 2009).

Fig. 2.

Boxplots of the posterior distribution of TCR diversity k for regulatory (Treg) and conventional T cells (Tconv) across the different samples of diabetic and healthy mice.

For these results we carried out separate inference for each sample in Table 2. Later we will extend model (2) to allow joint inference across samples in a single hierarchical model and compare abundance of each sequence across cell types and lab strains.

2.3. Simulation Study

We carried out a simulation study to confirm that the proposed semi-parametric model can indeed address some of the shortcomings of a traditional parametric model. We created a simulation truth with 172 unique TCR sequences by pooling all samples from the experiments with diabetic mouse strains described in Section 2.2. We decided for the use of such pooled data in the absence of a gold standard data set for TCR diversity estimation and because similar pooled data are commonly used in the immunological literature, presumably to obtain larger sample sizes. Experimental constraints make it difficult to obtain large individual samples (Wong et al., 2007; Hsieh et al., 2004). Also, pooling different data sets has the effect of producing intricate sequence-abundance distributions (Sepúlveda, 2009).

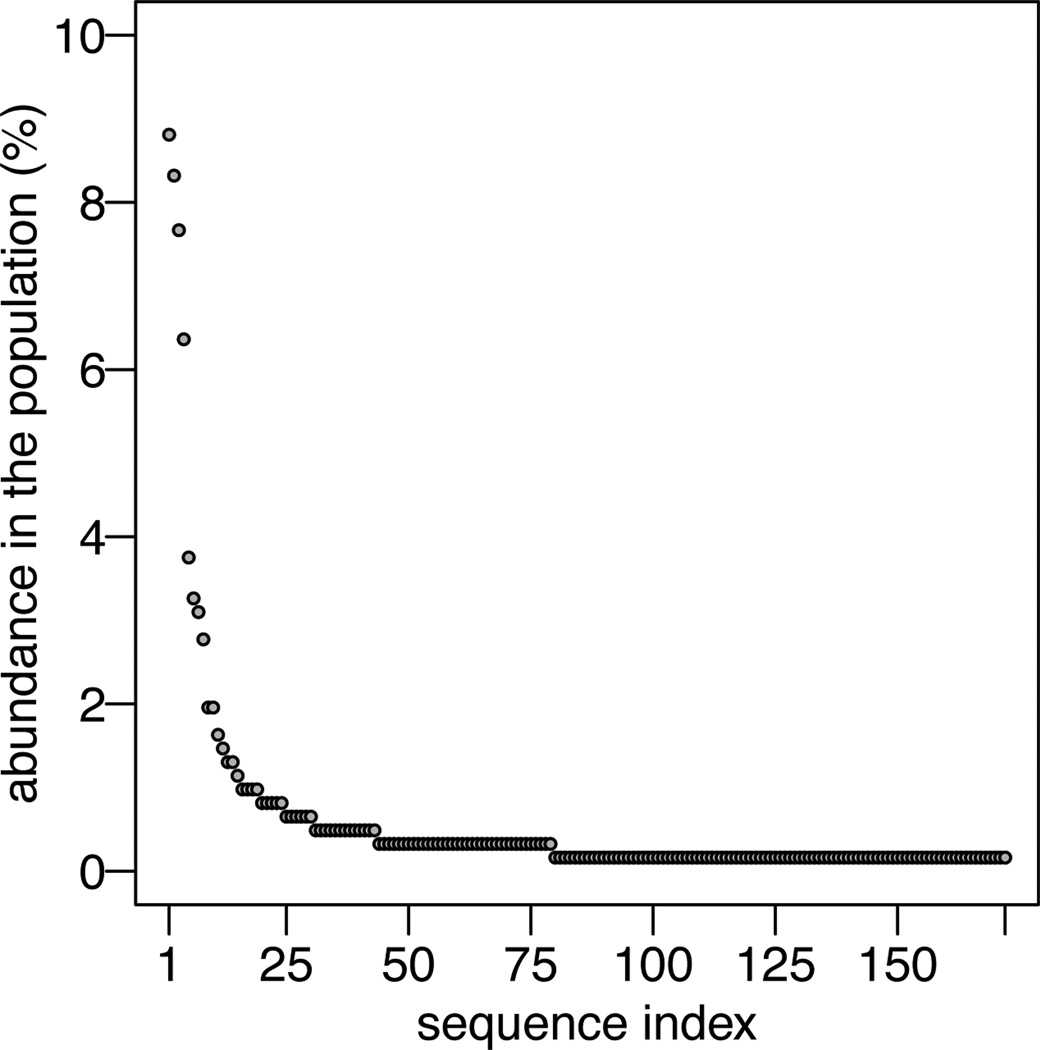
Figure 3 shows the proportions of the unique sequences in the pooled data. Data simulation was implemented as multinomial sampling of 250 sequences from the population of 172 unique sequences. The probabilities of each hypothetical sequence were defined by the corresponding relative abundances in the pooled data for the diabetic mouse strains.

Fig. 3.

Relative abundance of 172 unique TCR sequences resulting from pooling all samples of sick-mouse strain together.

We generated M = 100 different data sets. In each simulated data set we carried out inference under the proposed semi-parametric approach using a uniform prior with support between k′ and 5000 for the unknown true diversity k. Results were compared to the ones obtained under previously proposed parametric models for TCR diversity estimation, namely, the homogeneous Poisson, the geometric, the Poisson-gamma, the Poisson-lognormal, and the Yule model (Sepúlveda et al., 2010). The homogeneous Poisson model assumes a single Poisson distribution for all sequence counts. The other four models assume a mixture of Poisson sampling model as in (2) with exponential, gamma, and lognormal prior densities in the geometric, Poisson-gamma, and Poisson-lognormal models, respectively. The Yule model uses a mixture of exponential distributions (Sepúlveda et al., 2010). The five parametric models were estimated using the same uniform prior on k and appropriate uniform priors for the remaining parameters.

For each simulation and each model we computed bias and coverage of highest posterior density credible intervals. Bias was measured as the average difference (over the M repeated simulations) between a Bayesian point estimate (posterior mean or median) for k and the simulation truth (k = 172). Coverage is reported for 95% and 99% HPD credible intervals calculated according to the method proposed by Chen and Shao (1999). Results are summarized in Table 3.

Table 3.

Summary results of the simulation study based on M = 100 data sets from a population of 172 unique TCR sequences whose relative abundances are shown in Figure 3. The reported CI lengths are median lengths across simulations.

	Bias		CI Length		Coverage
Model	Mean	Median	95%	99%	95%	99%
homogenous Poisson	−77.2	−77.4	9	11	0.00	0.00
geometric	−35.4	−36.0	34	44	0.11	0.21
Poisson-gamma	2287.1	2001.9	4490	4669	0.00	0.00
Poisson-lognormal	1015.0	678.5	3588	4630	0.56	0.58
Yule	109.8	107.4	123	160	0.00	0.03
semi-parametric	56.75	53.24	173	245	1.00	1.00

Inference about the unknown true diversity relies on the assumed model and its ability to recover the salient features of the true sampling distribution from the observed counts. Inference under none of the models attains both a precise and close estimate of true diversity. However, inference under the proposed semi-parametric approach compares favorably with the other models in terms of small bias and high coverage. We believe that this is mostly due to the flexibility of the Bayesian semi-parametric specification, which does not constrain the sampling distribution to a specific shape. Also, compared to the parametric approaches, the lengths of the credible intervals (CI) under the Bayesian semi-parametric model are neither too tight nor too large to make inference meaningless. With respect to the 95% and 99% HPD credible intervals and the observed over coverage, we note that the (frequentist) coverage need not exactly match the nominal (posterior) probability of the C.I. In particular, in non-parametric Bayesian inference there is no equivalent to the Bernsteinvon Mises theorem, which states that credible sets for parametric models are asymptotically equivalent to confidence regions based on maximum likelihood estimators (see Freedman, 1999). We refer the interested reader to recent work that attempts to provide a better understanding of frequentist properties of nonparametric Bayes procedures, e.g. Knapik et al. (2011) and Castillo (2012). In summary, our comparison confirms some recent theoretical studies that have demonstrated that the sequence abundance distribution might be too complex to be captured by simple parametric models (Sepúlveda, 2009). The Bayesian semi-parametric approach provides a natural and flexible modeling choice to tackle TCR diversity and gives a reasonable account of all uncertainties of the specific estimation problem.

2.4. Estimation of SAGE Tag Abundances

We consider a SAGE library of normal colon epithelium tissue with a total number of 49, 610 recorded tags. Here, tags refer to the RNA fragments being counted in the experiment. The library is publicly available on SAGE Genie (http://cgap.nci.nih.gov/SAGE, NC1 library) and has been analyzed by many authors (Zhang et al., 1997; Stollberg et al., 2000; Morris et al., 2003). A total of 17, 703 distinct tags were observed from a healthy colon tissue of a single individual. Most distinct tags were recorded with low counts: 75% of the tags were observed once and 92% of the tags show frequencies less than five. However, tags with low counts represent only 26.4% of the total mRNA mass expressed in the sample. This skewed distribution with many scarce tags and few abundant tags is typical of SAGE experiments (Morris et al., 2003). We fit model (2)-(3) to this dataset, with the following choices of the hyperparameters. The base measure of the Dirichlet process is G* = Ga(1.0, 0.05) (mean=20, σ = 400), and the mass parameter is ν = 5.0, corresponding to E(L) ≈ 40. This allows for a large range of λ_i values as well as flexibility in the estimation of the density of the observed tag counts. We also investigated alternative choices of ν (not shown). As expected, different ν did not affect the estimate of E(k | data) but only the number of clusters in equation (2). We considered three values for the hyperparameter Ξ in a Poi(Ξ) prior for k: Ξ = 17, 703, which corresponds to centering around the observed number of distinct tags, k′, and is the most conservative estimate; Ξ = 25, 536, which is the number of unique tags estimated by Stollberg et al. (2000) in this normal colon tissue; and Ξ = 50, 000, as a realistic upper bound. The results are reported in Table 4 and suggest that the estimate reported by Stollberg et al. might be slightly over estimating the true diversity of tags, assuming similar bias as we observed in the simulation study.

Table 4.

Posterior quantiles of tag diversity k according to different prior mean choices

Prior expectation	Posterior quantiles
E(k)	0.05	0.50	0.95
17,703	19,934	21,371	23,124
25,536	21,279	23,437	25,541
50,000	24,962	28,218	31,763

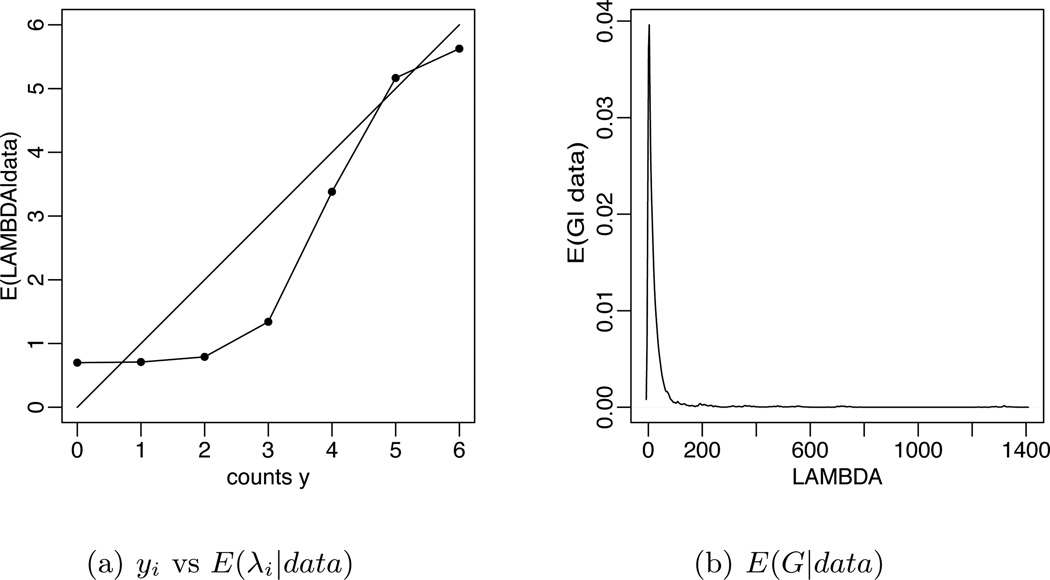
Also, we note that the influence of prior assumptions is tempered by the evidence in the data, as desired. Figure 4 summarizes posterior inference under Ξ = 25, 536. Figure 4(a) plots the semi-parametric Bayes estimates versus the observed counts. The plot demonstrates the shrinkage profiles relative to the empirical frequencies (diagonal solid line), which are the maximum likelihood estimates (m.l.e.) under a Poisson model. In particular, for censored sequences (with y_i = 0) the posterior mean estimate inflates the m.l.e. and reports E(λ_i|data) ≈ 0.9. The shrinkage profile induced by the semi-parametric model is nonlinear, and affects the rare sequences more than the abundant ones. For abundant sequences, posterior inference is driven only by the observed counts, and E(λ_i|data) ≈ y_i. Figure 4(b) shows the estimated distribution of sequence abundances λ_i. It is highly skewed, with high probability mass on low copy number values and small mass on extreme values.

Fig. 4.

Analysis of SAGE library of normal colon epithelium tissue. (a) Posterior means E(λ_i|data) on the vertical axis against observed counts y_i on the horizontal axis. (b) Estimated mixing measure G. The left panel zooms in to small counts, where the shrinkage with respect to the maximum likelihood estimates is most noticeable.

3. A Model for Comparison across Biological Conditions

3.1. Multiple Samples

When the data include samples across different biological conditions, then the desired inference extends beyond the estimation of the within sample abundances. The semi-parametric Bayesian approach introduced in the previous sections can be extended to accommodate the general case of sequence counts observed over several samples and different biological conditions. Let T and C denote, respectively, the total number of samples and conditions included in the data set.

As in Section 2, the total number of distinct sequences, k, is unknown due to sampling variability. Data consist of counts y_it of a sequence i in sample t = 1, …, T. Not all samples may include the same set of sequences. This is similar to the censoring of zero counts in the earlier setup, but now with many possible censoring patterns. The characterization of censoring patterns requires some additional notation. We introduce binary indicators γ_it with γ_it = 1 if a sequence i is present in sample t, otherwise γ_it = 0 and y_it = 0. Then γ_i = (γ_i1, …, γ_iT )′ is a binary vector that records the presence of sequence i. The set of k sequences can be partitioned into subsets of units appearing in the same samples according to γ_i. We denote the partitioning subsets by Κ_j, indexed by a running integer j = 0, …, 2^T− 1. The mapping from γ_i to j is determined by $j={\sum }_{t=1}^T{2}^{t-1}{\mathrm{\gamma }}_{\mathit{\text{it}}}$. Vice versa, the digits of j in a binary expansion are the γ_it. Let ${\mathrm{\gamma }}_j^{*}$ denote the common value of γ_i for all units in Κ_j, i.e., ${\mathrm{\gamma }}_i={\mathrm{\gamma }}_j^{*}$ for all i ∈ Κ_j. For example, if T = 2, then ${\mathrm{\gamma }}_0^{*}=(0,0),{\mathrm{\gamma }}_1^{*}=(1,0),{\mathrm{\gamma }}_2^{*}=(0,1)\text{and}{\mathrm{\gamma }}_3^{*}=(1,1)$.

Also denote by k_j = |Κ_j| the size of each one of these sets, which corresponds to the number of sequences with the same pattern of being observed and censored across samples. Here, k₀ is the number of sequences with zero counts across all samples, i.e., the number of sequences that are zero-censored in all samples. The model construction proceeds similar to before. We start with a model for censoring patterns, and then use a semi-parametric mixture model to specify G(·). Specifically, we extend the model discussed in section 2 by assuming that the distribution of k_j is multinomial,

$$p(k_j,j=0,\dots ,2^T-1|k,G)=(\begin{array}{c}\hfill k\hfill \\ k_0\dots k_{2^T-1}\hfill \end{array})\prod _{j=0}^{2^T-1}{[G_{+}(j)]}^{k_j},$$

where $G_{+}(j)=\mathit{\text{Pr}}({\cap }_{t:{\mathrm{\gamma }}_{\mathit{\text{jt}}}^{*}=0}\{y_{\mathit{\text{it}}}=0\}\cap {\cap }_{t:{\mathrm{\gamma }}_{\mathit{\text{jt}}}^{*}=1}\{y_{\mathit{\text{it}}}>0\})$ denotes the probability that a sequence belongs to the partition set Κ_j. Similar to the discussion in Section 2 and in accordance with the interpretation of the set Κ₀, G₊(0) denotes the probability of all zero counts. Denote the set of recorded observations by y₊ = {y_it : y_it > 0, i = 1, …, k, t = 1, …, T} and let y_i = {y_it, t = 0, …, T}. Also, let k = (k, k_j, j = 0, …, 2^T−1)^T. Then, we can write $p({\mathbf{y}}_{+}|\mathbf{k})={\prod }_{j=0}^{2^T-1}{\prod }_{i\in {{\rm K}}_j}G({\mathbf{y}}_i)/G_{+}(j)$, where G(y_i) = Pr(Y_it = y_it, i ∈ Κ_j) is the sampling distribution for the observations in the partition set Κ_j. Hence, the likelihood of the observed counts can be expressed as

$$p(\mathbf{y},k_j,j=0,\dots ,2^T-1|k,G)=(\begin{array}{c}\hfill k\hfill \\ k_0\dots k_{2^T-1}\hfill \end{array})\prod _{j=0}^{2^T-1}\prod _{i\in {{\rm K}}_j}G({\mathbf{y}}_i).$$ (5)

The framework is sufficiently general to accommodate a wide range of sampling distributions. In the following examples we will again assume the random mixture of Poissons models as in (2).

3.2. Multiple Conditions

We extend the model to study the abundance of sequences across different conditions. We denote with x_t = x, x ∈ {1, …, C} the type of tissue (or condition) collected in a sample t. Without loss of generality, we assume that x = 1 refers to samples from a reference tissue (e.g. a healthy cell), whereas x > 1 indexes treatment samples (e.g., tumor).

We replace the hierarchical model (3) by the more general

$$y_{\mathit{\text{it}}}|{\mathrm{\lambda }}_{i{x}_t},x_t,n_t~\text{Poi}({\mathrm{\lambda }}_{i{x}_t}{n}_t)i=1,\dots ,k,t=1,\dots ,T.,$$ (6)

where n_t is the size of sample t. Here, the abundance parameter λ_ixt is normalized with respect to the total level of abundance n_t in each sample t, t = 1, …, T. This accounts for between library variability (Baggerly et al., 2003). Also, we assume that the abundance rate is condition-specific, i.e., λ_ixt = λ_ix for all samples with x_t = x. When t is a library from the reference tissue, we assume

$${\mathrm{\lambda }}_{i{x}_t}|P\stackrel{i.i.d.}{~}P,\text{if}{x}_t=1,$$ (7)

as in (2), i = 1, …, k. For other type of tissues, x ≠ = 1, we allow for the possibility of different abundance rates λ_ixt ≠ λ_i1. We augment the hierarchical model (3) by an additional layer that models differential abundance across tissue types. We assume

$${\mathrm{\lambda }}_{i{x}_t}|\pi ,P,{\mathrm{\lambda }}_{i1}~\pi I({\mathrm{\lambda }}_{i{x}_t}={\mathrm{\lambda }}_{i1})+(1-\pi )P\text{if}{x}_t=2,\dots ,C.$$ (8)

For each condition, x_t, the prior probability of non-differential abundance with respect to the reference tissue is π + (1 −π) / (ν + 1), where the second term arises from the event that two independent draws from P are tied and ν is the mass parameter of the DP as in Section 2.1. The marginal distribution of λ_ix is P for any given x, i.e., $p({\mathrm{\lambda }}_{ix},i=1,\dots ,k|P)={\prod }_{i=1}^{k}P({\mathrm{\lambda }}_{ix})$. We introduce latent variables ω_ix ~ Bern(π) and reformulate (8) as

$${\mathrm{\lambda }}_{ix}|{\omega }_{ix},{\mathrm{\lambda }}_{i1}~\{\begin{array}{cc}I({\mathrm{\lambda }}_{ix}={\mathrm{\lambda }}_{i1}\hfill & \text{if}{\omega }_{ix}=1,\hfill \\ P\hfill & \text{if}{\omega }_{ix}=0.\hfill \end{array}$$

The use of the latent variables ω_ix results in an augmentation scheme that simplifies posterior simulation. In particular, it simplifies inference on the λ_ix, hence the probabilities of differential abundance, and hence also inference on k. Finally, note that we could always modify equation (8) to obtain more detailed inference across conditions. In particular, if three or more conditions were examined, it would be possible to include in (8) some terms that allow for non-differential abundance among any pairs of conditions.

3.3. Comparison of T cell Receptor Abundances

Many recent studies have tried to better understand the protective role of regulatory T cells against several autoimmune diseases, such as type I diabetes or lupus. Some of these studies were designed to ascertain core differences between the TCR frequency presented by these cells and their conventional T cell counterparts (Hsieh et al., 2004, 2006; Pacholczyk et al., 2006, 2007; Wong et al., 2007; Ferreira et al., 2009; Sepúlveda et al., 2010). In this section we extend the analysis reported in Section 2.2 to compare the abundances of each TCR sequence across different conditions.

We analysed the data under model (6) through (8) using the same prior specification as in section 2.2. Additionally, we chose π = 0.9. This choice limits findings to a small set of scientifically interesting prospects (Efron, 2008). For comparison we also considered π = 0.5. We will describe several comparisons. Each comparison is across C = 2 conditions. See below for details. Let υ_i = Pr(λ_i1 ≠ λ_i2 | data) be the posterior probability of differential abundance of TCR sequence i across the two conditions. When multiple comparison is set as a Bayesian decision problem, the optimal decision rule for many common loss functions can be defined as identifying a TCR sequence with differential abundance across cell type or mouse strain whenever υ_i > δ for some threshold δ (see Müller et al., 2007 and Bogdan et al., 2008). It is worth noting that the choice of π generally affects inferences over υ_i but not the resulting ordering of the TCR sequences.

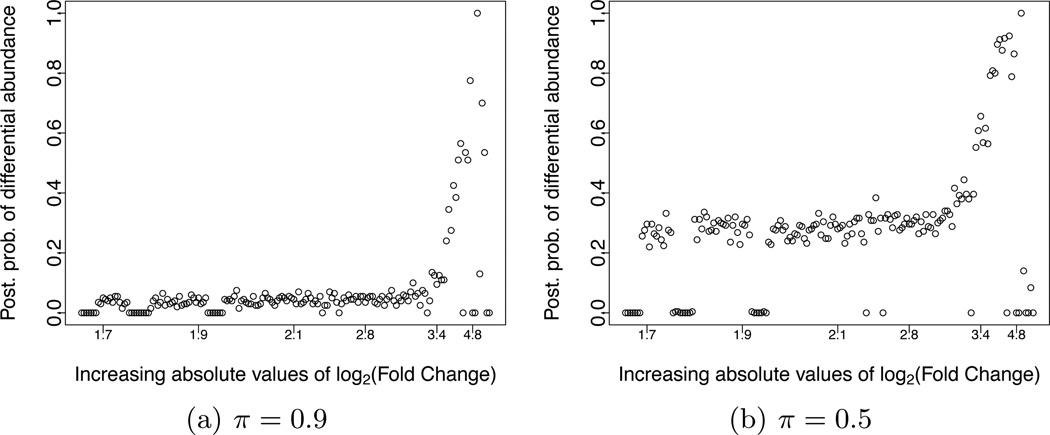
We start by comparing the abundances of each TCR sequence in the diabetic mice data. After pooling samples of the same cell type, we compare counts in regulatory T cells versus conventional T cells. Figure 5 plots the posterior probability υ_i under the proposed model versus the difference on a scale of base 2 logarithm (log₂ fold change) as calculated by the R package EdgeR (Robinson and Smyth, 2007). According to this figure, TCR sequences with differential abundances are usually associated with the highest log₂-fold change difference with few exceptions. The number of differentially abundant TCR sequences, i.e., υ_i δ, decreases rapidly with increasing threshold δ. But for a fixed threshold δ, the number of detections may depend on the choice of π.

Fig. 5.

Comparison of TCR sequence abundances in regulatory and conventional T cells collected diabetic mice. The figure plots υ_i versus the corresponding ranking based on the absolute values of log₂ Fold Changes as computed in EdgeR. The prior probability of differential expression in (8) is set to π = 0.9 (a) and π= 0.5 (b).

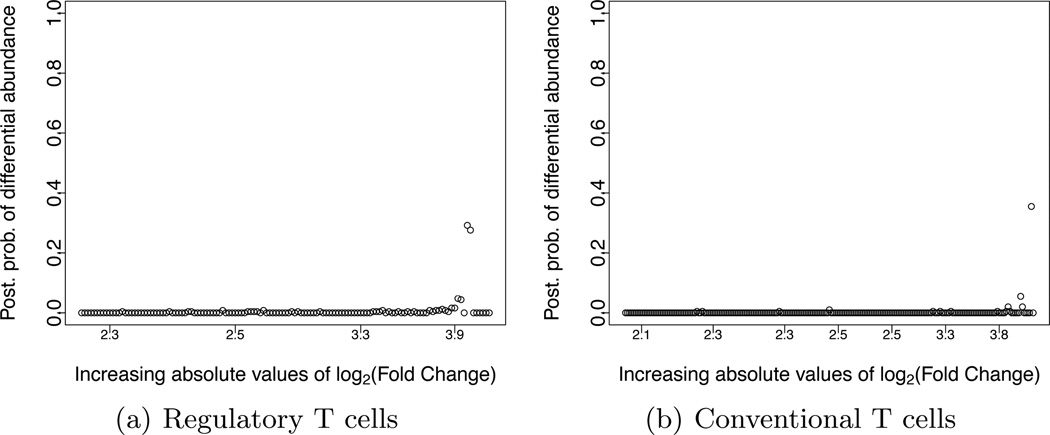
Next we compared counts across healthy versus diabetic mice. Figure 6 shows the comparison, for the regulatory T cells (panel a) and conventional T cells (panel b). The figure plots the posterior probability υ_i versus the log₂-fold change. The figure suggests that there are no TCR sequences with differential abundance across mouse strains. For this analysis we used π = 0.9. A qualitatively similar pattern was observed using π = 0.5 (results not shown), but the corresponding posterior values were inflated.

Fig. 6.

Comparison of TCR sequence abundances between diabetic and health mice: posterior probability of differential abundances across distinct TCR sequences as function of their ranking versus the corresponding ranking based on the absolute values of log₂ Fold Changes as computed in EdgeR for (a) regulatory T cells (b) conventional T cells.

For both comparisons, the R package EdgeR did not report any significantly different abundances. The smallest p-value was greater than 0.25 in all cases. The method by Robinson and Smyth (2007), which is implemented in the EdgeR package, relies on the estimation of a common overdispersion parameter across samples. The estimation of this overdispersion parameter improves with the sample size. However, in some cases, including the T cell sequences considered in this work, the number of sequences available in each sample is limited by the nature of the experiment. Hence, the estimation of a single overdispersion parameter can be particularly challenging and it might affect the overall inferential results.

3.4. Comparison of SAGE Libraries

The previous analysis is now extended to compare 4 libraries of normal and primary cancer colon epithelium tissues. The same data have been analyzed by several authors before (Zhang et al., 1997; Baggerly et al., 2004; Robinson and Smyth, 2007).

The number of unique tags recorded across the 4 libraries is 55,209. We implement model (6) through (8), with π = 0.9, and the specifications of the prior hyperparameters as described in Section 2.4. As a prior for the parameter k, we assumed a Poisson distribution Poi(Ξ), with Ξ = 55, 209. This reflects the prior belief that most tags should already be present in the collected libraries. This prior belief is in close agreement with the data as the mean posterior of the overall k is 56,125 tags. In Figure 7, we plot the percentage of tags assigned to the alternative hypothesis, i.e., 1/n∑_i I(υ_i > δ), against the threshold δ.

Fig. 7.

Percentage of tags that are declared differentially expressed versus the threshold δ in the rule υ_i > δ to determine differential expression. See section 3.3 for details.

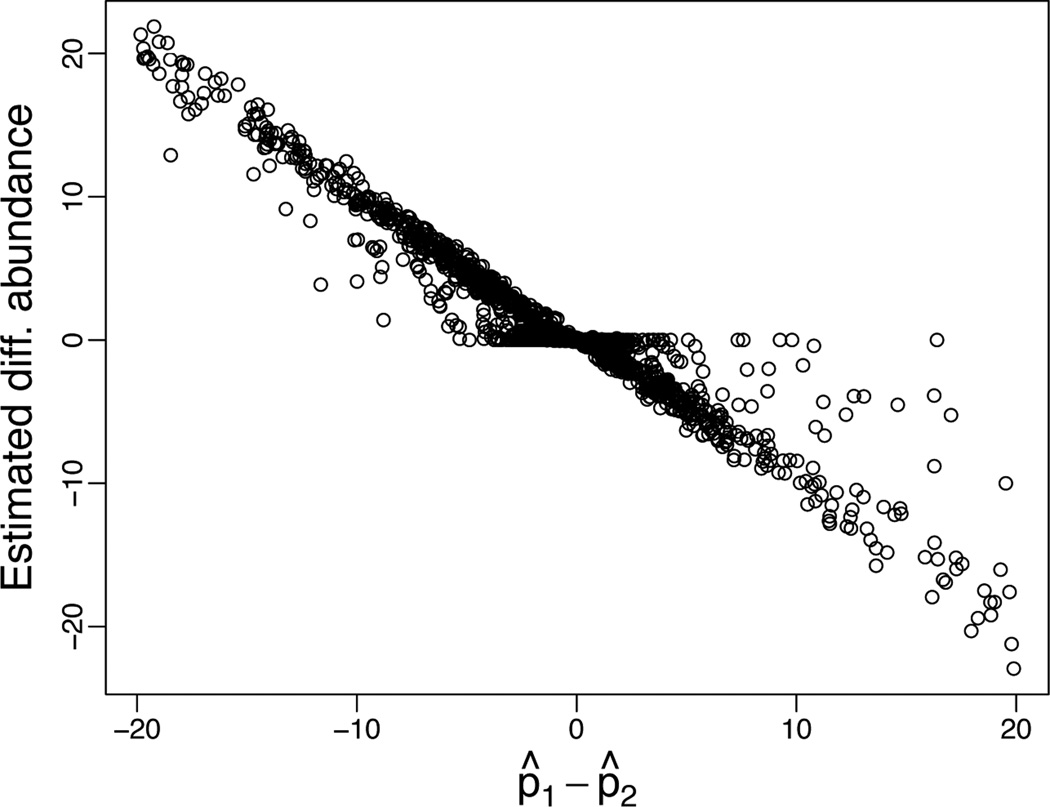
We compare our findings with the methods discussed in Baggerly et al. (2003) and Robinson and Smyth (2007). Baggerly et al. (2003) develop a beta-binomial sampling model to account for within and between library variability and discuss the use of test statistics $t_i^{\omega }=({\widehat{p}}_{i1}-{\widehat{p}}_{i2})/\sqrt{{\widehat{V}}_{i1}+{\widehat{V}}_{i2}}$ for the purpose of group comparisons. Here, p̂_ij, j = 1, 2 is a weighted sum of the proportions of tag i in each group and V̂_ij is an unbiased estimator of the variance of p̂_ij. For example, p̂_ij = ∑_t:xt=j ω_tp̂_it, with p̂_it = y_it/n_t and ω_t = n_t/∑_t:xt=jnt. Figure 8 compares the differences p̂_i1 − p̂_i2, as computed in Baggerly et al. (2003), against the estimated differential expressions from our model, computed as E(λ_i1|data) − E(λ_i2|data). Although the two quantities seem to be overall comparable, we observe many tags for which the difference p̂_i1 − p̂_i2 is significantly different from zero according to Baggerly et al. (2003) but are still assigned to the null hypothesis under the nonparametric prior. One of the reasons for the discrepancy is that our approach allows for “borrowing strength” across tags, whereas the test in Baggerly et al. (2003) works with one tag at a time.

Fig. 8.

Differential abundance estimated according to model (6) through (8) versus the difference of weighted proportions p̂₁ − p̂₂ as in Baggerly et al. (2003) for the SAGE libraries considered in section 3.3. The zoom to absolute differences less than 20 highlights the shrinkage implied by the nonparametric prior.

Finally, we also analyzed the same data with the R package EdgeR (Robinson and Smyth, 2007) and found substantial agreement between that method and ours. More specifically, the package EdgeR identifies 243 tags as differentially expressed with p-values less than 0.01. Out of the first 250 tags that our method flags as differentially expressed, we identify the same list as the one from EdgeR, except for five tags which are assigned probability of differential expression equal to zero by our model. The difference in absolute counts in those 5 cases may be explained by the slightly larger size of the two tumor libraries.

4. Summary

We have discussed a coherent probabilistic framework for the analysis of sequence counts data with a Bayesian semi-parametric approach. The strength of our modeling framework is that it adapts easily to analyze datasets of different dimensions. In particular, we can apply it to small but still overdispersed datasets as those described in sections 2.2 and 3.3, which may pose a challenge for alternative methods that strongly rely on an accurate estimate of some overdispersion parameter (e.g., Robinson and Smyth, 2007). Many experimental techniques imply data censoring in the sense that many sequences might not be observed. We account for unobserved sequences by explicitly modeling the discrepancy between population and sample diversity. We showed how the shrinkage properties implied by the nonparametric prior allow estimation of the true abundance of scarcely represented sequences without affecting the estimation of true expression for more abundant tags. Finally, we showed how our modeling framework can be extended to tackle the general multicomparison problem across samples and conditions.

The implementation of the proposed method is computationally intensive. For example, for the application in section 3, it took a C++ program 1 day to conclude approximately 1,000 iterations on an Intel Quad-Core processor with 4GB memory. The use of fast mixing samplers, such as the Sequentially Allocated Merge-Split (SAMS) sampler by Dahl (2003) is therefore particularly recommended. In particular, the application of this methodology to modern sequencing technologies may require the use of fast approximation algorithms such as the ones described in Blei and Jordan (2006), Daumé III (2007), Wang and Dunson (2011). In addition, models of sequence formation as the one recently proposed by Gilchrist et al. (2007) could be incorporated in the analysis to explicitly account for a varying probability of generating an observable unit across sequences and experiments.

Finally, the proposed corrections for censoring is not needed for all types of sequence count data. For example, for high-throughput data the correction is less meaningful, simply because censoring at zero counts is not an issue in that context with large total counts.