Significance
Understanding the complexity of anisotropic turbulent processes in engineering and environmental fluid flows is a formidable challenge with practical significance because energy often flows intermittently from the smaller scales to impact the largest scales in these flows. These complex features strongly impact practical prediction, uncertainty quantification, and data assimilation strategies in such anisotropic turbulent systems. The large scales in turbulence are chaotic whereas the small scales with low variance have relatively frequent extreme events––intermittency––which can impact the large scales. Here conceptual dynamical models of turbulence are developed which, despite their simplicity, capture many of these key features of anisotropic turbulent systems in a qualitative fashion. The paper is a self-contained treatment of these conceptual models and their properties.
Keywords: wave–mean interaction, stochastic model
Abstract
Understanding the complexity of anisotropic turbulent processes in engineering and environmental fluid flows is a formidable challenge with practical significance because energy often flows intermittently from the smaller scales to impact the largest scales in these flows. Conceptual dynamical models for anisotropic turbulence are introduced and developed here which, despite their simplicity, capture key features of vastly more complicated turbulent systems. These conceptual models involve a large-scale mean flow and turbulent fluctuations on a variety of spatial scales with energy-conserving wave–mean-flow interactions as well as stochastic forcing of the fluctuations. Numerical experiments with a six-dimensional conceptual dynamical model confirm that these models capture key statistical features of vastly more complex anisotropic turbulent systems in a qualitative fashion. These features include chaotic statistical behavior of the mean flow with a sub-Gaussian probability distribution function (pdf) for its fluctuations whereas the turbulent fluctuations have decreasing energy and correlation times at smaller scales, with nearly Gaussian pdfs for the large-scale fluctuations and fat-tailed non-Gaussian pdfs for the smaller-scale fluctuations. This last feature is a manifestation of intermittency of the small-scale fluctuations where turbulent modes with small variance have relatively frequent extreme events which directly impact the mean flow. The dynamical models introduced here potentially provide a useful test bed for algorithms for prediction, uncertainty quantification, and data assimilation for anisotropic turbulent systems.
Understanding the complexity of anisotropic turbulence processes over a wide range of spatiotemporal scales in engineering shear turbulence (1–3) as well as climate atmosphere ocean science (4–6) is a grand challenge of contemporary science. This is especially important from a practical viewpoint because energy often flows intermittently from the smaller scales to affect the largest scales in such anisotropic turbulent flows. The typical features of such anisotropic turbulent flows are the following (2–4):
-
(A)
The large-scale mean flow is usually chaotic but more predictable than the smaller-scale fluctuations. The overall single point probability distribution function (pdf) of the flow field is nearly Gaussian whereas the mean flow pdf is sub-Gaussian, in other words, with less extreme variability than a Gaussian random variable.
-
(B)
There are nontrivial nonlinear interactions between the large-scale mean flow and the smaller-scale fluctuations which conserve energy.
-
(C)
There is a wide range of spatial scales for the fluctuations with features where the large-scale components of the fluctuations contain more energy than the smaller-scale components. Furthermore, these large-scale fluctuating components decorrelate faster in time than the mean-flow fluctuations on the largest scales, whereas the smaller-scale fluctuating components decorrelate faster in time than the larger-scale fluctuating components.
-
(D)
The pdfs of the larger-scale fluctuating components of the turbulent field are nearly Gaussian, whereas the smaller-scale fluctuating components are intermittent and have fat-tailed pdfs, in other words, a much higher probability of extreme events than a Gaussian distribution (see figures 8.4 and 8.5 from ref. 3 for such experimental features in a turbulent jet).
The goal here is to develop the simplest conceptual dynamical model for anisotropic turbulence that captures all of the features in (A)–(D) in a transparent qualitative fashion. In contrast with deterministic models of turbulence which are derived by Galerkin truncation of the Navier–Stokes equation (7) and do not display all of the features in (A)–(D), the conceptual models developed here are low-dimensional stochastic dynamical systems; the nonlinear interactions between the large-scale mean-flow component and the smaller-scale fluctuating components are completely deterministic but the potential direct nonlinear interactions between the smaller-scale fluctuating components are modeled stochastically by damping and stochastic forcing (6, 8). The conceptual models developed here are not derived quantitatively from the Navier–Stokes equations but are developed to capture the key features in anisotropic turbulent flows listed in (A)–(D) by mimicking key physical processes. Besides aiding the understanding of anisotropic turbulent flows, such conceptual models are useful for designing and testing numerical algorithms for prediction and data assimilation in such complex turbulent systems.
Conceptual Model
The model has a mean scalar variable 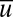 representing the largest scales and a family of small-scale variables
representing the largest scales and a family of small-scale variables  so that there are
so that there are 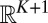 variables in the system
variables in the system 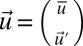 . The variables
. The variables 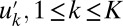 represent contributions to the turbulent fluctuations from increasingly smaller scales as k increases with
represent contributions to the turbulent fluctuations from increasingly smaller scales as k increases with
 |
the turbulent fluctuations. One can think of 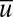 as the large-scale spatial average of the turbulent dynamics at a single grid point in a more complex system and
as the large-scale spatial average of the turbulent dynamics at a single grid point in a more complex system and 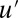 as the turbulent fluctuations at the grid point with
as the turbulent fluctuations at the grid point with
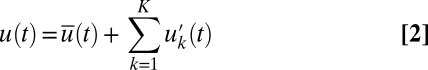 |
the total turbulent field. To add a sense of spatial scale, one can also regard 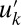 as the amplitude of the kth Fourier cosine mode evaluated at a grid point but such an interpretation is not necessary here. Note that the large-scale mean
as the amplitude of the kth Fourier cosine mode evaluated at a grid point but such an interpretation is not necessary here. Note that the large-scale mean 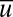 can have fluctuating, chaotic dynamics in time through interactions with turbulence and its own intrinsic dynamics. The nonlinear interactions in turbulence conserve the total energy of the mean and fluctuations and a key feature of the conceptual model is to use nonlinear interactions which conserve the energy E, which we take as given by
can have fluctuating, chaotic dynamics in time through interactions with turbulence and its own intrinsic dynamics. The nonlinear interactions in turbulence conserve the total energy of the mean and fluctuations and a key feature of the conceptual model is to use nonlinear interactions which conserve the energy E, which we take as given by
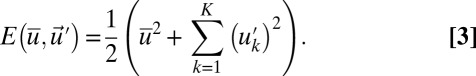 |
A hallmark of turbulence is that the large scales can destabilize the smaller scales in the turbulent fluctuations intermittently and this increased small-scale energy can impact the large scales; this key feature is captured in the conceptual models. With the above discussion, here are the simplest models with all these features, the conceptual dynamical models for turbulence:
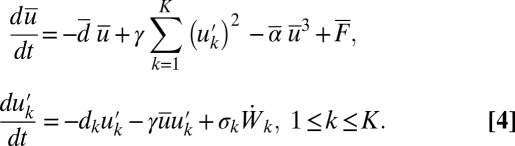 |
The reader can think of 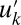 as the amplitude of the kth Fourier cosine mode to aid the interpretation of the model but this is not necessary here. The system of
as the amplitude of the kth Fourier cosine mode to aid the interpretation of the model but this is not necessary here. The system of 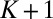 dimensional stochastic differential equations in 4 is written in physicist’s notation with
dimensional stochastic differential equations in 4 is written in physicist’s notation with 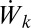 independent white noises for each k but the system in 4 is always interpreted in the Ito sense below. The reader easily verifies that the nonlinear interactions in 4 conserve the energy E in 3, which can be modified by the linear terms, the external forcing
independent white noises for each k but the system in 4 is always interpreted in the Ito sense below. The reader easily verifies that the nonlinear interactions in 4 conserve the energy E in 3, which can be modified by the linear terms, the external forcing 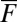 , nonlinearity of the large scales, and the random forcing of the small scales. The turbulence dissipation coefficients
, nonlinearity of the large scales, and the random forcing of the small scales. The turbulence dissipation coefficients 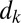 for
for 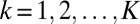 are positive,
are positive, 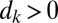 , in order for the turbulence to have a statistical steady state but the coefficient
, in order for the turbulence to have a statistical steady state but the coefficient 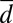 for the large scales can be either positive or negative reflecting large-scale instability. When
for the large scales can be either positive or negative reflecting large-scale instability. When 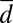 is negative so there is instability on the large scales we add the stabilizing cubic term with
is negative so there is instability on the large scales we add the stabilizing cubic term with 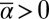 whereas for positive
whereas for positive 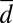 we assume
we assume 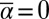 ; both cases are studied below. The external force
; both cases are studied below. The external force 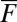 is a constant which is varied below to mimic fully turbulent regimes with (A)–(D). For a fixed coefficient of nonlinear interaction
is a constant which is varied below to mimic fully turbulent regimes with (A)–(D). For a fixed coefficient of nonlinear interaction 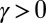 , there is local growth and instability in time for the kth turbulent scale provided that
, there is local growth and instability in time for the kth turbulent scale provided that
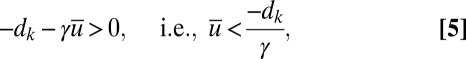 |
and chaotic fluctuations of 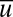 will create intermittency in
will create intermittency in 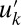 through this mechanism. Thus, the overall system can have a statistical steady state whereas there is intermittent instability on the small scales which increases their energy and impacts the large scales, creating non-Gaussian intermittent behavior in the system. With
through this mechanism. Thus, the overall system can have a statistical steady state whereas there is intermittent instability on the small scales which increases their energy and impacts the large scales, creating non-Gaussian intermittent behavior in the system. With 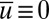 , the equation for the kth turbulent scale
, the equation for the kth turbulent scale 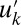 is a simple Langevin process with Gaussian statistical steady state with zero mean and variance
is a simple Langevin process with Gaussian statistical steady state with zero mean and variance 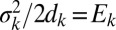 ; it is natural to pick these energy densities to have power-law behavior for this energy spectrum, i.e.,
; it is natural to pick these energy densities to have power-law behavior for this energy spectrum, i.e.,
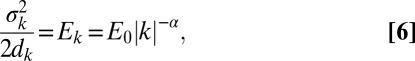 |
with 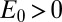 and
and 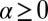 fixed constants (8). For example,
fixed constants (8). For example, 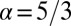 corresponds to the Kolmogorov spectrum (3, 8). Note that we could allow coefficient γ in 4 to vary with k for
corresponds to the Kolmogorov spectrum (3, 8). Note that we could allow coefficient γ in 4 to vary with k for 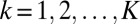 but we refrain from discussing this generalization here. On the other hand, it is natural to have the damping
but we refrain from discussing this generalization here. On the other hand, it is natural to have the damping 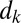 vary with k to represent various dissipative processes such as viscosity or Ekman friction (8). This completes the description of the conceptual models.
vary with k to represent various dissipative processes such as viscosity or Ekman friction (8). This completes the description of the conceptual models.
Mathematical Properties
Note that the equation for the large-scale mean 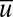 is deterministic and without any direct stochastic forcing; this deterministic structure mimics that at the large scales for realistic turbulent flows. Nevertheless, the large-scale mean
is deterministic and without any direct stochastic forcing; this deterministic structure mimics that at the large scales for realistic turbulent flows. Nevertheless, the large-scale mean 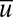 interacts with the fluctuations
interacts with the fluctuations 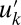 which are stochastically forced. We claim that even with the above degenerate noise, the conceptual models in 4 are geometrically ergodic (9); in other words, for any value of
which are stochastically forced. We claim that even with the above degenerate noise, the conceptual models in 4 are geometrically ergodic (9); in other words, for any value of 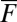 , a unique smooth ergodic invariant measure exists with exponential convergence of suitable statistics from time averages in the long time limit. To prove this, we apply the main theorem in ref. 9 with the Lyapunov function given by the total energy in 3. Two things need to be checked; the first is the coercivity of the generator applied to the Lyapunov function which is immediately satisfied given our hypotheses; the second condition is the hypoellipticity of the generator of 4. To check hypoellipticity we consider the K-vector fields
, a unique smooth ergodic invariant measure exists with exponential convergence of suitable statistics from time averages in the long time limit. To prove this, we apply the main theorem in ref. 9 with the Lyapunov function given by the total energy in 3. Two things need to be checked; the first is the coercivity of the generator applied to the Lyapunov function which is immediately satisfied given our hypotheses; the second condition is the hypoellipticity of the generator of 4. To check hypoellipticity we consider the K-vector fields
and
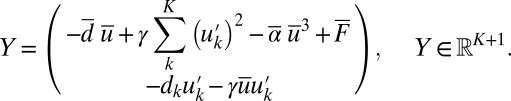 |
We only need to show that 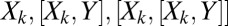 span all of
span all of 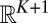 where
where 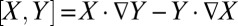 is the Lie bracket. Because
is the Lie bracket. Because 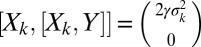 and the
and the 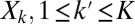 span the orthogonal complement, hypoellipticity is satisfied.
span the orthogonal complement, hypoellipticity is satisfied.
Phase Plane Analysis
Here we develop intuition regarding the parameters of the conceptual models which provide important guidelines to demonstrate below that these models with 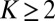 can capture all of the features of anisotropic turbulence listed in (A)–(D) above. For such intuition, there is a revealing phase plane analysis of the 2D system for
can capture all of the features of anisotropic turbulence listed in (A)–(D) above. For such intuition, there is a revealing phase plane analysis of the 2D system for 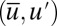 which is the special case of the model in 4 where
which is the special case of the model in 4 where 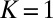 and without noise. This system is given by
and without noise. This system is given by
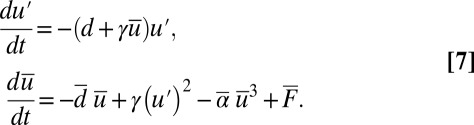 |
The linear subspace 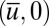 is invariant for the dynamics which reduces on this subspace to the scalar equation
is invariant for the dynamics which reduces on this subspace to the scalar equation
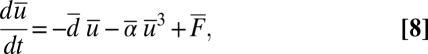 |
whereas the general dynamics of 7 is invariant under the flip symmetry 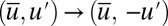 . Thus, there are between one and three critical points of 7 with the form
. Thus, there are between one and three critical points of 7 with the form 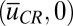 as
as 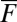 varies, provided that
varies, provided that 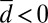 and
and 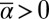 and only a single critical point of the form
and only a single critical point of the form 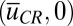 with
with 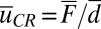 for
for 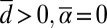 ; regardless of these stability properties along the
; regardless of these stability properties along the 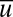 axis, such critical points are unstable to
axis, such critical points are unstable to 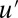 perturbations if and only if
perturbations if and only if 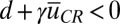 , i.e., the instability condition in 5 is satisfied. For suitable values of
, i.e., the instability condition in 5 is satisfied. For suitable values of 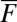 , there is another family of critical points for 7 with the form
, there is another family of critical points for 7 with the form 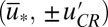 where
where
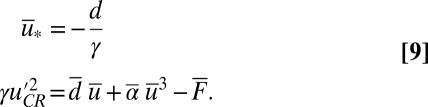 |
Note that 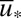 is exactly the critical value of neutral stability from 5 for the conceptual model. The linear stability matrix at these critical points for 7 has the form
is exactly the critical value of neutral stability from 5 for the conceptual model. The linear stability matrix at these critical points for 7 has the form
 |
with 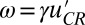 so these critical points are stable (unstable) if and only if
so these critical points are stable (unstable) if and only if 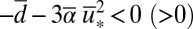 .
.
To develop guidelines in choosing parameters for the numerical experiments for 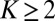 with the conceptual model in 4, we consider the phase plane analysis in two scenarios with positive and negative large-scale damping. In both cases, the parameters
with the conceptual model in 4, we consider the phase plane analysis in two scenarios with positive and negative large-scale damping. In both cases, the parameters 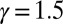 and
and 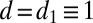 are fixed below, whereas for
are fixed below, whereas for
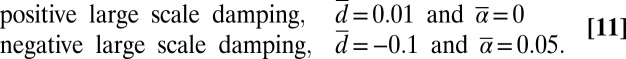 |
First consider positive large-scale damping; the two critical points 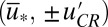 occur for
occur for 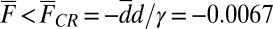 and are both stable by the criterion in 10, whereas the critical point
and are both stable by the criterion in 10, whereas the critical point 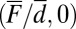 along the
along the 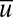 axis is unstable to
axis is unstable to 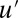 perturbation provided
perturbation provided 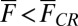 . Because the energy is a Lyapunov function for 7, trajectories off the
. Because the energy is a Lyapunov function for 7, trajectories off the 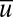 axis converge to either of the critical points
axis converge to either of the critical points 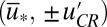 with
with 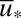 the marginally stable value; thus we can expect more turbulent behavior in the conceptual stochastic models with
the marginally stable value; thus we can expect more turbulent behavior in the conceptual stochastic models with 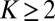 as the forcing
as the forcing 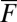 increases in magnitude through negative values,
increases in magnitude through negative values, 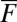 with
with 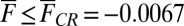 . A similar scenario occurs for the case with negative damping in 7 for
. A similar scenario occurs for the case with negative damping in 7 for 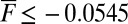 with a single critical point along the
with a single critical point along the 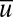 axis which is unstable to perturbations in
axis which is unstable to perturbations in 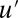 with two critical points
with two critical points 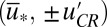 ,
, 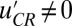 , which are also unstable because
, which are also unstable because  ; in this case, with all three equilibrium points unstable, trajectories off the
; in this case, with all three equilibrium points unstable, trajectories off the 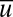 axis necessarily converge to periodic orbits encircling the critical points
axis necessarily converge to periodic orbits encircling the critical points 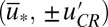 and frequently visit values of
and frequently visit values of 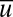 with instability in the
with instability in the 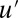 dynamics. We also anticipate different behavior for
dynamics. We also anticipate different behavior for 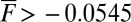 because a stable critical point appears at
because a stable critical point appears at 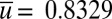 for this and larger values of
for this and larger values of 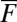 . See the tables in SI Appendix.
. See the tables in SI Appendix.
Numerical Experiments for K = 5 in the Conceptual Model
Here we use simple numerical experiments to demonstrate that the six-dimensional conceptual model in 4 with 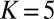 has all of the statistical features listed in (A)–(D) including intermittency of the small scales. The parameters
has all of the statistical features listed in (A)–(D) including intermittency of the small scales. The parameters 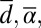 and
and 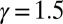 have already been discussed in 11. The damping coefficients
have already been discussed in 11. The damping coefficients 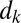 are a mixture of uniform and scale-selective damping with
are a mixture of uniform and scale-selective damping with 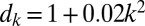 for
for 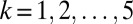 so that the smaller scales are damped more rapidly; the noise level set by
so that the smaller scales are damped more rapidly; the noise level set by 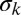 for the kth mode is determined by
for the kth mode is determined by
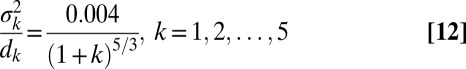 |
so that a −5/3 spectrum is calibrated to occur for these modes provided 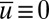 in the equations for
in the equations for 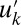 (8). This specifies all parameters in the conceptual model for turbulence used here. For all numerical simulations below and in SI Appendix, the Euler–Maruyama method is used with a time step
(8). This specifies all parameters in the conceptual model for turbulence used here. For all numerical simulations below and in SI Appendix, the Euler–Maruyama method is used with a time step 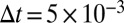 and the system is integrated for a long time
and the system is integrated for a long time 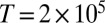 with the first
with the first 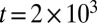 time data ignored for postprocessing the equilibrium statistics. In all simulations the initial value is
time data ignored for postprocessing the equilibrium statistics. In all simulations the initial value is 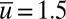 with
with 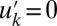 for
for 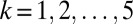 .
.
First we consider the case with large-scale instability for 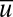 with negative damping,
with negative damping,  and
and 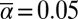 with the forcing value
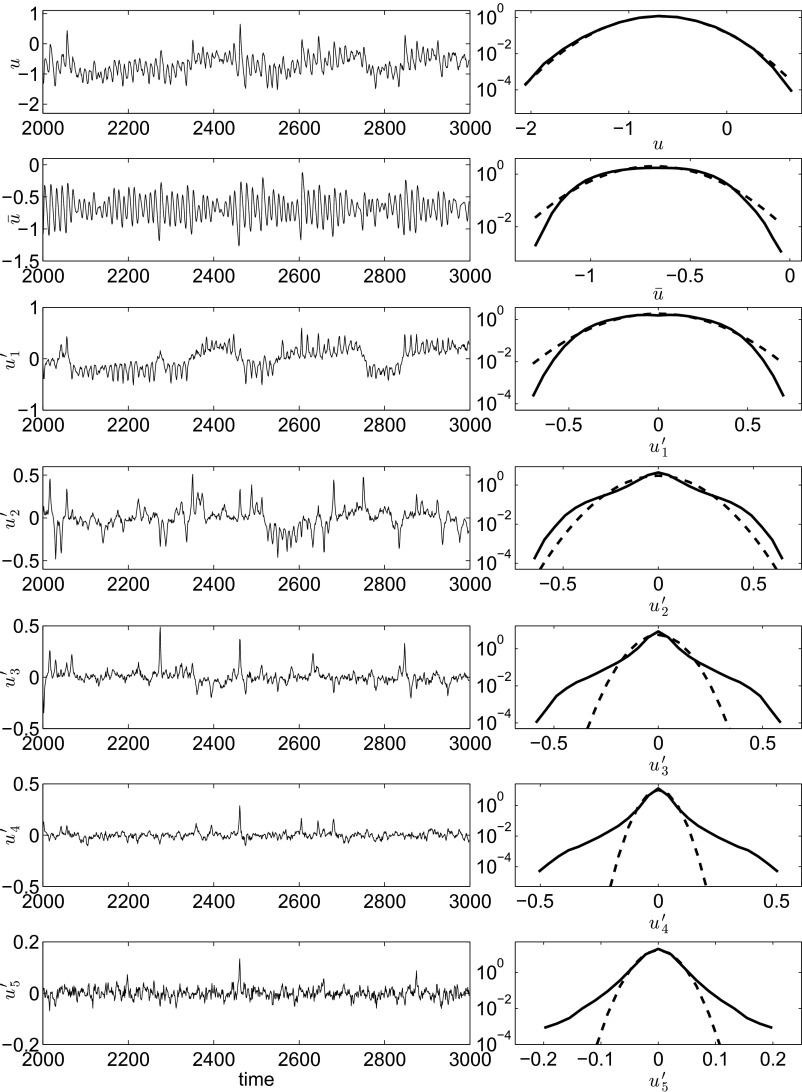
with the forcing value 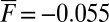 motivated by the phase portrait analysis above. Fig. 1 depicts the pdfs for the total turbulent field u, the large-scale mean
motivated by the phase portrait analysis above. Fig. 1 depicts the pdfs for the total turbulent field u, the large-scale mean  , and the turbulent fluctuations
, and the turbulent fluctuations 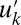 ,
, 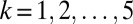 as well as a sample of the time series of each variable in the conceptual model; the pdfs are plotted with a logarithmic vertical coordinate to highlight fat tails of intermittency whereas the Gaussian distribution with the same variance is the parabola in the figure. The pdf for the overall turbulent field u in 2 is nearly Gaussian whereas the pdfs for the mean
as well as a sample of the time series of each variable in the conceptual model; the pdfs are plotted with a logarithmic vertical coordinate to highlight fat tails of intermittency whereas the Gaussian distribution with the same variance is the parabola in the figure. The pdf for the overall turbulent field u in 2 is nearly Gaussian whereas the pdfs for the mean 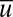 and the largest scale fluctuating mode
and the largest scale fluctuating mode 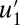 are both slightly sub-Gaussian. The variable
are both slightly sub-Gaussian. The variable 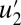 has a Gaussian tail whereas the variables
has a Gaussian tail whereas the variables 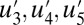 all have significant fat tails, which are a hallmark of intermittency. The time series for
all have significant fat tails, which are a hallmark of intermittency. The time series for 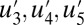 in Fig. 1 clearly display highly intermittent behavior of extreme values, with the amplitude of
in Fig. 1 clearly display highly intermittent behavior of extreme values, with the amplitude of 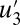 occasionally spiking to the typical amplitude of
occasionally spiking to the typical amplitude of 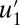 even though the statistical equilibrium variance of
even though the statistical equilibrium variance of 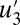 is nearly eight times smaller than that for
is nearly eight times smaller than that for 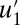 (see SI Appendix, Table S2). The statistical equilibrium mean value for
(see SI Appendix, Table S2). The statistical equilibrium mean value for 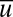 is
is 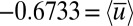 and
and 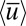 is very close to the marginal stability value
is very close to the marginal stability value 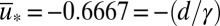 motivated from 7 whereas the standard deviation of
motivated from 7 whereas the standard deviation of 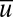 is 0.1993, indicating that the instability mechanism elucidated in 5 is operating on all modes and creating intermittency. The total energy of the mean flow
is 0.1993, indicating that the instability mechanism elucidated in 5 is operating on all modes and creating intermittency. The total energy of the mean flow 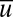 exceeds that of the fluctuations
exceeds that of the fluctuations 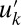 . The variables
. The variables 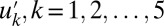 have essentially zero means with variances 0.0446, 0.0174, 0.0049, 0.0014, and 0.0005, respectively, with the correlation time for
have essentially zero means with variances 0.0446, 0.0174, 0.0049, 0.0014, and 0.0005, respectively, with the correlation time for 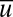 ∼34, whereas those for
∼34, whereas those for 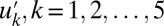 are decreasing with k and ∼29, 16, 6, 4, and 3, respectively. These are all of the features of anisotropic turbulence required from (A)–(D) and demonstrated in the conceptual dynamical models; furthermore, all of these conditions occur in a robust fashion for
are decreasing with k and ∼29, 16, 6, 4, and 3, respectively. These are all of the features of anisotropic turbulence required from (A)–(D) and demonstrated in the conceptual dynamical models; furthermore, all of these conditions occur in a robust fashion for 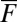 increasing in magnitude with
increasing in magnitude with 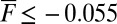 and
and 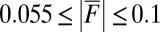 . All of the detailed data discussed above can be found in SI Appendix, Tables S1–S3. There is an evident role for the unstable damping of the large scales
. All of the detailed data discussed above can be found in SI Appendix, Tables S1–S3. There is an evident role for the unstable damping of the large scales 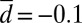 to increase the variance of
to increase the variance of 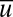 with its mean near the marginally critical value
with its mean near the marginally critical value 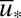 so that the instability mechanism from 5 operates vigorously in the model and creates more variance in
so that the instability mechanism from 5 operates vigorously in the model and creates more variance in 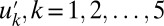 . Thus, we expect the system with stable damping and the same values of
. Thus, we expect the system with stable damping and the same values of 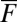 with
with 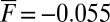 to have less variance.
to have less variance.
Fig. 1.
Negative large-scale damping: time series (Left) and pdfs (Right) of the turbulent signal u,  and
and 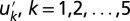 with
with 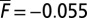 . Note the logarithmic scale of pdfs in the y axis. Dashed lines are Gaussian distributions with the same mean and variance.
. Note the logarithmic scale of pdfs in the y axis. Dashed lines are Gaussian distributions with the same mean and variance.
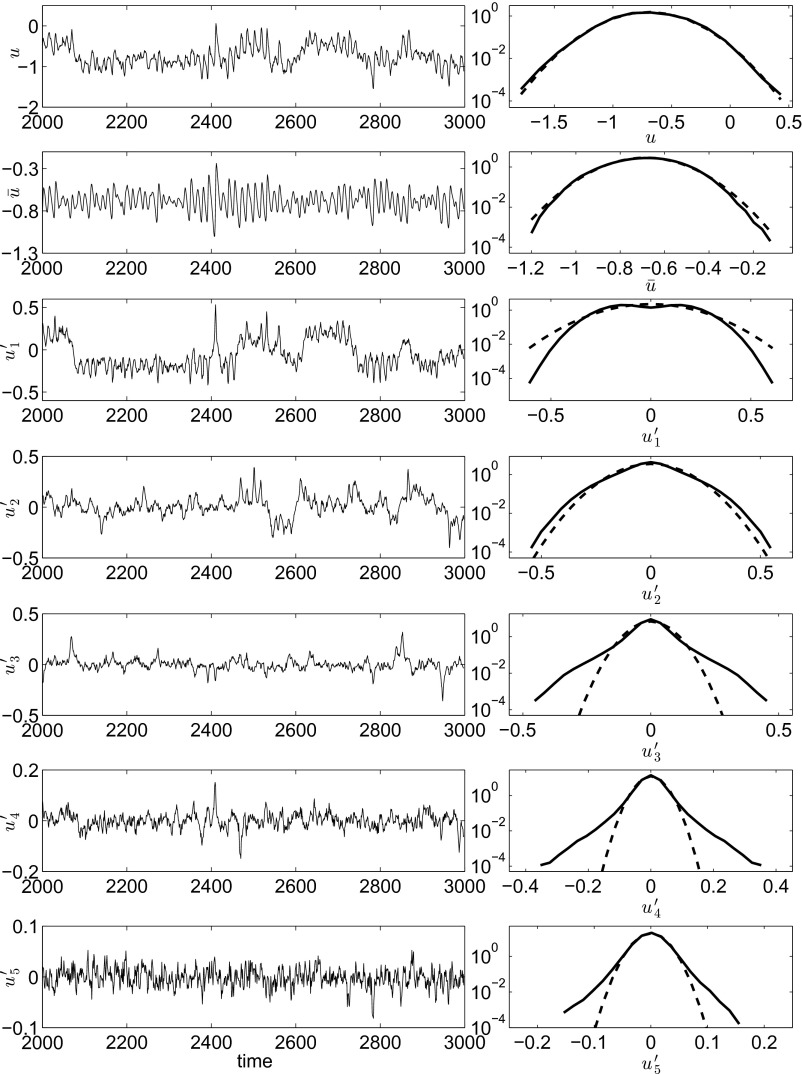
We consider the case with positive large-scale damping, 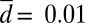 , for
, for 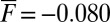 ; in Fig. 2 we show the pdfs of all variables as well as a piece of the time series of the turbulent signal
; in Fig. 2 we show the pdfs of all variables as well as a piece of the time series of the turbulent signal 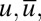 and
and 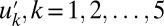 . The intermittency of the small-scale modes with less variance is evident in Fig. 2. The mean-flow variable
. The intermittency of the small-scale modes with less variance is evident in Fig. 2. The mean-flow variable 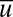 has the largest total energy with equilibrium statistical mean
has the largest total energy with equilibrium statistical mean 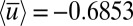 , which is very close to the marginal critical values
, which is very close to the marginal critical values 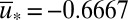 so the intermittent instability mechanism in 5 is operating once again. Both the variances and correlation times behave in a similar fashion as for the negative large-scale damping case discussed above and as required in (A)–(D) so the conceptual model with positive large-scale damping also is a qualitative dynamical model for anisotropic turbulence with all of the features in (A)–(D). Furthermore, all of these features persist for
so the intermittent instability mechanism in 5 is operating once again. Both the variances and correlation times behave in a similar fashion as for the negative large-scale damping case discussed above and as required in (A)–(D) so the conceptual model with positive large-scale damping also is a qualitative dynamical model for anisotropic turbulence with all of the features in (A)–(D). Furthermore, all of these features persist for 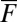 with
with 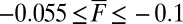 ; the pdfs are all Gaussian with no fat tails for
; the pdfs are all Gaussian with no fat tails for 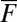 with sufficiently small absolute value such as
with sufficiently small absolute value such as 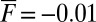 , as shown in SI Appendix. As expected from our discussion of the unstable case, for fixed forcing with
, as shown in SI Appendix. As expected from our discussion of the unstable case, for fixed forcing with 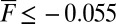 there is between a factor of 2 and 3 less variance in all variables in the positive large-scale damping case compared with the negative large-scale damping case. Documentation for all of the above claims is found in extensive tables in SI Appendix. For both cases cross-correlation among the variables
there is between a factor of 2 and 3 less variance in all variables in the positive large-scale damping case compared with the negative large-scale damping case. Documentation for all of the above claims is found in extensive tables in SI Appendix. For both cases cross-correlation among the variables 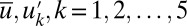 is negligible in the statistical equilibrium mean with values roughly less than the 5% level.
is negligible in the statistical equilibrium mean with values roughly less than the 5% level.
Fig. 2.
Positive large-scale damping: time series (Left) and pdfs (Right) of the turbulent signal u,  and
and 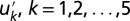 with
with 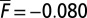 . Note the logarithmic scale of pdfs in the y axis. Dashed lines are Gaussian distributions with the same mean and variance.
. Note the logarithmic scale of pdfs in the y axis. Dashed lines are Gaussian distributions with the same mean and variance.
In the above paragraphs, we emphasized models with 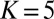 to mimic the many degrees of freedom in real anisotropic turbulence and their interaction with the mean flow. From a mathematical viewpoint, it is interesting to address the following: what is the lowest dimensional conceptual model with intermittency and satisfying all of the requirements in (A)–(D)? Versions of the conceptual model with
to mimic the many degrees of freedom in real anisotropic turbulence and their interaction with the mean flow. From a mathematical viewpoint, it is interesting to address the following: what is the lowest dimensional conceptual model with intermittency and satisfying all of the requirements in (A)–(D)? Versions of the conceptual model with 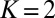 already exhibit intermittency in
already exhibit intermittency in  as well as all of the other features required in (A)–(D) for both positive and negative damping as shown in SI Appendix. However, the two mode models with
as well as all of the other features required in (A)–(D) for both positive and negative damping as shown in SI Appendix. However, the two mode models with 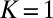 always exhibit either sub-Gaussian or at most Gaussian behavior in
always exhibit either sub-Gaussian or at most Gaussian behavior in 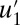 without intermittency as the noise level is varied in all of our numerical experiments.
without intermittency as the noise level is varied in all of our numerical experiments.
Concluding Discussion
Conceptual dynamical models for anisotropic turbulence have been introduced here which, despite their simplicity, capture key features of vastly more complicated systems. The conceptual dynamical models introduced here in 4 involve a large-scale mean flow 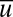 and turbulent fluctuations,
and turbulent fluctuations, 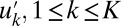 , on a variety of spatial scales and involve energy-conserving wave–mean-flow interactions as well as suitable degenerate stochastic forcing of the fluctuations
, on a variety of spatial scales and involve energy-conserving wave–mean-flow interactions as well as suitable degenerate stochastic forcing of the fluctuations 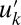 . The models have a transparent mechanism where the mean flow
. The models have a transparent mechanism where the mean flow 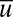 can destabilize the kth mode whenever
can destabilize the kth mode whenever 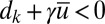 ; a phase plane analysis yields parameters and robust regimes of sufficiently strong large-scale external forcing
; a phase plane analysis yields parameters and robust regimes of sufficiently strong large-scale external forcing 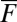 , where the models have a statistical equilibrium mean
, where the models have a statistical equilibrium mean 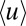 which is nearly neutrally stable in the sense that
which is nearly neutrally stable in the sense that 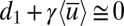 so that fluctuations in the mean
so that fluctuations in the mean 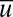 often introduce intermittent instability. Numerical experiments with a six-dimensional version of the model summarized here and in SI Appendix confirm that it captures key statistical features of vastly more complex anisotropic turbulent systems. These include chaotic statistical behavior of the mean flow
often introduce intermittent instability. Numerical experiments with a six-dimensional version of the model summarized here and in SI Appendix confirm that it captures key statistical features of vastly more complex anisotropic turbulent systems. These include chaotic statistical behavior of the mean flow 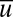 with a sub-Gaussian pdf for its fluctuations, whereas the turbulent fluctuations
with a sub-Gaussian pdf for its fluctuations, whereas the turbulent fluctuations  have decreasing energy and correlation times as k increases with nearly Gaussian pdfs for the large-scale fluctuations and fat-tailed non-Gaussian pdfs for the smaller-scale fluctuations; this last feature allows for intermittency of the small-scale fluctuations where turbulent modes with small variance can have relatively frequent large-amplitude extreme events which directly impact the mean flow
have decreasing energy and correlation times as k increases with nearly Gaussian pdfs for the large-scale fluctuations and fat-tailed non-Gaussian pdfs for the smaller-scale fluctuations; this last feature allows for intermittency of the small-scale fluctuations where turbulent modes with small variance can have relatively frequent large-amplitude extreme events which directly impact the mean flow 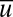 . Remarkably, vastly more complex realistic turbulent systems often exhibit such marginal critical behavior on average (4). As mentioned above (1 and 2), we can regard
. Remarkably, vastly more complex realistic turbulent systems often exhibit such marginal critical behavior on average (4). As mentioned above (1 and 2), we can regard 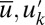 for
for 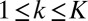 as defining turbulent fluctuations at a grid point in a vastly more complex spatially extended system. There are straightforward generalizations of the conceptual model to allow for many large-scale grid points
as defining turbulent fluctuations at a grid point in a vastly more complex spatially extended system. There are straightforward generalizations of the conceptual model to allow for many large-scale grid points 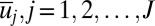 with associated turbulent fluctuations
with associated turbulent fluctuations 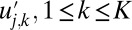 satisfying a coupled system of equations on the large scales,
satisfying a coupled system of equations on the large scales,
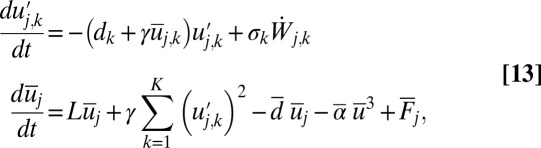 |
where L can be a linear or nonlinear operator coupling the 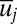 . The conceptual models in 13 are nonlinear generalizations with transparent physical mechanisms of those introduced to study stochastic superparameterization in anisotropic turbulence (6, 10). Besides their role as qualitative analog models of vastly more complicated anisotropic turbulence, the conceptual dynamical models introduced here are potentially useful as a simplified test bed for algorithms and strategies for prediction, uncertainty quantification (11), and data assimilation (8) in vastly more complex anisotropic turbulent systems. It also would be interesting to derive the limiting statistical behavior of the conceptual models as the number of fluctuating components k becomes large.
. The conceptual models in 13 are nonlinear generalizations with transparent physical mechanisms of those introduced to study stochastic superparameterization in anisotropic turbulence (6, 10). Besides their role as qualitative analog models of vastly more complicated anisotropic turbulence, the conceptual dynamical models introduced here are potentially useful as a simplified test bed for algorithms and strategies for prediction, uncertainty quantification (11), and data assimilation (8) in vastly more complex anisotropic turbulent systems. It also would be interesting to derive the limiting statistical behavior of the conceptual models as the number of fluctuating components k becomes large.
Supplementary Material
Acknowledgments
The research of A.J.M. is partially supported by Office of Naval Research (ONR) Grants, ONR-Departmental Research Initiative N0014-10-1-0554, ONR N0014-11-1-0306, and ONR Multidisciplinary University Research Initiative 25-74200-F7112. Y.L. is supported as a Postdoctoral Research Fellow on this last award.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1404914111/-/DCSupplemental.
References
- 1.Hinze J. Turbulence: An Introduction to Its Mechanisms and Theory. New York: McGraw-Hill; 1959. [Google Scholar]
- 2.Townsend AA. The Structure of Turbulent Shear Flow. Cambridge, MA: Cambridge Univ Press; 1976. [Google Scholar]
- 3.Frisch U. Turbulence. New York: Cambridge Univ Press; 1995. [Google Scholar]
- 4.Vallis GK. Atmospheric and Oceanic Fluid Dynamics: Fundamentals and Large-Scale Circulation. Cambridge, MA: Cambridge Univ Press; 2006. [Google Scholar]
- 5.Salmon R. Lectures on Geophysical Fluid Dynamics. New York: Oxford Univ Press; 1998. [Google Scholar]
- 6.Majda AJ, Grooms I. 2014. New perspectives on superparameterization for geophysical turbulence, J Comput Phys, 10.1016/j.jcp.2013.09.014.
- 7.Holmes P, Lumley JL, Berkooz G. Turbulence, Coherent Structures, Dynamical Systems and Symmetry. New York: Cambridge Univ Press; 1996. [Google Scholar]
- 8.Majda AJ, Harlim J. Filtering Complex Turbulent Systems. New York: Cambridge Univ Press; 2012. [Google Scholar]
- 9.Mattingly JC, Stuart AM, Higham DJ. Ergodicity for SDEs and approximations: Locally Lipschitz vector fields and degenerate noise. Stoch Proc Appl. 2002;101(2):185–232. [Google Scholar]
- 10.Majda AJ, Grote MJ. Mathematical test models for superparametrization in anisotropic turbulence. Proc Natl Acad Sci USA. 2009;106(14):5470–5474. doi: 10.1073/pnas.0901383106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Majda AJ, Branicki M. Lessons in uncertainty quantification for turbulent dynamical systems. Discrete Cont Dyn S. 2012;32(9):3133–3221. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.