Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2014 Apr 28;111(19):7156–7160. doi: 10.1073/pnas.1311231111

Controllability in protein interaction networks

Stefan Wuchty 1,1,2
PMCID: PMC4024882  PMID: 24778220

Significance

In human and yeast protein interaction datasets we determined minimum dominating sets (MDSets), proteins that play a role in the control of the underlying interaction webs. Such proteins are defined as optimized subsets from where each remaining protein can be immediately reached. Notably, MDSet proteins were enriched with cancer-related and virus-targeted genes. Furthermore, MDSet proteins have a higher impact on network resilience than hub proteins. Indicating their relevance for the controllability of biological networks, we also found a strong involvement in bottleneck interactions, regulatory and phosphorylation events as well as genetic interactions.

Abstract

Recently, the focus of network research shifted to network controllability, prompting us to determine proteins that are important for the control of the underlying interaction webs. In particular, we determined minimum dominating sets of proteins (MDSets) in human and yeast protein interaction networks. Such groups of proteins were defined as optimized subsets where each non-MDSet protein can be reached by an interaction from an MDSet protein. Notably, we found that MDSet proteins were enriched with essential, cancer-related, and virus-targeted genes. Their central position allowed MDSet proteins to connect protein complexes and to have a higher impact on network resilience than hub proteins. As for their involvement in regulatory functions, MDSet proteins were enriched with transcription factors and protein kinases and were significantly involved in bottleneck interactions, regulatory links, phosphorylation events, and genetic interactions.

Recently, the focus of modern network research shifted to the determination of nodes that allow the control of an entire network. In particular, Liu et al. (1) introduced a maximum matching approach to predict nodes for the control of various technical, social, and biological networks. Whereas their approach only applied to directed networks, Nacher and Akutsu (2) suggested an equivalent optimization procedure to determine minimum dominating sets (MDSets) of nodes that play an important role for the control of undirected networks. An intriguing question, however, remains if such nodes carry important functional characteristics. Generally, the importance of a protein in an interaction network is frequently considered a question of the number of interactions a given protein is involved in. For instance, the so-called centrality–lethality rule was first suggested by Jeong et al. (3) and Yu et al. (4), stating that highly connected proteins tend to be essential. Furthermore, such hubs are also involved in a rising number of protein complexes (5), suggesting that their essentiality is a consequence of their complex involvement (6, 7). In humans, human viruses and parasites target certain proteins to seize control of a host cell (8, 9) whereas such proteins play a decisive role in different cancer types (10, 11). Therefore, we wondered whether protein sets that are predicted to be important for the control of a protein interaction network would carry such biological significance as well. In other words, we expected that minimum dominating sets of proteins were enriched with, for example, disease or essential genes. Focusing on the currently best investigated interactomes we determined MDSets in human and yeast. Such sets are defined as finite subsets of proteins from where each remaining protein can be immediately reached by one interaction. Strongly suggesting that such well-defined protein groups have significance, MDSet proteins were indeed enriched with essential, cancer-related and virus-targeted genes. Furthermore, we found that MDSet proteins were preferably placed in central network positions, enabling MDSet proteins to connect protein complexes and significantly appear in bottleneck interactions, regulatory and phosphorylation events, and genetic interactions.

Results

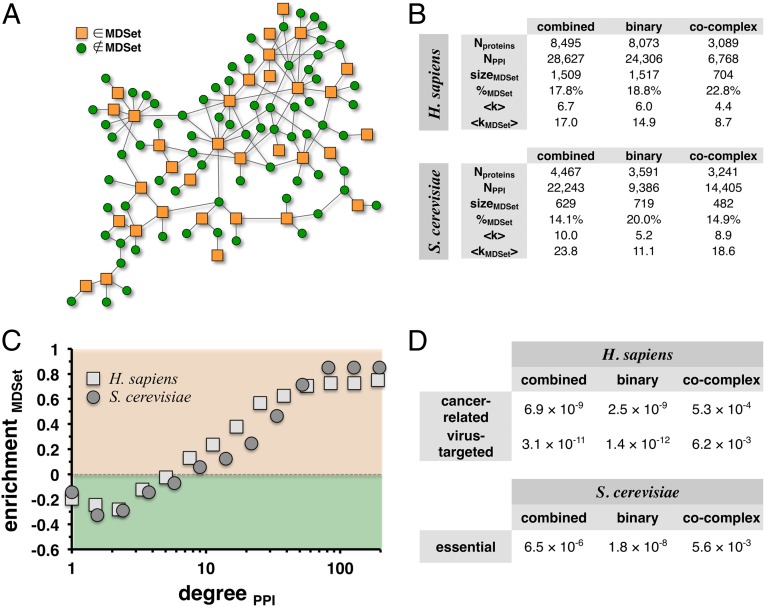
In a protein interaction network, an MDSet is defined as an optimized subset of proteins from where each remaining (i.e., non-MDSet) protein can be reached by one interaction. Therefore, each non-MDSet protein is connected to at least one MDSet protein (Fig. 1A). In protein interactions of Homo sapiens and Saccharomyces cerevisiae of the High-quality INTeractomes (HINT) database (12) we determined corresponding minimum dominating sets by solving an integer-based linear programming problem (Methods). Although we considered their combination, we separately accounted for binary and cocomplex interactions in each organism as well (Methods). The table in Fig. 1B indicates that the corresponding MDSets of human and yeast interaction networks involved fewer than 20% of all proteins. Compared with the mean degree of 6.7 in the combined human interaction network, the mean degree of MDSet proteins increased to 17.1. In the combined yeast network, each protein was on average involved in 10.0 interactions and the mean degree of MDSet proteins rose to 23.8. Such trends also applied to binary and cocomplex interaction sets of both organisms (Fig. 1B). Whereas the degree distributions of all proteins in interaction networks are generally characterized by fat tails (3, 13), the degrees of MDSet proteins showed the same distribution (Fig. S1A). To determine the enrichment of MDSet proteins as a function of their number of interactions we grouped proteins according to their degree in bins of logarithmic size. In each group we compared the protein’s frequency distributions in the combined interaction networks and the corresponding MDSets (Methods). Fig. 1C clearly demonstrates that MDSets were mostly enriched with proteins that roughly had more than 10 interactions. Fig. S1B shows similar results in the binary and cocomplex interaction sets of both organisms. Indicating a protein’s central role in an interaction network, we calculated a protein’s betweenness centrality. Fig. S2A shows that the frequency distributions of betweenness centralities of MDSet proteins in all interaction sets have fat tails. In Fig. S2B, we grouped proteins in bins of logarithmic size and compared the protein’s frequency distributions in the underlying interaction networks and their corresponding MDSets (Methods). Specifically, we observed that proteins with increasing betweenness predominantly appeared in the corresponding MDSets of all different interaction datasets of human and yeast.

Fig. 1.

Fig. 1.

Open in a new tab

Definition and characteristics of minimum dominating sets. (A) In a toy network we illustrate the concept of an MDSet. Specifically, an MDSet is defined as an optimized subset of nodes (orange squares) from where each remaining (i.e., non-MDSet) node (green circles) can be immediately reached by one step. As a consequence, each non-MDSet protein is linked to at least one MDSet protein. (B) In the table we present statistics of protein interaction networks and their corresponding MDSets in human and yeast. In particular, we accounted for binary and cocomplex interactions as well as combined interaction datasets. (C) We grouped proteins in logarithmic bins according to their number of interaction partners in the combined networks. In each bin, we separately calculated the frequency of proteins in the full networks and MDSets. In comparison, MDSet proteins mostly appeared enriched in groups of proteins with roughly more than 10 interactions. (D) By applying a Fisher’s exact test, we found that cancer-related genes and proteins that are targeted by human viruses are significantly enriched in human MDSets. Similarly, essential genes are significantly present in the corresponding yeast MDSets.

To account for false positives in the underlying interaction networks, we simulated their presence by randomly deleting a certain fraction of interactions. To investigate the robustness of MDSets toward such perturbations we evaluated the overlap of MDSets in the actual and the randomized networks with a Jaccard index. Fig. S3 shows that the overlap between the MDSets of the actual and randomized networks decreased but seemed to steady with an increasing rate of false positives. Notably, such trends applied to yeast and human networks of all interaction types.

To indicate the biological significance of MDSet proteins in a human interaction network we hypothesized that such sets may be significantly enriched with proteins that govern diseases. In particular, we collected 496 oncogenes and 876 tumor suppressor genes from the CancerGenes database, totaling 1,370 cancer-related genes (14). Applying Fisher’s exact test, we found that cancer-related genes were indeed significantly enriched in the MDSet of the combined human interaction network (P = 6.9 × 10−9). In human binary and cocomplex interaction data we obtained statistically significant enrichments of cancer genes as well (P < 10−3, Fig. 1D). Analogously, we used 770 human proteins that were involved in 4,474 interactions with proteins of various human viruses from the Molecular INTeraction (MINT) database (15). In all human interaction sets, targeted proteins were significantly enriched in the corresponding MDSets (P < 0.01, Fig. 1D) with the binary network showing the strongest signal (P = 1.4 × 10−12). To show the importance of MDSet proteins in yeast interaction networks we determined the enrichment of 1,110 essential genes in S. cerevisiae that were compiled from the Database of Essential Genes (DEG) (16). We observed that essential genes were significantly enriched in the MDSets of all yeast interactions datasets (P < 0.01, Fig. 1D), with the binary interaction network showing the strongest enrichment (P = 1.8 × 10−8).

To compare the enrichment levels of disease and essential genes we created sets of most connected proteins that matched the size of the corresponding MDSets in each interactions dataset. In Fig. S4A, we calculated the enrichment of cancer-related genes and proteins that were targeted by human viruses. We found that sets of most connected proteins showed much stronger enrichments of such disease genes, results that applied for essential genes in yeast as well. Analogously, we obtained similar results with sets of most central proteins in human and yeast interaction sets (Fig. S4B).

Protein complexes provide a different functional level of molecular organization, suggesting that MDSet proteins may appear in more complexes. Using data from the CORUM (Comprehensive Resource of Mammalian protein complexes) database, we collected 1,843 protein complexes in H. sapiens (17) and 409 protein complexes in S. cerevisiae from the CYC2008 database (18). Fig. S5 clearly indicates that MDSet proteins in the combined human interaction network appeared in significantly more protein complexes than non-MDSet proteins (P = 2.6 × 10−8, Wilcoxon test), results that also held for yeast protein complexes (P = 4.1 × 10−5). Furthermore, we determined the complex participation coefficient Pi of each protein i (19). Pi tends toward 1 if i interacts with proteins in the same protein complexes, and vice versa. Because MDSets are most central to reach all other proteins in a network, we hypothesized that MDSet proteins preferably connect many different protein complexes through their interactions. Therefore, we expected that MDSet proteins have lower complex participation coefficients. Comparing the coefficient distributions of (non)MDSet proteins in the combined yeast interaction network in Fig. S6, we indeed found that MDSet proteins provided lower values than non-MDSet proteins (P = 3.3 × 10−17, Wilcoxon test), a result that also applied to complexes in the combined human interaction network (P = 2.4 × 10−38).

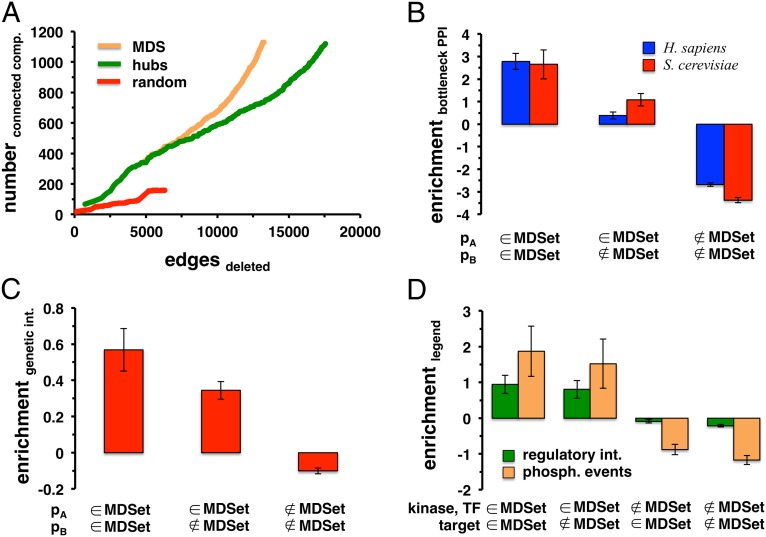
To measure a protein’s impact on an interaction network’s resilience, we performed a robustness analysis. Using the combined yeast network, we sorted all 629 MDSet proteins according to their degree. To compare, we created sets of equal size of the most connected yeast proteins as well as randomly picked proteins. Starting with the most connected protein we gradually deleted proteins and calculated the number of connected components after each deletion step. Successive deletion of MDSet proteins had a higher impact by producing more connected components and removing fewer interactions than their hub and random counterparts (Fig. 2A). In Fig. S7, we observed that such perturbations provided similar results in the combined human network.

Fig. 2.

Fig. 2.

Open in a new tab

Enrichment of topological and functional entities in MDSets. In A we sorted all MDSet proteins in the combined yeast interaction network according to their degree. To provide an equivalent set of equal size we collected and sorted the highest connected hub proteins. Furthermore, we randomly sampled a set of yeast proteins of the same size. Starting with the most connected protein, we gradually deleted proteins and calculated the number of connected components in the altered network. In comparison, the deletion of MDSet proteins had a higher impact on the resilience of the underlying networks than hubs alone. (B) Defined as the top 10% of interactions with the highest edge betweenness, we determined a set of bottleneck interactions in the combined human and yeast networks, respectively, and counted their occurrence between (non)MDSet proteins (pA and pB). Randomly sampling MDSets 10,000 times, we observed that bottleneck interactions were significantly enriched between MDSet proteins and depleted between non-MDSet proteins (P < 10−4). In C we determined the enrichment of genetic interactions between yeast (non)MDSet proteins (pA and pB) in the combined network. Randomly sampling MDSet proteins 10,000 times we clearly observed that genetic interactions preferably appeared between MDSet proteins, whereas the opposite applied for non-MDSet proteins (P < 10−4). (D) Human phosphorylation events and transcriptional, regulatory interactions were significantly enriched when at least kinases or transcription factors were involved in the MDSet of the combined human network (P < 10−4).

Whereas single MDSet proteins generally showed strong enrichments, we expected that similar signals emerge from topological and functional interactions between MDSet proteins. Specifically, we focused on bottleneck interactions, defined as the top 10% of interactions with the highest edge betweenness (20). In both the combined human and yeast networks we counted the number of bottleneck interactions that involved pairs of (non)MDSet proteins. As a null model, we randomly sampled MDSet proteins 10,000 times and expected to find similar numbers if their placement was a random process. After determining the corresponding enrichment/depletion of such bottleneck interactions we clearly observed that bottleneck interactions were significantly enriched between MDSet proteins whereas the opposite held for pairs of non-MDSet proteins (P < 10−4, Fig. 2B).

Genetic interactions can reveal important functional relationships between genes and pathways (21), suggesting that genetic interactions may be overrepresented between MDSet proteins. After collecting 108,899 genetic interactions between 5,364 genes in S. cerevisiae from the Biological General Repository for Interaction Datasets (BioGRID) database (22), we counted genetic interactions between (non)MDSet proteins. Randomly sampling MDSets 10,000 times we clearly observed that genetic interactions are significantly enriched when at least one protein participated in the MDSet (Fig. 2C). In turn, the opposite held for genetic interactions between non-MDSet proteins (P < 10−4).

Assuming that MDSets may significantly contribute to control processes we hypothesized that transcription factors and their target genes may significantly appear in MDSets. Specifically, we used 95,722 regulatory interactions between 209 human transcription factors and 8,910 target genes from the TRANScription FACtor (TRANSFAC) database (23, 24). Furthermore, we assumed that the same logic applies to phosphorylation events and collected 5,462 human phosphorylation events between 207 kinases and 1,661 from the networKIN database (25, 26). Applying Fisher’s exact test we found that transcription factors (P = 2.7 × 10−4) and kinases (P = 3.4 × 10−12) were significantly enriched in the MDSet of the combined human interaction network. Additionally, we counted how often a pair of transcription factors and a given target gene appeared between (non)MDSet proteins. Specifically, we observed that regulatory interactions and phosphorylation events were significantly enriched when corresponding transcription factors and kinases were involved in the MDSet (P < 10−4, Fig. 2D). In turn, interactions between a transcription factor and a target gene seemed generally depleted when both were not involved in the MDSet (P < 10−4). In yeast, we used 48,082 regulatory interactions between 183 yeast transcription factors and 6,403 genes from the Yeast Search for Transcriptional Regulators And Consensus Tracking (YEASTRACT) database (27). Furthermore, we obtained 3,466 experimentally determined interactions between 80 kinases and 1,172 substrates from (28), allowing us to find similar, albeit less significant, enrichment patterns (Fig. S8).

Discussion

Here, we determined minimum dominating sets of proteins in interaction networks that were defined as the smallest group of strategically placed proteins from where each remaining protein (i.e., non-MDSet protein) can be immediately reached through an interaction. As a consequence each non-MDSet protein therefore interacts with at least one MDSet protein. Although we observed that MDSet proteins are enriched among highly connected proteins, a large degree is not necessarily a criterion that qualifies a protein to participate in the MDSet. Notably, we observed that the degree distributions of MDSet proteins have fat tails, indicating that the majority of MDSet proteins have a small number of interaction partners, and vice versa. Such a characteristic is quite different compared with hubs that are widely considered the topologically and functionally most important proteins in an interaction network. In particular, the only criterion to consider a protein a hub is a preferably large number of interaction partners. Furthermore, the definition of hubs depends on an arbitrarily set threshold that only rigidly accounts for the local vicinity of a node. In turn, the way to determine MDSets considers the whole network, providing an optimal smallest set of strategically placed proteins, a procedure that does not need any arbitrary parameters. Still, MDSets manage to capture a considerable amount of highly connected proteins. Furthermore, MDSet proteins preferably appeared among proteins of high betweenness (i.e., bottleneck nodes), an observation that translated into bottleneck interactions as well. The direct comparison of MDSets with sets of protein hubs is a difficult undertaking, given that no generally applicable threshold or method for the detection of hubs actually exists. However, we generated sets of the most connected proteins that match the size of MDSets as an approximation. To directly compare the topological impact of MDSet proteins and hubs we sorted proteins according to their degree and successively deleted proteins from the underlying network. Notably, the deletion of MDSet proteins had a higher disruptive effect on the underlying network than hub proteins, demonstrating the topological relevance of MDSets.

On a different, more biologically relevant, level of network organization, we found that their strategic placement allowed MDSet proteins to participate in significantly more protein complexes than non-MDSet proteins. Furthermore, their interactions enabled MDSet proteins to reach more proteins in other complexes than non-MDS proteins. Whereas such observations indicate that MDSet proteins reach other proteins effectively, the question remains whether such characteristics translate into a governing role in the underlying networks. Indeed, we found that cancer-related genes and proteins that are targeted by human viruses are enriched with MDSet proteins. Onco- and tumorsuppressor genes play a fundamental causal role for the emergence of tumors whereas proteins that are targeted by viruses form a host–pathogen interface, allowing viruses to interfere with functions in the underlying host cell. Therefore, MDSet proteins may be important for the dissemination of causal information because their central placement provides a topological basis to reach all other proteins efficiently. In a similar vein, the central placement of MDSet proteins may complement functional interactions that exert biological control. In particular, transcription factors govern the expression of their underlying target genes, whereas kinases control the level of phosphorylation of their substrates as an effective means to process biological signals. Genetic interactions between genes indicate potential synergies when mutations in two genes may produce an unexpected phenotype given each mutation’s individual effects. Notably, genetic interactions preferably appeared when the interacting proteins were involved in MDSets. The strong involvement of MDSet proteins seems plausible, assuming that a genetic interaction may provide control of compensatory pathways or protein complexes. Considering expression and phosphorylation events, we obtained strongest enrichment signals when both the controlling (i.e., transcription factors, kinases) and controlled entity (i.e., target genes, substrates) occurred in the MDSets. In turn, such interactions seemed most diluted when both transcription factors/kinases and targets/substrates did not participate in the underlying MDSet. Such observations suggest that the topological characteristics of MDSets may be tapped for the collection and dissemination of biological information by transcription factors and kinases. Given that MDSet proteins connect to each remaining protein in the underlying networks by at most one step a transcription factor or kinase that participates in the MDSet may have an advantage to efficiently receive signals through corresponding interactions. In turn, a signal that is mediated by the expression levels of a target gene or the phosphorylation of substrate may have stronger efficacy when distributed through the interactions of an MDSet protein. Therefore, MDSets may be considered a complement that allows transcription and phosphorylation events to efficiently control biological processes.

Methods

Protein–Protein, Regulatory, and Phosphorylation Interactions.

We used a total of 28,627 high-quality protein interactions between 8,495 human proteins as well as 22,243 interactions between 4,467 yeast proteins from the HINT database (12). Accounting for methods that allow the detection of binary and cocomplex interactions (29) we obtained 27,254 binary interactions between 8,233 proteins and 7,692 cocomplex interactions between 3,188 proteins in human. As for yeast, we collected 11,435 binary interactions between 3,653 proteins and 16,294 cocomplex interactions between 3,380 proteins. Checking the interaction’s quality, Fig. S9 shows that the majority of binary interactions were confirmed by more than one publication. Cocomplex interactions were only accounted for when they were reported in at least two publications.

We collected 95,722 links between 209 human transcription factor and 8,910 human genes from the TRANSFAC (24) database as provided by mSigDB (23). As for regulatory interactions in yeast we used 48,082 regulatory interactions between 183 transcription factors and 6,403 genes from the YEASTRACT database (27). Specifically, such regulatory interactions were indicated if a binding site of given transcription factor appeared in the promoter of the underlying genes.

As for phosphorylation events in human we obtained 5,864 interactions between 63 kinases and 1,452 human proteins from the networKIN database (25, 26). Such links represent a kinase specific phosphorylation site in a given protein. Furthermore, we collected 3,466 experimentally determined phosphorylation events between 80 kinases and 1,172 substrates in yeast (28).

Determination of a Minimum Dominating Set.

A set 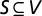Inline graphic of nodes in a network G = (V, E) is defined as an MDSet if every node 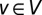Inline graphic is either an element of S or adjacent to an element of S. In other words, an MDSet is an optimized subset of nodes from where each remaining node can be immediately reached by one interaction (Fig. 1A). Specifically, we modeled and solved a binary integer-programming problem where each protein 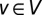Inline graphic that participates in interactions E in a protein interaction network G = (V, E) is assigned a binary variable xv. If v is an element of the MDSet we defined xv = 1, and 0 otherwise. We modeled the determination of an MDSet as 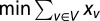Inline graphic, subject to the constraint Inline graphic, where Γ(v) was the set of interaction partners of protein v. Because the domination problem in graphs is NP-complete no algorithm necessarily exists that allows the determination of a minimum dominating set in arbitrary graphs in polynomial time (30). Specifically, we used a branch-and-bound algorithm (31) (see SI Methods and Fig. S10 for more details) as implemented by library lpSolve of the R programming language to solve our binary integer-programming problem.

Essential Genes in S. cerevisiae.

We used 1,110 essential genes from the DEG database, which collects data about essential genes from the literature (16).

Disease Genes in H. sapiens.

We collected 496 oncogenes and 876 tumor suppressor genes from the CancerGenes database (14), which collects such information from the literature. Furthermore, we considered 4,474 interactions between proteins of various human viruses and 770 human proteins that the MINT database collected from the literature (15).

Protein Complexes.

We used 1,843 protein complexes in H. sapiens from the CORUM database (17) and 409 protein complexes in S. cerevisiae from the CYC2008 database (18). Both databases collect information about experimentally determined protein complexes from the literature.

Protein Complex Participation Coefficient.

For each protein that is involved in at least one protein complex, we defined the protein complex participation coefficient of a protein i as 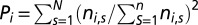Inline graphic, where ni,s is the number of links that protein i had to proteins in complex s out of N total complexes. If a protein predominantly interacted with partners of the same complex, P tended to 1, and vice versa (32).

Enrichment Analysis.

Using a protein interaction network, we grouped proteins according to their degrees or betweenness centrality in bins of logarithmically increasing size. In each group i we determined the corresponding frequency of proteins with a certain characteristic A, 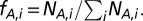Inline graphic Analogously, we calculated the corresponding frequency of proteins with characteristic A that appeared in a minimum dominating set (MDSet), 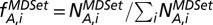Inline graphic. Finally, we defined the enrichment of proteins with characteristic A that appear in the MDSet in bin i as 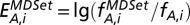Inline graphic. Therefore, 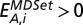Inline graphic points to an enrichment of feature A, and vice versa.

As for the enrichment of genetic interactions, regulatory interactions, or bottleneck interactions between (non)MDSet protein pairs, we counted the number of pairs that are connected by such links, NA. Randomly sampling minimum dominating sets, we analogously counted the corresponding random number, Nr,A, and defined the enrichment of such interactions as 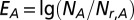Inline graphic.

Betweenness Centrality.

As a global measure of its centrality, we calculated an edges betweenness, indicating an interactions appearance in shortest paths through the whole network. In particular, we defined betweenness centrality cB of an edge e as 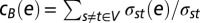Inline graphic, where σst was the number of shortest paths between proteins s and t and σst (e) was the number of shortest paths running through e. Analogously, we determined the betweenness centrality of node v as 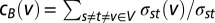Inline graphic. Furthermore, we normalized a node v’s centrality by 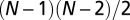Inline graphic, where N is the total number of nodes in the network.

Supplementary Material

Supporting Information
supp_111_19_7156__index.html (7.3KB, html)

Acknowledgments

We thank A.-L. Barabási, Peter Uetz, and Sawsan Khouri for fruitful discussions. This work was supported by the National Institutes of Health/Department of Health and Human Services (Intramural Research program of the National Library of Medicine) as well as start-up funds from the Department of Computer Science at the University of Miami.

Footnotes

The author declares no conflict of interest.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1311231111/-/DCSupplemental.

References

  • 1.Liu YY, Slotine JJ, Barabási AL. Controllability of complex networks. Nature. 2011;473(7346):167–173. doi: 10.1038/nature10011. [DOI] [PubMed] [Google Scholar]
  • 2.Nacher J, Akutsu T. Dominating scale-free networks with variable scaling exponent: Heterogeneous networks are not difficult to control. New J Phys. 2012;14(7):073005–073028. [Google Scholar]
  • 3.Jeong H, Mason SP, Barabási AL, Oltvai ZN. Lethality and centrality in protein networks. Nature. 2001;411(6833):41–42. doi: 10.1038/35075138. [DOI] [PubMed] [Google Scholar]
  • 4.Yu H, et al. High-quality binary protein interaction map of the yeast interactome network. Science. 2008;322(5898):104–110. doi: 10.1126/science.1158684. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Wuchty S, Almaas E. Peeling the yeast protein network. Proteomics. 2005;5(2):444–449. doi: 10.1002/pmic.200400962. [DOI] [PubMed] [Google Scholar]
  • 6.Zotenko E, Mestre J, O’Leary DP, Przytycka TM. Why do hubs in the yeast protein interaction network tend to be essential: Reexamining the connection between the network topology and essentiality. PLOS Comput Biol. 2008;4(8):e1000140. doi: 10.1371/journal.pcbi.1000140. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 7.Song J, Singh M. From hub proteins to hub modules: The relationship between essentiality and centrality in the yeast interactome at different scales of organization. PLOS Comput Biol. 2013;9(2):e1002910. doi: 10.1371/journal.pcbi.1002910. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Batada NN, Hurst LD, Tyers M. Evolutionary and physiological importance of hub proteins. PLOS Comput Biol. 2006;2(7):e88. doi: 10.1371/journal.pcbi.0020088. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Fraser HB, Hirsh AE, Steinmetz LM, Scharfe C, Feldman MW. Evolutionary rate in the protein interaction network. Science. 2002;296(5568):750–752. doi: 10.1126/science.1068696. [DOI] [PubMed] [Google Scholar]
  • 10.Kar G, Gursoy A, Keskin O. Human cancer protein-protein interaction network: A structural perspective. PLOS Comput Biol. 2009;5(12):e1000601. doi: 10.1371/journal.pcbi.1000601. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Jonsson PF, Bates PA. Global topological features of cancer proteins in the human interactome. Bioinformatics. 2006;22(18):2291–2297. doi: 10.1093/bioinformatics/btl390. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Das J, Yu H. HINT: High-quality protein interactomes and their applications in understanding human disease. BMC Syst Biol. 2012;6:92. doi: 10.1186/1752-0509-6-92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Lehner B, Fraser AG. A first-draft human protein-interaction map. Genome Biol. 2004;5(9):R63. doi: 10.1186/gb-2004-5-9-r63. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Higgins ME, Claremont M, Major JE, Sander C, Lash AE. CancerGenes: A gene selection resource for cancer genome projects. Nucleic Acids Res. 2007;35(Database issue):D721–D726. doi: 10.1093/nar/gkl811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Zanzoni A, et al. MINT: A Molecular INTeraction database. FEBS Lett. 2002;513(1):135–140. doi: 10.1016/s0014-5793(01)03293-8. [DOI] [PubMed] [Google Scholar]
  • 16.Zhang R, Ou HY, Zhang CT. DEG: A database of essential genes. Nucleic Acids Res. 2004;32(Database issue):D271–D272. doi: 10.1093/nar/gkh024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Ruepp A, et al. CORUM: The comprehensive resource of mammalian protein complexes—2009. Nucleic Acids Res. 2010;38(Database issue):D497–D501. doi: 10.1093/nar/gkp914. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 18.Pu S, Wong J, Turner B, Cho E, Wodak SJ. Up-to-date catalogues of yeast protein complexes. Nucleic Acids Res. 2009;37(3):825–831. doi: 10.1093/nar/gkn1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 19.Wuchty S, Siwo GH, Ferdig MT. Shared molecular strategies of the malaria parasite P. falciparum and the human virus HIV-1. Mol Cell Proteomics. 2011;10(10):M111 009035. doi: 10.1074/mcp.M111.009035. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Yu H, Kim PM, Sprecher E, Trifonov V, Gerstein M. The importance of bottlenecks in protein networks: Correlation with gene essentiality and expression dynamics. PLOS Comput Biol. 2007;3(4):e59. doi: 10.1371/journal.pcbi.0030059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Costanzo M, et al. The genetic landscape of a cell. Science. 2010;327(5964):425–431. doi: 10.1126/science.1180823. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Stark C, et al. BioGRID: A general repository for interaction datasets. Nucleic Acids Res. 2006;34(Database issue):D535–D539. doi: 10.1093/nar/gkj109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Subramanian A, et al. Gene set enrichment analysis: A knowledge-based approach for interpreting genome-wide expression profiles. Proc Natl Acad Sci USA. 2005;102(43):15545–15550. doi: 10.1073/pnas.0506580102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Matys V, et al. TRANSFAC and its module TRANSCompel: Transcriptional gene regulation in eukaryotes. Nucleic Acids Res. 2006;34(Database issue):D108–D110. doi: 10.1093/nar/gkj143. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Linding R, et al. Systematic discovery of in vivo phosphorylation networks. Cell. 2007;129(7):1415–1426. doi: 10.1016/j.cell.2007.05.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Linding R, et al. NetworKIN: A resource for exploring cellular phosphorylation networks. Nucleic Acids Res. 2008;36(Database issue):D695–D699. doi: 10.1093/nar/gkm902. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 27.Abdulrehman D, et al. YEASTRACT: Providing a programmatic access to curated transcriptional regulatory associations in Saccharomyces cerevisiae through a web services interface. Nucleic Acids Res. 2011;39(Database issue):D136–D140. doi: 10.1093/nar/gkq964. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Ptacek J, et al. Global analysis of protein phosphorylation in yeast. Nature. 2005;438(7068):679–684. doi: 10.1038/nature04187. [DOI] [PubMed] [Google Scholar]
  • 29.De Las Rivas J, Fontanillo C. Protein-protein interactions essentials: Key concepts to building and analyzing interactome networks. PLOS Comput Biol. 2010;6(6):e1000807. doi: 10.1371/journal.pcbi.1000807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Haynes TW, Hedetniemi ST, Slater PJ. Fundamentals of Domination in Graphs. Pure Applied Mathematics (Marcel Dekker, New York) [Google Scholar]
  • 31.Land AH, Doig AG. An automatic method of solving discrete programming-problems. Econometrica. 1960;28(3):497–520. [Google Scholar]
  • 32.Wuchty S, Siwo G, Ferdig MT. Viral organization of human proteins. PLoS ONE. 2010;5(8):e11796. doi: 10.1371/journal.pone.0011796. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_111_19_7156__index.html (7.3KB, html)
1311231111_pnas.201311231SI.pdf (865KB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES