Abstract
Based on the measurements of noise in gene expression performed during the past decade, it has become customary to think of gene regulation in terms of a two-state model, where the promoter of a gene can stochastically switch between an ON and an OFF state. As experiments are becoming increasingly precise and the deviations from the two-state model start to be observable, we ask about the experimental signatures of complex multistate promoters, as well as the functional consequences of this additional complexity. In detail, we i), extend the calculations for noise in gene expression to promoters described by state transition diagrams with multiple states, ii), systematically compute the experimentally accessible noise characteristics for these complex promoters, and iii), use information theory to evaluate the channel capacities of complex promoter architectures and compare them with the baseline provided by the two-state model. We find that adding internal states to the promoter generically decreases channel capacity, except in certain cases, three of which (cooperativity, dual-role regulation, promoter cycling) we analyze in detail.
Introduction
Gene regulation—the ability of cells to modulate the expression level of genes to match their current needs—is crucial for survival. One important determinant of this process is the wiring diagram of the regulatory network, specifying how environmental or internal signals are detected, propagated, and combined to orchestrate protein level changes (1). Beyond the wiring diagram, the capacity of the network to reliably transmit information about signal variations is determined also by the strength of the network interactions (the “numbers on the arrows” (2)), the dynamics of the response, and the noise inherent to chemical processes happening at low copy numbers (3–6).
How do these factors combine to set the regulatory power of the cell? Information theory can provide a general measure of the limits to which a cell can reliably control its gene expression levels. Especially in the context of developmental processes, where the precise establishment and readout of positional information has long been appreciated as crucial (7), information theory can provide a quantitative proxy for the biological function of gene regulation (8). This has led to theoretical predictions of optimal networks that maximize transmitted information given biophysical constraints (8–13), and hypotheses that certain biological networks might have evolved to maximize transmitted information (14). Some evidence for these ideas has been provided by recent high-precision measurements in the gap gene network of the fruit fly (15). In parallel to this line of research, information theory has been used as a general and quantitative way to compare signal processing motifs (16–29). Further theoretical work has demonstrated a relationship between the information capacity of an organism’s regulatory circuits and its evolutionary fitness (30–32).
Previously, information theoretic investigations primarily examined the role of the regulatory network. In this study, we focus on the molecular level, i.e., on the events taking place at the regulatory regions of the DNA. Little is known about how the architecture of such microscopic events shapes information transfer in gene regulation. Yet it is precisely at these regulatory regions that the mapping from the “inputs” in the network wiring diagram into the corresponding “output” expression level is implemented by individual molecular interactions. In this bottleneck various physical sources of stochasticity—such as the binding and diffusion of molecules (33–35), and the discrete nature of chemical reactions (36)—must play an important role. In the simplest picture, gene expression is modulated through transcriptional regulation. This involves molecular events such as the binding of transcription factors (TFs) to specific sites on the DNA, chemical events that facilitate or block TF binding (e.g., through chromatin modification), or events that are subsequently required to initiate transcription (e.g., the assembly and activation of the transcription machinery).
Although the exact sequence of molecular events at the regulatory regions often remains elusive (especially in eukaryotes), quantitative measurements have highlighted factors that contribute to the fidelity by which TFs can affect the expression of their target genes. These findings have been succinctly summarized by the so-called “telegraph model” of transcriptional regulation (37): the two-state promoter switches stochastically between the states “ON” and “OFF,” with switching rates dependent on the concentration(s) of the regulatory factor(s). This dependence can either be biophysically motivated (e.g., by a thermodynamic model of TF binding to DNA), or it can be considered as purely phenomenological. The switching itself is independent of mRNA production but determines the overall production rate. The production of mRNA molecules from one state is usually modeled as a Poisson process, with a first-order decay of messages; this is usually followed by a birth-death process in which proteins are translated from the messages. This two-state model is well-studied theoretically (37–43) and has been used extensively to account for measurements of noise in gene expression (44–47). An increasing amount of information about molecular details has motivated extensions to this model by introducing more than two states in specific systems (48–55), and recent measurements of noise in gene expression provided some support for such complex regulatory schemes (56–59).
In this article we address the general question of the functional effect of complex promoters with multiple internal states. How does the presence of multiple states affect information transmission? Under what conditions, if any, can multistate promoters perform better than the two-state model? We consider a wide spectrum of generic promoter models, such that many molecular “implementations” can share the same mathematical model. With this framework in hand, we derive the total noise in mRNA expression and discuss how measurements of this function can be diagnostic of the underlying mechanism of regulation. To answer the main question of this paper—namely if additional complexity at the promoter can lead to an improvement in controlling the output level of a gene—we compute the information transmission from transcription factor concentrations to regulated protein expression levels through two- and three-state promoters. Finally, we analyze in detail three complex promoter architectures that outperform the two-state regulation.
Methods
Channel capacity as a measure of regulatory power
We start by considering a genetic regulatory element—e.g., a promoter or an enhancer—as a communication channel, shown in Fig. 1 A. As the concentrations of the relevant inputs (for example, transcription factors) change, the regulatory element responds by varying the rate of target gene expression. In steady state, the relationship between input k and expression level of the regulated protein g is often thought of as a “regulatory function” (60). Although attractive, the notion of a regulatory function in a mathematical sense is perhaps misleading: gene regulation is a noisy process, and so for a fixed value of the input we have not one, but a distribution of different possible output expression levels, (see Fig. 1 B). When the noise is small, it is useful to think of a regulatory function as describing the average expression level, , and of the noise as inducing some random fluctuation around that average. The variance of these fluctuations, , is thus a measure of noise in the regulatory element; note that its magnitude depends on the input, k.
Figure 1.
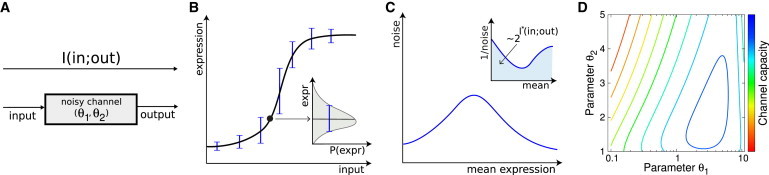
A genetic regulatory element as an information channel. (A) Mutual information I is a quantitative measure of the signaling fidelity with which a genetic regulatory element maps inputs (e.g., TF concentrations) into the regulated expression levels. In this schematic example, the properties of the element are fully specified by two parameters (; e.g., the switching rates between promoter states). (B) In steady state, the input/output mapping can be summarized by the regulatory function (solid black line) for target protein expression (equivalently, for target mRNA expression, not shown); noise, (respectively for mRNA), induces fluctuations around this curve (inset and error bars on the regulatory function). (C) The “noise characteristic” (noise vs. mean expression) is usually experimentally accessible for mRNA using in situ hybridization methods and can reveal details about the promoter architecture. The maximal transmitted information (channel capacity , see Eqs. 2 and 3) is calculated from the area under the inverse noise curve for the target protein, (inset). (D) Channel capacity is, in this example case, maximized for a specific choice of parameters (blue peak). To see this figure in color, go online.
The presence of noise puts a bound on how precisely changes in the input can be mapped into resulting expression levels on the output side—or inversely, how much the cell can know about the input by observing the (noisy) outputs alone. In his seminal work on information theory (61), Shannon introduced a way to quantify this intuition by means of mutual information, which is an assumption-free, positive scalar measure in bits, defined as follows:
| (1) |
In Eq. 1, is a property of the regulatory element, which we compute below, whereas is the distribution of inputs (e.g., TF concentrations) that regulate the expression; finally, is the resulting distribution of gene expression levels. With set by the properties of the regulatory element and the biophysics of the gene expression machinery, there exists an optimal choice for the distribution of inputs, , that maximizes the transmitted information. This maximal value, , also known as the channel capacity (62), summarizes in a single number the “regulatory power” intrinsic to the regulatory element (10–14).
Our goal is to compute the channel capacity between the (single) regulatory input and the target gene expression level for information flowing through various complex promoters. Under the assumption that noise is small and approximately Gaussian for all levels of input, the complicated expression for the information transmission in Eq. 1 simplifies, and the channel capacity can be computed analytically from the regulatory function, , and the noise, . The result (10–14) is as follows:
| (2) |
| (3) |
where in the last equality we changed the integration variables to express the result in terms of the average induction level, , using the regulatory function . This integral is graphically depicted in Fig. 1 C (inset). Finally, we will use this to explore the dependence of on parameters that define the promoter architecture (see Fig. 1 D), looking for those arrangements that lead to large channel capacities and thus high regulatory power.
Information as a measure of regulatory power has a number of attractive mathematical properties (for review, see (8)); interpretation-wise, the crucial property is that it roughly counts (the logarithm of) the number of distinguishable levels of expression that are accessible by varying the input—also taking into account the level of noise in the system. A capacity of 1 bit, therefore, suggests that the gene regulatory element could act as a binary switch with two distinguishable expression levels (note that this is different from saying that the promoter has two (or any other number) of possible internal states); capacities smaller than 1 bit correspond to (biased) stochastic switching, whereas capacities higher than 1 bit support graded regulation. An increase of information by 1 bit means that the number of tunable and distinguishable levels of gene expression has roughly doubled, implying that changes of less than a bit are meaningful. Careful analysis of gene expression data for single-input single-output transcriptional regulation suggest that real capacities can exceed 1 bit (14). Increasing this number substantially beyond a few bits, however, necessitates very low levels of noise in gene regulation, requiring prohibitive numbers of signaling molecules (10).
Multistate promoters as state transition graphs
To study information transmission, we must first introduce the noise model in gene regulation, which consists of two components: i) the generalization of the random telegraph model to multiple states, and ii), the model for input noise that captures fluctuations in the number of regulatory molecules. Starting with the first component, we compute the mean and variance for regulated mRNA levels, since these quantities are experimentally accessible when probing noise in gene expression. We assume that the system has reached steady state and that gene product degradation is the slowest timescale in the problem, i.e., that target mRNA or protein levels average over multiple state transitions of the promoter and that the resulting distributions of mRNA and protein are thus unimodal. Whereas for protein levels these assumptions hold over a wide range of parameters and include many biologically relevant cases, there exist examples where promoter switching is very slow and the system would need to be treated with greater care (e.g., (38,50,63)).
Let us represent the possible states of the promoter (and the transitions between them) by a state transition graph as in Fig. 2 A. Gene regulation occurs when an input signal modifies one (or more) of the rates at which the promoter switches between its states. To systematically analyze many promoter architectures, we choose not to endow from the start each graph with a mechanistic interpretation, which would map the abstract promoter states to various configurations of certain molecules on the regulatory regions of the DNA (as in Fig. 2 B). This is because there might be numerous molecular realizations of the same abstract scheme, which will yield identical noise characteristics and identical information transmission. In Fig. 3 and Fig. S1 in the Supporting Material, we discuss known examples related to different promoter architectures.
Figure 2.
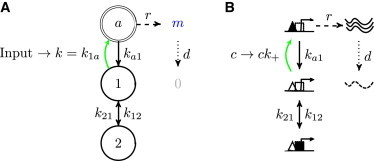
Promoters as state transition graphs. (A) A state transition graph for an example three-state promoter. Active state a (double circle) expresses mRNA m at rate r, which are then degraded with rate d. Transition into a (green arrow) is affected by the input that modulates rate . Stochastic transitions between promoter states are an important contribution to the noise, . (B) A possible mechanistic interpretation of the diagram in (A): state 1 is an unoccupied promoter, state 2 is an inaccessible promoter (occupied by a nucleosome or repressor, solid square). Transition to the active state (green arrow) is modulated by changing the concentration c of activators (solid triangles) that bind their cognate site (open triangles) at the promoter with the rate . To see this figure in color, go online.
Figure 3.
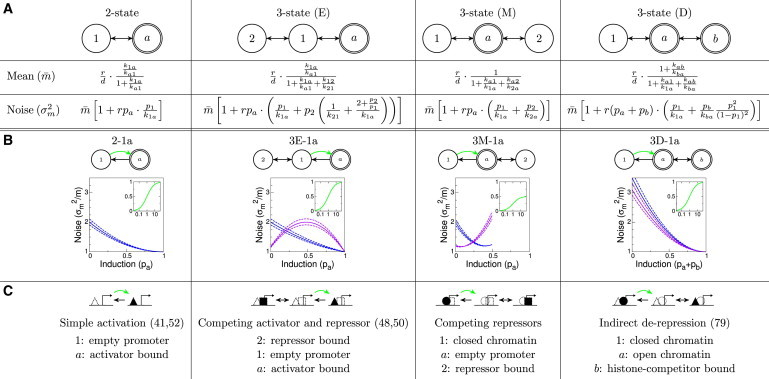
Mean expression level and noise for different promoter models. (A) Expressions for the mean (first row, ) and the variance (second row, ) of the mRNA distribution in steady state for different promoter architectures. In the limit of (respectively ), the expression for the two-state model is obtained from the models with three states. The names of the topologies indicate the position of the expressing state: E(nd), M(iddle), D(ouble). (B) Noise characteristics (pa on the x axis vs. the Fano factor, , on y axis) for different promoter models. Here, in all models is modulated (green arrow) to achieve different mean expression levels. For all rates (except k) equal to 1 (blue lines), the functional form of the noise characteristics is very similar. This remains true for a variation of of ±10% (blue dashed lines). Making the rates in/out of the third state (state 2 or b) slower by a factor of 5 (purple lines, dashed ±10%) yields qualitatively different results. Insets show the induction curve, , where k is the modulated rate. A full table and possible molecular interpretations of different promoter schemes are given in Fig. S1 (74–80). (C) Possible interpretations of the modulation schemes. Triangles represent activators, squares are repressors, and circles are histones. The dotted shapes denote (empty) binding sites. Cited references use similar models. To see this figure in color, go online.
Given a specific promoter architecture, we would like to compute the first two moments of the mRNA distribution under the above assumptions. Here, we only sketch the method for the promoter in Fig. 2 A; for a general description and details see the Supporting Material. We will denote the rate of mRNA production from the active state(s) by r and its degradation rate by d. Let further be the fractional occupancy of state and the rate of transitioning from state i to . Here, a is the active state, and 1, 2 are the nonexpressing states. Equations 4 and 5 then describe the behavior of the state occupancy and mRNA level m:
| (4) |
| (5) |
and ; and are Langevin white-noise random forces (36,64) (see the Supporting Material). In this setup it is easy to compute the mean and the variance in expression levels given a set of chosen rate constants. Using the assumption of slow gene product degradation, , we can write the noise in a generic way:
| (6) |
where is the occupancy of the active states ( or ), and the dimensionless expression for Δ depends on the promoter architecture and can be read out from Fig. 3 A for different promoter models. The expression for noise in Eq. 6 has two contributions. The first, where the variance is equal to the mean is the “output noise” attributable to the birth-death production of single mRNA molecules (also called “shot noise” or “Poisson noise”). The second contribution to the variance in Eq. 6 is attributable to stochastic switching of the promoter between internal states, referred to as the “switching noise.” This term does depend on the promoter architecture and has a more complicated functional form than being simply proportional to the mean. A first glance at the expressions for noise seems to imply that going from two to three promoter states can only increase the noise (and by Eq. 3 decrease information), since new, positive contributions appear in the expressions for ; we will see that, nevertheless, transmitted information can increase for certain architectures.
Input noise
In addition to the noise sources internal to the regulatory mechanism, we also consider the propagation of fluctuations in the input, which will contribute to the observed variance in the gene expression level. Can we say anything general about the transmission of input fluctuations through the genetic regulatory element? Consider, for instance, the modulated rate k that depends on the concentration c of some transcription factor, as in , where is the association rate to the TF’s binding site. Since the TF itself is expressed in a stochastic process, we could expect that there will be (at least) Poisson-like fluctuations in c itself, such that ; this will lead to an effective variance in k that will be propagated to the output variance in proportion to the “susceptibility” of the regulatory element, . Extrinsic noise would affect the regulatory element in an analogous way, as suggested in a previous study (65). Independently of the noise origin, we can write
| (7) |
where indicate output and switching terms from Eq. 6 and v is the proportionality constant that is related to the magnitude of the input fluctuations and, possibly, their subsequent time averaging (5).
Even if there were absolutely no fluctuations in the total concentration c of TF molecules in the cell (or the nucleus), the sole fact that they need to find their target by diffusion puts a lower bound on the variance of the local concentration at the regulatory site (33,34,66). This diffusion noise represents a substantial contribution to the total, as was shown by the analysis of high-precision measurements in gene expression noise (35,45). For this biophysical limit set by diffusion, we find yet again that the variance in the input is proportional to the input itself, and that the values of v are of order one when expressed in units of the relevant averaging time (see the Supporting Material and (66–68)). This, in sum, demonstrates that Eq. 7 can be used as a generic model for diverse kinds of input noise.
Results
Experimentally accessible noise characteristics
Could complex promoter architectures be distinguished by their noise signatures, even in the easiest case where the input noise can be neglected (as is often assumed (45))? The expressions for the noise presented in Fig. 3 A hold independently of which transition rate the input is modulating. We can specialize these results by choosing the modulation scheme, that is, making one (or more) of the transition rates the regulated one. This allows us to construct the regulatory function (insets in Fig. 3 B). Additionally, we can also plot the noise (shown in Fig. 3 B as the Fano factor, ) as a function of the mean expression, , thus getting the noise characteristic of every modulation scheme. These curves, shown in Fig. 3 B, are often accessible from experiments (44,69), even when the identity of the expressing state or the mechanism of modulation is unknown. We systematically organize our results in Fig. 3 B (for the case when is modulated) and provide a full version in Fig. S1; we also list four molecular schemes implementing these architectures in Fig. 3 C, while providing additional molecular implementations in Fig. S1. We emphasize that very different molecular mechanisms of regulation can be represented by the same architecture, resulting in the same mathematical analysis and information capacity.
Measured noise-vs.-mean curves have been used to distinguish between various regulation models (44,69,70). For this, two conditions have to be met (45,71). First, it must be possible to access the full dynamic range of the gene expression in an experiment, and this sometimes seems hard to ensure. The second condition is that the input noise is not the dominant source of noise: input noise can mimic promoter switching noise and can, e.g., provide alternative explanations for noise measurements in (44) that quantitatively fit the data (not shown).
Even if these conditions are met, it would be impossible to distinguish between certain promoter architectures (e.g., 2-a1 vs. 3E-a1) with this method, whereas some would require data of a very high quality to distinguish (e.g., activating 3E-1a vs. repressing 3E-12, see Fig. S1), at least in certain parameter regimes. On the other hand, there exist noise characteristics that can only be obtained with multiple states (e.g., 3M-1a).
One feature that can easily be extracted from the measured noise characteristics is the asymptotic induction: it can be equal to 1 (e.g., in 2-1a), or bounded away from 1 (e.g., in 3M-1a). Although this distinction between architectures cannot be inferred from the shapes of the regulatory functions, the effect on the noise characteristics is unambiguous: in the case where the expressing state is never saturated, the Fano factor does not drop to the Poisson limit of 1 even at the highest-expression levels (which seems to have been the case in a previous study (44)).
Taken together, when the range of promoter architectures is extended beyond the two-state model, distinguishing between these architectures based on the noise characteristics seems possible only under restricted conditions, emphasizing the need for dynamical measurements that directly probe transition rates (e.g., (59,72)), or for the measurements of the full mRNA distribution (rather than only its second moment). We note that dynamic rates are often reported assuming the two-state model, as they are inferred from the steady-state noise measurements (e.g., (44,47)), and only a few experiments probe the rates directly (e.g., (73)); for a brief review of the rates and their typical magnitudes, see the Supporting Material.
Information transmission in simple gene regulatory elements
Protein noise
In most cases the functional output of a genetic regulatory element is not the mRNA, but the translated protein. Incorporating stochastic protein production into the noise model does not affect the functional form of the noise, but only rescales the magnitude of the noise terms. To see this, we let proteins be produced from mRNA at a rate r' and degraded or diluted at d', such that is the slowest timescale in the problem. Then the mean protein expression level is . The output and promoter switching noise contributions are affected differently, so that the protein level noise can be written as (45):
| (8) |
where is the burst size (the average number of proteins translated from one mRNA molecule), and the other quantities are as defined in Eq. 6.
Information transmission in the two-state model
To establish the baseline against which to compare complex promoters, we look first at the two-state promoter (2-1a). Here the transition into the active state is modulated by TF concentration c via , as it would be in the simple case of a single TF molecule binding to an activator site to turn on transcription. Adding together the noise contributions of Eqs. 8 and 7, we obtain the following model for the total noise:
| (9) |
To compute the corresponding channel capacity, we use Eq. 3 with the noise given by Eq. 9 as follows:
| (10) |
| (11) |
Here, and is the dimensionless combination of parameters related to the off-rate for the TF dissociation from the binding site. can be interpreted as the number of independently produced output molecules when the promoter is fully induced (11–13). In the case where mRNA transcription is the limiting step for protein synthesis, corresponds to the maximal average number of mRNA synthesized during a protein lifetime: . With this choice of parameters, affects Z multiplicatively and thus simply adds a constant offset to the channel capacity (see Eq. 2) without affecting the parameter values that maximize capacity. In what follows we therefore disregard this additive offset, and examine in detail only . We also only use dimensionless quantities (as above, e.g., the rates are expressed in units of d'), but leave out the tilde symbols for clarity.
Optimizing information transmission
What parameters maximize the capacity of the two-state promoter 2-1a given by Eq. 10? Given that the dynamic range of input (e.g., TF concentration) is limited (10–13), , and given a choice of v that determines the type and magnitude of input noise, the channel capacity for the two-state promoter only depends nontrivially on the choice of a single parameter, . Fig. 4 shows the tradeoff that leads to the emergence of a well-defined optimal value for : at a fixed dynamic range for the input, , the information-maximizing solution chooses that balances the strength of binding (such that the dynamic range of expression is large), while simultaneously keeping the noise as low as possible. If this abstract promoter model were interpreted in mechanistic terms where a TF binds to activate gene expression, then choosing the optimal would amount to choosing the optimal value for the dissociation constant of our TF; importantly, the existence of such a nontrivial optimum indicates that, at least in an information-theoretic sense, the best binding is not the tightest one (10–13,27,81,82). This tradeoff between noise and dynamic range of outputs (also called “plasticity”) has also been noticed in other contexts (83,84).
Figure 4.
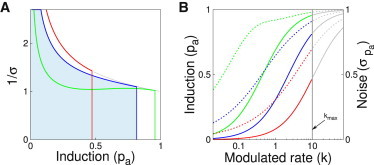
Finding that optimizes information transmission in a two-state promoter. The strength of the input noise is fixed at and the input dynamic range for k is from 0 to . (A) The integrand of Eq. 10 is shown for the optimal choice of (blue), and for two alternative values: a factor of 5 larger (red) or smaller (green) than the optimum. Although increasing lowers the noise, it also decreases the integration limit, and vice versa for decreasing . (B) The effect on the regulatory function (solid, left axis) and the noise (dashed, right axis), of choosing different values. Optimal (blue curves) from (A) leads to a balance between the dynamic range in the mean response (the maximal achievable induction), and the magnitude of the noise. Higher (red curves), in contrast, lead to smaller noise, but fail to make use of the full dynamic range of the response. The gray part of the regulation curves cannot be accessed, since the input only ranges over . To see this figure in color, go online.
Improving information transmission with multistate promoters
We would like to know if complex promoter architectures can outperform the two-state model in terms of channel capacity. To this end, we have examined the full range of three-state promoters, summarized in Fig. S1, and found that generally—as long as only one transition is modulated and only one state is active—extra promoter states lead to a decrease in the channel capacity relative to two-state regulation. However, by relaxing these assumptions, architectures that outperform two-state promoters can be found.
Cooperative regulation
The first such pair of architectures is illustrated in Fig. 5 A and B: three-state promoters with one (or two) expressing states, where two transitions into the expressing states are simultaneously modulated by the input. A possible molecular interpretation of these promoter state diagrams is an AND-architecture cooperative binding for the model with one expressing state, and an OR-architecture cooperative activation for the model with two expressing states. In case of an AND-architecture, a TF molecule hops onto the empty promoter (state 2) with rate 2k (since there are two empty binding sites), whereas a second molecule can hop on with rate (called “recruitment” if ), bringing the promoter into the active state. The first of two bound TF molecules falls off with rate (called “cooperativity” if ), bringing the promoter back to state 1, and ultimately, the last TF molecule can fall off with rate . The dynamics are now described (see Eq. 5) by the matrix
| (12) |
and , respectively . To compute the noise, we can use the solutions for the generic three-state model 3E from Fig. 3 A by making the following substitutions: .
Figure 5.
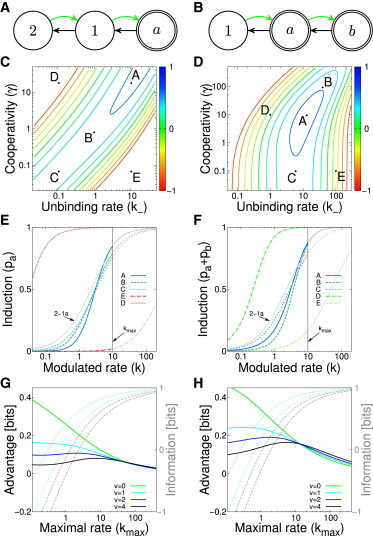
Improving information transmission via cooperativity. (A,B) The state transition diagram for the AND-architecture three-state promoter (at left, one active state) and OR-architecture (at right, two active states). (C,D) The information planes showing the channel capacity (color code) for various combinations of and γ at a fixed maximum allowed , for the AND- and OR-architectures and . (E,F) The regulatory functions of various models selected from parameters denoted by dots in the information planes in (B,C). Solutions that maximize the information denoted with a solid blue line. Colors indicate the channel capacities. The gray part of the regulation curves cannot be accessed, since the input only ranges over . For comparison, we also plot the regulation curve of the 2-1a scheme (with its optimal ). (G,H) Channel capacity (dashed lines, axes at right) and the advantage of the multistate scheme over the best two-state promoter, (solid lines, axes at left), of the AND and OR models, as a function of the maximal input range, , and the strength of the input noise (v, color). Since there is no globally optimal choice for γ for the AND-architecture, we fix in (G), and optimize only over values. To see this figure in color, go online.
To simplify our exploration of the parameter space, we choose (i.e., no recruitment), but keep (unbinding rate) and γ (cooperativity) as free parameters; the modulated rate k is proportional to the concentration of TF molecules and is allowed the range . For every choice of , we computed the regulatory function and the noise, and used these to compute the capacity, , using Eqs. 2 and 3. This information is shown in Fig. 5 C and D for the AND- and OR-architecture, respectively.
In the case of an AND-architecture, where both molecules of the TF have to bind for the promoter to express, there is a ridge of optimal solutions: as we move along the ridge in the direction of increasing information, cooperativity is increased and thus the doubly occupied state is stabilized, while the unbinding rate increases as well. This means that the occupancy of state 1 becomes negligible, and the regulation function becomes ever steeper, as is clear from Fig. 5 E, while maintaining the same effective dissociation constant (the input at which the promoter is half induced, i.e., ). In this limit, the shape of the regulation function must approach a Hill function with the Hill coefficient of 2, . Surprisingly, information maximization favors weak affinity of individual TF molecules to the DNA, accompanied by strong cooperativity between these molecules. The OR-architecture portrays a different picture: here, the maximum of information is well-defined for a particular combination of parameters , as shown in Fig. 5 D. As (increasing destabilization for ), the second active state (b) is never occupied, and the model reverts to a two-state model.
For both architectures we can assess the advantage of the three-state model relative to the optimal two-state promoter. Fig. 5 E and F show the information of the optimal solutions as a function of the input noise magnitude as well as the input range, . As expected, the information increases as a function of since the influence of input and switching noise can be made smaller with more input molecules. This increase saturates at high because output noise becomes limiting to the information transmission—this is why the capacity curves converge to the same maximum, the curve that lacks the input noise altogether. The advantage (increase in capacity) of the three-state models relative to the two-state promoter is positive for any combination of parameters and v. It is interesting to note that increasing and decreasing v have very similar effects on channel capacity, since both drive the system to a regime where the limiting factor is the output noise.
Regulation with dual-role TFs
In the second architecture that we consider a transcription factor can switch its role from repressor to activator, depending on the covalent TF modification state or formation of a complex with specific co-factors. A well-studied example is in Hedgehog (Hh) signaling, where the TF Gli acts as a repressor when Hh is low, or as an activator when Hh is high (85–87). Fig. 6 A shows a possible dual-role signaling scheme where the total concentration of dual-role TFs is fixed (at ), but the signal modulates the fraction of these TFs that play the activator role (k) and the remaining fraction that act as repressors , which compete for the same binding site. The channel capacity of this motif is depicted in Fig. 6 B as a function of promoter parameters and , showing that a globally optimal setting (denoted “A”) exists for these parameters; with these parameters, the input/output function, shown in Fig. 6 C, is much steeper than what could be achieved with the best two-state promoter, and that is true despite the fact that the molecular implementation of this architecture uses only a single binding site. The ability to access such steep regulatory curves allows this architecture to position the midpoint of induction at higher inputs k, thus escaping the detrimental effects of the input noise at low k, while still being able to induce almost completely (i.e., make use of the full dynamic range of outputs) as the input varies from 0 to . This is how the dual-role regulation can escape the tradeoff faced by the two-state model 2-1a (shown in Fig. 4). Sharper transition at higher input would lead us to expect that the advantage of this architecture over the two-state model is most pronounced when input noise is dominant (small , large v), which is indeed the case, as shown in Fig. 6 D.
Figure 6.

Improving information transmission via dual-role regulation. (A) The signal k increases the concentration of TFs in the activator role that favor the transition (green) to the expressing state, while simultaneously decreasing the rate of switching (red) into the inactive state with the repressor bound. (B) Channel capacity (color) as a function of off-rates shows a peak at A. and . (C) The regulatory functions for the optimal solution A (solid blue line) and other example points (B to E) from the information plane, show that this architecture can access a rich range of response steepnesses and induction thresholds. For comparison, we also plot the regulation curve of the scheme 2-1a (with its optimal ). (D) The channel capacity (dashed line) and information advantage over the optimal two-state architecture (solid line), as a function of . To see this figure in color, go online.
Promoter cycling
In the last architecture considered in this article, promoters “cycle” through a sequence of states in a way that does not obey detailed balance, e.g., when state transitions involve expenditure of energy during irreversible reaction steps. In the scheme shown in Fig. 7 A, the regulated transition puts the promoter into an active state a; before decaying to an inactive state, the promoter must transition through another active state b. Effectively, this scheme is similar to the two-state model in which the decay from the active state is not first-order with exponentially distributed transition times, but rather with transition times that have a sharper peak. The benefits of this architecture are maximized when the transition rates from both active states are equal. Although it always outperforms the optimal two-state model, the largest advantage is achievable for small . At large the advantage tends to zero: this is because the optimal off-rates are high, causing the dwell times in the expressing states to be short. In this regime the gamma distribution of dwell times (in a three-state model) differs little from the exponential distribution (in a two-state model). Note that this model would not yield any information advantage if the state transitions were reversible.
Figure 7.
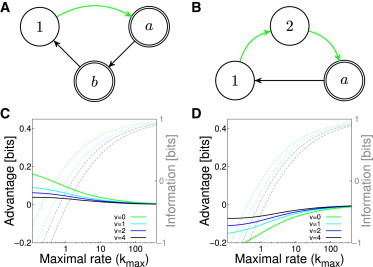
Improving information transmission via cycling. (A) Promoter cycles through two active states (a, b) expressing at identical production rates before returning to inactive state (1), from which the transition rate back into the active state (green) is modulated. For each value of , we look for the optimal choice of . The information and advantage relative to the optimal two-state model is shown in (C). (B,D) A similar architecture where turning the gene on is a multistep regulated process. This architecture always underperforms the optimal two-state model, indicated by a negative value of the advantage for all choices of v and . To see this figure in color, go online.
Fig. 7 C and D show that irreversible transitions alone do not generate an information advantage: a promoter that needs to transition between two inactive states (1, 2) to reach a single expressing state a from which it exits in a first-order transition, is always at a loss compared with a two-state promoter. This is because here the effective transition rate to the active state in the equivalent two-state model is lower (since an intermediate state must be traversed to induce), necessitating the use of a lower off-rate , which in turn leads to higher switching noise.
It is interesting to note that recent experimental data on eukaryotic transcription seem to favor models in which the distribution of exit times from the expressing state is exponential, whereas the distribution of times from the inactive into the active state is not (59), pointing to the seemingly underperforming architecture of Fig. 7 B. The three-state promoter suggested in this study is probably an oversimplified model of reality, yet it nevertheless makes sense to ask why irreversible transitions through multiple states are needed to switch on the transcription of eukaryotic genes (88,89) and how this observation can be reconciled with the lower regulatory power of such architectures. This is the topic of our ongoing research.
Discussion
When studying noise in gene regulation one is usually restricted to the use of phenomenological models, rather than a fully detailed biochemical reaction scheme. Simpler models, such as those studied in this paper, also allow us to decouple questions of mechanistic interpretation from the questions of functional consequences. Here, we extended a well-known functional two-state model of gene expression to multiple internal states. We introduced state transition graphs to model the “decision logic” by which changes in the concentrations of regulatory proteins drive the switching of our genes between various states of expression. This abstract language allowed us to systematically organize and explore nonequivalent three-state promoters. The advantage of this approach is that many microscopically distinct regulatory schemes can be collapsed into equivalent classes sharing identical state transition graphs and identical information transmission properties.
The functional description of multistate promoters confers two separate benefits. First, it is able to generate measurable predictions, such as the noise vs. mean induction curve. Existing experimental and theoretical work using the two-state model has demonstrated how the measurements of noise constrain the space of promoter models (44), how the theory establishes the “vocabulary” by which various measured promoters can be classified and compared with each other (90), and how useful a baseline mathematical model can be in establishing quantitative signatures of deviation that, when observed, must lead to minimal model revisions able to accommodate new data (59). Alternative complex promoters presented here could explain existing data better either because of the inclusion of additional states (see (52)), or because we also included and analyzed the effects of input (diffusive) noise, which can mimic the effects of promoter switching noise but is often neglected (45). As a caveat, it appears that in many cases discriminating between promoter architectures based on the noise characteristics alone would be very difficult, and thus dynamical measurements would be necessary.
The second benefit of our approach is to provide a convenient framework for assessing the functional impact of noise in gene regulation, as measured by the mutual information between the inputs and the gene expression level. We are interested in the question whether multistate promoters can, at least in principle, perform better than the simple ON/OFF two-state model. We find that generically, i.e., for all three-state models where one state is expressing and only one transition is modulated by the input, the multistate promoters underperform the two-state model. Higher information transmission can be achieved when these conditions are violated, and biological examples for such violations can be found. For example, we find that a multistate promoter with cooperativity has a higher channel capacity than the best comparable two-state promoter, even when promoter switching noise is taken into account (see (11).). Dual-regulation yields surprisingly high benefits, which are largest when input noise is high. In the context of metazoan development where the concentrations of the morphogen molecules can be in the nanomolar range and the input noise is therefore high (35), the need to establish sharp spatial domains of downstream gene expression (as observed (91),) might have favored such dual-role promoter architectures. Lastly, we considered the simplest ideas for a promoter with irreversible transitions and have shown that they can lead to an increase in information transmission by sharpening the distribution of exit times from the expressing state (92).
The main conclusion of this article—namely that channel capacity can be increased by particular complex promoters—is testable in dedicated experiments. One could start with a simple regulatory scheme in a synthetic system and then by careful manipulation gradually introduce the possibility of additional states (e.g., by introducing more binding sites), using promoter sequences that show weaker binding for individual molecules yet allow for stronger cooperative interaction. In both the simple and complex system, one could then measure the noise behavior for various input levels. Information theoretic analysis of the resulting data could be used to judge if the design of higher complexity, although perhaps noisier by some other measure, is capable of transmitting more information, as predicted.
The list of multistate promoters that can outperform the two-state regulation and for which examples in nature could be found is potentially much longer and could include combinations of features described in this article. Rather than trying to find more examples, we should perhaps ask about fundamentally different mechanisms and constraints that our analysis did not consider. By expending energy to keep the system out of equilibrium, one could design robust reaction schemes where, for example, the binding of a regulatory protein leads (almost) deterministically to some tightly controlled response cycle, perhaps evading the diffusion noise limit (93) and increasing information transmission. At the same time, cells might be confronted by sources of stochasticity we did not discuss in this article—for example, because of cross-talk from spurious binding of noncognate regulators. Finally, cells need to not only transmit information through their regulatory elements, but actually perform computations, that is, combine various inputs into a single output, thereby potentially discarding information. A challenging question for the future is thus about extending the information-theoretic framework to these other cases of interest.
Acknowledgments
We thank W. Bialek, T. Gregor, I. Golding, M. Dravecká, K. Mitosch, G. Chevereau, J. Briscoe, and J. Kondev for helpful discussions.
Supporting Material
References
- 1.Levine M., Davidson E.H. Gene regulatory networks for development. Proc. Natl. Acad. Sci. USA. 2005;102:4936–4942. doi: 10.1073/pnas.0408031102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ronen M., Rosenberg R., Alon U. Assigning numbers to the arrows: parameterizing a gene regulation network by using accurate expression kinetics. Proc. Natl. Acad. Sci. USA. 2002;99:10555–10560. doi: 10.1073/pnas.152046799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Elowitz M.B., Levine A.J., Swain P.S. Stochastic gene expression in a single cell. Science. 2002;297:1183–1186. doi: 10.1126/science.1070919. [DOI] [PubMed] [Google Scholar]
- 4.Ozbudak E.M., Thattai M., van Oudenaarden A. Regulation of noise in the expression of a single gene. Nat. Genet. 2002;31:69–73. doi: 10.1038/ng869. [DOI] [PubMed] [Google Scholar]
- 5.Paulsson J. Summing up the noise in gene networks. Nature. 2004;427:415–418. doi: 10.1038/nature02257. [DOI] [PubMed] [Google Scholar]
- 6.Raj A., van Oudenaarden A. Nature, nurture, or chance: stochastic gene expression and its consequences. Cell. 2008;135:216–226. doi: 10.1016/j.cell.2008.09.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Houchmandzadeh B., Wieschaus E., Leibler S. Establishment of developmental precision and proportions in the early Drosophila embryo. Nature. 2002;415:798–802. doi: 10.1038/415798a. [DOI] [PubMed] [Google Scholar]
- 8.Tkačik G., Walczak A.M. Information transmission in genetic regulatory networks: a review. J. Phys. Condens. Matter. 2011;23:153102. doi: 10.1088/0953-8984/23/15/153102. [DOI] [PubMed] [Google Scholar]
- 9.Ziv E., Nemenman I., Wiggins C.H. Optimal signal processing in small stochastic biochemical networks. PLoS ONE. 2007;2:e1077. doi: 10.1371/journal.pone.0001077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Tkačik G., Callan C.G., Jr., Bialek W. Information capacity of genetic regulatory elements. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2008;78:011910. doi: 10.1103/PhysRevE.78.011910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Tkačik G., Walczak A.M., Bialek W. Optimizing information flow in small genetic networks. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:031920. doi: 10.1103/PhysRevE.80.031920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Walczak A.M., Tkačik G., Bialek W. Optimizing information flow in small genetic networks. II. Feed-forward interactions. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:041905. doi: 10.1103/PhysRevE.81.041905. [DOI] [PubMed] [Google Scholar]
- 13.Tkačik G., Walczak A.M., Bialek W. Optimizing information flow in small genetic networks. III. A self-interacting gene. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:041903. doi: 10.1103/PhysRevE.85.041903. [DOI] [PubMed] [Google Scholar]
- 14.Tkačik G., Callan C.G., Jr., Bialek W. Information flow and optimization in transcriptional regulation. Proc. Natl. Acad. Sci. USA. 2008;105:12265–12270. doi: 10.1073/pnas.0806077105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Dubuis J.O., Tkačik G., Bialek W. Positional information, in bits. Proc. Natl. Acad. Sci. USA. 2013;110:16301–16308. doi: 10.1073/pnas.1315642110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tostevin F., ten Wolde P.R. Mutual information between input and output trajectories of biochemical networks. Phys. Rev. Lett. 2009;102:218101. doi: 10.1103/PhysRevLett.102.218101. [DOI] [PubMed] [Google Scholar]
- 17.Tostevin F., ten Wolde P.R. Mutual information in time-varying biochemical systems. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:061917. doi: 10.1103/PhysRevE.81.061917. [DOI] [PubMed] [Google Scholar]
- 18.Cheong R., Rhee A., Levchenko A. Information transduction capacity of noisy biochemical signaling networks. Science. 2011;334:354–358. doi: 10.1126/science.1204553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.de Ronde W.H., Tostevin F., ten Wolde P.R. Effect of feedback on the fidelity of information transmission of time-varying signals. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;82:031914. doi: 10.1103/PhysRevE.82.031914. [DOI] [PubMed] [Google Scholar]
- 20.de Ronde W.H., Tostevin F., ten Wolde P.R. Feed-forward loops and diamond motifs lead to tunable transmission of information in the frequency domain. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;86:021913. doi: 10.1103/PhysRevE.86.021913. [DOI] [PubMed] [Google Scholar]
- 21.de Ronde W., Tostevin F., ten Wolde P.R. Multiplexing biochemical signals. Phys. Rev. Lett. 2011;107:048101. doi: 10.1103/PhysRevLett.107.048101. [DOI] [PubMed] [Google Scholar]
- 22.Tostevin F., de Ronde W., ten Wolde P.R. Reliability of frequency and amplitude decoding in gene regulation. Phys. Rev. Lett. 2012;108:108104. doi: 10.1103/PhysRevLett.108.108104. [DOI] [PubMed] [Google Scholar]
- 23.Mugler A., Tostevin F., ten Wolde P.R. Spatial partitioning improves the reliability of biochemical signaling. Proc. Natl. Acad. Sci. USA. 2013;110:5927–5932. doi: 10.1073/pnas.1218301110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bowsher C.G., Swain P.S. Identifying sources of variation and the flow of information in biochemical networks. Proc. Natl. Acad. Sci. USA. 2012;109:E1320–E1328. doi: 10.1073/pnas.1119407109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Jost D., Nowojewski A., Levine E. Regulating the many to benefit the few: role of weak small RNA targets. Biophys. J. 2013;104:1773–1782. doi: 10.1016/j.bpj.2013.02.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hormoz S. Cross talk and interference enhance information capacity of a signaling pathway. Biophys. J. 2013;104:1170–1180. doi: 10.1016/j.bpj.2013.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Levine J., Kueh H.Y., Mirny L. Intrinsic fluctuations, robustness, and tunability in signaling cycles. Biophys. J. 2007;92:4473–4481. doi: 10.1529/biophysj.106.088856. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lalanne J.-B., François P. Principles of adaptive sorting revealed by in silico evolution. Phys. Rev. Lett. 2013;110:218102. doi: 10.1103/PhysRevLett.110.218102. [DOI] [PubMed] [Google Scholar]
- 29.Mancini F., Wiggins C.H., Walczak A.M. Time-dependent information transmission in a model regulatory circuit. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2013;88:022708. doi: 10.1103/PhysRevE.88.022708. [DOI] [PubMed] [Google Scholar]
- 30.Taylor, S. F., N. Tishby, and W. Bialek, 2007. Information and fitness. arXiv 0712.4382.
- 31.Rivoire O., Leibler S. The value of information for populations in varying environments. J. Stat. Phys. 2011;142:1124–1166. [Google Scholar]
- 32.Donaldson-Matasci M.C., Bergstrom C.T., Lachmann M. The fitness value of information. Oikos. 2010;119:219–230. doi: 10.1111/j.1600-0706.2009.17781.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Bialek W., Setayeshgar S. Physical limits to biochemical signaling. Proc. Natl. Acad. Sci. USA. 2005;102:10040–10045. doi: 10.1073/pnas.0504321102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bialek W., Setayeshgar S. Cooperativity, sensitivity, and noise in biochemical signaling. Phys. Rev. Lett. 2008;100:258101. doi: 10.1103/PhysRevLett.100.258101. [DOI] [PubMed] [Google Scholar]
- 35.Gregor T., Tank D.W., Bialek W. Probing the limits to positional information. Cell. 2007;130:153–164. doi: 10.1016/j.cell.2007.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.van Kampen N. North Holland; Amsterdam: 1981. Stochastic processes in physics and chemistry. [Google Scholar]
- 37.Peccoud J., Ycart B. Markovian modeling of gene-products synthesis. Theor. Popul. Biol. 1995;48:222–234. [Google Scholar]
- 38.Iyer-Biswas S., Hayot F., Jayaprakash C. Stochasticity of gene products from transcriptional pulsing. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;79:031911. doi: 10.1103/PhysRevE.79.031911. [DOI] [PubMed] [Google Scholar]
- 39.Shahrezaei V., Swain P.S. Analytical distributions for stochastic gene expression. Proc. Natl. Acad. Sci. USA. 2008;105:17256–17261. doi: 10.1073/pnas.0803850105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Dobrzynski M., Bruggeman F.J. Elongation dynamics shape bursty transcription and translation. Proc. Natl. Acad. Sci. USA. 2009;106:2583–2588. doi: 10.1073/pnas.0803507106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Kepler T.B., Elston T.C. Stochasticity in transcriptional regulation: origins, consequences, and mathematical representations. Biophys. J. 2001;81:3116–3136. doi: 10.1016/S0006-3495(01)75949-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Hu B., Kessler D.A., Levine H. Effects of input noise on a simple biochemical switch. Phys. Rev. Lett. 2011;107:148101. doi: 10.1103/PhysRevLett.107.148101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Hu B., Kessler D.A., Levine H. How input fluctuations reshape the dynamics of a biological switching system. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;86:061910. doi: 10.1103/PhysRevE.86.061910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.So L.-H., Ghosh A., Golding I. General properties of transcriptional time series in Escherichia coli. Nat. Genet. 2011;43:554–560. doi: 10.1038/ng.821. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tkačik G., Gregor T., Bialek W. The role of input noise in transcriptional regulation. PLoS ONE. 2008;3:e2774. doi: 10.1371/journal.pone.0002774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Raser J.M., O’Shea E.K. Control of stochasticity in eukaryotic gene expression. Science. 2004;304:1811–1814. doi: 10.1126/science.1098641. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Raj A., Peskin C.S., Tyagi S. Stochastic mRNA synthesis in mammalian cells. PLoS Biol. 2006;4:e309. doi: 10.1371/journal.pbio.0040309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Sánchez A., Kondev J. Transcriptional control of noise in gene expression. Proc. Natl. Acad. Sci. USA. 2008;105:5081–5086. doi: 10.1073/pnas.0707904105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Gutierrez P.S., Monteoliva D., Diambra L. Role of cooperative binding on noise expression. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:011914. doi: 10.1103/PhysRevE.80.011914. [DOI] [PubMed] [Google Scholar]
- 50.Karmakar R. Conversion of graded to binary response in an activator-repressor system. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:021905. doi: 10.1103/PhysRevE.81.021905. [DOI] [PubMed] [Google Scholar]
- 51.Coulon A., Gandrillon O., Beslon G. On the spontaneous stochastic dynamics of a single gene: complexity of the molecular interplay at the promoter. BMC Syst. Biol. 2010;4:2. doi: 10.1186/1752-0509-4-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Sanchez A., Garcia H.G., Kondev J. Effect of promoter architecture on the cell-to-cell variability in gene expression. PLOS Comput. Biol. 2011;7:e1001100. doi: 10.1371/journal.pcbi.1001100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Zhou T., Zhang J. Analytical results for a multistate gene model. SIAM J. Appl. Math. 2012;72:789–818. [Google Scholar]
- 54.Zhang J., Chen L., Zhou T. Analytical distribution and tunability of noise in a model of promoter progress. Biophys. J. 2012;102:1247–1257. doi: 10.1016/j.bpj.2012.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Gutierrez P.S., Monteoliva D., Diambra L. Cooperative binding of transcription factors promotes bimodal gene expression response. PLoS ONE. 2012;7:e44812. doi: 10.1371/journal.pone.0044812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Blake W.J., Balázsi G., Collins J.J. Phenotypic consequences of promoter-mediated transcriptional noise. Mol. Cell. 2006;24:853–865. doi: 10.1016/j.molcel.2006.11.003. [DOI] [PubMed] [Google Scholar]
- 57.Blake W.J., Kærn M., Collins J.J. Noise in eukaryotic gene expression. Nature. 2003;422:633–637. doi: 10.1038/nature01546. [DOI] [PubMed] [Google Scholar]
- 58.Kandhavelu M., Mannerström H., Ribeiro A.S. In vivo kinetics of transcription initiation of the lar promoter in Escherichia coli. Evidence for a sequential mechanism with two rate-limiting steps. BMC Syst. Biol. 2011;5:149. doi: 10.1186/1752-0509-5-149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Suter D.M., Molina N., Naef F. Mammalian genes are transcribed with widely different bursting kinetics. Science. 2011;332:472–474. doi: 10.1126/science.1198817. [DOI] [PubMed] [Google Scholar]
- 60.Setty Y., Mayo A.E., Alon U. Detailed map of a cis-regulatory input function. Proc. Natl. Acad. Sci. USA. 2003;100:7702–7707. doi: 10.1073/pnas.1230759100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Shannon C. A mathematical theory of communication. Bell Syst. Tech. J. 1948;27:379–423. 623–56. [Google Scholar]
- 62.Cover T., Thomas J. Wiley Interscience; New York: 2006. Elements of Information Theory. [Google Scholar]
- 63.Walczak A.M., Sasai M., Wolynes P.G. Self-consistent proteomic field theory of stochastic gene switches. Biophys. J. 2005;88:828–850. doi: 10.1529/biophysj.104.050666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gillespie D.T. The chemical Langevin equation. J. Chem. Phys. 2000;113:297. [Google Scholar]
- 65.Swain P.S., Elowitz M.B., Siggia E.D. Intrinsic and extrinsic contributions to stochasticity in gene expression. Proc. Natl. Acad. Sci. USA. 2002;99:12795–12800. doi: 10.1073/pnas.162041399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Berg H.C., Purcell E.M. Physics of chemoreception. Biophys. J. 1977;20:193–219. doi: 10.1016/S0006-3495(77)85544-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Berg O.G., von Hippel P.H. Diffusion-controlled macromolecular interactions. Annu. Rev. Biophys. Biophys. Chem. 1985;14:131–160. doi: 10.1146/annurev.bb.14.060185.001023. [DOI] [PubMed] [Google Scholar]
- 68.Endres R.G., Wingreen N.S. Accuracy of direct gradient sensing by single cells. Proc. Natl. Acad. Sci. USA. 2008;105:15749–15754. doi: 10.1073/pnas.0804688105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Carey L.B., van Dijk D., Segal E. Promoter sequence determines the relationship between expression level and noise. PLoS Biol. 2013;11:e1001528. doi: 10.1371/journal.pbio.1001528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.de Ronde W.H., Daniels B.C., Nemenman I. Mesoscopic statistical properties of multistep enzyme-mediated reactions. IET Syst. Biol. 2009;3:429–437. doi: 10.1049/iet-syb.2008.0167. [DOI] [PubMed] [Google Scholar]
- 71.Sanchez A., Choubey S., Kondev J. Regulation of noise in gene expression. Annu. Rev. Biophys. 2013;42:469–491. doi: 10.1146/annurev-biophys-083012-130401. [DOI] [PubMed] [Google Scholar]
- 72.Golding I., Paulsson J., Cox E.C. Real-time kinetics of gene activity in individual bacteria. Cell. 2005;123:1025–1036. doi: 10.1016/j.cell.2005.09.031. [DOI] [PubMed] [Google Scholar]
- 73.Geertz M., Shore D., Maerkl S.J. Massively parallel measurements of molecular interaction kinetics on a microfluidic platform. Proc. Natl. Acad. Sci. USA. 2012;109:16540–16545. doi: 10.1073/pnas.1206011109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Viñuelas J., Kaneko G., Gandrillon O. Quantifying the contribution of chromatin dynamics to stochastic gene expression reveals long, locus-dependent periods between transcriptional bursts. BMC Biol. 2013;11:15. doi: 10.1186/1741-7007-11-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Sanchez A., Osborne M.L., Gelles J. Mechanism of transcriptional repression at a bacterial promoter by analysis of single molecules. EMBO J. 2011;30:3940–3946. doi: 10.1038/emboj.2011.273. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Garcia H.G., Sanchez A., Phillips R. Operator sequence alters gene expression independently of transcription factor occupancy in bacteria. Cell Rep. 2012;2:150–161. doi: 10.1016/j.celrep.2012.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Yang H.-T., Ko M.S.H. Stochastic modeling for the expression of a gene regulated by competing transcription factors. PLoS ONE. 2012;7:e32376. doi: 10.1371/journal.pone.0032376. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Earnest T.M., Roberts E., Luthey-Schulten Z. DNA looping increases the range of bistability in a stochastic model of the lac genetic switch. Phys. Biol. 2013;10:026002. doi: 10.1088/1478-3975/10/2/026002. [DOI] [PubMed] [Google Scholar]
- 79.Mirny L.A. Nucleosome-mediated cooperativity between transcription factors. Proc. Natl. Acad. Sci. USA. 2010;107:22534–22539. doi: 10.1073/pnas.0913805107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Segal E., Widom J. What controls nucleosome positions? Trends Genet. 2009;25:335–343. doi: 10.1016/j.tig.2009.06.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Li G.-W., Berg O., Elf J. Effects of macromolecular crowding and DNA looping on gene regulation kinetics. Nat. Phys. 2009;5:294–297. [Google Scholar]
- 82.Grönlund A., Lötstedt P., Elf J. Transcription factor binding kinetics constrain noise suppression via negative feedback. Nat. Commun. 2013;4:1864. doi: 10.1038/ncomms2867. [DOI] [PubMed] [Google Scholar]
- 83.Lehner B. Conflict between noise and plasticity in yeast. PLoS Genet. 2010;6:e1001185. doi: 10.1371/journal.pgen.1001185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Bajić D., Poyatos J.F. Balancing noise and plasticity in eukaryotic gene expression. BMC Genomics. 2012;13:343. doi: 10.1186/1471-2164-13-343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Parker D.S., White M.A., Barolo S. The cis-regulatory logic of Hedgehog gradient responses: key roles for gli binding affinity, competition, and cooperativity. Sci. Signal. 2011;4:ra38. doi: 10.1126/scisignal.2002077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.White M.A., Parker D.S., Cohen B.A. A model of spatially restricted transcription in opposing gradients of activators and repressors. Mol. Syst. Biol. 2012;8:614. doi: 10.1038/msb.2012.48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Müller B., Basler K. The repressor and activator forms of Cubitus interruptus control Hedgehog target genes through common generic gli-binding sites. Development. 2000;127:2999–3007. doi: 10.1242/dev.127.14.2999. [DOI] [PubMed] [Google Scholar]
- 88.Larson D.R. What do expression dynamics tell us about the mechanism of transcription? Curr. Opin. Genet. Dev. 2011;21:591–599. doi: 10.1016/j.gde.2011.07.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Yosef N., Regev A. Impulse control: temporal dynamics in gene transcription. Cell. 2011;144:886–896. doi: 10.1016/j.cell.2011.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Zenklusen D., Larson D.R., Singer R.H. Single-RNA counting reveals alternative modes of gene expression in yeast. Nat. Struct. Mol. Biol. 2008;15:1263–1271. doi: 10.1038/nsmb.1514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Dessaud E., McMahon A.P., Briscoe J. Pattern formation in the vertebrate neural tube: a sonic hedgehog morphogen-regulated transcriptional network. Development. 2008;135:2489–2503. doi: 10.1242/dev.009324. [DOI] [PubMed] [Google Scholar]
- 92.Pedraza J.M., Paulsson J. Effects of molecular memory and bursting on fluctuations in gene expression. Science. 2008;319:339–343. doi: 10.1126/science.1144331. [DOI] [PubMed] [Google Scholar]
- 93.Aquino G., Endres R.G. Increased accuracy of ligand sensing by receptor internalization. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2010;81:021909. doi: 10.1103/PhysRevE.81.021909. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


