Fine-Granularity Functional Interaction Signatures for Characterization of Brain Conditions

Abstract

In the human brain, functional activity occurs at multiple spatial scales. Current studies on functional brain networks and their alterations in brain diseases via resting-state functional magnetic resonance imaging (rs-fMRI) are generally either at local scale (regionally confined analysis and inter-regional functional connectivity analysis) or at global scale (graph theoretic analysis). In contrast, inferring functional interaction at fine-granularity sub-network scale has not been adequately explored yet. Here our hypothesis is that functional interaction measured at fine-granularity subnetwork scale can provide new insight into the neural mechanisms of neurological and psychological conditions, thus offering complementary information for healthy and diseased population classification. In this paper, we derived fine-granularity functional interaction (FGFI) signatures in subjects with Mild Cognitive Impairment (MCI) and Schizophrenia by diffusion tensor imaging (DTI) and rsfMRI, and used patient-control classification experiments to evaluate the distinctiveness of the derived FGFI features. Our experimental results have shown that the FGFI features alone can achieve comparable classification performance compared with the commonly used inter-regional connectivity features. However, the classification performance can be substantially improved when FGFI features and inter-regional connectivity features are integrated, suggesting the complementary information achieved from the FGFI signatures.

Introduction

Resting-state functional magnetic resonance imaging (rsfMRI) measures spontaneous low-frequency fluctuations in the blood oxygen level-dependent (BOLD) signal that is correlated with intrinsic neuronal signaling (Biswal et al. 1995; Raichle and Mintun 2006). Considering the intrinsic neuronal signaling accounts for a large proportion of brain activity, the study of these spontaneous fluctuations has enabled systematical delineation of the functional brain architecture (e.g., Smith et al. 2009; Biswal et al. 2010; Sporns 2011; Behrens and Sporns 2011) and the examination of whether the functional architecture of intrinsic activity is altered in neurological and psychiatric conditions (e.g., Alzheimer's diseases (AD) and mild cognitive impairment (MCI) (Reiman and Jagust 2011), and Schizophrenia (SZ) (Fornito et al. 2012)). Several review articles (Barabasi et al. 2011; Bassett and Bullmore 2009; Zhang and Raichle 2010) have provided extensive surveys of relevant studies. In rsfMRI based disease pathophysiology studies, functional activity and/or functional architecture related measurements are typically derived from rs-fMRI for both patients and matched controls, followed by discriminative studies that usually involve feature selection, classifier training and evaluation through pattern analysis algorithms. The most discriminative features, often referred to as neuroimaging biomarkers, are then interpreted to elucidate the functional alterations in the brain conditions under study.

Recently, it has been realized that spatial scale is a critical issue when using intrinsic functional activity measured by rs-fMRI as a biomarker for brain diseases (Zhang and Raichle 2010). The reason is that functional activity occurs at multiple spatial scales, and various diseases at different stages might be sensitive to activity changes at different scales. For example, Autism is hypothesized to involve relative alterations in global connectivity (Courchesne and Pierce 2005; Li et al. 2012a). In this case, increased sensitivity might be accomplished by detecting global changes such as those constructed with graph theory, rather than by detecting localized connectivity deficits. In other diseases, the deficit might be highly localized (Seeley et al. 2009), thus the detection of functional activity alterations may be confined to the relevant locations. In our understanding, the spatial scales in previous studies can be briefly categorized into three groups: 1) Regionally-confined analysis; 2) Inter-regional connectivity analysis; and 3) Global network-level analysis based on graph theory, which will be discussed as follows.

Regionally-Confined Analysis

Regionally-confined analysis usually depends on the properties of the regional rs-fMRI time series. For example, the amplitude of low-frequency fluctuation (ALFF) measures the total power of the time course for a given voxel within a specific frequency range (e.g.,0.01–0.10 Hz) (Zang et al. 2007), and fractional ALFF (fALFF) measures the power within a specific frequency range divided by the total power in the entire detectable frequency range (Zou et al. 2008). In comparison, the regional homogeneity (ReHo) focuses on the functional coherence of a given voxel with its nearest neighbors (Zang et al. 2004). Both ALFF/fALFF and ReHo alterations have been widely reported in a variety of brain conditions (Liu et al. 2008). For example, Hoptman et al. showed that patients with SZ had reduced fALFF in the lingual gyrus, left cuneus, left insula/superior temporal gyrus and right caudate, and increased fALFF in the medial prefrontal cortex and the right parahippocampal gyrus. Also, the ALFF was reduced in SZ patients in the lingual gyrus, cuneus, and precuneus and increased in the left parahippocampal gyrus (Hoptman et al. 2010). Dai et al. reported that AD patients had significantly decreased ReHo in the posterior cingulate cortex/precuneus and increased ReHo in the bilateral cuneus, left lingual gyrus and right fusiform gyrus compared with healthy subjects (Dai et al. 2011).

Inter-Regional Connectivity Analysis

Inter-regional connectivity analysis usually involves the identification of correlations between distinct brain regions, commonly referred to as functional connectivity. Roughly, inter-regional functional connectivity analysis methods can be classified into two categories: model-dependent and model-free methods (van den Heuvel and Hulshoff Pol 2010).

One of the most popular model-dependent techniques for performing rs-fMRI analysis is seed-based correlation (Andrews-Hanna et al. 2007; Biswal et al. 1995; Cordes et al. 2000; Fransson 2005; Larson-Prior et al. 2009; Song et al. 2008). In seed-based correlation, the rs-fMRI time course is first extracted from a ‘seed’ region of interest (ROI). Correlations are then computed between the seed's fMRI time course and each voxel's fMRI signals in the brain, generating a functional connectivity map (fcMap). In general, fcMaps provide a clear view of with which regions the seed region is functionally connected, making it an elegant way of examining functional connectivity in normal and diseased human brains. For example, in one of the early studies that used rs-fMRI to examine disease pathophysiology in patients with either AD or MCI (Li et al. 2002), the authors used seed-based analysis and demonstrated that patients with AD showed decreased bilateral hippocampal connectivity compared with the control group.

However, the information of an fcMap is limited to the functional connections of the selected seed region, making it difficult to examine functional connectivity patterns on a whole-brain scale (van den Heuvel and Hulshoff Pol 2010). The first step towards mapping large-scale functional brain network is to define the network nodes (or ROIs) that cover the entire brain (Bressler and Menon 2010). To address this challenge, a popular model-dependent method is to use image/surface registration algorithms to warp the candidate brain to a predefined volume/cortical surface template, and parcellate the candidate brain into a set of anatomical ROIs (e.g., (Tzourio-Mazoyer et al. 2002)). Functional connectivity is then measured for each pair of regions, resulting in a large-scale functional brain networks. A rich set of studies have used this method to systematically investigate functional alterations in brain diseases. For example, a variety of increases and decreases in functional connectivity were detected in patients with AD/MCI versus controls in (Supekar et al. 2008; Wang et al. 2007), and relatively high sensitivity and specificity have been reported in differentiation diseased population from normal controls using those functional connectivity patterns (Fox and Greicius 2010). The limitations of registration based image/surface parcellation for brain ROIs identification have been discussed in (Liu 2011). As an alternative approach, we have developed and validated a cortical ROIs localization system named Dense Individualize Common Connectivity-based Cortical Landmark (DICCCOL) (Zhu et al. 2012b), in which 358 brain ROIs that provide intrinsically-established structural correspondences across different subjects can be accurately localized and each identified ROI was optimized to possess maximal group-wise consistency of DTI-derived fiber shape patterns (Zhu et al. 2012a, b). By using the DICCCOL system, our recent study investigated the discrepant brain regions of prenatal cocaine exposure (PCE) affected adolescents on the whole cortex, and identified 10 DICCCOLPCE ROIs that exhibit significant differences of functional connectivity between PCE brains and normal controls (Li et al. 2012a, b). It is notable that rather than the inter-regional functional connectivity patterns, statistical measures such as global/local connectivity strength and diversity of connectivity (e.g., (Lynall et al. 2010)) derived from the large-scale connectivity matrix have also been used as potential bio-markers for clinical studies.

Beside model-dependent methods, several model-free methods have also been proposed for rs-fMRI analysis including principal component analysis (PCA) (Friston 1998), independent component analysis (ICA) (Beckmann et al. 2005; Calhoun et al. 2001; De Luca et al. 2005; van de Ven et al. 2004) and hierarchical (Cordes et al. 2002; Salvador et al. 2005), Laplacian (Thirion et al. 2006) and normalized cut clustering (van den Heuvel et al. 2008). With those model-free methods, a set of resting-state functional brain networks such as visual network, motor network and default mode network (DMN) have been successfully identified (Beckmann et al. 2005; Damoiseaux et al. 2006; De Luca et al. 2005; van de Ven et al. 2004; van den Heuvel et al. 2008). Similarly, statistical measures including global/-local connectivity strength and diversity of connectivity derived from the identified functional networks have been used to investigate functional alterations in brain conditions, and promising results have been reported (Bassett and Bullmore 2009; Zhang and Raichle 2010).

Global Network Level Analysis Based on Graph Theory

The ascendancy of graph theoretical analysis of brain networks has been driven by the growing realization that the behavior of complex systems of the human brain is shaped by interactions among their constituent elements (Bullmore and Sporns 2009). Once the brain network has been represented in graphical form, its topological properties can be measured based on graph theory. The quantitative measurements offered by graph theory allow the characterization of the traditionally abstract concepts of integration (for example, high clustering and short path length) and segregation (for example, modularity and centrality), thereby providing a comprehensive understanding of how brain networks are structurally and functionally organized and how they generate complex dynamics, as well as a statistical means to distinguish between healthy and diseased populations. It is notable that current studies of graphical properties alterations in brain diseases are usually performed at global network scale. Preferential interests have been directed to graphical parameters that infer global organization of the human brain such as small-worldness, global efficiency, wiring cost, hierarchy and assortativity (Bullmore and Sporns 2009).

In general, using rs-fMRI, regionally confined analysis and inter-regional connectivity analysis investigate the brain at localized spatial scale, while graph theoretic analysis provides information about global organization of functional brain networks at global scale. Those studies have largely advanced our understanding of the neural mechanisms of neurological and psychological diseases. However, functional interactions at fine-granularity sub-network scale have not been adequately examined yet as far as we know. As mentioned before, functional activity occurs at multiple spatial scales, and brain diseases at different stages might exhibit functional activity alterations at different spatial scales. Thus, our hypothesis is that functional interactions measured at fine-granularity sub-network scale may provide new insight into the neural mechanisms of neurological and psychological conditions, thus offering complementary information for classification between healthy and diseased population using rs-fMRI. Compared with regionally-confined and inter-regional connectivity based analyses, fine-granularity functional interaction (FGFI) measures the functional integration among multiple (n>2) segregated brain regions. Compared with graph theoretical analysis, FGFI measures the functional interaction in brain networks with fine-granularity.

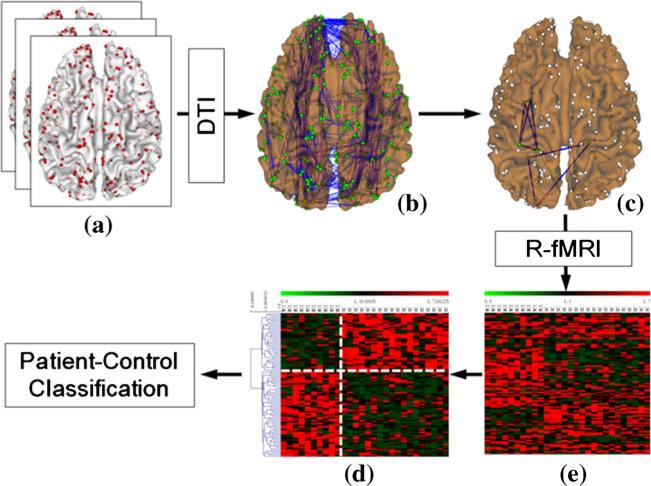
In this paper, we use rs-fMRI and DTI datasets of subjects with MCI and SZ as two test-beds to demonstrate their corresponding FGFI signatures, and examine how FGFI features can improve the performance in the differentiation of diseased population from healthy controls. The overview of our study is summarized in Fig. 1. Briefly, the DICCCOL system (Zhu et al. 2012b) was adopted to localize 358 cortical ROIs for each subject individually (Fig. 1(a)). Then, the whole-brain structural connectomes (Fig. 1(b)) were constructed from fiber tracts derived from DTI tractography (via MEDINRIA (Fillard and Gerig 2003)) (Zhu et al. 2012b; Li et al. 2012a, b). Afterwards, structural cliques (complete sub-graphs) were identified based on the structural connectomes, serving as the structural substrates of sub-networks for evaluating the FGFI signatures (Fig. 1 (c)). With concurrent rs-fMRI data, functional interactions in each graph clique were measured via the propensity for synchronization (PFS) (Fig. 1(d)). FGFI signatures for MCI/SZ were derived as the decreased and increased clusters of significant functional interaction alterations inferred by group-wise significance analysis between patients and matched normal controls (Fig. 1(e)). Finally, patient-control classification experiments were used to evaluate the discriminability of FGFI features in differentiation of patients from healthy controls.

Fig. 1.

The overview of our study. a Cortical ROIs (red dots) localized via DICCCOL system for each subject. b Structural connectomes constructed from fiber tracts derived from DTI tractography. c Examples of structural cliques (complete sub-graphs) (purple polygons) serving as the structural substrates of sub-networks for evaluating the FGFIs. d Significantly altered FGFIs in patients. e FGFI signatures. The vertical white dashed line separates patients and controls, while the horizontal dashed white line separates significantly increases and decreased FGFIs in patients

Materials and Methods

Data Acquisition and Preprocessing

MCI Dataset

This study included 28 volunteer participants (10 MCI patients and 18 socio-demographically matched controls) who were recruited and scanned in the Duke-UNC Brain Imaging and Analysis Center (BIAC). Informed consent was obtained from all participants, and the experimental protocols were approved by the Duke IRB. The criteria for MCI determination were in accordance with NACC procedures and NINCDS-ADRDA diagnostic guidelines. Confirmation of the diagnosis for all subjects was made by a clinical psychiatrist (Dr. Wang) at Duke University Medical Center. The characteristics of the participants in this study are summarized as follows: numbers of males in MCI and controls: 5 and 8; age: 74.2±8.6 (MCI) and 72.1± 8.2 (controls); MMSE: 28.4±1.5 (MCI) and 29.4±0.9 (controls); years of education: 17.7±4.2 (MCI) and 16.3± 2.4 (controls).

The DTI and rs-fMRI datasets were acquired on a 3.0 Tesla scanner (GE Signa EXCITE, GE Healthcare). For functional imaging, 34 slices were acquired in the same plane (as the low resolution T1-weighted images) using a SENSE inverse-spiral pulse sequence with echo time (TE)= 32 ms, repetition time (TR)=2000 ms, FOV=25.6 cm², matrix=64×64×34, 3.8 mm³. For diffusion tensor imaging, 25 direction diffusion-weighted whole-brain volumes were acquired axially parallel to the AC-PC line using diffusion weighting values, b=0 and 1000 s/mm², flip angle=90°, TR=17 s and TE=78 ms. The imaging matrix was 256× 256 with a rectangular field of view (FOV) of 256× 256 mm² and 72 slices with a slice thickness of 2.0 mm.

SZ Dataset

Multimodal T1 structural MRI, DTI and rsfMRI datasets of 10 SZ subjects and 10 healthy controls were downloaded from the publicly available NA-MIC dataset (http://hdl.handle.net/1926/1687). In brief, the multimodal imaging parameters are summarized as follows. The structural MRI acquisition protocol was based on spoiled gradient-recalled acquisition (fast-SPGR) with the following parameters: TR=7.4 ms, TE=3 ms, TI=600, 10° flip angle, 25.6 cm² field of view, matrix=256×256. The voxel dimensions are 1×1×1 mm³. Both DTI and rs-fMRI scans were acquired on a 3 Tesla GE system using an echo planar imaging (EPI) sequence. An 8 channel coil was used to perform parallel imaging using ASSET (Array Spatial Sensitivity Encoding Techniques, GE) with a SENSE-factor (speed-up) of 2. The DTI used 51 directions with b=900 and 8 baseline scans with b=0. Other imaging scan parameters include: TR 17000 ms, TE 78 ms, FOV 24 cm, 144× 144 encoding steps, 1.7 mm slice thickness. Totally, 85 axial slices parallel to the AC-PC line covering the whole brain were acquired. The rs-fMRI was 10 min long, and contained 200 repetitions of a high resolution EPI scan (96×96 in plane, 3 mm thickness, TR=3000 ms, TE=30 ms, 39 slices, ASSETT). Subjects were asked to close their eyes and rest during the scans. The same data pre-processing steps used in the above multimodal DTI and rs-fMRI MCI datasets were used here. Two cases of SZ subjects were discarded due to low quality of DTI data.

Cortical ROIs Localization

Localizing robust, reproducible and accurate cortical ROIs that are consistent and correspondent across individuals and populations is a critical problem for effective brain networks studies (Liu 2011). Recently, we developed and validated a novel data-driven discovery approach that identified 358 consistent and corresponding cortical ROIs in over 240 brains (Zhu et al. 2012a, b; Li et al. 2012a, b), in which each identified ROI was optimized to possess maximal group-wise consistency of DTI-derived fiber shape patterns. The neuroscience basis is that each brain's cyto-architectonic area has a unique set of extrinsic inputs/outputs, named the “connectional fingerprint” in (Passingham et al. 2002), which principally determine the functions that each brain area could possibly possess. Our prior studies have shown that these 358 DICCCOLs can be used to effectively construct large-scale structural connectomes (Zhu et al. 2012b) and to derive informative functional connectomics signatures (Li et al. 2012a, b). Thus, in this paper, we employ the DICCCOL system to localize dense cortical ROIs for each subject.

Localizing cortical ROIs using DICCCOL system includes steps of DICCCOL discovery (training) and prediction, which are briefly described as follows and more details are referred to (Zhu et al. 2012b; Zhang et al. 2011). In the training stage, a simple strategy is adopted to generate a regular grid initialization of 2056 cortical landmarks for each subject in ten training samples. The initialization aimed to place a dense map of cortical ROIs distributed over major brain regions, while establishing rough correspondences across those subjects by linear registration. After initialization, we formulated the problem of optimization of ROI locations as an energy minimization problem, which aimed to maximize the consistency of structural connectivity patterns across the ten training samples. The optimization was performed for each initialized ROI separately. Specifically, for a given ROI, we extracted white matter fiber bundles emanating from the small regions around the neighborhood of its initial location. Then a trace-map model (Zhu et al. 2012b) was employed to describe the shape pattern of the extracted fiber bundle. By searching the whole-space of candidate locations, we found an optimal combination of new landmarks that exhibited the least group variance of the fiber bundle shape pattern in the ten training samples. The optimization step was then followed by a determination step in which both quantitative and qualitative methods were used to evaluate the consistency of converged ROIs, and finally 358 ROIs with high consistency across the training samples were selected as the DICCCOL landmarks. In the prediction stage, the 358 DICCCOL landmarks were predicted for any new subject with DTI dataset (e.g., Fig. 1a). In current stage, the prediction was performed for each landmark separately. The initialization of the DICCCOL landmarks in the candidate new subject was achieved via a linear registration of the training samples to the candidate. Then, an optimization step was employed to finalize the landmarks so that the similarity of the fiber bundle shape patterns between the candidate and those training samples is maximized.

Sub-Networks Identification

In the literature, clustering algorithms (e.g., N-cut in (van den Heuvel et al. 2008)) are typically used to group predefined voxels/ROIs (358 DICCCOL landmarks in our study) into sub-networks based on their functional and structural connection patterns. However, a prerequisite to perform sub-network clustering is a predefined number of clusters. Such a prerequisite is somehow ambiguous since how many sub-networks exist in the human brain is unknown yet. Moreover, the spatial scale of the sub-networks, that is, the number of ROIs that compose a sub-network, is difficult to control in clustering approaches. For example, some resulted clusters may enclose dozens of ROIs while other clusters may include only several ROIs.

To address this challenge, we identify n-clique from the DTI-derived structural connectomes, serving as the structural substrates of sub-networks to measure the functional behavior of sub-networks at fine granularity. In graph theory, a clique in a graph is defined as a subset of its vertices such that every pair of two vertices in the subset are connected by an edge (Luce and Perry 1949). Clique is one of the basic concepts in graph theory and has been used in many mathematical problems (Kemp and Tenenbaum 2008), as well as in structural and functional brain network studies (Wu et al. 2012; Lohmann and Bohn 2002). More importantly, it has been observed that the spontaneous fluctuations measured in rs-fMRI are synchronous within brain regions that are anatomically connected by large white matter tracts (Vincent et al. 2007), and functionally correlated networks demonstrate a high degree of correspondence with DTI-reconstructed anatomy in a variety of networks (Honey et al. 2009; Greicius et al. 2009). Thus, the cliques extracted from the structural connectomes provide a natural way to define structural substrates for investigating functional interactions of a sub-network and possesses strong biological support given the intrinsic close relationships between structural and functional connectivities.

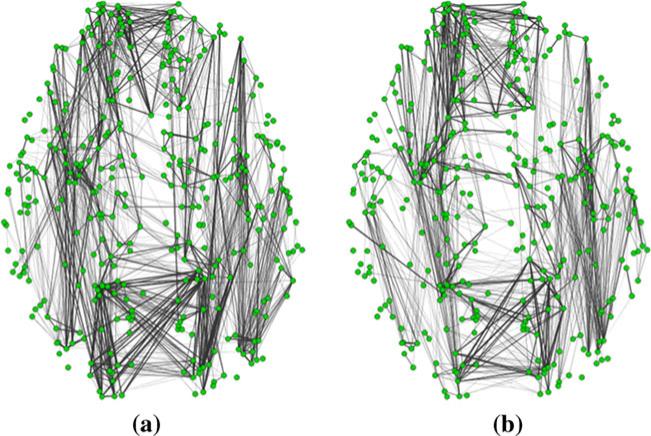
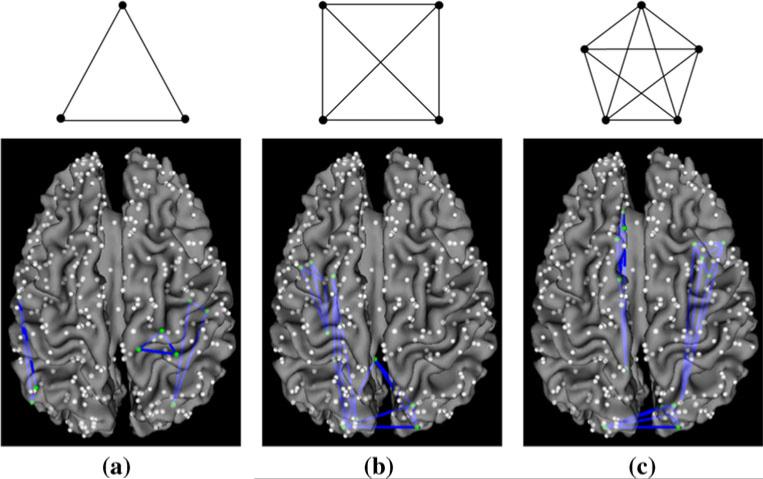
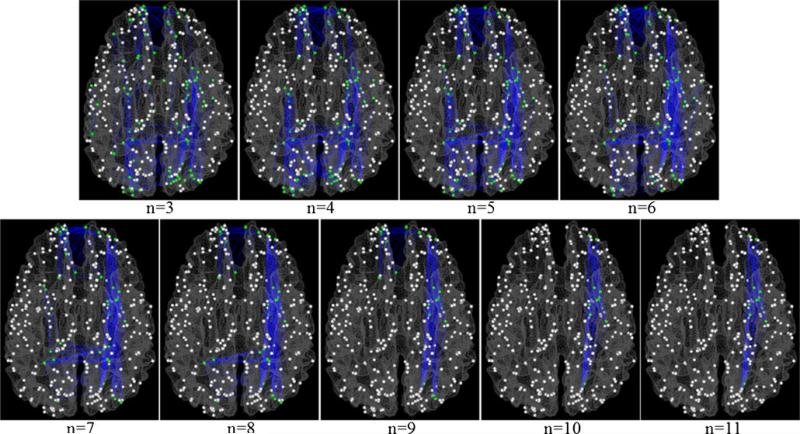
The structural connectivity matrix was derived from the DTI data for each subject. The structural connectivity between any pair of the 358 DICCCOL ROIs was approximately quantified as the number of the fiber tracks connecting the two ROIs (Zhu et al. 2012b). Figure 2 visualizes examples of structural connectivity matrices of two randomly selected subjects. It can be seen that the structural connectomes are reasonably consistent across subjects. The structural connectivity matrices of the subjects in the MCI or SZ dataset were averaged and a predefined threshold (5 in our study) was applied to remove the noise in fiber tracking. The resulted binary matrix, corresponding to the adjacent matrix of an undirected and un-weighted graph, was considered as the structural connectomes of the corresponding dataset. The cliques are identified for each dataset separately. Figure 3 illustrates the definition of cliques by taking those in the sizes of 3, 4 and 5 as examples, and shows some correspondence examples of structural graph cliques identified in our dataset. Notably, we can identify graph cliques with up to 11 and 13 nodes from the structural connectomes in the MCI and SZ datasets, respectively.

Fig. 2.

Examples of structural connectomes derived from DTI data of two randomly selected subjects. Green circles represent DICCCOL landmarks. Grey lines represent structural connectivities and the thickness indicates the strength of structural connectivities

Fig. 3.

Illustration of structural graph cliques and examples of cliques overlaid on a cortical surface. a, b and c corresponds to structural cliques with 3, 4 and 5 nodes, respectively. 3 cliques are shown as examples in each sub-figure

Functional Interaction of Sub-Network

In our study, the propensity for synchronization (PFS) (Hu et al. 2011) is used to characterize the functional interaction in each clique. In general, PFS describes the synchronizability of the network from which it is derived (Chung 1997; Hu et al. 2011; Boccaletti et al. 2006). Lower PFS indicates higher synchronizability of the network, while higher PFS indicates lower synchronizability of the network. We first describe the definition of PFS in a generic networked system and then demonstrate the calculation of PFS for the identified cliques.

Considering a generic, networked system of N coupled dynamical units, each of them gives rise to the evolution of an m-dimensional vector field x_i, the dynamical variables of the i-th node, governed by a local set of ordinary differential equations x = F_i (x_i. The equation of motion follows (Hu et al. 2011; Boccaletti et al. 2006)

$${\stackrel{.}{\mathrm{x}}}_i={\mathrm{F}}_i\left({\mathrm{x}}_i\right)-\sigma \sum _{j=1}^N{M}_{ij}\mathrm{H}\left({\mathbf{x}}_{\mathrm{j}}\right),i=1,2,\dots ,N$$ (1)

where x_i = Fi(xi) governs the local dynamics of the vector field xi in each node, H(x) is a vectorial output function, α is the overall coupling strength, and M is a zero row-sum N×N symmetric coupling matrix with strictly positive diagonal terms that specify the strength and topology of the underlying wiring connection. The Laplacian matrix of graph G has been typically used as M to characterize the topology of the networked system which G represents (Chung 1997). The definition of Laplacian matrix L(G) of a weighted graph G followed the description in (Chung 1997). Let d(v) denote the degree of v ∈ V(G). Given the connectivity matrix C(G), d(v) is defined as d(v) =Σ_u C(u,v). L(G) is calculated as

$$L(u,v)=\{\begin{array}{cc}1\hfill & ifu=v\hfill \\ 1-\frac{C(u,v)}{\sqrt{d_u{d}_v}}\hfill & ifu\ne v\hfill \end{array}\phantom{\}}$$ (2)

The spectrum of L, that is, the eigenvalues of L are nonnegative. Denote the eigenvalues of L by 0 = λ¹ ≤ λ²... ≤ λ. The variational equations governing the stability the synchronized state {x_i(t) = x_s (t),∀i} of the system in Eq. (1) follow the form (Boccaletti et al. 2006)

$$\stackrel{.}{\xi }=[1_N\otimes \mathrm{JF}\left({\mathrm{x}}_{\mathrm{s}}\right)-\sigma \mathrm{L}\otimes \mathrm{JH}\left({\mathrm{x}}_{\mathrm{s}}\right)]\xi$$ (3)

where ξ = (ξ¹, ξ², . . . ; ξ^N) is the collection of the variations of the units, ⊗ stands for the direct product between matrices, and J denotes the Jacobian operator. To assess the stability of the synchronous state of the system, Eq. (3) is further diagonalized and can be written in N-blocks variational equation with each block following

$${\stackrel{.}{\xi }}_k=\mathrm{JF}\left({\mathrm{x}}_{\mathrm{s}}\right){\xi }_{\mathrm{k}}-\sigma {\lambda }_{\mathrm{k}}\mathrm{JH}\left({\xi }_{\mathrm{k}}\right)$$ (4)

where λ_k is the k-th eigenvalue of the coupling matrix L. Replacing αλ_k by v in Eq. (4), the behavior of the largest Lyapunov exponent against v fully accounts for linear stability of synchronization manifold. For a large class of networked system, the master stability function is negative in a finite parameter interval I_st ≡ (v_min ≤ v ≤ v_max). The stability condition is satisfied when all the eigenvalues enter the interval I_st. Since v₁ and v₂ depend on the specific choice of F(x) and H(x), the key quantity for assessing the PFS on a network is the eigenratio r = λ_n/λ₂. The small r is, the more packed the eigenvalues are, leading to an enhanced interval I_st for any choice of F and H.

Given a graph clique with size of n, its functional connectivity matrix C_n×n is calculated according to the coincident rs-fMRI BOLD signals. Specifically, after co- registering the rs-fMRI with DTI data, the procedure of BOLD signal mapping, in which both the GM map and fiber tracks derived from DTI data are used as anatomical constraints (Li et al. 2010), is performed to find the corresponding rs-fMRI time series for each DICCCOL ROI for each subject. Note that each ROI typically contains multiple BOLD signals. In this paper, the first principal component derived from the principal components analysis performed on the multiple time series is used as the representative BOLD signal for the ROI. The functional connectivities are quantified as the temporal Pearson correlations between the representative BOLD signals for any possible pair of ROIs. The Laplacian matrix for the clique is calculated according to Eq. (2) and the PFS is measured as the eigenratio of the Laplacian matrix.

Derivation of FGFI Signatures

With the PFSs measured for all the cliques, we adopted the well-established approaches of deriving genomics signatures in genome-wide gene expression studies (Alizadeh et al. 2000) to discover FGFI signatures for the characterization of the brain conditions of MCI and SZ groups. Specifically, a hierarchical clustering algorithm (Alizadeh et al. 2000) was used to group FGFI attributes (equivalent to genes in genome-wide microarray data) on the basis of similarity in the pattern with which their attributes (equivalent to gene expression) varied over all brains (equivalent to samples). One of the prominently similar features between FGFI attributes and genome-wide gene expressions is that the increase or decrease in FGFI is equivalent to the up-regulated or down-regulated gene expression. Before the actual clustering procedure, we applied a preprocessing step of two-tailed t-test to remove those FGFIs that do not exhibit significance difference between MCI/SZ patients and controls. It is notable that false positive discovery rate correction was performed for the significant test in our study. Thus, the clustering procedure can not only be significantly speeded up, but also be less prone to the possible noises. For visual examination and interpretation (e.g., Fig. 1e), the FGFI signatures after the hierarchical clustering were shown in a matrix format (Alizadeh et al. 2000), with each row representing all attributes for a single element of the FGFIs, and each column representing the measured attributes for all FGFIs in a single brain.

Feature Selection, Classifier Training and Testing

Statistical t-test was performed to select the most discriminative features for classification. Features with p-values smaller than a predefined threshold (p-value<0.01) were selected to train the classifier. It is notable that the selected features might be in high dimensional while the number of training samples is relatively small (28 for MCI dataset and 18 for SZ dataset), thus the training of the classifiers is at the risk of over-fitting. To address this problem, we applied an unsupervised dimension reduction algorithm (Martinez and Kak 2001) based on principal component analysis for feature reduction. Specifically, the eigenvalues and eigenvectors of the covariance matrix of the feature set were calculated. Let λ = {λ₁; λ₂; . . . ; λ_m; λ₁ > λ₂ > . . . > λ_m denotes the set of eigenvalues. The number of the principalg components mx, that is, the dimension of the reduced feature is determined such that ${\sum }_{p=1}^{mx}{\lambda }_p\ge T\cdot {\sum }_{p=1}^m{\lambda }_p$, where 0 is a threshold revealing the percentage of information preserved in the new feature set compared with the original one. T=0.95 was used in our experiment.

With the reduced feature set, linear kernel based support vector machine (SVM) classifier implemented in LibSVM (Chang and Lin 2001) was used to evaluate the discriminability of the FGFI features. The leave-one-out cross-validation strategy was used in training and testing due to the limited number of samples. It is notable that the feature selection and reduction were performed in each run of leave-one-out cross-validation separately so that the training and testing are fully separated. The parameters used in SVM classifier are optimized via the grid search strategy.

For comparison study, the feature selection, feature reduction and classification experiments described above were also performed using functional connectivity features and fused features in which functional connectivity features and FGFI features were sequentially concatenated.

Results

FGFI Signatures in MCI

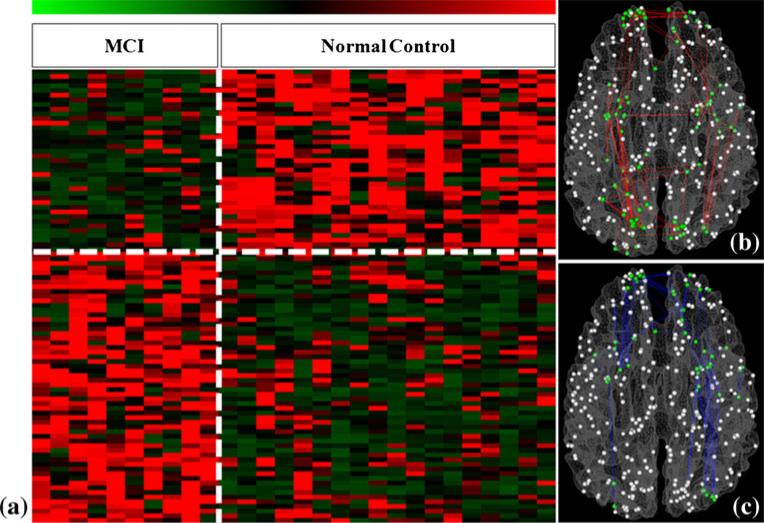
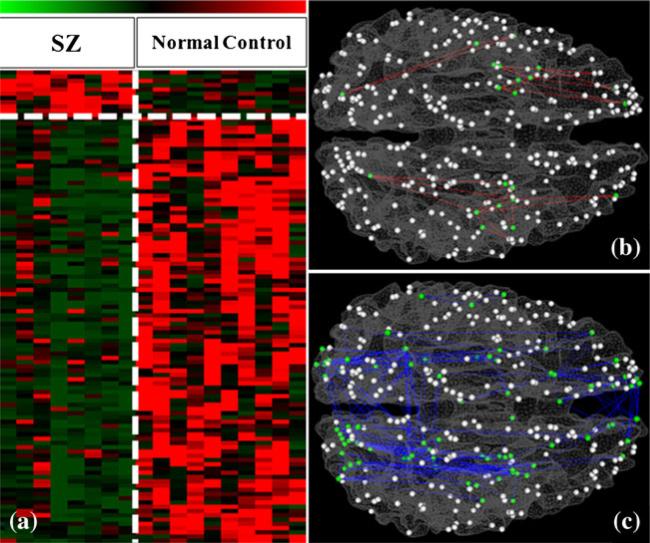
The total number of identified cliques (N_cliques), the number of cliques with significantly altered PFSs (N_altered), and the number of cliques with significantly increased (N_increased) and decreased (N_decreased) PFSs, and the ratio of cliques with significantly increased (R_increased) and decreased (R_decreased) PFSs are summarized in Table 1. For instance, we identified 58 cliques with consistently increased PFSs and 39 cliques with consistently decreased PFSs when the size of the clique is 3, as shown in Fig. 4(a). As these hyper- or hypo-interaction patterns in 10 MCI subjects, in comparison with 18 healthy controls, are very consistent across individuals (Fig. 4), thus we name these two patterns as FGFI signatures of MCI.

Table 1.

Altered FGFIs in MCI patients compared with normal controls

Clique size	NCliques	Naltered	Nincreased	Ndecreased	Rincreased	Rdecreased	Pincreased	Pdecreased
3	7593	97	58	39	59.79 %	40.21 %	53.45 %	66.67 %
4	16047	107	97	10	90.65 %	9.35 %	43.30 %	50.00 %
5	24404	177	154	23	87.01 %	12.99 %	48.05 %	30.43 %
6	27323	177	143	34	80.79 %	19.21 %	46.15 %	20.59 %
7	22760	133	107	26	80.45 %	19.55 %	51.40 %	26.92 %
8	14118	66	58	8	87.88 %	12.12 %	67.24 %	12.50 %
9	6453	22	22	0	100 %	0	68.18 %	/
10	2119	6	6	0	100 %	0	83.33 %	/
11	475	0	0	0	/	/	/	/

Fig. 4.

FGFI signatures for characterization of MCI when the size of the clique is 3. a The PFSs of the clustered cliques. Green and red stand for lower and higher PFSs, respectively. We identified 58 cliques showing consistently increased PFS and 39 cliques showing consistently decreased PFS in MCI group, compared with the normal control group. The vertical white dashed line separates MCI and controls, while the horizontal dashed white line separates significantly increases and decreased functional interactions in MCI. The spatial distributions of these cliques on the cortical surface are shown in b for increased PFSs and c for decreased PFSs. In (b) and (c), the DICCCOL landmarks are represented as spheres. Green ones are those landmarks involved in the cliques showing significantly altered PFSs

It can be clearly seen in Table 1 that decreased and increased PFSs co-exist in MCI patients, which corresponds to increased and decreased synchronization in the subnetworks, respectively. The result is in line with the literature in which the coexistence of dysfunction and functional compensation in functional brain networks of MCI patients (Liang et al. 2011; Buldu et al. 2012; Woodard et al. 2009; Qi et al. 2010; Staffen et al. 2011; Verma and Howard 2012). It is also notable that the functional interaction alterations in MCI are dominated by decreased ones, indicating the overall condition of the brain networks in MCI is disturbed and has resulted in reduced network efficiency (Buldu et al. 2012; Vannini et al. 2007; Iachini et al. 2009).

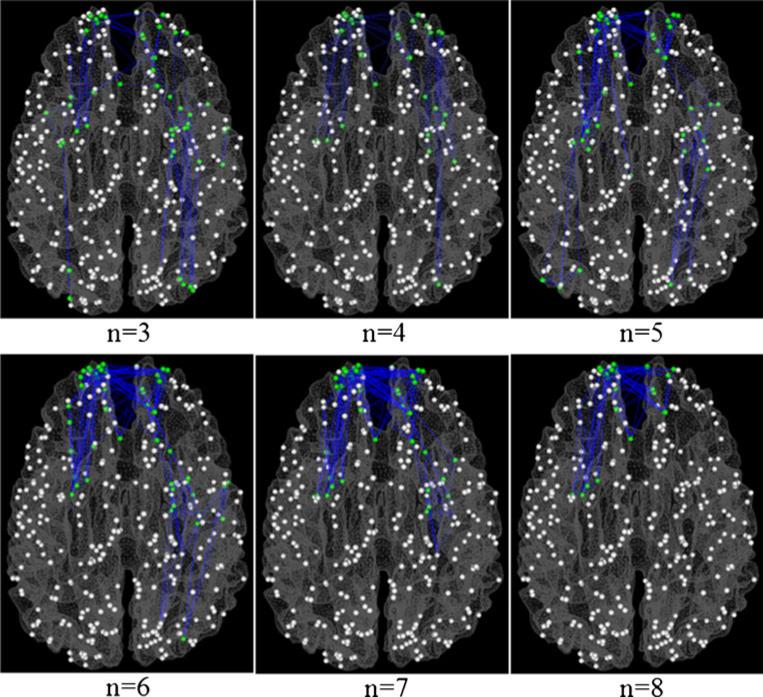
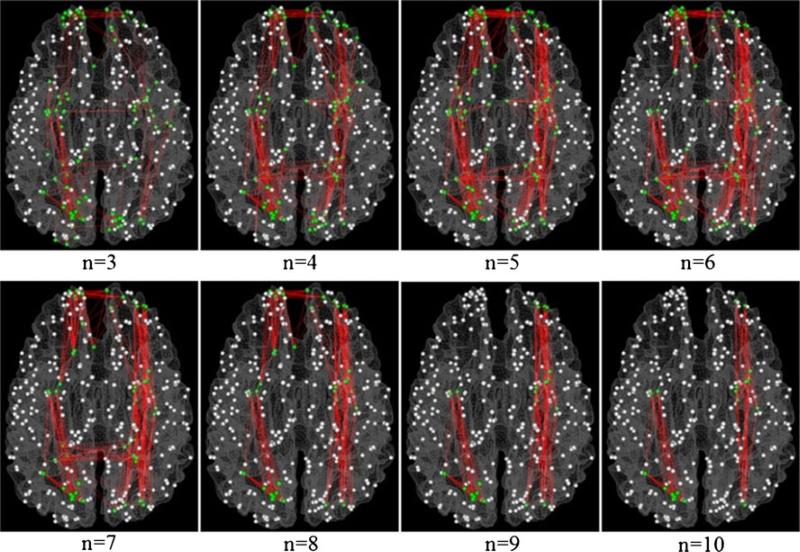
To demonstrate the spatial distributions of the cliques with altered PFSs, Fig. 4(b) and (c) visualize the cliques with increased and decreased PFSs in MCI respectively on a cerebral cortical surface when the clique size is 3. Figures 5 and 6 depict the distributions of the cliques with altered PFSs in other sizes. It should be noted that despite there is a certain degree of overlap between altered sub-graphs of different orders, e.g., some 3-clique sub-graphs might be contained in some 6-clique or 7-clique sub-graphs in Figs. 5 and 6, these different sub-graphs still provide rich information about the alterations of functional interactions in various spatial scales and their spatial distribution patterns are substantially different (Figs. 5 and 6). Quantitatively, the percentages on the left frontal, left parietal, left temporal, left occipital, right frontal, right parietal, right temporal and right occipital lobes are 28.89 %/20.44 %, 3.33 %/10.22 %, 11.11 %/13.14 %, 1.11 %/4.38 %, 31.11 %/19.71 %, 0 %/5.11 %, 16.67 %/17.52 %, and 7.78 %/9.49 %, respectively. It is evident that the majority of the functional interaction alterations occurs in the temporal and frontal lobes, which is consistent with the findings in the literature as well (Liang et al. 2011; Dickerson and Sperling 2009; Buldu et al. 2012; Sorg et al. 2007). The novel contribution here is that we systematically and comprehensively characterized and quantified those functional interaction alterations in fine granularity.

Fig. 5.

Spatial distributions of cliques with different sizes (from 3 to 8) with decreased PFS in MCI

Fig. 6.

Spatial distributions of cliques with different sizes (from 3 to 10) with increased PFS in MCI

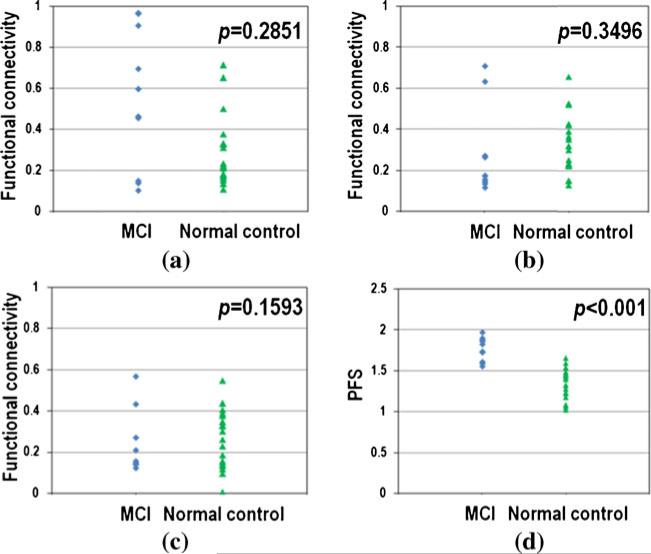
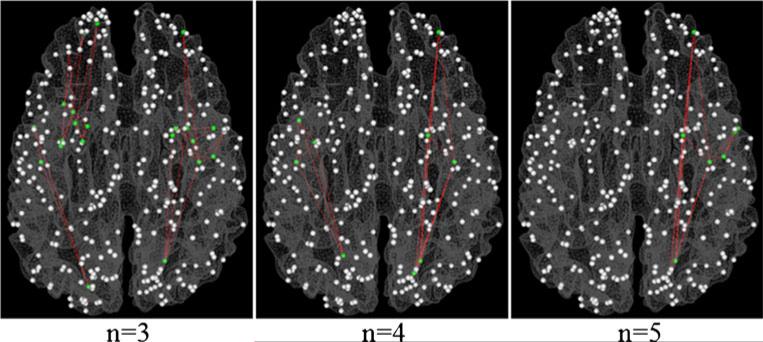
One interesting finding is that in a large proportion of cliques that show significantly altered PFSs in MCI compared with normal controls, none of the functional connectivities among the cortical ROIs that composed the clique is significantly different. The proportion of these cliques in all the identified cliques with increased (P_increased) and de- creased (P_decreased) PFSs in different size is summarized in Table 1 (last two columns). For example when the clique size is 3, 58 cliques show significantly increased PFSs, however, there is no significantly altered pairwise functional connections in 31 (53.45 %) cliques. Figure 7 illustrates an example of such a clique that has three nodes. Figure 7(a), (b) and (c) shows the distribution of the pairwise functional connectivities. The p-value in significance test (two-tailed t-test) for each edge is 0.2851, 0.3496 and 0.1593, respectively. The PFSs on this clique are shown in Fig. 7(d). The corresponding p-value is less than 0.001. This result indicates that FGFI can provide complementary information to currently used functional connectivity features in differentiation between MCI and normal controls. The reason to additional sensitivity and specificity provided by FGFI features compared with pairwise functional connectivity features may attribute to the fact that the realization of brain's function depends on the integration of multiple segregated brain regions. Pairwise functional connectivity is successful in capturing functional interactions between two brain regions, but it is limited when functional integration involves more brain regions (here, 3 to 11). In comparison, FGFI intrinsically measures the functional integration in widely distributed brain regions.

Fig. 7.

The distribution of inter-regional functional connectivities and PFSs for an exemplar 3-node clique that has significantly different PFS but has no significantly different inter-regional functional connectivities between MCI and normal controls. a, b and c shows inter-regional functional connectivity for the three edges of the clique, respectively. d shows the PFSs on the clique. p-value of significance test (two-tailed t-test) is at the right-top corner in each sub-figure

FGFI Signatures in SZ

The total number of identified cliques (N_cliques), the number of cliques (N_altered) with significantly altered PFSs, and the number of cliques with significantly increased (N_increased) and decreased (N_decreased) PFSs, and the ratio of cliques with significantly increased (R_increased) and decreased (R_decreased) PFSs for SZ compared with age-matched normal controls are summarized in Table 2. For example, we identified 11 cliques with consistently increased PFS and 100 cliques with consistently decreased PFS when the size of the clique is 3, as shown in Fig. 8. Figures 9 and 10 depict the distributions of the cliques with significantly decreased and increased PFSs in SZ group for various clique sizes, respectively.

Table 2.

Altered FGFIs in SZ patients compared with normal controls

Clique size	NCliques	Naltered	Nincreased	Ndecreased	Rincreased	Rdecreased	Pincreased	Pdecreased
3	6069	111	11	100	9.91 %	90.09 %	72.72 %	46.00 %
4	10943	94	6	88	6.38 %	93.62 %	66.67 %	46.59 %
5	14528	108	5	103	4.63 %	95.37 %	40.00 %	32.04 %
6	14951	103	0	103	0	100 %	/	13.59 %
7	12247	88	0	88	0	100 %	/	11.36 %
8	8040	90	0	90	0	100 %	/	0
9	4192	61	0	61	0	100 %	/	0
10	1697	30	0	30	0	100 %	/	0
11	514	8	0	8	0	100 %	/	0
12	110	0	0	0	/	/	/	/
13	15	0	0	0	/	/	/	/

Fig. 8.

FGFI signatures for characterization of SZ when the clique size is 3. a The PFSs of the clustered cliques. Green and red stand for lower and higher PFSs, respectively. We identified 11 cliques showing consistently increased PFS and 100 cliques showing consistently decreased PFS in SZ group, compared with the normal control group. The vertical white dashed line separates SZ and controls, while the horizontal dashed white line separates significantly increases and decreased PFSs in SZ. The spatial distributions of these cliques on the cortical surface are shown in b for increased PFSs and c for decreased PFSs

Fig. 9.

Spatial distributions of cliques with different sizes (from 3 to 11) with decreased PFS in SZ

Fig. 10.

Spatial distributions of cliques with different sizes (from 3 to 5) with increased PFS in SZ

The distributions of the ROIs involved in the cliques with decreased/increased PFS on brain lobes are assessed. Specifically, the percentages on the left frontal, left parietal, left temporal, left occipital, right frontal, right parietal, right temporal and right occipital lobes are 18.64 %/18.75 %, 6.78 %/0, 11.86 %/28.13 %, 8.47 %/6.25 %, 19.49 %/9.38 %, 1.69 %/0, 16.95 %/28.13 %, and 16.10 %/9.38 %, respectively. It is seen that the majority of the functional interaction alterations are in the temporal and frontal lobes, which is consistent with the findings in the literature (Calhoun et al. 2009; Schneider et al. 2007). It is also seen that the functional interaction alterations in SZ are dominated by decreased PFSs, which indicates that the functional interaction in SZ are substantially higher than healthy controls. This result is in agreement with the increased functional integration and the excessive salience of, and/or focus on, internal stimuli (Whitfield-Gabrieli et al. 2009) in SZ patients which may attribute to the disorder of the metastable balance between large-scale integration and independent processing in the cortex (Bressler 2003).

Similarly, we also find that in a large proportion of cliques that show significantly altered PFSs in SZ compared with normal controls, none of the functional connectivities among the cortical ROIs that composed the clique is significantly different. The proportion of these cliques in all the identified cliques with increased (P_increased) and decreased (P_decreased) PFSs in different size is summarized in Table 2 (last two columns). This result demonstrates that additional sensitivity and specificity in characterizing the functional alterations in SZ using rs-fMRI can be achieved by FGFI signatures.

Classification Performance in MCI and SZ

The classifiers are evaluated based on sensitivity and specificity. The classification performances when using FGFI features, functional connectivity features and directly fused features are summarized in Table 3. It is seen that FGFI features yield a relatively high sensitivity (80.00 % and 75.00 % in MCI and SZ dataset, respectively) and specificity (77.78 % and 80.00 % in MCI and SZ dataset, respectively). Despite the limited number of available samples, the relatively high accuracy classification demonstrated the good discriminability of FGFI features in characterizing functional alterations in MCI and SZ patients. It is also seen that FGFI features can achieve comparable performance compared with functional connectivity features (sensitivity: 80.00 % and 75.00 % in MCI and SZ dataset, respectively; specificity: 83.33 % and 80.00 % in MCI and SZ dataset). However, the sensitivity (90.00 % and 100.00 % in MCI and SZ dataset, respectively) and specificity (94.44 % and 90.00 % in MCI and SZ dataset, respectively) can be remarkably improved (sensitivity improvement: 10 % and 25 % in MCI and SZ dataset, respectively; specificity improvement: 11.11 % and 10.00 % in MCI and SZ dataset, respectively) when the directly fused features were used, demonstrating FGFI features can provide complementary information for patient-control classification using rs-fMRI.

Table 3.

Sensitivity and specificity in classification of MCI/SZ and normal controls using FGFI features, functional connectivity features and directly fused features

	MCI		SZ
	Sensitivity	Specificity	Sensitivity	Specificity
FGFI	80.00 %	77.78 %	75.00 %	80.00 %
Functional connectivity	80.00 %	83.33 %	75.00 %	80.00 %
Directly fused	90.00 %	94.44 %	100 %	90.00 %

Discussion and Conclusion

In this paper, we presented an algorithmic pipeline to systematically and comprehensively explore the functional interaction signatures of brain networks in fine granularity and applied them to characterize the functional alterations in MCI and SZ patients. Compared with the commonly used functional connectivity patterns used in current studies, the FGFI features yield comparable classification performance in differentiating patients and normal controls in both MCI and SZ datasets. More importantly, we showed that FGFI features can provide complementary information for examining disease pathophysiology using rs-fMRI. Performance of patient-control classification can be substantially improved by integrating FGFI features with functional connectivity/connectomes features. We also investigated the spatial distribution of the DICCCOL landmarks that involved in the brain condition alterations in MCI and SZ. The results are consistent with the literatures. Importantly, the FGFI features can capture functional interaction and dynamics in brain sub-networks at fine granularity level that inter-regional functional connectivities could not, and thus may shed novel light on the dysfunctions in MCI and SZ.

In the current study, the FGFI signatures were examined only in the complete sub-graphs extracted from the structural connectomes constructed from DTI data. The close relationship between structural and functional connectivity in human brain renders strong biological support for using structural cliques as the representation of brain subnetworks. However, it is also known that many functional pathways do not have corresponding direct structural pathways, and functional units may communication through indirect structural pathways (Honey et al. 2009). In our study, other possible sub-graphs connected by indirect structural connections were not considered for the purpose of computational feasibility. As a result, our study in this paper only assessed a sub-set of meaningful functional interaction patterns within the DICCCOL-based connectomes, and could possibly miss other meaningful functional interaction patterns that occur in non-complete sub-graphs. In the future, with the availability of additional pieces of information, other approaches of defining meaningful sub-graphs could be considered such as by integrating multimodal neuroimaging data into the definition of sub-network that is consistent multi-modalities. In addition to defining and including more sub-graphs, other quantitative metrics (in addition to the PFS used in this paper) including a variety of spectral graph theoretic measurements (Chung 1997; Boccaletti et al. 2006) could be used to assess the functional interactions and dynamics on these sub-graphs. It is expected that the improvements in these lines could contribute to deriving more informative functional interaction signatures for brain conditions in the future. In addition, the number of available samples is limited in our study, which may increase the risk of over-fitting in classifier training and prevent us from fully examining the potential benefit brought by FGFI features in differentiation between diseased populations from normal controls. In the future, we plan to validate the proposed FGFI features on larger dataset.

Despite the limitations discussed above, the proposed FGFI signatures investigate functional brain network at spatial scale that is in-between those spatial scales utilized in existing studies using inter-regional functional connectivities (local scale) and graphical analysis (global scale). In comparison with inter-regional functional connectivity analysis, the proposed FGFI signatures consider the interaction of functional integration in multiple (n>2) segregated brain regions. And compared with current graph theoretical studies, FGFI signatures measure the functional interaction in brain networks at fine granularity scale. Thus, FGFI signatures can provide complementary information for study functional brain network in both healthy and diseased populations and improve classification performance between them using rs-fMRI, as validated by our experimental results. It should be pointed out that the functional interactions measured by PFS were derived from the pair-wise connectivity matrix (“Functional Interaction of Subnetwork”) and there could exist intrinsic relationships between the derived functional interaction signatures and pairwise connectivity patterns, which should be further explored in the future. In the current patient/control classification experiments, we demonstrated improved classification performance can be achieved by integrating FGFI features and inter-regional functional connectivity features. It has been reported that the integration of functional and structural connectivity patterns can provide new avenues for brain disease classification. We envision that the classification performance can be further improved by integrating structural connectivity via advanced feature fusion algorithms (e.g., Multi-Modal Spectral based feature fusion (Cai et al. 2011)) and learning algorithm (e.g., multiple-kernel SVM (Wee et al. 2012), multi-view learning (Bickel and Scheffer 2004) and co-training (Kumar and Daume 2011)), rather than the straightforward direct concatenation used in our study. Further, our future work also lies in the joint analysis of FGFI signatures and structural connectivity patterns to investigate the relationship between brain structure and functions.

In the bioinformatics and genomics fields, genomics signatures such as genome-scale gene expression analyses are transforming medicine in many facets including disease sub- type identification, differential diagnosis, disease staging, personalized treatment, and follow-up. In parallel, in the neuro-science and neuroimaging fields, the mapping of human brain connectomes (Allen and Williams 2011; Buckner 2010; Behrens and Sporns 2011; Biswal et al. 2010; Kennedy 2010; Sporns 2011) and derivation of connectomics signatures (Li et al. 2012a, b) will fundamentally advance our understanding of brain structure and function and reveal widespread alterations in a variety of neurological or psychiatric conditions such as Alzheimer's disease and Schizophrenia. In particular, we believe quantitative mapping of functional interaction signatures in fine granularity (as shown in this paper) in healthy and disease populations have significant importance to systematically and comprehensively understand, characterize, diagnose and treat many devastating brain conditions. It has been shown in this work that the DICCCOL-based structural connectomes provide a common representation of human brain architecture and thus offer a solid foundation for deriving, integrating and comparing functional interaction signatures across individuals and populations. We predict that once those functional interaction signatures are cross-validated across different labs and datasets, they will play important roles in the clinical managements of many brain conditions.

Information Sharing Statement

Source codes of the proposed computational algorithms and methods are available at: http://www.cs.uga.edu/~tliu/neuroinformatics/neuroinformatics_FGFISignatures.rar

Multimodal neuroimaging datasets of 10 SZ subjects and 10 healthy controls were downloaded and available from the NA-MIC dataset: http://hdl.handle.net/1926/1687