Abstract
Comparative sequence analysis has become an essential component of studies aiming to elucidate genome function. The increasing availability of genomic sequences from multiple vertebrates is creating the need for computational methods that can detect highly conserved regions in a robust fashion. Towards that end, we are developing approaches for identifying sequences that are conserved across multiple species; we call these “Multi-species Conserved Sequences” (or MCSs). Here we report two strategies for MCS identification, demonstrating their ability to detect virtually all known actively conserved sequences (specifically, coding sequences) but very little neutrally evolving sequence (specifically, ancestral repeats). Importantly, we find that a substantial fraction of the bases within MCSs (∼70%) resides within non-coding regions; thus, the majority of sequences conserved across multiple vertebrate species has no known function. Initial characterization of these MCSs has revealed sequences that correspond to clusters of transcription factor-binding sites, non-coding RNA transcripts, and other candidate functional elements. Finally, the ability to detect MCSs represents a valuable metric for assessing the relative contribution of a species' sequence to identifying genomic regions of interest, and our results indicate that the currently available genome sequences are insufficient for the comprehensive identification of MCSs in the human genome.
A key component of genomics research beyond the Human Genome Project will be the rigorous interpretation of the recently finished human genome sequence (Collins et al. 2003). Central to these efforts will be the identification of all functional elements in the human genome. Recent comparative analyses of the human and mouse genome sequences suggest that ∼5% of the mammalian genome is under active selection and thus likely serves a functional role (International Mouse Genome Sequencing Consortium 2002; Roskin et al. 2003). Within this functional subset is an estimated 1% to 2% of the genome that encodes protein (International Mouse Genome Sequencing Consortium 2002). The prospects for comprehensive identification of these coding sequences are quite good, especially in light of the availability of data sets that are complementary to the genomic sequence (e.g., ESTs [Boguski et al. 1994; also see http://www.ncbi.nlm.nih.gov/dbEST] and full-length cDNA sequences [Strausberg et al. 2002; also see http://mgc.nci.nih.gov]) and ever-improving computational methods for gene prediction (Kulp et al. 1996; Burge and Karlin 1997; Rogic et al. 2001; Solovyev 2001; Flicek et al. 2003). The complete identification and characterization of the remaining 3% to 4% of the mammalian genome that likely corresponds to functional non-coding sequence will be profoundly more challenging, due to the lack of complementary data sets, the absence of robust tools for computational predictions, and the incomplete insight about the nature of such sequence. In short, the generation of a comprehensive “parts list” of functional elements in the human genome remains an immense and important challenge.
The comparison of orthologous genomic sequences has emerged as a powerful approach for identifying functional elements in the genome (Dermitzakis et al. 2002; DeSilva et al. 2002). The premise of this approach is that sequences conserved across millions of years of evolution are likely to have a functional role (Pennacchio and Rubin 2001). Comparative sequence analyses have been shown to facilitate the identification of both coding (Batzoglou et al. 2000; Korf et al. 2001; Pennacchio et al. 2001; Alexandersson et al. 2003; Flicek et al. 2003) and functional non-coding (Stojanovic et al. 1999; Dubchak et al. 2000; Göttgens et al. 2000; Loots et al. 2000, 2002; Wasserman et al. 2000; Dehal et al. 2001; Elnitski et al. 2003; Kellis et al. 2003) sequences. Among the latter are elements that regulate the spatial and temporal patterns of gene expression (Hardison 2000). When the generation of alignments between related sequences is not possible, motif-finding techniques have also been used to identify functional sequences, in particular for detecting transcription factor–binding sites (Bailey and Elkan 1995; Roth et al. 1998; Hertz and Stormo 1999; McCue et al. 2001; Blanchette and Tompa 2002).
Recent efforts have produced whole-genome sequences for several vertebrates, including human (International Human Genome Sequencing Consortium 2001), mouse (International Mouse Genome Sequencing Consortium 2002), rat (http://genome.ucsc.edu/cgi-bin/hgGateway?org=rat), and pufferfish (Aparicio et al. 2002), with the sequencing of additional vertebrate genomes well underway. Increasingly, methods for visualizing (Kent et al. 2002; Clamp et al. 2003; Karolchik et al. 2003) and comparing (Stojanovic et al. 1999; Mayor et al. 2000; Blanchette and Tompa 2002; Loots et al. 2002; Giardine et al. 2003; Schwartz et al. 2003a) genomic sequences from multiple species are emerging. As a complement to these efforts, we are generating the sequence of targeted genomic regions in multiple, phylogenetically diverse vertebrates (Thomas et al. 2003) and developing computational approaches for identifying the subset of sequences that confers function. In particular, we have focused on developing algorithms for detecting sequences that are highly conserved across multiple species, which we call Multi-species Conserved Sequences (or MCSs); such sequences represent candidates for being functionally important. Here we report the development and testing of methods for MCS detection, including analyses of MCSs identified using a recently generated set of orthologous sequences from 11 non-human vertebrates (Thomas et al. 2003).
RESULTS
Development of Approaches for Detecting MCSs
The detection of MCSs requires analytical approaches for identifying conserved regions across multiple orthologous sequences in a fashion that takes into account: (1) the phylogenetic diversity of the originating species and thus the general variation in sequence conservation; (2) the varying neutral substitution rate for different genomic regions; and (3) the characteristics of the generated genomic multi-sequence alignment. Since none of the previously described approaches (Stojanovic et al. 1999; Pennacchio and Rubin 2001; Loots et al. 2002; Alexandersson et al. 2003; Elnitski et al. 2003) completely satisfies these requirements, we developed and tested two independent methods for identifying MCSs from large sequence data sets derived from multiple species. Both methods utilize genomic multi-sequence alignments generated with the algorithms employed by MultiPipMaker (Schwartz et al. 2003a). To date, we have focused on the identification of highly conserved sequences in the human genome; thus, we generated human-referenced pair-wise alignments with each species' sequence. However, our methods can be readily adapted such that any species' sequence can serve as the reference. Details about each MCS-detection method are given in Methods, with a brief overview provided here.
In the binomial-based method, a “conservation score” is calculated in a fashion that weights the relative contribution of each species' sequence by accounting for its baseline neutral substitution rate (relative to the human reference sequence). Thus, conserved sequences from more diverged species make a greater relative contribution to the conservation score than those from less diverged species. Such a weighting scheme is established by calculating the cumulative binomial probability of detecting the observed number of base identities in each 25-base window, given the neutral substitution rate calculated using four-fold degenerate positions (the third position of codons for which any base codes for the same amino acid).
In the parsimony-based method, the amount of conservation within each column of the multi-sequence alignment is measured using a phylogenetic parsimony score (Fitch 1971). Such a score reflects the minimal number of substitutions needed along the branches of an established phylogenetic tree to account for the observed bases (Stojanovic et al. 1999; Blanchette and Tompa 2002). A P-value associated with the derived parsimony score is then calculated under a continuous-time Markov model of neutral evolution. This P-value is subsequently converted into a conservation score, with more highly conserved columns assigned higher scores. This approach is related to the method of Boffelli et al. (2003), who computed log-likelihood ratios for the bases observed in each column under a model of slow versus neutral evolution. However, our parsimony-based method does not require a model of functional sequence evolution (which is associated with inaccuracies due to the non-uniform evolutionary rates of functional regions), as it simply measures deviation from the null model.
Both the binomial- and parsimony-based methods calculate a conservation score for overlapping 25-base windows (incremented by one base). Therefore, a conservation score is calculated 25 times for each base (once for each of the overlapping 25-base windows), with the highest calculated score then assigned to that base. The two methods also have some fundamental differences. First, the binomial-based method only requires knowledge of the major lineages represented by the species under study, while the parsimony-based method requires a complete phylogenetic tree topology. Second, while the binomial-based method measures conservation with respect to one reference sequence (e.g., the human sequence), the parsimony-based method treats all sequences symmetrically (although the relative contribution of each species' sequence is then weighted based on its phylogenetic position). Thus, results with the two methods will markedly differ for regions that are only conserved among non-human species; in such cases, only the parsimony-based method would be capable of producing a higher conservation score. Finally, while both methods compare the observed conservation with that expected under neutral evolution, the binomial-based method more directly measures the significance of conservation levels below the neutral substitution rate (which can lead to a negative value for the conservation score; in principle, such scores could represent regions under positive selection). The development and testing of two independent methods based on distinct fundamental algorithms provided the opportunity to study the similarities and differences of the MCSs detected by each approach.
General Features of Detected MCSs
Both methods for detecting MCSs were used to analyze a set of sequences orthologous to a 1.8-Mb interval on human chromosome 7q31 that were generated from 11 non-human vertebrates (chimpanzee, baboon, cat, dog, cow, pig, rat, mouse, chicken, fugu, and tetraodon; Thomas et al. 2003). This genomic region contains 10 known genes, including the gene mutated in cystic fibrosis (CFTR; see OMIM 219700, http://www.ncbi.nlm.nih.gov/Omim). The entire data set, including individual sequences, alignments, and results of the analyses described below, is available at http://www.nisc.nih.gov/data and can be viewed at http://genome.ucsc.edu.
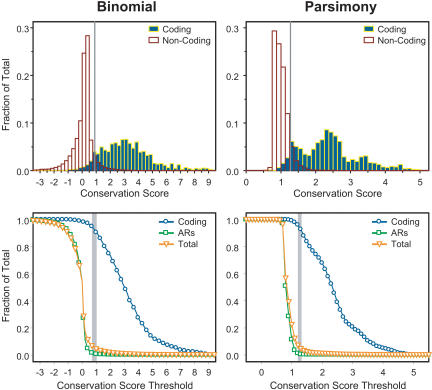
For both methods, the distribution of conservation scores calculated for individual bases was reasonably effective at distinguishing between known protein-coding sequence (typically actively conserved) and non-coding sequence (Fig. 1, top). More detailed analyses (Fig. 1, bottom) revealed a small range of conservation score thresholds that allow detection of almost all (>90%) known coding sequence, virtually no (<1.5%) ancestral repeats (ARs; ancient relics of transposons inserted prior to the eutherian radiation and presumed to not be under selection), and a small percentage of additional non-coding sequence. We presumed that the latter contains highly conserved sequences representing candidate functional elements. Given that the use of threshold values within this small range results in the detection of 4% to 7% of the total human sequence and that ∼5% of the mammalian genome is thought to be under active selection (International Mouse Genome Sequencing Consortium 2002; Roskin et al. 2003), we selected a conservation score threshold for each method such that the detected MCSs would contain 5% of the human reference sequence (see Methods for further details). Note that each MCS is simply defined as a segment of contiguous sequence where each base exceeds the conservation score threshold, with the minimum length of an MCS being 25 bases (see Methods).
Figure 1.
Discrimination of different types of sequence using conservation scores calculated by the binomial- (left) and parsimony- (right) based methods. The top two histograms depict the distribution of conservation scores calculated for coding (blue outlined in yellow) and non-coding (white outlined in red) sequence by each method. Note that the distributions are represented as a fraction of the total sequence in each annotated category and that only 1.1% of the sequence in the analyzed region represents coding sequence. The vertical lines indicate the conservation score thresholds used for defining MCSs (see text). The bottom two graphs show the detection of different types of sequence at increasing conservation score thresholds. The fraction of sequence in each annotated category (coding, ARs, and total) that exceeded the indicated conservation score threshold is plotted. The vertical bars (shaded in grey) reflect the small range of conservation score thresholds that optimally results in the detection of nearly all coding sequence along with a minimum amount of the total sequence (4% to 7%).
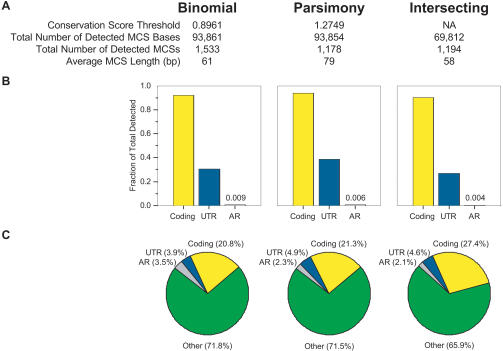
Using the established conservation score thresholds, the binomial- and parsimony-based methods identify 1533 and 1178 MCSs, respectively, within the 1.8-Mb target region (Fig. 2A). The positions of these MCSs relative to annotated genomic features in the target region can be seen at http://genome.ucsc.edu, with a representative example shown in Figure 3. For both methods, the detected MCSs at least partially overlap >97% of the 128 known exons and >76% of the 22 known UTRs in the region; these overlaps account for >93% and >30% of all coding and UTR bases, respectively (Fig. 2B). Just over 20% of the total MCS bases reside within coding sequence and an additional ∼4% to 5% within UTRs (Fig. 2C). Of note, MCSs containing exonic sequence are, on average, larger than those containing non-coding sequence (∼120 versus ∼45 bp, respectively). This relative size difference can be seen even when MCSs separated by short distances (e.g., 10, 20, or 50 bp) are merged together (data not shown). Only ∼3% of MCS bases are within ARs, even though ARs account for >19% (363,432bp) of the human reference sequence. Since this class of repeats is generally evolving in a neutral fashion (International Mouse Genome Sequencing Consortium 2002) and assuming that the amount of sequence conservation observed with ARs is representative of neutrally evolving regions, these results indicate that the detection of sequences not likely to be under active selection is low. It should be noted that the chicken and fish sequences do not have alignable ARs (at least by the alignment methods used here). Remarkably, for both methods, >70% of the MCS bases (residing in ∼83% of the MCSs) correspond to non-annotated sequence whose function is, at present, unknown (Fig. 2C).
Figure 2.
Characteristics of MCSs detected by different methods. The “Binomial” and “Parsimony” columns provide a summary of the MCSs generated by each respective method. The “Intersecting” column provides a summary of the MCSs derived by intersecting the results of the binomial- and parsimony-based methods (see Methods and Fig. 4). The general features of the detected MCSs are provided in A. The thresholds used for the binomial- and parsimony-based methods result in a virtually identical number of MCS bases; however, the total number of detected MCSs (and correspondingly their average length) varied between the two methods. Also, the greater number of intersecting MCSs compared to those detected by the parsimony-based method reflects the fact that some MCSs were fragmented by the intersection process. The bar graphs in B depict the fraction of coding, UTR, and AR bases in the target region that overlaps the indicated set of MCSs. For the fraction of AR bases, the exact values are also provided. The pie charts in C depict the percentage of MCS bases that corresponds to coding (yellow), UTR (blue), AR (grey), and other (green) sequence.
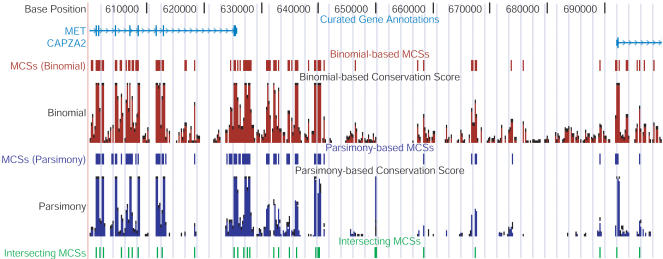
Figure 3.
Positions of MCSs relative to other annotated genomic features. A complete representation of the positions of MCSs within the ∼1.8-Mb targeted region is available at a customized version of the UCSC Genome Browser (see http://genome.ucsc.edu). A view depicting a ∼100-kb interval encompassing the intergenic region between MET and CAPZA2 is shown. The thick vertical boxes in the “Curated Gene Annotations” track correspond to exons. The positions of MCSs identified by the binomial- (red) and parsimony- (purple) based methods are shown in separate tracks, as are the underlying conservation scores calculated by each method (depicted as bar graphs). Also shown are the positions of the intersecting set of MCSs (green; see text and Fig. 2).
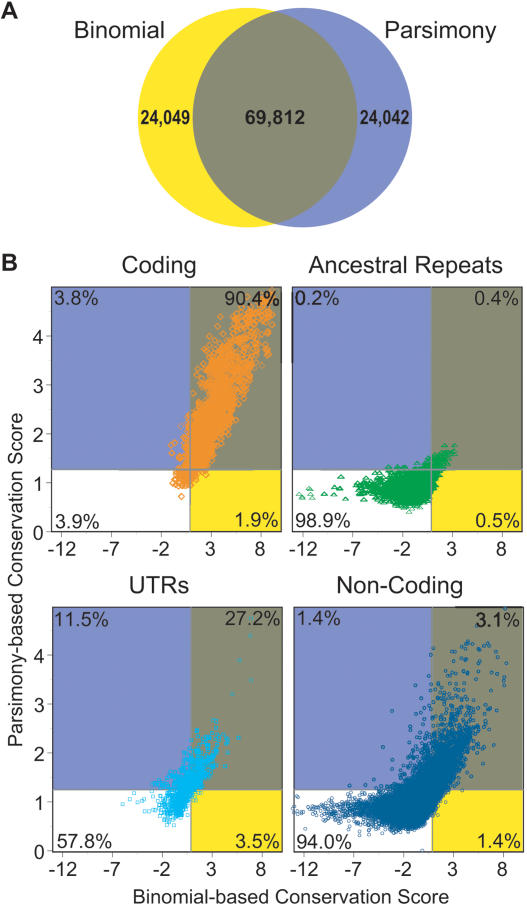
Comparison of the MCSs detected by the two methods revealed excellent concordance. This is evident from both qualitative examination of the positions of the MCSs within the target region (Fig. 3) and more quantitative analyses (Fig. 4). Indeed, 74.4% (69,812) of the MCS bases detected by either method were common to both (Fig. 4A). In addition, there is a strong correlation between the base-by-base conservation scores calculated by each method (Fig. 4B), with the tightest relationships seen for bases within coding regions and ARs. In the case of MCSs uniquely detected by one method, the conservation scores calculated by the other method for that sequence were typically just below the defining threshold.
Figure 4.
Concordance of the binomial- and parsimony-based methods for MCS detection. (A) Venn diagram showing the relationship of MCS bases detected by the binomial- (yellow circle) and parsimony- (purple circle) based methods, with the bases detected by both methods shown in brown. Also indicated is the total number of MCS bases in each category. (B) Scatter plots showing the relationship of the conservation scores calculated by each method for bases residing in different types of sequence. Each point represents a base that falls within coding sequence (orange), ARs (green), UTRs (light blue), or non-coding sequence (dark blue), with its position on the x- and y-axes reflecting the conservation score calculated by the binomial- and parsimony-based methods, respectively. The boundaries of each rectangular area (color coded to match the Venn diagram in A) correspond to the established conservation score threshold for each method (see Figs. 1, 2). The indicated percentages reflect the fraction of bases of the indicated type of sequence falling within that area. For visual clarity, every tenth base is plotted; however, the indicated percentages reflect all bases.
We examined more closely the sequence found to be conserved by both methods. The resulting intersecting set of 69,812 MCS bases coalesce into 1194 MCSs (defined as segments of contiguous sequence where each base exceeds the conservation score thresholds of both methods) and are associated with similar demographics as the individual data sets (Fig. 2; also see Fig. 3) These results further indicate that each method identifies a similar set of MCSs. Nonetheless, the presence of a slightly smaller fraction of AR bases within the intersecting set of MCSs makes this data set potentially more enriched for functionally important sequences. For these reasons, we chose to perform all subsequent analyses on the intersecting set of MCSs, which contains 3.7% of the human reference sequence in the region.
Uniqueness of MCSs in the Human Genome
We investigated the uniqueness of the detected MCSs within the human genome, particularly focusing on the 83% that do not overlap coding regions and that contain virtually no (<5%) repetitive sequence. Comparison of these MCSs to the human genome sequence (November 2002 assembly; http://genome.ucsc.edu) using MegaBlast (Zhang et al. 2000) revealed that 99.6% had no other significant match. The remaining MCSs matched only one additional location in the genome, over lengths of 24–292 bp (see http://www.nisc.nih.gov/data). Detailed inspection of these non-unique MCSs suggested that they likely reside in segmental duplications, in most cases specific to the primate lineage (data not shown). These analyses indicate that virtually all of the MCSs detected in this study that contain non-coding sequence are unique in the genome (at least by the homology search methods employed here), with the functional relevance of the small number of non-unique MCSs being unclear. Similar conclusions were reached by comparing the MCSs to the entire GenBank NR database with BLAST (Altschul et al. 1990; data not shown).
Correlating MCSs With Functional Elements
Conserved RNA Structures
Non-coding RNA genes are notoriously difficult to identify (Eddy 2002). While no non-coding RNA genes are known to reside in the genomic region examined here, we analyzed the detected MCSs using the QRNA program (Rivas and Eddy 2001). Although QRNA was designed to identify RNA genes, it also detects regions of pre-mRNA and mRNA predicted to have a conserved secondary structure, which may be involved in splicing, translational regulation, or mRNA localization or degradation.
A total of 29 MCSs were found to contain sequences that are candidates for RNA structural elements (see http://www.nisc.nih.gov/data). Strikingly, seven and five of these MCSs are located within 5′ and 3′ UTRs (or within 2kb upstream thereof), respectively. This represents a seven- and four-fold enrichment of MCSs in these positions, respectively (assuming a uniform distribution). These results are reassuring, especially since UTRs are known to contain structural elements involved in the regulation of translation (van der Velden and Thomas 1999) and mRNA localization (Etkin and Lipshitz 1999). Note that none of the UTRs studied here has previously been shown to contain a structural element. Finally, all but one of these 29 MCSs reside within known transcribed sequences, or within 2kb thereof; we thus suspect that some of these MCS sequences may be involved in the regulation of mRNA splicing (Akker et al. 2001).
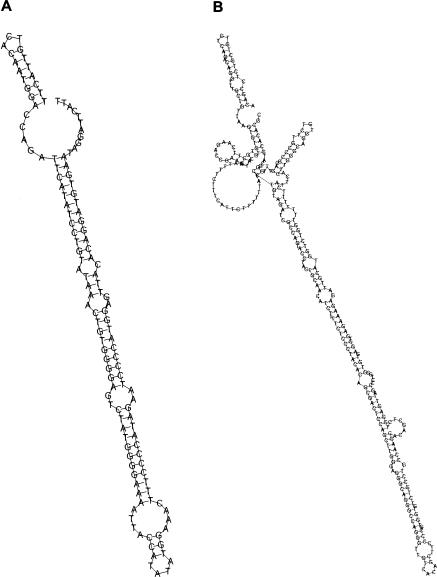
The predicted RNA secondary structures for sequences within two of these MCSs are shown in Figure 5. Both reside within introns of the ST7 gene, with each forming a long, highly conserved hairpin. The structure in Figure 5A was found to be associated with a number of base substitutions that were accompanied by a compensatory change at the partnering base (data not shown), thus adding credibility to the predicted structure. The structure in Figure 5B reflects a remarkably conserved sequence (a 206-base region with only one substitution among the nine mammals examined); this region is part of a transcript (GenBank AF400044) that contains some of the ST7 coding exons (Vincent et al. 2002). Both structures in Figure 5 appear to be good candidates for microRNAs (Lim et al. 2003).
Figure 5.
Representative RNA secondary structures predicted for sequences within two MCSs. The minimal free energy structures for the human sequences are depicted, as produced by the Vienna Package (Hofacker et al. 1994). (A) Hairpin structure within an MCS in intron 1 of ST7 (log-odds = 26.3, position of sequence displayed: 855569–855698). (B) Hairpin structure within an MCS in intron 11 of ST7 (log-odds = 46.7, position of sequence displayed: 1019625–1019879).
Transcription Factor-Binding Sites
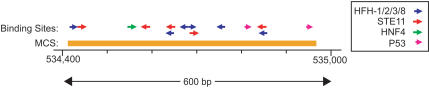
We searched the detected MCS sequences for potential binding sites of transcription factors cataloged in TRANSFAC 5.0 (Matys et al. 2003). Because the detection of small, individual sites is associated with false-positive predictions, we specifically looked for cases where an MCS contained multiple, clustered sites. Particularly interesting results were encountered with several MCSs (see http://www.nisc.nih.gov/data). One of these (Fig. 6) is located 4 kb downstream of the first coding exon of the MET protooncogene (encoding the hepatocyte growth factor receptor) and contains six predicted binding sites for transcription factors of the hepatocyte nuclear factor family as well as one for hepatic nuclear factor HNF4. Interestingly, HNF4 has been shown to be involved in the regulation of the murine Met gene (Spagnoli et al. 2000).
Figure 6.
A 600-bp region within MET intron 2 with clustered putative binding sites for the indicated transcription factors. The orange bar depicts the position of a detected MCS; note that this MCS is flanked by 4.6 kb and 26 kb of intronic sequence, respectively. Two of the binding sites for HFH (hepatocyte nuclear factor homolog) transcription factors overlap, and there are thus only six independent occurrences.
Contribution of Different Species' Sequences to the Detection of MCSs
We investigated how different species' sequences contributed to the detection of MCSs. Specifically, we systematically recomputed the binomial-based conservation score for all possible combinations of species, and then examined the relative performance of each in detecting the intersecting MCSs identified using the sequences from all 11 non-human species. To avoid problems created by the absence of sequence for certain species, we limited these analyses to a “reference set” of 561 MCSs (containing 33,322 bp) residing within a ∼560-kb interval for which sequence data were available in all species (see Methods).
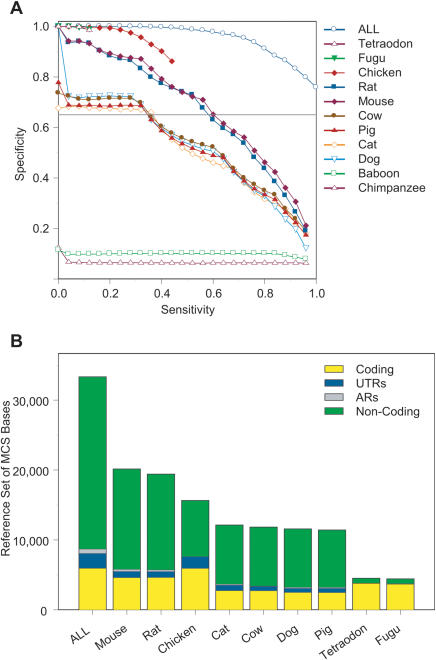
These studies required an understanding of the relationship between sensitivity (fraction of reference MCS bases detected) and specificity (fraction of detected MCS bases that corresponds to reference MCS bases) over a range of conservation score thresholds. This relationship is shown for individual species in Figure 7A. Note that since all results are compared to a set of intersecting MCSs (and not just the MCSs detected by the binomial-based method), in no case is 100% sensitivity and specificity achieved (even when all species' sequences are used). Importantly, the general trends seen for the various species are consistent across the entire range of sensitivity and specificity values.
Figure 7.
Ability of individual species' sequences to detect MCSs. (A) Using the indicated species' sequences, MCSs were identified by the binomial-based method over a range of conservation score thresholds. Shown is the resulting relationship between sensitivity (fraction of reference MCS bases detected; see Methods) and specificity (fraction of detected MCS bases that corresponds to reference MCS bases). Also indicated are the results using the sequences from all 11 non-human species (ALL). Note that the limited amount of alignable sequence from chicken and fish impedes the ability to obtain the full range of sensitivity/specificity values. (B) Detection of reference MCS bases, indicated for each type of sequence (coding, UTRs, ARs, and non-coding). This is shown for each species' sequence using the data obtained with a specificity of 65% (horizontal grey line in A), except for chicken and fish. For the latter species, data obtained with specificities of 81% and 99%, respectively, were used (since lower specificities cannot be achieved with these sequences; see A). ALL represents the entire set of reference MCS bases (which is detected by the binomial-based method with a 75% specificity when the sequences from all 11 non-human species are used). Data with non-human primate sequences were not included in B because of their inability to achieve a specificity of 65% (see A). Note that a specificity of 65% was chosen since it allowed the inclusion of most species' sequences. The underlying data associated with these analyses are available at http://www.nisc.nih.gov/data.
Analyses using individual species' sequences revealed differences in the types of sequence within the detected MCSs (Fig. 7B). For these comparisons, we used a conservation score threshold that yielded a specificity of 65%, except for chicken (81%), tetraodon (99%), and fugu (99%; sequences from these species are incapable of yielding lower specificities; see Fig. 7A). These results demonstrated that: (1) rodent sequences detect the greatest number of MCS bases as well as the largest fraction of non-coding sequence; (2) chicken sequence detects slightly fewer MCS bases than rodents, but with a considerably higher specificity (see Fig. 7A) and with the largest amount (indeed, 99.8%) of coding MCS bases; (3) the MCSs detected with fish sequences almost exclusively contain coding sequence, although this only accounts for 13% of the reference MCS bases; (4) non-human primate sequences are not useful for MCS detection by the methods described here; and (5) none of the individual species' sequence alone came close to identifying all of the reference MCS bases (consistent with a previous analysis performed with mouse sequence alone; Thomas et al. 2003).
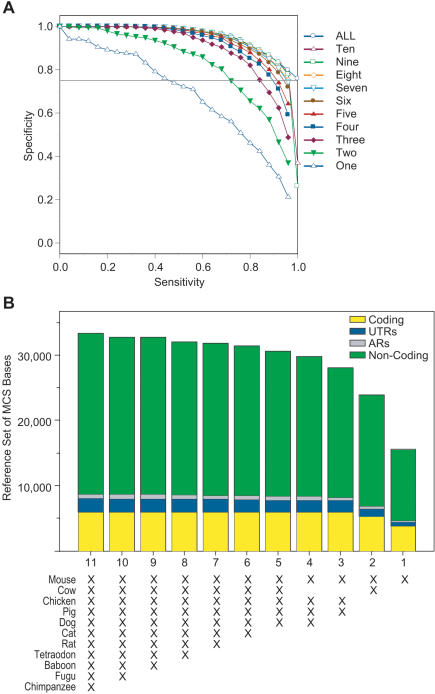
Analyses using different combinations of multiple species' sequences revealed additional important findings. First, the top 10 combinations of two species' sequences (used in conjunction with the human sequence) are virtually indistinguishable from one another, with the results obtained with mouse and cow sequences shown in Figure 8. All of these two-species combinations contain a rodent sequence (mouse or rat) along with one additional non-primate mammal (cat, cow, dog, or pig) or chicken. Similarly, the most effective subsets of three to five species' sequences are consistently those containing different combinations of mammals plus chicken (Fig. 8). The ability to detect reference MCS bases increases with additional species' sequences until there are about six species represented, both in terms of sensitivity/specificity characteristics (Fig. 8A) and total MCS bases detected (Fig. 8B). Beyond six species, the addition of non-human primate and/or fish sequences do not contribute significantly to the detection of the reference MCS bases. Finally, note that the ability to detect MCSs overlapping coding sequence plateaus with fewer species compared to detecting MCSs that overlap non-coding sequence.
Figure 8.
Ability of combinations of different species' sequences to detect MCSs. Sequences from every combination of the 11 non-human species were analyzed by the binomial-based method, and the subset of each possible number of species (from 1 to 10, in addition to human) yielding the highest sensitivity at 75% specificity was identified. Note that the ranking of the subsets remains essentially the same for a wide range of specificity thresholds. (A) The resulting relationship between sensitivity and specificity is shown for each subset (see Fig. 7A for details). (B) Detection of reference MCS bases (see Fig. 7B for details), shown for each best-performing subset of species using data obtained with a specificity of 75% (horizontal grey line in A). Note that the far-left bar represents the entire set of reference MCS bases (see Fig. 7B). The underlying data associated with these analyses are available at http://www.nisc.nih.gov/data.
DISCUSSION
The identification and characterization of all genomic elements that confer function will be central to gaining a global understanding of biological systems. With the generation of complete genome sequences from multiple vertebrates (Green 2001; International Human Genome Sequencing Consortium 2001; Aparicio et al. 2002; International Mouse Genome Sequencing Consortium 2002), the focus is rapidly shifting to the development of strategies for establishing comprehensive catalogs of functional sequences. One powerful route for this involves performing comparative analyses that distinguish between those sequences that are and are not highly conserved across large evolutionary distances. The premise of such efforts is that highly conserved sequences are more likely to reflect regions under active selection due to the presence of an element(s) that confers biological function.
Initial comparisons of the sequences of whole mammalian genomes (e.g., those of human and mouse; International Mouse Genome Sequencing Consortium 2002) have revealed strikingly high levels of similarity. For example, 40% of the human genome sequence forms alignments with the mouse genome sequence (International Mouse Genome Sequencing Consortium 2002; Schwartz et al. 2003b), and this figure is even higher for many other mammalian sequences (Thomas et al. 2003). These numbers are roughly an order of magnitude greater than the amount of the mammalian genome estimated to be under active selection (∼5%; International Mouse Genome Sequencing Consortium 2002; Roskin et al. 2003). These early glimpses thus suggest that pair-wise sequence comparisons will not be sufficient for precisely identifying the small fraction of the mammalian genome that is functionally important.
To extend comparative sequence analyses beyond simple pair-wise studies, we sought to develop approaches for identifying MCSs, discrete regions of DNA that are conserved across multiple species. Here we report the development of two independent methods for MCS detection and describe their relative performance in analyzing a recently generated data set of orthologous sequences derived from the same 1.8-Mb genomic region in 11 non-human vertebrates (Thomas et al. 2003). The strong concordance found between the two methods suggests that the identified MCSs indeed reflect the most evolutionarily conserved sequences in the studied genomic region. In addition, the detected MCSs were found to overlap virtually all known coding exons as well as some non-coding regions already shown to be functionally relevant (Thomas et al. 2003).
There are several important factors to consider about detecting MCSs by the methods described here. First, the total branch length of the phylogenetic tree consisting of the species being studied must be sufficiently large, ensuring that enough evolutionary time has elapsed so that non-functional regions have sufficiently diverged. This can be accomplished by utilizing either a small number of highly diverged species (such as that performed here) or a larger number of more closely related species (Boffelli et al. 2003; see below). Second, the reliable identification of smaller functional elements within MCSs will require a greater total branch length compared to the identification of larger functional elements (Cooper et al. 2003). Since coding exons and non-coding RNA genes are generally conserved over larger stretches of DNA, these elements can often be detected using a small set of species' sequences; however, the reliable detection of smaller functional regions, such as individual transcription factor-binding sites, is likely to require larger (and perhaps different) sets of species' sequences. The two methods for detecting MCSs described here utilize calculations performed with 25-base windows, which are much larger than most individual transcription factor–binding sites; despite this, these methods do appear to detect MCSs that contain such sites (see Fig. 6; Thomas et al. 2003). It should certainly be pointed out that the analyses performed in this study focused on a single region of the human genome. Additional work with larger sets of species and additional genomic regions is needed to establish how best to reliably identify smaller functional elements (Loots et al. 2002). Eventually, it will be of interest to know what sets of species are required to determine if an individual human base is conserved under various degrees of selection (Cooper et al. 2003).
It should also be noted that our methods are biased towards the identification of sequences that are conserved in most species (as opposed to only a subset of species), and thus they work best to find sequences that are predominantly under purifying selection (including several sequences previously characterized as ARs; see http://www.nisc.nih.gov/data). Genomic regions whose function (and thus sequence) has changed significantly in certain lineages may remain undetected. These include sequences undergoing significant positive selection for new function in specific lineages, as well as those that have lost function in specific lineages and started to accumulate mutations at the neutral rate. The development of algorithms for performing large-scale genomic comparisons that model richer, more complex modes of molecular evolution remains a significant challenge (Blanchette and Tompa 2002). Such issues have a significant bearing on the choice of species for performing such sequence comparisons—as the set of species being studied becomes very diverse, it becomes increasingly necessary to deal effectively with varied modes of evolution.
Algorithms that utilize diverse sets of species, such as those described here, also depend on the ability to align multiple orthologous sequences in a robust and accurate fashion. Imperfections in the multi-sequence alignments can result in the failure to detect an MCS (false negative) or the inappropriate prediction of an MCS (false positive). The development of newer-generation strategies for generating genomic multi-sequence alignments (Brudno et al. 2003; Bray and Pachter 2003; and W. Miller, pers. comm.) will be important for capturing the full power of comparative sequence analyses, especially using sequences generated from more divergent species.
As an alternative to searching for sequences shared over large evolutionary distances, some comparative analyses involve cataloging sequence differences among closely related species, with regions lacking such differences then presumed to be functionally important. Such a strategy was recently implemented for identifying functional regions (mainly coding exons and regulatory elements) using multiple primate sequences (Boffelli et al. 2003). This approach should be particularly effective at detecting primate lineage-specific functional elements, although sequences from numerous species will likely be needed to identify all such elements. Nonetheless, investigating the full potential of this strategy, especially within the primate lineage, is highly desirable.
The ability to enhance the detection of highly conserved genomic elements is one of many criteria being considered in choosing additional species for whole-genome sequencing. Our analyses thus included investigating the relative contribution of different species' sequences to the identification of MCSs using our targeted genomic region as a model. These studies revealed that the small number of vertebrate genomes whose sequence is at or near completion (human [International Human Genome Sequencing Consortium 2001], mouse [International Mouse Genome Sequencing Consortium 2002], fugu [Aparicio et al. 2002], and rat [http://genome.ucsc.edu/cgi-bin/hgGateway?org=rat]) will not be sufficient for detecting MCSs in a comprehensive fashion, especially those residing within non-coding regions. However, the addition of sequences from even one or two more mammals would likely improve MCS detection significantly.
The results obtained with chicken sequence deserve special comment. Most human–chicken sequence alignments fall within a detected MCS, and virtually all coding sequences are included in those alignments. This is in sharp contrast to human–mouse alignments, the vast majority of which do not fall within a detected MCS, and human–fish alignments, which are almost exclusively restricted to coding regions (but do not include all coding sequences). However, the virtue of the high sensitivity and relatively high specificity for identifying coding sequence that is provided by human–chicken alignments should be balanced against its relatively poor sensitivity for detecting conserved non-coding sequences. Given the striking differences between the ability of sequences from non-primate mammals versus chicken to detect MCSs (especially those within non-coding regions), it is of great interest to investigate the use of sequences from species whose evolutionary position relative to human resides between the placental mammals and birds, such as marsupials (Chapman et al. 2003) and monotremes.
The studies reported here and elsewhere (Thomas et al. 2003) provide tantalizing evidence that many MCSs are indeed biologically important. Provided appropriate sequence data sets, our methods can be readily used to prioritize genomic regions for functional testing. Critical next steps include correlating specific biological functions with individual MCSs, especially for the ∼70% of MCS bases that do not appear to encode protein. A major hardship for establishing such correlations is the paucity of existing information about non-coding functional elements in the human genome. While the MCSs described here overlap the majority of experimentally validated regulatory elements in the 1.8-Mb target region (Thomas et al. 2003), this accounts for only a small fraction (∼2%) of the detected MCSs (and inevitably the inventory of known regulatory elements in the region is far from complete). Efforts to test directly for the presence of regulatory sequences (e.g., enhancers and repressors) within the detected MCSs are ongoing. Similar studies will likely be performed under the auspices of the recently launched ENCODE project (see http://genome.gov/ENCODE), which aims to compile a comprehensive encyclopedia of functional elements in a selected 1% of the human genome. These and other studies should begin to solidify our understanding of the relationships between highly conserved sequences and the biological functions they confer.
METHODS
Multi-Species Genomic Sequence Data Set
The multi-species sequences analyzed in this study, which were generated by the NISC Comparative Sequencing Program (see http://www.nisc.nih.gov), are orthologous to a 1.8-Mb region on human chromosome 7q31 (Thomas et al. 2003). The specific data set utilized here (available at http://www.nisc.nih.gov/data) includes sequences from 11 non-human species: two primates (chimpanzee and baboon), two carnivores (cat and dog), two artiodactyls (cow and pig), two rodents (mouse and rat), one bird (chicken), and two fish (fugu and tetraodon).
Sequence Alignments and Annotations
Pair-wise sequence alignments were generated with repeatmasked sequences using blastz (Schwartz et al. 2000; 06/26/2002 build, available at bio.cse.psu.edu/dist) and the following parameters: B = 0 C = 2K = 2500 Y = 3400 T = 0. When a position in the human reference sequence aligned with multiple positions in the second species' sequence, the highest scoring alignment was chosen. A human-referenced Multiple Pair-wise Alignment (MPA) file was then generated using all of the pair-wise alignments. To keep each species' sequence alignments on the same coordinate system, insertions were removed from the human reference sequence in each pair-wise alignment prior to building the MPA file. Note that we have also used the optimized alignment generated from the Web-based MultiPipMaker program and found that the MCSs detected with the two alignment strategies were ∼95% concordant (data not shown). Also, aligning fish and chicken sequences to the human sequence is notoriously difficult; it should therefore be noted that our currently available strategies might not be aligning the maximum amount of sequence from these species. Nevertheless, in support of the validity of the multi-sequence alignment used here, we found that 99% of the conserved regions identified by the motif-finding program FootPrinter (Blanchette and Tompa 2002), which does not rely on a multi-sequence alignment, were correctly aligned by MultiPipMaker (data not shown).
The above multi-species sequence data set was systematically annotated for known coding exons and UTRs (Thomas et al. 2003). In addition, ARs (Hardison et al. 2003) were identified from the output of RepeatMasker (run in sensitive mode; A.F.A. Smit and P. Green, unpubl.; http://repeatmasker.genome.washington.edu) using an algorithm developed elsewhere (International Mouse Genome Sequencing Consortium 2002), kindly provided by S. Schwartz, and implemented with a Perl script available at http://www.nisc.nih.gov/data. These annotations can be viewed at http://genome.ucsc.edu.
Binomial-Based Method for MCS Detection
In the binomial-based method, a conservation score is calculated for each 25-base window of a multi-sequence alignment based on the probability of detecting the observed amount of conservation between the human and each other species' sequence, assuming neutral substitution rates. For each species, the neutral substitution rate is calculated from fourfold degenerate positions (the third base of codons for which any base will encode the same amino acid). In this way, sequence conservation detected with more diverged species (and their higher neutral substitution rates) is weighted more heavily when calculating the conservation score.
To generate the final conservation score and normalize for any phylogenetic biases (e.g., the use of two rodents but only one bird species), the data are “phylogenetically averaged” by first averaging the conservation scores within each represented clade and then averaging across the different clades. The final binomial-based conservation score is calculated from overlapping 25-base windows (incrementing the window position one base at a time).
More precisely, let pj be the probability that a given base in the human sequence has been conserved in species j, assuming the neutral substitution rate between human and species j. The conservation score Sbin(i) of the 25-base window centered at position i is calculated as follows:
-
For each species j,
- Let N be the number of aligned bases in the 25-base window of the human-species j alignment and let K be the number of perfect matches.
- Calculate the cumulative binomial probability of observing at least K matches in N bases, given the neutral substitution probability pj:
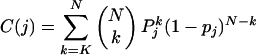
- If the proportion of matches is greater than or equal to the baseline conservation level for that species, K / N ≥ pj, the species score sj is set to -log(C(j)). Otherwise, set sj = log(1 - C(j)). In cases where N = 0, sj is set to zero.
- To obtain the final conservation score SBin(i), the individual species' scores sj are “phylogenetically averaged”:
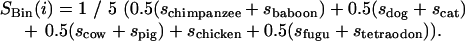
In this calculation, conservation scores below zero represent alignable regions that are more diverged (i.e., less conserved) than expected, while conservation scores greater than zero represent regions that are more conserved than expected.
The program used to identify MCSs by the binomial-based method is available at http://research.nhgri.nih.gov/MCS.
Parsimony-Based Method for MCS Detection
The parsimony-based method analyzes the multi-sequence alignment column by column. The conservation of each column is initially measured with a parsimony score. Given a phylogenetic tree T relating the sequences being analyzed, the parsimony score P(i) of the i-th column of the alignment is defined as the minimum number of substitutions, performed along the branches of the tree, needed to explain the bases observed at the leaves of the tree. The parsimony score is a tight lower bound on the number of substitutions having actually occurred at position i during evolution. Sequences with gaps in column i are ignored when computing the parsimony score P(i). A P-value is then computed that is associated with the parsimony score of column i, measuring the “surprise” of observing a parsimony score P(i) or lower if column i had evolved at a neutral substitution rate.
To quantify this notion of surprise, a model of neutral evolution needs to be defined. The phylogenetic tree T relating the species under study, as well as the length l(e) of each branch e, have previously been established (Thomas et al. 2003). Assuming an HKY neutral substitution rate matrix Q (Hasegawa et al. 1985), the transition probability matrix along a branch (u,v) is given by M(u,v) = el(u,v)Q. Together with a background base distribution π, this defines a null model of neutral evolution that generates a set of random but related bases at the leaves of the tree by simulating evolution. Let A(u) be the random variable representing the base generated by this random process at node u. We compute the probability that the parsimony score of the bases thus generated at the leaves of T have a parsimony score at most P(i). If this probability is small, the column is unlikely to have been generated under neutral evolution. Let r be the root of T; let Z(u) be a random variable describing the parsimony score of the bases at the leaves of the subtree rooted at u. We are interested in computing Pr[Z(r) ≤ P(i)]. To this end, we define Zj(u), for j ε{a,c,g,t} as the parsimony score obtained for the subtree rooted at u, if node u is forced to be labeled with base j. Notice that Z(r) = min(Za(r),Zc(r),Zg(r),Zt(r)). We compute the probability Pr[Za(u) = za, Zc(u) = zc, Zg(u) = zg, Zt(u) = zt | A(u) = α] for all possible choices of za, zc, zg, zt ε N and α ε {a,c,g,t} to obtain
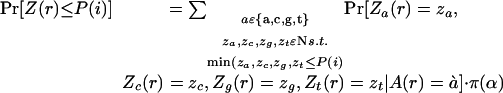 |
We compute Pr[Za(u) = za, Zc(u) = zc, Zg(u) = zg, Zt(u) = zt | A(u) = α] using a dynamic programming algorithm that proceeds from the leaves of T back to its root. When u is a leaf, this probability is zero everywhere except for Pr[Za(u) = 0, Zc(u) = +∞, Zg(u) = +∞, Zt(u) = +∞ | A(u) = a] = 1 and similarly for c, g, and t. In analogy to Sankoff and Rousseau's algorithm (1975) for computing parsimony scores, define (xa,xc,xg,xt) (ya,yc,yg,yt) = (min(xa + ya,xa + ya + 1, xa + ya + 1, xa + ya + 2),…, min(xt + yt, xt + yt + 1, xt + yt + 1, xt + yt + 2)) where xi = minj≠i xj. When u is an internal node with children v and w, we have (Za(u),…,Zt(u)) = (Za(v),…,Zt(v)) (Za(w),…,Zt(w)), and thus
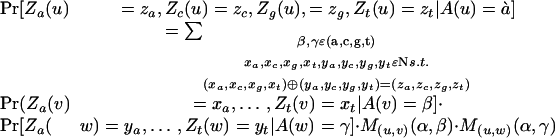 |
Note that the above sum is finite because Pr[Za(u) = za, Zc(u) = zc, Zg(u) = zg, Zt(u) = zt] is zero whenever za, zc, zg, zt differ from each other by more than two (for binary trees) or are larger than the number of leaves (Blanchette 2003). Finally, the score assigned to position i, computed on a 25-base window, is SPars(i) = -Σ j=i-12…i+12 log(Pr[Z(r) ≤ P(j)]). SPars(i) is high when i is at the center of a window of unusually well-conserved columns.
The program used to identify MCSs by the parsimony-based method is now part of the FootPrinter package (Blanchette and Tompa 2003), available at http://bio.cs.washington.edu.
Choosing an Appropriate Threshold for MCS Detection
We chose to use a threshold such that 5% of the human sequence from the analyzed region falls within an MCS for the following reasons. First, human–mouse sequence comparisons suggest that ∼5% of the human genome is under active selection (International Mouse Genome Sequencing Consortium 2002; Roskin et al. 2003). Second, additional studies estimate that the fraction of the human genome under active selection is in the range of 4% to 8% (F. Chairomonte and D. Haussler, pers. comm.). Third, we find a small range of threshold values where virtually all known actively conserved sequences (coding exons) are detected within MCSs while excluding the vast majority of non-coding sequences (Fig. 1); this range results in 4% to 8% of the human sequence residing within the detected MCSs. Finally, applying the methods utilized by the International Mouse Genome Sequencing Consortium (2002) to the multi-species sequences analyzed here (and described by Thomas et al. 2003), we obtain a similar estimate for the amount of human sequence under active selection (data not shown), suggesting that this genomic region is representative of the entire human genome.
Defining MCSs
Both the binomial- and parsimony-based methods assign a score to 25-base windows incremented one base at a time. Therefore, this score applies not only to column i but also to the whole window. To account for this, the final score assigned to position i is as follows: ScoreBinomial(i) = maxj=i-12…i+12 SBin(j) and ScoreParsimony(i) = maxj=i+12…i+12 SPars(j). These scores are then used to define MCSs by each method: For a given threshold t, position i is predicted to be part of an MCS if ScoreBinomial(i) ≥ t, and similarly for ScoreParsimony(i). Note that these calculations constrain the minimum MCS length to 25 bases. However, the minimum distance between two MCSs is not constrained (and, in fact, MCSs can be separated by as little as one base).
The “intersecting set of MCSs” was defined as segments of contiguous sequence where each base exceeds the conservation score thresholds of both the binomial- and parsimony-based methods (see Results; also note that these MCSs are not constrained to be a minimum of 25 bases in length). For some analyses (those described under “Uniqueness of MCSs in the Human Genome” and “Correlating MCSs with Functional Elements” in the Results), intersecting MCSs separated by <10 bases were merged to maximize detection of functional sequence spanning multiple MCSs. This reduced the total number of MCSs by 23%, while increasing the total number of MCS bases by only 1.4%. We refer to these below as the “merged MCSs”.
Assessing the Uniqueness of MCSs
Merged MCSs not overlapping known coding exons and containing <5% repetitive sequence were compared to the human genome sequence (November 2002 build; see http://genome.ucsc.edu) using MegaBlast (Zhang et al. 2000). A dropoff value of 50 was used to prevent small gaps from splitting an alignment into two parts. To minimize multiple hits associated with small MCSs (<34 bp), alignments containing <90% of the MCS length were not considered.
Conserved RNA Secondary Structures
To identify potential RNA secondary structures, MCS sequences were analyzed with the QRNA program (Rivas and Eddy 2001). This program uses two orthologous sequences to predict the presence of a protein-coding region, an RNA structural element, or neither by searching for conserved RNA secondary structures. Five pairs of species' sequences were analyzed: human–mouse, human–pig, human–dog, cat–cow, and dog–pig. A total of 29 MCSs were identified where the average (over the five species pairs) log-odds posterior probability of being an RNA structural element was greater than zero (see http://www.nisc.nih.gov/data). As a control, the QRNA program was used to analyze a data set where the multi-sequence alignments of the MCSs were “scrambled” (i.e., the aligned columns within an MCS were randomly re-ordered, thereby altering the primary sequence but yielding the same percent identity across the different species). Upon scrambling, fewer MCSs obtained a score above zero (19 versus 29). The number of predictions obtained with the scrambled MCSs could indicate a slight bias towards lower-complexity AT- or GC-rich regions.
Detection of Transcription Factor–Binding Sites
MCS sequences were analyzed for potential binding sites for transcription factors listed in TRANSFAC 5.0 (Matys et al. 2003). The TRANSFAC database catalogs transcription factor–binding sites using positional weight matrices (PWMs), which describe the probability of observing each base at each position of a binding site. Each candidate site for transcription factor binding can thus be evaluated under the PWM model as well as the null background model. The logarithm of the likelihood ratio is often used to then measure the quality of the match.
Using the aligned orthologous sequences containing candidate transcription factor–binding sites and the available PWM, we computed the score S as the sum of the log-likelihood ratios for all mammalian species. We then computed a P-value for S under a null model of neutral evolution identical to that used for the parsimony-based method. This was done using dynamic programming, similar to that presented above for computing parsimony score P-values and derived from Blanchette (2003). For each PWM in TRANSFAC 5.0, we identified all sites with P-values <10-7 (see http://www.nisc.nih.gov/data).
We then examined the clustering of predicted transcription factor–binding sites for each PWM. Suppose k of the N putative sites for a given PWM are located within the same MCS. Assuming a null model, where each position in each MCS is equally likely to have a match to one of the N sites, we used simulations to estimate the probability of a merged MCS with at least k sites. This probability is the P-value used in this study. Note that the sizes of the merged MCSs were taken into consideration during the simulations. To simplify the analysis, we considered only non-overlapping sites on both strands.
Assessing the Contribution of Different Species' Sequences to MCS Detection
A 695,679-bp subregion of the above data set (positions 247861–770083 and 839435–874186; see http://genome.ucsc.edu) was selected for these analyses because it is associated with near-complete sequence coverage in all species. Within this subregion are 561 intersecting MCSs that contain 33,322 bp (referred to as the “reference MCS bases”). For each of the 211 - 1 = 2047 subsets of species (all containing human), we measured the sensitivity and specificity of the binomial-based method to detect these intersecting MCSs at varying conservation score thresholds. The complete set of results from these analyses is available at http://www.nisc.nih.gov/data. It should be noted that analyses performed with the entire 1.8-Mb genomic region (which includes an occasional clone gap) yielded very similar results to that obtained with the above subregion. Also, because of the computational demands, it was not practical to use the parsimony-based method for analyzing all 2047 subsets. However, application of the parsimony-based method on a small number of the subsets yielded near-identical results as that obtained with the binomial-based method.
Acknowledgments
We thank numerous people associated with the NISC Comparative Sequencing Program, in particular Jim Thomas, Jeff Touchman, Bob Blakesley, Gerry Bouffard, Steve Beckstrom-Sternberg, Pam Thomas, Jenny McDowell, Baishali Maskeri, Nancy Hansen, Jackie Idol, Valerie Maduro, Shih-Queen Lee-Lin, Arjun Prasad, Matt Portnoy, and various other NISC staff members. We also thank Phil Green, Webb Miller, Adam Siepel, Matt Schwartz, Scott Schwartz, Mark Diekhans, and Ryan Weber for advice and support, as well as Webb Miller, Nancy Hansen, and Jim Mullikin for critical reading of the manuscript.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked “advertisement” in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.1602203.
References
- Akker, S.A., Smith, P.J., and Chew, S.L. 2001. Nuclear post-transcriptional control of gene expression. J. Mol. Endocrinol. 27: 123-131. [DOI] [PubMed] [Google Scholar]
- Alexandersson, M., Cawley, S., and Pachter, L. 2003. SLAM: Cross-species gene finding and alignment with a generalized pair hidden Markov model. Genome Res. 13: 496-502. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altschul, S.F., Gish, W., Miller, W., Myers, E.W., and Lipman, D.J. 1990. Basic local alignment search tool. J. Mol. Biol. 215: 403-410. [DOI] [PubMed] [Google Scholar]
- Aparicio, S., Chapman, J., Stupka, E., Putnam, N., Chia, J.M., Dehal, P., Christoffels, A., Rash, S., Hoon, S., Smit, A., et al. 2002. Whole-genome shotgun assembly and analysis of the genome of Fugu rubripes. Science 297: 1301-1310. [DOI] [PubMed] [Google Scholar]
- Bailey, L. and Elkan, C. 1995. Unsupervised learning of multiple motifs in biopolymers using expectation maximization. Machine Learning 21: 51-80. [Google Scholar]
- Batzoglou, S., Pachter, L., Mesirov, J.P., Berger, B., and Lander, E.S. 2000. Human and mouse gene structure: Comparative analysis and application to exon prediction. Genome Res. 10: 950-958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchette, M. 2003. A comparative analysis method for detecting binding sites in coding regions. In The Seventh Annual International Conference on Research in Computational Molecular Biology (RECOMB). Berlin, Germany.
- Blanchette, M. and Tompa, M. 2002. Discovery of regulatory elements by a computational method for phylogenetic footprinting. Genome Res. 12: 739-748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blanchette, M. and Tompa, M. 2003. FootPrinter: A program designed for phylogenetic footprinting. Nucleic Acids Res. 31: 3840-3842. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boffelli, D., McAuliffe, J., Ovcharenko, D., Lewis, K.D., Ovcharenko, I., Pachter, L., and Rubin, E.M. 2003. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science 299: 1391-1394. [DOI] [PubMed] [Google Scholar]
- Boguski, M.S., Tolstoshev, C.M., and Bassett Jr., D.E. 1994. Gene discovery in dbEST. Science 265: 1993-1994. [DOI] [PubMed] [Google Scholar]
- Bray, N. and Pachter, L. 2003. MAVID multiple alignment server. Nucleic Acids Res. 31: 3525-3526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brudno, M., Do, C.B., Cooper, G.M., Kim, M.F., Davydov, E., NISC Comparative Sequencing Program, Green, E.D., Sidow, A., and Batzoglou, S. 2003. LAGAN and Multi-LAGAN: Efficient tools for large-scale multiple alignment of genomic DNA. Genome Res. 13: 721-731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burge, C. and Karlin, S. 1997. Prediction of complete gene structures in human genomic DNA. J. Mol. Biol. 268: 78-94. [DOI] [PubMed] [Google Scholar]
- Chapman, M.A., Charchar, F.J., Kinston, S., Bird, C.P., Grafham, D., Rogers, J., Grutzner, F., Marshall Graves, J.A., Green, A.R., and Göttgens, B. 2003. Comparative and functional analyses of LYL1 loci establish marsupial sequences as a model for phylogenetic footprinting. Genomics 81: 249-259. [DOI] [PubMed] [Google Scholar]
- Clamp, M., Andrews, D., Barker, D., Bevan, P., Cameron, G., Chen, Y., Clark, L., Cox, T., Cuff, J., Curwen, V., et al. 2003. Ensembl 2002: Accommodating comparative genomics. Nucleic Acids Res. 31: 38-42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, F.S., Green, E.D., Guttmacher, A.E., and Guyer, M.S. 2003. A vision for the future of genomics research: A blueprint for the genomic era. Nature 422: 835-847. [DOI] [PubMed] [Google Scholar]
- Cooper, G.M., Brudno, M., NISC Comparative Sequencing Program, Green, E.D., Batzoglou, S., and Sidow, A. 2003. Quantitative estimates of sequence divergence for comparative analyses of mammalian genomes. Genome Res. 13: 813-820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehal, P., Predki, P., Olsen, A.S., Kobayashi, A., Folta, P., Lucas, S., Land, M., Terry, A., Ecale Zhou, C.L., Rash, S., et al. 2001. Human chromosome 19 and related regions in mouse: Conservative and lineage-specific evolution. Science 293: 104-111. [DOI] [PubMed] [Google Scholar]
- Dermitzakis, E.T., Reymond, A., Lyle, R., Scamuffa, N., Ucla, C., Deutsch, S., Stevenson, B.J., Flegel, V., Bucher, P., Jongeneel, C.V., et al. 2002. Numerous potentially functional but non-genic conserved sequences on human chromosome 21. Nature 420: 578-582. [DOI] [PubMed] [Google Scholar]
- DeSilva, U., Elnitski, L., Idol, J.R., Doyle, J.L., Gan, W., Thomas, J.W., Schwartz, S., Dietrich, N.L., Beckstrom-Sternberg, S.M., McDowell, J.C., et al. 2002. Generation and comparative analysis of approximately 3.3 Mb of mouse genomic sequence orthologous to the region of human chromosome 7q11.23 implicated in Williams syndrome. Genome Res. 12: 3-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dubchak, I., Brudno, M., Loots, G.G., Pachter, L., Mayor, C., Rubin, E.M., and Frazer, K.A. 2000. Active conservation of non-coding sequences revealed by three-way species comparisons. Genome Res. 10: 1304-1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddy, S.R. 2002. Computational genomics of non-coding RNA genes. Cell 109: 137-140. [DOI] [PubMed] [Google Scholar]
- Elnitski, L., Hardison, R.C., Li, J., Yang, S., Kolbe, D., Eswara, P., O'Connor, M.J., Schwartz, S., Miller, W., and Chiaromonte, F. 2003. Distinguishing regulatory DNA from neutral sites. Genome Res. 13: 64-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Etkin, L.D. and Lipshitz, H.D. 1999. RNA localization. FASEB J. 13: 419-420. [DOI] [PubMed] [Google Scholar]
- Fitch, W.M. 1971. Toward defining the course of evolution: Minimum change for a specified tree topology. Syst. Zool. 20: 406-416. [Google Scholar]
- Flicek, P., Keibler, E., Hu, P., Korf, I., and Brent, M.R. 2003. Leveraging the mouse genome for gene prediction in human: From whole-genome shotgun reads to a global synteny map. Genome Res. 13: 46-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Giardine, B., Elnitski, L., Riemer, C., Makalowska, I., Schwartz, S., Miller, W., and Hardison, R.C. 2003. GALA: A database for genomic sequence alignments and annotations. Genome Res. 13: 732-741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göttgens, B., Barton, L.M., Gilbert, J.G., Bench, A.J., Sanchez, M.J., Bahn, S., Mistry, S., Grafham, D., McMurray, A., Vaudin, M., et al. 2000. Analysis of vertebrate SCL loci identifies conserved enhancers. Nat. Biotechnol. 18: 181-186. [DOI] [PubMed] [Google Scholar]
- Green, E.D. 2001. Strategies for the systematic sequencing of complex genomes. Nat. Rev. Genet. 2: 573-583. [DOI] [PubMed] [Google Scholar]
- Hardison, R.C. 2000. Conserved non-coding sequences are reliable guides to regulatory elements. Trends Genet. 16: 369-372. [DOI] [PubMed] [Google Scholar]
- Hardison, R.C., Roskin, K.M., Yang, S., Diekhans, M., Kent, W.J., Weber, R., Elnitski, L., Li, J., O'Connor, M., Kolbe, D., et al. 2003. Covariation in frequencies of substitution, deletion, transposition, and recombination during eutherian evolution. Genome Res. 13: 13-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hasegawa, M., Kishino, H., and Yano, T. 1985. Dating of the human–ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22: 160-174. [DOI] [PubMed] [Google Scholar]
- Hertz, G.Z. and Stormo, G.D. 1999. Identifying DNA and protein patterns with statistically significant alignments of multiple sequences. Bioinformatics 15: 563-577. [DOI] [PubMed] [Google Scholar]
- Hofacker, I.L., Fontana, W., Stadler, P.F., Bonhoeffer, L.S., Tacker, M., and Schuster, P. 1994. Fast folding and comparison of RNA secondary structures. Monatsh Chem. 125: 167-188. [Google Scholar]
- International Human Genome Sequencing Consortium. 2001. Initial sequencing and analysis of the human genome. Nature 409: 860-921. [DOI] [PubMed] [Google Scholar]
- International Mouse Genome Sequencing Consortium. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420: 520-562. [DOI] [PubMed] [Google Scholar]
- Karolchik, D., Baertsch, R., Diekhans, M., Furey, T.S., Hinrichs, A., Lu, Y.T., Roskin, K.M., Schwartz, M., Sugnet, C.W., Thomas, D.J., et al. 2003. The UCSC Genome Browser Database. Nucleic Acids Res. 31: 51-54. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellis, M., Patterson, N., Endrizzi, M., Birren, B., and Lander, E.S. 2003. Sequencing and comparison of yeast species to identify genes and regulatory elements. Nature 423: 241-254. [DOI] [PubMed] [Google Scholar]
- Kent, W.J., Sugnet, C.W., Furey, T.S., Roskin, K.M., Pringle, T.H., Zahler, A.M., and Haussler, D. 2002. The human genome browser at UCSC. Genome Res. 12: 996-1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korf, I., Flicek, P., Duan, D., and Brent, M.R. 2001. Integrating genomic homology into gene structure prediction. Bioinformatics 17(Suppl 1): S140-S148. [DOI] [PubMed] [Google Scholar]
- Kulp, D., Haussler, D., Reese, M.G., and Eeckman, F.H. 1996. A generalized hidden Markov model for the recognition of human genes in DNA. Proc. Int. Conf. Intell. Syst. Mol. Biol. 4: 134-142. [PubMed] [Google Scholar]
- Lim, L.P., Glasner, M.E., Yekta, S., Burge, C.B., and Bartel, D.P. 2003. Vertebrate microRNA genes. Science 299: 1540. [DOI] [PubMed] [Google Scholar]
- Loots, G.G., Locksley, R.M., Blankespoor, C.M., Wang, Z.E., Miller, W., Rubin, E.M., and Frazer, K.A. 2000. Identification of a coordinate regulator of interleukins 4, 13, and 5 by cross-species sequence comparisons. Science 288: 136-140. [DOI] [PubMed] [Google Scholar]
- Loots, G.G., Ovcharenko, I., Pachter, L., Dubchak, I., and Rubin, E.M. 2002. rVista for comparative sequence-based discovery of functional transcription factor binding sites. Genome Res. 12: 832-839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matys, V., Fricke, E., Geffers, R., Gossling, E., Haubrock, M., Hehl, R., Hornischer, K., Karas, D., Kel, A.E., Kel-Margoulis, O.V., et al. 2003. TRANSFAC: Transcriptional regulation, from patterns to profiles. Nucleic Acids Res. 31: 374-378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayor, C., Brudno, M., Schwartz, J.R., Poliakov, A., Rubin, E.M., Frazer, K.A., Pachter, L.S., and Dubchak, I. 2000. VISTA: Visualizing global DNA sequence alignments of arbitrary length. Bioinformatics 16: 1046-1047. [DOI] [PubMed] [Google Scholar]
- McCue, L., Thompson, W., Carmack, C., Ryan, M.P., Liu, J.S., Derbyshire, V., and Lawrence, C.E. 2001. Phylogenetic footprinting of transcription factor binding sites in proteobacterial genomes. Nucleic Acids Res. 29: 774-782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pennacchio, L.A. and Rubin, E.M. 2001. Genomic strategies to identify mammalian regulatory sequences. Nat. Rev. Genet. 2: 100-109. [DOI] [PubMed] [Google Scholar]
- Pennacchio, L.A., Olivier, M., Hubacek, J.A., Cohen, J.C., Cox, D.R., Fruchart, J.C., Krauss, R.M., and Rubin, E.M. 2001. An apolipoprotein influencing triglycerides in humans and mice revealed by comparative sequencing. Science 294: 169-173. [DOI] [PubMed] [Google Scholar]
- Rivas, E. and Eddy, S.R. 2001. Non-coding RNA gene detection using comparative sequence analysis. BMC Bioinformatics 2: 8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogic, S., Mackworth, A.K., and Ouellette, F.B. 2001. Evaluation of gene-finding programs on mammalian sequences. Genome Res. 11: 817-832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roskin, K., Diekhans, M., and Haussler, D. 2003. Scoring two-species local alignments to try to statistically separate neutrally evolving from selected DNA segments. In The Seventh Annual International Conference on Research in Computational Molecular Biology (RECOMB), pp. 257-266. Berlin, Germany.
- Roth, F.P., Hughes, J.D., Estep, P.W., and Church, G.M. 1998. Finding DNA regulatory motifs within unaligned non-coding sequences clustered by whole-genome mRNA quantitation. Nat. Biotechnol. 16: 939-945. [DOI] [PubMed] [Google Scholar]
- Sankoff, D. and Rousseau, P. 1975. Locating the vertices of a Steiner tree in arbitrary space. Math. Programming 9: 240-246. [Google Scholar]
- Schwartz, S., Zhang, Z., Frazer, K.A., Smit, A., Riemer, C., Bouck, J., Gibbs, R., Hardison, R., and Miller, W. 2000. PipMaker: A web server for aligning two genomic DNA sequences. Genome Res. 10: 577-586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, S., Elnitski, L., Li, M., Weirauch, M., Riemer, C., Smit, A., NISC Comparative Sequencing Program, Green, E.D., Hardison, R.C., and Miller, W. 2003a. MultiPipMaker and supporting tools: Alignments and analysis of multiple genomic DNA sequences. Nucleic Acids Res. 31: 3518-3524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schwartz, S., Kent, W.J., Smit, A., Zhang, Z., Baertsch, R., Hardison, R.C., Haussler, D., and Miller, W. 2003b. Human–mouse alignments with BLASTZ. Genome Res. 13: 103-107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Solovyev, V.V. 2001. Statistical approaches in eukaryotic gene prediction. In Handbook of statistical genetics (eds. D.J. Balding, et al.), pp. 83-127. John Wiley & Sons, Ltd, New York.
- Spagnoli, F.M., Cicchini, C., Tripodi, M., and Weiss, M.C. 2000. Inhibition of MMH (Met murine hepatocyte) cell differentiation by TGFβ is abrogated by pre-treatment with the heritable differentiation effector FGF1. J. Cell. Sci. 113: 3639-3647. [DOI] [PubMed] [Google Scholar]
- Stojanovic, N., Florea, L., Riemer, C., Gumucio, D., Slightom, J., Goodman, M., Miller, W., and Hardison, R. 1999. Comparison of five methods for finding conserved sequences in multiple alignments of gene regulatory regions. Nucleic Acids Res. 27: 3899-3910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strausberg, R.L., Feingold, E.A., Grouse, L.H., Derge, J.G., Klausner, R.D., Collins, F.S., Wagner, L., Shenmen, C.M., Schuler, G.D., Altschul, S.F., et al. 2002. Generation and initial analysis of more than 15,000 full-length human and mouse cDNA sequences. Proc. Natl. Acad. Sci. 99: 16899-16903. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas, J.W., Touchman, J.W., Blakesley, R.W., Bouffard, G.G., Beckstrom-Sternberg, S.M., Margulies, E.H., Blanchette, M., Siepel, A.C., Thomas, P.J., McDowell, J.C., et al. 2003. Comparative analyses of multi-species sequences from targeted genomic regions. Nature 424: 788-793. [DOI] [PubMed] [Google Scholar]
- van der Velden, A.W. and Thomas, A.A. 1999. The role of the 5′ untranslated region of an mRNA in translation regulation during development. Int. J. Biochem. Cell. Biol. 31: 87-106. [DOI] [PubMed] [Google Scholar]
- Vincent, J.B., Petek, E., Thevarkunnel, S., Kolozsvari, D., Cheung, J., Patel, M., and Scherer, S.W. 2002. The RAY1/ST7 tumor-suppressor locus on chromosome 7q31 represents a complex multi-transcript system. Genomics 80: 283-294. [DOI] [PubMed] [Google Scholar]
- Wasserman, W.W., Palumbo, M., Thompson, W., Fickett, J.W., and Lawrence, C.E. 2000. Human–mouse genome comparisons to locate regulatory sites. Nat. Genet. 26: 225-228. [DOI] [PubMed] [Google Scholar]
- Zhang, Z., Schwartz, S., Wagner, L., and Miller, W. 2000. A greedy algorithm for aligning DNA sequences. J. Comput. Biol. 7: 203-214. [DOI] [PubMed] [Google Scholar]
WEB SITE REFERENCES
- http://www.nisc.nih.gov; NIH Intramural Sequencing Center (NISC) home page.
- http://www.nisc.nih.gov/data; Supplementary data, including annotated sequence for the studies reported here and supplemental tables.
- http://genome.ucsc.edu; UC Santa Cruz Genome Browser home page, including the multi-species “zoo browser.”
- http://bio.cs.washington.edu; Computational Molecular Biology Group (University of Washington, Computer Science & Engineering) home page.
- http://genome.gov/ENCODE; ENCODE project home page.
- http://www.ncbi.nlm.nih.gov/dbEST; Database of Expressed Sequence Tags at the National Center for Biotechnology Information.
- http://www.ncbi.nlm.nih.gov/entrez/query.fcgi?db=OMIM; Online Mendelian Inheritance in Man.
- http://mgc.nci.nih.gov; Mammalian Gene Collection home page.
- http://research.nhgri.nih.gov/MCS; Home page for binomial-based method for MCS detection.
- http://repeatmasker.genome.washington.edu; RepeatMasker home page.