Catalysis of electron transfer during activation of O₂ by the flavoprotein glucose oxidase

Abstract

Two prototropic forms of glucose oxidase undergo aerobic oxidation reactions that convert FADH⁻ to FAD and form H₂O₂ as a product. Limiting rate constants of k_cat/K_M(O₂) = (5.7 ± 1.8) × 10² M⁻¹⋅s⁻¹ and k_cat/K_M(O₂) = (1.5 ± 0.3) × 10⁶ M⁻¹⋅s⁻¹ are observed at high and low pH, respectively. Reactions exhibit oxygen-18 kinetic isotope effects but no solvent kinetic isotope effects, consistent with mechanisms of rate-limiting electron transfer from flavin to O₂. Site-directed mutagenesis studies reveal that the pH dependence of the rates is caused by protonation of a highly conserved histidine in the active site. Temperature studies (283–323 K) indicate that protonation of His-516 results in a reduction of the activation energy barrier by 6.0 kcal⋅mol⁻¹ (0.26 eV). Within the context of Marcus theory, catalysis of electron transfer is attributed to a 19-kcal⋅mol⁻¹ (0.82 eV) decrease in the reorganization energy and a much smaller 2.2-kcal⋅mol⁻¹ (0.095 eV) enhancement of the reaction driving force. An explanation is advanced that is based on changes in outer-sphere reorganization as a function of pH. The active site is optimized at low pH, but not at high pH or in the H516A mutant where rates resemble the uncatalyzed reaction in solution.

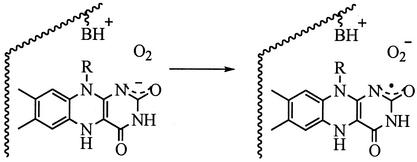
Flavins are highly versatile enzyme cofactors that undergo electron and proton-coupled electron transfer reactions (1–3). As a result, flavoenzymes are involved in an array of chemical and photochemical processes from C—H oxidations (4) to electron transport (5) to repair of cross-linked DNA (6). Glucose oxidase (GO) is a homodimeric protein found predominantly in fungi (National Center for Biotechnology Information, www.ncbi.nlm.nih.gov). Each protein subunit contains an equivalent of noncovalently bound FAD ≈15 Å below the surface (7). GO mediates net hydride transfer from the anomeric C—H bond of glucose to FAD in the reductive half-reaction (8, 9) and the oxidation of reduced cofactor (FADH⁻) by O₂ in the oxidative half-reaction, forming H₂O₂ as a product. All evidence points toward a rate-limiting electron transfer step during FADH⁻ oxidation as shown in Eq. 1 (10). This reaction involves the transfer of negative charge from cofactor to superoxide ion with no net change in charge at the active site.

To date, most mechanistic studies of O₂ activation have focused on metalloenzymes. In such reactions, electron transfer and electrostatic stabilization often occur within a single step (ref. 11 and references therein), causing rates to approach the diffusion limit (12). Additionally, ligands control metal coordination geometries and modulate redox potentials, thereby tuning reactivity toward O₂ (13). Enzymes that use organic cofactors do not enjoy such advantages, but may use specialized protein environments to help overcome the kinetic and thermodynamic barriers associated with activation of O₂.

The physical characterization of the protein dielectric is an area of growing interest (14–18) and may provide the key to understanding how proteins like GO facilitate the charge transfer reactions involved in their catalytic cycles. The importance of active-site electrostatics to proton transfer catalysis has been elucidated (19). The electrostatic environment of the protein is likely to be important for catalysis of electron transfer because of similar energy demands (17, 20). The work presented in this article allows us to dissect the thermodynamic and kinetic factors that contribute to O₂ reactivity in GO, showing how a single charged amino acid can create a polarized environment that is optimal for electron transfer.

Experimental Procedures

Reagents were obtained from commercial sources and used as received. Buffers were prepared from sodium salts of acetate (pH 5.0–7.0), pyrophosphate (pH 8.0–10.0), cyclohexylaminopropanesulfonate (pH 10.5–11.1), and hydroxide (pH >12). Kinetic measurements were performed at 298 K and μ = 0.1 ± 0.025 M by using solutions of 2-deoxy-d-glucose (grade III, Sigma) unless otherwise noted. The concentration of WT recombinant GO was determined by standard assay in an air-saturated solution of 0.5 M deoxyglucose (0.1 M acetate, pH 5) and referenced to k_cat = 41.7 s⁻¹. Corrections were applied for enzyme instability on the time scale of measurements by using activities determined from standard assays after preincubation of enzyme in reaction solutions. The largest correction corresponded to a 35% activity loss after incubation of enzyme in 0.1 M deoxyglucose at pH 12.4 and 313 K for 2 min.

Optical absorbance measurements were performed by using a Hewlett–Packard 8452a diode array spectrophotometer or a Hi Tech (Salisbury, U.K.) stopped-flow apparatus equipped with a rapid-scanning module and a UV-visible detector. Global analysis of kinetic data was performed by using specfit (Spectrum Software, Malborough, MA). Enzyme used in single-turnover experiments was prereduced with stoichiometric glucose under argon. Steady-state rates of O₂ consumption were measured by using a Clark electrode (model 5300, Yellow Springs Instruments). kaleidagraph (Synergy Software, Reading, PA) was used for linear and nonlinear regression analyses. To be as conservative as possible, errors in rate constants are reported as ±2σ, as are errors in activation parameters derived from linear fits of the 2σ-weighted data.

Oxygen-18 kinetic isotope effects (KIEs) were measured competitively on solutions containing deoxyglucose (30–50 mM) and natural abundance O₂ (0.4–1.0 mM) by using a custom-designed apparatus as described (21, 22). H₂O₂ was scavenged by using horseradish peroxidase with either guaiacol (pH 5.0 and 9.0) or potassium ferrocyanide (pH 12.5) as substrate. Samples were analyzed by isotope-ratio MS (Krueger, Cambridge, MA). Isotope effects were computed from enrichment of ¹⁶O¹⁸O as a function of O₂ consumed and are reported as the average of 5–10 independent measurements with errors of ±1σ.

GO from Aspergillus niger was heterologously expressed in Saccharomyces cerevisiae by using pSGO₂ and cell line GRF181 donated by Steven Rosenberg (formerly of Chiron) (23). The H516A variant was prepared by subcloning the gene from pSGO₂ into the BglII site of pMT/BiP/V5-His B (Invitrogen). Mutagenesis was performed with the QuikChange kit (Qiagen, Chatsworth, CA) and two primers: 5′-CCACTTCCGTCCTAACTACGCTGGCGTGGGTACTTGC-3′ and 5′-GCAAGTACCCACGCCAGCGTAGTTAGGACG-3′ (Operon Technologies, Alameda, CA). DNA was sequenced at the University of California, Berkeley, DNA Sequencing Facility. The mutant gene reinserted into the expression vector was amplified in E. coli XL10-Gold Ultracompetent cells (Stratagene). Sequencing (5.6 kB) and restriction analysis with SacI (Amersham Pharmacia) confirmed the presence of the mutant gene in the correct orientation. Overexpression of proteins was accomplished following Frederick et al. (23). The ≈320-kDa WT and H516A, purified as described (24, 25), exhibited identical migration patterns on SDS and native 7.5% polyacrylamide gels.

The H516A variant exhibited a weakened binding affinity for FAD evidenced by low OD at 450 nm and lack of measurable activity. Reconstitution of the apoenzyme (1–5 μM) with excess Na₂FAD (100 equivalents) resulted in a high yield of holoenzyme after incubation in the dark for 2 days at 295 K. The concentration of holoH516A was determined by spectrophotometric titration in an anaerobic cell with glucose as a reductant. The concentration of bound flavin was determined from the change in absorbance at 450 nm on converting oxidized FAD (ɛ = 12.83 mM⁻¹⋅cm⁻¹) to FADH⁻ (ɛ = 2.1 mM⁻¹⋅cm⁻¹) (24) and agreed to ±20% with concentrations of protein determined by Bio-Rad dye analysis using WT GO as the standard. Addition of excess Na₂FAD (100–1,000 equivalents) did not affect the initial rates or the decline in activity over the course of hours. Solutions of H516A (10–50 μM) and Na₂FAD (5.0 mM) were stored for up to 2 weeks at 277 K and assayed without removal of free flavin.

Results

GO reacts by a ping-pong mechanism, allowing steady-state analysis of the oxidative half-reaction independently of the reductive half-reaction (26, 27). The bimolecular rate constant k_cat/K_M(O₂) describes all steps beginning with interaction of enzyme and O₂ up to and including the first irreversible step. Optical absorbance measurements under single turnover conditions (pH 5, 278 K) show isosbestic points corresponding to conversion of FADH⁻ to oxidized FAD. Global analysis of the data yields no evidence of the known flavin semiquinones (1) consistent with previous studies (10, 28–30). Although electrochemical data acquired at pH 5.3 (30) indicate an equilibrium constant of K_278K ≅ 10 for the formation of the semiquinone/O state (see below), buildup of this intermediate apparently is precluded by its faster consumption in a subsequent reaction.

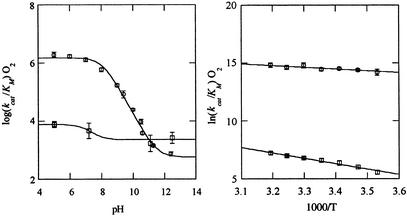
The data shown in Fig. 1 Left reveal two forms of WT GO that react with O₂. The slope of log k_cat/K_M(O₂) versus pH determined to be 0.93 is consistent with the ionization of a single base of pKa = 8.1. Data fitted to a two-state model and a single pKa {ref. 26 and log k_cat/K_M(O₂) = log[k_Min/(1 + 10 ^{pKa − pH}) + k_Max/(1 ± 10^{pH − pKa})} indicate maximum and minimum rate constants of k_cat/K_M(O₂) = (1.5 ± 0.3) × 10⁶ M⁻¹⋅s⁻¹ and k_cat/K_M(O₂) = (5.7 ± 1.8) × 10² M⁻¹⋅s⁻¹ at low and high pH, respectively. This analysis indicates that the rate constant at high pH is >100 times slower than reported (26). Because rate constants differ by 3 orders of magnitude, the low pH enzyme form is the dominant contributor to the observed rate constant up to pH 11, which is above the highest pH characterized in the earlier study.

Fig 1.

(Left) Profiles of log k_cat/K_M(O₂) for WT (○) and the H516A (□) versus pH at 298 K and μ = 0.1 M. Rate constants fitted to the expression log k_cat/K_M(O₂) = log[k_Min/(1 + 10^{pKa − pH}) + k_Max/(1 ± 10^{pH − pKa})] are given in Table 1. (Right) Temperature dependencies of ln k_cat/K_M(O₂) for WT at pH 5.0 (○) and pH 12.5 (□). Activation parameters are given in Table 1.

Assessment of the limiting k_cat/K_M(O₂) along with an unambiguous demonstration of two active enzyme forms requires experiments over a very broad pH range. The hyperglycosylated enzyme used in this study is stable for several hours above pH 3.0 and for short periods above pH 12. Although prolonged exposure to strongly basic conditions causes enzyme to denature irreversibly, only small changes in activity are observed on the time scale of the initial rate measurements. Rates determined in 96% D₂O show negligible solvent KIEs of 1.2 ± 0.2 at pL 5.0 and 1.1 ± 0.2 at pL 12.5. As anticipated from previous studies with the same glycoform of GO (26), the acidity of the active-site base is reduced in D₂O where the pKa = 8.7.

Changes in pKa are also seen in the presence of viscosogens ethylene glycol and glycerol, which were previously used to assess the extent of diffusion control on k_cat/K_M(O₂) (26). Reactions in glycerol and ethylene glycol at pH 9.0 (η = 4 cp) exhibit identical k_cat/K_M(O₂) and both are a factor of 4 slower than the buffer-only solutions. This finding originally was taken as support for a mechanism involving diffusion-controlled reaction of O₂ (26) but must be revised in light of the following: (i) Viscosogen effects disappear at the pH extremes where the limiting rate constants are manifest. (ii) The observed rate deceleration is larger than expected for an encounter-controlled reaction of O₂ based on a modified Stokes–Einstein equation (31). (iii) Control experiments with sucrose as viscosogen (η = 4 cp) show acceleration of k_cat/K_M(O₂) by ≈30%. Together, the results indicate that k_cat/K_M(O₂) is not affected through changes in the diffusion coefficient for O₂ but by a structural perturbation that is specific to the hydroxylic additive. The pH profile of k_cat/K_M(O₂) in 50% ethylene glycol is simply shifted from that of the 0% viscosogen solution, revealing a unit slope and pKa = 7.7 (see Figs. 3–6, which are published as supporting information on the PNAS web site, www.pnas.org). Thus, the previously reported viscosity effect at high pH (26) is now understood to result from a pKa perturbation that depletes the concentration of the more reactive, low-pH enzyme form.

Site-directed mutagenesis studies implicate His-516 as largely responsible for catalyzing the reaction between FADH⁻ and O₂. The pH profiles of WT and H516A are compared in Fig. 1 Left. The mutant shows a slightly increased rate at high pH, where k_cat/K_M(O₂) = (2.3 ± 1.7) × 10³ M⁻¹⋅s⁻¹ and a markedly decreased rate at pH 5 where k_cat/K_M(O₂) = (7.6 ± 3.8) × 10³ M⁻¹⋅s⁻¹. The elimination of His also affects k_cat/K_M(deoxyglucose) = (3.5 ± 1.0) × 10¹ M⁻¹⋅s⁻¹ and k_cat = 2.9 ± 0.3 × 10⁻² s⁻¹, which are slower than the WT reactions at pH 5.0 by approximately 1 and 3 orders of magnitude, respectively. This finding is consistent with those of Witt et al. that the analogous mutant in Pennicilium (H520A) exhibits a turnover rate with glucose that is 4 orders of magnitude slower than WT (32).

Within the superfamily of glucose-methanol-choline oxidases, a highly conserved active-site His has been suggested to function as a general acid during the oxidative half-reactions (33). This work supports the proposal that His-516 in GO is responsible for the acceleration of k_cat/K_M(O₂) at low pH (26). The absence of solvent KIEs at the pH extremes indicates, however, that proton transfer does not occur in the rate-determining steps. Rather, His-516 catalyzes the reaction with O₂ by contributing a positive point charge. The effect of His-516 protonation in WT GO is surprisingly large, up to 2,600-fold, neglecting any influence from His-559, the only other positively charged residue in proximity to the flavin. The effect of a single ionizing residue is consistent with the variation of k_cat/K_M(O₂) with pH. For H516A, the 7-fold rate acceleration observed on lowering the pH from 12.5 to 5.0 is likely the result of small effects from nonessential residues.

Competitive oxygen-18 KIEs (O-18 KIEs, ¹⁸V/K) reveal the extent to which a change in oxygen bond order occurs in the rate-limiting step. The ¹⁸V/K = 1.027 ± 0.003 obtained at pH 5.0 and 9.0 (26) reflects the reaction of the low-pH enzyme form for the reasons described above. The ¹⁸V/K = 1.028 ± 0.004 at pH 12.5 reported herein is caused by reaction of the high-pH form exclusively. Reported isotope effects are independent of fraction conversion and concentrations of peroxide scavenging agents. To avoid complications from the decomposition of H₂O₂, measurements at pH 12.5 were obtained within 10 min. Over this period, k_cat/K_M(O₂) is independent of peroxide scavengers and added H₂O₂ up to 2 mM. The H516A mutant exhibits ¹⁸V/K = 1.017 ± 0.007 at pH 5.0. The precision of this value is somewhat compromised by the low conversions of O₂ (≈0.1 mM) that result from slow turnover and enzyme instability. The isotope effect is within the error limits of that observed for WT, indicating a similar change in oxygen bond order during the rate-limiting step of k_cat/K_M(O₂).

The temperature dependence of k_cat/K_M(O₂) further distinguishes the high- and low-pH enzyme forms. The data fitted to the Arrhenius expression (Fig. 1 Right) indicate activation energies of E_a = 9.0 ± 1.0 kcal⋅mol⁻¹ (0.39 ± 0.04 eV) at pH 12.5 and E_a = 3.0 ± 1.0 kcal⋅mol⁻¹ (0.13 ± 0.05 eV) at pH 5.0. A negative E_a is obtained at intermediate pH (pH 9.0) because of the temperature dependence of the catalytic base pKa (27). The O-18 KIEs from 283 K to 323 K (pH 5.0 and 9.0) are the same within the error limits, indicating that the rate-determining step is unchanged over the temperature range studied. No attempt was made to measure the temperature dependence of the O-18 KIEs at pH 12.5 because of the reduced stability of enzyme and peroxide. The difference in reactivity between high- and low-pH enzyme forms is caused by the activation energies because the terms ln A = 20 ± 4 at pH 5.0 and ln A = 22 ± 3 at pH 12.5 are the same within experimental error.

Discussion

The classical Marcus theory of electron transfer (34, 35) gives the ΔG‡ for a unimolecular reaction as the result of the reorganization energy (λ) and the Gibbs free energy of reaction (ΔG°) according to Eq. 2. The ΔG° is equivalent to −nFΔE°, where n represents the moles of electrons transferred, F is the Faraday's constant, and ΔE° is the standard reduction potential difference of two half-reactions. Here, electron transfer to O₂ is treated by replacing ΔG° with ΔG°′ according to Eq. 3, which includes electrostatic work terms associated with formation of a reactant complex (w_R) and disassembly of a product complex (w_P).

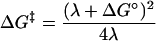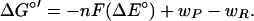The reorganization energy λ is the sum of inner-shell (λ_in) and outer-shell (λ_out) contributions. λ_in is the energy associated with changing the bond lengths and angles of the reactant state to match those of the product state without the transfer of an electron. λ_out is the energy associated with transforming the configuration of the surrounding medium in the reactant state to that of the product state also without transfer of electron. The harmonic approximation is commonly used to describe λ. The λ_in is approximated by Eq. 4 where f̄ is a reduced force constant an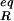d r and r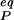 are the equilibrium bond lengths in the reactant and product states, respectively. A dielectric continuum model, where the orientation polarization of the surroundings is slow, relative to the electronic polarization, frequently is used to approximate λ_out (34, 35). In its most general form, Eq. 5 gives λ_out in terms of the electric fields (E_R and E_P) exerted at a distance (r) from the centers of the reactant and product states in a cavity of volume (V). The constant ɛ_o = 332.1 kcal⋅mol⁻¹ is the charge permittivity of vacuum. The inverse of the dielectric constants is used to describe the fast, electronic (1/ɛ_op) and slow, orientational (1/ɛ_s) responses of the surrounding medium. Although derived for reactions in solution, Eq. 5 has been extended to proteins (35–38), giving values of λ_out that typically range from 0.5 to 1.6 eV (38).

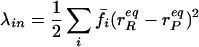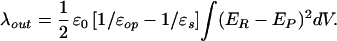Intrinsic Barrier to O₂ Activation.

The self-exchange reaction between O₂ and O sheds light on the factors that influence electron transfer activation of O₂. The self-exchange rate constant occurs by definition with ΔG°′ = 0. As a result, ΔG‡ = λ/4 and serves as a direct measure of the intrinsic barrier to reaction. Electron transfer from O to O₂ occurs with a rate constant of k_ET = (4.5 ± 1.6) × 10² M⁻¹⋅s⁻¹ in aqueous solution (39). Application of the adiabatic Marcus theory (35, 39) gives ΔG‡ = 11.5 kcal⋅mol⁻¹ (0.5 eV) and λ ≅ 46 kcal⋅mol⁻¹ (2.0 eV). [This assumes k_ET = κZ exp(−ΔG‡/RT), where κ = 1 and Z = 10¹¹ M⁻¹⋅s⁻¹.] A value of λ_in = 16 kcal⋅mol⁻¹ (0.69 eV) has been calculated from Eq. 4 (39) but may be as low as 11 kcal⋅mol⁻¹ according to recent quantum treatments (40). The former value is used here to estimate λ_out = 30 kcal⋅mol⁻¹ (1.3 eV) from the difference λ − λ_in (39). This finding indicates that reorganization of the surrounding medium presents a major energy cost for electron transfer to O₂. It follows that in proteins that are optimized for charge transfer such that ɛ_s ∼ ɛ_op, λ_out is expected to be greatly reduced from that in polar solutions where ɛ_op ≪ ɛ_s (17).

Mechanism of the Oxidative Half-Reaction.

Illumination of the rate-determining step during aerobic oxidations can be achieved by correlating changes in O—O bond order to the reaction kinetics (41). The first step in the oxidative half-reaction of GO is diffusion of O₂ near the active site. Although reaction between buried cofactor and O₂ at the surface is possible, the 15-Å distance makes such an event highly improbable. Encounter between protein-bound FADH⁻ and O₂ is expected to occur with a rate constant k_diff = 10⁹–10¹⁰ M⁻¹⋅s⁻¹ (42). The k_cat/K_M(O₂) in GO ranges from ≈10³ to 10⁶ M⁻¹⋅s⁻¹, arguing against a diffusion-controlled reaction; additionally, there is no effect of solvent viscosogen on rate.

There is no indication of a Michaelis-type complex or of oxygen binding to GO in reactions at low pH (8, 28, 29). Although there is a very large difference in K_M(O₂) at high pH (≥1 mM) and low pH (25 ± 5 μM), this is unrelated to the protein's affinity of O₂. The K_M(O₂) is simply the ratio of k_cat, which consists largely of the hydride transfer step (25) and k_cat/K_M(O₂). For the purposes of this analysis, O₂ in the active site is formulated as a weak interaction complex with K_D(O₂) ≈ 1 M, analogous to the reactant complex in Marcus theory (35).

The kinetic data presented here support mechanisms of rate-limiting electron transfer for the E(FADH⁻, His) and E(FADH⁻, HisH⁺) forms of WT GO (Eq. 1). Optical absorbance spectra show isosbestic points on reaction of reduced enzyme with O₂, consistent with a rate-limiting step after the formation of E(FADH⁻, HisH⁺)|O₂ and before the disappearance of E(FADH^•, HisH⁺)|O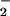. The O-18 KIEs indicate one electron reduction of O₂ during the irreversible steps of the WT and H516A mutant oxidative half-reactions. The O-18 KIEs range from 1.017 to 1.028 in agreement with the upper limit set by the equilibrium isotope effect; a value of ¹⁸K ≅ 1.03, is estimated from the difference in free energies associated with converting ^16,16O₂ to ^16,16O 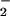and ^16,18O₂ to ^16,18O 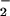using the Mayer–Bigeleisen approach (43). It is important to realize, however, that within the context of electron transfer theory the O-18 KIE originates from the difference in Franck–Condon factors for the electron transfer (44). This parameter, treated classically or quantum mechanically (45), gives the O-18 KIE as a function of O—O distances and normal mode force constants in the reactant and product states. Thus, O-18 KIEs are expected to exhibit a parabolic dependence on the free energy approaching a maximum as ΔG°^′ approaches zero and the difference in Franck–Condon factors is greatest (unpublished work).

With the present results, several alternative mechanisms of O₂ activation can be ruled out. An inner-sphere electron transfer by the direct addition of O₂ to FADH⁻ requires a change in the spin state of either the reduced flavin or O₂ that is accessible only by photochemical excitation. Because we find that observed rate constants are insensitive to the absence of light, such processes cannot be involved. Proton-coupled electron transfer pathways are inconsistent with the absence of solvent KIEs on k_cat/K_M(O₂). An independence of rate on solvent isotope caused by a lack of proton/deuteron exchangeability is precluded by the observed pKa shift in D₂O. The polar positions of the flavin in GO are known to be solvent accessible as well (46). A sequential process where electron and proton transfers occur before a rate-determining electron transfer may not show a solvent KIE. This reaction would involve oxidation of flavin semiquinone by HOO^• or O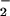. The reaction of neutral semiquinone and O 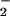has been studied in GO by pulse radiolysis. The reaction occurs with a second-order rate constant of 10⁹ M⁻¹⋅s⁻¹, suggesting that this is not a rate-limiting step (10). Siegbahn and coworkers (47) have suggested a variation of this mechanism wherein the putative triplet radical pair [E(FADH^•, HisH⁺)|O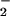] is formed rapidly and converts to the singlet spin state in the rate-determining step of k_cat/K_M(O₂). This finding appears incompatible with the pH dependence of the reaction, requiring an electron transfer step that is both reversible and orders of magnitude more favorable at low than high pH. Thus, their mechanism predicts substantial buildup of [E(FADH^•, HisH⁺)|O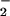], in contrast to the absence of detectable flavin semiquinone at low pH (8, 28–30). In an analogous manner, a rate-limiting conformational change subsequent to electron transfer can be ruled out because this would also predict accumulation of measurable semiquinone levels.

The Role of Charge in the Active Site.

The role of the protein during catalysis is the subject of long-standing debate and barrier-lowering effects are suggested to have both kinetic and thermodynamic origins (20, 48). Catalytic rates of O₂ activation by flavoprotein oxidases are found to correlate with the presence of positively charged amino acids in the active site (10, 49). The role of the protein during these processes has yet to be elucidated.

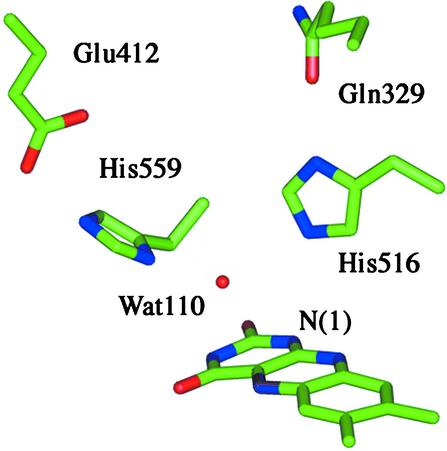
In reduced GO, FADH⁻ persists as an anion to pH 5 (50). Crystal structures of the oxidized enzymes from A. niger and Pennicilium amagasakiense are available at pH 5.6 and pH 7.4, respectively (7). Despite the pH difference, the active sites are conformationally identical with the exception of the imidazolium of His-516, which is rotated by 90°. Both structures contain a water molecule that forms bifurcated hydrogen bonds to the two conserved His residues and to the N(1) position of the flavin. In the Aspergillus structure (compare Fig. 2, bond distances given in parentheses), N^δ of His-516 is hydrogen-bonded to the carboxamide oxygen of Gln-329 (3.18 Å) and N^ɛ is hydrogen- bonded to Wat-110 (2.92 Å). Similarly in Pennicillium, N^δ of His-516 is hydrogen-bonded to the backbone carbonyl of Asn-514 while maintaining interaction with the water molecule positioned near the flavin N(1). Both structures indicate that N^ɛ of His-559 forms a strong hydrogen bond to the carboxylate of Glu-412 (2.64 Å) and N^δ is close to the water molecule (2.51 Å). The proximity of His-559 to Glu-412 implicates a strong dipolar interaction that presumably causes the pKa of His in the reduced enzyme to be elevated to outside of the range studied. If it is assumed that the active site of the reduced enzyme is similar to that depicted in Fig. 2, the dipolar network should facilitate O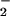 formation in the pocket occupied by Wat-110. It is expected that the dipolar network be altered at high pH where H516 is neutral and in the mutant where Ala is substituted for His.

Fig 2.

Active-site residues and conserved water molecule relative to the bound flavin in oxidized GO. (Structure from ref. 7.)

Ionic interaction with H516H⁺ makes FADH⁻ a thermodynamically less potent reductant. Removal of the positive charge effected by changing the pH or mutagenizing His to Ala makes the FADH⁻ more reducing toward O₂. As expected on the basis of similar redox potentials, the high pH form of WT GO and the H516A mutant show k_cat/K_M(O₂) values that are close to the k_ET = 1.3 × 10³ M⁻¹⋅s⁻¹ observed for the reaction of deprotonated 5-ethyl lumiflavin with O₂ in aqueous solution (51). Contrary to expectations, however, GO reacts fastest under acidic conditions where H516 and His-559 are protonated. This is also true to some extent for the mutant where His-559 presumably remains protonated.

Energetics of Electron Transfer.

The considerations outlined above indicate that the mechanism of the oxidative half-reaction in GO is an extraordinarily simple process where O₂ diffuses into the active site and reacts by rate-determining electron transfer. Analysis of rate constants as a function of temperature indicates a 6.0-kcal⋅mol⁻¹ (0.26 eV) difference in the E_a terms of E(FADH⁻, HisH⁺) and E(FADH⁻, His). The observation of pre-exponential factors (10⁸–10⁹ M⁻¹⋅s⁻¹), which are the same within experimental error, is taken to mean that electron transfers occur over short distances with similarly high probabilities for both enzyme forms (45). As a result, the difference in E_a from the temperature studies approximates the difference in ΔG‡. Ostensibly, the >10³ faster rate at low pH reflects the sensitivity of the free energy barrier to the charge on His-516.

To understand the decrease in ΔG‡ at low pH relative to high pH, the electrostatic effects on ΔG°′ and λ must be resolved. Analysis of the electrochemical data allows comparison of ΔG° for the two enzyme forms (30). A one-electron reduction potential for [E(FADH^•, HisH⁺)] of E°′ = −0.065 V vs. NHE has been determined at pH 5.3. This value was originally attributed to a proton-coupled process because at the time of measurement it was not known that FADH⁻ existed as an anion at this pH (50). The reported E°′ = −0.242 V vs. NHE at pH 9.3 corresponds to a proton-coupled reduction. The proton-uncoupled potential is calculated by assuming Nernstian behavior (52) and correcting the observed potential for the ionization of the flavin semiquinone (pKa = 7.3) determined in GO (30) (see Figs. 3–6). This gives E°′ = −0.12 V as the pH-independent reduction potential for [E(FADH^•, His)]. Thus, the reduction potentials for the two enzyme forms differ by only 0.055 V (1.3 kcal⋅mol⁻¹), which is comparable to the effect of charge at N(1) of the flavin on the pKa for the active site His (≈0.9 pKa unit or 1.2 kcal⋅mol⁻¹) (see Figs. 3–6). The pKa of the reduced flavin in GO is perturbed ≈3 pKa units from its value in aqueous solution (10), implicating factors other than protonation of His-516 in FADH⁻ stabilization. Note that the effect of His protonation on the flavin E°′ is opposite to the observed change in ΔG‡ of 6.0 kcal⋅mol⁻¹.

The Nature of Electron Transfer Catalysis.

It has been proposed that electrostatic stabilization of O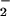 is responsible for catalysis of the oxidative half-reaction in GO (26, 27). In the active site, interaction with HisH⁺ may provide substantial stabilization to O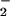, making the reaction driving-force greater than anticipated based on the reduction potentials (above). The interaction energy is essentially a correction to the reduction potential for conversion of O₂ to O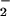, E° = −0.16 V vs. NHE (53). The result is Eq. 6, which is analogous to Eq. 4 except that the w_R term is now contained in the measured reduction potential of E(FADH^•, HisH⁺).

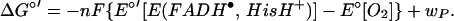The value of w_P is difficult to address computationally as it requires knowledge of active-site dielectric and charge screening effects (54, 55). Eqs. 7a and 7b give w_R and w_P within the continuum electrostatics approach (56). The free energies are a function of ionic charges (q_iand q_j), interaction distance (r), screening factor (f_ij), and static dielectric constant (ɛ_s) of the surroundings. The term ɛ₀ is the previously described permittivity of vacuum.

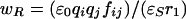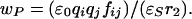Here w_P is estimated from w_R and the ratio of interionic distances r₁ and r₂. In comparing the stabilizing influence of HisH⁺ on FADH⁻ (w_R) to that of HisH⁺ on O (w_P), the values q_i and q_j are constant. If f_ij/ɛ_s is assumed constant, then the ratio r₁/r₂ is directly proportional to w_R/w_P. The x-ray crystal structure (7) indicates that r₁ ≅ 4 Å from the center of the charged ring of the flavin to the proton on N(ɛ) of His-516. A close contact distance of r₂ = 1.5 Å is assumed for the same proton and O. This approach, rather than one based on the edge-to-edge distance between charges, was used to maximize the calculated effect on O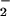. The distances above, together with w_R = −1.3 kcal⋅mol⁻¹ estimated from the 0.055 V difference in FADH⁻ reduction potentials at high and low pH, give w_P = −3.5 kcal⋅mol⁻¹. The resulting shift in electrochemical potential (+0.15 V) is in good agreement with measured effects of noncoordinating cations on the one-electron reduction of O₂ in organic solvents (53, 57).

Table 1 summarizes the kinetic and thermodynamic properties of WT GO as a function of solution pH. The electrostatic stabilization of O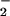 by E(FADH^•, HisH⁺) changes the effective free energy of reaction (Eq. 6) from ΔG°′ = 2.2 kcal⋅mol⁻¹ to ΔG°′ = −1.3 kcal⋅mol⁻¹. Note, however, that this difference cannot account for the 10³-fold rate acceleration over E(FADH⁻, His). Calculations performed with Eq. 2 and corrected values of ΔG°′ (Table 1) indicate that for E(FADH⁻, HisH⁺) λ is decreased by 19 kcal⋅mol⁻¹. The effect is caused by a change in λ_out because, by definition, λ_in is pH independent. Furthermore, because the electron transfers are concluded to occur over similar distances from the A factors (Table 1), the change in λ_out may reflect a change in [1/ɛ_op − 1/ɛ_s] of Eq. 5, the parameter decreasing as the pH is lowered. An alternative explanation based on reaction driving force would require an unusually large correction factor (w_P = −13.5 kcal⋅mol⁻¹) for the stabilization of O 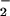by a positive point charge (54, 58). Such a large change would be expected to have a significant impact on the O-18 KIE, inconsistent with the virtually identical ¹⁸V/K values for E(FADH⁻, HisH⁺) and E(FADH⁻, His). Thus, studies of GO provide compelling experimental evidence that changes in the reorganization energy as a function of pH correlate with enzyme-catalyzed reduction of O₂.

Table 1.

Kinetic and thermodynamic data for WT GO

	E(FADH−, His)	E(FADH−, HisH+)
kcat/KM (O2)a,b	(5.7 ± 1.8) × 102	(1.5 ± 0.3) × 106
Ea (kcal⋅mol−1)	9.0 ± 1.0	3.0 ± 1.0
ln Aa,b	20 ± 4	22 ± 3
ΔH‡ (kcal⋅mol−1)c	8.3	2.3
ΔS‡ (cal⋅mol−1⋅K−1)a,d	9.0	9.0
ΔG‡ (kcal⋅mol−1)a,e	11.0	5.0
E°′ (V) vs. NHEf	−0.120	−0.065
ΔG°′ (kcal⋅mol−1)a,g	0.92h	−1.3i
λ (kcal⋅mol−1)j,k	42 (28–56)	23 (13–33)

At 298 K.

Units of M⁻¹⋅s⁻¹.

ΔH^‡ = E_a − RT.

Calculated from ΔS^‡ = ln(A/κZ) × k_B with κ = 1, Z = 10¹¹ M⁻¹⋅s⁻¹ and ln A = 21.

ΔG^‡ = ΔH^‡ − TΔS^‡.

pH-independent reduction potentials.

From Eq. 6 and E°(O₂) = −0.16 V vs NHE.

W_P = 0 kcal⋅mol⁻¹.

W_P = −3.5 kcal⋅mol⁻¹.

From Eq. 2, ΔG^‡ and ΔG°′ given in the table.

Range corresponding to the 2σ errors in ΔG^‡ is given in parentheses.

Conclusions

The present study provides a rare glimpse of the influence of protein environment on O₂ activation. Two distinct forms of GO react with O₂ by mechanisms of electron transfer at both high and low pH. Rate constants differ by more than 3 orders of magnitude in a direction that is opposite to the 0.055-V difference in flavin reduction potentials. Site-directed mutagenesis studies, coupled with the analysis of the temperature dependence of rate constants, uncover a 6.0-kcal⋅mol⁻¹ barrier-lowering effect caused by protonation of a single histidine residue in the active site. Within the context of Marcus theory, this corresponds to a 19-kcal⋅mol⁻¹ reduction in λ_out and only a modest 2.2-kcal⋅mol⁻¹ enhancement of ΔG°′.

O-18 KIEs are increasingly being used to elucidate redox changes at O₂ during enzyme catalysis (41). The large isotope effects on the reactions of E(FADH⁻, His) and E(FADH⁻, HisH⁺) indicate similar free energies of reaction, consistent with the analysis of the electrochemical data and the interpretation of O-18 KIEs within the framework of electron transfer theory. The possibility that nuclear tunneling during electron transfer (44, 59) is the physical origin of the oxygen KIE is presently under investigation. Because of its simplicity, this system should provide unprecedented insights regarding the barrier to O₂ reduction and the influences of temperature and driving force on KIEs.

Flavoprotein oxidases catalyze the activation of O₂ at rates that generally exceed the analogous solution-phase reactions by 3 orders of magnitude. The specific role of the protein during these reactions has not been understood (10, 49). van Berkel and coworkers (60) suggested that the sampling of highly reactive conformational states of the flavin accounts for the 10³ greater aerobic reactivity of FADH⁻ in p-hydroxybenzoate hydroxylase compared with the reaction in solution. A recent mechanistic study by Xu and Gunner (61) of photosynthetic reaction centers proposes that electron transfer between quinones is gated by a pH-dependent conformational change. With regard to GO, x-ray studies at pH 5.6 and 7.4 show nearly identical active-site conformations consistent with the majority of enzyme existing in the E(FADH⁻, HisH⁺) form (50). At elevated pH where the catalytic His-516 is deprotonated, loss of this key charge is likely to cause an increase in conformational flexibility at the active site and, consequently, an increase in the reorganization energy for electron transfer. In this manner, the protein's dielectric properties at high pH may resemble a polar solution, whereas at low pH the active site imposes a more rigid and structured network of dipoles. Our results on GO are consistent with theoretical studies, which suggest that proteins can enhance rates by preorganizing their active sites to minimize molecular reorientations during charge transfer (20, 36). We propose that enzymes that use nonmetal cofactors to activate O₂ are likely to have strategically placed charged amino acids that optimize the protein dielectric for electron transfer.

Abbreviations

• GO, glucose oxidase

• KIE, kinetic isotope effect

• O-18 KIE, oxygen-18 KIE