Fast protein folding kinetics

Abstract

Fast folding proteins have been a major focus of computational and experimental study because they are accessible to both techniques: they are small and fast enough to be reasonably simulated with current computational power, but have dynamics slow enough to be observed with specially developed experimental techniques. This coupled study of fast folding proteins has provided insight into the mechanisms which allow some proteins to find their native conformation well less than 1 ms and has uncovered examples of theoretically predicted phenomena such as downhill folding. The study of fast folders also informs our understanding of even “slow” folding processes: fast folders are small, relatively simple protein domains and the principles that govern their folding also govern the folding of more complex systems. This review summarizes the major theoretical and experimental techniques used to study fast folding proteins and provides an overview of the major findings of fast folding research. Finally, we examine the themes that have emerged from studying fast folders and briefly summarize their application to protein folding in general as well as some work that is left to do.

1. Introduction

Small globular proteins and peptides can fold very rapidly into their native structural ensemble (Jackson & Fersht, 1991). For this reason, they have received much attention as model systems from the protein science community (Kubelka, Hofrichter & Eaton, 2004). Experimental techniques have been developed to look at the fast (from an experimental point of view) time scales of microseconds or even nanoseconds necessary to study such proteins (Gruebele, 1999). Computational techniques have developed to look at the slow (from a computational point of view) timescales of microseconds and even milliseconds necessary to study such proteins (Zagrovic et al., 2002; Lindorff-Larsen et al., 2011). And a coarse grained statistical mechanical framework has been developed that ties experiment and computation together (Bryngelson et al., 1995; Dill et al., 1995). We are now in a new era where experiment, simulation and theory all overlap, allowing for rich comparisons, and teaching us where additions and refinements are needed to achieve the holy grail: an algorithm that describes the structure and dynamics of a globular protein from first principles based on its sequence, post-translational modifications, and solvation environment.

Small proteins fold fast for several related reasons. A short polypeptide chain obviously reduces the configurational search space, but there is more to it than that. Small size helps avoid imperfections that are intrinsic to the folding process. Protein folding has to work with a limited alphabet of about 20 amino acids. That is better than the four nucleobases available to RNA, but still makes energetic and structural imperfections unavoidable as chain length increases. As an example of structural imperfection, consider the old adage about ‘proteins fold into 3-dimensional structures.’ A truly three dimensional object can be arranged to completely pack a three dimensional volume. Analysis of the full Protein Data Bank (Berman et al., 2000) has shown that proteins are actually fractals with a dimension between 2.5 and 2.8 (Liang & Dill, 2001; Enright & Leitner, 2005). The reduced dimensionality of protein structures indicates that peptide sequence conformations are constrained. The constraint arises from the fact that a finite alphabet of amino acids cannot perfectly satisfy all packing requirements of a connected polypeptide chain, leaving ever larger voids of missing contacts in the structure as the chain grows (Chowdary & Gruebele, 2009). As an example of energetic imperfection, it is impossible to minimize the local free energy of every residue when the overall free energy of the protein is minimized. The effect is commonly called “frustration” (Panchenko, Luthey-Schulten & Wolynes, 1996). One consequence of frustration in protein folding is the existence of so-called “traps,” long-lived non-native states of relatively low free energy. The longer the protein sequence, the more likely there are to be unfavorable interactions which cannot be simultaneously eliminated by protein evolution or engineering. Fixing one ‘problem’ creates another. Each residue in a protein chain comes with its own set of competing requirements – only for small proteins do we have any chance at satisfying the requirements of all sidechains at once.

Initial investigations of protein folding focused on elucidating how proteins could possibly fold so quickly – on the order of seconds or minutes for most proteins (Levinthal, 1969). With the discovery of proteins folding in < 1 ms, in recent years attention has shifted towards discovering why most proteins fold “so slowly.” Since competing energetic and structural demands slow down the speed at which proteins find their free energy minimum, how fast might proteins fold if frustration were eliminated? Small proteins, with their minimally frustrated folding landscapes, can approach the speed limit for folding. The exact definition of the speed limit depends on the level of structural coarse-graining (Hagen et al., 1996; Liu & Gruebele, 2008). For example, at a very low level of coarse graining, many microscopic coordinates describe the system at the level of individual molecules and bonds. At this level of description, an ensemble of side chain torsions and their attendant interacting water molecules may mark the bottleneck of lowest population flux (the definition of a transition state) between denatured and folded states; such motions occur in picoseconds and this sets the ultimate “speed limit” for folding. From a biological perspective, it makes more sense to coarse grain to the level of loops and secondary structure elements forming and making tertiary contacts; then the fastest possible time scale is a fraction of a microsecond. Low-dimensional models of folding with one or a few reaction coordinates are naturally coarse grained to the biological level, and thus the fastest time scales of hopping from state to state are microseconds and barriers are low (less than a few tens of kJ/mole for fast folders). High dimensional models with many microstates hop between individual states much faster, but the overall folding speed remains the same: the time is now spent hopping rapidly but unproductively among microstates until one connected to the native ensemble is found (Fig. 1). Though proper coarse graining, necessarily, does not change actual observables such as the folding time, it does change our description of the folding process. In the coarse grained perspective, protein folding looks like a slow passage between macrostates, while the detailed folding pathway appears to be dominated by slow entropic search within a group of microstates, interrupted by rare transitions “forward” (and occasionally “backward”) in the folding pathway.

Fig. 1. Macro- and microstates.

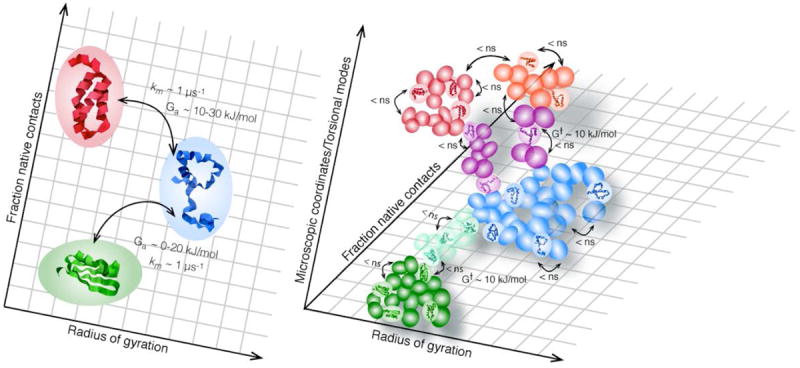
(a) Kinetics coarse grained to the level of secondary and tertiary structure formation, the level of resolution probed by many fast folding experiments. Shown is a folded macrostate (green), an unfolded macrostate (blue) and a compact helix-rich trap (red). k_a = k_m exp(-G_a/RT) is analogous to the Arrhenius equation in the main text. The prefactor k_m^-1 = τ_m, the inverse of the molecular time, is the rate for crossing from one macrostate to another in absence of a barrier (G_a≈0) (b) A very fine grained picture, including backbone torsional angles and side chain conformations, reveals each macrostate as an ensemble of many structurally related microstates. Microstates typically interconvert in a nanosecond or faster, with barriers G^† ≈ 10 kJ/mole and prefactors ≈ 1 ps (for torsional angles). The vast majority of these micro-conversions leave the protein in the same macrostate; the protein is “waiting,” not “folding.” Eventually, through thermal fluctuations, the protein finds “bottleneck” microstates (purple and turqoise). Not all motion within this transition state ensemble (TSE) is productive because there are so many coordinates the protein can stray in. Thus when motion through the TSE is projected onto a few macroscopic coordinates, the crossing takes τ_m ~ 1 μs instead of nanoseconds or less. This delay is often modeled as friction (of the protein with itself or solvent), although some of the microscopic processes involved may have barriers G^†. In analogy to the example from classical kinetics in the text, the splitting of the observed rate k_a into prefactor (e.g. friction) and Boltzman factor (G_a) depends on the choice of macro coordinates.

This ambiguity of reaction time scales is not unknown even in basic chemical kinetics: there the Arrhenius rate coefficient can be written as

$$k=A{e}^{­E_a/\mathit{RT}}=\mathit{ZW}{e}^{­E_a/\mathit{RT}}$$

where A is the Arrhenius prefactor, Z is the collision frequency (typically picoseconds), E_a is the activation energy, R=0.00831 kJ/mole and T is the temperature in Kelvin. W≤1 is the steric factor, which accounts for the observation that not every collision is correctly oriented to produce a product, even if the energy exceeds the activation energy. Rewriting W as exp(lnW) and combining the two exponential terms, we get

$$k=Z{e}^{­(E_a­\mathit{TR}\ln W)/\mathit{RT}}.$$

Finally, defining S_a=RlnW, this becomes

$$k=Z{e}^{­(E_a­T{S}_a)/\mathit{RT}}=Z{e}^{­G_a/\mathit{RT}}$$

So, is the speed limit of the reaction A and the barrier the energy E_a, or is the speed limit the much larger value Z, and the barrier the much larger free energy barrier G_a? The argument is pointless because the observable k is the same in both cases, and as long as we know where the steric factor is absorbed (into the prefactor or into the activation barrier) the models are equivalent. In the case of folding, self-friction, solvent interactions and heterogeneous transition ensembles (multiple reaction coordinates) complicate the analysis of prefactors and barriers (Lee et al., 2003; Hummer, 2005; Chahine et al., 2007; Best & Hummer, 2010). The resulting debates in the literature are a good sign: experiments are getting more informative, and models more detailed so that soon one-dimensional pictures will no longer suffice (Liu et al., 2009a; Scott & Gruebele, 2010).

An attempt to clarify the physics behind the prefactor was made by Eaton and co-workers in series of papers examining the effect of solvent viscosity in the folding kinetics of a variety of proteins (Ansari et al., 1992; Jas, Eaton & Hofrichter, 2001; Cellmer et al., 2008). There, the folding rate is modeled as

$$k=\frac{D}{s+h}{e}^{­E_a/\mathit{RT}}$$

where D is the diffusion constant across the activation barrier, σ is the internal friction of the protein, which acts as its own solvent during folding, and η is the solvent viscosity. Other formulas that scale as powers of viscosity have also been proposed. The dependence of the folding rate on η is in turn dependent on the relative value of the internal friction σ: in regimes where σ is much greater than η, the rate is insensitive to the solvent viscosity, while in regimes where η is much greater than σ there is a straightforward inverse dependence (Ansari et al., 1992). While this analysis provides some extra information about the contributions to the prefactor, the basic problem remains the same. A coarse-grained model will have slow diffusion across the barrier (small D and E_a), corresponding to relatively slow rearrangement of secondary structure elements, while a fine-grained picture will highlight fast rearrangements of atoms and bonds in the transition state (large D and small E_a).

Due to their complexity, proteins offer researchers many candidates for reaction coordinates that can track the folding process – e.g. percent of native contacts formed, backbone deviation from the native structure (Cα-RMSD), or the completeness of hydrophobic packing. Despite this complexity, many folding reactions have been well described relying on only 1 reaction coordinate, usually an easily measured experimental observable, in a so-called 1 dimensional analysis. The cooperativity of many folding reactions is what allows this simplification (see Section 4.2 for an extended discussion). Despite this success, improved experimental and computational techniques now allow the study of more complex systems like larger proteins or faster dynamics. It is increasingly clear that these systems are not, in general, well described by a single reaction coordinate and must be treated as depending on multiple coordinates at once – as multidimensional processes. Developing a general technique for determining and measuring the relevant reaction coordinates is a challenge for both experimental and computational studies.

The major hurdle to quantitatively comparing experimental and simulation studies of protein folding also lies in the choice and development of reaction coordinates. Experimental reaction coordinates probe only very global (e.g. FRET distances, radius of gyration) or very local (e.g. amino acid fluorescence) properties of protein unfolding, and no single probe provides a complete description of the folding process. Many experimental coordinates are extremely difficult to simulate. Theoretical reaction coordinates, on the other hand, can be difficult to measure with fast time resolution in the lab (e.g. the percentage of native contacts, or the a carbon root mean square deviation from the native structure). Finding a set of easily measured and simulated reaction coordinates which can capture the global and local behaviors of proteins will be crucial in allowing the comparison of experiments and models at a finer level of detail than has been possible so far.

In section 2 this review will go over computational and experimental techniques developed to study fast folders (proteins that fold to the native state in substantially less than a millisecond). Then those fast folders for which considerable experimental and computational data has been amassed will be briefly but critically reviewed in section 3. Section 4 lays out some of the useful concepts that have emerged to describe fast folding reactions, tying them together with the experimental data and simulations. Both experiment and simulation now can be understood in terms of simple concepts. Finally, we take a look at future developments. Some work that needs to be done has already been hinted at in the previous paragraph.

2. Learning from Simulation and Experiment

Dissecting the folding process of any protein requires the implementation of varied experimental and computational techniques. The difficulty is only increased when studying fast-folding proteins: the processes become more complex to analyze when the timescales of prefactors and activated folding approach each other. Studies of fast folders have not only employed all of the existing techniques for elucidating the folding process, but have also contributed new tools that are applied to varied biomolecular systems. Here we briefly review some of the most widely used techniques to study fast folding proteins, referring whenever possible to their application in the studies of the model proteins discussed below. This is by no means a complete list of techniques used to study fast folders – others are mentioned in the reviews of model proteins as they are applied.

2.1 A range of coarse grained models

The coarse grained description of protein folding described above sacrifices molecular details of the folding process for conceptual accessibility. Different coarse graining models represent different perspectives on the most meaningful parameters for describing the steps of protein folding. We will see that different choices for coarse graining highlight different aspects of the folding process. The evolution of coarse-grained models and their conceptual diversity is highlighted nicely by the progression from lattice models to Markov state analysis.

When computational resources were limited in the late 80s to late 90s, lattice simulations were the first simulations to connect ‘microstates’ and ‘macrostates.’ Lattice simulations model proteins as a sequence of balls, representing amino acids, connected by straight rods. The rigidity of the connecting segments (enhanced by restrictions on the allowable angles between segments) forces the model amino acids to sit at vertices of a grid. Thus both the molecular details and the conformational space have been coarse grained, in this case by brute force simplification. The interactions between residues can be modeled with a simple distance-dependent potential, or the complexity can be increased by implementing residue specific potentials. The geometric and mathematical simplicity of the system allowed simulations of protein folding well before computational power allowed for the simulation of real protein sequences in real solvent. Such models revealed that some folded states are not kinetically accessible from the denatured state (Shakhnovich et al., 1991), and folding rates are maximized at a special temperature (Socci & Onuchic, 1995).

A related strategy derives from helix-coil theories developed in the 50s and 60s (Poland & Scheraga, 1966), although in this case the coarse graining is kinetic instead of explicitly structural: the system is reduced to coupled kinetic master equations, each responsible for formation of a structural element. Such models have been extended to analyze the folding of small, fast folding proteins, including beta sheet or helix zipping (Muñoz & Eaton, 1999). The modern hidden Markov state analysis is now based on all-atom molecular dynamics, but uses the same underlying idea: the seemingly continuous distribution of structures in a simulation can be grouped into ensembles so that conversion within the ensemble is very fast, but conversion among the ensembles is slow because of bottlenecks. Helix-coil theories start with the assumption that the relevant ensembles are distinguished by their degree of secondary structure formation, while Markov state analysis builds up the ensembles via analysis of simulation trajectories. A good example is the Markov model for WW domain by Noé and coworkers (Noé et al., 2009) (Fig. 2). This small triple-stranded beta sheet protein is often approximated as a two-state folder in experimental analyses (Jäger et al., 2001). Although the protein folds by a consensus path (the formation of loop 1 connecting beta strands 1 and 2 is rate-limiting), Markov state analysis of trajectories shows that alternate paths are visited by a fraction of the proteins – the secondary structure of a conformation does not fully determine its place in the folding pathway. The principle of Figure 1 applies here, too: at higher resolution, 9 ensembles of states play a role, but upon strong coarse graining, just two ensembles connected by a single path account for the majority of population flux (Fig. 2).

Fig. 2. Multiple pathways for folding.

A more fine-grained analysis does not have to go all the way to torsions of the backbone and sidechains. The left shows a simplified network of ‘mesostates’ from the hidden Markov analysis in (Noé et al., 2009). The denatured ensemble moves through a network of states, some of which directly convert to the native state, others reaching the native state through alternative routes, including a trap accessible from both denatured and native states. Upon strong coarse graining and elimination of minority paths, a two-state interconversion from a denatured ensemble to the native state accounts for most of the experimentally observed dynamics. An experiment that probes only a low-resolution reaction coordinate (e.g. tryptophan fluorescence upon T-jump), may be satisfactorily explained by the scheme on the right, but data with more resolution (e.g. e,g. 2-D IR) may require a more mesosocopic level of description.

Molecular dynamics force fields have also been coarse grained directly (Tozzini, 2005). Although folding can now be simulated at the all-atom level, coarse-grained force fields or force fields modified by Go potentials (where a bias towards the known native state is built-in) can still be very useful in conducting low-resolution exploration over longer time scales (Pogorelov & Luthey-Schulten, 2004). Off-pathway or rare ensembles revealed may provide target ensembles for more costly full-atom simulation. Even as all-atom computation speeds up, there are always larger and slower-folding proteins around the corner.

2.2 Enhanced sampling methods in molecular dynamics

The promise of simulations for the study of both the native structure and folding dynamics of proteins and peptides has been recognized from the beginning of fast folding studies (Duan, Wang & Kollman, 1998). Up until very recently, limits on computational power ruled out simulation of real-time folding dynamics of even the smallest proteins (see section 2.3 for recent advances). Simplifying the protein-solvent system can reduce the computational cost of simulations. For example, distance cutoffs can be applied to electrostatic interactions and atomic solvent resolution can be exchanged for implicit solvent representations that treat the solvent as an embedding dielectric (Freddolino et al., 2008; Klepeis et al., 2009). More sophisticated techniques take advantage of parallelization to run multiple simulations at once to sample a greater range of conformations. The innovations of these techniques lie in different approaches to utilizing multiple simulations.

Either due to the roughness of the free energy landscape, or errors in force field parameters that deepen non-native free energy minima relative to the native state, protein folding simulations often get “trapped” in non-native states (Sugita & Okamoto, 1999; Freddolino et al., 2008; Piana et al., 2012). Replica exchange molecular dynamics (REMD) seeks to break out of these traps to better drive the simulation to the true native state. Many simulations (“replicas”) of the same protein are run simultaneously at a range of temperatures. At regular time intervals the momenta between two neighboring temperature replicas may be exchanged. The momenta are normalized by the initial and final temperature so that the average kinetic energy remains 3/2 k_BT per atom after exchange, but the momenta of individual atoms may change. This change can give the system the kick it needs to find the native state. Indeed, replica exchange simulations sample wider regions in conformational space and have lower average potential energy than conventional simulations at low temperatures (Hansmann, 1997; Sugita & Okamoto, 1999). Proteins are less likely to settle into traps in high temperature simulations, so replica exchange and conventional simulations are more similar to one another at higher temperatures.

Markov state modeling (MSM), already mentioned in 2.1, also employs parallel simulations. In MSMs, many short simulations are conducted simultaneously under identical conditions (except for the starting conformation of the protein, which are drawn from a weighted equilibrium ensemble). An MSM is constructed by analyzing the transitions that occur, by chance, during the short simulations. Conformations which quickly exchange over low barriers are grouped together into “mesostates” (moderate coarse graining) or “macrostates” (more coarse graining) (Fig. 2). Conversion between meso- or macrostates takes place more slowly than intra-state conversion: as shown in Fig. 1, entropy favors random exploration of microstates within a single macrostate over discovery of the few microstates that allow exiting to another macrostate. Meso- or macrostates are metastable. The kinetic clustering of MSMs allows the reconstruction of possible intermediate structures in the folding pathway, as well as the structural distribution within such meta-stable states (Bowman et al., 2009; Bowman, Voelz & Pande, 2010). Difficulties in constructing MSMs that can guide experimentalists lie in constructing appropriately weighted macrostates and in piecing trajectories together to calculate transition probabilities between macrostates (Bowman et al., 2009). Of course the resulting networks of states are limited by the accuracy of the molecular dynamics structural sampling from which they emerge, so MSMs are affected by force field errors just like conventional simulations.

2.3 Full solvent, all atom trajectories

Rapid increases in computational power and increased parallelization have led to the feasibility of conducting full solvent, all-atom simulations that can resolve dynamics on timescales of a millisecond or longer. These simulations are especially good at highlighting force field errors and force fields must be carefully optimized to avoid long-lived traps or unphysical native states (Freddolino et al., 2008; Raval et al., 2012). The difficulty of eliminating these states highlights an important feature of the protein free energy surface: several structurally distinct states lie at low free energy, separated only by a few RT units of free energy; even small computational inaccuracies may switch the native ground state with an excited misfolded state, creating a false native state. For example, the free energy surface of WW domain calculated using CHARMm22 with CMAP corrections has a helical ground state while the actual native beta sheet structure lies at higher energy. It is likely that the true free energy surface of WW domain does have a low-lying helical state, in addition to the true beta sheet ground state (Freddolino et al., 2008). Such alternative states of fast folding proteins have been observed experimentally by tuning the free energy surface via alteration of solvent conditions or selective mutation of protein sequence (Kim et al., 2009).

A recent paper compared experimental and simulated folding of 12 fast folding proteins using long, single trajectories. In most cases, the simulated trajectories agreed well with folding mechanisms proposed experimentally. In a few cases, the simulated trajectories can act to shed light on controversies that cannot be resolved via experiments due to the limited detail presented by experimental data (Lindorff-Larsen et al., 2011). These simulations will be discussed in more detail in Section 3.

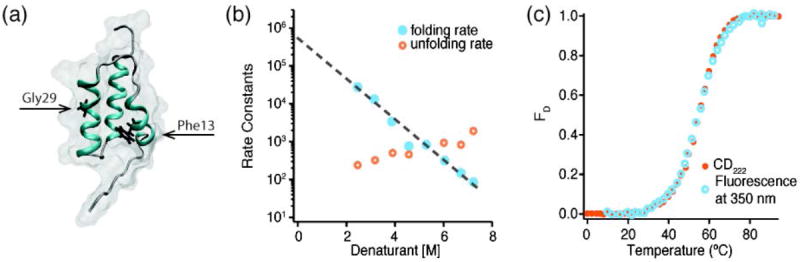
2.4 Thermodynamic experimental characterization

The desire to study fast folding processes in detail has led to the development of time resolved techniques fast enough to observe even sub-microsecond dynamics. Despite these technological innovations, it remains important to study fast folding proteins using steady-state, thermodynamic methods. The results of such studies provide boundary conditions by characterizing the most stable states of a protein. Many of these methods belong to the general biophysical toolbox: circular dichroism (CD), intrinsic fluorescence, infrared (IR) absorption, NMR chemical shifts and differential scanning calorimetry probe different experimental reaction coordinates as a protein is stressed by heating through its melting transition (Privalov, Khechinashvili & Atanasov, 1971), pressurizing it to unfold (Hawley, 1971), or exposing it to increasing concentrations of denaturant (Hopkins, 1930). Thermodynamic information allows the calculation of denaturation midpoints and provides information about the unfolding process.

The shape of the thermodynamic denaturation curves is related to the cooperativity of the protein folding transition, while comparison between different spectroscopic probes can give information about the number of stable intermediates (Garcia-Mira et al., 2002; Fung et al., 2008). Interpreting thermodynamic denaturation curves requires careful consideration of all possible sources of signal change under stress. For example, many proteins exhibit a non-zero signal baseline at low and/or high stress conditions – far from the folding-unfolding transition. Baselines can arise from two causes. First, the reaction coordinate being probed (e.g. fluorescence lifetime) may have an intrinsic dependence on the stress applied (e.g. temperature). Such a baseline has nothing to do with the folding process and can be subtracted without affecting the data interpretation. Alternatively, the native or other ensembles may structurally shift when a stress is applied (Fig. 3). In this case, the signal is shifting because the stress has modulated the protein’s energy landscape, moving the low energy basins to new locations in conformational space. In this context, it is important to note that strict two-state folding should have no native or denatured state baselines: the native and denatured wells stay fixed in conformational space while population moves between them. When baseline shifts are small we can still talk about a two-state transition. When they become very large, non-cooperative processes significantly participate in the folding thermodynamics and must be accounted for in the analysis of thermodynamic or kinetic data. In extreme cases, only a single native or denatured well may exist, and the protein no longer unfolds through population transfer between distinct states (Bryngelson et al., 1995). This is called “downhill folding in free energy” because there is no free energy barrier to folding (or unfolding) when the environment is changed to favor the native or denatured state: the protein only moves downhill in free energy to reach the new low energy state (see Sections 3 and 4 for further discussion of downhill folding). The first identification of downhill folding all the way to the native state was made by observing probe-dependent thermodynamics with large baselines (Garcia-Mira et al., 2002).

Fig. 3. Characterization of equilibrium ensembles.

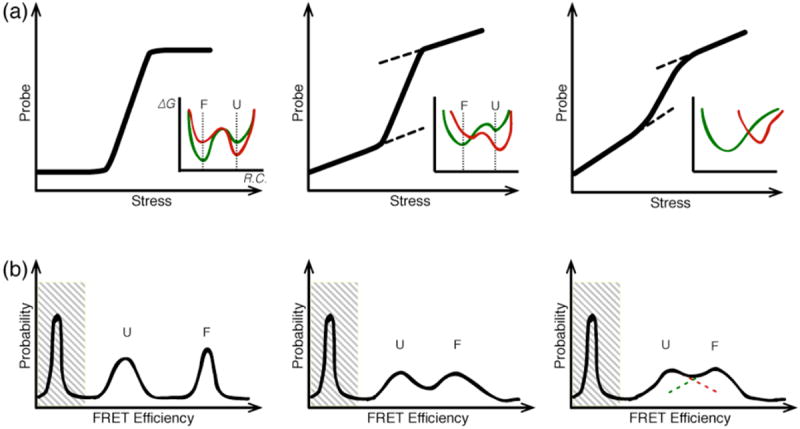
(a) Schematic denaturation curves characteristic of two-state to downhill folding mechanisms. The inset shows the free energy landscape as a function of reaction coordinate ‘R.C.’ Under low stress (green), the folded state ‘F’ is more stable, under high stress (red), the unfolded state is more stable. Low stress = physiological condition, or absence of denaturant. Consider the case where the probe signal depends upon R.C., but not on the stress. (Top Left) An ideal two-state folder should not have a folded or unfolded baseline because the location of the folded and unfolded basins does not move significantly upon stress. (Top Center) Significant folded and unfolded baselines indicate the presence of shifting F and U free energy minima upon stress; the barrier is much lower, but one could still approximately call this a two-state folder. (Top Right) As the baselines get steeper, it becomes difficult to distinguish the transition from folded to unfolded. In the most extreme cases (as shown in the inset), this corresponds to a single-well landscape. The protein population unfolds not over a barrier, but by diffusion as the well moves along R.C. (b) Schematic single-molecule distributions at the denaturation midpoint for the scenarios in (a). As the protein deviates from two-state folding, the unfolded and folded peaks broaden and begin to overlap. On the right, it makes no sense to label the overlapping peaks as separate populations. The peak at low FRET efficiency arises from singly-labeled molecules and does not report on the protein’s conformational distribution.

In addition, different structure sensitive probes like CD or IR absorption can also shed light on the dynamics of folding. Robust folders may permit the incorporation of fluorescent amino acids (tryptophan) or fluorescent dyes (for FRET or triplet-triplet energy transfer) to provide new measurable reaction coordinates. Particularly when barriers are low, as is likely for small fast folders, different probes may switch at different stresses (e.g. have different melting temperatures during thermal denaturation), hinting as to which secondary structures melt first, or what residual or emergent structure is present in the denatured state (Liu & Gruebele, 2007).

In addition to experiments that drive the system out of equilibrium, single-molecule studies of equilibrium fluctuations provide thermodynamic information. These studies must be done near the thermodynamic denaturation midpoint, so that both the folded and unfolded ensembles are sampled by the molecules. A large body of work exists applying single-molecule techniques to probe equilibrium ensembles or to study slower protein dynamics using surface immobilization or laminar flow techniques (Schuler, Lipman & Eaton, 2002; Lipman et al., 2003; Kuzmenkina, Heyes & Nienhaus, 2005; Huang, Ying & Fersht, 2009). A more complete review of these techniques and their results can be found in a recent review by Schuler and Eaton (Schuler & Eaton, 2008). Particularly common are studies on FRET-labeled proteins, which reveal structural distribution as a function of the FRET efficiency E=A/(A+D), where A is the acceptor fluorescence and D the donor fluorescence. For true two-state folders, such analysis should reveal completely non-overlapping peaks at low (unfolded) and high (folded) FRET efficiency, whereas proteins with low or absent barriers will produce FRET distributions that are non-zero at all values of E (see Fig. 3b).

2.5 Sub-millisecond NMR spectroscopy

Early attempts to use Nuclear Magnetic Resonance (NMR) to study protein folding and unfolding were limited to the study of slow-folding proteins, as fast folders would undergo conformational changes during the scan time, smearing out the acquired NMR spectrum (Dobson & Hore, 1998). NMR lineshape analysis takes advantage of exchange-broadening to reconstruct the population exchange dynamics during the scan (Huang & Oas, 1995b). If we consider a single resonance (e.g. a histidine proton) with different chemical shifts in the folded (F) and unfolded (U) states we can see how lineshapes can give both thermodynamic and kinetic information about protein folding. If F and U interconvert slowly, two resonance peaks are observed; if they interconvert rapidly, a single peak at the average position is observed; in-between, two broadened peaks that merge at higher folding rate are observed. Folding and unfolding can be studied by this technique only near the denaturation midpoint, where a significant fraction of molecules can be found in both the folded and unfolded state. Kinetic information is extracted from the broadened lineshape, in a range dependent on spin relaxation (≈100 μs for protons) (Huang & Oas, 1995b). Theoretically, lineshape analysis could be conducted for every labeled residue in a protein, allowing a residue-by-residue reconstruction of unfolding. Analyzed residues, however, must have individually distinguishable peaks even in the unfolded state, which limits the number of positions that can be analyzed in practice. When lineshape analysis has been conducted for multiple residues in the same protein, the unfolding processes are usually similar (Wang et al., 2003). This may be because lineshape analysis can only be used for fast-folding proteins on the 100 μs time scale, which exhibit largely two-state folding (see below). NMR lineshape analysis was the earliest technique to directly observe full sub-millisecond folding of a small protein (λ repressor fragment, see below) (Huang & Oas, 1995b).

More recent developments in sample manipulation and data analysis have enhanced the ability of NMR spectroscopy to follow protein folding and equilibrium fluctuations with near-atomic, sub-millisecond resolution. The development of rapid-mixing techniques for NMR has allowed Hydrogen/Deuterium (H/D) exchange measurements to resolve changes in residue solvent exposure at sub-millisecond timescales. In these experiments, protein refolding is initiated by rapid mixing with deuterated refolding buffer and is allowed to proceed for a mixing time t_f. After t_f, the protein is diluted into a deuterated buffer optimized to promote hydrogen-to-deuterium exchange for a time t_ex. Finally, exchange is quenched with a buffer that slows proton exchange. The sample can then be analyzed by NMR (Uzawa et al., 2008) to extract information about the residues that exchanged protons during t_ex. Residues that undergo HD exchange during t_ex are called “unprotected” and are usually assumed remain unfolded after the mixing time t_f. By changing t_f and the efficiency of exchange during t_ex researchers can obtain sub-domain information about the pathway of refolding. Experiments using this technique have, in some cases, shown significant differences between the kinetically formed folding intermediate and an equilibrium intermediate populated under denaturing conditions, highlighting that the difficulty of determining the folding mechanism extends to experimental techniques as well (Nishimura, Dyson & Wright, 2008). Similar labeling schemes are also used in conjunction with proteolysis assisted mass spectrometry (MS) (Hu et al., 2013) instead of NMR to detect residues or regions subject to exchange. This data can be compared with kinetic data (see section 2.6 below) and structural information about the native state to construct detailed maps of protein folding.

Other advances in solution NMR have allowed the detection and, in some cases, the characterization of sparsely populated excited-state structures that are normally hidden by closely related ground state structures, by analyzing line broadening under different NMR pulse sequences (relaxation dispersion) (Neudecker, Lundström & Kay, 2009; Sekhar & Kay, 2013). In some cases these excited states have been identified as folding intermediates, while in others they are pathways to aggregation or possibly functional fluctuations in the equilibrium structure (Sekhar & Kay, 2013). In other cases, the effect of mutations on the occupancy of the excited state can be used to conduct ϕ-value analysis on difficult to isolate intermediate states (Cho et al., 2010). This technique has also been used to characterize coupled folding and binding reactions (Sugase, Dyson & Wright, 2007).

2.6 Sub-millisecond relaxation methods

Relaxation methods to study fast folding proteins have borrowed liberally from techniques developed in the 50s through 70s to study chemical reactions in real time (Eigen & Maeyer, 1963). They are based on the application of a sudden small perturbation (in temperature or pH, for example) to study the recovery of equilibrium. After the perturbation, the system will relax to a new equilibrium at a rate determined by the equation

$$\frac{\partial \mathrm{D}a}{\partial t}=­\frac{1}{t}\mathrm{D}a(t)$$

where Δα(t) is the distance from the old equilibrium and τ is an experimentally determined relaxation time. Δα₀ and Δα_∞ are known; they are, respectively, 0, by definition, and the equilibrium value of Δα at the final experimental condition. The system therefore evolves as

$$\mathrm{D}a(t)=\mathrm{D}{a}_{•}(1­e^{­t/t}).$$

One of the most fruitful relaxation methods for studying fast folding proteins has been laser induced temperature jumps. In this class of experiments, IR laser light is focused onto a sample, heating the water in the solution on picosecond to nanosecond time-scale (Phillips, Mizutani & Hochstrasser, 1995; Ballew, Sabelko & Gruebele, 1996; Williams et al., 1996). Fluorescence (either lifetimes or intensities) from intrinsic or extrinsic fluorophores can be monitored using a probe laser during the time before and after the jump (Phillips et al., 1995; Ballew et al., 1996). Other probes, such as IR absorption, may also be used to track relaxation after the jump (Williams et al., 1996; Dyer et al., 1998; Liu et al., 2009a). The deviation of kinetics from the single exponential described above is a sign that even the coarse grained description of the energy landscape must include more than just the native and denatured states. Downhill folders (discussed above) increasingly deviate from single-exponential kinetics as protein stability increases – this is another experimental signature used to identify downhill folders (see Figs. 5, 10 15b discussed in section 3) (Yang & Gruebele, 2003; Yang & Gruebele, 2004b). Most temperature jump experiments monitor unfolding as the protein is jumped across its melting temperature. For a two-state folder the measured relaxation rate (1/τ) is the sum of the folding and unfolding rates at the final temperature. Some experiments have investigated refolding from the cold-denatured state; in this case, an upward temperature jump favors refolding and the final state is more folded than the initial state (Ballew et al., 1996; Sabelko, Ervin & Gruebele, 1999).

Fig. 5. Villin headpiece.

Local and global unfolding can have individual spectroscopic signatures. Kinetic relaxation trace of the K24,29Nle stablilized mutant after T-jump from 343 to 348 K (black line is a bi-exponential fit). Arrhenius analysis of the slower phase yields a folding time of 730 ns at melting temperature (360 K). The fast phase is well fit to decay time of 70 ns at all jump temperatures (data modified from (Kubelka et al., 2006)). The fast and slow phases are attributed to local unfolding near the tryptophan probe and global protein unfolding, respectively. Inset shows the structure of the 35-residue domain (PDB 1YRF, (Chiu et al., 2005)). The highlighted residues show the 3 phenylalanine hydrophobic core of F6, F10, and F17.

Fig. 10. Cold shock proteins.

One member of the Csp family exhibits a downhill folding phase. (a) Structure of CspB from Bacillus subtilis (PDB 1CSP (Schindelin, Marahiel & Heinemann, 1993)). (b) Two phase unfolding of CspA from E. coli detected by IR absorbance in the amide I band after a temperature jump from 60 to 80 °C. The double exponential fit (red and blue) matches the data better than the single exponential fit (black). The fast relaxation (27 μs, red) is attributed to a minority downhill folding process (data adapted from (Leeson et al., 2000)).

Fig. 15. λ repressor fragment.

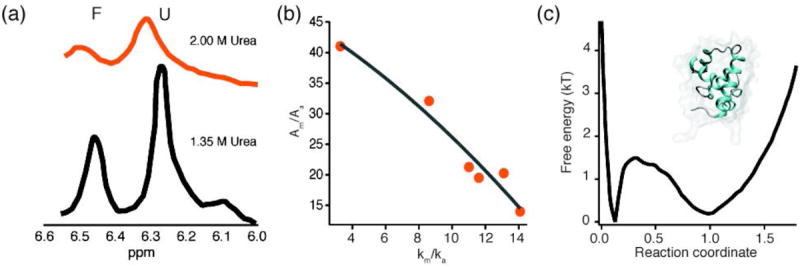
λ_6-85 downhill folding increases with protein stability. (a) NMR lineshapes at 1.35 M (black) and 2 M (orange) Urea. The folded peak amplitude decreases with increasing urea concentration (data adapted from (Huang & Oas, 1995b)). (b) The relative amplitude of the molecular phase (A_m/A_a) decreases when lambda repressor fragment is stabilized and the activated rate approaches k_m (data adapted from (Yang & Gruebele, 2004b)): when the barrier decreases towards downhill folding upon protein stabilization, the activated population becomes sizeable and reacts promptly upon T-jump. (c) Free energy landscape of λ repressor, calculated from molecular dynamics simulations. Note the extremely low barrier between the folded and unfolded states (data adapted from (Lindorff-Larsen et al., 2011)), in agreement with the experimental measurement (Yang & Gruebele, 2004b). Inset shows the structure of λ_6-85 (PDB 3KZ3 (Liu et al., 2010)).

High pressure is a denaturant, but was implemented only in steady-state or millisecond resolution experiments until recently. Large downward pressure jumps are a recent addition to the stable of sub-ms relaxation methods. Such jumps monitor protein folding, rather than unfolding. One study of pressure induced re-folding showed faster folding kinetics than were found with temperature jumps (Dumont, Emilsson & Gruebele, 2009). One suggested explanation for the discrepancy is that there is greater residual secondary structure in the pressure denatured state than in the temperature induced denatured state. The role of the denatured state in enabling fast folding is one of the major questions addressed by studies of fast folding proteins (see below).

While both temperature and pressure jumps change the thermodynamic environment of the protein, other methods change the chemical environment. Photoinduced pH jumps use the application of a laser pulse to induce proton transfer to or from a small molecule included in the reaction buffer. The proton transfer kinetics are extremely fast; the time resolution of a few nanoseconds is determined by shape of the pump laser pulse (Abbruzzetti et al., 2001a; Abbruzzetti et al., 2001b). As might be expected, pH jumps have been applied primarily to heme binding proteins (e.g. myoglobin and cytochrome C), where the pH change profoundly affects ligand binding affinity, and therefore the stability of the native state. Photochemically driven carbon monoxide desorption can also switch folded and denatured states of heme proteins rapidly (Jones et al., 1992; Mines et al., 1996). Similarly, in certain cases, laser excitation can induce chemical changes in the protein itself, which favor or disfavor folding (Chan, Hofrichter & Eaton, 1996; Pascher et al., 1996; Sabelko et al., 1999).

Though relaxation experiments offer powerful insight into folding mechanisms, their analysis has come under scrutiny because a kinetic signature such as non-exponential relaxation is consistent with more than one kind of folding. For example, non-exponential kinetics may be associated with downhill folding or with barrier limited folding over multiple barriers (Parker & Marqusee, 1999; Parker & Marqusee, 2001; Hagen, 2007; Lin, Culik & Gai, 2013). Thus, experiments investigating downhill folding have relied on trends of how kinetics tunes smoothly from fast non-exponential to slower single-exponential relaxation when stress is added (higher temperature, or unfavorable mutations as in Figure 8), presumably because stress destabilizes the native state and increases the refolding activation barrier (Gruebele, 2007; Liu et al., 2008; Liu & Gruebele, 2008; Liu, Gao & Gruebele, 2010; Lin et al., 2013).

Fig. 8. WW domain.

Mutations can move proteins into the downhill folding regime. (a) The native Pin1 WW domain (gray, PDB 1PIN, (Ranganathan et al., 1997)) has a long loop, responsible for its binding function, connecting beta sheets 1 and 2. A stabilized mutant (FiP35) ((Jäger et al., 2006) magenta, PDB 2F21) exhibits faster folding kinetics, but reduced binding activity, both due to its shortened loop. (b) A plot of activated folding time (blue dots) vs. melting temperature for 35 WW domain mutants highlights the correlation between stability and folding speed, calculated from a single exponential fit at the temperature of fastest folding. The fastest-folding WW domains show a molecular phase (open red circles) when the kinetics are fit using a double exponential (the activated time is shown as an open blue circle), showing that these mutants approach the ‘speed limit’ of downhill folding (adapted from (Liu et al., 2008)).

2.7 Sub-millisecond mixing experiments

Mixing experiments conducted with stopped flow are still one of the most common tools for measuring biomolecular dynamics. Conventional stopped flow instruments have millisecond dead times (mixing times), making them too slow for the study of fast folders whose kinetics are complete in less than a millisecond. Some mixer designs take advantage of mixing-initiated turbulence to create small domains within which mixing is extremely rapid. These instruments usually achieve ≈50 μs time resolution (Chan et al., 1997; Shastry, Luck & Roder, 1998).

The most common sub-millisecond mixing experiments use laminar flow of two solutions to achieve rapid mixing through diffusion across the solution interface (Knight et al., 1997; Lapidus et al., 2007; Gambin et al., 2011). Laminar flow mixers can achieve mixing times as fast as 10 μs, limited by diffusion through the interface. Mixing experiments are often used to study protein re-folding after denaturation and have shed light on the initial collapse of unfolded chains (Park, Shastry & Roder, 1999; Lapidus et al., 2007; Waldauer et al., 2008) and even the folding pathway of the fastest folders (DeCamp et al., 2009).

2.8 Sub-millisecond single-molecule experiments

Single-molecule techniques have only recently been applied to fast folding proteins. The main difficulty is the limited photon flux out of a single molecule. Fluorophores have nanosecond lifetimes, limiting the number of excitation-emission cycles in each sampling period. In addition, collection efficiency is well below 100%, cutting the number of photons further. The photon collection rate has to be comparable to the kinetics of interest so the reaction may be properly sampled.

Much effort in the last few years has been directed toward enabling the observation of time-resolved single-molecule folding events. In 2004, Rhoades, et al. studied FRET labeled CspTm (a fast folding cold shock protein, see below) at its denaturant midpoint and observed single-molecule transitions between the folded and unfolded states. They could not resolve the actual transition steps, even at time resolutions down to 100 μs.

This difficulty of resolving the actual folding event highlights the distinction between the “activated time” and the “molecular time” (Fig. 4) The activated time is related to the dwell time of molecules in one or the other state before making a rapid transition between states. As the dwell time t_a increases, the activated relaxation time τ_a gets slower. The activated rate dependence on free energy and temperature is described by the Arhennius rate law discussed in the introduction, although a viscosity- and temperature-dependent prefactor has to be utilized (Kramers, 1940). The activated time (or rate) is also measured by ensemble experiments like the ones described in section 2.5 or 2.6. The molecular time is the actual time for a protein to switch between two states after already being activated, and is related to the “transit time” across the transition state for a two-state folder (Fig. 4). The molecular rate was observed in 2003 in fast relaxation experiments (Yang & Gruebele, 2003), where it precedes the activated rate portion of the relaxation. Its measured (1-2 μs)^-1 value explains why it is so hard to observe by single-molecule experiments. Fig. 4 highlights how single-molecule trajectories and ensemble kinetic traces can be analyzed to yield similar information about the activated and molecular phases of a folding transition.

Fig. 4. Kinetics from single-molecule and ensemble traces.

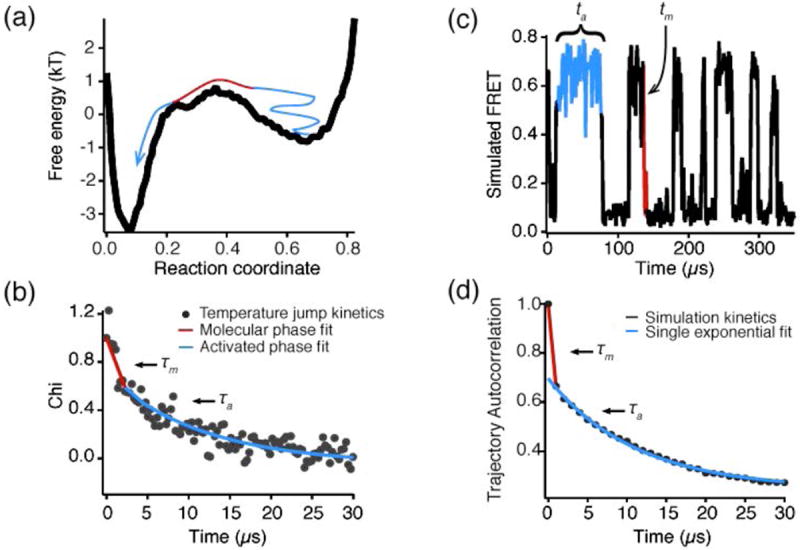
(a) A free energy landscape of WW domain; blue shows the ‘wait’ (time scale of kinetics) and red shows the actual transition from unfolded to folded (molecular time scale). (b) Single-molecule folding trajectory simulated on this free energy landscape (adapted from (Liu et al., 2009b)); the ‘wait’ time (activated kinetics time scale, blue) and molecular time scales (actual reaction event, red) are again shown. (c) This ensemble folding trace was simulated by auto-correlating the single-molecule trajectory in (b). The molecular phase is again highlighted in red and the activated phase in blue. (d) Experimental ensemble T-jump relaxation trace obtained by temperature-jumping FiP35 WW domain from 65 to 71°C. The fast time scale (~1 μs, red) corresponds to the molecular timescale of contact formation, the slow timescale (~10 μs, blue) corresponds to the distribution of ‘wait’ times in activated kinetics (adapted from (Liu et al., 2009b)).

Single-molecule experiments can observe the actual transit time – if they can be made fast enough to catch molecules reacting instead of just waiting to react. Conventional fluorescence microscopy techniques, in which donor and acceptor fluorescence is recorded on a CCD camera with a finite integration time, are not fast enough to resolve the transit between states. Chung and co-workers developed a technique to record single photons from both the donor and acceptor. They use the correlated donor and acceptor photon trajectories to reconstruct the FRET efficiency with 350 ps resolution (Chung, Louis & Eaton, 2009; Chung et al., 2011). They were able to resolve the transition path of a FRET labeled WW domain variant in the presence of denaturant and glycerol (see discussion below) and place an upper limit on the transition path transit time in the slower folder GB1. Though the folding rates of these proteins differ by a factor of ~ 10,000, the transit times of GB1 is less than five times slower than that of WW domain (Chung et al., 2012). This is consistent with the notion that molecular diffusion, not a highly activated process, controls the transit time. Molecular phases were previously observed in ensemble relaxation experiments (see WW domain, α3D, and λ repressor, below). The advantage of single-molecule experiments is that this transition can be seen as a rare event even when the barrier is high. In an ensemble experiment, an extraordinary signal-to-noise ratio would be required to see the minuscule molecular phase over the huge amplitude of the activated phase when the barrier is large, as for the slow folder GB1. Thus the single-molecule experiment converts a signal-to-noise problem into a waiting time problem.

3. The proteins

It has been only about 20 years since computational and experimental methods were developed to allow direct observation of fast (sub-millesecond) folding processes. During the subsequent technological and theoretical development, fast folders have yielded insights into the most fleeting processes that occur during protein folding. In this section, we review some of the most studied fast folders and highlight the major discoveries and their application to our understanding of protein folding in general. A figure for each protein highlights its structure (along with important mutations described in the text) and one or two important experimental results. These results are also referred to in Section 4.

Since many of the results discussed here were obtained by changing thermodynamic parameters such as temperature and pressure, the reported free energy differences and barrier heights are often not available at standard temperature and pressure (25 °C, 1 atm). Thus, for consistency, we use the general symbols ΔG and ΔG^‡, instead of their corrected counterparts ΔG° and ΔG^‡°, to report the experimentally determined values. When possible, we report the conditions under which the free energies are calculated.

3.1 Villin headpiece

The Villin headpiece is a 35-residue protein subdomain consisting of three short helices surrounding a three-phenylalanine hydrophobic core (see Fig. 5) (Chiu et al., 2005). Unlike many small protein folders, villin folds independently without the incorporation of disulfide bonds, ligand binding, or unnatural amino acids (McKnight et al., 1996), though such residues were eventually incorporated to study the effect of stabilization (Chiu et al., 2005; Kubelka et al., 2006). Early measurements of villin folding showed cooperative thermodynamics with a transition temperature of 342 K. Temperature jump measurements showed a 2 phase relaxation: the fast phase (70 ns) was attributed to local motions near the tryptophan probe, while the slow phase (5 μs at 300K) corresponded to global unfolding (Kubelka, Eaton & Hofrichter). Extensive subsequent work with villin has touched on many of the major themes of protein folding research. The first folding experiments were conducted after the first microsecond simulation ever performed (Duan et al., 1998), giving experimentalists clear theoretical predictions to test. While some simulations were in agreement with experimentally determined folding times, the suggested mutations for faster folding did not always result in significantly faster kinetics, calling into question how closely the simulated folding trajectories agree with the real microscopic mechanism of folding (Zagrovic et al., 2002; Kubelka et al.; Piana et al., 2012). Just because a simulation folds a protein to the correct native structure does not mean it also captures the correct folding mechanism: mechanism is more subtle than structure. Efforts to determine the dynamics of villin folding have extended to the incorporation of novel probes to study local vs global unfolding (Reiner, Henklein & Kiefhaber, 2010), revealing early melting (T_m = 319 K) in helix 2 (Brewer et al., 2007). Finally, successful attempts at stabilization have brought villin closer to the folding speed limit (k_fold = (730 ns)^-1) and lowered the activation barrier between the folded and unfolded states, bringing villin near the downhill folding regime (Kubelka et al., 2006). Full atom single trajectory simulations confirm a barrier of ≈2 RT near T_m when projected onto a single reaction coordinate.

3.2 Trp-cage

Trp-cage is a 20 residue peptide based on an exendin (a peptide hormone). It folds via the formation of a hydrophobic core of 3 prolines, a phenylalanine, and a tryptophan (the “trp-cage”). Trp-cage has a short N-terminal helix in addition to the core and NMR protection factors indicate the formation of tertiary structure, meaning that it displays the key features of a true protein (see Fig. 6). Trp-cage is relatively stable for a designed protein, showing a cooperative transition in both CD and NMR melts with a midpoint around 315 K (Neidigh, Fesinmeyer & Andersen, 2002). Hagen and co-workers find a folding rate of 4 μs and attribute the faster-than-expected rate (as predicted based on its stability) to its extremely small size and robust tertiary structure: once one native tertiary contact is made, the others are much more likely to be formed due to reduced conformational freedom, and folding proceeds quickly (Qiu et al., 2002). Gai and co-workers stabilized the hydrophobic core by replacing one of the prolines with a tryptophan and find not only that the protein is stabilized by ~15 °C, but also that folding speeds are sub-microsecond well below the transition temperature (see Fig. 6). While thermodynamic melts and exponential kinetics suggest a two-state folding mechanism, the Arrhenius fits to the folding rates give a negative value for the enthalpy of activation at the melting temperature, suggesting the possibility of barrierless, or “downhill”, folding (Bunagan et al., 2006). Recent experiments used IR temperature jumps to separately probe unfolding of different structural elements and identified an early event in the folding process (Culik et al., 2011), indicating some folding heterogeneity. Like other small proteins, Trp-cage has been the focus of many folding simulations, many of which predict different pathways and/or intermediates, again highlighting the subtlety of mechanism compared to structure (Zhou, 2003; Paschek, Hempel & Garcia, 2008). A recent 1D free energy surface along the reaction coordinate of native contact fraction calculates a barrier of 4 RT; however, the calculated and measured folding enthalpies are not in good agreement, explaining a discrepancy in melting temperature that still frequently occurs between experiment and simulation (Lindorff-Larsen et al., 2011).

Fig. 6. Trp-cage.

Folding speed and protein stability are often correlated. (a) Trp-cage structure (PDB 2JOF (Barua et al., 2005)) with W6 highlighted in blue. P12 (gray) was targeted for the stablilizing P12W mutation. (b) Thermodynamic stability of Trp-cage (orange) and Trp-cage P12W (blue), measured by CD at 222 nm. The P12W mutation stabilizes Trp-cage by ~15 °C and also speeds up the folding rate by a factor >4 (data adapted from (Bunagan et al., 2006)).

3.3 BBA

Many naturally occurring small proteins are able to nucleate and stabilize tertiary structure by binding metal cations. BBA is a small folder based on the zinc finger ββα motif (see Fig. 7). To encourage nucleation without ion binding, the loop connecting the beta hairpin was changed to a Type II’ β turn, and secondary structure enhancing amino acids were used to increase helix and sheet propensity (Struthers, Cheng & Imperiali, 1996). Selecting for the Type II’ β turn in BBA5 required the use of a nonstandard d-amino acid (d-proline). BBA5 maintains a stable, well defined fold in the absence of zinc ions (Struthers, Ottesen & Imperiali, 1998). For fast folding studies, BBA5 mutants F8W and F8W/V8Y were introduced to enhance the fluorescence signature of folding. These BBA5 mutants were simulated using a distributed computing platform and subjected to temperature jumps, allowing the first direct comparison of simulated and experimental folding time and thermal stability. Simulated folding times (~ 7.5 μs for the double mutant, 16 μs for the single mutant) were found to be roughly consistent with the experimentally determined values (6 μs for the double mutant, < 10 μs for the single mutant) (Snow et al., 2002). The difficulties hindering direct comparison between the experimental and theoretical results in this paper – force field inaccuracies resulting in shifts of the melting temperature, or how to map atomic coordinate data into low-resolution experimental probes, for example – are still active areas of research for collaborating theorists and experimentalists (Bowman et al., 2009; Lindorff-Larsen et al., 2011; Raval et al., 2012).

Fig. 7. BBA.

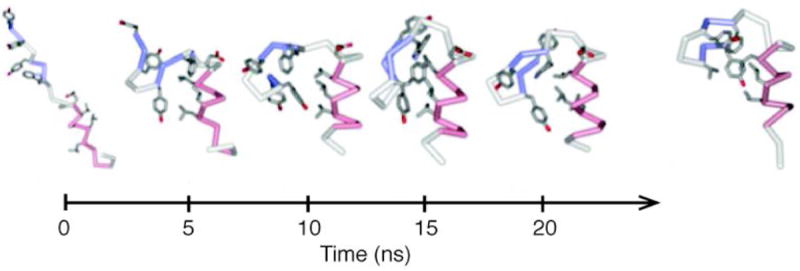
Comparison of BBA folding in simulation and in experiment. 20 ns folding trajectory of BBA5, terminating in a final structure with RMSD 2.2 Å. At the right is the folded structure of BBA5 (adapted from (Snow et al., 2002)). The simulated and experimental folding kinetics of two BBA mutants are comparable. This simulation was the first to be directly compared with experimental folding relaxation times and equilibrium constants.

3.4 WW domain

The WW domain comprises a family of ~40 residue proteins which fold into a three stranded anti-parallel sheet structure (Crane et al., 2000). They get their name from two highly conserved tryptophans that lay 20 to 22 residues apart (see Fig. 8). WW domain motifs are found as modules in many proteins. Loop 1 is an unusually long functional loop involved in binding proline-rich peptides during signaling, and WW domain is the smallest independently functional protein binding domain. The WW domain was the first fast beta sheet folder to be studied (Crane et al., 2000). WW domains vary widely in both thermodynamic stability and folding speed (Nguyen et al., 2003). Native WW domain sequences fold faster than 100 μs and engineered mutants can fold as fast as 3.5 μs (Piana et al., 2011). WW domains have been especially fruitful for folding studies due to the robustness of the WW domain fold: almost every residue can be mutated without disrupting the fold, allowing experimentalists to investigate the role of each residue in the folding pathway. The predominant folding pathway of Pin1 WW domain proceeds through formation of strand 1-loop 1-strand 2 (Jäger et al., 2001), with computational and experimental evidence for an alternative path through loop 2 (Nguyen et al., 2003).

In a series of papers, Gruebele, Kelly, and co-workers studied the folding pathway of WW domains via mutations analyzed by NMR structural studies, thermodynamic stability, ϕ-value analysis, and temperature jump spectroscopy (Jäger et al., 2001; Fuller et al., 2009). These studies were extended to examine the sometimes competing demands of protein folding and function: modification of the first loop in the commonly used Fip35 mutant significantly speeds up WW loop formation, but almost completely eliminates binding action (Jäger et al., 2006). Thus redesign of functional sites in proteins (shortening binding loops, replacing charged or polar residues in active sites by hydrophobic residues) emerged as a design criterion for faster folding.

WW domain folding has been tuned by both mutation and environmental perturbation. Crane, et al showed that the native content of the Pin1 WW domain transition state is highly dependent on temperature (Crane et al., 2000), while Nguyen and coworkers showed that FBP WW domain folding could be tuned from an apparent two- to a three-state mechanism using both sequence mutations and temperature (Nguyen et al., 2003). This variability as a function of sequence and solvent conditions indicates that folding barriers are small on the biological scale.

Indeed, Liu et al. have observed the characteristic appearance of a fast molecular phase after temperature jump when Fip35 WW domain is stabilized by mutations (Liu, Nakaema & Gruebele, 2009b) (see Fig. 8). The molecular phase originates from a significant population of molecules that are found in the transition state, not the native well, after temperature jump. These molecules promptly move downhill to the unfolded state and, since they don’t need to escape the native well for unfolding to proceed, the reaction is very fast – on the order of τ_m ≈ 1 μs. Molecules that remain in the native well after temperature jump unfold through normal, activated kinetics – giving rise to the fast (molecular) and slow (activated) phases. As predicted (Yang & Gruebele, 2004b; Gruebele, 2007; Gruebele, 2008), the observed amplitude of the molecular phase increases the more the protein is stabilized. A slight slow-down of the molecular phase at higher temperature, in contrast with the expected speed-up due to lower solvent viscosity, was attributed to stronger non-native transient contacts caused by the stronger hydrophobic effect at higher temperature. Recent single-molecule studies of FBP WW domain have estimated that the transition path “transit time” has an upper limit of 10 μs (Chung et al., 2012), very close to the molecular rate k_m for diffusing out of the transition region measured by T-jump relaxation (Yang & Gruebele, 2003).

The experiments have driven a large number of recent simulation studies, which in turn have helped interpret the experiments. (Karanicolas & Brooks, 2003; Freddolino et al., 2008; Ensign & Pande, 2009; Noé et al., 2009; Lindorff-Larsen et al., 2011). Full atom single trajectory simulations have yielded the WW domain native state, after some necessary adjustment to the force fields. Simulations of FBP WW domains indicated heterogeneous folding. Hidden Markov analysis of short trajectories also revealed a more complex network of interconverting mesostates (coarse graining level between micro- and macro-states), including ones forming either loop 1 or loop 2 first, the latter being a minority path, in agreement with experiment (Fig. 3). A single-trajectory explicit solvent simulation that sampled many folding/unfolding events determined a 2 RT barrier under conditions where the native state is favored by 2.5 RT (Lindorff-Larsen et al., 2011), in good agreement with temperature jump experiments that showed the molecular phase of downhill folding (Liu et al., 2009b). Simulations have also suggested mutations to accelerate WW domain folding, resulting in the development of GTT WW domain – the fastest folding β-sheet folder (Piana et al., 2011). This result shows that simulations are becoming capable of making mechanistic predictions, in addition to reaching the native fold and yielding reasonable rate coefficients.

3.5 NTL9

NTL9_1-39 is a 39 residue truncated N-terminal fragment of the ribosomal protein L9. Its structure is mixed α/β, giving it a more complicated fold topology than many other small proteins (see Fig. 9) (Horng, Moroz & Raleigh, 2003). For this reason one would expect it to fold somewhat slower, and be in the two-state limit. Temperature and denaturant melts are consistent with two-state folding. The two-state folding mechanism is also supported by a V-shaped chevron plot from stopped-flow folding measurements at a succession of Urea concentrations. A single mutation (K12M) significantly increases stability and speeds up folding from 1.5 ms to 700 μs (Horng et al., 2003), as probed by deuterium exchange NMR spectroscopy and stopped flow experiments.

Fig. 9. NTL9.

NTL9 shows two-state folding behavior in experiments, but simulations show multiple folding pathways. (a) Structure of NTL9 (PDB 2HBA). Highlighted in black is the mutated residue 12 (from lysine to methionine). The K12M mutant shows increased stability and folding speed. (b) Folding rate as a function of GuHCl denaturant concentration; native NTL9 (blue) and the K12M mutant (orange) relaxation kinetics were measured by stopped flow (adapted from (Horng et al., 2003)). The K12M mutant is more stable, determined by the position of intersection of the two arms of the chevron plot. The folding rate at 0 M GuHCl is determined by the intercept with the y-axis. The native protein folding time is 1.3 ms, while K12M folds in ~827 μs. Similar results are obtained with Urea induced folding. The straight arms at extreme GuHCl concentrations are consistent with 2 state folding. (c) The observation of two distinct folding energy landscapes in folding simulations of NTL9 (blue and orange) is inconsistent with the two-state behavior found in experiments. (d) Corresponding folding paths on the two energy landscapes for NTL9 observed in long all-atom simulations (c and d adapted from (Lindorff-Larsen et al., 2011)). The discrepancy between experimental and computational results may be due to force field errors, or to the existence of dynamics invisible to the experimental probe used (tryptophan fluorescence).

Interestingly, both Markov State Model (MSM) and long-trajectory simulations are able to fold NTL9_1-39 to its native structure, but both observe multiple pathways to the folded state (Voelz et al., 2010; Lindorff-Larsen et al., 2011). Non-two state kinetics have not been observed experimentally. This could be due force field errors leading to a mechanistic discrepancy, or it may be that additional experimental probes will reveal different time scales. NTL9 is a good example of a fast folder where simulations must push the millisecond boundary and additional experimental reaction coordinates deployed before mechanistic discrepancies between simulation and experiment can be resolved.

3.6 Cold shock proteins (Csps)

The Csp family is a group of highly homologous, approximately 70 residue, β-sheet folders (see Fig. 10). Almost all members of the family are two-state folders with overall folding times in the 1 ms range (as measured by stopped-flow) (Perl et al., 1998; Delbrück et al., 2001).

Two-state folding kinetics without observable intermediates was first observed in the folding of CspB from Bacillus subtilis (Schindler et al., 1995). An analysis of Csps from many organisms revealed a surprising decoupling of protein stability and kinetics: Csp stability varies by over 20°C, but the folding mechanism and kinetics remain the same. This showed that the two-state kinetics is not simply the result of low (or high) thermodynamic stability (Perl et al., 1998). Two-state equilibrium behavior was confirmed by single-molecule FRET experiments (Rhoades et al., 2004).

One member of the family – CspA from E. coli – deviates from the family’s two-state folding mechanism in IR temperature jump experiments. A rapid (~40 μs) relaxation phase is detected in large temperature jumps (> 12°C) that does not appear in smaller jumps to the same final temperature (see Fig. 10). This fast phase is attributed to downhill folding from part of the initially folded ensemble that ends up on the plateau of the energy landscape after temperature jump due to the large landscape changes during the jump. The slower (~ 130 μs) relaxation phase is attributed to activated folding (Leeson et al., 2000). Just as mechanistic variations between different force fields highlight the potential for several low energy pathways to the native state (even when one of these pathways is predominantly realized), so do mechanistic variations of proteins such as Csps and WW domains when sequence and solvent are varied experimentally. Again, the final fold is more robust than the folding mechanism.

Though folding experiments could not detect stable intermediates in Csp folding, stopped flow experiments showed that the starting “denatured” state is more compact than would be expected for an extended chain and that this so-called collapsed state forms quickly, before the onset of folding (Magg & Schmid, 2004). Further studies by both stopped flow and FRET showed that this collapsed state contains up to 20% of the native β sheet content, but maintained non-native backbone configurations (Buscaglia et al., 2003; Magg et al., 2006; Hoffmann et al., 2007; Nettels et al., 2009). Rapidly formed, compact unfolded states, often with some non-native structure, are also found in other fast folders (Dumont et al., 2006). Indeed, simulations started in extended states generally collapse very rapidly to more compact forms that can facilitate or hinder the folding process. Residual unfolded state structure in general contributes significantly to folding rate and mechanism (Waldauer et al., 2008). In some cases it can be difficult to distinguish residual unfolded state structure from folding intermediates (see homeodomain, below (Mayor et al., 2003a)), highlighting the difficulties of interpreting even detailed experimental data.

3.7 Protein A

“Protein A”, in fast-folding studies, refers to a 60 residue, 3-helix bundle from the B domain of staphylococcal protein A (out of a total protein length of 472 residues) (see Fig. 11) (Myers & Oas, 2001). Both theoretical and experimental studies support a folding mechanism where at least one of the helices forms before tertiary contacts are formed (Guo, Brooks & Boczko, 1997; Myers & Oas, 2001; Vu et al., 2004). The native form of the protein was unfolded via IR-detected temperature jump and found to have two kinetic phases – the fast (90 ns) phase is attributed to helix structure unfolding, while the slow (9 μs) relaxation accounts for the unfolding of the hydrophobic core and tertiary contacts (Vu et al., 2004). A fluorescent Phe13Trp/Gly29Ala mutation, designed to speed up helix formation, yields only a single <4 μs kinetic phase (Arora, Oas & Myers, 2004; Dimitriadis et al., 2004), consistent with fast two-state folding. Indeed, CD and fluorescence detected denaturation curves of the mutant can be globally fitted with the same T_m, further supporting two-state folding. Here again, a folding mechanism of a fast folder is heavily modified by a change in sequence, while the overall fold remains the same. Very fast single phases, such as the 730 ns for a villin headpiece mutant, the 3.8 μs for FiP GTT WW domain, or the 4 μs observed for the protein A mutant, are very useful for setting unambiguous lower limits on the prefactor or molecular rate k_m.

Fig. 11. Protein A.

The structure of Protein A is conserved even when the folding mechanism is altered. (a) Structure of Protein A (PDB 1BDC (Gouda et al., 1992)). The residues targeted by mutation are highlighted in black (F13W and G29A). (b) Folding rate constants for the F13W/G29A mutant calculated from NMR lineshape analysis upon denaturation using a mixture of Urea and Thiourea (3.3:1). The folding rate extrapolated to 0 M denaturant is 450,000 s^-1 (τ_fold ≈ 2 μs) (data adapted from (Arora et al., 2004)). (c) Unfolding of F13W/G29A in 2.2 M GuHCl. Traces monitored by CD (orange) and Tryptophan fluorescence (blue) are super-imposable, indicating that mutated protein exhibits 2-state folding (data adapted from (Dimitriadis et al., 2004)). The data in (b) and (c) show that, unlike the wild type, the mutated protein folds in a single, extremely fast, phase despite maintaining a similar folded structure.

3.8 Protein B

Protein B, like Protein A, is a small (47 residue) 3-helix subdomain of a larger protein (in this case, from protein PAB, an albumin binding protein from Peptostreptococcus magnus) (Johansson et al., 1995). Protein B is extremely stable – thermodynamic melts up to 100 °C do not reach the unfolded baseline (Johansson et al., 1995). Simulations of Protein B folding, like those for Protein A, predict the early formation of helices before hydrophobic collapse, with stabilization occurring via the formation of specific tertiary contacts (Takada, 2001).

Experimental infrared-detected T-jumps of two Protein B mutants (K5I and K5I/K39V, both designed to increase the hydrophobic content of the buried core) show not only extremely fast folding (2.5 μs for one mutant, 1 μs for the other), but also that increasing the hydrophobic content of the protein can bring folding close to the diffusion limited folding speed limit (predicted to be .5 μs for Protein B) (Wang, Zhu & Gai, 2004). This supports the idea, discussed for WW domain above, that function and folding efficiency can be at odds, and substitution of hydrophobic residues for charged or polar functional residues can speed up folding at the expense of function. The kinetic measurements of the mutants show no sign of a second, helix-forming phase.

3.9 Homeodomain

Homeodomain refers to a 60 residue, 3-helix DNA binding motif (Clarke et al., 1994). The most commonly studied homedomain is Engrailed Homeodomain (En-Hd) from Drosophila melanogaster (see Fig. 12) and it has served as a platform for studying both folding dynamics (with coupled simulations and experiments) and the sometimes competing demands of protein folding speed and stability (Mayor et al., 2000; Gillespie et al., 2003; Mayor et al., 2003b; Shah et al., 2007).

Fig. 12. Homeodomain.

Mutations can stabilize transiently formed intermediates. (a) Structure of wild-type homeodomain (top, PDB 2JWT (Religa, 2008)) and the isolable intermediate L16A (bottom, PDB 1ZTR (Religa et al., 2005)). Highlighted in black in each is the mutated residue 16. (b) Slow (circles) and fast (squares) rates of folding measured by of L16A as a function of temperature for different salt concentrations. Under low salt conditions, the L16A mutant forms a folding intermediate of the native protein, while under high salt its folding is similar to that of the native sequence. 100 mM NaCl (orange circles) has only a fast phase, corresponding to formation of the intermediate-like structure. 500 mM NaCl (blue circles and squares) shows both a fast and a slow phase, which matches well with the slow folding phase of the wild type protein (black line) (data adapted from (Religa et al., 2005)).

Kinetic studies with resistive- and laser- temperature jumps show that native En-HD folds in two distinct phases: a 1.5 μs fast phase and a 15 μs slower phase (Mayor et al., 2000; Mayor et al., 2003b). The 1.5 μs phase has been alternately described as the formation of a metastable intermediate (Mayor et al., 2003a; Mayor et al., 2003b; Religa et al., 2005; Religa et al., 2007) or taken as evidence of downhill folding (Naganathan et al., 2006). Earlier interpretations of the fast phase attribute it to collapse of the unfolded state (Mayor et al., 2003a). The time scale of the fast phase is consistent with the molecular rate k_m expected for prompt reaction of a barrier-top population (Yang & Gruebele, 2003). A very recent explicit solvent single trajectory simulation of a homeodomain sequence that sampled multiple folding and unfolding events yielded a 1D free energy surface that was indeed downhill along a native contact fraction reaction coordinate (Lindorff-Larsen et al., 2011). The interpretation of homeodomain’s folding and simulation data again highlights the difficulty of distinguishing purely downhill scenarios from folding through multiple short-lived intermediates. However, at some point these two scenarios are not really different: “shallow wells” (< 3 RT) in the free energy are equivalent to “residual roughness” on a downhill free energy surface obtained by averaging over many micro-states. Downhill folding on a rough energy landscape vs. rapid folding through very shallow intermediates is in the eye of the beholder. The important conclusion is that proteins can fold without significant barriers at the biologically relevant level of coarse graining discussed in the introduction.

Fersht and co-workers destabilized En-Hd via an L16A mutation to favor intermediate formation. Under physiological conditions, En-Hd L16A shows only a single fast phase forming the intermediate structure. At low pH, however, En-Hd L16A can fold completely, and shows wild-type two phase kinetics (Mayor et al., 2003a) (see Fig. 12). This observation highlights again how the folding mechanism of fast folders is easily modulated by varying the sequence or solvent conditions even though the native structure remains the same. It is proposed that the fast intermediate completes helix formation, while tertiary contacts stabilizing the helix bundle form in the slow phase (Mayor et al., 2003a; Mayor et al., 2003b; Religa et al., 2007). There is evidence for such tuning of local vs. non-local structure formation in other fast folders (Dumont et al., 2006). This local-global folding pathway also has been seen in simulations of homeodomain folding (Mayor et al., 2000; Hubner, Deeds & Shakhnovich, 2006; Lindorff-Larsen et al., 2011). Two groups have successfully stabilized En-HD, obtaining thermodynamic melting points up to 30°C higher than native En-HD; no significant changes in kinetics are observed in those cases (Gillespie et al., 2003; Shah et al., 2007).

3.10 Beta hairpin peptides

The early events of β sheet formation are studied through the kinetics of β hairpin formation. A β hairpin is a short, 2 strand peptide, usually 12-20 residues in length, held together by specific contacts in the loop or strands. We consider two examples here.

The trpzip peptides are a family of short (12 to 16 residue) β-hairpins designed to maximize the stability of the β-hairpin motif (see Fig. 13). The trpzip sequences optimize interstrand tertiary interactions via cross-strand tryptophan pairs to increase stability (Cochran, Skelton & Starovasnik, 2001). The trpzips exhibit broad, cooperative unfolding transitions, with melting temperatures from 315-351 K. Thermodynamic and replica exchange computational studies show that the trpzip free energy is a single basin at high temperature (α-carbon root mean square reaction coordinate, Cα RMSD), but becomes increasingly rough at low temperature (i.e. exhibits multiple shallow minima) (Yang et al., 2004) (see Fig. 13). Kinetic studies showed folding time scales on the order of a few microseconds (Snow et al., 2004; Yang et al., 2004). In particular, a wavelength-dependent fluorescence study showed that denatured states with more solvent protected tryptophans can end up folding more slowly than denatured states whose tryptophans are highly exposed to solvent (Yang & Gruebele, 2004a). This was interpreted as compact traps taking longer to unzip and refold to the native state than an extensively unfolded state. Analogous simulation and T-jump experimental results for some λ-repressor mutants have been interpreted in the same manner (Bowman et al., 2010; Prigozhin & Gruebele, 2011).

Fig. 13. Trpzips.

Temperature influences the shape and roughness of the energy landscape. (a) Computational studies of trpzip folding reveal that the shape and the location of the free energy minimum changes with temperature. Shown here are representative structures obtained in the low- and high- temperature basins (adapted from (Yang et al., 2004)). At low temperatures, multiple minima exist within ≈ 4 RT of the native basin. (b) The computational predictions are supported by kinetic measurements that detect temperature- and probe-dependent temperature jump unfolding traces. The observable χ₁ is a measure of how the tryptophan lifetime changes during the reaction. Population of multiple basins is detected via temperature jumps monitoring fluorescence from more (orange) or less (blue) solvent exposed tryptophan. Both probes exhibit 2 distinct phases, but the microsecond phase is faster for the more exposed probe (data adapted from (Yang & Gruebele, 2004a)). This difference increases at higher temperatures.

The first hairpin studies isolated one of the hairpin turns from the fast-folding protein G (Blanco, Rivas & Serrano, 1994). Kinetic studies of hairpin formation found a 6 μs folding time for the native protein G hairpin, which is an order of magnitude longer than a typical folding time for an isolated helix (Muñoz et al., 1997). The folding time is predicted to speed up as the hydrophobic core moves closer to the loop – a prediction confirmed by studies of both isolated hairpins (Espinosa, Muñoz & Gellman, 2001) and of the hairpin in Protein G (McCallister, Alm & Baker, 2000). Very recently, the speed limit for beta hairpin peptides has been raised with a 100 ns reported relaxation time of the peptide CLN025 (Davis et al., 2012). CLN025 also cannot be described by two-state folding, with times depending on the infrared wavelength being probed. This hairpin is thus in the downhill folding limit where kinetics are probe dependent and extremely fast. Thus beta sheets are not necessarily intrinsically slower to form than alpha helix peptides. There is a vast literature on dynamics of small hairpins and helices that lack a hydrophobic core, some of which is reviewed in (Kubelka et al., 2004).

3.11 α₃D

α₃D is one of the largest de novo designed proteins at 73 residues. It exhibits both a well-defined native structure (see Fig. 14) and natural protein-like thermodynamic stability (Bryson et al., 1998; Walsh et al., 1999). Unlike the other helix bundle proteins (Proteins A and B and homeodomain, for example), α₃D does not exhibit any signs of intermediates with some or part of helices folded. Instead, α₃D fully unfolds in infrared T-jump experiments with a relaxation time of less than 3 μs at all temperatures (Zhu et al.). In contrast, UV fluorescence monitored kinetics are temperature dependent (see Fig. 14). These probe dependent kinetics, coupled with the extremely fast observed rates, suggest that this relatively large protein is folding downhill (Liu et al., 2009a). Computational attempts at globally fitting the infrared and fluorescence data to a 1D free energy surface with a barrier were not successful (Scott & Gruebele, 2010); instead, a 2D surface with IR (secondary structure) and fluorescence (packing around tryptophan) reaction coordinates was required to account quantitatively for the data. The 2D surface had barriers < 3 RT, putting α₃D near the downhill folding limit.

Fig. 14. α₃D.

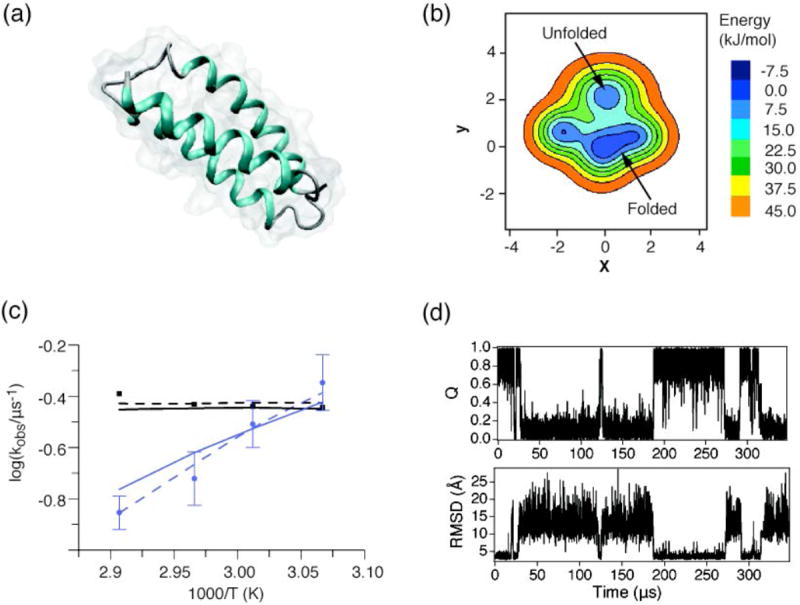
α₃D folding cannot be modeled as a 1-dimensional process. (a) Structure of α₃D (PDB 2A3D (Walsh et al., 1999)). (b) 2D free energy surface as calculated by (Scott & Gruebele, 2010) using Langevin dynamics. (c) Kinetic rates measured by fluorescence (purple) and IR absorption (black) spectroscopy. Only the fluorescence data show a significant temperature dependence. 1D (dashed) and 2D (solid) models both fit the data, but the 1D fit diffusion coefficient is unrealistic, signaling that the model cannot fully capture the dynamics (adapted from (Scott & Gruebele, 2010)). (d) Time traces of Q (percent native contacts) and C_α-RMSD from (Lindorff-Larsen et al., 2011) are similar, but not identical for these two different coordinates. The low calculated barriers (< 3 RT) and probe-dependent dynamics (in both experiment and simulation) suggest that α₃D may be an incipient downhill folder. Here a future temperature-dependence simulation would be very useful.

The α₃D results are an example of experimental data requiring more than a 1D model to interpret. As experiments combine multiple probes, more sophisticated simulation analyses, such as the hidden Markov networks for multiple trajectory simulations and multiple maximally orthogonal reaction coordinates for single trajectory simulations, will be required to explain the data quantitatively. The real difficulty will be for experiments and simulations to agree on probes that can be quantitatively modeled. Otherwise the comparison between computed low-dimensional free energy surfaces and experimental signals as a function of time cannot be made rigorous.

3.12 λ repressor fragment

The N-terminal segment of the bacteriophage λ CI transcription repressor is the largest of the proteins that reach the speed limit at a few microseconds, and thus fold downhill or nearly downhill. Lambda repressor fragment has been the focus of fast folding studies because of its high stability and tolerance for mutations (Sauer, Jordan & Pabo, 1990). The domain studied by Sauer and coworkers had ≈100 residues. This was whittled down to an 80 residue five helix bundle (λ_6-85) by Oas and coworkers, and shown to have similar structure as the full N-terminal domain (see Fig. 15) (Huang & Oas, 1995a). It was finally whittled down to a 58 residue two helix bundle by (Prigozhin et al., 2011). Remarkably, the 80 and 58 residue versions both have mutants with stabilities exceeding 60 °C and folding relaxation times below 20 μs.

Dynamic NMR experiments initially showed that native λ_6-85 folds in approximately 250 μs with no detectable intermediates (Huang & Oas, 1995b). A more stable variant, G46/48A (created via two stabilizing glycine to alanine mutations in helix 3), folds approximately 10 times faster, showing that the wild type helix 3 was not optimized for fast folding or stability (Burton et al., 1996). The native glycine residues provide flexibility during DNA binding, their mutation again highlights the competition between function and folding seen for WW domain and other examples. The NMR studies were able to map the native-like contacts of the barrier-limited transition state and to track how mutations affect the content of the transition state (Burton et al., 1996). A fluorescent mutant of G46/48A was studied via stopped flow and temperature jump (Ghaemmaghami et al., 1998; Yang & Gruebele, 2003).

Laser temperature jumps detected by fluorescence or infrared spectroscopy revealed a number of interesting features of the folding kinetics (Fig. 15). Proteins with relaxation times > 20 μs showed only a single exponential phase (Yang & Gruebele, 2004c), but proteins with relaxation times < 20 μs showed a new 1 μs fast phase (Yang & Gruebele, 2003), whose amplitude increased with folding speed (Yang & Gruebele, 2004b), until the two phases become indistinguishable at the highest folding speed (Liu & Gruebele, 2007). When the protein folds entirely downhill, only the fast rate k_m is observed. The λHA mutant of lambda repressor approaches this limit with a relaxation time of only 2.3 μs, very fast for such a large protein.

Other signatures of downhill folding were also observed for some mutants: infrared and fluorescence probes produce different observed rates, but only when the protein was stabilized (Ma & Gruebele, 2005). By using a fast microfluidic mixer, Lapidus and coworkers were able to observe λ_6-85 refolding under conditions more strongly favoring the native state than is possible by upward T-jumps, bringing near downhill-folding mutants into the full downhill limit (DeCamp et al., 2009). For one mutant, probe dependence was also observed in thermodynamic measurements, showing that the protein behaves like a downhill folder even near its melting point (Liu & Gruebele, 2007).

λ_6-85’s fast folding has made it a target of theoretical efforts to discern the molecular steps of its folding mechanism. A recent explicit solvent single trajectory simulation has calculated multiple folding and unfolding events. The barrier along a 1D native contact reaction coordinate is 1.5 RT (Lindorff-Larsen et al., 2011), in agreement with that reported from experiment (Yang & Gruebele, 2003). Other simulations have made experimentally verifiable predictions about off-pathway traps: even in downhill folders not all non-native interactions can be avoided (Bowman et al., 2010). T-jump experiments have shown that such traps exist for some mutants, in particular the most stable mutants (Prigozhin & Gruebele, 2011). This may seem counterintuitive, but previous measurements also showed that the most stable λ_6-85 mutants are the most aggregation prone. The mystery is resolved by realizing that fast barrierless downhill folding also means faster barrierless uphill unfolding, meaning such proteins explore partially folded states more frequently. Such states could be more prone to forming nonnative contacts (traps) or aggregating. Finally, a recent experimental and computational study suggests that pressure-denatured λ_6-85 populates a helix-rich non-native state that is different than the unfolded state reached via temperature denaturation (Prigozhin et al., 2013). Pressure-jump refolding experiments showed a large 1.4 ms refolding phase, which is much slower than the 60 μs phase principally observed in temperature jump experiments of the same mutant (Prigozhin & Gruebele, 2011). It was postulated that the slow refolding is due to the high helical content of the native state, once again highlighting the influence of the denatured state on folding kinetics.

3.13 BBL

BBL is an ~40 residue alpha-helical miniprotein, comprised of two short helices connected by a long loop (see Fig. 16) (Robien et al., 1992; Garcia-Mira et al., 2002). As BBL has no natural fluorophores, all folding experiments have been done with signals generated from extrinsic fluorophores (Garcia-Mira et al., 2002; Huang et al., 2009) or by mutating residues from the original sequence (Ferguson et al., 2005; Neuweiler et al., 2009). Structural studies of the folded state and its stability have been conducted with NMR (Ferguson et al., 2004; Sadqi, Fushman & Muñoz, 2006). T-jump experiments of a BBL tryptophan mutant show fast folding kinetics with a single 10 μs phase (Neuweiler et al., 2009). While this would seem to indicate the existence of a two-state folding mechanism, the interpretation of both thermodynamic and kinetic data of BBL folding has given rise to a significant debate over whether BBL is an extremely fast two-state folder or an example of a natural protein exhibiting single-well downhill folding. Calculations by Cho and Wolynes indicate that some mutants fold downhill, while others still fold over a small barrier. A recent explicit solvent long trajectory simulation of the tryptophan-containing BBL mutant studied by Neuweiler et al. shows that when projected on a native contact reaction coordinate, the free energy of folding has a single well with free energy roughness < 1 kT, consistent with a single-well downhill folder (Lindorff-Larsen et al., 2011). A recent study combined simulations and temperature jumps to show that the temperature dependence of BBL unfolding is consistent with downhill, not barrier limited, folding (Lin et al., 2013).

Fig. 16. BBL.

BBL exhibits signatures of downhill folding in both experiments and simulations. (a) BBL folding monitored by MRE₂₂₂ as a function of pH. The CD signal changes approximately linearly with stress, indicative of a single basin free energy minimum (adapted from (Cerminara et al., 2012)). (b) The calculated free energy landscape of BBL from long, all-atom trajectories. (c) Snapshot of a single-molecule folding trajectory (b, c adapted from (Lindorff-Larsen et al., 2011)). The transitions from folded to unfolded are rather ‘fuzzy,’ as expected when distinct populations no longer exist.

BBL is the most highly debated protein in the literature when it comes to downhill vs. fast two-state folding. The discussion has been fruitful because it led to demands for more rigorous interpretation and data to identify folding mechanisms. Muñoz and coworkers conducted the first study of BBL folding (Garcia-Mira et al., 2002) using a FRET labeled variant of BBL and found probe-dependent thermodynamic stabilities as a signature of downhill folding. A similar study by Fersht and coworkers using a tryptophan labeled BBL, however, reached the opposite conclusions: multiple mutants and multiple probes gave similar stabilities, leading to the conclusion that BBL employs a conventional, albeit extremely fast, folding mechanism (Ferguson et al., 2004; Ferguson et al., 2005). The discrepancy between these experiments has raised questions about how experimental conditions and data interpretation can influence the classification of protein folders (Ferguson et al., 2005; Naganathan et al., 2005; Cho, Weinkam & Wolynes, 2008). More recent studies have sought to resolve the controversy by mapping the equilibrium ensemble of BBL, but once again direct comparison is difficult because of the distinct methods of experiment and analysis that are employed (Sadqi et al., 2006; Cho et al., 2008; Campos, Liu & Muñoz, 2009; Huang et al., 2009). Currently the experimental, simulation (Lindorff-Larsen et al., 2011) and theoretical evidence favors downhill folding of at least some BBL sequences. Since BBL is a natural protein module, Muñoz and coworkers have raised the next question: when could natural downhill folding confer an evolutionary advantage? One possibility is signaling, where proteins acting as continuous “rheostats” rather than two-state “on-off” switches could help regulate cellular processes (Cerminara et al., 2012). The flycasting mechanism has been developed as a plausible way that binding can modulate folding of otherwise unfolded proteins all the way to the downhill scenario (Shoemaker, Portman & Wolynes, 2000).

3.14 Less studied fast proteins

The above list is not exhaustive, as many proteins and short peptides that undergo rapid conformational change have been studied. Examples range in size from the very short chignolin (Lindorff-Larsen et al., 2011) to the large protein cytochrome b562 (Kimura et al., 2009). A newly discovered downhill folder, gpW, is larger than most fast folders (62 residues) and exhibits a complex α/β fold (Fung et al., 2008; Sborgi et al., 2011). Like BBL, gpW is a natural protein domain, and its similar folding mechanism has raised similar questions about the functional or evolutionary advantage its downhill folding mechanism could provide (see below for an extended discussion).

Apomyoglobin does not fold rapidly to the native state (Jennings & Wright, 1993), but does form a metastable intermediate in a few microseconds (Ballew et al., 1996). Here the strife between function and folding is highlighted again. Apomyoglobin is an 8 helix bundle (helices A-H), and early folding models quite reasonably predicted that the C terminal A helix and N terminal GH helices, which share tertiary contacts, would be the last to fold. After all, the CDEF helices are directly connected and have to diffuse over a short distance to make tertiary contacts, whereas the A and GH helices are separated by about 100 residues. Kinetics experiments, however, showed that the A and H helices fold up to approximately 1 million times faster than CDE. This deviation from intuition has its roots in the original function of the CDEF helix group: the contiguous helices are optimized to bind a hydropobic heme group, not to fold on their own. Without their large hydrophobic anchor, CDEF lose out against A and GH, even though the tether connecting the latter is much longer (Ballew et al., 1996).

Other early examples of downhill or near-downhill folding from unfolded states to folding intermediates include phosphoglycerate kinase (PGK) (Sabelko et al., 1999) and RNAse H (Parker & Marqusee, 2001). The more PGK was destabilized by cold denaturation, the more its intermediate formed by slow single exponential kinetics. The more it was stabilized, the faster it folded with an additional fast spike in the kinetics at short times, modeled by a stretched exponential. Similarly, the early folding kinetics of RNAse H were interpreted in terms of a continuous distribution of populations based on thermodynamic tuning (downhill folding), rather than on a single two-state interconversion. Folding intermediates could generally be more likely to form via downhill folding: they often still have partly hydrated cores, eliminating the large barrier needed for concerted water removal to for a dry core of the fully native state.

4. What has been learned: Fast folding concepts

4.1 Population and free energy: from paths to landscapes

There is a long-standing argument in the literature about whether proteins fold on a single main pathway, or on many pathways. The answer we have learned from studying fast folders is that the population of a specific protein under specific solvent conditions generally follows a predominant pathway, but that multiple pathways of low free energy exist on the free energy landscape, allowing the same fold to form by quite different mechanisms.

We know that many low-lying pathways exist both from experiments and simulations discussed in section 3. In a few cases, simulations and experiments have detected multiple pathways that are highly populated simultaneously, such as for protein NTL9, whose beta sheets can assemble in different order (Lindorff-Larsen et al., 2011). In other cases, such as λ_6-85 and WW domain, the protein can fold through completely different mechanisms (downhill, two-state, three state) upon mutation or changes in solvent condition (Nguyen et al., 2003; Yang & Gruebele, 2004b; Liu et al., 2008; Kim et al., 2009; Liu et al., 2010). These perturbations are only a few kJ/mole, so the new paths must already lie at a low free energy before the perturbation is applied. A problem nagging current force fields is also indicative of multiple low energy paths: folding mechanisms simulated by molecular dynamics often differ from experiment, even when the final structure and folding times are nearly correct. The “cup half empty” view of this result is that force fields need further refinement before they can correctly predict folding mechanism. The “cup half full” view is that structure is much more robust than mechanism: simulations reveal pathways that lie just a little higher in free energy in the real protein, but end up lower in the force field implementation.

It is very likely that these alternative paths confer functional advantages on proteins, that they make folding more robust, and that they facilitate the evolution of new function and structure. The functional advantage arises because switching among conformations, required by function, is facilitated by easily accessible alternative structures. Most proteins have marginally stable native states (just 10s of kJ/mole) or even stable disordered states to achieve the required flexibility for binding or catalysis. Improving stability and folding speed by protein engineering can lead to overly rigid native states without function (Liu et al., 2010). The speeding up of λ_6-85 provides one example of this phenomenon – the glycine to alanine mutations in helix 3 stabilize the helix and speed folding, but reduce the flexibility needed for DNA binding (Burton et al., 1996). The robustness advantage arises because low-lying paths provide folding alternatives to the lowest free energy pathway that carries the majority of the population. These alternative paths can take over from the original lowest free energy path when the sequence is mutated or when environmental conditions change. Conversely, such low-lying paths could be evolutionary remnants of an alternative structure from which the modern protein structure evolved. Indeed, on rare occasions a protein can switch between two alternative native states. For example, human lymphotactin folds into two different structures with different functions depending on the temperature (Tuinstra et al., 2008).

If there are multiple low energy paths, how come a single pathway dominates the folding of most proteins under specific conditions? The answer lies in the sensitivity of population to energy, given by the Boltzmann factor

$$(\mathit{Population\; a})/(\mathit{Population\; b})~\exp (­\Delta G_{\mathrm{ab}}/\mathit{RT}).$$

Two paths a and b that differ only by 3 RT in free energy already differ by a factor of e³ ≈ 20 in population. Only the lower free energy path is seen. Thus it is very unlikely that parallel folding mechanisms are seen often (they are indeed rare), but it is very likely that fast-folding proteins have mechanisms sensitive to mutation or solvent environment (this has been observed many times over in section 3). The same sensitivity of population to free energy can have grave functional consequences: for example, Tay syndrome (a skin disorder associated with mental impairment) results from a 0.7 RT change in a helicase binding free energy (Fan et al., 2008).

4.2 The utility of proteins near the “speed limit”

Fast folding has attracted a lot of interest because experiments can be compared directly with simulations. Starting with the Duan and Kollman simulation of villin headpiece in 1999 (Duan et al., 1998), simulations have reached the microsecond and longer time scale on which proteins fold. Experiments point to the 0.1 to 10 μs time scale as the minimum where biological units of protein secondary and tertiary structure are assembled, making these simulations valuable for understanding general processes of structure formation employed by slower folding proteins. While further advances in computational power and force field quality will allow the simulation of millisecond and slower folders, in the meantime there is still much to learn from fast folders.

Just a few years ago, a simulation by Freddolino et al. using the CHARMm22 force field folded the FiP35 WW domain in a 10 μs trajectory with explicit solvent. The folded state was a two helix bundle, not the native β sheet structure (Freddolino et al., 2008). Subsequent analysis showed that the helix bundle was the lowest energy state for this force field – the simulation had found the native state, it just was not the real-world native state. The actual native state was raised to high free energy in this force field because the slightly non-linear hydrogen bonds of the sheet were not properly represented (Freddolino et al., 2009). In newer versions of the force field, this problem has been fixed and WW folds properly (Ensign & Pande, 2009; Lindorff-Larsen et al., 2011). Indeed, even mechanistic predictions made by newer versions have been experimentally verified (Piana et al., 2011). It is now becoming possible to train force fields on multiple α/β fast folders and tweak them to come closer to experimental structures, rates and stabilities. Objective measures of quality indicate that the force fields are improving; for example, the same force field can now be used to fold very different structures (Lindorff-Larsen et al., 2012). Despite this progress, there is still much room for improvement. Melting temperatures of proteins in silico are usually far too high and force fields are effective potentials valid only over a narrow temperature and pressure range. These discrepancies interfere with direct comparison of simulation and experiment, as experiments often employ temperature or pressure variation to reach denatured ensembles. In addition, current simulation water models are not necessarily accurate for the water molecules hydrating the protein because they are parameterized to reproduce bulk water properties. We know, however, that solvation water has properties quite different from bulk water (Halle & Davidovic, 2003), even to distances of nanometers from the protein surface (Ebbinghaus et al., 2007); improving solvation water models will improve the ability of force fields to accurately identify the true melting temperature of proteins.

Now that simulations can fold/unfold fast folders multiple times, it may become possible to more accurately simulate experimental probes. For example, consider T-jump unfolding kinetics of a protein with a nitrile probe mutation (absorbs in an infrared ‘window’ above 2000 cm^-1) and the same protein with a cyanophenylalanine-tryptophan FRET pair mutation (allowing pairwise distance measurement). Instead of doing a single ‘wild type’ simulation, both non-native sequences can now be simulated, alongside the wild type protein, because multiple long trajectories are no longer prohibitively expensive. This allows not only more direct comparison with experimental data, but may also shed light on possible perturbations caused by the addition of non-native probes to a sequence. Information about the probe itself, inaccessible in experiments, e.g. the possibly non-random orientational fluctuations of the dipoles in the FRET pair, could be directly simulated using molecular dynamics. The linear independence of two different experimental reaction coordinates could be quantified based on simulation, shedding light on the sometimes different answers obtained by experiments on the ‘same’ protein. These simulations could guide more efficient probe choices for experiments seeking to widely sample features of the folding process.

Some experimental reaction coordinates, such as tryptophan solvent exposure measured by fluorescence wavelength, cannot be simulated classically. Here it will be important to develop excellent correlations, for example between observed wavelength shift and computed solvent-exposed sidechain surface area. Once calibrated, the easily computed variable (sidechain exposure) can again be compared quantitatively with experiment (tryptophan wavelength shift). 1D pictures of folding have proved adequate for a rough comparison of molecular times τ_m, activated folding times τ_a, and other variables of interest between the current generation of experiments and computation. The increased richness of data (e.g. multiple orthogonal probes) and sophisticated analysis (e.g. Markov modeling combined with longer trajectories) will provide a more quantitative understanding of the folding process by putting stronger experimental constraints on simulations and requiring more than one reaction coordinate to describe the folding process.

Direct simulation of experimental protocols will also allow for a more direct comparison with experimental results. For example, the final ensemble of a laser temperature jump can be modeled by equilibrating the protein for a time comparable to its folding time. Indeed, the T-jump itself can be modeled in silico as a 10 ns temperature rise. For modeling purposes, temperature and pressure are particularly useful variables because their changes are easily controlled in molecular dynamics by thermostats and barostats. The resulting free energies can be analyzed as 2D projections onto the infrared and FRET coordinates, as every probe constitutes a more-or-less adequate reaction coordinate.

Though protein folding is often modeled as a one-dimensional process, its multidimensional nature is one of the reasons why the problem has been so difficult to solve (Fig. 17). Highly cooperative processes, like phase transitions, involve billions of microscopic degrees of freedom, but their cooperativity allows all of these to be reduced to a single order parameter. The material phase transitions between gas, liquid, and solid, for example, are well represented by simply tracking the density of the system as a whole. Small molecule reactions exist at the opposite end of the spectrum: though there is no significant cooperativity, there is also usually only one relevant coordinate which is able to capture most of the dynamics of the reaction. Small proteins are in-between: multiple interactions can cooperate for structure formation, producing a folding process that is sometimes like a mesoscopic version of a phase transition (two-state folding) and sometimes not (downhill folding). Most proteins require several reaction coordinates to describe the process in sufficient detail, making this problem harder than either the small molecule reaction or phase transition problem. Perhaps this is why small molecule reactions were initially understood in the 1930s, phase transitions in the 1960s, whereas folding is yielding only now to a quantitative understanding. The designed protein α₃D from section 3 is a good example. We saw above how α₃D’s folding mechanism initially appeared simple – a single, temperature-independent folding phase detected by IR Tjumps suggested a simple 2-state mechanism for folding. A UV probe, however, revealed significantly different kinetics. The simple 1-dimensional picture of the first experiments could not capture the full folding mechanism of this protein, and at a minimum a 2- reaction coordinate was needed (Scott & Gruebele, 2010). Even less coarse-grained MSM models (section 2) reveal further mesostates in small proteins (Bowman et al., 2009; Noé et al., 2009; Bowman et al., 2010).

Fig. 17. System size dependence of dynamical complexity.

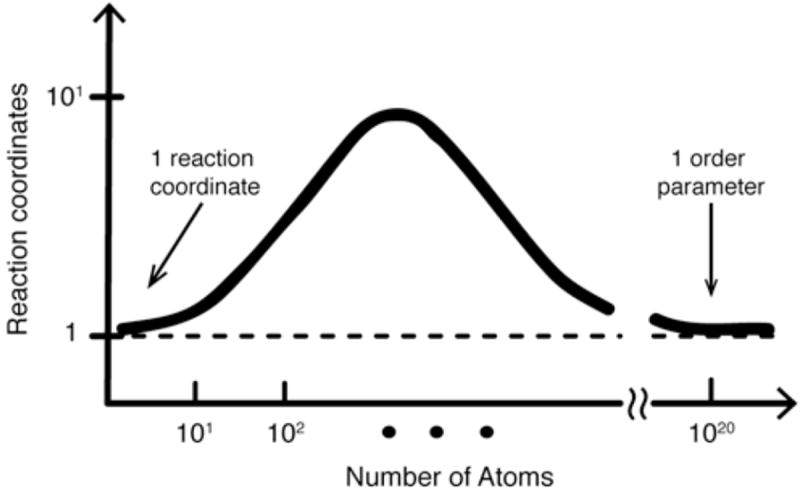
For small systems (e.g. organic chemical bond breaking), the dynamics are usually well captured by a single ‘reaction coordinate.’ For large and highly symmetrical systems that approach the thermodynamic limit (e.g. ice melting to water), system dynamics can be described by employing a single ‘order parameter.’ Intermediate-size systems, like proteins are not small enough for a single reaction coordinate, nor large and symmetrical enough for a single order parameter. They may require several coordinates for an adequate description.

Finally, further studies of fast folding natural protein domains will help to clarify the interplay of folding, function, and stability. Clearly folding is necessary to produce function – a random polypeptide chain cannot reliably respond in the complicated environment of the cell, it must fold at least upon crowding or binding, if not in isolation. However, there is evidence that fast folding and function are at least sometimes at odds. For example, the fastest two-state and downhill folding mutants of WW domain have lost that domain’s ability to bind phosphorylated target peptides. Mutations to speed up folding shortened the long binding loop (see Fig. 8), reducing the conformation entropy of the unfolded state and speeding up the search time for the transition state (recall that the formation of this loop is the first step in the dominant folding pathway, see above).

Therefore optimization of folding conflicts with the optimization of function. As mentioned above, stabilizing mutations necessarily reduce the flexibility of the native state - while this might seem beneficial, for binding domains like λ_6-85 this increased rigidity may interfere with the protein’s ability to find and bind its substrate (Burton et al., 1996). Indeed, flexibility is a hallmark of chaperone domains that must be able to bind a variety of protein substrates. In fact, it has been proposed that some chaperone domains remain disordered until substrate binding takes place, upending the rigid picture of protein binding shown in textbooks (see Section 4.4, below) (Reichmann et al., 2012). Finally, in some cases we saw that mutations and environmental modulation leave final structure intact even when the folding mechanism changes (Liu et al., 2010). In other cases, as for many members of the Csp family, changes in sequence and stability seem to leave both structure and folding mechanism unaffected. In the “cup half full” perspective, these observations all highlight the robustness of the folded state and support the widely impression that protein folding and function have evolved to be robust. On the other hand, this extreme redundancy undermines the naïve intuition that there is an approximate one-to-one correspondence between a polypeptide’s sequence, structure, and function. The irregular relationship between these characteristics highlights the complexity of how these related, though still clearly separate, features of polypeptide chains co-evolve to create a population of functional proteins.

4.3 Two-state and downhill folding

One of the nice features of small fast folders is that their folding mechanisms are simple in the following sense: Often only two states are populated, and sometimes the initial and final state are not even separated by a barrier ≫ 1 RT. The latter scenario, “downhill folding” was first proposed by Wolynes and coworkers based on a simple statistical mechanical model for folding, which posits that contact enthalpy increases monotonically with configurational entropy, giving rise to a folding funnel (Onuchic et al., 1995). However, “downhill folding” does not refer to the decrease of contact enthalpy when a protein moves down in the funnel. Rather, downhill folding in free energy occurs when the decreasing enthalpy overpowers the decreasing entropy so that even the free energy G=H-TS decreases monotonically from unfolded to folded state (see Fig. 18). Folding downhill in free energy was one of the most unexpected predictions of statistical mechanical folding models.

Fig. 18. Folding in enthalpy and free energy.

(Left) Protein enthalpy (H_c) as a function of configurational entropy (S_c) for two proteins. Enthalpy is reduced as both proteins fold because native contacts are made as the chain collapses. For one protein (red), the entropy decreases before the enthalpy decreases. For the other protein (blue), enthalpy and entropy decrease together. The enthalpy-entropy relationship is often plotted symmetrically (dotted red and blue) to convey the idea that many more coordinates are involved in this ‘funnel.’ Furthermore, the trace is usually roughened to convey the idea that non-native interactions may cause dips in the enthalpy. (Right) The ‘blue’ vs. ‘red’ difference is reflected in the free energy landscapes of the two proteins. While ΔG is similar for both proteins, only the ‘red’ protein encounters an activation barrier to folding (ΔG^†), caused by the initial drop in entropy without a compensating drop in enthalpy. The ‘blue’ protein folds downhill because enthalpy and entropy compensate along the way to the folded state. Solvent effects can be included in this description by modifying G(x). Non-native contacts can be included by adding small wells (‘roughness’), or by adding a coordinate-dependent diffusion coefficient, depending on how coordinates are chosen to describe the system. The ‘choice problem’ arises for the reasons illustrated by Fig. 17.

Although natural protein domains that fold downhill are still rare (Sborgi et al., 2011; Cerminara et al., 2012), many of the fast folders described in section 3 can be stabilized so that some fraction of the population folds without barrier crossing. Stabilization tilts the double well free energy towards a single well free energy by Hammond’s postulate: if the free energy of the folded protein is lowered, the free energy of the transition state is also lowered (albeit by a lesser amount). Many of the proteins discussed in section 3 have been stabilized and thus sped up (via mutations or solvent conditions) to exhibit downhill folding phases. It may not be obvious at first glance why thermodynamic stabilization should have any effect on the amplitude of the downhill folding phase (but see Figs. 3 and 4). Recall that for λ_6-85 the molecular phase emerged as the activated relaxation time dropped below 20 μs. The faster activated time indicates that the barrier between the native well and the transition state has decreased. As the barrier gets lower, it becomes more likely for molecules to find themselves resting on the barrier, poised to fold or unfold without waiting to hop over barrier (Chandler, 1987; Yang & Gruebele, 2004b; Liu & Gruebele, 2007). The larger Boltzmann factor discussed in section 4.1 is responsible for the larger barrier-top population. Increasing the size of the barrier-top population increases the size the downhill folding phase (or molecular phase). A similar phenomenon is implicated in the emergent molecular phase of CspA after large temperature jumps (Leeson et al., 2000).

Proteins may also be engineered so that they switch from two-state towards downhill folding even at the denaturation midpoint (Liu & Gruebele, 2007). And of course, it has been observed in a few natural proteins, such as BBL and gpW (Sborgi et al., 2011; Cerminara et al., 2012). In that case, a lower barrier occurs even without further biasing of the protein towards the native state. Instead of switching from a double well free energy near the melting temperature to a single well at low temperature, the free energy surface can be represented by a single well under all conditions.

Aside from putting a lower limit on the molecular speed limit, the observation of downhill folding phases along with activated phases (as is the case for most incipient downhill folders created by mutation) allows direct measurement of ΔG_a because the molecular rate fixes the ambiguous prefactor in the Arrhenius rate equation (see section 1). In this case, the Arrhenius equation at a temperature T for which k_m and k_a can be measured becomes (Yang & Gruebele, 2003):

$$k_a=k_m\exp (­\Delta G_{\mathrm{a}}/\mathit{RT})$$

which can be rearranged to find that

$$\Delta G_{\mathrm{a}}=\mathit{RT}\ln (k_m/k_a).$$

Two-state folding and downhill folding are surely not the most common folding mechanisms. Most proteins are larger than the model systems discussed in section 3. They contain multiple domains that fold independently on different time scales, or fold through metastable intermediates, or dwell in traps with non-native enthalpic contacts. However, small two-state and downhill folders fold very rapidly, and thus are the first proteins to be compared with molecular dynamics simulations. In addition, it seems likely that these more complicated folding behaviors are built up from the mechanisms (both productive and unproductive) observed in the study of fast folders. As computers become faster and our understanding of protein folding improves, it will become possible to study misfolding, metastable intermediates, and other complications of the folding process in simulations and experiments on appropriately modified fast folders. Directed studies of off-pathway protein dynamics will provide extra insight into consequences of misfolding and may shed light on the most dangerous conditions from the perspective of achieving successful folding. Avoiding these conditions provides evolutionary pressure on the development of folded states and folding pathways.

4.4 Folding and binding

Traditional pictures of proteins in the cell in do not incorporate the dynamism that studies of fast folders and other proteins have revealed. The textbook picture of protein binding, for example, postulates that two relatively rigid protein structures find each other like a lock and key (hence the “lock and key” mechanism that preceded more recent conformational selection and induced fit models). Such static models of protein function ignore evidence that protein structure and function are perturbed by the most general features of the cellular environment (Homouz et al., 2008; Dhar et al., 2010; McGuffee & Elcock, 2010). This environmental responsiveness is a consequence of the minimal stability of protein native states, and next generation models of binding incorporate this flexibility to drive, not inhibit folding.

Wolynes and co-workers have developed a theoretical treatment of “fly-casting,” a mechanism through which the formation of active multi-protein complexes induces folding in one or more component proteins (Shoemaker et al., 2000; Trizac, Levy & Wolynes, 2010). The fly-casting mechanism postulates that an unfolded protein can better form a binding interface with its partner because its increased conformational flexibility makes it easier to find favorable interface interactions. Theoretical treatments of complex formation show that an unfolded binding target increases the overall cooperativity of binding. Increased cooperativity may serve to increase the efficiency of complex formation: highly cooperative processes will tend towards completion more regularly than broad binding transitions. Fly-casting is not likely to induce global folding of multi-domain proteins, but rather folding of their signaling recognition modules: binding enhancement is greatest when the interface domain and the barrier to folding are small. Small, fast folding proteins generally share these characteristics, giving rise to the suggestion that some fast folders may bind in vivo substrates in a partially unfolded state, quickly folding when the binding interface or target sequence is found. This hypothesis is bolstered by the large fraction of natural multi-module proteins that have fast-folding DNA binding domains (e.g. λ repressor), where such fly-casting is most studied and thought to be most helpful. A folding simulation of a small, engineered homodimer indeed showed that folding of either monomer only proceeded when the dimer interface was stabilized by inter-monomer interactions, both native and non-native (Piana, Lindorff-Larsen & Shaw, 2013). Though these fly-casting interactions enhanced folding and complex formation, they also allowed formation of incorrect, trapped structures, just as downhill free energy landscapes speed up folding but also increase the tendency for aggregation (see Section 3.12, above). Similarly, the binding of an intrinsically disordered activation domain to its partner protein was shown by NMR to proceed through the formation of non-specific, intermolecular hydrophobic contacts while native contacts are formed during the folding of the disordered domain. Folding of the disordered domain was only detected in the presence of the binding partner (Sugase et al., 2007).

One emerging area of research into the interplay of protein binding and folding is the study of Intrinsically Disordered Proteins (IDPs) in the cellular environment. Despite their name, evidence is mounting that many IDPs are, in fact, well structured in the cells. The “switch” from disordered to folded is facilitated by binding: either to each other (alpha-synuclein is now thought to be a tetramer in vivo (Bartels, Choi & Selkoe, 2011)) or to a ligand (Kriwacki et al., 1996; Sugase et al., 2007; Gambin et al., 2011). It is possible that structured IDPs in vivo are an extreme example of the more general flycasting mechanism favoring coupled protein binding and folding. This possibility has interesting implications for the folding mechanism of IDPs in vivo. We saw above that putative fly-casting targets share many characteristics with fast folding domains. If IDPs are, in fact, extreme fly-casting targets, then this might suggest that, in the right environment, IDP domains fold quickly. This is in stark contrast to what we observe in vitro, which is that IDPs never fold – or at least fold very slowly. As techniques for studying IDPs are developed both in vitro and in vivo, researchers will be able to directly investigate the mechanism of folding and its relationship with binding.

The interplay between folding and binding has been suggested as a source of evolutionary pressure towards downhill folders. We have seen that reaching the global downhill folding limit with fast two-state proteins requires careful coordination of sequence mutations and environmental conditions (Liu & Gruebele, 2007). Slow ribosomal folding of these proteins certainly does not provide any evolutionary pressure towards downhill folding. To find such folding in naturally occurring domains like BBL and gpW suggests a high degree of selective pressure favoring this specialized folding mechanism (Fung et al., 2008).

But what role could downhill folding have to play in the molecular processes of the cell? We can look to in vitro experiments to guide our intuition. Studies of WW domain, λ repressor, and other fast folders have shown that downhill folding is exquisitely sensitive to environmental conditions: sequences that are downhill folders at one temperature or pH may not be at another (Leeson et al., 2000; Yang & Gruebele, 2004b; Liu et al., 2008). A corollary of this sensitivity is that the low-energy ensemble of downhill folders is extremely responsive to environmental changes. Muñoz and coworkers have proposed that this environmental responsiveness may be used by the cell to respond to changes in cellular conditions, modulating ligand binding or complex formation via the conformational state of downhill folding domains (Naganathan et al., 2006; Cerminara et al., 2012). Instead of acting like digital switches (bound or unbound), the continuously variable structure of single well downhill folders would act like a rheostat with variable folding-binding affinity (see Fig. 16). Since the equilibrium ensemble of a downhill folder is continuously adjustable by environmental conditions, the environmental changes needed to alter binding affinity may be much smaller than those required to move a two-state folder from one well to another (Cerminara et al., 2012). This may be a mechanism by which the cell can sensitively respond to small changes in its environment.

5. Whence from here?

In the 1960s through 1980, the way to determine an accurate structure of a small molecule was to measure its microwave spectrum or rotationally resolved infrared spectrum. Quantum chemistry, or ab initio, calculations were simply too crude. In the 1980s, experimental measurements on exotic molecules (ions, radicals) helped refine the computational packages for the most difficult cases, showing which methods converged best in the least time. Nowadays, the quickest and most accurate way to get a small molecule structure is to run an ab initio computer calculation.

Protein folding has not reached that holy grail yet, although signs of it are finally visible: for small proteins up to ~100 residues with folding times < 1 ms, good quality structures, and in some cases even mechanisms, can be obtained. The current generation of empirical force fields, as well as computational power, need to improve further before larger proteins, multi-domain proteins, or slower folders can be folded by physical modeling on the computer.

Force fields need to become less semi-empirical (be accurate over a wider range of solvent conditions). Validation over a range of temperature and pressures, together with improved water and solute models that bring folding temperatures to the experimental value, would be a good start, and are the subject of intensive study at present.

It is clear that even apparent two-state and downhill folders, once one goes from the macrostate to the mesostate level, can harbor complex mechanisms due to a combination of interactions distributed throughout the protein structure. Understanding these better will be important not just for folding, but for understanding protein functional dynamics. The paradigm of “conformational selection” is now becoming better established, and low energy structures explored by proteins during unfolding may well be top candidates for functional dynamics. So while functional requirements may slow down folding due to higher barriers or unnecessary intermediates, there is also synergy there: studies of folding can illuminate functional states. The same goes for dysfunctional states. Here experimenters must contribute by finding fast-reacting model systems for aggregation, misfolding and binding.

Simulations of folding binding are particularly important because biomolecular interactions are prime targets for drugs. More accurate simulations that include physical dynamics could make the process of whittling down drug targets much less expensive than high throughput experiments. Of course, the molecular recognition process itself is only one facet of the problem, others being biodeliverability and latency.

To make all this possible, simulators need to work on computing reaction coordinates that can be compared quantitatively: ones that do not require difficult quantum mechanical algorithms (too expensive for now), but relate directly to experiment. Standins that can be computed from atomic coordinates and momenta and that have been validated with large experimental data sets are a good start. (E.g.: computed Trp surface exposed area and local electric field to correlate with experimental peak fluorescence wavelength.) Good coordinates are more important than ever as we are able to compare experiment and simulations at ever finer levels of detail.

In the meantime, fast folding experiments must explore the effects of environment on folding and binding: ‘biological water’ at the surface of biomolecules, crowding, and chemical interactions in cells or at cell surfaces modulate folding, binding and function. There is evidence for another level of loose association above quaternary structure (sometimes dubbed ‘quinary structure’ (McConkey, 1982)) that corresponds to the ~ RT time scales relevant for fast folders, but has sufficient benefits to be selected for by evolution. The first coarse grained description of cell’s interiors are already coming on line, and they should be adapted to simulate protein folding soon.