Nonequilibrium Dissipation-free Transport in F₁-ATPase and the Thermodynamic Role of Asymmetric Allosterism

Abstract

F₁-ATPase (or F₁), the highly efficient and reversible biochemical engine, has motivated physicists as well as biologists to imagine the design principles governing machines in the fluctuating world. Recent experiments have clarified yet another interesting property of F₁; the dissipative heat inside the motor is very small, irrespective of the velocity of rotation and energy transport. Conceptual interest is devoted to the fact that the amount of internal dissipation is not simply determined by the sequence of equilibrium pictures, but also relies on the rotational-angular dependence of nucleotide affinity, which is a truly nonequilibrium aspect. We propose that the totally asymmetric allosteric model (TASAM), where adenosine triphosphate (ATP) binding to F₁ is assumed to have low dependence on the angle of the rotating shaft, produces results that are most consistent with the experiments. Theoretical analysis proves the crucial role of two time scales in the model, which explains the universal mechanism to produce the internal dissipation-free feature. The model reproduces the characteristic torque dependence of the rotational velocity of F₁ and predicts that the internal dissipation upon the ATP synthesis direction rotation becomes large at the low nucleotide condition.

Introduction

One of the major advances in modern statistical physics is the understanding of stochastic thermodynamics, where behavior of thermodynamic machines in the fluctuating world is the main target of study (1,2). In sharp contrast to macroscopic systems, fluctuations play significant roles in microscopic engines (3,4), as in the cases of biomolecular motors (5). Recent studies have further clarified the role of information in thermodynamics (6,7), which provides new perspectives on the design principle of molecular motors (8,9). In light of these developments both in theory and experiments, we are now in the position to reveal the fundamental rules that govern nonequilibrium molecular machines.

Among many molecular motors, the detailed energetics of F₁ has attracted special attention because of its important roles in the metabolic network, and its unique feature of reversibility (10–13). Rotational motion of F₁ in the ATP hydrolysis direction is roughly explained as follows: the $\alpha \beta$ subunits change their conformations following the events of the binding of ATP, the hydrolysis reaction ATP → adenosine diphosphate (ADP) + phosphate (Pi), and the release of Pi and ADP. These chemical-reaction coupled conformation changes induce the γ subunit (shaft) to rotate 120° per single ATP input and ADP + Pi output. Energetically (Fig. 1 A), in the absence of load, the income of this motor is the chemical free energy of ATP $\left(\Delta \mu \right)$, and the outflow is made either through the γ shaft rotation ($Q_{\text{ext}}$, external dissipation) or the switching of conformation in $\alpha \beta$ ($Q_{\text{int}}$, internal dissipation).

Figure 1.

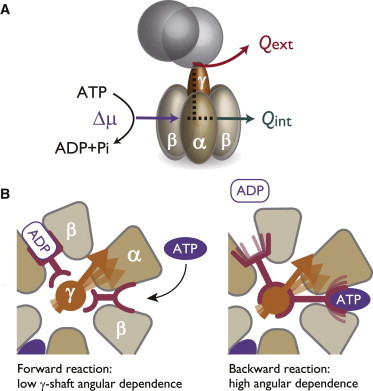
The totally asymmetric allosteric model (TASAM) explains the internal dissipation-free feature of F₁-ATPase. (A) Summary of the energy income and outflow of F₁ in the ATP hydrolysis rotation in the absence of external load. Free energy of the chemical fuel $\left(\Delta \mu \right)$ is dissipated through the rotary motion of the γ shaft $\left(Q_{\text{ext}}\right)$, or through the $\alpha \beta$ complex where the reactions take place $\left(Q_{\text{int}}\right)$. (B) Schematic of the TASAM. When the motor is waiting for the ATP to bind (left), the binding site is free from the control by the γ shaft rotary angle. Conversely, once the ATP is bound to the motor and the ADP release has proceeded (right), the affinity of the binding sites to the nucleotides strictly depends on the γ shaft angle. To see this figure in color, go online.

Recent precise experiments on F₁ have shown that, in the absence of external load, the chemical energy consumption is made almost 100% through the rotational motion, $Q_{\text{ext}}\sim \Delta \mu$, meaning that the internal dissipation is almost zero (14,15), $Q_{\text{int}}\sim 0$. This highly suggestive result prompts us to consider the hidden rules that govern molecular motors. In fact, the established theories in stochastic thermodynamics (e.g., the fluctuation theorem (16–18) and the second law) prove that the total energy dissipation is given by $\Delta \mu =Q_{\text{ext}}+Q_{\text{int}}$ but cannot explain any restrictions that rule the individual values of $Q_{\text{ext}}$ and $Q_{\text{int}}$. One study shows another surprising aspect of F₁; the internal dissipation-free feature does not depend on the rotational velocity (14). Conceptual interest lies in the fact that these observed data reflect the truly nonequilibrium character of F₁ and include more information than the equilibrium; the internal dissipation is a quantity that cannot be determined even if the full free energy landscape is measured or calculated.

Interestingly, the chemical reactions, which are the main source of the rotational motion, are themselves controlled by the rotary position of the γ shaft (19,20), which is a feature known as allosterism. The amount of internal/external dissipation in a model may be manipulated by setting various types of γ angular dependence of the chemical reactions. In a recent study (21), a load-sharing factor was introduced as a parameter for this angular dependence. It was observed that in the case where the load-sharing is assumed to be largely asymmetric, numerical simulation produces consistent results with the internal dissipation-free feature of F₁-ATPase (14).

Following the approach taken in (21), we reconsider the features of F₁ at the level of the phenomenological model, where only the rotary degree of freedom of the γ shaft and the nucletide state of the $\alpha \beta$ subunits are taken into account. Specifically, we introduce the totally asymmetric allosteric model (TASAM, Fig. 1 B) to explain the internal dissipation-free nature of F₁. The key assumption in this model is that the ATP binding to the motor, which is the limiting slow process, is allowed with equal probability over the γ shaft angle. The motor thus passively waits and lets the ATP to bind freely and decides whether or not to release this ATP depending on the angle of the γ shaft. As we shall see in detail (Fig. 2 C), numerical results in our model show that $Q_{\text{ext}}$ is kept close to $\Delta \mu$ for a broad range of rotational velocity. We identify the crucial role of two time scales in the TASAM, which explains the universal mechanism in the model to produce the internal dissipation-free feature. Moreover, we analyze the nucleotide concentration dependence on the torque-velocity relation (see Fig. 5), and we find that a certain asymmetric pattern observed in experiment is reproduced by the TASAM.

Figure 2.

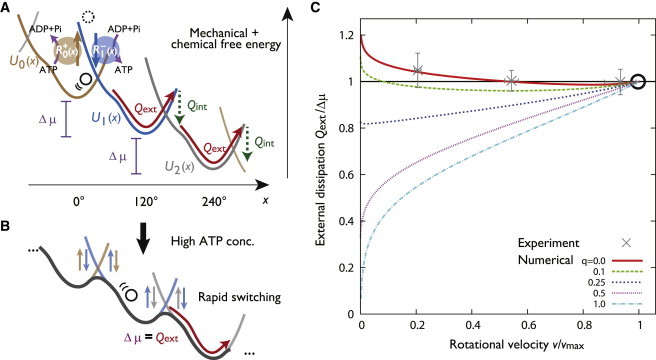
External heat dissipation defined in the molecular motor model and its dependence on transport velocity. (A) Potential switching model and schematic of the heat dissipation for the hydrolysis-driven rotation of F₁ in the absence of applied external torque (F = 0). The black circle represents the angular position of the probe bead attached to the γ subunit. The kinetics of x is described by an overdamped Brownian motion inside each potential. Potentials are switched according to the angular position dependent rates $R_n^{\pm }\left(x\right)$. (B) Effective potential in the high ATP concentration limit. Since the switching dynamics is fast, the independent potentials become invisible, and the dynamics follows the tilted periodic potential description, irrespective of the form of $R_n^{\pm }\left(x\right)$. In this limit, the external dissipation $Q_{\text{ext}}$ becomes equal to $\Delta \mu$. (C) Rotational velocity v versus the external heat dissipation per step $Q_{\text{ext}}$. The red line is the case of the TASAM (q = 0), and the other lines correspond to various $q\ne 0$ models introduced by Eq. 5. Experimental data were obtained from Toyabe et al. (14). (Errorbars: standard error of mean). The black circle indicates the high ATP concentration limit. To see this figure in color, go online.

Figure 5.

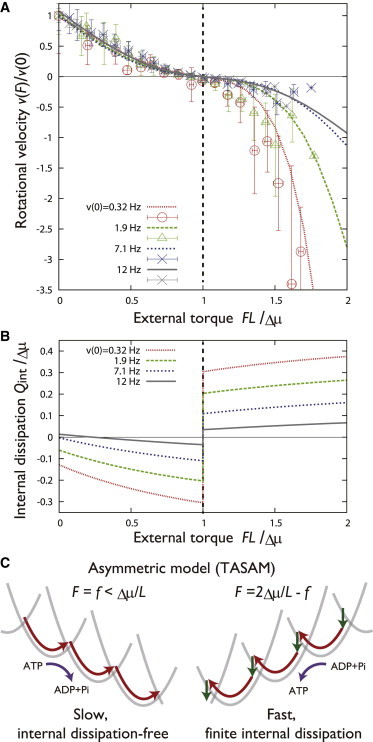
Characteristic torque dependence of velocity and dissipation in the TASAM. (A) External torque dependence of the rotational velocity in the TASAM (numerical, lines) and the corresponding values obtained from experiment (points with standard deviation errorbars (25)). Velocity is normalized using its value at F = 0, which is shown as the title of each lines. The, v = 0.32, 1.9, 7.1, and 12 Hz cases correspond to W = 1.7, 15, 120, and 1000 sec⁻¹ in the model, respectively, with other parameters fixed. (B) External torque dependence of the internal dissipation $Q_{\text{int}}$ in the TASAM. At low nucleotide conditions (small W), $Q_{\text{int}}$ significantly deviates from zero at the presence of large torque. (C) ATP hydrolysis and synthetic rotation cases in the TASAM at the low nucleotide concentration condition. In contrast to the symmetric model (Fig. 4B), the absolute velocity and the value of internal dissipation are different in the $F=f$ and $2\Delta \mu /L-f$ cases. To see this figure in color, go online.

Our stochastic model is based on confirmed properties of F₁, such as the discrete steps (22,23), mechanical potentials (24), and large stall force (25) with all the real parameters. However, we do not refer to the microscopic interactions, for example, at the amino acid residue level, which is typically required in molecular dynamic simulations. Nevertheless, the key feature of the F₁ energetics and dynamics seem to be well reproduced by the simple one-dimensional description. The existence of such consistent description encourages us to consider the fundamental design principle behind molecular machines, since at this coarse-grained scale, comparison between different biomotors (including linear processive motors) and blueprints of future nanomachines is possible.

Materials and Methods

Model description

We introduce a simple one-dimensional model based on the Brownian motion and potential switching scheme. The mechanical potentials $U_n\left(x\right)$ trap the rotational degree of freedom x of the probe attached to the tip of the γ subunit. Here, $n=0,\pm 1,\pm 2,\dots$ is the amount of ATP consumed through the rotary motion. Each potential is created by the interaction between the γ subunit and the $\alpha \beta$ subunits (22,24), and the joint between the γ subunit and the probe bead (26).

Because of the threefold symmetry of the motor (Fig. 1), the potentials are translationally identical $U_n\left(x\right)=U_0\left(x-120°\times n\right)$. Since the substeps corresponding to the hydrolysis/synthesis reactions + releasing/binding of Pi are fast (23), the hydrolysis dwell potentials are effectively included in $U_n\left(x\right)$, and the ATP binding followed by ADP release is considered as the rate-limiting step in the full reaction scheme. By assuming that the ATP binding dwell and the hydrolysis dwell potentials are harmonic with the same spring constants (19), k, the form of $U_n\left(x\right)$ is estimated as an effective potential, $U_0\left(x\right)/k_{\text{B}}T=k{x}^2/2-\text{log}\left[\text{exp}\left(-klx\right)+\text{exp}\left(\tilde{\Delta }\mu /k_{\text{B}}T+k{l}^2/2\right)\right]$. Here, $l=40°$ is the angle of the substep, and $\tilde{\Delta }\mu$ is the free energy difference between the ATP hydolysis dwell state and the binding dwell state. By fitting the data in another study (24), we obtained $k=0.0061$ deg⁻² and $\tilde{\Delta }\mu =5.2k_{B}T$, which are in good agreement with previous independent observations (19,23,26). See Supporting Material, Section A for the derivation of,$U_0\left(x\right)$.

The angular position of the probe bead, x, undergoes an overdamped Brownian motion inside each potential:

$$\text{Γ}\dot{x}=-\frac{\partial }{\partial x}{U}_n\left(x\right)-F+\sqrt{2\text{Γ}{k}_{\text{B}}T}{\xi }_t,$$ (1)

where ${\xi }_t$ is the Gaussian white noise with unit variance, $k_{\text{B}}$ is the Boltzmann constant, F is the applied external torque, $\text{Γ}$ is the friction coefficient determined by the size of the probe bead, and T is the temperature of the water (i.e., the heat bath). The potentials are switched according to chemical-reaction induced Poissonian transitions (Fig. 2 A). The switching rate in the forward direction $\left(n\to n+1\right)$, $R_n^{+}\left(x\right)$, corresponds to the ATP binding + ADP release reaction, and the rate in the backward $\left(n\to n-1\right)$ direction, $R_n^{-}\left(x\right)$, corresponds to the ADP binding + ATP release, where we assume $R_n^{\pm }\left(x\right)=R_0^{\pm }\left(x-120°\times n\right)$. The switching rate functions satisfy the local detailed balance condition (Fig. 2 A):

$$\frac{R_n^{+}\left(x\right)}{R_{n+1}^{-}\left(x\right)}=\text{exp}\left\{\frac{1}{k_{\text{B}}T}\left[U_n\left(x\right)-U_{n+1}\left(x\right)+\Delta \mu \right]\right\},$$ (2)

where we used the free energy difference between a single molecule ATP and ADP + Pi, $\Delta \mu =\Delta {\mu }_0+k_{\text{B}}T\text{log}\left(\left[\text{ATP}\right]\left[{\text{H}}_2\text{O}\right]/\left[\text{ADP}\right]\left[\text{Pi}\right]\right)$. The finite free energy input $\Delta \mu$ in Eq. 2 allows the motion of x to show a finite steady-state current in the plus direction, whereas at $\Delta \mu =0$ the rotational motion stalls and the dynamics is in equilibrium. The condition in Eq. 2 also guarantees that the rotational motion would stall when the external torque $F=\Delta \mu /L$ is applied to the motor, and would rotate backward (i.e., the ATP synthesis rotation) when $F>\Delta \mu /L$, corresponding to the tight-coupling feature of F₁ confirmed in the experiment (25).

Here we note on the requirement to introduce our potential switching model. Although it has been clarified that the discrete position of the gamma subunit (0°, 80°, 120° …) is coupled strongly to the nucleotide state and conformation of the alpha-beta subunits (11,22,23), what occurs in between these discrete angles has yet to be explained. In fact, it has been clarified in previous experiments (19,20) that the chemical reactions do not necessarily occur precisely at a certain angle of the γ shaft, meaning that the timing of chemical reaction is indeed a stochastic phenomena with respect to the angular position. Furthermore, it was shown in another study (24). that there exist separate potentials corresponding to the discrete positions with a certain extent of overlap. Taking these facts together, it is required to adopt the model depicted in Fig. 2 A to reproduce the experimentally observed kinetics and energetics of the F₁ motor.

In the stochastic dynamics of our model, there are two paths for the motor to exchange energy with the surrounding water (Fig. 2 A). One path is through the change of rotational position, which corresponds to the external dissipation, since this energy flows out from the γ shaft. The other path is through the change of mechanical potential, which is the internal dissipation corresponding to the energy used to change the conformation of $\alpha \beta$. To characterize these quantities, we introduce the probability density function $P_n^{\text{ss}}\left(x\right)$, which describes the steady-state probability of x under the condition that the trapping potential is $U_n\left(x\right)$. Note that $P_n^{\text{ss}}\left(x\right)=P_0^{\text{ss}}\left(x-120°\times n\right)$ because of the translational symmetry. We further define ${\text{Λ}}_n\left(x\right):=P_n^{\text{ss}}\left(x\right)R_n^{+}\left(x\right)-P_{n+1}^{\text{ss}}\left(x\right)R_{n+1}^{-}\left(x\right)$, which is the steady-state switching rate that characterizes the switching position. The first term in the right-hand side corresponds to the probability density of the position at which the forward switching $\left(n\to n+1\right)$ occurs, and the second term corresponds to that of the backward switching $\left(n+1\to n\right)$. By integrating ${\text{Λ}}_n\left(x\right)$, we obtain the net transport rate from potential n to $n+1$, $v:={\int }_{-\infty }^{\infty }dx{\text{Λ}}_n\left(x\right)/3$, which is the steady-state rotational velocity.

The heat dissipations $Q_{\text{int}}$ and $Q_{\text{ext}}$ in the model are defined as the steady-state average of the internal and external heat dissipation per 120° step, respectively (Fig. 2 A). $Q_{\text{int}}$, the energy dissipation accompanying the switching of n, is calculated by the following:

$$Q_{\text{int}}:=\frac{1}{3v}\int dx{\text{Λ}}_n\left(x\right)\left[U_n\left(x\right)-U_{n+1}\left(x\right)+\Delta \mu \right],$$ (3)

where $U_n\left(x\right)-U_{n+1}\left(x\right)+\Delta \mu$ corresponds to the total energy shift upon the potential switching $n\to n+1$ at position x, and the average is taken with respect to the probability distribution of the switching position. $Q_{\text{ext}}$, the dissipation through the spatial motion of x, is the difference between the total dissipation and the internal one:

$$Q_{\text{ext}}:=\left|\Delta \mu -FL\right|-Q_{\text{int}}.$$ (4)

Here, FL is the work performed by the motor against the external torque per forward step, and therefore $\left|\Delta \mu -FL\right|$ corresponds to the total dissipation per step. We take the absolute value since the average stepping direction changes its sign at $FL=\Delta \mu$.

Since direct measurement of $Q_{\text{ext}}$ is technically challenging, it has been estimated through indirect measurement in previous experiments (14,15). The key idea in these experiments is that $Q_{\text{ext}}$ is related to the extent of the violation of the fluctuation response relation (27), and thus may be quantified through the measurement of the angular velocity fluctuation and the response to small perturbative torque. Using this method, $Q_{\text{ext}}$ has been obtained without referring to $\Delta \mu$ or the detail of the mechanical potential (14,15).

Data of rotational velocity and external heat dissipation (Figs. 2 and 5) and the switching position probability densities (Fig. 3) were obtained by numerically solving the Fokker-Planck equation corresponding to the model (Eqs. 1 and 5). We used the diffusion constant $k_{\text{B}}T/\gamma L^2=3.3$ sec⁻¹ that was noted previously (24). $\Delta \mu$ was set as 18.3 $k_{\text{B}}T$ in Figs. 2 and 5, and 16.5 $k_{\text{B}}T$ in Fig. 3, corresponding to earlier experiments (14), (15), and (24), respectively.

Figure 3.

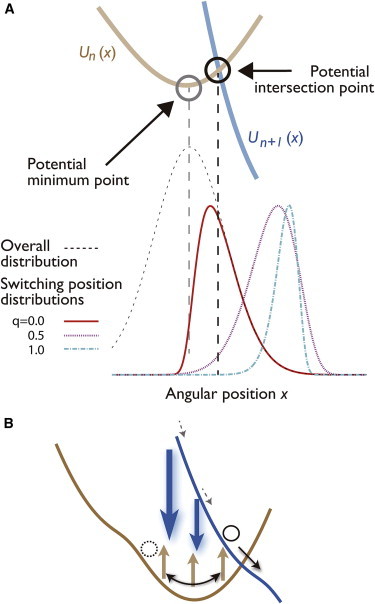
Switching position distribution of the TASAM. (A) Distribution of the switching angular position at the slow rotation rate condition. Numerically obtained switching position distribution in the q = 0 (red), 0.5 (pink), and 1 (light blue) models, compared for the same rotational rate v = 2 Hz (low velocity). The vertical axis is arbitrarily scaled. Although the steady-state distribution of the q = 0 model (black dotted line) has a peak at the minimum point of $U_n\left(x\right)$, the switching position density clearly has a peak around the intersection point, which is consistent with experiment (24). (B) Mechanism behind the internal dissipation-free feature of the TASAM. The potential switching may occur at any angle in the TASAM (brown arrows), whereas the backward switching of the potential follows instantaneously if the energy required for the forward switching was too large (blue arrows). Suppression of switching at high energy difference positions lets the switching to occur only around the potential intersection point, leading to the $Q_{\text{int}}\sim 0$ feature. To see this figure in color, go online.

Results

First, we consider the case where $\left[\text{ATP}\right]$ and $\left[\text{ADP}\right]$ are set high under a fixed ratio $\left[\text{ATP}\right]\left[{\text{H}}_2\text{O}\right]/\left[\text{ADP}\right]\left[\text{Pi}\right]$. We show in the model that the steady-state rotation rate v converges to a finite maximum velocity $v_{\text{max}}$, and the external dissipation $Q_{\text{ext}}$ converges to $\Delta \mu$. To illustrate this, we write $R_n^{\pm }\left(x\right)=W{f}_n^{\pm }\left(x\right)$, where W is the rate characterizing the chemical reaction, and $f_n^{\pm }\left(x\right)$ are dimension-less functions that do not explicitly depend on $\left[\text{ATP}\right]$, $\left[\text{ADP}\right]$, or $\left[\text{Pi}\right]$ but only depend on the ratio $\left[\text{ATP}\right]\left[{\text{H}}_2\text{O}\right]/\left[\text{ADP}\right]\left[\text{Pi}\right]$ through $\Delta \mu$. Note that the nucleotide concentration condition set by $\left[\text{ATP}\right]$ and $\left[\text{ADP}\right]$ may be described using the two parameters, W and $\Delta \mu$.

Under a fixed $\Delta \mu$, a high $\left[\text{ATP}\right]$ and $\left[\text{ADP}\right]$ situation is represented by large W. When W is sufficiently large (see Supporting Material, Section A), we can prove that the dynamics becomes independent of the form of $f_n^{\pm }\left(x\right)$, and the motion of the probe is then described by the one-dimensional Brownian motion in an effective tilted periodic potential (Fig. 2 B). This means that the switching of mechanical potentials becomes too fast to be observed as distinct steps. $v_{\text{max}}$, which is the steady-state velocity for $W\to \infty$ under fixed $\Delta \mu$, may be calculated using this effective potential. Velocity saturation at high ATP concentration is a well-known property in molecular motors, which has been phenomenologically understood through the Michaelis-Menten curve (5). Because in this limit the potential switching dynamics is sufficiently fast and reaches equilibrium, the energy dissipation accounting for the $\alpha \beta$ conformation change is balanced and becomes zero, $Q_{\text{int}}=0$. Therefore, the dissipation through the rotational motion equals the free energy input $Q_{\text{ext}}=\Delta \mu$, in the absence of torque. This result is also consistent with the observation in the previous experiment (15), where the external force dependence of $Q_{\text{ext}}$ was measured under the condition of high nucleotide concentrations (see also Fig. 5 B).

The previous torque-free experiment (14) shows that even when (ATP) is low enough and $v<v_{\text{max}}$, the external dissipation $Q_{\text{ext}}$ is still close to $\Delta \mu$ (Fig. 2 C, crosses). Although we have shown that the feature where $Q_{\text{ext}}\sim \Delta \mu$ is achieved for any switching rate function when $v\sim v_{\text{max}}$, the external dissipation has a strong dependence on the functional form of $f_n^{\pm }\left(x\right)$ in the low velocity regime, since the value of $Q_{\text{int}}$ (and consequently, $Q_{\text{ext}}$) is determined by the typical position x at which the switching occurs (Fig. 2 A). The experimental observation is striking, since the individual functional forms of $f_n^{\pm }\left(x\right)$ are arbitrary as long as the detailed balance condition Eq. 2 is satisfied; there is no general reason for $Q_{\text{ext}}$ to become close to $\Delta \mu$ in the low velocity regime.

To see the significance of the experimental result for lower velocities, and to demonstrate the uniqueness and validity of the TASAM (Fig. 1 B), we parameterize the switching rate functions by introducing a parameter q $\left(0\le q\le 1\right)$ as follows:

$$\begin{array}{ccc}{f}_n^{+}\left(x\right)& =& \text{exp}\left\{\frac{q}{k_{\text{B}}T}\left[U_n\left(x\right)-U_{n+1}\left(x\right)+\Delta \mu \right]\right\},\\ f_{n+1}^{-}\left(x\right)& =& \text{exp}\left\{\frac{q-1}{k_{\text{B}}T}\left[U_n\left(x\right)-U_{n+1}\left(x\right)+\Delta \mu \right]\right\}.\end{array}$$ (5)

This q determines the asymmetry in the x-dependence of the forward and backward switching rates, while respecting the detailed balance condition. The TASAM is the case where the switching rate in the forward direction (ATP binding rate) has no dependence on the γ angle, and therefore, corresponds to q = 0. The case of q = 1 corresponds to another type of totally asymmetric model that is opposite to the TASAM, where the ATP binding event is strictly controlled by the γ angle, whereas the reverse reaction (ADP binding) is instead independent of the angle. In this manner, q describes the asymmetry in the extent of coordination between the angle of γ subunit and the ATP binding site.

Fig. 2 C shows the numerically obtained relation between v and $Q_{\text{ext}}$ for various values of q. The TASAM produces the internal dissipation-free feature $\left(Q_{\text{ext}}\sim \Delta \mu \right)$, which indeed has low dependence on the rotational velocity in the broad range tested in the experiment (Fig. 2 C, red). This feature of the model is preserved for the larger $\Delta \mu$ case (Fig. S9 in Supporting Material). Note that under a fixed functional form of $U_n\left(x\right)$, the maximum velocity $v_{\text{max}}$ does not depend on q, which is why we may compare $Q_{\text{ext}}$ between various models for the same $v/v_{\text{max}}$. Although all models produce $Q_{\text{ext}}=\Delta \mu$ for $v=v_{\text{max}}$ (black circle), the values of $Q_{\text{ext}}$ for the cases of $q>0.1$ deviate from $\Delta \mu$ significantly at lower v. Thus, we propose that the internal dissipation-free motor is obtained only by assuming low coordination $\left(q\sim 0\right)$ in the ATP free state and high coordination in the ATP bound state.

As seen in Eq. 3, the value of $Q_{\text{int}}$ is determined by the typical switching position. We compare ${\text{Λ}}_n\left(x\right)$ for the various models in the low velocity regime in Fig. 3 A. Although the steady-state distribution of the γ angle $\left(P_n^{\text{ss}}\left(x\right)\right)$ has a peak at the potential minimum point in this low velocity regime (Fig. 3 A, black circle), the peak of ${\text{Λ}}_n\left(x\right)$ in the q = 0 model is positioned close to the point $x=x_{c,n}$ where $U_{n+1}\left(x_{c,n}\right)-U_n\left(x_{c,n}\right)-\Delta \mu =0$, which we shall refer to as the potential intersection point. The mechanism that produces this behavior is that, although the ATPs most likely approach the motor when the γ angle is around the potential minimum point, the bound ATP is almost always kicked out instantaneously, because of the large energy difference required to switch the potential at such points, $U_{n+1}\left(x\right)-U_n\left(x\right)-\Delta \mu \gg k_{\text{B}}T$ (Fig. 3 B). The switching would inevitably occur at positions close to $x_{c,n}$, resulting in low energy dissipation in the potential switching (low $Q_{\text{int}}$). ${\text{Λ}}_n\left(x\right)$ of the TASAM (Fig. 3 A) agrees with the estimated distribution presented in (24) whereas in the cases where $q=0.5$ and 1 (Fig. S6), the peaks clearly shifted more toward the forward direction than the intersection point.

On theoretical grounds, the low velocity dependence of $Q_{\text{ext}}$ could be understood through the existence of the time scale ${\tau }_{\text{p}}$, which determines the minimal value of W at which the model presents the internal dissipation-free feature. We have numerically verified that in the q = 0 model, ${\tau }_{\text{p}}$ is the time scale of the angular position to relax inside a single potential (see Supporting Material). The crucial point is that this time scale ${\tau }_{\text{p}}$ is much larger than the time scale ${\tau }_{\text{v}}$, which determines the rotational velocity saturation and the single effective potential description (Fig. 2 B). The large separation between the values of ${\tau }_{\text{p}}$ and ${\tau }_{\text{v}}$ causes the experimentally accessible region of the value of W (corresponding to the ATP concentration) to fit inside the inequality ${\tau }_{\text{p}}^{-1}<W\le {\tau }_{\text{v}}^{-1}$, and the internal dissipation-free feature is observed at all velocity conditions as a consequence. In more practical words, our theory shows that when the actual motor adopts the TASAM, $Q_{\text{ext}}\sim \Delta \mu$ holds if (ATP) is as large as 0.1 μM for the 0.3 μm probe bead case (14,15). Since the velocity saturation occurs at (ATP) $>$ 5 μM under this condition (23), this lower bound concentration to observe $Q_{\text{ext}}\sim \Delta \mu$ is significantly small.

We next show how other features of the TASAM appear in measurable quantities. For the sake of schematic explanation, let us consider that the mechanical potentials are harmonic, $U_0\left(x\right)=K{\left(x/L\right)}^2/2$ (Fig. 4 A). Then, the potential switching model would be symmetric concerning the change of parameters and coordinate, $\left(F,q,x\right)\to \left(2\Delta \mu /L-F,1-q,-x\right)$. It follows from this symmetric property that in the case of q = 0.5 (symmetric model, Fig. 4 B), the torque dependence of the steady-state rotational velocity, $v\left(F\right)$, would show an antisymmetric curve with respect to the $F=\Delta \mu /L$ line. Indeed, this property is observed even when we assume the nonharmonic and realistic form of $U_0\left(x\right)$ (see Fig. S7). On the contrary, in the TASAM (q = 0), this feature is lost especially at low W, and the torque dependence of the velocity becomes sharper at $F>\Delta \mu /L$ than at $F<\Delta \mu /L$ ($v\left(0\right)=0.32,1.9,7.1$ Hz lines in Fig. 5 A). Remarkably, this feature of the TASAM matches with the experimental observation (25) (line points in Fig. 5 A), whereas other models fail to capture the observed feature of F₁ (Fig. S7).

Figure 4.

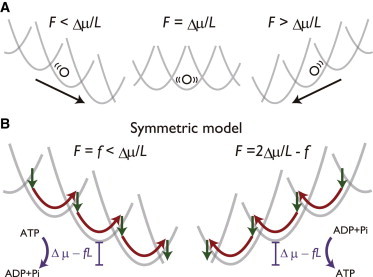
Property of the potential switching model under application of external force. (A) Schematic of the torque F dependence of the potential switching model. When the mechanical potential is harmonic, the model becomes symmetrical about the change $\left(F,q,x\right)\to \left(2\Delta \mu /L-F,1-q,-x\right)$. (B) In the case of q = 0.5, the absolute velocity and the balance between the internal/external dissipations become equivalent in the two cases, F = f and $2\Delta \mu /L-f$. To see this figure in color, go online.

We predict that similar difference between the torque-free and torque-applied cases would be observed in the internal dissipation, if the TASAM is adopted in the F₁ motor. In fact, Fig. 5 B shows that the internal dissipation-free nature of the TASAM is lost, especially when large torque $F>\Delta \mu /L$ is applied in the model. The low torque dependence of $Q_{\text{int}}$ at high nucleotide concentration has recently been measured and reported (15), which is consistent with the case of $v\left(0\right)=12$ Hz in Fig. 5 B. The validity of our model can be checked by further measuring $Q_{\text{int}}$ in the low nucleotide concentration condition ($v\left(0\right)=0.32,1.9$ and 7.1 Hz cases in Fig. 5 B).

The character of the torque dependence of TASAM could be understood through the property of the potential switching model discussed above. The dynamics of the TASAM at the presence of large applied torque, for instance $F=2\Delta \mu /L$, becomes equivalent to that of the q = 1 model with F = 0 with opposite velocity. As we show in Fig. 2 C and 3 A, the internal dissipation is large in the q = 1 case, which explains why we observe large internal dissipation in the presence of torque in the TASAM at low W. In this sense, adopting the TASAM in the forward step mechanism (ATP hydrolysis) is equivalent to adopting the q = 1 model in the backward step (ATP synthesis, Fig. 5 C). The absolute velocity at low nucleotide condition becomes faster at $F=2\Delta \mu /L$ than at F = 0 in the TASAM (Fig. 5 A), which is suggestive since the F₁ is forced to rotate in the ATP synthetic direction in physiological conditions. It shall be interesting to quantify how asymmetric the thermodynamic quantities and force-velocity relations are in other molecular motors.

Another way to verify our model is to directly estimate the switching rate functions. Recently, two groups have reported the angular position dependence of chemical reaction rates in the F₁ motor (19,20,28). By assuming that the ATP-on rates measured in these reports correspond to the forward switching rate in our model ($R_n^{+}\left(x\right)$), we obtain $q=0.07\sim 0.12$ when the harmonic potential model $U_0\left(x\right)=K{\left(x/L\right)}^2/2$ with $K=50k_{\text{B}}T$ is adopted (see Supplementary Material, Section B). This means that the angular position dependence of the ATP binding observed in experiment is relatively low compared with that of the ATP synthetic reaction ($R_n^{-}\left(x\right)$, corresponding to the combination of ADP-on and ATP-off), which is consistent with our assumption in the TASAM. We predict that if the direct measurement of $R_n^{-}\left(x\right)$ is possible, one should find a large dependence on the angle, since $0\sim q\ll 1-q\sim 1$.

Discussions

We now discuss the possibility of another model to explain the experimental results. Instead of the form we introduced in Eq. 5, we may choose a switching rate function that has a sharp peak at a fixed certain position that is very close to the potential intersection point $x_{c,n}$ under the experimental condition of $\Delta \mu =18.3k_{\text{B}}T$ (see Supporting Material, Section C). In such a model, the peak position of ${\text{Λ}}_n\left(x\right)$ would be independent of W, and the velocity independent feature of $Q_{\text{int}}\sim 0$ would be trivially obtained as long as $\Delta \mu$ is not changed. The first problem of this model is that it is difficult to explain the $\Delta \mu$ independence of small internal dissipation observed in (14). Since the intersection point is $\Delta \mu$ -dependent, the x-dependence of $R_n^{+}\left(x\right)$ must be explicitly changed depending on $\Delta \mu$ to preserve the intersection point switching. The second problem of this model is that the $v\left(F\right)$ curve would be antisymmetric for general W, opposed to the experimental observation (Fig. S8). This is because when $R_n^{+}\left(x\right)$ has a sharp peak at the intersection point, $R_{n+1}^{-}\left(x\right)$ would also have a sharp peak around the intersection point, and the model would effectively be symmetric about the parameter and coordinate change $\left(F,x\right)\to \left(2\Delta \mu /L-F,-x\right)$.

The motor conformation dependence of the chemical reaction has been understood as the diffusion-catch mechanism in various molecular motors (24,29,30). According to our theory, one way to realize such diffusion-catch feature is to simply make the chemical reaction that sets forward the desired motion to have flat dependence on the motor conformation. The potential switching scheme is a general model that appears for example in the context of electron transfer reactions (31). Therefore, it is of interest to find the applicability of the two scenarios of intersection point switching: the fast switching limit and the TASAM, in a wide range of problems in biological and physical chemistry.

In summary, we showed in this study that the general model for molecular motors is internal dissipation-free, but only when the chemical fuel concentration is high enough for the motor to reach maximum velocity. We introduced the TASAM to explain the internal dissipation-less feature of F₁ at the small velocity condition. We showed the consistency of the model with the experimentally observed feature in rotational velocity and the angular dependent chemical reactions, and further discussed on the possibility of large internal dissipation in the ATP synthetic rotation to be observed in future experiments. Since the basic scheme we considered is generic, and the assumption made on the TASAM is simple, we consider that our theory would serve as a prototype for physicists as well as biologists to further investigate the thermodynamics of nano-machines.