An efficient parallel algorithm for accelerating computational protein design

Abstract

Motivation: Structure-based computational protein design (SCPR) is an important topic in protein engineering. Under the assumption of a rigid backbone and a finite set of discrete conformations of side-chains, various methods have been proposed to address this problem. A popular method is to combine the dead-end elimination (DEE) and A* tree search algorithms, which provably finds the global minimum energy conformation (GMEC) solution.

Results: In this article, we improve the efficiency of computing A* heuristic functions for protein design and propose a variant of A* algorithm in which the search process can be performed on a single GPU in a massively parallel fashion. In addition, we make some efforts to address the memory exceeding problem in A* search. As a result, our enhancements can achieve a significant speedup of the A*-based protein design algorithm by four orders of magnitude on large-scale test data through pre-computation and parallelization, while still maintaining an acceptable memory overhead. We also show that our parallel A* search algorithm could be successfully combined with iMinDEE, a state-of-the-art DEE criterion, for rotamer pruning to further improve SCPR with the consideration of continuous side-chain flexibility.

Availability: Our software is available and distributed open-source under the GNU Lesser General License Version 2.1 (GNU, February 1999). The source code can be downloaded from http://www.cs.duke.edu/donaldlab/osprey.php or http://iiis.tsinghua.edu.cn/∼compbio/software.html.

Contact: zengjy321@tsinghua.edu.cn

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Structure-based computational protein design (SCPR) provides a promising tool in a wide range of protein engineering applications, such as drug design (Gorczynski et al., 2007), enzyme synthesis (Chen et al., 2009), drug resistance prediction (Frey et al., 2010) and design of protein–protein interactions (Roberts et al., 2012). The basic idea of SCPR is to find a new amino acid sequence based on a known structure, such that the total energy of the resulting molecular complex is minimized. In general, it is difficult to model an ideal protein design framework with the consideration of full backbone and side-chain flexibility, since there are usually a huge number of conformations that need to be sampled even for a small protein. Therefore, in practice assumptions are often made to reduce the complexity of the protein design problem. In most of protein design models (Roberts et al., 2012), the backbone structure is assumed as a rigid body, and only side-chains are allowed to rotate among a finite set of discrete conformations, called the rotamer library.

Under the rigid backbone assumption, the goal of SCPR is to search over all possible combinations of side-chain rotamer conformations of different allowed amino acids, trying to find the global minimum energy conformation (aka GMEC). Unfortunately, this problem has been proven NP-hard (Chazelle et al., 2004; Pierce and Winfree, 2002). Thus, a number of heuristic methods, such as Monte Carlo and genetic algorithms, have been proposed to find the approximate solutions to this problem (Kuhlman and Baker, 2000; Marvin and Hellinga, 2001; Shah et al., 2004; Street and Mayo, 1999). A recent study also suggests that we can split the entire task into small pieces so that a large-scale protein design problem can be solved in parallel (Pitman et al., 2014). However, these approaches cannot provide any provable guarantee of finding the global optimal solution (i.e., GMEC) as they may get trapped in a local optimum. In contrast, provable algorithms, such as tree decomposition (Xu and Berger, 2006), integer linear programming with a branch-and-bound technique (Althaus et al., 2002; Kingsford et al., 2005), dead-end elimination (DEE; Desmet et al., 1992) and A* search (Donald, 2011; Leach et al., 1998; Lippow and Tidor, 2007) assure that GMEC will be outputted as a final solution. In particular, the combination of DEE and A* search is popular in computational protein design (Donald, 2011; Lippow and Tidor, 2007). In this design strategy, DEE is first applied to prune a large number of unfavorable rotamers that are provably not part of the optimal solution. Next, the A* algorithm is used to search over all possible combinations of the remaining rotamers and compute the GMEC solution.

A number of DEE criteria have been proposed to improve the rotamer pruning and reduce the complexity of the rotamer conformation search space (Gainza et al., 2012; Georgiev et al., 2008, 2006). Although DEE can prune most rotamer conformations in the problem space, the A* algorithm still runs in exponential time in the worst case. In the DEE and A*-based framework, A* is generally one of the most time-consuming parts, especially for large-scale protein design problems. Thus it is vital to propose a faster algorithm to alleviate this bottleneck and therefore accelerate the protein design process.

In this article, we develop an efficient parallel A* tree search algorithm to accelerate computational protein design. By optimizing and parallelizing the computation of heuristic functions and the underlying data structure (i.e., the priority queue) for A* search, our algorithm significantly speeds up the A* search process. Our approach fully exploits the capacity of parallelism on a Graphics Processing Unit (GPU) to support the A* search for protein design. Tests on a benchmark dataset of 74 proteins show that our new algorithm runs up to 20 000 times faster than the original A*-based protein design algorithm, while still maintaining an acceptable amount of memory overhead. Thus, our parallel A* search algorithm can provide a practically useful tool for computational protein design.

2 METHODS

2.1 General-purpose computing on GPUs

General-purpose computing on graphics processing units (aka GPGPU), is a method to use a GPU together with a CPU to accelerate traditional computation. The main difference between CPU and GPU computational frameworks lies in the mechanisms they use to process calculation tasks. A CPU usually contains several highly optimized cores for sequential instruction execution, while a GPU typically contains thousands of simpler but efficient cores which are able to process different tasks in parallel. As an example, a high-end GPU, AMD Radeon 7970 Tahiti XT, has 2048 processing elements, while a powerful CPU such as Intel Xeon E7-8870 only contains 10 cores. Because of this characteristic, we must modify our algorithms originally designed for a CPU to take advantage of a large amount of parallelism to bring the full power of a GPU into play.

A GPU typically has a better performance in floating-point operation than a same-price CPU. For example, an NVIDIA GeForce GTX 580M has 952.3 theoretical GFLOPS (giga floating-point operation per second), while the theoretical GFLOPS of Intel Core i7-3960 is only 158.4, according to the specification released by Intel (Intel Corporation, 2011) and NVIDIA (NVIDIA Corporation, 2013), respectively. In our protein design problem, the main bottleneck is the floating-point operations for the heuristic function evaluation. Therefore, GPU acceleration is an appropriate tool to address such a problem.

A GPU has its own memory system. Thus it can provide a larger memory bandwidth than that of a CPU, which means GPU cores can retrieve and write data from/to the global memory faster than a CPU. This is especially suitable for those algorithms that are limited by the global memory bandwidth. However, before and after the computation, data need to be transferred between the memory of CPU and GPU through a relatively slow PCI-E bus. Thus, in general, we prefer a smaller ratio between the amount of time used to transfer input/output and the amount of time spent on computation. The A* search algorithm is suitable for such a computation framework, as the amount of floating-point computation makes the data transfer overhead negligible.

2.2 An A* search algorithm for protein design

In this section, we will first give some background about using A* algorithm to solve the protein design problem. In Section 2.2.1, we will provide a new approach to improve the computation of heuristic function in A* search. After that, Sections 2.3 and 2.4 will present a two-level parallelized A* algorithm that is suitable for a modern GPU. Finally, Section 2.5 will provide an extended A* algorithm that runs in bounded memory.

Under the assumption of a rigid backbone and discrete side-chain rotamers, SCPR can be generally formulated as an optimization problem, in which we aim to find an amino acid or rotamer sequence that minimizes the following objective function using 1- and 2-body energies:

(1)

where A is the set of discrete side-chain rotamer conformations (typically called the rotamer library), E₀ is the backbone or template energy, E₁(i_r) is the self energy of rotamer r for residue i (including intra-residue and rotamer-to-backbone energies), and E₂(i_r,j_s) is the pairwise interaction energy between rotamer i_r and j_s. The global optimal solution, i.e., GMEC, minimizes the above energy function in Equation (1).

The combination of DEE and A* search algorithm has been popularly used in computational protein design (Donald, 2011; Gainza et al., 2013; Georgiev et al., 2008; Leach et al., 1998; Lilien et al., 2005; Lippow and Tidor, 2007;). In this protein design strategy, the DEE algorithm is first applied to prune a number of rotamers that are provably not part of the optimal solution that minimizes the energy function in Equation (1). Next, an A* tree search algorithm is used to search over all possible combinations of the remaining rotamers and find the global optimal solution (i.e., GMEC). Traditional implementations of the A* search algorithm for protein design take a priority queue to decide the order of visiting nodes in the tree search. In this priority queue, elements are sorted by the following heuristic function as the evaluation measure for each expanding rotamer:

$$f(x)=g(x)+h(x),$$ (2)

where g(x) represents the actual cost from the starting node (i.e., the root of the A* search tree) to the current node x, and h(x) represents the estimated cost from the current node x to its destination (i.e., a leaf node in the A* search tree).

Each time, we extract a node with the smallest heuristic function value from the priority queue, expand it and then push the new expanded nodes back into the priority queue. We repeat this process until a target node (which is one of the leaf nodes with the minimum heuristic function value in the search tree) is found. Algorithm 1 describes a single-thread version of the traditional A* search procedure.

Algorithm 1 A single-thread version of the traditional A* search.

1: procedure A-Star(s, T)   ▹ s is the starting node and T is

2: Let Q be a priority queue   ▹ the set of target nodes

3: $Q\leftarrow \varnothing$

4: Push(Q, s)

5: while Q is not empty do

6:  $q\leftarrow$Pop(Q)

7:  if $q\in T$ then

8:   return the path found

9:  end if

10:  Let R be the set of expanded nodes from q

11:  Calculate f(x) for all nodes in R

12:  Push all the elements from R into Q

13: end while

14: end procedure

2.2.1 Improved computation of heuristic functions

In the A* search algorithm for solving the protein design problem, the actual cost from the starting node to current node x in the search tree is defined by

(3)

where D(x) is the set of residues in which rotamers have been already determined so far, E₀ is the backbone energy, E₁(i_r) is the self energy of rotamer i_r (including both intra-residue and rotamer-to-backbone energies), and E₂(i_r,j_s) is the pairwise interaction energy between rotamers i_r and j_s.

The estimated cost from current node x to the destination node is defined by

$$h(x)={\displaystyle \sum _{i\in U(x)}\stackrel{\min }{r}}(E_1(i_r)+{\displaystyle \sum _{j_s\in D(x)}{E}_2}(i_r,j_s)+{\displaystyle \sum _{k\in U(x)}\stackrel{\min }{u}}{E}_2(i_r,k_u)),$$ (4)

where U(x) represents the set of residues, in which rotamers have not been determined at current node x.

A brute-force method of calculating heuristic function f(x) = g(x) + h(x) takes O(n²m²) floating-point operations, where n is the length of protein sequence and m is the maximum possible number of rotamers per residue. Thus, it takes O(n²m²t) floating-point operations to compute heuristic functions for all nodes in the whole A* search tree using this brute-force method, where t is the total number of expanded nodes in the search tree. However, our analysis of Equation (4) reveals that we do not need to spend O(nm) time in repeatedly calculating ${\displaystyle {\sum }_{k\in U(x)}{\min }_u}{E}_2(i_r,k_u)$ each time when we evaluate the heuristic function. Since we search the conformation space residue by residue, there are only n possibilities for U(x). Therefore, we can use a two-dimension table T[U(x),i_r] to pre-compute all these possible values. This pre-computation process takes O(n²m) memory and O(n³m²) floating-point operations, but reduces time complexity of calculating f(x) down to O(n²m) when expanding a new node. Again suppose that the total number of expanded nodes in the final A* search tree is t. Then we bring down the overall time complexity from O(n²m²t) to O(n³m² + n²mt), which greatly improves the practical efficiency of the algorithm because in general t ≫ n.

We have also applied some technique to improve the computation of the g(x) function, which reduces its computational complexity from O(n²) to O(n). More details of the improved computation of g(x) can be found in Supplementary Material Section S1.

2.3 Parallelized computation of heuristic functions

The most time-consuming part of the A* tree search algorithm for protein design lies in the following two aspects: (i) Calculation of heuristic functions; (ii) Priority queue operations for expanding new nodes. To alleviate these two bottlenecks, we propose a new algorithm with two levels of parallelism to accelerate protein design. In this section, we will describe the first level of parallelism, that is, parallelized calculation of heuristic functions in A* search.

Although time complexity of calculating a heuristic function has been improved from O(n²m²t) to O(n³m² + n²mt) in Section 2.2.1, the computation of heuristic functions for new expanded nodes in A* search can be further sped up by exploiting the inherent parallelism capacity of a GPU. This step is quite straightforward, based on the observation that calculation of heuristic function f(x) for each expanded node is simply a series of independent arithmetic operations that can be directly parallelized. The flow chart of the first level parallelism can be found in Figure S1 in Supplementary Material Section S2.

2.4 Parallelized A* search for protein design

Although the method described in Section 2.3 can parallelize the A* search algorithm, the scale of the parallelism is still limited. In our protein design problem, the degree of parallelism in the computation of heuristic function is equal to the maximum number of rotamers per residue, which is normally in the order of 10 after pruning unfavorable rotamers using the combinations of different DEE criteria. Although this may be good enough for a single-machine CPU implementation, a GPU implementation definitely needs a larger degree of parallelism as we mentioned in Section 2.1.

Another problem is that the priority queue operations, including Push-back and Pop, take $O(\log N)$ time, where N stands for the total number of elements in the priority queue and usually is a large number. After computing the heuristic functions of newly expanded nodes, we need to push all of them back into a single priority queue. This part has not been parallelized and thus only exploits a small proportion of the parallel capacity of a GPU. Therefore, further improvement is needed.

A naïve idea is to pop a number of minimum elements from a single priority queue and then compute their heuristic function values. However, this method is still unable to parallelize the priority queue operations. Existing parallel priority queues (Rönngren and Ayani, 1997), such as pipelined binary heap (Moon et al., 2000), do not fit the GPU model well, mainly due to the high overhead of synchronization and branch divergence.

To address the aforementioned problems, we propose a new and parallel version of the A* search algorithm to fully exploit the power of parallelism in a GPU for accelerating protein design. This algorithm is mainly based on the observation that we do not need to extract the k lowest-energy conformations with the smallest f(x) values in gap-free sorted order. In fact, we only need to assure that the element with the smallest heuristic function value is extracted, and do not have to restrict others.

In our algorithm, we allocate hundreds of priority queues, and then let each thread operate on its own priority queue. Suppose we allocate k priority queues in total. The basic idea of our algorithm includes the following key steps:

1. Launch k threads to pop k minimum elements from k priority queues in parallel;

2. For each thread, expand new nodes for the extracted element;

3. Launch enough threads to perform parallelized computation of heuristic functions, using the procedure described in Section 2.3; and

4. Launch k threads to push all expanded nodes back into k priority queues.

The pseudocode of our algorithm, GA*, can be found in Algorithm 2. More details of this parallel algorithm are illustrated in Figure 1. The parallelism employed in our algorithm can directly address all the previously mentioned computational bottlenecks in A* search and thus greatly speed up the computational protein design process. In addition, our new algorithm introduces small overhead. It only requires a constant number of global synchronization points per round without much communication overhead.

Fig. 1.

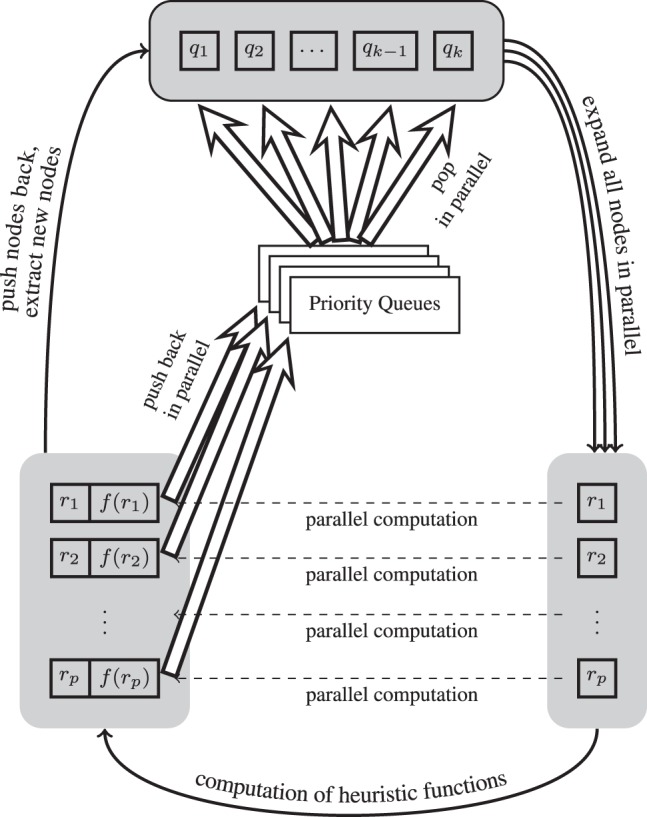
Flow chart of our GA* search algorithm for accelerating protein design. Symbols r_i represent all parallel expanded rotamers, and p is the total number of expanded nodes. A shaded and rounded square represents a global state, which can be regarded as a global synchronization point. The directional black edges mean that the procedure needs to be done between two synchronization points. The dashed arrows and the double bold arrows represent the data flow among different states and the priority queues, respectively. A group of similar arrows means that the operations are performed in parallel

Note that this pseudocode is just for computing the GMEC solution. Our algorithm can be easily extended to output all solutions within a specific energetic cutoff from the GMEC solution in gap-free sorted order, using the same strategy as in OSPREY (Chen et al., 2009; Gainza et al., 2013).

Algorithm 2 GA*: a GPU parallel A* algorithm for protein design.

1: procedure GA*(k, s, T)   ▹ k is the number of allocated

2: for $i\leftarrow 1$ to k in parallel do   ▹ priority queues, s is the

3:  Let Q_i be a priority queue   ▹ starting node, and T is

4:  $Q_i\leftarrow \varnothing$   ▹ the set of all target nodes,

5: end for

6: Push(Q₁, s)

7: $t\leftarrow \text{nil}$   ▹ t stores the best solution hitherto

8: while $\exists Q_i$ that is not empty do

9:  $R\leftarrow \varnothing$

10:  for i be the index where Q_i is not empty in parallel do

11:   $q_i\leftarrow$ Pop(Q_i)

12:   if $q_i\in T$ then

13:    if $t=\text{nil}$ or f(p_i) < f(t) then

14:     $t\leftarrow p_i$

15:    end if

16:    continue

17:   end if

18:   Let R′ be the nodes expanded from q_i.

19:   $R\leftarrow R\cup R\prime$

20:  end for

21:  if $t\ne \text{nil}$ and $f(t)={\min }_{j}f(p_j)$ then

22:   return t

23:  end if

24:  Reorder the nodes in R ▹ See Section 2.6

25:  Calculate f(x) for all nodes in R in maximum parallel

26:  for $i\leftarrow 1$ to k in parallel do

27:   Pick |R|/k nodes from R with different parents

28:   Push them into Q_i

29:  end for

30: end while

31: end procedure

Note that the nodes to be expanded are not necessarily the most optimal nodes. For example, suppose we have two priority queues, and the 1st, 2nd, 3rd most optimal nodes are in the first priority queue while the 4th one is in the second queue. In this situation, our algorithm will pop out the 1st and 4th most optimal nodes, which is not an ideal situation. This is the price of the parallelism of the priority queue. We try to alleviate this problem by separating the nodes with the same parent nodes, which may have similar heuristic function values, to different queues.

Because the parallelism of the priority queue changes the work flow of the overall A* algorithm, it is necessary to provide a proof to show that GA* is able to compute a global optimal solution. Here, our proof is derived mainly for the protein design problem, in which the underlying search graph is a tree.

Lemma 2.1 —

Let h_r(x) represent the real cost from x to an optimum target node. If the defined heuristic function satisfies h(x) ≤ h_r(x) for each node x and the search graph is a tree, for any optimal target $t\in T$, there exists a node t′ in the priority queues {Q_i} such that f(t′) ≤ f(t) in Algorithm 2 before each Pop operation is executed.

Proof —

Let d(x,y) = g(y)– g(x) denote the real cost from node x to node y, where x must be on the path from the starting node s to y. For all node t′ that is on the path from s to t, we have

$$\begin{array}{c}f(t\prime )=g(t\prime )+h(t\prime )\\ \le d(s,t\prime )+h_r(t\prime )\\ =d(s,t\prime )+d(t\prime ,t)\\ =d(s,t)\\ =f(t).\end{array}$$

Thus, it is sufficient to prove that there exists a node t′ in the priority queues along the path from s to t. At the beginning, the starting node s satisfies such a condition. At any time, if line 11 in Algorithm 2 pops node t′, line 18 will generate another node that is also on the path from s to t, which is then pushed back into the queues. Thus, such a node always exists.□

Theorem 2.2 —

Let h_r(x) represent the real cost from x to an optimum target node. If the defined heuristic function satisfies h(x) ≤ h_r(x) for every node x and the search graph is a tree, the first solution returned by GA* must be the optimal solution.

Proof —

We prove this theorem by contradiction. There exists two possible situations that may violate our conclusion:

1. The algorithm never terminates; and

2. When the algorithm terminates, it returns a solution that is not optimal.

For (1), it is impossible because the search space is a finite tree and our algorithm will never visit any node twice.

For (2), assume that our algorithm returns a node t₁, while the optimal solution is node t₂. Thus, we have f(t₁) > f(t₂). However, according to Lemma 2.1, we have a node t′ in the queues {Q_i} that satisfies f(t′) ≤ f(t₂) < f(t₁), which violates the condition in line 21 of Algorithm 2.□

Theorem 2.2 states that GA* guarantees to find the global optimal solution. However, GA* does not retain all the properties that the original version of A* search has. The optimality property (Dechter and Pearl, 1985), which guarantees that A* will expand fewer nodes than any other algorithm using the same heuristic function, is lost in GA*. The reason is that in GA*, it is possible to expand a node whose f(x) value is larger than the best solution due to the parallelism. However, as we will see in the Results section, the fraction of extra expanded nodes compared to the original A* algorithm is within an acceptable range.

2.5 Memory-bounded A* search for protein design

Although our parallel algorithm GA* can speed up the traditional A* algorithm by several orders of magnitude, the scale of the protein design problem that it can solve is still limited. For example, we may support at most 20 mutable residues if all types of amino acids are allowed in each residue. The bottleneck mainly lies in the limited memory available for each machine. In the worst case, A* produces an exponential number of expanded nodes in the search tree. Once the algorithm runs out of memory to store new expanded nodes, it cannot continue. Several efforts have been made to solve this problem. In particular, variants of the A* algorithm such as iterative deepening depth-first search (IDA*) (Korf, 1985) and simplified memory-bounded A* (SMA*) (Russell, 1992) have been proposed to address such an issue. IDA* uses a depth-first-search strategy to reduce the usage of memory, which is difficult to parallelize on a GPU. On the other hand, we found that SMA* could be well implemented on a GPU. We call this new algorithm GSMA*.

SMA* is almost identical to a normal A* algorithm, with the only exception that if a new expanded node does not fit in memory, we simply throw away the least promising node in the queue, which has the worst f(x) value. Using this method, SMA* can still assure to generate the optimal solution when the memory is large enough for the original A* algorithm, while it may miss the optimal solution if the size of the priority queue exceeds the memory limit. In this case, although our algorithm cannot guarantee to find the GMEC solution, we can still know whether the solution returned by SMA* is a GMEC solution. This can be done by tracking the lowest f(x) value among all nodes that we have thrown away. If the energy of the returned solution is below this value, we know that SMA* finds the GMEC solution. Otherwise, we can report that the energy of the GMEC solution must lie in the interval between this value and energy of the solution found by SMA*.

For GSMA*, when we run out of the memory, we first do a global scan operation (Sengupta et al., 2007) to pick those nodes which are the leaves of the current searching tree, while freeing the memory occupied by the internal nodes that have already been expanded. Then a global sorting operation is performed over all the remaining nodes according to their f(x) values. Finally, we keep a user-specified percentage of nodes with the lowest f(x) values and then reconstruct the priority queues evenly, in which nodes are stratified by their heuristic function values.

2.6 Implementation details

Our new parallel A* search algorithm is implemented based on the current open-source protein design package OSPREY (Chen et al., 2009; Gainza et al., 2013). The CPU code is written in C and the GPU code is written in CUDA. As the OSPREY library is implemented in Java, we use Java Native Interface (JNI) to communicate with the native C program.

At the beginning, our program copies the configuration and necessary information such as energy matrix and the original sequence from CPU memory to the global memory of a GPU. Then it allocates memory space for the nodes generated by GA* and a user-specified number of binary heaps. Each element in a binary heap stores a floating-point value of f(x) and a pointer to its corresponding node x.

After initializing the GPU data structure, the GPU circulates among the four states as shown in Figure 2 until a valid solution is found. Compared to Figure 1, we add a new Radix-Sorting state.

Fig. 2.

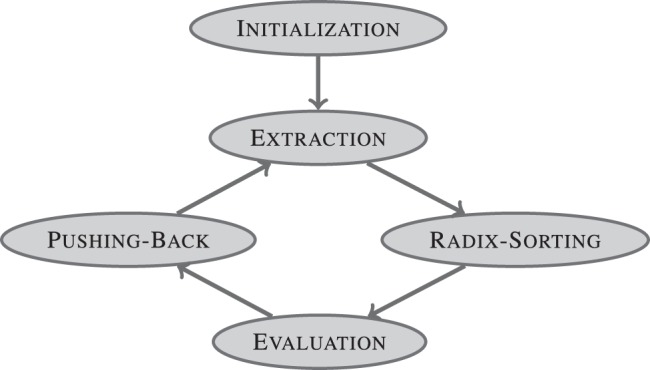
Diagram of the GPU states

In the Extraction phase, GA* launches a user-specified number of threads, each of which operates on its own priority queue and performs the Delete-Minimum operation to extract the node with the minimum f(x) value. Each priority queue is a vanilla binary heap. In addition, GA* checks whether the extracted node of the current thread is the optimal target node. Also, the expanding operation is done in this phase, which generates the children of the extracted nodes and then puts them into a global buffer.

The second phase is Radix-Sorting, which corresponds to line 24 in Algorithm 2. In this phase, the expanded nodes are sorted by their current depth, that is, the number of decided rotamers, before entering the Evaluation phase. The major motivation for this phase is that the range of the loop during the calculation of f(x) heavily depends on the depth of the corresponding node in the search tree. Thus, after sorting, all the threads in a single SIMD unit of a GPU will tend to have the same length of the loop during the evaluation phase, which thus can reduce the branch divergence overhead and improve the efficiency of the parallelized computation of heuristic functions. There are several efficient sorting algorithms available for GPUs, such as (Satish et al., 2009; Sintorn and Assarsson, 2008). As the number of elements to be sorted is not that large, we choose a classical and simple method, the GPU radix-sorting (Sengupta et al., 2007), to perform this task.

In the Evaluation phase, GA* launches the same number of threads as the number of expanded nodes to calculate the heuristic function of each node in order to exploit the full floating-point operation capacity of a GPU. Our tests show that a GPU would spend more than 80% time in this phase. Thus parallelizing the calculation of heuristic functions in this phase can significantly reduce the running time of A* search for protein design. Section 2.3 explains more details about parallelizing computation of heuristic functions in this phase.

In the final Pushing-Back phase, GA* pushes all the expanded nodes with their heuristic function values back into the priority queues, using the classical insert procedure of a binary heap. In addition, GA* pushes the different expanded nodes into priority queues so that the sizes of these queues are balanced and the new expanded nodes with the same parents, which may have similar heuristic function values, are stored in different queues.

3 RESULTS

3.1 Parallel protein design

In order to evaluate the performance of our new parallel A* algorithm, we performed several protein design experiments. The Results section is divided into two parts. In the first subsection, we will compare the running time and memory usage of our new algorithm GA* against the original A* algorithm for protein design. In the second subsection, we will evaluate the effectiveness of the combination of our parallel design algorithm GA* and the memory-bounded strategy (i.e., SMA*), by testing whether our algorithm is able to get a GMEC solution and calculating the proportion of recovered residues in native sequences recovery.

In addition to the original A* search algorithm in OSPREY (Gainza et al., 2013) and our parallel design algorithm GA*, we also implemented a single-thread version of the A* search algorithm on a CPU in C programming language using the new strategy of computing heuristic functions, as we have described in Section 2.2.1. There are two reasons for us to include this program in this benchmark. First, it measures improvement by using this new strategy to compute heuristic functions. Second, it is unfair to perform a direct comparison between algorithms implemented in Java and native machine code on a GPU, because the Java Virtual Machine and the garbage collection system may introduce a considerable amount of overhead.

We used 74 protein core redesigns provided by (Gainza et al., 2012) as the test data. We used the same parameters as those in (Gainza et al., 2012), including the set of allowed amino acids and the number of mutable residues. We used iMinDEE (Gainza et al., 2012) as the DEE strategy to prune those rotamers that are provably not in the part of the global optimal solution. The iMinDEE algorithm can give a more accurate result on rotamer pruning, but results in a much larger conformation space for the downstream A* algorithm to search over to find the GMEC solution. Strictly speaking, we are not trying to find the GMEC solution in A* when using iMinDEE. We are trying to find the lowest-energy bound conformation for iMinDEE. But from the point view of an A* algorithm, it treats that job as same as finding the GMEC solution. So we will not distinguish these terminologies in the Results section. In this part of the experiment, memory-bounded operations were not performed. Because GA* is a provable algorithm (see Theorem 2.2 in Section 2.4), it can still guarantee to find the optimal solution. For correctness, we also verified that our results are completely identical to those of original OSPREY.

The CPU and GPU we used in this benchmark test were an Intel Xeon^TME5-1620 3.6 GHz with 16 GB memory and an NVIDIA Tesla K20c GPU with 4.8 GB global memory and 2496 CUDA cores, respectively. The main point of this test is to measure the speed and the memory consumption of our algorithm, the results of which can be found in Tables 1 and 2, respectively. We ran the full experiment over all 74 protein structures, but we only show the list of the 10 slowest cases here as the others were finished too quickly even for the original A* algorithm implemented in OSPREY after rotamer pruning using iMinDEE. The results of all tests can be found in Tables S1 and S2 in Supplementary Material Section S3.

Table 1.

The comparison results about time efficiency of our parallel against original versions of A* search for protein design

PDB	Spacea	OSPREYb	A*1c	GA*768d	GA*4992d
2QCP	2·1017	21 551 916	51 091	3075	1146
1XMK	2·1014	247 585	2990	296	121
1X6I	7·1013	96 990	1406	138	73
1UCS	6·1012	88 135	1771	182	79
1CC8	3·1014	77 614	1078	99	53
2CS7	8·1012	64 187	1154	149	57
2BWF	9·1013	18 457	307	33	24
1I27	7·1011	8151	88	18	16
1T8K	2·1013	6806	89	18	15
1R6J	2·1014	6018	107	18	21

Notes: Time was measured in millisecond. The results were sorted by the running time needed by OSPREY and only the 10 largest cases are listed here. ^aThe second column, labeled with ‘Space’, reports the size of conformation search space after the rotamer pruning using iMinDEE. ^bThe third column, labeled with ‘OSPREY’, reports the running time of the original A* algorithm in OSPREY implemented in Java. ^cThe fourth column, labeled with ‘A*1’, reports the running time of our new implementation of a single-thread A* algorithm written in C programming language running on a CPU, which adopted the improved computation of heuristic functions, as described in Section 2.2.1. ^dThe fifth and sixth columns, labeled with ‘GA*768’ and ‘GA*4992’, respectively, report the running time of two fully parallelized A* algorithms running on a GPU, whose numbers of parallel priority queues are 768 and 4992, respectively.

Table 2.

The comparison results about memory consumption of our parallel against original versions of A* search for protein design

PDB	Space	A*1	GA*768	GA*4992
2QCP	2·1017	31 589 690	32 825 074	35 517 854
1XMK	2·1014	2 910 324	3 325 654	4 419 100
1X6I	7·1013	1 919 055	2 282 986	3 486 684
1UCS	6·1012	1 713 636	2 196 315	2 960 752
1CC8	3·1014	966 196	1 255 899	1 893 701
2CS7	8·1012	1 378 633	1 686 558	2 354 910
2BWF	9·1013	325 634	529 810	981 302
1I27	7·1011	121 920	260 825	737 328
1T8K	2·1013	129 767	211 003	618 794
1R6J	2·1014	117 053	244 399	837 359

Note: Each column has the same meaning as that in Table 1 except that the numbers in last three columns represent the numbers of expanded nodes in different programs.

In our GA* algorithm, the number of parallel priority queues, as described in Section 2.4, is a parameter that we can tune for the maximum performance. By increasing the number of priority queues, we can increase the degree of parallelism and further exploit the capability of the GPU hardware. On the other hand, when more parallel priority queues are used, the number of extra expanded nodes in the tree search compared to the original A* algorithm will also increase, which will cause both computation and memory overhead. In our computational experiments, we tested two choices of this parameter. One is 768, designed for the balance between time and space consumption. The other is 4992, targeting at maximizing the protein design speed.

From Table 1, we found that our parallel A* algorithm GA* can speed up the original A*-based protein design algorithm by several orders of magnitude. For the largest protein design problem related to 2QCP, the original A*-based protein design algorithm took ∼6 h, while GA*4992 (i.e., GA* algorithm that used 4992 parallel priority queues) was able to finish the search in 1.2 s. Such improvement is striking. In addition, as summarized in Table 2, the larger the conformation search space is, the more impact GA* will have. This is because for large problems, GA* is able to better exploit its parallelism, amortizing the overhead to a negligible level.

Furthermore, the test results on the memory consumption of GA* (Table 2) were also promising. Although for small-scale protein design problems, memory consumption of GA*4992 was several times higher than that of a single-thread version, the discrepancy in memory consumption became more and more negligible when the conformation space scaled up. For the largest design problem related to 2QCP, GA*4992 only generated 1.12 times more nodes than the single-thread algorithm. Therefore, such small growth of memory requirement was acceptable compared to the large improvement on time efficiency achieved by our algorithm.

3.2 Parallel protein design with bounded memory

Memory limitation is always a problem when we are conducting large-scale protein design. Although GSMA* can solve this problem, it does not guarantee to generate a GMEC solution anymore. Therefore, it is necessary to evaluate the quality of its solutions when the memory resource is not sufficient. Researches have shown that the sequences of native proteins tend to optimize their core structures for stability (Gainza et al., 2012; Kuhlman and Baker, 2000). Therefore we included the native sequence recovery experiments, in which we removed the types of some amino acids from the core of the wild-type proteins and recorded the percentage of correctly recovered residues by the design algorithm as an indicator of its quality besides other direct critera.

We randomly picked six PDBs from the protein sequence recovery dataset provided in (Gainza et al., 2012) to evaluate performance of our parallel GA* with limited memory (i.e., GSMA*). Unlike Section 3.1 in which we did not change any parameters on the original test dataset, this time we increased the number of mutable residues so that the total number of new nodes expanded by GA* just fitted the physical memory limit of the GPU without throwing any of them away, which had ∼3 × 10⁷ nodes. We did this because we need to have a set of optimal solutions as a reference for comparison, and we hoped that all the test data had the similar memory consumption so that their performance was comparable. The method for choosing the set of allowed amino acids and the positions of extra mutable residues was as same as that in (Gainza et al., 2012).

The number of parallel priority queues in this experiment was fixed to 768. We ran our experiments four times per test data. Each time we imposed a different restriction on the number of nodes that GSMA* was allowed to expand, which was 3 × 10⁴, 3 × 10⁵, 3 × 10⁶ and 3 × 10⁷, respectively. These restrictions can be approximately considered as using 1000th, 1%, 10% and 100% of memory needed by GA*. Each time the system ran out of memory, 50% of the nodes with larger f(x) values were thrown away.

We use four metrics to evaluate the quality of our algorithm. The first one is the availability of the GMEC solution. The second one is whether GSMA* is able to determine that the first solution it found is the GMEC solution. We have described this method in Section 2.5. The other two metrics are based on the first 50 solutions returned by A* rather than the GMEC solution. The third metric, correctness, measures the percentage of the top 50 solutions calculated with memory restriction that were also presented in the top 50 solutions calculated without such restriction. The fourth metric, recovery rate, reports the average percentage of amino acids in the top 50 solutions that are identical to those in the wild-type protein. Table 3 shows the results.

Table 3.

Performance of GSMA* with 768 parallel priority queues on 6 test datasets

	PDB	1OAI	1U2H	1ZZK	2CS7	2DSX	3D3B
	No. of mutable residues	16	18	14	15	15	15
	Conformation space	2·1022	2·1020	2·1015	2·1023	3·1020	6·1818
	GA*768 search spacea	4·107	8·106	8·106	4·107	4·107	3·107
3 × 104 nodes limit	Scan countb	252	104	99	202	182	109
	GMEC gotten	NO	YES	YES	NO	YES	NO
	GMEC assured	NO	NO	NO	NO	NO	NO
	Correctness	4%	100%	20%	12%	32%	6%
	Recovery ratio	62%	75%	85%	48%	46%	48%
3 × 105 nodes limit	Scan countb	139	43	36	103	97	55
	GMEC gotten	YES	YES	YES	YES	YES	YES
	GMEC assured	NO	YES	YES	NO	NO	NO
	Correctness	100%	100%	100%	100%	100%	44%
	Recovery ratio	74%	75%	87%	46%	48%	54%
3 × 106 nodes limit	Scan countb	22	3	3	24	22	18
	GMEC gotten	YES	YES	YES	YES	YES	YES
	GMEC assured	YES	YES	YES	YES	YES	YES
	Correctness	100%	100%	100%	100%	100%	100%
	Recovery ratio	74%	75%	87%	46%	48%	53%
3 × 107 nodes limit	Scan countb	1	0	0	1	1	1
	GMEC gotten	YES	YES	YES	YES	YES	YES
	GMEC assured	YES	YES	YES	YES	YES	YES
	Correctness	100%	100%	100%	100%	100%	100%
	Recovery ratio	74%	75%	87%	46%	48%	53%

Note: The meaning of each row is explained either in the text or here. ^aThe row labeled with ‘GA*768 search space’ represents the number of nodes expanded by GA*768 for calculating the best 50 solutions. ^bThe rows labeled with ‘Scan Count’ represent the number of times that the system ran out of memory, in which a series of operations described in Section 2.5 were executed.

The numbers reported in the row of GA*768 search space indicate that the numbers of new nodes expanded by parallel A* search did not exceed the memory limit of GPU so that the results computed without memory restriction can be used as references for evaluating their tests with memory restriction. We found that the native sequence recovery ratios of last three structures were a little low, even when no node was thrown away. Apart from that, the results look encouraging. The GMEC solution can be guaranteed by GSMA*768 on all our test data even if we only used ∼10% of memory required by GA*768. When we restricted the memory to 1%, GSMA*768 can still keep all GMEC solutions, though it cannot theoretically guarantee to find the GMEC solution in some cases.

In the test with the restriction of 0.1% memory, the algorithm achieved relatively poor performance. In this case, the algorithm was only allow to keep 30 000 nodes in memory, which is unfriendly to parallel A*, as discussed in Section 3.1. When the absolute size of allowed memory is too small, it is more probable for GSMA* to throw away an important node at the beginning of the tree expansion. In practice, we will always use all available memory to perform the protein design task. So this setting was only for the evaluation purpose.

4 CONCLUSION AND FUTURE WORK

Computational protein design is a challenging problem in the computation biology field. In this article, we have developed an innovative method to improve the A* algorithm for computational protein design, which significantly reduces running time of the original protein design algorithm by up to four orders of magnitude while maintaining low memory overhead. Another advantage of our algorithm is that we do not change the interface of the original protein design framework in OSPREY (Gainza et al., 2013). We have shown that it could be successfully integrated with iMinDEE (Gainza et al., 2012) to further improve SCPR with the consideration of continuous side-chain flexibility.

Memory limitation becomes a more important problem in protein design after A* is sped up. Thus, we introduce memory-bounded parallel A*, a variant of A* algorithm that only uses limited memory. In the Results section, we have shown that in practice, the memory-bounded parallel A* algorithm is able to guarantee the GMEC solution with only one-tenth of memory consumption that the original algorithm requires.

Currently GA* is only implemented on the Tesla GPU card. It would be interesting to know whether it can achieve similar performance on a more affordable GPU card such as NVIDIA GeForce GTX series. In addition, although currently GA* is only runnable on a single GPU platform, it should be easy to port it to other parallel computational platforms due to the parallel characteristic of our algorithm. If we can utilize the existing large clusters of CPUs and GPUs to run GA*, in which more memory and computation resource is available, we will be able to solve a larger protein design problem than ever before.