Accounting for a mirror-image conformation as a subtle effect in protein folding

Significance

Numerous diseases, including neurodegenerative diseases, are caused by misfolding of proteins; therefore, understanding the mechanism by which a protein folds to its native conformation is one of the most important problems of biophysics. This task becomes more complicated for proteins with a high degree of symmetry that, in addition to the native structure, allows the existence of another, energetically competitive conformation with the native one, a native-like “mirror-image” structure, which has not yet been detected experimentally. By investigating one of the representatives of such symmetrical proteins, reasons for formation of the mirror-image conformation are provided.

Abstract

By using local (free-energy profiles along the amino acid sequence and ¹³C^α chemical shifts) and global (principal component) analyses to examine the molecular dynamics of protein-folding trajectories, generated with the coarse-grained united-residue force field, for the B domain of staphylococcal protein A, we are able to (i) provide the main reason for formation of the mirror-image conformation of this protein, namely, a slow formation of the second loop and part of the third helix (Asp29–Asn35), caused by the presence of multiple local conformational states in this portion of the protein; (ii) show that formation of the mirror-image topology is a subtle effect resulting from local interactions; (iii) provide a mechanism for how protein A overcomes the barrier between the metastable mirror-image state and the native state; and (iv) offer a plausible reason to explain why protein A does not remain in the metastable mirror-image state even though the mirror-image and native conformations are at least energetically compatible.

To perform their functions in living organisms, most proteins must fold from unfolded polypeptides into their functional, unique 3D structures. Understanding protein-folding mechanisms is crucial because misfolded proteins can cause many diseases, including neurodegenerative diseases (1) such as Alzheimer’s, Parkinson, and Huntington diseases. From theoretical and conceptual points of view, it has been suggested that a native protein exists in a thermodynamically stable state with its surroundings (2) and that a study of free-energy landscapes (FELs) holds the key to understanding how proteins fold and function (3, 4).

The native structures of some proteins contain a high degree of symmetry that, in addition to the native structure, allows the existence of another, energetically very close to the native conformation, a native-like “mirror-image” structure. One of the representatives of such symmetrical proteins is the 10- to 55-residue fragment of the B domain of staphylococcal protein A [Protein Data Bank (PDB) ID: 1BDD, a three-α-helix bundle] (5). Protein A has been the subject of extensive theoretical (6–18) and experimental (19–23) studies because of its small size, fast folding kinetics, and biological importance. However, the mirror-image topology has never been a subject for discussion except for the earlier work by Olszewski et al. (7) and recent work by Noel et al. (24). The reason for this might be that it has never been detected experimentally and it was observed only in some theoretical studies (7–9, 12, 13, 15, 17, 18, 24) with different force fields. It is of interest to determine how realistic the mirror-image conformation is. Is it an artifact of the simulations or is it a conformation difficult to observe experimentally? Noel et al. (24) showed that the native and mirror-image structures have a similar enthalpic stability and are thermodynamically competitive and that the mirror image can be considered not just a computational annoyance, but as a real conformation competing with the native structure. Moreover, the mirror-image conformation is more entropically favorable than the native conformation (24). By making multiple mutations in the hydrophobic core and the first loop region, Olszewski et al. (7) found that the change in the handedness of the first loop induced by the mutations, the burial of the N cap of the second helix, and repacking of the hydrophobic core are responsible for formation of the mirror-image conformation. However, at the end, the authors stated: “… Whether the conclusion about the possible importance of turns in defining the global topology holds in general or is just specific to the three-helix bundles analyzed here requires additional investigation....” (ref. 7, p. 298).

The difficulties for experiments to detect the mirror-image topology arise because the secondary structures of the mirror-image and the native conformation are identical and the native-contact interactions are similar in both conformations (details in Fig. S1 and SI Native and Mirror-Image Structures of Protein A). Hence, with an experimental technique such as circular dichroism, used to estimate the fraction of secondary-structure content, it is almost impossible to distinguish the mirror-image structure from the native structure. It would have been desirable if the mirror-image conformation and its evolution to the native structure could be detected by NMR spectroscopy. Nevertheless, by using local [¹³C^α chemical shift (25) and free-energy profiles (FEPs) along the amino acid sequence (26–28)] and global [principal component (PC) (29)] analyses (SI Materials and Methods), we examined molecular dynamics (MD) trajectories of protein A, generated with the coarse-grained united-residue (UNRES) force field (27, 30–32) (Fig. S2 and SI Materials and Methods). These analyses of the MD trajectories, in which folding from a fully unfolded conformation occurs either almost instantly or through a metastable state formed by the mirror-image topology, enabled us to elucidate the origin of the formation of a mirror-image topology and how the protein emerges from the kinetic trap and folds to the native state.

The results presented in this work are based on the analysis of four pairs of MD trajectories at 270 K (in each pair, one trajectory folds directly to the native state and the other folds through the metastable mirror-image state) selected from 96 MD simulations, which we carried out in a broad range of temperatures (details in Materials and Methods). The mirror-image conformation is energetically competitive with the native conformation in the studied trajectories (an illustrative example of two trajectories is in Fig. S3), and these results are in agreement with those of earlier studies (12, 24).

Results

Free-Energy Profile.

To understand what induces protein A to fold into its native conformation from a fully unfolded conformation almost instantly or through a kinetic trap, the local motions of each residue were examined along the sequence. In particular, the FEPs along the backbone virtual-bond angle θ and the backbone virtual-bond dihedral angle γ of each residue (defined in Fig. S2) were examined.

The FEPs along the θ_i and γ_i angles of the entire trajectory [$\mu \left(\theta \right)=-k_{\text{B}}T\ln P\left(\theta \right)$, $\mu \left(\gamma \right)=-k_{\text{B}}T\ln P\left(\gamma \right)$, where P, T, and k_B are the probability distribution function (PDF), the absolute temperature, and the Boltzmann constant, respectively] are very helpful to identify the key residues in the folding process (26–28); however, the analysis of the FEPs of the entire trajectory does not provide information about the way in which each residue explores its own FEP in the course of time or to what extent the motion of each residue is coupled to the global motion of the protein as it proceeds toward its native state. To answer these questions, for selected trajectories, the FEPs along the θ_i and γ_i angles for certain periods of time, during which significant structural changes occur before the protein reaches its native state, were calculated.

It should be noted that the FEPs presented here are effective FEPs because they are computed from a nonequilibrium probability density and depend on the time duration and on the initial conditions of the trajectory. The effective FEP differs from the actual FEP, which is an equilibrium thermodynamic property, and should be computed from the entire sets of trajectories (folding and nonfolding). Because of the dependence of the effective FEP on the time duration of the trajectory and on the initial conditions, the effective FEP was used (27, 28) to analyze the MD trajectories in detail and extract the reasons why a protein folds or does not in a single MD trajectory. In the present work, the effective FEPs were used to explain why protein A folds with or without a kinetic trap.

In this work, selection of time intervals, over which the FEPs were calculated, was based on significant changes in the C^α root-mean-square deviation (rmsd) from the native structure of trajectories (details in Fig. S4 and SI Time Intervals for Free-Energy Profiles).

FEPs Along θ_i and γ_i Angles of the Folding Trajectories With and Without Kinetic Traps.

By comparing the FEPs along all of the θ and γ angles, computed at different time intervals, of two trajectories, one of which folds without and the other with a kinetic trap, we found that the FEPs along 17 of the θ angles and 17 of the γ angles differ noticeably from each other between the two trajectories and consequently play a crucial role in a folding pathway. The discrepancies between these FEPs are caused by different behaviors of the angles in different time intervals. Based on these differences, FEPs can, overall, be divided into two categories: (i) the FEPs in which differences appear at the beginning of the trajectory before the protein jumps into either the native or the mirror-image state and (ii) the FEPs in which differences appear after the collapse.

The first category includes the FEPs along the angles pertaining to the second loop and its vicinity including part of the third helix; the second category includes the FEPs along the angles pertaining to the first loop and its vicinity, including parts of the first and second helices. In particular, most of the angles of the first-category FEPs are flexible at the beginning of the trajectory and explore a large region of angle space before jumping into the global minimum in the trajectory with a kinetic trap, whereas the same angles of the trajectory without a kinetic trap gradually explore the region of only their own global minima during the entire trajectory (an illustrative example is shown in Fig. 1 A and B).

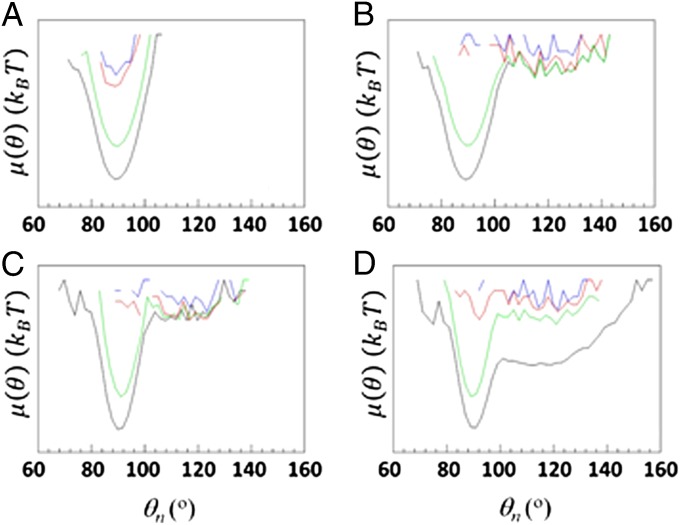
Fig. 1.

(A–D) FEPs, μ(θ), along the θ₃₁ (A and B) and θ₁₄ (C and D) angles, for the folding trajectory without a kinetic trap (A and C) and the folding trajectory with a kinetic trap (B and D) of protein A. Blue, red, green, and black curves correspond to FEPs computed over 300 ps, 650 ps, and 28 ns and over the entire MD trajectories, respectively.

The behavior of the angles of the second-category FEPs is more complicated; for example, some of these angles of the trajectory without a kinetic trap completely explore the shallow local minimum before the protein jumps to the native state, whereas the same angles of the trajectory in which protein A folds through a kinetic trap jump back and forth between the local and global minima during the entire trajectory (an illustrative example is shown in Fig. 1 C and D); differences in behavior of the remaining angles of the second-category FEPs do not have any particular pattern, although protein A explores a larger portion of conformational space when it folds through a kinetic trap, manifested by a small number of regions in which the FEPs are undefined (Fig. S5 and SI FEPs Along θ_iand γ_iAngles of the Folding Trajectories with and Without Kinetic Traps, in which the FEPs along all of the θ and γ angles are shown).

Based on the results of the FEP analysis, it can be concluded that all residues of the first and second loops and their edges, including the parts of all three helices, play a crucial role in the folding pathway of protein A. In particular, residues of the second loop, its edges, and part of the third helix are responsible for formation of the mirror-image topology; and residues of the first loop and its edges along with the parts of the first and second helices assist the protein to overcome a barrier between the metastable mirror-image and native states.

To justify and strengthen the aforementioned statements resulting from the analysis of only one pair of trajectories, we selected three additional pairs of MD trajectories, in which protein A folds without and through a kinetic trap, respectively, and computed the FEPs along the θ and γ angles for these trajectories. The obtained results are in agreement with those shown in Fig. 1 and Fig. S5; however, because of the tremendous number of FEPs (each trajectory contains 89 panels of FEPs), we do not show the results for the other three pairs. Instead, based on the results obtained from all four pairs of trajectories, we plotted the amino acid sequence of 1BDD (Fig. 2), in which the residues in rectangles belong to helices, the residues outside of the rectangles belong to the loops, the residues in red color are parts of both θ and γ angles along which the FEPs differ from each other, and the residues in green color are parts of only one of those θ or γ angles, the FEPs of which differ from each other.

Fig. 2.

Amino acid sequence of 1BDD. The numbers of residues forming the α-helices are in black rectangles, the residues outside of rectangles belong to the loops; residues in red color are parts of both θ and γ angles along which the FEPs differ from each other, and the residues in green color are parts of only one of those angles whose FEPs differ from each other.

¹³C^α Chemical Shift Analysis.

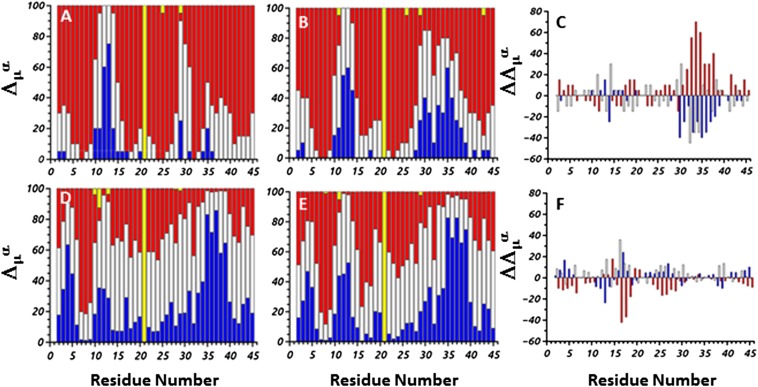
By using the CheShift-2 Server (25), the ¹³C^α chemical shifts were calculated for each conformation of the same MD trajectories and during the same time intervals as in the FEP analysis (Fig. S4). The results obtained from the analysis of the ¹³C^α chemical shifts coincide with those from the analysis of the FEPs. In particular, the main differences between the results, depicted in Fig. 3 A and B, which corresponds to the ¹³C^α chemical shifts calculated before the collapse of the protein, are in the second loop region (residues 30–32) and in part of the third helix (residues 33–39). The ¹³C^α chemical shifts of the residues of both of these portions of the protein are very close to the experimental ones (blue bars) for the trajectory folding without a kinetic trap (Fig. 3B), whereas the ¹³C^α chemical shifts of the residues of the same portions of the protein folding with a mirror image (Fig. 3A) are either acceptable (white bars) or unacceptable (red bars). A graphical representation of these differences is shown in Fig. 3C. In particular, each color bar of each residue in Fig. 3C is a difference between the corresponding color bars of the same residue in Fig. 3 A and B (interpretation of Fig. 3C in SI ¹³C^α Chemical Shift Analysis).

Fig. 3.

Δ_μ^α represents the differences between the observed and theoretical ¹³C^α chemical shifts computed from the MD trajectories. The different colors of the bars indicate the magnitude of the differences (Δ_μ) in terms of σ [σ = 1.7 ppm (25)]. In particular, blue bars correspond to $\langle {\mathrm{\Delta }}_{\mu }\rangle \le \sigma$, white bars correspond to $\sigma <\langle {\mathrm{\Delta }}_{\mu }\rangle \le 2\sigma$, and red bars correspond to $\langle {\mathrm{\Delta }}_{\mu }\rangle >2\sigma$. A full bar highlighted in yellow, as for residue Gly21, indicates that the chemical shift was not measured experimentally or (for all of the remaining partial bars highlighted in yellow) that the theoretical value could not be computed for a particular conformation. A, D and B, E illustrate the differences in ¹³C^α chemical shift per residue for the trajectories that fold with and without mirror image, respectively. In particular, A and B correspond to the time interval from the start of the simulation until the protein starts to collapse; and D and E correspond to the full trajectory of the simulation. C and F illustrate the second-order differences, computed as follows: $\mathrm{\Delta }{\mathrm{\Delta }}_{\mu \left(C\right)}^{\alpha }={\mathrm{\Delta }}_{\mu \left(A\right)}^{\alpha }-{\mathrm{\Delta }}_{\mu \left(B\right)}^{\alpha }$ and $\mathrm{\Delta }{\mathrm{\Delta }}_{\mu \left(F\right)}^{\alpha }={\mathrm{\Delta }}_{\mu \left(D\right)}^{\alpha }-{\mathrm{\Delta }}_{\mu \left(E\right)}^{\alpha }$.

Noticeable differences, between the ¹³C^α chemical shifts calculated during the time interval when the protein remains in the metastable mirror-image state (Fig. S6 D and E) and the full trajectory (Fig. 3 D and E), are in the region of the first loop (residues 11–15) (Fig. S6F, Fig. 3F, and SI ¹³C^α Chemical Shift Analysis). The reason for these differences is that the first loop does not reach the native geometry in the metastable mirror-image state and tries to emerge from the kinetic trap; during this time the structure of the first loop undergoes drastic changes. Consequently, the differences between ¹³C^α chemical shifts of the residues of the first loop and those from the experimental chemical shifts are larger (details in Fig. S6 and SI¹³C^α Chemical Shift Analysis). As for the FEPs, the analysis of the ¹³C^α chemical shifts was also performed for three other pairs of trajectories. The results obtained for those other pairs are in agreement with those presented here; therefore, we present the results for only one pair.

It should be noted that the observed ¹³C^α chemical shifts were obtained from the Biological Magnetic Resonance Bank (BMRB), deposited under accession no. 5656, which correspond to ¹³C^α chemical shift values obtained from the Z domain, rather than the B domain, of protein A (33). Nevertheless, the Z domain differs from the B domain by only two substitutions, namely Ala1 → Val and Gly30 → Ala. However, because we studied the 10- to 55-residue fragment of the B domain of staphylococcal protein A, the only relevant substitution is that of Gly30 → Ala, which is equivalent to Gly21 → Ala in our renumbered sequence. For this reason, all panels in Fig. 3 and Fig. S6 show the bar corresponding to residue Gly21 highlighted in yellow, i.e., indicating that the observed ¹³C^α chemical shift value is missing. Overall, because the B and Z domains exhibit identical binding affinity (33), the use of the observed information from the Z rather than the B domain of protein A is reasonable.

Principal Component Analysis of the Folding Trajectories With and Without Kinetic Traps.

Both trajectories, in which protein A folds with and without a kinetic trap, were also analyzed by principal component analysis (PCA). In particular, the contributions of the two main principal modes (with the largest eigenvalues) to the mean-square fluctuations along the θ and γ angles were calculated. The peaks in these contributions appear exactly in the regions where the main differences between the shapes of the FEPs and those of the ¹³C^α chemical shifts were found. However, differences between the contributions of the two main principal modes of these trajectories are not very noticeable, which indicates that the mirror image is a local property and cannot be detected by the global motions of PCA (details in Fig. S7 and SI Materials and Methods, Principal Component Analysis).

Origin of Formation of the Mirror-Image Conformation.

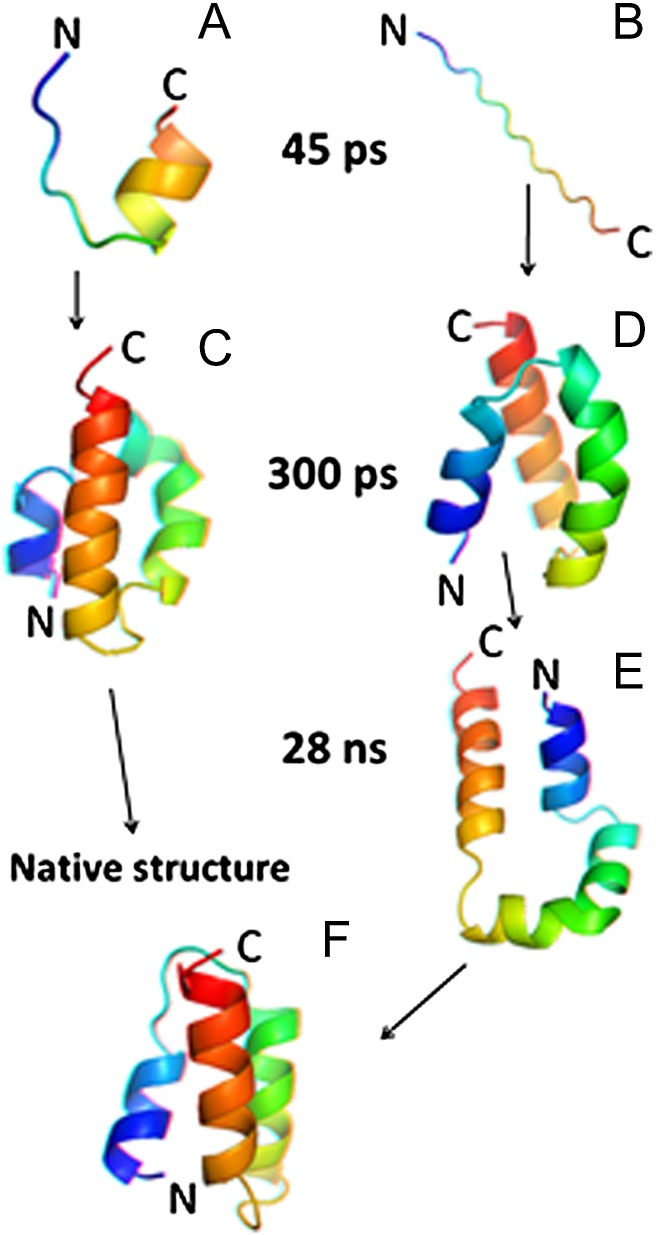
The FEPs and ¹³C^α chemical shift analyses enabled us to identify the parts of protein A involved in formation of the mirror-image conformation. However, the question of what induces protein A either to fold almost instantly or to misfold first and then emerge from the mirror-image state still needs to be answered. Therefore, we first examined, in detail, the dynamics of the 24- to 37-residue portion of protein A, which includes the second loop and parts of the second and third helices, at the beginning of the trajectory before the protein jumps into either the native or the mirror-image state. In particular, we examined the local interactions by computing the C^α····C^α distances between the residues as a function of time in the 24- to 37-residue portion. It appears that, in the trajectory with the kinetic trap, the residues of the second loop and part of the third helix (Asp29–Asn35) are in local conformational states that are in an extended region with larger values of virtual-bond angle θ [and, consequently, larger C^α····C^α distances (Fig. S8)]. The residence of some residues in the extended conformational states seems to make the second loop and part of the third helix reach the native geometry much slower in the trajectory with the kinetic trap (Fig. 4B) than in the trajectory without the kinetic trap (Fig. 4A). This delay of formation in Fig. 4B is enough to direct the N-terminal portion of the chain to pack against the wrong side of the helical hairpin formed by the second and the third helix (Fig. 4 C and D).

Fig. 4.

(A–F) Anaglyph stereo diagrams of the 24- to 37-residue portion of protein A at 45 ps of the trajectories without (A) and with (B) a kinetic trap. At 300 ps the whole protein collapses and forms either a molten globule (C) or a mirror-image (D) conformation; at 28 ns the protein emerges from a kinetic trap by opening the conformation of the first loop (E) and then proceeds to the native state (F) by adopting a closed-loop conformation.

Thus, the formation of the mirror-image conformation may be caused by the presence of multiple local conformational states in the second loop and part of the third helix (Asp29–Asn35). It should be noted that, based on the FEPs and ¹³C^α chemical shift analyses, the large portion of the third helix (Ser33–Lys42) might also be involved in formation of the mirror-image conformation; however, a visual inspection of each trajectory revealed that formation of the mirror-image conformation was initiated by the residues of the second loop and the neighboring part of the third helix (Asp29–Asn35).

Another three-helix bundle domain of staphylococcal protein A, namely the E domain (PDB code: 1edk), also forms the mirror-image topology (24). Remarkably, the B and E domains of protein A have identical sequences in the Asp29–Asn35 fragment, which are present in the second loop and in part of the third helix (Fig. 2). This observation reinforces our conclusion that this portion of protein A might be responsible for formation of the mirror-image conformation.

The Mechanism by Which Protein A Emerges from the Metastable Mirror-Image State.

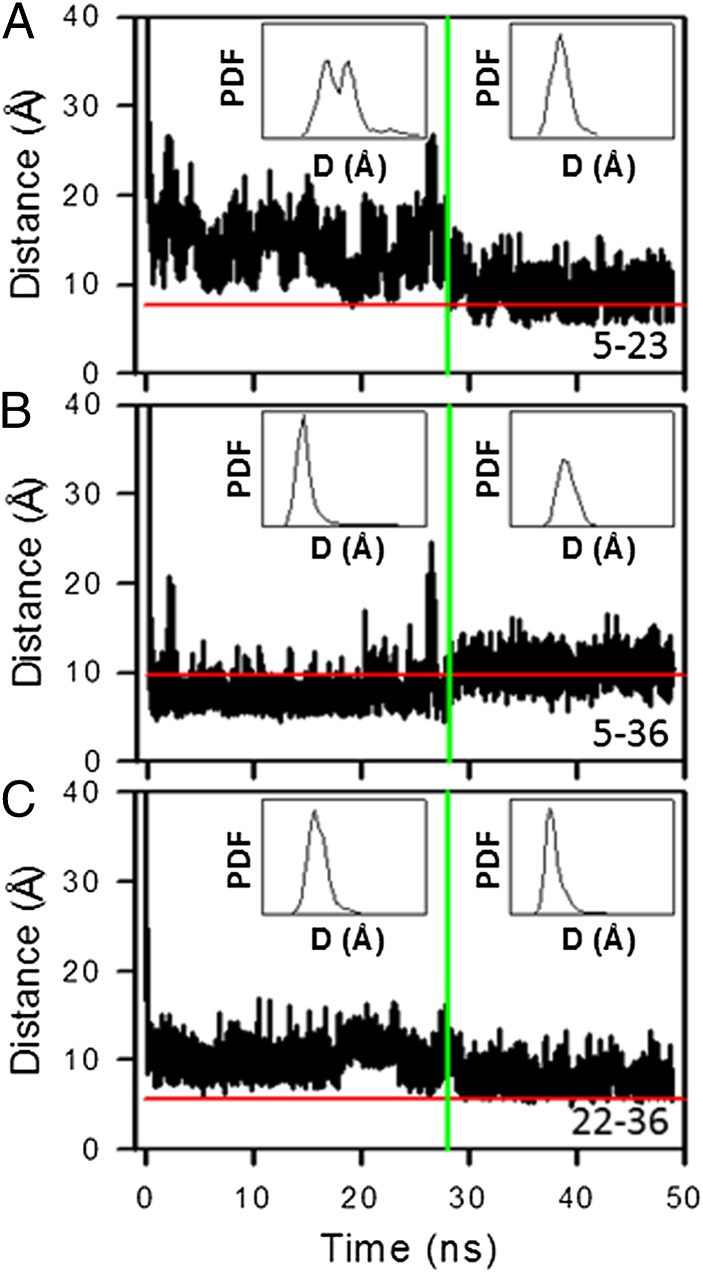
The FEPs and ¹³C^α chemical shift analyses enabled us to identify the fragment of the sequence of protein A that may be actively involved in surmounting the kinetic trap. However, the mechanism of how protein A overcomes the barrier between the metastable mirror-image state and the native state and what makes the protein undergo this transition has not yet been explained. That is why we examined the behavior of the helices in both the mirror-image and the native conformations. In particular, for the trajectory that folds through the mirror image, we calculated the distances between C^αs of selected nonpolar residues, pertaining to the first and second (Fig. 5A), the first and third (Fig. 5B), and the second and third (Fig. 5C) helices over 50 ns, which form hydrophobic contacts either in both the mirror-image (during the first 28 ns) and native conformations (Fig. 5 A and C) or in one of them (Fig. 5B). Insets in Fig. 5 A–C represent the PDF of each distance computed for both the mirror image state and the native state.

Fig. 5.

(A–C) The distances between C^αs of Phe5–Ile23 (A), Phe5–Leu36 (B), and Phe22–Leu36 (C), as functions of time for a 50-ns time interval (the 0- to 28-ns time interval corresponds to the mirror-image state, and the 28- to 50-ns time interval corresponds to the native state). Insets show the probability distribution functions of the distances (D) between these residues computed for both the mirror-image and the native states. Horizontal red lines correspond to experimental distances (5) between the C^αs of these selected residues. Vertical green lines indicate the time when the protein jumps from the metastable mirror-image state into the native state.

The average distance between C^αs of nonpolar residues, pertaining to the first and second helices, and the amplitudes of the fluctuations of this distance in the metastable mirror-image state (Fig. 5A) are greater than those of the other pairs (Fig. 5 B and C). Moreover, the bimodal broad distribution of the PDF in the mirror-image state is observed only for the pair of residues pertaining to the first and second helices (Fig. 5A), which is replaced by a narrow unimodal distribution in the native state. These results indicate that this portion of the protein is not stable in the metastable mirror-image state. The average distance between the nonpolar residues pertaining to the first and third helices (Fig. 5B) is smaller in the metastable mirror-image state than in the native state. Such behavior is understandable, because the Phe5–Leu36 pair forms hydrophobic contacts only in the mirror-image conformation. The average distance between the nonpolar residues pertaining to the second and third helices (Fig. 5C) is slightly larger in the metastable mirror-image state than in the native state. The amplitudes of fluctuations of the distances in the mirror-image state and in the native state are similar for both pairs of helices (first–third and second–third). However, the amplitudes of the fluctuations of the distance, between the nonpolar residues pertaining to the first and second (Fig. 5A) and the first and third (Fig. 5B) helices, increase significantly when the protein is about to overcome the barrier between the metastable mirror-image and native states. These results indicate that the first helix is the least stable helix in the metastable mirror-image state, and its instability induces the first loop to open and then close to place the third helix in the native location (Fig. 4 E and F). The behavior of the distances between the C^αs of other nonpolar residues than those shown in Fig. 5 is shown in Fig. S9.

Another visual justification of our conclusions can be seen in Fig. S4, in which the structures of protein A corresponding to significant changes in both trajectories clearly show how protein A misfolds (Fig. S4C) and then emerges from the metastable mirror-image state (Fig. S4B). Stereo diagrams of folding pathways for both trajectories are shown in Fig. S10.

Discussion and Conclusions

By analyzing the MD trajectories of the 10- to 55-residue fragment of the B domain of staphylococcal protein A generated with the coarse-grained UNRES force field, by FEPs along the amino acid sequence, by ¹³C^α chemical shift, and by PCA methods, we have investigated the reasons for formation of the mirror-image topology in protein A and found the following:

• i)The slow formation of the second loop and part of the third helix (Asp29–Asn35), which seems to play a crucial role in formation of the mirror-image conformation, appears to be caused by the presence of multiple local conformational states of the residues of the second-loop region (Asp29–Asn35).
• ii)In the trajectory with the mirror image, the residues of the second-loop region frequently visit more extended states (larger values of θ; Fig. 1B), whereas in the trajectory leading directly to the native structure, the second-loop region is more folded (smaller values of θ; Fig. 1A). Consequently, the second-loop region of the chain seems to reach the native geometry slowly and, in this way, it can enable the N-terminal portion of the chain to pack against the wrong side of the helical hairpin formed by the second and the third helix.
• iii)The “opening and closing” of the first loop may assist the first helix to jump over the plane of the second and third helices and consequently help protein A overcome the barrier, between the metastable mirror-image state and the native state, and fold to the native state. The computed difference between the total free energies of the mirror-image and the native conformations is only a few kilocalories per mole (12, 24) and, hence, it is not possible to identify only one particular type of interaction as being responsible for surmounting the kinetic trap during folding of protein A. In other words, any type of change in the intramolecular interactions could make protein A leave the energetically compatible metastable mirror-image state.
• iv)PCA was unable to detect formation of the mirror-image conformation, which might indicate that this conformation is a local property of protein A.

In the end, it should be noted that, although we computationally proved the plausibility of formation of the mirror-image conformation, we did not argue whether or how the mirror-image conformation could be detected experimentally. The point is that, based on our results, the differences in the local geometry of the second loop and part of the third helix regions between the pathways leading to the native and those leading to the mirror-image structures of protein A occur only at the beginning of the trajectories, before the protein collapses, within the tenth-of-microsecond timescale [because of the extension of the timescale of UNRES (27, 32)].

Another important point, which makes this problem very interesting, is the functional consequences that protein A may have because of the possible coexistence of the native and mirror-image folds. The point is that, besides the energetic closeness of these two conformations, the frequency of the transitions between the folded and mirror-image states increases with increase of temperature, and the mirror-image state becomes more and more probable with respect to the native state. In particular, the free-energy differences between the native and mirror-image folds that resulted from a cluster analysis of multiplexed replica exchange molecular dynamics (MREMD) simulations at different temperatures [$\mathrm{\Delta }F=-k_{\text{B}}Tln\left(x_{\text{mirror}}/x_{\text{native}}\right)$, where k_B, T, x_mirror, and x_native are the Boltzmann constant, the absolute temperature, and the populations of mirror-image and native clusters, respectively] are 4.15 kcal/mol (at 270 K), 3.15 kcal/mol (at 280 K), and 1.95 kcal/mol (at 300 K); and, at the folding-transition temperature, the populations of the conformations with the native and mirror-image topology are nearly equal (17). Hence, the question can be raised of whether protein A in the mirror-image conformation performs the same function as it does in the native conformation. In general, it should not be the same, because the mirror-image conformation is a misfolded conformation; however, without experimental evidence for the existence of the mirror-image conformation, we cannot argue this issue.

Materials and Methods

We carried out 96 canonical MD simulations in a broad range of temperatures (270 K ≤ T ≤ 350 K) with the UNRES force field parameterized (34) on the 1GAB (35) protein. The UNRES force field takes the solvent into account implicitly, through the mean-force potential of interactions between united side chains (34). The folding was found to occur either directly to the native state or through a kinetic trap, mainly the topological mirror image of the native three-helix bundle. The latter folding scenario was observed more frequently at low temperatures (e.g., protein A folds through a kinetic trap in 7 of 16 trajectories at 270 K). Therefore, the four pairs of trajectories that were selected for detailed analysis corresponded to those at low temperature (270 K). It should be noted that a visual inspection of the remaining pairs of MD trajectories at 270 K revealed a similar mechanism for formation of the mirror-image conformation and for its emergence from the metastable mirror-image state. The Berendsen thermostat (36) was used to maintain constant temperature. The time step in molecular dynamics simulations was δt = 0.1 mtu [1 mtu = 48.9 fs is the “natural” time unit of molecular dynamics (37)] and the coupling parameter of the Berendsen thermostat was τ = 1 mtu. A total of 10⁸ MD steps were run for each trajectory.