Exploring the collaboration between antibiotics and the immune response in the treatment of acute, self-limiting infections

Significance

We use a mathematical model and computer simulations to explore the design and evaluation of antibiotic treatment protocols for an acute, self-limiting bacterial infection. We consider the effect of dose, dosing frequency, and term of treatment on the time before clearance of the infection and the likelihood of resistance emerging and ascending during therapy. Our analysis supports high-dose, full-term antimicrobial chemotherapy as the most effective strategy for maximizing the rate of cure and minimizing the de novo evolution of resistance during the course of therapy. We discuss the current status of data in support of and against the predictions of this study and identify potential ways of testing the hypotheses derived from our analysis.

Abstract

The successful treatment of bacterial infections is the product of a collaboration between antibiotics and the host’s immune defenses. Nevertheless, in the design of antibiotic treatment regimens, few studies have explored the combined action of antibiotics and the immune response to clearing infections. Here, we use mathematical models to examine the collective contribution of antibiotics and the immune response to the treatment of acute, self-limiting bacterial infections. Our models incorporate the pharmacokinetics and pharmacodynamics of the antibiotics, the innate and adaptive immune responses, and the population and evolutionary dynamics of the target bacteria. We consider two extremes for the antibiotic-immune relationship: one in which the efficacy of the immune response in clearing infections is directly proportional to the density of the pathogen; the other in which its action is largely independent of this density. We explore the effect of antibiotic dose, dosing frequency, and term of treatment on the time before clearance of the infection and the likelihood of antibiotic-resistant bacteria emerging and ascending. Our results suggest that, under most conditions, high dose, full-term therapy is more effective than more moderate dosing in promoting the clearance of the infection and decreasing the likelihood of emergence of antibiotic resistance. Our results also indicate that the clinical and evolutionary benefits of increasing antibiotic dose are not indefinite. We discuss the current status of data in support of and in opposition to the predictions of this study, consider those elements that require additional testing, and suggest how they can be tested.

The goals of antibiotic treatment of bacterial infections are straightforward and interrelated: to maximize the likelihood and rate of cure, to minimize the toxic and other deleterious side effects of treatment, and to minimize the likelihood of resistance emerging during the course of therapy. How does one choose the most effective antibiotic(s) for a given infection and determine its optimum dose, frequency, and term of administration to achieve these goals?

One answer has been to combine in vitro studies of the pharmacodynamics (PD) of the antibiotics and bacteria and the in vivo pharmacokinetics (PK) of the antibiotics in treated patients or model organisms (1, 2). Central to this “rational” (as opposed to purely empirical) approach to antibiotic treatment are PK/PD indices. Although there have been efforts to develop more comprehensive measures of the relationship between the concentration of antibiotics and rate of bacterial growth (e.g., see refs. 3–5), in practice the lowest antibiotic concentration required to prevent the in vitro growth of the bacteria [the minimum inhibitory concentration (MIC)] is the sole pharmacodynamic parameter used for these indices (6). Depending on the drug, one of three PK parameters that quantify drug availability is combined with the MIC to generate these PK/PD indices: (i) the ratio of the peak antibiotic concentration achieved in vivo to the MIC, C_MAX/MIC, (ii) the ratio of the area under the concentration–time curve to the MIC, AUC/MIC, and (iii) the amount of time the antibiotic concentration exceeds the MIC, T > MIC. The therapeutic efficacies of different classes and regimens of antibiotics are assessed by determining the relative values of one of these indices. These evaluations are conducted in vitro, for example with hollow-fiber systems, or with experimental animals, typically neutropenic mice (7).

Although host variation in PK is sometimes considered in these analyses (2), by using the MIC as the single PD parameter, PK/PD indices have the virtues of reductionism and standardization; there are precisely prescribed ways by which MICs are estimated (8–10). While there is evidence that some antibiotic use protocols based on these indices are correlated with treatment success (11–14), it is not at all clear whether these protocols are optimal (15, 16). Treatment fails and resistance emerges even when PK/PD-based protocols are adhered to (12, 17). Are there antibiotic treatment regimens that would lead to lower rates of failure and reduced likelihood of resistance emerging than those based on simple PK/PD indices with MICs as the unique PD parameter?

Mathematical and computer simulation models are promising in their ability to provide a framework for the development and evaluation of optimal antibiotic treatment protocols. They have been successfully used to design and evaluate antibiotic use regimens for hospitals and to examine the relationship between antibiotic use and the epidemiology of resistance in open communities (e.g., refs. 18–21). Mathematical models have also been used to explore and evaluate protocols for the treatment of individual patients with single and pairs of antibiotics (22–26).

However, existing models of antibiotic treatment neglect a number of inconvenient but potentially important realities of bacterial infections. For instance, they commonly ignore within-host heterogeneities in access to antibiotics and differences in antibiotic susceptibility of bacteria in separate spatial compartments or physiological states. In addition, they consider inherited resistance as a discrete state, rather than as the continuum of susceptibility to the drugs that it is. Furthermore, although it is well known that the clearance of bacterial infections can be attributed to the combined action of immune defenses and antibiotics, there has been very limited exploration of how the interaction between antibiotics and the immune response affect the course of therapy. With few exceptions (e.g., refs. 22 and 27–29), mathematical models of antibiotic treatment of patients do not consider the contribution of the host’s immune defenses. Moreover, the models of antibiotic treatment of which we are aware that do consider these defenses typically assume that the intensity of the immune response depends on the density of the infecting population of bacteria (for an exception, see ref. 28). In theory, such interaction between antibiotics and the immune response could be antagonistic rather than synergistic; by reducing the density of the bacterial population, antibiotic cidal action could decrease the intensity of the immune response that would be mobilized to eradicate the infection. At another extreme, an alternative relationship between the immune system and antibiotics could also exist where immune responses could be independent of the density of the infecting bacteria, in which case the bactericidal immune activity would not be blunted by the action of antibiotics.

In this report, we use a mathematical model and computer simulations to explore the course of antibiotic-treated bacterial infections in immune-competent hosts. We restrict our consideration to the most common use of antibiotics in open communities, to reduce the morbidity and term of normally self-limiting acute infections (30). This application of these drugs is certainly a (and maybe the most) significant selective force responsible for the ascent and maintenance of antibiotic resistance in human communities. It is also the focus of pleas for and advice about the prudent use of antibiotics (see, for example, www.tufts.edu/med/apua/consumers/faqs.shtml).

The model combines the pharmacokinetics of periodic antibiotic dosing with multiparameter functions for the pharmacodynamics of the antibiotics and bacteria and innate and adaptive host immune responses. It allows for the contribution of phenotypic resistance, multiple states of inherent susceptibility of the bacteria to the treating drugs and within-host variation in the efficacy of immune responses. In analyzing the properties of this model, we explore the efficacy of different antibiotic dosing, frequency of administration, and term-of-use regimens on the rate of bacterial clearance (cure) and emergence of antibiotic resistance. We consider how pathogen density-dependent (PDD) and pathogen density-independent (PDI) immune responses affect the efficacy of treatment regimens. The results of our analysis make a number of predictions (hypotheses) about the consequences of different antibiotic treatment regimens, as well as different antibiotic-immune response interactions on the course of bacterial infections.

Methods

The Model.

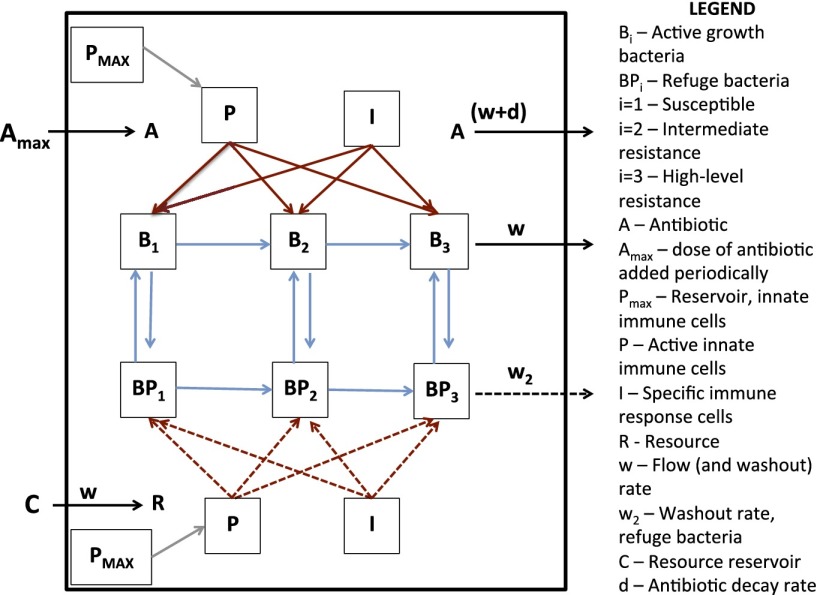
The model we develop here is an extension of that used in ref. 31 that incorporates innate and adaptive host immune responses and the emergence of resistance (Fig. 1). In the following, we outline the different elements of this model.

Fig. 1.

Schematic diagram showing the mathematical model of the population and evolutionary dynamics of bacteria with host immune responses and antibiotic treatment.

The bacterial populations.

In the absence of antibiotics, the maximum growth rate of bacteria of population B_i (ϕ_iMAX) is proportional to the concentration of a limiting resource, R µg/mL, as follows:

$${\varphi }_{iMAX}\left(R\right)=V_{iMAX}\left(\frac{R}{k+R}\right),$$

where k is the concentration of the resource at which the population is growing at one-half its maximum rate, and V_MAX is the maximum resource-independent growth rate (32). There are three populations of bacteria with densities and designations B₁, B₂, and B₃. These bacteria differ in their MIC_i, with the higher index number bacteria being less susceptible to the antibiotic than the lower index populations (9, 33). In our simulations, the intermediate (B₂) and high-level (B₃) resistant populations have MICs, respectively, 2- and 10-fold greater than that of the most susceptible population (B₁). The bacteria can also exhibit different maximum rates of growth, V_iMAX, due to fitness costs of resistance in the B₂ and B₃ populations. Bacteria of more susceptible states can generate those of lower susceptibility by mutation: B₁ → B₂ at a rate µ₁ per cell per generation and B₂ → B₃ at a rate µ₂ per cell per generation. For convenience and also because the effect is negligible, we do not consider reverse mutation. The cells of each of these bacterial populations can be in one of two states: (i) rapidly replicating and phenotypically susceptible to the antibiotics, or (ii) slowly replicating and phenotypically refractory to the antibiotics. The latter subpopulations, BP₁, BP₂, and BP₃, represent a refuge from the antibiotics as would be expected for persisters (34) as well as cells in biofilms and other subhabitats where the efficacy of the antibiotics is reduced (35). These refuge populations divide at a low rate, ψ_pi(R), as follows:

$${\psi }_{Pi}\left(R\right)=V_{Pi}\left(\frac{R}{k+R}\right),\text{ where }{\mathit{V}}_{\mathit{p}}\mathit{<< }{\mathit{V}}_{\mathit{MAX}}\text{. }$$

We assume that bacteria change from susceptible to phenotypically refractory states at rate f_SP per cell per hour and return to the susceptible state at a rate f_PS per cell per hour, f_SP < f_PS.

Pharmacodynamics and pharmacokinetics.

Central to the PD of this model is a Hill function in which the net rate of growth or death of a bacterial population, ψ_i, is a function of the concentration of the antibiotic, A µg/mL, and the limiting resource, R µg/mL (36), as follows:

$${\psi }_i\left(A,R\right)={\varphi }_{iMAX}\left(R\right)-\left[\frac{\left({\varphi }_{iMAX}\left(R\right)-{\varphi }_{iMIN}\left(R\right)\right){\left(\frac{A}{MI{C}_i}\right)}^{\kappa }}{{\left(\frac{A}{MI{C}_i}\right)}^{\kappa }-\frac{{\varphi }_{iMIN}\left(R\right)}{{\varphi }_{iMAX}\left(R\right)}}\right],$$

where ϕ_iMAX(R) is the maximum resource-limited growth rate of the bacteria; ϕ_iMIN(R) is the minimum resource-limited growth rate of the bacteria, and ${\varphi }_{iMIN}\left(R\right)=V_{iMIN}\left(R/\left(k+R\right)\right)$, where V_MIN is the resource-independent minimum bacterial growth rate (maximum antibiotic kill rate); κ, the Hill coefficient is a shape parameter that describes the sensitivity of the bacterial growth rate to changes in antibiotic concentration; and MIC_i is the minimum inhibitory concentration of the antibiotic.

For the pharmacokinetics, we assume that in the absence of input the concentration of the antibiotic declines exponentially at rate d per hour, and is also lost due to flow from the site of infection at rate w as follows:

$$\frac{dA}{dt}=-\left(d+w\right)A.$$

Resources.

Resources continually infuse into the site of the infection out of a resource reservoir C at a rate w µg/mL per day and are consumed by the bacteria at a rate proportional to their maximum growth rate and a conversion efficiency parameter, e µg per cell (37). The latter is the amount of resource required to produce a single new cell. The rate of change in the resource concentration is therefore given by the following:

$$\frac{dR}{dt}=w\left(C-R\right)-e\left({\displaystyle \sum _{i=1}^n{B}_i{\psi }_i\left(A,R\right)+}{\displaystyle \sum _{i=1}^{n}B{P}_i{\psi }_{Pi}\left(R\right)}\right).$$

The immune response.

Our model incorporates two components of mammalian immune defenses, a rapid innate response and a more slowly developing adaptive response.

The innate immune response.

Our model of the innate immune response is similar to that in ref. 38. Activated effector cells are recruited into the site of the infection at a rate proportional to the density of cells in an inactive reservoir and a rate parameter η per hour. The total density of cells in the reservoir is P_MAX, and P represents the density of activated effector cells, with the latter becoming inactive at a rate γ per hour. We consider two different forms of this immune response:

• i)a PDD form in which the rate of recruitment is proportional to the total density of the infecting bacterial population, N = B₁ + B₂ + B₃ + BP₁ + BP₂ + BP₃ via a Monod-like hyperbolic function as follows:

$$\frac{dP}{dt}=\eta \left(P_{MAX}-P\right)\left(\frac{N}{N+{\sigma }_P}\right)-\gamma P,$$

• where σ_P >0 is a saturation constant used to reflect the relationship between the rate of recruitment of the innate immune cells and the density of bacteria in the site of the infection, and

• ii)a PDI form, where the rate of recruitment of activated innate immune cells does not depend on bacterial density:

$$\frac{dP}{dt}=\eta \left(P_{MAX}-P\right)-\gamma P.$$

The adaptive (specific) immune response.

• i)The PDD form: The adaptive immune response proceeds via a clonal expansion of effector cells, I, that are specific for the collective of antigens borne on the infecting bacteria. We assume that the intensity of this response changes at a rate determined by the maximum rate at which the I population increases, α per hour, and the density of the target population of bacteria. The constant σ_I is the density of bacteria at which the adaptive immune response increases at one-half its maximum rate (39):

$$\frac{dI}{dt}=\alpha I\left(\frac{N}{N+{\sigma }_I}\right).$$

• ii)The PDI form: The adaptive immune response is independent of pathogen density and continues to increase until it reaches a maximum saturation level:

$$\frac{dI}{dt}=\alpha I\left(1-\frac{I}{{\delta }_I}\right),$$

• where δ_I is the maximum density attainable by adaptive immune cells.

Because we are modeling short-term infections, we assume that there is no waning of the adaptive immune response over the course of the infection.

Bacterial population dynamics under immune action.

We assume the sensitivity to growth inhibition (killing) by the innate and adaptive immune response is the same for all replicating populations of bacteria and proportional to the product of their densities, P or I, and the mass action constants k_p or k_I (per immune cell per hour), respectively. We also assume that the three phenotypically refractory populations of bacteria are killed at a lower rate than the more rapidly replicating subpopulations. The mass action constants for the innate and adaptive immune responses for these refuge populations are, respectively, j_p and j_I, where j_p < k_p and j_I < k_I.

With the above definitions and assumptions, the rates of change in the densities of the bacterial populations are given by the following:

$$\frac{d{B}_i}{dt}={\psi }_i\left(A,R\right)B_i-k_P{B}_{i}P-k_I{B}_{i}I+f_{PS}B{P}_i-f_{SP}{B}_i,$$

$$\frac{dB{P}_i}{dt}={\psi }_{Pi}\left(R\right)B{P}_i-j_{P}B{P}_{i}P-j_{I}B{P}_{i}I-f_{PS}B{P}_i+f_{SP}{B}_i.$$

Computer Simulations.

We use a semistochastic algorithm to solve the above array of coupled differential equations. The changes in the densities of the bacteria, immune cells, and concentrations of the resource and antibiotic are deterministic. The corresponding differential equations are solved by the Euler method with a finite step size Δt. The generation and loss of phenotypically resistant refuge bacteria and mutation to antibiotic resistance are stochastic. We incorporate these stochastic elements into the model via a Monte Carlo protocol, used for its relative simplicity. To illustrate this algorithm, we consider that used for the generation of refuge bacteria. At each finite time interval Δt, the probability that a single refuge cell BP₁ will be produced from the B₁ population is f_SPB₁Δt, where Δt is chosen so that this product is less than 1. If a random number x (0 < x < 1) is less than or equal to f_SPB₁Δt, a single B₁ is removed from that population and enters the refuge BP₁ population. Mutations that change the resistance state of the bacteria are generated using a similar protocol, at rates proportional to bacterial growth rates and the product of the number of individuals of the ancestral state and the mutation rate, μ₁ or μ₂. In addition, because stochastic extinction processes are important at lower population densities (40, 41), we assume that when the density of a bacterial population is less than 5 cells per mL, there is a 50% chance of extinction of that population with each iteration of the simulation. In Table S1, we list the variables and parameters of the model and the ranges and/or standard values of the parameters used in our simulations. Whenever possible, we use parameter values in the ranges of those estimated experimentally for Staphylococcus aureus and Escherichia coli (16, 36, 42, 43). For more justifications of the parameter values used, see the footnotes to Table S1.

We initiate the simulations with a single bacterium of state B₁, a single phagocyte P = 1 and a single adaptive immune cell I = 1. We choose parameter values to address the reality that the infecting bacterial population increases exponentially and reaches substantial densities before the host response begins to control it. Because we are exploring the dynamics of a self-limited infection, the combined innate and adaptive immune responses will, in the absence of antibiotics, clear the infection over a clinically realistic term (44, 45). The simulation used for this model was programmed in Berkeley Madonna. Copies of the program are available at www.eclf.net/programs.

Results

Dynamics of the Self-Limiting Infection With and Without Antibiotic Treatment.

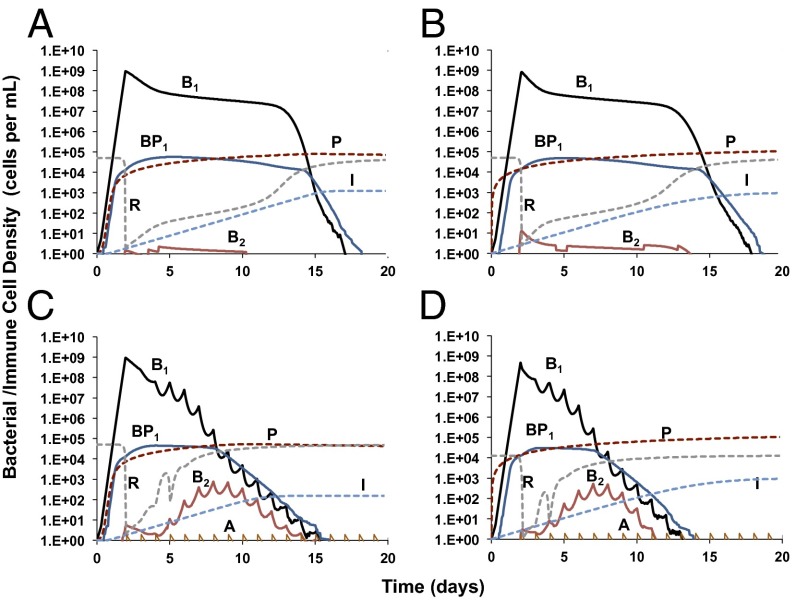
In Fig. 2, we illustrate the dynamics of the self-limiting infection with and without antibiotic treatment. In the absence of antibiotics, for both PDD (Fig. 2A) and PDI (Fig. 2B) immune responses, the susceptible bacteria grow to densities that are high enough to produce a substantial density of refuge bacteria (BP₁). Intermediate-resistance bacteria (B₂) are generated but do not ascend due to resource restriction. Because the infection is self-limited, all bacteria are cleared well before the end of the 20th day (see Fig. S1 for the dynamics of the infection in the absence of an immune response). In our simulations, antibiotic treatment commences after the bacteria reach their peak, resource-limited density (presumably when symptoms are manifest). The addition of a small dose of antibiotics at this time reduces the amount of time before the infection is cleared (Fig. 2 C and D). As a consequence of the antibiotics reducing the density of the infection, resources are freed and bacteria with intermediate resistance to the antibiotic, B₂ ascend. However, these too are eventually cleared by the immune response. This consequence of antibiotic therapy obtains with both PDD and PDI immune responses, respectively (Fig. 2 C and D). The rate of clearance, however, is somewhat greater for the PDI response.

Fig. 2.

Bacterial population dynamics of a self-limited infection with immune action and antibiotic treatment. Changes in the densities of the bacteria (B₁, antibiotic-susceptible, undergoing active growth; B₂, intermediate-resistant, undergoing active growth; BP₁, refuge bacteria), resources (R), and immune cells (P, innate immune cells; I, adaptive immune cells) under the following conditions: (A) pathogen density-dependent (PDD) innate and adaptive immune action, (B) pathogen density-independent (PDI) innate and adaptive immune action, (C) PDD innate and adaptive immune action with antibiotic treatment (dose, 2 μg/mL), and (D) PDI innate and adaptive immune action with antibiotic treatment (dose, 2 μg/mL). The parameter values used for the simulations are listed in Table S1.

Dose and Frequency of Administration.

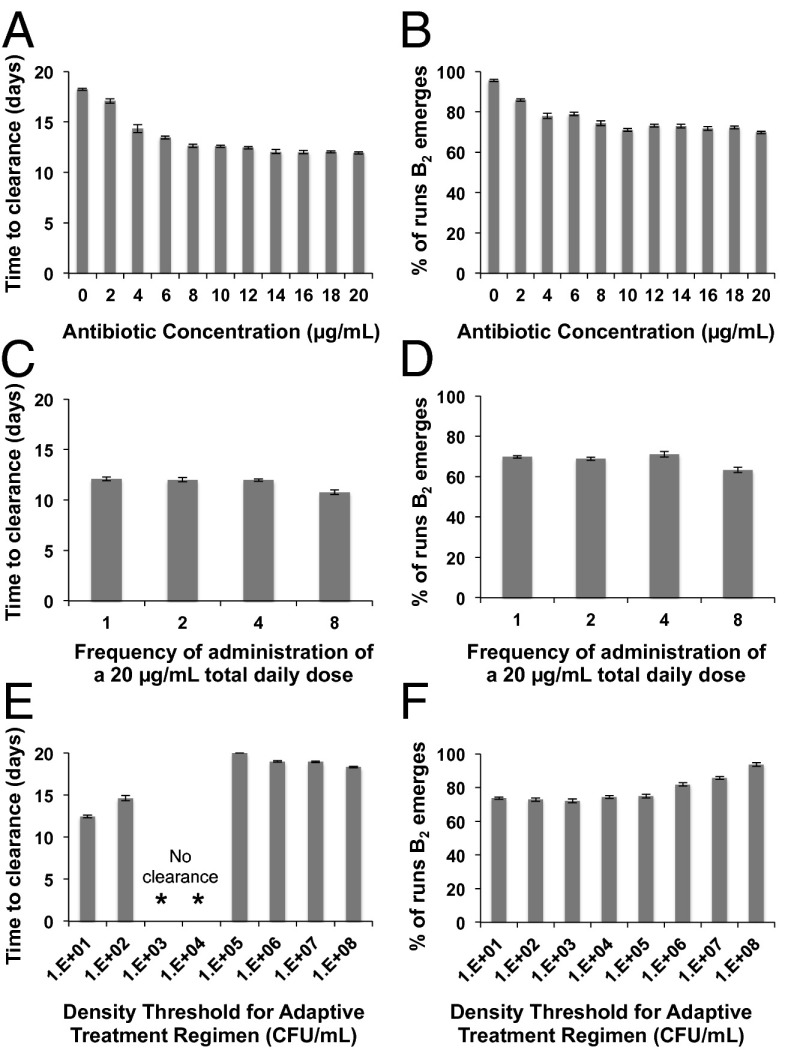
How do different doses and frequencies of administration affect the time to clearance of the bacteria and the rate of evolution of intermediate and high-level resistance? As our measure of clearance, we consider the average number of days required for the density of the total bacterial population to be less than 1 CFU/mL over 10 independent simulations. To explore the effects of treatment on the emergence of resistance, we estimate the average number of Monte Carlo simulations in which the density of B₂ or B₃ exceeds 1 before the infection is cleared at day 20. With PDD immune dynamics, the average time to clearance and the fraction of runs in which B₂ bacteria emerge declines with increasing concentrations of the antibiotic (dose) (Fig. 3 A and B). This decline, however, is not monotonic. After a point, increasing the dose of the drug has little or no effect on either of these measures of antibiotic efficacy. This is a reflection of the saturable Hill function pharmacodynamics.

Fig. 3.

The effects of different treatment regimens and pathogen density-dependent (PDD) immune dynamics on the average time to clearance of the infection (left column) and fraction of 100 simulations in which bacteria with intermediate levels of resistance emerge (right column). Means and SEs for 10 independent simulations (left column) and means and SEs for 10 independent simulations each with 100 runs (right column). (A and B) Single daily doses of different concentrations of the antibiotic; (C and D) 20 µg/mL of the antibiotic administered at different frequencies ranging from one dose of 20 µg/mL to eight doses of 2.5 µg/mL per day; (E and F) different density thresholds for the cessation of antibiotic dosing in adaptive treatment regimens, standard treatment of 10 µg/mL per day.

In Fig. 3 C and D, we illustrate the effect of the frequency of administration on clearance and resistance. On first consideration, it may seem surprising that dosing rates have little effect on these measures of the efficacy of treatment. Why this is the case can be seen in Fig. S2, where we follow the changes in density of bacteria for situations where the same total concentration of the drug is administered in a single daily dose, or partitioned into eight separate doses. When the dose is high and the frequency of administration low, between doses, the antibiotic concentration wanes to low levels due to decay and washout. However, as a result of the high initial concentration, the density of the bacterial population is markedly reduced before it starts to recover (Fig. S2A). Although the magnitude of antibiotic-mediated killing at each dose is decreased by partitioning the total amount of drug into more frequently administered doses, the amplitude of the oscillations in concentration is damped and the rate of antibiotic-mediated killing is more constant (Fig. S2B). The net effect is that both the rate of clearance and intensity of selection for resistance are relatively insensitive to changes in the frequency of administration of the drug.

Treatment Hiatuses.

In Fig. 3 E and F, we consider the effects of an “adaptive treatment” regimen, whereby drugs are only administered when the density of bacteria exceeds a threshold level. Our assumption is that this threshold represents the density below which symptoms would be abrogated. In this way, we examine a type of regimen in which administration of antibiotics depends on the presence of symptoms in a patient. This type of regimen would affect the frequency at which dosing occurs, the total time over which treatment is undertaken (term) and, ultimately, the total concentration of antibiotic that a patient would be exposed to during the course of their therapy. We explore the potential effects of this type of regimen by varying the thresholds at which dosing occurs and examining the impact on the rates of bacterial clearance (Fig. 3E) and emergence of resistance (Fig. 3F). Clearance occurs more rapidly at lower than at higher threshold densities, and the rate of emergence of resistance is also lower in the former. At the very low threshold densities (10¹ and 10²), the hiatuses in treatment are relatively rare and the antibiotics are effective in reducing the density of the bacterial population. At high threshold densities (10⁵ and above), hiatuses in dosing occur frequently and antibiotic cidal activity is decreased. Because the intensity of the immune response is directly proportional to the density of the infecting bacteria, immune-mediated killing plays a major role in clearance under these conditions. As the numbers of bacteria are relatively large, mutants of intermediate resistance are more likely to be generated at these high threshold densities (Fig. 3F). Hence, high-level resistant bacteria are also generated at threshold densities of 10⁶ and above, although this occurred infrequently, in less than 1% of simulations. At “intermediate” threshold densities (10³ and 10⁴), we observe an intriguing result in which clearance does not occur in any of the runs. This result is due to the interplay between the density of the bacteria and the immune response. At these threshold densities, the hiatuses in antibiotic dosing keep the average density of bacteria during treatment at levels that only marginally stimulate the adaptive immune response, and, as a result, clearance does not occur (Fig. S3).

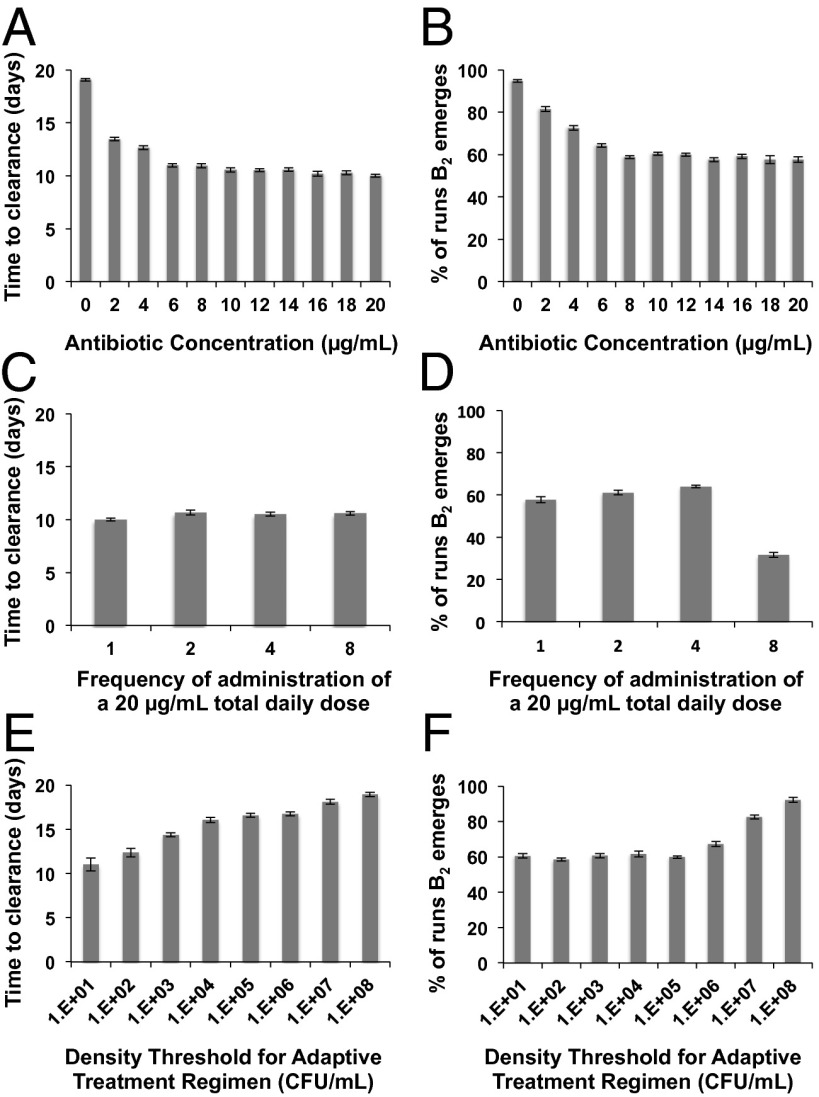
In Fig. 4, we illustrate the corresponding simulation results as those in Fig. 3, but for PDI immune dynamics. With the same antibiotic concentrations, bacterial clearance occurs relatively earlier for PDI than for the PDD immune dynamics. Moreover, the effect of increasing antibiotic concentration is much less pronounced; with PDI immune dynamics, lower antibiotic concentrations (2 and 4 µg/mL) clear the infection more rapidly and are less likely to generate intermediate resistance than when the immune response depends on the pathogen density (Fig. 4 A and B). For PDI immune dynamics, we generally observe a relatively modest effect of varying dosing frequencies for the same reasons as described for PDD dynamics (Fig. 4 C and D). The exception to this is that, at the most frequent dosing rate, the likelihood of the emergence of intermediate-resistant bacteria is about one-half that at the other dosing rates (Fig. 4D). This result occurs because, under PDI conditions, the most frequent dosing regimen leads to a lower maximum density of ancestral B₁ cells and thereby appreciably decreases the likelihood of B₂ cells emerging.

Fig. 4.

The effects of different treatment regimens and pathogen density-independent (PDI) immune dynamics on the average time to clearance of the bacteria (left column) and fraction of simulations in which bacteria with intermediate levels of resistance emerge (right column). Means and SEs for 10 independent simulations (left column) and 10 independent simulations each with 100 runs (right column). (A and B) Single daily doses of different concentrations of the antibiotic; (C and D) 20 µg/mL of the antibiotic administered at different frequencies ranging from one dose of 20 µg/mL to eight doses of 2.5 µg/mL per day; (E and F) different density thresholds for the cessation of antibiotic dosing in adaptive treatment regimens, standard treatment of 10 µg/mL per day.

For adaptive treatment regimens, clearance occurs at all threshold densities, and time to clearance is directly proportional to the threshold densities (Fig. 4E). At threshold densities of 10⁵ and lower, emergence of resistance occurs at equivalent rates that are lower than for the corresponding thresholds under PDD immune dynamics (Fig. 4F). High-level resistant bacteria are generated at thresholds of 10⁶ and above, but as for PDD dynamics, they occur infrequently, in less than 1% of simulations.

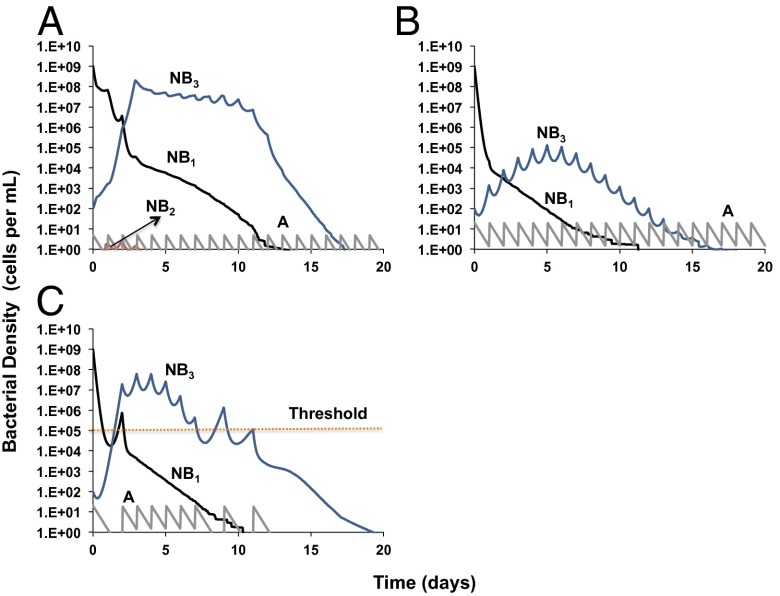
Preexisting Resistance.

In Fig. 5, we consider the treatment dynamics of an infection for which there is already a minority population of resistant B₃ cells before the initiation of therapy. When treated with a low antibiotic concentration, the density of susceptible bacteria is rapidly reduced while the resistant minority population ascends to high densities. In this self-limiting infection, however, these antibiotic resistant cells are eventually cleared by the immune response (Fig. 5A). In Fig. 5B, we illustrate how treating with higher antibiotic concentrations can reduce the rate of ascent and the maximum density attained by these resistant bacteria. This result occurs because of the reality that resistance is a continuum of levels of susceptibility in which even the least susceptible bacteria are not completely refractory to the antibiotic. If there are hiatuses in dosing due to an adaptive treatment regimen, even at the higher antibiotic concentrations used in Fig. 5B, the resistant bacteria ascend more rapidly, reach higher densities, and increase the time to clearance of the infection (Fig. 5C). Similar dynamics obtain for both PDD immune responses (Fig. 5) and PDI responses (Fig. S4), but clearance occurs earlier with the PDI immune response.

Fig. 5.

Bacterial population dynamics of a self-limited infection with preexisting high-level resistant bacteria and PDD immune dynamics. Changes in the densities of the bacteria (NB₁ = B₁ + BP₁, NB₂ = B₂ + BP₂, NB₃ = B₃ + BP₃) under the following conditions: (A) dose of 5 μg/mL; (B) dose of 20 μg/mL; (C) dose of 20 μg/mL, adaptive treatment threshold of 10⁵ bacteria per mL. The parameter values used for the simulations are listed in Table S1.

Discussion

“Essentially, All Models Are Wrong, but Some Are Useful” (46).

Ultimately, the utility of mathematical and computer simulation models depends on their ability to explain existing observations and generate testable hypotheses for empirical studies. Some of the predictions made in this study have been supported experimentally in vitro, in laboratory animals and in treated patients, others have yet to be evaluated, and some experimental and clinical observations are inconsistent with what this model predicts. In the following, we discuss the major predictions of this study, the evidence in their support and opposition, the limitation of this evidence, and the implications of this theoretical study for the optimal design of antibiotic treatment regimens.

Our analysis of the properties of our model predicts that the term of acute, self-limiting infections (and presumably the magnitude of morbidity) will be inversely proportional to the dose of the antibiotic used for treatment. This prediction has been corroborated in a number of in vitro studies (47–49), in animal model experiments (50–52), and in patients (11, 12, 53–55). Our results also suggest that if at the onset of treatment all of the target bacteria are susceptible to the antibiotic, the likelihood of de novo resistance evolving will decline with the dose of the drug. There is support for this prediction from in vitro experiments (47, 49, 56–59), animal models (60, 61), and human studies (62–64). By rapidly reducing the density of the infecting bacteria, higher doses of antibiotics supplement the action of immune defenses and bring the numbers of bacteria down to levels where resistant mutants are not likely to be generated. Moreover, the generation of clinically significant levels of resistance can be a multistep process, as for fluoroquinolone resistance in S. aureus and E. coli (65). Our model suggests that if first-step or intermediate-resistance mutants are already present at the onset of or evolve during treatment, the likelihood of high-level clinical resistance emerging also declines with antibiotic dose. This prediction is supported by in vitro (48, 59, 66, 67) and animal model experiments (52, 68). Although not responsible for mortality, there are three compelling reasons to control the ascent of resistance in acute self-limiting infections: to minimize (i) the term of morbidity, (ii) the reservoir of resistant commensal and potentially invasive bacteria in the treated host, and (iii) the extent of transmission of resistant bacteria into the community.

Although it is convenient to consider susceptibility and resistance as qualitatively distinct states, in reality the susceptibility of bacteria to antibiotics is a quantitative rather than a qualitative phenomenon (9, 33). Our analysis indicates that as long as the dose is high enough, even if there are preexisting populations with reduced susceptibility, antibiotics can retard their rate of ascent and densities and thereby the likelihood that these “resistant cells” will be transmitted. For Streptococcus pneumoniae infections, for instance, there is both in vitro and in vivo evidence to show that, by using higher doses, β-lactam antibiotics can be used to treat some infections containing populations of bacteria that are officially “nonsusceptible” to the drug (69–71). Of course, because of toxicity and other side effects, there are limits to the concentrations at which most antibiotics can be used. Nevertheless, the doses at which some antibiotics are used could be increased to enhance their efficacy with little or no toxic side effects (72–74).

Although our analysis supports the use of higher doses of antibiotics for treatment, it also suggests that there are diminishing returns to increasing antibiotic doses. In addition to the potential deleterious side effects, after a point the gain in antibiotic-mediated killing and the capacity to limit the de novo evolution of resistance declines as the concentration of drug increases. This can be attributed to the saturation effect associated with Hill function pharmacodynamics. It is worth noting that a number of in vitro studies (36, 75–78) and experiments using animal models (79–82) have demonstrated that the pharmacodynamics of antibiotics are consistent with saturating functions like those used in our model. There have also been studies that support the proposition that, after a point, increasing doses of antibiotics have diminishing effects on clinical outcome (83, 84). It would seem particularly useful for the optimal use of existing antibiotics to have more studies determining the doses of antibiotics beyond which there is little or no effect on clinical outcome.

Our results also suggest that the relationship between the intensity of the immune response and pathogen burden can affect the net bactericidal effect generated by different doses of antibiotics. If the immune response develops at a rate that depends on bacterial load, by reducing the density of bacteria, antibiotics can decrease the stimulation of the immune response. This antagonism is particularly apparent at lower antibiotic doses, in which the course of the infection is prolonged due to a combination of relatively low antibiotic-mediated bactericidal activity and decreased stimulation of the immune response. If the rate at which the immune response develops is independent of pathogen burden, then no such antagonistic interactions occur. As a result, the advantages of increasing the dose of the drug are much less pronounced than when efficacy of the immune response is dependent on the density of the infection.

The two scenarios we have considered for the relationship between the intensity of immune responses and pathogen load, PDI and PDD, are heuristic extremes. There is experimental evidence to indicate that there can be both PDD (6, 85, 86) and PDI (87–89) immune responses to bacterial infection. Our results suggest that further experimental effort should be put into investigating the correlation between immune-mediated killing and pathogen burden for various bacterial diseases. This information may help modulate treatment doses, as the optimal dose might be different depending on the type of immune dynamics in play.

What about the frequency at which antibiotics are administered? The results of our analyses of situations in which the same total dose of an antibiotic is administered at different frequencies suggest that if the total concentration of the drug is sufficiently great, the frequency of administration would have little effect on the rate of clearance. This result supports using antibiotics at higher doses administered at lower frequencies, a practice that improves the logistics of treatment and the likelihood of adherence. Implicit in this interpretation is that adverse side effects are not dependent on the dose or frequency of administration. For at least some antibiotics, like the cyclic peptide daptomycin, the toxic side effects are lower when the drug is administered at high doses than when that dose is fractionated and administered more frequently (90).

What about the term, the length, of therapy? Is there justification for the common physician admonishment to “finish the course of treatment”? It has been suggested that using lower doses for short amounts of time would be an effective way to reduce the rate of ascent of resistance and thereby constitute a prudent use of antimicrobials (91). The assumption is that by reducing the density, rather than rapidly clearing the bacteria, such “light-touch therapy” would augment the contribution of immune responses while reducing the intensity of selection for resistance. To explore this light-touch approach, we used an adaptive treatment model of antibiotic treatment in which drugs are only administered when the density of bacteria is above some minimum threshold. We assume that the thresholds correlate with bacterial densities that elicit symptoms in a patient. Because of the hiatuses in treatment, the total amount of drugs used and the amount of time a patient is under therapy are less than they would be for a treatment regimen with a predefined term. The results of our analysis suggest that relative to a “heavier touch” treatment regimen, this form of light-touch therapy can extend the time before clearance and promote the evolution of antibiotic resistance.

Our model points to questions that should be addressed to evaluate moderate treatment regimens based on the manifestation of symptoms: (i) What are the densities of bacteria at which patients can cease taking antibiotics without affecting the rates of microbiological cure? (ii) What is the relationship between these bacteriological loads and patient symptoms? To obtain answers to these questions, it will be critical to monitor the densities of infecting populations of bacteria and determine the relationship between these densities and the symptoms of the infection during the course of treatment. When this information is available, the term of therapy may then be modulated by the manifestation of symptoms rather than a preprescribed term. Of note, although we assume that symptoms are a direct reflection of bacterial load, immunopathology is another crucial component of patient morbidity (34). Monitoring the extent of immune responses and determining correlations with immunopathology would also provide useful information for the design of more moderate treatment regimens.

Taken at large, the results of this study are inconsistent with the arguments by Read et al. (91) against the “orthodoxy” of high-dose antimicrobial chemotherapy and experimental support for their arguments (92). The basis of their argument and evidence is “competitive suppression.” If, as seems reasonable, the intensity of selection for resistance is proportional to the dose of a drug, the rate of ascent of resistance would be directly proportional to that dose as well (93). If resistance engenders a fitness cost on the pathogen, at lower doses of the antimicrobial the advantage gained by resistance may not exceed its cost; the ascent of the resistant strains would then be “competitively suppressed” by the intrinsically more fit coinfecting susceptible pathogens. How relevant is “competitive suppression” for antibiotics and bacteria? Even when resistance initially engenders a fitness cost, compensatory mutations may ameliorate these costs (94–98). Moreover, the rate of clearance and population dynamics of resistance in bacteria are not uniquely determined by the concentration of the antibiotic at a point in time. As in our model, this rate and the intensity of selection for resistance depends on a complex interplay between the pharmacokinetics, pharmacodynamics, and the contribution of the immune system.

“Frapper Fort et Frapper Vite” (Hit Hard and Hit Fast).

This quotation was Paul Ehrlich's recommendation to maximize the rate at which microbes are cleared, i.e., chemotherapeutic drugs should be used as early in the infection as possible and at high doses (99). The results of this computer-assisted theoretical study support this century-old recommendation. They also raise a number of questions about the details of this “hit them hard” protocol with respect to the microbiological, immunological, and evolutionary components of the rational design of antibiotic treatment regimens. These questions can and certainly have to be answered empirically.