Protein Mass-Modulated Effects in the Catalytic Mechanism of Dihydrofolate Reductase: Beyond Promoting Vibrations

Abstract

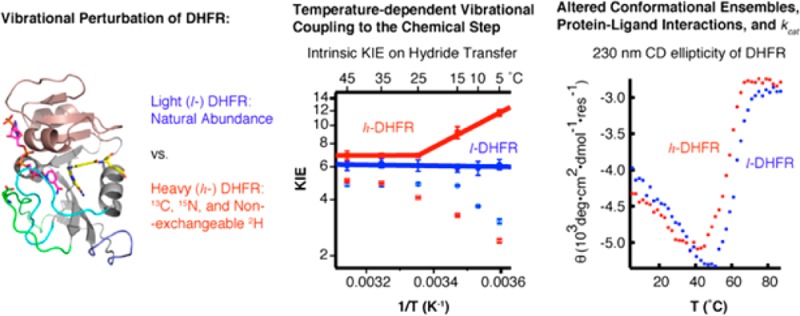
The role of fast protein dynamics in enzyme catalysis has been of great interest in the past decade. Recent “heavy enzyme” studies demonstrate that protein mass-modulated vibrations are linked to the energy barrier for the chemical step of catalyzed reactions. However, the role of fast dynamics in the overall catalytic mechanism of an enzyme has not been addressed. Protein mass-modulated effects in the catalytic mechanism of Escherichia coli dihydrofolate reductase (ecDHFR) are explored by isotopic substitution (¹³C, ¹⁵N, and non-exchangeable ²H) of the wild-type ecDHFR (l-DHFR) to generate a vibrationally perturbed “heavy ecDHFR” (h-DHFR). Steady-state, pre-steady-state, and ligand binding kinetics, intrinsic kinetic isotope effects (KIE_int) on the chemical step, and thermal unfolding experiments of both l- and h-DHFR show that the altered protein mass affects the conformational ensembles and protein–ligand interactions, but does not affect the hydride transfer at physiological temperatures (25–45 °C). Below 25 °C, h-DHFR shows altered transition state (TS) structure and increased barrier-crossing probability of the chemical step compared with l-DHFR, indicating temperature-dependent protein vibrational coupling to the chemical step. Protein mass-modulated vibrations in ecDHFR are involved in TS interactions at cold temperatures and are linked to dynamic motions involved in ligand binding at physiological temperatures. Thus, mass effects can affect enzymatic catalysis beyond alterations in promoting vibrations linked to chemistry.

Introduction

Protein structures in solution fluctuate on a broad range of time scales, from atomic vibrations in femtoseconds to conformational changes in milliseconds or longer. Enzyme dynamics on the catalytic turnover (k_cat) time scale (usually ≥ms) are known to play important roles in substrate binding, product release, and conformational sampling in the catalytic cycle.¹⁻⁴ However, the role of fast protein dynamics (e.g., in fs) in the full catalytic cycle of enzymes remains elusive. Computational studies suggest that some enzymes employ “protein-promoting vibrations” (PPVs, from fs to ps)⁵ to modulate bond vibrations of substrates and promote passage over the energy barrier of the chemical step (i.e., covalent bond changes).⁶⁻⁸ These PPVs were predicted to extend beyond the active site, across the protein architecture of the enzyme.⁸ To examine this computational suggestion, Schramm and co-workers devised an experimental tool known as “heavy enzymes”,⁹ where all the amino acids are uniformly labeled with ¹³C, ¹⁵N, and non-exchangeable ²H (D) to perturb the bond vibrations without affecting the electrostatics of the protein (based on the Born–Oppenheimer approximation). All the heavy enzymes reported have shown slower rates in the chemical steps than the corresponding light enzymes,⁹⁻¹² supporting mass-dependent contributions of PPVs in crossing the chemical barriers.

While the coupling of PPVs to chemical barrier crossing in several enzymes is compelling, some heavy enzymes have shown altered substrate binding or product release steps,¹⁰ indicating a mass-dependent dynamics in slower motions than those coupled to the transition state (TS). Heavy enzymes have slower bond vibrational frequencies, which are proposed to disrupt coordinated vibrations of the protein (including but not limited to PPVs). In addition, the substitution of non-exchangeable H by D causes slight geometry and dipole moment changes in C–H bonds.¹³ Although such differences have been reported to be negligible in small molecules,¹⁴ small effects may be multiplied in the extended structure of an enzyme. Thus, altering protein mass and bond vibrations may not only affect the “chemical step(s)” but also modulate enzyme dynamics on slower time scales involved in “physical steps” of the catalytic cycle. Here we study protein mass-modulated effects in the catalytic mechanism of Escherichia coli dihydrofolate reductase (ecDHFR), a widely used model system for studying enzyme catalysis, protein–drug interactions, and protein folding. DHFR catalyzes the hydride transfer from the reduced nicotinamide adenine dinucleotide phosphate (NADPH) to 7,8-dihydrofolate (DHF) to produce 5,6,7,8-tetrahydrofolate (THF, Figure 1A). This reaction is ubiquitous in all organisms and is the sole source of THF, the precursor for all folate coenzymes involved in biosynthesis of nucleic acids, proteins, lipids, and neurotransmitters, by providing one-carbon additions at different oxidation states. DHFR is the target of antifolate drugs (e.g. methotrexate) used to treat childhood leukemia and other diseases involving rapid cellular proliferation.¹⁵

Figure 1.

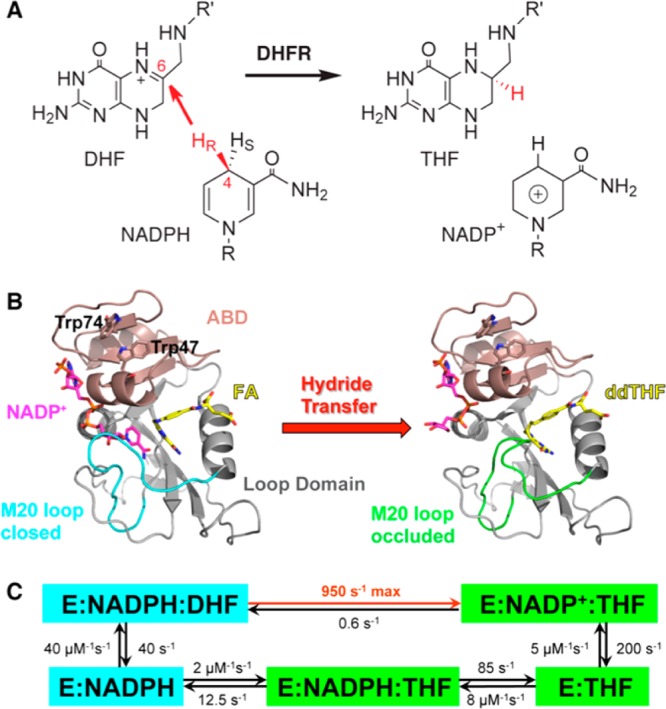
(A) DHFR catalyzes the stereospecific transfer of the pro-R hydride of C4 on NADPH to C6 of DHF, producing the product THF and oxidized cofactor NADP⁺. (B) The active-site cleft of ecDHFR divides the protein into two domains: the adenosine binding domain (ABD, residues 38–88) binds the adenosine moiety of the cofactor NADPH, while the loop domain (∼100 residues) is dominated by three loops surrounding the active site. The ternary complex of ecDHFR with NADP⁺ (magenta) and folic acid (FA, yellow) mimics the Michaelis complex (structure on the left, PDB code: 1RX2), where the M20 loop (cyan) closes over the active site to ensure close proximity of the hydride donor (C4 of NADPH) and acceptor (C6 of DHF). The ternary complex of ecDHFR with NADP⁺ (magenta) and 5,10-dideazatetrahydrofolic acid (ddTHF, yellow) mimics the product complex (structure on the right, PDB code: 1RX4), where the M20 loop (green) protrudes into the binding site of the nicotinamide ribose moiety of the cofactor to facilitate product release. (C) Under cellular conditions (with abundant NADPH concentrations), ecDHFR cycles through five kinetic intermediates, which are colored on the basis of the M20 loop conformations (cyan, closed; green, occluded). The rate constants of each step are from ref (27). The maximum (pH-independent) hydride-transfer rate (950 s^–1) was obtained from nonlinear regression of the pH dependence of observed rate constants (pH 5.5–9) in stopped-flow experiments.²⁷

The protein fold of ecDHFR contains large loop regions connecting a central eight-stranded β-sheet and four flanking α-helices (Figure 1B). This relatively unstable structural feature leads to ground-state (GS) conformational heterogeneity of ecDHFR in various ligand-bound states,^16,17 while apo-ecDHFR exists as two conformational isomers that slowly interconvert (0.034 s^–1).¹⁸ During the catalytic cycle, ecDHFR undergoes extensive backbone motions, especially in the loop domains, where the flexible M20 loop alternates between closed and occluded conformations in concert with binding and release of the substrates and products (Figure 1C).¹⁶ A “network of coupled motions” ^19,20 throughout the protein has been suggested to facilitate the reaction by generating conformational ensembles favorable for hydride transfer.^4,21 Remote mutations that disrupt this network of coupled motions (from ps to ms²²) lead to slower reactions and altered TS for hydride transfer.^23,24 The origin of TS effects can be explored computationally by transition path sampling.²⁵

Quantum mechanics/molecular mechanics (QM/MM) calculations using transition path sampling reported that ecDHFR does not employ PPVs to promote passage over the chemical barrier at 27 °C.²⁵ This report differed from those of other enzymes studied by the same method^7,8 and predicted that the TS barrier for DHFR might be independent of protein mass, in contrast to previous reports for heavy enzymes. In agreement with this report, more recent QM/MM calculations using ensemble-averaged variational transition state theory demonstrated equal barrier heights and tunneling contributions in the hydride-transfer steps of light ecDHFR (l-DHFR) and heavy ecDHFR (h-DHFR).²⁶ Despite this prediction, kinetic experiments in the same study reported slower hydride-transfer rates for h-DHFR than for l-DHFR.²⁶ But no kinetic isotope effects (KIEs) of the substrates were reported to explore TS effects.

Here we explore protein bond vibrational dynamic contributions in both the GS²⁸ and TS of ecDHFR. Our study not only examines the nature of hydride-transfer step by measuring intrinsic KIEs but also reveals protein mass-modulated effects on reactant affinity and rates of release from DHFR. Kinetic and thermal unfolding experiments indicate that mass-altered h-DHFR has distinct GS conformational fluctuations, leading to varied protein–ligand interactions from l-DHFR. Measurements of hydride-transfer rates and KIEs indicate that, at temperatures below 25 °C, the mass-altered atomic vibrations of DHFR are linked to TS conformations and the energy barrier of hydride transfer. Together with previous DHFR studies, our findings provide new insights into the role of protein dynamics in DHFR catalysis.

Results and Discussions

Different Steady-State Kinetic Parameters of l- and h-DHFR

The molecular weights of purified l- and h-DHFR were determined to be 18.1 and 20.1 kDa (11% mass increase), respectively, by protein mass spectroscopy, confirming 98.3% heavy isotope enrichment of ¹³C, ¹⁵N, and non-exchangeable ²H in h-DHFR (Figure S1). We measured the initial reaction rates of l- and h-DHFR at 25 °C (pH 7 and 9) with varying concentrations of NADPH and DHF. We used methotrexate titration^29,30 to quantitate the active enzyme concentrations for all comparative experiments, and we measured full saturation kinetic curves for both substrates to obtain the k_cat values (Figure 2). We also measured deuterium KIEs on k_cat (^Dk_cat) with saturating concentrations of both DHF and [4R-^xH]NADPH (^xH = H or D) and found that the ^Dk_cat values are within statistical experimental errors of each other for l- and h-DHFR at the same pH (pH 7 or 9, Table 1). The ^Dk_cat at pH 7 is close to unity, while the ^Dk_cat at pH 9 is large, in agreement with previous findings that hydride transfer becomes more rate-limiting for k_cat at higher pH values.²⁷ Our measurements showed the k_cat values of l- and h-DHFR at pH 9 are within statistical experimental errors of each other (Figure 2 and Table 1), suggesting the same hydride-transfer rate (k_hyd) for both enzymes. At pH 7, the k_cat of h-DHFR is ca. 10% slower than that of l-DHFR (Figure 2 and Table 1), suggesting that THF release from the DHFR·NADPH·THF complex (rate limiting for k_cat at pH 7)²⁷ is slower for h-DHFR. In addition, h-DHFR shows larger Michaelis constants of DHF (K_M^DHF) and smaller (k_cat/K_M)^DHF than l-DHFR at both pH’s (Table 1), indicating differences in DHF binding kinetics. The larger K_M, smaller (k_cat/K_M)^DHF, and slower k_cat (at pH 7) of h-DHFR suggest that the interactions between DHFR and folate substrate/product are sensitive to the altered protein mass and vibrations. In summary, our steady-state kinetic data suggest that the changes in protein mass affect DHFR catalysis beyond alterations in promoting vibrations linked to the hydride transfer.

Figure 2.

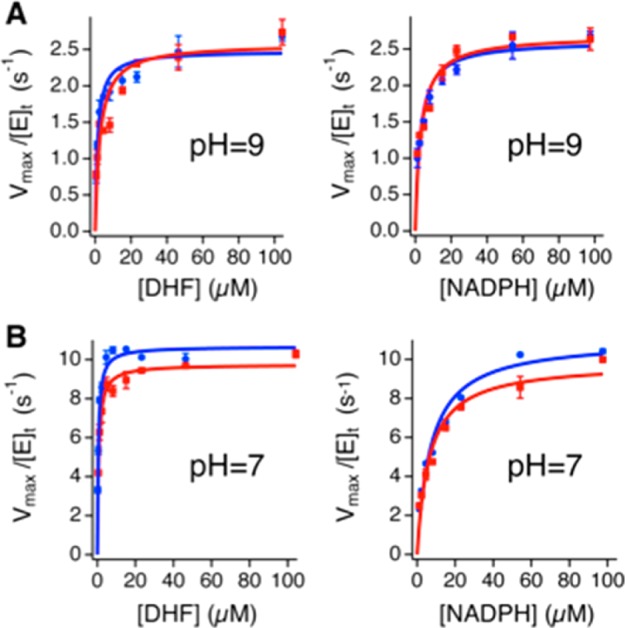
Michaelis–Menten kinetics of l-DHFR (blue) and h-DHFR (red), measured with 2.5 nM enzyme and varying concentrations of DHF (left) or NADPH (right), in the presence of 100 μM NADPH or DHF, respectively, at 25 °C. (A) The k_cat values of l- and h-DHFR are within experimental error at pH 9. (B) The k_cat of h-DHFR is ca. 10% slower than that of l-DHFR at pH 7.

Table 1. Steady-State Parameters of l-DHFR and h-DHFR at 25 °C.

	25 °C, pH 9			25 °C, pH 7
	l-DHFR	h-DHFR	h-KIEd	l-DHFR	h-DHFR	h-KIEd
kcatDHF (s–1)a	2.48 ± 0.06	2.58 ± 0.09	0.96 ± 0.04	10.7 ± 0.1	9.7 ± 0.1	1.09 ± 0.02
kMDHF(μM)a	1.4 ± 0.2	2.7 ± 0.5	0.5 ± 0.1	0.53 ± 0.04	0.72 ± 0.06	0.74 ± 0.08
(kcat/KM)DHF	1.8 ± 0.2	1.0 ± 0.2	1.9 ± 0.4	20 ± 1	14 ± 1	1.5 ± 0.2
kcatNADPH (s–1)b	2.61 ± 0.06	2.68 ± 0.09	0.97 ± 0.04	11.0 ± 0.3	9.8 ± 0.3	1.12 ± 0.04
kMNADPH (μM)b	2.7 ± 0.3	3.1 ± 0.4	0.9 ± 0.2	7.2 ± 0.8	6.4 ± 0.6	1.1 ± 0.2
(kcat/KM)NADPH	1.0 ± 0.1	0.9 ± 0.1	1.1 ± 0.2	1.5 ± 0.2	1.5 ± 0.2	1.0 ± 0.1
Dkcatc	2.5 ± 0.4	2.5 ± 0.2		1.18 ± 0.07	1.11 ± 0.08

^ak_cat^DHF and K_M are the turnover number and Michaelis constant of DHF measured with 100 μM NADPH and varying concentrations of DHF.

^bk_cat^NADPH and K_M are the turnover number and Michaelis constant of NADPH measured with 100 μM DHF and varying concentrations of NADPH.

^cDk_cat is the deuterium KIE on k_cat when NADPH is replaced by NADPD.

^dh-KIE is the heavy enzyme KIE, calculated by taking the ratio between the kinetic parameter of l-DHFR and the same parameter of h-DHFR.

Similar Hydride-Transfer Rates of l- and h-DHFR

While previous heavy enzyme experiments have all found protein mass-modulated effects on the chemical steps of catalyzed reactions,⁹⁻¹² our steady-state experiments at pH 9 implicate no effects on k_hyd caused by h-DHFR. However, the ^Dk_cat at pH 9 (ca. 2.5, Table 1) is smaller than the intrinsic KIE (KIE_int) on the hydride transfer (H/D KIE_int is ^Dk_hyd = 3.6 ± 0.2 for l-DHFR³¹ and 3.88 ± 0.05 for h-DHFR, Table S1), suggesting that k_cat is not fully limited by k_hyd. In order to quantitate k_hyd, we conducted pre-steady-state experiments by rapidly mixing the DHFR·NADPH binary complex with DHF on a stopped-flow instrument. The reaction rates were followed by the decay of the Förster resonance energy transfer (FRET) from tryptophan residues of DHFR to the bound NADPH cofactor during the rapid mixing (Figure 3).²⁷ The time traces of the FRET decay fit well to eq 1, where k_burst is the observed rate constant of the initial burst phase, and v is the steady-state rate of FRET decrease.

1

Figure 3.

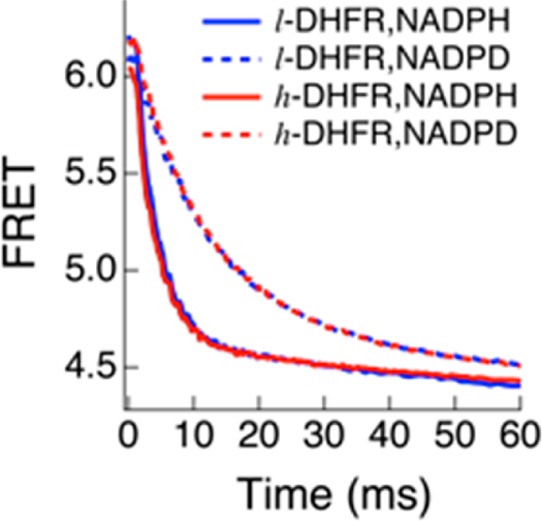
Pre-steady-state kinetics of l-DHFR (blue) and h-DHFR (red) are the same when either NADPH (solid curve) or NADPD (dashed curve) is used as the cofactor at 25 °C, pH 7.

We measured the pre-steady-state kinetics of l- and h-DHFR in the pH 5–9 range at 25 °C to find the conditions where the observed KIEs are the closest to KIE_int on the hydride transfer and thus permit comparison of the chemical steps. Replacing NADPH by NADPD causes a deuterium KIE on k_burst (^Dk_burst), which is generally smaller than ^Dk_hyd due to the kinetic complexity on k_burst from other steps during the burst phase. The ^Dk_burst values at pH 7 are close to ^Dk_hyd for both l- and h-DHFRs (Table 2), suggesting that k_burst closely approximates k_hyd under those experimental conditions. Compared with k_burst of l-DHFR (k_burst^light), k_burst of h-DHFR (k_burst) is statistically the same at 25 °C, pH 7 (Table 2). The similarity of k_hyd for l- and h-DHFRs agrees with previous QM/MM calculations that found no promoting vibrations for DHFR in catalyzing the hydride transfer.²⁵ In summary, our stopped-flow experiments suggest that, at 25 °C, h-DHFR catalyzes the hydride-transfer step as fast as l-DHFR.

Table 2. Observed Rate Constants of the Burst Phase in the Pre-Steady-State Kinetic Experiments When NADPH or NADPD Were Used as Cofactor (k_burst^NADPH and k_burst, Respectively), and Observed KIEs (^Dk_burst = k_burst^NADPH/k_burst) for l- and h-DHFR at 25 °C, pH 7.

enzyme	kburstNADPH	kburstNADPD	Dkburst	Dkhyda
l-DHFR	270 ± 7	84 ± 2	3.2 ± 0.1	3.6 ± 0.2
h-DHFR	264 ± 6	83.8 ± 0.9	3.15 ± 0.08	3.88 ± 0.05

^aThe intrinsic deuterium KIEs on the hydride transfer, determined by the competitive experiments described below.

Different TS Conformational Ensembles of l- and h-DHFR

To interrogate protein mass-modulated effects explicitly on the chemical step, we determined KIE_int on the hydride transfer of l- and h-DHFR in the 5–45 °C temperature range. We used the competitive method to measure H/T and D/T KIEs on the second-order rate constant k_cat/K_M^NADPH (^T(V/K) and ^T(V/K)_D, respectively) and extracted the KIE_int by Northrop’s method.^23,32,33 The H/T KIE_int (^Tk_hyd) values were fit to the Arrhenius equation (eq 2) to evaluate the temperature dependence of KIE_int, based on the isotope effects on the pre-exponential factors (A_H/A_T) and the activation energy difference (ΔE_a,H-T) between protium and tritium isotopes in k_hyd. (In eq 2, R and T are gas constant and absolute temperature, while “T” in the subscripts and superscripts of other parameters indicates the tritium isotope.) Table S1 in SI presents the observed and intrinsic KIEs as well as the commitment factors (discussed in detail below) at various temperatures for both l- and h-DHFR.

2

Recent experimental and theoretical studies have indicated a relationship between temperature dependence of KIE_int and protein dynamics that modulates the donor–acceptor distance (DAD, e.g., the distance between C4 of NADPH and C6 of DHF here) to affect the contribution of QM tunneling in hydride-transfer reactions.³⁴ The ^Tk_hyd values of l- and h-DHFR were also fit to a Marcus-like model using the formula developed by Roston et al.³⁵ to estimate the average DAD at the TS of hydride transfer. Figure 4 and Table 3 summarize the results for both l- and h-DHFR. The ^Tk_hyd of l-DHFR³¹ is temperature independent (i.e., ΔE_a,H-T ≈ 0), and A_H/A_T is larger than the upper limit of semiclassical prediction (s.c. A_H/A_T = 0.5–1.6),^36,37 suggesting hydride transfer with large contribution from QM tunneling at a well-organized TS, often denoted as tunneling ready state (TRS),³⁴ that is insensitive to thermal fluctuations of the global protein environment. In contrast, h-DHFR shows a two-phase temperature dependence of ^Tk_hyd, similar to the observations for a thermophilic alcohol dehydrogenase³⁸ and a mutant of thymidylate synthase.³⁹ In the temperature range of 25–45 °C, the values of ^Tk_hyd and estimated DAD (ca. 3.06 Å) of h-DHFR are within statistical experimental errors of those of l-DHFR, indicating the same TRS for both enzymes. At temperatures below 25 °C, the ^Tk_hyd of h-DHFR becomes larger than that of l-DHFR (Figure 4A), suggesting that the TS conformational ensembles shift away from the TRS of l-DHFR. Fitting the ^Tk_hyd of h-DHFR in the 5–25 °C range to the Marcus-like model (assuming two DAD distributions³⁵) yields a longer DAD (3.36 ± 0.01 Å) than the DAD of TRS at higher temperatures. These results suggest that, at lower temperatures, the altered protein mass and vibrational spectrum lead to changes in the protein motions that now modulate the DAD fluctuations at the TS for hydride transfer.³⁴ Temperature-dependent phase transitions have been attributed to trapping of the protein dynamics into a different ensemble of dynamic conformations at lower temperatures.^36,37 Thus, the heavy enzyme may have an altered reactive conformational distribution at low temperatures coupled to the hydride transfer.

Figure 4.

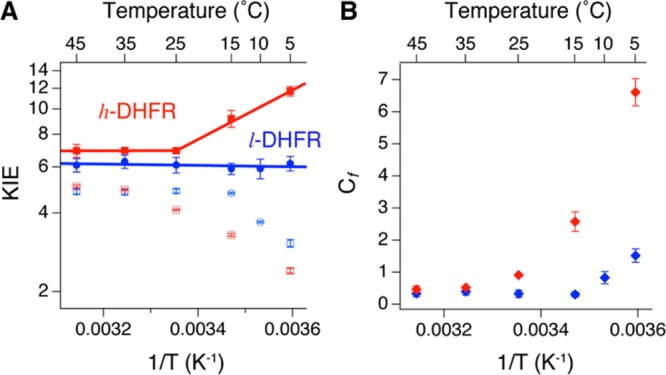
KIEs and forward commitment factors (C_f) of l-DHFR (blue, data from ref (31)) and h-DHFR (red) measured from competitive experiments at pH 9. (A) The observed H/T KIEs on k_cat/K_M^NADPH (empty symbols) and intrinsic H/T KIEs (^Tk_hyd, filled symbols) are plotted on the logarithmic scale against inverse absolute temperature. The lines are nonlinear regression of ^Tk_hyd to the Arrhenius equation (eq 2). (B) C_f of h-DHFR is either statistically equal to (25–45 °C) or larger than (5–25 °C) C_f of l-DHFR.

Table 3. Isotope Effects on the Arrhenius Parameters^a of the Hydride Transfer of l- and h-DHFR in the Temperature Range 5–45 °C.

enzyme	l-DHFR	h-DHFR
temp, °C	5–45	25–45	5–25
AH/AT	7.0 ± 1.5b	5.6 ± 1.9	0.01 ± 0.003d
ΔEa,H-T (kcal/mol)	–0.1 ± 0.2b	0.1 ± 0.2	4.1 ± 0.3
DAD (Å)c	3.06 ± 0.08	3.06 ± 0.0008	3.36 ± 0.01

^aThe values of these parameters are obtained by fitting temperature dependence of ^Tk_hyd to eq 2, measured by competitive experiments at pH 9 (Figure 4).

^bData from ref (31).

^cDAD is the average distance between C4 of NADPH and C6 of DHF in the dominant population at the TRS. This parameter is estimated from fitting KIE_int to a Marcus-like model following the method published in ref (35).

^dThe steeply temperature-dependent KIEs and small ratio of pre-exponential factors (A_H/A_T) can be interpreted either by the semiclassical TS theory corrected with moderate tunneling,³⁴ or by a Marcus-like model with multiple populations with different DADs.³⁵

In competitive KIE experiments, the observed ^T(V/K) is usually smaller than ^Tk_hyd due to kinetic commitment factors on V/K caused by other steps in the reaction:^40,41

3

where EIE is the equilibrium isotope effect, and C_f and C_r are the forward and reverse commitment factors. For DHFR-catalyzed hydride transfer, C_r is negligible because (1) the reverse rate constant of the hydride transfer is almost 3 orders of magnitude slower than the dissociation of NADP⁺ from the product complex DHFR·NADP⁺·THF (0.6 s^–1 vs 200 s^–1, Figure 1C)²⁷ and (2) the overall DHFR reaction is essentially irreversible under our aerobic experimental conditions due to instability of THF. Thus, eq 3 can be rearranged to solve C_f from the experimentally determined ^T(V/K) and ^Tk_hyd values:

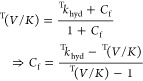4

C_f is the ratio between k_hyd and the net rate for the bound NADPH to dissociate from the DHFR·NADPH·DHF ternary complex,^40,41 which reflects the probability for the Michaelis complex to cross the barrier of the chemical step relative to dissociation of the cofactor. In a previous study, heavy purine nucleoside phosphorylase (PNP) showed the same substrate KIEs but smaller rate of chemical step and smaller C_f than light PNP,⁹ which agrees with the reduced probability of crossing the same chemical barrier in heavy PNP suggested by QM/MM calculations.⁴² In contrast, h-DHFR shows statistically the same ^Tk_hyd, similar k_hyd, and equal barrier crossing probability as l-DHFR in the physiological temperature range (25–45 °C), consistent with the computational results at 27 °C.²⁵ At temperatures below 25 °C, h-DHFR shows different ^Tk_hyd and larger C_f than l-DHFR (Figure 4B), implicating an increase in the relative probability of barrier-crossing that is concomitant with changes in TS conformations of the hydride transfer (Table 3). The increased C_f of h-DHFR is also likely associated with changes in GS conformational fluctuations that affect the rate of NADPH dissociation from the Michaelis complex.

In summary, our pre-steady-state kinetic measurements and competitive KIE experiments suggest that the altered mass and vibrational modes of h-DHFR do not affect the hydride-transfer TS or barrier-crossing probability in the physiological temperature range (25–45 °C). However, a phase transition at 25 °C changes the nature of hydride transfer for h-DHFR. This may indicate either a temperature-dependent coupling between DHFR protein dynamics and the catalyzed hydride transfer or a different conformational ensemble of the heavy enzyme at low temperatures that leads to a longer DAD at the TRS for the hydride transfer.

Different Ligand Binding Kinetics of l- and h-DHFR

All the results above suggest that altering the mass and vibrations of DHFR affects its catalysis in a manner distinct from previously studied heavy enzymes.⁹⁻¹² Besides the functional phase transition of h-DHFR that affects the temperature dependence of KIE_int, h-DHFR also shows larger K_M^DHF, slower k_cat at pH 7 (when hydride transfer is not rate limiting), and increased C_f at temperatures below 25 °C than l-DHFR. These results suggest that the altered vibrational modes of h-DHFR affect the interactions between the protein and substrates at GS²⁸ (as opposed to TS of the chemical step). To investigate these effects, we conducted stopped-flow experiments to measure the binding kinetics of NADPH and DHF for both l- and h-DHFR using the method described by Fierke et al.²⁷ Although the association and dissociation rate constants (k_on and k_off, respectively) of NADPH do not show statistical difference for the two enzymes (Table 4a), h-DHFR shows slower k_on and faster k_off for DHF than l-DHFR (Table 4b, k_on/k_on^heavy = 1.36 ± 0.03 and k_off/k_off^heavy = 0.48 ± 0.04). These differences lead to a larger dissociation constant of DHF (K_d/K_d^heavy = 0.35 ± 0.03), in agreement with increased K_M of h-DHFR than l-DHFR (Table 1). Interestingly, the presence of NADP⁺ diminishes the differences between l- and h-DHFR in the binding kinetics of DHF (Table 4c, only small difference in k_on^light/k_on = 1.09 ± 0.02 for the DHFR·NADP⁺ binary complex), suggesting that the bound cofactor can compensate for the deteriorated interactions between h-DHFR and DHF.

Table 4. Association and Dissociation Rate Constants (k_on and k_off, Respectively) That Describe the Interactions between Different Ligands and ecDHFR Species (l-, Light DHFR; h-, Heavy DHFR), As Measured by Rapid Mixing of the Ligand with ecDHFR or a Binary Complex at 25 °C, pH 7.

	ligand	enzyme species		kon (μM–1 s–1)	koff (s–1)	Kd = koff/kon (μM)
(a)	NADPH	DHFR	l-	17.3 ± 0.4	3 ± 2a	0.18 ± 0.09
			h-	16.8 ± 0.4	5 ± 2a	0.28 ± 0.09
(b)	DHF	DHFR	l-	41.0 ± 0.5	54 ± 4	1.3 ± 0.1
			h-	30.1 ± 0.6	113 ± 6	3.8 ± 0.2
(c)		DHFR·NADP+	l-	42.1 ± 0.5	10 ± 3	0.24 ± 0.07
			h-	38.5 ± 0.6	11 ± 4	0.3 ± 0.1
(d)	FA	DHFR	l-	34.3 ± 0.4	110 ± 3	3.22 ± 0.09
			h-	35.9 ± 0.5	125 ± 4	3.5 ± 0.1
(e)		DHFR·NADPH	l-	5.9 ± 0.1	90.0 ± 0.8	15.2 ± 0.3
			h-	6.0 ± 0.1	91.7 ± 0.8	15.4 ± 0.3
(f)	methotrexate	DHFR	l-	28.4 ± 0.3	2.0 ± 0.6	0.07 ± 0.02
			h-	28.1 ± 0.4	1.9 ± 0.6	0.07 ± 0.02
(g)		DHFR·NADPH	l-	52.2 ± 0.4	–0.7 ± 0.7b	–0.01 ± 0.01
			h-	47.2 ± 0.4	0.9 ± 0.8b	0.02 ± 0.02

^aSmall differences within the limits of experimental error may exist for k_off of NADPH between l- and h-DHFR.

^bThe k_off for methotrexate dissociating from the DHFR·NADPH·methotrexate ternary complex cannot be accurately determined by this method.

The variation in DHF binding kinetics of l- and h-DHFR supports the involvement of protein mass-modulated vibrations in the interactions between DHFR and folates and antifolates. To test this hypothesis, we also measured the binding kinetics of the substrate analogue folic acid (FA) and the classical antifolate drug methotrexate. Similar to DHF, FA dissociates from the h-DHFR·FA binary complex faster than from l-DHFR·FA (Table 4d, k_off^light/k_off = 0.88 ± 0.04), and the presence of NADPH diminishes this difference (Table 4e). Conversely, while the binding kinetics of methotrexate do not show statistical difference between l- and h-DHFR apoenzymes (Table 4f), methotrexate binds more slowly to the h-DHFR·NADPH binary complex than to l-DHFR·NADPH (Table 4g, k_on^light/k_on = 1.11 ± 0.01). These results suggest that the altered mass of h-DHFR causes differential impacts on the interactions between the apo-/halo-DHFR and folates/antifolates, implicating the possibility of exploiting unique vibrational modes in the design of new antifolate drugs. The pteridine ring of methotrexate is flipped 180° with respect to that of DHF/FA when binding to ecDHFR,¹⁶ which may explain their different sensitivity to protein mass-altered vibrational modes. Although the structure of methotrexate is not analogous to the TS of hydride transfer, crystallographic studies suggest that the unique binding geometry of methotrexate induces DHFR to adopt a conformation resembling the TS of the enzyme complex.¹⁶ Thus, the DHFR·NADPH·methotrexate ternary complex has been widely accepted as an analogue of the TS of DHFR·NADPH·DHF ternary complex. The variation in the k_on of methotrexate with l- and h-DHFR·NADPH binary complexes may correlate with the differences in TS conformational ensembles of l- and h-DHFR·NADPH·DHF ternary complexes.

Differences in Ground-State Conformations of l- and h-DHFR

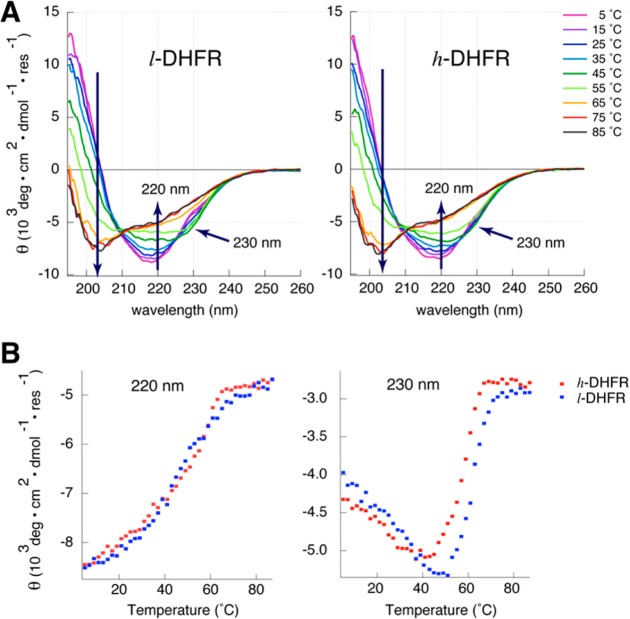
Previous heavy enzyme studies focused on the chemical step, and protein mass-modulated GS conformations have not been discussed in the context of enzyme catalysis. Our data above suggest that the altered mass of h-DHFR can affect the GS interactions between the enzyme and ligands. To investigate the protein conformational differences between the l- and h-DHFR, we studied their circular dichroism (CD) spectra and thermal unfolding from 5 to 85 °C (Figure 5).

Figure 5.

Protein mass-modulated CD spectra and thermal unfolding of DHFR, measured in 10 mM potassium phosphate buffer (pH 7 at 25 °C). (A) Compared with l-DHFR (left), the isoelliptic point at 225 nm is altered in the CD spectra of h-DHFR (right), indicating altered conformations in 5–45 °C. (B) The l- and h-DHFR show similar temperature dependence of the mean residue ellipilicity (θ) at 220 nm, implying the same overall fold and thermal stability for both enzymes. However, l- and h-DHFR show differences in the temperature dependence of θ at 230 nm, suggesting small variance in the GS conformations of the protein at each temperature.

As temperature increases, ecDHFR undergoes an initial collapse of the adenosine binding domain (ABD), followed by loss of key tertiary interactions in the loop domain, and unfolding of the remaining secondary structures.⁴³⁻⁴⁶ The early transition (5–45 °C) shows equal changes in the mean residue ellipticity (MRE, θ) at 230 and 220 nm with an isoelliptic point at 225 nm due to disruption of the exciton coupling between Trp47 and Trp74 in the ABD region.⁴⁵ This early transition likely represents the shift of equilibrium between the two conformational isomers¹⁸ rather than denaturation of the protein, since the catalytic activity of ecDHFR increases with temperature in the 5–45 °C range. The overall CD spectra and melting curve of θ_220nm of h-DHFR (monitoring protein backbone) are very similar to those of l-DHFR, suggesting the same overall fold and thermal stability. However, the isoelliptic point at 225 nm is altered in the CD spectra of h-DHFR, and the melting curve of the θ_230nm feature of h-DHFR shifts toward lower temperatures with respect to that of l-DHFR. These differences suggest that the altered protein mass and vibrational modes of h-DHFR modulate the conformational ensembles of the protein, which may be correlated with the different ligand binding kinetics discussed above. In summary, our protein unfolding experiments suggest that the mass-altered h-DHFR shows different GS conformational ensembles from l-DHFR.

Protein Mass-Modulated Effects in the Catalysis of ecDHFR

Our experiments discussed above reveal that altering the protein mass affects GS²⁸ and TS conformational ensembles of ecDHFR in a temperature-dependent fashion. Recent computational studies proposed that the “network of coupled motions” (from ps to ms²²) in ecDHFR facilitates the reaction by generating conformational ensembles favorable for the hydride transfer, rather than directly promoting hydrogen tunneling.^4,21 Similarly, our current study suggests that the altered mass and vibrational modes of h-DHFR cause more significant effects on the GS conformational ensembles than by altering the barrier crossing for hydride transfer (i.e., by PPVs). These findings imply an extension of the “network of coupled motions” to the bond vibrational time scale (fs), and the importance of DHFR dynamics may generally lie in accessing catalytically competent states rather than promoting the chemical barrier crossing. The differences in the CD spectra and melting curves of l- and h-DHFR suggest that the altered protein vibrational dynamics can affect the interconversion between the two conformational isomers and shift the GS conformational ensembles of ecDHFR (Figure 5). The altered GS conformational ensembles can cause variations in the kinetics of binding interactions of DHF, FA, and methotrexate with apo-/halo-DHFR (Table 4). Similarly, slower atomic vibrational frequencies of h-DHFR can also shift the accessible TS conformational ensembles for the hydride transfer at temperatures below 25 °C (Figure 4). The same KIE_int of l- and h-DHFR at temperatures above 25 °C suggests that the thermal fluctuations of protein backbone and side-chain dynamics in the physiological temperature range can overcome the limitations imposed by slower atomic vibrations of h-DHFR, allowing the enzyme to access the same TRS as l-DHFR. Consistent with our current findings and previous transition path sampling calculations,²⁵ recent QM/MM calculations with ensemble-averaged variational transition state theory found no difference in the barrier heights or tunneling contributions in the hydride-transfer reactions of l- and h-DHFR at 300 K (27 °C).²⁶ The only difference between l- and h-DHFR was observed by analyzing all-atom root-mean-square deviation from the TS structure in reactive trajectories, which suggest that the atomic motions with lower frequencies in h-DHFR respond slower to the changes along the reaction coordinate. This computational finding corroborates with our experimental results that suggest h-DHFR causes global effects on the protein dynamics, altering the accessible conformational ensembles of both GS and TS.

Conclusions

The current study applied different experimental techniques to investigate and distinguish the “heavy enzyme” effects on both the GS²⁸ and TS of the reaction catalyzed by ecDHFR. The altered protein mass of h-DHFR affects the GS conformational ensembles and protein–ligand interactions, but it does not affect the hydride transfer in the physiological temperature range (25–45 °C). At lower temperatures, h-DHFR shows different TS ensembles and increased barrier-crossing probability compared with l-DHFR, suggesting temperature-dependent protein vibrational coupling to the chemical step that is beyond the promoting vibrations investigated by previous heavy enzyme studies. The protein mass-modulated effects on different kinetic parameters of various heavy enzymes suggest that the specific dynamics–catalysis relationship may depend on the protein architecture, the nature of catalyzed reaction, and other physical and chemical properties of the enzymatic system. We hope future research can extend the model enzyme studies and advance our understanding of how protein motions at different time scales are coordinated to catalyze chemical reactions.

Materials and Methods

Materials and Software

[U-¹³C₆,1,2,3,4,5,6,6-²H₇]glucose and [¹⁵N]ammonium chloride (NH₄Cl) were purchased from Cambridge Isotope Laboratories, Inc. The isotopically labeled cofactor compounds, [4R-^xH]-NADPH (^xH = D or T, and the specific activity of [4R-T]-NADPH is 680 mCi/mmol) and [Ad-¹⁴C]-NADPH (50 mCi/mmol), were synthesized and purified following published procedures.⁴⁷ Ultima Gold liquid scintillation cocktail reagent was purchased from Packard Bioscience. Liquid scintillation vials were purchased from Research Products International Corp. All other chemicals were purchased from Fisher Scientific or Sigma-Aldrich and used without further purification. The concentrations of compounds in solution were determined by UV absorbance on an Agilent Cary 300 UV–vis spectrophotometer using the following molar extinction coefficients: NADPH, 6.2 mM^–1 cm^–1 at 339 nm; NADP⁺, 16 mM^–1 cm^–1 at 259 nm; DHF, 24.7 mM^–1 cm^–1 at 277 nm; FA, 25.1 mM^–1 cm^–1 at 283 nm; methotrexate, 23.25 mM^–1 cm^–1 at 258 nm.²⁹ All the reagent concentrations refer to the final concentrations in the reaction mixture, unless otherwise specified. All the kinetic experiments were conducted in 50 mM MES, 25 mM Tris, 25 mM ethanolamine, and 100 mM sodium chloride (“MTEN buffer”) because previous studies demonstrated that the ionic strength of MTEN buffer is constant in a wide pH range (pH 5–10).⁴⁸ Figure 1B was generated with Pymol v1.5.0.4.⁴⁹ The kinetic and thermal unfolding data (Figures 2–5 and Figure S2) were analyzed and plotted with IGOR Pro v6.34 from WaveMetrics, Inc.

Preparation of l- and h-DHFR

The ecDHFR gene was inserted into a PJexpress411 vector by DNA2.0 Gene Synthesis Service, and the protein was expressed in E. coli BL21 (DE3) cells with 30 mg/L kanamycin. The l-DHFR was expressed in either LB medium or M63 minimum medium supplemented with glucose and NH₄Cl (natural abundance). The difference in medium conditions did not cause measurable differences in the kinetic parameters (e.g., k_cat, K_M, and k_hyd) of l-DHFR. The h-DHFR was expressed in M63 minimum medium in ²H₂O (D₂O) supplemented with [U-¹³C₆,1,2,3,4,5,6,6-²H₇]glucose and [¹⁵N]NH₄Cl. Both l- and h-DHFR were purified and stored in buffered solutions in ¹H₂O following previously published procedures.⁵⁰ The molecular weights of purified l- and h-DHFR were determined to be 18.1 and 20.1 kDa, respectively (11% increase), by protein mass spectroscopy using a 12T Fourier transform ion cyclotron mass spectrometer, confirming 98.3% heavy isotope enrichment of ¹³C, ¹⁵N, and non-exchangable ²H in h-DHFR (Figure S1). Both l- and h-DHFR were stored in 50 mM sodium phosphate buffer with 1 mM dithiolthreitol (DTT), 10% glycerol, pH 7. Under these conditions, the enzymes can be kept on ice for up to a week without noticeable loss in activity. For longer storage, the stock enzyme solutions were divided into small aliquots, flash-frozen in liquid nitrogen, and kept at −80 °C until use.

Steady-State Kinetic Experiments

To accurately determine k_cat, we quantitated the active enzyme concentrations of l- and h-DHFR by fluorescence titration with methotrexate in MTEN buffer (pH 7) with 5 mM dithiothreitol (DTT) following published procedures.²⁹ The experiments were conducted on a FluoroMax-3 spectrofluorometer (Horiba Scientific) equipped with a temperature-controlled cuvette assembly. The ligands fluorescence and inner filter effects were corrected by titrating methotrexate into the solution where DHFR was replaced by free tryptophan at a concentration that gave the same amplitude of fluorescence signal. Methotrexate titration into the apo-DHFR (monitoring tryptophan fluorescence at 350 nm) or DHFR·NADPH complex (monitoring FRET at 450 nm) gave the same values for enzyme concentration. To reduce the possible errors caused by protein degradation, the steady-state kinetic experiments were conducted in the same day for l- and h-DHFR, within a week of storage on ice after the enzyme concentrations were measured by methotrexate titration.

The steady-state kinetic experiments were conducted on an Agilent Cary 300 UV–vis spectrophotometer equipped with a temperature-controlled cuvette assembly. The initial reaction rates were measured at 25 °C by monitoring the decrease of absorbance at 340 nm that follows conversion of NADPH and DHF to NADP⁺ and THF (accumulative Δε_340nm = 11.8 mM^–1 cm^–1). The reaction mixture contained 2.5 nM DHFR in MTEN buffer, pH 7 or 9. The K_M values of DHF were measured with 100 μM NADPH, and the K_M values of NADPH were measured with 100 μM DHF. To avoid the hysteresis effect,²⁷ DHFR was pre-incubated with NADPH in the cuvette for 3 min before DHF was added to initiate the reaction. Each data point in Figure 2 is an average of three independent measurements with the same ligand concentrations. The initial reaction rates vs concentrations of substrate/cofactor were fit to the Michaelis–Menten equation, using the nonlinear regression available in IGOR Pro (Figure 2). The k_cat values were also measured with saturating concentrations (100 μM) of NADPD and DHF in MTEN buffer, at pH 7 and 9, to obtain the deuterium isotope effects on the turnover rates (^Dk_cat, Table 1).

Stopped-Flow Experiments: Ligand Binding and Pre-Steady-State Kinetics

The ligand binding (Table 4) and pre-steady-state kinetic experiments (Figure 4) were conducted on an Applied Photophysics model SX20 stopped-flow instrument, which has a dead time of 1 ms. Each data set included at least two independent experiments, and each experiment is an average of at least five measurements under the same conditions.

Ligand Binding Kinetics

Enzyme tryptophan residues are photoexcited at 290 nm and emit fluorescence at 350 nm. When NADPH is present, FRET occurs from the tryptophan residues to NADPH at the active site, resulting in fluorescence emission at 450 nm. The kinetics of ligand binding was measured by monitoring either the quenching of protein fluorescence through a 305 nm cutoff filter, when NADPH is absent, or the change in FRET through a 405 nm cutoff filter, when NADPH is present. We measured the observed rate constant (k_obs) of the fast exponential phase by rapidly mixing apo-/halo-DHFR with the ligand, using the published procedure.²⁷ The k_obs values were plotted against ligand concentrations to obtain k_on and k_off for each ligand (k_obs = k_on[L] + k_off, respectively, Table 4 and Figure S2).²⁷ The experiments were conducted with 5 mM DTT in MTEN buffer, pH 7 at 25 °C. The final enzyme concentration was 0.25 μM, and the ligand concentrations in each experiment can be found in Figure S2.

Pre-Steady-State Kinetics

The pre-steady-state kinetics was measured by monitoring the decrease in FRET (through a 405 nm cutoff filter) that follows the hydride transfer. DHFR was pre-incubated with NADPH or NADPD for 3 min before rapid mixing with DHF. The final reaction mixture contained 5 μM DHFR, 120 μM NADPH or NADPD, 100 μM DHF, and 5 mM DTT in MTEN buffer. The experiments were conducted at various pHs (5–9) at 25 °C. The pH of MTEN buffer was adjusted at 25 °C prior to each experiment. The FRET signal was monitored for 200 ms after rapid mixing DHFR·NADPH complex with DHF, and the data were fit to eq 1 to estimate k_hyd under different pH and temperature conditions. Figure 3 only shows the time traces in the first 60 ms to clearly compare the pre-steady-state kinetics of l- and h-DHFR. The observed rate constants and deuterium KIEs of the burst phase are summarized in Table 2.

Competitive KIE Experiments

The KIE_int on the hydride transfer was measured by the competitive KIE method developed for l-DHFR.²³ The reaction mixture contained 0.85 mM DHF (200-fold molar excess over NADPH) in MTEN buffer, and the pH was adjusted to 9 before DHFR (concentrations in nM range) was added to initiate the reaction at each temperature (5–45 °C). The reaction was monitored by HPLC to reach the fraction conversion of 25–70% (see eq 6) and was quenched by adding excess amount of methotrexate (final concentration 1.7 mM in the quenched mixture). Bubbling oxygen to quenched samples converts all the tritium from unstable THF (hydride acceptor) into stable species that are separated from NADPH on HPLC,⁵¹ which allows calculating the observed H/T and D/T KIEs on V/K. The radioactive compounds were separated by a Supelco Discovery C18 reverse-phase column on HPLC and analyzed on a liquid scintillation counter (LSC).

The observed KIEs were determined from three measured values—the fraction conversion (f), the ³H/¹⁴C ratio in the products ([4R-T]- and [Ad-¹⁴C]-NADP⁺) at each quenched time point (R_t), and the ³H/¹⁴C ratio in the products at the infinity time point (R_∞):

5

The fraction conversion f was calculated by

6

We used the modified Northrop method to extract the intrinsic KIEs from the observed H/T and D/T KIEs:^40,41,52

7

or

8

Equations 7 and 8 are equivalent with the Swain–Schaad exponential relationship of H/T and H/D KIE_int: ^Tk_hyd = (^Dk_hyd)^1.44.^53,54 We have developed an online program, as well as a Mathematica script, to solve eq 7 numerically for ^Tk at each temperature (http://ccs14.chem.uiowa.edu/faculty/kohen/group/tools.html). Fitting KIE_int values to the Arrhenius equation (eq 2) allows analysis of their temperature dependence.⁵²Table S1 summarizes the observed and intrinsic KIEs, as well as C_f, at each experimental temperature for both l- and h-DHFR.

Thermal Unfolding of DHFR

Thermal unfolding of DHFR was studied by recording its CD spectra every 2 °C as temperature increased from 5 to 85 °C, in a sealed quartz cuvette with a path length of 0.1 cm. The sample contained 15 μM l- or h-DHFR in 10 mM potassium phosphate buffer with 0.1 mM DTT, and the pH was adjusted to 7 at 25 °C prior to the experiment. The experiments were conducted on a Jasco J-180 (Jasco, Essex, UK) spectrophotometer with a PTC-423S/L Peltier type temperature control system. The temperature was increased at a rate of 1 °C/min, and the CD spectra were recorded after 1 min equilibration at each temperature. The Spectra Analysis and Interval Analysis software on the same instrument was used to analyze the data. Mean residue ellipticities (MRE, θ) were calculated using the equation θ = Θ/(10ncl), where Θ is the measured ellipticity in mdeg, n is the number of backbone amide bonds, c is the concentration of protein in molar, and l is the path length in cm. Figure 5A only shows the recorded spectra every 10 °C for clarity.

Supporting Information Available

Protein mass spectra of l- and h-DHFR; plots of observed rate constants vs ligand concentrations from the stopped-flow binding kinetic experiments; observed rate constants and KIEs from the stopped-flow pre-steady-state experiments; and observed KIEs, intrinsic KIEs, and C_f values at different temperatures. This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^§ Department of Chemistry, Yale University, 350 Edwards St., New Haven, CT 06511

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States