Abstract
Linkage analysis in autotetraploid species has been an historical challenge in quantitative genetics theory and is a stumbling block that urgently needs to be removed in the rapidly emerging genome research on this species, such as cultivated potato. This article presents theory of a full model of tetrasomic linkage and develops a statistical framework for the linkage analysis. The model considers both double reduction and recombination, the most essential features of tetrasomic inheritance with linked loci, whereas the statistical method takes appropriate account of the major complexities in analyzing both dominant and codominant molecular marker data during map reconstruction in tetraploid species. These complexities include the problems arising from multiple dosage of allelic inheritance, the null allele, allelic segregation distortion, mixed bivalent and quadrivalent pairing in meiosis, and incomplete information of marker phenotype data. The theoretical analysis established the relationship between the coefficients of double reduction at linked loci, which is essential in the present tetrasomic linkage analysis and in assessing the impact of double reduction on the evolution of tetraploid populations. The statistical method, based on the combination of theoretical analysis and a computer-based algorithm, provided analytical tools for predicting the maximum-likelihood estimates of the model parameters. A simulation study showed the feasibility of a practical implementation of the method, detailed the procedure of the analysis, validated the power and reliability in the parameter estimation, and compared the present method with those proposed in the current literature.
Understanding the genetic mechanisms of polyploidy has long been considered an important topic of the evolutionary biology of eukaryotes, in particular, flowering plant species, and for their genetic improvement (1–5). In the era of genomics, genetic linkage maps are now or quickly becoming available for humans and for almost all important diploid animal and plant species, and they have provided the first milestone for genome projects in these species. In sharp contrast, the corresponding study of polyploid species is still in its infancy. Recently, significant research efforts have been made to develop linkage maps for many important polyploids, such as cultivated potato, sugarcane, alfalfa, and sour cherry (6–10). Because of a lack of well established theory for linkage analysis with polysomic inheritance, these studies had been based either on the use of single-dose (simplex) dominant markers (e.g., AFLPs and RAPDs) that segregate in a simple 1:1 ratio in segregation of mapping populations or use of the corresponding diploid relatives as an approximation to the polyploid case. Several reasons exist why genetic linkage analysis at a polyploid level is necessary. First, meiotic processes in autopolyploids differ greatly from those in diploids (11). This finding suggests a requirement to take account of the distinct features of gene segregation of autopolysomic inheritance. Second, polyploidization and subsequent evolution of polyploid genomes is an extremely dynamic process (3), implying that it may not be appropriate to approximate a polyploid genome directly with its diploid relative. Third, the diploid relatives of some polyploid species may not exist. Finally, use of more informative genetic markers such as DNA microsatellites requires modeling the inheritance of multiplex alleles of the polyploids.
Genetic linkage analysis in autotetraploid species has been a theoretically difficult topic in the history of quantitative genetics ever since the pioneering work of Fisher (12) and Mather (13). To meet the need of genome projects of recently launched genome studies in several polyploid species, much research has focused on developing theory and statistical methods for constructing genetic linkage maps in autotetraploid species (14–18). However, these studies have been based on various assumptions that have avoided various degrees of complexity of the analyses, on the one hand, but ignored some essential features of autotetrasomic inheritance and practical data analysis on the other. The assumption of bivalent pairing of homologous chromosomes in autotetrasomic meiosis, which was made in almost all currently relevant literature (14–21), remarkably reduces the challenges in modeling autotetrasomic linkage analysis.
One of the most important features of autotetrasomic inheritance is the phenomenon of double reduction, i.e., sister chromatids can end in the same gamete as a result of homologous chromosomes forming a quadrivalent, followed by crossing over between the locus and spindle attachment (13). The probability of the meiotic event is defined as the coefficient of double reduction. Double reduction is the major biological cause of segregation distortion in autotetrasomic linkage analysis, and the coefficient of double reduction at any locus depends to a great extent on its genetic distance from the centromere (11–13). It also plays a dominant role in evolution of autotetraploid genomes (22). Bailey (11) pointed out that no theoretical basis exists for predicting the frequency of any given mode of gamete formation in terms of the recombination fraction between the two loci and the two double-reduction parameters. Thus, double reduction has been a historical problem in autotetrasomic genetic linkage analysis. More recently, Wu and his colleagues (23) attempted to integrate double reduction into linkage analysis in autotetraploids. However, their study was restricted only to the unrealistic assumption that the two parental genotypes, which were crossed to initiate the mapping populations, had to differ at all four alleles at each of the two loci. With such an assumption, the analysis becomes trivial because both double reduction and recombination events can be resolved directly from segregation of these alleles. This assumption concealed the essential challenge arising from the problem. Second, their analysis was based entirely on modeling segregation of gamete genotypes at two such loci. In practice, the parental lines that match such a requirement are extremely rare, and so the major difficulties in statistically modeling real data were not properly addressed. Thus, genetic linkage analysis of autotetraploids remains a theoretical and methodological problem to be solved.
In this article, we present a general theory for linkage analysis in autotetraploid species and propose a statistical framework for predicting double reduction and recombination frequency between two loci with tetrasomic inheritance. The theory models both double reduction and recombination simultaneously, and the method takes appropriate account of a series of practical problems involved in tetrasomic linkage analysis by using dominant or codominant DNA-marker data.
Theory of Autotetraploid Linkage Analysis: Model and Notation
The theoretical analysis considers a full-sib family derived from crossing two autotetraploid parental individuals. For simplicity, but without loss of generality, we first consider segregation and recombination of genes at two marker loci A and B (with dominant or codominant inheritance). Let G1 and G2 be the genotypes at the marker loci for the two parents. When we are considering linked loci, it is often necessary to specify how the alleles at different loci are grouped into homologous chromosomes, i.e., linkage phases of the alleles. Thus, a general presentation for an autotetraploid genotype at the two loci can be A1B1/A2B2/A3B3/A4B4, indicating that alleles Ai and Bi (i = 1, 2, 3, 4) locate on the same homologous chromosome. Let the two loci be linked with recombination frequency r.
To incorporate double reduction in the linkage analysis, we need to consider the locations of the two linked loci relative to the location of the centromere. Without loss of generality, we assume the order of their map locations is the centromere, locus A, and locus B. Because the probability of double reduction at a locus is proportional to its distance from the centromere (11), this assumption implies that α, the coefficient of double reduction at locus A ≤ β, the coefficient of double reduction at locus B. To model the gametogenesis, Fisher (12) classified the gametes generated from an autotetraploid individual into 11 modes of gamete formation according to the occurrence of double reduction and recombination events in meiosis but was unable to express frequencies of these gamete types in terms of the recombination and double-reduction parameters. After a tedious and careful analysis on probability distribution of double reduction and recombination events under the two-loci model, we are able to express the probability distribution for each of the gamete formation modes (mi) and, in turn, for each individual gamete genotype as functions of α and r. These findings are summarized in Table 1. It can be seen from the table that β, the coefficient of double reduction at locus B, can be expressed in term of a function of α and r as:
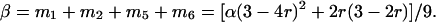 |
[1] |
This equation bridges a relationship between the coefficients of double reduction at two linked loci, which is mediated by the recombination frequency between them. Given that the maximum value of the coefficient of double reduction is 1/6, Eq. 1 also provides prediction of the largest possible recombination frequency between locus A and a locus linked to it, which is given as
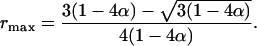 |
[2] |
Eq. 2 is useful not only for the linkage analysis discussed in the present study but for evaluation of the extent of double reduction in shaping the evolution of autotetraploid genomes (22).
Table 1. Probability distribution of the modes of gamete formation and gamete genotypes at two linked loci from a quadrivalent meiosis of autotetraploid species.
| Gametes (1 ≤ i, j, k, l ≤ 4)
|
Double reduction and recombination events
|
Probabilities (i = 1, 2,..., 11)
|
||
|---|---|---|---|---|
| Frequency | Modes (mi) | Gametes (gi) | ||
| AiBi/AiBi | 4 | A and B (0) | α(1 - r)2 | 27α(1 - r)2/108 |
| AiBj/AiBj | 12 | A and B (2) | αr2/3 | 3αr2/108 |
| AiBi/AiBj | 12 | A (1) | 2αr(1 - r) | 18αr(1 - r)/108 |
| AiBj/AiBk | 12 | A (2) | 2αr2/3 | 6αr2/108 |
| AiBi/AjBi | 12 | B (1) | 2(1 - α)r(1 - r)/3 | 6(1 - α)r(1 - r)/108 |
| AiBj/AkBj | 12 | B (2) | 2(1 - α)r2/9 | 2(1 - α)r2/108 |
| AiBi/AjBj | 6 | — (0) | (1 - α)(1 - r)2 | 18(1 - α)(1 - r)2/108 |
| AiBi/AjBk | 24 | — (1) | 4(1 - α)r(1 - r)/3 | 6(1 - α)r(1 - r)/108 |
| AiBj/AjBi | 6 | — (2) | (1 - α)r2/9 | 2(1 - α)r2/108 |
| AiBj/AjBk | 24 | — (2) | 4(1 - α)r2/9 | 2(1 - α)r2/108 |
| AiBj/AkBl | 12 | — (2) | 2(1 - α)r2/9 | 2(1 - α)r2/108 |
The number in parentheses denotes the number of recombinant chromosomes in the gametes; — means that neither loci A nor B involves double reduction.
For any given individual genotype, at the most, 136 distinct gamete genotypes exist. A general formula for the frequency of these gametes can be written as:
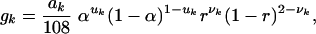 |
[3] |
where ak is a constant, such as 27, 3, 18,..., 2 in Table 1, uk takes a value of 1 if the gamete is generated from double-reduction meiosis or 0 otherwise, whereas νk = 0, 1, or 2, corresponding to the number of recombinant chromosomes carried by the gamete. Since, at the most, 16 different alleles exist between two tetraploid individuals at two loci, a total of at the most 1362 = 18,496 zygote genotypes of offspring occur by crossing any two parental individuals.
This formulation assumed complete quadrivalent pairing among homologous chromosomes during meiosis. Much cytogenetic evidence shows that homologous chromosomes may segregate due to a mixture of quadrivalent and bivalent pairings. Luo et al. (18) showed that a general formula for the frequency of a gamete from a bivalent pairing was given by:
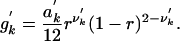 |
[4] |
To model the mixed chromosomal pairings, we denote λ for the probability of a randomly chosen diploid gamete being from bivalent pairing. With the assumption of a random union of gametes from two parents, a general expression for the frequency of zygote j, which is composed of gametes k and l, may be in form of
 |
where aj = akal, bj = a′kal + aka′l, ωj = uk + ul, and νj = νk + νl. a′j, u′j, and ν′j are similarly defined.
The first difficulty involved in tetrasomic linkage analysis is that no simple one-to-one relationship usually exists between the phenotype and the genotype of molecular markers scored in tetraploid individuals. Three reasons for this exist. First, a multiple dosage of an allele cannot be distinguished from a single dosage on the basis of the gel band pattern. Second, some alleles may not be revealed as the presence of a corresponding gel band, i.e., the null alleles (24). Third, dominance may mask the presence of recessive alleles. We have developed the relationship between marker phenotypes and genotypes at a single tetraploid locus and pointed out that as many as six genotypes could exist for one phenotype (18). Thus, the probability of zygote pheno-type i can be expressed in the different forms of the model parameters λ, α, and r.
 |
[5] |
 |
[6] |
 |
[7] |
In Eq. 5 Σg∈i indicates the sum over the frequencies of all those genotypes g that are compatible with the same phenotype i. It will become clear in the next section of statistical analysis that the offspring phenotype probability is expressed alternatively by Eqs. 5, 6, 7.
Statistical Analysis
Maximum Likelihood Estimation of the Model Parameters. In the model above, the unknown parameters are λ, α, and r. The statistical analysis predicts these model parameters based on P1 and P2, the phenotype scored on the two parents, and O = (o1, o2,..., on), the phenotype records of a random sample of n offspring individuals from the parental lines. Let G = (g1, g2..., gn) be the genotypes of the offspring individuals, respectively. The likelihood function of the parameters Ω = (λ, α, r) given P1, P2, and O can be written as:
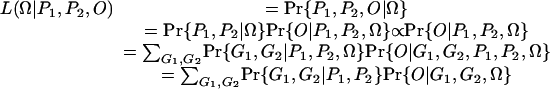 |
[8] |
In the likelihood function, the probability Pr{G1, G2|P1, P2} can be calculated easily from various parental genotypes G1 and G2, which are compatible with the given phenotypes P1 and P2. Thus, the analysis is focused on the probability Pr{O|G1, G2, Ω}, which is also the likelihood function Lg(G1, G2, Ω|O). We assume that the offspring phenotype is randomly sampled from a multinomial distribution with probability parameters given by fi, then the likelihood function has a form of
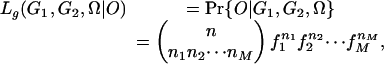 |
[9] |
where ni (i = 1, 2,..., M) is the number of individuals with the ith phenotype class in the sample. The logarithm of the likelihood is thus
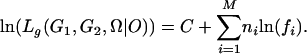 |
[10] |
The derivatives of the function with respect to the unknown parameters λ, α, and r are
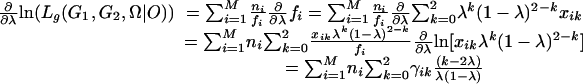 |
[11] |
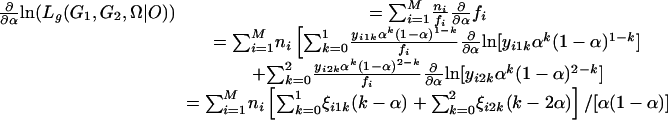 |
[12] |
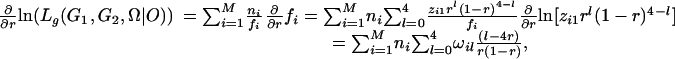 |
[13] |
where γik = xikλk(1 - λ)2-k/fi is the conditional probability of individuals with the ith phenotype having k gametes from meiosis with bivalent chromosome pairing, ξijk = yijkαk(1 - α)j-k/fi is the conditional probability of individuals of the ith phenotype with k double-reduction gametes, and ωik = zikrk(1 - r)4-k/fi, the probability of individuals of the ith phenotype with k recombinant chromosomes. Set Eqs. 11, 12, 13 to be zero, the maximum-likelihood estimates (MLEs) of the parameters can be calculated as:
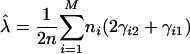 |
[14] |
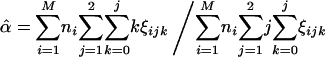 |
[15] |
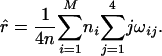 |
[16] |
This procedure represents a version of the EM algorithm for achieving the MLEs of the model parameters (25) in the present context. The algorithm starts with a given set of arbitrary values of the unknown parameters λ, α, and r; uses these values as estimates of the parameters to calculate the conditional probability, γik, ξijk, and ωik (the expectation step); and these probabilities are then incorporated into Eqs. 14, 15, 16 to calculate the new estimates of λ, α, and r, respectively (the maximization step). These two steps are iterated until the sequence of the likelihood function given by Eq. 9 converges.
The second challenge of the linkage analysis is to calculate the expected frequencies of phenotypes of offspring from any given pair of parental genotypes. It is obviously impractical to carry out the calculation manually. We developed a computer-based algorithm that automates calculation of cijkl, the constant coefficients in Eqs. 5, 6, 7 for fi, the ith phenotype frequency. The algorithm is detailed and illustrated in Supporting Text, which is published as supporting information on the PNAS web site. With cijkl and parameter values, the terms γik, ξijk, and ωik can be worked out easily and, in turn, this statistical algorithm can be programmed accordingly.
The likelihood analysis discussed above can be carried out for all possible pairs of parental genotypes that are compatible with their given phenotypes. For a given marker phenotype, at the most, six possible genotypes exist at a locus, 36 possible configurations of these genotypes are at two loci for one individual, and 36 × 36 = 1,296 possible configurations exist for a pair of parental genotypes. However, to combine two one-locus genotypes into one two-locus genotype one must take into account the linkage phase of alleles at the two loci. The number of possible different linkage phases depends on the number of distinct alleles at each locus and increases exponentially with the number of loci under consideration. In a two-locus system of tetrasomic inheritance, an individual genotype may have a maximum of 24 distinct linkage phases, and a pair of individuals may have a maximum of 24 × 24 = 576 distinct linkage-phase configurations. Therefore, the number of pairs of parental genotypes, which need to be considered in this statistical analysis, could be as large as 1,296 × 576 = 764,496! It is certainly possible by use of a fast computer, but computationally inefficient, to predict the most likely parental genotypes from all these possibilities. We have developed a statistical method for predicting the probability distribution of all possible parental genotype pairs at a dominant or codominant marker locus on the basis of their own and their progeny's phenotypes scored at that locus (17). This method enables the number of all possible parental genotype pairs, the most probable genotype pair, and the MLEs of the coefficient of double reduction to be estimated at each individual locus. Simulation study and analysis of 74 offspring of a tetraploid potato cross-demonstrated that the most likely parental genotypes were predicted usually with a probability value of >90%. To reduce computational demand in searching over all possible two-locus parental genotypes, we suggest use of the single-locus method to determine the most likely parental genotypes at each of the linked loci. Then we focus on these predicted one-locus genotypes in searching for the most likely phase of the linked alleles and, thus, the most likely parental genotypes at the linked loci. This may reduce the computational demand dramatically.
Information and Power of the MLE. The likelihood-based analysis described previously provides a framework for calculating the asymptotic variance–covariance matrix of the MLEs of the model parameters and for predicting statistical power for testing the significance of double reduction at locus A or/and genetic linkage. Let G1 and G2 be the most likely parental genotype searched, and 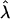 ,
, 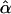 , and r̂ be the MLEs of λ, α, and r, respectively. The likelihood-ratio test statistics for testing significance of double reduction and linkage are given by
, and r̂ be the MLEs of λ, α, and r, respectively. The likelihood-ratio test statistics for testing significance of double reduction and linkage are given by
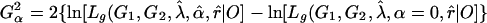 |
[17] |
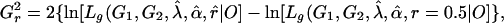 |
[18] |
respectively. In ref. 26, it was shown that these test statistics have an approximate large-sample noncentral chi-square distribution with 1 df, and the noncentrality parameters in the present context are, respectively:
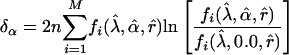 |
[19] |
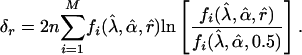 |
[20] |
Thus, the power for the statistical test at a given significance level ε is given by the probability
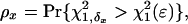 |
[21] |
where x = α or r corresponds to the test for double reduction or linkage, respectively. χ21,δ denotes a random variable with a noncentral chi-square distribution with 1 df and the noncentrality parameter δ, and χ21 (ε)isthe1 - ε percentile of a central chi-square distribution, also with 1 df. The expectation of the second derivatives of the likelihood function with respect to the model parameters x and y, π2xy = E[(∂2/∂x∂y) ln(Lg(G1, G2, Ω|O)], can be expressed as the simplified forms of
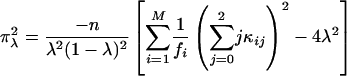 |
[22] |
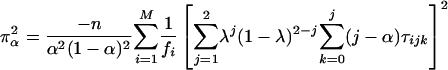 |
[23] |
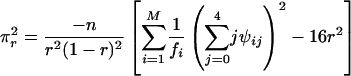 |
[24] |
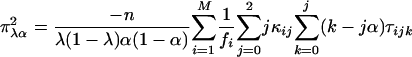 |
[25] |
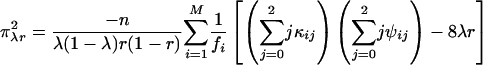 |
[26] |
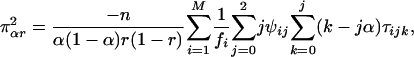 |
[27] |
where κij = λj(1 - λ)2-jxi(j-1), τijk = αk(1 - α)j kyijk, and ψij = rj(1 - r)4-jzij, with xij, yijk, and zij being defined in Eqs. 5, 6, 7, respectively. The simplified forms can be derived by use of the formulae illustrated in Supporting Text. Thus, the asymptotic variance–covariance matrix of the MLEs of  ,
, 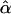 , and r̂ is given by:
, and r̂ is given by:
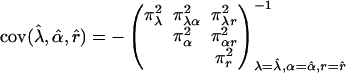 |
[28] |
Simulation Examples. For illustration of the theoretical analysis and statistical method developed in the present study, we simulated a full-sib family of 200 individuals from crossing two autotetraploid genotypes AA/BB/BB/OB and CA/DA/EC/EO, where O denotes a “null allele” or a recessive allele. For a given simulated value of λ, the simulated values of α and r were independently chosen, but the values of β were determined from Eq. 1 for given α and r. Six sets of simulation parameters were considered and tabulated as the first four columns of Table 2.
Table 2. Simulated parameters and means and standard errors (in parentheses) of their MLEs.
| λ | α | β | r | 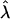 |
α̂ | β̂ | r̂ | ρα | ρr | p1 | p2 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.10 | 0.14 | 0.10 | 0.002 (0.001) | 0.1024 (0.0027) | 0.1375 (0.0018) | 0.0985 (0.0025) | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.25 | 0.10 | 0.14 | 0.10 | 0.259 (0.009) | 0.1028 (0.0030) | 0.1390 (0.0024) | 0.0994 (0.0023) | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.50 | 0.10 | 0.14 | 0.10 | 0.510 (0.013) | 0.1085 (0.0042) | 0.1434 (0.0033) | 0.0993 (0.0027) | 1.00 | 1.00 | 1.00 | 1.00 |
| 0.75 | 0.10 | 0.14 | 0.10 | 0.748 (0.016) | 0.1094 (0.0051) | 0.1443 (0.0041) | 0.1020 (0.0027) | 0.98 | 1.00 | 1.00 | 1.00 |
| 0.50 | 0.05 | 0.10 | 0.10 | 0.489 (0.015) | 0.0534 (0.0032) | 0.1049 (0.0025) | 0.1052 (0.0026) | 0.95 | 1.00 | 1.00 | 1.00 |
| 0.50 | 0.10 | 0.12 | 0.05 | 0.506 (0.010) | 0.1041 (0.0034) | 0.1229 (0.0030) | 0.0501 (0.0018) | 1.00 | 1.00 | 1.00 | 1.00 |
λ, α, β, and r (r̂) are simulated values (or MLEs) of the proportion of bivalent pairing, the coefficients of double reduction and recombination frequency between two linked loci. ρα and ρr represent the empirical statistical power for testing significance of double reduction and genetic linkage. p1 and p2 are frequencies of correct diagnosis of the linkage phase of two parental genotypes.
Table 2 tabulates the means and standard errors (in brackets) of the MLEs based on 100 repeated simulations. The MLEs were searched from all possible linkage phases for each of all possible parental genotypes based on the phenotype data of the parents and their offspring. It can be seen that the model parameters were predicted adequately by the corresponding MLEs. We calculated empirical powers for testing significance of double reduction and linkage as a proportion of the corresponding significant tests over the repeated simulation trials, and these were denoted as ρα and ρr respectively. It showed that the likelihood-ratio statistic had a power of 100% for detecting linkage in all these simulated populations. However, the statistical power for testing double reduction was decreased as expected when bivalent pairing accounted for a high proportion (i.e., 75%) of meioses or when it occurred at a low frequency (i.e., α = 0.05). Table 3 lists the top 10 most likely parental genotypes, the MLEs of α and r, and the corresponding log-likelihood value from the first single data set from simulation with λ = 0.05, α = 0.1, and r = 0.1. It indicated that the true parental genotypes were diagnosed as the most likely genotypes, which was as many as e(689.31–679.33) ≃ 22,026 times more likely than the second most possible prediction of the genotypes. To demonstrate the present algorithm in resolving different linkage phases of parental genotypes, we investigated distribution of values of the likelihood of all the possible linkage phases of the most likely parental genotypes. Fig. 1, which is published as supporting information on the PNAS web site, illustrated change in the likelihood values over change in the MLEs of r, which were calculated at these linkage phases. It showed that the true linkage phases were distinguished without ambiguity from the remaining possibilities regardless of varying proportions of bivalent pairing in the simulated autotetrasomic meiosis.
Table 3.
The top 10 most likely parental genotypes at the two linked loci (G1 and G2), the maximum likelihood estimates of α and r which were calculated at these genotypes, and the log-likelihood values (L)
| G1 | G2 | α | r | L | |
|---|---|---|---|---|---|
| 1 | AA/BB/BB/OB | CA/DA/EC/EO | 0.0102 | 0.1132 | —679.33 |
| 2 | AA/BB/BB/OB | CA/DA/EC/EA | 0.0837 | 0.1804 | —689.31 |
| 3 | AA/AB/BB/BB | CA/DA/EC/EO | 0.3376 | 0.1372 | —709.83 |
| 4 | AA/BB/BB/OB | CA/DO/EC/EO | 0.3431 | 0.2305 | —710.45 |
| 5 | AA/BB/BB/OB | CA/DA/EC/EC | 0.0496 | 0.3923 | —718.72 |
| 6 | AA/BO/BB/OB | CA/DA/EC/EO | 0.2307 | 0.1861 | —719.99 |
| 7 | AA/BB/BB/OA | CA/DO/EC/EO | 0.4120 | 0.2601 | —724.81 |
| 8 | AA/BB/BB/OA | CA/DA/EC/EO | 0.2465 | 0.2759 | —726.74 |
| 9 | AA/BB/OB/OB | CA/DA/EC/EO | 0.0628 | 0.1450 | —729.50 |
| 10 | AA/BB/BB/OO | CA/DA/EC/EA | 0.1205 | 0.2981 | —729.83 |
Discussion
Theoretical analysis of a full model of genetic linkage in autotetraploid species that considers double reduction and recombination has been a challenging problem in the history of genetic linkage studies (11–13) and an important topic in the era of genome research in autotetraploids (14–18). Taking advantage of advances in modern statistics, computational technology, and molecular biotechniques, the present study addresses a series of key problems in such an analysis.
The present study has succeeded in modeling the distribution of offspring genotypes at two linked loci from crossing any two parental genotypes in terms of the coefficient of double reduction at one of the two loci and recombination fraction between them. This analysis has filled the gap left by the pioneering works (11–13), which was subsequently addressed but not properly solved in more recent studies (22, 23).
This tetrasomic model of gene segregation and recombination created a theoretical basis for the statistical method developed in the present study, which takes appropriate account of most, if not all, essential features of the molecular marker data in the current construction of the genetic map of the autotetraploid species. These features include inheritance of alleles with multiple dosages, existence of null alleles, allelic segregation distortion due to double reduction, mixture of bivalent and quadrivalent pairings among homologous chromosomes in meiosis, and incomplete information of phenotype in regard to genotype. The method was built on a combination of a computer-based approach for calculating the conditional probability distribution of offspring phenotypes given their parental phenotypes and the EM algorithm for calculating the MLEs of the model parameters. In addition, the likelihood-based method provides a prediction of the most likely parental genotypes at linked loci, a direct evaluation of the statistical power for detecting significance of double reduction and linkage, and calculation of the asymptotic variances and covariances of the MLEs. Simulation examples demonstrated the feasibility of implementing the algorithm to analyze practical data, validated the adequacy of parameter estimation under various models of chromosomal pairing, and showed a sharp resolving power in diagnosing the most likely parental genotypes and their linkage phases from a large number of possible rivals. Moreover, the present method offers appropriate modeling of both bivalent and quadrivalent chromosomal pairing during autotetraploid meiosis, distinguished sharply from the methods that appeared in almost all recent literature and considered bivalent pairing only (14–21). These methods cannot be used to cope with complexities in patterns of gene segregation and recombination due to double reduction. For instance, a total of 41 possible offspring phenotypes exist for the simulated parental genotypes in the present simulation study when double reduction is taken into account, but this number reduces to 36 if only bivalent pairing is assumed. Thus, these methods are seriously limited in analyzing data in practice.
The present study involved a pairwise approach, but the theoretical analysis of the study has built a key stepping stone for the analysis of multiple loci. In practical implementation, we may either implement the least-squares method that was originally developed by Stam (27) for joining the pairwise loci linkage analysis into reconstruction of multiple loci linkage maps in diploids and extended to the tetraploid case (18) or use the hidden Markov chain model first proposed by Lander and Green (28) to construct genetic linkage maps of multiple loci in diploid species. Integration of the present study into the least-squares method is straightforward for the estimates of recombination frequencies between all pairwise loci, and the corresponding likelihood values are all required for joining the pairs of linked loci into linkage maps. On the other hand, the present probabilistic model of gene segregation and recombination at two linked loci may be readily converted into the transition probabilities of the Markov chain process, a key component of the hidden Markov chain model analysis. However, the major challenge of the hidden Markov chain model-based multiple loci analysis lies in the computational demand in searching over the huge number of all possible orders of multiple loci and linkage phases at these loci. It is no longer appropriate to investigate all these alternatives exclusively. An effective approach is to treat this question as a combinatorial optimization problem, which can be solved by implementing the simulated annealing algorithm (29) to search for optima of the multiple loci likelihood function of discrete variables of the linkage orders and phases.
Double reduction has been recognized as a significant factor in evolution of breeding structure (30), in maintenance of genetic polymorphism (1), and in affecting persistence of recessive deleterious mutations (31) in polyploid populations. More recently, Butruille and Boiteux (22) stressed its role in determining gametophytic selection–mutation equilibrium based on a single-locus model of double reduction and pointed out the need to incorporate recombination into the system. The multilocus model allows not only the extent of effect of double reduction on the genome to be assessed but also enables a joint effect of double reduction and recombination to be investigated. The model proposed here has thus created such an opportunity to address these evolutionary questions in addition to its central utility in genetic map construction in autopolyploid species.
Supplementary Material
Acknowledgments
We thank Drs. John Bradshaw and Jim McNicole for comments on an earlier version of this paper. This study was supported by research grants from the United Kingdom Biotechnology and Biological Sciences Research Council and The Pilot Research Project Fund of the University of Birmingham and by a grant from the Natural Environment Research Council.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviation: MLE, maximum-likelihood estimate.
References
- 1.Stebbins, G. L. (1971) Chromosome Evolution in Higher Plants (Edward Arnold, London).
- 2.Lewis, W. H. (1980) Polyploidy: Biological Relevance (Plenum, New York).
- 3.Song, K., Lu, P., Tang, K. & Osborn, T. C. (1995) Proc. Natl. Acad. Sci. USA 92, 7719-7723. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Soltis, P. S. & Soltis, D. E. (2000) Proc. Natl. Acad. Sci. USA 97, 7051-7057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bradshaw, J. E., Hackett, C. A., Meyer, R. C., Milbourne, D. & McNicol, J. W. (1998) Theor. Appl. Genet. 97, 202-210. [Google Scholar]
- 6.Meyer, R. C., Milbourne, D., Hackett, C. A., Bradshaw, J. E., McNicol, J. W. & Waugh, R. (1998) Mol. Gen. Genet. 259, 150-160. [DOI] [PubMed] [Google Scholar]
- 7.Wang, D., Karle, R., Brettin, T. S. & Tezzoni, A. F. (1998) Theor. Appl. Genet. 97, 202-210. [Google Scholar]
- 8.Brouwer, D. J. & Osborn, T. C. (1999) Theor. Appl. Genet. 97, 202-210. [Google Scholar]
- 9.Tai, G. C. C., Seabrook, J. E. A. & Aziz, A. N. (2000) Theor. Appl. Genet. 101, 126-130. [Google Scholar]
- 10.Gregan, P. B., Jarvik, T., Bush, A. L., Shoemaker, G. C., Lark, K. G. & Specht, J. E. (1999) Crop Sci. 39, 1464-1490. [Google Scholar]
- 11.Bailey, N. T. J. (1961) Introduction to the Mathematical Theory of Genetic Linkage (Clarendon, Oxford).
- 12.Fisher, R. A. (1947) Philos. Trans. R. Soc. London B 233, 55-87. [Google Scholar]
- 13.Mather, K. (1936) J. Genet. 32, 287-314. [Google Scholar]
- 14.Hackett, C. A., Bradshaw, J. E., Mayer, R. C., McNicol, J. W. & Milbourne, D. (1998) Genet. Res. 71, 143-154. [Google Scholar]
- 15.Ripol, M. I., Churchill, G. A., da Silva, J. A. G. & Sorrells, M. (1999) Gene 135, 31-41. [DOI] [PubMed] [Google Scholar]
- 16.Doerge, R. W. & Craig, B. A. (2000) Proc. Natl. Acad. Sci. USA 97, 7951-7956. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Luo, Z. W., Hackett, C. A., Bradshaw, J. E., McNicol, J. W. & Milbourne, D. (1999) Theor. Appl. Genet. 100, 1067-1073. [Google Scholar]
- 18.Luo, Z. W., Hackett, C. A., Bradshaw, J. E., McNicol, J. W. & Milbourne, D. (2001) Genetics 157, 1067-1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Xie, C. & Xu, S. (2000) Genet. Res. 76, 105-115. [DOI] [PubMed] [Google Scholar]
- 20.Hackett, C. A., Bradshaw, J. E. & McNicole, J. W. (2001) Genetics 159, 1819-1832. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ma, C. X., Casella, G., Shen, Z. J., Osborn, T. C. & Wu, R. (2002) Genome Res. 12, 1974-1981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Butruille, D. V. & Boiteux, L. S. (2000) Proc. Natl. Acad. Sci. USA 97, 6608-6613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Wu, S. S., Wu, R. L., Ma, C. X., Zeng, Z. B., Yang, M. C. & Casella, G. (2001) Genetics 159, 1339-1350. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Callen, D. F., Thompson, A. D., Shen, Y., Phillips, H. A. & Richards, R. I. (1993) Am. J. Hum. Genet. 52, 922-927. [PMC free article] [PubMed] [Google Scholar]
- 25.McLachlan, G. J. & Krishnan, T. (1997) The EM Algorithm and Extensions (Wiley, New York).
- 26.Agresti, A. (1990) Categorical Data Analysis (Wiley, New York).
- 27.Stam, P. (1993) Plant J. 3, 739-744. [Google Scholar]
- 28.Lander, E. S. & Green, P. (1987) Proc. Natl. Acad. Sci. USA 84, 2363-2367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.van Laarhoven, P. J. M. & Aarts, E. H. L. (1987) Simulated Annealing: Theory and Application (D. Reidel Publishing Company, Dordrecht, The Netherlands).
- 30.Fisher, R. A. (1949) The Theory of Inbreeding (Hafner, New York).
- 31.Soltis, D. & Rieseberg, L. H. (1986) Am. J. Bot. 73, 310-338. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


