Skip to main content
PMC home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 1995 Sep 26;92(20):9206–9209. doi: 10.1073/pnas.92.20.9206

Lattice model for rapidly folding protein-like heteropolymers.

I Shrivastava 1, S Vishveshwara 1, M Cieplak 1, A Maritan 1, J R Banavar 1
PMCID: PMC40953  PMID: 7568102

Abstract

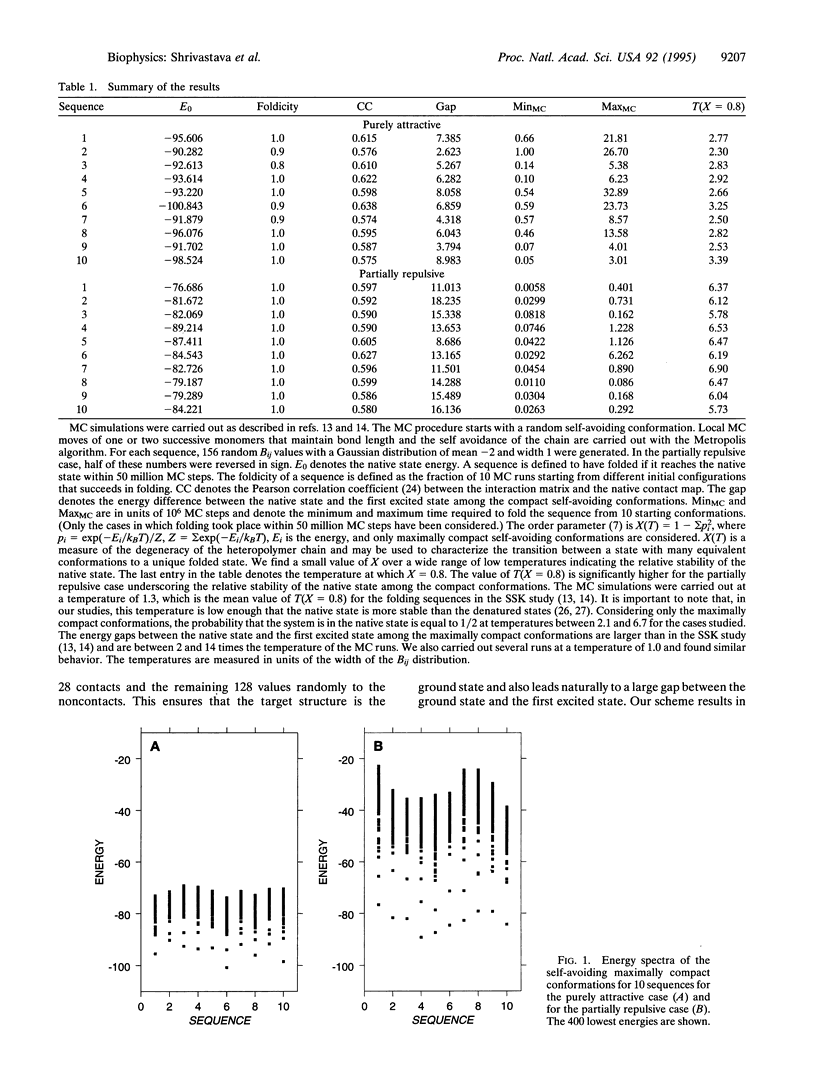
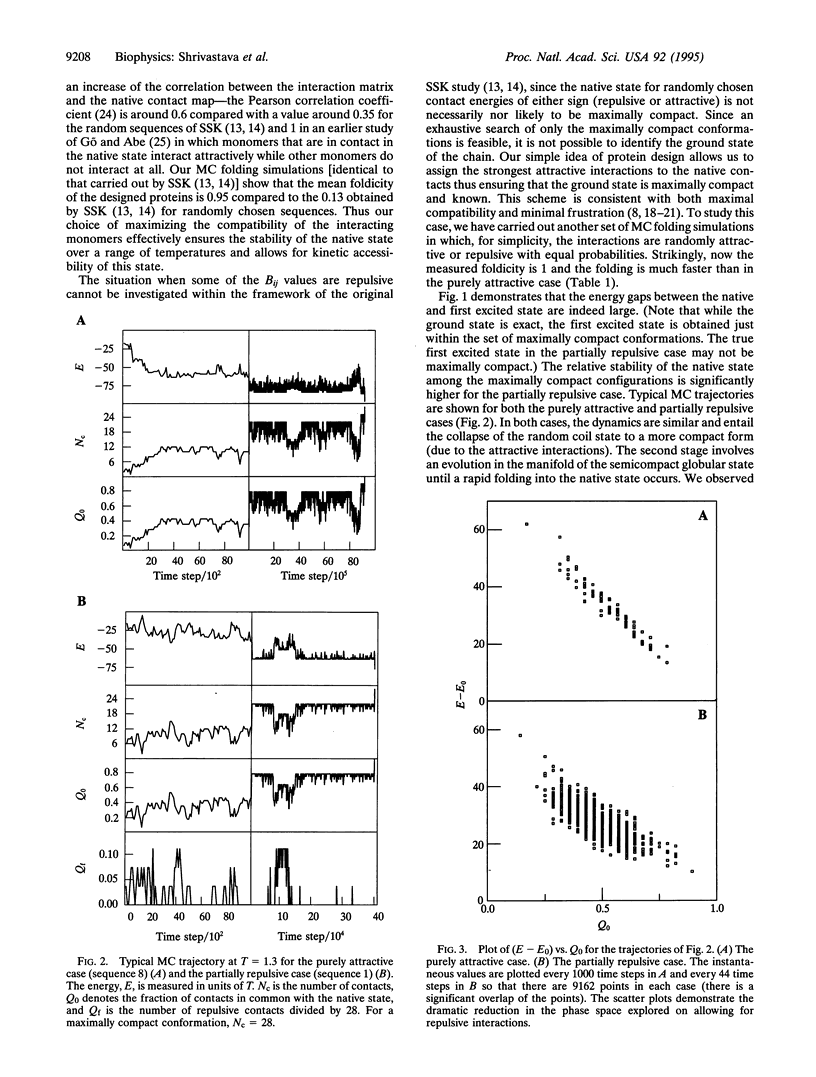
Protein folding is a relatively fast process considering the astronomical number of conformations in which a protein could find itself. Within the framework of a lattice model, we show that one can design rapidly folding sequences by assigning the strongest attractive couplings to the contacts present in a target native state. Our protein design can be extended to situations with both attractive and repulsive contacts. Frustration is minimized by ensuring that all the native contacts are again strongly attractive. Strikingly, this ensures the inevitability of folding and accelerates the folding process by an order of magnitude. The evolutionary implications of our findings are discussed.

Full text

PDF
9209

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Abe H., Go N. Noninteracting local-structure model of folding and unfolding transition in globular proteins. II. Application to two-dimensional lattice proteins. Biopolymers. 1981 May;20(5):1013–1031. doi: 10.1002/bip.1981.360200512. [DOI] [PubMed] [Google Scholar]
  2. Bryngelson J. D., Onuchic J. N., Socci N. D., Wolynes P. G. Funnels, pathways, and the energy landscape of protein folding: a synthesis. Proteins. 1995 Mar;21(3):167–195. doi: 10.1002/prot.340210302. [DOI] [PubMed] [Google Scholar]
  3. Bryngelson J. D., Wolynes P. G. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci U S A. 1987 Nov;84(21):7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Chan H. S., Dill K. A. Polymer principles in protein structure and stability. Annu Rev Biophys Biophys Chem. 1991;20:447–490. doi: 10.1146/annurev.bb.20.060191.002311. [DOI] [PubMed] [Google Scholar]
  5. Chan H. S. Kinetics of protein folding. Nature. 1995 Feb 23;373(6516):664–665. doi: 10.1038/373664a0. [DOI] [PubMed] [Google Scholar]
  6. Chothia C., Finkelstein A. V. The classification and origins of protein folding patterns. Annu Rev Biochem. 1990;59:1007–1039. doi: 10.1146/annurev.bi.59.070190.005043. [DOI] [PubMed] [Google Scholar]
  7. Cieplak M, Maritan A, Banavar JR. Optimal paths and domain walls in the strong disorder limit. Phys Rev Lett. 1994 Apr 11;72(15):2320–2323. doi: 10.1103/PhysRevLett.72.2320. [DOI] [PubMed] [Google Scholar]
  8. Dill K. A., Bromberg S., Yue K., Fiebig K. M., Yee D. P., Thomas P. D., Chan H. S. Principles of protein folding--a perspective from simple exact models. Protein Sci. 1995 Apr;4(4):561–602. doi: 10.1002/pro.5560040401. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Flores T. P., Orengo C. A., Moss D. S., Thornton J. M. Comparison of conformational characteristics in structurally similar protein pairs. Protein Sci. 1993 Nov;2(11):1811–1826. doi: 10.1002/pro.5560021104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Gokhale R. S., Agarwalla S., Francis V. S., Santi D. V., Balaram P. Thermal stabilization of thymidylate synthase by engineering two disulfide bridges across the dimer interface. J Mol Biol. 1994 Jan 7;235(1):89–94. doi: 10.1016/s0022-2836(05)80018-x. [DOI] [PubMed] [Google Scholar]
  11. Goldstein R. A., Luthey-Schulten Z. A., Wolynes P. G. Optimal protein-folding codes from spin-glass theory. Proc Natl Acad Sci U S A. 1992 Jun 1;89(11):4918–4922. doi: 10.1073/pnas.89.11.4918. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Goldstein R. A., Luthey-Schulten Z. A., Wolynes P. G. Protein tertiary structure recognition using optimized Hamiltonians with local interactions. Proc Natl Acad Sci U S A. 1992 Oct 1;89(19):9029–9033. doi: 10.1073/pnas.89.19.9029. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Kirkpatrick S., Gelatt C. D., Jr, Vecchi M. P. Optimization by simulated annealing. Science. 1983 May 13;220(4598):671–680. doi: 10.1126/science.220.4598.671. [DOI] [PubMed] [Google Scholar]
  14. Lim W. A., Sauer R. T. Alternative packing arrangements in the hydrophobic core of lambda repressor. Nature. 1989 May 4;339(6219):31–36. doi: 10.1038/339031a0. [DOI] [PubMed] [Google Scholar]
  15. Matthews B. W. Genetic and structural analysis of the protein stability problem. Biochemistry. 1987 Nov 3;26(22):6885–6888. doi: 10.1021/bi00396a001. [DOI] [PubMed] [Google Scholar]
  16. Newman CM, Stein DL. Spin-glass model with dimension-dependent ground state multiplicity. Phys Rev Lett. 1994 Apr 4;72(14):2286–2289. doi: 10.1103/PhysRevLett.72.2286. [DOI] [PubMed] [Google Scholar]
  17. Ponder J. W., Richards F. M. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J Mol Biol. 1987 Feb 20;193(4):775–791. doi: 10.1016/0022-2836(87)90358-5. [DOI] [PubMed] [Google Scholar]
  18. Rabow A. A., Scheraga H. A. Lattice neural network minimization. Application of neural network optimization for locating the global-minimum conformations of proteins. J Mol Biol. 1993 Aug 20;232(4):1157–1168. doi: 10.1006/jmbi.1993.1468. [DOI] [PubMed] [Google Scholar]
  19. Reidhaar-Olson J. F., Sauer R. T. Combinatorial cassette mutagenesis as a probe of the informational content of protein sequences. Science. 1988 Jul 1;241(4861):53–57. doi: 10.1126/science.3388019. [DOI] [PubMed] [Google Scholar]
  20. Sali A., Shakhnovich E., Karplus M. How does a protein fold? Nature. 1994 May 19;369(6477):248–251. doi: 10.1038/369248a0. [DOI] [PubMed] [Google Scholar]
  21. Sali A., Shakhnovich E., Karplus M. Kinetics of protein folding. A lattice model study of the requirements for folding to the native state. J Mol Biol. 1994 Feb 4;235(5):1614–1636. doi: 10.1006/jmbi.1994.1110. [DOI] [PubMed] [Google Scholar]
  22. Shakhnovich EI. Proteins with selected sequences fold into unique native conformation. Phys Rev Lett. 1994 Jun 13;72(24):3907–3910. doi: 10.1103/PhysRevLett.72.3907. [DOI] [PubMed] [Google Scholar]
  23. Skolnick J., Kolinski A. Computer simulations of globular protein folding and tertiary structure. Annu Rev Phys Chem. 1989;40:207–235. doi: 10.1146/annurev.pc.40.100189.001231. [DOI] [PubMed] [Google Scholar]
  24. Unger R., Moult J. Finding the lowest free energy conformation of a protein is an NP-hard problem: proof and implications. Bull Math Biol. 1993 Nov;55(6):1183–1198. doi: 10.1007/BF02460703. [DOI] [PubMed] [Google Scholar]

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES