Clinal Variation at Phenology-Related Genes in Spruce: Parallel Evolution in FTL2 and Gigantea?

Abstract

Parallel clines in different species, or in different geographical regions of the same species, are an important source of information on the genetic basis of local adaptation. We recently detected latitudinal clines in SNPs frequencies and gene expression of candidate genes for growth cessation in Scandinavian populations of Norway spruce (Picea abies). Here we test whether the same clines are also present in Siberian spruce (P. obovata), a close relative of Norway spruce with a different Quaternary history. We sequenced nine candidate genes and 27 control loci and genotyped 14 SSR loci in six populations of P. obovata located along the Yenisei river from latitude 56°N to latitude 67°N. In contrast to Scandinavian Norway spruce that both departs from the standard neutral model (SNM) and shows a clear population structure, Siberian spruce populations along the Yenisei do not depart from the SNM and are genetically unstructured. Nonetheless, as in Norway spruce, growth cessation is significantly clinal. Polymorphisms in photoperiodic (FTL2) and circadian clock (Gigantea, GI, PRR3) genes also show significant clinal variation and/or evidence of local selection. In GI, one of the variants is the same as in Norway spruce. Finally, a strong cline in gene expression is observed for FTL2, but not for GI. These results, together with recent physiological studies, confirm the key role played by FTL2 and circadian clock genes in the control of growth cessation in spruce species and suggest the presence of parallel adaptation in these two species.

IDENTIFYING the loci underlying the variation in quantitative traits and detecting the selection acting on them remains, to this day, one of the main challenges in biology (Rockman 2012; Marjoram et al. 2013). In his Nobel lecture Sidney Brenner (Brenner 2003) predicted that genome-wide association studies (GWAS) would become the main approach to identifying the genetic factors controlling complex traits. The past decade has amply vindicated Brenner’s prediction: GWAS have blossomed and identified a large number of single nucleotide polymorphism (SNP) associated to various quantitative traits (Visscher et al. 2012). Limitations of GWAS have, however, started to become evident and different strategies have been offered to alleviate those (Rockman 2012; Marjoram et al. 2013; Vilhjalmsson and Nordborg 2013). In particular, GWAS have limited power unless very large data sets are used. They therefore remain prohibitively expensive, and often not so informative, for nonmodel organisms with limited or nascent genome resources such as conifers. In such organisms a more targeted strategy, combining population genetics, physiology, and expression studies of candidate genes remains a very fruitful approach, at least in the short term. We recently adopted such a strategy in an attempt to unravel the genetic basis of growth cessation, a trait of adaptive value with a strong and well-documented clinal variation, in Norway spruce (Picea abies) (Chen et al. 2012a and references therein). Two of the most promising candidate genes that emerged from these studies are PaFTL2, from the photoperiodic pathway, and the circadian clock gene Gigantea (PaGI). PaFTL2 expression level is associated with growth cessation (Gyllenstrand et al. 2007), transgenic studies in Norway spruce confirm that high expression induces growth cessation (Karlgren et al. 2013), and SNPs within its promoter show a strong clinal variation in Scandinavia (Chen et al. 2012a). Gigantea harbors nonsynonymous variants showing clinal variation correlating with growth cessation. Gigantea is further of focal interest as there is mounting evidence of its involvement with phenology in a broad range of tree species (poplars, Rohde et al. 2011, Keller et al. 2012; oaks, Alberto et al. 2013; and spruces, Holliday et al. 2010, Chen et al. 2012a).

In this study we analyzed the relationship between latitude and variation at PaFTL2, PaGI, and other candidate genes for growth cessation in Siberian spruce. One major difficulty when studying clines from Scandinavia is the complex genetic structure of species found in this region. In great parts this complex population structure reflects the extent of the glaciations in this area and the existence of at least three major postglaciation recolonization routes (e.g., Giesecke and Bennett 2004, Chen et al. 2012a for spruce). In contrast, central Siberia, from where the Siberian spruce populations studied here originate, was much less affected by glaciations than northwestern Europe (Binney et al. 2009; Väliranta et al. 2011). Most of central and western Siberia was likely a cold desert as westerly moisture, which is today the source of both rain and snow in this region, was blocked by the Scandinavian ice sheet during the glacial periods (Velichko et al. 2011). The extent and the depth of permafrost during the last glacial maxima were also much greater than they are today. However, macrofossils collected on lower river terraces, high floodplains, and mountain areas suggest that, while most of the region consisted of aeolian dunes, mountain areas and river valleys were a separate habitat where spruce trees were likely able to survive. Some of these populations were even found at high latitudes (Binney et al. 2009; Väliranta et al. 2011) and there is genetic evidence in Siberian larch that southern montane refugia did not contribute to the recolonization of western Siberia (Semerikov et al. 2013). We therefore expect the population history and genetic structure of the Siberian spruce to differ markedly from that of Norway spruce and, based on what has been observed in Siberian larch (Semerikov et al. 2013), to be weaker. Significant associations between candidate genes for growth cessation and latitude are therefore less likely to be false positives than in Scandinavia. The observation of association with latitude for the same candidate genes in both species will also constitute a nice example of parallel evolution, a phenomenon that has recently received a lot of attention (Stern 2013). Because, Scandinavia and western Siberia were glaciated or inhospitable during the last glacial maximum (LGM), the current latitudinal clines are, by necessity, at most 20,000 years old. Hence the presence of parallel clines at candidate genes for growth cessation would suggest the presence of parallel adaptation.

To test for the latter, we first investigated to what extent there are similar phenotypic clines for growth cessation and pattern of gene expression at candidate genes in Siberian spruce. To avoid sampling any putative hybrids between Norway and Siberian spruces we focused on six central Siberian populations growing along the Yenisei river from latitude 56°N to latitude 67°N (Supporting Information, Figure S1). As our previous studies of Norway spruce suggested that variation in photoperiodic and circadian clock genes explain some of the difference in growth cessation along latitudinal clines, we resequenced nine of these genes in Siberian spruce. Five of the genes belong to the photoperiodic pathway—PoFTL2, PoMFTL1, PoPhyP, PoPhyN, PoPhyO—and four of them to the circadian clock—PoCCA1, PoPPR3, PoPRR7, and PoGI.

Below we show that growth cessation and expression patterns for PoFTL2 correlate with latitude in Siberian spruce, much like they do in Norway spruce. We also show that despite an almost complete lack of population genetic structure and deviation from standard neutral model variation, three of these nine genes show clinal variation and/or signs of selection. Furthermore, in the circadian clock-related gene Gigantea (PoGI) the same nonsynonymous mutation as in Norway spruce exhibits clinal variation and signs of selection. Our study therefore suggests the presence of parallel adaptation in these two species. Taken together with physiological studies, these data confirm the key role played by PoFTL2 in the control of growth cessation in spruce species.

Materials and Methods

Measurement of growth cessation

Three experiments were performed to compare the pattern of growth cessation over different latitudes. Two of them were carried out in growth chambers in 2012 and 2013 and a larger one in a greenhouse during the summer 2013. The populations used in each experiment are given in Table 1 and the number of families and seedlings per families is reported in Table S1.

Table 1. Geographic location of the Picea obovata populations used in this study.

Population name	Abbreviation	Latitude (N)	Longitude (E)	Altitude (m)
Koshurnikovoa,b	KOS-54	54.29	93.36	912
Shebertac	SHE-54	54.63	99.90	1045
Baironovkac	BAI-56	55.88	98.12	268
Krasnoyarska,b,d	KRQ-56	55.98	92.75	217
Enyseyska,b,d	ENI-58	58.45	92.20	71
Yartsevoa,b,d	YAR-60	60.23	90.22	52
Bora,b,d	BOR-61	61.58	90.00	38
Turukhanska,b,d	TYR-66	65.78	87.97	15
Igarkab,d	IGA-67	67.43	86.53	15

^aPopulations used in growth cessation study 1 (growth chamber) and 3 (greenhouse).

^bPopulations used in the SSR study.

^cPopulations used in growth cessation study 2 (growth chamber).

^dPopulations used in allele frequency spectrum analyses.

Both growth chamber experiments followed the procedure outlined in detail in Chen et al. (2012a). In short, seeds were germinated and the seedlings were then cultured in a growth chamber under continuous light (250 μmol/m²/sec light and 400–700 nm). The seedlings were then grown under increasing night length from 2- to 9.5-hr night lengths. Each photoperiod lasted 1 week and the weekly increase in night length was 1.5 hr. The temperature in the growth chamber was 20° and the seedlings were watered regularly to keep the substrate moist during the whole duration of the experiment. The first experiment comprised seedlings from six of the seven Yenisei populations used for population genetic analysis, whereas the second one included two southern populations and one very northern one also originating from the Yenisei region (Table 1). Plant height was measured every 7 days and growth cessation was defined as the time at which the weekly length increase was <10% of the total plant height to account for the measurement error.

Patterns of growth cessation and bud set in populations were further studied in a greenhouse experiment. The experiment comprised seeds from five populations located along the Yenisei river and that were used in all genetic analyses (Table 1). The number of half-sib families per population varied from 8 to 20, and each family was represented by 25 seedlings. Seeds were planted in five completely randomized blocks, with five seeds from each half-sib family in every block. Seeds were planted in row pots (Plantek49F, volume of a pot being 155 cm³) filled with peat (Kekkilä, White 420 W F6) and density in the experiment was 330 seedlings/m². Seedlings were grown in a fully computerized greenhouse at Haapastensyrjä Unit of the Finnish Forest Research Institute (METLA, Finland) (60°62’ N, 24°43’ E). Photoperiodic conditions and temperature followed the natural conditions at Haapastensyrjä in southern Finland. Seeds were planted between May 13 and May 17, 2013, one block per day. The number of individuals that germinated from each population varied between 133 and 422 (Table S1). Altogether 1291 seedlings germinated. Plant height was measured and time of bud set observed every 7 days after 7 weeks of growth. Growth cessation was determined as in the growth chamber experiments.

In all three experiments the length of the growth period was then regressed on population latitude (see Chen et al. 2012a, Materials and Methods, for details).

PoFTL2 and PoGI expression pattern

Levels of gene expression during growth cessation were estimated by sampling needles at 09:00 am the last day of each night-length period. For each week and for almost all populations, needles from four unrelated seedlings were collected twice and pooled into two samples for RNA extraction. For the most northern population where fewer seeds germinated, a single pooled sample of four seedlings was collected. RNA was extracted using the STRN250 Spectrum Plant Total RNA kit (Sigma-Aldrich). cDNAs were synthesized from 0.5 mg total RNA, using Superscript III reverse transcriptase and random hexamer primers. The expression of PoFTL2 and the control gene α-tubulin was assessed by quantitative PCR (qPCR) on the Eco Real-Time PCR system (Illumina) using primers described in Gyllenstrand et al. (2007) and Chen et al. (2012a). Reactions were performed in 10-μl reactions containing 5 μl DyNAmo Flash SYBR Green (Thermo Scientific), 0.5 mM of each primer, and 4 μl cDNA (diluted 1:100). αBot (AlphaHelix Molecular Diagnostics AB, Uppsala, Sweden) performed all pipetting prior to runs in the Eco.The qPCR was a standard protocol of 7 min at 95° followed by 40 cycles of 10 sec at 95° and 30 sec at 60°, and finally, 15 sec at 95°, 15 sec at 55°, and 15 sec at 95°. We used both replicates when possible and when these were not available we performed replicated reactions for the same cDNA. The cycle threshold (CT) value was recorded for all qPCR runs for PoFTL2 and α-tubulin and averaged over the two runs per locus in each individual. Relative expression was calculated as ΔCT (CT_α-tubulin − CT_TARGET). Weekly estimates of relative expression of PoFTL2 and PoGI were then regressed over latitude using R (R Core Team 2013).

DNA extraction, genotyping, and sequencing

Two data sets were used for genetic analysis. The first data set consisted of seven populations with latitudes ranging from 54.3°N to 67.4°N (Table 1). Diploid DNA was extracted using needle tissue. A total of 14 nuclear SSR loci were genotyped: three loci by Scotti et al. (2002a) (EATC2B02, EATC1E03, and EATC2G05), one locus by Scotti et al. (2002b) (EAC2C08), one locus by Pfeiffer et al. (1997) (SPAC1F7), six loci by Rungis et al. (2004) (WS0022.B15, WS00111.K13, WS0016.O09, WS00716.F13, WS0073.H08, and WS0092.A19), and three loci by Fluch et al. (2011) (Pa05, Pa28, and Pa44). These 14 loci were amplified in six tubes by multiplex PCR using a Type-it Microsatellite PCR kit (Qiagen) in 5.0-μl mixtures containing 0.7 μl of 1–10 ng of genomic DNA, 2.5 μl of Multiplex PCR master mix buffer, 1.3 μl of H₂O, and 0.5 μl of primer mix (with the concentration of each primer pair adjusted from 0.2 to 0.3 μM). Samples were amplified with a DNA thermal cycler using the following program: initiation of hot-start DNA polymerase and denaturation at 95° for 5 min; 30 cycles of 95° for 30 sec, 57° for 90 sec, and 72° for 30 sec; and a final 30-min extension step at 60°. The amplified products were loaded into an ABI 3130 autosequencer (Applied Biosystems) and MegaBACE1000 (GE Healthcare Life Science) and their sizes and genotypes were determined using GeneMapper software (Applied Biosystems) and Genetic Profiler software (Amersham Biosciences, 2003), respectively. Although two types of autosequencers were used in this study, the samples amplified by the same multiplexed markers were always loaded into the same autosequencer and genotyped with the corresponding software.

The second data set included 96 individuals originating from six of these populations (population KOS-54 was not used here). Genomic DNA was extracted with DNeasy plant mini kit (Qiagen, Germantown, MD) from single megagametophytes using seeds collected from individuals trees in the different populations. In total, 36 PCR fragments covering a total of 48,359 bp were amplified and sequenced using Sanger sequencing technology. The program suite Phred/Phrap/Consed (Ewing et al. 1998; Ewing and Green 1998; Gordon et al. 1998) was used for base calling, sequence assembly, and editing. Nine of the amplified fragments are candidate genes for local adaptation to latitude. These nine genes were chosen as they show sequence similarity to genes related to photoperiod or circadian rhythm in flowering plants and have expression pattern and/or SNP variation consistent with their involvement in local adaptation in Norway spruce (Chen et al. 2012a). Five of the genes belong to the photoperiodic pathway—PoFTL2, PoMFTL1, PoPhyP, PoPhyN, PoPhyO—and four of them to the circadian clock—PoCCA1, PoPPR3, PoPRR7, and PoGI. The 27 control loci were randomly chosen genes and primers were initially developed by Pavy et al. (2012).

Nucleotide diversity, linkage disequilibrium, and neutrality tests

The number of segregating sites (S), the pairwise nucleotide diversity (π) (Nei and Li 1979), and Watterson’s estimate of the scaled population mutation rate (θ_w) (Watterson 1975) were calculated with Dnasp v. 4.50.2 (Librado and Rozas 2009) at noncoding, synonymous, and nonsynonymous sites. Linkage disequilibrium (LD) within and between genes was calculated separately in the pooled data and in individual populations. SNPs were considered to be part of the same LD group if r² ≥ 0.5 and the adjusted P-value ≤ 5% (χ² test with Bonferroni correction for multiple comparisons). The overall decay of LD with physical distance within genes was evaluated by nonlinear regression of r² on a distance between polymorphic sites measured in base pairs, using the formula suggested by Remington et al. (2001). Neutrality tests such as Tajima’s D (Tajima 1989) and Fay and Wu’s H (Fay and Wu 2000) were also calculated using P. sylvestris or P. taeda as outgroups.

Population structure

SSR:

Null allele frequencies and corrected F_ST values were estimated for each of SSR loci using FreeNA (Chapuis and Estoup 2007). The difference between corrected and observed values of F_ST was negligible (data not shown). We selected three statistics to evaluate the genetic diversity within populations, namely allelic richness (Elmousadik and Petit 1996), Nei’s unbiased expected heterozygosity (H_e, Nei 1987), and Wright’s fixation index (F_IS), using the program Fstat v. 2.9.3.2 (Goudet 1995). F_IS was also used to examine the deviation from Hardy–Weinberg equilibrium. In addition, unbiased F_IS values after correction for null alleles were calculated in INEST (Chybicki and Burczyk 2009). The population genetic differentiation was evaluated by both F_ST and the isolation-by-distance (IBD) test (Rousset 1997) implemented in GenAlEx v. 6 (Peakall and Smouse 2006). Finally we investigated the population genetic structure using the Bayesian algorithm implemented in the program STRUCTURE v. 2.3.3 (Pritchard et al. 2000; Hubisz et al. 2009). Each individual was assigned to different clusters based on its multilocus genotype at 14 SSR loci. The program was performed for a number of clusters from K = 1 to K = 7, using an admixture model with correlated allele frequencies. Results were collected from 10 replicates, with each replicate of 100,000-step burn-in followed by 1,000,000-step iteration.

SNP:

We also performed a structure analysis on 240 unlinked control SNPs. The same parameters were applied as those for the SSR data with K values varying from 1 to 6 (population KOS-54 was not included here).

Demographic inference and posterior predictive simulations

A null demographic model of constant effective population size was considered (SNM) consisting of two parameters: the population scaled mutation rate (θ = 4N_eμ) and the population scaled recombination rate (ρ = 4N_er), where N_e is the effective population size, and μ and r are the mutation rate and recombination frequency per base pair per generation, respectively. To test for deviations from this null model, two other simple demographic models were considered. The bottleneck model (BOT) consisted of a population of effective population size N_e that reduces to an effective population size of xN_e at t coalescent time units in the past (measured in 4N_e generations). After a duration of 0.2 coalescent time units, the effective population size returns to N_e. We choose to fix the duration as it is confounded with the severity (x) of the bottleneck. The BOT model therefore consisted of four parameters θ, ρ, x, and t. An exponential growth model (EXP) that includes three parameters, θ, ρ and α, was also considered. The growth parameter α controls the rate of growth of the effective population size (looking forward in time) such that N_t = N(e^−αt). For the three models, the prior bounds were (0: 0.01), (0: 0.01), (0: 1), (0: 2), and (0: 5) for θ, ρ, x, t, and α, respectively.

For each model, 6 × 10⁵ simulations were performed using the coalescent simulator MS (Hudson 2002), with summary statistics calculated using the LIBSEQUENCE package MSSTATS (Thornton 2003). Three summary statistics were used: nucleotide diversity, π, Watterson’s estimate of θ, θ_w, and Tajima’s D (Tajima 1989). For each iteration step, a fragment was simulated for each locus matching the length of those in the observed data set. The summary statistics for each iteration are therefore an average over the simulated loci. Parameters were estimated using the local linear regression method according to Beaumont et al. (2002) giving a posterior distribution of 6000 accepted points. Model choice was performed using the rejection-based method described in Fagundes et al. (2007). Both parameter estimation and model choice were implemented using the package EggLib (Mita and Siol 2012). We performed parameter estimation and model choice based on summary statistics calculated from silent sites only to capture the effect of neutral demographic processes. The choice between competing models was assessed using Bayes factors calculated as the ratio of the marginal likelihoods of the two competing models: p(y|M₁)/p(y|M₀). A Bayes factor ≥3 was considered enough to reject model M₀ in favor of model M₁ (Kass and Raftery 1995). To assess the fit of each locus to the chosen demographic model, 10,000 parameters were randomly sampled with replacement from the posterior distribution of the model. This resulted in posterior predictive distributions for each locus, which were then compared to summary statistics calculated from the observed data using all sites. For Tajima’s D, a normal distribution was assumed for the calculation of P-values for each locus. (The fit to a normal distribution was based on an inspection of the distribution of Tajima’s D values and of a Q–Q plot given in Figure S2. The latter indicates a good fit for negative values.) Fay and Wu’s H, however, had distributions that were highly skewed so a rank transformation of the data was performed using the rntransform function of the R package GenABEL (Aulchenko et al. 2007).

Analysis of the cline

SNPs were extracted and sites with more than two segregating nucleotides were removed. The rate of missing data was kept <5%. This led to a total number of 659 SNPs including 303 candidate SNPs and 356 control SNPs. Control SNPs were used to build the empirical distribution of selected summary statistics. We considered only SNPs whose summary statistics fell into the 5 or 1% empirical tails as outliers under selection and checked the enrichment of candidate outliers at the tails to reduce the false-positive rate.

Linear regression on latitude:

Allele frequencies in each population were calculated and transformed using a square-root arcsine function (Berry and Kreitman 1993) and then regressed on population latitude. We used the coefficient of determination, R², as a statistic of clinality to measure the proportion of total variance in frequency that could be explained by latitude (Berry and Kreitman 1993).

Bayesian generalized linear mixed-model analysis:

To correct for the effect of population history when assessing the relationship between allele frequency and latitude, we used a Bayesian generalized linear mixed model implemented in the program Bayenv (Coop et al. 2010). Allele frequencies in each population are assumed to follow a multinomial distribution and an estimated variance–covariance matrix accounts for the random effects due to shared population history (Nicholson et al. 2002). Environmental or geographic factors (e.g., latitude) are incorporated as fixed linear effects (see Coop et al. 2010 and Hancock et al. 2010, 2011 for more details). The 356 control SNPs were used to generate the variance–covariance matrix and then all 659 SNPs were scanned for regression on latitude. Results were averaged across eight runs of 1,000,000 iterations each.

F_ST outliers:

We tested for F_ST outliers using the program BayeScan v. 2.1 (Foll and Gaggiotti 2008; Foll et al. 2010; Fischer et al. 2011) since it was reported to be more reliable than others when an island model can be assumed (Narum and Hess 2011). In this Bayesian approach, F_ST has two components, a population-specific component and a locus-specific component. The alternative (selection) model for a given locus is retained when the locus-specific component is necessary to explain the observed pattern of diversity. The support for the selection model is estimated with the posterior odds ratio, comparing the posterior probabilities of the data with and without locus-specific components. We ran BayeScan with 20 pilot runs and a burn-in of 50,000 steps followed by 50,000 output iterations. The prior odds ratio was set to 1, which is approximately the ratio of candidate/control SNPs. We also tested a prior odds ratio equal to 10 as this should reduce the number of false positives.

Results

Growth cessation and clinal variation in gene expression

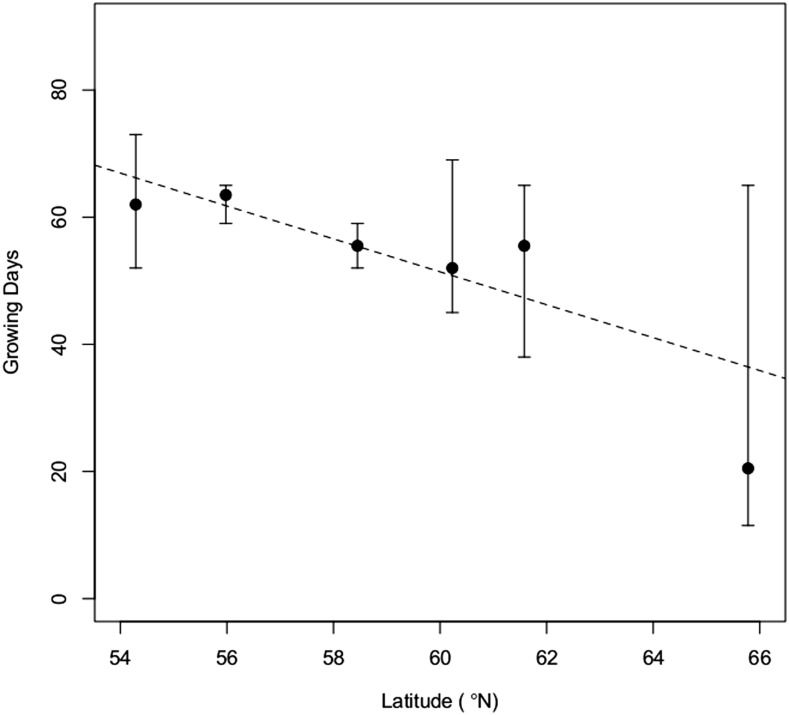
In the two growth chamber experiments, seedlings originating from populations located at different latitudes along the Yenisei river were exposed to periods of increasing night length to trigger growth cessation. In the first and largest growth chamber experiment, the average lengths of the growth period varied significantly between populations of different latitudinal origins (d.f. = 49, r² = 0.455, P-value = 2.52E − 08). The two most southern populations grew for >60 days, whereas the most northern ones ceased to grow after <20 days (Figure 1). In a replicated experiment including two southern and one northern population, the pattern was largely the same with the two southern populations growing significantly longer than the northern population and the response to altered light conditions was consistent between experiments (pairwise Wilcoxon test: P-value = 9.1E − 08) (Figure S3).

Figure 1.

Average number of growing days for six populations along the Yenisei river, estimated in a growth chamber experiment. Vertical bars represent the standard deviation for each measurement. Photoperiodic treatments started with 1 week of constant light, followed by 1 week at 22 hr light/2 hr dark, and so on. The dark period was extended by 1.5 hr each week until a photoperiod of 14.5 hr light/9.5 hr dark was reached. Growth cessation was defined as the time at which the weekly length increase was <10% of the total plant height. The dotted line is a regression line (d.f. = 49, r² = 0.455, P-value = 2.52E − 08).

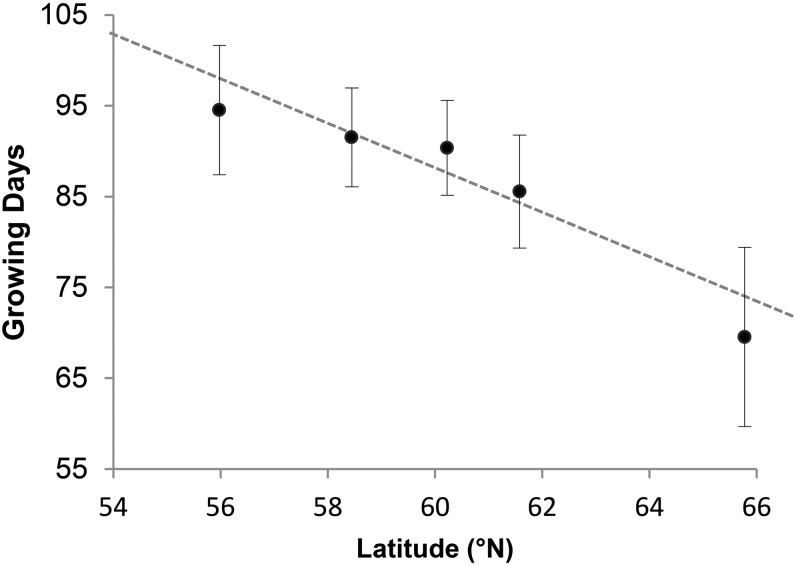
The growth cessation pattern in the greenhouse experiment was very similar to that in the growth chamber experiments. Average lengths of growth period varied significantly between populations of different latitudinal origins (d.f. = 1289, r² = 0.473, P-value < 0.001). The most southern population grew >90 days, while the most northern one ceased to grow after <70 days (Figure 2). The timing of bud set exhibited the same clinal pattern and differed between populations of different latitudinal origins (d.f. = 1288, r² = 0.432, P-value < 0.001). The southernmost population set bud >110 days after sowing, whereas bud formation was observed after <70 days in the northernmost population (Figure S4). Interestingly, in both the first growth chamber experiment and the greenhouse experiment, the cline was weak up to 62°N, with a sharp decline in growth cessation time thereafter.

Figure 2.

Average number of growing days for five populations along the Yenisei river, estimated in a greenhouse experiment. Vertical bars represent the standard deviation for each measurement at Haapastensyrjä in southern Finland (60.62°N, 24.43°E). Growth cessation was defined as the time at which the weekly length increase was <10% of the total plant height. The dotted line is a regression line (P-value < 0.001, r² = 0.473, d.f. = 1289).

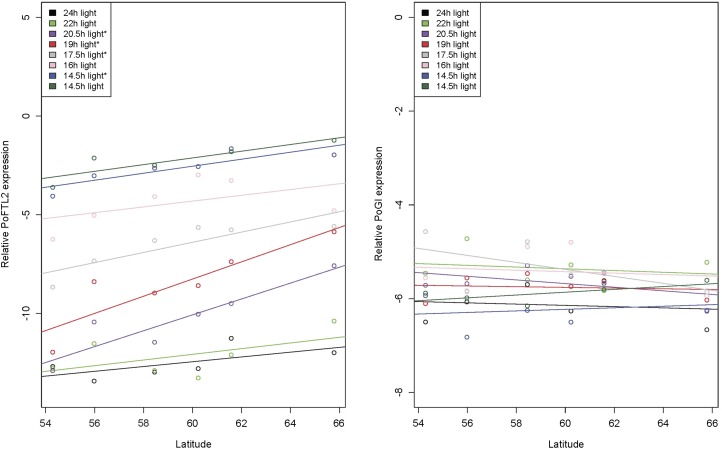
Two of the top candidate genes, PoFTL2 and PoGI, were tested for the presence of clinal variation in gene expression, by monitoring expression in the different populations over the course of the experiment. As night length extended, the expression level of PoFTL2 increased in all populations and was significantly correlated with latitude during several of the night-length periods. In contrast, the expression of PoGI stayed more or less stable over the whole experiment and there was no clear effect of population’s latitude (Figure 3).

Figure 3.

Expression patterns of PoFTL2 (left) and PoGI (right) during growth cessation in P. obovata seedlings originating from different latitudes. Seedlings were grown under increasing night length (see text for details). For each photoperiodic period the expression level was modeled as a function of population latitude. Photoperiodic periods during which there is a significant effect of latitude on expression level are highlighted with a star. For PoFTL2 there is, over all treatments and populations, a general increase in expression level as night length increases, whereas the expression of PoGI remains largely unaltered over both photoperiodic periods and populations.

Nucleotide diversity, neutrality tests, and LD

Summary statistics of the site-frequency spectrum were calculated for all 36 genes and are given in Table S2. The total number of SNPs was 357 and 356 and the average nucleotide diversity (π) was 0.002 and 0.003 for candidate and control loci, respectively. Tajima’s D was −0.5 for both control and candidate genes and one candidate gene (PoPRR3) and two control loci showed values significantly different from 0. Nucleotide diversity (π) was higher at synonymous sites than at nonsynonymous sites for all genes except PoGI and PoPRR3 where the opposite pattern was observed. The value of Fay and Wu’s H test was positive for loci PoCCA1 and PoGI but negative or close to zero for other loci.

Intragenic and intergenic linkage disequilibrium is fairly limited (median values of r² = 0.006 and 0.002, respectively) and r² decays <0.1 within 400 bp (Figure S5). Linkage disequilibrium decays at a similar pace between populations but gets steeper when data are pooled, which suggests the existence of population specific haplotypes. On average, candidate loci show slightly higher r² than control loci but the difference is not significant (median r² = 0.006 and 0.007, respectively; Wilcoxon test P-value >0.1). We assigned all control SNPs to 244 LD groups and all candidate SNPs to 163 LD groups, based on pairwise LD test (Bonferroni adjusted P-value ≤ 0.05 and r² ≥ 0.5). For both candidate and control SNPs only intragenic linked SNPs were considered due to the lack of intergenic linkage disequilibrium (Figure S6).

Population structure

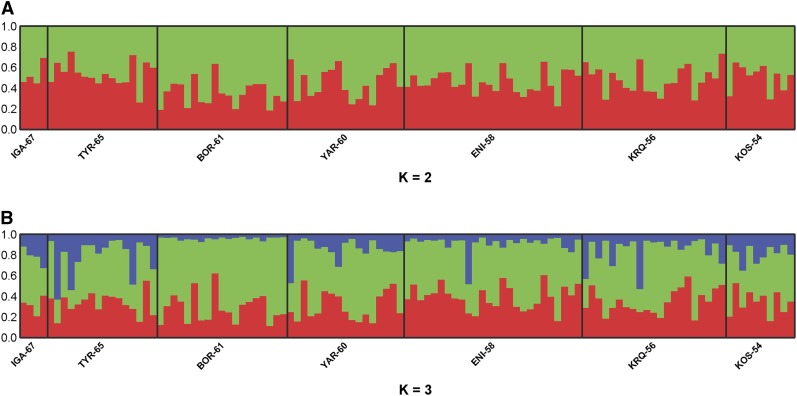
Using 14 SSR loci the overall F_ST value was 0.0152 and STRUCTURE failed to delineate any meaningful clusters: all individuals appear admixed, reflecting the lack of population genetic structure in the data set (Figure 4, A and B, and Figure S7). Isolation-by-distance was significant but weak (Figure S8). None of the SSR genetic diversity statistics showed any significant latitudinal geographic patterns (Table S3). No population structure could be detected when the 240 unlinked SNPs stemming from the 27 control genes were analyzed with STRUCTURE (Figure S9).

Figure 4.

Clustering analysis conducted in STRUCTURE using 14 SSR loci. For each data set, K = 1 to K = 7 were tested. K = 2 and K = 3 are shown to illustrate the lack of population genetic structure.

Demographic inference and posterior predictive simulations

Bayes factors and model probabilities for the different demographic models are given in Table S4. If a Bayes factor ≥3 is considered as an appropriate threshold (Kass and Raftery 1995) then a null model of constant effective population size (SNM) cannot be rejected. When tested against the BOT, the bottleneck model (BNM) and the exponential growth model (EXP) gave Bayes factors of 1.1394 and 0.6062, respectively. However, it should be noted that the Bayes factor for the BOT was a little >1 and that the model probability (0.4135) was also higher when compared simultaneously with the SNM (0.3647) and the EXP model (0.2218). To address this we estimated parameters under the BOT but found that the severity (x) and the time of the bottleneck (t) were poorly estimated so that only the SNM of constant effective population size was considered for the remainder of the analysis.

For the posterior predictive simulations, we first estimated the parameters of the SNM (Figure S10) to get a posterior distribution of 6000 points. We then sampled 10,000 times with replacement from the posterior distribution and calculated Tajima’s D and Fay and Wu’s H to obtain the posterior predictive distributions for each locus. The same statistics were then calculated using both nonsynonymous and synonymous sites from the observed data to test for departures from neutrality. Figure S11 shows the simulated and observed values of Tajima’s D. While most loci do not depart from the SNM, PoPRR3 shows a significant excess of rare variants when all sites are considered. For Fay and Wu’s H (Figure S12), PoMFTL1 shows an excess of high-frequency variants, while PoGI and PoPhyP exhibit positive values of H. To assess the significance of these deviations we rank transformed the data to normality and calculated P-values (Figure S13). After transformation, none of the loci deviate significantly from neutrality, although PoMFTL1, PoGI, and PoPhyP give the lowest P-values of 0.14, 0.07, and 0.11, respectively.

Clinal variation in allele frequencies

In the following sections, we assess the effect of latitude on the variance of allele frequency of individual SNPs by linear regression and using a recently developed Bayesian generalized linear mixed model that controls for population structure (Coop et al. 2010). We then used an F_ST outlier test to assess whether the clinal variation shown by these SNPs could be due to diversifying selection (Foll and Gaggiotti 2008; Foll et al. 2010; Fischer et al. 2011). We evaluated the enrichment of candidate outliers in the tails of empirical distribution to help reduce the false discovery rate (FDR).

Linear regression:

The adjusted coefficient of determination, R², was used to assess the variance in allele frequency explained by latitude. We built the empirical R² distribution based on the control SNPs and reported the numbers of outliers in both SNP categories, at 90, 95, 97.5, and 99% (see Table S5). We observed a slight enrichment of candidate SNPs at each of the tails examined, except 99%, by comparing to the total data set. However, none of the enrichment ratios was significant for Fisher’s exact test. Among all the empirical outliers, 15 candidate SNPs (7 LD groups) and 12 control SNPs (10 LD groups) had a linear regression slope of allele frequency change significantly different from zero (adjusted P-value ≤0.05).

Bayesian generalized linear mixed model:

We used the control loci to build a variance–covariance matrix that accounted for the effect of random genetic drift caused by population history and reevaluated the latitudinal variation using the method of Coop et al. (2010). Enrichment of candidate SNPs toward empirical tails was also observed and was statistically significant at 95%. A total of 71.4% of the candidate SNPs and 63.9% of the control SNPs that showed latitudinal variation in the linear regression tests were confirmed, which indicates that population structure is indeed weak and that our empirical approach does pick more selection signals in candidate SNPs than in control SNPs.

F_ST outliers:

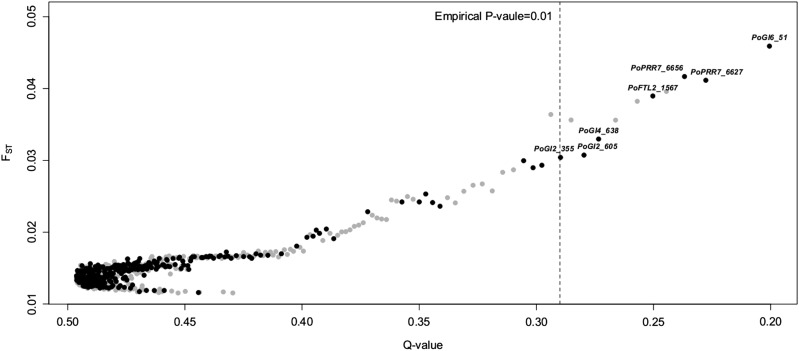
Locus-specific F_ST values estimated under Bayes model are heavily positively skewed with a median equal to 0.014. However, FDR-based outlier selection failed to detect any outliers (Figure 5). One possible reason could be that, compared to our study in Norway spruce (Chen et al. 2012a), the overall population differentiation is very weak and altogether not sufficient to be able to distinguish higher F_ST values. However, when outliers in the empirical tails >95% threshold were considered, a slight enrichment of candidate SNPs was observed with 14 (31.8%) candidate outliers and 8 (22%) control outliers. These 14 candidate SNPs are enriched with nonsynonymous changes (Fisher’s exact test, P-value= 1.05E − 2) with PoGI (P-value= 3.25E − 6) contributing 5 of 7 of them. Considering a prior odd equal to 10 did not alter the conclusion.

Figure 5.

Distribution of locus-specific F_ST values along with Q-values. Control SNPs are represented by shaded dots and candidate SNPs by solid dots. The dotted vertical line indicates the 1% empirical significant level based on control SNPs.

Summary of SNP variation analyses:

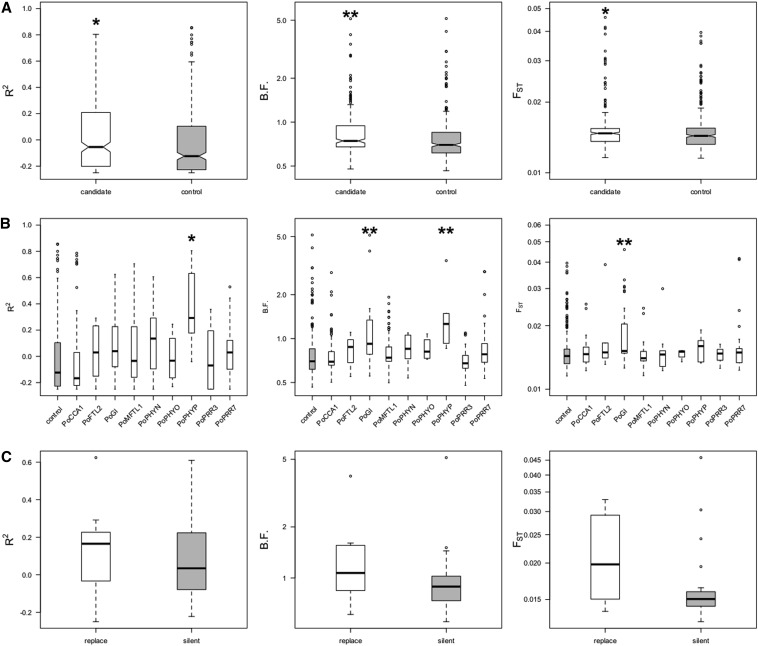
Information on putative outliers is summarized in Table 2 and additional information is given in File S1. The enrichment of candidate outliers under selection is quite clear when empirical tails are examined, especially when combining any of the approaches used (Table S5). To further remove the possible bias caused by linkage disequilibrium, we compared only the maximum values of the statistics used [R², Bayes Factor (B.F.), F_ST] in each LD groups (note that patterns are the same if the median, mean, or minimum values are used). Candidate SNPs exhibited significantly higher statistic values than controls (Wilcoxon test, P-value= 1.1E − 2, 1.56E − 4, 1.3E − 2 for R², B.F., and F_ST, respectively Figure 6A). Pairwise gene comparisons further revealed that genes PoPhyP and PoGI, especially the latter, contributed the majority of the statistical significance (Tukey honest significant difference, HSD, test, adjusted P-value <0.05, Figure 6B). The 12 nonsynonymous SNPs of PoGI had higher R², B.F. and F_ST values than the 3 synonymous and 17 noncoding SNPs (Figure 6C). If we assume that those nonsynonymous SNPs are potential targets of selection and the effect is distributed through linkage disequilibrium, pairwise comparison of these statistics further points at LD group PoGI_{F2_605} (containing 3 nonsynonymous SNPs and 2 noncoding SNPs) and PoGI_{F4_638} (containing 1 nonsynonymous SNPs and 1 noncoding SNPs, Figure S14) as both have significantly higher values than those of other LD groups (Tukey HSD adjusted P-value <0.05).

Table 2. SNPs that are significant at empirical threshold 5% with different analysis of allele frequencies in the six Yenisei populations.

Gene	SNPa	#SNP linked	Methodsb	Mutationc
PoCCA1	570	2	BEV, FST	Intron
	582	2	FST	Intron
	1016	2	LR, BEV	Intron
	2803	5	LR	Intron
	4113	1	LR, BEV	NS: Ser/Leu
PoFTL2	1567	1	FST	Promoter
PoGI	F2_605	5	BEV, FST	NS: His/Tyr (F4_138, F4_810)
	F4_134	1	BEV	NS: Gly/Arg
	F4_638	2	LR, BEV, FST	NS: Phe/Leu
	F6_8	1	BEV	Intron
	F6_39	1	BEV	Intron
	F6_76	1	FST	Intron
PoMFTL1	273	1	BEV, FST	Intron
	322	3	LR, BEV	Intron
	416	12	LR, BEV	Intron
	1487	1	BEV	Intron
	2888	1	FST	Intron
PoPHYN	583	1	FST	Intron
	2695	5	LR	SYN (2478)
PoPHYP	562	1	LR, BEV	SYN
	726	1	LR, BEV	NS: Leu/Pro
	802	1	BEV	SYN
PoPRR7	4758	1	BEV	Syn
	5687	1	BEV, FST	NS: Asn/Asp
	6627	1	BEV, FST	Intron
	6656	1	BEV, FST	Intron
	6717	1	LR, BEV	Intron

^aOnly the most significant outlier SNP in the LD group listed.

^bLR, linear regression empirical significance; F_ST, BayeScan empirical significance; BEV, Bayenv empirical significance;

^cMutation type of the SNP: NS, nonsynonymous; SYN, synonymous; positions of all nonsynonymous SNPs linked to are also indicated in the parentheses.

Figure 6.

Distribution of R², B.F., and F_ST (A) between candidate and control SNPs, (B) between nine candidate genes, and (C) between replacement and silent SNPs in gene PoGI. (*) P-value < 0.05; (**) P-value < 0.01.

Discussion

The results presented here, with results from a previous study in white spruce based on a similar experimental design (Prunier et al. 2012), demonstrate that the study of parallel clines can be a useful approach to detecting the parts of the genome involved in the control of clinal traits and to characterizing the selection acting on them. One of the core ideas of this approach is that different geographical regions of the same species, or different species, had different demographic histories and thereby constitute independent replicates of the evolutionary process. We therefore start by discussing this aspect of the study before addressing the consequences of the results for our understanding of the genetic control of growth cessation in spruce species.

Weak population structure over 12 degrees of latitude

Based on the fossil record, one of the premises of the study was that population structure of Siberian spruce would differ from the population structure of Norway spruce and would likely be weaker. It indeed turned out to be even weaker than we had expected, with no clustering among the populations and a rather weak pattern of isolation-by-distance along the river. This lack of population genetic structure is unlikely to solely reflect a lack of statistical power since population structure was detected when a more limited set of SNPs was used in Scandinavian populations of Norway spruce (Chen et al. 2012a). A plausible explanation of the pattern revealed by the STRUCTURE analysis is that what is captured by the six populations along the Yenisei river is a slice of a broader, more general longitudinal structure. This is supported by a large-scale investigation of population structure at 12 SSR loci in Norway and Siberian spruces that reveals large overlapping clusters, each of which has its center at a different longitude (Y. Tsuda, T. Källman, M. Lascoux, L. Parducci, D. Politov, V. Semerikov, J.H. Sønstebø, C. Sperisen, M.M. Tollefsrud, M. Väliranta, and G.G. Vendramin, unpublished results). The presence of scattered refugia along the river during the late glacial and possibly even the last glacial maximum (LGM) (Binney et al. 2009) might explain the weak isolation-by-distance observed along the river, which has generally been perceived as a major corridor for recolonization of higher latitudes. A similar lack of structure has also been observed in Larix sibirica and explained by rapid recolonization from scattered refugia within the Siberian plains during glacial periods and extensive gene flow thereafter (Semerikov et al. 2013). Independently of its exact causes there is, in any case, no doubt that the population genetic structure along the Yenisei latitudinal gradient differs markedly from the one in Norway spruce populations from Scandinavia. The lack of population structure observed in conifer species of central and western Siberia makes the area a very interesting one for association studies, as population structure is one possible source of false positives. Yet, in spite of this weak population structure, there is significant clinal variation in growth cessation.

Clinal variation in growth cessation

Three experiments were carried out: two of them in growth chambers, where growth cessation was induced by progressively increasing the night length, and one much larger, in a greenhouse, under more natural conditions. The cline in growth cessation was concordant across the two types of experiment indicating that the artificial shortening of the growth season in the first type of experiment did not affect the overall pattern of bud set. Interestingly, the slope of the cline was rather weak up to 62°N and much steeper thereafter. Since the same pattern has been observed for growth cessation in Norway spruce and in Scots pine seedlings grown under the same greenhouse conditions (T. Huotari, K. Käkkäinen, M. Lascoux, T. Källman, and O. Savolainen, unpublished results) this abrupt change probably reflects adaptation to a concomitant shift of environmental conditions as one approaches the tree line. As a matter of fact, the northernmost populations collected along the Yenisei river at 66°N and 67°N grew on much poorer soil and had a significantly smaller dominant height than populations below latitudes 62°N. It could also reflect differences in the perception of light: Norway spruce populations from latitudes between 49°N and 64°N exhibited a clear latitudinal cline in their requirement of far-red light to prevent growth cessation and bud set, with a clear increase north of latitude 61°N (Clapham et al. 1998). It would be interesting in future studies to sample more densely between 62°N and 67°N and to characterize more finely the environmental conditions.

Targets of selection: the key role of FT and GI in plants

The weak population structure confers more weight to the fact that using the same set of analyses as in Norway spruce, albeit in a slightly different way, we retrieved evidence of clinal variation or local selection at some of the nine candidate loci. In one case, selection was even detected at the same SNP as in Norway spruce. Hence, the present study lends further support to the involvement of genes from the photoperiodic pathway and the circadian clock in local adaptation of forest trees (Holliday et al. 2010; Hall et al. 2011; Rohde et al. 2011; Keller et al. 2012; Chen et al. 2012a). As in Chen et al. (2012a,b), three genes seem particularly interesting: PoFTL2, PoPRR3, and PoGI. All three include SNPs with high F_ST values and high heterozygosity. The strongest evidence of selection in PoFTL2 is found in the promoter, suggesting that adaptation occurs through changes in expression level. Indeed, assessment of clinal variation in expression in the present study confirms this. Like in Norway spruce, PoFTL2 expression levels increased with latitude (Chen et al. 2012a). These results, together with recent work by Karlgren et al. (2013) showing that overexpression of FTL2 in Norway spruce led to early growth cessation, demonstrate the central role played by FT genes in the control of phenology in plants.

While the combination of expression data and allele frequency pattern at FTL2 makes for a very convincing case, Gigantea probably offers the most intriguing case. Gigantea seems to be highly pleiotropic and associated with fitness-related traits in both Arabidopsis thaliana (Brock et al. 2007) and forest trees (Rohde et al. 2011; Keller et al. 2012). In spruce species, which generally have a high level of shared polymorphisms but a low number of fixed sites, GI displays almost the opposite pattern (Chen et al. 2010). The structure of its polymorphism pattern is also remarkable: in this study, the ratio of π_NS over π_S is 11.6 while it is <1 in all other genes but PoPRR3. If we compare with Norway spruce, this high ratio is due to the dearth of synonymous mutations, estimates of the nonsynonymous nucleotide diversity being almost equal in the two species. This pattern is consistent with recurrent selective sweeps occurring in PoGI and was already observed in genes from the photoperiodic pathway in Populus tremula (Hall et al. 2011). The pattern of polymorphism observed in GI in P. balsamifera by Keller et al. (2012) was also suggestive of recurrent episodes of selection, although perhaps not of selective sweeps. Despite these specific features it has been difficult to detect significant departures from neutrality at PoGI because of its overall low polymorphism. It might well be too that the evidence of local selection found in the present study and in Norway spruce reflects only recent local selection related to life at high latitudes.

The nonsynonymous change corresponding to PoGI_{F2_605} is found in both Scandinavia and along the Yenisei River but is absent in the Alpine domain of Norway spruce and in other spruce species that have been investigated so far (Chen et al. 2012a). Genomic regions that share the same patterns of sequence variation in ecologically similar but geographically separated regions are characteristic of parallel evolution (Hoekstra 2012). The shared polymorphism can be ancestral, i.e., was already present in the ancestor of the two species, can be due to migration since the split of the two populations, or can result from the same mutation occurring in both species (homoplasy). Shared polymorphisms are common among spruce species (Chen et al. 2010). In the nine candidate genes sequenced in both P. obovata and P. abies we found a total of 508 and 368 polymorphic sites in P. abies and P. obovata, respectively, and 133 were shared between the two species. The proportion of shared polymorphic sites per gene varies from 0.07 to 0.54 with an average value equal to 0.26. For the three GI fragments the average proportion is 0.15. So, shared polymorphism is certainly a possibility. However, if true then one needs to explain the lack of polymorphism in the Alpine part of the range at PoGI_{F2_605}. The survey of SSR diversity across the range of the two species referred to above indicates that the Alpine and Baltico-Nordic parts of the Norway spruce range separated after the Baltico-Nordic part of the Norway spruce range and Siberian spruce did. Hence in that case the mutation was apparently lost in the Alpine domain. The same data also suggest that the mutation is unlikely to be the result of recent gene exchange between the Yenisei populations and Norway spruce as the Yenisei area is clearly outside of the hybrid zone between the two species (see Figure S1). A more ancient introgression after the two species separated is, however, possible. We cannot rule out homoplasy but, given the low mutation rate in conifers (Chen et al. 2012a,b) and the time scale considered here, this seems unlikely. So, in summary, PoGI_{F2_605} seems to have been segregating in the ancestor species of Norway and Siberian spruce or to have been introgressed after the two species separated but, in any case, before the LGM. The mutation was then lost in the Alpine part of the range and driven to high frequency by selection at higher latitudes during the development of the clines after the LGM.

The PoGI_{F2_605} substitution causes an amino acid change from His78 to Tyr78. It is hard to evaluate the putative functional effect of PoGI_{F2_605} and other nonsynonymous changes in PoGI since, due to its very large size, the protein structure of Gigantea remains poorly characterized (Black et al. 2011). It is known, however, that in Arabidopsis GI interacts with several repressors of FT, as well as with FT itself (Kim et al. 2007; Sawa et al. 2007; Sawa and Kay 2011). Because we have repeatedly found clines and signature of selection in both FTL2 and GI in spruce it would be highly interesting to test whether a direct interaction between GI and FTL2 exists in spruce. In A. thaliana the interaction with the flowering repressor ZTL is mediated through the N-terminal half of GI (probably the first 394 amino acids; Black et al. 2011) although the exact location of the receptor is not known. We also note that the amino acids of this region are highly conserved among orthologous sequences from 17 plant genus. Analysis based on 3D-structure predictions using (PS)²-v2 (Chen et al. 2009) and Swiss-PdbViewer (Guex and Peitsch 1997) shows a small decrease in distance of H-bonds from His78 to Phe74 and to Glu80 when changed to Tyr78 (2.88–2.65 and 3.13–2.92 Å, respectively).

High F_ST and QTL

Recent theoretical as well as empirical work (Le Corre and Kremer 2012; Berg and Coop 2013) indicates that local adaptation in quantitative traits is expected to be primarily the consequence of a coordinated shift in allele frequency across many loci rather than significant allele frequency changes at individual loci. If the loci underlying the trait are numerous, the shift in allele frequency at individual loci will be modest. Growth cessation bears all the hallmarks of a quantitative trait, yet, in the present study, as well as in Chen et al. (2012a), we did detect SNPs in candidate genes for bud set with a significantly higher F_ST than control ones. At least in the case of FTL2 there is now solid evidence that polymorphism at this gene is truly associated with variation in the timing of growth cessation. This could indicate that genes such as FTL2 or GI have a larger effect on growth cessation than would be expected if the control of growth cessation variation was strictly following the infinitesimal model. It could also simply indicate that traits that are under strong local adaptation, such as clinal traits, do not have the same genetic architecture as traits that are under weaker local adaptation. As a matter of fact, local adaptation could lead, under certain levels of gene flow and mutation, to more or less compact genetic architecture (Yeaman and Whitlock 2011; Yeaman 2013). At this stage we can make conjectures only but it would certainly be interesting to test whether genes that play a crucial role in the control of a given trait or occupy a specific place within the regulatory network controlling the trait are more prone to show high levels of differentiation than other genes in the network of genes controlling the trait. Up to now it has been difficult to make solid predictions on the association between the position of a gene within a regulatory network controlling a trait and the intensity and type of selection acting on it (Olson-Manning et al. 2012) but the increasing amount of information on gene regulatory networks may help.

Conclusion

This study is a first step toward a more systematic use of parallel cline studies for understanding local adaptation in forest trees. Our study indicates that the same genes, and possibly the same mutations, could underly patterns of local adaptation for growth cessation in Norway spruce and Siberian spruce. They thereby belong to a series of recent studies highlighting the ubiquity of parallel or convergent adaptation (Ralph and Coop 2010; Hoekstra 2012; Jones et al. 2012). Apart from confirming the functional implication of the mutation in the variation of growth cessation it would also be very interesting, especially with the results of Ralph and Coop (2010) in mind, to extend them spatially by adding other latitudinal clines in both species. This should allow us to eventually link local adaptation to the demographic history of the two species and better understand the interaction of natural selection and demographic history.