Quantifying Extrinsic Noise in Gene Expression Using the Maximum Entropy Framework

Abstract

We present a maximum entropy framework to separate intrinsic and extrinsic contributions to noisy gene expression solely from the profile of expression. We express the experimentally accessible probability distribution of the copy number of the gene product (mRNA or protein) by accounting for possible variations in extrinsic factors. The distribution of extrinsic factors is estimated using the maximum entropy principle. Our results show that extrinsic factors qualitatively and quantitatively affect the probability distribution of the gene product. We work out, in detail, the transcription of mRNA from a constitutively expressed promoter in Escherichia coli. We suggest that the variation in extrinsic factors may account for the observed wider-than-Poisson distribution of mRNA copy numbers. We successfully test our framework on a numerical simulation of a simple gene expression scheme that accounts for the variation in extrinsic factors. We also make falsifiable predictions, some of which are tested on previous experiments in E. coli whereas others need verification. Application of the presented framework to more complex situations is also discussed.

Introduction

Recent experiments show that the life cycle of a gene product inside the cell is stochastic. For any gene, there exists great cell-to-cell variation in the expression level of both the protein and the mRNA (1–10) and changing this variation has phenotypical and fitness effects (11–14). Recently, it was also shown that coregulated proteins have correlated variability (15). This variation arises from

• 1.The intrinsic statistical mechanical fluctuations in diffusion and binding of the molecules involved in gene expression; and
• 2.The variation in extrinsic factors that determine the state of the cell. Examples of extrinsic factors include the external environment (16,17), the epigenetic state of the cell (18,19), the time from last cell division, and levels of molecular machines such as RNA polymerase, ribosome, proteases, and RNases (3,4,20).

In a given population of cells, the total noise (coefficient of variation)

$${\eta }_{\text{T}}=\frac{\langle m^2\rangle -{\langle m\rangle }^2}{{\langle m\rangle }^2}$$ (1)

serves as a useful experimental quantification of the variability in gene expression where 〈m〉 is the mean level of the gene product m (mRNA or protein) and 〈m²〉–〈m〉² is the variance.

For a constitutively expressing promoter, under simplifying conditions, the contribution to η_T associated with extrinsic factors, the extrinsic noise η_E, can be experimentally measured separately from the intrinsic noise η_I (3,6,15,20). The decomposition experiment usually involves expression of two identical copies of a single gene inside cells. Variation in local effects, e.g., binding and unbinding of transcription factors, affects the expression of the two genes in an uncorrelated manner. On the other hand, variation in global factors such as RNAP/ribosome/RNase levels affects them in a correlated manner. After comparing the statistics of the joint-expression system with that of a single gene expression system, the correlation between the two genes is identified as the extrinsic noise. It is now known that the extrinsic noise is the dominant contributor to gene expression (3,15) and can change the profile of gene expression in a nontrivial manner (21). Evidently, an important step toward the conceptual understanding of the noisy gene expression is to quantitatively account for the effect of variations in extrinsic factors on gene expression.

The major technical hurdle in building a comprehensive theory for extrinsic variation originates in the multitude of factors that contribute to it. Consequently, theoretical exploration of noisy gene expression has concentrated on intrinsic noise. Here, one generally employs the master equation framework (9,10,22–24). Briefly, we define a set of reactions $\mathcal{R}$ involving species $\mathcal{G}$ (protein, mRNA, etc.). A transition matrix for evolution of the probability distribution of $\mathcal{G}$ is constructed. The transition matrix contains information about the chemistry (rates, allosteric binding, etc.) and the topology (feedback, loops, etc.) of the reactions. The probability distribution P($\mathcal{G}$|t,$\mathcal{K}$) is then sought in terms of the rate constants $\mathcal{K}$ = {k₁,k₂,…} of all reactions and time t. Because closed form solutions for the master equation exist only for a few simple systems, much theoretical development explores efficient ways of simplifying the solution of the master equation (10,23,25).

The chemical reactions are carried out by molecular machines such as RNA polymerase, ribosomes, and enzymes, among others. Moreover, these chemical reactions also depend on the chemical state of the cell, such as, for example, the time from cell division, the chromatin structure of DNA, the presence of DNA binding proteins, RNA degradation by small RNAs, and the presence of RNA binding proteins. All these variables differ from cell to cell and as a function of time. Hence, the rate constants $\mathcal{K}$ depend on the state of the cell and are themselves stochastic variables. This makes gene expression a doubly stochastic process (26,27). In the theoretical analysis, we interpret the variability in $\mathcal{K}$—which represents the variability in global factors—as the extrinsic variability. The theoretical decomposition will faithfully represent the experimentally quantified one if:

• 1.The underlying model of intrinsic noise is an accurate description of gene expression; and
• 2.If the effect of within-cell variation in the parameters on gene expression is negligible at timescales relevant for gene expression.

Due to the very large number of affectors, it is impossible to model the extrinsic variability from first principles. Consequently, the theoretical treatment has either assumed a small extrinsic contribution resulting in a linear susceptibility-like analysis (20) or assumed an ad hoc structure for the distribution of extrinsic factors (21,28). Here, instead of accounting for all the extrinsic contributors ab initio, we develop a maximum entropy framework to estimate $P$($\mathcal{K}$), from limited information about the gene expression profile. We successfully test our results on a simplified numerical scheme for mRNA production that explicitly incorporates the variability in molecular machinery. Most importantly, we show that extrinsic factors can qualitatively and quantitatively affect the experimentally observed histogram of the gene expression product (protein or mRNA).

Theory

For concreteness, consider a constitutively expressing promoter in a bacterial setting (see Fig. 1). Later, we will substantially simplify this example. Here, an inactive gene is converted to an active gene with rate constant k₁ and vice versa (rate constant k₋₁). An mRNA molecule is transcribed from the active gene at a rate constant k₂. A protein is translated from the mRNA at a rate k₄. The mRNA and the protein are degraded at rates k₃ and k₅, respectively. The number of activated genes g, the number of mRNA molecules m, and the number of protein molecules p represent $\mathcal{G}$. The time from last division is itself a stochastic variable for a heterogeneous population (29) and can be included as a parameter with the reaction rate constants. We assume that the conditional distribution $P$($\mathcal{G}$|$\mathcal{K}$) is known. Here, $\mathcal{G}$ = {g,m,p} and $\mathcal{K}$ = {k₁,k₋₁,k₂,k₃,k₄,k₅}.

Figure 1.

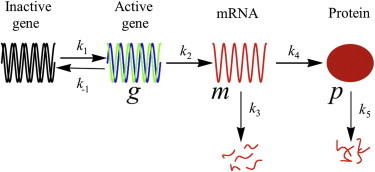
The most general case of a constitutively expressing promoter. An inactive gene (black) is turned into an active gene (and vice versa). The active gene (blue and green) is transcribed into an mRNA (red), which is then translated to a protein (red ellipse). The mRNA and the protein are also degraded. Various rate constants $\mathcal{K}$ govern the time evolution of P(g,m,p|$\mathcal{K}$), the joint probability distribution of g (number of activated genes), results for m (number of mRNA molecules), and the parameterization of p (number of protein molecules).

The maximum entropy framework

We now estimate the distribution of $\mathcal{K}$ using the maximum entropy (ME) framework (30). A brief introduction to ME can be found in the Supporting Material. Note that each point in the multidimensional $\mathcal{K}$-space represents a probability distribution in the $\mathcal{G}$-space. Consequently, the distribution whose entropy should be maximized is not $P$($\mathcal{K}$) but the joint distribution $P$($\mathcal{G}$,$\mathcal{K}$) of species and rates (26,31).

The entropy S[P($\mathcal{G}$,$\mathcal{K}$)] of the joint distribution $P$($\mathcal{G}$,$\mathcal{K}$) is given by

$$S\left[P\left(\mathcal{G},\mathcal{K}\right)\right]=-\sum _{\mathcal{G},\mathcal{K}}P\left(\mathcal{G},\mathcal{K}\right)\log P\left(\mathcal{G},\mathcal{K}\right)$$ (2)

$$=S\left[P\left(\mathcal{K}\right)\right]+\sum _{\mathcal{K}}S\left(\mathcal{G}|\mathcal{K}\right)P\left(\mathcal{K}\right).$$ (3)

Here,

$$P\left(\mathcal{K}\right)=\sum _{\mathcal{G}}P\left(\mathcal{G},\mathcal{K}\right),$$ (4)

$$S\left[P\left(\mathcal{K}\right)\right]=-\sum _{\mathcal{K}}P\left(\mathcal{K}\right)\log P\left(\mathcal{K}\right),$$ (5)

and

$$S\left(\mathcal{G}|\mathcal{K}\right)=-\sum _{\mathcal{G}}P\left(\mathcal{G}|\mathcal{K}\right)\log P\left(\mathcal{G}|\mathcal{K}\right)$$ (6)

is the entropy of the conditional distribution $P$($\mathcal{G}$|$\mathcal{K}$).

If we constrain the mean values of the rate constants 〈k₁〉, 〈k₂〉,…, the ME framework predicts that the joint distribution maximizes the entropy S[P($\mathcal{G}$,$\mathcal{K}$)] subject to the constraints. To find the distribution, we introduce Lagrange multipliers α_1, α₂,… corresponding to rate constants k_1, k₂,… and γ for normalization. The modified objective function is

$$S\left[P\left(\mathcal{G},\mathcal{K}\right)\right]-\sum _j{\alpha }_j\left(\sum _{\mathcal{G},\mathcal{K}}P\left(\mathcal{G},\mathcal{K}\right)k_j-\langle k_j\rangle \right)+\gamma \left(\sum _{\mathcal{G},\mathcal{K}}P\left(\mathcal{G},\mathcal{K}\right)-1\right)$$ (7)

$$=S\left[P\left(\mathcal{K}\right)\right]+\sum _{\mathcal{K}}S\left(\mathcal{G}|\mathcal{K}\right)P\left(\mathcal{K}\right)-\sum _j{\alpha }_j\left(\sum _{\mathcal{K}}P\left(\mathcal{K}\right)k_j-\langle k_j\rangle \right)+\gamma \left(\sum _{\mathcal{K}}P\left(\mathcal{K}\right)-1\right).$$ (8)

Note that the mean values of the rate constants are not directly observable from experiments. Employing them as constraints is a departure from the canonical understanding of the ME framework wherein probability distributions are predicted from moments calculated from experimental data. Yet, the ME framework can also be seen as an inference tool (26,31,32): ME predicts the logically consistent probability distribution if mean values of certain important parameters of an experiment are fixed.

Because we know the functional form of $P$($\mathcal{G}$|$\mathcal{K}$), in Eq. 8 we have summed over all possible values of $\mathcal{G}$ at a given value of $\mathcal{K}$. Setting the derivative of Eq. 8 with respect to $P$($\mathcal{K}$) equal to zero and solving, we get

$$P\left(\mathcal{K}\right)\propto \text{exp}\left(S\left(\mathcal{G}|\mathcal{K}\right)-\sum _j{\alpha }_j{k}_j\right).$$ (9)

Equation 9 is the maximum entropy estimate of the distribution of $\mathcal{K}$ if we constrain only the mean values of the rate constants. Note that in addition to the usual exponentials (see the Supporting Material), the distribution also depends on the entropy $\mathcal{S}$($\mathcal{G}$|$\mathcal{K}$) of the conditional distribution $P$($\mathcal{G}$|$\mathcal{K}$).

Estimating $P$($\mathcal{K}$) in an N-reporter experiment

Experimental advances allow us to construct more than one identical reporter for a gene inside a single cell (3,15). Mathematically, instead of generating samples of $\mathcal{G}$ from the distribution $P$($\mathcal{G}$|$\mathcal{K}$) for a fixed value of $\mathcal{K}$, we can conceive an experiment where we can sample N identical experiments of the same species $\mathcal{G}$ from the joint distribution P($\mathcal{G}$₁,$\mathcal{G}$₂,…,$\mathcal{G}$_N|$\mathcal{K}$) at a fixed value of $\mathcal{K}$. Note that the variability in the extrinsic factors respecting the distribution $P$($\mathcal{K}$) bears no relation to the number of reporters employed in a particular experiment. Consequently, we require the ME framework-predicted $P$($\mathcal{K}$) to be independent of N (31).

If we assume that the N experiments are sampled independently of each other—this is a crucial assumption in N-reporter experiments (3,15)—we can write

$$P\left({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_N|\mathcal{K}\right)=\prod _{n=1}^{N}P\left({\mathcal{G}}_n|\mathcal{K}\right).$$ (10)

Similar to the considerations above, to estimate $P$($\mathcal{K}$) from this N-reporter experiment, we maximize the entropy of the joint distribution P($\mathcal{G}$₁,$\mathcal{G}$₂,…,$\mathcal{G}$_N,$\mathcal{K}$) constraining the mean values of the rate constants 〈k₁〉,〈k₂〉,…. The entropy of the joint distribution can be simplified using the independence in Eq. 10 as

$$S\left[P\left({\mathcal{G}}_1,{\mathcal{G}}_2,\dots ,{\mathcal{G}}_N,\mathcal{K}\right)\right]=S\left[P\left(\mathcal{K}\right)\right]+N\sum _{\mathcal{K}}S\left(\mathcal{G}|\mathcal{K}\right)P\left(\mathcal{K}\right).$$ (11)

The modified objective function is given by (see Eq. 8)

$$S\left[P\left(\mathcal{K}\right)\right]+N\sum _{\mathcal{K}}S\left(\mathcal{G}|\mathcal{K}\right)P\left(\mathcal{K}\right)-\sum _j{\alpha }_j\left(\sum _{\mathcal{K}}P\left(\mathcal{K}\right)k_j-\langle k_j\rangle \right)+\gamma \left(\sum _{\mathcal{K}}P\left(\mathcal{K}\right)-1\right).$$ (12)

Consequently, the ME framework estimates the distribution $P$($\mathcal{K}$) as

$$P\left(\mathcal{K}\right)\propto \text{exp}\left(NS\left(\mathcal{G}|\mathcal{K}\right)-\sum _j{\alpha }_j{k}_j\right).$$ (13)

Interestingly, the estimate of the variability $P$($\mathcal{K}$) depends on the number of reporters (see Eq. 9 and Eq. 13) used in the experiment. This problem will be alleviated if we introduce the average entropy of a given experiment 〈S($\mathcal{G}$|$\mathcal{K}$)〉 as an additional constraint. This additional constraint is not an experimentally observable constraint but merely a requirement of consistency in the prediction over multiple experiments (26,31,33). Introducing the additional constraint 〈S($\mathcal{G}$|$\mathcal{K}$)〉 in the objective function by introducing a Lagrange multiplier μ_N, we write the modified objective function as

$$S\left[P\left(\mathcal{K}\right)\right]+N\sum _{\mathcal{K}}S\left(\mathcal{G}|\mathcal{K}\right)P\left(\mathcal{K}\right)-\sum _j{\alpha }_j\left(\sum _{\mathcal{K}}P\left(\mathcal{K}\right)k_j-\langle k_j\rangle \right)+\gamma \left(\sum _{\mathcal{K}}P\left(\mathcal{K}\right)-1\right)+{\mu }_N\left(\sum _{\mathcal{K}}S\left(\mathcal{G}|\mathcal{K}\right)P\left(\mathcal{K}\right)-\langle S\left(\mathcal{G}|\mathcal{K}\right)\rangle \right).$$ (14)

Writing N + μ_N = μ and maximizing with respect to $P$($\mathcal{K}$), we get

$$P\left(\mathcal{K}\right)\propto \text{exp}\left(\mu S\left(\mathcal{G}|\mathcal{K}\right)-\sum _j{\alpha }_j{k}_j\right).$$ (15)

Equation 15 is the main theoretical result of this work. Briefly, if we know that the rate constants $\mathcal{K}$ vary from cell to cell and as a function of time, and if, rather than precisely knowing them, we constrain only their mean values, the ME framework predicts the distribution $P$($\mathcal{K}$) as Eq. 15. Note that in addition to the usual exponentials, the distribution also depends on the conditional entropy S($\mathcal{G}$|$\mathcal{K}$). Similar results have been obtained for thermodynamic systems (26,33) and in estimating prior distributions in Bayesian inference (31).

Experimentally observed distribution of chemical species

The experimentally observable distribution $P$($\mathcal{G}$) is obtained by summing over all possible variations in $\mathcal{K}$. We get

$$P\left(\mathcal{G};\mu ,{\alpha }_1,{\alpha }_2,\dots \right)\propto \sum _{\mathcal{K}}P\left(\mathcal{G}|\mathcal{K}\right)·\text{exp}\left(\mu S\left(\mathcal{G}|\mathcal{K}\right)-\sum _j{\alpha }_j{k}_j\right).$$ (16)

Note that the distribution in Eq. 16 is parameterized by μ and α_1, α₂,…. Each α_i corresponds to one rate constant k_i whereas μ governs the extrinsic variability. In short, the ME framework predicts extrinsic variability only with one additional parameter μ. Note that Eq. 16 provides a functional form for the $P$($\mathcal{G}$) distribution. The parameters μ and {α_i} can be fit to suitable experimental measurements such as the moments of the distribution. Below, we will work out in detail the noise in the production of mRNA molecules from a constitutive promoter.

The distribution of mRNA copy numbers

Consider the simplified reaction scheme

$$\text{DNA}\stackrel{\gamma }{\to }\text{mRNA}\stackrel{\delta }{\to }\varphi$$ (17)

of transcription and degradation of mRNA molecules of a particular gene. The value γ is the rate of transcription and δ is the rate of degradation.

In Eq. 17, we have neglected the activation states of the DNA molecule e.g., promoter fluctuations (4,5,10). Promoter fluctuations are thought to occur from (among other things) chromatin remodeling and binding and unbinding of transcription factors (11,18,19). The chromosome of the DNA of a bacteria like E. coli is structured in ∼100–500 nucleoids (34). It is very likely that the chromatin structure extends locally to 10–50 genes around the gene studied and affects the transcription of all genes in a local region. Consequently, in a hypothetical dual-reporter experiment to study noise in mRNA production similar to Elowitz et al. (3), promoter fluctuations due to chromatin remodeling are likely to affect the expression of all genes localized in a given region on the DNA in a correlated fashion and will contribute to the extrinsic noise. On the other hand, promoter fluctuations arising due to noisy binding of transcription factors will act in an uncorrelated fashion in a hypothetical dual-reporter experiment. The contribution to mRNA noise due to noisy transcription factor binding will contribute to the intrinsic noise. Noisy transcription factor binding will result in a nonPoissonian process of mRNA production and will result in mRNA distributions that are wider than the Poisson statistics (18,19). In what follows, we neglect the contribution of noisy transcription factor binding to promoter fluctuations and effectively treat them as one of the local albeit extrinsic contributor to the variation in the effective rate of synthesis for the given gene. Below, we briefly discuss how to further parse the variability in the effective rate of synthesis into a contribution from promoter fluctuations and a contribution from other global extrinsic factors.

The solution of the reaction scheme at any time t and at steady state is a Poisson distribution

$$P\left(m|k\right)=\frac{e^{-k}{k}^m}{m!}$$ (18)

of mRNA copy number m with effective synthesis rate k = γ/δ(1−e^−δt) (24).

The effective synthesis rate k depends, in a complicated manner, on various factors including chromatin remodeling (11,18,19), the states of many molecules in the cell including the components of RNA polymerase, the dynamics of assembly of the RNA polymerase holoenzyme, various RNase molecules, and other competing genes (3,20). Consequently, it varies from cell to cell and as a function of time from the start of the cell cycle. Thus, while studying gene expression in a population, instead of fixing a particular value of the effective synthesis rate k, we need to consider P(k) the probability distribution of k. P(k) quantifies the extrinsic contribution noisy gene expression.

For a given gene, experimentally assessing the variability in k is nontrivial—P(k) has to be inferred from limited experimental information in respect to mean expression level, variation in gene expression level, etc. From Eq. 15, we see that the distribution P(k) is given by

$$P\left(k\right)\propto \text{exp}\left[\left(\mu \alpha -1\right)S\left(k\right)-\alpha k\right].$$ (19)

Here, S(k) is the entropy of the conditional distribution P(m|k), a Poisson distribution. Unfortunately, S(k) does not have a closed form but S(k) ∼ log k. Thus,

$$P\left(k;\mu ,\alpha \right)\propto k^{\mu \alpha -1}{e}^{-\alpha k}.$$ (20)

In Eq. 20, μ is the mean expression level and α = η₁/η_E is the ratio of the intrinsic and the extrinsic noise. The joint distribution P(m,k) is then given by

$$P\left(m,k\right)=P\left(m|k\right)P\left(k\right)\propto \frac{e^{-\alpha k}{k}^{m+\mu \alpha -1}}{m!}.$$ (21)

The experimentally accessible histogram P(m) is obtained by summing over all variations in k, i.e., summing over the variation in extrinsic factors,

$$P\left(m\right)=\sum _{k}P\left(m,k\right)\propto \sum _k\frac{e^{-\alpha k}{k}^{m+\mu \alpha -1}}{m!}.$$ (22)

We estimate P(m) to be the negative binomial distribution (the discrete version of the γ-distribution),

$$P\left(m\right)\propto \frac{1}{{\left(1+\alpha \right)}^m}\times \frac{\text{Γ}\left[m+\alpha \mu \right]}{m!}.$$ (23)

Noise decomposition of experimental data

We estimate the total noise η_T from Eq. 23 (see the Supporting Material for details) as

$${\eta }_{\text{T}}=\frac{1}{\mu }\left(1+\frac{1}{\alpha }\right)=\frac{1}{\mu }\left(1+\frac{{\eta }_{\text{E}}}{{\eta }_{\text{I}}}\right)\ge \frac{1}{\mu }$$

and

$$\begin{array}{l}{\eta }_{\text{I}}=\frac{1}{\mu },\\ {\eta }_{\text{E}}={\eta }_{\text{T}}-\frac{1}{\mu }.\end{array}$$ (24)

The greater-than-Poisson relationship between η_T and the mean mRNA copy number μ (see Eq. 24) is sometimes attributed to nonPoissonian dynamics such as promoter fluctuations, chromatin remodeling, and mRNA synthesis bursts, among other causes (4,5,7,10,18,19). These effects themselves are thought to arise from cell-to-cell and dynamic variability in chromatin state and the state of DNA binding molecules (11,18,19). Additionally, we suggest that the cell-to-cell variation in other extrinsic factors (3,20) also contributes to the greater-than-Poisson relationship.

The ME framework predicts that Eqs. 23 and 24 completely determine the histogram of mRNA copy numbers from experimentally measured mean expression level μ and total noise η_T. Moreover, η_T is always >1 and η_I and η_E can be estimated from the histogram alone. Importantly, the framework estimates the hitherto elusive effect of extrinsic factors on gene expression regarding the distribution P(k) of the effective synthesis rate k.

The joint distribution Eq. 21 also allows us to estimate potentially interesting moments; for example, we predict that the Pearson correlation coefficient

$${\rho }_{mk}=\frac{1}{\sqrt{1+\alpha }}=\sqrt{\frac{{\eta }_{\text{E}}}{{\eta }_{\text{T}}}}$$ (25)

between effective mRNA synthesis rate and the mRNA copy number is the square-root of the ratio of extrinsic and total noise. These are some of the falsifiable predictions of the development presented here.

Results and Discussion

Numerical validation of the ME-predicted distribution

We analyze a simple numerical scheme for the synthesis of rGene, the mRNA of a constitutively expressed gene. In the scheme, the variability in the effective synthesis rate k arises from the stochasticity in the production and degradation of the machinery (RNAP and RNase). We show that the ME-predicted distribution (Eq. 23) describes very accurately the numerically predicted distribution of mRNA copy number for different strengths of extrinsic noise (see Fig. 2 for a cartoon and the Supporting Material for details).

Figure 2.

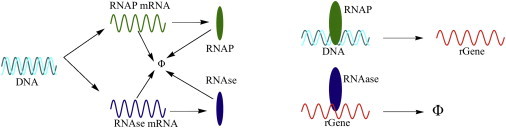
A cartoon of the simplified scheme of mRNA production that takes into account extrinsic factors in gene expression levels (see the Supporting Material for details). In the scheme, RNAP serves as the proxy for the RNA polymerase holoenzyme complex and RNase is the proxy for RNA degradation machinery. The rate of synthesis of rGene, the RNA of a given gene, is directly proportional to the concentration [RNAP] of the protein product of the RNAP gene. Similarly, the rate of degradation of rGene is directly proportional to the concentration [RNase], the protein product of RNase gene. RNAP and RNase themselves are synthesized and degraded stochastically.

Let [X] denote the concentration of species X. In the model, the rate of synthesis γ = γ₀[RNAP] and the rate of degradation δ = δ₀[RNAse] of rGene, the mRNA of the gene under consideration, both depend on the concentration of the cellular proteins that carry out those reactions for [RNAP] (a proxy for the RNA polymerase complex) and [RNase] (a proxy for RNase), respectively. Both the proteins are themselves are stochastically synthesized and degraded. The variation in the proxies mimics the cell-to-cell variations in extrinsic factors. The effective synthesis rate k is directly proportional to the ratio [RNAP]/[RNase]. We implement the Gillespie algorithm (35) to estimate the steady-state distribution of [rGene], the mRNA copy number. The correlated dynamics of production of rGene, RNAP, and RNase play an important part in determining the dynamics of the variability in [rGene]. The steady-state joint distribution [RNAP] and [RNase] completely determines the steady-state distribution of [rGene] if the dynamics of synthesis and degradation of RNAP and RNase are not too fast compared to that of rGene. The parameters chosen for the simulation make sure that the timescale of synthesis and degradation of RNAP and RNase is of the same order as that of rGene. We only sample the distribution of mRNA copy numbers at long times ensuring that the steady state has been reached (see the Supporting Material for details). To clearly elucidate the effect of extrinsic factors on gene expression profile, in Fig. 3, we show the histogram of mRNA copy numbers for three different levels of noise, quantified by

$${\eta }_k\equiv \frac{\langle k^2\rangle -{\langle k\rangle }^2}{{\langle k\rangle }^2}={\eta }_{\text{E}},$$ (26)

the coefficient of variation in k, keeping the mean expression constant. The equality η_k = η_E is a consequence of the underlying single-step process and will not hold true for other cases.

Figure 3.

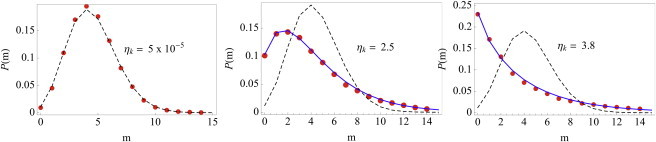
The histogram of mRNA copy numbers (red dots), the Poisson distribution fit (dashed black lines), and the marginal distribution fit (solid blue, see Eq. 23) for three different scenarios in the numerical simulation. The mean mRNA copy number μ ≈ 4.4 for all three cases. (Left) Small variations in extrinsic factors (η_k ≈ 5 × 10⁻⁵) results in a histogram of mRNA copy numbers that is well described by a Poisson distribution. (Middle) Higher variation in extrinsic factors (η_k ≈ 2.5) broadens the histogram of mRNA copy numbers. The marginal distribution P(m) (see Eq. 23) fits the data well. (Right) High variation in extrinsic factors (η_k ≈ 3.8). Again, note that the histogram of mRNA copy numbers is wider than a Poisson distribution and the marginal distribution P(m) fits the simulation well.

In the left panel of Fig. 3, we show the histogram of mRNA copy numbers when the coefficient of variation η_k is low (η_k ≈ 5 × 10⁻⁵). Observe that the histogram of mRNA copy numbers (red circles) is well described by a Poisson distribution (black dashes), as is expected. If we increase the variation in k (η_k ≈ 2.5 in the middle panel and η_k ≈ 3.8 in the right panel), the histogram of mRNA copy numbers gets broader and is best described by P(m) (Eq. 23, solid blue) rather than Poisson distribution (black dashes). Thus, even though the mRNA synthesis and degradation is governed by a Poisson process with an effective synthesis rate k, the variation in the rate itself makes gene expression a doubly stochastic process (26,27) and leads to a histogram of mRNA copy numbers that is not Poisson-distributed and is best described by a Gamma-like distribution.

Interpreting experiments

Fig. 4 shows the best fit to the histogram of mRNA copy numbers for the E. coli gene TufA (7). The Poisson distribution does not capture the mRNA histogram whereas Eq. 23 describes it well (for a comparison with numerical simulations, see the right panel of Fig. 3). Also, recently, So et al. (18) showed that the distribution of mRNA copy numbers in E. coli is well described by a negative binomial distribution.

Figure 4.

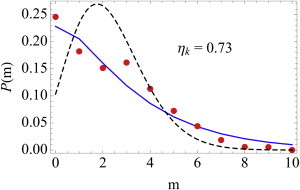
(Dashed black lines). Our results predict that the experimentally measured mRNA copy number histogram is described by Eq. 23 (solid blue). η_k ≈ 0.7 is the estimated coefficient of variation of the effective synthesis rate k.

In Fig. 5, we show the measured total noise and the predicted log-binned average trends in the decomposition of the total noise into its intrinsic and extrinsic components. The components are estimated from Eq. 24 for ∼130 genes, as reported in Taniguchi et al. (7). The noise decreases as mean expression level increases and both intrinsic and extrinsic components contribute significantly to the total noise. The total noise and the extrinsic noise saturate at high expression levels that are sometimes referred to as the “extrinsic limit” (4,7,8,15). Importantly, our framework also allows us to directly estimate the variation P(k) of the effective synthesis rate k.

Figure 5.

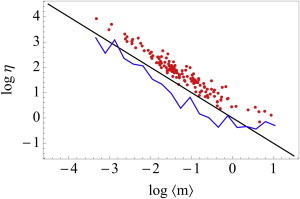
The experimentally measured total noise η_T (red dots) is always higher than what is expected from a Poisson distribution (black line, see Eq. 24). Our framework also allows us to predict the extrinsic noise η_E and the variation in the effective synthesis rate η_k. (Blue line) Log-binned average of η_E (also equal to η_k). Note that as opposed to proteins, for most mRNAs, intrinsic noise dominates the total noise for mRNAs. At higher mRNA numbers, the η_E dominates η_T. Within the ME framework, we can explicitly estimate the hitherto inaccessible variation in the effective synthesis rate as well.

Incorporating promoter fluctuations explicitly

The mRNA histogram from a slightly involved model that captures the activation state of the DNA molecule (10,18,19) results in a distribution identical to Eq. 23. In that model, the deviation from Poisson distribution is ascribed entirely to promoter fluctuations. As mentioned above, promoter fluctuations arise, among other things, from chromatin remodeling (11,19) and are likely to affect the local region around the given gene (34). Within our framework, the variation in mRNA synthesis rate due to promoter fluctuations is treated as extrinsic and is automatically incorporated in the distribution of the effective synthesis rate.

We can further separate the variability in k due to promoter fluctuations from the variability due to other extrinsic factors. The presence of other extrinsic factors can be tested in a number of ways. For example, if promoter fluctuations are the major contributor to the variation of effective synthesis rate, it can be shown that the experimentally estimated skewness

$${\gamma }_1=\frac{\langle m^3\rangle -3\langle m\rangle \langle m^2\rangle +2{\langle m\rangle }^3}{{\left(\langle m^2\rangle -{\langle m\rangle }^2\right)}^{3/2}}$$ (27)

of the distribution of mRNA numbers will be roughly equal to twice the square-root of the total noise η_T. In the presence of other extrinsic noise, this relationship is somewhat modified (see the Supporting Material for details).

If promoter fluctuations are explicitly modeled, the distribution of mRNA copy numbers is characterized by at least two parameters (10,18). The development presented here will add one additional parameter to characterize the extrinsic variability beyond promoter fluctuations. Thus, the resulting distribution will be characterized by three parameters. Analyzing the reported experimental measurements of total noise to predict extrinsic noise beyond promoter fluctuations will consequently be an overfit. Yet, we note that if experimental measurements reliably estimate the third moment of the mRNA distribution, the presented framework will be able to parse the total noise into its extrinsic and intrinsic (which will include promoter fluctuations) contributions without the assistance of a two-color experiment (see the Supporting Material for details).

Concluding Remarks

Measurements of the cell-to-cell variation in protein numbers show that the extrinsic contributions play a dominant role (3). Yet, much of the theoretical development in understanding noise in gene expression has focused on the effect of intrinsic contributors on statistical mechanical fluctuations in binding and diffusion of molecules. The limited treatment extrinsic noise has received (7,20,28) employs the linear fluctuation-dissipation like susceptibility analysis (20) or ad hoc assumptions about the nature of variation in extrinsic parameters (7,28).

To the best of our knowledge, for the first time, we have presented a framework that systematically estimates the static variation in the rate parameters of gene expression. In the context of the model, the extrinsic noise in gene expression arises solely because of the variation in the parameters, allowing us to separate the intrinsic and the extrinsic contributors to noisy gene expression from limited information about the gene expression profile. Consequently, a weakness of the presented framework is that the decomposition of the total noise in its intrinsic and extrinsic contributions depends on the accuracy of the gene expression model. We conclude that extrinsic factors can change the experimentally accessible histogram of mRNA copy numbers quantitatively and qualitatively. More importantly, the framework allows us to directly estimate the hitherto elusive variation in global extrinsic factors.

Specifically, we show that even if mRNA synthesis and degradation is described by a simple Poisson process, owing to the variation in the effective synthesis rate k, the experimentally accessible histogram of mRNA copy numbers is broader and we estimate it to be the negative binomial distribution (see Eq. 23). Consequently, we find that variation in the effective synthesis rate k contributes to the greater-than-Poisson relationship between noise η_T and the mean mRNA copy number 〈m〉 (see Eq. 24). We also predict that, in contrast to proteins (3), intrinsic and extrinsic factor variations both contribute significantly to the noisy expression of mRNA. Moreover, we directly probe the variation in effective mRNA synthesis rate k and show that the coefficient of variation η_k saturates at high expression levels (see Fig. 5, bottom).

Arguably, biologically interesting situations where noise is important are not limited to production of mRNA molecules. One would like to know how noise affects the regulation of internal circuits, response to external stimuli, and fitness and evolution. It is clear that once the distribution of $\mathcal{G}$ is known as a function of $\mathcal{K}$, the application of the presented framework is, in principle, straightforward. Unfortunately, the conditional distribution P($\mathcal{G}$|$\mathcal{K}$) is known for very few simple cases (similar to the one discussed in this work). We propose the following algorithm to overcome this difficulty.

Even though the entire distribution P($\mathcal{G}$|$\mathcal{K}$) is almost always analytically inaccessible, the first two moments $\left\{{\langle \mathcal{G}\mathcal{i}\rangle }_{\mathcal{K}}\right\}$ and $\left\{{\langle \mathcal{G}\mathcal{i}\mathcal{G}\mathcal{j}\rangle }_{\mathcal{K}}\right\}$ can be estimated very accurately as analytical functions of $\mathcal{K}$ for a number of complicated situation using the well-known Ω expansion (9). Moreover, under the assumption of linear noise, the entropy S($\mathcal{G}$|$\mathcal{K}$) can itself be approximated as S($\mathcal{G}$|$\mathcal{K}$) ∼ log det Σ, where ${\sum }_{ij}=\langle {\mathcal{G}}_i{\mathcal{G}}_j\rangle -\langle {\mathcal{G}}_i\rangle \langle {\mathcal{G}}_j\rangle$ is the covariance matrix. From here onwards, it is a straightforward exercise to compute P($\mathcal{K}$) using Eq. 15. The intrinsic and extrinsic components can then be separated out analytically. We will implement the proposed program for protein synthesis and networks in the future.