Assessing the Significance of Global and Local Correlations under Spatial Autocorrelation; a Nonparametric Approach

Summary

We propose a method to test the correlation of two random fields when they are both spatially auto-correlated. In this scenario, the assumption of independence for the pair of observations in the standard test does not hold, and as a result we reject in many cases where there is no effect (the precision of the null distribution is overestimated). Our method recovers the null distribution taking into account the autocorrelation. It uses Monte-Carlo methods, and focuses on permuting, and then smoothing and scaling one of the variables to destroy the correlation with the other, while maintaining at the same time the initial autocorrelation. With this simulation model, any test based on the independence of two (or more) random fields can be constructed. This research was motivated by a project in biodiversity and conservation in the Biology Department at Stanford University.

1. Motivation

Assessing significance of the correlation coefficient is not straightforward if the values of the variables involved vary smoothly with location (throughout the paper smooth refers to spatial autocorrelation, and it may be the case that the variable changes abruptly over a short distance). With spatially autocorrelated data, nearby points may provide almost identical information. Hence there is a tension between sample size, resolution and the number of independent measurements; i.e. at some level, more data, meaning sampling the process at a higher resolution, does not mean more information. As a result, classical tests Fisher (1915) tend to incorrectly reject the null (larger type II errors). Some work has been done, particularly in the field of Geostatistics, to overcome this problem. For instance, Clifford, Richardson, and Hemon (1989) propose a method that estimates an effective sample size M < N to be used in such tests, in an attempt to capture the real uncertainty. The correlation coefficient is thus evaluated with a Student’s t distribution with M degrees of freedom (distribution with larger variance), which accounts for the loss of precision due to the underlying spatial component. The method, however, is developed for Gaussian random fields and in reality smoothed processes tend to be non-Gaussian.

We propose a Monte-Carlo method to test the correlation of two random fields that takes account of the spatial autocorrelation. By

1. randomly permuting the values of one of the fields across space we eliminate the dependence between them, and

2. smoothing and scaling the permuted field we approximately recover, with the help of the variogram, the spatial structure suppressed in (1).

In the same spirit, Allard, Brix, and Chadoeuf (2001) propose a method that is based on random local rotations, but applied to the characteristics of the spatial structure of point processes, where the intensity (rate parameter) is assumed to be constant at small scales and varies at large scales, the opposite situation we encounter with random fields, were the autocorrelation usually fades away as the distance increases.

By repeating steps 1) and 2) many times, we can obtain approximate realizations of the null distribution of interest. In fact, with this simulation model, it is possible to examine the null distribution of a larger variety of statistics. In particular any test based on the independence of two (or more) random fields can be constructed, the simplest example being the test for a single Pearson’s correlation coefficient between the two random fields. We will call it global correlation.

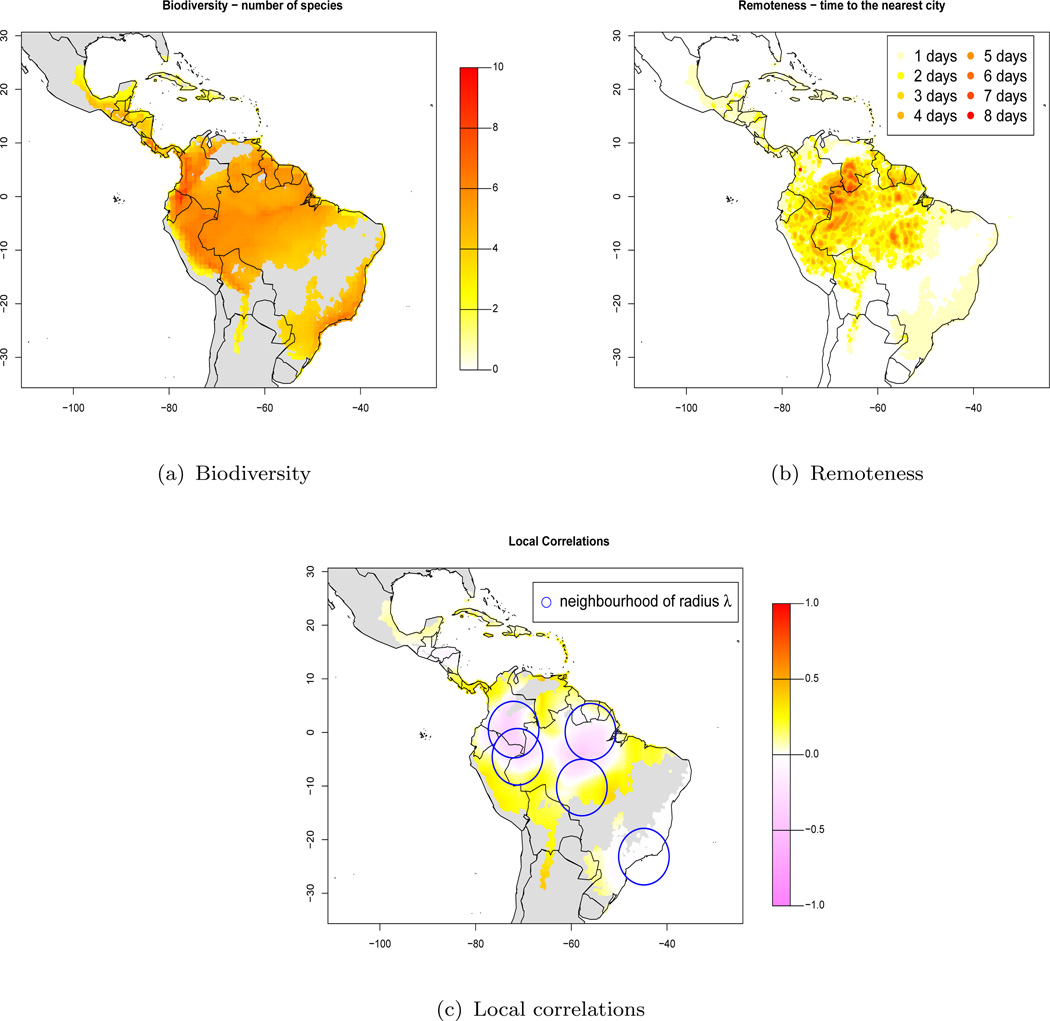
Other spatially local tests may be of interest — for example, which regions show strong correlation between the two fields — the question that our collaborators posed (McCauley et al., 2012). They mapped the locations of sites over the world using two criteria:

• amount of species richness — biodiversity, and

• travel time in days needed to reach the nearest city — remoteness.

Figures 1(a) and 1(b) represent both these fields, and we see that they are spatially very smooth. Are remoteness and biodiversity correlated with one another? i.e. are there more species in remote areas that are better insulated from human disturbance? To succinctly communicate the strength of these correlations, the authors were interested in reporting a p-value map for the areas where overlap between remoteness and biodiversity occurs. Initially they used Geographically Weighted Regression methods (Fotheringham, Brunsdon, and Charlton, 2002), a set of regression techniques that tackle spatially varying relationships. This book has captured considerable attention in the Geostatistics community. However, these methods focus on comparing coefficients for different spatial areas, and identifying the areas with stronger relationships, but with no assessment to whether the coefficients in the model are significant or not.

Figure 1.

Top right: Biodiversity as a function of domain. Top left: Remoteness as a function of domain. Bottom: Local correlations between biodiversity and remoteness using a Gaussian kernel with bandwidth λ = 5.281 (see Appendix 2), where the blue circles indicate the extent of the neighborhood for 5 locations at random. The grey areas correspond to areas with no data.

Given the map of correlations in Figure 1(c), where each value corresponds to the correlation between biodiversity and remoteness in a given neighborhood (we will call them local correlations), we will apply our method and produce a map of p-values, where each p-value assesses significance of the correlation in that particular location. See Appendix 2 for details on how to calculate the local correlations.

We organize the paper as follows. In section 2 we show the results of applying our method to the biodiversity dataset. Section 3 illustrates the limitations of the standard test under spatial autocorrelation. Section 4 describes in detail the algorithm proposed in this paper, and in Section 5 we study the behavior of the method by performing power and type I error analyses, and compares it to the approach in Clifford et al. (1989). We conclude and summarize our findings in the discussion.

2. Biodiversity Data

Protecting remote ecosystems is the future of global diversity, WWF ecologists divided the world into 16 unique regions (Biomes) based on land cover and climate. In this paper, and for simplicity, we will focus on the part of the biodiversity dataset that corresponds to the American region of Biome 1 (Tropical and subtropical moist broadleaf forests) to illustrate our methodology.

Biodiversity (X) is the result of estimating the number of species of plants, amphibians, birds and mammals in an area of 100 × 100 km and centered at location s. The estimates for the 4 groups is normalized to a maximum score of 10, with X being the average of those normalized counts. Remoteness (Y) combines a number of data sets that influence speed of travel: road networks, angle of slope, density of vegetation, river courses, etc. It takes values between 1 – 8 and indicates the travel time in days needed to reach the nearest city larger than 50, 000 inhabitants from location s, where 8 represents any travel time larger than 7 days. Our sample is denoted by (X_s, Y_s) = [(X_s1, Y_s1), …, (X_sN, Y_sN)], s = (s₁ … s_N), where s_i ∈ ℝ² are the longitude and latitude coordinates of observation i and N = 19, 926.

2.1 The empirical and smoothed variogram for Biodiversity

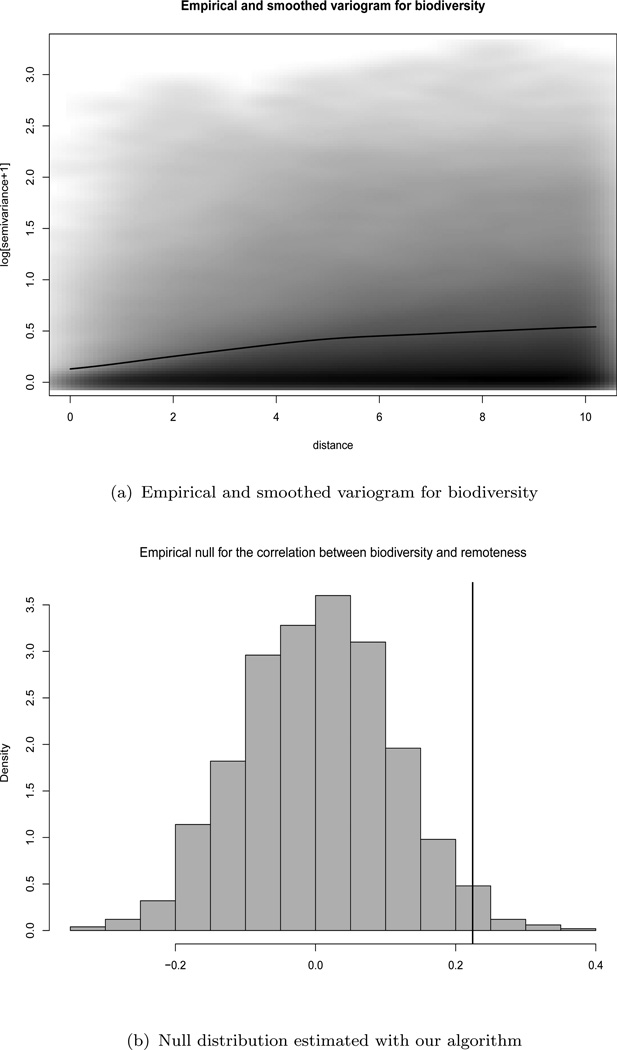
The theoretical variogram is a function describing the degree of spatial dependence of a random field X_s. It is defined as the variance of the difference between field values at two locations s_i and s_j across realizations of the field: $\gamma (s_i,s_j)=\frac{1}{2}\text{Var}(X_{s_i}-X_{s_j})$, see Cressie (1993). The empirical variogram for the sample X_s1, …, X_sN is the collection of pairs of distances u_ij = ‖s_i − s_j‖ between s_i and s_j, and their corresponding variogram ordinates ${\upsilon }_{ij}=\frac{1}{2}{(X_{s_i}-X_{s_j})}^2$. The empirical variogram for biodiversity is plotted in Figure 2(a). Since γ is expected to be a smooth function of distance, it is common to smooth the empirical variogram to improve its properties as an estimator for γ. In our algorithm, we will use the smoothed variogram γ̂, which is obtained using a kernel smoother and defined in Appendix 1. The black curve in Figure 2(a) is the smoothed variogram for biodiversity with bandwidth h = 0.746, and truncated at distance u = 10, which corresponds to the 25% percentile of the distribution of pairs of distances. We truncate the variogram because the precision of the estimate is expected to decrease as the distance increases, since a decreasing number of pairs are involved.

Figure 2.

Top: empirical (scatter plot in grey scale) and smoothed (black line) variogram for biodiversity in a logarithmic scale. The variograms are truncated at distance 10 and the smoothed variogram is calculated using a Gaussian kernel with bandwidth h = 0.746 (see Appendix 1). The intensity of the grey color in the empirical variogram indicates the density of the data. Bottom: Null distribution of r_{Xs, Ys} for the biodiversity dataset estimated with our algorithm. The black line corresponds to the observed correlation r̂_{Xs, Ys} = 0.224. The p-value is 0.057.

When pairs of distances are small, the variance of X_si − X_sj is small, indicating that observations close to each other are very similar. As pair distances increase, the autocorrelation dies off and the variogram grows; as farther apart observations are less similar. The increasing nature of the variogram as the distance increases is a common behavior that corroborates the spatial autocorrelation present in the variable biodiversity.

2.2 Applying our Method to the Biodiversity Dataset

In this section we apply to the biodiversity dataset the algorithm that we describe in Section 4. Given X_s and Y_s, we will test significance of 1) the global correlation coefficient [H₀ : ρ_{Xs, Ys} = 0], and 2) the set of local correlations ${\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}^{\lambda }(s_1),\dots ,{\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}^{\lambda }(s_N)$ plotted in Figure 1(c) [H₀ : ρ_{Xs, Ys}(s_j) = 0, ∀j], and calculated using a Gaussian kernel with neighborhood window truncated at bandwidth λ = 5.281 (see Appendix 2).

We will see that the algorithm returns ${\mathbf{X̂}}_{\mathbf{s}}^1,\dots ,{\mathbf{X̂}}_{\mathbf{s}}^B$ as a result of randomizing and smoothing X_s B = 1000 times, with bandwidths Δ ∈ (0.005, 0.785). These are proxies for X_s with approximately the same autocorrelation but with the characteristic of being independent of Y_s. The pairs $({\mathbf{X̂}}_{\mathbf{s}}^1,{\mathbf{Y}}_{\mathbf{s}}),\dots ,({\mathbf{X̂}}_{\mathbf{s}}^B,{\mathbf{Y}}_{\mathbf{s}})$ will be used to test the situations 1) and 2) above.

We chose to randomize X_s (biodiversity), as we are free to pick the most convenient one, since the purpose is to break the dependence between both variables.

2.2.1 Testing the Global Correlation

The observed global correlation coefficient between biodiversity and remoteness is γ̂_{Xs, Ys} = 0.224. We use r = (r₁, …, r_B) as an estimate of the sampling distribution of r_{Xs, Ys} under the null hypothesis of independence, where $r_i=\text{cor}({\mathbf{X̂}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}})$; see Figure 2(b). Using this null distribution to test H₀ : ρ_{Xs, Ys} = 0, the p-value is $p_{\mathrm{r̂}}=P(|r_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}|>|{\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}|)=\frac{1}{B}{\sum }_{i=1}^{B}I[|r_i|>|{\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}|]=0.057$ (indicated with a black line in Figure 2(b)). Had we assumed that the sample pairs were independent, and used instead a Student’s t with N − 2 degrees of freedom, the p-value would have been effectively zero, since the variance of the Student’s t distribution is significantly smaller.

2.2.2 Testing Local Correlations

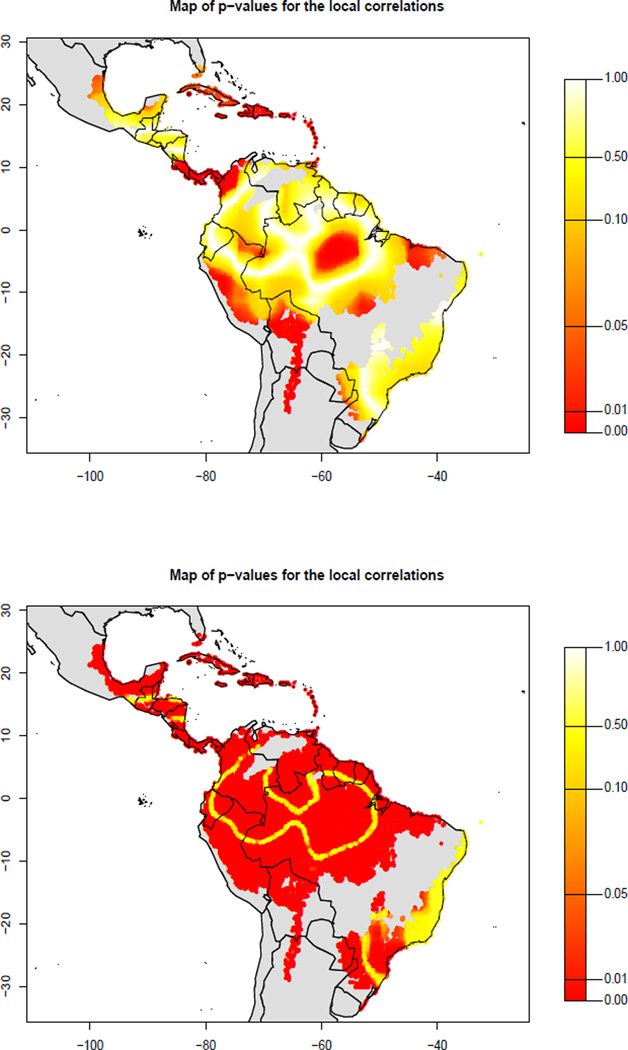
Each pair of random fields $({\mathbf{X̂}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}}),i=1,\dots ,B$, can be used to calculate a new map of local correlations under the null hypothesis (${\mathbf{X̂}}_{\mathbf{s}}^i$ and Y_s are constructed to be independent). Hence we can compute local p-values in exactly the same was as was done globally above. A sample distribution of the statistic r_{Xs, Ys}(s_j) under the null is r(s_j) = (r₁(s_j), …, r_B(s_j)), where $r_i(s_j)=r_{{\mathbf{X̂}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}}}^{\lambda }(s_j)$. The p-value for testing H₀ : ρ_{Xs, Ys}(s_j) = 0 at location s_j is $p_{s_j}=P(|r_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}(s_j)|>|{\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}^{\lambda }(s_j)|)=\frac{1}{B}{\sum }_{i=1}^{B}I[|r_i(s_j)|>|{\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}^{\lambda }(s_j)|]$. The resulting p-value map is plotted in Figure 3, where we can identify the regions that are strongly correlated. For comparison, we also plot the map of p-values had we used the standard test.

Figure 3.

Top: map of p-values for the correlations between biodiversity and remoteness in Figure 1(c), obtained with our method with B = 1000 and Δ ∈ (0.005, 0.785). Bottom: p-values map if we assume that there is no spatial autocorrelation and use the standard test to assess the local correlations.

3. Behavior of r_{Xs, Ys} under Spatial Autocorrelation

If (x₁, y₁), …, (x_N, y_N) is an independent and normally distributed sample, the distribution for the Pearson’s correlation coefficient under ρ_X,Y = 0 is

$$f_N(r)=\frac{{(1-r^2)}^{\frac{N-4}{2}}}{B\{\frac{1}{2},\frac{1}{2}(N-2)\}},\Vert r\Vert \le 1$$ (1)

The statistic $t=\frac{{(N-2)}^{\frac{1}{2}}r}{{(1-r^2)}^{\frac{1}{2}}}$ is used to test for H₀ : ρ_X,Y = 0, which follows a Student’s t distribution with N − 2 degrees of freedom, see Kenney and Keeping (1951).

In the previous section we have seen that even though the sample size of the biodiversity dataset was very large (N = 19, 296), the sample distribution for r_{Xs, Ys} was somewhat wide (Figure 2(b)).

This emphasizes the following point, which we demonstrate via a simulation. For a pair of spatially correlated random fields, the sample size or, more precisely, the resolution at which the fields are sampled, can play less of a role in the behavior of the distribution of r_{Xs, Ys}; rather it is the extent of the spatial autocorrelation that determines this distribution (see Walther (1997) for an equivalent problem with time series).

Let W_s be a stationary and isotropic Gaussian random field, s ∈ ℝ², with Matérn auto-correlation function φ(u) = [2^κ−1Γ(κ)]⁻¹(u/ϕ)^κK_κ(u/ϕ) where ϕ > 0 is the scale, and the shape parameter κ > 0 determines the smoothness of the process, var(W_s) = σ². For κ = 0.5, the Matérn autocorrelation function reduces to the exponential, and when κ → ∞ to the Gaussian.

Suppose X_si is generated by a stationary process

$$X_{s_i}=W_{s_i}+Z_i,$$ (2)

with Z_i being mutually independent and identically distributed with zero mean and nugget variance τ² (measurement error), see Diggle and Ribeiro (2007). The theoretical variogram of X_si under stationarity is described in Appendix 1 and illustrated in Web Figure 4.

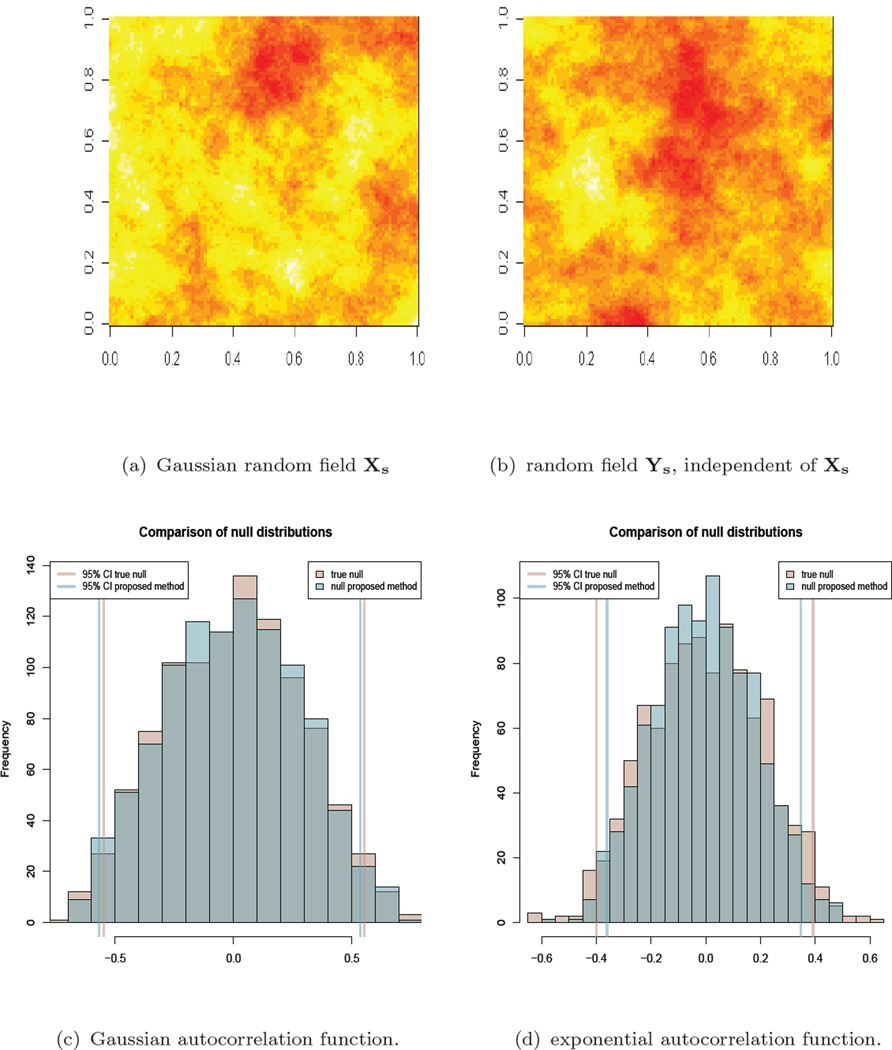
Figures 4(a) and 4(b) are X_s and Y_s, two independent realizations of this process in the grid [0, 1] × [0, 1] with resolution N = 101 × 101 = 10, 201, and parameters κ = 0.5 and ϕ = 0.30. We have used the R package RandomFields to simulate these processes (R Core Team, 2013; Schlather et al., 2013).

Figure 4.

Top, left and right: Illustration of X_s and Y_s, two independent realizations of a Gaussian random field with exponential autocorrelation function with ϕ = 0.03 and grid size g = 0.01. Bottom, left and right: null distribution for r_{Xs, Ys} returned by the algorithm (blue), for a Gaussian and exponential autocorrelation function respectively, together with the true null (pink) obtained by simulating from model (2). The corresponding 95% Confidence Intervals are added to the plot.

In Web Figure 1, Figure (a) is the scatter plot of X_s and Y_s, whereas Figure (d) is the scatter plot of two independent samples, each of them mutually independent (non-spatially correlated) and normally distributed. The correlation coefficient is much larger for X_s and Y_s (r̂_{Xs, Ys} = 0.3). Figure (b) and (c) are two new sets of independent simulated processes X_s and Y_s, showing negative strong correlation and a correlation closer to zero respectively. Thus, as we have seen, a consequence of the spatial autocorrelation is a larger variance for the distribution of r_{Xs, Ys}. In fact, the larger κ, the larger the variance. Intuitively, consider the extreme case of two very smooth one-dimensional fields (i.e lines) with randomly chosen orientations (slopes); the correlation of sampled pairs will either be −1 and +1 depending on the randomly chosen orientation; a maximal variance situation. The same intuition applies to higher-dimensional fields.

The null distribution for r_{Xs, Ys} under ρ_{Xs, Ys} = 0 can be estimated by generating the independent pairs $({\mathbf{X}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}}^i)$. With this distribution, the probability of observing values as extreme or more than 0.3 is 0.16, with no evidence against H₀.

Although X_s and Y_s have been constructed to be independent of each other, if we use the Student’s t distribution to test H₀ : ρ_{Xs, Ys} = 0, the p-value for r̂_{Xs, Ys} = 0.3 is 0.

4. The Algorithm

We propose a method that approximately recovers the null distribution of r_{Xs, Ys}, or any other statistic based on the independence of X_s and Y_s. The following scheme summarizes the main steps of the algorithm.

Let X_s and Y_s be a realization of two random fields. Repeat the following two steps B times:

1. Randomly permute the values of X_s over s, which we denote by X_π(s); this means X_π(s) and Y_s are independent.

2. Smooth and scale X_π(s) to produce X̂_s, such that its smoothed variogram γ̂ approximately matches γ̂(X_s); i.e. the transformed variable X̂_s has approximately the same autocorrelation structure as X_s.

The random fields ${\mathbf{X̂}}_{\mathbf{s}}^1,\dots ,{\mathbf{X̂}}_{\mathbf{s}}^B$ have approximately the same autocorrelation structure as X_s, but are each independent of Y_s. Hence, the pairs $({\mathbf{X̂}}_{\mathbf{s}}^1,{\mathbf{Y}}_{\mathbf{s}}),\dots ,({\mathbf{X̂}}_{\mathbf{s}}^B,{\mathbf{Y}}_{\mathbf{s}})$ are the ingredients for the calculation of a null distribution. For instance, the distribution of r_{Xs, Ys} under H₀ : ρ_{Xs, Ys} = 0 can be approximated by r = (r₁, …, r_B), where $r_i=\text{cor}({\mathbf{X̂}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}})$, but we could proceed equivalently with any other statistic based on the independence of X_s and Y_s.

Note that we do not pose restrictions on which random field to permute, but the algorithm assumes that X_s is stationary.

Step (2) of the algorithm is described in detail in the following section.

4.1 Step 2: Matching Variograms

This step focuses on recovering the intrinsic spatial structure of X_s that was eliminated with the random permutation. As we have seen, the null distribution of r_{Xs, Ys} is mainly determined by the amount of autocorrelation, and this step will determine how well we are able to recover it. Our approach is non-parametric, which implies that the variogram matching does not rely on model assumptions, such as choosing a parametric model for the variogram.

Formally, the problem reduces to choosing a variogram from the family

$$\beta \mathrm{\gamma ̂}({\mathbf{X}}_{\mathbf{s}}^{\delta })+\alpha$$ (3)

that best approximates γ̂(X_s), the smoothed variogram of X_s.

Let X_π(s) be the permuted random field obtained in step (1) above. Choose Δ to be a set of values for the proportion of neighbors to consider for the smoothing step.

1. Calculate the smoothed variogram γ̂(X_s) by smoothing the empirical variogram of X_s (see Appendix 1).

2. For each δ ∈ Δ repeat:

   1. Construct the smoothed variable ${\mathbf{X}}_{\mathbf{s}}^{\delta }$ using a kernel smoother that fits a constant regression to X_π(s) at each location s_j (see Appendix 2).
   2. Calculate $\mathrm{\gamma ̂}({\mathbf{X}}_{\mathbf{s}}^{\delta })$ as in (1).
   3. Fit a linear regression between $\mathrm{\gamma ̂}({\mathbf{X}}_{\mathbf{s}}^{\delta })$ and γ̂(X_s), where (α̂_δ, β̂_δ) are the least-squares estimates.

3. Choose δ* ∈ Δ such that the sum of squares of the residuals of the fit in (2) (c) is minimized.

4. Transform ${\mathbf{X}}_{\mathbf{s}}^{{\delta }^{*}}$ by ${\mathbf{X̂}}_{\mathbf{s}}^{{\delta }^{*}}=|{\mathrm{\beta ̂}}_{{\delta }^{*}}{|}^{\frac{1}{2}}{\mathbf{X}}_{\mathbf{s}}^{{\delta }^{*}}+|{\mathrm{\alpha ̂}}_{{\delta }^{*}}{|}^{\frac{1}{2}}\mathbf{Z}$, where Z is a vector of mutually independent and identically distributed Z_i’s with zero mean and unit variance.

By varying the tuning parameter or proportion of neighbors δ in step (2) we obtain a family of variograms with different shapes, choosing the one more similar to the variogram of the original variable X_s.

The linear transformation in Step (4) ensures that the scale and intercept of $\mathrm{\gamma ̂}({\mathbf{X̂}}_{\mathbf{s}}^{{\delta }^{*}})$ match those of γ̂(X_s), since the smoothing in step (2)(a) has changed the scale of X_s (the smoother ${\mathbf{X}}_{\mathbf{s}}^{{\delta }^{*}}$, the smaller the variance), in addition to the intercept (nugget variance) of γ̂(X_s).

The variogram of the random field ${\mathbf{X̂}}_{\mathbf{s}}^{{\delta }^{*}}$ is a member of the family in (3), and ${\mathbf{X̂}}_{\mathbf{s}}^{{\delta }^{*}}$ has been constructed to match γ̂(X_s) in shape, scale, and intercept.

Note that $|{\mathrm{\beta ̂}}_{{\delta }^{*}}|\text{var}({\mathbf{X}}_{\mathbf{s}}^{{\delta }^{*}})$ is an estimate of σ² in (A.2), |α̂_δ*|is an estimate of τ², and correspondingly $\text{var}({\mathbf{X̂}}_{\mathbf{s}}^{{\delta }^{*}})=|{\mathrm{\beta ̂}}_{{\delta }^{*}}|\text{var}({\mathbf{X}}_{\mathbf{s}}^{{\delta }^{*}})+|{\mathrm{\alpha ̂}}_{{\delta }^{*}}|$ is an estimate of σ² + τ².

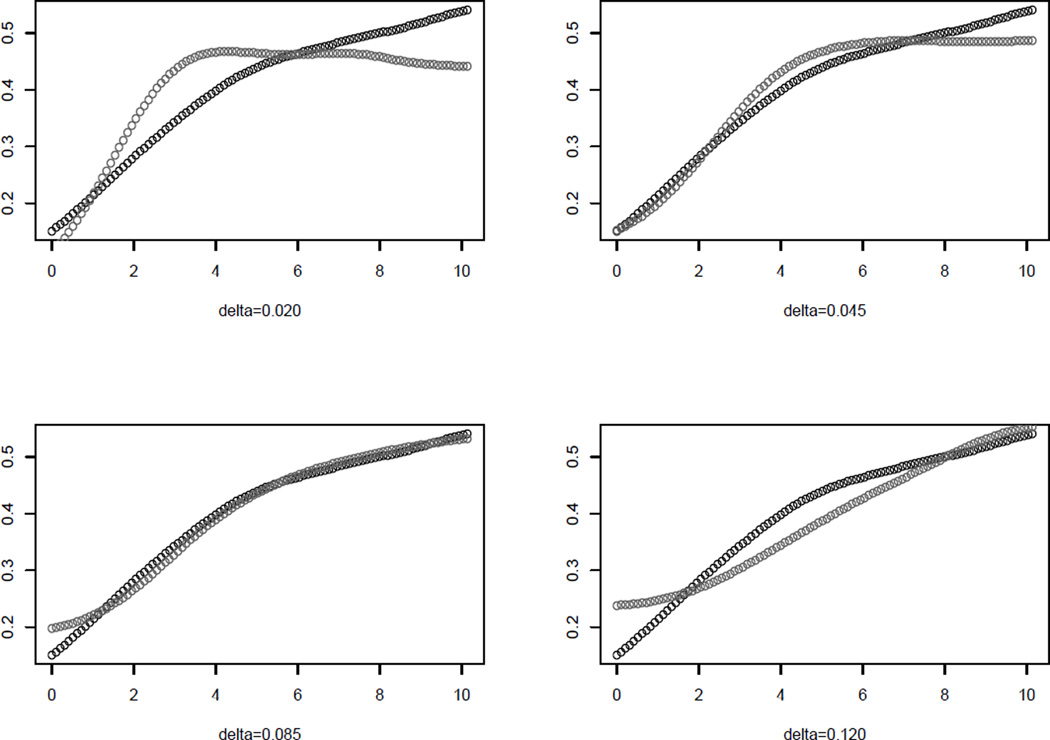
For an illustration of the variogram matching see Figure 5. Different δs result in different shapes for $\mathrm{\gamma ̂}({\mathbf{X}}_{\mathbf{s}}^{\delta })$, and the best match between γ̂(X_s) and $\mathrm{\gamma ̂}({\mathbf{X}}_{\mathbf{s}}^{\delta })$ (grey) is reached with δ = 0.085. The residual sum of squares of linearly regressing $\mathrm{\gamma ̂}({\mathbf{X}}_{\mathbf{s}}^{\delta })$ on γ̂(X_s) for different values of δ are plotted in Web Figure 2.

Figure 5.

Variogram matching between the original biodiversity variable X_s (black) and the transformed variable ${\mathbf{X̂}}_{\mathbf{s}}^{\delta }$ (grey) for 4 different values of bandwidth: Δ = (0.020, 0.045, 0.085, 0.120). The best match is reached with δ = 0.085.

5. Simulation Results

In this section we study the performance of our method for testing H₀ : ρ_{Xs, Ys} = 0 by comparing the estimate of the null distribution for r_{Xs, Ys} provided by our algorithm with an estimate of the true null distribution.

In addition to that, we carry out power and type I error analyses (Section 5.2), and compare the results to Clifford’s approach.

Let X_s and Y_s be two independent Gaussian random fields in the grid [0, 1] × [0, 1] with resolution N = 101 × 101 = 10, 201, following model (2) with σ² = 1, μ = 0, and:

1. Gaussian autocorrelation function φ(u) = exp[−(u/ϕ)²] with scale parameter ϕ = 0.3.

2. exponential autocorrelation function φ(u) = exp(−u/ϕ) with ϕ = 0.3.

We apply our algorithm to one realization of the pair (_{Xs, Ys}) in situations (1) and (2), with B = 1000 and bandwidths Δ_gauss = (0.1, 0.2, …, 0.9) and Δ_exp = (0.07, 0.080, …, 0.18) respectively.

The null distributions that the algorithm returns are plotted respectively in Figures 4(c) and 4(d), together with the true nulls obtained by simulating 1000 times the pairs $({\mathbf{X}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}}^i)$ from the models above. The results are slightly better for (1), but we manage to recover the null in both situations.

5.1 Clifford’s Effective Sample Size

We briey review Clifford’s procedure prior to using it as a comparator. Clifford et al. (1989) propose to use f_M (r) in (1) as the distribution of reference under the null. The variance of f_M(r) is $\frac{1}{M-1}$. Their suggestion is to estimate the effective sample size M by $\mathrm{M̂}=\lfloor 1+\frac{1}{\mathrm{\sigma ̂}\frac{2}{r}}\rfloor$, as a result of equating $\frac{1}{M-1}$ to ${\sigma }_r^2$, the variance of the sample correlation. Hence, an estimate for the null distribution of r_{Xs, Ys} is f_M̂(r).

How to Estimate ${\sigma }_r^2$

In Clifford et al. (1989)’s Appendix they prove that ${\sigma }_r^2=\frac{\mathrm{var}(S_{{\mathbf{X}}_{\mathbf{s}}{\mathbf{Y}}_{\mathbf{s}}})}{E(S_{{\mathbf{X}}_{\mathbf{s}}}^2)E(S_{{\mathbf{Y}}_{\mathbf{s}}}^2)}$ to the first order, and under the assumption of normality, where S_XsYs is the sample covariance, $S_{{\mathbf{X}}_{\mathbf{s}}}^2$ and $S_{{\mathbf{Y}}_{\mathbf{s}}}^2$ are the sample variances of X_s and Y_s, var(S_XsYs) = trace(Σ_ξsΣ_ηs), Σ_ξs = PΣ_XsP, Σ_ηs = PΣ_YsP, Σ_Xs and Σ_Ys are the covariance matrices of X_s and Y_s respectively, $\mathit{P}=\mathit{I}-\frac{1}{N}\mathbf{11}\prime$ and 1 is a vector of 1’s of dimension N.

An estimate for var(S_XsYs) is obtained by imposing a stratified structure on Σ_Xs and Σ_Ys. More precisely, they assume that the set of all ordered pairs of elements of s can be divided into strata S₀, S₁, S₂, …, and that the covariances within strata are constant. Then, ${\mathrm{\sigma ̂}}_r^2=\frac{{\sum }_k{N}_k{Ĉ}_{{\mathbf{X}}_{\mathbf{s}}}(k){Ĉ}_{{\mathbf{Y}}_{\mathbf{s}}}(k)}{N^2{S}_{{\mathbf{X}}_{\mathbf{s}}}^2{S}_{{\mathbf{Y}}_{\mathbf{s}}}^2}$, where N_k is the number of pairs in stratum S_k and ${Ĉ}_{{\mathbf{X}}_{\mathbf{s}}}(k)=\frac{1}{N_k}{\sum }_{(i,j)\in S_k}(X_{s_i}-{\mathrm{X̅}}_k)(X_{s_j}-{\mathrm{X̅}}_k)$ is an autocovariance estimate for stratum S_k. They use the sample variogram to choose the number of strata.

5.2 Power Analysis and Type I Error Estimates

In this section we estimate the power and type I error of the test for our procedure, and compare it to Clifford’s approach.

Web Figure 3 summarizes different scenarios for the null and alternative distributions, as a function of the effect ρ we would like to detect and the amount of spatial autocorrelation ϕ. The power to detect a fixed effect ρ decreases as the spatial autocorrelation increases. Equivalently, for a fixed ϕ the power decreases with the effect size. These data have been simulated assuming we know the truth, and indicates how well we can do in each situation. The grid size g is set to 0.05 (N = 441), but identical results were obtained for grid size g = 0.01 (N = 10, 201).

The simulation experiment goes as follows. For each combination of autocorrelation in ϕ ∈ (0.05, 0.1, 0.3) and resolution in g ∈ (0.05, 0.01), and for the power calculations, for each size effect in ρ ∈ (0.2, 0.5, 0.8), we simulate 10 independent pairs $({\mathbf{X}}_{\mathbf{s}}^j,{\mathbf{Y}}_{\mathbf{s}}^j)$ from the usual model in the grid [0, 1] × [0, 1], with grid size g and Gaussian autocorrelation function with scale parameter ϕ. Then we do the following:

1. apply our algorithm to each pair $({\mathbf{X}}_{\mathbf{s}}^j,{\mathbf{Y}}_{\mathbf{s}}^j)$ with B = 1000, Δ_ϕ=0.3 = (0.1, 0.2, …, 0.9), Δ_ϕ=0.1 = (0.03, 0.034, …, 0.074), and Δ_ϕ=0.05 = (0.013, 0.014, … 0.027) respectively. Let (r₁, …, r₁₀) be the resulting 10 nulls.

2. apply Clifford’s method to each pair $({\mathbf{X}}_{\mathbf{s}}^j,{\mathbf{Y}}_{\mathbf{s}}^j)$ by generating B independent and normally distributed random vectors X_i and Y_i of dimension M̂. Let $({\mathbf{r}}_1^{\mathrm{C}\mathrm{l}},\dots ,{\mathbf{r}}_{10}^{\mathrm{C}\mathrm{l}})$ be the resulting 10 nulls, where ${\mathbf{r}}_j^{\mathrm{C}\mathrm{l}}=(r_{1j}^{\mathrm{C}\mathrm{l}},\dots ,r_{Bj}^{\mathrm{C}\mathrm{l}})$ and $r_{ij}^{\mathrm{C}\mathrm{l}}=\text{cor}({\mathit{X}}_i,{\mathit{Y}}_i)$.

In addition to that, $({\mathbf{r}}_1^{\mathrm{T}\mathrm{r}},\dots ,{\mathbf{r}}_{10}^{\mathrm{T}\mathrm{r}})$ are 10 nulls under the truth, by simulating B independent pairs $({\mathbf{X}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}}^i)$ from the same model, where ${\mathbf{r}}_j^{\mathrm{T}\mathrm{r}}=(r_{1j}^{\mathrm{C}\mathrm{l}},\dots ,r_{Bj}^{\mathrm{T}\mathrm{r}})$ and $r_{ij}^{\mathrm{T}\mathrm{r}}=\text{cor}({\mathbf{X}}_{\mathbf{s}}^i,{\mathbf{Y}}_{\mathbf{s}}^i)$.

The type I error of the test should be equal to the significance level α = 0.05. We use the nulls $({\mathbf{r}}_1^{\mathrm{T}\mathrm{r}},\dots ,{\mathbf{r}}_{10}^{\mathrm{T}\mathrm{r}})$, (r₁, …, r₁₀) and $({\mathbf{r}}_1^{\mathrm{C}\mathrm{l}},\dots ,{\mathbf{r}}_{10}^{\mathrm{C}\mathrm{l}})$ to estimate the type I errors associated to both methods and the truth. We draw 100 samples from $({\mathbf{X}}_{\mathbf{s}}^k,{\mathbf{Y}}_{\mathbf{s}}^k)$ under H₀ : ρ_{Xs, Ys} = 0, and use respectively ${\mathbf{r}}_j^{\mathrm{T}\mathrm{r}}$,r_j and ${\mathbf{r}}_j^{\mathrm{C}\mathrm{l}}$ to assess significance of ${\mathrm{r̂}}_k=\text{cor}({\mathbf{X}}_{\mathbf{s}}^k,{\mathbf{Y}}_{\mathbf{s}}^k)$, for k = 1, …, 100. Out of the 100 samples, the proportion of times the p-values are smaller than α = 0.05 is an estimate of the type I error. We repeat the same process for 100 replicates, obtaining 100 type I error estimates. We then repeat the process again for each null j = 1, …, 10 and average the 10 × 100 type I error estimates, which are shown in Table 1. Estimates of the standard errors are obtained by computing the standard deviation of the 10 × 100 estimates, and appear in brackets in the table.

Table 1.

Type I error estimates obtained by contrasting pairs simulated under H₀ : ρ_{Xs, Ys} = 0, to the null distribution returned by our algorithm and Clifford’s method, in addition to the true null obtained by simulating independent pairs under model (2). Results are presented for different levels of autocorrelation and resolution: ϕ ∈ (0.05, 0.1, 0.3) and g ∈ (0.05, 0.01). The standard errors are in brackets.

Type I Error Estimates
	ϕ = 0.05	ϕ = 0.1	ϕ = 0.3
grid size = 0.05	0.052 (0.024)	0.046 (0.022)	0.048 (0.024)	true
	0.059 (0.029)	0.056 (0.035)	0.051 (0.041)	ours
	0.055 (0.027)	0.055 (0.029)	0.093 (0.045)	Clifford
grid size = 0.01	0.053 (0.027)	0.049 (0.023)	0.051 (0.022)	true
	0.075 (0.030)	0.051 (0.027)	0.050 (0.045)	ours
	0.055 (0.027)	0.058 (0.026)	0.086 (0.044)	Clifford

The power of the test is calculated using a similar sampling scheme. We generate pairs $({\mathbf{X}}_{\mathbf{s}}^k,{\mathbf{Y}}_{\mathbf{s}}^k)$ as before, but then transform ${\mathbf{Y}}_{\mathbf{s}}^k\leftarrow \eta {\mathbf{X}}_{\mathbf{s}}^k+{\mathbf{Y}}_{\mathbf{s}}^k$ with $\eta =\rho /\sqrt{(}1-{\rho }^2)$ (leading to a population correlation of ρ). The r̂_k’s are thus obtained under the alternative hypotheses H₁ : ρ_{Xs, Ys} = ρ. We then follow the same procedure as was done for the type-I errors, namely steps (1) and (2) above, leading to the power estimates in Table 2.

Table 2.

Power estimates obtained by contrasting pairs simulated under H₁ : ρ_{Xs, Ys} = ρ, to the null distribution returned by our algorithm and Clifford’s method, in addition to the true null obtained by simulating correlated pairs under model (2). Results are presented for different levels of autocorrelation, effect size and resolution: ϕ ∈ (0.05, 0.1, 0.3), ρ ∈ (0.2, 0.5, 0.8) and g ∈ (0.05, 0.01).

Power Estimates
		ϕ = 0.05	ϕ = 0.1	ϕ = 0.3
grid size = 0.05	ρ = 0.2	0.921 (0.026)	0.418 (0.059)	0.103 (0.034)	true
		0.926 (0.031)	0.444 (0.087)	0.089 (0.042)	ours
		0.926 (0.030)	0.446 (0.077)	0.153 (0.045)	Clifford
	ρ = 0.5	1 (0)	0.997 (0.005)	0.426 (0.055)	true
		1 (0)	0.997 (0.005)	0.420 (0.089)	ours
		1 (0)	0.997 (0.005)	0.558 (0.100)	Clifford
	ρ = 0.8	1 (0)	1 (0)	0.951 (0.021)	true
		1 (0)	1 (0)	0.879 (0.127)	ours
		1 (0)	1 (0)	0.950 (0.045)	Clifford
grid size = 0.01	ρ = 0.2	0.915 (0.033)	0.405 (0.052)	0.104 (0.030)	true
		0.935 (0.031)	0.404 (0.073)	0.124 (0.069)	ours
		0.927 (0.030)	0.415 (0.064)	0.169 (0.046)	Clifford
	ρ = 0.5	1 (0)	0.996 (0.007)	0.424 (0.059)	true
		1 (0)	0.996 (0.007)	0.391 (0.154)	ours
		1 (0)	0.996 (0.007)	0.510 (0.111)	Clifford
	ρ = 0.8	1 (0)	1 (0)	0.937 (0.022)	true
		1 (0)	1 (0)	0.949 (0.030)	ours
		1 (0)	1 (0)	0.972 (0.018)	Clifford

We highlight the values in Table 1 that most deviate from α. Type I error estimates for our method are close to α, which is less of a case for Clifford’s method, except for ϕ = 0.05.

Note also in Table 2 that power results for our method are typically closer to the power obtained under the truth, and that better power results in Clifford’s case go along with larger type I error estimates, these values are highlighted in the table.

Finally, observe that there are no obvious differences between both resolutions, where the grid sizes g = 0.01 and g = 0.05 correspond to N = 101 × 101 = 10201 and N = 21 × 21 = 441 respectively. This is important, as it highlights the fact that the power of the analysis is mainly driven by the autocorrelation, and even if we increase significantly the resolution, the power stays the same as it is constrained by ϕ.

6. Discussion

This papers addresses the consequences of spatial autocorrelation on the distribution of statistics like correlation between random fields. We develop a nonparametric approach for sampling from the null-hypothesis of independence, that involves three steps:

1. pick one of the fields and estimate the spatial autocorrelation structure via its variogram

2. randomly permute the values in this field

3. apply a local smoothing to the permuted values, using a bandwidth and rescaling so that its resulting variogram matches the original in step (1).

Steps (2) and (3) are repeated B times to obtain B realizations from the null. These realizations can be used to measure many different kinds of independence, including measures of local dependence.

A referee of an earlier draft of this paper made a useful suggestion for an alternative and more direct approach. Their suggestion was to simulate a Gaussian random field according to a model of the variogram, with parameters estimated by weighted least square, maximum likelihood or composite likelihood, with non-Gaussian data transformed to normal scores prior to the estimation of the variogram. One of the advantages of our method, though, is that it does not rely on model assumptions, which turns it into a more flexible, non-parametric approach.

Allard et al. (2001) address a related problem in the context of pairs of point processes, where the focus is on local correlations between pairs of realizations of counts. They randomize one of the processes using local rotations, under the assumption that locally the process rates are constant. Our randomization scheme treats broader range correlations, so the locally constant assumption is not appropriate.

Another approach is proposed by Clifford et al. (1989), where they estimate an effective sample size that takes the autocorrelation into account. We compare this approach to our method through simulations, which show that our algorithm behaves well in practice, with type I error estimates close to α, and power estimates close to the maximum power for each combination of ϕ and ρ.

Since correlation may exist simultaneously at a number of different geographical scales, the method can be used to calculate a p-value for the global correlation, as well as p-values for the local correlations (p-values map), summarizing the strength of the relationship between both fields in a particular location.

One of the important consequences of autocorrelation is that increasing the sample size does not necessarily increase the power to find significance. There is no concept of sample size, since what we observe is one realization of the random field, and the amount of data that we have is the resolution. The information that the sample provides is limited by the spatial autocorrelation. Consequently, in practice it may be more important to focus on using methods that adjust for autocorrelation, than on collecting more data.

Appendix 1

The smoothed variogram γ̂ for X_s is defined by smoothing the empirical variogram using a kernel smoother:

$$\mathrm{\gamma ̂}(u_0)=\frac{{\sum }_{i=1}^N{\sum }_{j=i+1}^N{w}_{ij}{\upsilon }_{ij}}{{\sum }_{i=1}^N{\sum }_{j=i+1}^N{w}_{ij}}.$$ (A.1)

It assigns weights that die off smoothly as distance to u₀ increases, with w_ij = K_h(‖u₀−u_ij‖), u_ij = ‖s_i−s_j‖, ${\upsilon }_{ij}=\frac{1}{2}{(X_{s_i}-X_{s_j})}^2$ and $K_h(x)=\text{exp}\{\frac{-{(2.68x)}^2}{2h^2}\}$, the Gaussian kernel is scaled so that their quartiles are at ±0.25h, with h being the bandwidth (R function ksmooth). The variogram γ̂ is obtained by evaluating (A.1) at distances u = (u₁, …, u₁₀₀) uniformly chosen within the range of pair distances u_ij.

The theoretical variogram of a stationary random field X_si = W_si + Z_i in (2) is:

$$\gamma (u)={\sigma }^2\{1-\phi (u)\}+{\tau }^2,$$ (A.2)

where φ(u) is the autocorrelation function of W_si, typically a monotone decreasing function with φ(0) = 1 and φ(u) → 0 as u → ∞. Its most important feature is its behavior near u = 0, and how quickly it approaches zero when u increases, which reflects the physical extent of the spatial autocorrelation in the process. When φ(u) = 0 for u greater than some finite value, this value is known as the range of the variogram. The intercept τ² corresponds to the nugget variance, the conditional variance of each measured value X_si given the underlying signal value W_si. The sill is the asymptote τ² + σ² and corresponds to the variance of the observation process X_si. Web Figure 4 gives a schematic illustration.

Appendix 2

We smooth a given random field X_s by fitting a local constant regression at locations s₁, …, s_N using the R package locfit (Loader, 2013):

$${\mathrm{f̂}}_{\delta }(s)=\frac{{\sum }_{\Vert s-s_i\Vert \le {\lambda }_s}{w}_{s_i}{X}_{s_i}}{{\sum }_{\Vert s-s_i\Vert \le {\lambda }_s}{w}_{s_i}},$$ (A.3)

where w_si = K_λs(‖s − s_i‖), $K_{{\lambda }_s}(x)=\text{exp}(\frac{-2.5x^2}{2{\lambda }_s^2})$ is a Gaussian kernel, and λ_s controls the smoothness of the fit. For a fitting point s, λ_s is such that the neighborhood contains the k = ⌊Nδ⌋ nearest points to s in Euclidean distance, where δ ∈ (0, 1) is a tuning parameter that indicates the proportion of neighbors. Each f̂_δ(s) is estimated with the k observations that fall within the ball B_λs(s) centered at s and of radius λ_s (the kernel truncates at one standard deviation). We use a varying λ_s because it reduces data sparsity problems by increasing the radius in regions with fewer observations.

The smoothed variable ${\mathbf{X}}_{\mathbf{s}}^{\delta }$ in Section 4.1 in step (2)(a) of the algorithm is the result of fitting the function (A.3) to X_π(s).

The local correlations in Figure 1(c) are calculated using this same approach. The local correlation at location s is defined as:

$${\mathrm{r̂}}_{{\mathbf{X}}_{\mathbf{s}},{\mathbf{Y}}_{\mathbf{s}}}^{\lambda }(s)=\frac{{\sum }_{\Vert s-s_i\Vert \le \lambda }{w}_{s_i}(X_{s_i}-{\mathrm{X̅}}_{\mathbf{s}})(Y_{s_i}-{\mathrm{Y̅}}_{\mathbf{s}})}{\sqrt{{\sum }_{\Vert s-s_i\Vert \le \lambda }{w}_{s_i}{(X_{s_i}-{\mathrm{X̅}}_{\mathbf{s}})}^2{\sum }_{\Vert s-s_i\Vert \le \lambda }{w}_{s_i}{(Y_{s_i}-{\mathrm{Y̅}}_{\mathbf{s}})}^2}}$$ (A.4)

where ${\mathrm{X̅}}_{\mathbf{s}}=\frac{\sum w_{s_i}{X}_{s_i}}{\sum w_{s_i}}$ and ${\mathrm{Y̅}}_{\mathbf{s}}=\frac{\sum w_{s_i}{Y}_{s_i}}{\sum w_{s_i}}$. We then compute (A.4) by breaking it down and separately evaluating the quantities Σw_siX_si, Σw_siY_si, Σw_siX_siY_si, $\sum w_{s_i}{X}_{s_i}^2$ and $\sum w_{s_i}{Y}_{s_i}^2$ using locfit as above.