Tunable Vapor-Condensed Nanolenses

Abstract

Nanostructured optical components, such as nanolenses, direct light at subwavelength scales to enable, among others, high-resolution lithography, miniaturization of photonic circuits, and nanoscopic imaging of biostructures. A major challenge in fabricating nanolenses is the appropriate positioning of the lens with respect to the sample while simultaneously ensuring it adopts the optimal size and shape for the intended use. One application of particular interest is the enhancement of contrast and signal-to-noise ratio in the imaging of nanoscale objects, especially over wide fields-of-view (FOVs), which typically come with limited resolution and sensitivity for imaging nano-objects. Here we present a self-assembly method for fabricating time- and temperature-tunable nanolenses based on the condensation of a polymeric liquid around a nanoparticle, which we apply to the high-throughput on-chip detection of spheroids smaller than 40 nm, rod-shaped particles with diameter smaller than 20 nm, and biofunctionalized nanoparticles, all across an ultralarge FOV of >20 mm². Previous nanoparticle imaging efforts across similar FOVs have detected spheroids no smaller than 100 nm, and therefore our results demonstrate the detection of particles >15-fold smaller in volume, which in free space have >240 times weaker Rayleigh scattering compared to the particle sizes detected in earlier wide-field imaging work. This entire platform, with its tunable nanolens condensation and wide-field imaging functions, is also miniaturized into a cost-effective and portable device, which might be especially important for field use, mobile sensing, and diagnostics applications, including, for example, the measurement of viral load in bodily fluids.

With researchers’ ever-increasing interest in observing the nanoscale world and in controlling light at wavelength-scale dimensions and smaller, micro- and nano-optical elements are gaining widespread use. Applications include high-resolution lithography,^1,2 extreme miniaturization of couplers and interconnects in photonic circuits,³ spatial control of surface plasmon polaritons,^4,5 sensitivity enhancement for CCD and CMOS image sensors,⁶ emissivity enhancement for LEDs,⁷ near-field imaging for subdiffraction-limit resolution,⁸⁻¹⁰ and sensitivity enhancement in detection of nanoparticles and viruses.¹¹⁻¹³ In each of these applications, control of the optical properties of the lens is key to success.

Existing methods for fabricating micro- and nanolenses include both top-down and bottom-up approaches. Top-down methods of fabricating micro- and nanolenses include photolithography with thermal reflow,^8,14 gray-scale lithography,^4,15 and laser-induced bubble formation.⁵ Other bottom-up self-assembly methods have also been pursued, including harnessing thin-film fluid instabilities such as controlled dewetting,¹⁶ thermocapillary instabilities,^17,18 and electrohydrodynamic instabilities,¹⁹ as well as other forms of self-assembly such as of CHQ molecules,²⁰via liquid drainage and pinch-off,¹³ and via solvent evaporation.²¹ Another classical approach to fabricating microscale lenses, although not particularly well-controlled, is to condense a mist or vapor onto a substrate to form so-called “breath figures”.^22,23 Typically, this approach forms random arrays of droplets with varying size whose mean value depends on the substrate wettability. Based on differences in this mean size, breath figures have been used to identify patches of different types of self-assembled molecular monolayers, with horizontal length scales typically 10’s of micrometers or larger.^24,25 Research into the optical properties of condensate formed around single isolated nanoscale features is more limited.²⁶ Beyond surface characterization, breath figures have also been used to fabricate large structures such as well-defined channels²⁷ and porous materials,²⁸ as well as in designing more efficient heat exchangers.²⁹⁻³²

Here we present a controlled bottom-up method to fabricate time- and temperature-tunable nanoscale lenses based on the condensation of a polymeric liquid around a nanoparticle (Figure 1), with the goal of detecting individual spherical and rod-shaped nanoparticles on a surface. While other methods exist for detecting nanoparticles, vapor-condensed nanolenses improve our detection signal-to-noise ratio (SNR) by more than a factor of 50 and enable the detection of particularly small particles including spheres <40 nm and rods <20 nm in diameter across an ultralarge field of view (FOV) of 20 mm², i.e., >1000-fold larger compared to the FOV of, for example, a 100× objective lens. Wide-field optical microscopy is advantageous for analyzing rare events and low particle concentrations,³³⁻³⁶ as well as for high-throughput monitoring of multiplexed assays;³⁷ however it has in general limited resolution and sensitivity for imaging nano-objects. Previous nanoparticle imaging techniques that have similar FOVs cannot detect spheroids smaller than 100 nm,^13,21 and therefore our results present the detection of particles >15-fold smaller in volume, which in free space have >240 times weaker Rayleigh scattering compared to the particle sizes detected in previous wide-field imaging techniques.³⁸ These vapor-condensed nanolenses are also compatible with chemically functionalized surfaces for specific and sensitive capture and detection of bioparticles such as viruses.

Figure 1.

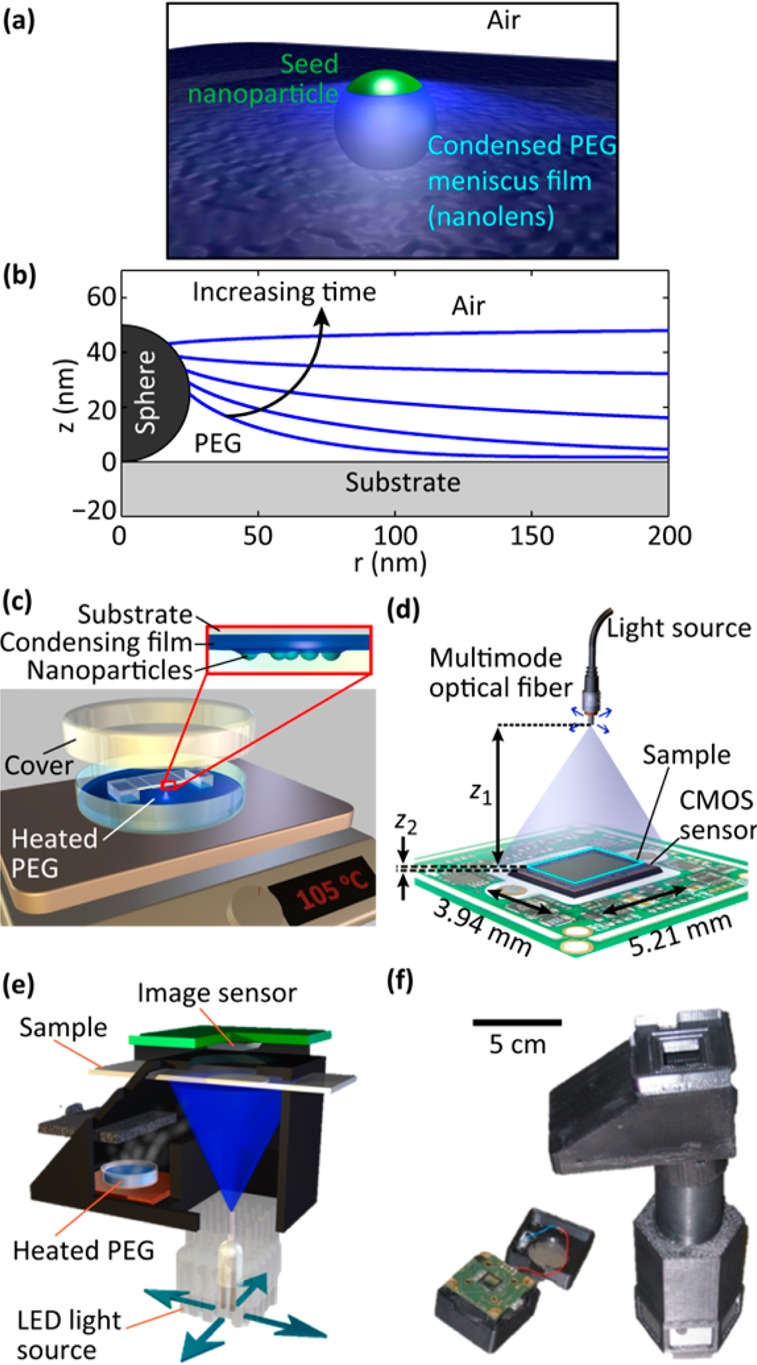
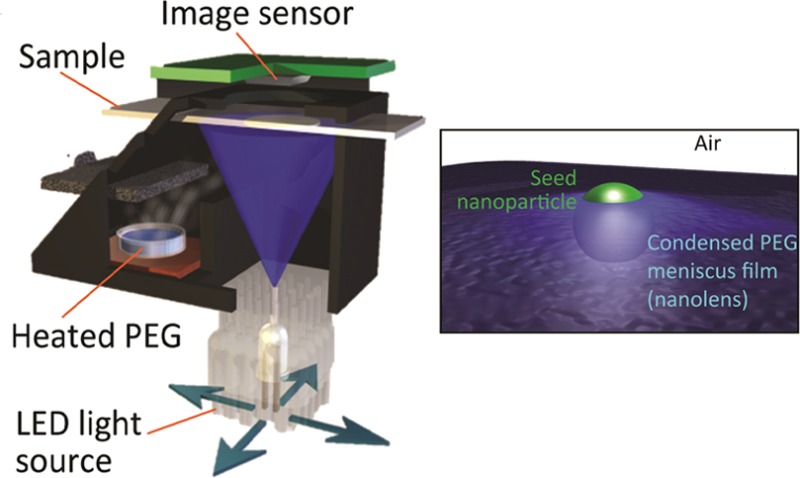
Nanolens formation and imaging. (a) Artistic 3D rendering of the bead and nanolens. (b) As liquid condenses on the substrate, the lens surrounding a spherical nanoparticle thickens and changes shape. (c) Condensation of PEG is performed by suspending the substrate over a heated pool of liquid PEG in a closed chamber. (d) The nanoparticle sample with vapor-condensed nanolenses is imaged using an ultrawide field of view lens-free holographic on-chip microscope. (e, f) The condensation and imaging steps are integrated into a single field-portable device, such as the prototype shown here in schematic (e) and photograph (f). This portable device could be used in field settings for both the creation and simultaneous imaging of vapor-condensed tunable nanolenses.

To form these nanolenses, we first deposit the nanoparticles of interest on a hydrophilic plasma-treated glass coverslip, using any one of a variety of methods such as evaporation of a solvent, adsorption from a slowly flowing suspension,^13,39 or specific biochemical linkage (see Materials and Methods section for details). Next, the sample with adsorbed particles is suspended over a shallow pool of liquid polyethylene glycol (PEG) preheated to 105 °C, as shown in Figure 1c. The particles are exposed to PEG vapor for, for example, 2 min, during which a nanofilm of PEG condenses on the sample substrate. In the vicinity of the nanoparticles on the substrate, this film rises in the form of a meniscus, which forms a nanolens (Figure 1b). Other materials may also be used to form the nanolenses, such as water, glycerol, or other polymeric liquids. Here, we chose to use PEG because of its low toxicity and its availability at a molecular weight having low vapor pressure when moderately heated, but high vapor pressure at room temperature so that the lenses do not evaporate immediately after deposition.

To quantify these nanolenses’ ability to enhance the scattering signals of the embedded nanoparticles, we use a pixel super-resolved lens-free holographic on-chip microscope⁴⁰⁻⁴³ (Figure 1d). This imaging modality provides a number of advantages over conventional microscopy, including cost-effectiveness⁴⁴ (no expensive imaging optics), field-portable implementations⁴⁴⁻⁴⁶ (see, for example, Figure 1e and f), high resolution up to 0.9–1 effective numerical aperture,^42,47,48 the ability to generate phase-contrast images, and an ultralarge field of view of >20 mm² (Figure 2a) that is more than 1000 times larger than that obtained with a typical high-NA objective lens. In this lens-free on-chip imaging configuration (Figure 1d), the transparent sample is placed in close proximity to the image sensor (z₂ = 50–300 μm) and is illuminated with a narrow-band light source, emanating from an effective aperture size of ∼100 μm. In this form of partially coherent on-chip microscopy, the captured raw frames are in-line holograms of the specimen with unit magnification, which can be computationally reconstructed to form high-fidelity phase and amplitude images of the sample with submicrometer resolution over the entire active area of the optoelectronic sensor array.^44,49

Figure 2.

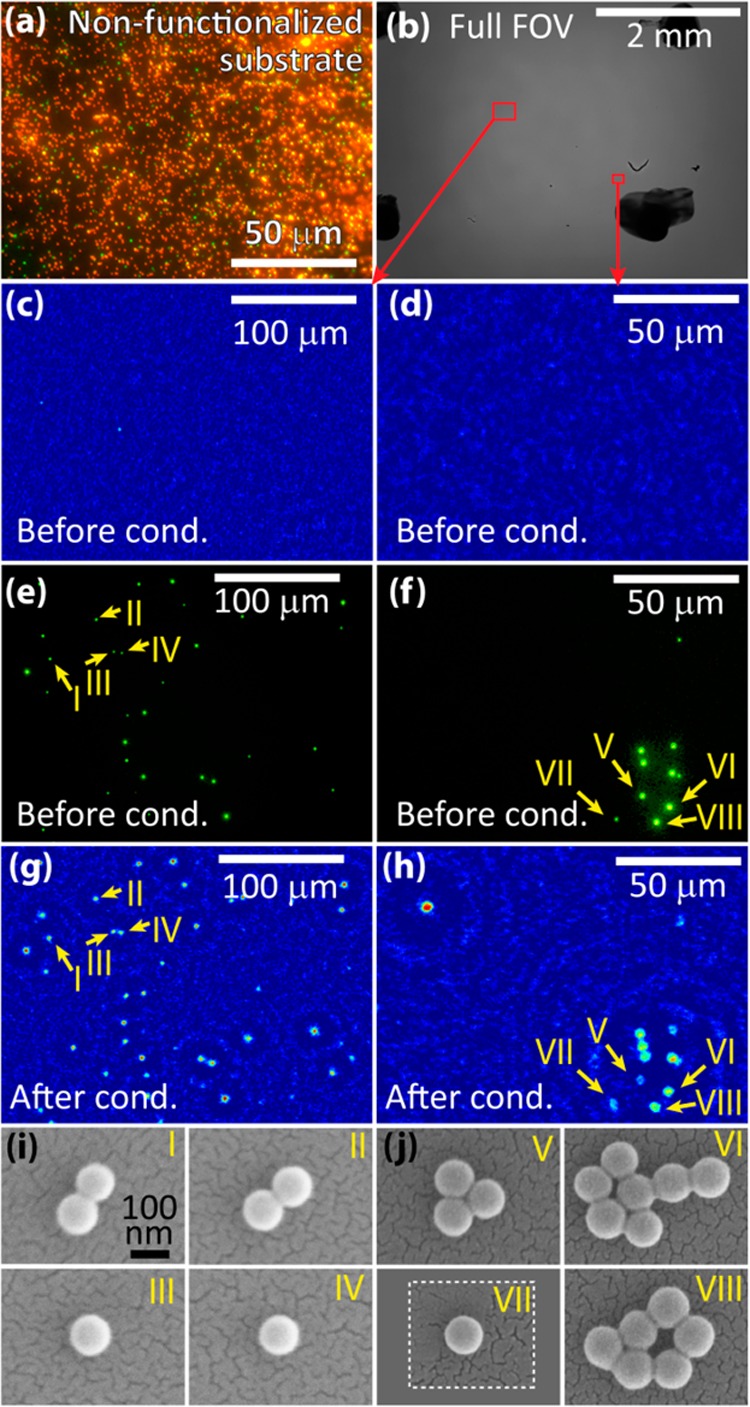
Nano-objects imaged with the aid of vapor-condensed nanolenses. (a–e) Detection of polystyrene nanoparticles. The full field of view hologram is shown in (a), with a super-resolved zoom-in in (b). The reconstructed phase image of a region of interest is shown in (c), where no particles are visible because their holographic signals are too weak. After the condensation of nanolenses, individual particles in the same region of interest become visible in (d). SEM is used to verify the size of the particles that were detected (e). (f–h) Another region of interest with polystyrene particles. This region shows two larger, irregular particles, along with a particularly small, sub-40 nm particle. (i–k) Detection of gold nanoparticles. In addition to these nanoparticles, this region of interest includes two very large dust particles, which can be seen in both the “before” image (i) and the “after” image (j), showing that the two images are correctly registered. (l–n) Imaging of large, multiwalled carbon nanotubes, where the curved shapes of the nanotubes are visible. (o–q) Detection of smaller multiwalled carbon nanotubes with diameters below 20 nm. These tubes are too short for their shape to be correctly resolved; however they are still detectable. (r–t) Imaging of a platinum pattern deposited on an indium–tin-oxide substrate using a focused electron beam. Although parts of this pattern are still visible in the “before” image, the contrast is significantly improved by condensation of nanolenses. Throughout the entire figure, for each pair of “before” and “after” images, the same color map is used for both figures, although the working distance, z₂, may be slightly different (see the Materials and Methods section).

Results

In Figure 2, we show the results of a variety of different nano-objects whose imaging is enabled through the combination of vapor-deposited nanolenses and lens-free holographic on-chip microscopy. Types of particles include polystyrene beads (Figure 2a–h), gold nanoparticles (Figure 2i–k), carbon nanotubes (Figure 2l–q), and a platinum-based pattern written on an indium–tin-oxide substrate (Figure 2r–t). For each set of nano-objects, we show control images of lens-free reconstructions of the sample without condensed nanolenses, lens-free reconstructions of the same regions of interest with condensed nanolenses (see Supporting Figures S1 and S2 for larger regions of interest), and SEM images of the target particles for true size determination. For our lens-free images, we use reconstructed phase images, which provide us the highest sensitivity and contrast for these small particles.

In addition to our ability to detect significantly smaller particles, this condensation-based approach to nanolens formation provides flexibility in terms of the particle surface chemistry. One example of this is the carbon nanotubes shown in Figure 2l–n. These nanotubes are highly hydrophobic and incompatible with aqueous solutions. Here we performed their deposition on the substrate by first suspending them in acetone and then letting the acetone evaporate. Despite the nanotubes’ hydrophobic surface chemistry, PEG nanolenses provided commensurate enhancement as found for the more hydrophilic polystyrene beads.

Biochemically functionalized particles can also be detected using vapor-condensed nanolenses after specific capture. This capability is particularly useful when trying to identify a specific type of particle from a heterogeneous solution (e.g., a virus or protein in whole blood⁵⁰). In Figure 3, we demonstrate a proof-of-concept approach to image specific nanoparticles captured based on the interaction between biotin and streptavidin.

Figure 3.

Specific capture and wide-field imaging of individual biofunctionalized nanoparticles on a chip. (a) Conventional 40× fluorescent microscope image of the bead mixture on a nonfunctionalized substrate. Many plain red 100 nm beads can be seen, as can a few streptavidin-coated green 110 nm beads. (b–j) Images of green streptavidin-coated beads specifically captured on biotinylated glass, mimicking the capture of virus-sized particles. (b) Full FOV holographic on-chip microscope image before deposition of vapor-condensed nanolenses. (c, d) Two regions of interest showing that beads cannot be detected without condensed nanolenses. (e, f) Conventional fluorescent 40× objective microscope images showing specific capture of only streptavidin-coated beads. (g, h) Holographic images of the sample with vapor-condensed nanolenses showing particle detection. (i, j) SEM images that verify the sizes of the detected particle clusters. For all lens-free images, the working distance is z₂ ≈ 280 μm.

We first prepare an aqueous mixture of plain red fluorescent nanobeads and streptavidin-coated green fluorescent nanobeads, both ∼100 nm. When a drop of this solution is deposited on a substrate and left to evaporate, we can measure the ratio of plain red beads to streptavidin green beads, which was 3.9:1 (Figure 3a). To achieve specific capture of the green streptavidin-coated beads, we use a biotinylated glass slide as a substrate (see Materials and Methods section). This process provides excellent specificity with minimal nonspecific binding, as verified using fluorescent microscopy in Figure 3e and f, which show many green beads and no red beads. See Supporting Figure S3 for quantification of the sensitivity and specificity of our surface capture. After using surface chemistry to provide specific capture of the desired nanobeads, we use holographic on-chip microscopy and vapor-condensed nanolenses to image the captured particles. As a control experiment, we first use on-chip holographic imaging without nanolenses to attempt to detect the specifically captured beads (Figure 3c and d). As expected, beads this small are undetectable in this lens-free on-chip imaging setup. After vapor-condensing nanolenses on the sample with a short plasma treatment to make the surface hydrophilic, the captured beads are now easily visible using on-chip holographic microscopy. The particle locations observed after nanolens deposition (Figure 3g and h) coincide with the particle locations measured using a conventional fluorescence microscope before plasma treatment and deposition (Figure 3e and f). SEM images are also used to verify the size and shape of the objects we are detecting (Figure 3i and j).

To quantify the signal enhancement provided by vapor-condensed nanolenses, we plot in Figure 4 the peak reconstructed phase signal (i.e., greatest pixel value) from holographic on-chip images for both polystyrene spheroidal particles (e.g., those shown in Figure 2a–h) and carbon nanotubes (e.g., those shown in Figure 2l–q). These plots show that phase signal scales with particle diameter and that the threshold for particle detection using nanolenses lies below 40 nm for spheres and 20 nm for carbon nanotubes. The performance of this platform can be further improved in terms of limit of detection by using, for example, a high-bit-depth and cooled image sensor chip to further push the noise level down. The analysis reported in Figure 4 reveals that for objects with <50 nm feature size our vapor-condensed nanolenses improve the detection SNR by as much as 35 and 20 dB for spherical and rod-shaped nanoparticles, respectively.

Figure 4.

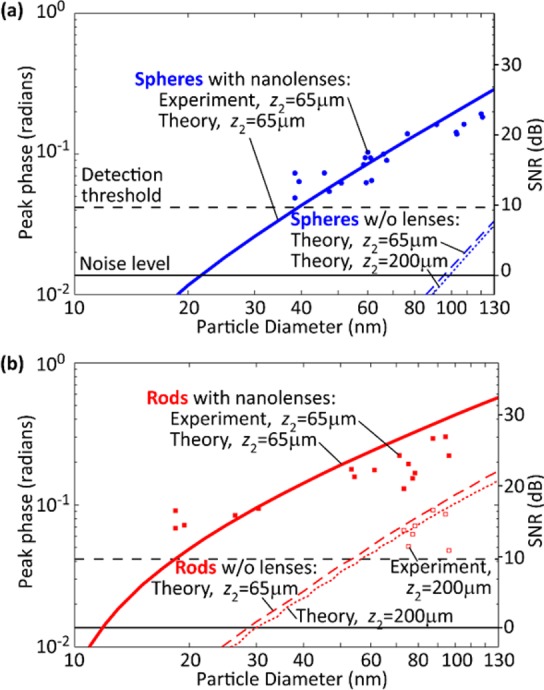
Experimental and simulated signal levels of nanoparticles with and without vapor-condensed nanolenses. (a) Spheroidal polystyrene particles. Vapor-condensed nanolenses raise the nanoparticle signal levels above the detection threshold. The solid blue line was determined using the vapor density as a fitting parameter, with value of 3.6 × 10¹⁵ molecules/m³. The blue dashed lines used no fitting parameters. For 40 nm particles, there is ∼50-fold improvement in signal level for particles with nanolenses compared to those without. The root-mean-square noise level was measured experimentally in several experiments and found to be ∼0.014 radians. The empirically determined detection threshold is set at 3 times the background noise level, which also corresponds to what a human observer can reliably discern relative to background fluctuations. (b) Rod-shaped carbon nanotubes. The minimum detectible diameter (D) is smaller for rod-shaped particles than for spheroidal particles. The larger carbon nanotubes are experimentally detectable without nanolenses. Their signal values agree well with theoretical predictions. No fitting parameters were used in this panel; the solid red line uses the same vapor density as in (a).

Discussion

To better understand how vapor-condensed nanolenses enhance the phase signal and what kinds of nanolenses perform best, we have modeled the nanolens growth, along with their optical responses, and compared these results to experimental measurements in Figure 4. In modeling the nanolens growth, we assume that the condensation is film-wise; that is, any PEG vapor molecule that hits the substrate will condense, and the driving force for condensation is sufficiently strong due to the undercooling of the substrate such that there is no nucleation barrier. In Supporting Figure S4, we provide further evidence for this assumption, ruling out the dropwise condensation model. Under the film-wise model, surface tension causes the film to rise in the form of a meniscus around embedded nanoparticles (Figure 1b), thereby forming the signal-enhancing nanolens. As detailed in the Materials and Methods section, the shape of the nanolens can be calculated from the Young–Laplace equation with the inclusion of a van der Waals disjoining pressure, which can be significant for films this thin.^21,51 The boundary conditions we use for the Young–Laplace equation are the contact angle at the particle and the film thickness at large r. At the particle, we assume a contact angle of 50°, based on the macroscopically measured contact angle of PEG on polystyrene, as well as measurements of PEG contact angles on carbon nanotubes, which have a similar value of 57.4 ± 5.9°.⁵² However, it is important to note that, especially for the polystyrene beads we are using, the particle contact angle has not been well-characterized in our nanoscale system, and effects resulting from surface chemistry of the particle, surface roughness, and van der Waals interactions could alter the contact angle. Fortunately, simulations show that the results of this model are not especially sensitive to moderate variations in contact angle (see Supporting Figure S5). The second boundary condition, the film thickness far away from nanoparticles, is determined by the time and temperature of the condensation process. It grows linearly in time at a rate determined by the vapor density.⁵³ With the governing equation and boundary conditions established, the lens shapes can be calculated as a function of time for both spherical particles (Figure 1b) and rod-shaped particles (Supporting Figure S6).

The optical properties of the nanoparticles and lenses are modeled using a thin-lens approximation with a laterally varying vertically integrated optical path length determined by the nanoparticle and lens topography. In a previous study, we have compared this type of model to a finite-difference time-domain model and found the two models to be equivalent.¹³ Based on this thin-lens approximation, we compute the in-line hologram formed by the object using the angular spectrum approach, which simulates the complex optical field at the complementary metal-oxide-semiconductor (CMOS) image sensor plane.^49,54 As the CMOS image sensor can only sense the intensity of the hologram, we keep only the amplitude information from the field at this plane, down-sample it to a super-resolved pixel size of 0.28 μm, and then back-propagate to the object plane, again using the angular spectrum approach. This simulation thus replicates the way the experimental data are processed to retrieve phase and amplitude images of specimens. After back-propagation, we record the peak value of the phase for different particle diameters and plot the data as lines in Figure 4.

In performing these simulations, a single fitting parameter was used, the effective PEG vapor density, which depends on the PEG heating temperature. This parameter was chosen to provide the best fit between experiment and theory for spheres with nanolenses in Figure 4a. We find this fitting parameter necessary to accurately simulate the nonequilibrium condensation with our steady-state model. In the experiment, it is difficult to quantify the true PEG vapor density due to the short duration of the experiment and initial transient fluctuations from mixing with ambient air during sample insertion. However, we would expect the true PEG vapor density to lie somewhere between the saturated vapor densities at room temperature (25 °C) and at the heated PEG reservoir temperature of 105 °C. Indeed, the best-fit PEG vapor density of 3.6 × 10¹⁵ molecules/m³ corresponds to the saturated vapor density at 40 °C and, thus, falls within the expected bounds. Supporting Figure S4 shows additional curves for different effective vapor densities.

Further validation of the theoretical model is obtained by testing its predictions for carbon nanotubes using the same value of the effective PEG vapor density, shown in Figure 4b. These results, along with the results of the control simulations (nanotubes without nanolenses, dashed lines in Figure 4b), which used no fitting parameters, show a continued good match between experiment and simulation. Note that spheroidal particles do not provide a strong enough signal to be measured without nanolenses and, thus, cannot be directly compared with simulation predictions. Although it does not significantly affect the recovered signal, the control simulations of particles without nanolenses were conducted at two different working distances to match experimental conditions.

Interestingly, the addition of nanolenses changes the characteristic scaling of the phase signal ϕ with respect to particle diameter, reducing its exponent (q, where ϕ ∼ D^q), as evident from the reduction in slope shown on the log–log plots in Figure 4 upon deposition of nanolenses. A reduction in exponent corresponds to enhanced signals from smaller particles. Rayleigh scattering theory predicts a scattered power from nanoparticles P ∝ D⁶, which would apply to microscopy modalities such as dark-field microscopy.³⁸ In contrast, holographic microscopy records the interference of the scattered wave with a reference wave, with a signal that is proportional to scattered field amplitude, reducing the scaling exponent from q = 6 to q = 3. Note that the simulations for spherical particles without nanolenses shown in Figure 4a show consistent scaling with q = 3.0 for z₂ = 200 μm and q = 2.9 for z₂ = 65 μm. After the deposition of vapor-condensed nanolenses, the exponent reduces even further to q = 1.6, based on a linear fit to the solid blue curve for 100 nm < D < 130 nm. For rod-shaped particles, the exponents do not initially follow Rayleigh scattering theory (q = 2) because the rods are simulated with a complex refractive index (absorption) and with a length significantly longer than the wavelength of light, where Rayleigh theory fails. The rod simulation exponents, again for 100 nm < D < 130 nm, are q = 1.5 for z₂ = 65 μm without nanolenses, q = 1.4 for z₂ = 200 μm without nanolenses, and q = 1.1 for z₂ = 65 μm with nanolenses. Therefore, we can conclude that vapor-condensed nanolenses reduce the scaling exponent for rod-shaped particles, just as they did with spherical particles. This reduction in scaling exponent is commensurate with significantly improved signal.

We have also investigated the effect of condensation time and PEG vapor density on recovered phase signal in Figure 5, which provide two modes of tunability to improve our detection performance by >30 dB for the 50 nm spherical particles simulated here. For a given vapor density, the phase signal shows an optimum in time because small levels of condensation generate only small lenses, while very large amounts of condensation end up burying a particle under a thick continuous film, entirely eliminating the lensing effect. As one might expect, greater vapor densities produced from higher PEG heating temperatures speed up the lens growth rates. For comparison to previous work, we also show the phase signal that is theoretically predicted for a catenoid-shaped minimal-surface nanolens of the type formed through a previous liquid flow method of producing nanolenses.¹³ We see that such a nontunable minimal-surface-based nanolens would not boost the phase signal above the detection threshold for, for example, D = 50 nm and that the tunability afforded by vapor-condensed nanolenses provides significant detection advantages.

Figure 5.

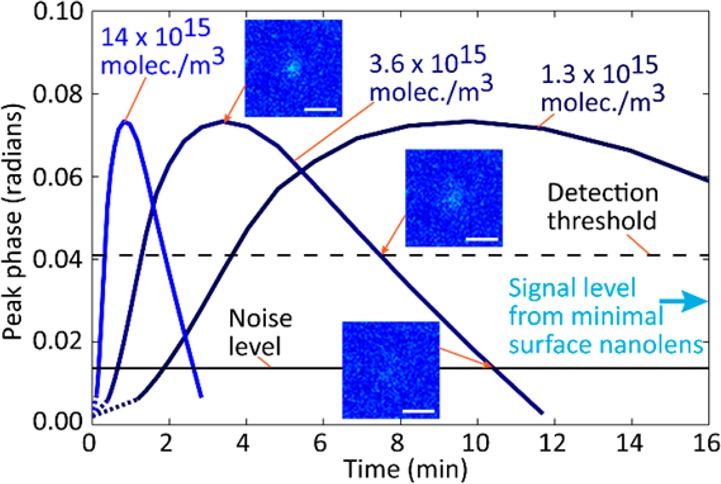
Tunability of signal enhancement based on time and vapor density. The level of the phase signal for 50 nm beads is simulated for three different vapor densities, corresponding to different heating temperatures. The three insets show the simulated reconstruction images with signal levels at the maximum, at the detection threshold, and at the noise level. Scale bars are 5 μm. The noise level and detection threshold are based on experimental measurements (see Figure 4). The minimal surface nanolens phase (0.030 rad) is the result of a simulation of a catenoid-shaped nanolens with a substrate contact angle of 2.5°.¹³

Conclusions

In summary, we have shown a method to fabricate tunable self-assembled nanolenses around nanoparticles using the condensation of PEG from the vapor phase. We have applied these nanolenses to significantly boost SNR for the detection and localization of nanoparticles across an ultralarge field of view using lens-free holographic on-chip microscopy. These vapor-condensed PEG nanolenses perform significantly better than previous nontunable nanolenses, enabling the detection of spherical particles below 40 nm and rod-shaped particles with diameters below 20 nm. The optical enhancement provided by these nanolenses agrees very well with theory. This vapor-based condensation approach also provides the advantages of compatibility with various surface chemistries and compatibility with specific and sensitive particle capture based approaches necessary for isolating bionanoparticles from multicomponent samples. Furthermore, both the nanolens vapor condensation and its wide-field on-chip imaging can be performed within a cost-effective and portable device (see, for example, Figure 1e), which may find wide-scale use in field settings as well as mobile sensing and diagnostics applications. These developments can pave the way for label-free and field-portable detection of biological nanoparticles such as viruses in complex heterogeneous samples including, for example, whole blood. With further enhancements in SNR so that particles as small as ∼10 nm diameter are detectible, it may be possible to perform single biomolecule detection using this vapor-condensation technique. Whispering gallery mode detection schemes can already detect individual particles at approximately this scale,⁵⁵⁻⁵⁷ and it is possible that the use of vapor condensation may enhance the signal found in these devices too. However, one limitation regarding this technique that should be considered is that the target nanoparticles must be adsorbed on a bare substrate, and thus nanoparticles must be removed from their solution before they are detected.

In a broader context, this method of constructing tunable nanolenses may prove useful for fabricating lithographically controlled nanolenses for other nanoimaging and detection applications. Creating a regular array or particular pattern of nanolenses would require the controlled deposition of nanoparticles or formation of nanoprotrusions on a substrate, tasks that are possible using standard nanolithography techniques. A resulting hybrid nanofabrication approach that incorporates vapor condensation would therefore provide a way to fabricate 3D nanolenses starting from standard 2D lithography approaches.

Materials and Methods

Sample Preparation

Deposition of nanoparticles on the substrate, a #1 cover glass, depends on the type of nanoparticles. For polystyrene beads (Figure 2a–h, Figure 4, Supporting Figure S1, and Supporting Figure S4), manufacturer stock solutions (Invitrogen F8800, F20886, F8783) are diluted between 5 million-fold and 500 million-fold in alcohol (either ethanol or 2-propanol), and a 1–5 μL drop is deposited on a plasma-treated (Electro-Technic Products, BD-10AS) cover glass and left for the solvent to evaporate. For gold nanoparticles (Figure 2i–k), manufacturer stock solutions (nanoComposix, DAC1278) are diluted several hundred times in a Tris/PEG-600/HCl mixture (Sigma-Aldrich, 07066), a 6 μL drop of which is deposited on a plasma-treated cover glass and left to sediment for 5 min, after which the excess liquid is removed by tilting the substrate. This procedure forms minimal-surface nanolenses,¹³ which are further improved by the vapor-condensed nanolenses added later. For multiwalled carbon nanotubes (Figure 2l–q and Figure 4), the as-received powder (CheapTubes, 03040203, 03040204, 030104, 030106, 030107) is suspended in acetone at concentrations between 0.1 μg/mL and 1 mg/mL and is deposited on a plasma-treated cover glass and left to evaporate. For the platinum direct-write pattern (Figure 2r–t), the substrate is an indium–tin-oxide-coated glass, 0.5 mm thick. A focused ion beam/scanning electron microscope system (FEI Nova 600 NanoLab) is used to locally deposit platinum on the substrate where the scanning electron beam is focused. The height-to-width aspect ratio of these patterns is approximately 1:1, and the line cross sections are approximately Gaussian.

For the specificity experiments (Figure 3 and Supporting Figure S3), the sample preparation was more specialized. First, a coverslip is biotinylated using the following procedure: (1) dissolve biotin-PEG-silane (Laysan Bio, Biotin-PEG-SIL-3400-1g) at a concentration of 6.8 mg/mL in 95% ethanol, 5% water, (2) plasma-treat using hand-held plasma treater (Electro-Technic Products, BD-10AS), (3) drop 10 μL of biotin solution onto cover glass, (4) wait for cover glass to dry, then rinse with deionized (DI) water. The bead mixture was prepared by combining 1 μL of the manufacturer stock solution of 110 nm green fluorescent streptavidin-coated beads (Bangs Laboratories, CP01F) and 0.4 μL of the manufacturer stock solution of 100 nm red fluorescent carboxylate-coated beads (Invitrogen, F8800) in 1 mL of water with 3% sodium dodecyl sulfate (SDS). In Figure 3, this solution was diluted by a factor of 1:9 in water and 3% SDS, while in Supporting Figure S3 many different dilution factors were used. A 0.5 μL droplet of the solution was placed on the biotinylated cover glass, and an untreated cover glass was placed on top with 40 μm spacers between the two glasses. The sample was left for 3 min and then disassembled, and the biotinylated cover glass was washed with DI water. The sample was imaged using fluorescence and lens-free imaging to acquire “before” images. Finally, before condensing the nanolenses, the back side of the sample was plasma treated to make the sample more hydrophilic.

Vapor Condensation

Polyethylene glycol 300 (Sigma-Aldrich, 202371) was poured into a 4 in. glass Petri dish to form a pool of liquid 2 mm deep. This Petri dish was heated on a hot plate at 105 °C (110 °C in the case of Figure 2i–k) for 30 min to allow for the evaporation of water and any particularly short PEG chains that happened to be present in the PEG 300. The nanoparticle sample was mounted upside-down on a bridge-shaped structure using double-sided tape such that the gap between the liquid pool of PEG and the sample was 4 mm (see Figure 1c). The chamber was covered and left for 2 min, and then the sample was removed.

Holographic on-Chip Imaging

We use a lens-free holographic on-chip microscope to image our samples (Figure 1d). This imaging platform has been described extensively in previous publications.^13,40,42,48 The microscope includes automated source-shifting to capture pixel-super-resolved in-line holograms, resulting in a spatial resolution below 0.3 μm even under unit magnification, where the sample field of view equals the active area of the CMOS imager. We image using 480 nm light with a bandwidth of 3 nm generated using a monochromator (Newport, 74100), projected from the end of a 100 μm core diameter fiber. The distance between the light source and the sample is z₁ = 6 cm. The working distance between the sample and the sensor (Sony, 16 megapixel, 1.12 μm pixel pitch) varied among the experiments: for Figure 2c, f, i, j, l, and o, z₂ was between 197 and 212 μm; for Figure 2d, g, m, p, r, and s, z₂ was between 61 and 66 μm; for Figure 3, all lens-free images were acquired with z₂ between 280 and 290 μm; and for Figure 4, all of the experimental data points after nanolens condensation were acquired with z₂ between 61 and 71 μm, while all of the experimental data points before nanolens condensation were acquired with z₂ between 181 and 198 μm. Raw low-resolution holograms were melded into a super-resolved hologram using a pixel super-resolution procedure.^40,58−60 These holograms are digitally reconstructed using the angular spectrum method,^49,54 with the phase channel being used to report results. Noise levels were computed by finding the standard deviation of the background fluctuations in a region without particles.

Scanning Electron Microscopy for Independent Size Quantification

Samples were coated with 13.6 nm of gold (8.5 nm of AuPD alloy in the case of Figure 2k) using an ion beam sputterer and imaged on a scanning electron microscope (FEI Nova 600 NanoLab). These coating thicknesses were calculated by observing the apparent change in size of nanoparticles as a function of coating time in the ion beam sputterer. When quoting SEM-measured particle sizes here, these coating thicknesses were subtracted from the raw measurement of the thickness.

Lens Shape Modeling

In the following analysis, we leave the effective vapor density, n₀, variable to be used as a fitting parameter in comparing with experimental data. The molecular flux in the vapor can be derived from the Maxwell–Boltzmann distribution and is given by⁶¹

where k is Boltzmann’s constant, m₁ = 4.69 × 10^–25 kg is the mass of a single PEG molecule (assumed to have 6 monomer units so that the molecular weight is ∼300 Da), and we have chosen the temperature to be that of a saturated vapor with density n₀ at ambient pressure. Based on the ideal gas law,

where p_vap is the partial pressure of the saturated vapor, which is also a function of temperature. Using the curves for the vapor pressure of ethylene glycol, diethylene glycol, triethylene glycol, and tetraethylene glycol,⁶² we have extrapolated the vapor pressure of PEG to be

where M = 6 is the number of monomers and T_sat^Cel is the saturation temperature in Celsius. These two equations can be solved numerically to find T_sat(n₀), which is expected to lie somewhere between room temperature and the heated PEG temperature (typically 105 °C).

Under the assumption of filmwise condensation, there is no nucleation barrier to condensation on the substrate, and therefore the condensing film thickness is given by

where V₁ = m₁/ρ_PEG is the volume of a single molecule of PEG (ρ_PEG = 1130 kg/m³),⁶³ and t is time.

The shape of the nanolens (meniscus) that forms around an embedded particle is found by solving the Young–Laplace equation with a disjoining pressure:^21,51,64

where Δp is the pressure drop across the liquid–vapor interface, g is acceleration due to gravity, h is the local height of the interface, γ = 42.2 mN/m is the surface tension of the PEG at 40 °C,⁶⁵K_m is the local mean curvature of the interface, and ∏(h) is the disjoining pressure of the film due to van der Waals interactions, given by

where A₁₂₃ = −6.3 × 10^–21 J is the Hamaker constant for a glass–PEG–air system.²¹ As Δp is space-invariant, we can compute it far from the nanoparticle, where the film is essentially flat (K_m = 0):

In a cylindrical coordinate system, which applies to modeling the lens formed around spherical nanoparticles, the mean curvature can be derived from a cylindrical parametrization of the surface and expressed in either of the two forms⁶⁶

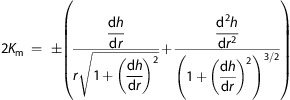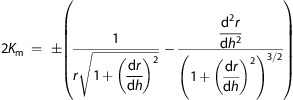The analytical form that is most convenient depends on the local slope and curvature of the interface (i.e., is h a single-valued function of r, or is r a single-valued function of h?). After substituting these expressions into the Young–Laplace equation, it can be seen that the Young–Laplace equation is a second-order nonlinear ordinary differential equation (ODE) and, thus, requires two boundary conditions. The film thickness at infinity, h₀, is one boundary condition, and the contact angle of the film at the particle, θ_p, is the other boundary condition.

We numerically solve this nonlinear ODE using a custom-written MATLAB program that sequentially solves a number of initial value problems that trace the interface starting from the particle, moving outward. These initial value problems are characterized by the initial slope of the interface based on the assumed θ_p and the contact height of the interface at the particle (0 ≤ h_p ≤ D), where D is the particle diameter. As this interface is traced outward from the particle, the solver intelligently switches between the two forms of the mean curvature and so can handle interfaces that completely curve back on themselves. This approach automatically satisfies the boundary condition given by θ_p, while the boundary condition of the film thickness at infinity being h₀ is satisfied by selecting the film shape corresponding to the initial contact height h_p that results in h → h₀ as r → ∞. These results are shown in Figure 1b and Supporting Figure S4a for the time-varying h₀.

For modeling the lens shape around rod-shaped particles, the approach is similar. Here we will assume that the rod is oriented along the x-direction such that the meniscus falls away from the rod in the y-direction. Then, the Young–Laplace equation becomes

and the two mean curvature expressions are⁶⁶

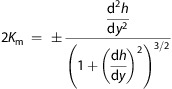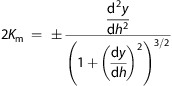We generally model the rods as being 5 μm long; rods between 500 nm and 10 μm long show approximately constant signal with variations less than ±15% (Supporting Figure S7). For the rod end-caps we use hemispheres with lens shapes predicted by the spherical particle solution. This approximation in lens shape at the edge does not reflect the true lens shape at the edges, which would require a more advanced finite-element approach to model, which is beyond the scope of this paper. However, these errors in edge effects should have only a minor contribution to the recovered phase signal compared to the long body of the rod being simulated. The remaining steps in modeling lenses around rod-shaped particles are the same as for modeling lenses around spherical particles, and the results can be seen in Supporting Figure S6.

Optical Modeling

To numerically model the holographic microscopic imaging of the nanoparticles and nanolenses, we first treat the nanoparticles and nanolenses using the thin-lens approximation, which has been shown to be equivalent to an FDTD simulation for similar objects,¹³ although here we model the materials using complex refractive indices to account for absorption and scattering. For polystyrene particles, we use n = 1.61;^67,68 for multiwalled carbon nanotubes, we use the refractive index of amorphous carbon, n = 1.80 + 0.692i;^67,69 for PEG 300, we use n = 1.46.⁶³ Using the above model for the lens shapes, we compute the net optical path length (particle and lens together) through each (x, y) point of the system, on a grid with an interval size 3.5 nm and full dimensions of 83 μm × 83 μm. Using the angular spectrum method, we compute the hologram that is generated a distance z₂ away when this material system is illuminated with a plane wave,^49,54 which represents the hologram at the sensor plane. This hologram is then down-sampled to a super-resolved pixel-size of 1.12 μm/4 = 0.28 μm, and its phase is set to zero, simulating the hologram that would be recorded experimentally. The resulting hologram is interpolated by a factor of 2 and then back-propagated, again using the angular-spectrum approach, which is the same procedure used to recover images experimentally. In these recovered images, we record the peak value of the phase image, which we then plot in Figure 4, Figure 5, and Supporting Figures S4, S5, and S7.

The authors declare the following competing financial interest(s): A.O. is the founder of a start-up company (Holomic LLC) that aims to commercialize lens-free microscopy tools.

Supporting Information Available

Larger lens-free fields of view corresponding to Figure 2 reconstructions, sensitivity and specificity of streptavidin-coated bead capture, comparison between filmwise and dropwise condensation models, peak phase signal dependence on particle contact angle, nanolens shape formed around nanorods, nanorod peak phase signal dependence on rod length, methods for modeling the shape of isolated nanolenses, and supporting references. This material is available free of charge via the Internet at http://pubs.acs.org.

Funding Statement

National Institutes of Health, United States