Abstract
We previously demonstrated that individual molecules of single-stranded DNA can be driven electrophoretically through a single Staphylococcus aureus -hemolysin ion channel. Polynucleotides thread through the channel as extended chains and the polymer-induced ionic current blockades exhibit stable modes during the interactions. We show here that polynucleotides can be used to probe structural features of the -hemolysin channel itself. Specifically, both the pore length and channel aperture profile can be estimated. The results are consistent with the channel crystal structure and suggest that polymer-based “molecular rulers” may prove useful in deducing the structures of nanometer-scale pores in general.
I. INTRODUCTION
High-resolution x-ray crystal structures of proteins are invaluable tools for basic research in biology, biophysics, and biotechnology.1 Although there are notable exceptions (e.g., Refs. 2 and 3), membrane-bound proteins are difficult to crystallize compared to their water-soluble counterparts. Thus, other methods are usually needed to reveal the salient features of transmembrane proteins.
Ion channels4 lend themselves to simple structure determination techniques because their functional aspect can be probed by conductance measurements. For example, scanning cysteine mutagenesis and covalent chemical modification were used to identify amino acid side chains that line the pore of the nicotinic acetylcholine receptor channel,5 the Staphylococcus aureus -hemolysin channel,6–14 and the active form of Bacillus anthracis protective antigen (i.e., ).15,16
Nonelectrolyte water soluble polymers have been used to deduce channel structural features. For example, in the pioneering study by Zimmerberg and Parsegian,17 pore-impermeant poly(ethylene glycol) (PEGs) molecules were used to estimate the change in volume that occurs when the voltage dependent anion channel18 gates between two predominant conductance states. In addition, Krasilnikov and others used PEGs to estimate the radii of ion channels from the ability of size-selected PEGs to partition into the channel pore.11,19–36
Protein translocation across membranes, which plays a key role in many biological processes, can be facilitated by ion channels.37–39 Other biomolecules can be detected as they transport through ion channels. For example, we demonstrated that individual molecules of single-stranded DNA (ssDNA) could be characterized as they are driven electrophoretically into and through a single channel.40 Because the mobility of negatively charged polynucleotides is less than that of monovalent ions (i.e., , , and ) in those solutions, the channel conductance decreases significantly when the anionic polymer is inside the pore. The mean lifetime of the polynucleotide-induced current blockades is proportional to the polymer contour length,40 which suggested that the polymer threads through the pore as a linear chain, as illustrated schematically in Fig. 1. Theoretical models and Monte-Carlo simulations that describe the transport of polynucleotides and idealized polymers through idealized nanoscale pores have been developed.41–55 In addition, the ability of another ion channel to catalyze DNA transport has been identified by Szabo and colleagues.56
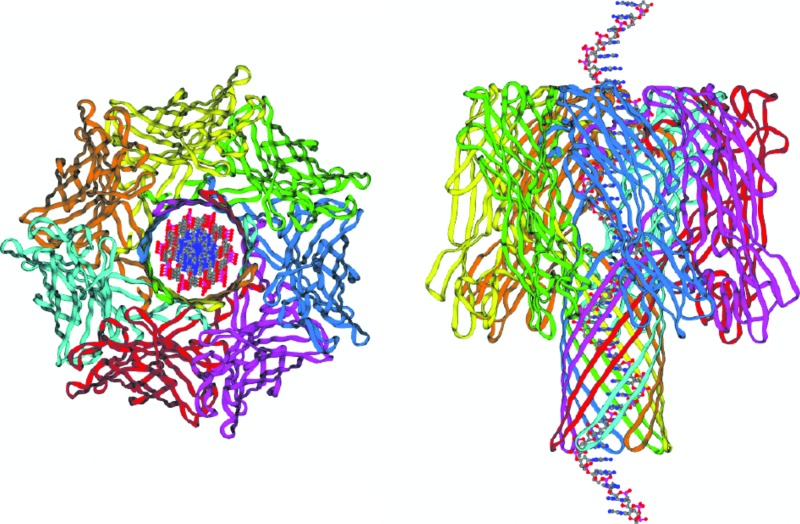
FIG. 1.
Model nanopore for DNA transport studies. The alpha-hemolysin ion channel crystal structure is shown (Ref. 2) along with an idealized single-stranded DNA molecule superposed inside the channel. The exterior length and width of the channel are both approximately 10 nm. The narrowest constriction within the pore is approximately 1.5 nm in diameter (Refs. 2, 11, 20, 26, 32, and 33), which is much wider than that of highly ion selective protein ion channels (e.g., Ref. 3). We show here how DNA can be used to probe the structure of the channel pore.
The rate at which polynucleotides enter the channel is voltage dependent.57 Assuming that the interaction between the polymer and the pore could be treated as a chemical reaction, a Van’t Hoff–Arrhenius rate law was used to estimate the height of the energy barrier for polymer entry into the pore57 and a more detailed stochastic simulation to describe this effect was developed by Ambjörnsson and colleagues.58 We demonstrate here how polynucleotides can be used as molecular rulers to better understand the interaction of a nanopore with individual polymers, and to determine the location of the energy barriers to polynucleotide transport.
II. MATERIALS AND METHODS
The ability of polynucleotides to partition into a nanometer-scale pore was studied by measuring the polymer-induced effects on the ionic current flowing through a single channel in a planar lipid bilayer membrane.8,10 The current was measured before and after the addition of polymer to the bulk aqueous phase on one side of the membrane. Polynucleotides were driven into the channel pore by an applied electrical potential of the appropriate polarity. Individual polynucleotides that enter the pore cause transient blockades in the single channel current.40 These events were digitally recorded and the lifetime, amplitude, and pattern of the ssDNA-induced current blockades were measured.59–61
A. Membrane and channel formation
Solvent-free planar lipid bilayer membranes62 were formed from diphytanoyl phosphatidylcholine (Avanti Polar Lipids, Inc., Alabaster, AL) in pentane (Burdick and Jackson, Muskegon, MI). The membranes were made on diameter holes in a thick Teflon partition that separates two identical Teflon chambers. The hole was pretreated with a solution of 10% (v/v) hexadecane (Aldrich) in pentane. Both chambers contained 1 M KCl (Mallinckrodt, Paris, KY), 5 mM HEPES (Calbiochem, San Diego, CA), titrated to pH 7.5 with concentrated NaOH (Mallinckrodt).
Single channels were formed by adding approximately of to a chamber on one side of the partition (herein called cis), which contained approximately 2 ml of 1 M KCl aqueous buffer solution. After a single channel formed, the cis chamber was rapidly perfused with fresh buffer to prevent further channel incorporation. An electrical potential of −120 mV, which drives anions from the cis to the trans side, was applied using Ag–AgCl electrodes in 3 M KCl, 1.5% (w/v) agar bridges. The current was converted to voltage and amplified using an Axopatch 200A patch-clamp amplifier and a CV 201 AU headstage (Axon Instruments, Foster City, CA). The signal was filtered using a Frequency Devices 9002 low-pass Bessel filter (Haverhill, MA) with a corner frequency set to 3/8 the sampling rate of either a National Instruments AT-MIO-16X 16-bit analog to digital converter board (Austin, TX) or an Axon Instruments analog to digital converter. The temperature was .
B. Polynucleotides and other reagents
The polynucleotides were purchased from Midland Certified Reagents (Midland, TX). The final concentrations of the polynucleotides in the cis and trans chambers were , unless otherwise noted. Neutravidin (Pierce Biochemicals), streptavidin (Molecular Probes) or -BRDU polyclonal antibody (Fitzgerald Industries International Inc., Concord, MA) was added to cis or trans sides as noted.
III. RESULTS AND DISCUSSION
A. Polynucleotides partition into single channels
Figure 2 illustrates typical blockades of the single channel ionic current caused by individual molecules of singe-stranded DNA. This and previous work demonstrated that the lifetimes of polynucleotide transits are typically per base.40,59,63,64
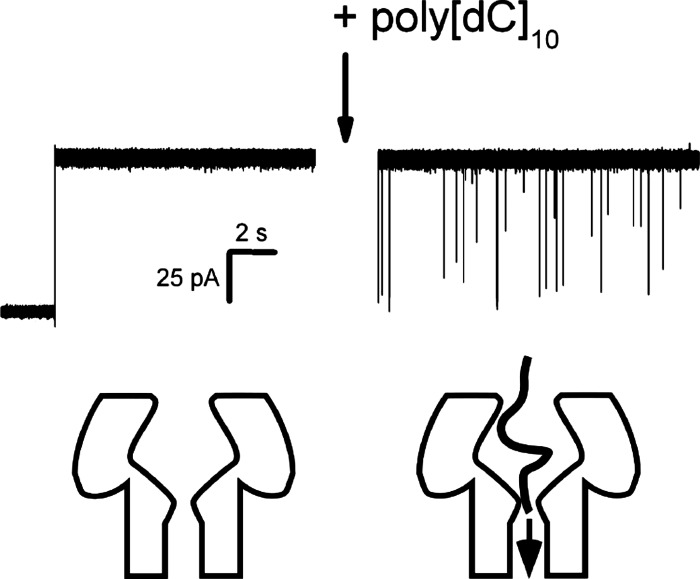
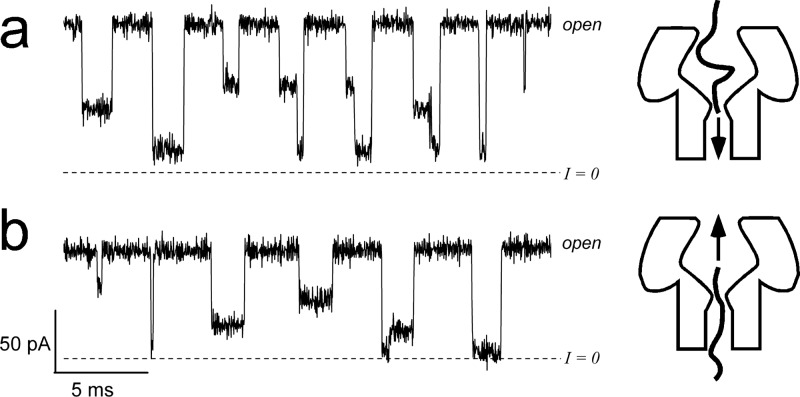
FIG. 2.
Single channel recordings show that polynucleotides partition into the pore, and transiently reduce the channel conductance. The step increase in current corresponds to the formation of a single channel (left). In the absence of single-stranded DNA, the current is quiescent. Addition of 10-nucleotide long poly[dC] (i.e., ) causes short-lived blockades in the ionic current (right). Each transient blockade in the ionic current is due to the partitioning of a single polynucleotide into the channel. There is a stable and repeatable state structure in the amplitude distribution of the current blockades over large event ensembles (e.g., Ref. 61).
B. Location of polynucleotide transport barrier
Previously, we demonstrated that the addition of a large protein cap at one end of a polynucleotide would inhibit the complete translocation of the polymer through the channel.57,59,65 Here, we provide more detailed experimental results that show how different length polymers can act as semiquantitative “molecular rulers” to determine how far the polymer must thread into the pore before it is committed to transport through the channel.
Different length biotinylated poly[dC] (i.e., bT-poly[dC]) molecules were added to the cis side in separate experiments. For illustrative purposes, the effects of 20 and 30-nucleotide long bT-poly[dC] are shown on the single channel current recordings (Fig. 3, top right). As expected, both polymers cause transient current blockades (Fig. 3 top, two single channel recordings, minus avidin). After adding avidin, the results show that the complex between avidin:bT-, but not avidin:bT-, occluded the pore virtually indefinitely [Fig. 3(a), plus avidin]. Similar experiments with different length bT-poly[dC] molecules showed that polymers containing more than 25 nucleotides occlude the pore in the presence of avidin (data not shown). Qualitatively similar results are observed when both biotinylated single-stranded DNA (ssDNA) and avidin are added to the trans side (Fig. 3, bottom). However, in that case, the minimum-length capped poly[dC] that occluded the pore is between 10 and 20 nucleotides. A statistical mechanical description for the interaction between a stretched polymer and an attractive well (which keeps the polymers beyond a critical length in the pore) is outlined in the Appendix.
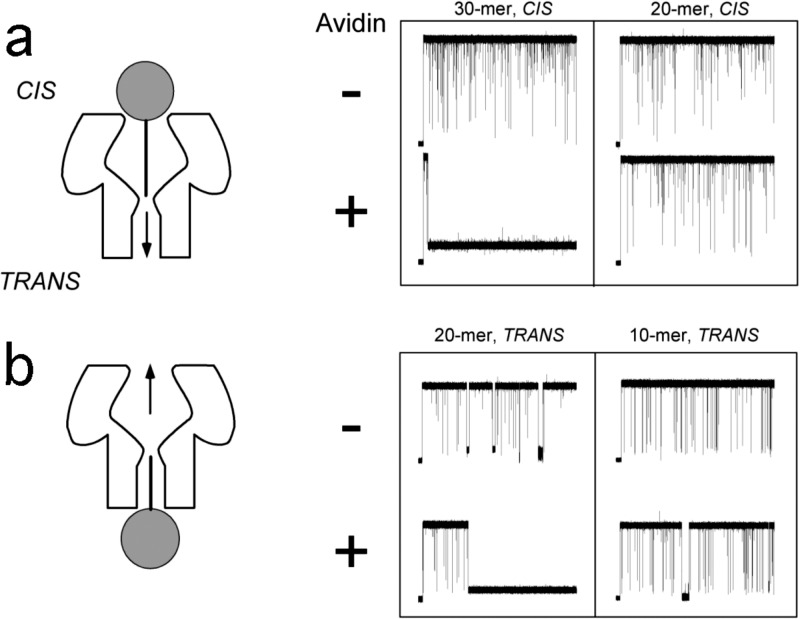
FIG. 3.
The use of DNA “molecular rulers” to locate the barrier for polynucleotide transport in the channel. (a) 30- or 20-nucleotide long biotinylated poly[dC] (bT on the -end of the polymer) added to the cis side cause transient blockades in the single channel current. The subsequent addition of avidin, which binds to biotin, causes the 30-nucleotide long polymer to occlude the pore but not the 20-nucleotide strand. (b) A qualitatively similar result was observed for polymer added the trans side. The data suggest there is a critical depth inside the channel at which the polymer is committed to transport through the pore.
The results shown in Fig. 3 suggest that the barrier to polynucleotide transport is approximately 25 and 15 nucleotides from the cis and trans pore entrances, respectively. The barrier probably corresponds to the smallest geometric constriction inside the pore near the amino acid side chain M113.2 Indeed, the steepest gradient of the electrostatic potential occurs over the region with the smallest cross-sectional area inside the pore.66
C. Length of the channel
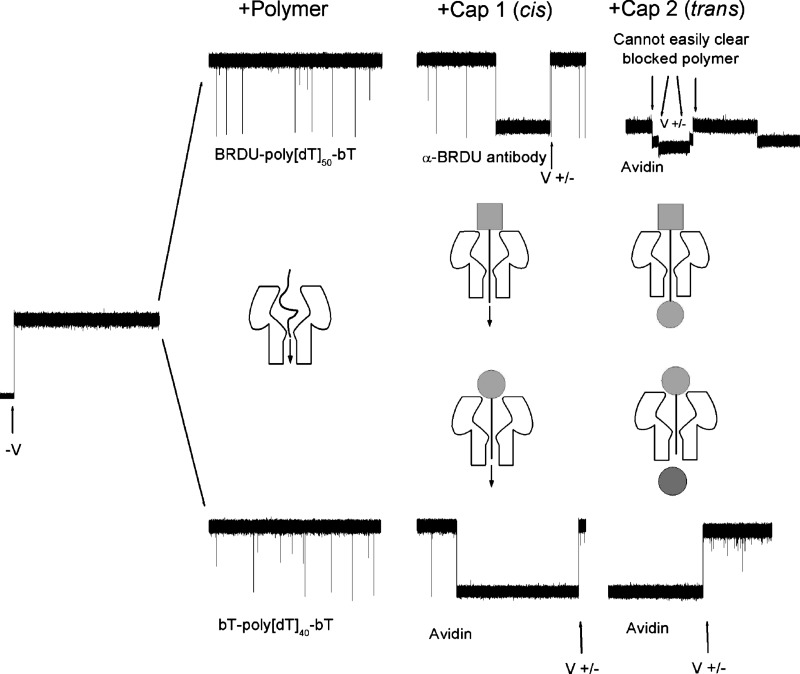
To deduce additional structural information about the channel, we used polynucleotides that can be capped at both ends. These polymers have binding sites for large macromolecules at both the and ends of the polynucleotide (e.g., -BRDU-poly[dC]-bT-; where BRDU is brominated deoxy U). In the absence of the polymers, the single channel recordings are quiescent (Fig. 4, left). The addition of uncapped polymer to the cis side causes transient current blockades as illustrated in Fig. 4 (, top). A relatively large capping protein (e.g., -BRDU) that binds to one end of the polymer is subsequently added to the cis side. The polymers that complex with the cap protein occlude the pore (Fig. 4, 1 cis). Once occluded, the capped polymer can be cleared from the pore by momentarily reversing the sign of the applied potential (Fig. 4, 1 cis, , top). If the capped polymer is long enough to extend past the trans pore entrance, that uncapped end interacts with a second ligand or cap (e.g., avidin) subsequently added to the trans side. The doubly capped polymer is thus trapped within the pore (Fig. 4, 2 trans, top). Similar experiments using shorter polymers (e.g., Fig. 4, bottom) show that the ssDNA homopolymers must contain between 45 to 50 nucleotides of either thymine or cytosine to span the entire pore’s length.
FIG. 4.
The length of the channel determined using differing length polynucleotides. The leftmost time series shows the open channel current. The addition of different polynucleotides (top: ; bottom: ) cause transient blockades in the current. Subsequent addition of a large cap protein that binds to one end of the polymer occludes the pore until the potential is reversed. A second cap protein, which can bind to the free end of the polynucleotide, is then added to the trans side. The 40-mer (bottom right), but not the 50-mer (top right) can be cleared from the pore by reversing the applied potential. This result suggests the 40-mer does not completely span the channel and that the 50-mer does.
These results demonstrate conclusively that ssDNA can partition into and thread completely through the pore, in agreement with results from our earlier study.40 Also, because the pore is 10 nm long,2 the relative length of each nucleotide in the pore is , consistent with the structures of polynucleotides in solution.67 Because 45 nucleotides are sufficient to traverse the pore, the region inside the pore that commits the DNA to traversing the channel is approximately 5 nucleotides long. This zone corresponds to the narrowest segment inside the channel as determined by x-ray crystallography.2
D. Geometry of the channel probed with ssDNA
The ionic current blockades, e.g., of poly[dT], do not always have a simple binary structure.59,60 Instead, they are noisy and many are piecewise stationary in multiple states. These multi-state events most likely relate, at least in part, to the nature of the channel aperture at various depths. The quantitative measurement of such a signal requires a statistical state identification and decoding procedure to make maximum a posteriori (MAP) state sequence estimates of the individual events based on the ionic current amplitude distribution. We then apply the decoding procedure to the individual events.
The single channel recordings in Fig. 5 show that the state structure is particularly rich for induced blockades. Still, the signals are simple enough to be tractable. These data demonstrate that the signal state structure depends on the direction of polynucleotide transport through the pore. Note that occasionally causes step structures that depend on the direction of transport and, as we show below, this provides information about the pore geometry.
FIG. 5.
Representative ionic current blockades for interactions with the channel. The polymer is added to either the (a) cis or (b) trans side and the applied potential is or , respectively. The patterns of the blockades, which illustrate the states of the bimolecular interactions, are consistent across large ensembles and can be classified. The blockade morphologies correlate with the geometry of the channel. Most of the open channel current recording between events is removed for clarity.
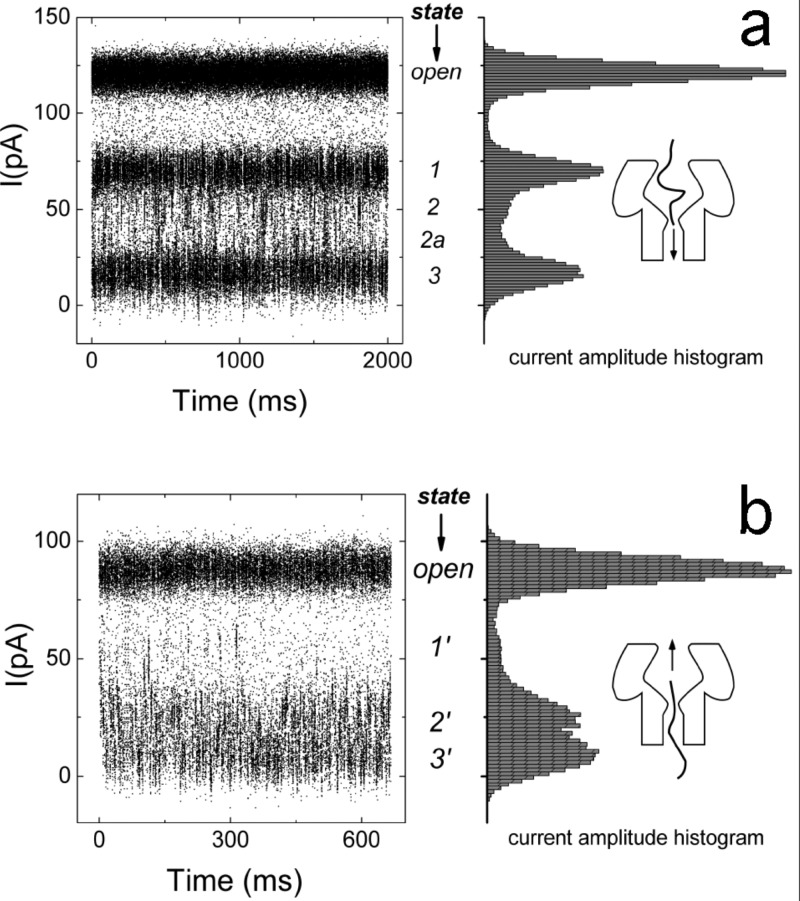
Moreover, for events with lifetimes (Fig. 6) the amplitude distributions for polymer entry from the cis and trans sides can each be modeled using five-kernel, and four-kernel gaussian mixture models (GMMs), respectively. These states (i.e., Gaussian kernels) are enumerated in Fig. 6. The general form of these models is:
where is the ionic conductance amplitude, is the number of Gaussian kernels in the mixture sum, A is the set of positive mixture weights that sum to one, M is the set of kernel means, and is the set of kernel standard deviations. We obtained two distinct GMMs, one for each transport direction. The kernels for cis and trans occluded states are numbered 1, 2, 2a, 3, and , , , respectively.
FIG. 6.
Ionic current time series for blockade events with lifetimes (left) and current amplitude distributions (right) for polymers entering from either the (a) cis or (b) trans pore entrances. The two time series depict bands for the open channel current and the most probable occluded states. The occluded states represent the negotiation of the polymer through the various pore apertures. The probability weight of the open state is arbitrary because most of the open channel recording between the randomly occurring blockades is removed.
The Gaussian mixture parameters, estimated as described below, result in a mixture probability density function that cannot be rejected at the 0.05 probability level using the Kolmogorov–Smirnov goodness of fit test. They are subsequently incorporated as output distributions of a hidden Markov model (HMM) with a persistent, but ergodic, transition matrix.60,61
Interestingly, the blockade structure for cis to trans polymer transport evolves with increasing event duration, as shown in Fig. 7. Qualitatively similar results were obtained with events caused by polymer transport from the trans to the cis side (data not shown). The morphologies are mostly confined to state 1 for the short lifetimes, bifurcate to state 1 or state 3 for intermediate lengths, and show a characteristic event step from state 1 to state 3 within events for longer blockade lifetimes [Fig. 5(a)]. This is consistent with the polymer entering the cis-side vestibule, being dislodged in the short events, and progressively exploring the narrower apertures further in the channel for events with increasing lifetimes. Very long-lived events (sometimes up to seconds, data not shown) tend to show an irregular transition between these and additional states, and are more difficult to interpret.
FIG. 7.

Event time-amplitude histograms showing characteristic ionic current signatures for increasing blockade duration. -induced blockades stratified by duration show that the event structure evolves in a simple manner. Sixty microsecond events show a state 1 conductance level; long events show a bimodal conductance morphology (states 1 and 3); long events show state 1 and increasingly frequent state 3 blockades. The blockades also show the emergence of events with transitions from state 1 to state 3. These signatures most likely represent the progress of the polymer through the various limiting apertures of the nanopore (see text). In these experiments, the polynucleotide entered the channel from the cis pore mouth. The color scale is adjusted to the declining frequency of longer events to best visualize the common event morphologies. The numbered conductance states correspond to those illustrated in Fig. 6.
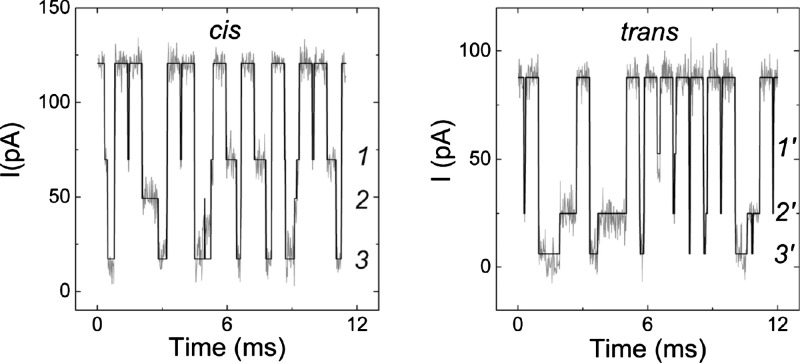
Figure 8 illustrates the MAP state sequence decoded using the signal amplitude Gaussian mixtures as the output distributions of our HMM, and the statistical decoding procedure based on that of Viterbi.68 This results in a state sequence of the current blockades in terms of the GMM amplitude distribution kernels. Partial-then-deep blockade for cis polymer entry and a deep-then-partial blockade for trans polymer entry emerge as common patterns. The results are consistent with the channel structure because the cis-side vestibule is larger than the pore trans side.2
FIG. 8.
Morphologies of poly[dT]-induced blockades of the single channel current for polymer entering the cis (left) or trans (right) entrances. The data, and the decoded state sequences are illustrated in light gray and black, respectively. Note that two-step blockade events are observed for polymers that partition into either pore entrance. The numbered conductance states correspond to those illustrated in Fig. 6.
We modified the original HMM technique introduced by Baum,69 by replacing the Baum–Welsh forward-backward iteration training procedure with the ionic current amplitude GMM estimates.70 The Kolmogorov-Smirnov test offers a stopping rule for unsupervised training of the GMM output distributions using expectation maximization. This algorithm learns the system modes from the data automatically and therefore offers an unsupervised variant of the classical HMM that is data driven, because it does not require independently generated ground truth annotations of the training data. Also, the classical Baum–Welsh procedure does not readily lend itself to a statistical goodness of fit test. In contrast, our signal amplitude GMM allows to us to assess the statistical model’s accuracy, and thus permits unsupervised state identification.
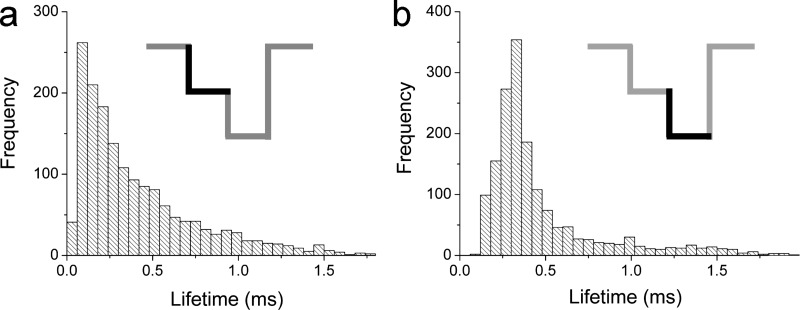
The detailed nature of the two-state blockades provide additional information about the interaction between poly[dT] and the channel. Figure 9 shows the lifetime distributions for two predominant blocked states; the most common shallow blockade state (state 1) and the deeper blockade state (state 3) are shown in Figs. 9(a) and 9(b), respectively. The state 1 lifetime distribution appears to be approximately exponential and thus consistent with the polymer partitioning into, and randomly exploring the cis-side vestibule interior. An exponential lifetime distribution implies a constant hazard rate , where , and is the cumulative of the density .71 State 1 events are followed by the polymer either retreating whence it came (state 1 only events, Figs. 5–8) or threading into the narrower segment of the pore (transition to state 3); which commits the polymer to vectorial transport. In contrast to the exponential distribution [Fig. 9(a)], the more symmetrical mode for the state 3 lifetime distribution [Fig. 9(b)] suggests a more deterministic phenomenon; as would be expected for a population of uniform-length polymers threading through the channel.40
FIG. 9.
Lifetime distributions for both segments of two-state blockades caused by . The distribution of lifetimes for the lesser blocked states (a) is approximately exponential; whereas that of the deeper blockade state (b) is clearly different. The result suggests the mechanism for the two blockade states are different. The polymer was added to the cis side.
IV. CONCLUSIONS
We demonstrated here that steady-state and kinetic information gleaned from the interactions between DNA polymers and a single nanometer-scale pore provide structural information about the latter. Different polynucleotides were used to deduce gross structural details of the channel, such as the pore length and the depth at which a polymer is committed to transport. We also showed that for a given polymer type, the polymer-induced ionic current blockade patterns are consistent with a small set of archetypal exemplars (Figs. 5–9) that most likely correlate with the channel geometry; e.g., poly[dT] current blockade patterns with two steps and three predominant blockade levels (Fig. 5).
One possible interpretation of the latter results, which is illustrated in Fig. 10, is that the degree of ionic current blockade correlates with the amount of poly[dT] mass in the cap domain vestibule (partial blockades), or in the smallest aperture (deeper blockade) between the vestibule and the -barrel stem region of the pore. This simple hypothesis is consistent with the blockade patterns caused by poly[dT] transport in either direction (Fig. 8) and the lifetime distributions of poly[dT]-induced blockades (Fig. 9). These results, and others shown here, demonstrate that DNA can be used to probe the geometry of channel. By inference, this technique might also prove useful for probing the structures of other nanometer-scale pores, including those in solid-state materials.72–81
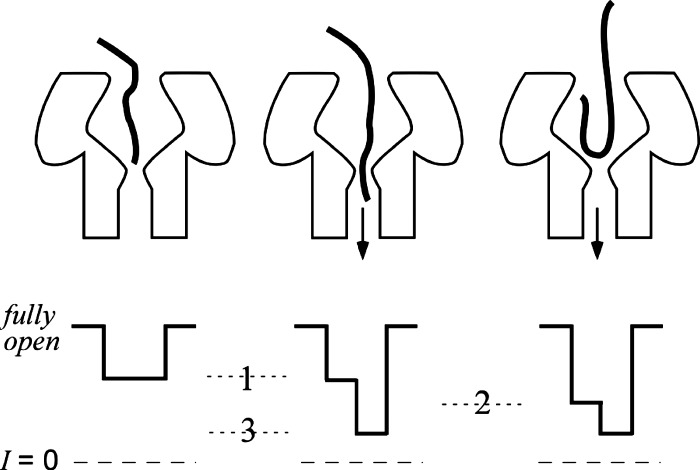
FIG. 10.
A toy model to describe the interaction of individual poly[dT] polynucleotides with the ion channel. Illustrations of the polynucleotide entry into and possible transport through the pore (top) and the resulting stylized current blockades (bottom) caused by the presence of a polymer either in the cis vestibule only (left and right) or in the tightest constriction (center). The 3 predominant conductance states caused by poly[dT] probably correspond to the amount of polymer in the pore. The two shallow conductance states (1 and 2) may be caused by significantly different amounts of polymer in a relatively narrow region within the cap. Conductance state 3 most likely is caused by polymer entry into the narrowest segment of the channel, which leads to the subsequent transport of the polymer through the pore. If the conductance in a particular blockade never reaches state 3, the polymer probably exits from the same mouth it entered.
We also demonstrated the use of our unsupervised state identification process and subsequent state sequence decoding technique using an HMM-like statistical model to quantify the kinetics of interactions between nanopores and biomolecules. This technique allows us to measure complex multi-state signals generated by this system, and elucidate the information contained therein. It also permits quantification of a large number of events, thus allowing a detailed statistical study of the polynucleotide-nanopore kinetic interactions.
The ability to entrap indefinitely an individual polynucleotide in a single nanometer-scale pore may help extract information from the polymer with higher fidelity than is currently possible.70 For example, it has been suggested that averaging the ionic current time series by flossing the polymer back and forth may improve the signal to noise ratio in an averaged ensemble.60,82–85
ACKNOWLEDGMENTS
This work was funded in part by the NIST Advanced Technology Program (J.J.K.), the NIST Single Molecule Manipulation and Measurement Competence program (J.J.K and V.M.S.), the National Science Foundation: NIRT Grant No. CTS-0304062 (J.J.K.), and the NIST Office of Law Enforcement Standards (J.J.K.).
APPENDIX: STATISTICAL MECHANICAL DESCRIPTION OF A STRETCHED POLYMER IN AN ATTRACTIVE WELL
Predicting when the current blockade is persistent [Fig. 3(a), 30 mer] or transient [Fig. 3(a), 20 mer] can be approached using statistical mechanics. Suppose the chain is stretched by the electric field as shown in Fig. 3 (left). Then the total potential energy, PE, in the presence of a uniform electric field, , is given by:
where is the distance between monomers and is the total number of monomers. The rate, , at which the polymer escapes from the well depends on the well depth and is:
where has its usual meaning. diminishes rapidly with increasing . Consequently there is a critical value of beyond which the rate is so small that the particle is trapped in the pore.
The rate of escape depends on other variables including the pore width. Imagine an enclosure bounded by a cylindrical wall given by and by horizontal planes at and . One end of the polymer is tied to the center of the plane and the other monomers of the chain reside within the cylinder as before under the influence of an electric field . The surfaces can be attractive or repulsive to the monomers. Computer modeling and the relevant thermodynamic properties could be used to determine the partition function :
will be a function of , , and , wall attraction if any, and a functional of . Knowledge of should allow us to estimate and . This problem can be viewed as a generalization of a chromatography problem solved by Cassasa86 (and references therein)
Finally, the chain may undergo a coil-stretch transition. From the formula for the PE, the forces on monomer segments near the point of attachment to the biotinylated blob increase linearly in both and . Thus for long chains, there is a point where the “elastic limit” of the spring constant is reached, which leads to the coil-stretch transition.
REFERENCES
- 1.Beauchamp J. C. and Isaacs N. W., Curr. Opin. Chem. Biol. 3, 525 (1999). 10.1016/S1367-5931(99)00003-4 [DOI] [PubMed] [Google Scholar]
- 2.Song L. Z., Hobaugh M. R., Shustak C., Cheley S., Bayley H., and Gouaux J. E., Science 274, 1859 (1996). 10.1126/science.274.5294.1859 [DOI] [PubMed] [Google Scholar]
- 3.Doyle D. A., Cabral J. M., Pfuetzner R. A., Kuo A. L., Gulbis J. M., Cohen S. L., Chait B. T., and MacKinnon R., Science 280, 69 (1998). 10.1126/science.280.5360.69 [DOI] [PubMed] [Google Scholar]
- 4.Hille B., Ionic Channels of Excitable Membranes (Sinauer Associates, Sunderland, 1992). [Google Scholar]
- 5.Akabas M. H., Stauffer D. A., Xu M., and Karlin A., Science 258, 307 (1992). 10.1126/science.1384130 [DOI] [PubMed] [Google Scholar]
- 6.Bhakdi S. and Tranum-Jensen J., Microbiol. Rev. 55, 733 (1991). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Menestrina G., J. Membr. Biol. 90, 177 (1986). 10.1007/BF01869935 [DOI] [PubMed] [Google Scholar]
- 8.Bezrukov S. M. and Kasianowicz J. J., Phys. Rev. Lett. 70, 2352 (1993). 10.1103/PhysRevLett.70.2352 [DOI] [PubMed] [Google Scholar]
- 9.Gouaux J. E., Braha O., Hobaugh M. R., Song L. Z., Cheley S., Shustak C., and Bayley H., Proc. Natl. Acad. Sci. U.S.A. 91, 12828 (1994). 10.1073/pnas.91.26.12828 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Kasianowicz J. J. and Bezrukov S. M., Biophys. J. 69, 94 (1995). 10.1016/S0006-3495(95)79879-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bezrukov S. M., Vodyanoy I., Brutyan R., and Kasianowicz J. J., Macromolecules 29, 8517 (1996). 10.1021/ma960841j [DOI] [Google Scholar]
- 12.Valeva A., Weisser A., Walker B., Kehoe M., Bayley H., Bhakdi S., and Palmer M., EMBO J. 15, 1857 (1996). [PMC free article] [PubMed] [Google Scholar]
- 13.Gouaux E., J. Struct. Biol. 121, 110 (1998). 10.1006/jsbi.1998.3959 [DOI] [PubMed] [Google Scholar]
- 14.Kasianowicz J. J., Burden D. L., Han L., Cheley S., and Bayley H., Biophys. J. 76, 837 (1999). 10.1016/S0006-3495(99)77247-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Benson E. L., Huynh P. D., Finkelstein A., and Collier R. J., Biochemistry 37, 3941 (1998). 10.1021/bi972657b [DOI] [PubMed] [Google Scholar]
- 16.Halverson K. M., Panchal R. G., Nguyen T. L., Gussio R., Little S. F., Misakian M., Bavari S., and Kasianowicz J. J., J. Biol. Chem. 280, 34056 (2005). 10.1074/jbc.M507928200 [DOI] [PubMed] [Google Scholar]
- 17.Zimmerberg J. and Parsegian V. A., Nature (London) 323, 36 (1986). 10.1038/323036a0 [DOI] [PubMed] [Google Scholar]
- 18.Schein S. J., Colombini M., and Finkelstein A., J. Membr. Biol. 30, 99 (1976). 10.1007/BF01869662 [DOI] [PubMed] [Google Scholar]
- 19.Sabirov R. Z., Krasilnikov O. V., Ternovsky V. I., Merzliak P. G., and Muratkhodjaev J. N., Biol. Membr. 8, 280 (1991). [Google Scholar]
- 20.Krasilnikov O. V., Sabirov R. Z., Ternovsky V. I., Merzliak P. G., and Muratkodjaev J. N., FEMS Microbiol. Immunol. 105, 93 (1992). 10.1111/j.1574-6968.1992.tb05891.x [DOI] [PubMed] [Google Scholar]
- 21.Sabirov R. Z., Krasilnikov O. V., Ternovsky V. I., and Merzliak P. G., Gen. Physiol. Biophys. 12, 95 (1993). [PubMed] [Google Scholar]
- 22.Bezrukov S. M. and Vodyanoy I., Biophys. J. 64, 16 (1993). 10.1016/S0006-3495(93)81336-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Korchev Y. E., Bashford C. L., Alder G. M., Kasianowicz J. J., and Pasternak C. A., J. Membr. Biol. 147, 233 (1995). 10.1007/BF00234521 [DOI] [PubMed] [Google Scholar]
- 24.Bezrukov S. M., Vodyanoy I., and Parsegian V. A., Nature (London) 370, 279 (1994). 10.1038/370279a0 [DOI] [PubMed] [Google Scholar]
- 25.Parsegian V. A., Bezrukov S. M., and Vodyanoy I., Biosci. Rep. 15, 503 (1995). 10.1007/BF01204353 [DOI] [PubMed] [Google Scholar]
- 26.Bezrukov S. M. and Kasianowicz J. J., Eur. Biophys. J. 6, 241 (1997). [DOI] [PubMed] [Google Scholar]
- 27.Ternovsky V. I., Grigoriev P. A., Berestovsky G. N., Schlegel R., Dornberger K., and Grafe U., Membr. Cell Biol. 11, 497 (1997). [PubMed] [Google Scholar]
- 28.Desai S. A. and Rosenberg R. L., Proc. Natl Aca. Sci. USA 94, 2045 (1997). 10.1073/pnas.94.5.2045 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Coates G. M. P., Bashford C. L., and Smart O. S., Biochem. Soc. Trans. 26, S193 (1998). [DOI] [PubMed] [Google Scholar]
- 30.Merzlyak P. G., Rodrigues C. G., Carneiro C. M. M., Krasilnikov O. V., and Bezrukov S. M., Biophys. J. 77, 3023 (1999). 10.1016/S0006-3495(99)77133-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Berestovskii G. N., Ternovskii V. I., and Kataev A. A., Biofizika 45, 69 (2000). [PubMed] [Google Scholar]
- 32.Krasilnikov O. V., in Structure and Dynamics of Confined Polymers, NATO Science Series, 3. High Technology, edited by Kasianowicz J. J., Kellermayer M. S. Z., and Deamer D. W. (Kluwer, Dordrecht, The Netherlands, 2002) Vol. 87, pp. 97–115 [Google Scholar]
- 33.Bezrukov S. M. and Kasianowicz J. J., in Structure and Dynamics of Confined Polymers, NATO Science Series, 3. High Technology, edited by Kasianowicz J. J., Kellermayer M. S. Z., and Deamer D. W. (Kluwer, Dordrecht, The Netherlands, 2002) Vol. 87, pp. 117–130 [Google Scholar]
- 34.Rostovtseva T. K., Nestorovich E. M., and Bezrukov S. M., Biophys. J. 82, 160 (2002). 10.1016/S0006-3495(02)75383-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nablo B. J., Halverson K. M., Robertson J. W. F., Nguyen T. L., Bavari S., Panchal R. G., Gussio R., Krasilnikov O. V., and Kasianowicz J. J., Biophys. J. 95, 1157 (2008). 10.1529/biophysj.107.121715 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Krasilnikov O. V. and Bezrukov S. M., Macromolecules 37, 2650 (2004). 10.1021/ma030374n [DOI] [Google Scholar]
- 37.Simon S. M. and Blobel G., Cell 65, 371 (1991). 10.1016/0092-8674(91)90455-8 [DOI] [PubMed] [Google Scholar]
- 38.Simon S. M. and Blobel G., Cell 69, 677 (1992). 10.1016/0092-8674(92)90231-Z [DOI] [PubMed] [Google Scholar]
- 39.Koriazova L. K. and Montal M., Nat. Struct. Biol. 10, 13 (2003). 10.1038/nsb879 [DOI] [PubMed] [Google Scholar]
- 40.Kasianowicz J. J., Brandin E., Branton D., and Deamer D. W., Proc. Natl. Acad. Sci. U.S.A. 93, 13770 (1996). 10.1073/pnas.93.24.13770 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Sung W. and Park P. J., Phys. Rev. Lett. 77, 783 (1996). 10.1103/PhysRevLett.77.783 [DOI] [PubMed] [Google Scholar]
- 42.Lubensky D. K. and Nelson D. R., Biophys. J. 77, 1824 (1999). 10.1016/S0006-3495(99)77027-X [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Muthukumar M., J. Chem. Phys. 111, 10371 (1999). 10.1063/1.480386 [DOI] [Google Scholar]
- 44.de Gennes P., Proc. Natl. Acad. Sci. U.S.A. 96, 7262 (1999). 10.1073/pnas.96.13.7262 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Kumar K. K. and Sebastian K. L., Phys. Rev. E 62, 7536 (2000). 10.1103/PhysRevE.62.7536 [DOI] [PubMed] [Google Scholar]
- 46.Sebastian K. L. and Paul A. K. R., Phys. Rev. E 62, 927 (2000). 10.1103/PhysRevE.62.927 [DOI] [PubMed] [Google Scholar]
- 47.Muthukumar M., Phys. Rev. Lett. 86, 3188 (2001). 10.1103/PhysRevLett.86.3188 [DOI] [PubMed] [Google Scholar]
- 48.Lee S. K. and Sung W., Phys. Rev. E 63, 021115 (2001). 10.1103/PhysRevE.63.021115 [DOI] [PubMed] [Google Scholar]
- 49.Kong C. Y. and Muthukumar M., Electrophoresis 23, 2697 (2002). [DOI] [PubMed] [Google Scholar]
- 50.Sung W. and Park P. J., in Structure and Dynamics of Confined Polymers, NATO Science Series, 3. High Technology, edited by Kasianowicz J. J., Kellermayer M. S. Z., and Deamer D. W. (Kluwer, Dordrecht, The Netherlands, 2002) Vol. 87, pp. 261–280 [Google Scholar]
- 51.Muthukumar M., Electrophoresis 23, 1417 (2002). [DOI] [PubMed] [Google Scholar]
- 52.Slonkina E. and Kolomeisky A. B., J. Chem. Phys. 118, 7112 (2003). 10.1063/1.1560932 [DOI] [Google Scholar]
- 53.Troisi A., Nitzan A., and Ratner M. A., J. Chem. Phys. 119, 5782 (2003). 10.1063/1.1601600 [DOI] [Google Scholar]
- 54.Muthukumar M., J. Chem. Phys. 118, 5174 (2003). 10.1063/1.1553753 [DOI] [Google Scholar]
- 55.Kong C. Y. and Muthukumar M., J. Chem. Phys. 120, 3460 (2004). 10.1063/1.1642588 [DOI] [PubMed] [Google Scholar]
- 56.Szabo I., Bathori G., Tombola F., Brini M., Coppola A., and Zoratti M., J. Biol. Chem. 272, 25275 (1997). 10.1074/jbc.272.40.25275 [DOI] [PubMed] [Google Scholar]
- 57.Henrickson S. E., Misakian M., Robertson B., and Kasianowicz J. J., Phys. Rev. Lett. 85, 3057 (2000). 10.1103/PhysRevLett.85.3057 [DOI] [PubMed] [Google Scholar]
- 58.Ambjörnsson T., Apell S. P., Konkoli Z., DiMarzio E., and Kasianowicz J. J., J. Chem. Phys. 117, 4063 (2002). 10.1063/1.1486208 [DOI] [Google Scholar]
- 59.Kasianowicz J. J., Henrickson S. E., Weetall H. H., and Robertson B., Anal. Chem. 73, 2268 (2001). 10.1021/ac000958c [DOI] [PubMed] [Google Scholar]
- 60.Kasianowicz J. J., Henrickson S. E., Masakian M., Weetall H., Robertson B., and Stanford V., in Structure and Dynamics of Confined Polymers, NATO Science Series, 3. High Technology, edited by Kasianowicz J. J., Kellermayer M. S. Z., and Deamer D. W. (Kluwer, Dordrecht, The Netherlands, 2002) Vol. 87, pp. 141–163 [Google Scholar]
- 61.Stanford V. and Kasianowicz J. J., Proceedings of the IEEE Workshop on Genomic Signal Processing and Statistics, Raleigh, NC, 11–13 October 2002. (unpublished). [Google Scholar]
- 62.Montal M. and Mueller P., Proc. Natl. Acad. Sci. U.S.A. 69, 3561 (1972). 10.1073/pnas.69.12.3561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Akeson M., Branton D., Kasianowicz J. J., Brandin E., and Deamer D. W., Biophys. J. 77, 3227 (1999). 10.1016/S0006-3495(99)77153-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Meller A., Nivon L., and Branton D., Phys. Rev. Lett. 86, 3435 (2001). 10.1103/PhysRevLett.86.3435 [DOI] [PubMed] [Google Scholar]
- 65.Chandler E. L., Smith A. L., Burden L. M., Kasianowicz J. J., and Burden D. L., Langmuir 20, 898 (2004). 10.1021/la035728i [DOI] [PubMed] [Google Scholar]
- 66.Aksimentiev A. and Schulten K., Biophys. J. 88, 3745 (2005). 10.1529/biophysj.104.058727 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Saenger W., Principles of nucleic acid structure (Springer-Verlag, New York, 1984). [Google Scholar]
- 68.Viterbi A. J., IEEE Trans. Inf. Theory 13, 260 (1967). 10.1109/TIT.1967.1054010 [DOI] [Google Scholar]
- 69.Baum L., Inequalities 3, 1 (1972). [Google Scholar]
- 70.Stanford V. M. and Kasianowicz J. J., Proceedings of the IEEE Workshop on Genomic Signal Processing and Statistics, Baltimore, MD, 26 May 2004. (unpublished). [Google Scholar]
- 71.Mann N. R., Schafer R. E., and Singpurwalla N. D., Methods for Statistical Analysis of Reliability and Life Data (Wiley, New York, 1974) p. 124 [Google Scholar]
- 72.Li J., Stein D., McMullan C., Branton D., Aziz M. J., and Golovchenko J. A., Nature (London) 412, 166 (2001). 10.1038/35084037 [DOI] [PubMed] [Google Scholar]
- 73.Stein D., Li J., and Golovchenko J. A., Phys. Rev. Lett. 89, 276106 (2002). 10.1103/PhysRevLett.89.276106 [DOI] [PubMed] [Google Scholar]
- 74.Li J., Gershow M., Stein D., Brandin E., and Golovchenko J. A., Nat. Mater. 2, 611 (2003). 10.1038/nmat965 [DOI] [PubMed] [Google Scholar]
- 75.Aksimentiev A., Heng J. B., Timp G., and Schulten K., Biophys. J. 87, 2086 (2004). 10.1529/biophysj.104.042960 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Heng J. B., Ho C., Kim T., Timp R., Aksimentiev A., Grinkova Y. V., Sligar S., Schulten K., and Timp G., Biophys. J. 87, 2905 (2004). 10.1529/biophysj.104.041814 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Fologea D., Gershow M., Ledden B., McNabb D. S., Golovchenko J. A., and Li J., Nano Lett. 5, 1905 (2005). 10.1021/nl051199m [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Storm A. J., Storm C., Chen J., Zandbergen H., Joanny J. F., and Dekker C., Nano Lett. 5, 1193 (2005). 10.1021/nl048030d [DOI] [PubMed] [Google Scholar]
- 79.Storm A. J., Chen J. H., Zandbergen H. W., and Dekker C., Phys. Rev. E 71, 051903 (2005). 10.1103/PhysRevE.71.051903 [DOI] [PubMed] [Google Scholar]
- 80.Ho C., Qiao R., Heng J. B., Chatterjee A., Timp R. J., Aluru N. R., and Timp G., Proc. Natl. Acad. Sci. U.S.A. 102, 10445 (2005). 10.1073/pnas.0500796102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Heng J. B., Aksimentiev A., Ho C., Marks P., Grinkova Y. V., Sligar S., Schulten K., and Timp G., Nano Lett. 5, 1883 (2005). 10.1021/nl0510816 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Henrickson S. E., “Polynucleotide transport through a single nanometer-scale pore: biophysical and biotechnological applications,” thesis, Harvard University, Cambridge, MA, 2001 [Google Scholar]
- 83.Di Marzio E. A. and Kasianowicz J. J., J. Chem. Phys. 119, 6378 (2003). 10.1063/1.1603725 [DOI] [Google Scholar]
- 84.Sánchez-Quesada J. A., Saghatelian A., Cheley S., Bayley H., and Ghadiri M. R., Angew. Chem. Int. Ed. 43, 3063 (2004). 10.1002/anie.200453907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Kasianowicz J. J., Nat. Mater. 3, 355 (2004). 10.1038/nmat1143 [DOI] [PubMed] [Google Scholar]
- 86.Casassa E. F., Macromolecules 9, 182 (1976). 10.1021/ma60049a029 [DOI] [PubMed] [Google Scholar]