Inference and validation of predictive gene networks from biomedical literature and gene expression data

Abstract

Although many methods have been developed for inference of biological networks, the validation of the resulting models has largely remained an unsolved problem. Here we present a framework for quantitative assessment of inferred gene interaction networks using knock-down data from cell line experiments. Using this framework we are able to show that network inference based on integration of prior knowledge derived from the biomedical literature with genomic data significantly improves the quality of inferred networks relative to other approaches. Our results also suggest that cell line experiments can be used to quantitatively assess the quality of networks inferred from tumor samples.

1. Introduction/Methods

We have increasingly come to recognize that cellular regulatory processes are more complex than we had once imagined and that it is generally not individual genes, but networks of interacting genes and gene products, which collectively interact to define phenotypes and the alterations that occur in the development of a disease [4]. The first application of network reconstruction to gene expression used data from a yeast cell cycle experiment in which synchronized cells were profiled over a carefully planned time-course [28]. Friedman and colleagues analyzed these data in a Bayesian Network framework to develop a predictive cell-cycle model. Since this early work, there have been many other methods developed to model networks while addressing the intrinsic complexity of high-throughput genomic data (high feature-to-sample ratio and high level of noise) [22]. However, few methods have been widely used and often fail to produce useful network models, mainly because there are no gold standards on how to build and validate large gene networks [12, 35].

One challenge in developing network inference methods is validation of the resulting models. Most published network inference methods attempt to validate their models through comparison with biological databases, calculating the proportion of interactions found both in the inferred networks and those databases [2]. However, this assumes that the network topologies are static and do not change between phenotypes or in response to perturbations. Others have validated small network models using targeted biological experiments to assess interactions between genes, but this is not feasible for a large number of genes and new potential interactions. An alternate route based on simulated interventional data was used in the NIPS2008 workshop on causality validating inferred networks by trying to predict the results of interventions [16], but this method is biased to those network inference models most closely resembling the simulation model.

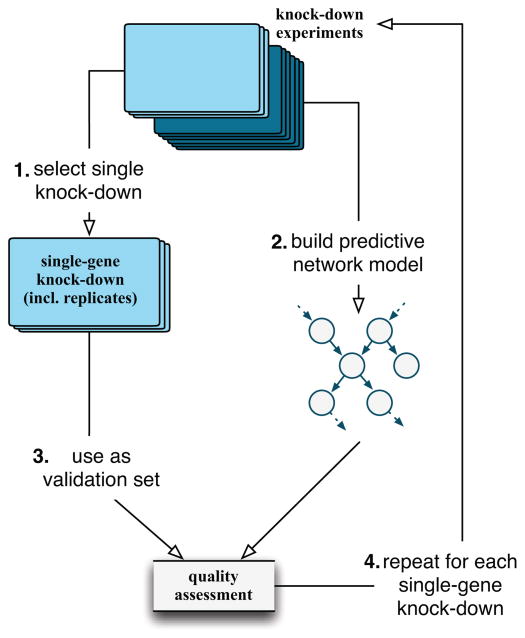
Here we propose a new validation framework that enables a quantitative and unbiased assessment of the performance of an inferred network model. This framework relies on generating independent, single-gene knock-down experiments targeting a collection of genes in a network or pathway of interest, and measuring gene expression data before and after the knockdowns. With this data in hand, we apply the following iterative leave-one-out cross-validation approach to assess the performance of a given network inference method (Fig. 1):

Fig. 1.

Validation algorithm using single-gene knock-down experiments in a leave-one-out cross-validation scheme.

1. Select a single gene knock-down, including all replicates, from the collection as validation set.

2. From the remaining knock-down experiments, build a predictive network model.

3. Use the validation set to assess the network’s quality, focused on connections local to the perturbation.

4. Repeat steps 1–3 until all perturbations have been tested in the models and their local predictive power assessed.

This “dual use” of the data for model inference and validation allows the computation of a performance score that quantitatively assesses the inferred network’s quality based on a comparison between the genes that are empirically determined to be affected based on the validation data set and those genes inferred to be affected based on the models. Since this validation framework is not tied to a specific network inference method, it can be used to assess the relative performance of different network inference methods. As a test of the approach, we applied it to two methods that infer directed (causal) interaction network from gene expression data: GeneNet [27] and predictionet [17]. GeneNet computes full partial correlations and then orders the genes based on partial variances to identify directed acyclic causal networks. This approach improves on Bayesian network inference methods as it allows inference of large interaction networks containing hundreds of genes. However, its current implementation (version 1.2.5) does not integrate prior knowledge about likely network structure captured in published biomedical literature and pathway databases [9, 14, 18, 32]. Bayesian networks are inferred from different sources of information in [19, 29, 32] but to the best of our knowledge there is no such method publicly available in R.

The use of prior network structures is at the heart of predictionet, which builds on reported gene-gene interactions cataloged in the Predictive Networks (PN), web application [17]. predictionet infers an undirected network using mRMR (minimum Redundancy-Maximum Relevance; [8, 26]) feature selection and then orients the edges in this network using the interaction information [25]. In both steps, prior information can be used to adjust the respective rankings based on the confidence in the interactions, as further described in Section 1.1 of the Supplementary Information.

Here we will describe the application of our validation framework, which combines knock-down experiments and network inference, to quantitatively assess inference methods for large gene interaction networks. We will show that the integration of priors with gene expression data yielded networks best at predicting the genes affected by a targeted perturbation.

2. Results

In this section we will present our validation framework and the combination of targeted perturbations and network inference methods it relies on. The data and the main parameters used in our framework will be described in detail.

2.1. Targeted perturbations

One of the best approaches to test the quality of a network model is to quantify how well it can predict the system’s response to perturbations. As a demonstration, we use a well-studied model system - the RAS signaling pathway in colorectal cancer. We performed RNAi-mediated gene knockdown experiments in two colorectal cancer cell lines, SW480 and SW620 [20], targeting eight key genes in the RAS pathway: CDK5, HRAS, MAP2K1, MAP2K2, MAPK1, MAPK3, NGFR and RAF1¹. The experiments were done in six biological replicates of each knockdown and controls in both cell lines. From each sample, we profiled gene expression (Supplementary File 1) using the A ymetrix GeneChip HG-U133PLUS2 platform. CEL files were normalized using frma [24]. We used the jetset package to select a unique probeset for each of the 19,218 unique gene symbols represented on the arrays; further annotations were obtained using biomaRt [11]. The raw and normalized data are available from the NCBI Gene Expression Omnibus (GEO) repository [5] with accession number GSE53091. A more detailed description of the knock-down experiments is available in Section 1.6 in Supplementary Information.

Although our experimental perturbations were limited to eight genes, the goal was to infer a larger network. Consequently, we needed to identify a broader set of genes linked to the RAS pathway. We compared gene expression profiles of quiescent cell lines over-expressing RAS [6]. These data were generated using the Affymetrix GeneChip HG-U133PLUS2 and normalized using MAS5 [1] (GEO accession number: GSE3151). We used the Wilcoxon Rank Sum test to compare the ten control cell lines with the ten cell lines over-expressing RAS and selected the most differentially expressed genes (false discovery rate FDR < 10% and fold change ≥ 4) between groups; this identified 332 RAS-associated genes including HRAS itself. The unique set of 339 RAS-associated genes and our knock-down genes are listed together with their corresponding statistics in Supplementary File 2.

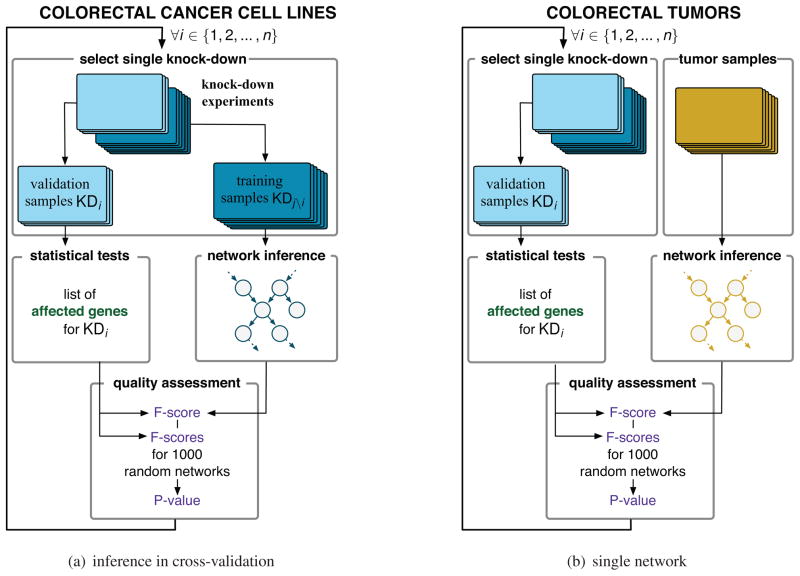
With the gene expression data from the eight knock-down experiments, we used the validation framework illustrated in Figure 2(a). Each knock-down was considered separately during the validation process. In a first step this entails the separation of the samples into those not related to the knock-down under consideration (the training samples) and the samples related to it (the validation samples). The validation samples are then analyzed to identify the list of RAS-associated genes significantly affected by the target knock-down. To compare the expression of genes in control versus knock-down experiments we used the Wilcoxon Rank Sum test with a FDR < 10%. The list of affected genes and their annotations are reported in Table 1 and Supplementary File 3, respectively.

Fig. 2.

In Fig. 2(a) a gene interaction network is inferred at each fold of the cross-validation whereas in Fig. 2(b) a single network is inferred from all the tumors in the data set. In both settings we used the knock-downs (KD) of n = 8 key genes of the RAS pathway performed in colorectal cancer cell lines in order to quantitatively assess the network’s quality.

Tab. 1.

Number of genes significantly affected by KD (out of 339 genes) based on gene expression data with FDR < 10%.

KD	CDK5	HRAS	MAP2K1	MAP2K2
Number of affected genes	73	122	33	38
	MAPK1	MAPK3	NGFR	RAF1
	117	59	99	61

2.2. Network inference methods

Using the training samples (Figure 2(a)) we then proceed to the inference of a network using either GeneNet or predictionet with different weights on the priors (prior weight w ∈ {0, 0.25, 0.5, 0.75, 0.95, 1}; see Supplementary Information Sections 1.1 and Section 1.2 for details of the inference algorithm and the parameter choices, respectively). To define these priors we used the Predictive Networks (PN) web-application to identify gene-gene interactions reported in the biomedical literature and in structured biological databases [17] for this collection of genes. The PN database was generated, in part, from PubMed abstracts and full-text papers using a text mining method in which each interaction is represented as a triplet [Subject, Predicate, Object] such as [PGC, is inhibited by, SIRT1] or [CCNT1, regulates, PGC]. While the Subjects and Objects represent genes, the Predicates capture the interactions between these genes and include terms like ‘regulates’ or ‘is inhibited by’ that describe directional interactions, here Subject → Object or Subject ← Object, respectively. PN contains 81,022 interactions from PubMed documents and 1,323,776 interactions from the Human Functional Interaction [34] and the Pathways Common [7] databases (both retrieved on 2012-11-16).

Among the 339 RAS-associated genes, 325 are present in the PN database with a total of 37,212 interactions of which 602 occurred between pairs of RAS-associated genes (Supplementary File 4). Each interaction was characterized by an evidence score represented as the difference between the number of positive evidence citations and the number of negative evidence represented by a predicate such as ‘does not regulate’. More details on how the priors are used in predictionet are available in Section 1.1 in Supplementary Information.

2.3. Inferred networks

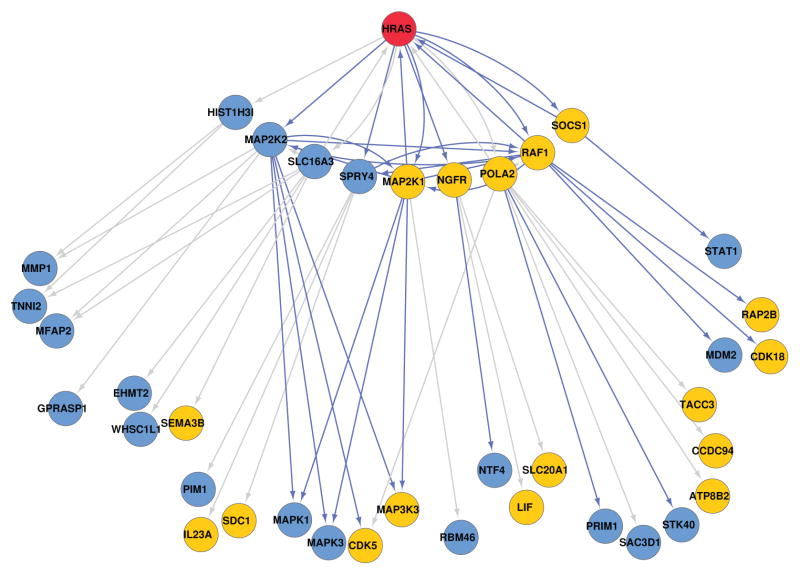
Next, we used the genomic data and priors to infer a gene interaction network for each knock-down (CDK5, HRAS, MAP2K1, MAP2K2, MAPK1, MAPK3, NGFR and RAF1) and each network inference methods (GeneNet and predictionet with increasing prior weights). As an example, we will describe the network inferred for the HRAS knock-down using predictionet with prior weight w = 0.5 (Figure 3). Due to the size of the network and the fact that we are primarily interested in the effect of the targeted perturbation (knock-down of HRAS), we focus on that part of the inferred network which models these effects, that are the children and grand-children (referred to as CH2) of HRAS.

Fig. 3.

Children and grandchildren of HRAS (red node) inferred using predictionet, equal weight between training data and prior knowledge (prior weight w = 0.5). The yellow nodes (genes) are the ones identified as significantly affected by HRAS based on the validation samples. The remaining nodes, colored in blue, have been predicted as affected during network inference while they were not identified as significantly affected in the validation samples. Blue edges are known interactions (priors) while grey edges represent new interactions.

In theory, the genes inferred to be descendants of the knockdown should correspond to the genes identified as significantly affected in the validation experiments. That is, when considering our validation samples one can evaluate which genes exhibit a significant change in expression compared to the control samples; these affected genes should ideally be present in the knock-down’s childhood (CH).

We then tested whether the inferred interactions (edges) in the network were present in the prior (the blue edges) or not (grey edges). This together with the knowledge of which genes were truly affected by the knock-down allows us to identify possible new paths such as HRAS-POLA2-CCDC94 that although not previously reported in the literature, have empirical support in the perturbation data set.

We find (Figure 3) that truly affected genes are present within the set of children as well as with the grandchildren of HRAS; these nodes are colored yellow. Although there are additional genes that are differentially expressed in response to HRAS knockdown, for visualization purposes we focus on those that are predicted to be first or second-generation descendants of the knockdown target. To evaluate the network’s overall quality, we measured the ratio of those genes in the KD’s childhood that are affected by the perturbation relative to those genes predicted to be in the childhood that are not affected. In the following section we will use this idea to design a systematic quantitative validation procedure by properly defining true positives, false positives and false negatives nodes.

2.4. Systematic validation

Given an inferred network and a list of genes significantly affected by a specific knock-down, we can now classify the descendants of the knock-down in the inferred network depending on their response to the perturbation. If this is the case, each of these descendants is classified as true positive (TP), as false positive (FP) if it was not affected by the perturbation, and finally if we know that a gene was affected by the knock-down experiment but it is not inferred as a descendant in the network, it is classified as false negative (FN), as illustrated in Figure 4.

Fig. 4.

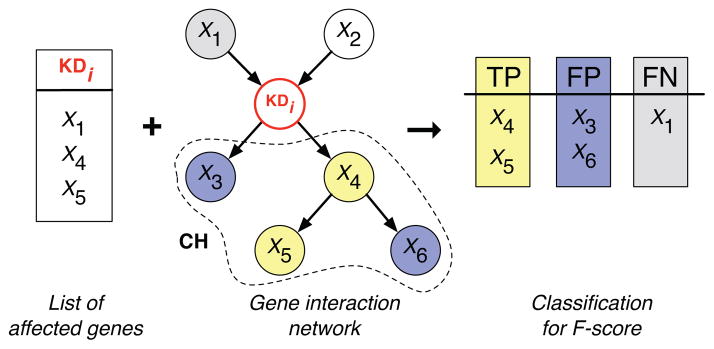
Given a set of genes affected by a knock-down gene KD_i and a gene interaction network, one can define nodes as true positives (TP), false positives (FP) and false negatives (FN). In theory, all the affected genes should be inferred to be members of the knock-down’s childhood, denoted by CH. If they are found within CH, they are classified as true positives (TP). All other genes in CH are classified as false positives (FP). Affected genes that are not inferred to be in the knock-down’s CH are classified as false negatives (FN). This classification of nodes into TP, FP and FN is then used to compute a quality score, such as the F-score.

This classification then allows us to compute, for the inferred network, a quality measure such as the F-score

$$F=\frac{2TP}{2TP+FP+FN},F\in [0,1],$$ (1)

where F=1 corresponds to perfect classification of the affected genes and F=0 to no correctly identified affected genes.

The question of which genes in the network qualify as ‘descendant’ is difficult to answer and we chose to consider the knock-down’s children and its grandchildren, that is the childhood of distance two (CH2). In our experiments, we see that considering only the direct children (CH1) will include too few genes and it is not possible to compute meaningful F-scores. On the other hand, considering larger childhoods such as that of distance three (CH3) or even all descendants usually leads to too many genes predicted as affected. Therefore, we focus on analyzing results obtained for CH2 while reporting those for CH1 and CH3 in Supplementary Information, Figure 4.

Because increasing the size of the childhood almost automatically leads to higher F-score values due to the greater weight given to true positives versus false positives, one cannot solely rely on this quality measure. Therefore, a second measure is needed that will penalize networks with a greater number of edges. Our strategy is to generate a large number n of random networks and compare their F-scores to the F-score obtained with the inferred network to assess its significance using the following formula:

$$\text{pval}=\frac{{\sum }_{i=1}^n{𝟙}_{({\mathrm{F}}_{{\text{random}}_i}\ge {\mathrm{F}}_{\text{inferred}})}}{n}$$ (2)

The larger the number of edges is, the easier it will be to beat the inferred network’s performance with these random networks as the variation between networks is reducing with growing number of edges.

We generated random networks by mimicking the inference using feature selection strategies as implemented by predictionet. Keeping the number of edges and the maximum number of parents equal to those of the inferred network, the random network generator adds a uniformly distributed number of parents in [1, maxparents] to each gene in the random network. This allows us to show that the feature selection and arc orientation strategy implemented in predictionet indeed performs statistically significantly better than a random edge addition procedure. Network performance is computed in terms of F-score values associated with a knock-down’s childhood and any network with a p-value as defined in equation (2) lower than 0.05 is considered to be significantly better than random networks.

2.4.1. Inferring networks with different prior weights for all knock-downs

With this combination of two complementary quantitative validation measures we can now evaluate the inferred networks, those obtained using GeneNet with only genomic data and those obtained using predictionet with genomic data and priors for different weighing schemes. We allowed the prior weights w to vary between 0 and 1, the former corresponding to networks inferred from genomic data only and the latter to networks inferred from prior knowledge only: w ∈ {0, 0.25, 0.5, 0.75, 0.95, 1}.

To assure a fair comparison between GeneNet and the network inferred from data only with predictionet and the associated random network topologies, we constrained GeneNet networks to have the same number of edges as those networks inferred using predictionet. We chose to take the number of edges obtained with predictionet using prior weight of 0.5 for two reasons. Firstly, although GeneNet is not designed to natively integrate prior knowledge, we tested whether combining data and prior using predictionet will yield better results than a widely-used method that only use data. Secondly, F-score values tend to be higher for networks with greater numbers of edges, therefore choosing a prior weight which results in an advantageous number of edges, such as 0.5, seems reasonable.

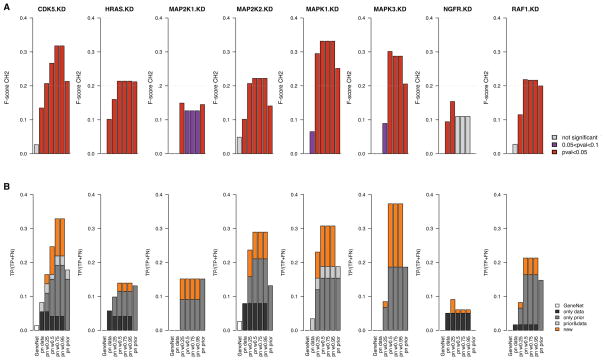
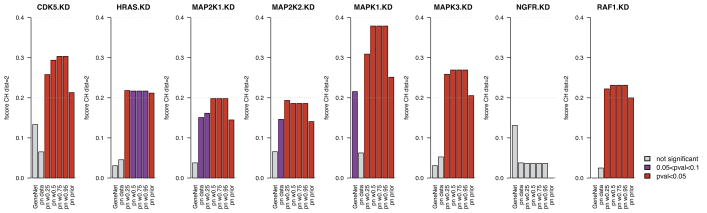
Using our validation framework (Figure 2(a)), we analyzed our set of colorectal cancer cell lines and computed F-scores of the inferred networks in cross-validation for each of the eight KDs (Figure 5A). We first investigated the performance of networks inferred from prior knowledge only (prior weight w = 1). To the best of our knowledge, the informational value of priors retrieved from biomedical literature and structured biological databases has not yet been quantitatively assessed in the context of gene network inference. Indisputable, these known interactions are often the result of biological experiments that are valid in the context in which they have been performed. However, this does not necessarily mean that they carry information with respect to biological data sets generated outside of this context. In our study we found that networks inferred from priors only are informative as they yielded significant F-scores for all the knock-downs except NGFR (Figure 5A and Table 2). This is due to the fact that we found only few prior information regarding the downstream effects of NGFR, with only one direct child and no grandchild in the priors, which is not sufficient to compute a meaningful F-score.

Fig. 5.

Bar plots reporting the performance of gene interaction networks, in cancer cell lines, inferred from genomic data only (GeneNet and predictionet (pn) with prior weight w = 0), predictionet with priors only (prior weight w = 1) and predictionet using combinations of both data sources (prior weight w = {0.25, 0.5, 0.75, 0.95}). Each column reports the performance of the network validated in each KD. (A) Bars represent the F-scores of each network in each validation experiment; they are colored with respect to their significance, that is in red and purple when network’s F-score is higher than 5% and 10% of random networks, respectively. (B) Bars’ heights represent the percentage of true positives with respect to the total number of affected genes for each KD’s network; they are colored based on their origin: black for true positives identified in the network inferred from genomic data only, dark grey from priors only, light grey in both, and orange for true positives that are uniquely found in networks inferred by combining genomic data and priors.

Tab. 2.

Inference using knock-down data in cross-validation:

	CDK5				HRAS				MAP2K1				MAP2K2
	# edges	CH2	TP	Fscore	# edges	CH2	TP	Fscore	# edges	CH2	TP	Fscore	# edges	CH2	TP	Fscore
GeneNet	1006	2	1	0.026667	1058	0	0	0	1044	0	0	0	1025	3	1	0.04878
pn data	586	16	6	0.13483	661	16	7	0.10145	637	0	0	0	610	21	3	0.10169
pn w0.25	802	43	12	0.2069	861	28	12	0.16	831	34	5	0.14925	811	49	9	0.2069
pn w0.5	1006	62	18	0.26667	1058	37	17	0.21384	1044	46	5	0.12658	1025	61	11	0.22222
pn w0.75	1024	78	24	0.31788	1077	37	17	0.21384	1062	46	5	0.12658	1043	61	11	0.22222
pn w0.95	1029	78	24	0.31788	1080	37	17	0.21384	1066	46	5	0.12658	1048	61	11	0.22222
pn prior	313	49	13	0.21311	313	29	16	0.21192	313	36	5	0.14493	313	33	5	0.14085

	MAPK1				MAPK3				NGFR				RAF1
	# edges	CH2	TP	Fscore	# edges	CH2	TP	Fscore	# edges	CH2	TP	Fscore	# edges	CH2	TP	Fscore
GeneNet	1017	0	0	0	1016	0	0	0	1014	0	0	0	1025	0	0	0
pn data	607	6	4	0.065041	593	13	0	0	578	7	5	0.09434	603	11	1	0.027778
pn w0.25	818	66	27	0.29508	783	53	5	0.089286	787	18	9	0.15385	792	26	5	0.11494
pn w0.5	1017	100	36	0.3318	1016	87	22	0.30137	1014	10	6	0.11009	1025	58	13	0.21849
pn w0.75	1033	100	36	0.3318	1031	94	22	0.28758	1027	10	6	0.11009	1044	59	13	0.21667
pn w0.95	1035	100	36	0.3318	1033	94	22	0.28758	1031	10	6	0.11009	1049	59	13	0.21667
pn prior	313	58	22	0.25143	313	48	11	0.20561	313	1	0	0	313	29	9	0.2

^#denotes the number of edges in the inferred network; CH2 denotes the number of genes in the KD’s childhood consisting of children and grandchildren; TP and Fscore denote the number of true positives and F-score for the childhood consisting of children and grandchildren.

To test whether combining prior knowledge with genomic data leads to an improved inference of gene interaction networks, we compared F-scores obtained for networks inferred from data only (GeneNet and predictionet with prior weight w = 0), from priors only (prior weight w = 1) and a combination of data and priors (prior weight w ∈ ]0, 1[). As can be seen in Figure 5A, networks inferred from combination of priors and genomic data yielded consistently higher F-scores than networks inferred from genomic data alone (Wilcoxon signed rank test p = 0.004 for prior weight w = 0.5). When compared to networks inferred from priors only, we observe statistically significant improvement in the F-score for five out of eight KDs (CDK5, MAP2K2, MAPK1, MAPK3 and NGFR; Wilcoxon signed rank test p = 0.01 for prior weight w = 0.5). Moreover the networks inferred from combined data sources are significantly better than random networks in most cases, except for NGFR for which the prior knowledge is limited (Figure 5A).

We then assessed the benefit of combining data sources by counting how many true positives can only be found by combining priors and genomic data, that is they are not present in the data only and/or priors only networks (Figure 4). In other words it does not suffice to fuse the data and prior-only networks to get these true positives. Figure 5B represents the portion of true positives that can be found in the networks inferred from genomic data only, priors only or the combination of both. We observe in Figure 5B that there is little overlap between true positives identified in networks inferred from genomic data only or priors only, suggesting that priors and genomic data provide very different information regarding gene interactions. Moreover, we find that a substantial proportion of new true positives could have only been found by combining data sources, highlighting the benefit of combining priors and data to infer networks (Figure 5B, Table 2).

2.4.2. Extrapolate to tumor patient data

Having shown that the knock-down experiments enable quantitative assessment of the quality of an inferred network, we apply our validation framework to a large data set of 292 colorectal human tumors (expO data set²). We infer gene interaction networks using the entire data set as training set and used the knock-down experiments to assess networks quality as before (Figure 2(b)). Such comparison between patient samples and laboratory models is recognized as imperfect as colorectal cell lines are not precise models for patient’s tumors [15, 23].

The networks inferred from colorectal tumor data were denser than those inferred from cell lines (Supplementary Information, Table 1); this is expected due to the larger sample size of the tumor data set (~300 vs ~100 for the colorectal tumor and cell lines, respectively) and its correspondingly greater diversity. Despite the difference in network density the F-scores were not statistically significantly different to those found for the cell line knock-down experiments (Wilcoxon signed rank test p ≥ 0.10, Figure 6).

Fig. 6.

Bar plots reporting the performance of gene interaction networks, in patients’ tumors, inferred genomic data only (GeneNet and predictionet (pn) with prior weight w = 0), predictionet using priors only (prior weight w = 1) and predictionet using a combination of both data sources (prior weight w=0.25, 0.5, 0.75, 0.95). Each column reports the performance of the network validated in each KD. Bars represent the F-scores of each network in each validation experiment; they are colored with respect to their significance, that is in red and purple when network’s F-score is higher than 5% and 10% of random networks, respectively.

We found that GeneNet performed better on the tumor data than on the KD data, possibly due to the larger sample size. However GeneNet only provides significant results for MAPK1 compared to random networks (Figure 6). On the contrary, networks inferred using combination of genomic data and priors with predictionet yielded significant F-scores in most cases, except for NGFR which is consistent with the cell line knock-down experiments. Again, combining data with the prior knowledge improved F-scores for CDK5, MAP2K1, MAP2K2, MAPK1, MAPK3 and RAF1. This is again consistent with the cell line results.

Given that the networks inferred from colorectal cancer cell lines and tumor data (Supplementary Files 5–8) yielded similar F-scores, we compared their topologies to identify the edges inferred in both data sets and those specific to either cell lines or tumors. For this, because we do not use the test data for validation, we infer a single network using the entire knock-down data set. This cell line network and the tumor network shared on average 22% of edges depending on the methods (4%, 5%, 20%, 31%, 33%, 33% for GeneNet, predictionet with prior weight w=0, 0.25, 0.5, 0.75, 0.95, respectively; Supplementary Information, Table 2). As expected, the proportion of common edges increases with the prior weight; however the networks shared fewer than one third of their edges, suggesting that either the gene interactions present in cell lines and tumors significantly differ from each other or that the sample size in the cell line knockdown experiments was not sufficient to infer networks that are generalizable to other data sets.

Moreover we observed that most of the common interactions involve one of the eight KD genes (41%, p<0.001) for predictionet with prior weight w=0.5), suggesting that more generalizable networks could be inferred when performing targeting experiments, which is supported by recent studies [3, 30]. We illustrated this result in Supplementary Information, Figure 8 which represents the gene interaction network surrounding HRAS, which shows that most common interactions involve at least one of the KD gene.

3. Discussion

Inference of biological networks from genomic and other data has the potential to provide insight into mechanisms driving complex phenotypes including diseases such as cancer. However, the validation of large gene interaction networks remains a challenging task. The most widely used validation approaches consist of comparing network edges to ‘known’ gene-gene interactions derived from the literature or pathway databases. However, such validation is in many ways limiting and imperfect.

Firstly, it prevents the use of prior knowledge in network inference if this is to be used subsequently for validation as it would lead to over-fitting and thus provide an overoptimistic performance evaluation for the inferred networks. Secondly, it may be that most prior knowledge are not specific to the biological conditions or phenotypes under investigation, which makes it difficult to identify a set of standard references of relevant interactions. Further, we and others have suggested that prior knowledge could be used to improve network inference [9, 18]; therefore we developed a new network inference approach, called predictionet, to efficiently integrate priors, in the form of gene-gene interactions extracted from biomedical literature and structured biological databases [17].

The field of network inference lacks quantitative, unbiased validation frameworks purely driven by data [10, 21, 31]. In this paper we present a new validation framework using (I) experimental knock-down data to compute the inferred network’s performance (F-score) and (II) to assess network’s performance based on p-values computed using random networks as null hypothesis to ensure statistical significance of the results. These two parts are complementary as only relatively sparse networks are likely to be significantly better than random networks and networks with more interactions are more likely to yield higher F-scores. Within this framework, we showed how difficult it is to infer networks solely based on genomic data both for GeneNet and predictionet. Furthermore, we provided evidence for the quality of prior knowledge retrieved through the Predictive Networks web-application. Finally, we were able to show that combining genomic data and prior networks lets us achieve higher F-scores than either of the sources achieves by themselves, while at the same time inferring networks that were also significantly better than random networks. When using patients’ tumor data, we obtained comparable results, suggesting that cell line experiments can be used for the validation of patient data.

This study has some potential limitations. First, we targeted a small set of eight key genes from the RAS signaling pathway but assessed their effect on other genes from the entire genome. Second, these KDs were performed for single genes, which do not allow us to assess the effect of multiple simultaneous KDs. Third we performed the KD experiments on two colorectal cancer cell lines; extension of our validation framework to a larger number of cell lines and additional single and multiple gene KDs is likely to improve our ability to infer robust gene interaction networks. Lastly, we focused on a RAS signature of 339 genes to limit the computational time required to infer multiple networks; we are working on parallelizing the predictionet package to enable network inference from more genes, potentially the whole genome.

In conclusion, we demonstrated that performance of gene interaction networks inferred from high-throughput genomic data can be quantitatively assessed and compared using targeted experiments. Moreover we showed that priors, in the form of gene-gene interactions extracted from biomedical literature and structured biological databases using the Predictive Networks web-application, produce relevant networks on their own and substantially improve networks’ performances when efficiently integrated in the inference process. Finally we were able to use the gene perturbation data generated in cell lines to assess the performance of networks inferred from patient tumor samples, suggesting that our validation framework could be applied in a translational research setting.

Supplementary Material

01

Supplementary File 1 In this file each sample of the knock-down data set is described in terms of “samplename”, “scan.name”, “filename”, “cell.line”, “KD”, “biological.replicate”, “sample” and “sample2”.

Supplementary File 2 In this file we provide the values of the statistical comparison, these are the log2 fold change, the p-value of the Wilcoxon test and the associated false discovery rate, for each of the 339 unique genes. The first sheet comprises the 332 genes identified from the Bild 2005 RAS signature and the second sheet the 332 plus the core genes for a total of 339 genes. HRAS was identified in the Bild 2005 signature.

Supplementary File 3 This table provides the mapping for each of the 339 genes to their probe, gene symbol and Entrez gene. Furthermore, for each knocked down gene it provides the log2 fold change, p-value and false discovery rate determining whether the genes were affected by the perturbation experiment.

Supplementary File 4 This file contains the gene-gene interactions as retrieved from Predictive Networks between the 325 genes present in the database including the source of the corresponding citation as well as the citation itself.

Supplementary File 5 The inferred network from the complete knock-down data set exported to *gml format. This file contains the general network properties.

Supplementary File 6 The inferred network from the complete knock-down data set exported to *gml format. This file contains additional edge properties.

Supplementary File 7 The inferred network from the expO data set exported to *gml format. This file contains the general network properties.

Supplementary File 8 The inferred network from the expO data set exported to *gml format. This file contains additional edge properties.

Supplementary File 9 Detailed of selected eight core genes including links to GeneBank and RefSeq.

Highlights.

Although many methods have been developed for inference of biological networks, the validation of the resulting models has largely remained an unsolved problem. Here we present a framework for quantitative assessment of inferred gene interaction networks using knock-down data from cell line experiments and show that network inference based on integration of prior knowledge significantly improves the quality of inferred networks.