Abstract
In eukaryotic proteins, intrinsically disordered regions (IDRs) are ubiquitous and often exist in linker regions that flank the functional domains of modular proteins, regulating their functions. For detailed structural ensemble modeling of IDRs, we propose a multiscale method for IDRs that possess significant long-range order in modular proteins and apply it to the eukaryotic transcription factor p53 as an example. First, we performed all-atom (AA) molecular dynamics (MD) simulations of the explicitly solvated p53 linker region, without experimental restraint terms, finding fractional long-range contacts within the linker. Second, we fed this AA MD ensemble into a coarse-grained (CG) model, finding an optimal set of contact potentials. The optimized CG MD simulations reproduced the contact probability map from the AA MD simulations. Finally, we performed the CG MD simulation of the tetrameric p53 fragments including the core domains, the linker, and the tetramerization domain. Using the obtained ensemble, we theoretically calculated the small angle x-ray scattering (SAXS) profile of this fragment. The obtained SAXS profile agrees well with the experiment. We also found that the long-range contacts in the p53 linker region are required to reproduce the experimental SAXS profile. The developed framework in which we calculate the long-range contact probability map from the AA MD simulation and incorporate it to the CG model can be applied to broad range of IDRs.
Introduction
It has become clear that intrinsically disordered regions (IDRs) are ubiquitous in eukaryotic proteins: 30% to 50% of eukaryotic proteins have been predicted to have IDRs with at least 30 consecutive residues (1–3). IDRs often play crucial roles in molecular recognition and signaling, protein modification, molecular assembly, entropic chain activities, and so on (4). Furthermore, IDRs are related to various human diseases, such as cancer, cardiovascular diseases, amyloidosis, neurodegenerative diseases, and diabetes (5,6). Notably, in eukaryotic proteins, most IDRs exist either at the tails or at the linkers that flank folded domains in multidomain and modular proteins (see Fig. 1 A as an example) (7). Such flexible linkers can control the relative location of the flanking domains, which is important for the proteins to regulate their functions (8,9).
Figure 1.
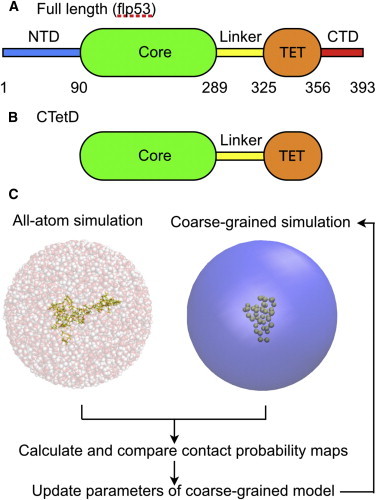
The domain maps of (A) the full length p53 and (B) the CTetD. The ellipses represent domains that have stable tertiary structure in solution, whereas the rectangles represent disorder regions. (C) The strategy to determine the parameters of the CG linker model based on the AA V-McMD simulation result. Snapshots show the AA V-McMD simulation of the linker region (left) and the CG MD simulation (right). To see this figure in color, go online.
Biophysically, IDRs possess energy landscapes with many shallow and competing minimums at room temperature and thus encompass the broad spectrum of conformational ensembles (4,10–13). The dominant feature of these ensembles is the lack of persistent secondary and tertiary structures, with a flexible chain transiently sampling fractional local secondary structure as well as some long-range contacts (14–16). An accurate description of the conformational ensemble is crucial to fully understand its functions. It is, however, difficult to obtain detailed information of conformational ensembles of IDRs solely by conventional experimental techniques. Therefore, combining experimental data with computational method has been used and shows some promise (14–16).
First, one can generate a large variety of conformations and then select the subset of conformations that have ensemble averages that agree with experimental data (17,18). Another approach uses a restrained MD simulation that is performed with experimental restraint terms for biasing the conformational sampling (19). These approaches help researchers obtain IDR conformational ensembles consistent with experiments (14–16). However, they commonly suffer from a so-called “degeneracy problem”—that is, given the low-resolution information from experiments, there can be many different ensembles that are consistent with the experiments. Sophisticated methods to determine weights for each conformation in the ensemble have been developed to mitigate the problem (20). An alternative way that does not suffer from the degeneracy problem is to perform MD simulations without the experimental restraint term. However, conformational sampling by AA MD itself is highly nontrivial for systems with transient long-range contacts. The purpose of this paper is to develop a multiscale method that can deal with IDRs with long-range residual contacts.
In addition, IDRs are often flanked by folded domains and thus the full-length proteins are large and beyond the reach of current AA MD simulations. Modular proteins, comprising two or more folded domains tethered by IDR linkers, are common in nature (21–23), among which is the eukaryotic transcription factor p53, which we used in this study. The full-length p53 contains two folded domains (the core domain and the tetramerization domain (Fig. 1 A)) that are flanked with both N- and C-terminal disordered tails and the disordered linker region (24). Interestingly, of these five distinct regions, two regions bind to DNA: the core and the C-terminal domains. Our previous CG MD simulation study showed that tetrameric full-length p53 slides on DNA with its C-terminal IDR while its core domains repeat dissociation from and association to DNA (25). These are in accord with a recent single molecule experiment (26). This result points to the functionally important role of the p53 linker region that connects two DNA binding regions. Tidow et al. reported the SAXS profiles of the p53 fragment that lacks N- and C-terminal intrinsically disordered domains (CTetD; Fig.1 B) and modeled a static structure that is consistent with the experimental data (27). As another study found, obtaining a unique static structure that could describe the SAXS profiles did not exclude the possibility that the CTetD is flexible in solution (28). In this construct, the linker region controls a relative location between the core domain and the tetramerization domain. Therefore, the model of this linker region has the dominant effect on the overall shape of the CTetD and consequently its SAXS profile. We also know, a posteriori, that the linker region contains transient long-range order. This makes the CTetD construct an ideal system to verify quantitative modeling of IDRs in modular proteins.
In this study we extended previous multiscale approaches (29–32) and proposed a multiscale ensemble modeling method that can be used on IDRs with long-range residual contacts. For the p53 linker, we first performed atomistic structure modeling by taking the recently developed enhanced sampling techniques, a virtual-system coupled multicanonical MD (V-McMD) simulation (33). This AA MD based ensemble was utilized to obtain an optimal set of CG interaction parameters (Fig. 1 C). Using the obtained CG model of the p53 linker, we performed CG MD simulations for the p53 CTetD, and theoretically calculated the SAXS profile of the obtained CG conformational ensemble. We find that the profile agrees well with that of the experiment. Finally, we investigated the effect of the long-range order in the linker on biological functions, focusing on the contact probabilities between two core domains. The results suggest that the linker conformations modulate the inter-core domain contacts to a certain degree. In this work, we successfully modeled the p53 linker region that has long-range contacts and obtained structural ensemble of p53 CTetD that cannot be obtained easily by the previously established modeling methods. The framework in which we calculate the long-range contact probability map from the AA MD simulation and incorporate it to the CG model can be applied to broad range of IDRs.
Methods
Multiscale method for intrinsically disordered region
We next outline the multiscale method for IDR modeling, in which we use AA MD simulations to tune parameters in a CG model. We suppose the case that a relatively large modular protein contains IDRs and that the IDRs possess long-range residual order. Here, the long-range residual order means a structural order stabilized by nonlocal interactions. For this IDR region, first, we obtained the conformational ensemble by performing AA MD simulations. Then, using this AA MD-based ensemble, we tuned the CG model.
For the IDR that has long-range order, we write the potential energy function of our CG model as follows:
| (1) |
where represents a CG potential previously developed for IDRs that are supposed to approximate local residual order (see the following sections for the explicit formula); is the distance between the i-th and the j-th CG particles; and and are parameters to be determined via the multiscale method.
First, from the AA ensemble, we calculated the modes of distances between CG particle pairs and set them to the parameters. We also calculated the contact probability map from the AA ensemble . We considered a residue pair was contacted, if the distance between its CG particles (the atoms of these residues for AA ensemble) was less than 8.5 Å.
To determine the parameters, we first performed CG MD simulations of this region with the parameters set to 0.0. Then, we calculated the contact probability map from the CG ensemble . By comparing the contact probability map with , we updated the parameters that were initially set to 0.0, according to the following equation:
| (2) |
Then, we performed the CG MD simulation again, using the new parameters. We repeated 1), the CG MD simulation, 2), the contact probability calculation, and 3), the parameter update until the contact probability map from the CG ensemble converged to that from the AA ensemble as shown below. The strategy is outlined in Fig. 1 C. Previously, a similar procedure was utilized to incorporate interaction information from experiments into their CG model (34).
All-atom simulation of p53 linker region
In this section we describe the AA MD simulation method for the p53 linker (for details of the method, see the Supporting Material). The system consists of the p53 linker segment with a few residue extensions at both ends (40 residues long, residue ID: 288 to 327), which is solvated with water molecules. The amino-acid sequence is Ace- NLRKKGEPHHELPPGSTKRALPNNTSSSPQPKKKPLDGET-Nme, where Ace and Nme are, respectively, the N-terminal acetyl and C-terminal N-methyl groups introduced to cap the segment termini. We generated a random conformation of the linker segment for the initial conformation and put it into a solvent sphere (diam. = 80 Å), setting the center of mass at the center of the sphere. The system consisted of 30,937 atoms (640 polypeptide atoms, 36 Cl-, 30 Na+, and 10,077 water molecules). To sample the conformation of the linker region with reduced influence of the boundary condition, we fixed the linear and the angular momenta of the linker segment to zero by rescaling the velocities. We did not use the periodic boundary condition in this study because the periodicity may cause artificially interchain entangling among the different periodic boxes. The solvent sphere was set as large as possible, yet small enough so that the multicanonical sampling can be done within a feasible simulation time.
The force field parameters for the polypeptides were from an AMBER-based hybrid force field (35) defined as , where and denote the AMBER parm94 (36) and parm96 force fields, respectively (37). Previous McMD simulations with revealed that a peptide with a helical propensity folds into an -helix, whereas a peptide with a -hairpin propensity forms a -hairpin (35). Therefore, we used for the present study. We have successfully applied this force field to protein folding (38–40) and an ensemble modeling of an intrinsically disordered protein (IDP) (41). Although there is no perfect atomistic force field that can be applicable to any amino-acid sequence, our preceding works (35,41) have suggested that the force field we used in the present study does not have an apparent bias in secondary structure formation and is appropriate for IDRs.
The AA simulation procedure consists of two stages: 128 pre-V-McMD simulations were performed with a high temperature. These 128 simulations were all started from different random conformations. Then, for the pre-V-McMD simulations, the biased potential was computed for the first V-McMD simulation. Then, we started the first V-McMD simulations using the biased potential (see the Supporting Material for the accuracy of the biased potential estimation). Each of these simulations was started from the final conformation of each of the pre-V-McMD simulations. The length of the production run was 1.2 107 steps for each of the 128 runs. Finally, we assigned a statistical weight at 300 K to each snapshot of the production run according to the reweighting technique (33).
Coarse-grained simulation of p53 linker region
As a starting point of development of a new CG model, we began with a concise CG model that we developed previously (“pure-CG” model in (42)). This model does not take into account long-range contacts. The potential energy function of that model is as follows:
| (3) |
where , , and are the bond-stretching term, the electrostatics term, and the excluded volume effect term, respectively. (For complete description of the potential energy function, refer to an earlier study (42)). This model reproduced the SAXS profile of the p53 N-terminal IDR whose conformational ensemble did not have extensive long-range contacts. However, the direct application to the system with fractional long-range contacts fails to reproduce the SAXS profile, as is shown below.
The molecular system of the CG MD simulation was the same as that of the AA MD simulation except for the absence of the cap of the segment termini. We used the one-bead-per-one-amino-acid CG model and put a CG particle on each position of the 40-residues-long linker segment. We generated a random conformation of the linker segment for the initial conformation and put it into a sphere. The diameter of the sphere was 80 Å, the same as that of sphere 2 in the AA MD simulation. Because the diameter of the sphere was same between the AA and the CG MD simulations, the confinement was expected to affect similarly the AA and the CG conformational samplings. Therefore, we thought that the confinement effect on the parameter calibration procedure was negligible. Production runs for the CG simulations were performed by Langevin dynamics for 108 MD steps using CafeMol 2.0 (43).
Coarse-grained simulation of two core domains
Experimentally, it has been shown that two p53 core domains form a loose dimer with the dissociation constant of 2 mM at 100 mM monovalent ion (44). Using NMR spectroscopy, Tidow et al. revealed that transient interaction between core domains in solution involved the same interface as that observed in the crystal structure of the core domain-DNA complex (27). To model this intercore-domain interaction so that the dissociation constant was essentially the same as that measured in the previous experiment, we performed the CG MD simulation of the system containing the two core domains (Fig. S1 A). The initial coordinate of the core domain was taken from the x-ray crystal structure (45) (PDB ID: 2XWR). We put two core domains into a sphere with the diameter of 50 Å. We adopted recently developed Go-like AICG2 model (46) for the intramolecular potential energy function that stabilizes the native structure (45) (PDB ID: 2XWR). The intercore-domain potential energy function is defined as follows:
| (4) |
where and were electrostatics term and excluded volume effect term, respectively (for complete description of these terms, refer to the Supporting Material). The i and j run over the CG particle pairs that contacted in the experimentally indicated interface in the x-ray crystal structure (47) (PDB ID: 3KMD). The is the distance between two CG particles i and j in the native structure. The ’s are the AICG2 model parameters (46). These parameters were tuned so that the fluctuation of isolated proteins was reproduced. Thus, there is no guarantee that these parameters reproduce the strength of interprotein-interaction. Accordingly, to reproduce the dissociation constant, we scaled the intermolecular native contact interaction by an additional factor = 0.65 (the determination process of is described in detail in the Supporting Material). The ion strength was set to the same value as that of the experiment (100 mM) (44).
In previous NMR studies (27,48), the other interdomain interactions (i.e., core-linker, core-Tet, and linker-Tet interactions) were not identified. Therefore, we imposed only repulsive and electrostatic interactions to the other interdomain interactions.
Construction of coarse-grained conformational ensemble of CTetD
To validate the parameters of the CG linker model, we performed the CG MD simulation of the tetrameric CTetD (Fig. 1 B), obtained the CG conformational ensemble, and theoretically calculated the SAXS profile from this conformational ensemble using the CRYSOL program (49) after reconstructing AA model using the PULCHRA program (50). We used 2XWR (45) and 1AIE (51) as the template structure for the core (residues 91 to 289) and the tetramerazation (residues 326 to 356) domains, respectively, and modeled the linker region (residues 290 to 325) as a random coil. We used Eq. 1 as the potential energy function (with and without intrachain contact interactions) for the linker region, the AICG2 model as that for the core and the teramerization domains, and Eq. 4 as that for the intrachain-domain interaction. The ion strength was set to the same value as the experiment (150 mM) (27). Each production run was performed by Langevin dynamics for 109 MD steps.
Results and Discussions
All-atom simulation of p53 linker region
First, we performed the AA V-McMD simulation of the p53 linker region with a few residue extensions in both ends (residue ID: 288 to 327). We obtained the well-converged conformational ensemble (see the end of this section for the convergence test). To characterize structures in the ensemble, we grouped the structures into clusters. The clustering was done by the gromos algorithm (52) implemented in GROMACS 4.5.5 (53) using the root mean square deviation (RMSD) between each pair of structures as a distance metric. In the clustering analysis, we chose 200 conformations that had large Boltzmann weights at 300 K out of 30,000 stored conformations. Using the RMSD cutoff 3.0 Å, we obtained 31 clusters. In Fig. 2, we show the representative structures of the top-six largest clusters, together with the ranking by the cluster size. We find that the conformational ensemble is very diverse.
Figure 2.
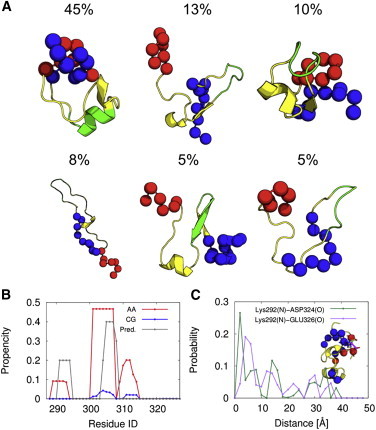
The representative structures of the top-six largest clusters obtained using the AA V-McMD simulation. The blue spheres represent the atoms of the N-terminal residues (residue ID: 288 to 297). The red spheres represent the atoms of the C-terminal residues (residue ID: 321 to 327). The helical region of the largest cluster (residue ID: 301 to 307) is colored green. To see this figure in color, go online.
Interestingly, each conformation has its specific secondary structure and tertiary contact pattern. For example, the top-cluster structure contains a helical region (light green in Fig. 2), although the same region in the other five clusters does not contain a helical region. The secondary structure prediction also indicated that this region have high helical probability (Fig. S2 in Supporting Material). A recent study revealed that the iASPP protein, whose function is to modulate p53-dependent apoptosis, is bound to the p53 linker region although its binding site in the linker region has not been elucidated yet (54). It was also reported that a significant number of molecular recognition events often involved loosely structured regions within IDRs (55). Taken together, we speculate that either or both of these regions (residue ID: 289 to 293 and 301 to 307) with relatively high helical propensities recognize the iASPP by the “coupled folding and binding” manner.
Moreover, the N-terminal region (blue) and C-terminal region (red) in the simulated peptide form the long-range contacts in the most and the third-most populated clusters, but not in the other clusters (Fig. 2). We speculate that some of these long-range contacts are caused by the electrostatic interaction (Fig. S3). Overall, it is suggested that the conformational ensemble of the p53 linker region cannot be described by the simple random coil model and is composed of the structures with the transient secondary structures and long-range contacts.
We assessed the convergence of the conformational ensemble obtained by V-McMD simulations. To do so, we randomly divided the 128 simulation trajectories into two groups, extracted the structures from each of them to make two conformational ensembles (“AA_1” and “AA_2”), calculated contact probability maps and the distributions of the radius of gyration, and compared them (left panel in Fig. 3 A). In drawing the contact maps, we identify two residues forming contact when the distance between two atoms is less than 8.5 Å. From Fig. 3 A, we see that these two contact maps are similar, suggesting that the AA ensemble converges relatively well in this perspective. This information is directly incorporated into the CG model below. Therefore, the convergence in this perspective is critically important. From this map, we also see that, in addition to the transient long-range contacts between N- and C-terminal regions, there are several fractional but noticeable contacts in the AA conformational ensemble. We listed the prominent contacts in Table S3. In Fig. 3 C, distributions of radius of gyration from AA_1 and AA_2 are completely overlapped, suggesting that the AA ensemble converges relatively well in this perspective, too.
Figure 3.
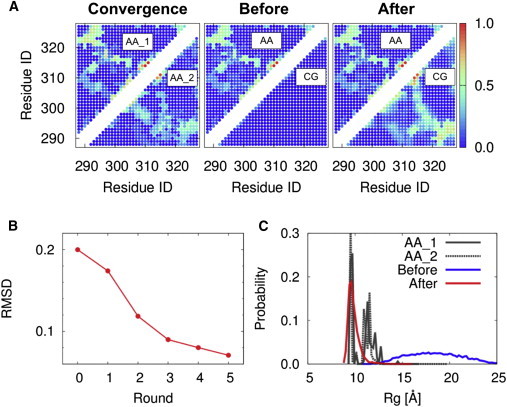
The determination of parameters of the CG linker model. (A) The contact probability maps from AA V-McMD simulation (left) using two halves of ensemble (AA_1 and AA_2; see text for details). The contact probability maps from the AA V-McMD simulation (center; above diagonal), from the coarse-grained (CG) simulation with all of the ε’s in Eq. 1 set to 0.0 (center; below diagonal), and from the CG simulation with the updated parameters (right; below diagonal). (B) The RMSD between the contact probability maps from the AA V-McMD simulation and those from the CG MD simulation of each round of the parameter update procedure. (C) The probability distributions of the radius of gyration from the AA V-McMD simulation (“AA_1” and “AA_2”), from the CG simulation with all of the ε’s in Eq. 1 set to 0.0 (blue), and from the CG simulation with the updated parameters (red). To see this figure in color, go online.
Determination of parameters of coarse-grained linker model
For the p53 linker region, we seek a set of CG model parameters in Eq. 1 that can reproduce the residue-residue contact probabilities computed by the AA simulations as close as possible.
First, we performed the CG MD simulation with the parameters in Eq. 1 set to zero. Then, we calculated the contact probability map from the obtained CG conformational ensemble (the bottom-right triangle region in the center panel of Fig. 3 A) using the same cutoff distance as above for the definition of contacts. The map shows almost no fractional contact in this CG conformational ensemble. For comparison, the top-left triangle region in the same panel shows the contact map by AA simulations. We see clear difference between the two halves.
Then, we updated the parameters according to the Eq. 2. Using the updated parameters, we repeated the CG MD simulation and calculated the contact probability maps. As a result, the difference between the AA map and the CG map became smaller (the RMSD plotted in Fig. 3 B). We repeated this cycle five times. Fig. 3 B shows that, as we repeated the cycle, the RMSD monotonically decreased and finally converged to a small value. In the bottom-right triangle region of the right panel of Fig. 3 A, we show the contact probability map calculated from the final CG conformational ensemble. By comparing the elements above (the contact map by AA simulations) and below the diagonal, we see that the CG map and the AA maps are essentially the same. Thus, the parameter set in the fifth round reproduced the AA contact probability map well and was used for the subsequent CG MD simulations of the CTetD (Fig. 1 B).
To investigate the characteristics of the CG conformational ensemble in the final round, we calculated and plotted probability distributions of radius of gyration (; Fig. 3 C). The plot shows that the average of the ensemble (red) is smaller than that in the initial round with all of the parameters set to zero (blue). In Fig. 3 C, we also plotted the probability distribution of of the AA conformational ensemble (black or gray, see the previous section). Interestingly, there are three peaks in this probability distribution, which indicates that several distinct states with different ’s coexist in the AA conformational ensemble. By comparing these probability distributions, we can see that the most intense peak with the smaller average of the AA probability distribution is reproduced by the CG conformational ensemble in the final round, but not by the initial round. This suggests that the AA conformational ensemble is more compact than expected from the random coil model and the fractional long-range contacts are required to reproduce this conformational ensemble. We can also see that the other two peaks are reproduced by neither of the CG conformational ensembles. This suggests that the Lenard-Jones-type contact term in Eq. 1 is not sophisticated enough to reproduce the transition between several distinct states in the AA conformational ensemble. The development of more sophisticated CG model for contact interaction is desirable in future. For example, a simple way to improve the model is to impose the contact potential (Eq. 1) only to the interaction between beads representing a hydrophobic or bulky and polar amino acid (i.e., Leu, Ala, Asn, and Gln). However, we consider that the simple model can be used for the p53 linker region, because these less populated conformations do not seem to affect the conformational ensemble of the CTetD.
Validation of parameters of the coarse-grained model
To validate the parameters of the CG linker model obtained above, we performed 109-step CG MD simulation of the tetrameric CTetD (Fig. 1 B), obtained the CG conformational ensemble, theoretically calculated the SAXS profile from this ensemble using CRYSOL (49) after reconstructing the AA model using PULCHRA (50), and compared it with that of the previous experiment (27). We note that, except for the linker region, the other parts of the CTetD have stable tertiary structures in solution (Fig. 1 B). Therefore, the overall shape of the CTetD is mostly decided by the flexible linker region, which makes this system suitable for validation of the parameters of the CG linker model.
First, we compared the normalized SAXS intensity profile calculated from the CG MD simulation with that of the experiment (Fig. 4 A). We see that the SAXS profile from the CG MD simulation with the contact interactions in the linker region (all of the ’s in Eq. 1 calibrated based on the AA MD simulation; red in Fig. 4 A) reproduces that of the experiment well (gray in Fig. 4 A) ( = 0.38, where is the sum of square difference of each data point). On the other hand, the SAXS profile from the CG MD simulation without the contact interactions (all of the ’s in Eq. 1 were set to 0; blue in Fig. 4 A) exhibits clear deviation from the experimental data ( = 2.60).
Figure 4.

Comparison of the experimentally observed and theoretically calculated SAXS profiles. (A) The SAXS intensity profile from the experiment (gray points), from the CG MD simulation with the updated parameters (red solid line), and from the CG MD simulation with all of the ’s in Eq. 1 set to 0.0 (blue solid line). Inset shows representative structures from the CG MD simulation with all the ε’s in Eq. 1 set to 0.0 (left) and from the CG MD simulation with the updated parameters (right). (B) Kratky plot. The color assignment is same as that of A. (C) Guinier plot. The color assignment is the same as that of A. To see this figure in color, go online.
Second, we compared the Kratky plots ( versus , where is a scattering vector and is a scattering intensity) (Fig. 4 B). The experimental Kratky plot (gray) shows a single pronounced peak that is indicative of a spatial decorrelation between the different globular domains (28). This peak is nearly perfectly reproduced by the CG MD simulation with the contact interaction in the linker region (red in Fig. 4 B), whereas the peak position is clearly different when all of the ’s in Eq. 1 are set to zero. This result indicates that the relative position of the different core domains is well decorrelated in the CG MD simulation with the optimal ’s.
Third, we compared the Guinier plots ( versus ) (Fig. 4 C). From the slope of the linear region in the small-angle limit, we can estimate the radius of gyration of the molecule. From this figure, we can see that the slope of the CG MD simulation with the contact interactions in the linker region is essentially the same as that of the experiment, whereas that of the CG MD simulation without the contact interaction is quite different. This result indicates that the experimental radius of gyration (52.2 Å) is closer to the CG MD simulation with the contact interactions in the linker region (45.8 Å). The latter is significantly smaller than that of the CGMD simulation without long-range order in the linker (64.8 Å). This result also indicates that the structures from the CG MD simulation with the contact interaction (right panel of the inset of Fig. 4 A) tend to be more compact than those from the CG MD simulation without them (left panel of the inset of Fig. 4 A). In the CG MD simulation with the contact interaction, the average radius of gyration is smaller than that of the experiment. We think that this can partly be attributable to the bias in the conformational ensemble obtained using the AA MD simulation to the relatively compact structures. This is a previously reported problem in almost all of the current generation force fields (56). Thus, it is desired that next generation force fields are designed to mitigate this problem.
Taken together, these results show that we can obtain the CG conformational ensemble of the CTetD that fairly well reproduces the experimental SAXS profile using the CG MD simulation with the contact interaction in the linker region. Thus, the parameters of the CG linker model obtained based on the AA MD simulation are valid.
Intercore-domain interaction in CTetD
In the “Determination of parameters for intercore-domain interaction” section, we tuned the CG model parameters in Eq. 4 for the intercore-domain interaction. The parameters were determined so that the experimental dissociation constant of the intercore-domain interaction was reproduced. In the tetrameric CTetD, four core domains are tethered by tetramerization domains and thus tethering by the linker modulates the inter-core domain associations. To reveal the effect of the tethering on the inter-core-domain association, we plot the probability distributions of intercore-domain Q-score of each pair of core domains in Fig. 5. The Q-score represents the ratio of the transiently formed contacts to the natively formed contacts.
Figure 5.
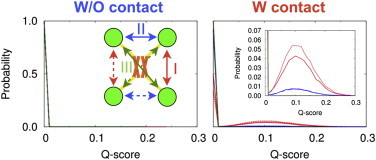
Probability distributions of the inter-core-domain Q-score from the CG MD simulation with all of the ’s in Eq. 1 set to 0.0 (left) and from the CG MD simulation with the updated parameters (right and right inset). The Q-score represents the ratio of the transiently formed contacts to the natively formed contacts. Natively formed contacts are defined using the x-ray crystal structure in which four core domains bind to its specific DNA (PDB ID: 3KMD) as a template structure. We calculated the probability distribution of each pair of the core domains. Because of the symmetry of the molecule, these pairs can be divided into three classes. Therefore, we mapped these three classes on to the cartoon of tetramerized CTetD (left inset). The color assignment is the same as that of Fig. 1A and B. To see this figure in color, go online.
We note that the tetramerization domain of p53 takes dimer-of-dimers. The primary dimer makes tight contacts including interchain sheet formation. Interactions between two primary dimers are via helix-helix contacts and are weaker. Because of the nature of the dimer-of-dimer form of tetramerization, inter-core-domain interactions have three types of pairings: 1), the pairing of core domains, of which chains form the primary dimer in the tetramerization domain; 2), the pairing of core domains, of which chains form contacts via secondary dimer interface in the tetramerization domain; and 3), the pairing of core domains, of which chains are most distant and thus form the least contacts in the tetramerization domain (arrows in the inset of the left panel of Fig. 5). In Fig. 5, we used different colors for different types of pairings: red for the type 1, blue for the type 2, and green for the type 3. Because of the symmetry of the molecule, there are two pairs in each of the three types. We distinguished the two pairs using the solid and the dashed curves.
The right panel of Fig. 5 shows that, when we included long-range interaction in the linker region, we see a weak yet significant probability of contacts between core domains (a low and broad peak around the intercore domain Q-score of 0.1). On the other hand, we do not see significant probability of intercore domain contact when the linker does not contain long-range interactions (left panel of Fig. 5: the correlation coefficient between red (blue) curves in left and right panels of Fig. 5 is around 0.15). Note that the inter-core-domain contact strengths are identical between the two simulations and that the origin of the difference is purely in the treatment of the linker region. This result indicates that the long-range contact interaction in the linker region increases the local effective concentration of the core domains and thereby enhances the inter-core-domain association. However, even with the contact interaction in the linker region, the contact probability is rather low. Therefore, our data show that the p53 predominantly exists as an open form, i.e., the core domains are not in contact, in the absence of its response element (RE) on DNA, whereas there is a low probability to take a topologically closed form, i.e., the core domains are in contact. This may facilitate p53 to wrap the DNA when p53 finds the response element. When p53 binds to its RE, the core domains form interchain contacts, taking the closed form. Bound to the nonspecific DNA, p53 would primarily take an open form although intercore domain contact probability may be slightly higher than that in the absence of DNA. This conformation could be somewhat different from the RE wrapping conformation previously observed using cryo-electron microscope (27). On the nonspecific DNA, the inter-core domain contact probability would be quite low. Thus, we can reasonably argue that the inclusion of the inter-core domain does not affect the main conclusion of the previous work.
From this figure, we also see the peak of type 1 interaction (red) is the most pronounced. The distribution of the intercore-domain Q-score of one core-domain-pair is similar to that of the other core-domain-pair (compare the solid and dashed line in the right panel in Fig. 5), suggesting that the initial-structure-dependency is almost diminished by repeated dissociation and association of the core domains. This result indicates that each core cannot freely diffuse because of the tethering and that the type 1 interaction is preferred. Because the interaction energy parameters for each pair of the core domains are set identically, this preference arises from the topology of the tetramerization domain and from the restraint of the linker region.
Conclusion
Although the SAXS profile is not sensitive enough to test the detail of the model, the SAXS can monitor the shape of the molecular envelope. Therefore, comparison of the SAXS profile provided validation of the compactness of the compact linker structural ensemble obtained in our CG MD simulations.
At the moment, limited experimental information is available for structural and dynamic properties of the p53 isolated linker domain. In this study, we found that the long-range contacts in the linker region alter the structure of the p53 as a whole, affecting the function of this protein. Thus, more structural study of this region would be beneficial. To address biological functions of p53 more directly, we need to characterize conformations of p53 binding to the RE on DNA. This is beyond the scope of the present work and should be addressed in future studies.
The structural analysis of p53 CTetD indicates that the long-range contact in the linker region increases the local effective concentration of the core domains and thereby enhances the inter-core-domain association, though the contact probability is rather low. Therefore, our data show that the p53 predominantly exists as an open form, whereas it takes a closed form in a low probability. We speculate that this low-probability closed form in DNA-free state may facilitate the closed form on the DNA and to wrap its recognition element.
Modular proteins comprising two or more folded domains tethered by intrinsically disordered linker regions are ubiquitous in nature (21–23). Our results strongly suggest that the multiscale modeling strategy employed in this work can be used in the conformational ensemble modeling of modular proteins that usually have fractional long-range contacts in its disordered regions. Although the method itself is general, the CG potential function obtained in this work is specific to the target molecule, and is not transferable to other systems. For each of the target molecules, we started with the AA MD simulation to obtain conformational ensemble of a disordered region because different amino-acid sequences have different conformational ensembles. Therefore, the applicable range of the proposed method is limited by the capability of obtaining an equilibrium AA conformational ensemble of a disordered region, i.e., the longer the IDR, the more difficult the conformational sampling. Although various promising methods including the one we used in this work (33) have been developed, further improvement is definitely desired to overcome the limits of the present method.
Acknowledgments
We thank Prof. Alan Fersht for kindly providing with experimental SAXS profile of the CTetD.
The calculations in this work were, in part, performed by using the supercomputer of ACCMS, Kyoto University. T. T. thanks to the support of a JSPS fellowship. This work was supported by Grant-in-Aid for JSPS Fellows, by Grant-in-Aid for Scientific Research on Innovative Area, by Strategic Program for Innovative Research, by the Global COE Program “Formation of a Strategic Base for Biodiversity and Evolutionary Research: from Genome to Ecosystem” of the Ministry of Education Culture, Sports, Science, and Technology (MEXT) and by the Excellent Graduate School Program “Biodiversity and Evolution from Genome to Ecosystem.” J. H. appreciates a Grant-in-Aid for Scientific Research on Innovative Areas (21113006) provided by the MEXT. J. H. was supported by grants from the New Energy and Industrial Technology Development Organization (NEDO) Japan.
Supporting Material
References
- 1.Ward J.J., Sodhi J.S., Jones D.T. Prediction and functional analysis of native disorder in proteins from the three kingdoms of life. J. Mol. Biol. 2004;337:635–645. doi: 10.1016/j.jmb.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 2.Xue B., Dunker A.K., Uversky V.N. Orderly order in protein intrinsic disorder distribution: disorder in 3500 proteomes from viruses and the three domains of life. J. Biomol. Struct. Dyn. 2012;30:137–149. doi: 10.1080/07391102.2012.675145. [DOI] [PubMed] [Google Scholar]
- 3.Peng Z., Mizianty M.J., Kurgan L. Genome-scale prediction of proteins with long intrinsically disordered regions. Proteins. 2014;82:145–158. doi: 10.1002/prot.24348. [DOI] [PubMed] [Google Scholar]
- 4.Dunker A.K., Brown C.J., Obradović Z. Intrinsic disorder and protein function. Biochemistry. 2002;41:6573–6582. doi: 10.1021/bi012159+. [DOI] [PubMed] [Google Scholar]
- 5.Uversky V.N., Oldfield C.J., Dunker A.K. Intrinsically disordered proteins in human diseases: introducing the D2 concept. Annu Rev Biophys. 2008;37:215–246. doi: 10.1146/annurev.biophys.37.032807.125924. [DOI] [PubMed] [Google Scholar]
- 6.Metallo S.J. Intrinsically disordered proteins are potential drug targets. Curr. Opin. Chem. Biol. 2010;14:481–488. doi: 10.1016/j.cbpa.2010.06.169. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Good M.C., Zalatan J.G., Lim W.A. Scaffold proteins: hubs for controlling the flow of cellular information. Science. 2011;332:680–686. doi: 10.1126/science.1198701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Chong P.A., Lin H., Forman-Kay J.D. Coupling of tandem Smad ubiquitination regulatory factor (Smurf) WW domains modulates target specificity. Proc. Natl. Acad. Sci. USA. 2010;107:18404–18409. doi: 10.1073/pnas.1003023107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Smagghe B.J., Huang P.-S., Springer T.A. Modulation of integrin activation by an entropic spring in the beta-knee. J. Biol. Chem. 2010;285:32954–32966. doi: 10.1074/jbc.M110.145177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Uversky V.N., Gillespie J.R., Fink A.L. Why are ‘natively unfolded’ proteins unstructured under physiologic conditions? Proteins. 2000;41:415–427. doi: 10.1002/1097-0134(20001115)41:3<415::aid-prot130>3.0.co;2-7. [DOI] [PubMed] [Google Scholar]
- 11.Dyson H.J., Wright P.E. Intrinsically unstructured proteins and their functions. Nat. Rev. Mol. Cell Biol. 2005;6:197–208. doi: 10.1038/nrm1589. [DOI] [PubMed] [Google Scholar]
- 12.Huang A., Stultz C.M. Finding order within disorder: elucidating the structure of proteins associated with neurodegenerative disease. Future Medicinal Chem. 2009;1:467–482. doi: 10.4155/fmc.09.40. [DOI] [PubMed] [Google Scholar]
- 13.Tompa P. Unstructural biology coming of age. Curr. Opin. Struct. Biol. 2011;21:419–425. doi: 10.1016/j.sbi.2011.03.012. [DOI] [PubMed] [Google Scholar]
- 14.Eliezer D. Biophysical characterization of intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2009;19:23–30. doi: 10.1016/j.sbi.2008.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fisher C.K., Stultz C.M. Constructing ensembles for intrinsically disordered proteins. Curr. Opin. Struct. Biol. 2011;21:426–431. doi: 10.1016/j.sbi.2011.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Jensen M.R., Ruigrok R.W.H., Blackledge M. Describing intrinsically disordered proteins at atomic resolution by NMR. Curr. Opin. Struct. Biol. 2013;23:426–435. doi: 10.1016/j.sbi.2013.02.007. [DOI] [PubMed] [Google Scholar]
- 17.Marsh J.A., Neale C., Forman-Kay J.D. Improved structural characterizations of the drkN SH3 domain unfolded state suggest a compact ensemble with native-like and non-native structure. J. Mol. Biol. 2007;367:1494–1510. doi: 10.1016/j.jmb.2007.01.038. [DOI] [PubMed] [Google Scholar]
- 18.Nodet G., Salmon L., Blackledge M. Quantitative description of backbone conformational sampling of unfolded proteins at amino acid resolution from NMR residual dipolar couplings. J. Am. Chem. Soc. 2009;131:17908–17918. doi: 10.1021/ja9069024. [DOI] [PubMed] [Google Scholar]
- 19.Dedmon M.M., Lindorff-Larsen K., Dobson C.M. Mapping long-range interactions in alpha-synuclein using spin-label NMR and ensemble molecular dynamics simulations. J. Am. Chem. Soc. 2005;127:476–477. doi: 10.1021/ja044834j. [DOI] [PubMed] [Google Scholar]
- 20.Fisher C.K., Huang A., Stultz C.M. Modeling intrinsically disordered proteins with Bayesian statistics. J. Am. Chem. Soc. 2010;132:14919–14927. doi: 10.1021/ja105832g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lim W.A. The modular logic of signaling proteins: building allosteric switches from simple binding domains. Curr. Opin. Struct. Biol. 2002;12:61–68. doi: 10.1016/s0959-440x(02)00290-7. [DOI] [PubMed] [Google Scholar]
- 22.Levitt M. Nature of the protein universe. Proc. Natl. Acad. Sci. USA. 2009;106:11079–11084. doi: 10.1073/pnas.0905029106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Ekman D., Björklund A.K., Elofsson A. Multi-domain proteins in the three kingdoms of life: orphan domains and other unassigned regions. J. Mol. Biol. 2005;348:231–243. doi: 10.1016/j.jmb.2005.02.007. [DOI] [PubMed] [Google Scholar]
- 24.Joerger A.C., Fersht A.R. Structural biology of the tumor suppressor p53. Annu. Rev. Biochem. 2008;77:557–582. doi: 10.1146/annurev.biochem.77.060806.091238. [DOI] [PubMed] [Google Scholar]
- 25.Terakawa T., Kenzaki H., Takada S. p53 searches on DNA by rotation-uncoupled sliding at C-terminal tails and restricted hopping of core domains. J. Am. Chem. Soc. 2012;134:14555–14562. doi: 10.1021/ja305369u. [DOI] [PubMed] [Google Scholar]
- 26.Tafvizi A., Huang F., van Oijen A.M. A single-molecule characterization of p53 search on DNA. Proc. Natl. Acad. Sci. USA. 2011;108:563–568. doi: 10.1073/pnas.1016020107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tidow H., Melero R., Fersht A.R. Quaternary structures of tumor suppressor p53 and a specific p53-DNA complex. Proc. Natl. Acad. Sci. USA. 2007;104:12324–12329. doi: 10.1073/pnas.0705069104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Bernadó P. Effect of interdomain dynamics on the structure determination of modular proteins by small-angle scattering. Eur. Biophys. J. 2010;39:769–780. doi: 10.1007/s00249-009-0549-3. [DOI] [PubMed] [Google Scholar]
- 29.Kamerlin S.C.L., Vicatos S., Warshel A. Coarse-grained (multiscale) simulations in studies of biophysical and chemical systems. Annu. Rev. Phys. Chem. 2011;62:41–64. doi: 10.1146/annurev-physchem-032210-103335. [DOI] [PubMed] [Google Scholar]
- 30.Hyeon C., Thirumalai D. Capturing the essence of folding and functions of biomolecules using coarse-grained models. Nat. Commun. 2011;2:487. doi: 10.1038/ncomms1481. [DOI] [PubMed] [Google Scholar]
- 31.Takada S. Coarse-grained molecular simulations of large biomolecules. Curr. Opin. Struct. Biol. 2012;22:130–137. doi: 10.1016/j.sbi.2012.01.010. [DOI] [PubMed] [Google Scholar]
- 32.Vuzman D., Levy Y. Intrinsically disordered regions as affinity tuners in protein-DNA interactions. Mol. Biosyst. 2012;8:47–57. doi: 10.1039/c1mb05273j. [DOI] [PubMed] [Google Scholar]
- 33.Higo J., Umezawa K., Nakamura H. A virtual-system coupled multicanonical molecular dynamics simulation: principles and applications to free-energy landscape of protein-protein interaction with an all-atom model in explicit solvent. J. Chem. Phys. 2013;138:184106. doi: 10.1063/1.4803468. [DOI] [PubMed] [Google Scholar]
- 34.Matysiak S., Clementi C. Optimal combination of theory and experiment for the characterization of the protein folding landscape of S6: How far can a minimalist model go? J. Mol. Biol. 2004;343:235–248. doi: 10.1016/j.jmb.2004.08.006. [DOI] [PubMed] [Google Scholar]
- 35.Kamiya N., Watanabe Y.S., Higo J. AMBER-based hybrid force field for conformational sampling of polypeptides. Chem. Phys. Lett. 2005;401:312–317. [Google Scholar]
- 36.Cornell W.D., Cieplak P., Kollman P.A. A second generation force field for the simulation of proteins, nucleic acids, and organic molecules. J. Am. Chem. Soc. 1996;117:5179–5197. [Google Scholar]
- 37.Kollman P., Dixon R., Pohorille A. The development/application of a ‘minimalist’ organic/biochemical molecular mechanic force field using a combination of ab initio calculations and experimental data. In: van Gunsteren W.F., Weiner P.K., Wilkinson A.J., editors. Vol. 3. Springer; New York: 1997. pp. 83–96. (Computer Simulations of Biomolecular Systems). [Google Scholar]
- 38.Ikebe J., Kamiya N., Higo J. Conformational sampling of a 40-residue protein consisting of alpha and beta secondary-structure elements in explicit solvent. Chem. Phys. Lett. 2007;443:364–368. [Google Scholar]
- 39.Ikebe J., Standley D.M., Higo J. Ab initio simulation of a 57-residue protein in explicit solvent reproduces the native conformation in the lowest free-energy cluster. Protein Sci. 2011;20:187–196. doi: 10.1002/pro.553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Ikebe J., Umezawa K., Higo J. Theory for trivial trajectory parallelization of multicanonical molecular dynamics and application to a polypeptide in water. J. Comput. Chem. 2011;32:1286–1297. doi: 10.1002/jcc.21710. [DOI] [PubMed] [Google Scholar]
- 41.Higo J., Nishimura Y., Nakamura H. A free-energy landscape for coupled folding and binding of an intrinsically disordered protein in explicit solvent from detailed all-atom computations. J. Am. Chem. Soc. 2011;133:10448–10458. doi: 10.1021/ja110338e. [DOI] [PubMed] [Google Scholar]
- 42.Terakawa T., Takada S. Multiscale ensemble modeling of intrinsically disordered proteins: p53 N-terminal domain. Biophys. J. 2011;101:1450–1458. doi: 10.1016/j.bpj.2011.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Kenzaki H., Koga N., Takada S. CafeMol: a coarse-grained biomolecular simulator for simulating proteins at work. J. Chem. Theory Comput. 2011;7:1979–1989. doi: 10.1021/ct2001045. [DOI] [PubMed] [Google Scholar]
- 44.Rippin T.M., Freund S.M., Fersht A.R. Recognition of DNA by p53 core domain and location of intermolecular contacts of cooperative binding. J. Mol. Biol. 2002;319:351–358. doi: 10.1016/S0022-2836(02)00326-1. [DOI] [PubMed] [Google Scholar]
- 45.Natan E., Baloglu C., Joerger A.C. Interaction of the p53 DNA-binding domain with its n-terminal extension modulates the stability of the p53 tetramer. J. Mol. Biol. 2011;409:358–368. doi: 10.1016/j.jmb.2011.03.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Li W., Terakawa T., Takada S. Energy landscape and multiroute folding of topologically complex proteins adenylate kinase and 2ouf-knot. Proc. Natl. Acad. Sci. USA. 2012;109:17789–17794. doi: 10.1073/pnas.1201807109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Chen Y., Dey R., Chen L. Crystal structure of the p53 core domain bound to a full consensus site as a self-assembled tetramer. Structure. 2010;18:246–256. doi: 10.1016/j.str.2009.11.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Bista M., Freund S.M., Fersht A.R. Domain-domain interactions in full-length p53 and a specific DNA complex probed by methyl NMR spectroscopy. Proc. Natl. Acad. Sci. USA. 2012;109:15752–15756. doi: 10.1073/pnas.1214176109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Svergun D., Barberato C., Koch M.H.J. CRYSOL—a program to evaluate x-ray solution scattering of biological macromolecules from atomic coordinates. J. Appl. Cryst. 1995;28:768–773. [Google Scholar]
- 50.Rotkiewicz P., Skolnick J. Fast procedure for reconstruction of full-atom protein models from reduced representations. J. Comput. Chem. 2008;29:1460–1465. doi: 10.1002/jcc.20906. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Mittl P.R., Chène P., Grütter M.G. Crystallization and structure solution of p53 (residues 326-356) by molecular replacement using an NMR model as template. Acta Crystallogr. D Biol. Crystallogr. 1998;54:86–89. doi: 10.1107/s0907444997006550. [DOI] [PubMed] [Google Scholar]
- 52.Daura X., Gademann K., Mark A.E. Peptide folding: when simulation meets experiment. Angew. Chem. 1999;38:236–240. [Google Scholar]
- 53.Pronk S., Páll S., Lindahl E. GROMACS 4.5: a high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics. 2013;29:845–854. doi: 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Ahn J., Byeon I.-J.L., Gronenborn A.M. Insight into the structural basis of pro- and antiapoptotic p53 modulation by ASPP proteins. J. Biol. Chem. 2009;284:13812–13822. doi: 10.1074/jbc.M808821200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Kotta-Loizou I., Tsaousis G.N., Hamodrakas S.J. Analysis of molecular recognition features (MoRFs) in membrane proteins. Biochim. Biophys. Acta. 2013;1834:798–807. doi: 10.1016/j.bbapap.2013.01.006. [DOI] [PubMed] [Google Scholar]
- 56.Piana S., Klepeis J.L., Shaw D.E. Assessing the accuracy of physical models used in protein-folding simulations: quantitative evidence from long molecular dynamics simulations. Curr. Opin. Struct. Biol. 2014;24:98–105. doi: 10.1016/j.sbi.2013.12.006. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


