Integration of biological data by kernels on graph nodes allows prediction of new genes involved in mitotic chromosome condensation

A gene function prediction method suitable for the design of targeted RNAi libraries is described and used to predict chromosome condensation genes. Systematic experimental validation of candidate genes in a focused RNAi screen by automated microscopy and quantitative image analysis reveals many new chromosome condensation factors.

Abstract

The advent of genome-wide RNA interference (RNAi)–based screens puts us in the position to identify genes for all functions human cells carry out. However, for many functions, assay complexity and cost make genome-scale knockdown experiments impossible. Methods to predict genes required for cell functions are therefore needed to focus RNAi screens from the whole genome on the most likely candidates. Although different bioinformatics tools for gene function prediction exist, they lack experimental validation and are therefore rarely used by experimentalists. To address this, we developed an effective computational gene selection strategy that represents public data about genes as graphs and then analyzes these graphs using kernels on graph nodes to predict functional relationships. To demonstrate its performance, we predicted human genes required for a poorly understood cellular function—mitotic chromosome condensation—and experimentally validated the top 100 candidates with a focused RNAi screen by automated microscopy. Quantitative analysis of the images demonstrated that the candidates were indeed strongly enriched in condensation genes, including the discovery of several new factors. By combining bioinformatics prediction with experimental validation, our study shows that kernels on graph nodes are powerful tools to integrate public biological data and predict genes involved in cellular functions of interest.

INTRODUCTION

Gene knockdowns are typically used to induce cellular phenotypes from which gene functions can be inferred. This reverse-genetics approach to cell biology has long been limited to genetically tractable model organisms such as the budding yeast Saccharomyces cerevisiae. With the advent of RNA interference (RNAi), reverse genetics has become routine also in human cells, and experimentally assigning functions to each human gene is in principle possible. However, many cellular functions can only be studied through complex assays or require high-content microscopy readouts, and both assay complexity and cost associated with large-scale RNAi screens keep genome-wide studies beyond the reach of most laboratories. As a consequence, most RNAi screens are conducted with a small set of often poorly selected candidate genes. For example, the set of all protein kinases is often selected for screening on the basis of the lower cost of the corresponding small interfering RNA (siRNA) libraries. This situation leads to a small number of genes being functionally overannotated, such as oncogenes and protein kinases, whereas most of the human genome contains genes whose functions remain to be characterized. In a few cases, candidate genes are identified after extensive literature and database searches by association with genes already implicated in the process under consideration. Given the multiplicity of data sources for gene similarity and the fact that links between genes can be indirect, candidate gene selection is a difficult task. An efficient data-mining method to select genes relevant to a biological process of interest would allow investigators to focus experimental screens on the most likely candidates. In addition, such a tool would allow the user to fill gaps in hit lists of RNAi screens, which in human cells typically do not reach saturation.

Many methods for predicting gene function have been developed (see Wang and Marcotte, 2010), and some predictions have been experimentally tested in different systems (Lee et al. 2008; Qi et al. 2008; Hu et al. 2009; Rojas et al. 2012). For human genes, methods have mostly focused on finding association with diseases (Tranchevent et al., 2011) rather than basic biological functions. Because different studies use different approaches, it is difficult to compare performance of the prediction in successfully guiding experiments. However, among the different methods, those that represent genes as nodes in a graph linked by their functional associations and then exploit the graph structure to compare genes perform well in retrieving known functional annotations in mouse (Peña-Castillo et al., 2008). These methods can be seen as propagating the characteristics of functionally annotated example genes to unannotated genes using a similarity measure between genes that takes into account the graph structure. One such state-of the art algorithm is GeneMANIA (Mostafavi et al., 2008; Mostafavi and Morris, 2010). In this algorithm, different data sources are combined into one graph, and then a measure of similarity between genes as nodes of the graph is computed, taking into account the global structure of the graph.

Among the different ways of measuring similarity between genes, kernel functions are particularly suited for data mining because they can be applied to nonvectorial data such as sequences or nodes of interaction graphs. Furthermore, kernels allow integration of many data sources because linear combinations of kernel matrices are still interpretable as similarity matrices (Shawe-Taylor and Christianini, 2004). Because most biological data can be viewed as weighted undirected graphs with genes as nodes and “interactions” or “functional links” as edges, kernels on graph nodes represent a natural measure of similarity between genes.

Previous applications of the kernel concept have generally focused on kernels with free parameters (e.g., radial basis kernels, polynomial kernels, diffusion kernels) and on learning an ad hoc combination of kernels for data integration (Lanckriet et al., 2004; De Bie et al., 2007; Roth and Fischer, 2007; Yu et al., 2010). These approaches require tuning of free parameters using an extensive training data set often requiring both positive and negative examples. For practical applications to guide experimental work, this has two drawbacks. First, parameter tuning may have to be done for each new query, since a training set appropriate for one biological function may not be adequate for another. Second, for new or poorly understood biological functions, the training set is typically limited to very few genes, and negative examples are often not known.

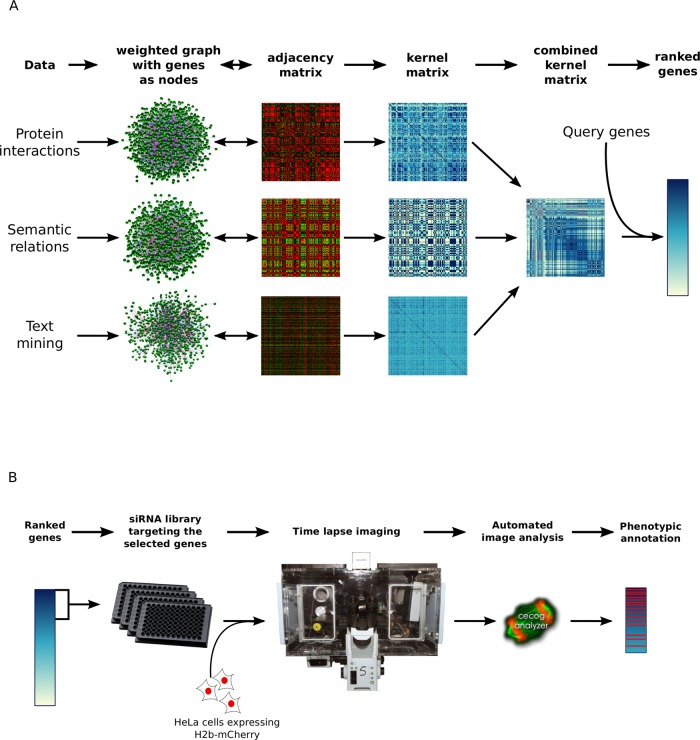
The goal of this study is therefore to demonstrate the performance of a parameter-free gene function prediction method using kernels on graph nodes to select candidate genes for a focused RNAi screen. However, which kernel would provide the most useful representation for a particular data set was an open question. To this end, we first compared how well different kernels on graph nodes derived from various public gene characterization data sources retrieve known functional relationships between genes. After identifying the best kernel combination, we then used kernel similarity to genes known to be involved in a biological process of interest to predict new genes with the same function (Figure 1A). To validate experimentally the quality of the kernel prediction, we targeted the top 100 ranked genes in a microscopy-based RNAi screen (Figure 1B).

FIGURE 1:

Overview of the data integration, gene selection, and experimental testing procedure. (A) Each data source is viewed as an undirected weighted graph whose adjacency matrix is used to derive a kernel matrix representing similarities between genes. Data integration is performed by averaging kernels from different data sources. Genes are ranked by the sum of their similarities to a list of query genes representing a biological process of interest. (B) Genes from the top of the ranked list are targeted by RNA interference, and the resulting phenotypes are captured by automated microscopy of live cells, followed by computational image analysis.

As biological process, we chose mitotic chromosome condensation as an example of an essential yet poorly understood step of cell division. Condensation transforms interphase chromatin into rod-shaped compact mitotic chromosomes that allow faithful genome partitioning. The condensation process starts during prophase (before nuclear envelope breakdown in the case of open mitosis), and the only genes known to be involved belong to the condensin protein complex, identified almost 20 years ago (Hirano and Mitchison, 1994; Strunnikov et al., 1995), with two isoforms, condensin I and II in metazoans. Condensin I is formed by SMC2, SMC4, NCAPD2, NCAPG, and NCAPH and is present in all eukaryotes, whereas condensin II is formed by SMC2, SMC4, NCAPD3, NCAPG2, and NCAPH2 and is restricted to metazoans (Ono et al., 2003; Hirota et al., 2004). Although depletion of condensin I and II reduces chromosome condensation in prophase, chromosomes appear normally condensed at later stages of mitosis (Hudson et al., 2003; Ono et al., 2003; Hirota et al., 2004), and a lack of condensin most prominently affects chromosome segregation (Gerlich et al., 2006; Renshaw et al., 2010) rather than condensation. Which factors promote chromosome condensation in the first place therefore remains an open question, and new proteins that are required for mitotic chromosome condensation in human cells still need to be identified.

RESULTS

Computational validation of the gene function prediction method

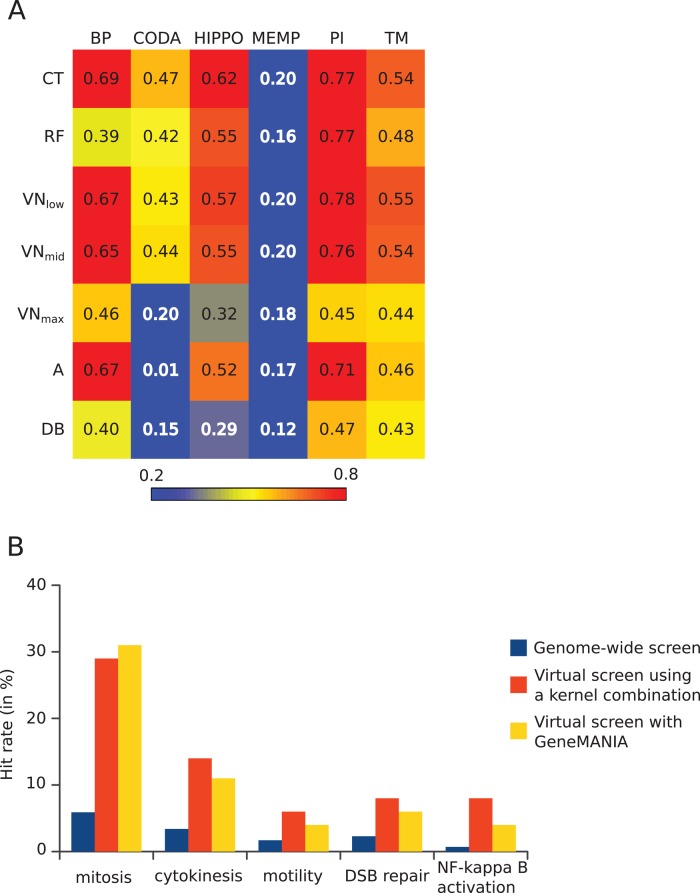
We represented biological information on gene function from various sources as undirected weighted graphs and computed different kernels as similarity measures between genes. We mined six sources of data: protein interactions (PI), homology-inferred protein interactions (HIPPO), Gene Ontology (GO) biological process (BP), text mining (TM), a gene expression network from aggregation of many gene expression data sets (MEMP), and ab initio–predicted protein interactions from co-occurring protein domain architectures (Co-Occurrence Domain Analysis [CODA]), to which we applied three different kernel functions—the commute time, random forest, and von Neumann diffusion kernels (see Materials and Methods). To ensure that the kernels captured relevant relationships between genes, we first examined which kernel on which data source gave the best performance in retrieving known functional relationships between genes as defined in the Panther pathways database (Mi et al., 2005). Using a few pathway genes as query, we ranked each gene in the genome by the sum of its similarities to the query genes and then counted how many genes from the whole pathway were found above different thresholds (see Materials and Methods). We found that the commute time (CT) kernel gave the best overall performance for all data sources (Figure 2A and Supplemental Figure S1) and that combining the best kernels for each data source for data integration further improved function retrieval (Table 1 and Supplemental Figure S2). This approach only slightly outperformed the GeneMANIA method (Table 1), which integrates data sources first by computing an average graph before applying a single kernel function (see Supplemental Information). Although these tests showed that most kernels in principle represent gene functional similarity well, they are likely to give an overoptimistic view of the prediction performance due to the interdependence between the Panther pathways and source databases. For example, defining pathway genes in Panther relies on functional information from the same literature used to establish protein interactions and GO databases. To avoid circularity in biological databases, we tested whether we could predict hits from human genome-wide RNAi screens published after the establishment of the source data. As example sources of phenotypic functional gene relations, we used the outcome of the MitoCheck genome-wide RNAi screen (Neumann et al., 2010), which scored several cell division–related phenotypes and increased motility, as well as a screen on DNA double-strand-break repair (Słabicki et al., 2010) and a screen for NF-κB activation (Gewurz et al., 2012). Suitable query genes representing prior knowledge were chosen from genes already annotated with GO terms of the biological process targeted by each screen (Supplemental Table S1) and were used to query the similarity matrix formed by our best kernel combination or by the GeneMANIA approach. To assess the performance of the gene function prediction, we performed a virtual screen by counting the fraction of hits from the experimental genome-wide screen found among the top 100 predicted genes and compared the resulting hit rate to that of the genome-wide screen (Figure 2B). Whereas the genome-wide screens have an average hit rate of 3%, the virtual screens produced a hit rate average of 13% with our kernel combination and 11% with the GeneMANIA approach. In all cases, the hit rate of the virtual screen was significantly higher than the hit rate of the corresponding genome-wide screen, demonstrating that the predicted genes are strongly enriched in genes involved in the biological function of interest.

FIGURE 2:

Summary of bioinformatics tests of the gene selection method. (A) Kernels on graph nodes differ in their global performance at information retrieval: heatmap view of areas under the curve (AUC) of true positives vs. false positives for all kernels and data sources tested. Colors go from blue for low values (<0.2) to red for high values (>0.8). Data sources are in columns: BP, semantic similarities across GO biological processes; CODA, predicted interactions based on domain co-occurrence; HIPPO, protein interactions from other species mapped to human; MEMP, gene coexpression network; PI, protein interactions in human; TM, iHOP-generated interactions. Kernels are in rows: CT, commute time; RF, random forest; VN, Von Neumann diffusion; A, adjacency matrix; DB, degree-based similarity. (B) Screening of selected genes outperforms genome-wide screening. For each screen, the hit rate is expressed as percentage of tested genes having the desired phenotype. For virtual screens, the tested genes are the top 100 predicted genes, and the numbers represent the fraction of these that were found as hits in the corresponding genome-wide screen.

TABLE 1:

Performance of different data integration schemes.

Data integration scheme	AUC up to 25% false-positive rate
KRF(PI) + KCT(HIPPO) + KCT(BP) + KCT(TM)	0.88
KCT(averaged graph PI + HIPPO + BP + TM)	0.84
GeneMANIA (= KRF(averaged graph PI + HIPPO + BP + TM))	0.86
KCT(combined binary graphs PI + HIPPO + BP + TM)	0.70

These results showed that the approaches used have the ability to predict genes involved in a specific biological function. We were therefore confident that graph-derived kernel-based gene ranking can be used to predict candidate genes involved in a particular biological process. Whereas the kernel combination approach and the GeneMANIA approach gave roughly similar performances, the kernel combination outperformed GeneMANIA by a small margin, as illustrated by the fact that the median number of hits retrieved by the GeneMANIA approach that were missed by our approach was one whereas the median number of hits retrieved by our approach but missed by GeneMANIA was four. We therefore chose to use the kernel combination to select candidate genes involved in mitotic chromosome condensation and assessed the quality of this selection by carrying out a new RNAi screen.

Prediction of human chromosome condensation genes and construction of siRNA library

The similarity matrix formed by the best kernel combination was queried with genes known to function in chromosome condensation, that is, the eight genes encoding human condensin subunits plus KIF22, which was previously shown to contribute to chromosome arm compaction in anaphase (Mora-Bermudez et al., 2007; Ohsugi et al., 2008). As a result of this query, each gene in the genome was assigned a score that is the sum of its similarity values to the query genes and ranked by decreasing value of this score. Plotting score against rank number is an additional way to help the experimentalist assess up to which rank there is high predictive power for a functional relationship to the query genes. In the case of chromosome condensation predictions, the score curve dropped to low values and flattened after the top 100 genes (see Supplemental Figure S3), which suggested that screening the top 100 genes as candidates for chromosome condensation should reveal most true positives. We therefore decided to build a custom siRNA library for the top 100 genes (two siRNAs per gene; for the full list of the 200 siRNAs, see Supplemental Table S2). Although used as a query, KIF22 had rank 4849, suggesting that there is no functional link between KIF22 and the condensin genes. To nevertheless represent all query genes in the library, we added KIF22 to the list of candidate genes.

Validation of chromosome condensation gene predictions by microscopy-based RNAi screening

Mitotic chromosome condensation defects have often been inferred indirectly from the detection of chromosome segregation defects such as the presence of chromatin bridges because this is the dominant phenotype observed in the absence of condensins. However, chromosome segregation defects are not an ideal reporter for chromosome condensation defects because segregation defects can be independent of condensation, and condensation defects may not always result in segregation problems (Cuylen and Haering, 2011; Petrova et al., 2013). Therefore we assayed chromosome condensation more directly by imaging human cells at sufficiently high spatial and temporal resolution to analyze the changes in chromatin texture during condensation in prophase. HeLa cells stably expressing H2B-mCherry to mark chromatin and LMNA–enhanced green fluorescent protein (eGFP) to mark the nuclear lamina and report on nuclear envelope breakdown (NEBD) as an independent temporal reference for the prophase/prometaphase transition (Mall et al., 2012) were transfected with 200 siRNAs targeting the 100 selected candidate genes individually, using solid-phase transfection in siRNA-coated, microscopy-compatible 96-well plates (Erfle et al., 2008; see Materials and Methods). At 24 h after plating, cells were imaged at 20× magnification for 44 h with a time lapse of 8.5 min. Four independent experimental replicates were acquired for each siRNA, resulting in a set of 800 time-lapse movies.

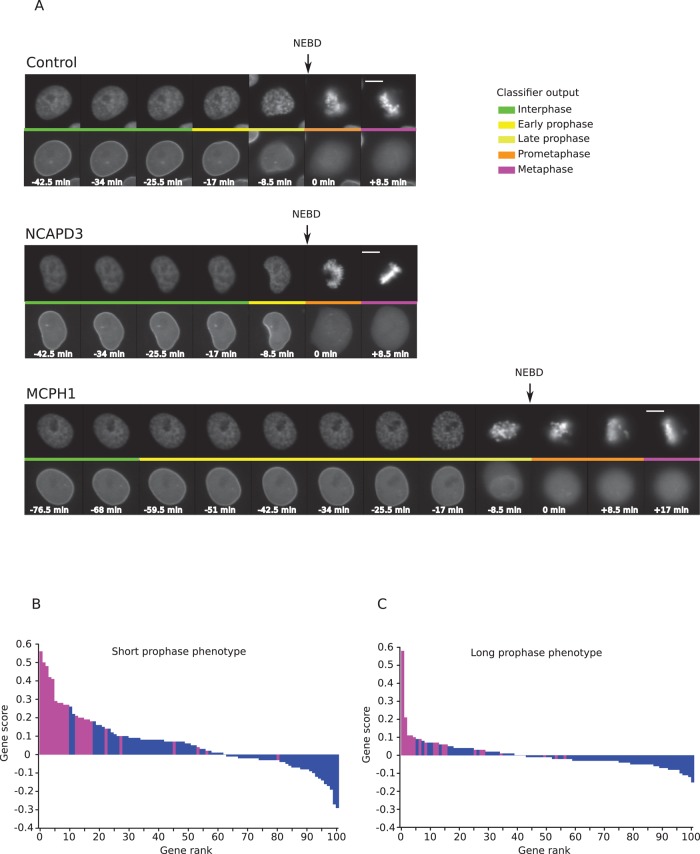
To score chromosome condensation phenotypes in this large amount (2 TB, >0.5 million images) of time-resolved image data, we used the CellCognition software (Held et al., 2010) to automatically classify the different cell cycle stages in the recorded movies and track single cells through the interphase-to-mitosis transition (see Materials and Methods for details). Because our prophase class definition is based on the morphological changes of chromatin taking place before NEBD, a lack of mitotic chromosome condensation in prophase would be detected as a shorter prophase. Conversely, premature or delayed condensation would be detected as a longer prophase. In cells treated with nontargeting siRNAs, the duration of prophase varied with a median of 17 min, in agreement with previous measurements (Hirota et al., 2004; Landsverk et al., 2010). Examples of the short- and long-prophase phenotypes are shown in Figure 3A. To get an overview of the screen, we derived for each gene a short-prophase score (Figure 3B) and a long-prophase score (Figure 3C) (for details see Materials and Methods) whose distributions show that knockdowns of more genes result in a shortening rather than a lengthening of prophase. For the purpose of validating our gene function prediction algorithm and taking genes forward to further validation analysis (see later discussion), a gene was considered to score if at least two replicates of at least one siRNA resulted in a significant change to prophase duration (see Materials and Methods).

FIGURE 3:

Screen for chromosome condensation genes. (A) Example of nuclei classification outputs for a negative control cell (top, control), a cell from NCAPD3 knockdown (middle, NCAPD3), and MCPH1 knockdown (bottom, MCPH1). Scale bar, 10 μm. Time is in minutes relative to NEBD. The colored line in the middle of each row represents the class assigned to each nucleus of the top showing H2B-mCherry. Bottom, corresponding status of the nuclear envelope in the LMNA-eGFP channel. (B) Short-prophase score distribution for all tested genes. The gene score is the median of the difference with control in the fraction of mitoses with short prophase over all replicates involving the gene. A positive value indicates more mitoses with short prophase than in control. Genes identified as short-prophase hits are shown in magenta. (C) Long-prophase score distribution for all tested genes. The gene score is the median of the difference with control in the fraction of mitoses with long prophase over all replicates involving the gene. A positive value indicates more mitoses with long prophase than in control. Genes identified as long prophase hits are shown in magenta.

As expected, siRNA silencing of all condensin II subunits (SMC2, SMC4, NCAPD3, NCAPG2, and NCAPH2) led to a marked shortening of prophase, indicative of reduced condensation and validating our microscopy-based assay and computational scoring. In addition, knockdown of 17 other genes caused significantly shorter prophases (Figure 3B and Table 2). In contrast, knockdown of 18 genes caused significant delays in prophase (Figure 3C and Table 2). In particular, knockdown of MCPH1 and CDK1, two known regulators of condensin II function (Abe et al., 2011; Yamashita et al., 2011), showed a considerable lengthening of prophase with both siRNAs, which suggests that this phenotypic category also identified true regulators of mitotic chromosome condensation. In total, our screen validated six of the nine query genes and identified 32 potential new genes that showed defects in chromosome condensation in early mitosis, corresponding to an initial hit rate of 32%. Although this hit rate is defined by single siRNA hits and follow-up experiments are required to confirm individual genes as bona fide chromosome condensation genes, this definition is adequate to demonstrate that the gene selection method produced a library strongly enriched in genes with the expected phenotypes. For comparison, similarly defined hit rates are typically ∼5% in many other primary screens of genome-scale or protein family–based (e.g., kinome) siRNA libraries (Sigoillot and King, 2011).

TABLE 2:

Genes with chromosome condensation phenotypes.

Hits with short prophase	Hits with long prophase
SMC2	MCPH1
NCAPH2	DNMT3B
NCAPD3	CDK1
NCAPG2	PAPD5
RAN	GINS1
CDCA5	NAA10
SMC4	TOP2A
TRAF3IP1	RUVBL2
CBX5	NEK6
HDAC1	MYC
AKAP8	SIAH1
TAL1	SMC1A
KIF22	POLR3C
HILS1	H1FNT
NUTF2	PTP4A3
BRF1	INTS1
PJA1	BRCA2
TOP1	MYST3
SEP15_HUMAN
NAA10
CHFR
INTS1

Quantitative analysis of chromosome condensation phenotypes

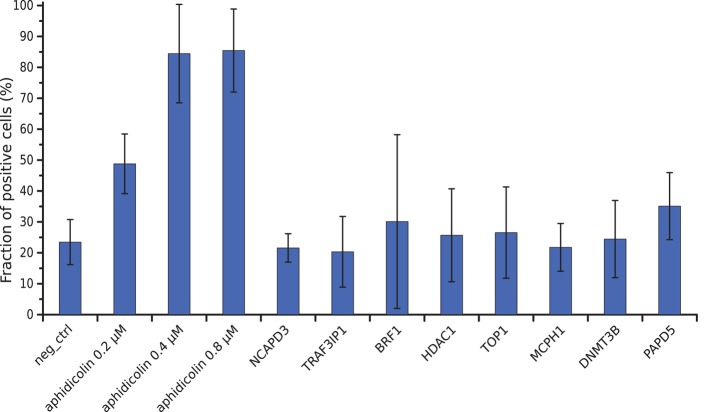
Some of our hits—for example, condensin II and MCPH1—have also been implicated in DNA double-strand-break repair (Wood et al., 2008). To rule out that our mitotic condensation assay detected indirect effects of a primary function in DNA repair, we tested whether knockdown of our hits led to increased DNA damage, using immunostaining for a phosphorylated form of H2AX induced by DNA double-strand breaks (Rogakou et al., 1998). Knockdown of the condensation genes did not lead to a detectable increase in the fraction of γ-H2AX–positive cells above the basal levels of spontaneous DNA damage present in HeLa cells (Figure 4), whereas low doses of the DNA polymerase inhibitor aphidicolin readily led to increased DNA damage, as reported previously (Lukas et al., 2011). Therefore the changes in mitotic chromatin texture detected in our screen are unlikely to be caused by DNA double-strand breaks.

FIGURE 4:

Fraction of cells showing signs of DNA damage. The fraction of γ-H2AX–positive cells is expressed as the average percentage of the total number of cells from three experiments. Error bars represent SDs of the means.

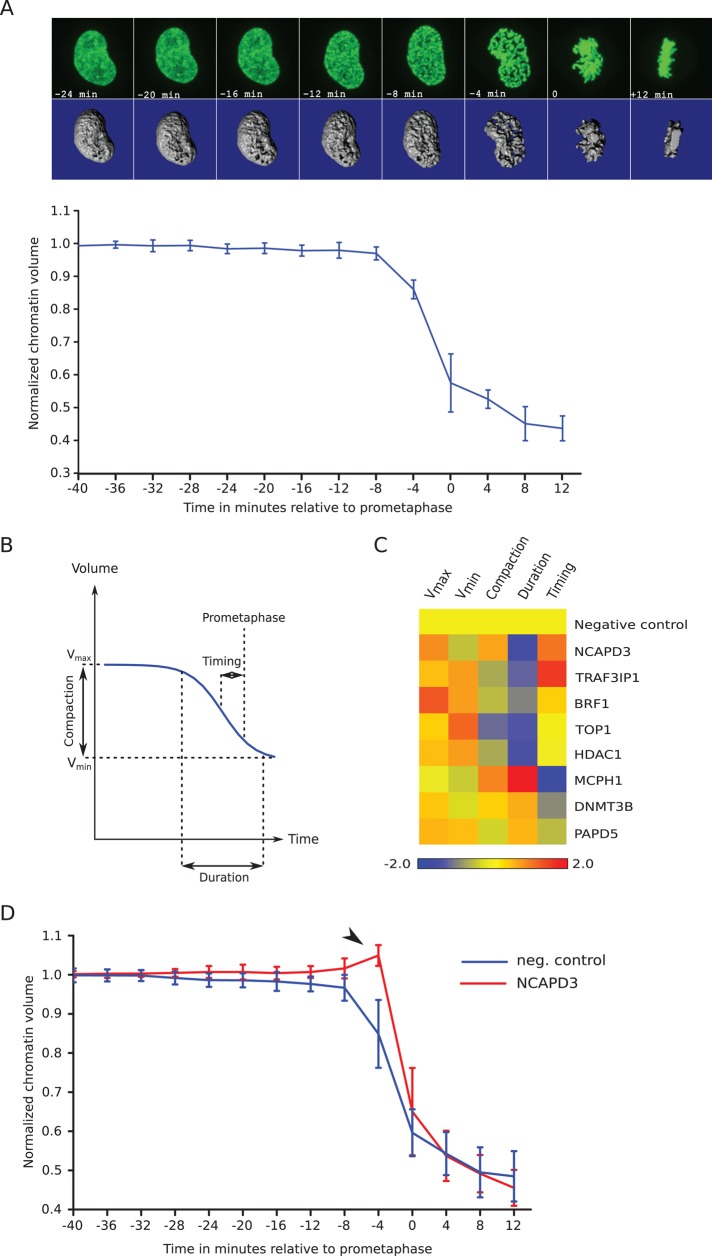
To characterize the chromosome condensation defects in prophase of several of the hits in more depth, we next used high-resolution three-dimensional (3D) confocal time-lapse imaging of HeLa cells expressing H2B-eGFP to quantify changes in chromatin volume from prophase to anaphase onset. Our previous approaches to chromatin volume measurements relied on time-consuming manual processing of image stacks (Mora-Bermudez et al., 2007). To be able to process dozens of cells from different gene knockdowns, we implemented a computational pipeline to segment the chromatin signal in three dimensions and compute its volume. Because changes in chromatin compaction cause large variations in intensity, which could cause undersegmentation or oversegmentation, segmentation was constrained such that the total intensity of the chromatin volume remained constant and equal to the intensity in prometaphase. Segmentation was implemented using a combination of image stack–level threshold and slice-specific threshold. The image stack threshold was determined by analyzing the histogram constructed from all the pixels within the image stack under consideration, and a slice-specific threshold was determined in a similar way using only pixels from the slice under consideration. An iterative algorithm was then used to adjust global and local thresholds to minimize the deviation between the total intensity in the prometaphase image stack and that in the processed stack (see Materials and Methods). The absolute volume of chromatin was estimated by the number of segmented voxels multiplied by the voxel size. Finally, to minimize cell-to-cell variations, we normalized chromatin volumes relative to interphase chromatin volume. In control cells, reduction in chromatin volume followed a sigmoidal decay curve (Figure 5A) consistent with previous measurements of chromatin volume (Mora-Bermudez et al., 2007) and similar to the diminution of the distance between two loci observed during chromosome condensation in Schizosaccharomyces pombe (Petrova et al., 2013). Therefore, as in this study, we fitted the changes in chromatin volume over time with a sigmoidal function to derive parameters for the duration of condensation, the compaction ratio, and the time of the midpoint of condensation relative to prometaphase (Figure 5B; see Materials and Methods). All knockdowns showed differences from control cells in several parameters (Figure 5C; representative curves in Supplemental Figure S4). In control cells, most of the chromatin compaction proceeded over 10–11 min, resulting in an about twofold reduction in volume (Supplemental Table S3). In contrast, chromatin compaction required only 5–7 min in knockdowns with short prophase and 12–23 min in knockdowns with long prophase (Supplemental Table S3). Shortened prophase condensation correlated with a time of mid-condensation closer to NEBD, whereas longer prophase correlated with mid-condensation time much before NEBD. As previously observed (Petrova et al., 2013), cells with a strong phenotype gave aberrant curves that were poorly fitted with the chosen sigmoid function (see example in Supplemental Figure S6), resulting in underestimation of the deviation from normal cells. Of interest, we noticed that in some knockdown cells with reduced prophase, NEBD was accompanied by a transient increase in chromatin volume. To investigate this further, we analyzed 25 NCAPD3-knockdown cells. Of these, 10 exhibited a small increase in chromatin volume at NEBD (Figure 5D) associated with very short or undetectable prophase. This effect is significant, as it is never observed in control cells (10 of 25 NCAPD3 knockdowns vs. 0 of 25 control cells; Fisher exact test, p < 0.003) or in NCAPD3-knockdown cells with weaker or no phenotype, revealing that chromatin would expand in the absence of a confining nuclear envelope unless mitotic condensation compacts it before NEBD.

FIGURE 5:

Quantification of chromosome condensation. (A) Evolution of normalized chromatin volume in control cells. Top, maximum intensity projection images (top) and isosurface reconstruction (bottom) of the chromatin from a representative scrambled siRNA–treated control cell at different time points. Occasionally cell rounding in metaphase brings chromatin slightly out of imaging range, resulting in a missing image slice. The missing part is then estimated (see Materials and Methods). The curve represents the average of 10 control cells from four independent experiments. Error bars represent SDs of the means. (B) Definition of chromosome condensation parameters. A sigmoidal decay curve (blue line) is fitted to normalized chromatin volume over time. The fit defines the maximum and minimum volumes, the compaction ratio, and the duration and timing of condensation relative to prometaphase. (C) Heatmap of chromosome condensation parameters in gene-knockdown experiments. The color scale encodes the number of pooled SDs away from the negative control mean. Values smaller than in control are in blue, and values higher than in control are in red. (D) Absence of prophase condensation correlates with chromatin expansion before NEBD. NCAPD3-knockdown cells with almost no prophase (red curve) show transient chromatin decondensation at the time of NEBD (arrowhead), whereas this is never seen in control cells (blue curve). Error bars show SDs of the means (n = 25 for control cells, n = 10 for NCAPD3-knockdown cells).

Independent validation of chromosome condensation genes

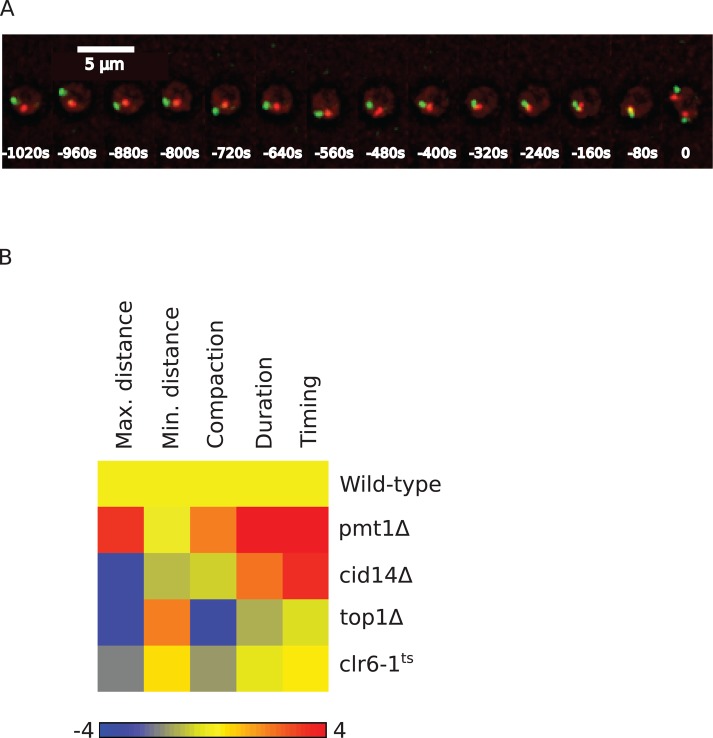
siRNA-mediated gene silencing has the potential of hitting other genes than the intended targets. We used two different approaches to validate the gene targets of the siRNAs that scored in our chromosome condensation assay. First, we checked whether the same phenotype could be reproduced by both independent siRNA sequences targeting the same gene. Several genes scored as hits with two siRNAs (shorter prophase: BRF1, CBX5, RAN, and TRAF3IP1, in addition to NCAPD3, NCAPG2, NCAPH2, and SMC2; longer prophase: CDK1, H1FNT, and MCPH1) and can therefore be considered high-confidence hits. Second, to test some of the hits that scored with one siRNA—that is, DNMT3B and PAPD5 from the “longer-prophase” and HDAC1 and TOP1 from the “shorter-prophase” category, we assayed the condensation phenotype in a genetic mutant of the orthologous genes in the fission yeast S. pombe. For this, we took advantage of a recently developed chromosome condensation assay that measures the distance of two fluorescently labeled loci located ∼1 Mb apart on the same chromosome arm (Petrova et al., 2013). As wild-type cells enter mitosis, the 3D distance between the two loci decreases as a consequence of condensation until the onset of anaphase (Figure 6A). By fitting of the condensation kinetics with a sigmoidal function, the maximum and minimal distances between the loci, the corresponding compaction ratio, and the duration and timing of compaction can be determined in a similar manner to our chromatin volume measurements. We introduced mutations in the S. pombe orthologues of these genes (pmt1Δ, cid14Δ, clr6-ts, and top1Δ, respectively) into the yeast strain with the fluorescently marked chromosome arm loci and analyzed their condensation behavior. In all mutants, we could observe significant differences from wild-type cells for several condensation parameters (Figure 6B, Supplemental Information, and Supplemental Table S4), demonstrating that they affect mitotic chromosome condensation. This is consistent with the phenotype of their orthologues in HeLa cells (Supplemental Figure S5; see Supplemental Information for a more detailed comparison). We therefore consider them also high-confidence hits. In total we could thus validate 11of 32 new chromosome condensation genes as high-confidence hits and expect that the remaining 21 new genes contain a number of additional high-confidence hits.

FIGURE 6:

Mitotic chromosome condensation in S. pombe mutants. (A) Chromosome condensation assay in S. pombe. Images of S. pombe cell in which two loci are labeled by binding of TetR fused to tdTomato (red) and LacR fused to GFP (green), respectively, to TetO and LacI tandem arrays integrated ∼1 Mb apart on the same arm of chromosome I. (B) Heatmap of chromosome condensation parameters in tested S. pombe mutants. The color scale encodes the number of SDs away from the wild-type mean. Values smaller than in wild type are in blue and values higher than in wild type are in red.

DISCUSSION

Combined kernels on graphs of biological information are effective at information retrieval

We chose to view individual data types on gene function as graphs and measure functional similarity between genes as nodes of these graphs using kernels because of their attractive properties for data integration and mining. We limited our study to a few kernel functions with a preference for those that are parameter free. We demonstrated that the commute time was a powerful and parameter-free measure of similarity between genes across various biological data types viewed as graphs. It performed well in retrieving known functional relationships from various data sets, and among all kernels tested, it appeared the most robust, since it always gave the best or close to the best performance for each data type. In contrast, performance varied more widely for the other kernels depending on the data type. In particular, the diffusion kernel performed poorly for some values of its parameter, illustrating the importance of parameter choice for kernels with free parameters. Except for the diffusion kernel, the graph-derived kernels we used were less sensitive to bias introduced by highly connected genes. To our knowledge, our approach is the first to compare performances of different kernels and identify the best kernel for a particular data set before integrating it with other data. We furthermore showed that integration of several data types improved information retrieval power and that these data types were best integrated by combining the graph-derived kernels using the best kernel function for each data type rather than the graphs themselves as in GeneMANIA (Mostafavi and Morris, 2010). Therefore our approach compares favorably with state-of-the-art algorithms on information retrieval.

Combined kernels are powerful predictors of gene function

The interdependent nature of biological databases can lead to a good performance of computational methods in information retrieval but makes it difficult to assess performance for predicting new genes for biological functions. To test the kernel performance, we therefore tested new gene function predictions more stringently using data from genome-scale RNAi screens that were not included in our data sources. We could show that the top-ranked kernel-predicted genes are significantly enriched in the expected phenotypes for all five phenotypes queried with example genes (mitosis defect, cytokinesis defect, increased cell motility, DNA damage response, and NF-κ B activation). Nevertheless, many of the top kernel-predicted genes did not score as hits in the screens examined. This can be explained by either false positives in the predictions or false negatives in the screens. False-positive predictions could be produced if most of the genes in the query are not relevant. Therefore care has to be taken in the selection of query genes, and there may be better ways of selecting query genes for a particular process than using annotations from Gene Ontology as used here. In addition, it is likely that a significant fraction of the kernel-predicted genes that did not score correspond to false negatives in the screens. Indeed, false-negative rates between 8 and 34% have been reported in Drosophila (Liu et al., 2009; Booker et al., 2011) and human cells (Neumann et al., 2010). It is therefore likely that our virtual screen validation underestimated the kernel prediction power and instead provides a lower bound on the prediction performance.

It should also be noted that genes not represented in the source data are not accessible to the method. To be able to select completely uncharacterized genes, genome-wide experimental data sets or ab initio (e.g., sequence-derived) data would have to be included. However, our preliminary tests of genome-wide microarray data and sequence-based predicted interactions led us to exclude these data sets for making predictions because of poor performance.

Although the kernel combination approach slightly but consistently outperformed GeneMANIA, we note that it is difficult to demonstrate that any approach is the best possible without extensive experimental validation of all alternative methods. Nevertheless, the success rate of our predictions represents a fivefold increase over genome-wide screening, which in this context makes graph-derived, kernel-based gene ranking of practical value. For example, scaling up our high-resolution time-lapse imaging assay to cover the ∼21,000 protein-coding genes identified in the human genome would require more than 200 TB of disk space just to store the microscopy images, and the cost in reagents and consumables alone would reach several hundred thousand dollars. Therefore in silico genome-wide prescreening of genes to focus experimental testing on the top-ranked candidates can be an excellent alternative to costly and labor-intensive genome-wide experiments. Kernels on graph nodes represent a powerful method for gene function prediction, representing an easy-to-use “funnel” for the selection of candidate genes, and we therefore make our software freely available to the community at http://funl.org.

Kernels predict new genes that function in chromosome condensation

Finding new chromosome condensation genes has proven to be difficult for many years. This is possibly because condensation requires multiple contributing activities that, when singly inactivated, would produce only minor and transient condensation defects. Capturing these subtle phenotypes therefore requires quantitative monitoring of chromosome condensation in living cells, which is very difficult to do on the genome scale but is feasible with a candidate gene set. We therefore used this very sensitive phenotypic readout to screen the top-100-ranked kernel-predicted genes involved in mitotic chromosome condensation. Strikingly, these contained 32 new genes that caused a reproducible mitotic chromosome condensation phenotype upon knockdown that had not been previously described in mammalian cells. Eleven of the 32 genes score as high-confidence positives and therefore open new avenues for experiments. For example, TRAF3IP1 is involved in primary cilium formation (Berbari et al., 2011) and has also been implicated in signal transduction pathways (Niu et al., 2003; Ng et al., 2011) but not in chromosome condensation. Our study also clarifies several leads from the literature that had not been followed up. For example, histone deacetylases have been implicated in chromosome condensation with conflicting results (e.g., Cimini et al., 2003; Dowling et al., 2005) and without resolving the identity of the HDAC(s) involved. Similarly, DNA methylase DNMT3B was found associated with chromatin genes, including several condensin subunits (Geiman et al., 2004), but its role in mitotic chromosome condensation had not been demonstrated. Our work also highlights how a computational approach can find indirect connections between genes that would otherwise be difficult to find manually. For example, whereas PAPD5 is postulated to be a component of the human TRAMP complex involved in polyadenylation of RNAs and their subsequent targeting for degradation by the exosome (Schmidt and Butler, 2013), a mutation in trf4, a PAPD5 homologue in Saccharomyces cerevisiae, genetically interacts with top1 deletion to cause defects in ribosomal DNA condensation (Castaño et al., 1996).

Quantitative analysis of prophase chromosome condensation reveals a new functional aspect

Although mitotic chromosome condensation is inherently a dynamic process, very few studies have quantified it in live cells with a high temporal resolution, and, to our knowledge, no live-cell analyses of perturbations of the condensation process have been reported. Changes in the texture of fluorescently labeled chromatin between interphase and prometaphase are commonly used to define prophase. Our screen was based on the assumption that this definition of prophase reflects changes in chromatin volume. To test this assumption and further characterize chromosome condensation, we computationally analyzed high-resolution images from 3D time-lapse confocal microscopy to quantify chromatin volume during mitosis in control cells and in knockdowns of several hits from the screen. The observed variations in chromatin volume correlated well with the length of prophase as defined by texture classification under all conditions, confirming that chromatin texture is a good indicator of chromosome condensation. The volume measurements showed that gene knockdowns affected primarily the kinetics of compaction rather than the final compaction state of chromatin, consistent with the assumption of subtle phenotypes due to additive requirements of multiple factors. Volume analysis furthermore revealed that in the absence of prophase condensation, chromatin transiently expanded when the constraint of the nuclear envelope boundary was released by its breakdown at the end of prophase. Although the prompt prometaphase chromosome compaction rapidly reversed this expansion, this observation suggests a potential new function for prophase condensation, that is, to prevent chromatin leakage from the nucleus at NEBD.

MATERIALS AND METHODS

Reference genome

For building graphs and evaluating the kernels, we considered only human protein-coding genes from the Ensembl 56 release (September 2009). In preparing the data sources and pathways for evaluation, any identifier that could not be unambiguously assigned to an Ensembl56 protein-coding gene was discarded.

Ensembl 61 (February 2011) was used for the inference of siRNA target genes.

Data sources of gene interactions

BP: GO similarities across biological processes were calculated using the Ensembl56 GO assignments, computed as root term frequency/frequency of the most informative common ancestor term and discarding pairs with score less than some threshold to remove unspecific connections through high-level GO terms. Here the threshold is arbitrarily set as the information content of the term “chromosome condensation.” Similarities between genes were calculated using the maximum GO similarity between them.

HIPPO: iRefIndex (Razick et al., 2008; accessed 29 June 2010) binary interactions from other organisms mapped to human using Ensembl orthology information. Edge weights are set to 1 over the product of the number of human orthologues of each interaction partner to reflect confidence of association. In this scheme, interactions whose partners both have a unique orthologue in human get a weight of 1.

MEMP: Gene coexpression network using absolute Pearson correlation and rank aggregation across many data sets. All-against-all coexpression was calculated from 764 public data sets and aggregated using the MEM tool with default parameters (Adler et al., 2009). Probe sets were mapped to Ensembl 56, and ambiguous probe sets were removed. In case of multiple probe sets mapping to the same Ensembl ID, median score was used. To construct the graph, edge weights were taken as negative log of the best corrected p value associated with each edge.

PI: compilation of physical protein–protein interactions from the following databases: IntAct, MINT, MIPS, STRING, BIOGRID, DIP, HPRD, and Reactome (accessed 11 October 2010). Each protein was assigned to an Ensembl56 gene using Ensembl56’s external references if the gene was not already identified by an Ensembl ID in the source database. We noticed that some genes considered common contaminants in pull-down experiments analyzed by mass spectrometry (e.g., UBC) have a high number of interactors. In an attempt to reduce nonspecific interactions, eight genes with >300 interaction partners were removed: ENSG00000078369 (GNB1), ENSG00000150991 (UBC), ENSG00000170027 (YWHAG), ENSG00000164924 (YWHAZ), ENSG00000141510 (TP53), ENSG00000197122 (SRC), ENSG00000146648 (EGFR), ENSG00000177885 (GRB2), and ENSG00000127928 (GNGT1).

TM: An interaction graph was generated using the iHOP natural language processing protocol (Hoffmann and Valencia, 2004, 2005). Genes were identified in abstracts in September 2010 using iHOP by mapping to their HGNC names. A physical interaction link was created between two genes if they were connected by a verb implying physical binding (e.g., AURKB binds INCENP). Each identified interaction was given a weight corresponding to the confidence of the genes in the interaction being the correct HGNC genes.

CODA: CODA is a reliable fused domain prediction method. This method looks for and scores protein pairs in a given target genome (e.g., human) found as fused (co-occurring) domain architectures in homologues from genomes of other species (Reid et al., 2010). The CODA method was run against all sequences in the human proteome using CATH and Pfam protein domain annotations, and both (CODAcath and pfam) were combined into one single data set (Morilla et al., 2010). CODA predictions were benchmarked using the BP data set as positive examples and randomizations of this data set as negative examples. The CODA data set used in this work was formed by CODA-predicted interactions at a cut-off precision of at least 80%.

Kernels

Kernel methods work by mapping data points (e.g., genes) into some high-dimensional space (called feature space) and computing the dot product of the corresponding vectors. That is, for a mapping function Φ and two genes x and y, the kernel function K computes K(x, y) = 〈Φ(x), Φ(y)〉. A kernel matrix contains the evaluation of a kernel function for all pairs of data points under consideration and can be viewed as a similarity matrix. It can be shown that any symmetric, positive-semidefinite matrix represents a kernel corresponding to a dot product in some feature space (Shawe-Taylor and Christianini, 2004). So, if we can compute the kernel matrix directly, we do not need to know the mapping function or the feature space. This property makes kernel methods applicable to nonvectorial data such as nodes of graphs or sequences as long as some similarity matrix that is symmetric and has no negative eigenvalues can be computed. An additional property of kernels that is of interest for data integration is that various mathematical operations on kernels produce a valid kernel. In particular, a linear combination of several kernels is a kernel (Shawe-Taylor and Christianini, 2004). This means that a combination of similarity matrices can still be interpreted as a matrix of similarities if the combined matrices are valid kernels. This property makes kernels particularly attractive for data integration because it provides a principled way of combining information from different sources into one similarity matrix.

In this work, each data set is viewed as the adjacency matrix A of a weighted undirected graph, and a value A_ij of 0 indicates no edge between i and j. In the following, D denotes the diagonal degree matrix, I the identity matrix, and L the graph Laplacian (L = D − A). The following kernels on graph nodes were computed.

Kernelized adjacency matrix (A).

Our data sources already represent a measure of similarity between genes. To compare them with the derived kernels, we ensure that the original matrix is positive semidefinite by shifting its eigenvalues. This is accomplished by adding a sufficiently large constant to the diagonal of each matrix. Here we use λ, the absolute value of the smallest eigenvalue of A:

Commute time kernel (CT).

This kernel arises from the computation of the average number of steps a random walker on a graph needs to go from one node to another and back (Fouss et al., 2007; Qiu and Hancock, 2007). It also has an interpretation in terms of electrical networks, as the commute time is equal to the effective resistance between two nodes (Xiao and Gutman, 2003). Note that the commute time kernel does not represent the commute time itself but corresponds to the dot product of the vectors representing the nodes in a space where these nodes are exactly separated by their commute time:

Random forest kernel (RF).

This kernel arises from the enumeration of the spanning rooted forests in the graph and measures the relative “forest accessibility” between nodes (Chebotarev and Shamis, 1997). It also has an interpretation in terms of probabilities of reaching a node in a random walk with a random number of steps (Chebotarev, 2008). This kernel is used by the GeneMANIA algorithm in the context of Gaussian random field label propagation (Mostafavi and Morris, 2010):

von Neumann diffusion kernel (VN).

This kernel enumerates all paths between two nodes while penalizing the longer paths and has an interpretation in terms of diffusion on the graph (Shawe-Taylor and Christianini, 2004):

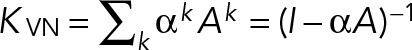The penalizing factor is α^k (k being the length of the path). and the kernel is defined for 0 < α < ρ⁻¹, with ρ being the spectral radius of A. Although α could be learned from the data, we chose here to explore three values toward the lowest, middle, and highest point of the valid range. We compare three VN kernels:

which correspond, respectively, to upper, middle, and lower values of the admissible range for α, ρ being the spectral radius of A and κ the proportion of nonzero elements in A (κ is very low, and so for VN_max, α ≈ ρ⁻¹).

Each kernel is computed separately for each connected component of the graph.

Genes with multiple functions or that are more studied tend to have more links to other genes. To compensate for this effect, each kernel is normalized by diag(K)^−1/2K diag(K)^−1/2 (which corresponds to computing the cosine of the vectors in the feature space of the kernel).

Degree-based similarity (DB).

We also computed a similarity matrix based only on node degree as in Gillis and Pavlidis (2011):

Ranking algorithm.

For a kernel K and a given pathway, we compute the score s = Ky, where y(x) = 1 if gene x is part of the query and is 0 otherwise. Genes are then ranked by s(x), which is the sum of the similarities between gene x and all query genes. For a given gene, the higher the score, the more similar this gene is to the query. We note that this procedure does not use the fact that the matrices are valid kernels, only that they encode some notion of similarity. Unlike in supervised classification (e.g., using support vector machines), the similarity depends on the distribution of the unlabeled points because the kernels are computed over the whole graph.

Kernel performance evaluation

We want to evaluate how well the kernels recapitulate current biological knowledge. As representation of established knowledge about a diverse range of biological functions, we chose to use all Panther pathways (Mi et al., 2005; from version 3.01) with ≥12 genes (79 pathways). Each pathway is evaluated using the leave-one-out cross-validation procedure. Similar results were obtained using a simple holdout method in which, for each pathway, 10 genes were randomly selected as targets and the rest used as query. Sensitivity is defined as the fraction of target genes from the pathway such that rank[target] ≤ N. Because different kernels can return a different number of ranked genes for a given query, a kernel that ranks more genes is more likely to rank some as-yet-unknown true positives better than the known ones. This means that test genes could get a worse rank with a kernel that retrieves more genes than with a kernel that returns fewer genes. To account for this and obtain a fairer comparison, ranks are normalized by the percentage of the genes returned. To estimate the false-positive rate, we assume that random selection yields unrelated genes and apply leave-one-out cross-validation to randomly formed lists of genes of the same sizes as the Panther pathways.

RNAi screen in HeLa cells

We prepared siRNA-coated 96-well plates as described previously (Neumann et al., 2010). We seeded 4000 HeLa cells stably expressing HIST1H2BJ-mCherry and LMNA-eGFP in each well and incubated them for 17 h at 37 C and 5% CO₂. After 17 h of incubation, the medium was replaced by preheated CO₂-independent imaging medium (Invitrogen; containing 10% heat-inactivated fetal calf serum, 2 mM glutamine, 100 U/ml penicillin, and 100 μg/ml streptomycin). Gas exchange was prevented by sealing the plates with Baysilone paste (Bayer, Leverkusen, Germany). Plates were then kept at least 1 h in the preheated incubation chamber of the microscope before imaging. Images were acquired with an automated epifluorescence microscope (IX-81; Olympus-Europe, Hamburg, Germany) with a 20× objective and a time interval of 8.5 min for 44 h. Four independent replicates were acquired for each siRNA treatment.

Screen image analysis

Images were processed using the CellCognition software (Held et al., 2010). Only the H2B-mCherry channel was used. After segmentation, a training set was assembled by manually assigning ∼1800 nuclei from negative control wells to one of the following 10 classes based on the morphological aspect of the nuclei: interphase, early prophase, late prophase, prometaphase, metaphase, early anaphase, late anaphase, apoptosis, artifact, and out of focus. Early prophase was defined as the first visually detectable changes in the texture of chromatin after interphase, and late prophase was defined as the first appearance of clearly condensed chromatin before prometaphase. This late-prophase definition corresponds to events preceding complete disassembly of the nuclear envelope as judged by the LMNA-eGFP marker. All nuclei were then automatically assigned by a multiclass support vector machine to one of these classes. Mitoses were detected as any transition from interphase to one or more of prophase, prometaphase, or metaphase followed by at least one of either metaphase or anaphase. Mitotic nuclei were then tracked for 22 frames (eight before the detected transition and 14 after). Mitoses with too-dark nuclei or for which the first eight frames before the transition were not classified as interphase (e.g., out-of-focus nuclei) were discarded. Wells with fewer than five valid mitoses were discarded.

Hit detection

Lack of condensin function, which results in absence of condensation in prophase, translated in our screen as a shorter prophase because the prophase class definition is based on the visual appearance of condensation before nuclear envelope breakdown. In negative control cells (i.e., treated with nontargeting siRNAs), the mode of duration of prophase was two frames (17 min). To get an overview of the screen, we derived a short prophase score for each gene as the median of the difference in the fraction of shorter prophase between all replicates involving the gene and corresponding negative controls (i.e., nontargeting siRNA). Similarly, we defined a long-prophase score by looking at the fraction of mitoses with prophase lasting >17 min. Then for each well, we tested whether the fraction of mitoses with prophase less (respectively more) than two frames was significantly different from the corresponding plate's pooled negative controls (Fisher's exact test with p < 0.1). A siRNA was then considered to affect mitotic chromosome condensation if it produced the same significant change in prophase duration in at least two replicates. A combined p value over replicates was calculated using the QFAST algorithm (Bailey and Gribskov, 1998), and siRNAs with combined p > 0.05 were not considered as hits.

Confocal microscopy

HeLa cells stably expressing H2B-eGFP were seeded in siRNA-coated wells of 96-well plates as for the screen 48 h before imaging. For imaging, culture medium was replaced by prewarmed, CO₂-independent imaging medium; the plate was then sealed with silicon grease and set in the confocal microscope incubation chamber at 37°C. Imaging was performed with a Zeiss LSM 780 confocal microscope (Carl Zeiss Microscopy, Jena, Germay) using a 63×/1.4 numerical aperture (NA) objective with a resolution of 0.132 × 0.132 × 0.9 μm × 4 min over a period of 18 h during which three cells were imaged for each of the following siRNAs: Neg9 (negative control), s25157 (TRAF3IP1), s74 (HDAC1), s4223 (DNMT3B), s23531 (NCAPD3), s6323 (BRF1), s14304 (TOP1), s36005 (MCPH1), and s34602 (PAPD5). Four such imaging rounds were carried out, except for NCAPD3 and negative control, for which images were acquired over additional rounds to image a total of 25 mitotic cells for each siRNA treatment. Under these conditions, no significant cell death or eGFP photobleaching was observed, and mitosis was not affected. Images of cells not entering mitosis were discarded. To account for variable phenotypic penetrance in gene knockdowns, cells were manually annotated for prophase duration using maximum intensity projection images, and cells with the same phenotype (i.e., shorter or longer prophase) as in the screen were kept for further processing.

Chromatin volume quantification

A fully automated computational pipeline to derive chromatin volume from confocal image stacks was implemented in Matlab and is described below.

Intensity decay with increasing distance from the coverslip surface was modeled as an exponential function of distance from the surface (Kervrann et al., 2004). Intensity-corrected stacks were interpolated to have an isotropic resolution along xy and z to provide greater flexibility in 3D image analysis. A 3D Gaussian filter was then applied on the interpolated stacks to reduce the effects of noise. Large variations in chromatin compaction in different mitotic phases lead to highly variable intensity/brightness of the chromatin area, which can cause undersegmentation or oversegmentation, depending on the mitotic phase. To deal with this, segmentation was constrained such that the intensity sum contained in the segmented chromatin volume within a 3D stack remained constant for all time points (Mora-Bermudez et al., 2007). To enforce this constraint, the stack containing the first prometaphase was selected as a reference and processed first. A global threshold was determined by analyzing the histogram constructed from all the pixels within the stack. This threshold was adapted for each slice by combining a second (local) threshold determined similarly for which only pixels within a particular slice were considered to construct the histogram. This combination of local and global thresholds within a stack significantly avoided oversegmentation and undersegmentation. To segment the stacks at other time points, the intensity sum contained in the segmented chromatin volume in the prometaphase stack was used as a reference. This also allowed estimation of small missing parts of chromatin in metaphase when cell rounding occasionally pushed the chromatin mass slightly out of imaging range. Highly compacted chromatin sometimes resulted in sections with saturated pixels. Loss of intensity due to saturation was estimated based on a logarithmic function of the number of saturated pixels. Then an iterative approach was applied that increased/decreased the global threshold and readjusted the local thresholds proportionally in order to obtain a refined segmentation that minimized the deviation between the total intensity in the reference stack and that in the processed stack. The absolute volume of chromatin was estimated by the number of segmented voxels multiplied by the voxel size.

For compaction analysis, chromatin volumes were normalized relative to interphase chromatin volume, defined as the average of the volumes at the first three time points starting 1 h before anaphase onset. Curves were then aligned on the first prometaphase image taken as time t = 0 min. The curves of volumes over time were fitted (as in Petrova et al., 2013) with the following sigmoidal function:

where V is the chromatin volume and t the time relative to prometaphase. From this, we derived the following parameters:

Compaction ratio: r = V_max/V_min.

Duration: Δt = t_95% – t_5% (where t_95% and t_5% represent the time points at which the volume has decreased by 95 and 5% of the total compaction, respectively).

Time to prometaphase: t_prometa = t(0) – t_50% (where t_50% represent the time point at which the distance has reached 50% of the total compaction).

Average values of these parameters for different gene knockdowns are given in Supplemental Table S3. Parameters from poorly fitted curves to MCPH1 knockdown data were discarded (see example in Supplemental Figure S6).

γ-H2AX immunostaining and analysis

We prepared 96-well plates as for the screen (Neumann et al., 2010) with the following siRNAs: Neg9 (negative control), s25157 (TRAF3IP1), s74 (HDAC1), s4223 (DNMT3B), s23531 (NCAPD3), s6323 (BRF1), s14304 (TOP1), s36005 (MCPH1), and s34602 (PAPD5). In addition, three wells were treated with 0.2, 0.4, and 0.8 μM aphidicolin to serve as positive controls.

HeLa cells stably expressing H2B-mCherry were grown on the siRNAs for 48 h and then fixed with a solution of 3.7% paraformaldehyde in phosphate-buffered saline (PBS) for 15 min at room temperature, permeabilized with 0.5% Triton X-100 in PBS for 10 min, incubated with a mouse monoclonal antibody against phosphorylated H2AX (ab22551; Abcam, Cambridge, UK) in PBS plus 0.1% Tween 20 plus 2% bovine serum albumin, washed three times, incubated with an Alexa 488–conjugated anti-mouse antibody, washed three times, and incubated 5 min with 0.1 mg/ml Hoechst 33342 in PBS and washed twice. Images were acquired from four fields in each well with an automated epifluorescence microscope (IX-81; Olympus-Europe) with a 40× objective. Using the CellCognition software, nuclei were segmented in the Hoechst channel, and a classifier was trained on a set of nuclei with positive and negative γ-H2AX staining.

S. pombe experiments

We give here a brief summary of the procedure described in Petrova et al. (2013). A yeast strain with two fluorescently labeled loci was constructed by integrating a tandem array of lactose operators and a tandem array of tetracycline operators ∼1 Mb apart on the arm of chromosome I and expressing a tetracycline repressor fused to tdTomato and a lactose repressor fused to GFP. Mutations for the tested genes were then introduced into this strain. For live-cell imaging, cells enriched for G2 phase were attached onto lectin-coated microscopy dishes, and images were taken on a DeltaVision (Applied Precision, Issaquah, WA) microscope using an Olympus UPlanApo (100×, NA 1.35) objective. Z-stacks with a step size of 0.4 μm were recorded every 40 s for a period of 60 min using a dual-band filter set for GFP or tdTomato fluorescence. Image processing to determine the distance between the marked loci was implemented in ImageJ (Schneider et al., 2012). For each experiment, distances measured from at least 14 cells were averaged, and the resulting curve was fitted with the same function used for chromatin volume. Average values and SDs for all parameters in wild-type yeast cells were computed from four different experiments. Parameter values are listed in Supplemental Table S4, and Supplemental Table S5 lists the genotypes of the yeast strains used.

Abbreviations used:

AUC

area under the curve

CT

commute time

eGFP

enhanced green fluorescent protein

NEBD

nuclear envelope breakdown

RF

random forest

RNAi

RNA interference

siRNA

small interfering RNA

VN

Von Neumann diffusion