Ionic Permeability and Mechanical Properties of DNA Origami Nanoplates on Solid-State Nanopores

Abstract

While DNA origami is a popular and versatile platform, its structural properties are still poorly understood. In this study we use solid-state nanopores to investigate the ionic permeability and mechanical properties of DNA origami nanoplates. DNA origami nanoplates of various designs are docked onto solid-state nanopores where we subsequently measure their ionic conductance. The ionic permeability is found to be high for all origami nanoplates. We observe the conductance of docked nanoplates, relative to the bare nanopore conductance, to increase as a function of pore diameter, as well as to increase upon lowering the ionic strength. The honeycomb lattice nanoplate is found to have slightly better overall performance over other plate designs. After docking, we often observe spontaneous discrete jumps in the current, a process which can be attributed to mechanical buckling. All nanoplates show a non-linear current-voltage dependence with a lower conductance at higher applied voltages, which we attribute to a physical bending deformation of the nanoplates under the applied force. At sufficiently high voltage (force), the nanoplates are strongly deformed and can be pulled through the nanopore. These data show that DNA origami nanoplates are typically very permeable to ions and exhibit a number of unexpected mechanical properties which are interesting in their own right, but also need to be considered in the future design of DNA origami nanostructures.

Solid-state-nanopore research^{1, 2} is an area which has been gaining much attention due to its potential applications in sequencing, biosensing, and as a tool for biophysics. In this technique an electric field is applied across a membrane containing a single pore. Charged molecules such as DNA experience an electrophoretic force which pulls them through the pore. Molecules are detected by the temporary reduction (or increase at low salt) in the ionic current which they cause as they pass through the pore. Despite recent advances^{1, 2} in solid-state-nanopore research, biological pores still offer several advantages such as a higher signal-to-noise ratio,³ slower DNA translocation velocity,⁴ and the possibility for adding chemical modifications to the channel by creating mutant proteins.⁵ In an attempt to combine the advantages of solid-state pores with those of biological pores, in 2010, our group demonstrated that a stable hybrid pore could be built by capturing an α-hemolysin protein pore with a DNA tail into a solid state nanopore.⁶ This work subsequently opened up a new stream of research into combining biological structures with solid-state nanopores in order to open up new functionalities.

This approach can be extended to DNA origami, a technique introduced by Paul Rothemund in 2006 which allows complex shapes to be built from DNA by designing short oligonucleotide “staples” which upon hybridization bring two defined parts of a large single-stranded DNA template together.⁷ Through the rational design of staples, the single-stranded DNA template can thus be folded into any desired shape. Since its introduction, DNA origami has grown into a robust technique capable of reliably producing 3D structures^{8, 9} such as boxes, spheroids, and complex objects with curved surfaces.^{10, 11}

DNA origami can be used to create DNA origami nanopores. Recent literature has reported the creation of hybrid nanopores by capturing DNA origami nanoplates containing apertures¹² as well as funnel-like structures¹³ onto solid state nanopores and glass nanocapillaries.¹⁴ Synthetic lipid membrane channels^{15, 16} have also been made using DNA origami nanostructures. The versatile approach, of docking DNA origami nanostructures onto solid-state nanopores, allows great control over both the geometry and the chemical functionality of the pore. Wei et al created a square honeycomb-lattice-based DNA-origami nanoplate with a central aperture. Their nanoplate contained a long ssDNA tail extending from the side of the aperture (close to the center of the nanoplate) to facilitate proper insertion. Initial work with this system showed translocation of DNA and protein through a docked nanoplate and stochastic sensing of target molecules using a bait-prey scheme. Bell et al focused on a hollow pyramid type structure with an aperture and a tail at the apex, reminiscent of the structure of α-hemolysin or MspA, with a top side larger than the diameter of the solid state pore. Their work showed the ability to capture and insert these structures into the pore and subsequently translocate dsDNA through docked nanostructures. These first experiments provided a good proof-of-concept and established that this technique can be used to add additional functionalities to solid-state nanopores. In addition, this approach can be used to study the inherent properties of DNA origami at the single-molecule level and measure properties, such as ionic permeability, which cannot be determined with other methods.

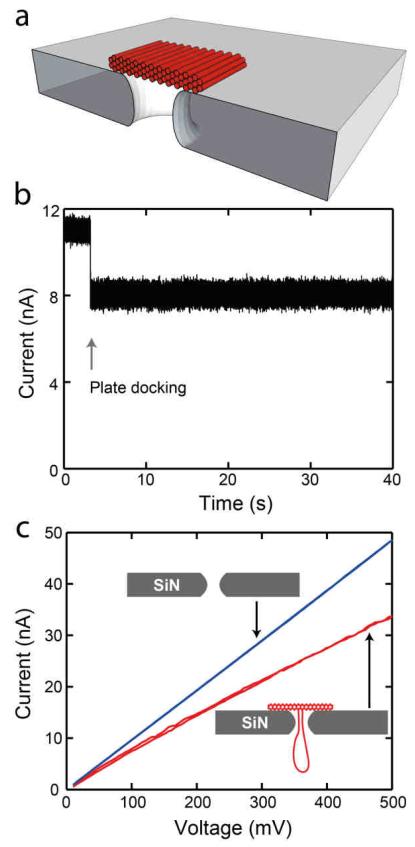
Here, we carry out a fundamental investigation into the ion conduction and mechanical properties of DNA origami nanoplates, by docking them onto solid-state nanopores. The approach begins with electrophoretically capturing an origami plate (without an aperture) by use of a long centrally located DNA tail into a pore, as shown in Figure 1. The tail allows the guided insertion of the nanostructure with a well-defined orientation onto a solid-state nanopore. An example 3D cross section of a honeycomb lattice nanoplate docked onto a 20 nm nanopore is shown in Figure 1a. The docking of a nanoplate is observed in real time by a reduction in the current level as shown in Figure 1b. Once docked, a current-voltage sweep such as shown in Figure 1c, reveals a lower conductance when the nanoplate is docked (red curve) compared to the conductance for a bare nanopore (blue) taken before the nanoplate was added. Nanoplates can be undocked from the nanopore by reversing the polarity of the applied voltage or by pulling them through the pore by significantly increasing the voltage, as shown below. The docking time is found not to be an intrinsic property but dependent on the experiment. Most nanoplates would stay docked forever if kept at low voltages.

Figure 1.

a) 3D representation showing a cross-sectional view of a honeycomb lattice DNA nanoplate docked onto a SiN nanopore. The tail has been omitted for visual clarity. b) Current trace of a honeycomb nanoplate captured onto a 14 nm pore at 100 mV. c) IV curve for a bare 14 nm SiN pore (blue) as well as for the same pore after a honeycomb nanoplate was docked (red).

The ionic permeability of the nanoplate is an important parameter for origami nanopores to optimize because it sets the magnitude of the current blockade in sensing single biomolecules relative to the baseline current. The ideal nanoplate should have minimal leakage of ions through the nanoplate itself, with the majority of the ionic current given by ionic transport through the open aperture, leading to a high ratio between the excluded volume of the translocating molecule and the total volume available to carry ions. This would result in a high signal-to-noise ratio. Secondly, the nanoplate should have a high mechanical stability under any applied voltage. We investigate these issues by experimenting with different nanoplate designs, varying the diameter of the solid-state nanopores, probing a wide range of voltages, and altering buffer conditions. We find that the conductance of the nanoplates is high and increases as a function of pore diameter and ionic strength. Additionally we see interesting mechanical effects including deformation, buckling, and structural failure under increasing applied force.

RESULTS AND DISCUSSION

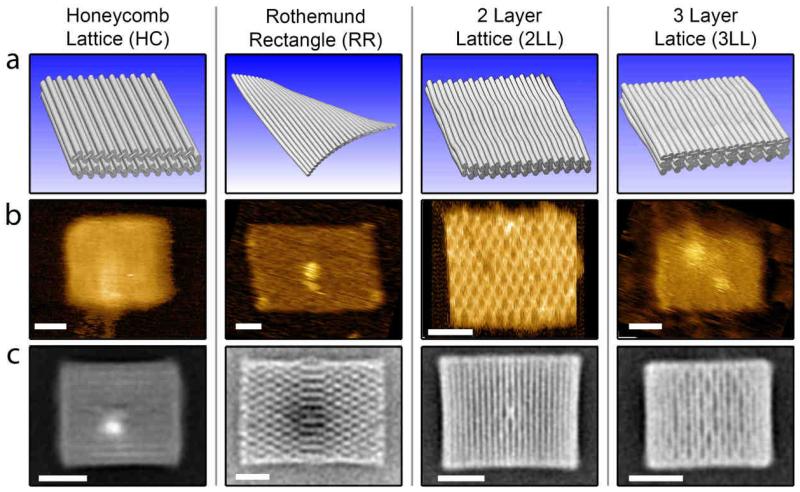
First, we investigated how the geometry of the DNA nanoplates influences their ionic permeability. Four different nanoplate designs were used, as shown in Figure 2a. None of the designs contained an aperture, to ensure that the measured current was only due to the ionic permeability of the nanoplate itself. The first design (HC) utilized a honeycomb-type DNA-packing architecture and has lateral dimensions of 45 nm × 52 nm with a thickness of 6.75 nm and an ideal spatial filling factor¹² of 0.605. The other designs are all based on the square-lattice rectangular DNA origami nanoplates introduced⁷ by Paul Rothemund with varying thicknesses of one, two, or three DNA layers. The filling factor for these plates is expected to be below 0.785, as several studies^{17, 18} have shown the DNA helices in the square-lattice are not close packed. The one-DNA-layer-thick Rothemund rectangle (RR) has lateral dimensions of 98 nm × 54 nm, the two-DNA-layer-thick rectangle (2LL) has 51 nm × 54 nm, and the three-DNA-layer-thick design (3LL) has 40 nm × 45 nm. Since each design is based on oligo-staple hybridization with a standard M13 single-stranded DNA template (RR and HC 7560 bases, 2LL and 3LL 7704 bases), the lateral dimensions of the designs are reduced as the thickness is increased. CanDo^{19, 20} finite-element modeling was used to predict the flexibility of each plate (Supplementary Section 8). This revealed that the RR plate should be quite deformed, as evident in Figure 2a, due to a large twist along the plate, although thermal fluctuations and surface effects should be able to force it into a flat state. This twist is caused by the square lattice and was compensated for in the 2LL and 3LL designs by designing staples which skip hybridization to some bases of the scaffold.¹¹ The predicted plate stiffness, as established from the range of RMS fluctuations (provided in the brackets) over different parts of the structure can be ordered from highest to lowest as follows: HC (0.3 to 0.8 nm) ≈ 3LL (0.3 to 1.0 nm) > 2LL (0.6 to 1.7 nm) > RR (1.2 to 3.5 nm). In addition to the electrophysiological measurements which are the main focus of this work, the DNA nanoplates were characterized using TEM and high-speed liquid AFM. Negative-stain TEM was used to verify proper nanoplate assembly with averaged micrographs for each design shown in Figure 2c. The high-speed liquid AFM provides high-resolution images of the plates (Figure 2b) but also allowed us to confirm the good stability of each design in a variety of buffer conditions. Details of the TEM and AFM characterization have been provided in Supplementary Section 7.

Figure 2.

Properties of four different DNA origami nanoplates. a) 3D representations of each design. b) Liquid tapping-mode AFM scans for each nanoplate design. Variations in image resolution can be attributed to differences in AFM tip sharpness. c) TEM class averages of negative stain micrographs for each plate (RR adapted from Sobczak et al.³⁰). All scale bars are 20 nm.

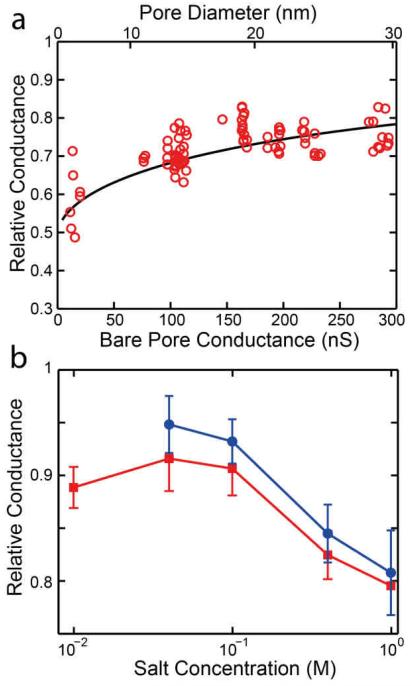
We first report how the ionic conductance of the nanoplates varies among the different designs, how it depends on the nanopore diameter, and how the observed trends can be reproduced with a simple model. The diameter of the solid-state nanopores onto which nanoplates were docked was varied from 5 nm to 30 nm. Figure 3a shows the observed relative conductances (i.e. the conductance of the pore with the plate relative to that of the bare pore) for the honeycomb (HC) nanoplate at 200 mV in 1 M KCl. The relative conductance decreases as the diameter on the solid-state nanopore is reduced. We see the relative conductance decrease from about 0.8 in large 30 nm pores down to below 0.6 in small 5 nm pores. Similar plots for the other nanoplate designs and at different voltages are shown in Supplementary Section 1.

Figure 3.

a) The relative conductance, G_hybrid/G_pore for the honeycomb nanoplate design at 200 mV in 1 M KCl buffer plotted versus the pore conductance, which scales inversely with pore diameter (see nonlinear scale at the top). Solid line denotes a fit of Eq. 6 giving α = 0.112 ± 0.06 nm⁻¹. b) Salt dependence of the relative conductance for the 2LL nanoplates docked onto 24 nm pores at 300 mV (red squares) and 200 mV (blue circles).

The solid line in Figure 3a represents a least-squares fit to the data using the model outlined below, with only one free parameter (α). Experimentally we measure G_hybrid, the conductance of the nanopore in series with the conductance of the nanoplate. As in previous work¹² this can be modeled as

$$G_{hybrid}={\left[\frac{1}{G_{pore}}+\frac{1}{G_{plate}}\right]}^{-1}$$ (1)

where the conductance of the pore²¹ is given by

$$G_{pore}=\kappa {\left[\frac{4l_{pore}}{\pi d^2}+\frac{1}{d}\right]}^{-1}$$ (2)

where κ is the conductivity of the buffer, l_pore is the effective thickness of the solid-state nanopore, and d is its diameter. Note that Eq. 2 also includes the access-resistance²¹ contribution which was ignored in previous work.¹² We model the conductance of the nanoplate using

$$G_{plate}=\frac{\pi \alpha \kappa d^2}{4}$$ (3)

where α is a phenomenological parameter with units of inverse length given by

$$\alpha =\frac{f\left(V\right)}{l_{plate}}$$ (4)

where l_plate is the nanoplate’s thickness and f(V) is a dimensionless function related to the applied voltage and the filling factor (F). If we ignore the (non-linear) voltage dependence discussed later on, f(V) equals

$$f\left(V\right)=1-F$$ (5)

where F is the filling factor of the nanoplate. It is useful to examine the limiting behavior of α. When the nanoplate becomes very thick (l_plate, → ∞) α approaches zero. In the other limit of very thin plates, we encounter the minimum plate thickness which is set by the diameter of a single DNA helix (2.25nm). Here, the value of α approaches zero for a fully filled plate (F=1), whereas it goes to 1/(2.25nm) as the filling factor goes to zero. In the context of optimizing the nanoplate design, the value of α should be as low as possible, since this represents the smallest leakage through the nanoplate, thus giving the highest signal-to-noise ratio in DNA translocation experiments through a nanopore in the nanoplate. The nanoplate designs are experimentally best characterized by their relative conductance (RC), the ratio of G_hybrid to G_pore. Combining equations 1, 2, and 3, we thus obtain

$$RC=\frac{G_{hybrid}}{G_{pore}}=\frac{1}{1+\frac{4}{\alpha (4l+\pi d)}}$$ (6)

This model nicely captures the observed trend of a decreasing relative conductance as the diameter of the solid-state nanopore is reduced, as seen in the solid line of Figure 3a. For the example in Figure 3a, α = 0.112 ± 0.06 nm⁻¹. Generally, we find values for α in the range from 0.10 to 0.18 nm⁻¹, see Figure S7, where we plot the value of the fit parameter α as a function of voltage. We find that the honeycomb nanoplate has the lowest leakage (lowest α). Surprisingly, the one-layer-thick Rothemund rectangle nanoplate has the next best characteristics, while the two and three-layer-thick nanoplates are worst. Although the differences are small, this observation is counterintuitive as we would expect the thicker nanoplates to have less leakage. Even though the higher leakage as the lateral dimensions of the origami nanoplate are decreased could indicate the presence of some leakage currents flowing in between the nanoplate and the solid-state nanopore substrate, we do not believe this to be a significant effect given the small size of the nanopores relative to the large size of the nanoplates involved as well as other factors discussed in detail in Supplementary Section 1. This phenomenon, of the thicker square-lattice plates being leakier, is therefore attributed to differences in the particular design of the nanoplates such as the arrangement of the oligo staples.

The dependence of the RC on the ionic strength of the buffer is shown in Figure 3b. The relative conductance is found to increase as the salt concentration is decreased. In other words, the nanoplates appear to become more leaky as the salt concentration drops. The relative conductance is observed to increase from around 0.8 at 1 M KCl up to 0.9 at salt concentration of 100 mM KCl or lower. Similar trends are observed for all other nanoplate designs and different pore sizes (see Supplementary Section 2 and 3). For the salt concentrations tested (1 M KCl, 400mM KCl, 100 mM KCl, 40mM KCl, and 10 mM KCl) the Debye screening length is 0.31 nm, 0.47 nm, 0.89 nm, 1.26 nm, and 1.82 nm, respectively. At 100 mM and lower, the Debye layer from neighboring DNA strands should begin to overlap in many areas of the DNA origami nanoplate. As the salt concentration is lowered from the (typically used) 1 M value, the reduced electrostatic screening could have two effects on a nanoplate’s ionic permeability. First, increased electrostatic repulsion between neighboring strands could increase the size of the holes present in-between the crossover points¹⁷, allowing more ions to pass though the structure, thus increasing the ionic permeability. This effect is a contributing factor, together with mechanically induced twist, in the diamond-like pattern clearly visible in the AFM and TEM characterization (Figure 2) of some plates, and has been observed in previous Cryo-EM¹⁷ and AFM²² studies of DNA origami structures. The structure swells up to the point where it is constrained by the oligo-staples. In addition to this, the higher effective negative charge and larger Debye screening lengths of the DNA leads to a higher cation selectivity, attracting more positive potassium (K⁺) ions while repelling the negatively charged chloride (Cl⁻) ions present in the solution.²³ This may result in higher conductivities than the bulk conductivity of the solution, as reported previously for small charged nanopores in low salt conditions.²⁴ The observed increase at low ionic strengths is likely due to a combination of these two effects. The measurements reveal that, while high salt concentrations should be preferred, the docking of nanoplates into nanopores can be detected in salt concentrations as low as 10 mM, opening up the possibility of conducting measurements on docked nanoplates at physiological conditions.

We found that the presence of magnesium in the buffer was unimportant for the behavior of the nanoplates. Although it has been recently shown that Magnesium divalent cations are not required for proper folding of the DNA origami structures,²⁵ the need for a divalent cation such as magnesium in the buffer can be rationalized as a means to allow the negatively charged nanoplate to stick to the negatively charged surface (an effect well known from AFM literature) of the SiN surface at pH 8, where all measurements are carried out. All nanoplates were folded in a buffer containing 20 mM Mg. Before measuring, these stock solutions are diluted into the proper salt concentration with new buffers containing 11 mM Mg. As a control, we also diluted some samples into magnesium-free buffer resulting in a final Mg concentration of around 0.5 mM. No differences were observed in the relative conductance measurements for these samples compared to those carried out in buffer with 11 mM Mg (data not shown). Furthermore, no issues were encountered with the docking of the nanoplates, suggesting that the electrophoretic force and van der Waals adhesion are stronger than the electrostatic forces. Over typical experimental timescales of several hours, no deterioration in the stability of the nanoplates was observed. These results show that the presence of high concentrations of magnesium in the buffer is not a stringent requirement for either maintaining nanoplate stability or facilitating the docking of nanoplates into solid-state nanopores.

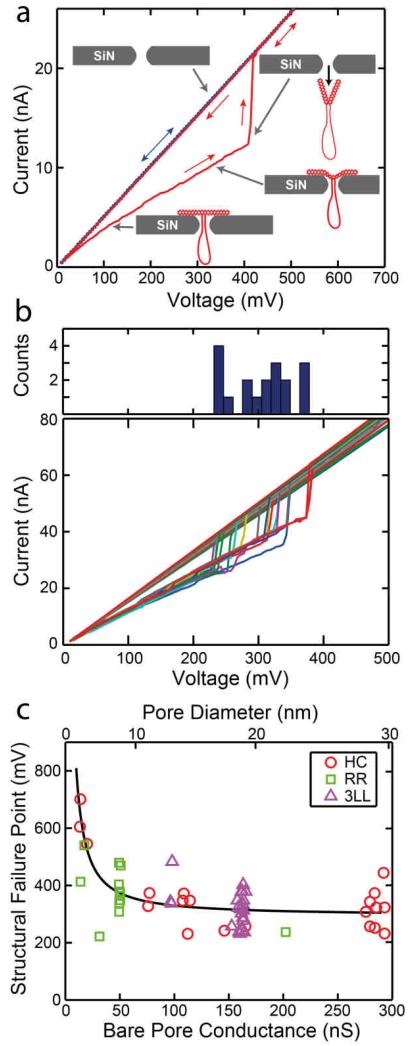
Next, we report an interesting observation that was not anticipated, namely the effects of mechanical deformation of the nanoplates. We find that docked nanoplates may undergo physical deformation as the voltage is increased and can even be pulled through the pore if sufficient force is applied. Once a nanoplate is docked into a pore, we can subject the nanoplate to a voltage ramp in order to probe its current-voltage (IV) characteristics. Voltage sweeps begin at 10 mV and go to 800 mV in steps of 5 mV (each 103 ms long), and subsequently we ramp back down to 10 mV. Examples of typical IV curves can be seen in Figure 1c for a HC nanoplate on a 14 nm pore and in Figure 4a for a 2LL nanoplate on a 9 nm pore. All nanoplates exhibit non-linear IV behavior with the conductance of the nanoplate being reduced as the voltage is increased. This trend can also be seen in the decrease of the fit parameter alpha as a function of voltage (Figure S7). We attribute this effect to the nanoplate undergoing increased physical deformation as the voltage is increased, which brings more DNA material into the pore (cf. sketch in the bottom right inset to Figure 4a).

Figure 4.

a) IV curve (red) showing a 2LL nanoplate undergoing structural failure and being pulled through a 9 nm pore. Once pulled through, the conductance of the pore returns to the level seen for the bare pore (blue dots). b) IV curves of 18 different 3LL nanoplates being pulled through a 19 nm pore. Top panel displays a histogram of the structural failure points. c) The structural failure points for three nanoplate designs docked onto different-diameter pores. It can be seen that smaller pores require a greater force to pull the nanoplate through. The solid line has been added to guide the eyes.

This idea is supported by the fact that beyond a critical voltage value, the current level is observed to suddenly return to the bare pore level as shown in Figure 4a, after which the IV curve is linear, reproducible, and back to the conductance value for the bare nanopore, indicating that the nanoplate has been pulled through the pore, as also proven using recapture experiments described below. We term the voltage level at which this occurs the structural failure point (SFP). This effect is quite reproducible and we are able to repeatedly capture nanoplates and pull them through, as shown in Figure 4b, where 18 different 3LL nanoplates are pulled through a 19 nm pore. The histogram at the top shows that the mean SFP is at a voltage of 307 ± 51 mV. If we plot the observed SFP for different nanoplate designs in different pores, as shown in Figure 4c, we observe that, not surprisingly, a higher voltage, and thus higher force, is required to pull the nanoplates through smaller pores compared to larger pores. The dependence on pore diameter is in fact even stronger than apparent for Figure 4c, since our detection method misses many SFPs with a large value (exceeding our maximum voltage of 800 mV) in small pores and additionally, it misses SFPs with a small value in larger pores. In small pores (~5 nm) it is often very difficult to pull a nanoplate through the pore (as evidenced by the low number of SFP events occurring). Instead, almost all nanoplates docked onto small pores remain stable up to the maximum applied voltage of 800 mV and are not pulled through. In large-diameter pores, some nanoplates are instantly pulled through already at the typical docking voltage (200 mV), thus creating short translocation events that are observed as spikes in the recorded current trace as they pass through the pore. The short spikes are observed to occur most frequently for the most flexible nanoplate, the single-layer Rothemund rectangle. This is expected because more flexible plates will undergo more deformation at a given level of applied force compared to stiffer plates. Figure S15 shows the spikes observed from RR nanoplates being pulled through a 24 nm pore at 200 mV and higher. This effect underlies the lack of data collected for the RR nanoplate in large-diameter pores, as evident in Figure 4c, Figure S1, and elsewhere. In addition to flexible plates, plates containing structural defects, such as those caused by missfolding are likely to be pulled through the pore very quickly.

In order to conclusively prove that the nanoplates were actually being pulled through the pore (rather than undocking back into the cis insertion chamber), we carried out recapture experiments where the electric field was reversed shortly after a spike was observed. If a nanoplate is being pulled through the pore, it should be recaptured if the electric field is reversed quickly enough and thus produce another spike. As shown in Figure S16, we indeed were able to recapture many nanoplates. The ability to recapture nanoplates when switching even 3 seconds after the translocation event at an applied voltage of 200 mV shows that the nanoplates were pulled through and undergo a slow drift-diffusion away from the pore. All our observations thus reveal that the nanoplates undergo mechanical deformation as the force applied on them is increased, and furthermore that the nanoplates can be completely pulled through the pore if sufficient force is applied. Flexible nanoplates can easily be pulled through larger pores, something which should be taken into account in future designs of origami nanopores.

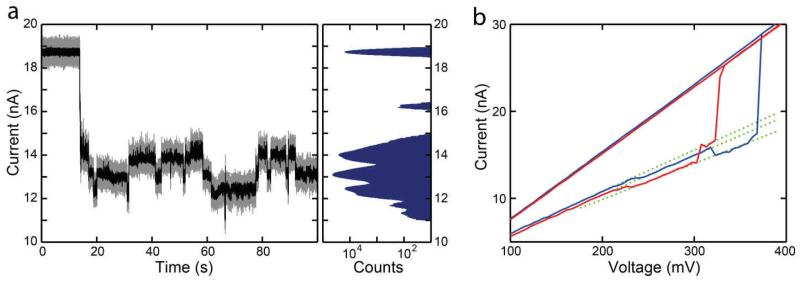
Another surprising observation is that the current through a docked nanoplate can suddenly and randomly jump between discrete levels. Observations of many such spontaneous jumps over time indicate that these jumps occur to and from quantized levels as shown in Figure 5a for a RR nanoplate docked in a 20 nm pore. These levels are clearly visible as discrete peaks in the histogram of the current trace, shown on the right. The magnitude of the jumps is up to about 10% of their relative conductance. Examples for other plate designs are provided in Supplementary Section 5. These jumps are also often seen during IV sweeps, as shown in Figure 5b. Here an HC nanoplate was docked in a 10 nm pore and subjected to a voltage ramp during which it transitioned through three distinct levels before being pulled through at the SFP. Subsequently another HC plate was docked in the same pore and showed similar behavior when subjected to the same voltage ramp. Interestingly, the conductance switched among the same discrete values for these two independent plates (cf. dotted green lines). We often observe these level jumps occurring in a docked nanoplate at constant voltage just before a nanoplate is pulled through, as shown in Figure S18 and Figure S19.

Figure 5.

a) Current is seen to jump among a number of discrete levels for a Rothemund rectangle nanoplate docked onto a 20 nm pore at 100mV. The black trace shows data filtered at 20 kHz while the gray data is unfiltered. The histogram on the right shows the frequency of all of the current values in the trace on a log scale, with each peak representing a discrete level. b) IV curve of two different honeycomb nanoplates docked onto the same 10 nm pore. As the voltage is ramped up, the two nanoplates each jump through three distinct levels before being pulled through. Three dotted green lines have been added for visualization purposes.

All these observations indicate that the source of these jumps is a physical change in the nanoplate structure. Although not every nanoplate tested exhibits these jumps, statistics at 100 mV on the occurrence reveal the majority (69% of HC, 60% of RR, 44% of 2LL, and 75% of 3LL nanoplates) exhibit these jumps. At 200 mV applied voltage these percentages all increase, to 82%, 80%, 68%, and 76% respectively, as shown in Figure S20. The 2LL nanoplate thus appears to exhibit a smaller effect compared to the other plates. We have previously seen that the 2LL nanoplate, unlike the other nanoplates, shows a very weak voltage dependence for its conductance (Figure S7). Ideally for origami nanopore experiments, these jumps should be absent or as small as possible in order to distinguish them from the signals produced by translocations.

Several different mechanisms could explain the physical origin of these jumps. Jumps occurring right after the nanoplate has docked could be attributed to the nanoplate orienting itself into the most energetically favorable position. We have indeed observed some events, which represent only a small fraction of the total events, where some jumps occurred within a short time after docking, after which the nanoplate remains at a stable current level for a long period of time (minutes) or indefinitely. The majority of jumps, however, continue occurring long after the nanoplate has docked and can be attributed to mechanical buckling of the nanoplate. Such buckling could be associated with various distinct mechanical modes of the plates. Temporary melting of the strands hybridized to the M13 template seems less likely since we see no evidence that ssDNA staples are ripped off of the nanoplates as jumps occur in both directions and will often return to the original conductance level after a number of jumps. It should be noted that Langeker et al¹⁵ attributed part of the current gating they observed in their DNA origami nanochannel to a similar effect. Although melted strands could in principle rehybridize, they are unlikely to do so in the presence of the high electric field of the nanopore where the highly charged melted strand is pulled away from its hybridization counterpart. For unzipping of the strands, the orientation of the staples is also very important, as it is known that a lower force is required to unzip a DNA helix if it is applied to the 5′ and 3′ ends²⁶ of complementary strands compared to the 5′ and 5′ ends.²⁷ In summary, we see discrete jumps in the current levels in many docked nanoplates, an effect which may be attributed mechanical readjustments such as nanoplate re-orientation and mechanical buckling.

How does the tail of the nanoplates affect the relative conductance measurements? The DNA origami nanostructures tested all contained a tail, 648 bp to 798 bp in length, protruding from the center of the nanoplate in order to facilitate their proper insertion into the solid-state nanopore. Since this single-stranded tail will form a blob of secondary structures, as confirmed by AFM and in previous nanopore experiments,²⁸ we attempted to investigate if this blob impacts the observed conductance by comparing it to an identical nanoplate design where the single-stranded loop had been hybridized with short oligos into a fully double-stranded loop which due to its large persistence length should stick out far from the pore. Comparison of these two tail designs in a honeycomb nanoplate showed no significant differences (Supplementary Section 6). Based on the observations, we conclude that the tail design does not affect the conductance of the nanoplate.

CONCLUSION

The experimental results in this work present a detailed study of ionic permeability through DNA origami objects. The conductance data reveal that the honeycomb structure is the best design for minimizing the leakage through the nanoplate, while the 2LL nanoplate appears to have the best mechanical stability. A number of methods could be explored in the future to reduce the ionic permeability of the nanoplates. For example, groove binders and possibly intercalators could provide an interesting route. We have seen that, counterintuitively, creating a thicker nanoplate (up to 3 DNA helices thick) does not necessarily reduce the resulting ionic leakage through the nanoplate. The availability of ssDNA templates longer than M13 could allow much thicker structures to be created. Such structures could reveal whether there is an inherent minimum ionic permeability of DNA nanostructures which is independent of thickness, as our data suggests. Investigation into the behavior of the nanoplates in different ionic regimes revealed an increased leakage through the nanoplates as the monovalent salt concentration was reduced, whereas the reduction of the magnesium concentration was shown to have no detectable effect.

DNA origami is beginning to move beyond the early static structures towards active machines with advanced functionalities. The design of such machines requires insight into the dynamics of these structures, as explored in this study. We have seen that the force applied on the nanoplates can deform the structures, cause them to buckle, and even pull them through the pore if sufficient voltage is applied. Alternative versions of the designs tested here, with different oligo-stapling or alternative scaffold routing may reveal how much the observed effects are dependent on minute design details connected to the stapling. Mechanical defects can be designed into plates to observe their effect on the plates mechanical properties such as the SFP. The combination of solid-state nanopores with DNA origami structures promises to open up a number of new possibilities that cannot be realized with other methods, including the ability to simultaneously integrate multiple receptors, binding sites, enzymes, protein, and simple mechanical machines directly within or adjacent to the nanopore.

METHODS

Nanopore fabrication and measurements

SiN pores were fabricated as described previously.²⁹ Nanopore membranes were mounted in a PEEK flowcell separating two aqueous chambers into which Ag/AgCl electrodes were inserted. Solutions of nanoplates at approximately 200 pM concentration were added to the CIS reservoir and a voltage was subsequently applied. The measurement buffer (unless otherwise stated) consisted of 1 M KCl, 10 mM Tris, 1 mM EDTA, 11 mM Mg at pH 8. Ionic currents were detected using an Axopatch 200B amplifier at 100 kHz bandwidth and digitized with a DAQ card at 500 kHz. Current traces were analyzed using Matlab and Clampfit.

AFM and TEM

AFM measurements were carried out under solution on a RIBM High-Speed AFM 1.0. Imaging buffers contained 10 mM Tris pH 7.6, 10 mM MgCl and KCl concentrations varying between 10 and 1000 mM. No significant differences were observed between different KCl concentrations (Figure S25). Samples were prepared by applying a drop of origami nanostructures in their folding buffer to plates of freshly cleaved muscovite mica. After an incubation time of 10 minutes, unadhered origamis were gently rinsed off with imaging buffer. Without drying, the samples were then transferred to the liquid cell of the AFM and imaged in tapping mode using Nanoworld USC-f1.5-k0.6 cantilevers. The TEM protocol and image processing followed the method described in Wei et al.¹²

Nanoplate design and assembly

The structures were designed using caDNAno v 0.2. DNA staple oligonucleotide strands were prepared by solid-phase chemical synthesis (Eurofins MWG) with Eurofins MWG high purity salt-free purification grade. The folding buffer was 5 mM Tris-base, 1 mM EDTA, 20 mM MgCl2 (except for RR 12.5 mM), and 5 mM NaCl at pH8. For the scaffold strand either 7560 (RR & HC) or 7704 (2LL & 3LL) base long M13mp18-phage-derived genomic DNA was used (20 nM). Staple strands were added with 10× excess (200 nM). The RR plate was folded in a thermocycler by ramping the temperature from 95°C to 25°C at 66 s/°C. For HC, 2LL, 3LL plates the temperature was ramped from 65°C to 60°C at 15 min/°C and then 59°C to 40°C with 3 h steps. All plates were subsequently stored at 4°C. The quality of folding was verified by 2% agarose gel electrophoresis (running buffer 0.5×TBE+11 mM MgCl2) showing that all structures fold with an acceptable yield. All the samples were 4× filter-purified after folding by using the folding buffers indicated above. Briefly, 50 μL of folded sample and 450 μL of buffer were added to Amicon Ultra 0.5 mL filter having molecular weight cutoff of 100 kDa. The sample was centrifuged with 14,000 rcf for 3 minutes. This step was repeated 3 times by adding 450 μL of buffer each round (final round 5 min centrifugation). Then the structures were collected to a fresh tube by placing the filter upside down and centrifuging with 1,000 rcf.