FamLBL: detecting rare haplotype disease association based on common SNPs using case-parent triads

Abstract

Motivation: In recent years, there has been an increasing interest in using common single-nucleotide polymorphisms (SNPs) amassed in genome-wide association studies to investigate rare haplotype effects on complex diseases. Evidence has suggested that rare haplotypes may tag rare causal single-nucleotide variants, making SNP-based rare haplotype analysis not only cost effective, but also more valuable for detecting causal variants. Although a number of methods for detecting rare haplotype association have been proposed in recent years, they are population based and thus susceptible to population stratification.

Results: We propose family-triad-based logistic Bayesian Lasso (famLBL) for estimating effects of haplotypes on complex diseases using SNP data. By choosing appropriate prior distribution, effect sizes of unassociated haplotypes can be shrunk toward zero, allowing for more precise estimation of associated haplotypes, especially those that are rare, thereby achieving greater detection power. We evaluate famLBL using simulation to gauge its type I error and power. Compared with its population counterpart, LBL, highlights famLBL’s robustness property in the presence of population substructure. Further investigation by comparing famLBL with Family-Based Association Test (FBAT) reveals its advantage for detecting rare haplotype association.

Availability and implementation: famLBL is implemented as an R-package available at http://www.stat.osu.edu/∼statgen/SOFTWARE/LBL/.

Contact: shili@stat.osu.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Genome-wide association studies (GWAS) have identified >1500 common variants that are associated with common diseases with genome-wide significance. However, GWAS failed to explain a majority of the heritability, and hence, it is hypothesized that rare single-nucleotide variants (rSNVs), which cannot be detected by GWAS platforms, are responsible for at least part of the missing heritability (Manolio et al., 2009). With the next-generation sequencing (NGS) technology, it becomes possible to investigate the role of rSNVs. However, the extremely low frequencies and high dimensionality render the tests developed for GWAS powerless when applied to rare variants.

Numerous methods aiming at detecting rSNVs for case-control studies have been developed in recent years. One class of tests, ‘burden tests’, focus on aggregating rare variants and then using the collapsed super-variant for the test. Tests of this category include the combined multivariate and collapsing method (Li and Leal, 2008) and the weighted-sum method (Madsen and Browning, 2009). Collapsing multiple variants into a single variant can indeed effectively reduce the dimension of the data and increase the frequency of the super-variant; however, power can be diminished when the rare variants being collapsed are of opposite effects on the trait of interest. Other tests, like C-alpha (Neale et al., 2011), Sequence Kernel Association Test (SKAT) (Wu et al., 2011) and a hierarchical modeling approach (Yi et al., 2011), are more powerful if there exist different directionality and variability in the coefficients of the regression parameters.

Most of the methods proposed thus far can only detect regions of interests. To identify the combination of causal variants responsible for the disease, it is advantageous to investigate haplotypes within each region. While association between common haplotypes and diseases is well studied in GWAS, those methods typically fail to detect individual effects of rare haplotypes. Traditionally, rare haplotypes are either ignored, combined into a super-variant or grouped with common haplotypes of similar sequence variation. Such a practice is clearly deficient, as causal rare haplotypes can result from common single-nucleotide polymorphisms (SNPs) (Guo and Lin, 2009). Further, rare haplotypes that are disease associated may tag rSNVs that are causal (Lin et al., 2012, 2013), and can even lead to greater power for detecting association (Supplementary Tables S1 and S2 and Figure S1). To remedy this situation so that rare haplotypes can be investigated, Guo and Lin (2009) proposed a LASSO regularization of logistic regression model for case-control data that effectively combat the problem of non-convergence of the EM algorithm due to estimation instability. Although methods are available for selecting optimal penalty parameters for LASSO-type regularization methods, they are typically computationally intensive. Moreover, uncertainty resulted from setting the tuning parameters is hard to be investigated and be accounted for. To avoid the need for specifying tuning parameters, Biswas and Lin (2012) proposed a Bayesian model in which Laplace distribution is used as prior distribution for effect size, effectively shrinking the coefficient toward zero. This approach also allows for testing individual haplotype effects and constructing confidence intervals for effect sizes. Further, in their model, a retrospective likelihood is used, which is more appropriate than a prospective formulation for case-control data given the data collection process.

It has been argued recently that linkage peaks detected by family-based methods can potentially be caused by rare variants (Bowden, 2011), and that using family data can avoid heterogeneity and be more fruitful for detecting such rare variant association (De et al., 2013). Further, family-based design should provide an increase in power compared with population-based designs for rare variants, as such variants are enriched in a family if it does exist (Zhu et al., 2010). Most importantly, family-based design will not be affected by population stratification, whereas case-control design may see an increase in type I error rate if left unadjusted.

The stage is therefore set for detecting associated rare (and common) haplotypes using family data. Commonly used family-based methods for detecting common haplotypes such as FBAT (Laird and Lange, 2006) may suffer from loss of power if used for detection of rare haplotypes, because the estimated variance of rare haplotype effects could be large. Recent extension of FBAT does provide a way to analyze rSNVs by collapsing and optionally weighting each variant (De et al., 2013), but the method is not amenable to haplotypes. In this article, we propose a family-based method aiming to detect both rare and common haplotype associations using common SNP data on case-parent trios. Our retrospective likelihood correctly reflects the ascertainment procedure, and its factorization resembles a ‘match-pair’ design as we will see in Section 2. To shrink the coefficients of unassociated haplotypes so that the effects of rare associated haplotypes can be more precisely estimated to increase the statistical power of detection, we adopted the Logistic Bayesian Lasso (LBL) methodology for parameter estimation and statistical inference (Biswas and Lin, 2012), leading to the famLBL algorithm. The proposed famLBL method is thoroughly investigated to gauge its power and type I error rate. We also compare famLBL with LBL and FBAT in terms of robustness to population stratification and effectiveness in detecting rare haplotype association. Finally, we apply famLBL to the Framingham Heart Study (FHS) data to illustrate its utility.

2 METHODS

Likelihood, logit and haplotype distribution modeling

Suppose we have n case-parent triads for which the families are ascertained due to the child being affected with a particular disease. Let ${\mathit{Z}}_i=(Z_{if},Z_{im},Z_{ic})$ denote the familial haplotype configuration of triad i (i.e. father, mother and child haplotype pairs, in that order), which is typically unobservable, as phase information is usually not deductible from genotype data ${\mathit{G}}_i=(G_{if},G_{im},G_{ic})$. We assume the SNPs are located close to one another so that there is no recombinant haplotype in the child. Thus, we may write ${\mathit{Z}}_i$ equivalently as ${\mathit{Z}}_i=(Z_{iu},Z_{ic})$, where Z_iu is the haplotype pair that was not passed to the child. Note that parental ordering is not necessary if allelic exchangeability is assumed, a weaker condition than Hardy–Weinberg Equilibrium (HWE) (Yang and Lin, 2013). Let D_i denote the event that family i is ascertained; for case-parent triad design, this is equivalent to the event that the child is affected, i.e. Y_ic = 1. The complete data likelihood for a collection of n triads is then

$$L(\varphi )={\displaystyle \prod _{i=1}^{n}P}(Z_{ic}|Y_{ic}=1,\mathit{\varphi })P(Z_{iu}|\mathit{\varphi }),$$ (1)

where $\mathit{\varphi }=(\mathit{\beta },\mathit{\delta })$ denotes the collection of individual haplotype effects (β, regression coefficients) and parameters associated with haplotype frequencies (δ), which will be specified more explicitly as our formulation unfolds. Note the similarity between this likelihood and that based on case-control data (Biswas and Lin, 2012); thus, this may be interpreted as a ‘matched-pair’ design, although the pseudo individual with the Z_iu haplotype pair comes from the target, not the control, population. We use logistic regression to model the odds of disease for a given haplotype Z: ${\theta }_Z=P(Y=1|Z)/P(Y=0|Z)$. Specifically,

$$\log {\theta }_Z=\alpha +{\mathit{X}}_Z\mathit{\beta },$$

where ${\mathit{X}}_Z$ is a row vector associated with haplotype Z, α is the intercept and β is a vector of coefficients representing the haplotype effects. Note that ${\mathit{X}}_Z$ can code for dominant/recessive/additive effects, which can be specified by the investigator (Guo and Lin, 2009).

Let $\mathit{f}=(f_1,\dots ,f_m)$ denote the frequencies of a total of m haplotypes with the constraints that f_k > 0 and ${\displaystyle {\sum }_{k=1}^m{f}_k}=1.$ For a haplotype pair $Z=z_k/z_{k\prime }$, we model its frequency in the target population by

$$a_Z(\mathit{\delta })=\{\begin{array}{cc}{f}_k^2+d{f}_k(1-f_k)& \text{if}{z}_k=z_{k\prime }\\ 2(1-d)f_k{f}_{k\prime }& \text{if}{z}_k\ne z_{k\prime }\end{array},$$

where $d\in (-1,1)$ is the within-population inbreeding coefficient that can be used to capture excess/reduction of homozygosity (Weir, 1996). By modeling the frequency in this way, we do not need to make the assumption of HWE. Assuming that the haplotype pair distribution in the control population is the same as in the target population, we can express the distribution in the diseased population as

$$b_Z=P(Z_{ic}|Y_{ic}=1,\mathit{\varphi })=\frac{{\theta }_Z{a}_Z}{{\displaystyle \sum _H{\theta }_H}{a}_H}.$$

The complete data likelihood in (1) can now be rewritten more fully as:

$$\begin{array}{ccc}L(\mathit{\varphi })& =& {\displaystyle \prod _{i=1}^n{a}_{Z_{iu}}}(\mathit{\delta })a_{Z_{ic}}(\mathit{\delta })·\frac{\exp \left\{X_{Z_{ic}}\mathit{\beta }\right\}}{{\displaystyle \sum _H(}\exp \left\{X_H\mathit{\beta }\right\}{a}_H(\mathit{\delta }))},\end{array}$$ (2)

which, we note, does not contain the regression parameter α, as it is canceled out.

Specification of priors

To shrink the coefficients of the unassociated haplotypes toward zero so that the effects of the associated ones can be estimated more precisely to increase statistical power, we cast the problem into the Bayesian Lasso framework (Park and Casella, 2008). As such, we need to assign prior distributions to the parameters $\mathit{\varphi }=(\mathit{\beta },\mathit{\delta }=\{\mathit{f},d\})$. For each β_j in β, we use the Laplace distribution, leading to the following density function:

$$\pi ({\beta }_j|\lambda )=\frac{\lambda }{2}\exp \left(-\lambda |{\beta }_j|\right),-\infty <{\beta }_j<\infty ,j=1,\dots ,m-1,$$

where the variance is 2/λ², and the hyperparameter λ controls the level of shrinkage. Instead of picking a fixed value of λ, we let it follow Gamma(a, b) with pdf $\pi (\lambda )=\frac{b^a}{\Gamma (\gamma )}{\lambda }^{a-1}\exp (-\lambda b)$. This specification of the priors has been shown to give the Bayesian version of LASSO when normal likelihood is used (Park and Casella, 2008) and has led to satisfactory shrinkage in LBL (Biswas and Lin, 2012). The hyperparameters a and b are selected to realistically reflect the odds ratio (OR) of associated haplotypes for complex diseases; the range of [15, 25] will be explored following Biswas and Lin (2012).

The parameters for modeling haplotype-pair frequencies, f and d, are not independent. Because $a_Z(\mathit{\delta })$ must be non-negative, it poses the following constraint: $d>\max \{-f_k/(1-f_k),k=1,\dots ,m-1\}$. Therefore, we let f follow Dirichlet(1,1,…,1). Then, we use the $\text{Uniform}\left({\max }_{k=1}^{m-1}\{-f_k/(1-f_k)\},1\right)$ distribution to model d given f.

Statistical inference based on posterior distributions

Markov chain Monte Carlo (MCMC) methods are used to draw samples of the parameters from the posterior distributions. We use the Metropolis–Hastings algorithm to update the β parameters with a double exponential proposal distribution whose mean is the current estimate and whose variance is proportional to the absolute value of the current estimate to facilitate shrinkage. The Metropolis–Hastings algorithm is also used to update the inbreeding parameter d using a uniform proposal distribution observing the constraints as described in the above Subsection. For the rest of the parameters (i.e. $\lambda ,\mathit{Z}$ and f), we update them using the Gibbs sampler, as the posterior distributions are of conjugate forms and can be sampled conveniently. Based on the MCMC samples after convergence has been achieved, we draw inference regarding association by testing for the significance of each β coefficient. Specifically, we carry out a hypothesis test of $H_0:|\beta |\le \mathrm{ϵ}$ $\text{versus}{H}_a:|\beta |>\mathrm{ϵ}$, where ε is set to a small number, using Bayes Factor (BF) (Raftery and Lewis, 1995), the ratio of posterior odds to prior odds. If the BF exceeds a certain threshold, we conclude that the corresponding β is significant, i.e. the haplotype is associated with the disease. Based on the work of Biswas and Lin (2012) after extensive simulation, setting ε = 0.1 and the BF threshold of 2 appear to be satisfactory and leads to a type I error rate at or below 5%, so these tuning parameters are adopted in the current study for most of the analyses. The R package (with dynamic loading of C program) implementing this method, famLBL, is publicly available.

3 RESULTS

We carried out extensive simulation to thoroughly evaluate the performance of famLBL and compared it with LBL and FBAT. A total of three sets of simulation are considered to evaluate power, type I error, sensitivity to population substructure and comparisons with LBL and FBAT. We describe the three simulation settings, data generation process and results in the following. In the last Subsection, we present an application of famLBL to the FHS data.

3.1 Simulation settings and data generation

3.1.1 Simulation 1

The setting for the first simulation study portraits data from a homogeneous population. This setting is used to demonstrate that famLBL, utilizing triad family data, controls type I error adequately, and to compare its power with that of LBL based on case-control data. Three haplotype distributions, HS1, HS2 and HS3, consisting of 6, 9 or 12 haplotypes, respectively, are considered. For each distribution, three scenarios are considered: only a common haplotype (frequency ≥ 0.05) is causal (C); a common and a rare haplotypes (frequency < 0.05) are causal (RC); and two rare haplotypes are causal (RR). The disease model is taken to be additive, in that two copies of the risk haplotype double the log odds of being affected. These haplotype distributions (column Pop1) and ORs for the disease models are given in Table 1. Two phenocopy rates at 5% and 10% are considered for this and the other two simulations, with the corresponding population prevalence for each combination of disease model and haplotype distribution given in the Supplementary Table S3. To simulate trio data, haplotypes for parents are generated first, and one haplotype from each parent is chosen at random to pass down to the descendant. Disease status of the descendant is simply based on the binomial probability inferred from the models described above. A total of 500 case-parent triads are obtained based on this simulation procedure. Phase information is removed and only triad genotype data are used in famLBL. Because LBL is only applicable to case-control data, we only retained the genotype data for the affected children, leading to 500 affected cases. We then randomly sample 500 unaffected individuals as controls.

Table 1.

Haplotype settings and association scenarios for the simulation

Haplotype		Frequency		OR
Setting	Hap	Pop1	Pop 2	RR	RC	C
HS1	01100	0.3	0.3	1	1	1
	10100	0.005	0.005	3	3	1
	11011	0.01	0.01	2	1	1
	11100	0.155	0.155	1	1	1
	11111	0.11	0.42	1	2	2
	10011	0.42	0.11	1	1	1
HS2	01010	0.06	0.06	1	1	1
	01100	0.25	0.25	1	1	1
	10000	0.08	0.005	1	2	2
	10100	0.005	0.08	3	3	1
	11011	0.01	0.01	2	1	1
	11100	0.09	0.09	1	1	1
	11101	0.085	0.085	1	1	1
	11111	0.1	0.1	1	1	1
	10011	0.32	0.32	1	1	1
HS3	00111	0.07	0.07	1	1	1
	01000	0.02	0.02	1	1	1
	01011	0.05	0.05	1	1	1
	01101	0.06	0.06	1	1	1
	01110	0.14	0.14	1	1	1
	10010	0.08	0.005	1	2	2
	10100	0.005	0.08	3	3	1
	11011	0.01	0.01	2	1	1
	11101	0.09	0.09	1	1	1
	11110	0.13	0.13	1	1	1
	11111	0.1	0.1	1	1	1
	10001	0.245	0.245	1	1	1

3.1.2 Simulation 2

In the second simulation study, the setting simulates a stratified population. The purpose of this setting is to show that famLBL is not sensitive, whereas the original LBL based on case-control data is sensitive, to population stratification. We hypothesize a stratified population with two subpopulations. The haplotype distributions under these two subpopulations (columns Pop1 and Pop2) are given in Table 1. The RR, RC and C disease models are the same for both populations. For trio data, parents are assumed to come from a 50–50% mixture of populations 1 and 2. The descendants’ haplotypes are retained as cases for the case-control data. The controls are generated randomly from a 80–20% mixture of populations 1 and 2. Again, phase information is deleted (i.e., only genotypes are retained) before the famLBL and LBL analyses.

3.1.3 Simulation 3

The last simulation study is casted under the same homogeneous population, haplotype settings and disease models as in the first simulation study. This set of simulation is aimed to compare the performance of two family-based methods for detecting haplotype association: famLBL versus FBAT.

3.2 Results and comparisons

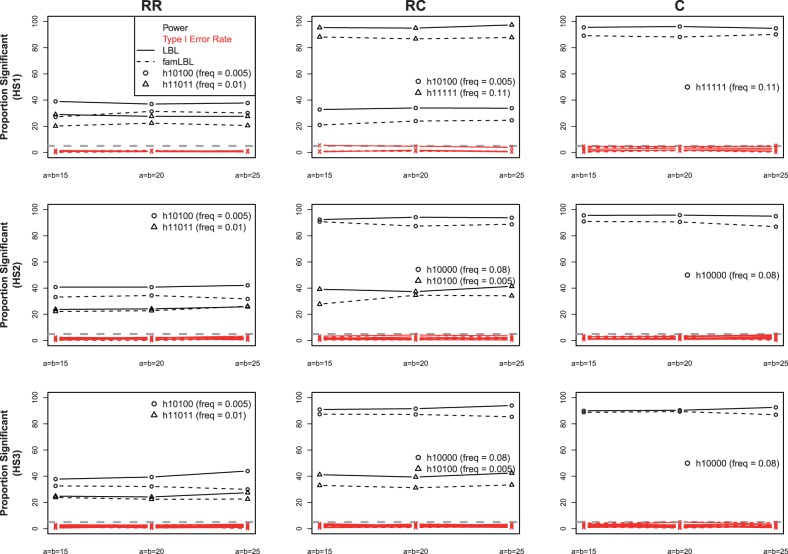
For each analysis, 40 000 MCMC iterations were run, which appears to be sufficiently large for obtaining meaningful results based on convergence diagnostics developed by Raftery and Lewis (1992). Results for both famLBL and LBL from the first set of simulation assuming a homogeneous population with 10% phenocopy rate are presented in Figure 1. Recall that famLBL uses 500 trios (which may be thought of as 500 affected children and 500 matched ‘pseudo controls’), whereas LBL uses 500 affected children and 500 independent controls. We can see that both famLBL and LBL are able to control the type I error rates; they are all at or below 5%, marked by the gray dashed line. The exact numbers are given in Supplementary Table S4. We also considered a larger BF threshold to control the type I error rate at the 1% level (Supplementary Table S5). Both methods are powerful for detecting common variants, but the power is much lower when the variants are rare, even though the effect size is larger for the rare variant in the RC scenario. On the other hand, when both associated haplotypes are rare, the effect size plays a larger role, leading to greater power for detecting the rarer haplotype with larger OR. As expected, the power of famLBL is universally smaller than LBL due to dependency in data, although the differences are all quite small. Results for the 5% phenocopy rate convey the same information (Supplementary Figure S2). Because the results are very similar for the three sets of a and b parameter values that we considered (a = b = 15, 20, 25), we choose to only use a = b = 20 for the next two sets of simulation.

Fig. 1.

Comparison of power and type I error rate between famLBL (using trio data) and LBL (using case-control data) under population homogeneity. Lines with ‘o’ and ‘Δ’ represent power, whereas those with ‘x’ denote type I error; solid: LBL, dashed: famLBL

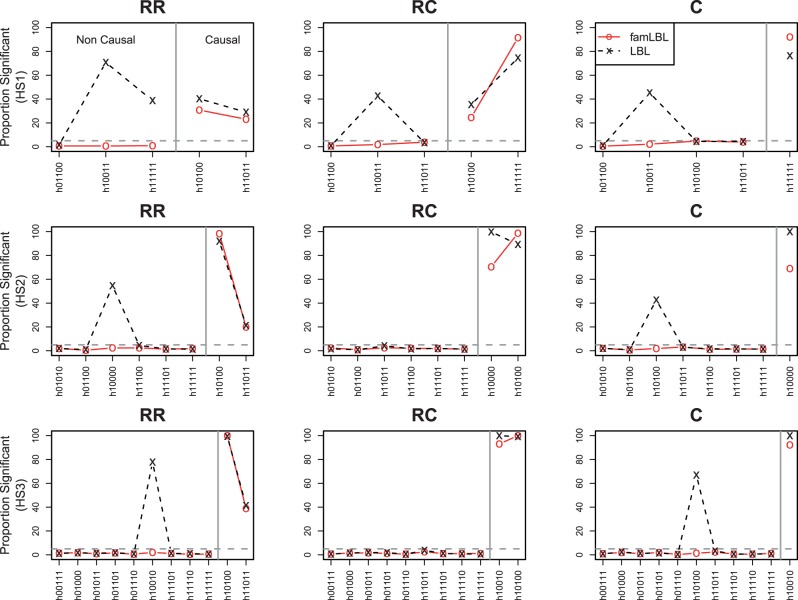
For the second set of simulation under population substructure, the type I error rates and the power are presented in Figure 2. Each plot depicts both type I error (for non-causal variant; left side) and power (for causal variants; right side) that are separated by a vertical line. In the presence of population substructure, we can see that LBL can have wildly inflated type I error rates, affirming the lack of robustness for population-based designs. For example, haplotype 10011 and 11111 under haplotype setting 1 (HS1) and the RR disease model (top-left plot) have quite different frequencies in the two subpopulations and thus greatly inflated type I error rates. On the other hand, because the internal matched ‘pseudo control’ in the trio design comes from the same population as the affected child, the results are not affected by population stratification, and thus, the type I error remains well controlled, as in the first set of simulation.

Fig. 2.

Comparison of type I error rate and power between famLBL (using trio data) and LBL (using case-control data) in the presence of population stratification. Type I error for non-causal haplotypes is plotted on the left, and power for causal haplotypes is plotted on the right; ‘x’: LBL, ‘o’: famLBL

We saw in our first set of simulation with a homogeneous population that the power of LBL is always higher than that for famLBL when the number of cases and ‘controls’ (true controls in LBL and ‘pseudo controls’ in famLBL) are the same. However, this is no longer the case when there is population substructure. The power of famLBL can exceed that of LBL. For example, the power for detecting the causal haplotype h11111 is higher for famLBL under the HS1 RC disease model scenario (right side of top-middle plot). As such, under population substructure, famLBL not only can control the type I error as expected, but it may potentially also have higher power for detecting causal variants compared with its population counterpart. Results for the 5% phenocopy rate are the same qualitatively and are given as Supplementary Figure S3.

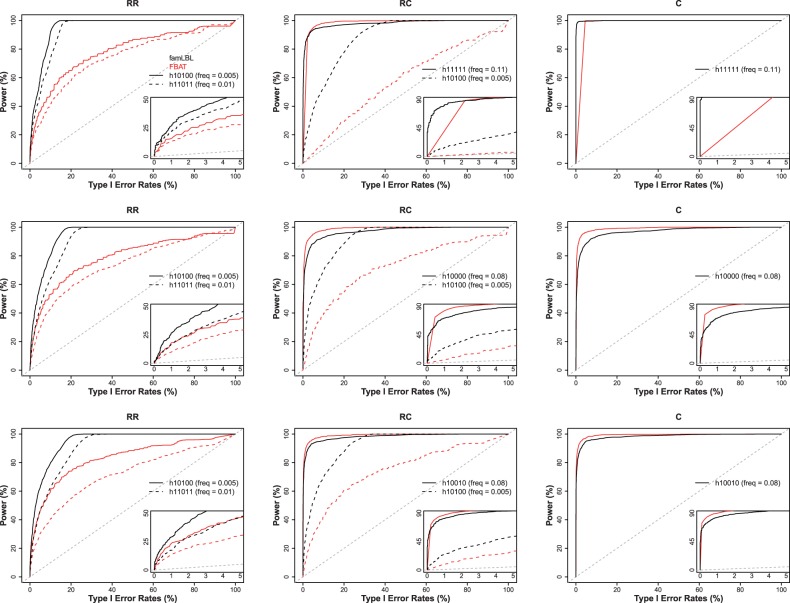
Results for comparing famLBL with FBAT in terms of both type I error and power are summarized as receiver operating characteristic (ROC) curves in Figure 3 for 10% phenocopy rate and Supplementary Figure S4 for the 5% phenocopy rate, where the x-axis plots the type I error while the y-axis plots the power for each corresponding type I error rate. The power for detecting common causal variants is high and comparable between famLBL and FBAT, with one slightly outperforming the other in a subset of the settings. However, for rare variants, famLBL dominates FBAT, as expected, as FBAT is not designed for detecting rare variant association. The power gain with famLBL can be very significant. For example, the famLBL’s power for detecting the rare associated haplotype (h10100) in the RC scenario for all three haplotype settings (dashed lines in all three plots in the middle column of Figure 3 and Supplementary Figure S4) is much higher, especially when type I error rate is in the small, acceptable, range (insets in the plots).

Fig. 3.

ROC curves comparing the performance of famLBL (black curves) with FBAT (dark gray (or red when in color) curves). Inset in each plot zooms in on the portion where type I error is at most 5%. A diagonal line is also added for reference

3.3 Application to the FHS data

To illustrate the utility of famLBL, we applied it to the FHS data, available at dbGaP through the Genetic Analysis Workshop 16. One of the objectives of FHS is to identify genetic risk factors for cardiovascular diseases. Following Han et al. (2013), we focus on a dichotomous hypertensive trait, in which hypertension is defined to be systolic blood pressure ≥140 mm Hg or diastolic blood pressure ≥90 mm Hg. Further, as the primary utility of famLBL is to follow up on regions with initial association signals to understand the causal mechanism, we focus on nine top associated SNPs (referred to as target SNPs) identified in Han et al. (2013) (Supplementary Table S6). For each of the nine target SNPs, we considered haplotypes spanning seven-SNP regions including the target SNP. Table 2 presents part of the results, with the full results given in Supplementary Tables S7 and S8. Six of the nine target SNPs return significantly associated haplotypes, with many of them being rare (frequency ≤ 0.05), signaling their potential roles of tagging rare SNVs.

Table 2.

Hypertension-associated haplotypes, with LB and UB denoting the lower and upper bounds of the OR, respectively

SNP	Haplotype	Frequency	OR	LB	UB
rs684596	0101110	0.006	0.082	0.003	0.806
rs2229188	1100111	0.023	9.207	1.322	96.93
rs7559838	0000000	0.079	2.184	1.066	4.923
rs2736483	0111010	0.165	0.418	0.169	0.917
rs16881524	1111001	0.028	2.942	1.276	6.228
rs7657817	1011000	0.024	3.397	1.070	12.31

Note: The bold type within each haplotype indicates the position and the allele of the target SNP.

4 DISCUSSION AND FUTURE WORK

In this article, we propose famLBL, a family-based method for detecting haplotype association with common diseases, specifically gearing toward rare haplotypes yet retaining sufficient power for detecting common haplotype associations. Such a method is timely in that there is a continuing recognition that rare haplotype constructed based on GWAS common SNPs may tag multiple rare causal SNVs not genotyped in GWAS. It is even more attractive considering the fact that the use of common SNPs from the GWAS era is much more economical (in fact, ‘free’, as no further genotyping is needed) than using new SNVs obtained from NGS. In addition, the use of a haplotype-based method can provide greater statistical power for detecting association compared with a collapsing-based method. Most importantly, by detecting specific associated haplotypes instead of simply a regional significant result from a collapsing-based test, a haplotype-based method can uncover crucial information useful for designing follow-up experiment to identify/validate causal variants.

Based on an extensive simulation study, we thoroughly investigated the properties of famLBL and documented its success in detecting haplotype associations, both rare and common. This is a significant step forward in two fronts. First, compared with population-based methods for detecting rare associated haplotypes, famLBL is not sensitive to population stratification, and thus, its type I error is well under control with good power. This finding is important because of recent surge of interests in returning to family data to find rare causal variants (Bowden, 2011; De et al., 2013; Zhu et al., 2010). Second, our results show that famLBL can be much more powerful than popular traditional family-based association methods for detecting rare associated haplotypes. Even though the underlying methodology of famLBL is geared toward the detection of associations that involve rare haplotypes by shrinking the estimated effect sizes of the unassociated ones, the power of famLBL for detecting associations of common haplotypes is still comparable with a method that has much smaller power for detecting rare associated haplotypes. Application of famLBL to the FHS illustrates its practical utility.

From a methodological perspective, the statistical approach adopted in famLBL is Bayesian LASSO, a method proven to be effective for detecting rare associated haplotypes by shrinking the coefficients (representing effect sizes) of unassociated haplotypes toward zero (signifying no association) (Biswas and Lin, 2012). By doing so, the effect sizes of the truly associated ones can be more precisely estimated. This leads to increased statistical power for detecting rare associated haplotypes without increasing type I error nor sacrificing power for detecting common associated ones.

Implementation of famLBL requires the use of MCMC methodology for parameter estimation and statistical inference. This versatile statistical technique, however, is computationally intensive. For each dataset simulated under the homogeneous population model, the computational time for famLBL with 40 000 MCMC iterations running on an Intel i3 2520 (2.5G) CPU with 8 GB memory took about 12, 20 and 50 s for haplotype settings 1 (6 haplotypes), 2 (9 haplotypes) and 3 (12 haplotypes), respectively. The amount of time taken to analyze a dataset simulated under the population stratification model is similar. As such, famLBL is not intended to be used as a genome-wide initial screening method. Rather, famLBL is likely to be most profitable as a follow-up tool on regions showing signals in initial screening, especially in regions under linkage peaks uncovered in family studies.

In the current article, we focus on detecting rare haplotype association with a binary trait. Nevertheless, famLBL can be extended to other phenotypes, including general qualitative or quantitative traits. Extension to extended pedigrees, on the other hand, is much more complicated. The most difficult issue stems from the potential of missing data with larger pedigrees and the no-recombination constraints, making an efficient MCMC algorithm much more difficult to devise. However, given the greater information contained in larger pedigrees and the availability of such data already in existence, research into this extension is warranted.