Dynamics of Active Semiflexible Polymers

Abstract

Active fluctuations, driven by processes that consume ATP, are prevalent in living cells and are mostly driven by different forms of molecular motors. Such motors often move and transmit forces along biopolymers, which in general can be treated as semiflexible chains. We present a theoretical analysis of the active (out of thermal equilibrium) fluctuation of semiflexible polymers, using both analytical and simulation methods. We find that enhanced diffusion, even superdiffusive, occurs in a well-defined temporal regime, defined by the thermal modes of the chain and the typical timescale of the activity. In addition, we find a dynamic resonance-like condition between the elastic modes of the chain and the duration of the active force, which leads to enhanced spatial correlation of local displacements. These results are in qualitative agreement with observations of cytoskeletal biopolymers, and were recently observed for the dynamics of chromatin in interphase cells. We therefore propose that the interplay between elasticity and activity is driving long-range correlations in our model system, and may also be manifest inside living cells.

Introduction

In recent years, active systems have spawned a lot of interest among researchers in different fields. Active systems have components that utilize chemical energy to perform work and are away from equilibrium, although they may exhibit nonequilibrium steady states. Active processes in cell biology have been a field of vigorous research activity. One of the most striking examples of active cellular process is the utilization of chemical energy by motor proteins that interact with filamentous biopolymers (1, 2). Examples include the contractile forces produced by myosin-II motors within the actin cytoskeleton, both in actin myosin gels and inside living cells (3, 4, 5). Another biopolymer is the DNA, and there is growing interest in its dynamics inside the nucleus of both eukaryotes (6, 7, 8) and in bacteria (9, 10), which seem to be actively driven by processes that consume ATP and affect the overall organization and expression of the genome (11, 12, 13). However, the exact process of energy transduction on the DNA remains unclear (14). A detailed recent study (15) has found evidence for long-range coherence in the active motion of the chromatin, which seems to be driven by the activity.

Motivated by these experimental studies of active motion, we study the active dynamics of a single semiflexible polymer in solution. We model the activity by stochastic forces that are exerted in the direction of the local normal, and with random orientation (we also investigate the effects of applying tangential active forces; see the Supporting Material). The active force is characterized by a fixed magnitude (F_a) and a temporal duration (τ), such that it is a colored-noise, violating the fluctuation-dissipation theorem (16). We implement a minimal model for the active shot-noise (16, 17), which has only two free parameters: its amplitude, and its burst timescale. We show below that the critical component distinguishing this noise from thermal, is the finite timescale. These properties give a coarse-grained description of the activity, for example of the myosin-induced contractility in the actin-myosin network. In the case of DNA transcription this description of the activity represents, in a coarse-grained manner, the complex processes of histone remodeling, DNA unwrapping, supercoiling, and RNA production that accompany the activity of transcription compartments (or transcription factories) (18, 19). We do not include hydrodynamic interactions in this study; without these interactions, we already find apparently novel behavior that is easier to investigate in a simpler description. In addition, the densely packed polymer inside the chromatin, or in actin-myosin gels, may diminish long-range hydrodynamic interactions.

From the theoretical side, our study is somewhat complementary to an earlier work (17) in that here the active effects are primarily transverse- and fluctuation-dominated. Several theoretical works that are related to ours include Loi et al. (20, 21), who had studied the effective temperature of active polymers, and Jiang and Hou (22), who had studied the effects of hydrodynamic interactions. In Liverpool et al. (23), Laskar et al. (24), and Jayaraman et al. (25), the directional drift of a polymer driven by directed active forces was studied, whereas we are interested here in the effects of active noise with zero mean. The motion of a filament embedded in an active gel was studied in Kukuchi et al. (26), whereas we examine the motion of an active polymer embedded in a passive background. In the active-gel case, there are additional length-scales arising from the range of coherent flows generated spontaneously, and these do not apply to our system. Most recently, a continuum description for the activity in the chromatin was suggested (27), which is very different and somewhat complimentary to our microscopic study.

We find several apparently new properties of the active polymer, such as a temporal regime where the motion of the segments follow a superdiffusive behavior. More strikingly, we find that the interplay between activity and the elasticity of the polymer leads to a resonance-like condition, whereby the activity stabilizes bending modes that have relaxation times of the order of the duration of the active bursts. We compare our results to experimental observations and in particular, we find that our work suggests a possible mechanism that can account for the puzzling correlations found in interphase chromatin motion (15).

Theoretical Model and Analytical Calculations

Most biopolymers are semiflexible in nature (2), and we therefore model them as wormlike chains, which are unstretchable (i.e., the local metric is preserved) and resist bending. We treat a single, free semiflexible chain embedded in a viscous medium. We use the approximation of local friction, thereby neglecting long-range hydrodynamic interactions. This should be a good description in the regime of a highly dense environment, such as exists in the cytoskeletal network and for chromatin inside the nucleus (or inside bacteria). In addition, we neglect elastic forces that may trap the chain, by treating it as freely moving in space. For the case of chromatin, therefore, we do not describe the very short timescales (t ≤ 1 s) where it is found to be elastically localized (28).

In the continuum model, the free energy of the chain can be written as (29)

$$F\left[\overrightarrow{r}\left(s\right)\right]={\int }_0^{L}ds\left(\frac{1}{2}{b}_o\kappa \frac{\partial \hat{t}}{\partial s}\cdot \frac{\partial \hat{t}}{\partial s}+g\left(s\right)\hat{t}\left(s\right)\cdot \hat{t}\left(s\right)\right),$$ (1)

where L is the length of the polymer, b₀ is the thickness of the chain, κ is the bending rigidity,

$$\hat{t}\left(s\right)=\frac{\partial \hat{r}}{\partial s}$$

is the unit tangent vector to the chain at location s along the chain, and g(s) is a Lagrange multiplier preserving the local metric; g(s) has the interpretation of tension, and is assumed to be independent of time (although this is not strictly true). Defining ζ to be the friction γ per unit length (also b₀) and ${\overrightarrow{f}}_s\left(t\right)$ to be the noise, the equation of motion for the segment at location s may be written as

$$\zeta \frac{\partial \overrightarrow{r}\left(s\right)}{\partial t}=-b_o\kappa \frac{{\partial }^4\overrightarrow{r}}{\partial s^4}+2\frac{\partial }{\partial s}\left(g\left(s\right)\frac{\partial \overrightarrow{r}}{\partial s}\right)+\overrightarrow{f}\left(s,t\right).$$ (2)

Equation 2 is difficult to solve exactly. Various methods such as gradient expansion have been used in the past to study the dynamics (17). We resort to a simple approximation in which the tension g(s) along the chain is replaced by the mean tension g; Eq. 2 then simplifies to

$$\zeta \frac{\partial \overrightarrow{r}\left(s\right)}{\partial t}=-b_o\kappa \frac{{\partial }^4\overrightarrow{r}}{\partial s^4}+2g\frac{{\partial }^2\overrightarrow{r}}{\partial s^2}+\overrightarrow{f}\left(s,t\right).$$ (3)

This equation, being linear, is amenable to Fourier mode analysis (30) as

$$\overrightarrow{r}\left(s,t\right)={\overrightarrow{X}}_0\left(t\right)+2\sum _{p=1}^{\infty }{\overrightarrow{X}}_p\left(t\right)\cos \left(p\pi s/L\right).$$ (4)

The inverse transform is given by

$${\overrightarrow{X}}_p\left(t\right)=\left(1/L\right){\int }_0^{L}ds\cos \left(p\pi s/L\right)\overrightarrow{r}\left(s,t\right).$$ (5)

Note that the trigonometric basis functions give errors near the chain ends, of order 1/L (31), and therefore are commonly used (17). In terms of modes, the equation of motion, Eq. 2, takes the form

$${\zeta }_p\frac{\partial {\overrightarrow{X}}_p}{\partial t}=-k_p{\overrightarrow{X}}_p\left(t\right)+{\overrightarrow{f}}_p\left(t\right),$$ (6)

where

$${\overrightarrow{f}}_p\left(t\right)=\left({\zeta }_p/L\zeta \right){\int }_0^{L}ds\text{cos}\left(p\pi s/L\right)\overrightarrow{f}\left(s,t\right).$$ (7)

The factor is

$$k_p=a{p}^4+b{p}^2,$$

where

$$a=\kappa b_0\left({\zeta }_p\text{/}\zeta \right){\left(\pi \text{/}L\right)}^4,$$

$$b=2g\left({\zeta }_p\text{/}\zeta \right){\left(\pi \text{/}L\right)}^2,$$

and

$${\zeta }_{p=0}=L\zeta ,{\zeta }_{p\ne 0}=2L\zeta .$$

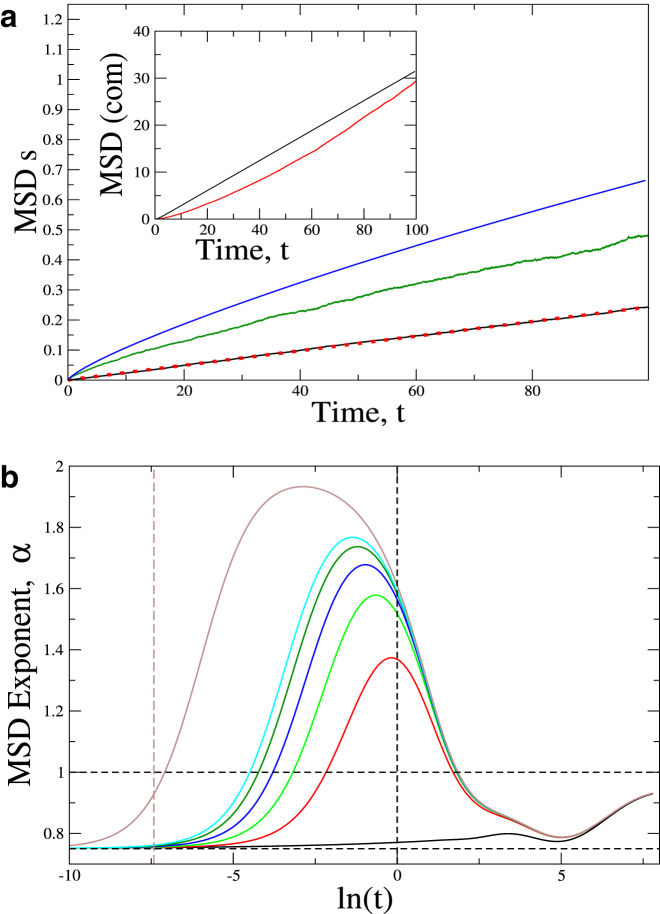
The motion of the polymer due to purely thermal fluctuations is calculated in the Supporting Material (Fig. 1 a), where we recover the well-known result that the mean-square displacement (MSD) exponent α, 〈r²〉 ≡ D_efft^α, at short times is α = 3/4 (32) (Fig. 2 a).

Figure 1.

(a) MSD-s of the COM (black, simulations; red, theory) and the middle bead (green, simulations; blue, theory) in the absence of active forces. (Inset) MSD-s for the COM (same color code) when an active force of magnitude F = 200 is applied in the direction of the local normal to the polymer; L = 25 and τ = 1 were used. (b) Exponents for the MSD-s of the middle bead obtained from the analytical theory for active forces of magnitude 0.0 (black), 50.0 (red), 90.0 (green), 130.0 (blue), 170.0 (dark green), 200.0 (cyan) and 1000.0 (brown); using τ = 1.0, L = 25. The crossover time t_c (Eq. 15) for F_a = 1000.0 is denoted by the red dashed vertical line, while the burst time τ is denoted by the vertical dashed black line. To see this figure in color, go online.

Figure 2.

(a) Time evolution of the exponent α from the analytical theory for the middle bead of the polymer for purely thermal excitation (black), and in the presence of applied active forces F_a = 50, 90, 130, 170, and 200 (red, green, blue, dark green, and cyan, respectively); for F_a = 1000 (brown); and the corresponding t_c (vertical dashed brown line; see Eq. 15). The active peak is seen to shift to smaller times with increasing magnitude of the active forces, in accordance with Eq. 15. (Horizontal black, dashed lines) Values 3/4 and 1. (b) Plot of the time evolution of the MSD exponents obtained from simulations (solid lines) for different values of active forces F_a = 0, 50, 90, 130, 170, and 200 (black, red, green, blue, dark green, and cyan, respectively). Horizontal dashed lines denote the values of 3/4 and 1. Vertical dashed lines denote: (Black) τ and (red) t_c for F_a = 50. The values L = 25, τ = 1 were used. To see this figure in color, go online.

We now consider the effect of active noise, which we model as an exponentially correlated colored noise (33). This describes the force exerted on the biopolymer by the active motors (16)

$$\langle F_{\alpha }\left(s,t\right)F_{\beta }\left(s^{\prime },t^{\prime }\right)\rangle =C\delta \left(s-s^{\prime }\right)\text{exp}\left[-|t-t^{\prime }|/\tau \right]{\delta }_{\alpha \beta },$$ (8)

where τ is the average timescale for the burst of motor activity. The prefactor C is the noise-strength measurement, which involves the strength of the kicks imparted by the motors walking on the polymer and the probability for a single motor to be active (16). By dimensional analysis, it can be seen that C can be expressed as a product of ζ and a factor that has the dimensions of power. It can be interpreted as the rate of consumption of chemical energy by the motor, and is proportional to the square of the amplitude of the active forces C ∝ F_a². We express C = p_onF_a²/b₀, where p_on is the probability for a motor to be active. In terms of modes, we have

$$\langle F_{p\alpha }\left(t\right)F_{q,\beta }\left(t^{\prime }\right)\rangle =LC{\zeta }_p{\zeta }_q/{\left(L\zeta \right)}^2\text{exp}\left[-|t-t^{\prime }|/\tau \right]{\delta }_{\alpha \beta }\left(1+{\delta }_{p,0}\right){\delta }_{pq}.$$ (9)

The active diffusion of the center of mass (COM) is given by (inset of Fig. 1 a)

$$\langle {\left({\overrightarrow{X}}_0\left(t\right)-{\overrightarrow{X}}_0\left(0\right)\right)}^2\rangle =\frac{2C\tau }{L{\zeta }^2}\left(t+\tau \left(\text{exp}\left[-t/\tau -1\right]\right)\right).$$ (10)

For t << τ, by expanding the exponential we get

$$\langle {\left({\overrightarrow{X}}_0\left(t\right)-{\overrightarrow{X}}_0\left(0\right)\right)}^2\rangle =N{\left(\frac{F_a}{N\gamma }\right)}^2{t}^2,$$ (11)

where N = L/b₀ is the number of beads along the chain. The right-hand side of Eq. 11 can be interpreted as the active velocity of the COM, i.e.,

$$v_{a,COM}=\sqrt{N}{F}_a/\left(N\gamma \right).$$

The evaluation of the MSD for an arbitrary segment of the polymer diffusing under active noise is considerably involved (see the Supporting Material). The result is

$$\langle {\left(\overrightarrow{r}\left(s,t\right)-\overrightarrow{r}\left(s,0\right)\right)}^2\rangle =T_{cm}+\frac{4C}{L{\zeta }^2}\sum _{p=1}^{\infty }{\text{cos}}^2\left(p\pi s/L\right)\left(T1-T2\right),$$ (12)

where T_cm is the COM term for active diffusion,

$$T1=\left(1-\text{exp}\left[-k_{p}t/{\zeta }_p\right]\right)/\left(k_p/{\zeta }_p\left(k_p/{\zeta }_p+1/\tau \right)\right)$$ (13)

and

$$T2=\left(\text{exp}\left[-t/\tau \right]-\text{exp}\left[-k_{p}t/{\zeta }_p\right]\right)/\left({\left(k_p/{\zeta }_p\right)}^2-{\left(1/\tau \right)}^2\right).$$ (14)

We use Eqs. 12–14 to evaluate numerically the MSD of the middle bead of the chain and the corresponding exponent α as a function of the time (Fig. 2). From the model, we can identify two different crossover times:

• 1.At times longer than the burst duration τ, the MSD approaches the behavior of random diffusion α → 1.
• 2.The MSD is dominated by thermal fluctuations for very short times.

We can then estimate the crossover timescale above which the active fluctuations begin to dominate, by equating the contributions of the thermal and active components to the MSD of the first mode as

$$t_c\simeq \frac{6k_{\text{B}}T\zeta }{C}\sim \frac{D_{\text{seg}}}{v_a^2},$$ (15)

where D_seg = k_BT/γ is the thermal diffusion coefficient of a polymer segment and v_a = p_onF_a/ζ is the active transverse velocity scale of a single polymer segment. This approximate form is valid in the limit of large damping and τk_p/ζ_p << 1 (see the Supporting Material). The crossover time is indicated by a dashed vertical line in Fig. 2 a, and it agrees quite well with the calculated behavior.

Simulation Results

Simulation method

We carried out extensive simulations to test the predictions of our simple analytical model and to go beyond it. We have simulated the dynamics of a semiflexible polymer in solution, where the polymer is modeled as a chain of connected beads that are subjected to the following interactions: The potential between neighboring beads

$$V_{\text{bonded}}={\left(|{\overrightarrow{r}}_{i+1}-{\overrightarrow{r}}_i|-b_o\right)}^2/2K$$ (16)

accounts for the nearest neighbor or bonded interactions. The spring constant K was set to a very high value to ensure the condition of inextensibility (a standard method employed extensively in the literature (34, 35)). Bond-length fluctuations were monitored during the simulation of the dynamics, and were always found to be a negligible (<1%) fraction of the equilibrium separation b_o at the temperatures and active forces involved. Here

$$V_{\text{self}\text{-}\text{avoidance}}=4ϵ\left({\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^6\right)+ϵ$$ (17)

if the separation distance r between any two beads is <2^1/6σ; which takes care of self-avoidance and prevents distant parts of the chain from crossing each other if they come too close, although such a situation almost never arises in our simulations because of the strictly semiflexible regime (L < L_p) that we explore.

Finally, the bending rigidity between adjacent bonds is implemented through the potential,

$$V_{\text{bonded}}=\frac{1}{2}\kappa {\theta }_j^2,$$ (18)

where θ_j is the angle between the bond vectors j and j + 1. Calculation of the bending forces involves relatively involved calculations that can be found in Allison (34).

The simulation procedure involved a two-step process:

• Step 1: Initialization of polymer conformations, and

• Step 2: Obtaining bead velocities using Monte Carlo methods (and, subsequently, an implementation of the dynamics).

Monte Carlo initialization

The Monte Carlo conformation initialization procedure was carried out as follows:

The first bead was positioned at some arbitrarily fixed origin, and the subsequent beads were placed at a mean separation of b_o from each other, with fluctuations in bond lengths given by the equipartition theorem for the bonded harmonic potential described in Eq. 16; the angles between the subsequent bonds were chosen using the equipartition theorem for the bending potential described in Eq. 18. Because semiflexible polymers of contour length less than the persistence length are anisotropic, the longitudinal direction was set along the x axis without loss of generality. Several tests were performed to test that the equilibrium properties of semiflexible polymers (end-to-end distance for different chain lengths, estimation of the persistence length from the tangent-tangent correlations, etc.) could be obtained with high degree of accuracy from the conformations thus generated. The velocities of the beads were initialized according to the Maxwell-Boltzmann distribution at the chosen temperature. We have neglected hydrodynamic interaction in our simulations; implementation of hydrodynamic interactions would be a natural extension of this work.

Simulation of dynamics

The active forces were generated as a time series of pulses for each of the beads. For the purely thermal simulations, the magnitude of the pulses were set to zero. These active pulses act on the beads along the direction of the local normal to the polymer turning on and off, stochastically. The pulses are treated as an external force while integrating the equations of motion; this is justified because the duration of the on- and off-periods are set as considerably larger than the integration time step, thus minimizing numerical errors. The integration scheme used is a standard procedure for simulating Brownian dynamics and can be found in Ermak and Buckholz (36). The results obtained from simulations were checked for zero active forces in the existing literature, and the agreement was excellent in all the cases, thus establishing the credibility of the simulation procedure beyond doubt. Unless otherwise mentioned, the parameters used in the simulations were set at the following values: ambient temperature T = 1, ambient friction ξ = 100, p_on ∼ 1, b_o = 1, and κ = 375 → L_p = 250.

MSD

In Fig. 1 a, we show the MSD-s with purely thermal fluctuations (COM and middle bead) and with active noise (COM, inset). In the thermal case, the MSD for the COM shows perfect agreement with theoretical result, whereas that of the middle bead shows a small deviation. This deviation is most probably due to nonlinearity of the tension, which our simple analytical model does not incorporate.

The discrepancy in the MSD of the COM for the case of active noise (inset of Fig. 1 a) results from a small overestimation of the mean-square velocity 〈v²_c.o.m.〉 for the active polymer, as shown in Fig. 1 b (as a function of F_a). The simulations give a quadratic dependence on F_a, in agreement with the analytic expression of the COM mean-square velocity (details in the Supporting Material),

$$\langle v_{\text{COM}}^2\rangle =\frac{k_{\text{B}}T}{M}+v_{a,\text{COM}}^2\frac{p_{\text{on}}}{1+m/\left(\gamma \tau \right)},$$ (19)

where v_a,COM = F_a/(Nγ), M = Nm, and m is the mass of a polymer segment. Note that for our choice of parameters (m = 1, γ = 100), the τ-dependent term in Eq. 19 is negligible.

The velocity distribution of a segment is found to be Gaussian (Fig. 1 b, inset), wider than the thermal distribution due to the active forces. Because the activity is distributed along the chain, we have the effect of N >> 1 active centers, thereby resulting in a Gaussian distribution (16).

MSD exponent α

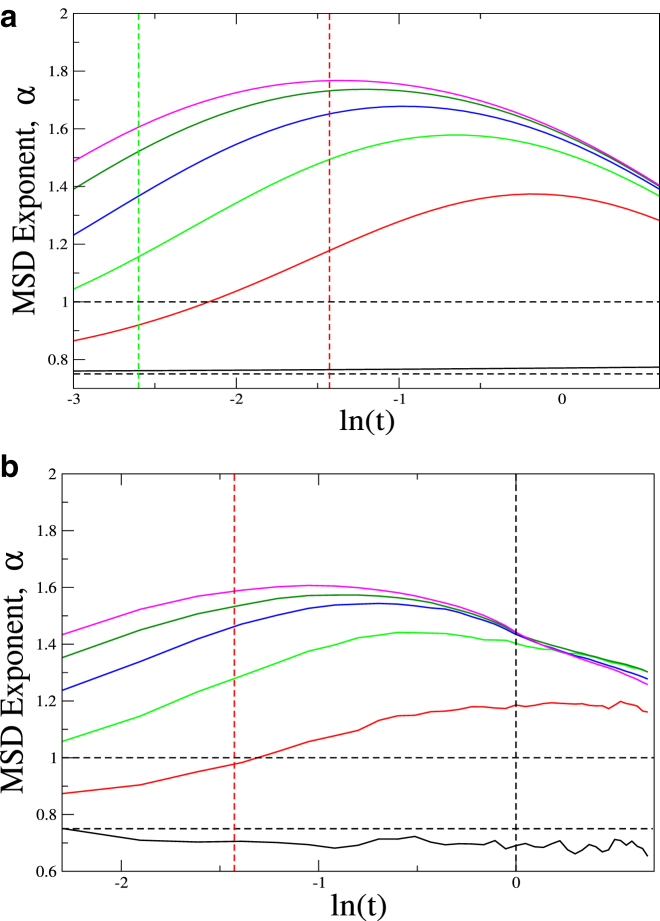
In Fig. 2 b, we show the simulated time evolution of the MSD exponent for the middle bead of the chain (solid lines) and theory (dashed lines). Several distinct regimes can be clearly identified: for very short times, there is a subdiffusive regime, exponent α ∼ 3/4, as is well known for semiflexible polymers (32). At longer times, we find a superdiffusive regime due to active excitation, followed by a gradual evolution to the diffusive regime for very long times. The overall agreement between the simulations and the analytic calculation (Fig. 2, a and b) is very good. For example, we note that the crossover to the superdiffusive regime happens at earlier times (indicated by the position of the activity-induced peak) for higher values of the active forces, as expected from our estimate of the crossover time, derived in Eq. 15. In the simulations, we were limited to smaller values of the active forces to avoid numerical instabilities. The analytical calculation seems to overestimate the exponent systematically; the overall qualitative agreement, however, is good.

Directional correlations

Semiflexible polymers are characterized by a persistence length that is the length along the polymer over which the tangent-tangent correlations decay. In Fig. 3 a, we plot the tangent-tangent correlations obtained from simulations, measured from the middle of the polymer. For purely thermal noise, we find that the simulations agree with the theoretical calculation of an exponential decay

$$C_t=\langle \hat{t}\left(s\right)\cdot \hat{t}\left(s^{\prime }\right)\rangle =\text{exp}\left[-|s-s^{\prime }|/L_p\right],$$ (20)

where L_p = 2κb₀/(3k_BT) is the persistence length of the polymer (37) (see details in the Supporting Material).

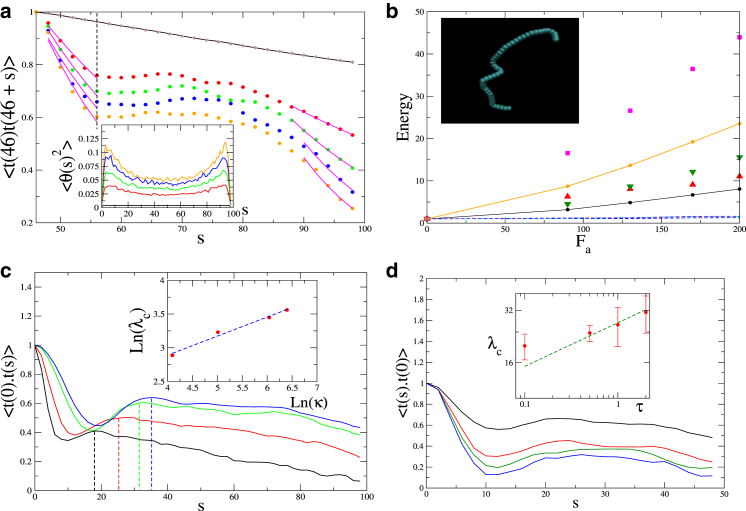
Figure 3.

(a) Decay of tangent-tangent autocorrelation function, measured from the middle of the chain, for different magnitudes of active forces F_a = 0, 90, 130, 170, and 200 (black, red, green, blue, and orange, respectively), chain length L = 100, L_p = 250, and τ = 1. (Brown) Exponential fit, according to Eq. 20, yields excellent agreement for the value of the persistence length (L_p) for the purely thermal case (F_a = 0). (Pink lines) Fit of the decay, for both short- and long ranges, to the same exponential form, for the correlations in the presence of active forces, thereby yielding L_p,eff. (Vertical dashed line) Length-scale of the onset of the plateau in the correlations. (Inset) Ensemble-averaged bending angles for different bonds along the chain. (b) Comparison of the effective temperatures (T_eff) obtained from the exponential fits of the decay of the orientational correlations from the middle bead, as shown in panel a (red, short range; green, long range). Mean bending energy (black) averaged over all the bonds and mean kinetic energy (lower dashed lines) associated with the components of velocities of the middle bead. (Inset) A typical conformation of the chain that provides visual evidence for the results shown in panel a (inset). (Pink symbols) Higher T_eff (and shorter persistence length) when the orientations are measured with respect to the end of the polymer, and compared to the mean bending energy of the first seven beads of the chain (orange line). (c) Orientational correlations calculated for polymer of different bending modulus κ; (inset) length-scale of the resonance increases as λ_c ∝ κ^1/4 (see Eq. 21). (d) As in panel c, we plot for different values of τ = 0.1, 0.5, 1, and 2 (top to bottom), showing (inset) that the length-scale of the resonance (extracted from a spline fit to the maximum of the plateau) increases in rough agreement with the predicted behavior as λ_c ∝ τ^1/4 (see Eq. 21). To see this figure in color, go online.

When the active forces are present, we find that the correlations decay faster (Fig. 3 a), but level off beyond a length-scale denoted by L_c, until the decay resumes at longer lengths. We fit the initial (and final) fast decay by an exponential form (Eq. 20), and find the corresponding effective persistence length L_p,eff from which we extract an effective temperature:

$$k_{\text{B}}{T}_{\text{eff}}=2\kappa b_0/\left(3L_{p,\text{eff}}\right).$$

Because we find that L_p > L_p,eff, we also get that T_eff > T. In Fig. 3 b, we plot the values of T_eff from the simulation, as a function of the active force, and compare to the mean kinetic and bending energy of the polymer segments. Both increase quadratically with F_a, as is expected from the contribution of the active noise to the energy (Eq. 19, and Ben-Isaac et al. (16)). However, there is a huge difference in magnitude between the mean kinetic and bending energies. We therefore conclude that the main contribution to the large T_eff comes from the energy stored in the bending modes of the polymer, excited by the active forces (see example configuration in the inset of Fig. 3 b). This situation is unlike thermal equilibrium where the kinetic and potential energies are equal. The case of purely tangential forces is given in the Supporting Material, and although it is qualitatively similar, it exhibits lower values of T_eff due to the weaker bending (see Fig. S1 in the Supporting Material). Note that the ends of the polymer tend to develop larger bending (inset of Fig. 3 a), as manifested by the shorter persistence lengths (higher T_eff) for the tangent-tangent correlations measured from the end of the polymer (Fig. 3 b, and see Fig. S3).

For nonzero active forces, we find an interesting intermediate region where the correlations decay much more slowly or have a plateau (Fig. 3 a, sometimes even showing a peak in Fig. 3 c), separating the two regions of exponential decay, which are described above by L_p,eff. This seems to imply stabilization of a bending mode (or rather a band of bending modes) in a form of resonance with the timescale of motor activity. We can estimate the length-scale for this resonance, by equating the motor activity timescale with the relaxation time of the bending modes of the chain

$$k_p/{\zeta }_p=1/\tau \Rightarrow {\lambda }_c=L/p=\pi {\left(\kappa b_0\tau /\zeta \right)}^{1/4}.$$ (21)

For the parameters used in Fig. 3 a, we get λ_c/b₀ ∼ 4.4, which is of the order of the length at which we find the onset of the plateau (denoted by the vertical dashed line in Fig. 3 a). Using Eq. 21, we predict a particular dependence of this length-scale on the bending modulus (κ, Fig. 3 c) and the mean burst duration (τ, Fig. 3 d), which we indeed find in the simulations. Note that because the activity excites many modes, the condition of the single mode resonance given by Eq. 21 is an approximation. We find that the regime of L_p ∼ L exhibits a very similar resonance (see Fig. S2).

Discussion and Comparison to Experiments

We now compare the results of our model to experimental observations. The most trivial result, that activity increases the MSD of the chain, is borne out by our model, as is observed in chromatin under different conditions (6, 7, 8, 9, 15, 28), and for cytoskeletal networks of actin-myosin (3). Next, we wish to compare our prediction about the regime of larger-than-thermal MSD exponent α. In chromatin there are indications for activity giving rise to exponents that are superdiffusive i.e., α > 1, in a certain temporal regime (6, 7, 15, 38, 39), as we predict. A similar superdiffusive regime was found in simulations (40) and experiments (41) of active two-dimensional biopolymer gels.

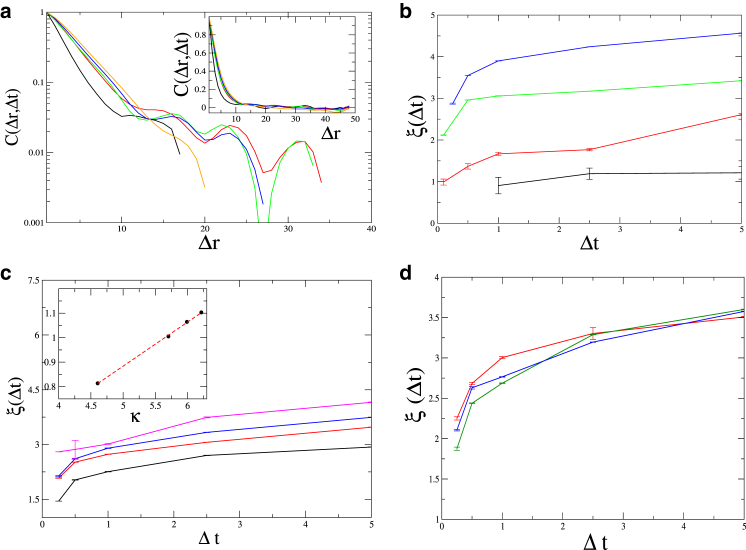
We next compare the shape correlations along the chain, arising from the activity. We find that the activity-driven deformation of the chain leads to a smaller effective persistence length L_p,eff, as was previously found theoretically (17), and experimentally (5). In Zidovska et al. (15), the displacement correlations, denoted by C_d(Δr, Δt), were quantified. We calculated this correlation function in an active chain, as a function of Δr for different values of Δt (Fig. 4 a). As we see, the long bursts of activity induce longer range spatial correlations compared to short pulses and purely thermal fluctuations. The typical length-scale for the decay of correlations is extracted by an exponential fit, in the small Δr regime:

$$C_d\left(\Delta r,\Delta t\right)\sim \text{exp}\left(-\Delta r/\xi \left(\Delta t\right)\right)$$

(Fig. 4 a). We find that ξ increases with the temporal window Δt (Fig. 4 b), and reaches a maximal value at a plateau (or maybe even a small peak), for Δt of order τ.

Figure 4.

(a) Displacement correlation function C(Δr, Δt), for displacements in the (transverse) z direction (F_a = 200, τ = 1, L_p = 250, and L = 50), as function of Δr (in microns), for Δt = 0.1, 0.5, 1, 2.5, and 5 (from bottom to top). Main panel shows the initial roughly exponential decay used to extract the correlation length ξ. (Inset) Correlations in linear scale. (b) Correlation lengths (ξ) as function of Δt, for the active case (τ = 5, 1, and 0.1; blue, green, and red, respectively), and for the purely thermal case (black). (c) The correlation length ξ(Δτ) as a function of Δt, for different values of the bending modulus κ = 100, 300, 400, and 500 (from bottom to top). (Inset) Log-log plot shows that ξ(τ) has a power-law dependence with an exponent 0.25 (dashed line in the exponent), as predicted by Eq. 21 (see Fig. 3c). (d) Plot of ξ(Δτ) for different values of the active force F = 130, 170, and 200 (green, blue, and red, respectively). We find that ξ is largely independent of F_a, as predicted by Eq. 21. To see this figure in color, go online.

This maximal value of the correlation length ξ of the displacement correlations C_d (Fig. 4 b) is found to be very similar to the length-scale of the onset of the plateau we found in the tangent-tangent correlations (C_t, Fig. 3 a). We therefore conclude that these two length-scales have the same order of magnitude and are determined by the same resonance-like condition (Eq. 21), i.e.: max(ξ) ∼ O(λ_c). In Fig. 4, c and d, we demonstrate that this relation between ξ and λ_c is indeed borne out by the dependence of ξ on the bending modulus and its independence of the magnitude of the active force F_a, exactly as λ_c behaves according to Eq. 21.

This leads us to propose that the increased displacement correlations seen in experiments (15) indeed arise from the resonance-like condition of the elastic modes of the chromatin and the timescale of the active forces. Comparing the findings of our model (shown in Fig. 4 b) to the experimental observations (see Fig. 2G in Zidovska et al. (15)), we conclude that the typical timescale for activity in the cell is τ ∼ 5–10 s. Using the relation that we propose between max(ξ) and λ_c, we can use Eq. 21 and the measured values of the relevant parameters to check for overall consistency. The effective bending modulus of chromatin is κb₀ ≃ 10⁻²² − 10⁻²³ Nm² (42), the effective viscosity of chromatin is ζ ∼ 10⁵ζ_water ∼ 10² Pa-s (43), and our estimate of τ is ∼10 s. Using these values in Eq. 21, we get λ_c ∼ O(1)μm, which is of the order of max(ξ) found in the experiments (15).

We can use Eq. 21 to analyze the observed reduction in the correlation length when the cells were treated with drugs targeting various nuclear enzymes that affect chromatin stability (15). It was proposed that the reduced displacement correlations under these conditions are somehow related to the reduced condensation of the chromatin in the presence of these drugs. This would correspond to a lower elastic modulus of the chromatin, which in our single-chain model is represented by lowering the bending modulus κ in Eq. 21, resulting in a lower value of λ_c, and therefore max(ξ). In addition, from Eq. 21 we predict that shorter active bursts will also result in reduced displacement correlations. The relative roles of activity and elasticity, which together determine the correlation length, need to be farther explored systematically in future experiments. It is important to note that the activity, which we have considered, is described by simple kicking of the polymer, while in the chromatin more complex remodeling can occur, involving bending, stretching, and twisting (44).

A similar resonance-like peak was reported for the displacement correlations of a fluorescent microtubule embedded in a network of actin-myosin (3). In Fig. 2 of Brangwynne et al. (3), a peak is found for this correlation function (in q-space) in the presence of myosin-II motors, corresponding to a distance of ∼2–3 μm. We can use the measured values of the parameters in this system (3) to check whether this length corresponds to our λ_c of Eq. 21: ζ ∼ 1 Pa-s, L_p = 2κb₀/³k_BT ∼ 10⁻³ m, which gives λ_c ∼ 2 μm if τ ∼ 5 s. The observed durations of the myosin-induced force fluctuations were measured to be of order of a few seconds (see Fig. 4c of Brangwynne et al. (3)), in agreement with our calculation based on the concept of resonance between the active timescale and the relaxation time of the bending model (Eq. 21).

Conclusions

In this study, we have analyzed the dynamics of an active semiflexible chain embedded in a viscous medium, using a minimal model for the active shot-noise (16, 17), and found the following main features:

• 1.The MSD exponents of the motion of individual segments display a marked maximum at an intermediate temporal regime (which corresponds to the transition from a thermal- to an activity-dominated, i.e., ballistic behavior) and then return to thermal-like behavior at times longer than the intrinsic timescale of motor activity.
• 2.We observe that the alignment of the polymer decays over shorter length-scales when there is activity (in addition to the thermal noise, which is always present), and the decay is dominated by activity-driven bending modes.
• 3.In addition to the decay, however, we also observe a resonance-like effect, due to matching between the timescale of motor activity and the relaxation time of the bending modes of the polymer. We find that the critical component distinguishing the active noise from the thermal, is the finite timescale, i.e., the temporal correlations.

The experimental observations on chromatin motion in living cells (6, 7, 8, 9, 10, 15, 28) show similarities with the behavior we find in our simple model, specifically the observed activity-driven coherence of the displacements (15). Despite the obvious simplicity of the model and the fact that it does not take into account the full complexity of the cytoskeletal network or chromatin packing, our work demonstrates that the interplay between activity and elasticity (related to bending and stretching in our single polymer case) is enough to qualitatively explain some puzzling experimental observations, and therefore may be a basic underlying property of such systems. Our relatively simple model allows for more complex additional components to be added, and can be used to motivate future experiments.

Editor: Levi Gheber.