Conditional Asymmetric Linkage Disequilibrium (ALD): Extending the Biallelic r² Measure

Abstract

For multiallelic loci, standard measures of linkage disequilibrium provide an incomplete description of the correlation of variation at two loci, especially when there are different numbers of alleles at the two loci. We have developed a complementary pair of conditional asymmetric linkage disequilibrium (ALD) measures. Since these measures do not assume symmetry, they more accurately describe the correlation between two loci and can identify heterogeneity in genetic variation not captured by other symmetric measures. For biallelic loci the ALD are symmetric and equivalent to the correlation coefficient r. The ALD measures are particularly relevant for disease-association studies to identify cases in which an analysis can be stratified by one of more loci. A stratified analysis can aid in detecting primary disease-predisposing genes and additional disease genes in a genetic region. The ALD measures are also informative for detecting selection acting independently on loci in high linkage disequilibrium or on specific amino acids within genes. For SNP data, the ALD statistics provide a measure of linkage disequilibrium on the same scale for comparisons among SNPs, among SNPs and more polymorphic loci, among haplotype blocks of SNPs, and for fine mapping of disease genes. The ALD measures, combined with haplotype-specific homozygosity, will be increasingly useful as next-generation sequencing methods identify additional allelic variation throughout the genome.

THE definition of the linkage disequilibrium (LD) parameter D_ij of nonrandom association between a pair of alleles A_i and B_j at two loci (A and B) is straightforward and unequivocal. It is the difference between the observed (or estimated) haplotype (chromosomal or gametic) frequency (f_ij) and that expected under random association of the two allele frequencies $(p_{A_i}\mathrm{and}{p}_{B_j}):D_{ij}=f_{ij}-p_{A_i}{p}_{B_j}$. While this is the base of all other measures of LD, defining the strength of any observed nonrandom association is complicated by the fact that the maximum value D_ij can take is a function of the observed allele frequencies. A number of normalized measures to reflect the strength of LD have been proposed; both for bi- and multiallelic data (Hedrick 1987; Lewontin 1988). However, since these are all a single summary of multidimensional data, no proposed measure of the strength of LD can be perfect; although each may have strengths and weaknesses with respect to the question being addressed.

The two most common measures of the strength of LD are: (1) the normalized measure of the individual LD values (Lewontin 1964), D_ij′ = D_ij/D_max (see Supporting Information, File S1 for details) and (2) the correlation coefficient r for biallelic data, which is most often reported as r² = D_ij² / (p_A1 p_A2 p_B1 p_B2). Hedrick (1987) extended the D′ measure for multiallelic data as a weighted average over all alleles at each locus of the individual normalized LD values: D′ = Σ_i Σ_j p_{${}_{A_i}$} p_{${}_{B_j}$}|D_ij′| . The multiallelic extension of the r² measure is

$$W_n^{\mathit{2}}=\left[{\displaystyle {\sum }_i{\displaystyle {\sum }_j{D}_{ij}^{\mathit{2}}}}/\left(p_{{}_{A_i}}{p}_{B_j}\right)\right]/\min \left(k_A-1,\hspace{0.5em}{k}_B-1\right),$$

where k_A and k_B indicate the number of alleles at each locus. It is also known as Cramer’s V statistic (Cramer 1946), defined on the contingency table relating two categorical variables and is a reexpression of the χ² statistic, normalized to be between zero and one (Hill 1975; Hedrick 1987; Single et al. 2007, 2011). With N individuals (2N alleles/haplotypes), (2N)(W_n²)min(k_A − 1, k_B − 1) has a χ² distribution with (k_A – 1)(k_B − 1) degrees of freedom and can be used to test for significant LD between two loci.

For biallelic data, D′ = 1 whenever one or more of the four possible haplotypes are not observed, irrespective of the expected frequencies. In contrast, r directly measures the correlation coefficient of the biallelic variation at two loci. Specifically, r = 1 only when the allelic variations at the two loci show 100% correlation, i.e., when both loci have equal allele frequencies and only two complementary haplotypes are observed. This correlation property is of interest to many research questions. For example, if two loci show associations with a disease but r is close or equal to one (i.e., nearly complete allelic association), then there is little or no variation that can be assessed by a stratified analysis for risk heterogeneity between two potentially disease-predisposing genetic variants.

Due to these inherent differences between the properties of the D′ measure and the correlation measure r, we focus on the correlation measure and its multiallelic extension W_n. We developed the pair of conditional asymmetric LD (ALD) measures, W_A/B and W_B/A, to complement the W_n measure especially when there are different numbers of alleles at the two loci. This leads to cases where W_n is equal or close to one while one of the two ALD measures is substantially less than one.

Other conditional LD measures have been proposed (Nei and Li 1980; Chakravarti et al. 1984; Hudson 1985; Guo 1997). Nei and Li (1980) developed a statistic that quantifies the association between alleles at a marker locus and a disease locus for studies where individuals are not randomly sampled from a single population, but sampling intensity varies within (disease) categories (Kaplan and Weir 1992; Maiste and Weir 1992). See File S1 for additional detail. In contrast to the above, the ALD measures introduced below are defined for a randomly ascertained sample from a demographically defined population or control group.

When there are different numbers of alleles at the two loci, the direct correlation property discussed above for the r measure is not retained by its multiallelic extension W_n. Consider example 1 with two and three alleles at the first and second loci, with f₁₁ = 0.3, f₂₂ = 0.5, f₂₃ = 0.2 for A₁B₁, A₂B₂, and A₂B₃ haplotypes. W_n = 1; however, there is variation at the B locus on haplotypes containing the A₂ allele. Thus, there is not 100% correlation, and there never can be with differing numbers of alleles at the two loci. In this example the two ALD measures (defined below) reflect that while there is no variation of A locus alleles on any of the haplotypes conditioned on the B locus alleles (W_A/B = 1), there is variation in the B₂ and B₃ alleles on haplotypes carrying A₂ (W_B/A = 0.73). The ALD measures directly indicate that with appropriate sample size, stratification analyses could be carried out for certain comparisons. In contrast, a naive interpretation of the fact that W_n = 1 could result in passing over these data for conditional or stratified haplotype analyses of risk heterogeneity (Thomson et al. 2008).

The definition of the ALD measures begins with the homozygosity (F) and heterozygosity (H) values expected under Hardy–Weinberg proportions (HWP) at a single locus (see Table 1). While there are other measures of association and LD that are based on allelic diversity statistics (see File S1 for details), these measures are all symmetric (Ohta 1980; Maruyama 1982; Hedrick and Thomson 1986; Hedrick 1987). The composite LD measure of Wu et al. (2008) is designed to test interaction between two unlinked loci.

Table 1. Linkage disequilibrium and genetic diversity measures.

Description	Definition of measuresa
1. Single locus homozygosity (F) and heterozygosity (H)b	FA = ∑i pAi2, HA = 1 − FA
2. Haplotype-specific homozygosity (HSF)c	FA/Bj = ∑i (fij / pBj)2, FB/Ai = ∑j (fij / pAi)2
3. Overall weighted HSF values FA/B and FB/A	FA/B = ∑j (FA/Bj) (pBj), FB/A = ∑i (FB/Ai) (pAi)
4. Multiallelic ALD squared (overall asymmetric LD squared)	WA/B2 = (FA/B−FA) / (1−FA) = [∑i ∑j (Dij2 / pBj)] / (1−FA) WB/A2 = (FB/A−FB) / (1−FB) = [∑i ∑j (Dij2 / pAi)] / (1−FB)

^aIn all cases, ∑_i indicates summation over all i = 1, 2, …, k_A, and similarly ∑_j over all j = 1, 2, …, k_B, where k_A and k_B are the number of alleles at the A and B loci, respectively, with ∑_i p_Ai = 1, and ∑_j p_Bj = 1. ∑_i ∑_j D_ij = 0, ∑_i D_ij = 0, ∑_j D_ij = 0, ∑_i ∑_j f_ij = 1, ∑_j f_ij = p_Ai, ∑_i f_ij = p_Bj. For biallelic data: D₁₁ = −D₁₂ = −D₂₁ = D₂₂ = D. Alternate expressions are given in the Appendix along with biallelic results.

^bThe values of F_A and H_A (F_A + H_A = 1) are those expected under Hardy–Weinberg proportions.

^cThe HSF_A/Bj values are the extension of the single-locus F_A values but now restricted to haplotypes containing the allele B_j (similarly for HSF_B/Ai). Haplotype-specific heterozygosity values are HSH_A/Bj = 1–HSF_A/Bj, and HSH_B/Ai = 1–HSF_B/Ai.

The conditional two-locus extensions of F and H, called haplotype-specific homozygosity (HSF) and haplotype-specific heterozygosity (HSH), measure the level of genetic variation at locus A on haplotypes with a specific allele on the B locus (and vice versa), i.e., F_A/Bj, and F_B/Ai (see Table 1). We developed the HSF and HSH measures (Malkki et al. 2005) to ascertain informative microsatellites (MSATs) in HLA transplantation and disease studies. The complementary pair of conditional ALD measures are defined by normalizing an extension of the HSF measure across all haplotypes.

Materials and Methods

Definition of the asymmetric LD measures

There are two conditional ALD measures, depending on which locus is conditioned upon. For simplicity, we often describe the measure in detail conditioning on the B locus. The derivation of the complementary measure, conditioning on the A locus, is given by swapping the roles of loci A and B.

The individual HSF values (Table 1) are combined as a weighted average over all alleles at the conditioned locus to obtain the two overall haplotype specific homozygosity measures: F_A/B and F_B/A (Table 1 and see Appendix for alternate expressions). The maximum value F_A/B can take is 1.0, when each A allele occurs with only one B allele.

W_A/B² (the square of the ALD measure) is obtained by normalizing the overall weighted HSF value based on the range of possible values that it can achieve (Table 1):

$$W_{A/B}^2=\left(F_{A/B}-F_A\right)/\left(1-F_A\right)=\left[{\displaystyle {\sum }_i{\displaystyle {\sum }_j\left(D_{ij}^2/p_{Bj}\right)}}\right]/\left(1-F_A\right).$$

For biallelic data at both loci $W_{A/B}{}^2\hspace{0.17em}=\hspace{0.17em}{W}_B{{}_{/}}_A{}^2\hspace{0.17em}=\hspace{0.17em}{D}^2/(p_{A_1}{p}_{A_2}{p}_{B_1}{p}_{B_2})\hspace{0.17em}=\hspace{0.17em}{r}^2$ (see Appendix).

Once we deviate from having two alleles at both loci, the two ALD measures are only equal in certain specific cases (see below). For biallelic data the correlation coefficient is given by r; for multiallelic data W_n and the ALD measures, W_A/B and W_B/A, give the appropriate correlation coefficients.

Other factors being equal, the ALD increases with stronger LD between the two loci. The ALD values are also influenced by the number of alleles at each locus. Specifically, for multiallelic loci with unequal numbers of alleles, e.g., k_A < k_B (with k_A ≥ 2), in the extreme case each B_j allele will occur with only one A_i allele and W_A/B = 1 (indicating no variation at the A locus on any haplotype containing a specific B_j allele) and also W_n = 1 (mirroring this effect). However, W_B/A < 1 reflects the required variation, given the inequality of allele numbers, at the B locus on some or all haplotypes containing a specific A_i allele (see special case e, below).

Special cases

1. Biallelic loci with two haplotypes of the four possible, e.g., A₁B₁ and A₂B₂, (hence $p_{A_1}\hspace{0.17em}=\hspace{0.17em}{p}_{B_1}\text{and}{p}_{A_2}\hspace{0.17em}=\hspace{0.17em}{p}_{B_2}$). LD is maximal with D = $p_{A_1}{p}_{B_1}$, and there is symmetry in all measures: D′ = 1 and r = W_n = W_A/B = W_B/A = 1.

2. Biallelic loci with three haplotypes of the four possible, e.g., A₁B₁, A₁B₂, and A₂B₂. With the following allele frequencies $p_{A_2}\hspace{0.17em}=\hspace{0.17em}{p}_{B_2},p_{A_1}\hspace{0.17em}<\hspace{0.17em}{p}_{B_1},\text{and}{p}_{A_1}\hspace{0.17em}<\hspace{0.17em}{p}_{B_2}$, LD is maximal (D = $p_{A_2}{p}_{B_1}$): D′ = 1, but r (= W_n = W_A/B = W_B/A) < 1. This reflects that the allele frequencies at the two loci are not 100% correlated.

3. Multiallelic loci with equal number of alleles (i.e., k_A = k_B = k) and only symmetric haplotypes (i.e., f_ii > 0, for all i = 1, 2, …, k, and f_ij = 0 otherwise). As above for the biallelic case a, there is complete symmetry and 100% correlation of allele frequencies at the two loci: D′ = 1, and W_n = W_A/B = W_B/A = 1. An example with three alleles at both loci is f₁₁ = 0.5, f₂₂ = 0.3, f₃₃ = 0.2, with all other f_ij = 0. There is no variation of A locus alleles on any of the haplotypes conditioned on the B locus alleles, and vice versa.

4. The same as c above, except that one or more of f_ij > 0 for i ≠ j: W_n < 1, W_A/B <1, W_B/A < 1.

5. Multiallelic loci with unequal number of alleles (e.g., k_A < k_B), with each B_j allele occurring with only one A_i allele (see example 1 in the Introduction). While W_n = W_A/B = 1, W_B/A < 1.

6. One locus biallelic and the other multiallelic (e.g., k_A = 2, k_B > 2): W_n = W_A/B ≠ W_B/A. In a variety of cases examined, W_B/A < W_A/B, but we have no proof that this is always the case.

See File S1 for proofs of special cases c–f.

Results

HLA classical loci

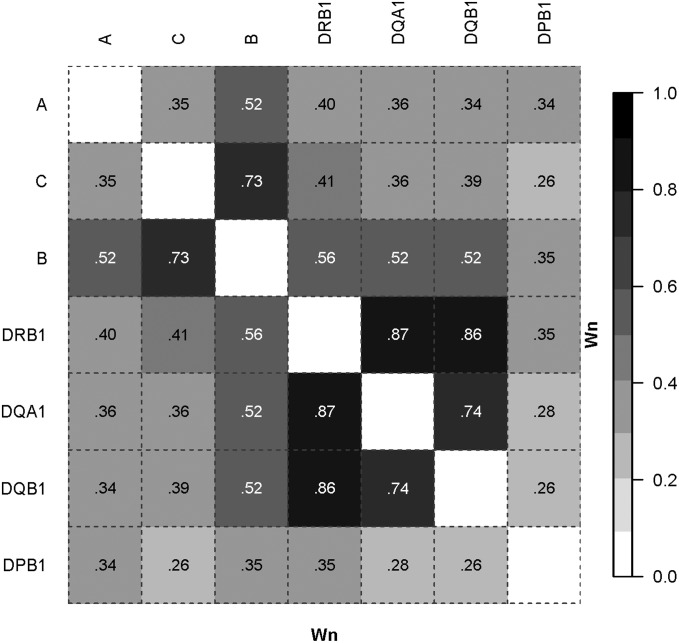
We applied the ALD measures to data for the polymorphic HLA classical genes (Wilson 2010): class I (A, C, and B) and class II (DRB1, DQA1, DQB1, and DPB1). Figure 1 and Figure 2 respectively show the standard overall LD measure W_n and the ALD measures W_A/B and W_B/A. The W_n measure assumes/forces symmetry (as does the overall D′ measure, not shown) even though with more than two alleles per locus, differing numbers of alleles at each locus, and different levels of LD between loci this is not the case.

Figure 1.

W_n Measure for classical HLA genes. LD plot based on the W_n measure (the multiallelic extension of the r correlation measure). Data source: ImmPort Study#SDY26 with N = 300 controls typed for HLA (Wilson 2010). The number of alleles (k) are as follows (given in parentheses after each locus): A (33), C (29), B (61), DRB1 (40), DQA1 (9), DQB1 (14), DPB1 (24).

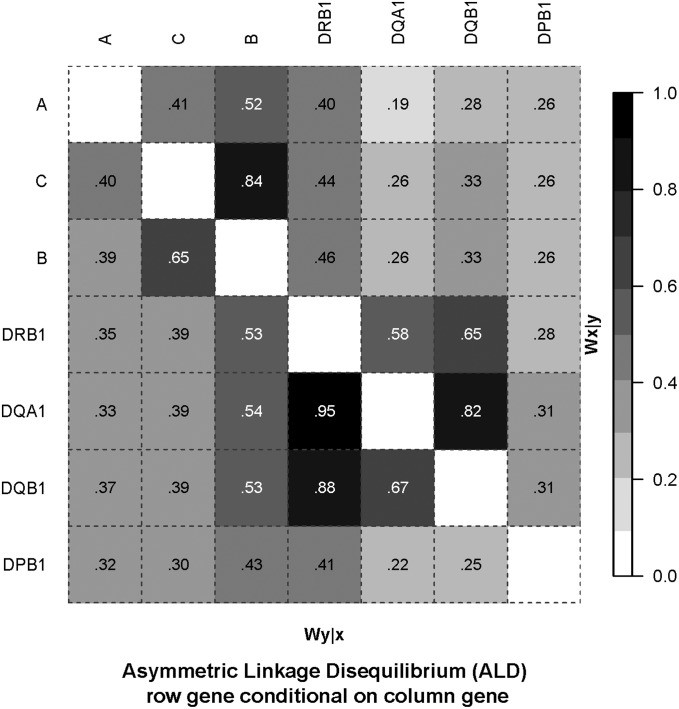
Figure 2.

ALD measures for classical HLA genes. LD plot based on the ALD measures. Our usual generic notation for the ALD measures of W_A/B and W_B/A is replaced by W_x/y and W_y/x to avoid confusion with the HLA-A and -B loci used in this example. Data source as for Figure 1.

The ALD values show considerable heterogeneity. For example (with numbers of alleles for each locus given in parentheses), the ALD for DRB1(40) conditioning on DQA1(9) is 0.58 = W_DRB1/DQA1; i.e., the overall variation for DRB1 is relatively high given specific DQA1 alleles. In contrast, the ALD for DQA1 conditioning on DRB1 is 0.95 = W_DQA1/DRB1; i.e., the overall variation for DQA1 is relatively low given specific DRB1 alleles. This reflects both the smaller number of alleles at DQA1 compared to DRB1 and the high LD between the two loci (most DRB1 alleles occur with only one DQA1 allele, but not vice versa). Similarly with the B(61) and C(29) loci, W_B/C = 0.65, and W_C/B = 0.84. In both these examples the standard (symmetric) overall pairwise LD values are intermediate to the ALD values: W_n = 0.87 and 0.73 for the DRB1:DQA1 and C:B locus pairs, respectively. In almost all comparisons, if the number of alleles k_X > k_Y then W_X/Y < W_Y/X. An exception is with the A(33) and C(29) loci, i.e., k_A > k_C, but W_A/C (0.41) > W_C/A (0.40).

SNP and HLA data

HLA and SNP data from de Bakker et al. (2006) characterized patterns of LD among highly polymorphic HLA genes and a large number of SNP sites. The extensive LD across the extended HLA region (∼8 Mb) makes the identification of additional non-HLA genomic effects on disease difficult to assess. The SNP sites used here were selected on the basis of their ability to identify or tag specific alleles at each of the HLA classical loci (i.e., tag-SNPs for HLA alleles). We chose this example, with a subset of the HLA and SNP data in the class II region, to highlight the properties of the ALD measures and what distinguishes them from the symmetric r and W_n measures.

Figure 3 and Figure 4 show plots of the W_n and ALD measures for 90 unrelated individuals with European ancestry from the Centre d’Etude du Polymorphisme Humain (CEPH) collection (CEU) obtained from the Tagger/MHC webpage. The ALD measures (Figure 4) provide a visualization of the tag-SNP properties that is not captured by the symmetric W_n measure. Looking down the column for any one of the HLA loci (i.e., conditioning on an HLA locus), one can see the particular SNPs that tag specific HLA alleles. These show up as a dark column in the figure. However, conditioning on any given SNP does not show this pattern of high LD. In contrast with the figure for W_n, there are no dark rows of high LD for the ALD measures, indicating that the ALD measures capture the different degree of overall association for each individual SNP.

Figure 3.

The W_n measure applied to SNP and HLA–DRB1, DQA1, and DQB1 data. LD plot based on the W_n measure. The data are for 90 unrelated individuals from de Bakker et al. (2006) with European ancestry from the CEU obtained from the Tagger/MHC webpage.

Figure 4.

The ALD measures applied to SNP and HLA–DRB1, DQA1 ,and DQB1 data. LD plot based on the ALD measures. Data source as for Figure 3.

Note that the information displayed in Figure 3 and Figure 4 captures different aspects of LD from the results reported in the de Bakker et al. (2006) article, as we present overall LD between each pair of loci. The r² values reported in their article represent the squared correlation between a given SNP and presence/absence of each particular HLA allele (e.g., A*0101 vs. other). The tag-SNPs were chosen such that this r² value is 1.0 (or nearly so) for a specific HLA allele, not for the overall locus. The values in Figure 3 and Figure 4 represent overall LD combining over all alleles at both loci.

For example, the SNP rs4988889 is listed as a tag-SNP in the CEU population for the HLA-DQB1*02:01 allele in Table S3 of de Bakker et al. (2006), with an r² (symmetric) value of 0.958. It does not show up as a tag-SNP for any other HLA allele in their Table S3. In Table 2 below, one can see that the values for W_HLA|SNP and W_SNP|HLA are quite different (0.4083 vs. 0.9788). The rs7743506 SNP is listed in de Bakker et al. (2006) as a tag-SNP for three class II alleles, each with an r² value of 1.0: HLA-DQA1*04:01, HLA-DQB1*04:02, and HLA-DRB1*08:01. Thus, allele 2 for this SNP is completely correlated with the presence of each of these three class II HLA alleles. This 100% correlation is captured by the ALD measure (W_SNP|HLA = 1.0), while the low values for W_HLA|SNP for each of the three class II loci indicates that there is a large amount of variability remaining at the HLA loci after conditioning on this SNP. Note that for the examples in Table 2, W_SNP|HLA is equal to W_n. This is an example of special case f above.

Table 2. Overall LD measures applied to data from de Bakker et al. (2006).

WHLA|SNP	WSNP|HLA	D’	Wn	Locus 1a	Locus 2
0.2611	0.8214	0.9150	0.8214	DRB1	rs4988889
0.2824	0.6256	0.8255	0.6256	DQA1	rs4988889
0.4083	0.9788	1.0000	0.9788	DQB1	rs4988889
0.1980	1.0000	1.0000	1.0000	DRB1	rs7743506
0.2164	1.0000	1.0000	1.0000	DQA1	rs7743506
0.2056	1.0000	1.0000	1.0000	DQB1	rs7743506

^aThe loci listed under locus 1 are the three classical class II loci HLA–DRB1, –DQA1, and –DQB1

HLA disease association data

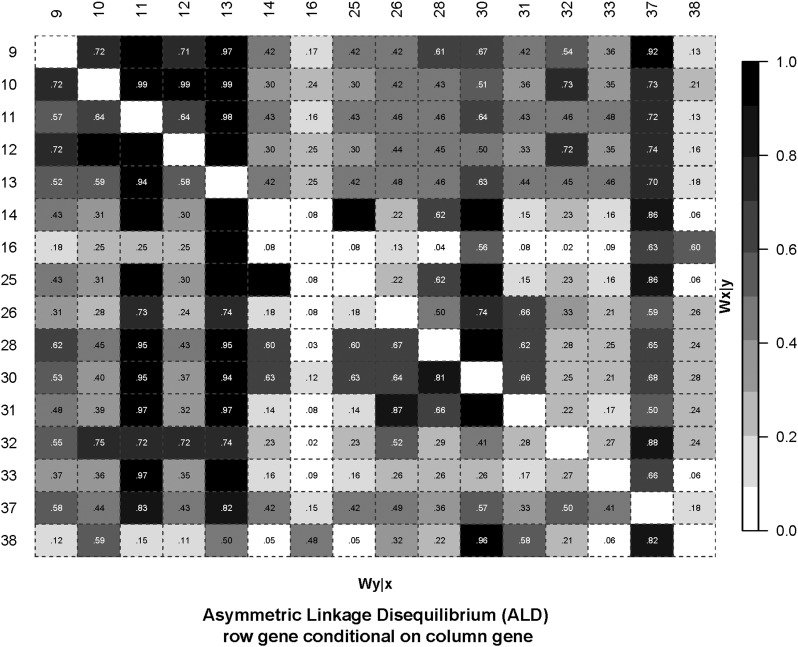
The HLA class II DRB1 gene is strongly associated with juvenile idiopathic arthritis (oligoarticular-persistent) (JIA-OP), with a hierarchy of predisposing through intermediate (“neutral”) to protective effects (Hollenbach et al. 2010; Thomson et al. 2010). Amino-acid position 13 (AA13) of DRB1 shows the strongest single AA association with JIA-OP. This association is also stronger than other potentially biologically relevant combinations of AAs defined under sequence feature variant-type (SFVT) analysis (Karp et al. 2010; Thomson et al. 2010). AA13 is also identified as potentially causative in disease using an extension of Salamon’s unique combinations algorithm (Salamon et al. 1996; Thomson et al. 2010). The overall AA LD (W_n) patterns are quite complex for each of the classical HLA loci, with DRB1 control data for JIA-OP shown in Figure 5. AA13 shows high LD via the W_n measure with quite a few other AAs (note only AAs 9–38 within exon 2 are shown). However, ALD analyses show additional variation that can be tested via conditional analyses (Figure 6).

Figure 5.

The W_n measure applied to HLA-DRB1 AMINO Acids 9-38. LD plot based on the W_n measure. Black colored cells have a numeric value of 1. The data are for the control sample in a study of JIA.(Hollenbach et al. 2010; Thomson et al. 2010) For clarity, only amino acids 9-38 are shown.

Figure 6.

The ALD measures applied to HLA-DRB1 AMINO Acids 9-38. LD plot based on the ALD measures. The data are as for Figure 5.

For illustration, we consider the block of high LD AAs 11(6), 12(2), and 13(6) (the number of “alleles,” or different AA residues segregating, at each AA site are given in parentheses). AA 10(2) and AA 12 are 100% correlated apart from a very rare allele, and hence AA 10 is not considered here. The ALD values indicate which pairs of AAs may allow for stratification and conditional analyses. For example (see Figure 5 and Figure 6), with AAs 11 and 12, W_n = 1, and while W_12/11 = 1, W_11/12 = 0.64, and hence some stratification analyses can be carried out (this is also an illustration of special case f above). Table 3 shows the results of specific tests of risk heterogeneity: variation at AA 13 is significantly associated with disease on haplotypes with AA 11 and AA 12. In contrast, AA 11 does not show heterogeneity on haplotypes with AA 13. This does not exclude a role for AA 11, nor AA 12, in disease predisposition, but the conditional analyses do show a potential role for AA 13 in being directly involved in disease risk.

Table 3.

Conditional Analyses of JIA-OP Data for HLA DRB1 Amino Acids 11-13^a

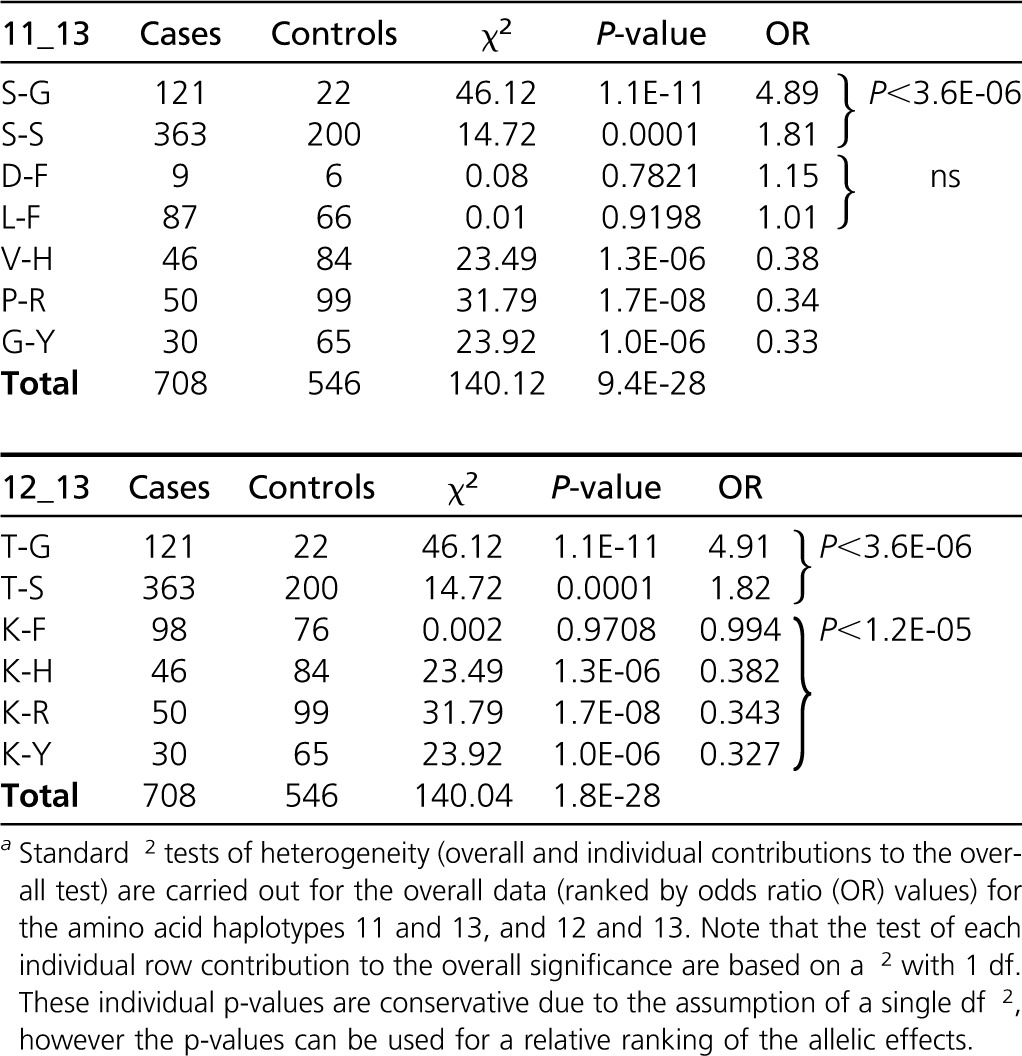
Selection on HLA–DRB1 amino acids

A role for balancing selection maintaining much of the extensive variation at the HLA classical loci is well established (Meyer and Thomson 2001; Meyer et al. 2006). In particular, application of the Ewens–Watterson (EW) neutrality test of allele-frequency distributions at the classical HLA loci has revealed the action of balancing selection in maintaining diversity at the HLA-A, -C, -B, DRB1, DQA1, and DQB1 loci (Salamon et al. 1999; Lancaster 2006; Solberg et al. 2008). Allele frequency distributions at these loci are generally more even than expected under neutral conditions. The distributions of DPB1 alleles do not show evidence of balancing selection (Salamon et al. 1999; Begovich et al. 2001; Lancaster 2006; Tsai and Thomson 2007; Solberg et al. 2008). However, extension of the EW test to the AA level has shown evidence for balancing selection acting on some AAs for all the classical HLA loci, including DPB1 (Salamon et al. 1999; Valdes et al. 1999; Lancaster 2006).

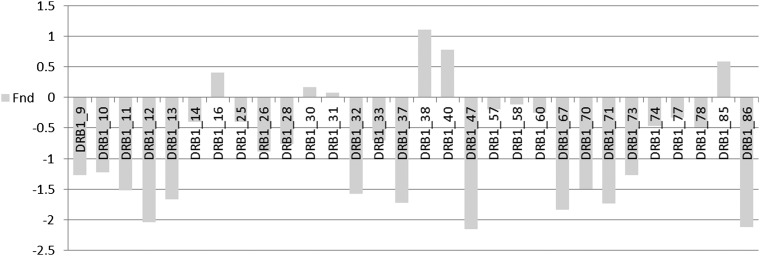
At both the allele and AA levels, the statistic used for the above analyses is the mean across populations of the normalized deviate F_nd of the homozygosity statistic F (Salamon et al. 1999). Balancing selection results in significantly negative F_nd values compared to neutral expectations, whereas directional selection, along with certain demographic events, leads to significant positive values. An observation of interest from previous studies is that pairs of AAs that show high LD may nonetheless show quite different F_nd values (Salamon et al. 1999; Lancaster 2006). To illustrate this point in the context of ALD measures applied to the JIA-OP DRB1 control data, consider AA positions 37 and 38, which have a moderately high W_n value of 0.71 (Figure 5). However, the ALD values are quite disparate (W_37/38 = 0.18 and W_38/37 = 0.82) (Figure 6), and explain how the observed F_nd values can show different evolutionary histories with significant evidence for balancing selection for AA 37 and possible directional selection for AA 38 (Figure 7). This pattern is not unique to this particular population. Similar patterns of this differential selection can be seen in meta-analyses across several populations (see Figure S1 for F_nd values across 57 populations for DRB1 data (Lancaster 2006)). For these data, P-values for deviation from neutral expectations in the direction of balancing selection are 2.5E−24 and 0.11 for AAs 37 and 38, respectively (Lancaster 2006).

Figure 7.

Selection at DRB1 AA sites measured by F_nd values. The F_nd measure of selection for polymorphic amino acid sites in HLA–DRB1 exon 2. The data are as for Figure 5 and Figure 6.

Discussion

From analyses of allele and haplotype data in disease-association studies, HLA researchers have long recognized that high pairwise LD (W_n) between two loci has limited our ability in some cases to distinguish the primary disease gene or genes. It is also well known that there are instances, particularly with differing numbers of alleles at two loci, where the W_n value does not accurately reflect our ability to perform stratified or conditional analyses to identify disease-risk heterogeneity. With multiallelic data, the ALD measures presented here are more appropriate and informative than the W_n measure. For example, with type 1 diabetes (T1D), DRB1–DQB1 haplotypes carrying the DRB1*04:01 allele can be subdivided by the DQB1*03:02 (predisposing) and *03:01 (protective) alleles. This approach, termed for HLA studies “within serogroup comparisons” (based on a specific variant in the first field, or serotype, of the DQB1 allele name, and comparing AA variation related to disease risk in the second field) focuses on a smaller number of AAs to compare. In this case the analysis of DRB1–DQB1 haplotypes is stratified on DQB1 based on the presence of DRB1*04:01. This led to identification of AA 57 of DQB1 in T1D risk. In fact, for T1D both DRB1 and DQB1 are directly involved in disease risk, with confirmation coming from cross-ethnic studies (Thomson et al. 2007, 2008, 2011; Erlich et al. 2008).

Another example of stratification on a particular site aiding in the identification of additional effects comes from a SNP in the PTPN22 gene. In a study of rheumatoid arthritis, Begovich et al. (2004) demonstrated an association with the minor allele of the R620W missense SNP (rs2476601) in PTPN22. In a follow-up study, similar to the above HLA study on T1D, Carlton et al. (2005) used AA analyses of closely related haplotypes of SNPs to show a direct role of R620W in risk heterogeneity. With stratification of the data by R620W, the role in disease risk of at least one additional SNP in PTPN22 was identified.

The ALD measures were initially developed to aid two separate lines of research for AA variation at classical HLA genes: to determine the actual disease-predisposing AAs in disease-association studies and to identify which AA sites are independently subject to selection in population studies. The major problem encountered in both research areas is the high level and complex patterns of LD between many AA sites, combined with more than two (and up to six) distinct AAs (“alleles”), seen at many sites. When evidence of strong balancing selection is seen at a number of AA sites (Salamon et al. 1999; Valdes et al. 1999; Lancaster 2006), how does one determine which AA sites could potentially show independent evolution vs. correlation due to high LD? Similarly with disease-association studies of individual AAs and biologically relevant sequence features (SFs) and their variant types (VTs) (Karp et al. 2010; Thomson et al. 2010), how can one distinguish between potentially causal effects vs. those due to LD? These AA-level analyses showed that there are cases with different numbers of “alleles” (AAs or SFVTs) at two loci where W_n = 1; nonetheless a stratified analysis could be applied to potentially distinguish disease predisposing variants. Also in population studies there are cases of two AA sites with W_n ≈ 1, which show variation that appears to be under different selection pressures (Salamon et al. 1999; Lancaster 2006). The ALD measures can help provide additional insight in these situations.

The ALD measures are applicable to the study of any genetic variation, and the fact that they are measured on the same scale as the well-documented correlation measure r enhances their comparability and interpretation. They will be increasingly useful as next-generation sequencing methods identify more allelic variation, including nonbiallelic SNPs, insertion/deletion polymorphisms, and copy-number variants. Currently, these nonbiallelic SNP sites are often excluded from analyses. Linkage disequilibrium analyses among SNPs and among polymorphic genes are typically handled separately and polymorphic genes are often recoded as a set of dichotomous indicator variables (presence/absence of each allele) to simplify analyses at the expense of interpretation. The ALD statistics provide a measure of linkage disequilibrium that is on the same scale for comparisons among SNPs, among SNPs and more polymorphic loci, among haplotype blocks of SNPs, and for fine mapping of disease genes. The ALD measures are especially useful when there is asymmetry in the number of alleles at each locus, and it is suspected that even with very high W_n values, some haplotypes will allow for a stratified analysis. The ALD values, combined with the HSF values (Table 1), give us a numeric evaluation of the variation available for stratification analyses. It can be challenging to conduct several analyses, synthesizing results from various combinations and types of genetic variants as risk factors. The ALD measures form a base for such studies, along with consideration of other complementary summary measures of the strength and structure of LD in multiallelic data.

Appendix: Alternate Expressions for ALD Statistics

Alternate expressions for F_A/B and F_B/A for multiallelic data

The two overall HSF measures can also be expressed as haplotype and allele frequencies (line 1 below), or as a deviation from the single-locus homozygosity (second line below) using individual LD (D_ij) values and allele frequencies.

$$\begin{array}{c}{F}_{A/B}={\displaystyle {\sum }_j\left(F_{A/Bj}\right)\left(p_{Bj}\right)}\\ ={\displaystyle {\sum }_j{\displaystyle {\sum }_i{\left(f_{ij}/p_{Bj}\right)}^{\mathit{2}}\left(p_{Bj}\right)}={\displaystyle {\sum }_i{\displaystyle {\sum }_j\left[f_{ij}^{\mathit{2}}/p_{Bj}\right]}}}\\ ={\displaystyle {\sum }_i{\displaystyle {\sum }_j{\left[p_{Ai}{p}_{Bj}+D_{ij}\right]}^{\mathit{2}}/p_{Bj}}}={\displaystyle {\sum }_i{\displaystyle {\sum }_j\left[p_{Ai}^{\mathit{2}}{p}_{Bj}+2p_{Ai}{D}_{ij}+D_{ij}^{\mathit{2}}/p_{Bj}\right]}}\\ =F_A+{\displaystyle {\sum }_i{\displaystyle {\sum }_j{D}_{ij}^2/p_{Bj}}}\end{array}$$

$\left(\mathrm{since}\hspace{0.5em}{\displaystyle {\sum }_j{D}_{ij}}=0;\hspace{0.5em}\mathrm{see}\hspace{0.5em}\mathrm{Table}\hspace{0.5em}1\hspace{0.5em}\mathrm{footnote}\right)$. Similarly, $F_{B/A}=F_B+{\displaystyle {\sum }_i{\displaystyle {\sum }_j{D}_{ij}^2/p_{Ai}}}$. It follows that F_A/B ≥ F_A with equality only when all D_ij = 0 (a “Wahlund” effect).

Alternate expressions for F_A/B and F_B/A for biallelic data

If both loci are biallelic:

$$\begin{array}{c}{F}_{A/B}=F_A+{\displaystyle {\sum }_i{\displaystyle {\sum }_j{D}_{ij}^2/p_{Bj}}}=F_A+\left[D_{11}^2/p_{B_1}\right]+\left[D_{12}^2/p_{B_2}\right]+\left[D_{21}^2/p_{B_1}\right]+\left[D_{22}^2/p_{B_2}\right]\\ =F_A+2\left[D^2/p_{B_1}\right]+2\left[D^2/p_{B_{\mathit{2}}}\right],\hspace{0.5em}\text{since}\hspace{0.5em}{D}_{11}=-D_{12}=-D_{21}=D_{22}=D,\\ =F_A+2\hspace{0.5em}{D}^{\mathit{2}}/\left(p_{B_1}\hspace{0.17em}{p}_{B_2}\right).\end{array}$$

Similarly, $F_{B/A}=F_B+2\hspace{0.5em}{D}^{\mathit{2}}/\left(p_{A_{\mathit{\prime }}}\hspace{0.17em}{p}_{A_{\mathit{2}}}\right).$

Alternate expressions for W_A/B² and W_B/A² for multiallelic data

W_A/B² and W_B/A² (Table 1) can also be expressed using haplotype and allele frequencies or using individual LD (D_ij) values and allele frequencies:

$$\begin{array}{c}{W}_{A/B}^2=\left(F_{A/B}-F_A\right)/\left(1-F_A\right)=\left({\displaystyle {\sum }_i{\displaystyle {\sum }_j\left[f_{ij}^{\mathit{2}}/p_{Bj}\right]-F_A}}\right)/\left(1-F_A\right)\\ =\left[{\displaystyle {\sum }_i{\displaystyle {\sum }_j\left(D_{ij}^{\mathit{2}}/p_{Bj}\right)}}\right]/\left(1-F_A\right),\end{array}$$

$$\begin{array}{c}{W}_{B/A}^2=\left(F_{B/A}-F_B\right)/\left(1-F_B\right)=\left({\displaystyle {\sum }_i{\displaystyle {\sum }_j\left[f_{ij}^{\mathit{2}}/p_{Ai}\right]-F_B}}\right)/\left(1-F_B\right)\\ =\left[{\displaystyle {\sum }_i{\displaystyle {\sum }_j\left(D_{ij}^{\mathit{2}}/p_{Ai}\right)}}\right]/\left(1-F_B\right).\end{array}$$

Alternate expressions for W_A/B² and W_B/A² for biallelic data

If both loci are biallelic:

$$\begin{array}{c}{W}_{A/B}^2=\left(F_{A/B}-F_A\right)/\left(1-F_A\right)=\left({\displaystyle {\sum }_i{\displaystyle {\sum }_j\left[f_{ij}^2/p_{Bj}\right]-F_A}}\right)/\left(1-F_A\right)\\ =\left[{\displaystyle {\sum }_i{\displaystyle {\sum }_j\left(D_{ij}^2/p_{Bj}\right)}}\right]/\left(1-F_A\right)=D^2/\left(p_{A_1}\hspace{0.17em}{p}_{A_2}\hspace{0.17em}{p}_{B_1}\hspace{0.17em}{p}_{B_2}\right)=r^2.\end{array}$$

Similarly, $W_{\mathit{B}/A}^{\mathit{2}}=r^{\mathit{2}}$.