Bacterial Motility Patterns Reveal Importance of Exploitation over Exploration in Marine Microhabitats. Part I: Theory

Abstract

Bacteria use different motility patterns to navigate and explore natural habitats. However, how these motility patterns are selected, and what their benefits may be, are not understood. In this article, we analyze the effect of motility patterns on a cell’s ability to migrate in a chemical gradient and to localize at the top of the gradient, the two most important characteristics of bacterial chemotaxis. We will focus on two motility patterns, run-tumble and run-reverse-flick, that are observed and characterized in enteric bacterium Escherichia coli and marine bacterium Vibrio alginolyticus, respectively. To make an objective comparison, master equations are developed on the basis of microscopic motions of the bacteria. An unexpected yet significant result is that by adopting the run-reverse-flick motility pattern, a bacterium can reduce its diffusivity without compromising its drift in the chemical gradient. This finding is biologically important as it suggests that the motility pattern can improve a microorganism’s ability to sequester nutrients in a competitive environment.

Introduction

Cell motility comes with a big cost. This is the reason its associated genes are tightly regulated (1,2). A high cost is usually accompanied by a high benefit, suggesting that motility is important for cell survival. The ultimate benefit of bacterial motility is that it allows a cell to sequester essential resources more efficiently in a competitive environment. A pelagic ocean is one of those habitats in which the average nutrient level is very low, e.g., the concentration of amino acids is in the range of ∼10⁻⁹ M, and evidence suggests that for small bacteria, the availability of metabolizable carbons is the limiting factor for how fast these bacteria can swim (3). Moreover, in oceans, nutrients appear and disappear in a sporadic fashion, demanding a swift chemical response, a fast swimming speed, and being able to localize near a nutrient patch once it is found. This raises an intriguing question about what motility pattern is better suited for such an environment.

The best studied and characterized bacterial motion is that of the enteric bacterium Escherichia coli, which we will call a two-step swimmer. In a homogeneous environment, the cell incorporates a run-tumble swimming pattern to navigate. In an inhomogeneous environment, the cell extends (shortens) its run intervals when it moves up (down) a chemoattractant gradient, leaving the tumbling interval that randomizes the swimming direction relatively unchanged (4). By modulating the run intervals based on chemical cues, the bacterium executes a biased random walk, allowing it to home in on the source of beneficial chemicals and away from harmful ones. However, as far as we know, marine bacteria do not use run-tumble to navigate. Instead, they use the forward-reverse pattern, which has been the most documented in works by Taylor and Koshland (5) and Luchsinger et al. (6). In a study in 2011 (7), we found that marine bacteria Vibrio alginolyticus, and possibly others, swims using a cyclic three-step motility pattern, forward-reverse-flick. Specifically, the bacterium swims forward for an interval Δ_CCW propelled by a CCW-rotating left-handed polar flagellum, and then swims backward for an interval Δ_CW pulled by the CW-rotating flagellum. Upon another motor reversal, which causes the bacterium to swim forward again, the polar flagellum deflects, causing the cell body to reorient in a new random direction. Compared to Δ_CCW or Δ_CW, which is ∼0.5 s, the flick is very brief, lasting ∼0.05 s.

Despite the different motility pattern of the marine bacterium, which we will call a three-step swimmer, its trajectory is still a random walk but with a reduced net displacement within a swimming cycle (Δ_CCW+Δ_CW) because of the backtracking (7). This raises an interesting question about the benefit for a microorganism to adopt the three-step run-reverse-flick motility pattern instead of the two-step run-tumble pattern. In a more general sense, one may ask whether certain motility patterns are better suited for a given environment than others. These important questions are difficult to address by laboratory experiments because different microorganisms have different swimming speeds, chemical sensitivities, and intrinsic switching rates. Indeed, our previous experiment showed that V. alginolyticus can migrate in an attractant gradient much faster than E. coli, which may be expected because its swimming speed is 2–3 times greater (7). However, the marine bacteria also form a tighter aggregate at the top of a gradient, which is not evident and appears at odds with its high swimming speed. Hence, unless the problem can be analyzed in an objective manner, there will be no satisfactory answer to these questions.

To overcome this impasse, we resort to mathematical modeling using master equations. A swimming bacterium is represented by a random walker obeying specific local dynamics in a chemical gradient. The two-step and three-step swimmers are identical in all aspects except their motility patterns. We found that for a microorganism executing the run-tumble cycles, the master equation is the standard convection-diffusion equation, or, in the biological context, known as the Keller-Segal (KS) equation (8). On the other hand, for a microorganism executing the run-reverse-flick cycles, the master equation is not of the standard form. It contains an extra flux term, which we show to be negligible. A simple but surprising physical picture emerging from our calculation is that a microorganism can alter its microscopic motility pattern to significantly reduce its diffusivity without compromising the drift velocity in a chemical gradient. This suggests that in oceans, the motility pattern such as run-reverse-flick or, for that matter run-reverse, is selected for its localization or exploitative behavior rather than its exploration potential.

This article is organized in the following fashion: To begin, the two-step and three-step motility patterns, which may be viewed as the chemotactic strategies, are implemented at a microscopic level in one spatial dimension. This results in differential equations similar to diffusion equations of the telegraph model (9). By specifying the switching rate k(x) as a function of local chemical concentration c(x), we show that the master equation is equivalent to the KS equation that contains two phenomenological constants, the bacterial diffusivity D and the chemotactic coefficient χ = v_d/∇c, where v_d is the drift velocity and ∇c is the chemical gradient. The KS equation is thus a general description of bacterial chemotaxis, and different motility patterns result in different D and χ. Analytic solutions are then obtained approximately for the one-dimensional case and compared with numerical solutions without approximations. Finally, the one-dimensional calculation is generalized to higher spatial dimension d, and we show that our central finding is independent of the spatial dimension.

Results and Discussions

The theoretical models in one dimension

The movement of a bacterium is akin to that of a random walker. The cell swims with a constant velocity for a time Δ and turns to a new random direction, where Δ is exponentially distributed. A model describing a diffusing particle with a finite mass is thus appropriate for mimicking chemotactic behavior of a bacterium. Here, we are only interested in the long-time diffusive regime of particle dynamics. We define the probability density functions (PDFs) of particles moving in the $\hat{x}$ and $-\hat{x}$ directions as $P\left(\hat{x},x,t\right)$ and $P\left(-\hat{x},x,t\right)$, respectively (9). These particles are subject to random collisions or directional randomization that occur at rates k₊(x) and k₋(x) when moving in the $\hat{x}$ and $-\hat{x}$ directions, respectively. After a collision, the particles have an even chance of continuing in the same or opposite direction. The PDFs are then given by

$$\frac{\partial P\left(\hat{x},x,t\right)}{\partial t}=-v\frac{\partial P\left(\hat{x},x,t\right)}{\partial x}-\frac{k_{+}\left(x\right)}{2}P\left(\hat{x},x,t\right)+\frac{k_{-}\left(x\right)}{2}P\left(-\hat{x},x,t\right),$$ (1)

$$\frac{\partial P\left(-\hat{x},x,t\right)}{\partial t}=v\frac{\partial P\left(-\hat{x},x,t\right)}{\partial x}+\frac{k_{+}\left(x\right)}{2}P\left(\hat{x},x,t\right)-\frac{k_{-}\left(x\right)}{2}P\left(-\hat{x},x,t\right).$$ (2)

In a homogeneous medium, the collision rates are expected to be constant, k_±(x) = k₀, independent of x. However, for chemotaxis, a bacterium follows chemical cues by modulating k_±(x): if the bacterium swims up an attractant gradient, it lowers the switching rate, and if it swims down the gradient, it increases the switching rate. This assumption is valid in the case of V. alginolyticus (10).

Previous experiments have shown that a bacterium performs chemosensing by temporal comparison. In E. coli, for example, the chemoreceptors average the receptor occupancy by chemoeffectors in the present one-second and compare it with that of the previous three seconds (11). The result of the comparison is used to alter the phosphorylation level of the regulator protein CheY that determines the flagellar motor switching probability. In 2011, we found that marine bacteria V. alginolyticus also perform temporal comparison, but the response time is shorter (10). Hence, even though bacterial chemotaxis is modeled as a random walk, the actual process is non-Markovian because k_±(x) is determined by the history of a particular trajectory (12,13). Because of this memory effect, a rigorous treatment requires averaging over all possible trajectories, which is beyond the scope of this work. The bacterial sensory response can be significantly simplified if the chemoeffector, say an attractant, c(x), has a shallow gradient that does not change much during a swimming interval, v|∂²c/∂x²| ≪ k₀ |∂c/∂x|. In this case, the switching rate is a linear function of the chemical gradient k_±(x) ≈ k₀ $\mp$ Δk(x) (9) with Δk(x) = gv∂c(x)/∂x and g being a gain factor. In an early work by Mesibov et al. (14), it was shown that instead of linear sensing, bacteria actually use logarithmic sensing to respond to a chemical cue. In this case, Δk(x) = (g′/c(x))v∂c(x)/∂x, where g′ is a constant. Work in 2009 showed that c(x) in g ≡ g′/c(x) can be replaced by $\overline{c}$, the average concentration experienced by the bacterium in an attractant profile if $\partial c\left(x\right)/\partial x\ll k_{0}c\left(x\right)/v$ (15).

The master equation for two-step swimmers

For the run-tumble motility pattern in a shallow gradient, Eqs. 1 and 2 can be used directly by replacing k_± with k₀ $\mp$ Δk. This yields

$$\frac{\partial P\left(\hat{x},x,t\right)}{\partial t}=-v\frac{\partial P\left(\hat{x},x,t\right)}{\partial x}-\frac{k_0-\Delta k\left(x\right)}{2}P\left(\hat{x},x,t\right)+\frac{k_0+\Delta k\left(x\right)}{2}P\left(-\hat{x},x,t\right),$$ (3)

$$\frac{\partial P\left(-\hat{x},x,t\right)}{\partial t}=v\frac{\partial P\left(-\hat{x},x,t\right)}{\partial x}+\frac{k_0-\Delta k\left(x\right)}{2}P\left(\hat{x},x,t\right)-\frac{k_0+\Delta k\left(x\right)}{2}P\left(-\hat{x},x,t\right).$$ (4)

Adding and subtracting Eqs. 3 and 4, we obtain

$$\frac{\partial P\left(x,t\right)}{\partial t}=-\frac{\partial J\left(x,t\right)}{\partial x},$$ (5)

$$\frac{\partial J\left(x,t\right)}{\partial t}=-v^2\frac{\partial P\left(x,t\right)}{\partial x}-k_{0}J\left(x,t\right)+v\Delta k\left(x\right)P\left(x,t\right),$$ (6)

where

$$P\left(x,t\right)=P\left(\hat{x},x,t\right)+P\left(-\hat{x},x,t\right)$$

is the total probability and

$$J\left(x,t\right)=v\left(P\left(\hat{x},x,t\right)-P\left(-\hat{x},x,t\right)\right)$$

is the flux. Taking the time derivative of Eq. 5 and replacing ∂J/∂t by Eq. 6 gives

$$\frac{{\partial }^{2}P\left(x,t\right)}{\partial t^2}=-\frac{\partial }{\partial x}\left[-v^2\frac{\partial P\left(x,t\right)}{\partial x}-k_{0}J\left(x,t\right)+v\Delta k\left(x\right)P\left(x,t\right)\right].$$ (7)

Because only the long-time behavior (k₀t ≫ 1) of the bacterial population is of interest, it is justifiable to set ∂²P(x,t)/∂t² = 0. This yields

$$\frac{\partial J\left(x,t\right)}{\partial x}=-\frac{v^2}{k_0}\frac{{\partial }^{2}P\left(x,t\right)}{\partial x^2}+\frac{v}{k_0}\frac{\partial \left(\Delta k\left(x\right)P\left(x,t\right)\right)}{\partial x}.$$ (8)

Inserting this equation into Eq. 5, we arrive at the master equation for the two-step swimmer,

$$\frac{\partial P_E\left(x,t\right)}{\partial t}+\frac{\partial \left(v_E\left(x\right)P_E\left(x,t\right)\right)}{\partial x}=D_E\frac{{\partial }^2{P}_E\left(x,t\right)}{\partial x^2},$$ (9)

where the subscript E stands for E. coli, v_E(x) = vΔk(x)/k₀ is the drift velocity, and D_E = v²/k₀ is the diffusivity. We observed that for the two-step swimmer, the master (or KS) equation can be derived with the single assumption k₀t ≫ 1. As we shall see, this is insufficient for the three-step swimmer.

The master equation for three-step swimmers

The major difference between a two-step and a three-step swimmer is that the latter has motility even when the flagellar motor rotates in the CW direction, backtracking its forward path. For the three-step swimmer, therefore, there are four possibilities depending on the swimming direction and the state of motor rotation: $\left(\hat{x},\text{CCW}\right)$, $\left(-\hat{x},\text{CCW}\right)$, $\left(\hat{x},\text{CW}\right)$, and $\left(-\hat{x},\text{CW}\right)$. The corresponding PDFs evolve in time according to

$$\frac{\partial P_{\text{CCW}}\left(\hat{x},x,t\right)}{\partial t}=-v\frac{\partial P_{\text{CCW}}\left(\hat{x},x,t\right)}{\partial x}-\left(k_0-\Delta k\right)P_{\text{CCW}}\left(\hat{x},x,t\right)+\frac{k_0-\Delta k}{2}{P}_{\text{CW}}\left(\hat{x},x,t\right)+\frac{k_0+\Delta k}{2}{P}_{\text{CW}}\left(-\hat{x},x,t\right),$$ (10)

$$\frac{\partial P_{\text{CCW}}\left(-\hat{x},x,t\right)}{\partial t}=v\frac{\partial P_{\text{CCW}}\left(-\hat{x},x,t\right)}{\partial x}-\left(k_0+\Delta k\right)P_{\text{CCW}}\left(-\hat{x},x,t\right)+\frac{k_0-\Delta k}{2}{P}_{\text{CW}}\left(\hat{x},x,t\right)+\frac{k_0+\Delta k}{2}{P}_{\text{CW}}\left(-\hat{x},x,t\right),$$ (11)

$$\frac{\partial P_{\text{CW}}\left(\hat{x},x,t\right)}{\partial t}=-v\frac{\partial P_{\text{CW}}\left(\hat{x},x,t\right)}{\partial x}-\left(k_0-\Delta k\right)P_{\text{CW}}\left(\hat{x},x,t\right)+\left(k_0+\Delta k\right)P_{\text{CCW}}\left(-\hat{x},x,t\right),$$ (12)

$$\frac{\partial P_{\text{CW}}\left(-\hat{x},x,t\right)}{\partial t}=v\frac{\partial P_{\text{CW}}\left(-\hat{x},x,t\right)}{\partial x}-\left(k_0+\Delta k\right)P_{\text{CW}}\left(-\hat{x},x,t\right)+\left(k_0-\Delta k\right)P_{\text{CCW}}\left(\hat{x},x,t\right).$$ (13)

In the above, the cyclic run-reverse-flick motility pattern is explicitly implemented, i.e., when a bacterium swims in a CCW state, a motor reversal simply makes the cell swim in the opposite direction, but when a bacterium swims in a CW state, a motor reversal causes the cell to flick and swim either in its current or opposite direction with equal probability.

Similar to the two-step case, we define the total probability

$$P\left(x,t\right)=P_{\text{CCW}}\left(\hat{x},x,t\right)+P_{\text{CCW}}\left(-\hat{x},x,t\right)+P_{\text{CW}}\left(\hat{x},x,t\right)+P_{\text{CW}}\left(-\hat{x},x,t\right)$$

and the flux

$$J=v\left(P_{\text{CCW}}\left(\hat{x},x,t\right)+P_{\text{CW}}\left(\hat{x},x,t\right)-P_{\text{CCW}}\left(-\hat{x},x,t\right)-P_{\text{CW}}\left(-\hat{x},x,t\right)\right)$$

for the three-step swimmer. Summing up Eqs. 10–13 yields the equation of conservation of total number of bacteria,

$$\frac{\partial P\left(x,t\right)}{\partial t}=-\frac{\partial J\left(x,t\right)}{\partial x},$$ (14)

which is expected. However, the flux equation is more complicated with the result

$$\frac{\partial J\left(x,t\right)}{\partial t}=-v^2\frac{\partial P\left(x,t\right)}{\partial x}-2k_{0}J\left(x,t\right)+2v\Delta k\left(x\right)P\left(x,t\right)+k_0\delta J_{\text{CW}}\left(x,t\right),$$ (15)

where

$$\delta J_{\text{CW}}\left(x,t\right)\equiv v\left(P_{\text{CW}}\left(\hat{x},x,t\right)-P_{\text{CW}}\left(-\hat{x},x,t\right)\right)-\frac{v\Delta k\left(x\right)}{k_0}\left(P_{\text{CW}}\left(\hat{x},x,t\right)+P_{\text{CW}}\left(-\hat{x},x,t\right)\right)$$

is the extra flux term, which makes this equation different from Eq. 6. Following the same procedure as above, i.e., taking the time derivative of Eq. 14 and replacing ∂J/∂t using Eq. 15, we found in the long-time limit,

$$\frac{\partial P\left(x,t\right)}{\partial t}=\frac{v^2}{2k_0}\frac{{\partial }^{2}P\left(x,t\right)}{\partial x^2}-\frac{v}{k_0}\frac{\partial \left(\Delta k\left(x\right)P\left(x,t\right)\right)}{\partial x}-\frac{1}{2}\frac{\partial \delta J_{\text{CW}}\left(x,t\right)}{\partial x}.$$ (16)

In the Supporting Material, it is shown that δJ_CW ∼ o(Δk) and can be neglected when Δk/k₀ ≪ 1. This is also confirmed by numerical calculations in which all terms are included. Dropping the last term in Eq. 16, we finally obtained the master equation for the three-step swimmer,

$$\frac{\partial P_V\left(x,t\right)}{\partial t}+\frac{\partial \left(v_V\left(x\right)P_V\left(x,t\right)\right)}{\partial x}=D_V\frac{{\partial }^2{P}_V\left(x,t\right)}{\partial x^2},$$ (17)

where the subscript V stands for V. alginolyticus, v_V(x) = vΔk(x)/k₀, and D_V = v²/2k₀. We note that by dropping the ∂δJ_CW/∂x term, the master equation for the three-step swimmer is mathematically identical to that of the two-step swimmer. Importantly, we found that the bacterial diffusivity of the three-step swimmer is a factor of two smaller than that of the two-step swimmer, D_V = D_E/2, but the drift velocity is the same for both v_V = v_E = v_d(≡ vΔk/k₀); the latter is unexpected because, due to backtracking, one anticipates v_V < v_E. The result is in contrast with inanimate particles. For example, for a colloidal particle in an external field, diffusion and drift are related; when one increases, the other must increase, inasmuch as both share the same frictional factor.

The above finding has important biological implications because it shows that by altering the motility pattern, a microorganism can reduce its diffusivity without compromising its drift velocity, a niche that can be exploited by the microorganism. Indeed, Eqs. 9 and 17 provide clues about how well a two-step and three-step swimmer can perform chemotaxis in a chemical gradient. It shows that for everything being equal, such as the swimming speed v, the switching rate k₀, and the gain factor g (or g′), the three-step swimmer can aggregate around a source of an attractant more tightly than its two-step counterpart, allowing a higher exposure to nutrients. Such a trait is very significant for competitive foraging in habitats where nutrients are scarce and localized. The high ability for the cell to localize evidently comes with a cost. It reduces the chance for the three-step swimmer to explore habitats efficiently. However, it may be argued that, in vast oceans, searching is unproductive unless a chemical signal is present. In this case, it is more important to follow closely and rapidly an existing chemical cue. This exploitative behavior appears to be encoded in the swimming pattern of V. alginolyticus.

Analytical and numerical solutions of the master equations

It is difficult to obtain analytical solutions to the master equation with an arbitrary drift velocity v_d(x). However, when the chemical gradient is linear, Δk and v_d become constant and the problem is simplified. Below we attempt to find analytical solutions in the domain [−L, L] with different initial conditions when an chemoattractant concentration increases linearly along x. Using the method of separation of variables, we found that the solution to the master equation is given by

$$P\left(x,t\right)=\frac{q^{\prime }}{\text{sinh}\left(2q^{\text{′}}L\right)}\text{exp}\left(2q^{\text{′}}x\right)+\exp \left(q^{\text{′}}x\right)\left[\sum _{n=\mathrm{1,2},\mathrm{..}}{A}_n{\psi }_n\left(x\right)\text{exp}\left(-{\lambda }_{n}t\right)+\sum _{m=\mathrm{0,1,2},\mathrm{..}}{B}_m{\varphi }_m\left(x\right)\text{exp}\left(-{\lambda }_{m}t\right)\right],$$ (18)

where q′ = v_d/2D is the wavenumber characterizing the steady-state profile, ψ_n(x) and ϕ_m(x) are the eigenfunctions, and λ_n and λ_m are the corresponding decay rates. In terms of wavenumbers

$$q_n=\frac{\pi n}{L}\text{and}{q}_m=\frac{\pi \left(2m+1\right)}{2L},$$

they are given by

$$\{\begin{array}{c}{\psi }_n\left(x\right)={\psi }_{0n}\left(q_n\cos \left(q_{n}x\right)+q^{\prime }\sin \left(q_{n}x\right)\right)\\ {\varphi }_m\left(x\right)={\varphi }_{0m}\left(q^{\prime }\cos \left(q_{m}x\right)-q_m\sin \left(q_{m}x\right)\right)\end{array},$$ (19)

$$\{\begin{array}{cc}{\lambda }_n=& {\lambda }_0\left[1+{\left(\frac{q_n}{q^{\prime }}\right)}^2\right],\\ {\lambda }_m=& {\lambda }_0\left[1+{\left(\frac{q_m}{q^{\prime }}\right)}^2\right],\end{array}$$ (20)

where

$${\lambda }_0=\frac{v_d^2}{4D},$$

$${\psi }_{0n}=\frac{1}{\sqrt{L\left(q^{\text{′}2}+q_n^2\right)}},\text{and}$$

$${\varphi }_{0m}=\frac{1}{\sqrt{L\left(q^{\text{′}2}+q_m^2\right)}},$$

and m and n are positive integers.

Consider the situation when the bacteria are released at x = 0, and we watch how they spread in space and time. The initial condition in this case is P(x,0) = δ(x), and it yields the Fourier amplitudes A_n = ψ_n(0) and B_m = ϕ_m(0). Fig. 1 displays our analytical solutions of P(x,t) for the two-step (blue lines) and three-step (purple lines) swimmers, and the results are compared with the numerical solutions (green squares and red circles, respectively) using the full equations, Eqs. 3 and 4 and Eqs. 10–13. Because of the approximations made in deriving Eqs. 9 and 17, specifically ∂²P/∂t² ≃ 0 and δJ_CW ≃ 0, the numerical method provides a quantitative means to check their validity. In all numerical calculations, we set Δx = 0.1 and Δt = 1 so that the bacterial swimming speed is v = Δx/Δt = 0.1, the switching rate is k₀ = 0.l/Δt (or the mean swimming interval k₀⁻¹ = 10Δt), and the change in switching rate is Δk = k₀/10.

Figure 1.

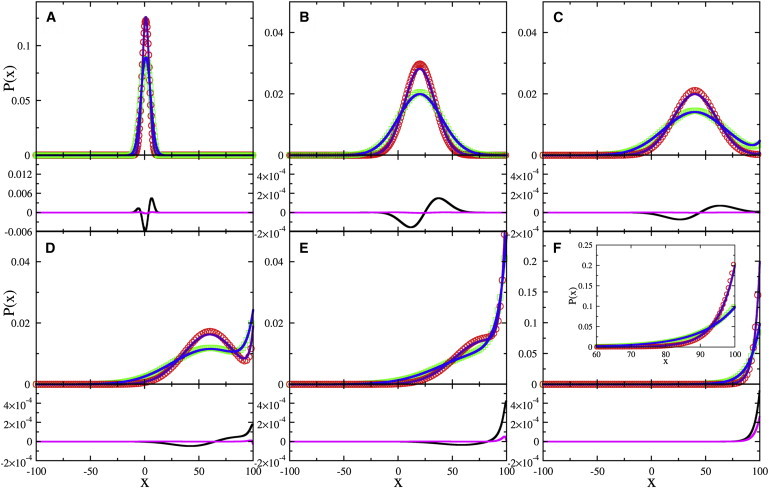
Evolution of P(x,t) starting from the δ-distribution P(x,0) = δ(x). The bacterial profiles of the two-step (blue line) and three-step (purple line) swimmers, calculated based on Eq. 18 at reduced times t/t_v = 0.01, 0.2, 0.4, 0.6, 0.8, and 2, are plotted in panels A–F, respectively. Here the chemoattractant concentration increases linearly along x, t_v (≡ L/v_d) 10⁴Δt, and Δt = 1 is the computation step. As seen, the steady-state exponential profiles are formed at t/t_v ≃ 2. (Green squares and red circles) Numerical solutions for Eqs. 3 and 4, and 10–13, respectively. (F, inset) Close-up for the steady-state profiles, where colored symbol and line designations are the same as above. Beneath each PDF, the first two terms $\left(v^2/2k_0\right)\left({\partial }^{2}P/\partial x^2\right)-v\left(\Delta k/k_0\right)\left(\partial P/\partial x\right)$ (black lines) and the last term $1/2\left(\partial /\partial x\right)\delta J_{\text{cw}}$ (magenta lines) on the right-hand side of Eq. 16 are plotted based on the numerical solutions. As seen, the extra flux term is significant only for late times. However, the analytic calculation without this term still yields a quantitatively good result, as demonstrated in panel F (inset). To see this figure in color, go online.

One observes that for the two-step swimmer, the analytical and numerical solutions are nearly identical, indicating that the short-time, ballistic-like motion of bacteria does not contribute significantly to the evolution of the bacterial profile. For the three-step swimmer, on the other hand, small discrepancies can be seen at the peak of bacterial profiles, indicating that in this region the extra flux term, ∂δJ_CW/∂x, in Eq. 16 has a small but discernible contribution. However, the overall good agreement between the analytic and the numerical solutions demonstrates that 1), our derivation of the master equations is sound, and 2), the approximations are reasonable.

It is noteworthy that the numerical solutions support our analysis that the microscopic motility patterns do not affect the drift velocity v_d. They only modify the bacterial diffusivity D. This is illustrated by Fig. 1, which shows that the two bacteria migrate up the chemical gradient with identical speed, but the bacterial pack for the three-step swimmer is narrower than its two-step counterpart. Our calculations also show that because of the spatial separation between the chemical source (x = L) and the initial bacterial position (x = 0), a waiting time of t_v ∼ L/v_d is required for the bacteria to aggregate around the top of the attractant concentration. As delineated by Fig. 1 F, the steady state is reached when t/t_v ≃ 2.

For a better comparison with experimental measurements, we also calculated evolution of bacterial profiles starting from a uniform distribution, P(x,0) = 1/2L. The result of this calculation and the accompanied discussion are included in the Supporting Material.

Comparison of nutrient exposure to two-step and three-step swimmers

Biologically it is useful to quantify nutrient exposure due to different motility patterns because this quantity is closely related to the fitness of the bacteria (16). In the steady state, the nutrient exposure can be calculated by the overlapping integral between the bacterial distribution P(x) and the attractant distribution c(x). For simplicity, we assumed that the nutrient is confined in the domain [−L, L] and has an exponential profile

$$c\left(x\right)=c\left(L\right)\text{exp}\left(\left(x-L\right)/l\right),$$

where c(L) is the attractant concentration at x = L and l is the decay length. The linear gradient is the special case when l ≫ L. In the steady state, the bacterial profile P(x) satisfies the equation

$$D\frac{\partial P\left(x\right)}{\partial x}-v_d\left(x\right)P\left(x\right)=0,$$ (21)

where

$$v_d\left(x\right)=\frac{g{v}^2}{k_0}\frac{\partial c}{\partial x}$$

and the gain factor g is assumed to be a constant. Solving Eq. 21 and using the general expression D = v²/εk₀, we found

$$P\left(x\right)=P\left(L\right)\exp \left[ϵgc\left(L\right)\left(\text{exp}\left(\frac{x-L}{l}\right)-1\right)\right],$$

where ε = 1 and 2 correspond to two-step and three-step swimmers, respectively. It follows that the average nutrient exposure per bacterium is given by

$$C={\int }_{-L}^{L}P\left(x\right)c\left(x\right)dx\text{/}{\int }_{-L}^{L}P\left(x\right)dx.$$

This allows us to compute the ratio of the nutrient exposure C_V/C_E of the two bacteria,

$$\frac{C_V}{C_E}=\frac{{\int }_{-2L}^0\text{exp}\left[2gc\left(L\right)\left(\text{exp}\left(x/l\right)-1\right)\right]\text{exp}\left(x/l\right)dx}{{\int }_{-2L}^0\text{exp}\left[gc\left(L\right)\left(\text{exp}\left(x/l\right)-1\right)\right]\text{exp}\left(x/l\right)dx}\times \frac{{\int }_{-2L}^0\text{exp}\left[gc\left(L\right)\left(\text{exp}\left(x/l\right)-1\right)\right]dx}{{\int }_{-2L}^0\text{exp}\left[2gc\left(L\right)\left(\text{exp}\left(x/l\right)-1\right)\right]dx}.$$

The above expression was numerically integrated, and the result is presented in Fig. 2. As can be seen, the advantage of the three-step motility pattern over the two-step pattern is significant only when gc(L) is large and l/L is small. For a shallow gradient l/L ≫ 1, the improvement

$$\Delta C\text{/}{C}_E\left(\equiv \frac{C_V-C_E}{C_E}\right)$$

is only a few percent in the best case. This result suggests that the three-step motility pattern is better suited for a localized source, and to benefit from such a strategy, the cell must have a large gain g.

Figure 2.

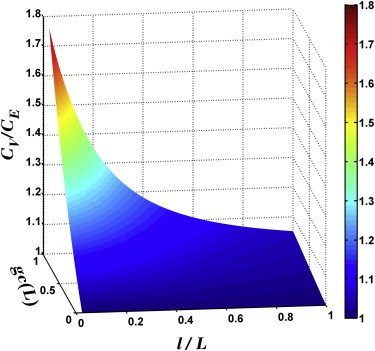
The ratio of nutrient exposure C_V/C_E versus l/L and gc(L). Here C_V (C_E) is the average nutrient exposure when the three-step (two-step) swimmers are exposed to exponentially distributed chemoattractant in a box of size 2L. The advantage of three-step over two-step swimming becomes more significant when the scale of the chemical distribution, l, is small compared to the size of the box L and the bacteria have a large gain factor g. To see this figure in color, go online.

Master equations in high spatial dimensions

It is possible to generalize the one-dimensional calculations to higher spatial dimensions d (9). Let $\hat{u}$ be a unit vector specifying the swimming direction of a bacterium. We define two subpopulations $P_{\text{CCW}}\left(\hat{u},x,t\right)$ and $P_{\text{CW}}\left(\hat{u},x,t\right)$ based on their motor directions. These two populations evolve according to

$$\frac{\partial P_{\text{CCW}}\left(\hat{u},x,t\right)}{\partial t}=-v\overrightarrow{\nabla }\cdot \left(\hat{u}{P}_{\text{CCW}}\left(\hat{u},x,t\right)\right)-k\left(x,\hat{u}\right)P_{\text{CCW}}\left(\hat{u},x,t\right)+\int k\left(x,{\hat{u}}^{\text{′}}\right)P_{\text{CW}}\left({\hat{u}}^{\text{′}},x,t\right)W\left(\hat{u},{\hat{u}}^{\text{′}}\right)d{\text{Ω}}_{{\hat{u}}^{\text{′}}},$$ (22)

$$\frac{\partial P_{\text{CW}}\left(\hat{u},x,t\right)}{\partial t}=-v\overrightarrow{\nabla }\cdot \left(\hat{u}{P}_{\text{CW}}\left(\hat{u},x,t\right)\right)-k\left(x,\hat{u}\right)P_{\text{CW}}\left(\hat{u},x,t\right)+\int k\left(x,{\hat{u}}^{\text{′}}\right)P_{\text{CCW}}\left({\hat{u}}^{\text{′}},x,t\right)W\text{′}\left(\hat{u},{\hat{u}}^{\text{′}}\right)d{\text{Ω}}_{{\hat{u}}^{\text{′}}},$$ (23)

where $k\left(x,\hat{u}\right)$ is the switching rate, which is assumed to be identical for both CCW and CW intervals; $W\left(\hat{u},{\hat{u}}^{\text{′}}\right)$ $\left(W^{\text{′}}\left(\hat{u},{\hat{u}}^{\text{′}}\right)\right)$ is the probability that upon a motor reversal from CW (CCW) to CCW (CW), the bacterium changes swimming direction from ${\hat{u}}^{\text{′}}$ to $\hat{u}$; and $d{\text{Ω}}_{{\hat{u}}^{\text{′}}}$ indicates integration over the solid angle spanned by ${\hat{u}}^{\text{′}}$. For a bacterium that executes a run-reverse-flick motility pattern, $W^{\text{′}}\left(\hat{u},{\hat{u}}^{\text{′}}\right)={\delta }_{\hat{u},-{\hat{u}}^{\text{′}}}$ so that $W^{\text{′}}\left(\hat{u},{\hat{u}}^{\text{′}}\right)=1$ if $\hat{u}=-{\hat{u}}^{\text{′}}$ and otherwise $W\text{′}\left(\hat{u},{\hat{u}}^{\text{′}}\right)=0$. Moreover, if $\hat{u}$ and ${\hat{u}}^{\text{′}}$ are uncorrelated, i.e., when a flick completely randomizes the swimming direction which is approximately valid for V. alginolyticus (7), $W\left(\hat{u},{\hat{u}}^{\text{′}}\right)={\text{Ω}}_d^{-1}$, where

$${\text{Ω}}_d\left(\equiv \int d{\text{Ω}}_{{\hat{u}}^{\text{′}}}\right)=2\pi$$

for d = 2 and Ω_d = 4π for d = 3.

Following the one-dimensional derivation, we define

$$P_{\text{CCW}}\left(x,t\right)\equiv \int P_{\text{CCW}}\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}},$$

$$P_{\text{CW}}\left(x,t\right)\equiv \int P_{\text{CW}}\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}},$$

$${\overrightarrow{J}}_{\text{CCW}}\left(x,t\right)\equiv v\int P_{\text{CCW}}\left(\hat{u},x,t\right)\hat{u}d{\text{Ω}}_{\hat{u}},\text{and}$$

$${\overrightarrow{J}}_{\text{CW}}\left(x,t\right)\equiv v\int P_{\text{CW}}\left(\hat{u},x,t\right)\hat{u}d{\text{Ω}}_{\hat{u}}.$$

The total probability density function P(x,t) and the total current $\overrightarrow{J}\left(x,t\right)$ are then given by P(x,t) ≡ P_CCW(x,t) + P_CW(x,t) and $\overrightarrow{J}\left(x,t\right)\equiv {\overrightarrow{J}}_{\text{CCW}}\left(x,t\right)+{\overrightarrow{J}}_{\text{CW}}\left(x,t\right)$. By adding Eqs. 22 and 23 and integrating both sides over all possible directions $\hat{u}$, we find

$$\frac{\partial P\left(x,t\right)}{\partial t}=-\overrightarrow{\nabla }\cdot \overrightarrow{J}\left(x,t\right).$$ (24)

To compute ${\overrightarrow{J}}_{\text{CCW}}\left(x,t\right)$, multiply both sides of Eqs. 22 by $v\hat{u}$, and integrate over $\hat{u}$. Because

$$\int W\left(\hat{u},{\hat{u}}^{\text{′}}\right)\hat{u}d{\text{Ω}}_{\hat{u}}=0,$$

we have

$$\frac{\partial {\overrightarrow{J}}_{\text{CCW}}\left(x,t\right)}{\partial t}=-v^2\int \hat{u}\overrightarrow{\nabla }\cdot \left(\hat{u}{P}_{\text{CCW}}\left(\hat{u},x,t\right)\right)d{\text{Ω}}_{\hat{u}}-v\int \hat{u}k\left(x,\hat{u}\right)P_{\text{CCW}}\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}.$$ (25)

Likewise, using Eq. 23, we obtain

$$\frac{\partial {\overrightarrow{J}}_{\text{CW}}(x,t)}{\partial t}=-v^2\int \hat{u}\overrightarrow{\nabla }\cdot \left(\hat{u}{P}_{\text{CW}}\left(\hat{u},x,t\right)\right)d{\text{Ω}}_{\hat{u}}-v{\int \hat{u}k\left(x,\hat{u}\right)\left(P_{\text{CW}}\left(\hat{u},x,t\right)+P_{\text{CCW}}\left(\hat{u},x,t\right)\right)d\text{Ω}}_{\hat{u}}.$$ (26)

Adding Eqs. 25 and 26 results in

$$\frac{\partial \overrightarrow{J}\left(x,t\right)}{\partial t}=-v^2\int \hat{u}\overrightarrow{\nabla }\cdot \left(\hat{u}P\left(\hat{u},x,t\right)\right)d{\text{Ω}}_{\hat{u}}-2v\int \hat{u}k\left(x,\hat{u}\right)P\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}+v\int \hat{u}k\left(x,\hat{u}\right)P_{\text{CW}}\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}.$$ (27)

For shallow chemoattractant gradients, the switching rate is expanded about the steady-state value k₀, resulting in

$$k\left(x,\hat{u}\right)\approx k_0-\Delta k\left(x,\hat{u}\right)$$

where $\Delta k\left(x,\hat{u}\right)=gv\hat{u}\cdot \overrightarrow{\nabla }c\left(x\right)$. The equation of motion for the current becomes

$$\frac{\partial \overrightarrow{J}\left(x,t\right)}{\partial t}=-v^2\int \hat{u}\overrightarrow{\nabla }\cdot \left(\hat{u}P\left(\hat{u},x,t\right)\right)d{\text{Ω}}_{\hat{u}}-2k_0\overrightarrow{J}\left(x,t\right)+2v\int \hat{u}\Delta k\left(x,\hat{u}\right)P\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}+k_0\delta {\overrightarrow{J}}_{\text{CW}}\left(x,t\right),$$ (28)

where the extra flux term is given by

$$\delta {\overrightarrow{J}}_{\text{CW}}\left(x,t\right)={\overrightarrow{J}}_{\text{CW}}\left(x,t\right)-\frac{v}{k_0}\int \hat{u}\Delta k\left(x,\hat{u}\right)P_{\text{CW}}\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}.$$

This term originates from the flicking step in the CW interval (see the last term on the right-hand-side of Eq. 22), and directional randomization accounts for its smallness compared to the flux term in the CCW interval. Taking an additional time derivative on both sides of Eq. 24, plugging in Eq. 28, and dropping both ∂²P/∂t² and $\delta \overrightarrow{J}\left(x,t\right)$ terms, we arrive at the master equation for d dimensions:

$$\frac{\partial P_V\left(x,t\right)}{\partial t}=\frac{v^2}{2k_0}\overrightarrow{\nabla }\cdot \left[\int \hat{u}\overrightarrow{\nabla }\cdot \left(\hat{u}{P}_V\left(\hat{u},x,t\right)\right)d{\text{Ω}}_{\hat{u}}\right]-\frac{v}{k_0}\overrightarrow{\nabla }\cdot \left[\int \hat{u}\Delta k\left(x,\hat{u}\right)P_V\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}\right].$$ (29)

Equation 29 should be compared with the master equation for the two-step swimmers, which has been derived in the work by Schnitzer (9) as

$$\frac{\partial P_E\left(x,t\right)}{\partial t}=\frac{v^2}{k_0}\overrightarrow{\nabla }\cdot \left[\int \hat{u}\overrightarrow{\nabla }\cdot \left(\hat{u}{P}_E\left(\hat{u},x,t\right)\right)d{\text{Ω}}_{\hat{u}}\right]-\frac{v}{k_0}\overrightarrow{\nabla }\cdot \left[\int \hat{u}\Delta k\left(x,\hat{u}\right)P_E\left(\hat{u},x,t\right)d{\text{Ω}}_{\hat{u}}\right].$$ (30)

Using the near-equilibrium assumption of Schnitzer (9), which amounts to

$$\left|\overrightarrow{J}\left(x,t\right)\right|\ll vP\left(x,t\right),$$

the distribution $P\left(\hat{u},x,t\right)$ is nearly independent of the swimming direction $\hat{u}$, $P\left(\hat{u},x,t\right)\approx P\left(x,t\right)/{\text{Ω}}_d$, so that Eqs. 29 and 30 can be written as

$$\frac{\partial P_V\left(x,t\right)}{\partial t}=\frac{v^2}{2d{k}_0}{\nabla }^2{P}_V-\frac{v^{2}g}{d{k}_0}\overrightarrow{\nabla }\cdot \left(\overrightarrow{\nabla }c\left(x\right)P_V\right),$$ (31)

and

$$\frac{\partial P_E\left(x,t\right)}{\partial t}=\frac{v^2}{d{k}_0}{\nabla }^2{P}_E-\frac{v^{2}g}{d{k}_0}\overrightarrow{\nabla }\cdot \left(\overrightarrow{\nabla }c\left(x\right)P_E\right),$$ (32)

where we have used the mathematical identity

$$\int {\hat{u}}_i{\hat{u}}_{j}d{\text{Ω}}_{\hat{u}}={\delta }_{ij}{\text{Ω}}_d/d.$$

These equations define the bacterial drift velocity and diffusivity with the results

$${\overrightarrow{v}}_d\equiv v^{2}g\overrightarrow{\nabla }c/\left(d{k}_0\right)\text{and}$$

$$D=v^2/\left(ϵd{k}_0\right),$$

where ε = 1 for a two-step swimmer and ϵ = 2 for a three-step swimmer. It is seen, therefore, that the central result obtained in one dimension remains valid in higher spatial dimensions d.

Conclusion

The main point of this article is the demonstration that a microorganism can modify its motility pattern at microscopic scales to significantly reduce its diffusivity without compromising its drift velocity in a chemical gradient. This counterintuitive effect results from the fact that, for a two-step swimmer, it “hedges its bet” for each swimming cycle, and on average it moves up the chemical gradient by a distance

$$\frac{1}{2}\left(\frac{v}{k_0-\Delta k}-\frac{v}{k_0+\Delta k}\right)\simeq v\Delta k\text{/}{k}_0^2$$

during the time k₀⁻¹, resulting in the drifting velocity v_E = vΔk/k₀. Despite the fact that a three-step swimmer also hedges its bet for each swimming cycle, the forward and backward intervals are compensatory. The cell migrates up the gradient by a distance

$$\frac{v}{k_0-\Delta k}-\frac{v}{k_0+\Delta k}\simeq 2v\Delta k\text{/}{k}_0^2$$

during the time 2k₀⁻¹, yielding the same drifting velocity v_V = vΔk/k₀. In this regard, the three-step motility pattern can be exploited by microorganisms to improve their fitness in an environment where nutrients exist in small and sparse patches. Earlier observations that marine bacteria V. alginolyticus (7), and possibly Pseudoalteromonas haloplanktis as well (16), can form a tighter cluster around a small chemical source more rapidly than their E. coli counterpart is consistent with such a scenario.

The study of chemotaxis ability of a bacterium cannot be disconnected from its natural habitat, which is characterized by its chemical compositions, concentrations, and distributions of individual components. Bacteria developed different niches to explore and exploit these features. Our model makes specific predictions about how macroscopic chemotaxis behaviors of a microorganism depend on niches such as microscopic motility pattern, swimming speed, and chemical sensitivity, which are characterized by ε, v, and Δk/k₀, respectively. This permits a quantitative and objective comparison of chemotaxis abilities of different microorganisms. Issues that are of biological and ecological significance, and can be quantified based on our calculation, include the following:

• 1.Dynamic evolution of bacterial profiles in the presence of different chemical distributions,
• 2.The ability to localize or disperse near a small source of attractant or repellent, and
• 3.The dynamic range and sensitivity in sensing a chemical.

The comparative study can give us a glimpse of the characteristics of the environment that the microorganism inhabits.

Finally, it should be pointed out that the minimal model presented here has not addressed the issues of memory and nonexponential run-time distribution in bacterial chemotaxis; the latter was observed in V. alginolyticus (7,17). Physically, bacterial memory is a result of signal transduction in the chemotaxis network and causes a delay in sensing the chemical gradient. Such a delay in general reduces the drift velocity of the cell, inasmuch as after a swimming direction reversal the memory inherited from the previous swimming interval is always in conflict with the gradient experienced by the cell at the presented interval (18). This increases the chance of the bacterium to move in a wrong direction, resulting in a reduced drift velocity. To minimize such an effect, it is necessary to diminish the delay in sensing the chemical gradient. In our minimal model, it is assumed that the cell modulates its switching rate according to the local chemical gradient, which corresponds to the limiting case where there is no delay in computing dc/dt or dc/dx.

As shown in the Supporting Material using the formula developed by de Gennes (17), when the signal processing time is much shorter than the intrinsic run time k₀⁻¹ of the microorganism so that the delay in computing dc/dt can be ignored, the drift velocity of the two-step swimmer is the same as that of the three-step swimmer, consistent with the outcome of the minimal model. In contrast, if the delay time is comparable to k₀⁻¹, the drift velocity of the three-step swimmer is cut by half compared to that of the two-step swimmer, as shown in Taktikos et al. (19). At present we do not know the significance of the memory effect and nonexponential run-time distribution in real microorganisms, but these effects can be assessed by comparing experiments with the minimal model. Thus, high-quality measurements specifically designed to test our model is urgently called for.

Supporting Citations

References (20,21) appear in the Supporting Material.