Abstract
It has been more than 50 years since the elucidation of the structure of double-helical DNA. Despite active research and progress in DNA biology and biochemistry, much remains to be learned in the field of DNA biophysics. Predicting the sequence-dependent curvature and flexibility of DNA is difficult. Applicability of the conventional worm-like chain polymer model of DNA has been challenged. The fundamental forces responsible for the remarkable resistance of DNA to bending and twisting remain controversial. The apparent “softening” of DNA measured in vivo in the presence of kinking proteins and superhelical strain is incompletely understood. New methods and insights are being applied to these problems. This review places current work on DNA biophysics in historical context and illustrates the ongoing interplay between theory and experiment in this exciting field.
1. Introduction
1.1 Biological and engineering relevance of DNA stiffness
Duplex DNA is the genetic material of all cells and some viruses. Genome management begins with DNA management. Amazingly, eukaryotic genome size ranges over 3 orders of magnitude from 29 million base pairs (bp) to 130 billion bp (Bennett & Leitch, 2005; Gregory, 2005), and the smallest prokaryotic endosymbiont genome is a mere 160,000 bp [160 kbp; (Nakabachi et al., 2006)]. Viral DNA content can also vary from coding capacity for 1 to 1,000 genes, with packaging pressures as high as 50 atmospheres in bacteriophage heads with ultra-compressed double-stranded DNA genomes (Gelbart & Knobler, 2009). Packaging the extremely long, information-rich double helix is therefore a fundamental problem in biology, and DNA stiffness is what really makes packaging difficult.
Moreover, the genome is not simply cargo to be stowed. Extracting the information encoded in DNA requires control of promoters, the entry sites for the RNA polymerases that transcribe genes. From the earliest examples of bacterial gene control in the E. coli lactose operon (Jacob & Monod, 1961), to gene control by recombination (Paull et al., 1993), to the most complex cases of locus control in animal cell development (Zhou et al., 2006), DNA looping appears to play a significant role. Sites separated along DNA by various distances must physically interact, through solution, to facilitate such looping (Allemand et al., 2006; Rippe, 2001; Rippe et al., 1995). Thus, DNA function requires both compression for packaging, and accessibility for looping.
Given the interesting requirements placed on DNA as a coding biopolymer, it is important to understand how the physical properties of the double helix relate to function. To what extent is auxiliary machinery needed to make the inherent properties of DNA compatible with biological requirements? How do DNA sequence and protein binding modify the shape and flexibility of DNA? These are among the questions addressed in this review.
In fact, DNA is among the stiffest natural polymers. The resistance of DNA to bending exceeds that of amino acid polymers polyglycine, polyalanine, and polyproline by 80-fold, 25-fold, and 2-fold, respectively (Cantor & Schimmel, 1980). This means that DNA stiffness is a potential obstacle to processes requiring bending, twisting, and looping. As described above, such processes include DNA compaction in precipitating agents, tight wrapping around histone octamers in chromatin, and loading into virus particles, and DNA looping in gene regulation and recombination.
Apart from appreciating the impact of DNA shape and stiffness on biological function, DNA is also increasingly considered as an engineering material for nanofabrication (Rothemund, 2006; Seeman, 2006). Such applications require an understanding of local and long-range polymer characteristics of the double helix. Manipulation of DNA stiffness may therefore become an important requirement in nanotechnology. The ability to artificially condense and package DNA is also of great interest to facilitate gene delivery to cells for gene therapy applications.
1.2 The worm-like chain model of DNA
The classic framework for understanding long-range DNA shape and resistance to bending is embodied in the worm-like (WLC) model of DNA flexibility (Kratky & Porod, 1949; Rippe et al., 1995; Shimada & Yamakawa, 1984). The development of this model for DNA and other semi-flexible (semi-stiff) chains has been a crucial contribution of polymer theory. The WLC model describes behavior intermediate between a rigid rod and a random coil to account for the striking local stiffness but long-range flexibility of DNA. Evolution of the WLC model proceeded by sequentially constraining more features of a random polymer chain.
A brief tutorial of the development of the WLC model is instructive. First, a discrete polymer chain is constructed by connecting successive steps in a random walk to yield a random flight chain or random coil. Constraining this chain so that all segments have the same length yields a freely jointed chain. As the name indicates, there are no restrictions on the bend or torsion angles between chain segments. Constraining the valence angles of this new chain, i.e. adding short-range interference, results in a freely rotating chain. Again, the name suggests that no restrictions are placed on torsion angles between chain segments so that rotations are permitted. Consider a freely rotating chain consisting of n segments of length a (not related to base pairs) joined linearly with valence angle θ, where free rotation about every segment is permitted. The contour length of the chain is given by the product na. The first segment r1 can be placed in the direction of the z-axis. If ez is a unit vector in the direction of the z-axis, then the average of the z component of the end-to-end vector R is given by
| (1) |
It is evident that 〈r1·r2〉 is the scalar projection of r2 onto r1 given by
| (2) |
since the angle between r1 and r2 is π−θ and cos(π−θ)=−cosθ. The value of 〈r1·r3〉 can be found by projecting r3 onto r2 and then projecting the result onto r1. This iterative process can be applied to each chain segment, so that, upon repeating scalar projections, the scalar products r1·ri are given by
| (3) |
Therefore, the desired sum is a geometric series a+a(−cosθ)+a(−cosθ)2+…+a(−cosθ)n−1 so that the sum of the first n terms is given by
| (4) |
In the limit n→∞
| (5) |
The length P is the persistence length of this chain, i.e. a measure of the “persistence,” or the memory, of the initial chain direction.
The Kratky-Porod worm-like chain (WLC) is defined as a limiting continuous chain formed from this discrete chain by letting n→∞, a→0, and θ→π under the restriction that na≡l, the chain contour length, and a/(1+cosθ)≡P remain constant. The WLC model can be used to express the mean-squared end-end distance of DNA fragments in terms of persistence length and contour length
| (6) |
Because of the biological significance of action at a distance along DNA, this kind of prediction is particularly important. Under physiological conditions, conventional values for P are near 50 nm or ~150 bp. For contour lengths l » P, DNA can be described as a flexible polymer (essentially, a self-avoiding freely jointed chain) whose entropic component of energy is dominant. In contrast, for contour lengths l ≤ P, DNA can be imagined as more rod-like with an elastic dominated energy.
1.3 The j-factor
The ring-closure probability for a given DNA length, an experimentally accessible measure of polymer stiffness, is an extremely useful parameter. The different regimes of DNA flexibility predicted by the WLC model are captured well in plots of the relative concentrations of two sites on DNA (j-factor) as a function of the length of the intervening DNA tether. Such plots (Fig. 1) have two domains. For DNA tether lengths less than a few multiples of the persistence length, the j-factor is low, reflecting rod-like behavior, and climbs dramatically with DNA length. Reaching a maximum value (optimal cyclization probability) near 500 bp, the plot then drops gradually with DNA length, reflecting dilution of DNA termini and coil-like behavior. Beyond these general features, details of the predicted j-factor depend upon how interaction between the two specified sites is defined (Allemand et al., 2006; Rippe, 2001; Rippe et al., 1995). If the sites are considered to interact when they reach some finite separation (as in the case of bridging proteins, neglecting the issue of helical face requirements), the length-dependence of the j-factor is least extreme (Fig. 1A). If the two sites interact by direct contact (neglecting helical face or axial alignment requirements), the length-dependence of the j-factor is much stronger (Fig. 1B). If interaction requires helix axis alignment (as in the case of ligation of cohesive DNA termini or contact between two particular helix faces) the length-dependence of the j-factor is most extreme (Fig. 1C). When torsional alignment of helical termini is considered, the j-factor oscillates through maxima and minima for every ~10 bp of increased length, due to DNA torsional inflexibility (Fig 1C, top vs. bottom). Experimental assessment of the j-factor is most commonly made using ligase-dependent DNA cyclization assays (Fig. 1C) based on the altered electrophoretic gel mobility of cyclized DNA.
Figure 1.
Depiction of the theoretical j-factor (predicted from the WLC model of DNA) as a function of DNA length and the nature of interaction between the two DNA sites. Note that both axes are plotted on logarithmic scales. Curves show behavior predicted for DNA with persistence length 46.5 nm, torsional constant 2.4 × 10−19 erg-cm, and helical repeat 10.48 bp. A. Sites are considered to interact when they are separated by distances of 20 nm (purple) or 10 nm (green). Helical face requirements are neglected. B. Sites are considered to interact upon direct contact, with no requirement for helix axis alignment or specification of helical face (blue). C. Sites are considered to interact when they collide and share a common helix axis. Consideration of the energy of DNA twisting to allow proper torsional alignment of DNA termini (as required for enzymatic ligation) results in an oscillating curve (black). Neglecting torsional alignment would result in a smooth curve (orange). Hatch marks indicate transition between fitting equations using expansions of the rod or coil limit. Curves were generated using formulas of Shimada and Yamakawa (Shimada & Yamakawa, 1984) as well as Douarche and Cocco (Douarche & Cocco, 2005) as discussed by Rippe (Rippe, 2001; Rippe et al., 1995) and Allemand et al. (Allemand et al., 2006).
1.4 Organization of review
This review will focus on intrinsic DNA curvature and flexibility and perturbations by sequence non-specific architectural proteins. DNA bending by histone octamers and sequence-specific DNA binding proteins will not be discussed in detail. Our strategy will be to provide sufficient historical context to illuminate the significance of recent progress and explore controversy in this field. An intentional theme of this presentation is the persistence of fundamental uncertainty and debate even after more than five decades of intense theoretical and experimental research.
At any given time, the shape of a DNA molecule is determined by sequence-dependent DNA curvature and sequence-dependent DNA deformability (flexibility or “softness”) driven by thermal energy or external force. This review will continue the conventional terminology of Hagerman (Hagerman, 1990; Hagerman, 1988; Hagerman, 1992): the sequence-dependent ensemble of DNA shapes in a hypothetical thermal bath without external forces is termed DNA “curvature.” Sequence-dependent DNA deformation driven by external force is termed “bending.”
There are at least five outstanding questions related to the biophysics of DNA curvature and flexibility: i. Why is DNA stiff? ii. How adequate is the WLC model for describing DNA in vitro? iii. What causes sequence-dependent DNA curvature and flexibility? iv. Can sequence-dependent DNA curvature and flexibility be predicted? v. How do cells manage the DNA stiffness problem? After summarizing relevant experimental methods, the remainder of this review will be organized around these questions.
2. Experimental methods for studying DNA stiffness in vitro and in vivo
A variety of experimental tools can be applied to measure intrinsic DNA curvature, flexibility, and the changes in DNA shape and flexibility caused by sequence non-specific architectural proteins. The following discussion is not exhaustive but highlights primary tools presently utilized. Particular attention is paid to recently developed methods and new applications of existing methodologies. These approaches can be broadly divided into three categories: passive methods (no applied force), methods involving exertion of an external force on DNA, and in vivo assays of DNA flexibility.
2.1 Passive methods
Optical spectroscopies measure equilibrium DNA conformations. These methods often assess DNA dynamics by virtue of end labeling (Fig. 2A). Fluorescence resonance energy transfer (FRET) measurements monitor the distance between fluorescent donor and acceptor dyes attached along a DNA duplex (Kuznetsov et al., 2006; McDonald et al., 2007; Morgan et al., 2005; Williams et al., 2006). Distance-dependent resonance interaction between the two fluorophores results in the direct transfer of the excited state energy from the donor to the acceptor. Since the rate of energy transfer varies according to the inverse sixth power of distance between the fluorophores, the emission of the fluorophores is very sensitive to fluctuations in DNA helix geometry. The rotational dynamics of DNA have also been assessed using steady-state and time-resolved fluorescence polarization anisotropy experiments (Noothi et al., 2009). Small-angle X-ray scattering (SAXS) interference between gold nanoparticles has also been utilized to measure the mean end-to-end lengths of short DNAs (and variance of these distribution) (Mastroianni et al., 2009; Mathew-Fenn et al., 2008). For these experiments gold nanocrystals (with radii of a few Å) are site-specifically attached to the ends of DNA via coupling to a deoxycytidine residue with a 3’-thiol modification.
Figure. 2.
Schematic illustration of some experimental methods applied to the measurement of DNA flexibility. A. Analysis of DNA re-orientation (electric dichroism), or interaction of tethered [X,Y] probes (FRET, EPR) or scattering agents (SAXS). B. Atomic force microscopy on a surface. C. Single molecule imaging in solution in an anti-Brownian electrophoretic (ABEL) trap. D. DNA ligase-mediated cyclization kinetics assay in vitro. E. Single molecule force spectroscopy in optical tweezers. F. Single molecule force spectroscopy in magnetic tweezers. G. In vivo assay of genetic switches (e.g. lac operon) involving DNA repression loops. Repressor is shown in red and RNA polymerase in purple. H. Chromosome conformation capture assay involving in vivo protein/DNA cross-linking, restriction digestion, DNA ligation, deproteination with cross-link reversal, and analytical polymerase chain reaction. DNA looping proteins are shown in red. Molecular models were rendered with PyMOL (DeLano Scientific).
Electron paramagnetic resonance (EPR) spectroscopy is a method for studying species that have one or more unpaired electrons. EPR is analogous to NMR, but excitation involves electron spins rather than nuclear spins. Thus, EPR has the requirement that the species being studied are paramagnetic. While this requirement limits the applicability of this technique, it also means that EPR has greater specificity. For example, site-specific EPR-active spin probes have been utilized to study the internal dynamics of DNA in solution and to measure a dynamic persistence length for DNA (Okonogi et al., 1999).
In the technique of transient electric birefringence (TEB) a brief (~1 µs) electric field is pulsed in a solution containing DNA. DNA and other charged molecules become partially (and transiently) oriented so that the solution becomes optically anisotropic (birefringent). In the absence of the electric field there is a return to a state of rotational isotropy and decay of birefringence. The measured rotational decay times of this process are very sensitive to changes in DNA conformation with more elongated molecules having longer decay times (Hagerman, 1981; Mills & Hagerman, 2004).
Atomic force microscopy (AFM, also known as scanning force microscopy, SFM) is an imaging technique that has been applied to study DNA shape and flexibility [(Scipioni et al., 2002a; Scipioni et al., 2002b); Fig. 2B]. This method of imaging can be applied to both trapped and dynamic DNA molecules. Operation takes place in either aqueous or ambient environments. Samples are deposited on a surface (commonly mica, graphite, or gold) with or without activation by surface reactive cations such as Mg2+, Ni2+ or (3-aminopropyl)triethoxysilane (APTES). There are three primary modes of AFM: contact, non-contact, and tapping. In each AFM mode, a tip at the end of an oscillating cantilever scans across the surface of the sample. The cantilever is typically oscillated at or near its resonance frequency, and changes in the deflection of the cantilever are measured by the displacement of a laser beam (detected using a photodiode detector) reflected from the cantilever. A feedback loop maintaining a constant signal to the photodiode detector is established in each mode by vertically adjusting the position of the scanning apparatus. Critical issues in AFM are the effects of different deposition methods DNA geometry and possible effects of the tip on the relatively soft samples.
Cryo-electron microscopy (cryo-EM) can also provide topographic images and three-dimensional reconstructions of DNA molecules, e.g. (Bednar et al., 1994; Demurtas et al., 2009). For this technique, DNA samples are loaded in micron-size holes on an electron microscope grid and immersed into liquid ethane at −160 °C for rapid cooling (vitrification) that avoids the freezing damage associated with the formation of ice-crystals. The DNA samples, which are almost instantly immobilized, are then transferred to a cryo-specimen holder in a pre-cooled electron microscope where they can be observed. The modest contrast between the electron density of the DNA sample and the surrounding solution allows multiple images from different incident angles that can be combined to allow 3D reconstructions of the sample.
Recently, a new means of trapping and measuring biological molecules was developed (Cohen & Moerner, 2005). This technique, the anti-Brownian electrophoretic (ABEL) trap, can gently and sensitively trap individual nanoscale objects that acquire a charge in solution (Fig. 2C). The ABEL trap consists of four electrodes on a glass slide. The electrodes can be individually controlled to generate an arbitrary electric field. By monitoring the Brownian motion of a small object with fluorescence microscopy, a time-dependent feedback voltage is applied so that induced electrophoretic drift cancels the Brownian motion of the object. A computer interfaced with a CCD camera and fluorescence microscope provides real-time images of the object diffusing among the electrodes. Using position information for the particle in the previous video frame, the computer generates a feedback voltage to return the object to a target position in the subsequent frame. The unique advantage of this approach is that it allows estimation of DNA conformational properties and dynamics in a state without physical tethering.
Detection of DNA curvature in the absence of external force has been achieved by X-ray crystallography and nuclear magnetic resonance (NMR) spectroscopy. Implications of crystallographic precipitants and co-solvents such as 2-methyl-2,4-pentanediol (MPD) have been actively debated in the literature (Dickerson et al., 1996; Harvey et al., 1995). It has been argued that dehydrating agents and crystal packing forces, i.e. the tendency of DNA molecules to make coaxial stacks through the crystal, may limit the ability of X-ray crystallography to illuminate sequence-directed curvature and flexibility. X-ray results are particularly problematic for A-tract sequences where results disagree with other methods. The applicability of NMR spectroscopy has advanced with the application of residual dipolar coupling information, making more confident long-range structural models built from NMR constraints (MacDonald et al., 2001). The exquisite shape-dependence of duplex DNA mobility in native polyacrylamide gel electrophoresis (PAGE) has been exploited for semi-quantitative measurement of DNA curvature. Because curved DNAs migrate more slowly, native PAGE has been utilized to detect DNA curvature or protein-induced bending in ligation ladders, circular permutation, and phasing assays (Crothers & Drak, 1992; Crothers et al., 1992; Crothers et al., 1990; Kahn & Crothers, 1992; Kahn et al., 1994; Koo & Crothers, 1988; Koo et al., 1990; Koo et al., 1986; Ross et al., 1999; Strauss & Maher, 1994; Zinkel & Crothers, 1987). It is often difficult or impossible to distinguish effects of DNA curvature versus anisotropic flexibility in such experiments (Kahn et al., 1994).
By exploiting the altered gel mobility of circular DNA, ring closure kinetics measure j-factors by sampling extreme DNA conformations. For a stiff chain like a double-stranded DNA of ~200 bp, conformations susceptible to ligation into circles (Fig. 2D) are exceedingly rare. Ligase-catalyzed DNA cyclization has received widespread theoretical and experimental consideration (Crothers et al., 1992; Du et al., 2005; Hagerman & Ramadevi, 1990; Kahn & Crothers, 1992; Podtelezhnikov et al., 2000; Shore et al., 1981; Taylor & Hagerman, 1990; Vologodskaia & Vologodskii, 2002; Zhang & Crothers, 2003). The extreme sensitivity of this technique for measuring intrinsic or induced DNA flexibility is practically unmatched. However, details of experimental conditions and key assumptions can be crucial, as will be discussed later (Cloutier & Widom, 2004; Du et al., 2005). Accordingly, the theoretical framework underlying analysis of ligase-catalyzed DNA cyclization kinetics is presented now in some detail along the lines of the original derivation of Shore and Baldwin (Shore & Baldwin, 1983; Shore et al., 1981). Cyclization converts a linear DNA molecule (L) with cohesive termini into a circular substrate (Sc) for DNA ligase (E). The ligation reaction produces a covalently closed DNA circle as product (Pc). Cyclization is proposed to proceed through the following kinetic mechanism:
| (7) |
The subscripts on the rate constants indicate which sets of species are being converted. For example, kab indicates a conversion from species a to species b.
If the concentrations of Sc and E are small, the dissociation of cohesive ends is fast compared to ligase-catalyzed ring closure, which involves the bimolecular formation of an enzyme-substrate complex (ESc). Since the formation of ESc is slow relative to end dissociation (i.e., there exists a rapid pre-equilibrium between L and Sc), the rate of ligase-catalyzed covalent ring closure (kC) is directly proportional to the equilibrium fraction of cyclized molecules (fSc) given by
| (8) |
An equation for kC can be derived by applying the steady-state approximation to the kinetic mechanism given in equation 7. First, the rate of change for the concentration of each species is written according to mass action as follows:
| (9) |
| (10) |
| (11) |
| (12) |
| (13) |
It is assumed that the fraction of cyclized molecules is small (fSc≤0.1), so that the steady-state approximation can be applied to both cyclized DNA (Sc) and to the enzyme substrate complex (ESc):
| (14) |
| (15) |
Expressions for the steady-state concentrations of Sc and ESc can then be found using equations 10 and 12 and the steady states equations 14 and 15:
| (16) |
| (17) |
with f34 defined as the efficiency of ligation of the ES complex
| (18) |
The rate of appearance of product d[Pc]/dt equals the rate of disappearance of unreacted DNA, i.e. the sum of the concentrations of linear and circular DNA
| (19) |
The measured rate constant for the formation of covalently closed circles kC is then defined as the (first-order) rate constant for the disappearance of L+Sc
| (20) |
It can be shown from equations 14, 19, 13, 17, and 18 that
| (21) |
Additionally, it follows from rearrangement of 16 that
| (22) |
so that from equations 20 – 22
| (23) |
On imposing the requirement for a rapid pre-equilibrium (L ↔ Sc) preceding the formation of ESc, i.e.
| (24) |
equation 23 simplifies to
| (25) |
Experimentally it is desirable to relate kC to the total enzyme concentration (E0). From equation 17 it can be shown that
| (26) |
where Km is the Michaelis constant for ESc given by
| (27) |
It follows from equation 26 that
| (28) |
so that for a fast pre-equilibrium
| (29) |
where Ka,circular is the equilibrium constant for cyclization (L ↔ Sc) given by
| (30) |
It should be noted that for fSc « 1 and Km » [Sc ], equation 29 becomes kC = (k34/Km) Ka,circular E0, which is a standard Michaelis-Menten expression for an enzyme-catalyzed reaction at low substrate concentration.
A similar approach can be applied to the kinetics of bimolecular joining of linear DNA molecules to form dimers (subscript d) with the same complementary cohesive ends:
| (31) |
For simplicity, it is assumed that each half molecule is distinguishable and has a single cohesive end (and one blunt end). A discussion of the case of indistinguishable half molecules will be come later. In the derivation that follows it is shown that the second-order rate constant for covalent bimolecular end joining (kD) is proportional to the equilibrium constant for bimolecular association (Ka,bimolecular) given by
| (32) |
Analogous rate equations, distinguished with subscript d and superscript * (as necessary), can be written for equations 11 – 13 as before, but rate equations for L and Sd are now
| (33) |
| (34) |
Steady state equations 14 and 15 (and therefore equation 17) are analogous to before, so the steady-state concentration of Sd is
| (35) |
Imposing the requirement (analogous to equation 24) for a rapid pre-equilibrium (2L ↔ Sd), this equation becomes
| (36) |
The measured rate constant for the formation of covalently closed linear dimer kD is defined as the (second-order) rate constant for the disappearance of unreacted DNA (L+2Sd)
| (37) |
From equations analogous to 13, 14, 17, and
| (38) |
it follows that
| (39) |
and since
| (40) |
with
| (41) |
it follows from equations 37, 39, and 40 that
| (42) |
and using the analog of equation 28 this becomes
| (43) |
Earlier, it was assumed that each half molecule is distinguishable and has a single cohesive end (and one blunt end). However, in the case of dimerization of (distinguishable or indistinguishable) DNA molecules with two cohesive ends, the apparent rate constant for dimerization is given by 4kD, where an expression for kD is given in equation 43. Taking the ratio of equation 29 to equation 43
| (44) |
If fSc and fSd are negligible compared to 1 and Km » [Sc] and [Sd], then
| (45) |
It should be noted that there is an implicit assumption that k34/Km for ligase is independent of the nature of the substrate, which conceivably is not true if there is significant local curvature or if the binding of ligase can alter curvature.
This is the key result of the derivation. Equation 45 illustrates that, subject to the specified assumptions, the j-factor (defined as a ratio of equilibrium constants) is given by a ratio of experimentally measurable rate constants. It should be noted that the rate constants defined here (kC and kD) are taken to be functions of DNA length and of temperature. However, for DNA lengths between 126 to 4361 bp, kD has been shown to be essentially independent of DNA length (Shore et al., 1981). Thus, the length dependence of j reflects kC. Several factors affect kC, including the energy required to bend the DNA to form a small circle and the energy required to twist the DNA upon cyclization so that 3’ and 5’ termini lie opposite each other and the opposed phosphodiester backbones (though nicked) follow a geometrically continuous path (along the co-linear helix axes) with the proper torsional alignment. This twist requirement is energetically costly for DNA fragments less than ~500 bp in length (Fig. 1).
Of recent interest are key assumptions required for the validity of equation 45. These assumptions include the requirements for rapid pre-equilibria (equation 24), Km »[substrate], and that the fraction of substrate is small (for each substrate type). The former is necessary so that the rate of product formation is proportional to ligase concentration. This requirement is met when the rate of substrate decay is much higher than the rate of ligase binding to the (nicked but) joined substrate ends. The later assumptions are necessary so the two reactions can be accurately compared. The requirement Km »[substrate] must be met for both circular and bimolecular substrates (which are likely at different concentrations) so that the relative equilibrium populations of each are faithfully reported. Implications of unmet assumptions are discussed in a later section.
2.2 Active methods: force spectroscopies
Investigations of the behavior of DNA under the influence of an applied force (particularly single molecule methods) have significantly enhanced our understanding of the energetic, elastic, mechanical, and structural properties of the DNA double helix (Baumann et al., 1997; Bustamante et al., 2000; McCauley et al., 2005; Podesta et al., 2005; Rouzina & Bloomfield, 2001a; Rouzina & Bloomfield, 2001b; Scipioni et al., 2002a; Scipioni et al., 2002b; Tinoco et al., 2006; Van Noort et al., 2004; Wiggins et al., 2006). Single molecule nanomanipulations utilize the technology of optical or magnetic traps and tweezers, microfibers, or atomic force microscopy (AFM) cantilevers to exert a range of forces on DNA molecules. In particular, experiments involving DNA stretching can be achieved with all of these methods. These technologies can also be combined with a buffer-flow system to examine hydrodynamic forces (drag) and to probe distinct buffer conditions, e.g. ionic strength. These techniques all employ the same basic principle. One terminus of a DNA molecule is anchored and a force sensor (viz. a trapped bead or a cantilever) is used to measure the applied force via displacement of the other terminus. Typically, DNA termini are specifically attached to the mobile and immobile components of a given system using tight associations of either biotin and streptavidin or digoxigenin (DIG) and anti-DIG.
In an optical trap or tweezer (Fig. 2E), a DNA molecule is tethered between two micron-sized polystyrene beads. One (immobile) bead is optically “trapped” in a focused laser beam or “tweezed” in the overlap of two convergently directed counter propagating laser beams while the other bead is held on the tip of a glass micropipette mounted on a piezoelectric stage. Movement of the micropipette tip (and possibly flow cell) relative to the trap causes the tethered DNA molecule to be stretched between the two beads, and the magnitude of extension is determined from the bead separation distance in simultaneous images of the micropipette tip and laser beams acquired from charge-coupled device (CCD) cameras. As the beams leave the trap, the light is directed into lateral effect (position-sensitive) photodetectors that determine the deflection of each beam to within a few microns. The magnitude of the applied force exerted on the DNA is inferred from this displacement, as the refraction of rays within a focused laser results in a restoring force. Whereas optical tweezers immobilize an (typically spherical) object within an optical trap, as their name suggests magnetic tweezers trap a micron-sized superparamagnetic bead using small magnets (Fig. 2F). Again, one end of a DNA molecule is immobilized on a glass surface (e.g. the bottom of a capillary tube that can again be linked to a buffer-flow system) while the other end is attached to a mobile magnetic bead. By controlling the position and rotation of the external permanent magnets, the bead can be pulled and/or rotated, thus stretching and/or twisting the tethered DNA molecule. The applied force is measured by video analysis of the Brownian fluctuations of the magnetic bead.
In the microfiber system, an optical fiber fed by a laser serves as the immobile component (Cluzel et al., 1996). A micron-sized polystyrene bead held on the tip of a glass micropipette mounted on a piezoelectric stage is the mobile component. Movement of the micropipette tip causes the DNA molecule tethered between the optical fiber and the bead to be stretched. The deflection (bending) of the optical fiber is detected by a position-sensitive photo-diode. For a microfiber of known stiffness, the applied force is proportional to the measured bending. Similarly, the force necessary to stretch a DNA tethered between a mobile piezoelectric stage and an immobile AFM cantilever is proportional to the deflection of the cantilever detected by the displacement of a laser beam reflected from the cantilever.
2.3 In vivo methods
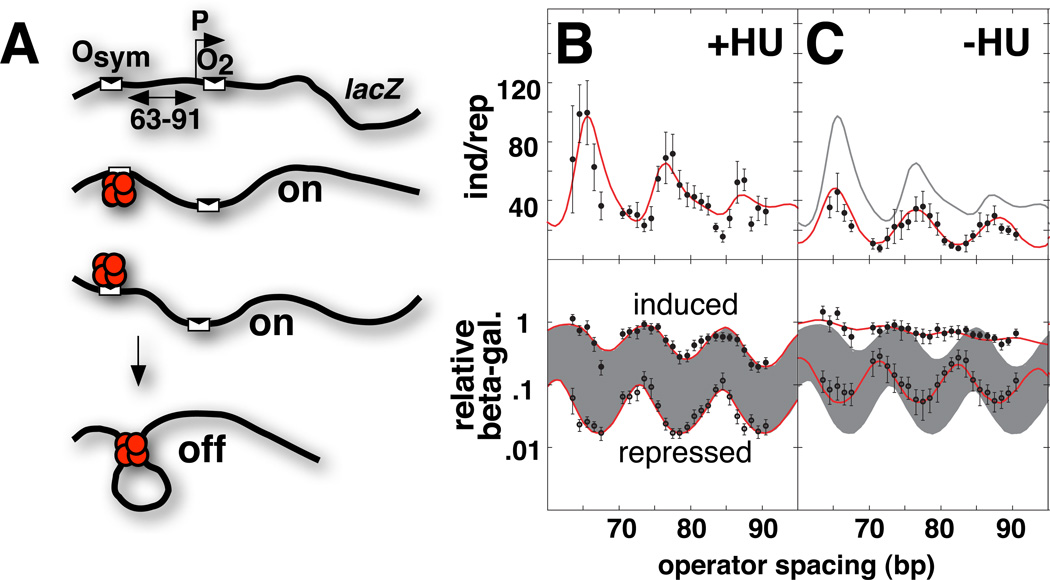
In vivo assays provide approaches to measuring DNA flexibility and looping propensity in the cellular context. Genetic assays reveal DNA flexibility through cooperativity at a distance (Fig. 2G). One particularly well-studied example is the lac looping system (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Kramer et al., 1987; Law et al., 1993; Mossing & Record, 1986; Muller et al., 1996; Oehler et al., 1990). The general biophysical principles embodied in this example have recently been elegantly reviewed (Oehler & Müller-Hill, 2009). In this system, one operator (O2) overlaps with the promoter of the lacZ reporter gene and serves as a very weak lac repressor binding site. The lacZ gene is poorly repressed by repressor occupancy of this operator alone. Repression is dramatically enhanced by placement of a strong operator (Osym) upstream of the promoter. The bidentate lac repressor tetramer occupying this upstream site creates a local concentration at the weaker downstream operator O2 that is higher than the concentration of free repressor, increasing the probability of binding at O2. This enhances the degree of saturation of the downstream operator through DNA looping. The need for DNA twisting when the operators are out-of-phase causes looping to be less energetically favorable. Analysis of lacZ repression as a function of operator spacing distance is a highly sensitive assay of the bending and twisting flexibility of DNA in vivo (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Garcia et al., 2007; Zhang et al., 2006a; Zhang et al., 2006b). The E. coli lac looping system allows for quantitative analysis of repression as a function of operator spacing via β-galactosidase (the product of the lacZ reporter gene) activity extracted from living cells. Cells are analyzed for β-galactosidase activity in the absence (uninduced) or presence (induced) of IPTG, a lactose analog that reduces the affinity of lac repressor for DNA. The repression ratio (induced relative to repressed activity) serves as a gauge of DNA deformation energetics within cells. Thermodynamic modeling is also possible and allows for identification of subtle trends in the data (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Law et al., 1993; Zhang et al., 2006a; Zhang et al., 2006b).
DNA looping propensity has also been estimated in vivo through recombination assays (Ringrose et al., 1999). Site-specific recombination was first used to measure ease of DNA looping in vitro by construction a series of flip recombinase (FLP) excision substrates with intervening DNA lengths ranging from 74 bp to 15 kbp between recognition target (FRT) sites. Purified FLP recombinase was added at known concentrations, aliquots were removed at specified time points, and percent recombination was measured. Percent recombination (plotted as a function of distance between FRTs) was shown to be proportional to the j-factor. This recombination assay was further adapted in this study to measure looping of chromatin in vivo by stable integration of FLP excision substrates in human cell lines.
Relative DNA looping propensity is also estimated in vivo through the chromosomal conformation capture (3C) assay (Fig. 2H). Looped chromatin segments in intact cells are first covalently linked by formaldehyde cross-linking. The cross-linked chromatin is then solubilized, digested with a restriction enzyme, and ligated. Intramolecular ligation of the crossed-linked fragments measures proximity of the free termini, and produces a large collection of products that serve as template for quantitative PCR. Since each ligation product results from the interaction of two sites, the abundance of each product reflects the frequency of interaction between the given sites in the three-dimensional cross-linked state. The 3C assay, and the more recent Hi-C variation, capture and quantify looping among chromatin sites both in cis and in trans. This technique has been applied to study the looping propensity of DNA in protein complexes (Dekker et al., 2002; Gondor et al., 2008; Lieberman-Aiden et al., 2009; Zhou et al., 2006).
3. Why is DNA stiff?
3.1 The forces responsible for DNA stiffness are not understood
As predicted by the WLC model, DNA exhibits a profound local stiffness but global flexibility. Consequently, over nanometer length scales DNA is among the stiffest biopolymers. Why is DNA so stiff? Surprisingly, this simple question remains controversial. The most likely contributors to DNA stiffness are favorable base pair stacking interactions that contract the double helix (Fig. 3A) or mutual phosphate diester charge repulsions that expand it (Fig. 3B). At present, it remains disputed which of these two factors is the dominant contributor to DNA stiffness. It remains possible that each contributes significantly to a balance of forces explaining the unique stiffness of the DNA polymer.
Fig. 3.
Schematic illustration of concepts and experimental approaches to exploring the basis for DNA stiffness. DNA stiffness may involve compressive base pair stacking forces (A) and/or electrostatic stretching forces along the negatively-charged sugar-phosphate backbone (B). See discussion of terms in text. C. Asymmetric phosphate neutralization by targeted methylphosphonate substitution to measure induced DNA bending toward the neutralized helix face. D. AFM study of apparent DNA stiffness on cationic surfaces. E. Hemicharged meroduplex model for measuring DNA stiffness when free bases stack onto a single helix without a second sugar-phosphate backbone.
The roles of local and long-range electrostatic effects in DNA structure and stiffness are not resolved. In his 1978 theory, Manning made predictions concerning residual DNA charge after counterion condensation. In this model, the high negative charge density of DNA induces a concentrated layer of mobile and hydrated cationic counterions along the DNA surface. The extent to which this “condensed” layer of counterions neutralizes DNA charge is governed by the valence of the counterions present in solution and, surprisingly, not by the bulk counterion concentration. The enthalpic attraction of the counterion to the DNA balances the entropic cost of localizing the ion even at very low bulk concentration. In particular, the parameter ξ governs counterion binding to DNA, and is defined as follows
| (46) |
where e is the charge of an electron, ε is the bulk dielectric constant of the solvent, kB is the Boltzmann constant, T is the absolute temperature, and b is the average axial charge spacing of the DNA. The quantity e2/(εkBT)=ℓB is the Bjerrum length for the pure solvent, the separation distance at which the electrostatic interaction between two elementary charges (e) is comparable in magnitude to the thermal energy scale (kBT). According to the theory, counterion condensation occurs when
| (47) |
where Z is the (unsigned) valence of the counterion. The saturated charge fraction r, that is, the fractional charge of DNA remaining after counterion condensation, in this theory is given by
| (48) |
It is important to restate this key result. Counterion condensation theory predicts that effective phosphate charge is controlled by counterion valence rather than concentration. Accordingly, DNA is predicted to carry some counterion-dependent residual charge that cannot be quenched by increasing bulk salt concentration. Though increased bulk salt may screen long-range interactions among phosphate charges, local electrostatic stretching interactions persist and make a constant local contribution to DNA stiffness for a given counterion. Manning theory predicts that monovalent cations neutralize ~76% of DNA phosphate charge, divalent cations ~88%, and trivalent cations ~92%. In short, Manning’s counterion condensation theory predicts that DNA stiffness should depend upon counterion valence because counterions of increasing valence should decrease the residual thermodynamic charge fraction on DNA and thus reduce the electrostatic contribution to DNA stiffness via phosphate screening. This trend has been observed in optical tweezers experiments where the persistence length was fit to force-extension data as a function of counterion valence. Decreasing DNA persistence was observed for increasing counterion valence (Baumann et al., 1997). Additionally, Schurr and co-workers have contributed considerably to the theoretical treatment of experimental polyelectrolyte effects (Fujimoto & Schurr, 1990; Rangel et al., 2008; Schurr & Allison, 1981; Schurr & Fujimoto, 2002), as recently reviewed (Schurr, 2009).
Manning counterion condensation theory also predicts a favorable entropy for the binding of cationic molecules to DNA, which releases condensed counterions into bulk solution. This prediction has been studied in detail by Record and co-workers (deHaseth et al., 1977; Lohman et al., 1980; Record et al., 1978; Record et al., 1977).
Manning has recently expanded this analysis to address the contribution of phosphate charge to DNA stiffness (Manning, 2006). In this model, bare DNA charge (not residual charge after condensation) produces an electrostatic stretching force (internal tension) on DNA due to phosphate-phosphate repulsions. To quantitatively investigate the effects of this force, Manning devised the notion of a “null” isomer of DNA, the hypothetical structure that would be adopted by a DNA if its electrostatic charge were set to zero (without affecting solvation). This model for null DNA consists of fully charged DNA supplemented by an applied compression force that is equal but oppositely directed to the internal electrostatic tension present in charged DNA. The key result of this model is a prediction for the relationship between the DNA persistence length P and the persistence length of its null isomer P*. This prediction invokes quantities already identified as well as the Debye screening length for the solution, 1/κ, the separation distance beyond which charges are screened (the only term dependent on ionic strength), and the polymer radius, R:
| (48) |
Thus, through κ there exists a dependence of the persistence length of DNA on salt concentration. Although equation 48 has no adjustable parameters, it is shown to give a reasonable value and counterion-dependence for P. A key result of this prediction is that the relationship between the bending persistence length of DNA and the persistence length of its null isomer is multiplicative, not additive. In contrast to other theories (Skolnick & Fixman, 1977) there is no “electrostatic persistence length.” That is to say, there is no additive electrostatic component. Importantly, the model quantitatively predicts how charge spacing (b) or its reciprocal (linear charge density) governs DNA persistence length. This prediction may be subject to experimental verification. For example, the charge-dependence of DNA persistence length and the role of electrostatics in mediating DNA stiffness can be addressed by novel chemistries coupled with traditional assays of DNA stiffness.
Several other theoretical studies have explored whether charge should contribute significantly to DNA stiffness. Results have been mixed. While calculations of charge crowding in bent DNA suggested a strong electrostatic opposition to deformation (Hardwidge et al., 2009; Range et al., 2005), other analyses suggest negligible effects of DNA charge on stiffness under physiological conditions (Ariel & Andelman, 2003; Guo et al., 2008; Nguyen & Shklovskii, 2002; Skolnick & Fixman, 1977).
There is experimental evidence that DNA shape depends on charge balance (Williams & Maher, 2000). Both theoretical and experimental investigations of asymmetric charge neutralization have been conducted (Kosikov et al., 2002; Manning et al., 1989; Okonogi et al., 2002; Rouzina & Bloomfield, 1998). DNAs with one helical face partially modified by incorporation of neutral phosphate analogs have been created (Fig. 3C). These modified DNAs are spontaneously deformed towards the neutralized surface, as would be predicted from Manning electrostatic theory (Strauss & Maher, 1994). Moreover, in an X-ray crystallography experiment involving tethering of cations (directed radially outward) in the major groove of DNA, it was demonstrated that the bound cations interacted electrostatically with the DNA to induce collapse of the major groove around the bound cations (Moulaei et al., 2005). Crucially, no other apparent structural changes were induced by the bound cations, suggesting that the tethered cations mediated their effect through electrostatics and did not disrupt base stacking. Thus, both phosphate neutralization and cation adduction induce spontaneous DNA bending (Williams & Maher, 2000), and they may cause DNA bending through a common mechanism.
More recently, experiments using SFM of DNA deposited on mica coated with positively charged molecules suggest that surfaces with increasing positive charge densities increase the flexibility of DNA [(Podesta et al., 2004; Podesta et al., 2005); Fig. 3D]. Addition of divalent and multivalent cations known to more completely neutralize the phosphate backbone with the potential to condense duplex DNA (Bloomfield, 1997; Gosule & Schellman, 1978; Hud et al., 1995) enhance the rotational dynamics of DNA, as evidenced by rotational correlation times from steady-state fluorescence anisotropy experiments (Noothi et al., 2009). Furthermore, studies have shown that DNA is more compact when complexed with an oppositely-charged amphiphile in organic solvent (Sergeyev et al., 1999). The hypothesis is that DNA in a DNA-surfactant complex behaves as though it was electrically neutralized and, as a result of enhanced flexibility, assumes a more compact state. These studies suggest dominant effects of DNA charge in modulating DNA flexibility and shape.
Fueling the controversy, there is experimental evidence that DNA stiffness is dominated by base stacking rather than charge repulsion. Transient electric birefringence (TEB) has been extensively developed to access DNA flexibility via persistence length, as it relates to base pair stacking (Hagerman & Hagerman, 1996; Hagerman, 1981; Mills et al., 1999; Vacano & Hagerman, 1997). In particular, TEB was utilized to explore the flexibility of the so-called “meroduplex,” an unstructured single-stranded polypyrimidine that attains duplex character upon addition of excess free purine base [(Hagerman & Hagerman, 1996); Fig. E]. A variant of the meroduplex was created with ~20 nucleotides of meroduplex flanked by double-stranded DNA at either end. This “gapped” meroduplex was shown to be much more flexible than the equivalent full duplex, but upon addition of free N6-methyladenine the flexibility became essentially indistinguishable from that of full duplex, suggesting that base pair stacking is the dominant contributor to DNA stiffness (Mills & Hagerman, 2004). There is also evidence that sequence-dependent differences in base stacking forces can measurably influence DNA persistence length (Caserta et al., 2009; Protozanova et al., 2004; SantaLucia, 1998; Virstedt et al., 2004). However, the scale of these stacking effects has never been experimentally compared with electrostatic effects.
Thus, the force (or likely, balance of forces) responsible for the bending stiffness of DNA remains unresolved. The issue remains of fundamental importance for at least three reasons. First, understanding the forces responsible DNA stiffness might allow engineering of DNA-like polymers with altered stiffness properties that could be helpful in creation of novel nanomaterials. Second, such an understanding would illuminate the mechanism responsible for eukaryotic DNA compaction by histone octamers in chromatin. Third, this understanding may suggest design principles for artificial DNA bending proteins and devices.
4. How adequate is the WLC model for describing DNA in vitro?
The worm-like chain (WLC) model of Kratky and Porod was formulated in 1949 (Kratky & Porod, 1949), and has since been extensively scrutinized and modified (Shimada & Yamakawa, 1984). The longevity and durability of the WLC model is remarkable. This course-grained approach treats DNA as an inextensible elastic rod lacking atomic detail. Despite its simplicity, the model has proven extremely accurate in describing DNA from thousands of base pairs down to fewer than one hundred. Recently, the validity of this model for short DNA molecules (less than one persistence length) has become controversial.
4.1 Challenges to the WLC model
T4 DNA-ligase mediated cyclization studies by Cloutier and Widom (Cloutier & Widom, 2004; Cloutier & Widom, 2005) suggested that ~100 bp DNA fragments formed circles at rates 3–5 orders of magnitude faster than predicted by the WLC model (Fig. 4A). In order to explain these unexpected findings, both theoreticians and experimentalists invoked the notion of DNA kinking (local base pair unstacking). Kinking of the DNA duplex would allow unusually large local bend angles as a possible means to explain these findings. DNA kinking is not a new idea. In 1975, Klug and Crick proposed that the energetic cost of forming small circles or loops could be reduced if DNA were to kink rather than uniformly distort (bend) throughout a looping region (Crick & Klug, 1975). Later, experimental evidence for DNA kinking came from the nucleosome, in which a persistence length of DNA is wound nearly twice around a histone octamer (Hogan et al., 1987; Luger et al., 1997). From the high-resolution nucleosome crystal structures it was shown that six of twelve 5’-CA-3’ steps exhibit kinking to narrow the minor groove toward the histone octamer, whereas the remainder of DNA bending in the nucleosome occur smoothly without kinking (Richmond & Davey, 2003). The other preferred base step for kinking was 5’-TA-3’, which also exhibits low base stacking energy (Fig. 4B).
Fig. 4.
Controversy surrounding a report of spontaneous sharp bending of double-stranded DNA. A. Data are presented from Shore and Baldwin [(Shore & Baldwin, 1983); times signs], Taylor and Hagerman [(Taylor & Hagerman, 1990); plus signs], Vologodskaia and Vologodskii [(Vologodskaia & Vologodskii, 2002); open circles], and Rueter and Maher [unpublished; stars]. Contrasting experimental findings for j-factors of short DNAs by ligase-catalyzed DNA cyclization kinetics where solid black symbols correspond to the data of Cloutier and Widom (Cloutier & Widom, 2004) and asterisks correspond to the data of Du et al. (Du et al., 2005) collected with particular attention to required assay assumptions (inset). Squares, circles, and triangles reflect data from the Widom group for different sequences. Both datasets have been modeled here using a DNA helical repeat of 10.54 bp/turn and a torsional rigidity of 2.4 × 10−19 erg-cm. Best fits for the DNA persistence length are 31 nm (data of Cloutier and Widom) or 46.5 nm (data of Du et al.). B. DNA kink that unstacks base pairs and widens the minor groove induced upon strong DNA bending in the X-ray crystal structure of the E. coli catabolite activator protein (Schultz et al., 1991). C. DNA kink that widens the major groove predicted from the molecular dynamics simulations of strained DNA circles by Lankas et al. (Lankas et al., 2006).
Theorists therefore proposed alternative kink-prone models for DNA flexibility. These models suggested the transient appearance of localized weakly stacked segments in the DNA that might be prone to kinking. Such kinks might either preserve base pairing but not base stacking, be accompanied by “bubbling” (local base unpairing to create a flexible hinge), base pair opening (disruption of both base pairing and stacking), or base flipping (where only a flipped base has disrupted base paring and stacking). Two such models, the kinked worm-like chain model (KWLC) and the single-stranded bubble model, both propose local distortions that could strongly enhance bending and bidirectional torsional flexibility (Wiggins et al., 2005; Yan & Marko, 2004). Consideration of the importance of short DNA loops in gene regulation, particularly in bacteria, also prompted models in which short DNA loops readily form with spontaneous kinking to relieve elastic strain, or alternatively, that accessory kinking proteins facilitate such loops. At the same time a model including more microscopic detail to supplement the WLC model was shown to predict enhanced apparent flexibility of short DNAs, due to intrinsically-curved sequences, without the necessity of kinks (Czapla et al., 2006).
Computationally intense all-atom molecular dynamics simulations were also applied to determine if kinking could be justified as an explanation for the Cloutier and Widom result. Lankas and coworkers in 2006 predicted the formation of DNA kinks in 94 bp DNA circles, modeled both with and without torsional strain [(Lankas et al., 2006; Maher, 2006); Fig. 4C]. Interestingly, the kinks most commonly occurred at 5’-CG-3’ steps rather than the predicted 5’-TA-3’ and 5’-CA-3’ steps. This simulation again suggested that kinks might be an inherent DNA response to strong bending and twisting strain. More modeling of DNA kinks ensued (Ghatak & Das, 2007; Popov & Tkachenko, 2005; Randall et al., 2009). Results of these studies indicated that severe DNA distortions, such as the formation of circles smaller than ~85 bp in length, may require alteration of the WLC model to include sharp bending or kinking of DNA.
Controversy has continued in experiments based on AFM and SAXS. Results of some AFM experiments were interpreted as being consistent with unexpectedly flexible DNA (Wiggins et al., 2006), while others agreed well with standard persistence lengths (Witz et al., 2008). Recent SAXS data examining the equilibrium end-to-end distance distributions of short DNAs fragments with gold nanocrystal labels again challenged the WLC model at short DNA lengths (Mathew-Fenn et al., 2008). In this work, the authors reported that stretching fluctuations were much larger than expected from WLC predictions, and that stretching was correlated over at least two turns of the DNA double helix. This interpretation suggested new flexibility regimes for DNA beyond WLC predictions. There have been further Technical Comments challenging and defending this work in the same journal.
4.2 The WLC model fights back
Amidst the flurry of theoretical and experimental work seeking support for new kink-prone models for DNA flexibility, there was renewed support for the applicability of the WLC model to sub-persistence length DNA. Vologodskii and co-workers revisited cyclization experiments of DNA fragments 105–130 bp in length and demonstrated that the WLC model remains adequate for predicting cyclization probabilities of these fragments when assumptions of the assay are scrupulously met (Du et al., 2005). Their experimental study reported a technical flaw explaining the unusually high cyclization probabilities observed by Cloutier and Widom. Because cyclization becomes an increasingly rare event for short, stiff DNAs at low ligase concentration, addition of increasing ligase had been necessary. However, the requirement that formation of both circular and bimolecular ligation products is proportional to ligase concentration (equation 24 above) had not been substantiated for the dimerization reaction under the necessarily high T4 DNA ligase concentrations of the Cloutier and Widom study (Cloutier & Widom, 2004). Du et al. showed that the rate of dimerization lacked a dependence on ligase concentration beyond a threshold value (~100 units/mL for their particular cohesive ends) (Du et al., 2005). Under conditions where assumptions of the fitting model could be shown valid, the WLC chain faithfully predicted the measured values of j-factor from ligation experiments. Du et al. went on to perform experiments with DNA minicircles under high bending strain (but no twisting strain) using nuclease attack to detect kinks in continuous or gapped control DNAs (Du et al., 2008). Minicircles as small as 85 bp in length resisted kinking or other apparent bending deformations unless torsionally strained. Additionally, recent cryo-electron microscopy experiments with the exact sequences studied by Cloutier and Widom suggest that circle formation occurs through smooth bending without DNA kinks (Demurtas et al., 2009). These results suggest that the WLC model is applicable to DNA lengths down to 85 bp.
Likewise, recent analysis of more extensive SAXS experiments led Mastroianni et al. to conclude that when care is taken to model DNA-gold linkages and to study a broad range of DNA lengths, the WLC model (with a conventional 50 nm persistence length estimate) is completely sufficient to explain the SAXS data (Mastroianni et al., 2009). This study considers sequence and salt effects, reporting that they contribute negligibly to the conclusions. Monte Carlo simulation is combined with experimentation to carefully consider the implications nonlinear elasticity versus the classical WLC model. The authors find that the WLC model can adequately describe conformational fluctuations of double-stranded DNA in the range of 1/3 to 2/3 of one persistence length.
Thus, although recent high-profile cyclization and SAXS studies raised the provocative possibility that DNA molecules on the length scale of the persistence length (~150 bp) are unexpectedly flexible, both the cyclization and SAXS studies have been contradicted by subsequent clarifying experiments. The subject remains intriguing, controversial and important. This is because the true character of local DNA behavior determines the energetics of nucleosome positioning, DNA looping, and transcriptional regulation.
5. What causes sequence-dependent DNA curvature and flexibility?
5.1 Sequence-dependence of DNA curvature
One of the first observations suggesting sequence-dependent DNA curvature was anomalously slow electrophoretic mobility through native polyacrylamide gels for certain DNA molecules. A noteworthy example was a segment of protozoan kinetoplast DNA, part of a natural DNA minicircle chromosome. Sequence analysis and subsequent clever gel assays revealed that A4–6 tracts phased with the DNA helical repeat are responsible for the observed mobility effects (Hagerman, 1985; Koo et al., 1986; Wu & Crothers, 1984). This result emphasized a challenging puzzle: what is it about phased A-tracts that causes a gel mobility anomaly? Are the sequences intrinsically curved, or anisotropically flexible? Exactly what sub-sequences have the unusual property (the A-tracts or the intervening ‘non-A’-tracts)? What is the molecular basis for the anomaly? Why do phased 5’-A4T4-3’ sequences induce curvature while 5’-T4A4-3’ sequences do not?
Work in this area led to classical models of DNA curvature that invoked either virtual wedges in dinucleotide stacks (Bolshoy et al., 1991; Cacchione et al., 1989; Calladine et al., 1988) or helical axis deformation at junctions between different doublehelical forms (Crothers et al., 1990; Koo & Crothers, 1988; Koo et al., 1990; Koo et al., 1986; Nadeau & Crothers, 1989). The concept of DNA curvature at such junctions had been predicted earlier (Selsing et al., 1979). The development of these classic models [reviewed by Hagerman (Hagerman, 1990; Hagerman, 1985; Hagerman, 1992)] and recent approaches to predict DNA curvature are addressed in the next section. Discussion here will focus on the possible physical basis for sequence-dependent DNA curvature. It is important to note that all of these models were essentially empirical, assigning microscopic properties to junctions or wedges that would explain the experimental data.
5.2 Electrostatic effects in DNA curvature and flexibility
It is evident that different DNA sequences commonly adopt polymorphic geometries in solution over the range of B, B* and A double helices. Is this polymorphism due only to base pair stacking preferences, or could counterions play a role (Williams & Maher, 2000)? The role of counterions in controlling DNA structure is not understood. As described in section 3 (above), Manning’s influential counterion condensation theory expresses the notion that highly-charged polyelectrolytes, such as DNA, essentially condense counterions from the diffuse bathing solution into a layer of ~1M local concentration near the polymer surface (Manning, 1978). The concentration of this condensed counterion “phase” is predicted to be essentially independent of the bulk counterion concentration. Substantial (but not complete) polyelectrolyte charge screening accompanies counterion condensation, but the magnitude of stretching forces between residual unscreened nearest-neighbor phosphate anion charges along DNA remains poorly understood. Furthermore, NMR experiments have detected counterion distributions that are asymmetric and sequence-dependent (Hud & Feigon, 1997; Hud & Feigon, 2002; Hud et al., 1998; Hud et al., 1999). Related results have been observed using X-ray crystallography (Hamelberg et al., 2000; Hamelberg et al., 2001; Howerton et al., 2001; McFail-Isom et al., 1999; Shui et al., 1998a; Shui et al., 1998b; Sines et al., 2000; Williams & Maher, 2000), free electrophoresis (Dong et al., 2009; Lu & Stellwagen, 2008; Stellwagen et al., 2001) and simulation (Beveridge et al., 1998; McConnell & Beveridge, 2000; Sprous et al., 1998; Young & Beveridge, 1998; Young et al., 1997a; Young et al., 1997b). This has raised stimulating discussion about the degree to which sequence-dependent asymmetric counterion recruitment into the DNA grooves could alter groove geometry and cause double helix polymorphism by unbalancing charge repulsions across the groove (McConnell & Beveridge, 2000; McFail-Isom et al., 1999; Williams & Maher, 2000) or across the double helix (Strauss & Maher, 1994).
These interesting results suggest strong correlations between asymmetry in cation localization, DNA groove geometry, and DNA curvature. However, the cause/effect role of counterion distribution remains both unknown and controversial. Does the asymmetry in counterion distribution arise because preferred cation binding sites are specified by the sequence of base pair edges? Do these cation distributions then exert electrostatic forces that restructure DNA by asymmetrically neutralizing interphosphate stretching forces? Is polymorphism in groove geometry driven by base pair stacking, and counterions simply decorate these sequence-dependent features without influence on DNA structure? These fundamental questions remain unresolved, even in molecular dynamics simulations.
An important contribution to unifying the concepts of ion distributions, helical polymorphisms, and sequence-dependent DNA curvature has been formulated by Hud and co-workers (Hud & Plavec, 2003; Hud & Polak, 2001). The revised junction model of Hud and Plavec invokes the correlation between groove polymorphism and counterion localization. The authors conceive of DNA sequences as participating in structural equilibria between different double-helical forms. In particular, they categorize DNA sequences into three groups (A-tracts, G-tracts, and generic DNA) with different equilibrium distributions between B, B* and A forms (Fig. 5). According to this model, the A-tract group of sequences (length >4, AA, TT, or AT base steps with no TA steps) is more likely to adopt the B*-form with a narrow minor groove rich in counterions. G-tracts are defined as containing only G and C residues with prominent GG steps. These sequences are argued to be more likely to sample the A-DNA conformation featuring a narrow major groove rich in counterions. All other DNA sequences are considered “generic” and most likely to assume B-form. The Hud-Plavec model then proposes a junction explanation for helix curvature. Simple conservation of base stacking between DNA segments with different helical forms alters the helix axis. Phasing of such junctions relative to the DNA helical repeat determines the global curvature of a DNA sequence. The Hud-Plavec model adds coherence to the interpretation of sequence-directed DNA curvature without resolving the cause/effect puzzle of cations and groove geometry.
Fig. 5.
Schematic depiction of the Hud-Plavec model linking counterion distributions, helix polymorphism, and sequence-directed DNA curvature at junctions. I. Proposed sequence-dependent duplex DNA polymorphism between generic DNA (canonical B-form, center), G-tract sequences (propensity for A-form, left) and A-tract sequences (B*-form, right). Grooves (M, major; m, minor) and simplified cation (+) distributions (magenta) are shown. II. Example of sequence-dependent DNA curvature due to junctions between B-form DNA and a 5 bp segment of A-form DNA (red). Helical structures were generated with 3DNA (Zheng et al., 2009). DNA backbones are shown in yellow.
5.3 Sequence-dependence of DNA flexibility
DNA conformation has been shown to be sequence-dependent. In fact, local DNA deformability (softness) with respect to bending and twisting is also sequence-dependent. It remains unknown how sequence-dependent anisotropic deformability influences anomalous gel mobility. Protein recognition of DNA depends on the initial DNA structure (including groove shape and curvature). For protein-DNA complexes involving distorted DNA, the stability of the complex depends on the sequence-dependent pliability of the double helix. An early study suggested that the DNA persistence length could vary 4-fold between the relatively flexible poly(dA)•poly(dT) and the relatively rigid poly(dG)•poly(dC), and the torsional DNA stiffness could vary at least 40-fold (Hogan et al., 1983). Subsequent work has explored relationships between stacking energy, thermal stability, and persistence length (Protozanova et al., 2004; SantaLucia, 1998; Sivolob & Khrapunov, 1995; Virstedt et al., 2004).
As will be discussed in greater detail below, packaging of eukaryotic DNA onto histone octamers in nucleosomes involves substantial DNA deformation. DNA sequences can be characterized or selected for their histone octamer affinity, thus presumably measuring flexibility rather than curvature (Lowary & Widom, 1998). Sequences with a high proclivity for nucleosome formation were shown by DNA cyclization analysis to have 2-fold increased longitudinal flexibility and one third lower torsional constants (Roychoudhury et al., 2000). Among such sequences, the flexibility of alternating A-T was one third higher than mixed sequences (Zhang & Crothers, 2003). Analysis of nucleosome positioning in genomic DNA has proven a fertile approach to deducing apparent sequence requirements for flexibility (Caserta et al., 2009; Drew & Travers, 1985; Kaplan et al., 2009; Satchwell et al., 1986; Segal et al., 2006; Trifonov & Sussman, 1980; Widom, 2001). To a first approximation, sequences favored for deformation in nucleosomes are over-populated by AA/TT/TA dinucleotides phased with the DNA helical repeat (i.e. occurring at intervals of ~10 bp), with GC dinucleotide steps phased 5 bp away. Such sequences appear not to be intrinsically curved, but anisotropically flexible (Lowary & Widom, 1997; Lowary & Widom, 1998; Segal et al., 2006). It should be noted, however, that it remains formally possible that the phased AA/TT/TA pattern favored in nucleosomal DNA is not predominantly due to enhanced bend flexibility. Instead, this sequence signature could endow the DNA with a particularly narrow minor groove that enhances local negative electrical potential in the groove, stabilizing histone binding by strengthening electrostatic contacts with protruding cationic arginines that engage the DNA minor groove at these positions (Rohs et al., 2009).
Once assumed to be monotonous in structure, even fully base-paired DNA displays local sequence-dependent groove geometry, axial curvature, and flexibility. These features may be crucial in the energetics of DNA recognition and deformation by sequence-specific proteins. The importance of these properties for indirect DNA readout by sequence-nonspecific proteins (including histone octamers) suggests that DNA sequence also encodes chromatin packaging and gene expression signals (Segal et al., 2006).
6. Can sequence-dependent DNA curvature and flexibility be predicted?
6.1 Base-pair step models
Given the significance of sequence-dependent DNA curvature and flexibility, the prediction of such properties is an important challenge. A number of early models deduced or proposed sequence-dependent base pair twist, roll, and tilt values for each of the ten unique base pair steps. Examples of models include those involving curvature at non-A-tract sequences (Calladine et al., 1988; Satchwell et al., 1986), those involving curvature within A-tracts (Bolshoy et al., 1991; Cacchione et al., 1989), and those invoking curvature at junctions between helical forms (Koo & Crothers, 1988). The various models have both strengths and weaknesses in their predictive power (Goodsell & Dickerson, 1994). It is important to note that they sought empirically to predict DNA properties without the goal of explaining these properties.
Increasingly sophisticated dinucleotide step models allow prediction of both DNA curvature (Liu & Beveridge, 2001; Young et al., 1995) and flexibility (Czapla et al., 2006; Czapla et al., 2008; Matsumoto & Olson, 2002; Olson et al., 1998; Olson et al., 2004; Olson & Zhurkin, 2000; Swigon et al., 2006; Zheng et al., 2009) from the growing databases of high-resolution DNA and DNA-protein structures. The impressive strategy implemented by Olson and co-workers mines average values and deviations for six base pair step parameters in known structures, allowing DNA structure prediction implemented in a web server tool (Lu & Olson, 2003). Empirical energy functions are deduced, allowing specification of the expected range of thermal motion for each base pair step. These estimates substantiate many established features of duplex DNA deformability, including the conclusion that pyrimidine-purine base pair steps are especially flexible. Recent publications have extended the prediction of DNA stiffness to parameters based on trinucleotide step datasets (Gromiha, 2000).
6.2 Molecular dynamics (MD) simulations and other models
Approaches to both understand and predict sequence-dependent DNA curvature and flexibility have also been undertaken using MD simulations. These strategies have grown in sophistication with increasingly facile parallel computing. MD simulations have been applied to sequence-directed DNA curvature. Initial studies were performed with unstrained DNA segments (Beveridge et al., 1998; Dixit et al., 2005; Flatters et al., 1997; Jayaram et al., 1998; Sprous et al., 1998; Young & Beveridge, 1998; Young et al., 1997b). An international collaboration has resulted in extended MD simulations of DNA sequences representing multiple samples of the 136 possible unique tetranucleotide sequences in duplex DNA (Beveridge et al., 2004). Such efforts have allowed the creation of reference datasets from which to deduce trends and compare results with flexibility parameters extracted from crystal structures. The work also firmly addresses issues of reproducibility, sampling, ion fluctuations, and convergence.
More recent simulations have modeled DNA under various bending and twisting forces to explore induced conformational changes (Harris, 2006). Forces include bending in small minicircles (Curuksu et al., 2009; Lankas et al., 2006; Maher, 2006), stretching (Harris et al., 2005), protein-mediated DNA looping (Balaeff et al., 2004; Czapla et al., 2008; Swigon et al., 2006; Villa et al., 2005), and supercoiling (Harris et al., 2008; Liverpool et al., 2008). Even more complex challenges to predictive modeling include DNA deformed into loops by proteins, or bent onto the surface of proteins.
As discussed in the next section, loop structures are involved in transcriptional repression in bacteria. In eukaryotic cells, DNA commonly exists wrapped tightly onto the histone octamer surface and DNA looping may be important in eukaryotic gene regulation as well. Approaches to modeling these structures and dynamics of such assemblages include several interesting approaches. A statistical mechanical treatment of DNA polymer behavior (Zhang et al., 2006b) has been applied to rationalize length-dependent in vivo DNA looping data in the lac operon (Zhang et al., 2006a). Multiscale modeling and simulation of the same complex were presented by Schulten and co-workers (Balaeff et al., 2004; Villa et al., 2005). This approach coupled molecular dynamics for all-atom models of the protein components with a continuous polymer model of the DNA. Modeling and prediction of lac DNA looping was also undertaken by Olson and co-workers (Swigon et al., 2006) using a theory of sequence-dependent DNA elasticity based on base-pair step sequence. It remains to be seen if tri- or tetranucleotide step data will enrich this approach (Dixit et al., 2005). The complexity of even this simplest of bacterial gene regulatory switches represents a daunting challenge for simulation. This is an expansive area for collaboration to generate experimental data that distinguish between the predictions of the different models. It is crucial that highly-accurate in vivo gene regulation data are available in order to create meaningful quantitative models of gene regulation.
6.3 Predicting DNA shape
An important recent contribution to the prediction of sequence-dependent DNA structure has come through cataloging patterns of base pair accessibility to damage by hydroxyl radicals. This reactive species is similar in size to water, and hydrogen abstraction reaction rates report solvent accessibility of the DNA grooves. It has been demonstrated that hydroxyl radical reactivity patterns measured for a collection of test sequences can then be used to accurately predict reaction patterns for new sequences through di- and trinucleotide matches. This approach to prediction of DNA “topology” (shape accessible to solvent) has sufficient accuracy to allow a survey of genome-wide protein binding site conservation, even when sequence conservation is difficult to detect (Parker et al., 2009).
Careful bioinformatics analysis of three-dimensional structures of protein-DNA complexes has also recently led Honig and co-workers to propose that minor groove negative electrostatic potential is a key recognition element for some proteins (Rohs et al., 2009). This study suggests that minor groove narrowing is a feature of focused electrostatic potential that may be predicted from sequence-structure correlation.
7. How do cells manage the DNA stiffness problem?
7.1 DNA softening in vivo
There have been hints that the apparent stiffness of DNA is lower in living cells than would be predicted from in vitro measurements. This is an intriguing result. Apparent softening of DNA with respect to both bending and twisting is observed in vivo. Initial results came from classic studies of E. coli lactose (lac) operon transcriptional regulation (Fig. 2G) where a DNA repression loop forms in the presence of lac repressor tetramer (Becker et al., 2005; Eismann & Müller-Hill, 1990; Kramer et al., 1988; Kramer et al., 1987; Mossing & Record, 1986; Muller et al., 1996; Oehler et al., 1990). Early estimates suggested enhanced DNA softness to bending (7-fold) and twisting (2-fold) relative to naked DNA studied in solution (Bellomy et al., 1988; Law et al., 1993; Mossing & Record, 1986). Using a statistical-mechanical model of DNA bending and protein-DNA looping, recent revised estimates for the bending and twisting anomalies are 1.6-fold and 3-fold, respectively (Zhang et al., 2006a). The DNA flexibility mystery also applies to eukaryotic DNA organized into chromatin. The spooling of DNA onto histone octamers to form nucleosomes should not, in principle, change its inherent flexibility. The naked “linker” segments of DNA between nucleosomes might be expected to determine the flexibility of the resulting fiber. However, careful comparison of DNA persistence length estimates based on genetic recombination in vitro and in vivo suggest a 2-fold reduction in the DNA bending persistence length (from 50 nm to 27 nm) in vivo (Ringrose et al., 1999).
7.2 Architectural DNA binding proteins
It has been hypothesized that cellular DNA, both prokaryotic and eukaryotic, displays unexpected apparent flexibility because of negative supercoiling and DNA bending proteins that are abundant in cells. Sequence-nonspecific architectural DNA bending proteins have been proposed to decrease the apparent persistence length of DNA by introducing random and transient sites of kinking and bending (Crothers, 1993; Paull et al., 1996; Paull et al., 1993; Paull & Johnson, 1995; Travers et al., 1994). This may be a universal property of architectural DNA binding proteins including the eukaryotic high mobility group B (HMGB) non-histone chromatin proteins and the heat unstable (HU) protein of bacteria (Bianchi, 1994; Thomas & Travers, 2001). A dramatic increase in apparent DNA cyclization propensity was observed when linear DNAs were ligated in the presence of crude heat-treated nuclear extract from human cells, demonstrating the profound capabilities of these proteins (Ross et al., 2001).
High mobility group (HMG) proteins are small, abundant eukaryotic chromatin-associated proteins of three unrelated families (Bustin, 2001; Grosschedl et al., 1994; Hock et al., 2007). HMGA proteins contain AT-hook motifs, HMGN proteins have nucleosome binding domains, and HMGB proteins contain one or two tandem “HMG box” motifs. Structures and DNA bending properties of bacterial HU and eukaryotic HMGB proteins are compared to each other and the histone octamer in Fig. 6. Although all have unrelated structures, HMGB monomers and HU dimers cause strong DNA bending through a combination of minor groove intercalation (by amino acid side chains) and electrostatic interactions involving cationic amino acids that asymmetrically neutralize the DNA double helix.
Fig. 6.
Sequence-nonspecific architectural protein complexes with bent DNA. A. Top and side views of the nucleosome core particle (pdb 1AOI) in which the histone octamer (red) bends 146 bp of DNA by 600°. B. Bacterial HU protein (red) bending DNA (pdb AHU2). C. Yeast Nhp6A (pdb 1J5N), a single-box HMGB protein (red) bending DNA through partial minor groove intercalation of amino acid side chains (white and green) and asymmetric charge neutralization (magenta). D. Two-box mammalian HMGB construct bending DNA (pdb 2GZK). DNA backbones are shown in yellow.
The role of architectural proteins in enhancing apparent flexibility of DNA and chromatin is under study. Architectural proteins appear to influence DNA looping in bacterial gene control. HU has been shown to participate in bending and kinking DNA in the repression loop of the gal operon in vitro (ensemble and single molecules experiments) and in vivo (Aki & Adhya, 1997; Lewis & Adhya, 2002; Lia et al., 2003). Despite decades of study it had not been known if HU might be involved in DNA looping at other repression loops such as lac. New evidence raises this possibility. In vivo assays of lac looping have been performed in several variations (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Kramer et al., 1987; Law et al., 1993; Mossing & Record, 1986; Muller et al., 1996; Oehler et al., 1990). Classic studies by Record and Müller-Hill showed that promoter repression by a weak downstream lac operator is dramatically strengthened by a strong upstream lac operator. Repression as a function of inter-operator distance gives a sensitive readout of the unfavorable energetics associated with DNA (and protein) bending and twisting (Fig. 7A). Repression is leaky when operators are positioned on opposite DNA faces because DNA looping also requires unfavorable DNA twisting. The result is an oscillating dependence of repression looping on inter-operator DNA length, with a period near 10 bp, the helical repeat of DNA (Fig. 7B). Repression is enhanced for properly-phased operators because DNA looping increases the effective repressor concentration experienced by the downstream operator by including collisions with repressor tetramers bound upstream. This in vivo looping system can be analyzed quantitatively (for example, Fig. 7B). Data in the lower panels show reporter gene expression as a function of DNA loop size in the absence or presence of IPTG inducer. It was both interesting and unexpected that faint oscillations in repression were observed even in the presence of saturating IPTG inducer concentrations. Data in the upper panels show the +IPTG/−IPTG ratio.
Fig. 7.
Experimental model of DNA looping in the control of the lactose operon in E. coli. A. Control states of the promoter. Strong (Osym) and weak (O2) operators for binding lac repressor tetramer (red) flank the lac promoter. Unfavorable operator positions that require DNA bending or twisting strain are poorly repressed (“on”), while operator spacings compatible with DNA looping allow gene repression (“off”). B and C. Example data (Becker et al., 2005a) comparing repressed and induced lac promoter expression for different operator spacings. B. Wild type cells under induced (IPTG) or repressed conditions showing lac promoter activity as normalized reporter activities (bottom), or their ratio (top). C. Results for E. coli cells lacking the sequence non-specific protein, HU, showing DNA looping disability.
Thermodynamic modeling of lac looping data has been performed in several ways, all based on the notion that the probability of proximal operator occupancy by repressor is inversely proportional to transcription (Becker et al., 2005; Becker et al., 2007; Becker et al., 2008; Bellomy et al., 1988; Bintu et al., 2005; Law et al., 1993; Zhang et al., 2006a). Fitting of the data in Fig. 7B led Zhang and co-workers (Zhang et al., 2006a) to conclude that the apparent in vivo persistence length of DNA was 95 bp (one-third lower than the in vitro value) and the twist constant was 0.7 × 10−19 erg cm (less than half of the in vitro value). Repression experiments were repeated in isogenic E. coli strains with disruption of the genes encoding HU [(Becker et al., 2005); Fig. 7C]. DNA looping was strongly disabled. In fact, the fit value for the DNA bending persistence length in this strain (128 bp) is close to that expected based on in vitro analysis (Zhang et al., 2006a). This study suggests that HU protein directly participates in lac repression loops, a hypothesis that is now under further investigation.
This in vivo result should not be interpreted as indicating that lac repressor cannot induce short DNA loops without architectural proteins. Indeed, such loops can be elegantly detected in vitro by single molecule tethered particle motion and AFM experiments (Han et al., 2009; Wong et al., 2008) and by classical methods (Kramer et al., 1987). Loop stability may be enhanced in vivo by architectural proteins.
Strikingly, expression of structurally unrelated eukaryotic HMGB architectural proteins can rescue DNA looping in E. coli cells lacking HU (Becker et al., 2005; Becker et al., 2008; Sebastian et al., 2009). This result suggests a fundamental mechanism of architectural proteins in altering DNA physical properties in vivo.
Repression loops comparable to those observed in prokaryotes have not been found in eukaryotic systems, but have been proposed (Zeller et al., 1995). Eukaryotic gene activation involves recruitment of both chromatin remodeling factors (Bhaumik & Green, 2001) and basal transcription machinery (Buratowski, 1994; Ptashne & Gann, 1997; Tjian & Maniatis, 1994) to promoters. Models for eukaryotic promoter and enhancer function have often invoked DNA loops (Ptashne & Gann, 1997; Rippe et al., 1995), but it has been unclear if the looped DNA is naked or assembled into nucleosomal chromatin. Long-range DNA looping in eukaryotes has been suggested by studies of telomeres, locus control regions, and yeast gene transcription termination (Ansari & Hampsey, 2005; Greider, 1999; Zhou et al., 2006). Proof of short-range DNA looping in transcription activation is lacking, though there are intriguing data (Dobi & Winston, 2007). An alternative model is that enhancers function by recruiting chromatin remodeling agents that regionally loosen histone octamers, increasing the exposure of promoter DNA to basal transcription factors and RNA polymerase. On the other hand, powerful new mapping techniques such as the chromosome conformation capture (3C) method [(Dekker et al., 2002; Gondor et al., 2008; Lieberman-Aiden et al., 2009); Fig. 2H] are being applied to monitor DNA folding and looping after cross-linking in living cells. These studies suggest long-range chromatin flexibility (Tolhuis et al., 2002; Vernimmen et al., 2007; Zhou et al., 2006). It is interesting to ask whether the DNA flexibility required for these structures is supported by polymer theory, or if factors such as architectural proteins could play roles. Long-range looping should not be constrained by the stiffness of naked DNA (Allemand et al., 2006; Rippe et al., 1995). Short-range looping is a more challenging question.
Spooling onto histone octamers is not a priori expected to change the bend and twist flexibilities of the unbound linker DNA segments that control the overall flexibility of the chromatin fiber. However, single molecule force-extension studies of reconstituted chromatin fibers have allowed flexibility studies in vitro (Brower-Toland et al., 2002; Kruithof et al., 2009). For example, it was found that the stretch behavior of chromatin was not consistent with the classical WLC model, but showed Hookian spring behavior where linear force-extension plots were obtained at low forces.
Constraints on DNA looping in living eukaryotic cells have also been measured. As described above, rates of site-specific recombination by FLP recombinase as a function of site separation distance (Ringrose et al., 1999). The authors reported in vitro measurements consistent with WLC polymer theory for naked DNA (persistence length near 50 nm). In contrast, simple fits to data obtained in transfected mammalian cells were interpreted as evidence for a 2-fold shorter apparent in vivo persistence length (~27 nm). If true, this result is reminiscent of DNA behavior in bacteria. The result is striking because of the predominance of nucleosomal DNA packaging in vivo. It remains possible that architectural proteins influence DNA looping in eukaryotes by altering the apparent flexibility of the ~50 bp segments of internucleosomal linker DNA.
A particularly interesting study was a genetic approach to understand what factors limit transcription regulation to a local phenomenon in the compact genome of budding yeast (Dobi & Winston, 2007). In this organism, long-range effects of cis regulatory elements could be deleterious. The authors identified mutations that conferred longer-range transcription activation. Interestingly, one of the mutants inactivated the sequence non-specific architectural DNA binding protein Spt2p. This result raises the intriguing possibility that average DNA loop size might be governed by the concentration of architectural proteins in vivo. On the other hand, Johnston and co-workers found that removal of yeast HMGB proteins Nhp6A/B did not influence the distance-dependence of transcription activation, but the potency of the activators themselves (Paull et al., 1996). Thus, it remains unclear whether and how enhanced apparent DNA flexibility is required in eukaryotes, and the role played by architectural DNA binding proteins in eukaryotes vs. prokaryotes (Fig. 8).
Fig. 8.
Architectural DNA binding protein effects on naked DNA. A. The locally stiff DNA double helix (left) adopts more compact conformations (center) in the presence of randomly-bound architectural DNA binding proteins (red triangles), decreasing the average end-end distance (double-headed arrows) as detected by enhanced cyclization rate (right) in the presence of DNA ligase. B. Example of ~ 200 bp circular protein-DNA complex facilitated by HMGB protein Nhp6A (red) in Monte-Carlo simulation. C. Potential role of architectural protein (e.g. HU, red triangle) in stabilizing bacterial repression loops.
8. Future Challenges
Five questions were posed in this review: Why is DNA stiff? How adequate is the WLC model for describing DNA in vitro? What causes sequence-dependent DNA curvature and flexibility? Can sequence-dependent DNA curvature and flexibility be predicted? How do cells manage the DNA stiffness problem? Although progress continues to be made toward answering each of these questions, it is exciting (and sobering) that much remains to be learned. Some particularly fundamental problems remain unresolved. Some future challenges and opportunities in understanding DNA curvature and bending are described here.
Though their roles remain unresolved after more than 50 years, electrostatic effects on the physical properties of DNA clearly deserve further study. The common view, that interphosphate repulsions are effectively screened under physiological conditions, predicts a small effect of bulk salt concentration on DNA persistence length. This leaves unresolved the question of whether (and to what extent) residual phosphate charges after counterion condensation contribute to a stretching tension in double-helical DNA. As described in section 3, there are arguments on both sides of the issue. A convergence of theory, experiment, and simulation is needed. Our own experimental approach has been to perturb DNA electrostatics using chemical or biochemical methods, and to measure resulting changes in DNA shape. Because each kind of perturbation has both electrostatic and non-electrostatic consequences, any given strategy may yield misleading results due to unforeseen non-electrostatic effects. We have sought a consistent pattern (such as DNA bending toward its asymmetrically-neutralized surface) that appears to be independent of the neutralization method. Additional experimental approaches are needed to test theories of DNA stiffness. Furthermore, fundamental electrostatic effects ought to be amenable to molecular dynamics simulations. Current limitations include the proper treatment of ions, the length of simulation, and the need to simulate DNA molecules of sufficient length to deduce bending fluctuations and persistence length. Improved computational methods may provide new opportunities (Materese et al., 2009).
The WLC model has proven to be remarkably effective at predicting aspects of DNA behavior over a wide length range. This review has touched on current efforts to define the lower length limit for applicability of the WLC model. There is now evidence that the WLC model will apply well even to tightly bent and twisted DNA molecules below 100 bp in length. The classic method of DNA ligase-catalyzed cyclization kinetics remains a central tool. There are opportunities for new single molecule or bulk experimental methods to collect DNA flexibility data more rapidly across a wide range of lengths in solution.
Improved prediction of sequence-dependent DNA conformation and flexibility is needed. The mining of knowledge-based dinucleotide and trinucleotide helical parameters from databases of structures and simulations has been impressive. These approaches provide a framework for understanding many cases of sequence-dependent curvature. Similar approaches applied to nucleosome positioning sequences are addressing the problem of predicting sequence-dependent deformability (Caserta et al., 2009). These approaches have not reached consensus (Caserta et al., 2009; Kaplan et al., 2009; Segal et al., 2006). There remains uncertainty about the forces and processes that cause the properties detected when sequence and structure are correlated. Structural databases could be biased, and simulation databases could be inadequate. Many future opportunities exist for accurate prediction of sequence-dependent DNA curvature and flexibility.
Even as new approaches are required to monitor DNA curvature and flexibility over tens to thousands of base pairs in vitro, this is even more true for measuring these properties in vivo. As described in this review, proteins both spool and kink DNA, yielding a material (bacterial or eukaryotic chromatin) whose properties appear different from naked DNA. Powerful qualitative assays such as chromatin conformation capture have created new opportunities. Improvements are needed in our ability to measure in vivo chromatin flexibility and dynamics, whether by functional, optical, or spectroscopic means. Such tools may allow us (finally) to understand how the properties of DNA measured by the biophysicist in dilute solution are managed, exploited, and manipulated by the cell to enable genome packaging, replication, and expression as measured by the biologist.
Acknowledgements
The authors acknowledge the important contributions of present and past students (Joe Azok, John Paul Bida, Laura Bond, Laura Cassiday, Tessa Davis, Robert Den, Phil Hardwidge, Anne Keating, Bob McDonald, Andy Rodrigues, Eric Ross, Nadia Sebastian, Julie Soukup), staff scientists (Matt Ferber, Claudia McDonald, Emily Rueter, Jeff Zimmerman) and collaborators (Anjum Ansari, Luke Czapla, Michael Fried, Barry Gold, Nathan Israeloff, Jason Kahn, Bill Kirk, Stephen Levene, Gerald Manning, Luis Marky, Udayan Mohanty, Wilma Olson, Yuan Ping Pang, Larry Parkhurst, Rob Phillips, Peter Privalov, Ivan Rasnik, Chris Switzer, Yitzhak Tor, Alex Vologodskii, Loren Williams, Mark Williams, Darrin York). The important contributions of Nicole Becker are especially noted. Jason Kahn and Nick Hud provided extremely helpful comments on the manuscript. Work on HMGB proteins in the authors’ lab is funded by the Mayo Foundation for Medical Education and Research and by NIH grant GM75965.
References
- Aki T, Adhya S. Repressor induced site-specific binding of HU for transcriptional regulation. EMBO Journal. 1997;16(12):3666–3674. doi: 10.1093/emboj/16.12.3666. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allemand JF, Cocco S, Douarche N, Lia G. Loops in DNA: an overview of experimental and theoretical approaches. The European physical journal E, Soft matter. 2006;19(3):293–302. doi: 10.1140/epje/i2005-10073-y. [DOI] [PubMed] [Google Scholar]
- Ansari A, Hampsey M. A role for the CPF 3'-end processing machinery in RNAP II-dependent gene looping. Genes and Development. 2005;19(24):2969–2978. doi: 10.1101/gad.1362305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ariel G, Andelman D. Persistence length of a strongly charged rodlike polyelectrolyte in the presence of salt. Physical Reviews E. 2003;67(1 Pt 1):11805–11814. doi: 10.1103/PhysRevE.67.011805. [DOI] [PubMed] [Google Scholar]
- Balaeff A, Mahadevan L, Schulten K. Structural basis for cooperative DNA binding by CAP and lac repressor. Structure. 2004;12(1):123–132. doi: 10.1016/j.str.2003.12.004. [DOI] [PubMed] [Google Scholar]
- Baumann CG, Smith SB, Bloomfield VA, Bustamante C. Ionic effects on the elasticity of single DNA molecules. Proceedings of the National Academy of Sciences USA. 1997;94(12):6185–6190. doi: 10.1073/pnas.94.12.6185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker NA, Kahn JD, Maher LJ., 3rd Bacterial repression loops require enhanced DNA flexibility. Journal of Molecular Biology. 2005;349(4):716–730. doi: 10.1016/j.jmb.2005.04.035. [DOI] [PubMed] [Google Scholar]
- Becker NA, Kahn JD, Maher LJ., 3rd Effects of nucleoid proteins on DNA repression loop formation in Escherichia coli. Nucleic Acids Research. 2007;35(12):3988–4000. doi: 10.1093/nar/gkm419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Becker NA, Kahn JD, Maher LJ., 3RD Eukaryotic HMGB proteins as replacements for HU in E. coli repression loop formation. Nucleic Acids Research. 2008;36(12):4009–4021. doi: 10.1093/nar/gkn353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bednar J, Furrer P, Stasiak A, Dubochet J, Egelman EH, Bates AD. The twist, writhe and overall shape of supercoiled DNA change during counterion-induced transition from a loosely to a tightly interwound superhelix. Possible implications for DNA structure in vivo. Journal of Molecular Biology. 1994;235(3):825–847. doi: 10.1006/jmbi.1994.1042. [DOI] [PubMed] [Google Scholar]
- Bellomy G, Mossing M, Record M. Physical properties of DNA in vivo as probed by the length dependence of the lac operator looping process. Biochemistry. 1988;27:3900–3906. doi: 10.1021/bi00411a002. [DOI] [PubMed] [Google Scholar]
- Bennett MD, Leitch IJ. Genome size evolution in plants. In: Gregory TR, editor. The evolution of the genome. San Diego: Elsevier; 2005. pp. 89–162. [Google Scholar]
- Beveridge DL, Barreiro G, Byun KS, Case DA, Cheatham TE, 3RD, Dixit SB, Giudice E, Lankas F, Lavery R, Maddocks JH, Osman R, Seibert E, Sklenar H, Stoll G, Thayer KM, Varnai P, Young MA. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. I. Research design and results on d(CpG) steps. Biophysical Journal. 2004;87(6):3799–3813. doi: 10.1529/biophysj.104.045252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beveridge DL, Young MA, Sprous D. Modeling of DNA via molecular dynamics simulation: structure, bending, and conformational transitions. In: Leontis NB, Santa Lucia J, editors. Molecular Modeling of Nucleic Acids. Washington, D.C.: American Chemical Society; 1998. pp. 260–284. [Google Scholar]
- Bhaumik SR, Green MR. SAGA is an essential in vivo target of the yeast acidic activator Gal4p. Genes & Development. 2001;15:1935–1945. doi: 10.1101/gad.911401. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bianchi ME. Prokaryotic HU and eukaryotic HMG1: a kinked relationship. Molecular Microbiology. 1994;14(1):1–5. doi: 10.1111/j.1365-2958.1994.tb01261.x. [DOI] [PubMed] [Google Scholar]
- Bintu L, Buchler NE, Garcia HG, Gerland U, Hwa T, Kondev J, Phillips R. Transcriptional regulation by the numbers: models. Current opinion in genetics & development. 2005;15(2):116–124. doi: 10.1016/j.gde.2005.02.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bloomfield VA. DNA condensation by multivalent cations. Biopolymers. 1997;44(3):269–282. doi: 10.1002/(SICI)1097-0282(1997)44:3<269::AID-BIP6>3.0.CO;2-T. [DOI] [PubMed] [Google Scholar]
- Bolshoy A, Mcnamara P, Harrington RE, Trifonov EN. Curved DNA without A-A: Experimental estimation of all 16 DNA wedge angles. Proceedings of the National Academy of Sciences USA. 1991;88:2312–2316. doi: 10.1073/pnas.88.6.2312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brower-Toland BD, Smith CL, Yeh RC, Lis JT, Peterson CL, Wang MD. Mechanical disruption of individual nucleosomes reveals a reversible multistage release of DNA. Proceedings of the National Academy of Sciences USA. 2002;99(4):1960–1965. doi: 10.1073/pnas.022638399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buratowski S. The basics of basal transcription by RNA polymerase II. Cell. 1994;77:1–3. doi: 10.1016/0092-8674(94)90226-7. [DOI] [PubMed] [Google Scholar]
- Bustamante C, Smith SB, Liphardt J, Smith D. Single-molecule studies of DNA mechanics. Current Opinion in Structural Biology. 2000;10(3):279–285. doi: 10.1016/s0959-440x(00)00085-3. [DOI] [PubMed] [Google Scholar]
- Bustin M. Revised nomenclature for high mobility group (HMG) chromosomal proteins. Trends in Biochemical Science. 2001;26(3):152–153. doi: 10.1016/s0968-0004(00)01777-1. [DOI] [PubMed] [Google Scholar]
- Cacchione S, De Santis P, Foti D, Palleschi A, Savino M. Periodical polydeoxynucleotides and DNA curvature. Biochemistry. 1989;28(22):8706–8713. doi: 10.1021/bi00448a006. [DOI] [PubMed] [Google Scholar]
- Calladine CR, Drew HR, Mccall MJ. The intrinsic curvature of DNA in solution. Journal of Molecular Biology. 1988;201(1):127–137. doi: 10.1016/0022-2836(88)90444-5. [DOI] [PubMed] [Google Scholar]
- Cantor C, Schimmel P. Biophysical Chemistry Part III: The behavior of biological macromolecules. New York: W. H. Freeman; 1980. [Google Scholar]
- Caserta M, Agricola E, Churcher M, Hiriart E, Verdone L, Di Mauro E, Travers A. A translational signature for nucleosome positioning in vivo. Nucleic Acids Research. 2009;37(16):5309–5321. doi: 10.1093/nar/gkp574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cloutier TE, Widom J. Spontaneous sharp bending of double-stranded DNA. Molecular Cell. 2004;14(3):355–362. doi: 10.1016/s1097-2765(04)00210-2. [DOI] [PubMed] [Google Scholar]
- Cloutier TE, Widom J. DNA twisting flexibility and the formation of sharply looped protein-DNA complexes. Proceedings of the National Academy of Sciences USA. 2005;102(10):3645–3650. doi: 10.1073/pnas.0409059102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cluzel P, Lebrun A, Heller C, Lavery R, Viovy JL, Chatenay D, Caron F. DNA: an extensible molecule. Science. 1996;271(5250):792–794. doi: 10.1126/science.271.5250.792. [DOI] [PubMed] [Google Scholar]
- Cohen AE, Moerner WE. Method for trapping and manipulating nanoscale objects in solution. Applied Physics Letters. 2005;86(9):093109. [Google Scholar]
- Crick FH, Klug A. Kinky helix. Nature. 1975;255(5509):530–533. doi: 10.1038/255530a0. [DOI] [PubMed] [Google Scholar]
- Crothers DM. Architectural elements in nucleoprotein complexes. Current Biology. 1993;3(10):675–676. doi: 10.1016/0960-9822(93)90065-v. [DOI] [PubMed] [Google Scholar]
- Crothers DM, Drak J. Global features of DNA structure by comparative gel electrophoresis. Methods in Enzymology. 1992;212:46–71. doi: 10.1016/0076-6879(92)12005-b. [DOI] [PubMed] [Google Scholar]
- Crothers DM, Drak J, Kahn JD, Levene SD. DNA bending, flexibility, and helical repeat by cyclization kinetics. Methods in Enzymology. 1992;212:3–29. doi: 10.1016/0076-6879(92)12003-9. [DOI] [PubMed] [Google Scholar]
- Crothers DM, Haran TE, Nadeau JG. Intrinsically bent DNA. Journal of Biological Chemistry. 1990;265:7093–7096. [PubMed] [Google Scholar]
- Curuksu J, Zacharias M, Lavery R, Zakrzewska K. Local and global effects of strong DNA bending induced during molecular dynamics simulations. Nucleic Acids Research. 2009;37(11):3766–3773. doi: 10.1093/nar/gkp234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Czapla L, Swigon D, Olson WK. Sequence-Dependent Effects in the Cyclization of Short DNA. Journal of Chemical Theory and Computation. 2006;2(3):685–695. doi: 10.1021/ct060025+. [DOI] [PubMed] [Google Scholar]
- Czapla L, Swigon D, Olson WK. Effects of the Nucleoid Protein HU on the Structure, Flexibility, and Ring-Closure Properties of DNA Deduced from Monte Carlo Simulations. Journal of Molecular Biology. 2008 doi: 10.1016/j.jmb.2008.05.088. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dehaseth PL, Lohman TM, Record MT., Jr Nonspecific interaction of lac repressor with DNA: an association reaction driven by counterion release. Biochemistry. 1977;16(22):4783–4790. doi: 10.1021/bi00641a004. [DOI] [PubMed] [Google Scholar]
- Dekker J, Rippe K, Dekker M, Kleckner N. Capturing chromosome conformation. Science. 2002;295(5558):1306–1311. doi: 10.1126/science.1067799. [DOI] [PubMed] [Google Scholar]
- Demurtas D, Amzallag A, Rawdon EJ, Maddocks JH, Dubochet J, Stasiak A. Bending modes of DNA directly addressed by cryo-electron microscopy of DNA minicircles. Nucleic Acids Research. 2009;37(9):2882–2893. doi: 10.1093/nar/gkp137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickerson RE, Goodsell D, Kopka ML. MPD and DNA bending in crystals and in solution. Journal of Molecular Biology. 1996;256(1):108–125. doi: 10.1006/jmbi.1996.0071. [DOI] [PubMed] [Google Scholar]
- Dixit SB, Beveridge DL, Case DA, Cheatham TE, Giudice E, Lankas F, Lavery R, Maddocks JH, Osman R, Sklenar H, Thayer KM, Varnai P. Molecular dynamics simulations of the 136 unique tetranucleotide sequences of DNA oligonucleotides. II: sequence context effects on the dynamical structures of the 10 unique dinucleotide steps. Biophysical Journal. 2005;89(6):3721–3740. doi: 10.1529/biophysj.105.067397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobi KC, Winston F. Analysis of transcriptional activation at a distance in Saccharomyces cerevisiae. Molecular and Cellular Biology. 2007;27(15):5575–5586. doi: 10.1128/MCB.00459-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dong Q, Stellwagen E, Stellwagen NC. Monovalent cation binding in the minor groove of DNA A-tracts. Biochemistry. 2009;48(5):1047–1055. doi: 10.1021/bi8020718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Douarche N, Cocco S. Protein-mediated DNA loops: effects of protein bridge size and kinks. Physical Reviews E, Statistical, Nonlinear, and Soft Matter Physics. 2005;72(6 Pt 1):061902. doi: 10.1103/PhysRevE.72.061902. [DOI] [PubMed] [Google Scholar]
- Drew HR, Travers AA. DNA bending and its relation to nucleosome positioning. Journal of Molecular Biology. 1985;186:773–790. doi: 10.1016/0022-2836(85)90396-1. [DOI] [PubMed] [Google Scholar]
- Du Q, Kotlyar A, Vologodskii A. Kinking the double helix by bending deformation. Nucleic Acids Research. 2008;36(4):1120–1128. doi: 10.1093/nar/gkm1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Q, Smith C, Shiffeldrim N, Vologodskaia M, Vologodskii A. Cyclization of short DNA fragments and bending fluctuations of the double helix. Proceedings of the National Academy of Sciences USA. 2005;102(15):5397–5402. doi: 10.1073/pnas.0500983102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eismann ER, Müller-Hill B. Lac repressor forms stable loops in vitro with supercoiled wild-type lac DNA containing all three natural lac operators. Journal of Molecular Biology. 1990;213(4):763–775. doi: 10.1016/S0022-2836(05)80262-1. [DOI] [PubMed] [Google Scholar]
- Flatters D, Young M, Beveridge DL, Lavery R. Conformational properties of the TATA-box binding sequence of DNA. Journal of Biomolecular Structure & Dynamics. 1997;14(6):757–765. doi: 10.1080/07391102.1997.10508178. [DOI] [PubMed] [Google Scholar]
- Fujimoto BS, Schurr JM. Dependence of the torsional rigidity of DNA on base composition. Nature. 1990;344(6262):175–177. doi: 10.1038/344175a0. [DOI] [PubMed] [Google Scholar]
- Garcia HG, Grayson P, Han L, Inamdar M, Kondev J, Nelson PC, Phillips R, Widom J, Wiggins PA. Biological consequences of tightly bent DNA: The other life of a macromolecular celebrity. Biopolymers. 2007;85:115–130. doi: 10.1002/bip.20627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gelbart WM, Knobler CM. Virology. Pressurized viruses. Science. 2009;323(5922):1682–1683. doi: 10.1126/science.1170645. [DOI] [PubMed] [Google Scholar]
- Ghatak A, Das AL. Kink instability of a highly deformable elastic cylinder. Physical review letters. 2007;99(7):076101. doi: 10.1103/PhysRevLett.99.076101. [DOI] [PubMed] [Google Scholar]
- Gondor A, Rougier C, Ohlsson R. High-resolution circular chromosome conformation capture assay. Nature Protocols. 2008;3(2):303–313. doi: 10.1038/nprot.2007.540. [DOI] [PubMed] [Google Scholar]
- Goodsell DS, Dickerson RE. Bending and curvature calculations in B-DNA. Nucleic Acids Research. 1994;22:5497–5503. doi: 10.1093/nar/22.24.5497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosule LC, Schellman JA. DNA condensation with polyamines. I. Spectroscopic studies. Journal of Molecular Biology. 1978;121:311–326. doi: 10.1016/0022-2836(78)90366-2. [DOI] [PubMed] [Google Scholar]
- Gregory TR. Genome size evolution in animals. In: Gregory TR, editor. The evolution of the genome. San Diego: Elsevier; 2005. pp. 3–87. [Google Scholar]
- Greider CW. Telomeres do D-loop-T-loop. Cell. 1999;97(4):419–422. doi: 10.1016/s0092-8674(00)80750-3. [DOI] [PubMed] [Google Scholar]
- Gromiha MM. Structure based sequence dependent stiffness scale for trinucleotides: a direct method. Journal of Biological Physics. 2000;26:43–50. doi: 10.1023/A:1005250718139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grosschedl R, Giese K, Pagel J. HMG domain proteins: architectural elements in the assembly of nucleoprotein structures. Trends in Genetics. 1994;10(3):94–100. doi: 10.1016/0168-9525(94)90232-1. [DOI] [PubMed] [Google Scholar]
- Guo Z, Taubes CH, Oh J-E, Maher LJ, III, Mohanty U. DNA on a Tube: Electrostatic Contribution to Stiffness. J. Phys. Chem. B. 2008;112(50):16163–16169. doi: 10.1021/jp806260h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagerman KR, Hagerman PJ. Helix rigidity of DNA: the meroduplex as an experimental paradigm. Journal of Molecular Biology. 1996;260(2):207–223. doi: 10.1006/jmbi.1996.0393. [DOI] [PubMed] [Google Scholar]
- Hagerman P. Sequence-directed curvature of DNA. Annual Review of Biochemistry. 1990;59:755–781. doi: 10.1146/annurev.bi.59.070190.003543. [DOI] [PubMed] [Google Scholar]
- Hagerman PJ. Investigation of the flexibility of DNA using transient electric birefringence. Biopolymers. 1981;20(7):1503–1535. doi: 10.1002/bip.1981.360200710. [DOI] [PubMed] [Google Scholar]
- Hagerman PJ. Sequence dependence of the curvature of DNA: a test of the phasing hypothesis. Biochemistry. 1985;24(25):7033–7037. doi: 10.1021/bi00346a001. [DOI] [PubMed] [Google Scholar]
- Hagerman PJ. Flexibility of DNA. Annual Review of Biophysics and Biophysical Chemistry. 1988;17:265–286. doi: 10.1146/annurev.bb.17.060188.001405. [DOI] [PubMed] [Google Scholar]
- Hagerman PJ. Straightening out the bends in curved DNA. Biochimica et Biophysica Acta. 1992;1131:125–132. doi: 10.1016/0167-4781(92)90066-9. [DOI] [PubMed] [Google Scholar]
- Hagerman PJ, Ramadevi VA. Application of the method of phage T4 DNA ligase-catalyzed ring-closure to the study of DNA structure. I. Computational analysis. Journal of Molecular Biology. 1990;212(2):351–362. doi: 10.1016/0022-2836(90)90130-E. [DOI] [PubMed] [Google Scholar]
- Hamelberg D, Mcfail-Isom L, Williams LD, Wilson WD. Flexible structure of DNA: Ion dependence of minor-groove structure and dynamics. Journal of the American Chemical Society. 2000;122(43):10513–10520. [Google Scholar]
- Hamelberg D, Williams LD, Wilson WD. Influence of the dynamic positions of cations on the structure of the DNA minor groove: sequence-dependent effects. Journal of the American Chemical Society. 2001;123(32):7745–7755. doi: 10.1021/ja010341s. [DOI] [PubMed] [Google Scholar]
- Han L, Garcia HG, Blumberg S, Towles KB, Beausang JF, Nelson PC, Phillips R. Concentration and length dependence of DNA looping in transcriptional regulation. PLoS ONE. 2009;4(5):e5621. doi: 10.1371/journal.pone.0005621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardwidge PR, Pang YP, Zimmerman JM, Vaghefi M, Hogrefe R, Maher LJ. Nucleic Acids: Curvature and Deformation. Washington, DC: American Chemical Society; 2009. Phosphate Crowding and DNA Bending; pp. 111–131. [Google Scholar]
- Harris SA. Modelling the biomechanical properties of DNA using computer simulation. Philosophical transactions Series A, Mathematical, physical, and engineering sciences. 2006;364(1849):3319–3334. doi: 10.1098/rsta.2006.1906. [DOI] [PubMed] [Google Scholar]
- Harris SA, Laughton CA, Liverpool TB. Mapping the phase diagram of the writhe of DNA nanocircles using atomistic molecular dynamics simulations. Nucleic Acids Research. 2008;36(1):21–29. doi: 10.1093/nar/gkm891. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris SA, Sands ZA, Laughton CA. Molecular dynamics simulations of duplex stretching reveal the importance of entropy in determining the biomechanical properties of DNA. Biophysical Journal. 2005;88(3):1684–1691. doi: 10.1529/biophysj.104.046912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey SC, Dlakic M, Griffith J, Harrington R, Park K, Sprous D, Zacharias W. What is the basis of sequence-directed curvature in DNAs containing A tracts? Journal of Biomolecular Structure and Dynamics. 1995;13(2):301–307. doi: 10.1080/07391102.1995.10508841. [DOI] [PubMed] [Google Scholar]
- Hock R, Furusawa T, Ueda T, Bustin M. HMG chromosomal proteins in development and disease. Trends in Cell Biology. 2007;17(2):72–79. doi: 10.1016/j.tcb.2006.12.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hogan M, Legrange J, Austin B. Dependence of DNA helix flexibility on base composition. Nature. 1983;304(5928):752–754. doi: 10.1038/304752a0. [DOI] [PubMed] [Google Scholar]
- Hogan ME, Rooney TF, Austin RH. Evidence for kinks in DNA folding in the nucleosome. Nature. 1987;328(6130):554–557. doi: 10.1038/328554a0. [DOI] [PubMed] [Google Scholar]
- Howerton SB, Sines CC, Vanderveer D, Williams LD. Locating monovalent cations in the grooves of B-DNA. Biochemistry. 2001;40(34):10023–10031. doi: 10.1021/bi010391+. [DOI] [PubMed] [Google Scholar]
- Hud NV, Downing KH, Balhorn R. A constant radius of curvature model for the organization of DNA in toroidal condensates. Proceedings of National Academy of Science USA. 1995;92:3581–3585. doi: 10.1073/pnas.92.8.3581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hud NV, Feigon J. Localization of divalent metal ions in the minor groove of DNA A-tracts. Journal of the American Chemical Society. 1997;119(24):5756–5757. [Google Scholar]
- Hud NV, Feigon J. Characterization of divalent cation localization in the minor groove of the AnTn and TnAn DNA sequence elements by 1H NMR spectroscopy and manganese(II) Biochemistry. 2002;41(31):9900–9910. doi: 10.1021/bi020159j. [DOI] [PubMed] [Google Scholar]
- Hud NV, Plavec J. A unified model for the origin of DNA sequence-directed curvature. Biopolymers. 2003;69(1):144–158. doi: 10.1002/bip.10364. [DOI] [PubMed] [Google Scholar]
- Hud NV, Polak M. DNA-cation interactions: The major and minor grooves are flexible ionophores. Current Opinion in Structural Biology. 2001;11(3):293–301. doi: 10.1016/s0959-440x(00)00205-0. [DOI] [PubMed] [Google Scholar]
- Hud NV, Schultze P, Feigon J. Ammonium ion as an NMR probe for monovalent cation coordination sites of DNA quadruplexes. Journal of the American Chemical Society. 1998;120(25):6403–6404. [Google Scholar]
- Hud NV, Sklenar V, Feigon J. Localization of ammonium ions in the minor groove of DNA duplexes in solution and the origin of DNA A-tract bending. Journal of Molecular Biology. 1999;286(3):651–660. doi: 10.1006/jmbi.1998.2513. [DOI] [PubMed] [Google Scholar]
- Jacob F, Monod J. Genetic regulatory mechanisms in the synthesis of proteins. Journal of Molecular Biology. 1961;3:318–356. doi: 10.1016/s0022-2836(61)80072-7. [DOI] [PubMed] [Google Scholar]
- Jayaram B, Sprous D, Young MA, Beveridge DL. Free energy analysis of the conformational preferences of A and B forms of DNA in solution. Journal of the American Chemical Society. 1998;120(41):10629–10633. [Google Scholar]
- Kahn JD, Crothers DM. Protein-induced bending and DNA cyclization. Proceeding of the National Academy of Sciences USA. 1992;89:6343–6347. doi: 10.1073/pnas.89.14.6343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kahn JD, Yun E, Crothers DM. Detection of localized DNA flexibility. Nature. 1994;368:163–166. doi: 10.1038/368163a0. [DOI] [PubMed] [Google Scholar]
- Kaplan N, Moore IK, Fondufe-Mittendorf Y, Gossett AJ, Tillo D, Field Y, Leproust EM, Hughes TR, Lieb JD, Widom J, Segal E. The DNA-encoded nucleosome organization of a eukaryotic genome. Nature. 2009;458(7236):362–366. doi: 10.1038/nature07667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koo H-S, Crothers DM. Calibration of DNA curvature and a unified description of sequence-directed bending. Proceedings of National Academy of Science USA. 1988;85:1763–1767. doi: 10.1073/pnas.85.6.1763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koo H-S, Drak J, Rice JA, Crothers DM. Determination of the extent of DNA bending by an adenine-thymine tract. Biochemistry. 1990;29:4227–4234. doi: 10.1021/bi00469a027. [DOI] [PubMed] [Google Scholar]
- Koo H-S, Wu H-M, Crothers DM. DNA bending at adenine-thymine tracts. Nature. 1986;320:501–506. doi: 10.1038/320501a0. [DOI] [PubMed] [Google Scholar]
- Kosikov KM, Gorin AA, Lu XJ, Olson WK, Manning GS. Bending of DNA by asymmetric charge neutralization: all-atom energy simulations. Journal of the American Chemical Society. 2002;124(17):4838–4847. doi: 10.1021/ja0125218. [DOI] [PubMed] [Google Scholar]
- Kramer H, Amouyal M, Nordheim A, Müller-Hill B. DNA supercoiling changes the spacing requirements of two lac operators for DNA loop formation with lac repressor. EMBO Journal. 1988;7:547–556. doi: 10.1002/j.1460-2075.1988.tb02844.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kramer H, Niemoller M, Amouyal M, Revet B, Von Wilcken-Bergmann B, Müller-Hill B. lac repressor forms loops with linear DNA carrying two suitably spaced lac operators. EMBO Journal. 1987;6(5):1481–1491. doi: 10.1002/j.1460-2075.1987.tb02390.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kratky O, Porod G. Röntgenuntersuchung gelöster fadenmoleküle. Recueil des Travaux Chimiques des Pays-Bas. 1949;68:1106–1123. [Google Scholar]
- Kruithof M, Chien FT, Routh A, Logie C, Rhodes D, Van Noort J. Single-molecule force spectroscopy reveals a highly compliant helical folding for the 30-nm chromatin fiber. Nature Sructural & Molecular Biology. 2009;16(5):534–540. doi: 10.1038/nsmb.1590. [DOI] [PubMed] [Google Scholar]
- Kuznetsov SV, Sugimura S, Vivas P, Crothers DM, Ansari A. Direct observation of DNA bending/unbending kinetics in complex with DNA-bending protein IHF. Proceedings of the National Academy of Sciences USA. 2006;103(49):18515–18520. doi: 10.1073/pnas.0608394103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lankas F, Lavery R, Maddocks JH. Kinking occurs during molecular dynamics simulations of small DNA minicircles. Structure. 2006;14(10):1527–1534. doi: 10.1016/j.str.2006.08.004. [DOI] [PubMed] [Google Scholar]
- Law SM, Bellomy GR, Schlax PJ, Record MT., Jr In vivo thermodynamic analysis of repression with and without looping in lac constructs. Estimates of free and local lac repressor concentrations and of physical properties of a region of supercoiled plasmid DNA in vivo. Journal of Molecular Biology. 1993;230(1):161–173. doi: 10.1006/jmbi.1993.1133. [DOI] [PubMed] [Google Scholar]
- Lewis DE, Adhya S. In vitro repression of the gal promoters by GalR and HU depends on the proper helical phasing of the two operators. Journal of Biological Chemistry. 2002;277(4):2498–2504. doi: 10.1074/jbc.M108456200. [DOI] [PubMed] [Google Scholar]
- Lia G, Bensimon D, Croquette V, Allemand JF, Dunlap D, Lewis DE, Adhya S, Finzi L. Supercoiling and denaturation in Gal repressor/heat unstable nucleoid protein (HU)-mediated DNA looping. Proceedings of the National Academy of Sciences USA. 2003;100(20):11373–11377. doi: 10.1073/pnas.2034851100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E, Van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, Sandstrom R, Bernstein B, Bender MA, Groudine M, Gnirke A, Stamatoyannopoulos J, Mirny LA, Lander ES, Dekker J. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326(5950):289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, Beveridge DL. A refined prediction method for gel retardation of DNA oligonucleotides from dinucleotide step parameters: reconciliation of DNA bending models with crystal structure data. Journal of Biomolecular Structure and Dynamics. 2001;18(4):505–526. doi: 10.1080/07391102.2001.10506684. [DOI] [PubMed] [Google Scholar]
- Liverpool TB, Harris SA, Laughton CA. Supercoiling and denaturation of DNA loops. Physical review letters. 2008;100(23):238103. doi: 10.1103/PhysRevLett.100.238103. [DOI] [PubMed] [Google Scholar]
- Lohman TM, Dehaseth PL, Record MT., Jr Pentalysine-deoxyribonucleic acid interactions: a model for the general effects of ion concentrations on the interactions of proteins with nucleic acids. Biochemistry. 1980;19(15):3522–3530. doi: 10.1021/bi00556a017. [DOI] [PubMed] [Google Scholar]
- Lowary PT, Widom J. Nucleosome packaging and nucleosome positioning of genomic DNA. Proceedings of the National Academy of Sciences USA. 1997;94(4):1183–1188. doi: 10.1073/pnas.94.4.1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowary PT, Widom J. New DNA sequence rules for high affinity binding to histone octamer and sequence-directed nucleosome positioning. Journal of Molecular Biology. 1998;276(1):19–42. doi: 10.1006/jmbi.1997.1494. [DOI] [PubMed] [Google Scholar]
- Lu XJ, Olson WK. 3DNA: a software package for the analysis, rebuilding and visualization of three-dimensional nucleic acid structures. Nucleic Acids Research. 2003;31(17):5108–5121. doi: 10.1093/nar/gkg680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Y, Stellwagen NC. Monovalent cation binding by curved DNA molecules containing variable numbers of a-tracts. Biophysical Journal. 2008;94(5):1719–1725. doi: 10.1529/biophysj.107.121236. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luger K, Mader AW, Richmond RK, Sargent DF, Richmond TJ. Crystal structure of the nucleosome core particle at 2.8 A resolution. Nature. 1997;389(6648):251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- Macdonald D, Herbert K, Zhang X, Pologruto T, Lu P. Solution structure of an A-tract DNA bend. Journal of Molecular Biology. 2001;306(5):1081–1098. doi: 10.1006/jmbi.2001.4447. [DOI] [PubMed] [Google Scholar]
- Maher LJ., 3rd DNA kinks available…if needed. Structure. 2006;14(10):1479–1480. doi: 10.1016/j.str.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Manning GS. The molecular theory of polyelectrolyte solutions with applications to the electrostatic properties of polynucleotides. Quarterly Reviews of Biophysics. 1978;2:179–246. doi: 10.1017/s0033583500002031. [DOI] [PubMed] [Google Scholar]
- Manning GS. The persistence length of DNA is reached from the persistence length of its null isomer through an internal electrostatic stretching force. Biophysical Journal. 2006;91(10):3607–3616. doi: 10.1529/biophysj.106.089029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manning GS, Ebralidse KK, Mirzabekov AD, Rich A. An estimate of the extent of folding of nucleosomal DNA by laterally asymmetric neutralization of phosphate groups. Journal of Biomolecular Structure and Dynamics. 1989;6:877–889. doi: 10.1080/07391102.1989.10506519. [DOI] [PubMed] [Google Scholar]
- Mastroianni AJ, Sivak DA, Geissler PL, Alivisatos AP. Probing the conformational distributions of subpersistence length DNA. Biophysical Journal. 2009;97(5):1408–1417. doi: 10.1016/j.bpj.2009.06.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Materese CK, Savelyev A, Papoian GA. Counterion atmosphere and hydration patterns near a nucleosome core particle. Journal of the American Chemical Society. 2009;131(41):15005–15013. doi: 10.1021/ja905376q. [DOI] [PubMed] [Google Scholar]
- Mathew-Fenn RS, Das R, Harbury PA. Remeasuring the double helix. Science. 2008;322(5900):446–449. doi: 10.1126/science.1158881. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsumoto A, Olson WK. Sequence-dependent motions of DNA: a normal mode analysis at the base-pair level. Biophysical Journal. 2002;83(1):22–41. doi: 10.1016/S0006-3495(02)75147-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mccauley M, Hardwidge PR, Maher LJ, 3rd, Williams MC. Dual binding modes for an HMG domain from human HMGB2 on DNA. Biophysical Journal. 2005;89(1):353–364. doi: 10.1529/biophysj.104.052068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mcconnell KJ, Beveridge DL. DNA structure: What's in charge? Journal of Molecular Biology. 2000;304(5):803–820. doi: 10.1006/jmbi.2000.4167. [DOI] [PubMed] [Google Scholar]
- Mcdonald RJ, Dragan AI, Kirk WR, Neff KL, Privalov PL, Maher LJ., 3rd DNA bending by charged peptides: electrophoretic and spectroscopic analyses. Biochemistry. 2007;46(9):2306–2316. doi: 10.1021/bi061921a. [DOI] [PubMed] [Google Scholar]
- Mcfail-Isom L, Sines CC, Williams LD. DNA structure: cations in charge? Current Opinion in Structural Biology. 1999;9(3):298–304. doi: 10.1016/S0959-440X(99)80040-2. [DOI] [PubMed] [Google Scholar]
- Mills JB, Hagerman PJ. Origin of the intrinsic rigidity of DNA. Nucleic Acids Research. 2004;32(13):4055–4059. doi: 10.1093/nar/gkh740. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mills JB, Vacano E, Hagerman PJ. Flexibility of single-stranded DNA: use of gapped duplex helices to determine the persistence lengths of poly(dT) and poly(dA) Journal of Molecular Biology. 1999;285(1):245–257. doi: 10.1006/jmbi.1998.2287. [DOI] [PubMed] [Google Scholar]
- Morgan MA, Okamoto K, Kahn JD, English DS. Single-molecule spectroscopic determination of lac repressor-DNA loop conformation. Biophysical Journal. 2005;89(4):2588–2596. doi: 10.1529/biophysj.105.067728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mossing MC, Record MT., Jr Upstream operators enhance repression of the lac promoter. Science. 1986;233(4766):889–892. doi: 10.1126/science.3090685. [DOI] [PubMed] [Google Scholar]
- Moulaei T, Maehigashi T, Lountos GT, Komeda S, Watkins D, Stone MP, Marky LA, Li JS, Gold B, Williams LD. Structure of B-DNA with cations tethered in the major groove. Biochemistry. 2005;44(20):7458–7468. doi: 10.1021/bi050128z. [DOI] [PubMed] [Google Scholar]
- Muller J, Oehler S, Müller-Hill B. Repression of lac promoter as a function of distance, phase and quality of an auxiliary lac operator. Journal of Molecular Biology. 1996;257(1):21–29. doi: 10.1006/jmbi.1996.0143. [DOI] [PubMed] [Google Scholar]
- Nadeau JG, Crothers DM. Structural basis for DNA bending. Proceedings of the National Academy of Sciences USA. 1989;86:2622–2626. doi: 10.1073/pnas.86.8.2622. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakabachi A, Yamashita A, Toh H, Ishikawa H, Dunbar HE, Moran NA, Hattori M. The 160-kilobase genome of the bacterial endosymbiont Carsonella. Science. 2006;314(5797):267. doi: 10.1126/science.1134196. [DOI] [PubMed] [Google Scholar]
- Nguyen TT, Shklovskii BI. Persistence length of a polyelectrolyte in salty water: Monte Carlo study. Physical Reviews. E. 2002;66(2 Pt 1) doi: 10.1103/PhysRevE.66.021801. 021801. [DOI] [PubMed] [Google Scholar]
- Noothi SK, Kombrabail M, Kundu TK, Krishnamoorthy G, Rao BJ. Enhanced DNA dynamics due to cationic reagents, topological states of dsDNA and high mobility group box 1 as probed by PicoGreen. FEBS Journal. 2009;276(2):541–551. doi: 10.1111/j.1742-4658.2008.06802.x. [DOI] [PubMed] [Google Scholar]
- Oehler S, Eismann ER, Kramer H, Müller-Hill B. The three operators of the lac operon cooperate in repression. EMBO Journal. 1990;9(4):973–979. doi: 10.1002/j.1460-2075.1990.tb08199.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oehler S, Müller-Hill B. High Local Concentration: A Fundamental Strategy of Life. Journal of Molecular Biology. 2009;395(2):242–253. doi: 10.1016/j.jmb.2009.10.056. [DOI] [PubMed] [Google Scholar]
- Okonogi TM, Alley SC, Harwood EA, Hopkins PB, Robinson BH. Phosphate backbone neutralization increases duplex DNA flexibility: A model for protein binding. Proceedings of National Academy of Science USA. 2002;99:4156–4160. doi: 10.1073/pnas.072067799. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Okonogi TM, Reese AW, Alley SC, Hopkins PB, Robinson BH. Flexibility of duplex DNA on the submicrosecond timescale. Biophysical Journal. 1999;77(6):3256–3276. doi: 10.1016/S0006-3495(99)77157-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson WK, Gorin AA, Lu XJ, Hock LM, Zhurkin VB. DNA sequence-dependent deformability deduced from protein-DNA crystal complexes. Proceedings of the National Academy of Sciences USA. 1998;95(19):11163–11168. doi: 10.1073/pnas.95.19.11163. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olson WK, Swigon D, Coleman BD. Implications of the dependence of the elastic properties of DNA on nucleotide sequence. Philosophical transactions Series A, Mathematical, physical, and engineering sciences. 2004;362(1820):1403–1422. doi: 10.1098/rsta.2004.1380. [DOI] [PubMed] [Google Scholar]
- Olson WK, Zhurkin VB. Modeling DNA deformations. Current Opinion in Structural Biology. 2000;10(3):286–297. doi: 10.1016/s0959-440x(00)00086-5. [DOI] [PubMed] [Google Scholar]
- Parker SC, Hansen L, Abaan HO, Tullius TD, Margulies EH. Local DNA topography correlates with functional noncoding regions of the human genome. Science. 2009;324(5925):389–392. doi: 10.1126/science.1169050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paull TT, Carey M, Johnson RC. Yeast HMG proteins NHP6A/B potentiate promoter-specific transcriptional activation in vivo and assembly of preinitiation complexes in vitro. Genes & Development. 1996;10:2769–2781. doi: 10.1101/gad.10.21.2769. [DOI] [PubMed] [Google Scholar]
- Paull TT, Haykinson MJ, Johnson RC. The nonspecific DNA-binding and -bending proteins HMG1 and HMG2 promote the assembly of complex nucleoprotein structures. Genes & Development. 1993;7(8):1521–1534. doi: 10.1101/gad.7.8.1521. [DOI] [PubMed] [Google Scholar]
- Paull TT, Johnson RC. DNA looping by Saccharomyces cerevisiae high mobility group proteins NHP6A/B. Journal of Biological Chemistry. 1995;270:8744–8754. doi: 10.1074/jbc.270.15.8744. [DOI] [PubMed] [Google Scholar]
- Podesta A, Imperadori L, Colnaghi W, Finzi L, Milani P, Dunlap D. Atomic force microscopy study of DNA deposited on poly L-ornithine-coated mica. Journal of Microscopy. 2004;215(Pt 3):236–240. doi: 10.1111/j.0022-2720.2004.01372.x. [DOI] [PubMed] [Google Scholar]
- Podesta A, Indrieri M, Brogioli D, Manning GS, Milani P, Guerra R, Finzi L, Dunlap D. Positively charged surfaces increase the flexibility of DNA. Biophysical Journal. 2005;89(4):2558–2563. doi: 10.1529/biophysj.105.064667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Podtelezhnikov AA, Mao C, Seeman NC, Vologodskii A. Multimerization-cyclization of DNA fragments as a method of conformational analysis. Biophysical Journal. 2000;79(5):2692–2704. doi: 10.1016/S0006-3495(00)76507-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Popov YO, Tkachenko AV. Effects of kinks on DNA elasticity. Physical Reviews E, Statistics, Nonlinear, and Soft Matter Physics. 2005;71(5 Pt 1) doi: 10.1103/PhysRevE.71.051905. 051905. [DOI] [PubMed] [Google Scholar]
- Protozanova E, Yakovchuk P, Frank-Kamenetskii MD. Stacked-unstacked equilibrium at the nick site of DNA. Journal of Molecular Biology. 2004;342(3):775–785. doi: 10.1016/j.jmb.2004.07.075. [DOI] [PubMed] [Google Scholar]
- Ptashne M, Gann A. Transcriptional activation by recruitment. Nature. 1997;386(6625):569–577. doi: 10.1038/386569a0. [DOI] [PubMed] [Google Scholar]
- Randall GL, Zechiedrich L, Pettitt BM. In the absence of writhe, DNA relieves torsional stress with localized, sequence-dependent structural failure to preserve B-form. Nucleic Acids Research. 2009 doi: 10.1093/nar/gkp556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Range K, Mayaan E, Maher LJ, 3rd, York DM. The contribution of phosphate-phosphate repulsions to the free energy of DNA bending. Nucleic Acids Research. 2005;33(4):1257–1268. doi: 10.1093/nar/gki272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rangel DP, Fujimoto BS, Schurr JM. Estimation of the persistence length of DNA from the torsion elastic constant and supercoiling free energy: effect of ethylene glycol. Journal of Physical Chemistry B. 2008;112(42):13359–13366. doi: 10.1021/jp801526w. [DOI] [PubMed] [Google Scholar]
- Record MT, Jr, Anderson CF, Lohman TM. Thermodynamic analysis of ion effects on the binding and conformational equilibria of proteins and nucleic acids: the roles of ion association or release, screening, and ion effects on water activity. Quarterly Reviews of Biophysics. 1978;11(2):103–178. doi: 10.1017/s003358350000202x. [DOI] [PubMed] [Google Scholar]
- Record MT, Jr, Dehaseth PL, Lohman TM. Interpretation of monovalent and divalent cation effects on the lac repressor-operator interaction. Biochemistry. 1977;16(22):4791–4796. doi: 10.1021/bi00641a005. [DOI] [PubMed] [Google Scholar]
- Richmond TJ, Davey CA. The structure of DNA in the nucleosome core. Nature. 2003;423(6936):145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- Ringrose L, Chabanis S, Angrand PO, Woodroofe C, Stewart AF. Quantitative comparison of DNA looping in vitro and in vivo: chromatin increases effective DNA flexibility at short distances. EMBO Journal. 1999;18(23):6630–6641. doi: 10.1093/emboj/18.23.6630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rippe K. Making contacts on a nucleic acid polymer. Trends in Biochemical Science. 2001;26(12):733–740. doi: 10.1016/s0968-0004(01)01978-8. [DOI] [PubMed] [Google Scholar]
- Rippe K, Von Hippel PH, Langowski J. Action at a distance: DNA-looping and initiation of transcription. Trends is Biochemical Science. 1995;20(12):500–506. doi: 10.1016/s0968-0004(00)89117-3. [DOI] [PubMed] [Google Scholar]
- Rohs R, West SM, Sosinsky A, Liu P, Mann RS, Honig B. The role of DNA shape in protein-DNA recognition. Nature. 2009;461(7268):1248–1253. doi: 10.1038/nature08473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross ED, Den RB, Hardwidge PR, Maher LJ., 3rd Improved quantitation of DNA curvature using ligation ladders. Nucleic Acids Research. 1999;27(21):4135–4142. doi: 10.1093/nar/27.21.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ross ED, Hardwidge PR, Maher LJ., 3rd HMG proteins and DNA flexibility in transcription activation. Molecular and Cellular Biology. 2001;21(19):6598–6605. doi: 10.1128/MCB.21.19.6598-6605.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rothemund PW. Folding DNA to create nanoscale shapes and patterns. Nature. 2006;440(7082):297–302. doi: 10.1038/nature04586. [DOI] [PubMed] [Google Scholar]
- Rouzina I, Bloomfield VA. DNA bending by small, mobile multivalent cations. Biophysical Journal. 1998;74(6):3152–3164. doi: 10.1016/S0006-3495(98)78021-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzina I, Bloomfield VA. Force-induced melting of the DNA double helix 1. Thermodynamic analysis. Biophysical Journal. 2001a;80(2):882–893. doi: 10.1016/S0006-3495(01)76067-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzina I, Bloomfield VA. Force-induced melting of the DNA double helix. 2. Effect of solution conditions. Biophysical Journal. 2001b;80(2):894–900. doi: 10.1016/S0006-3495(01)76068-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roychoudhury M, Sitlani A, Lapham J, Crothers DM. Global structure and mechanical properties of a 10-bp nucleosome positioning motif. Proceedings of the National Academy of Sciences USA. 2000;97(25):13608–13613. doi: 10.1073/pnas.250476297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Santalucia J. A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proceedings of the National Academy of Sciences USA. 1998;95(4):1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Satchwell SC, Drew HR, Travers AA. Sequence periodicities in chicken nucleosome core DNA. Journal of Molecular Biology. 1986;191(4):659–675. doi: 10.1016/0022-2836(86)90452-3. [DOI] [PubMed] [Google Scholar]
- Schultz SC, Shields GC, Steitz TA. Crystal structure of a CAP-DNA complex: the DNA is bent by 90 degrees. Science. 1991;253(5023):1001–1007. doi: 10.1126/science.1653449. [DOI] [PubMed] [Google Scholar]
- Schurr JM. Polyanion Models of Nucleic Acid-Metal Ion Interactions. In: Hud NV, editor. Nucleic acid - metal ion interactions. Cambridge: RSC; 2009. pp. 307–349. [Google Scholar]
- Schurr JM, Allison SA. Polyelectrolyte contribution to the persistence length of DNA. Biopolymers. 1981;20(2):251–268. doi: 10.1002/bip.1981.360200202. [DOI] [PubMed] [Google Scholar]
- Schurr JM, Fujimoto BS. Extensions of counterion condensation theory. I. Alternative geometries and finite salt concentration. Biophysical Chemistry. 2002;101–102:425–445. doi: 10.1016/s0301-4622(02)00178-3. [DOI] [PubMed] [Google Scholar]
- Scipioni A, Anselmi C, Zuccheri G, Samori B, De Santis P. Sequence-dependent DNA curvature and flexibility from scanning force microscopy images. Biophysical Journal. 2002a;83(5):2408–2418. doi: 10.1016/S0006-3495(02)75254-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scipioni A, Zuccheri G, Anselmi C, Bergia A, Samori B, De Santis P. Sequence-dependent DNA dynamics by scanning force microscopy time-resolved imaging. Chemistry and Biology. 2002b;9(12):1315–1321. doi: 10.1016/s1074-5521(02)00282-x. [DOI] [PubMed] [Google Scholar]
- Sebastian NT, Bystry EM, Becker NA, Maher LJ., 3rd Enhancement of DNA flexibility in vitro and in vivo by HMGB box A proteins carrying box B residues. Biochemistry. 2009;48(10):2125–2134. doi: 10.1021/bi802269f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seeman NC. DNA enables nanoscale control of the structure of matter. Quarterly Reviews of Biophysics. 2006:1–9. doi: 10.1017/S0033583505004087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segal E, Fondufe-Mittendorf Y, Chen L, Thastrom A, Field Y, Moore IK, Wang JP, Widom J. A genomic code for nucleosome positioning. Nature. 2006;442(7104):772–778. doi: 10.1038/nature04979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Selsing E, Wells RD, Alden CJ, Arnott S. Bent DNA: visualization of a base-paired and stacked A–B conformational junction. The Journal of Biological Chemistry. 1979;254(12):5417–5422. [PubMed] [Google Scholar]
- Sergeyev V, Pyshkina O, Lezov A, Mel'nikov A, Ryumtsev E, Zezin A, Kabanov V. DNA complexed with oppositely charged amphiphile in low-polar organic solvents. Langmuir. 1999;15:4435–4444. [Google Scholar]
- Shimada J, Yamakawa H. Ring-closure probabilities for twisted wormlike chains. Application to DNA. Macromolecules. 1984;17:689–698. [Google Scholar]
- Shore D, Baldwin RL. Energetics of DNA twisting. I. Relation between twist and cyclization probability. Journal of Molecular Biology. 1983;170:957–981. doi: 10.1016/s0022-2836(83)80198-3. [DOI] [PubMed] [Google Scholar]
- Shore D, Langowski J, Baldwin RL. DNA flexibility studied by covalent closure of short fragments into circles. Proceedings of the National Academy of Sciences USA. 1981;78(8):4833–4837. doi: 10.1073/pnas.78.8.4833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shui X, Mcfail-Isom L, Hu GG, Williams LD. The B-DNA dodecamer at high resolution reveals a spine of water on sodium. Biochemistry. 1998a;37:8341–8355. doi: 10.1021/bi973073c. [DOI] [PubMed] [Google Scholar]
- Shui X, Sines C, Mcfail-Isom L, Vanderveer D, Williams LD. Structure of the potassium form of CGCGAATTCGCG: DNA deformation by electrostatic collapse around inorganic cations. Biochemistry. 1998b;37:16877–16887. doi: 10.1021/bi982063o. [DOI] [PubMed] [Google Scholar]
- Sines CC, Mcfail-Isom L, Howerton SB, Vanderveer D, Williams LD. Cations mediate B-DNA conformational heterogeneity. Journal of the American Chemical Society. 2000;122(45):11048–11056. [Google Scholar]
- Sivolob AV, Khrapunov SN. Translational positioning of nucleosomes on DNA: The role of sequence-dependent isotropic DNA bending stiffness. Journal of Molecular Biology. 1995;247:918–931. doi: 10.1006/jmbi.1994.0190. [DOI] [PubMed] [Google Scholar]
- Skolnick J, Fixman M. Electrostatic persistence length of a wormlike polyelectrolyte. Macromolecules. 1977;10:944–948. [Google Scholar]
- Sprous D, Young MA, Beveridge DL. Molecular dynamics studies of the conformational preferences of a DNA double helix in water and an ethanol/water mixture: Theoretical considerations of the A–B transition. Journal of Physical Chemistry. 1998;102(23):4658–4667. [Google Scholar]
- Stellwagen NC, Magnusdottir S, Gelfi C, Righetti PG. Preferential counterion binding to A-tract DNA oligomers. Journal of Molecular Biology. 2001;305(5):1025–1033. doi: 10.1006/jmbi.2000.4362. [DOI] [PubMed] [Google Scholar]
- Strauss JK, Maher LJ., 3rd DNA bending by asymmetric phosphate neutralization. Science. 1994;266(5192):1829–1834. doi: 10.1126/science.7997878. [DOI] [PubMed] [Google Scholar]
- Swigon D, Coleman BD, Olson WK. Modeling the lac repressor-operator assembly: the influence of DNA looping on lac repressor conformation. Proceedings of the National Academy of Sciences USA. 2006;103(26):9879–9884. doi: 10.1073/pnas.0603557103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor WH, Hagerman PJ. Application of the method of phage T4 DNA ligase-catalyzed ring-closure to the study of DNA structure. II. NaCl-dependence of DNA flexibility and helical repeat. Journal of Molecular Biology. 1990;212(2):363–376. doi: 10.1016/0022-2836(90)90131-5. [DOI] [PubMed] [Google Scholar]
- Thomas JO, Travers AA. HMG1 and 2, and related 'architectural' DNA-binding proteins. Trends in Biochemical Science. 2001;26(3):167–174. doi: 10.1016/s0968-0004(01)01801-1. [DOI] [PubMed] [Google Scholar]
- Tinoco I, Jr, LI PT, Bustamante C. Determination of thermodynamics and kinetics of RNA reactions by force. Quarterly Reviews of Biophysics. 2006;39(4):325–360. doi: 10.1017/S0033583506004446. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjian R, Maniatis T. Transcriptional Activation: A Complex Puzzle with Few Easy Pieces. Cell. 1994;77:5–8. doi: 10.1016/0092-8674(94)90227-5. [DOI] [PubMed] [Google Scholar]
- Tolhuis B, Palstra RJ, Splinter E, Grosveld F, De Laat W. Looping and interaction between hypersensitive sites in the active beta-globin locus. Molecular Cell. 2002;10(6):1453–1465. doi: 10.1016/s1097-2765(02)00781-5. [DOI] [PubMed] [Google Scholar]
- Travers AA, Ner SS, Churchill MEA. DNA chaperones: A solution to a persistence problem. Cell. 1994;77:167–169. doi: 10.1016/0092-8674(94)90306-9. [DOI] [PubMed] [Google Scholar]
- Trifonov EN, Sussman JL. The pitch of chromatin DNA is reflected in its nucleotide sequence. Proceedings of the National Academy of Sciences USA. 1980;77(7):3816–3820. doi: 10.1073/pnas.77.7.3816. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vacano E, Hagerman PJ. Analysis of birefringence decay profiles for nucleic acid helices possessing bends: the tau-ratio approach. Biophysical Journal. 1997;73(1):306–317. doi: 10.1016/S0006-3495(97)78071-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Noort J, Verbrugge S, Goosen N, Dekker C, Dame RT. Dual architectural roles of HU: Formation of flexible hinges and rigid filaments. Proceedings of the National Academy of Sciences USA. 2004;101(18):6969–6974. doi: 10.1073/pnas.0308230101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vernimmen D, De Gobbi M, Sloane-Stanley JA, Wood WG, Higgs DR. Long-range chromosomal interactions regulate the timing of the transition between poised and active gene expression. EMBO Journal. 2007;26(8):2041–2051. doi: 10.1038/sj.emboj.7601654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Villa E, Balaeff A, Schulten K. Structural dynamics of the lac repressor-DNA complex revealed by a multiscale simulation. Proceedings of the National Academy of Sciences USA. 2005;102(19):6783–6788. doi: 10.1073/pnas.0409387102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Virstedt J, Berge T, Henderson RM, Waring MJ, Travers AA. The influence of DNA stiffness upon nucleosome formation. Journal of structural biology. 2004;148(1):66–85. doi: 10.1016/j.jsb.2004.03.007. [DOI] [PubMed] [Google Scholar]
- Vologodskaia M, Vologodskii A. Contribution of the intrinsic curvature to measured DNA persistence length. Journal of Molecular Biology. 2002;317(2):205–213. doi: 10.1006/jmbi.2001.5366. [DOI] [PubMed] [Google Scholar]
- Widom J. Role of DNA sequence in nucleosome stability and dynamics. Quarterly Reviews of Biophysics. 2001;34(3):269–324. doi: 10.1017/s0033583501003699. [DOI] [PubMed] [Google Scholar]
- Wiggins PA, Phillips R, Nelson PC. Exact theory of kinkable elastic polymers. Physical Review E, Statistics, Nonlinear and Soft Matter Physics. 2005;71(2 Pt 1) doi: 10.1103/PhysRevE.71.021909. 021909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiggins PA, Van Der Heijden T, Moreno-Herrero F, Spakowitz A, Phillips R, Widom J, Dekker C, Nelson PC. High flexibility of DNA on short length scales probed by atomic force microscopy. Nature Nanotechnology. 2006;1:137–141. doi: 10.1038/nnano.2006.63. [DOI] [PubMed] [Google Scholar]
- Williams LD, Maher LJ., 3rd Electrostatic mechanisms of DNA deformation. Annual Reviews of Biophysics and Biomolecular Structure. 2000;29:497–521. doi: 10.1146/annurev.biophys.29.1.497. [DOI] [PubMed] [Google Scholar]
- Williams SL, Parkhurst LK, Parkhurst LJ. Changes in DNA bending and flexing due to tethered cations detected by fluorescence resonance energy transfer. Nucleic Acids Research. 2006;34(3):1028–1035. doi: 10.1093/nar/gkj498. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witz G, Rechendorff K, Adamcik J, Dietler G. Conformation of circular DNA in two dimensions. Physical review letters. 2008;101(14):148103. doi: 10.1103/PhysRevLett.101.148103. [DOI] [PubMed] [Google Scholar]
- Wong OK, Guthold M, Erie DA, Gelles J. Interconvertible lac repressor-DNA loops revealed by single-molecule experiments. PLoS biology. 2008;6(9):e232. doi: 10.1371/journal.pbio.0060232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu H-M, Crothers DM. The locus of sequence-directed and protein-induced DNA bending. Nature. 1984;308:509–513. doi: 10.1038/308509a0. [DOI] [PubMed] [Google Scholar]
- Yan J, Marko JF. Localized single-stranded bubble mechanism for cyclization of short double helix DNA. Physical review letters. 2004;93(10):108108. doi: 10.1103/PhysRevLett.93.108108. [DOI] [PubMed] [Google Scholar]
- Young MA, Beveridge DL. Molecular dynamics simulations of an oligonucleotide duplex with adenine tracts phased by a full helix turn. Journal of Molecular Biology. 1998;281(4):675–687. doi: 10.1006/jmbi.1998.1962. [DOI] [PubMed] [Google Scholar]
- Young MA, Jayaram B, Beveridge DL. Intrusion of counterions into the spine of hydration in the minor groove of B-DNA: fractional occupancy of electronegative pockets. Journal of the American Chemical Society. 1997a;119:59–69. [Google Scholar]
- Young MA, Ravishanker G, Beveridge DL. A 5-nanosecond molecular dynamics trajectory for B-DNA: analysis of structure, motions, and solvation. Biophysical Journal. 1997b;73(5):2313–2336. doi: 10.1016/S0006-3495(97)78263-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Young MA, Ravishanker G, Beveridge DL, Berman HM. Analysis of local helix bending in crystal structures of DNA oligonucleotides and DNA-protein complexes. Biophysical Journal. 1995;68(6):2454–2468. doi: 10.1016/S0006-3495(95)80427-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeller RW, Griffith JD, Moore JG, Kirchhamer CV, Britten RJ, Davidson EH. A multimerizing transcription factor of sea urchin embryos capable of looping DNA. Proceedings of the National Academy of Sciences USA. 1995;92(7):2989–2993. doi: 10.1073/pnas.92.7.2989. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Crothers DM. High-throughput approach for detection of DNA bending and flexibility based on cyclization. Proceedings of the National Academy of Sciences USA. 2003;100(6):3161–3166. doi: 10.1073/pnas.0530189100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Mcewen AE, Crothers DM, Levene SD. Analysis of in-vivo LacR-mediated gene repression based on the mechanics of DNA looping. PLoS ONE. 2006a;1:e136. doi: 10.1371/journal.pone.0000136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Mcewen AE, Crothers DM, Levene SD. Statistical-mechanical theory of DNA looping. Biophysical Journal. 2006b;90(6):1903–1912. doi: 10.1529/biophysj.105.070490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng G, Lu XJ, Olson WK. Web 3DNA–a web server for the analysis, reconstruction, and visualization of three-dimensional nucleic-acid structures. Nucleic Acids Research. 2009;37:W240–W246. doi: 10.1093/nar/gkp358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou GL, Xin L, Song W, Di LJ, Liu G, Wu XS, Liu DP, Liang CC. Active chromatin hub of the mouse alpha-globin locus forms in a transcription factory of clustered housekeeping genes. Molecular and Cellular Biology. 2006;26(13):5096–5105. doi: 10.1128/MCB.02454-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zinkel SS, Crothers DM. DNA bend direction by phase sensitive detection. Nature. 1987;328:178–181. doi: 10.1038/328178a0. [DOI] [PubMed] [Google Scholar]