Transient Changes in Intercellular Protein Variability Identify Sources of Noise in Gene Expression

Abstract

Protein levels differ considerably between otherwise identical cells, and these differences significantly affect biological function and phenotype. Previous work implicated various noise mechanisms that drive variability in protein copy numbers across an isogenic cell population. For example, transcriptional bursting of mRNAs has been shown to be a major source of noise in the expression of many genes. Additional expression variability, referred to as extrinsic noise, arises from intercellular variations in mRNA transcription and protein translation rates attributed to cell-to-cell differences in cell size, abundance of ribosomes, etc. We propose a method to determine the magnitude of different noise sources in a given gene of interest. The method relies on blocking transcription and measuring changes in protein copy number variability over time. Our results show that this signal has sufficient information to quantify both the extent of extrinsic noise and transcription bursting in gene expression. Moreover, if the mean mRNA count is known, then the relative contributions of transcription versus translation rate fluctuations to extrinsic noise can also be determined. In summary, our study provides an easy-to-implement method for characterizing noisy protein expression that complements existing techniques for studying stochastic dynamics of genetic circuits.

Introduction

Genetically identical cells exhibit considerable intercellular variations in mRNA and protein levels. Many studies over the last decade have implicated different noise mechanisms that drive expression variability (Fig. 1) (1–12). These include the following:

• 1.Poissonian fluctuations (shot noise) in mRNA and protein levels;
• 2.Random switching between different promoter states, which leads to transcriptional bursting of mRNAs; and
• 3.Extrinsic noise arising from variations in transcription/translation rates due to cell-to-cell differences in size, environment, abundance of ribosomes/RNA polymerases, etc.

Because stochasticity plays important functional roles in diverse cellular processes (13–20), it is essential to identify the contributions of different noise sources in a given gene/promoter of interest.

Figure 1.

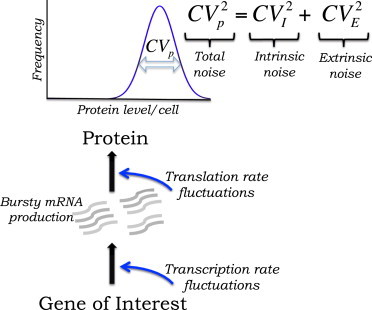
Different sources of noise in gene expression. Transcriptional bursting of mRNAs generates considerable intercellular variability in protein level. Additional variability (extrinsic noise) arises from fluctuations in transcription/translation rates. Total noise in protein level (${CV}_p^2$), measured by the coefficient of variation (CV) squared, is decomposed into intrinsic and extrinsic noise (see text for details). To see this figure in color, go online.

Two-color reporter assay and mRNA single-molecule fluorescence in situ hybridization are used for quantifying extrinsic noise and transcriptional bursting, respectively (21,22). These techniques are hard to implement, and mRNA fluorescence in situ hybridization becomes challenging in the regime of high mRNA concentrations. Recent work has shown that changes in protein copy number variability across a cell population (measured via flow cytometry) after transcriptional blockage can determine the extent of transcriptional bursting in a gene (23). This work was restricted to intrinsic noise in gene expression, and we extend these results to consider extrinsic noise at the transcriptional and translational stages of gene expression. Our results show that transient changes in protein noise levels after perturbation contain signatures to determine both the extent of extrinsic noise and transcription bursting. By taking into account the effects of extrinsic noise, this method provides better estimates of the transcriptional burst size. Finally, complementing this technique with additional data (such as independent measurement of the mean mRNA copy number) can quantify the relative contributions of transcription versus translation rate fluctuations to extrinsic noise. We begin by describing a general stochastic gene expression model with transcriptional bursting, and later extend it to include extrinsic noise arising from fluctuations in model parameters.

Results and Discussion

Stochastic gene expression model formulation

Consider a gene where transcriptional bursts occur at a rate k_m, and each burst creates B_m mRNA transcripts with distribution

$$\begin{array}{c}\text{Probability}\left\{B_m=i\right\}={\alpha }_i,\\ i\in \left\{\mathrm{0,1,2,3},\dots \right\}.\end{array}$$ (1)

Proteins are produced from each mRNA at a translation rate k_p. Proteins and mRNAs degrade at constant rates γ_p and γ_m, respectively. Let m(t) and p(t) denote the number of mRNA and protein molecules inside the cell at time t, respectively. Then, steady-state mean levels are given by

$$\begin{array}{c}\langle m\rangle =\frac{k_m\langle B_m\rangle }{{\gamma }_m},\\ \langle p\rangle =\frac{k_p{k}_m\langle B_m\rangle }{{\gamma }_m{\gamma }_p},\end{array}$$ (2)

where 〈⋅〉 denotes the expected value (24–26). Moreover, the steady-state mRNA and protein noise levels, measured by the coefficient of variation (CV) squared (variance/mean²), have been shown to be

$$\begin{array}{c}C{V}_m^2=\frac{B_e}{\langle m\rangle },\\ C{V}_p^2=\frac{B_e{\gamma }_p}{\langle m\rangle \left({\gamma }_p+{\gamma }_m\right)}+\frac{1}{\langle p\rangle },\end{array}$$ (3)

respectively (24–26). The first term on the right-hand-side of ${CV}_p^2$ represents protein noise arising from underlying fluctuations in mRNA population counts. The 1/〈p〉 term is the Poissonian noise arising due to random birth-death of individual protein molecules. Because the magnitude of noise in mRNA copy number is controlled by

$$B_e=\frac{\langle B_m^2\rangle +\langle B_m\rangle }{2\langle B_m\rangle },$$ (4)

the value B_e is used as a metric for quantifying the extent of transcription bursting. Note B_e = 1 for constitutive transcription (B_m = 1 with probability one), and B_e ≫ 1 for bursty transcription. Extrinsic noise is incorporated next by assuming k_m (mRNA burst arrival rate) and k_p (protein translation rate) to be random processes.

Incorporating fluctuations in model parameters

Let z_j(t), j ∈ {1,2} denote independent random processes representing levels of cellular factors Z_j (such as transcription factors, cell volume, etc.). Fluctuations in z_j(t) are modeled via a bursty birth-death process, where Z_j is synthesized in bursts of size B_j, with

$$\begin{array}{c}\text{Probability}\left\{B_j=i\right\}={\alpha }_{ji},\\ i\in \left\{\mathrm{0,1,2,3},\dots \right\},\\ j\in \left\{\mathrm{1,2}\right\}.\end{array}$$ (5)

Bursts arrive at constant rate k_j, and Z_j degrades with rate γ_j. The steady-state mean, CV², and autocorrelation function of z_j(t) are obtained as

$$\begin{array}{c}\langle z_j\rangle =\frac{k_j\langle B_j\rangle }{{\gamma }_j},\\ C{V}_{z_j}^2=\frac{\langle B_j^2\rangle +\langle B_j\rangle }{2\langle B_j\rangle \langle z_j\rangle },\\ \text{exp}\left(-{\gamma }_j\tau \right),\end{array}$$ (6)

respectively (26). A key advantage with this formulation is that the mean, magnitude, and timescale of fluctuations in z_j(t) can be independently modulated via k_j, B_j, and γ_j. Extrinsic noise is introduced by modifying the mRNA burst arrival rate to k_mz₁(t), and the protein translation rate to k_pz₂(t). The overall model, capturing stochastic gene expression with varying transcription/translation rates, is presented in Table 1. It comprises different events that fire at exponentially distributed time intervals. Whenever the event occurs, the population counts are reset based on the second column of the table. The third column lists the event propensity functions f(z₁, z₂, m, p), which determine how often an event occurs. In particular, the probability that an event will occur in the next infinitesimal time interval (t,t + dt] is given by f(z₁, z₂, m, p)dt. Next, steady-state statistical moments of p(t) are derived. Note that the propensity function for the translation event is nonlinear, which leads to the well-known problem of moment closure (27). Our recent work has shown that independence of random processes (for example, m(t) and z₂(t) are independent) can be exploited to solve moments exactly, despite nonlinear propensity functions (26). Here we use this technique to compute the steady-state protein noise level for the above model. Moreover, we study changes in noise levels in response to transcriptional perturbations and how this signal can be used for inferring underlying noise mechanisms.

Table 1.

Different events in the stochastic gene expression model and the corresponding changes in population counts when events occur probabilistically

Model events	Reset in population count	Propensity function f(z1, z2, m, p)
Zj production	zj(t) → zj(t) + i	kjαji, i ∈ {0,1,…}
Zj degradation	zj(t) → zj(t) − 1	γjzj(t)
Transcription	m(t) → m(t) + i	kmαiz1(t), i ∈ {0,1,…}
mRNA degradation	m(t) → m(t) − 1	γmm(t)
Protein translation	p(t) → p(t) + 1	kpm(t)z2(t)
Protein degradation	p(t) → p(t) − 1	γpp(t)

Third column lists the event propensity function that determines how often an event fires. Random processes m(t) and p(t) denote the number of mRNA and protein molecules inside the cell at time t, respectively. The values z_j(t), j ∈ {1,2} represent levels of cellular factors z_j that affect transcription and translation rates.

Quantifying protein noise level

To compute protein copy number CV² (noise level), differential equations describing the time evolution of the different statistical moments of z₁(t), z₂(t), m(t), and p(t) are first derived. To derive moment dynamics we use the result that the time-derivative of the expected value of any differentiable function φ(z₁, z₂, m, p) is given by

$$\frac{d\langle \phi \left(z_1,z_2,m,p\right)\rangle }{dt}=\langle \sum _{\text{Events}}\Delta \phi \times f\left(z_1,z_2,m,p\right)\rangle ,$$ (7)

where Δφ(z₁, z₂, m, p) is the change in φ when an event occurs and f(z₁, z₂, m, p) is the event propensity function (27,28). Using the resets in population counts and propensity functions in Table 1, this corresponds to

$$\frac{d\langle \phi \left(z_1,z_2,m,p\right)\rangle }{dt}=\langle \theta \left(z_1,z_2,m,p\right)\rangle ,$$ (8)

where the formula for θ(z₁, z₂, m, p) is provided in the Supporting Material (27,28). Moment dynamics is obtained by choosing φ to be monomials of the form $z_1^i{z}_2^j$m^kp^l. For example, time evolution of the second-order moment of the mRNA can be obtained by choosing φ = m², in which case we obtain

$$\frac{d\langle m^2\left(t\right)\rangle }{dt}=k_m\langle B_m^2\rangle \langle z_1\left(t\right)\rangle +{\gamma }_m\langle m\left(t\right)\rangle +2k_m\langle B_m\rangle \langle m\left(t\right)z\left(t\right)\rangle -2{\gamma }_m\langle m^2\left(t\right)\rangle .$$ (9)

Let μ be a 14-dimensional vector containing all the first- and second-order uncentered moments of the joint stochastic process {z₁(t), z₂(t), m(t), p(t)}. Then, the time evolution of μ can be compactly represented as

$$\frac{d\mu }{dt}=a_1+A_1\mu +B_1\overline{\mu },$$ (10)

where vector a₁ and matrices A₁ and B₁ depend on model parameters and

$$\overline{\mu }={\left[\langle z_2{m}^2\rangle ,\langle z_2^{2}m\rangle ,\langle m{z}_{2}p\rangle ,\langle z_1{z}_{2}m\rangle \right]}^T,$$ (11)

is a vector of third-order moments. The nonlinear propensity function leads to unclosed moment dynamics, i.e., the time derivative of second-order moments depends on third-order moments. Fortunately, for this system, including certain higher-order moments in μ closes moment equations. In particular, the time derivative of the 16-dimensional vector

$$\hat{\mu }={\left[{\mu }^T,\langle z_1{z}_{2}p\rangle ,\langle m{z}_{2}p\rangle \right]}^T$$ (12)

is given by

$$\frac{d\hat{\mu }}{dt}=a_2+A_2\mu +B_2\stackrel{\text{˘}}{\mu }$$ (13)

for some vector a₂ and matrices A₂ and B₂ and

$$\stackrel{\text{˘}}{\mu }={\left[\langle z_2{m}^2\rangle ,\langle z_2^{2}m\rangle ,\langle z_2^2{m}^2\rangle ,\langle z_1{z}_{2}m\rangle ,\langle z_1{z}_2^{2}m\rangle \right]}^T.$$ (14)

Recall that stochastic processes z₁(t) and z₂(t) are independent. Moreover, inasmuch as z₂(t) affects gene expression at the translational stage, m(t) and z₂(t) are also independent. Exploiting this independence,

$$\stackrel{\text{˘}}{\mu }={\left[\langle z_2\rangle \langle m^2\rangle ,\langle z_2^2\rangle \langle m\rangle ,\langle z_2^2\rangle \langle m^2\rangle ,\langle z_{1}m\rangle \langle z_2\rangle ,\langle z_{1}m\rangle \langle z_2^2\rangle \right]}^T$$ (15)

can be expressed as a function of first- and second-order moments already present in $\hat{\mu }$. Thus, Eqs. 13 and 15 form a closed system of differential equations and its steady-state analysis reveals the following protein noise:

$$C{V}_p^2=\frac{B_e}{\langle m\rangle }\left(\frac{{\gamma }_p}{{\gamma }_p+{\gamma }_m}+\frac{C{V}_{z_2}^2{\gamma }_p}{{\gamma }_p+{\gamma }_m+{\gamma }_2}\right)+\frac{1}{\langle p\rangle },$$ (16a)

$$+\frac{C{V}_{z_2}^2{\gamma }_p}{{\gamma }_p+{\gamma }_2}+\frac{C{V}_{z_1}^2{\gamma }_p{\gamma }_m\left({\gamma }_p+{\gamma }_m+{\gamma }_1\right)}{\left({\gamma }_p+{\gamma }_m\right)\left({\gamma }_p+{\gamma }_1\right)\left({\gamma }_1+{\gamma }_m\right)},$$ (16b)

$$+\frac{C{V}_{z_1}^{2}C{V}_{z_2}^2{\gamma }_p{\gamma }_m\left({\gamma }_p+{\gamma }_m+{\gamma }_1+{\gamma }_2\right)}{\left({\gamma }_p+{\gamma }_m+{\gamma }_2\right)\left({\gamma }_p+{\gamma }_1+{\gamma }_2\right)\left({\gamma }_1+{\gamma }_m\right)},$$ (16c)

where the mean mRNA and protein abundances are given by

$$\begin{array}{c}\langle m\rangle =\frac{k_m\langle B_m\rangle \langle z_1\rangle }{{\gamma }_m},\\ \langle p\rangle =\frac{k_p\langle z_2\rangle \langle m\rangle }{{\gamma }_p}.\end{array}$$ (17)

The above closure technique results in an exact protein noise level (expressions in Eq. 16) for the stochastic model described in Table 1. As expected, the expressions in Eq. 16 reduce to Eq. 3 when $C{V}_{z_j}^2=0$ (i.e., no parameters fluctuations). When the timescale of parameter fluctuations are much slower than the mRNA and protein turnover rates (γ_j ≪ γ_m, γ_p),

$$C{V}_p^2=\frac{B_e}{\langle m\rangle }\left(1+C{V}_{z_2}^2\right)\frac{{\gamma }_p}{{\gamma }_p+{\gamma }_m}+\frac{1}{\langle p\rangle }+C{V}_{z_1}^2+C{V}_{z_2}^2+C{V}_{z_1}^{2}C{V}_{z_2}^2.$$ (18)

As per previous studies (22,29,30), ${CV}_p^2$ is next decomposed into extrinsic and intrinsic noise components.

Decomposing protein expression variability into extrinsic and intrinsic noise

Extrinsic noise (${CV}_E^2$) can be interpreted as the expression variability arising solely due to parameter fluctuations. In contrast, intrinsic noise (${CV}_I^2$) is the expression variability that cannot be accounted for by extrinsic noise, and is defined as

$$C{V}_I^2=C{V}_p^2-C{V}_E^2,$$ (19)

where ${CV}_p^2$ is the total noise given by the expressions in Eq. 16. Experimentally, correlation in the expression of two identical copies of a gene (measured using a two-color assay) is used to quantify the extrinsic noise component, and the intrinsic noise is computed through Eq. 19 (22,29,30). Recent work has shown that ${CV}_E^2$ can be quantified by computing the steady-state protein CV² in a deterministic gene-expression model with corresponding parameter fluctuations (31). Toward that end, we consider the deterministic counterpart to the stochastic model,

$$\frac{dm\left(t\right)}{dt}=k_m\langle B_m\rangle z_1\left(t\right)-{\gamma }_{m}m\left(t\right),$$ (20a)

$$\frac{dp\left(t\right)}{dt}=k_p{z}_2\left(t\right)m\left(t\right)-{\gamma }_{p}p\left(t\right),$$ (20b)

driven by stochastic processes z₁(t) and z₂(t) representing transcription and translation rate fluctuations. Moment dynamics for the models in Eqs. 20a and 20b is obtained by choosing φ to be an appropriate monomial of the form $z_1^i{z}_2^j$m^kp^l in

$$\frac{d\langle \phi \left(z_1,z_2,m,p\right)\rangle }{dt}=\langle \delta \left(z_1,z_2,m,p\right)\rangle ,$$ (21)

where the formula for δ(z₁, z₂, m, p) is provided in the Supporting Material (32). To determine ${CV}_E^2$, we solve for the steady-state protein CV² using a procedure identical to the previous section: time evolution for vector $\hat{\mu }$ (defined in Eq. 12) is derived using Eq. 21 and closed using Eq. 15. Steady-state analysis of the resulting closed moment equations yields the extrinsic noise, which is subtracted from the total noise to obtain the intrinsic noise. These computations show that the terms in Eqs. 16b and 16c make up the extrinsic component of ${CV}_p^2$. In the limit γ_j ≪ γ_m, γ_p, the total noise (18) can be decomposed as

$$C{V}_p^2=C{V}_I^2+C{V}_E^2,$$ (22a)

$$C{V}_E^2=C{V}_{z_1}^2+C{V}_{z_2}^2+C{V}_{z_1}^{2}C{V}_{z_2}^2,$$ (22b)

$$C{V}_I^2=\frac{B_e}{\langle m\rangle }\left(1+C{V}_{z_2}^2\right)\frac{{\gamma }_p}{{\gamma }_p+{\gamma }_m}+\frac{1}{\langle p\rangle }.$$ (22c)

Note that ${CV}_I^2$ is different from the protein noise level when the transcription and translation rates are constant (see Golding et al. (3)). This result is consistent with previous work that has shown that intrinsic expression noise based on the two-color assay can be different from the protein noise in the absence of extrinsic parameter fluctuations, particularly for models with nonlinear propensity functions (30,33). Next, the technique for estimating ${CV}_E^2$ and the extent of transcriptional bursting (B_e) is presented.

Identification of B_e and ${\mathit{C}\mathit{V}}_{\mathit{E}}^{\mathbf{2}}$ from transient changes in protein statistical moments

Our method relies on measuring changes in protein mean and CV² after blocking transcription at time t = 0. The method is easy to implement, because drugs such as Actinomycin D are routinely used to rapidly and efficiently block transcription for measuring mRNA stability (34). Given the large sample sizes of single-cell flow cytometry measurements, mean and CV² can be measured with high precision over time. We make the following assumptions on the mRNA and protein decay rates of the fluorescent protein used to measure expression levels:

• 1.The decay rates γ_p and γ_m are known and the degradation reactions follow first-order kinetics. These rates are easily determined by tracking changes in the mean protein population counts after blocking transcription and translation using small-molecule drugs (23). We further assume that the protein half-life is not significantly larger than the mRNA half-life.
• 2.To isolate noise sources in gene expression, one should choose fluorescent reporters that have half-lives shorter than the cell-cycle length. This is important to minimize noise contributions from random cell-division events and errors incurred in partitioning of molecules between daughter cells (35,36). Because the timescale of extrinsic factor fluctuations is typically comparable to the cell-cycle time, short protein/mRNA half-lives allow us to assume γ_j ≪ γ_m, γ_p, which simplifies the formulas reported later on.

For mammalian cells that typically have 24-h cell cycle, an ideal fluorescent reporter that satisfies these assumptions is d2GFP, a destabilized version of GFP where both the mRNA and protein have an ∼2.5 h half-life (21,23,37). GFP variants with half-life <10 min can be used for other organisms with shorter cell-cycle lengths (38). It is important to point out that the above constraints on γ_p and γ_m are not on the native protein, but on the reporter used. For example, when quantifying transcriptional bursting in a promoter of interest, one constructs a cell line with the promoter driving a fluorescent reporter such as d2GFP. In this case γ_p and γ_m corresponds to the mRNA and protein decay rates of d2GFP. If one uses a native protein tagged with d2GFP, then the above constraints on γ_p and γ_m would be on the tagged system.

Considering the system is at equilibrium when transcription is stopped, and short protein/mRNA half-lives (γ_j ≪ γ_m, γ_p), the total noise (${CV}_p^2$) and extrinsic noise (${CV}_E^2$) in the protein level at t = 0 is given by Eqs. 22a–22c. Recall that Eqs. 13 and 15 represent closed moment dynamics of vector $\hat{\mu }$. Let $\hat{\mu }\left(\infty \right)$ be the steady-state solution of Eqs. 13 and 15. Then, the protein mean and CV² after transcriptional blockage is obtained by solving Eqs. 13 and 15 with k_m = 0 and initial condition $\hat{\mu }\left(0\right)=\hat{\mu }\left(\infty \right)$. After perturbation, the mean protein copy numbers decay as

$$\langle p\left(t\right)\rangle =\langle p\rangle \frac{{\gamma }_p\text{exp}\left(-{\gamma }_{m}t\right)-{\gamma }_m\text{exp}\left(-{\gamma }_{p}t\right)}{{\gamma }_p-{\gamma }_m},$$ (23)

where 〈p〉 is the mean level at t = 0. Moreover, the protein noise level monotonically increases over time (Fig. 2). Analysis in the software MATHEMATICA (Wolfram Research, www.wolfram.com/mathematica/) yields the following transient protein CV²:

$$C{V}_p^2\left(t\right)=C{V}_E^2+\left(C{V}_p^2-C{V}_E^2-\frac{1}{\langle p\rangle }\right)f\left(B_e,{\gamma }_p,{\gamma }_m,t\right)+\frac{1}{\langle p\left(t\right)\rangle },$$ (24)

where function f(B_e, γ_p, γ_m, t) increases with t and f(B_e, γ_p, γ_m, 0) = 1, implying ${CV}_p^2$(0) = ${CV}_p^2$. Equation 24 reveals that transient changes in the protein noise level after stopping transcription are dependent on both the extent of extrinsic noise and the extent of transcriptional bursting B_e (Fig. 2). Because the form of f(B_e, γ_p, γ_m, t) is too complicated, we present the function in four different limits:

$$\underset{B_e\to \infty }{\text{lim}}f\left(B_e,{\gamma }_p,{\gamma }_m,t\right)=1+\frac{{\gamma }_m{\gamma }_p{\left(\text{exp}\left({\gamma }_{p}t\right)-\text{exp}\left({\gamma }_{m}t\right)\right)}^2}{{\left({\gamma }_p\text{exp}\left({\gamma }_{p}t\right)-{\gamma }_m\text{exp}\left({\gamma }_{m}t\right)\right)}^2},$$ (25)

$$\underset{{\gamma }_m\to {\gamma }_p}{\text{lim}}f\left(B_e,{\gamma }_p,{\gamma }_m,t\right)=1+\frac{4\left(\text{exp}\left({\gamma }_{p}t\right)-1\right)+{\gamma }_{p}t\left(\left(B_e-2\right){\gamma }_{p}t-4\right)}{B_e{\left(1+{\gamma }_{p}t\right)}^2},$$ (26)

$$\begin{array}{c}\underset{{\gamma }_p\to \infty }{\text{lim}}f\left(B_e,{\gamma }_p,{\gamma }_m,t\right)=1+\frac{\text{exp}\left({\gamma }_{m}t\right)-1}{B_e},\\ \underset{{\gamma }_m\to \infty }{\text{lim}}f\left(B_e,{\gamma }_p,{\gamma }_m,t\right)=1.\end{array}$$ (27)

Combining the second expression in Eq. 27 with Eq. 24 shows that in the limit γ_m → ∞ (i.e., mRNA half-life is significantly shorter than the protein half-life),

$$\underset{{\gamma }_m\to \infty }{\text{lim}}C{V}_p^2\left(t\right)=C{V}_p^2+\frac{1}{\langle p\left(t\right)\rangle }-\frac{1}{\langle p\rangle },$$ (28)

and contains no information about B_e or ${CV}_E^2$. Thus fluorescent reporters where γ_m ≫ γ_p are not useful for this method, and reporters such as d2GFP where γ_m ≈ γ_p may be more appropriate. Note Eq. 26, where γ_m = γ_p is relevant for d2GFP. Because ${CV}_p^2$(t) and 〈p(t)〉 are measured in Eq. 24, γ_p and γ_m are known, ${CV}_E^2$ and B_e can be estimated by fitting Eq. 24 to data. For example, consider γ_p = γ_m = 1 h⁻¹ and the total protein noise level at equilibrium ${CV}_p^2$ = 0.5. If after 2 and 5 h of transcription blockage, the protein noise level increases by 1.5-fold and fivefold compared to ${CV}_p^2$, respectively, then by using Eqs. 24 and 26, B_e ≈ 2 and ${CV}_E^2$ ≈ 0.25. From Eq. 23, after 5 h the mean protein level would decay by 25-fold for γ_p = γ_m = 1 h⁻¹.

Figure 2.

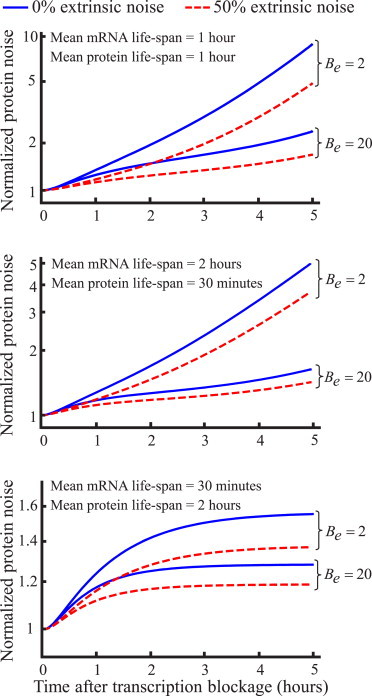
Transient changes in protein copy number variation after transcription blockage identifies noise mechanisms. Protein noise level (${CV}_p^2$(t)) monotonically increases after mRNA production is blocked. Shape of ${CV}_p^2$(t) for different percentages of extrinsic noise (${CV}_E^2$/${CV}_p^2$) and B_e (extent of transcriptional bursting) are shown, with higher values of B_e and ${CV}_E^2$ resulting in a lower rate of increase. Low (high) transcriptional bursting corresponds to B_e = 2(20). Protein noise levels are normalized by their values at t = 0 given by ${CV}_p^2$(0) = ${CV}_p^2$. Three cases of protein (γ_p) and mRNA (γ_m) degradation rates are considered: γ_p = γ_m (top); γ_p = 2 h⁻¹, γ_m = 0.5 h⁻¹ (middle); and γ_p = 0.5 h⁻¹, γ_m = 1 h⁻¹ (bottom). To see this figure in color, go online.

Recall that in our analysis we modeled fluctuations in the transcription and translation rates through independent random processes z₁(t) and z₂(t), respectively. Our analysis show that Eq. 24 holds even if z₁(t) and z₂(t) are dependent, as long as the timescale of extrinsic parameter fluctuations is slow compared to the mRNA and protein half-lives (see the Supporting Material). Thus transient changes in protein noise levels can be used to estimate both B_e and extrinsic noise even if transcriptional and translational rate fluctuations are correlated. Finally, assuming independence of z₁(t) and z₂(t), the relative contributions of $C{V}_{z_1}^2$ (transcription rate fluctuations) and $C{V}_{z_2}^2$ (translation rate fluctuations) to extrinsic noise can also be teased out if the mean mRNA level 〈m〉 is known. Assuming B_e and ${CV}_E^2$ have been estimated using the above procedure, then using Eqs. 22a–22c, the extent of parameter fluctuations can be quantified as

$$C{V}_{z_2}^2=\frac{C{V}_p^2-C{V}_E^2-\frac{1}{\langle p\rangle }}{\frac{B_e}{\langle m\rangle }\frac{{\gamma }_p}{{\gamma }_p+{\gamma }_m}}-1,$$ (29a)

$$C{V}_{z_1}^2=\frac{C{V}_E^2-C{V}_{z_2}^2}{1+C{V}_{z_2}^2}.$$ (29b)

In summary, our proposed method allows characterization of both transcription bursting and extrinsic noise in gene expression from a single experiment. Given additional information on the average mRNA abundance (using, for example, quantitative polymerase chain reaction), contributions of transcription and translation rate fluctuations to extrinsic noise can also be determined. By taking into account different sources of errors in singe-cell measurements (such as background autofluorescence and noise in flow cytometry reading), the proposed technique can be made robust to measurement noise. A key assumption for this technique to work is that the time delay between drug administration and transcriptional blockage is small compared to the mRNA and protein half-lives. One could also use synthetic approaches, such as placing the promoter under the control of a tetracycline-repressible transactivator, for faster shutdown of transcription (39,40). An added advantage of this approach is that it only stops transcription from the promoter of interest and does not create a global transcription block, as would be in the case of adding Actinomycin D.