Population Genetics Inference for Longitudinally-Sampled Mutants Under Strong Selection

Abstract

Longitudinal allele frequency data are becoming increasingly prevalent. Such samples permit statistical inference of the population genetics parameters that influence the fate of mutant variants. To infer these parameters by maximum likelihood, the mutant frequency is often assumed to evolve according to the Wright–Fisher model. For computational reasons, this discrete model is commonly approximated by a diffusion process that requires the assumption that the forces of natural selection and mutation are weak. This assumption is not always appropriate. For example, mutations that impart drug resistance in pathogens may evolve under strong selective pressure. Here, we present an alternative approximation to the mutant-frequency distribution that does not make any assumptions about the magnitude of selection or mutation and is much more computationally efficient than the standard diffusion approximation. Simulation studies are used to compare the performance of our method to that of the Wright–Fisher and Gaussian diffusion approximations. For large populations, our method is found to provide a much better approximation to the mutant-frequency distribution when selection is strong, while all three methods perform comparably when selection is weak. Importantly, maximum-likelihood estimates of the selection coefficient are severely attenuated when selection is strong under the two diffusion models, but not when our method is used. This is further demonstrated with an application to mutant-frequency data from an experimental study of bacteriophage evolution. We therefore recommend our method for estimating the selection coefficient when the effective population size is too large to utilize the discrete Wright–Fisher model.

WITH the advent of high-throughput sequencing, large and frequent longitudinal samples of segregating alleles are becoming increasingly abundant. The allele-frequency trajectories of such samples reflect the combined forces of genetic drift, selection, and mutation and can therefore be used to infer these population genetics parameters. Models of mutant-frequency changes over time are either deterministic or stochastic (Rouzine et al. 2001). The choice between these models depends on the variance effective population size N: the size of a Wright–Fisher population that is identical to the natural population in terms of genetic diversity (Kouyos et al. 2006). Deterministic models assume that the effective population size is infinitely large and therefore that mutant frequencies are not subject to genetic drift, while stochastic models allow the random sampling of variants across generations to influence the likelihood of mutant fixation and extinction.

Most stochastic population genetics models, including the classic coalescent (Kingman 1982), consider the extreme case where selection is so weak that the fate of an allele is determined entirely by random genetic drift. Several methods have been developed to infer N based on this assumption (Williamson and Slatkin 1999; Anderson et al. 2000; Wang 2001; Berthier et al. 2002; Beaumont 2003; Anderson 2005; Jorde and Ryman 2007). There is a growing literature on estimating the selection coefficient, s, using stochastic models of allele-frequency changes (Bollback et al. 2008; Malaspinas et al. 2012; Mathieson and McVean 2013; Feder et al. 2014; Nishino 2013; Foll et al. 2014). Most existing methods implicitly assume weak selection by relying on diffusion approximations that hold when s is of the order of the reciprocal of N and N is large. Weak selection is also assumed in the deterministic paradigm where allele-frequency trajectories are often modeled with a logistic curve obtained in the diffusion limit of the Wright–Fisher and Moran models (Illingworth and Mustonen 2011; Illingworth et al. 2012). All of these approaches are inappropriate when the selective pressure is strong, as is frequently the case, for example, in experimental studies of microbe adaptation and for immune-escape and drug-resistant mutations in intrahost viral populations. Furthermore, these methods will provide attenuated estimates of N if selection is strong, thereby exaggerating the role of random genetic drift (Liu and Mittler 2008).

Illingworth et al. (2014) recently presented a method to infer selection of arbitrary magnitude from longitudinal haplotype frequencies that are assumed to evolve deterministically. However, their definition of the selection coefficient is not consistent with the population genetics definition of this parameter: for every one offspring contributed to the next generation by the wild type, a mutant contributes 1 + s offspring. Consequently, the authors report estimates of the “selection coefficient” that are <−1, which is not possible in traditional population genetics models.

Recently, Foll et al. (2014) developed an approximate Bayesian computation method to infer selection based on a stochastic model of frequency change. Their two-step approach considers multiple longitudinal samples of segregating alleles from different locations in a genome that are all assumed to have the same effective population size. First, the posterior distribution of N is estimated from the frequency trajectories at all genetic loci under the assumption of neutral evolution. The posterior distribution of s is then inferred for each locus using the previously estimated distribution of N as a prior. Although the estimation of s in the second step does not make any assumptions about its magnitude, it is conditioned on the estimate of N that was inferred assuming no selection. The method is therefore appropriate only if selection is negligible at most loci and genetic drift does not vary between loci. This would not appear to be the case for protein-coding sequences where most positions are usually under strong functional or structural constraints.

Here, we present a simple approximation to the Wright–Fisher process that does not make any assumptions about the magnitude of selection and mutation and is therefore better suited to inferring selection acting on populations evolving under strong selective pressures. We use simulation studies to demonstrate that our approach, based on the delta method of statistics, outperforms the standard and Gaussian diffusion approximations when selection is strong, while all three methods perform comparably when selection is weak. Importantly, maximum-likelihood estimates of the selection coefficient are severely attenuated when selection is strong under the two diffusion models, but not when the delta method is used.

Methods

Model of mutant-frequency evolution

Consider a population of constant effective size N composed of individuals of two types: wild type and mutant. Let X_i ∈ {0, 1, …, N} denote the number of mutants in the population in generation i. If the mutant frequency evolves according to the Wright–Fisher model, then the conditional number of mutants in the next generation is (X_i+1|X_i = x_i) ∼ Bin(N, ϕ(x_i)/N) with

$$\varphi \left(x\right)=\frac{\left(1+s\right)x\left(1-\alpha \right)+\left(1-x\right)\beta }{1+sx},$$

where s is the selection coefficient, α is the probability of a mutation from a mutant to the wild type, and β is the probability of a mutation in the reverse direction. This defines a Markov chain {X_n, n = 1, 2, …} on the state space S = {0, 1, …, N} with a binomial one-step transition probability matrix ℙ.

Of course, we do not observe the number of mutants in the population at each generation. Instead, we collect samples at m time points and observe the mutant frequency y_k in a sample of size n_k at generation i_k for k = 1, …, m. If the population size N is large relative to the sample size n_k, then $\left(Y_k|X_{i_k}=x_{i_k}\right)\sim \text{Bin}\left(n_k,x_{i_k}/N\right)$. The data-generation process can therefore be described by a hidden Markov model with binomial emissions conditional on the latent number of mutants in the population (Bollback et al. 2008).

The likelihood function of the population genetics parameters θ = {N, s, α, β} under this model is

$$L\left(\theta \right)={\displaystyle \sum _{X_{i_1}}\cdots }{\displaystyle \sum _{X_{i_m}}p\left(X_{i_1}\right){\displaystyle \prod _{k=2}^{m}p\left(X_{i_{k+1}}|X_{i_k},\theta \right)}\hspace{0.5em}{\displaystyle \prod _{k=1}^{m}p\left(y_k|X_{i_k}\right)}},$$ (1)

where $p\left(y_{i_k}|X_{i_k}\right)$ is the binomial sampling probability and $p\left(X_{i_1}\right)$ is a prior distribution for the number of mutants in the first sampled generation. The transition probability distribution $p\left(X_{i_{k+1}}|X_{i_k},\theta \right)$ under the Wright–Fisher model is obtained by raising ℙ to the power of i_k+1 − i_k. The maximum-likelihood estimates of the population genetics parameters are obtained by maximizing (1) with respect to θ.

Approximating the transition probability distribution

Summary:

Since there is no analytical solution for $p\left(X_{i_{k+1}}|X_{i_k},\theta \right)$ and exponentiation of the (N + 1)-dimensional transition matrix ℙ is computationally prohibitive when N is large, Bollback et al. (2008) compute the transition function by approximating the Wright–Fisher process with a diffusion process (Fisher 1922; Wright 1945; Kimura, 1955a,b,c, 1957, 1962, 1964). The diffusion approximation is obtained by measuring time in units of N generations and letting N → ∞ under the assumption that s, α, β = O(N⁻¹). The consequence of this assumption is that the mean of the transition density will be upwardly biased when |s| > 0 (see Details section). Under strong positive and purifying selection, this bias can be significant, as is demonstrated by the simulation studies in the next section.

Norman (1975) relaxed this assumption with a Gaussian diffusion approximation in which mutant frequencies are centered about their deterministic trajectory with asymptotically normal deviations attributable to random genetic drift. The approximation still requires that the selection coefficient and mutation rates tend to zero as N → ∞, but assumes that the variability in mutant-frequency changes dies off faster in the limit. When selection or mutation is strong, the mean and variance of the Gaussian transition density will be biased.

While the moments derived under the assumptions of the Gaussian diffusion will be inappropriate when selection is strong, a normal approximation of the transition distribution is still reasonable. The skewness in the mutant-frequency distribution that results from stochastic loss will not develop for mutants under strong positive selection (Ns ≫ 1) once the mutant has reached a frequency of ≈1/Ns in the population (Maynard Smith 1971). In this case, the mutant frequency will track its expected value closely with small, symmetric departures due to genetic drift. We used the delta method to approximate the mean and variance of the Wright–Fisher process with a system of nonlinear difference equations that do not make any assumptions about the magnitude of s, α or β (see Details section). These equations can be solved numerically and the transition density can then be approximated by a Gaussian distribution with these two moments. The implementation of this method is extremely efficient; it requires only the routine computation of the Gaussian density, as opposed to the standard diffusion approximation, which requires specialized numerical techniques to solve Kolmogorov’s forward equation.

Details:

Here, we provide a detailed description of the three methods used to approximate the transition probability function.

Diffusion approximation:

The diffusion approximation to the Wright–Fisher process was first considered by Fisher (1930) and Wright (1931) and later substantially extended by Kimura (1955a,b,c, 1957, 1962, 1964). To approximate the discrete-state, discrete-time Wright–Fisher model with a diffusion process, it is necessary to scale the state space and time so that they are both approximately continuous. If X_n represents the proportion of mutants in a population of effective size N at generation n, then the state space will be approximately continuous on [0, 1] if N is large. Similarly, if time is measured in units of N generations such that changes occur in steps of size N⁻¹, then it too will converge to a continuous measure in the limit as N → ∞. Hence, the diffusion approximation holds when N is large. Fortunately, it is precisely in this context that the approximation is required to overcome the computational burden of exponentiating the large transition matrix, ℙ, of the discrete Wright–Fisher Markov chain.

Let {X_t, t ≥ 0} denote the proportion of mutants at time t measured in units of N generations in the limit as N → ∞. The diffusion process {X_t} is defined by its infinitesimal mean

$$\begin{array}{c}\mu \left(x\right)=\underset{N\to \mathrm{\infty }}{\text{lim}}\text{E}\left[d{X}_t|X_t=x\right]/dt\\ =\underset{N\to \mathrm{\infty }}{\text{lim}}\frac{Nsx\left(1-x\right)-N\alpha x\left(1+s\right)+N\beta \left(1-x\right)}{1+sx}\\ =\left[\underset{N\to \mathrm{\infty }}{\text{lim}}Ns\right]x\left(1-x\right)-\left[\underset{N\to \mathrm{\infty }}{\text{lim}}N\alpha \right]x+\left[\underset{N\to \mathrm{\infty }}{\text{lim}}N\beta \right]\left(1-x\right)\end{array}$$ (2)

and infinitesimal variance

$$\begin{array}{c}{\sigma }^2\left(x\right)=\underset{N\to \mathrm{\infty }}{\text{lim}}\text{Var}\left[d{X}_t|X_t=x\right]/dt\\ =\underset{N\to \mathrm{\infty }}{\text{lim}}\left(\frac{\left(1+s\right)x\left(1-\alpha \right)+\left(1-x\right)\beta }{1+sx}\right)\left(1-\frac{\left(1+s\right)x\left(1-\alpha \right)+\left(1-x\right)\beta }{1+sx}\right)\\ =x\left(1-x\right)\end{array}$$

(see, for example, Ewens 2004). Importantly, the last line in each of the above derivations requires that s, α, β = O(N⁻¹), so that Ns, Nα, and Nβ are constants and s, α, and β → 0 as N → ∞. To understand the consequences of this assumption for inference, consider a population that evolves as a Wright–Fisher process without mutation. The expected change in the mutant frequency in one generation is then

$$\frac{sx\left(1-x\right)}{1+sx},$$

while the diffusion approximation of this change is

$$\mu \left(x\right)dt=sx\left(1-x\right).$$

The expected mutant frequency therefore evolves according to a logistic function under the diffusion approximation. This will be a good approximation only for |s| ≈ 0, but will be upwardly biased for strong positive or negative selection. This implies that the mutant-frequency distribution will drift over toward fixation too rapidly under strong positive selection (s ≫ 0) and will move toward loss too slowly under strong negative selection (s ≪ 0). The diffusion approximation will therefore lead to attenuated estimates of |s| when selection is strong.

Given the infinitesimal mean and variance, the transition density φ(x, t) ≡ p(X_t|X₀, N, s, α, β) is the solution to Kolmogorov’s forward equation

$$\frac{\partial }{\partial t}\phi \left(x,t\right)=-\frac{\partial }{\partial x}\mu \left(x\right)\phi \left(x,t\right)+\frac{1}{2}\frac{{\partial }^2}{\partial x^2}{\sigma }^2\left(x\right)\phi \left(x,t\right).$$

The analytical solution to this equation was derived in a series of articles by Kimura (1955a,b,c 1957) for the special cases of pure random drift and random drift with selection and no mutation. The solutions in these special cases are extremely complex, involving infinite sums of Gegenbauer polynomials. Consequently, numerical methods for partial differential equations are typically employed to solve for the transition density φ(x, t). We used the exponentially fitted difference scheme of Duffy (1980), which is better suited than the Crank–Nicolson method employed by Bollback et al. (2008) to problems with singular initial conditions. When the discrete transition distribution is approximated with a continuous density function such as φ(x, t), the summations in (1) must be replaced with integrations. We used the trapezoidal rule to perform all integrations numerically.

Gaussian diffusion:

The assumption that Ns = O(1) is not appropriate in a regime where selection dominates genetic drift. Norman (1975) considered the case where stochastic changes due to genetic drift die off faster than the effects of selection and mutation in the limit as Nε → ∞ and ε → 0, where ε = max{|s|, α, β}. With time measured in units of ε⁻¹ generations, the mean and variance of an infinitesimal change in the mutant frequency are then

$$\begin{array}{c}\mu \left(x\right)=\underset{\mathit{\epsilon }\to 0}{\text{lim}}\frac{{\mathit{\epsilon }}^{-1}sx\left(1-x\right)-{\mathit{\epsilon }}^{-1}\alpha x+{\mathit{\epsilon }}^{-1}\beta \left(1-x\right)}{1+sx}\\ =\left[\underset{\mathit{\epsilon }\to 0}{\text{lim}}{\mathit{\epsilon }}^{-1}s\right]x\left(1-x\right)-\left[\underset{\mathit{\epsilon }\to 0}{\text{lim}}{\mathit{\epsilon }}^{-1}\alpha \right]x+\left[\underset{\mathit{\epsilon }\to 0}{\text{lim}}{\mathit{\epsilon }}^{-1}\beta \right]\left(1-x\right)\end{array}$$ (3)

and

$$\begin{array}{c}{\sigma }^2\left(x\right)=\underset{\mathit{\epsilon }\to 0,\hspace{0.17em}N\mathit{\epsilon }\to \mathrm{\infty }}{\lim }\left(\frac{\left(1+s\right)x\left(1-\alpha \right)+\left(1-x\right)\beta }{1+sx}\right)\left(1-\frac{\left(1+s\right)x\left(1-\alpha \right)+\left(1-x\right)\beta }{1+sx}\right)\frac{1}{N\mathit{\epsilon }}\\ =\underset{N\mathit{\epsilon }\to \mathrm{\infty }}{\lim }\frac{x\left(1-x\right)}{N\mathit{\epsilon }},\end{array}$$

respectively. The standard diffusion is a special case where ε = N⁻¹. Note that the assumption of weak selection and mutation through ε → 0 leads to the simplification in the second line of both equations. In particular, we note that the infinitesimal mean will suffer from the same bias as that of the standard diffusion approximation when selection is strong. The Gaussian diffusion is obtained by assuming that Nε → ∞ as N → ∞ and ε → 0 such that the variance of a displacement tends to zero faster than its expected value in the limit. Under these conditions, Norman (1975) showed that the transition density after n generations with initial mutant frequency p is approximately Gaussian with mean f(nε, p) and variance g(nε, p)/Nε, where f is the solution to

$$\frac{d}{dt}f\left(t,x\right)=\mu \left[f\left(t,x\right)\right]$$

subject to f(0, x) = x and g is given by

$$g\left(t,x\right)={\displaystyle {\int }_0^t\text{exp}\left\{2{\displaystyle {\int }_u^t{\mu }^{\prime }\left[f\left(\xi ,x\right)\right]d\xi }\right\}\nu \left[f\left(u,x\right)\right]du},$$

where ν(x) = x(1 − x). Here, we are interested in the case where selection is stronger than mutation, that is, ε = |s|. In this case, the transition density of the Gaussian diffusion after n generations has mean

$$E\left[X_n|X_0=p\right]=\frac{p}{p+\left(1-p\right)e^{-sn}}$$

and variance

$$\text{Var}\left[X_n|X_0=p\right]=\frac{p\left(1-p\right)e^{ns}\left[p^2{e}^{2ns}+\left(1-2p-2nsp\left(p-1\right)\right)e^{ns}-{\left(p-1\right)}^2\right]}{Ns{\left[1+p\left(e^{ns}-1\right)\right]}^4}.$$

Obtaining the transition density under the Gaussian diffusion is therefore computationally straightforward. Note that the expected mutant frequency is described by the same logistic function as the standard diffusion approximation, but that the dispersion about this deterministic trajectory will necessarily be symmetric.

Delta method:

The moments of the transition densities under both the standard and Gaussian diffusion approximations were derived under the assumption of weak selection and mutation. We obtained approximate expressions for the mean and variance of this distribution without making any assumptions about the strength of selection and mutation using the delta method (see, for example, Rice 2007, Chap. 4). For a random variable X with mean μ and variance σ², the mean and variance of a function f(X) can be approximated with first-order Taylor expansions about μ:

$$\begin{array}{c}E\left[f\left(X\right)\right]\approx f\left(\mu \right)\\ \text{Var}\left[f\left(X\right)\right]\approx {\left[f^{\prime }\left(\mu \right)\right]}^2{\sigma }^2.\end{array}$$

If {X_n, n = 0, 1, …} is a Wright–Fisher process, the mean μ_n ≡ E[X_n|X₀] and variance ${\sigma }_n^2\equiv \text{Var}\left[X_n|X_0\right]$ of the transition function can therefore be approximated as

$$\begin{array}{c}{\mu }_n=E\left[E\left[X_n|X_{n-1}\right]|X_0\right]\\ =E\left[\frac{\left(1+s\right)X_{n-1}\left(1-\alpha \right)+\left(1-X_{n-1}\right)\beta }{1+s{X}_{n-1}}|X_0\right]\\ \approx \frac{\left(1+s\right){\mu }_{n-1}\left(1-\alpha \right)+\left(1-{\mu }_{n-1}\right)\beta }{1+s{\mu }_{n-1}}\end{array}$$

and

$$\begin{array}{c}{\sigma }_n^2=E\left[\text{Var}\left[X_n|X_{n-1}\right]|X_0\right]+\text{Var}\left[E\left[X_n|X_{n-1}\right]|X_0\right]\\ =\frac{1}{N}E[\left(\frac{\left(1+s\right)X_{n-1}\left(1-\alpha \right)+\left(1-X_{n-1}\right)\beta }{1+s{X}_{n-1}}\right)\times \left(1-\frac{\left(1+s\right)X_{n-1}\left(1-\alpha \right)+\left(1-X_{n-1}\right)\beta }{1+s{X}_{n-1}}\right)|X_0]\\ +\text{Var}\left[\frac{\left(1+s\right)X_{n-1}\left(1-\alpha \right)+\left(1-X_{n-1}\right)\beta }{1+s{X}_{n-1}}|X_0\right]\\ \approx \frac{1}{N}[\left(\frac{\left(1+s\right){\mu }_{n-1}\left(1-\alpha \right)+\left(1-{\mu }_{n-1}\right)\beta }{1+s{\mu }_{n-1}}\right)\times \left(1-\frac{\left(1+s\right){\mu }_{n-1}\left(1-\alpha \right)+\left(1-{\mu }_{n-1}\right)\beta }{1+s{\mu }_{n-1}}\right)]\\ +{\left[\frac{\left(1+s\right)\left(1-\alpha -\beta \right)}{{\left(1+s{\mu }_{n-1}\right)}^2}\right]}^2{\sigma }_{n-1}^2,\end{array}$$

respectively. Hence we obtain a system of nonlinear recurrence equations that can be solved numerically for the mean and variance of the transition distribution given an initial frequency X₀ = p. For large populations with strong selection or mutation, the transition density can then be approximated by a Gaussian distribution with these moments.

The usual delta method of statistics uses a second-order Taylor series approximation for the mean. We considered this and a second-order Taylor series approximation for the variance. We investigated the behavior of the resulting systems of equations empirically for different values of s, N, and p with α = β = 0. We found that the system began to oscillate when p < 1/Ns for s > 0 when second-order approximations were used for either the mean only or the mean and the variance, but not when first-order approximations were used for both of these moments. Interestingly, when P < 1/Ns, the frequency of the mutant is too low to ensure its ultimate fixation and the resulting transition distribution will involve singularities at the boundaries. Clearly, such a mutant-frequency distribution cannot be accurately modeled with a Gaussian density. We ran all of our simulations using both the first-order approximation to the mean and variance and the second-order approximation to the mean. Although the true and inferred deterministic paths were indistinguishable when a second-order approximation was used for the mean, the improvement in accuracy did not substantively affect our simulation results. We have included the transition densities that we obtained with the second-order approximation to the mean in Supporting Information, Figure S1. Consequently, we report only the results obtained with the first-order approximations to the mean and variance, which did not lead to spurious oscillations for any of the parameter values investigated.

Implementation

All computer code was written in the R Language and Environment for Statistical Computing and is freely available from the corresponding author. The maximum-likelihood estimates were obtained with a steepest-ascent hill-climbing algorithm and were checked by plotting the likelihood surface when possible.

Results

Comparison of model approximations

For small N, the exact transition distribution of a discrete Wright–Fisher process can be evaluated numerically. We compared the approximate distribution obtained with each of the above three methods to the exact distribution for N = 100, 1000, and 5000 after n = 5, 10, and 20 generations starting with an initial mutant frequency of p = 0.1, 0.5, and 0.9. For each of these 27 combinations, we computed the mutant-frequency distribution for selection coefficients of 0, ±0.001, ±0.01, ±0.1, ±0.3, and ±0.5 and no mutation. The complete set of results is presented in Figure S1.

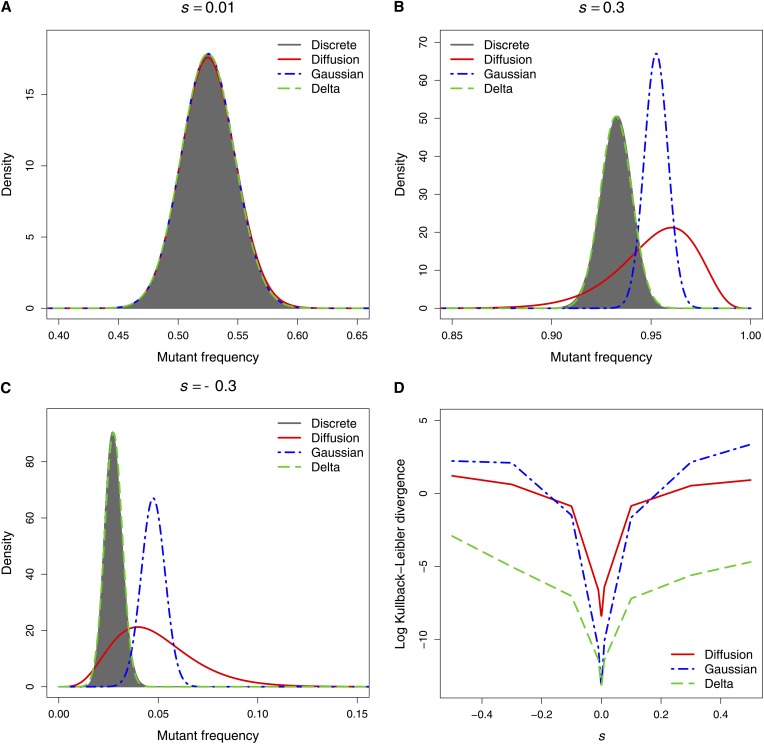
As expected all three methods provided an excellent approximation to the exact transition distribution when selection was weak (|s| < 0.01) and the population size was large (see Figure 1A, for example). When N = 5000, the standard and Gaussian diffusion approximations performed poorly under strong selection (|s| > 0.1). As is evident from Figures 1, B and C, the approximate transition distributions obtained with these methods are located too far to the right, a direct consequence of the assumption that s = O(N⁻¹) (see Methods). In contrast, our delta method approach provided an excellent approximation to the true distribution when the population size was large, irrespective of the strength of selection. Figure 1D, which plots the Kullback–Leibler divergence of each approximate distribution from the exact distribution, demonstrates the superior performance of our method compared to the standard and Gaussian diffusion approximations under strong positive and negative selection in a large population with an initial mutant frequency of 0.5. For large populations with initial mutant frequencies of 0.1 and 0.9, the delta method performed particularly well when there was strong selection away from the absorbing boundaries at 0 and 1, respectively (see the Kullback–Leibler divergence plots in Figure S1).

Figure 1.

The exact transition distribution of the Wright–Fisher process and its three approximations after n = 10 generations when N = 5000 and p = 0.5. (A) Weak selection (s = 0.01). (B) Strong positive selection (s = 0.3). (C) Strong negative selection (s = −0.3). (D) Kullback–Leibler divergence from the exact distribution.

When the population size was small (N = 100), the two methods that approximated the transition distribution with a Gaussian density performed less well compared to the standard diffusion approximation when selection was weak (see Figure S1). This result is unsurprising since random departures from the mean mutant frequency will be approximately normal only when the population size is large and selection is strong enough to prevent stochastic loss. When genetic drift dominates selection, the mutant-frequency distribution will develop singularities and skewness that cannot be captured by the Gaussian density. Interestingly, the standard diffusion model, which is derived in the limit as N → ∞, performs remarkably well when N is this small, provided, of course, that selection is weak. This is in agreement with the findings of Ewens (1963). When selection is strong, all three methods provide rather poor approximations to the true density if the population size is small (see Figure S1). However, no approximation is necessary when the population size is small, since the exact Wright–Fisher transition distribution can then be computed numerically from the transition matrix and initial mutant-frequency distribution.

Simulations

To assess how the three approximations affect population genetic inferences, we simulated 1000 realizations of a Wright–Fisher process with selection and no mutation for 20 generations. A relatively small effective population size of N = 1000 was used, because the matrix multiplications required to simulate a discrete Wright–Fisher process were computationally burdensome for larger values of N. For each simulated process, N and s were estimated by maximizing the likelihood function (1) with a uniform prior distribution for the initial population mutant frequency using each of the three approximations to the transition distribution. As a check that the three approaches perform as expected, the data were initially simulated with s = 0 and p = 0.5, and the parameters were estimated from large samples of size 10000 observed at all 20 generations. Under these conditions, all three methods performed similarly, yielding unbiased estimates, $\widehat{N}$ and $\widehat{s}$, of N and s with similar standard errors (see Table 1 and Figure S2).

Table 1. Medians of the maximum-likelihood estimates of N and s obtained in 1000 data sets simulated under the conditions given in the first three columns.

			Standard diffusion		Gaussian diffusion		Delta method
True selection	Sample sizes	No. of samples	$\widehat{N}$	$\widehat{s}$	$\widehat{N}$	$\widehat{s}$	$\widehat{N}$	$\widehat{s}$
0	10000	20	1150	0	1130	0	1130	0
			(890, 1530)	(−0.011, 0.009)	(870, 1510)	(−0.011, 0.010)	(870, 1510)	(−0.011, 0.010)
0.2	10000	20	1510	0.178	1200	0.182	1150	0.199
			(1070, 2330)	(0.166, 0.189)	(920, 1580)	(0.170, 0.193)	(890, 1510)	(0.185, 0.213)
0.2	1000	20	2310	0.177	1560	0.182	1490	0.199
			(1048, 12280)	(0.165, 0.190)	(900, 4695)	(0.169, 0.195)	(858, 4512)	(0.184, 0.215)
0.2	1000	5	11290	0.176	408000	0.181	446400	0.199
			(2292, >108)	(0.162, 0.190)	(1168, 1.526⋅107)	(0.167, 0.195)	(1118, 2.068⋅107)	(0.181, 0.216)
0.5	10000	20	3630	0.397	1160	0.406	1120	0.501
			(1688, >108)	(0.384, 0.411)	(888, 1570)	(0.392, 0.419)	(858, 1512)	(0.482, 0.521)
0.5	1000	20	3485	0.396	1610	0.405	1530	0.500
			(1620, >108)	(0.381, 0.411)	(888, 3905)	(0.391, 0.421)	(850, 3740)	(0.479, 0.523)
0.5	1000	5	5730	0.394	6700	0.405	7545	0.500
			(2672, >108)	(0.376, 0.413)	(1130, 1.675⋅107)	(0.388, 0.422)	(1070, 2.711⋅107)	(0.474, 0.525)

In all cases, the true population size was N = 1000. The interquartile ranges are indicated in parentheses.

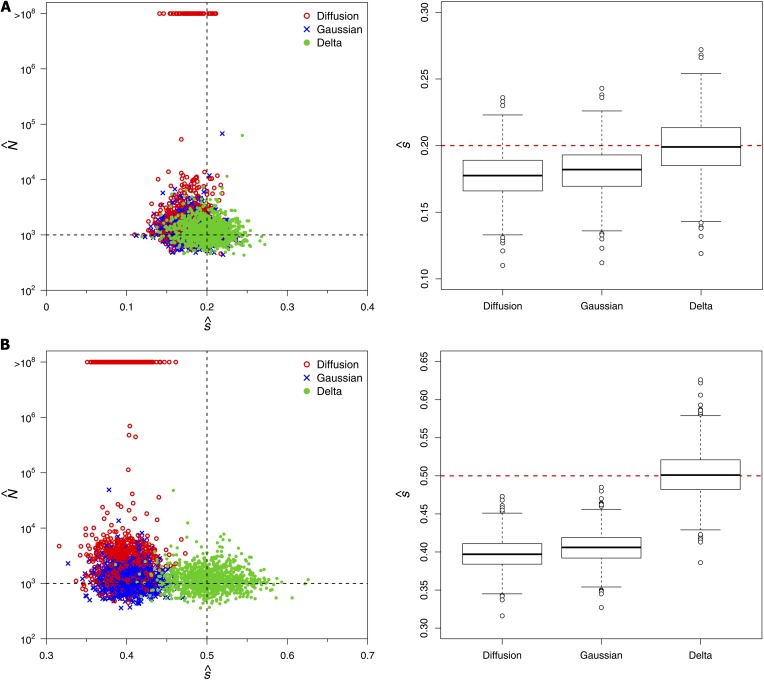
For the remaining simulations, we considered selection coefficients of s = 0.2 and s = 0.5 with initial mutant frequencies of p = 0.05 and P = 0.01, respectively. Bollback et al. (2008) inferred a selection coefficient of 0.43 for the C206U mutation of the bacteriophage MS2 using the standard diffusion approximation to the transition distribution. Given the results of the previous subsection, we would expect this estimate to be downwardly biased. To assess the severity of this bias using simulations, we first considered the ideal case in which large samples of 10000 sequences were observed at every generation for all 20 generations. Although these conditions may be unrealistic in practice, the purpose of this simulation study was to establish benchmark performances to serve as a basis for comparison when these ideal conditions are not met. We found that the Gaussian diffusion and delta methods provided reasonable maximum-likelihood estimates (MLEs) of N with interquartile ranges that included the true value of 1000 (see Table 1). The estimates of N obtained with the standard diffusion were more variable than those of the other two methods, and the median and interquartile range were upwardly biased. The selection coefficient s was underestimated with both the standard and Gaussian diffusion approximations. The bias was particularly severe when s = 0.5, with all of the 1000 MLEs falling below the true value for the standard and Gaussian diffusion approximations (median $\widehat{s}$ values of 0.397 and 0.406, respectively). Our delta method approximation, on the other hand, yielded estimates of s that were centered about the true value and only slightly more variable than those of the other two methods (see Table 1 and Figure 2).

Figure 2.

MLEs for N and s obtained in 1000 data sets simulated with N = 1000 and (A) s = 0.2 and (B) s = 0.5. Estimates were based on the mutant frequencies observed in samples of size 10000 taken every generation for 20 generations of the process, starting with an initial population mutant frequency of p = 0.05 in A and p = 0.01 in B.

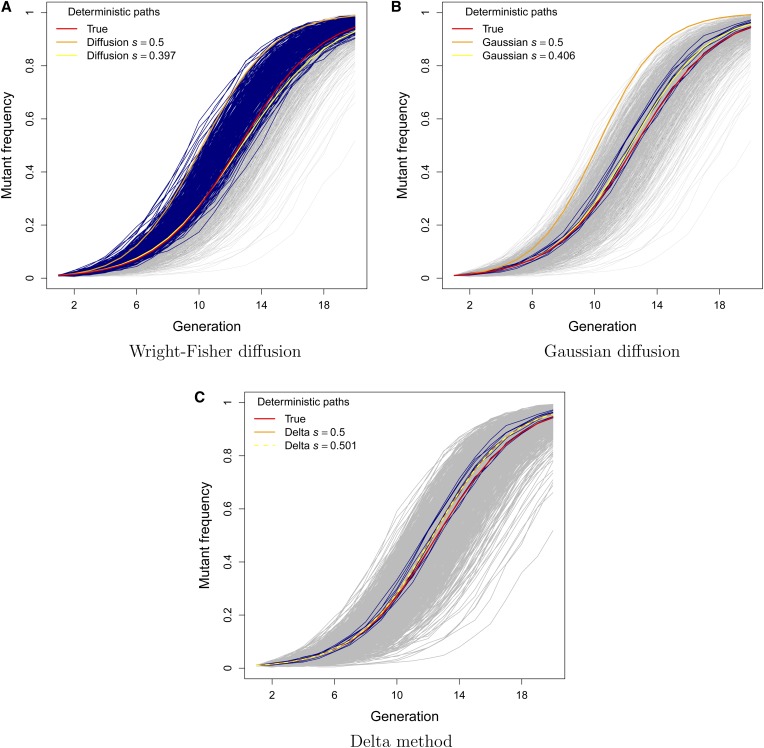
Approximately one-third of the simulated data sets produced MLEs of N in excess of 100 million when the standard diffusion approximation was employed with s = 0.5 (see Figure 2). These corresponded to data sets where the mutant frequency rose rapidly toward fixation (see Figure 3A). For a given level of selection, a large population size increases the expected displacement of the mutant frequency in an infinitesimal amount of time under this model (see Equation 2 in Methods). The larger estimates of N were therefore compensating for the downwardly biased estimates of s when the mutant-frequency trajectory rose sharply. Interestingly, such large estimates of N were not observed under the Gaussian diffusion approximation, even though $\widehat{s}$ was also downwardly biased under this model. This is because the infinitesimal mean of the Gaussian diffusion is not a function of N and therefore increasing the effective population size would not help to explain the rapid rise in mutant frequency (see Equation 3 in Methods). Instead, the simulated trajectories that yielded large N estimates with the Gaussian diffusion and delta methods closely tracked the true deterministic path (that is, the expected values of the discrete Wright–Fisher process used to simulate the data; see Figures 3, B and C). Note that the deterministic paths implied by the standard and Gaussian diffusion models rise much more rapidly than the true deterministic path of the data-generating process when s = 0.5. The downwardly biased estimates of s ensure that the deterministic trajectory based on the median $\widehat{s}$ represents the center of the data in both cases (see Figures 3, A and B). This was not the case for our delta method approximation, where the true and inferred deterministic paths were very similar (see Figure 3C).

Figure 3.

Trajectories with large N estimates based on the (A) Wright–Fisher diffusion model, (B) Gaussian diffusion model, and (C) delta method. Navy lines indicate data sets with $\widehat{N}>{10}^8$ in A and $\widehat{N}>5 000$ in B and C. The deterministic path based on the true data-generating process with s = 0.5 and N = 1000 is indicated with a red line. The deterministic path based on the model is indicated with an orange line for s = 0.5 and with a yellow line for the median value of $\widehat{s}$.

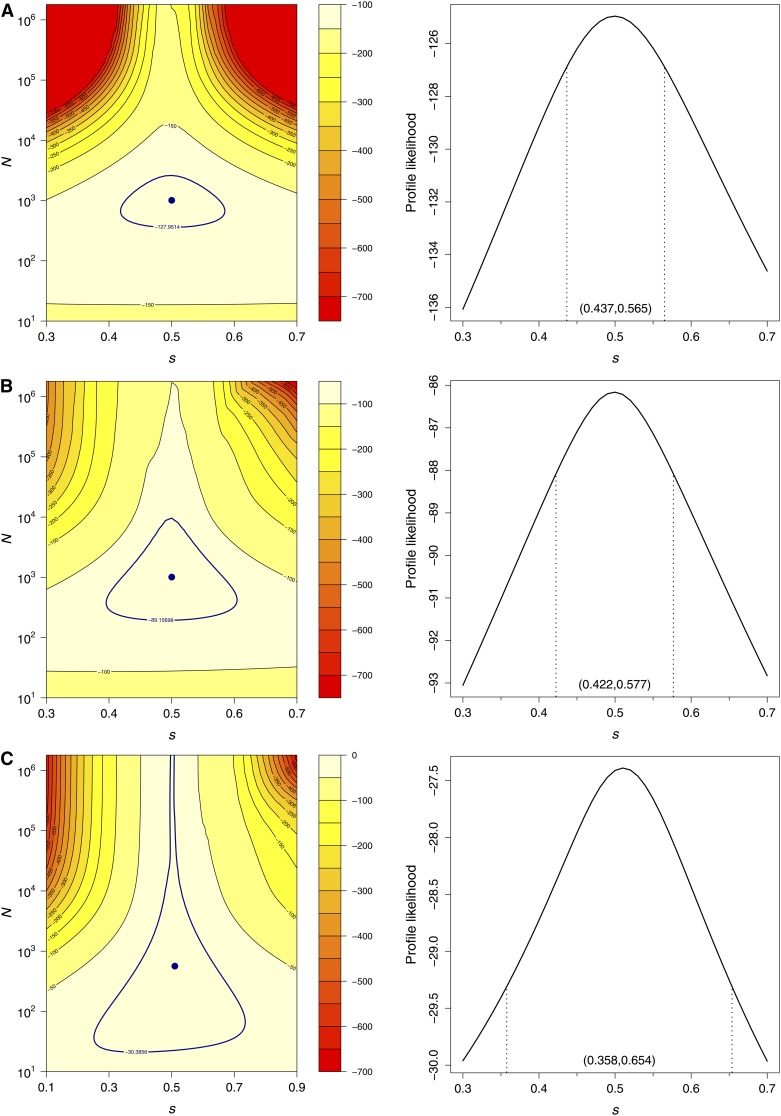
We conducted two further simulation studies to assess the effect of reducing the sample size and sampling frequency. In the first of these, the sample size was reduced to 1000 sequences per generation. In the second study, we assumed that the smaller samples were observed at only five equally spaced time points rather than for all 20 generations. The resulting estimates of N and s are summarized in Table 1, Figure S3, and Figure S4. As expected, reducing the sample size and, particularly, the sampling frequency increased the variability of the estimates of N. Interestingly though, the variability of $\widehat{s}$ did not increase notably in either of these cases. However, reducing the sampling frequency did have a profound effect on likelihood intervals for (N, s). As illustrated in Figure 4 for one simulated data set with s = 0.5, the 95% likelihood interval based on the delta method widened considerably when the sampling frequency was reduced fourfold. This expansion was particularly conspicuous along the N dimension, since fewer sample points implies less information on the genetic drift of the process. This was also noted by Malaspinas et al. (2012) in their simulations. There was also a more notable widening of the 95% profile likelihood intervals for s when fewer samples were taken compared to when the size of each sample was reduced.

Figure 4.

Log-likelihood surfaces (left) and profile likelihoods for s (right) obtained with the delta method for a selected simulated data set with N = 1000 and s = 0.5. (A) Samples of size 10,000 observed every generation for 20 generations. (B) Samples of size 1000 observed every generation for 20 generations. (C) Samples of size 1000 observed every fourth generation for 20 generations. Navy points indicate MLEs and navy contour lines indicate 95% likelihood regions. Dashed lines on the profile likelihood panels mark the 95% likelihood intervals for s given in parentheses.

Application

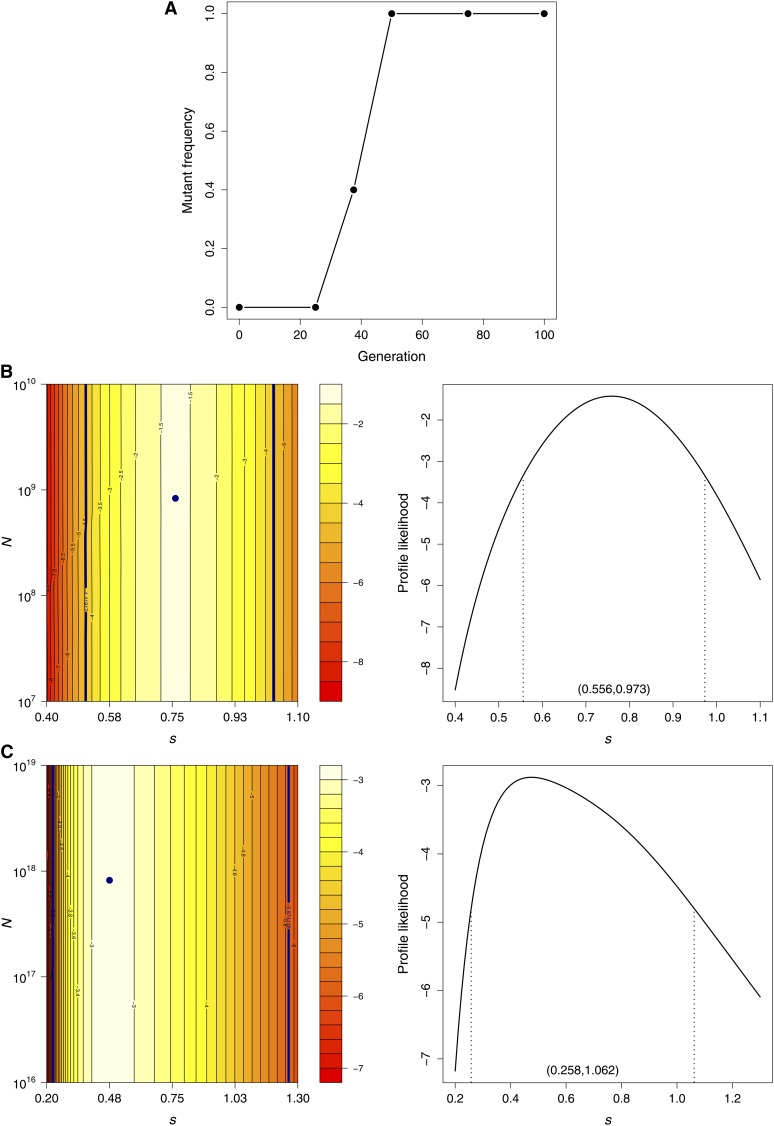
We applied our method to a mutant-frequency trajectory from an experimental study of bacteriophage adaptation (Bollback and Huelsenbeck 2007). Briefly, this study evolved large populations (census size of 5 × 10⁷) of the bacteriophage MS2 for 100 generations at elevated temperatures and tracked nucleotide substitutions occurring during adaptation. Since the mutants in this study evolved under strong selective pressure, we anticipated that our delta method approach would provide more accurate estimates of the population genetics parameters than the standard diffusion approximation.

We chose to apply our method to the U1685C mutation in experimental line 3, which rose rapidly in frequency once it appeared and is therefore likely to have a particularly large selection coefficient (see Figure 5A). The frequency of this mutation was measured at six time points based on 10 sequences at each time point (9 sequences at the second time point). Note that the sample size in this application is much smaller than that which we considered in our simulation studies, and we therefore expect much wider confidence intervals for the parameters. Since no mutants were observed until after the second time point, we assumed that the mutant arose only thereafter and used an informative prior with a point mass at zero for the population mutant frequency at generation 25. The mutation rates from C to U (α) and from U to C (β) were both set to $\frac{1}{3}\times {10}^{-3}$ (Drake 1993).

Figure 5.

Data and results for the bacteriophage U1685C mutation. (A) Mutant frequency trajectory. The log-likelihood surface (left) and profile likelihood for s (right) were computed with the (B) delta method and the (C) Wright–Fisher diffusion approximation. The navy points on the log-likelihood surfaces indicate the MLEs and the navy contour lines indicate the 95% likelihood regions. Dashed lines on the profile likelihood plots mark the 95% likelihood intervals for s given in parentheses.

The log-likelihood surface for U1685C obtained with our delta method approach is plotted in Figure 5B. The MLE of the effective population size was $\widehat{N}=8.32\times {10}^8$, although it is clear from the likelihood surface plot that this parameter cannot be reliably estimated from these data (the likelihood surface was flat along the N dimension for N values in the range 10⁴–10¹⁹). Indeed, this nucleotide site was observed to be polymorphic only at one time point and it is therefore not possible to confidently infer the extent of genetic drift. In contrast, the trajectory does contain information about the selection coefficient. We obtained a large MLE of $\widehat{s}=0.759$ with a 95% profile likelihood interval of (0.559, 0.973) using the delta method (see Figure 5B).

As expected, the MLE based on the standard diffusion approximation was substantially smaller at $\widehat{s}=0.475$ and was less than the lower bound of the 95% likelihood interval obtained with the delta method (see Figure 5C). The corresponding profile likelihood interval based on the diffusion approximation was also much wider at (0.258, 1.062). As we observed in our simulation studies, the MLE of the effective population size obtained with the diffusion approximation, $\widehat{N}=8.19\times {10}^{17}$, was much larger than that obtained with the delta method and appears to compensate for the downwardly biased estimate of s. However, as with the delta method, this parameter could not be reliably estimated with the diffusion approximation.

Discussion

Developments in ultra-deep sequencing technologies have greatly enhanced our ability to track changes in the genetic diversity of measurably evolving populations over time. Large genetic samples collected at several time points permit efficient statistical inference of the population genetics parameters that govern the fate of mutant variants.

In this article, we considered a stochastic model of mutant-frequency evolution that can be used to infer the effective population size, selection coefficient, and mutation rates from temporal allele-frequency data using the method of maximum likelihood. In this hidden Markov model, the observed mutant frequencies are obtained through binomial sampling from a population in which the mutant frequency evolves according to the Wright–Fisher process. Because there is no simple analytical expression for the transition distribution of this process and its numerical evaluation is computationally prohibitive for large effective population sizes, the Wright–Fisher model is commonly approximated with a diffusion process (Fisher 1922; Wright 1945; Kimura, 1955a,b,c, 1957, 1962, 1964). However, this approximation assumes that the forces of selection and mutation are weak. This assumption is not always appropriate. For example, mutations in intrahost viral populations are likely to be under strong selection to evade the immune response and drug therapy, and microbes are often subjected to strong selective pressures in experimental studies of adaptation. Moreover, the assumption of weak selection and mutation is often overlooked in the literature, although, as we have demonstrated, it has profound implications for inferences.

Norman (1975) derived an alternative approximation to the Wright–Fisher process, known as the Gaussian diffusion, in which the effects of selection and mutation die off less rapidly compared to genetic drift as the population size gets larger and the selection and mutation parameters tend to zero. Here, we developed a novel approximation that is extremely accurate for a population with a large effective size. Like Norman (1975), we approximate the transition distribution with a Gaussian density, but use the delta method of statistics to derive a set of recurrence equations for the mean and variance of this distribution without making any assumptions about the strength of selection and mutation.

By comparing the approximate transition densities to the exact distribution, we showed that all three methods perform well when the effective population size is large and selection is weak. However, the quality of the standard and Gaussian diffusion approximations was severely compromised when selection was strong. In both cases, the transition distribution shifts too rapidly toward mutant fixation under strong positive selection and too slowly toward mutant loss under strong purifying selection. In contrast, our approximation was remarkably accurate for large effective population sizes irrespective of the strength of selection.

The accuracy of the approximation has important consequences for estimates of the selection coefficient. Using simulated Wright–Fisher trajectories, we demonstrated that maximum-likelihood estimates of the selection coefficient are severely attenuated when selection is strong using either the standard or Gaussian diffusion approximations to the transition distribution. On the other hand, our delta method approach yielded unbiased estimates of the selection coefficient, irrespective of the sampling frequency or sample size. We applied our method to infer selection for a mutant in an experimental study of bacteriophage adaptation under heat stress. As expected from our simulation study, the estimated selection coefficient of 0.759 obtained with the delta method was much larger than the estimate of 0.475 obtained with the standard diffusion approximation.

Frequent sampling is needed to obtain robust and precise parameter estimates. In our simulation study, we demonstrated that reducing the sampling frequency leads to wider confidence regions, particularly in the direction of the effective population size. Indeed, we were unable to reliably infer this parameter in our bacteriophage application where the nucleotide site was observed to be polymorphic at only one time point. Interestingly though, this mutant-frequency trajectory still contained enough information with which to obtain a bounded likelihood interval for the selection coefficient. Given sufficient time points, it would also be possible to allow the selection coefficient to vary over time, which often occurs in natural populations. Ignoring time-varying selection could lead to attenuated estimates of the effective population size.

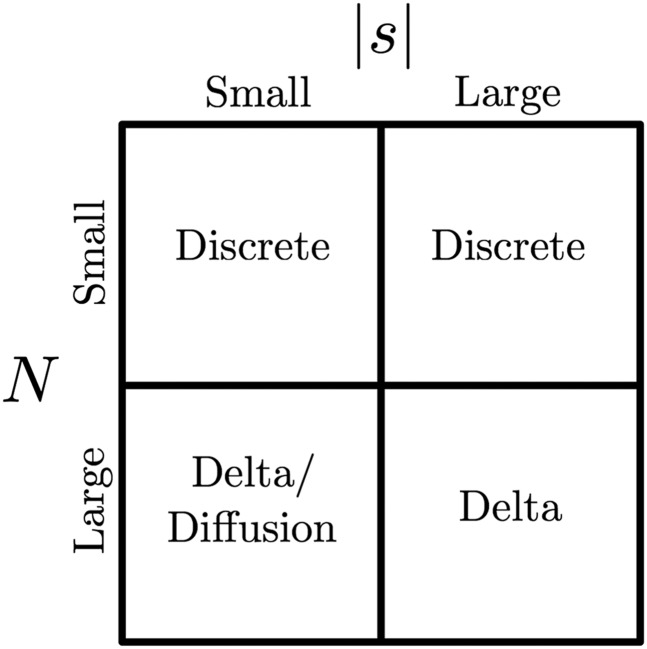
Figure 6 summarizes the appropriate statistical methods for different regions the (N, s) parameter space. When the effective population size is small (N < 5000), exponentiation of the one-step transition probability matrix of the discrete Wright–Fisher Markov chain is computationally feasible and should be used for inferences. For mutants evolving under weak selection (|s| < 0.01) in populations with a large effective size (N > 5000), either of the diffusion approximations or the delta method approach can be used for accurate inferences. However, we recommend the delta method over the standard diffusion approximation as it is computationally far more efficient. Finally, when the effective population size is large and selection is strong, only our delta method approach will provide an unbiased estimate of the selection coefficient.

Figure 6.

Parameter space with appropriate method of inference.

In practice, we may not have a priori information on the magnitudes of the parameters for a given data set. In this case, one could begin by first optimizing the likelihood based on the discrete Wright–Fisher model over small values of N (N < 5000). If the optimal (N, s) point lies on the upper boundary of N, then one would proceed to perform the optimization over larger values of N using the delta method approximation. Alternatively, one could plot the likelihood surface using the appropriate method in each region of the parameter space.