Partitioning Heritability of Regulatory and Cell-Type-Specific Variants across 11 Common Diseases

Abstract

Regulatory and coding variants are known to be enriched with associations identified by genome-wide association studies (GWASs) of complex disease, but their contributions to trait heritability are currently unknown. We applied variance-component methods to imputed genotype data for 11 common diseases to partition the heritability explained by genotyped SNPs ($h_g^2$) across functional categories (while accounting for shared variance due to linkage disequilibrium). Extensive simulations showed that in contrast to current estimates from GWAS summary statistics, the variance-component approach partitions heritability accurately under a wide range of complex-disease architectures. Across the 11 diseases DNaseI hypersensitivity sites (DHSs) from 217 cell types spanned 16% of imputed SNPs (and 24% of genotyped SNPs) but explained an average of 79% (SE = 8%) of $h_g^2$ from imputed SNPs (5.1× enrichment; p = 3.7 × 10⁻¹⁷) and 38% (SE = 4%) of $h_g^2$ from genotyped SNPs (1.6× enrichment, p = 1.0 × 10⁻⁴). Further enrichment was observed at enhancer DHSs and cell-type-specific DHSs. In contrast, coding variants, which span 1% of the genome, explained <10% of $h_g^2$ despite having the highest enrichment. We replicated these findings but found no significant contribution from rare coding variants in independent schizophrenia cohorts genotyped on GWAS and exome chips. Our results highlight the value of analyzing components of heritability to unravel the functional architecture of common disease.

Introduction

Recent work by ENCODE and other projects^1,2 has shown that specific classes of variants can have complex and diverse impacts on cell function and phenotype.^3–10 Although the importance of coding variation has long been understood, these projects identified other genomic regions that can contribute to function and highlighted the role of regulatory variants. With many potentially informative functional categories and competing biological hypotheses, quantifying the contribution of variants in these categories to heritability of complex traits would inform trait biology and focus genetic mapping.

The availability of significantly associated variants from hundreds of genome-wide association studies (GWASs)¹¹ has opened one avenue for quantifying enrichment. Indeed, 11% of GWAS hits lie in coding regions,¹¹ 57% of noncoding GWAS hits lie in broadly defined DNaseI hypersensitivity sites (DHSs; spanning 42% of the genome),³ and still additional GWAS hits tag these regions. The full distribution of GWAS association statistics exhibits enriched p values in coding regions and UTRs.¹² Analysis of DHS subclasses and other histone marks has revealed a complex pattern of cell-type-specific relationships with known disease associations.⁶ Recent work has also shown that functional enrichment can be leveraged for increasing association mapping power.¹³

Although relative enrichment has been documented, the question of how much each category contributes to disease heritability remains unanswered.^14,15 Recently, investigators have used variance-component methods to estimate the total additive variance explained by all genotyped SNPs ($h_g^2$),^16,17 and to estimate the $h_g^2$ of many quantitative and dichotomous traits.^18–22 We propose joint estimation of $h_g^2$ from functional-category-specific variance components for assessing enrichment. In contrast to analyses of top GWAS hits, the variance-component approach leverages the entire polygenic architecture of each trait and accounts for pervasive linkage disequilibrium (LD) across functional categories. Indeed, our simulations showed that this approach provides accurate genome-wide estimates of functional enrichment in diverse genetic architectures. We applied variance-component methods to functional categories in GWAS- and exome-chip data from over 100,000 samples in 11 traits.

Material and Methods

Estimating Enrichment of $h_g^2$ with Variance Components

For a single component of genotyped (or imputed) SNPs, we define $h_g^2$, an underlying parameter in the population, as the r² between the true phenotype and the best linear prediction over those SNPs. With multiple components, the goal of the partitioned analysis is to quantify the $h_g^2$ directly explained by SNPs in each functional category while excluding tagging of SNPs in other categories. We thus define the $h_g^2$ for each functional category as the r² between the true phenotype and the prediction only from SNPs in that functional category when all functional categories are jointly analyzed for a best linear prediction. When SNPs are in LD, this definition remains valid as long as the individual causal effect sizes are independent, as we would expect in highly polygenic traits. For disease traits, we model the phenotype (and corresponding $h_g^2$) by using the liability-threshold model, in which individuals whose underlying unobserved continuous liability exceeds a threshold are labeled as disease case subjects.^19,23

We estimate $h_g^2$ jointly across multiple variance components, each constructed from variants belonging to nonoverlapping functional categories. The underlying model assumes that SNP effect sizes are drawn from a normal distribution with category-specific variance. (We note that the normality assumption is unrealistic; previous work in the single-variance-component case has indicated that this does not introduce bias, although modeling a more realistic mixture distribution can increase precision.²⁴ Because of computational constraints, we do not consider mixture distributions here.) The model relates the observed phenotypic covariance to a weighted sum of genetic relationship matrices computed from SNPs in each category. The joint estimate allows all components to compete for shared variance due to LD.

Formally, for a functional categories each containing the set of SNPs S_i (of size M_i), we model the phenotype as a sum of individual SNP effect sizes:

$$y=\sum _{i=1}^a\sum _{s\in S_i}{W}_s{\beta }_s^i+e,$$

where $W_s$ is the genotype at SNP s, ${\beta }_s^i$ is the effect size at SNP s in category i and is drawn from category-specific normal distribution ${\beta }^i\sim N\left(0,{\sigma }_i^2\right)$, and e is the residual effect $e\sim N\left(0,{\sigma }_e^2\right)$. We assume that for each annotation i, SNPs normalized to have mean 0 and variance 1 are contained in the matrix $W_i$. The variance of the phenotype is then modeled as

$$V\left(y\right)=\sum _{i=1}^a{K}_i{\sigma }_i^2+e,$$

where each $K_i$ represents a genetic-relationship matrix (GRM) computed directly from the SNPs in annotation i as

$$K_i=W_i{W}_i^{\prime }/M_i.$$

The corresponding σ are then jointly inferred with the REML algorithm in GCTA (Genome-wide Complex Trait Analysis),^16,17 yielding

$$h_{gi}^2=\frac{{\sigma }_{gi}^2}{{\sum }_{j=1}^a{\sigma }_{gi}^2+{\sigma }_e^2}.$$

The inverse of the final average-information matrix yields an estimate of the corresponding error-covariance matrix of the variance-component estimates.²⁵ We use the error-covariance matrix and delta method²⁶ to compute SEs on $h_g^2$ and the percentage of $h_g^2$ while accounting for error correlations (referred to here as the analytical SE²⁷). All estimates of $h_g^2$ were transformed to the liability scale¹⁹ with the prevalence values in Table S1 (available online). We evaluated the accuracy of the analytical SE for both quantitative and ascertained traits and found it to correspond well to the true SD under reasonable polygenicity (see Appendix A). Meta-analysis estimates were computed with inverse-variance weighting:²⁸ given individual study estimates $h_{gi}^2$, analytical SE_i, and corresponding weight $w_i=1/{\text{SE}}_i^2$, the meta-analysis mean is equal to

$$\frac{{\sum }_i{w}_i\times h_{gi}^2}{{\sum }_i{w}_i},$$

and the meta-analysis SE is equal to $\sqrt{1/{\sum }_i{w}_i}$.

Enrichment is computed for each category i as the ratio of the percentage of $h_{gi}^2$ (the percentage of $h_g^2$ in category i) to the percentage of SNP_i (the percentage of SNPs in category i) and is tested for significance by Z score relative to a null of 1:0 with the (likewise-rescaled) analytical SE. Under the assumption that all causal variants are typed, this statistic is equivalent to the relative risk that a SNP in category i is causal in comparison to an average SNP. To achieve unbiasedness, the estimate of $h_g^2$ is not constrained to lie inside the plausible 0–1 bound, which can lead to negative estimates in rare instances.

Estimating Enrichment from Summary Statistics

We considered alternative methods for estimating functional enrichment from summary association statistics. The simplest approach is to directly count the number of individual genome-wide-significant variants in each functional annotation and compare to the null expectation from all SNPs (or random SNPs matched on certain features). This approach can either include all significant markers or restrict to the most significant variant in each locus. The genome-wide-significant-SNP approach has been extended to the full distribution of association statistics for quantifying overall p value enrichment.³ Over increasingly restrictive p value thresholds, the fraction of SNPs passing a given threshold and belonging to each category is computed and normalized by the category-specific genome-wide fraction. The distributions are then inspected visually for enrichment or assessed by permutation. For completeness, we considered two additional methods—stratified quantile-quantile (Q-Q) plots¹² and Bayesian hierarchical modeling (fgwas)¹³—which assess functional enrichment but are primarily focused on improving association mapping power (see Discussion).

Data Sets Analyzed

11 Diseases from WTCCC1 and WTCCC2

We analyzed seven traits from Wellcome Trust Case Control Consortium 1 (WTCCC1) and four traits from WTCCC2 for a total 47,000 samples (Table S1). Estimates of $h_g^2$ are particularly sensitive to individually small artifacts or batch effcts,^19,29 and we followed the rigorous quality-control (QC) protocol outlined previously²¹ by removing any SNPs that were below a minor allele frequency (MAF) of 0.01, were above 0.002 missingness, or deviated from Hardy-Weinberg equilibrium at a p value below 0.01. For each case-control cohort, we removed SNPs that had differential missingness with a p value below 0.05. We excluded one of any pair of samples with kinship entries ≥ 0.05¹⁹ and performed five rounds of outlier removal whereby all individuals more than 6 SDs away from the mean along any of the top 20 eigenvectors were removed and all eigenvectors were recomputed³⁰ (Figure S1). For all autoimmune diseases analyzed (rheumatoid arthritis [RA], Crohn disease [CD], type 1 diabetes [T1D], ulcerative colitis [UC], multiple sclerosis [MS], and ankylosing spondylitis [AS]), we also excluded from the analysis any SNPs in the well-studied major histocompatibility complex (MHC) locus (chr6: 26–34 Mb), which is known to have a complex LD structure, and many heterogeneous variants of strong effect for these traits.

The WTCCC1 samples were phased and imputed as described in Gusev et al.²¹ The WTCCC2 samples were split into two cohorts by platform, and each cohort was imputed separately according to the following protocol. All samples in a cohort were phased together in 10 Mb blocks with HAPI-UR (Haplotype Inference for Unrelated Samples)³¹ (see Web Resources) and three rounds of phasing and consensus voting. All phased samples in a cohort were then imputed in 1 Mb blocks with IMPUTE2³² (see Web Resources) and the 1000 Genomes³³ Phase I integrated haplotypes (September 2013 release; see Web Resources) with no singletons. Where relevant, the Oxford recombination map³⁴ was used. Markers with an information (info) score greater than 0.5 were retained. Finally, SNPs were excluded if they met any of the following criteria in any case or control population: Hardy-Weinberg p value < 0.05, per-locus missingness > 0.05, MAF < 0.01, or case-control differential missingness p value < 0.05.

Schizophrenia Cohort from the Psychiatric Genomics Consortium

We analyzed 24,926 schizophrenia (SP) subjects and 33,271 control individuals from 33 cohorts from the Psychiatric Genomics Consortium (PGC2); they were typed on a variety of platforms, quality controlled, and imputed to the 1000 Genomes reference panel as previously described³⁵ (Tables S1 and S2). Because of computational constraints, we split the cohort into four subgroups of individuals typed on similar platforms; each contained roughly 10,000–20,000 samples. We performed all analyses on the intersection of well-imputed SNPs within each subgroup, ranging from four to five million, and reported meta-analyzed results. Individual study identifiers and 20 multidimensional-scaling components were included as fixed-effect covariates in all analyses.

Swedish SP Exome Chip

We analyzed 12,674 Swedish samples typed on GWAS and exome chips (Tables S1 and S3). The exome chip yielded 238,652 SNPs (including monomorphic sites), of which 10,567 were also typed on a mix of Affymetrix GWAS chips (exome-chip calls were retained). The GWAS-chip data contained an intersection of 163,051 SNPs typed on all platforms in addition to per-platform imputation from 1000 Genomes for a total of 5,053,934 SNPs imputed on all platforms. Principal-component analysis (PCA) of the GWAS data revealed a large cluster of “homogenous” Swedish samples and clines related to Northern Swedish and Finnish admixture (Figure S2). After excluding samples that (1) were not typed on both GWAS and exome chips, (2) failed QC, (3) were PCA outliers by 6 SDs, or (4) were in a pair with GRM values > 0.05 (close relatives), we retained a total of 8,967 samples, of which 6,375 were of “homogenous” Swedish ancestry. In all of our analyses, rare variants had a MAF < 0.01, and common variants had a MAF ≥ 0.01. Simulations were performed on the homogenous samples (without principal components). We performed analyses of real phenotypes on the homogeneous samples and included the top 20 principal components as covariates (to account for any residual population structure; analyses on the full cohort are reported in Tables S23 and S25).

Functional Annotations

We annotated the genome by using six primary categories (Table S4): (1) coding, (2) UTR, (3) promoter, (4) DHS in any of 217 cell types, (5) intronic, and (6) intergenic. Each SNP was then assigned a unique annotation defined by the first of these categories with which it was annotated, resulting in six nonoverlapping variance components (the DHS category was thus restricted to distal regions). Each resulting category exhibited similar average allele frequency and imputation accuracy, although the DHS category had systematically lower LD³⁶ (Table S5). We also computed the “effective” number of SNPs in each category by using an LD-based metric that does not depend on sample size.^36,37 Table S6 shows that this metric was not substantially different from the actual percentage of SNPs used in imputed data, given that DHSs harbored slightly more effective SNPs (15.7% SNPs versus 18.9% effective SNPs) as a result of lower LD. For the imputed categories analyzed here, the differences in the percentage of SNPs, percentage of effective SNPs, and percentage of physical size were relatively minor. A greater difference was observed for genotyped SNPs: 23.6% of DHS SNPs corresponded to 33.6% of effective SNPs, suggesting that DHS enrichments from genotyped data might be indicative of better tagging.

For the DHS annotation, we used DNase sequencing libraries downloaded from ENCODE and Epigenome Roadmap projects in May 2012 and merged biological replicates into a single library (GEO accession numbers are available in Table S7). We used BOWTIE v.1.0³⁸ to align raw read sequences to UCSC Genome Browser hg19 and used MACS v.2.0 with false-discovery rate < 0.01 (the default cutoff) and Benjamini–Hochberg correction³⁹ to call DHS peaks. For the primary analysis, all peaks were merged into a single DHS annotation spanning 16% of the genome. We note that 98% of the primary DHS annotation was covered by the DHSs released by Maurano et al.³ (spanning 37% of the genome), and 67% of the primary DHS annotation was covered by the DHSs analyzed in Thurman et al.⁴ (spanning 15% of the genome). For the cell-type-specific analysis, duplicate lines were merged to form a final set of 83 unique cell types. The resulting annotations are available for download (see Web Resources).

Segway-chromHMM combined genome segmentations⁴⁰ were downloaded for six cell lines (see Web Resources). All regions classified as enhancers or weak enhancers were then combined into a single enhancer annotation. DNaseI digital genomic footprinting (DGF) regions were downloaded for 57 cell lines (see Web Resources). All regions from the narrow-peak classification were then merged into a single DGF annotation.

Simulation Framework

The goal of our simulations was to demonstrate that the partitioned $h_g^2$ properly recovers the heritability explained by causal variants in a given functional category under a variety of disease architectures. We performed simulations in genotyped and imputed data in 4,414 samples from the WTCCC1 coronary artery disease (CAD) case-control cohort together with the six main functional annotations to evaluate robustness and accuracy of the proposed variance-component method and the p-value-enrichment approach; we note that the genome-wide-significant-SNP approach is subsumed by the latter and is not reported separately in most analyses. For each simulation, 10% of the (genotyped or imputed) SNPs were randomly sampled to be causal, and normally distributed effect sizes were assigned to each SNP such that each explained equal variance in expectation. Additive phenotypes were then constructed, and random noise was added for an overall $h_g^2$ of 0.50. Except when evaluating $h_g^2$ between genotyped and imputed SNPs, we did not hide causal variants from the analyses, corresponding to the assumption that all causal variants are typed. We evaluated the variance-component model by using multiple components with GCTA in the unconstrained mode. For approaches based on summary statistics, we computed Z scores, SEs, and p values for the univariate regression of each SNP to a simulated phenotype.

Results

Simulations

We first evaluated the calibration of the methods in simulations of no enrichment by assuming a MAF-independent architecture where causal variants were uniformly sampled from the genome (see Material and Methods). We observed no significant deviations from the null for any categories estimated by variance components or p value enrichment (Figure 1). To evaluate possible biases due to MAF-dependent architectures,^21,41,42 we also considered a low-frequency architecture where only SNPs with a MAF below 0.05 can be causal and a DHS-low-frequency architecture where causal DHS variants are drawn from MAF below 0.05 and all other variants are drawn from any MAF (Figures S3 and S4). Results were generally similar to the MAF-independent architecture, although variance-component estimates exhibited slight but statistically significant deviations for the promoter and UTR categories, which were very small and in tight LD with each other.

Figure 1.

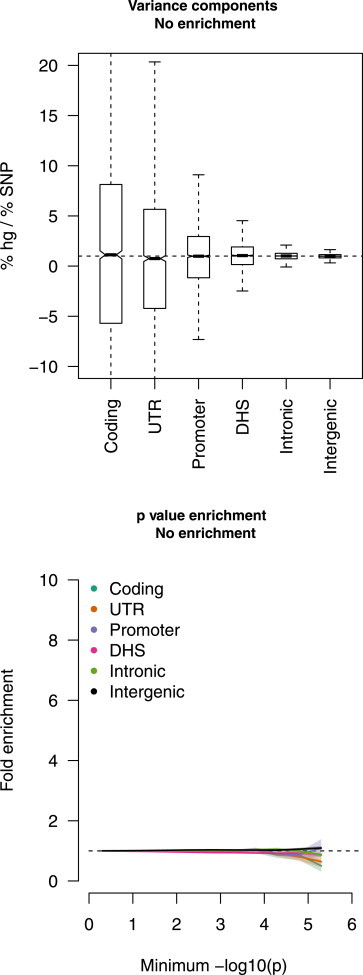
Estimates of Functional Enrichment under the Null

We simulated a polygenic disease architecture in imputed data with no functional enrichment (see text). Simulated phenotypes were tested with the variance-component method (top) from 3,000 simulations and with p value enrichment (bottom) from 100 simulations. In the variance-component subplot, the thin line represents the median, boxes represent the first and third quartiles, and whiskers represent the 1.5× interquartile range from the first to the third quartile. A subplot of p value enrichment shows 1.96× SE as shaded regions.

We next considered simulations with maximal enrichment, where all causal variants were drawn from a single functional category. MAF-independent results for the coding and DHS categories are shown in Figure 2 (see Figure S5 for other results). The variance-component estimate of the percentage of $h_g^2$ was again around 100% for the true causal category and 0% for all others. The plots of p value enrichment correctly demonstrated significant enrichment for five of the categories, but not the DHS category, which, when causal, was not significantly different from the null. This lack of enrichment at DHSs and not at other large categories was most likely due to the uniquely lower LD of DHS SNPs (Table S5). For the small categories (coding, UTR, and promoter), true causals in one category always yielded false p value enrichment in the others because of their close proximity and high LD (Figure 2; Figures S6 and S7). In the MAF-dependent scenarios, the variance-component estimate of $h_g^2$ was nearly unbiased: it had slight but significant inflation at the coding and UTR categories when they contained 100% of $h_g^2$ (Figure S8). Plots of p value enrichment exhibited similar patterns as in the MAF-independent simulations, and the DHS category was further falsely depleted (Figure S7).

Figure 2.

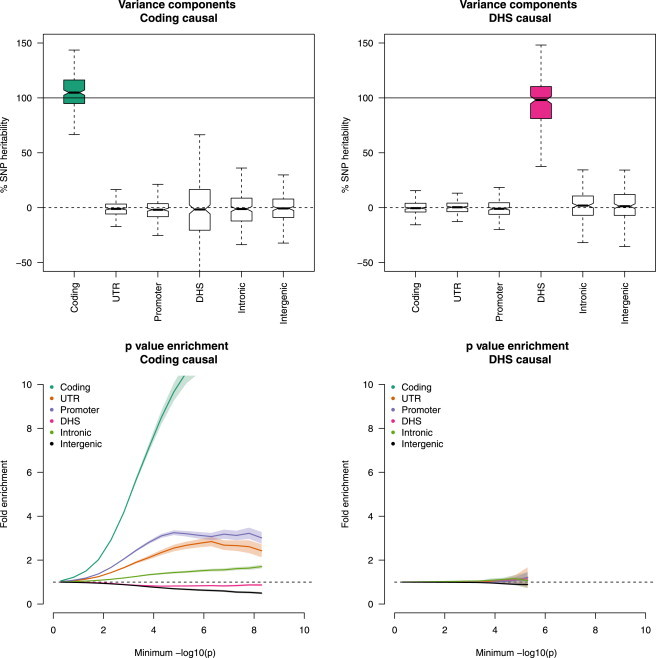
Estimates of Functional Enrichment from a Single Causal Category

We simulated a polygenic disease architecture in imputed data with causal SNPs drawn from a single functional category, corresponding to complete enrichment. Simulated phenotypes were tested with the variance-component method (top) from 200 simulations and with p value enrichment (bottom) from 100 simulations. In the variance-component subplot, the thin line represents the median, boxes represent the first and third quartiles, and whiskers represent the 1.5× interquartile range from the first to the third quartile. Subplots of p value enrichment show 1.96× SE across simulations as shaded regions. For each method, only the coding-causal and DHS-causal scenarios are shown (additional simulations appear in Figures S6 and S7).

To investigate the differences between genotype- and imputation-based estimates, we partitioned $h_g^2$ of category-specific phenotypes simulated from imputed SNPs by using components constructed from genotyped SNPs only. If the genotypes are reasonable proxies for imputed variants, 100% of $h_g^2$ should again be partitioned into each truly causal category. Instead, we observed significant deviations for all of the categories, and $h_g^2$ was partitioned into nearby categories as a result of incomplete tagging (Figures S9 and S10). In particular, less than half of the $h_g^2$ at imputed DHSs was partitioned into the DHS category in genotype data. Thus, estimates produced with only genotyped SNPs can severely underestimate enrichment. The difference between genotyped and imputed simulations suggests that estimates from imputed SNPs could also underestimate the true enrichments or depletions for rare causal variants that are absent from 1000 Genomes or are poorly imputed. We investigated this possibility by using the exome-chip SP data (see below). We separately assessed the impact of imputation error by simulating phenotypes with induced genotype noise proportional to the per-SNP imputation quality score (info score; Supplementary information S3 in Marchini et al.⁴³) but observed no significant biases in null or causal simulations (Tables S8 and S9), most likely as a result of the stringent postimputation QC.

We evaluated multiple other complex architectures with respect to LD (see Appendix A) but observed significant bias in only one deliberately severe scenario: causal variants sampled from intronic and intergenic regions either directly adjacent to or proximal to a DHS (within 1 kb of a DHS boundary). Although no substantial false DHS heritability was observed in genotyped SNPs, the imputed DHS component picked up 50% (0–500 bp) and 20% (500–1,000 bp) of the non-DHS $h_g^2$ (Figure S11). Given our findings that genotyped SNPs are expected to greatly underestimate DHS enrichment, we consider genotyped and imputed estimates to be lower and upper bounds, respectively, on the true causal enrichment.

Heritability of Functional Categories across 11 Diseases

We analyzed a total of 11 WTCCC1 and WTCCC2 phenotypes.^44–46 After QC,²¹ the seven WTCCC1 traits each included an average of 1,700 affected subjects and a set of 2,700 shared control subjects; the four WTCCC2 traits included 1,800–9,300 affected subjects and 5,300 shared control subjects (see Material and Methods; Table S1). In all analyses of autoimmune traits, SNPs in the well-studied MHC region were excluded, although inclusion of the MHC as a separate component did not significantly affect the results. Each cohort was imputed to the 1000 Genomes reference panel, yielding four to six million SNPs per trait after QC (see Material and Methods; Table S1). This analysis is expected to be skewed toward the autoimmune traits, which composed 6/11 traits analyzed and 20,461/30,158 affected subjects analyzed. We computed meta-analysis values by using inverse-variance weighting with the analytical SE to account for different levels of error across $h_g^2$ estimates. After meta-analysis, resulting SEs were adjusted for the use of shared controls by genomic control (unless otherwise stated), and p values were computed by a simple Z score comparing the mean enrichment and adjusted SE to a null of 1.0 enrichment. Estimating enrichment from shifted functional annotations yielded null enrichments and p values (Tables S10 and S11), confirming that this null is comparable to random SNP comparisons used in previous work.^3,11,40,47

Combined results meta-analyzed across all traits are reported in Figure 3 (Tables S10, S12, and S13). In genotyped data, DHS variants (spanning 24% of genotyped SNPs) were the most significantly enriched and explained an average of 38% (SE = 4%) of the total $h_g^2$, a 1.6× enrichment (p = 1.0 × 10⁻⁴). Coding variants were the only other category significantly enriched (after six tests were accounted for) and explained 4% (SE = 1%; p = 1.1 × 10⁻³). All enrichments or depletions were stronger when imputed SNPs were analyzed in terms of both significance and information content, consistent with our previous simulations (Figures S9 and S10; Table S16). Variants in DHSs again exhibited the greatest $h_g^2$ and most significant enrichment: imputed DHS SNPs explained an average of 79% (SE = 8%) of the total $h_g^2$, a 5.1× enrichment (p = 3.7 × 10⁻¹⁷). The enrichment varied across traits (Figure S12; Table S14), and there was a nominally significant difference between the six autoimmune traits (AS, CD, MS, RA, T1D, and UC) and the five nonautoimmune traits (SP, bipolar disorder, CAD, hypertension, and type 2 diabetes [T2D]) at 5.5× and 3.3×, respectively (p = 0.01 for difference without accounting for shared control subjects). Coding variants exhibited the greatest overall enrichment at 13.8× (p = 1.8 × 10⁻³) but accounted for 8% of $h_g^2$ because of the much smaller category size. Correspondingly, we observed a significant depletion for both intronic regions (0.1×; p = 4.9 × 10⁻⁹) and intergenic regions (−0.1×; p < 10⁻²⁰) and $h_g^2$ that was not significantly different from 0. We note that compared to genotyped SNPs, imputation in these traits generally does not explain additional $h_g^2$,²¹ but it can more precisely partition heritability into functional categories. We performed additional simulations mimicking the enrichment observed in imputed data with 8,300 causal variants (as inferred in a large GWAS of a polygenic trait⁴⁸) and found that 79% of heritability was explained by imputed DHS SNPs, 8% was explained by imputed coding SNPs, and the remainder was uniformly drawn from the other variant categories. This “realistic” scenario yielded much weaker estimates of enrichment from genotyped SNPs, and they were similar to estimates from genotyped SNPs in real data (Figure 3).

Figure 3.

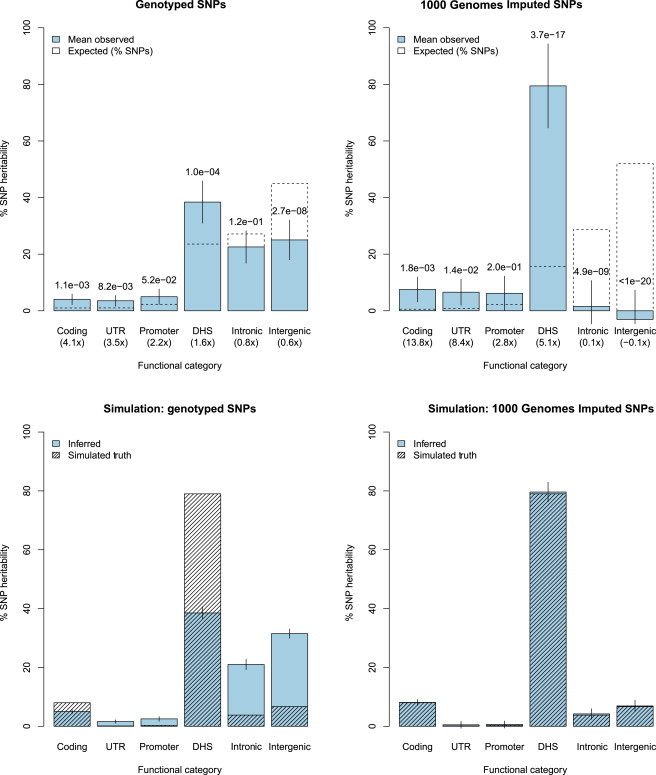
Functional Partitioning of SNP Heritability across 11 Traits

(Top panels) Joint estimates of the percentage of $h_g^2$ from six functional components are shown in filled bars (meta-analyzed over 11 traits). The null expectation, equal to the percentage of SNPs in each category, is shown by dashed, unfilled bars, and p values report the difference from this expectation. Fold enrichment relative to the null expectation is shown in parentheses below each category. The left panel shows results from analyses of genotyped SNPs only, and the right panel shows analysis of genotyped and 1000 Genomes imputed SNPs. Error bars show 1.96× SE after adjustment for shared controls.

(Bottom panels) Partitioned $h_g^2$ in simulations of a “realistic” trait where DHS and coding variants explained 79% and 8% of $h_g^2$, respectively (with no enrichment elsewhere). Filled bars show the mean inferred percentage of $h_g^2$ from genotyped (left) and imputed (right) SNPs over 100 simulations. Patterned bars show the simulated true partition. Error bars show 1.96× SE (on average, SEs on imputed data were 2.2× higher than SEs on genotype data as a result of the abundance of new variants).

We considered alternative estimation procedures to rule out potential biases. Although we allowed individual values of $h_g^2$ to fluctuate outside the 0–1 bound on variance to achieve unbiased estimates prior to averaging across traits,⁴⁹ a constrained analysis yielded similar results (see Table S15). Individual point estimates escaping the 0–1 bound were consistent with our imputed simulations under realistic enrichment, which showed that the percentage of $h_g^2$ for DHSs exceeded 1.0 10% of the time, whereas the percentage of $h_g^2$ for intronic and intergenic regions fell below 0.0 30% and 23% of the time, respectively, for a typical 7,000-sample cohort. Using flat instead of inverse-variance weighting yielded a comparable estimate such that DHS SNPs explained an average of 85% (SE = 15%) of $h_g^2$. With the flat weighting, the SD of imputed DHS estimates across different traits was 48%, which corresponds to a SD of 32% in the true unobserved values after the analytical SE of each estimate is accounted for (Table S14). We further evaluated the robustness of these estimates and found that biases arising from analytical SEs, ancestry, or case-control ascertainment were unlikely to significantly affect the enrichment (see Appendix A).

To investigate whether enrichment in $h_g^2$ from all SNPs at known loci was consistent with the genome-wide estimates, we partitioned the $h_g^2$ explained by SNPs within 1 Mb of published GWAS loci for each trait (NHGRI GWAS catalog;¹¹ see Web Resources) (Figure S13). Because some traits had a small number of loci, the DHS component was jointly analyzed with only a single other component containing all non-DHS SNPs. We again observed a highly significant DHS enrichment in imputed data and a significant difference between the genotyped and imputed estimates (p = 7.3 × 10⁻¹⁴). We observed a marginally significant difference between the DHS enrichment at known loci versus genome-wide in the imputed data (3.6× versus 5.5×, p = 0:003). Although it does not pass multiple-test correction, this p value suggests that genome-wide-significant SNPs of large effects might be less enriched with DHS variants than the rest of the genome.

We have shown by simulation that estimates from genotyped SNPs are expected to provide a lower bound on enrichment or depletion and that estimates from imputed SNPs are biased upward only when causal variants are very close to the annotation boundary. For brevity, subsequent results focus primarily on the analysis of imputed SNPs.

Comparison to Estimates of Enrichment from Summary Statistics

We compared our imputed variance-component estimates of 5.1× DHS enrichment for the 11 traits to the DHS enrichment of genome-wide-significant variants identified in these data or from published loci (NHGRI GWAS catalog;¹¹ see Web Resources). The enrichments from genome-wide-significant variants were much smaller (0.91× and 1.74× for variants in these data and published loci, respectively; Table S17). This is roughly consistent with previous results indicating that 57% of noncoding GWAS hits (from any trait) lie in broadly defined DHSs spanning 42% of the genome (1.4× noncoding enrichment; 1.2× overall enrichment) and that this percentage increases to 77% of noncoding GWAS hits when SNPs in perfect LD with a DHS SNP are included (1.8× noncoding enrichment; 1.6× overall enrichment).³ Similarly, 30% of the noncoding GWAS hits analyzed in Maurano et al.³ lay in our DHS annotation, yielding a comparable 1.8× noncoding enrichment. Extending to the full distribution of association statistics did not reveal significant DHS enrichment in any of these traits (Figure 4, left panel; Figure S14). This is consistent with our previous simulations showing the variance-component approach to be more effective than the p-value-enrichment approach at identifying DHS enrichment from complex-disease architectures (Figure 2).

Figure 4.

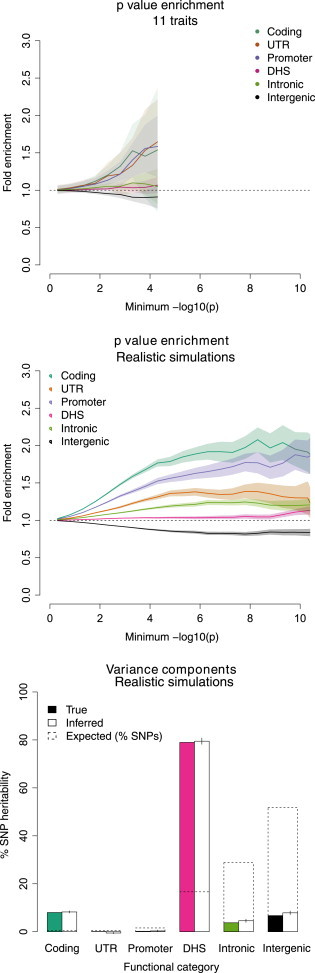
Enrichment from GWAS Summary Statistics

(Left panel) Estimates of p value enrichment are averaged over 11 analyzed traits and are restricted to minimum p value thresholds (x axis) for which at least one association meeting the threshold was observed in every trait.

(Middle panel) p value enrichment from a “realistic” simulation.

(Right panel) Variance-component enrichment from a “realistic” simulation. Realistic traits were simulated with DHS and coding variants explaining 79% and 8% of $h_g^2$, respectively, and with computed GWAS statistics in a cohort of 32,000 samples. Shaded regions and error bars represent the SE from meta-analysis (left) and 50 replicates (middle and right).

We sought to further confirm this observation by extending our simulations to a single large cohort with realistic levels of enrichment on the basis of the above results. We simulated the “realistic” level of enrichment (see above) in 33,000 combined WTCCC2 samples, corresponding to a large GWAS. We then conducted a standard GWAS on the simulated traits and plotted functional enrichment by using p value enrichment (see Material and Methods). The strategy yielded enrichment at coding variants through the full distribution of association statistics (Figure 4, middle panel). However, proximal categories such as UTR and promoter, which were truly depleted, also appeared enriched through tagging of significant coding variants. DHS variants were the least-enriched nonintergenic category, even though they made the single largest contribution to heritability. This was likely due to lower power to detect DHS SNPs as a result of their lower average effect size (relative to that of coding SNPs) and less LD. On the other hand, applying the variance-component strategy to the simulated cohorts correctly recovered the enrichment factors (Figure 4, right panel). These simulations further demonstrate that GWAS p values, although partially informative, can yield false-positive and false-negative enrichment to make functional interpretation difficult, motivating further development of methods that can produce robust estimates of partitioned heritability from summary statistics.

Analysis of PGC2 SP Data

We replicated our functional-enrichment results in an independent cohort of 58,197 samples from PGC2 (Tables S1 and S2). In the PGC2 data, the imputed DHS enrichment was significant at 3.2× (SE = 0.29, p = 1.4 × 10⁻¹³), and the intergenic category was significantly depleted at 0.3× (SE = 0.06, depletion p < 1 × 10⁻²⁰; Table S18). For comparison, the WTCCC2 analysis restricted to SP produced a nonsignificant DHS enrichment of 2.6× (SE = 1.47, p = 0.28) and intergenic $h_g^2$ of 0.4× (SE = 0.27, depletion p = 0.02; Table S14). The consistency of WTCCC2 and PGC2 estimates indicates that platform artifacts are unlikely to be a major confounder. Moreover, the substantially lower SE in this large cohort demonstrates the effectiveness of our methods at characterizing a single complex trait. As in our previous simulations, p value enrichment did not identify substantial enrichment at DHS variants (Figure S15).

Partitioning $h_g^2$ within DHSs

We further partitioned DHS enrichment in the WTCCC1 data into functional subcategories to assess significance in relation to all DHSs. We used Segway-chromHMM combined classifications of enhancer regions⁴⁰ to partition DHSs (15.7% of the genome) into those that overlapped predicted enhancers (3.2% of the genome) and those that did not (Figure 5A). The enhancer DHSs explained 31.7% (SE = 3.3%) of the total $h_g^2$, yielding an enrichment of 9.8× versus all SNPs (1.9× versus all DHSs; p = 5.1 × 10⁻⁴). We also partitioned DHSs into regions that were called in two or fewer cell types (“specific”; after merging similar tissues) and those that were not (Figure 5B). We observed a significant enrichment for cell-type-specific DHSs (6.1× versus all SNPs; 1.3× versus all DHSs; p = 3.2 × 10⁻³). The enrichment was not significant when we repeated this analysis for enhancer and nonenhancer DHSs separately. We next split the DHSs into SNPs overlapping and not overlapping the ENCODE database of DGF regions (8.5% of the genome), which are expected to precisely map sites where regulatory factors bind to the genome⁵⁰ (Figure 5C). We observed no difference in $h_g^2$ between these DHSs and other DHSs (1.0×, p = 0.90). However, DGF annotations were collected for only a subset of DHS cell types analyzed, and analysis in additional cell types is needed. Lastly, we partitioned the $h_g^2$ by using an expanded DHS annotation (including regions overlapping coding regions, UTRs, and promoters) into the remaining five major categories (Table S19), which yielded 34.4× enrichment at DHS coding variants versus all SNPs (5.3× versus all DHSs, p = 1.35 × 10⁻³) and 13.2× enrichment at DHS promoter variants versus all SNPs (2.3× versus all DHSs, p = 7.90 × 10⁻³). Notably, unlike the non-DHS introns, DHS introns did not show substantial depletion (0.9× versus all DHSs, p = 0.037).

Figure 5.

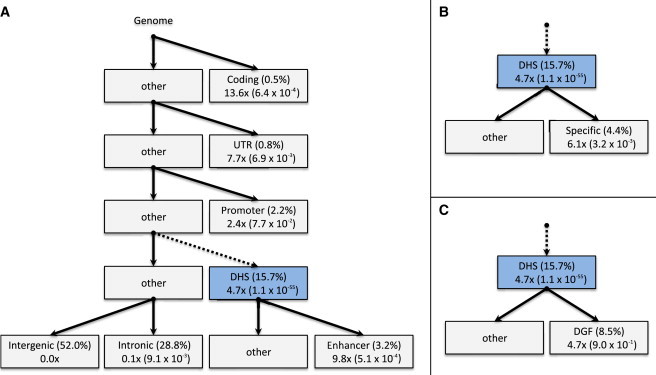
Hierarchical Analysis of Functional Enrichment

DHS variants were further partitioned into three subcategories: predicted enhancers (A), cell-type-specific DHSs (B), and DGF targets (C). Each block contains (on the top line) the functional category and fraction of the genome (in parentheses) and (on the bottom line) the fraction enriched in relation to the rest of the genome and the p value of enrichment in relation to the parent category (in parentheses). DHS enrichment of 4.7× nonsignificantly differed from 5.1× in Figure 3 as a result of additional free parameters.

To investigate the role of specific cell types, we separately estimated enrichment in $h_g^2$ for DHSs in each of 83 unique cell types (see Material and Methods). For each trait and cell type, we estimated $h_g^2$ jointly from three components corresponding to DHSs observed in that cell type, other DHSs not observed in that cell type, and all other SNPs; we assessed enrichment in relation to all DHSs. On the basis of our previous observation of heterogeneity, we performed meta-analyses across the six autoimmune traits (excluding the MHC) and across the five nonautoimmune traits. We observed seven cell types that were significantly enriched in autoimmune traits in genotype data (we conservatively adjusted for 83 tests, although the cell types are highly correlated), and none were significantly enriched in nonautoimmune traits (Table 1). Four of these seven cell types have previously been implicated in autoimmune diseases: Trynka et al.⁶ found that GWAS hits for RA were enriched within H3K36me3 peaks from CD8⁺ primary cells (at p = 0.0042), and Maurano et al.³ found that nominally significant SNPs in a GWAS of CD were enriched within DHS peaks from primary T helper 1 cells and that nominally significant SNPs in a GWAS of MS were enriched in DHS peaks from lymphoblastoid and monocyte CD14⁺ cells. The remaining three significant cell types were leukemia cells, fetal pelvis cells, and fetal thymus cells (additional nominally significant cell types are listed in Table S20). The enrichment was typically observed in all autoimmune traits individually; CD was the least enriched on average (2.8×), and UC was the most enriched on average (5.1×; Table S21). As before, the signal was stronger and more significant when we included imputed SNPs (Table 1).

Table 1.

Cell-Type- and Phenotype-Specific DHS Enrichment

Tissue Type	Cell Type	Autoimmune		Nonautoimmune	Published
		Genotyped	Imputed	Genotyped
Blood	Primary T helper 1 cells	5.8 (4.2 × 10−6)	10.2 (1.3 × 10−12)	2.1 (3.5 × 10−1)	Maurano et al.3 (CD)
	leukemia cells	3.5 (6.7 × 10−6)	4.7 (5.3 × 10−10)	1.0 (9.8 × 10−1)	–
	lymphoblastoid cells	3.3 (1.1 × 10−5)	4.9 (5.4 × 10−11)	1.0 (9.4 × 10−1)	Maurano et al.3 (MS)
	CD8+ primary cells	3.0 (3.0 × 10−4)	5.4 (1.8 × 10−10)	1.0 (9.6 × 10−1)	Trynka et al.6 (RA)
Fetal kidney	fetal right renal pelvic cells	5.4 (1.4 × 10−4)	8.2 (5.7 × 10−8)	1.5 (7.4 × 10−1)	–
Bone marrow	CD14+ monocytes	4.1 (1.6 × 10−4)	5.7 (2.2 × 10−7)	1.3 (7.6 × 10−1)	Maurano et al.3 (MS)
Fetal thymus	Fetal thymus cells	2.6 (4.0 × 10−4)	4.5 (3.2 × 10−9)	0.8 (6.6 × 10−1)	–

Fold enrichment of $h_g^2$ reported for cell-type-specific DHSs observed as significant in genotype data (after adjustment for 83 cell types tested). We measured enrichment in comparison to $h_g^2$ at DHSs to account for the background DHS enrichment. Results are shown separately from meta-analyses of six autoimmune traits and five nonautoimmune traits. Instances where enrichment was also observed in Trynka et al.⁶ or Maurano et al.³ are indicated.

On the basis of the hypothesis that most regulatory sites lie at the center of the called DHS peaks, we considered the enrichment after progressively narrowing the DHS annotations. Specifically, we trimmed the ends of each DHS peak (without removing any individual peaks) to a maximum length set such that the resulting overall DHS annotation covered 1%, 5%, or 10% of the physical genome. We then tested these three narrowed annotations in two models: (1) a univariate model in which $h_g^2$ was inferred from only the narrowed DHS component, thereby including any tagged heritability from other functional categories; and (2) a six-component model in which the full DHS component was replaced with the narrowed DHS component and the remaining DHS SNPs were distributed into the intron and other components. We found the DHS centers to be particularly strongly enriched (Table S22); the 1% annotation explained 19.8% of the total $h_g^2$ in the multivariate model (p = 2.6 × 10⁻⁶) and 61.0% of the total $h_g^2$ in the univariate model. For comparison, the coding component covering roughly 1% of the genome explained 30.0% of the total $h_g^2$ in the univariate model. The monotonic increase in $h_g^2$ from narrowed annotations is further evidence of enrichment at the DHS centers. We caution that this experiment might have been particularly susceptible to bias from causal variants very close to the annotation boundary.

Unbiased Estimates of $h_g^2$ with Rare and Common Variants

We separately analyzed a cohort of 2,500 SP subjects and 3,875 control subjects who were of homogenous Swedish origin and had been typed on both GWAS and exome chips (see Material and Methods; Tables S1 and S3) to investigate the possible contribution of rare coding variants to missing heritability,⁵¹ defined as the gap between our genome-wide estimates of $h_g^2$ and the total narrow-sense heritability. The exome-chip variants were primarily rare and consisted of 18% singletons and 64% nonsingletons with a MAF below 0.01. A concern is that $h_g^2$ estimates from exome-chip data can be substantially biased as a result of the abundance of rare variants.^21,41,42 To address this, we performed simulations across the full causal-allele frequency spectrum and found that joint estimates from two frequency-stratified⁴² components computed from rare (MAF ≤ 0.01) and common (MAF > 0.01) SNPs eliminated most of the observed bias. Subsequently adjusting each component for LD completely eliminated bias for normalized effect sizes (Figure S17) and yielded the most accurate estimate for standard effect sizes (Figure S18). We report estimates from joint components with (Table 2) and without (Table S23) LD adjustment.

Table 2.

${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}$ of SP from Exome Chip

Variant Class	${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}$	Percentage of${\mathit{h}}_{\mathit{g}}^{\mathbf{2}}$
Separately
All	0.370 ± 0.040	–
Noncoding	0.317 ± 0.042	–
Coding	0.158 ± 0.034	–
Jointly
Noncoding	0.291 ± 0.028	79% ± 8%
Coding	0.079 ± 0.034 (p = 1.2 × 10−2)	21% ± 6%
Coding (rare)	0.037 ± 0.029 (p = 1.0 × 10−1)	10% ± 7%
Coding (common)	0.042 ± 0.017 (p = 7.7 × 10−3)	11% ± 4%

Estimates of $h_g^2$ (adjusted for biases due to LD; see Figure S17 and Table S23) are reported from variance components in the homogenous Swedish subpopulation. The top section shows estimates that include tagging of variants in other classes. The bottom section shows joint estimates accounting for tagged variance due to LD. The p values from a likelihood-ratio test are shown in parentheses.

We partitioned the heritability explained by GWAS-chip and exome-chip data into three separate variance components: noncoding, rare coding (MAF < 0.01), and common coding variants. This partitioned analysis identified a total $h_g^2$ of 0.079 (SE = 0.034) from all coding variants (Table 2); only the $h_g^2$ of 0.042 (SE = 0.017) from common coding variants was significantly different from 0 (p = 7.7 × 10⁻³; rare coding p = 0:10). Moreover, the estimate of DHS enrichment from common SNPs was unaffected by the inclusion of rare coding variants (Table S24), confirming that DHS enrichment was not an artifact of untagged coding variation in this cohort. The $h_g^2$ from rare variants remained nonsignificant even after we partitioned according to PolyPhen-2 scores,⁵² restriction to putative SP-associated genes (see Appendix A), or gene collapsing (Tables S25 and S41–S43). This does not invalidate the use of collapsed-gene burden tests for association and genetic mapping because the individual collapsed gene is still a fundamentally informative unit of association. It does, however, demonstrate that the maximum variance that can be explained by such methods is guaranteed to be substantially lower than that of association with the full model, as has been shown in previous analyses of burden tests.⁵³ For singleton variants, we can place a 95% upper bound on collapsed $h_g^2$ at 0.014. We caution that our exome-chip results pertain to rare variants included in the chip design (ascertained from 12,000 samples) but do not extend to extremely rare variants. However, our findings are consistent with a recent analysis of SP exome sequencing data, which identified a significant but modest rare-coding burden (0.4%–0.6% of total variance) in a subset of ∼2,500 genes.⁵⁴

Fine Mapping with Functional Priors

Estimates of functional $h_g^2$ enrichment can guide fine-mapping analysis, where the goal is to identify a minimal set of SNPs that include the underlying causal variant(s).⁵⁵ To investigate the potential benefits of fine mapping on the basis of our estimates of functional enrichment, we applied these estimates as priors for fine mapping in four traits (RA, T2D, CAD, and SP) with publicly available imputed summary statistics (Table S26; see Web Resources). We used corresponding estimates of functional enrichment in the WTCCC1 data for RA, T2D, and CAD (while implicitly assuming a best-case scenario in which functional enrichment was accurately estimated for each trait) and used estimates of functional enrichment in PGC2 data for SP. Given that SNPs at genome-wide-significant loci explain only a small proportion of the trait variance, we do not expect partial sample overlap to be a significant confounder. Although fine-mapping analysis ideally involves targeted sequencing or genotyping, Maller et al.⁵⁵ observed that the latter had little impact on their fine-mapping analysis in comparison to imputed data, so we expect imputed markers to be a reasonable proxy. Each locus was defined as the union of 1 Mb windows around any SNP with a p value < 5 × 10⁻⁸. Association statistics consisting of individual SNP effect sizes and SEs were converted to Bayes factors as described in Pickrell¹³ and Wakefield⁵⁶ and were multiplied by either a flat prior or the genome-wide functional prior (computed as the estimated $h_g^2$ per SNP of the SNP category in the corresponding trait). We then computed the credible set for each locus for each scenario by including SNP Bayes factors from highest to lowest until the sum of the Bayes factors in the set was at least 95% of the sum of the Bayes factors at the locus. On average, we found that the six main functional priors reduced the credible set of causal variants by 30% across the four traits (Table 3). The largest reduction of 63% was observed in RA, where the total credible set for five loci (excluding the MHC) was reduced from 69 SNPs to 26. For comparison, including only coding-variant enrichment as a prior reduced the credible sets by 5% on average and had no reduction for RA. We showed by simulation that the credible sets were well calibrated with the correct priors and miscalibrated by less than 10% when the priors were at the extremes of the meta-analysis estimates (Table S27), demonstrating that this functional fine-mapping strategy might become robust and effective as individual trait sample sizes reach the current meta-analysis sample size. However, we caution that our estimates of functional enrichment for individual traits, except SP, are not tight enough for this strategy to be actionable at the current time.

Table 3.

Credible Sets of Causal SNPs at Known Associated Loci

Phenotype	No. of Loci	Total SNPs	Flat Prior	Coding Prior	Main Functional Priors	Main and Enhancer Priors
RA	5	8,393	69	69	26	26
T2D	13	24,799	101	90	84	83
CAD	16	27,685	112	112	90	86
CAD (metabo-chip)	34	7,498	325	325	264	260
PGC2	146	582,401	5,696	5,660	4,756	not available

For each trait, genome-wide-significant loci from meta-analysis association statistics were reduced to 95% credible sets with and without functional priors. The right-most four columns describe the number of SNPs in the credible set obtained from each prior type. “Flat prior” corresponds to standard analysis with no functional information. “Coding prior” uses only enrichment at coding variants. “Main functional priors” include all six priors from the main functional analysis. “Main and enhancer priors” include all six main priors and the enhancer-DHS prior.

Discussion

The importance of regulatory and cell-type-specific variation in common disease has previously been recognized,^3–10 but in contrast to previous work, we provide a quantification of this contribution to disease heritability. We have demonstrated by extensive simulations that our variance-component strategy yields robust estimates that account for LD between categories and complex-disease architecture. Across 11 traits, we found that regulatory regions marked by DHSs explained an average of 79% of imputed $h_g^2$ and 38% of genotyped $h_g^2$. We replicated our results in a large SP cohort, yielding a single-trait estimate of 3.2× (SE = 0.29, p = 1.4 × 10⁻¹³) from imputed SNPs, and found that the contribution from rare, exome-chip variants was nonsignificant and did not affect the enrichment.

Given that GWASs primarily identify noncoding variants, many hypotheses have been developed to explain the architecture of complex traits, including noncoding RNA, DNA methylation, alternative splicing, and unannotated transcripts.^14,57 Several previous studies have demonstrated an excess of significant GWAS associations in regulatory categories.^5,6,11,58 In particular, Ernst et al.⁵⁹ observed 2× enrichment in cell-type-relevant enhancers, Schaub et al.⁸ identified 1.12× enrichment at DHSs, and Maurano et al.³ identified 1.4×−1.8× enrichment at DHSs (relative to noncoding SNPs) and enrichment at cell-type-relevant DHSs. In our analyzed cohorts, known variants were1.7× enriched with DHSs, but there was less enrichment at variants identified only in these cohorts. In contrast, our findings constrain most of $h_g^2$ to the 16% of SNPs that lie in the DHS marks tested (or to SNPs that lie very close to DHSs; see below), particularly in those that overlap enhancers, and suggest that the other proposed mechanisms are unlikely to make substantial independent contributions. A deeper analysis of DHSs narrowed to cover 1% of the genome still explained 20% of $h_g^2$ directly (and 61% in total), potentially motivating a DHS-targeted genotyping chip analogous to the exome chip.⁶⁰ More generally, our approach provides a means of assessing biological hypotheses of contributions to disease heritability.

Unlike previous methods, our approach infers disease-relevant biological function from all SNPs simultaneously instead of one GWAS hit at a time. Over multiple simulated disease architectures, we show that variance-component methods are more accurate in partitioning heritability than summary-statistic-based approaches, such as p value enrichment, despite the appeal of analyses of summary statistics in many contexts.^61–64 For completeness, we also considered two additional methods, stratified Q-Q plots¹² and Bayesian hierarchical modeling (fgwas),¹³ which assess functional enrichment but are primarily focused on strong associations and improving mapping power. These methods did not produce consistent estimates of $h_g^2$ enrichment either in simulations or in real data (Figure S19–S29), although we note that they have different objectives. In addition to having implications for mapping power,^{12,13,65–68} functional enrichment has direct implications for fine mapping^55,69,70 and risk prediction. Enrichments at the level we observed could substantially reduce the set of potential causal variants in the four traits we tested by downweighing SNPs in low-heritability categories. On the other hand, the improvement in polygenic risk prediction was limited because of pervasive LD across categories (Table S28).

Several limitations of our approach remain as avenues for future work. The variance-component method might still be subject to subtle biases^21,41,42 under disease architectures or annotations with complex LD structure, although our analyses indicate that it is generally less biased than published methods. In particular, we found that imputed data might lead to an overestimate of category enrichment from causal variation very close to that category. For computational reasons, we did not make use of the mixture of the normal-effect-size approach, which has been shown to increase precision.²⁴ The method also requires individual-level genotype data and is computationally infeasible for extremely large cohorts or a very large number of components, motivating further work on methods that analyze summary statistics. A limitation of assessing enrichment from GWAS platforms is that we cannot account for untagged causal variation, which represents roughly half of total narrow-sense heritability.⁷¹ Although we have shown that rare coding variants are unlikely to alter the DHS enrichment, the missing heritability could lie in other categories. The precision of inferred enrichment is also limited by the underlying annotations and variants. It is possible that certain biological features could be subject to systematically poorer variant calling or imputation and exhibit decreased $h_g^2$ as a result of artifacts,⁷² although we did not observe substantial differences in the categories we analyzed. Because of the data available, our meta-analysis estimates were weighted toward autoimmune traits both in the number of individual studies and in total sample size; estimates of DHS enrichment were higher in autoimmune than in nonautoimmune traits, which could be partly due to the abundance of hematopoietic cell types in available DHS annotations. Except for SP, for which many samples are available, we could not provide precise estimates for single traits. However, we have shown by simulation that the individual estimates and errors were well calibrated, justifying meta-analysis of estimates that are not constrained to the plausible 0–1 range (an established strategy⁴⁹). Further partitioning of DHSs can yield additional enrichment, and it is likely that other functional categories—including additional chromatin marks, histone modifications, formaldehyde-assisted isolation of regulatory elements, transcription factor binding sites,⁷³ gene expression,^58,74,75 and measures of conservation⁷—will be highly informative.

Consortia

The members of the Schizophrenia Working Group of the Psychiatric Genomics Consortium are Stephan Ripke, Benjamin M. Neale, Aiden Corvin, James T.R. Walters, Kai-How Farh, Peter A. Holmans, Phil Lee, Brendan Bulik-Sullivan, David A. Collier, Hailiang Huang, Tune H. Pers, Ingrid Agartz, Esben Agerbo, Margot Albus, Madeline Alexander, Farooq Amin, Silviu A. Bacanu, Martin Begemann, Richard A. Belliveau, Jr., Judit Bene, Sarah E. Bergen, Elizabeth Bevilacqua, Tim B. Bigdeli, Donald W. Black, Anders D. Børglum, Richard Bruggeman, Nancy G. Buccola, Randy L. Buckner, William Byerley, Wiepke Cahn, Guiqing Cai, Dominique Campion, Rita M. Cantor, Vaughan J. Carr, Noa Carrera, Stanley V. Catts, Kimberly D. Chambert, Raymond C.K. Chan, Ronald Y.L. Chen, Eric Y.H. Chen, Wei Cheng, Eric F.C. Cheung, Siow Ann Chong, C. Robert Cloninger, David Cohen, Nadine Cohen, Paul Cormican, Nick Craddock, James J. Crowley, David Curtis, Michael Davidson, Kenneth L. Davis, Franziska Degenhardt, Jurgen Del Favero, Lynn E. DeLisi, Ditte Demontis, Dimitris Dikeos, Timothy Dinan, Srdjan Djurovic, Gary Donohoe, Elodie Drapeau, Jubao Duan, Frank Dudbridge, Naser Durmishi, Peter Eichhammer, Johan Eriksson, Valentina Escott-Price, Laurent Essioux, Ayman H. Fanous, Martilias S. Farrell, Josef Frank, Lude Franke, Robert Freedman, Nelson B. Freimer, Marion Friedl, Joseph I. Friedman, Menachem Fromer, Giulio Genovese, Lyudmila Georgieva, Elliot S. Gershon, Ina Giegling, Paola Giusti-Rodrguez, Stephanie Godard, Jacqueline I. Goldstein, Vera Golimbet, Srihari Gopal, Jacob Gratten, Jakob Grove, Lieuwe de Haan, Christian Hammer, Marian L. Hamshere, Mark Hansen, Thomas Hansen, Vahram Haroutunian, Annette M. Hartmann, Frans A. Henskens, Stefan Herms, Joel N. Hirschhorn, Per Hoffmann, Andrea Hofman, Mads V. Hollegaard, David M. Hougaard, Masashi Ikeda, Inge Joa, Antonio Julià, René S. Kahn, Luba Kalaydjieva, Sena Karachanak-Yankova, Juha Karjalainen, David Kavanagh, Matthew C. Keller, Brian J. Kelly, James L. Kennedy, Andrey Khrunin, Yunjung Kim, Janis Klovins, James A. Knowles, Bettina Konte, Vaidutis Kucinskas, Zita Ausrele Kucinskiene, Hana Kuzelova-Ptackova, Anna K. Kähler, Claudine Laurent, Jimmy Lee Chee Keong, S. Hong Lee, Sophie E. Legge, Bernard Lerer, Miaoxin Li, Tao Li, Kung-Yee Liang, Jeffrey Lieberman, Svetlana Limborska, Carmel M. Loughland, Jan Lubinski, Jouko Lnnqvist, Milan Macek, Jr., Patrik K.E. Magnusson, Brion S. Maher, Wolfgang Maier, Jacques Mallet, Sara Marsal, Manuel Mattheisen, Morten Mattingsdal, Robert W. McCarley, Colm McDonald, Andrew M. McIntosh, Sandra Meier, Carin J. Meijer, Bela Melegh, Ingrid Melle, Raquelle I. Mesholam-Gately, Andres Metspalu, Patricia T. Michie, Lili Milani, Vihra Milanova, Younes Mokrab, Derek W. Morris, Ole Mors, Preben B. Mortensen, Kieran C. Murphy, Robin M. Murray, Inez Myin-Germeys, Bertram Mller-Myhsok, Mari Nelis, Igor Nenadic, Deborah A. Nertney, Gerald Nestadt, Kristin K. Nicodemus, Liene Nikitina-Zake, Laura Nisenbaum, Annelie Nordin, Eadbhard O’Callaghan, Colm O’Dushlaine, F. Anthony O’Neill, Sang-Yun Oh, Ann Olincy, Line Olsen, Jim Van Os, Psychosis Endophenotypes International Consortium, Christos Pantelis, George N. Papadimitriou, Sergi Papiol, Elena Parkhomenko, Michele T. Pato, Tiina Paunio, Milica Pejovic-Milovancevic, Diana O. Perkins, Olli Pietilinen, Jonathan Pimm, Andrew J. Pocklington, John Powell, Alkes Price, Ann E. Pulver, Shaun M. Purcell, Digby Quested, Henrik B. Rasmussen, Abraham Reichenberg, Mark A. Reimers, Alexander L. Richards, Joshua L. Roffman, Panos Roussos, Douglas M. Ruderfer, Veikko Salomaa, Alan R. Sanders, Ulrich Schall, Christian R. Schubert, Thomas G. Schulze, Sibylle G. Schwab, Edward M. Scolnick, Rodney J. Scott, Larry J. Seidman, Jianxin Shi, Engilbert Sigurdsson, Teimuraz Silagadze, Jeremy M. Silverman, Kang Sim, Petr Slominsky, Jordan W. Smoller, Hon-Cheong So, Chris C.A. Spencer, Eli A. Stahl, Hreinn Stefansson, Stacy Steinberg, Elisabeth Stogmann, Richard E. Straub, Eric Strengman, Jana Strohmaier, T. Scott Stroup, Mythily Subramaniam, Jaana Suvisaari, Dragan M. Svrakic, Jin P. Szatkiewicz, Erik Sderman, Srinivas Thirumalai, Draga Toncheva, Paul A. Tooney, Sarah Tosato, Juha Veijola, John Waddington, Dermot Walsh, Dai Wang, Qiang Wang, Bradley T. Webb, Mark Weiser, Dieter B. Wildenauer, Nigel M. Williams, Stephanie Williams, Stephanie H. Witt, Aaron R. Wolen, Emily H.M. Wong, Brandon K. Wormley, Jing Qin Wu, Hualin Simon Xi, Clement C. Zai, Xuebin Zheng, Fritz Zimprich, Naomi R. Wray, Kari Stefansson, Peter M. Visscher, Wellcome Trust Case Control Consortium, Rolf Adolfsson, Ole A. Andreassen, Douglas H.R. Blackwood, Elvira Bramon, Joseph D. Buxbaum, Anders D. Brglum, Sven Cichon, Ariel Darvasi, Enrico Domenici, Hannelore Ehrenreich, Tõnu Esko, Pablo V. Gejman, Michael Gill, Hugh Gurling, Christina M. Hultman, Nakao Iwata, Assen V. Jablensky, Erik G. Jönsson, Kenneth S. Kendler, George Kirov, Jo Knight, Todd Lencz, Douglas F. Levinson, Qingqin S. Li, Jianjun Liu, Anil K. Malhotra, Steven A. McCarroll, Andrew McQuillin, Jennifer L. Moran, Preben B. Mortensen, Bryan J. Mowry, Markus M. Nthen, Roel A. Ophoff, Michael J. Owen, Aarno Palotie, Carlos N. Pato, Tracey L. Petryshen, Danielle Posthuma, Marcella Rietschel, Brien P. Riley, Dan Rujescu, Pak C. Sham, Pamela Sklar, David St. Clair, Daniel R. Weinberger, Jens R. Wendland, Thomas Werge, Mark J. Daly, Patrick F. Sullivan, and Michael C. O’Donovan.

The members of the SWE-SCZ Consortium are Stephan Ripke, Colm O’Dushlaine, Kimberly Chambert, Jennifer L. Moran, Anna K. Kähler, Susanne Akterin, Sarah Bergen, Patrik K.E. Magnusson, Benjamin M. Neale, Douglas Ruderfer, Edward Scolnick, Shaun Purcell, Steve McCarroll, Pamela Sklar, Christina M Hultman, and Patrick F. Sullivan.

Appendix A

LD

We further interrogated the role of LD and violations of model assumptions in the variance-component estimate. We considered two contrived annotations constructed from either the 16% of SNPs with the most LD partners or the 16% of SNPs with the fewest LD partners to mimic a high or low LD category, respectively, approximately equal in SNP number to the DHS category. Testing the uniformly drawn MAF-independent architecture, we again observed no enrichment for either the high-LD (1.02×, SE = 0.01) or the low-LD (1.02×, SE = 0.03) annotations over 1,000 trials. Finally, we considered a disease architecture in which causal variants were strongly enriched at the centers of DHSs such that variants in the middle 7% of the DHS (1% of the genome) explained 25% of the $h_g^2$ and the remaining DHS variants explained 75% of the $h_g^2$. We observed a slight deflation of the DHS estimate, but no significant false enrichment, at the neighboring categories (Figure S20).

Jackknife Estimates of SEs

The analytical SE used for significance testing was accurate in our simulations (Table S29) and has previously been shown to be robust in real data^21,27 but can be biased when the number of causal variants is very small.⁴¹ We assessed this directly with a weighted-block jackknife estimate⁷⁶ of the enrichment in the real traits by dropping each chromosome in turn, constructing new GRMs, and recomputing the percentage of $h_g^2$ for each functional category (and the corresponding enrichment). The jackknife estimate of the enrichment and its variance was then computed as described in Busing et al.⁷⁶ Although there is a demonstrable relationship between chromosome length and $h_g^2$, we do not expect to observe such a relationship with respect to the percentage of $h_g^2$ because of the normalization. However, this estimate of the variance does capture true biological variation in enrichment across chromosomes and is therefore conservative. Although we observed little difference between the jackknife and standard estimates in genotyped data (Table S30), the jackknife estimate of the imputed percentage of $h_g^2$ (71%, SE = 7.7%; Table S31) was indeed more conservative than the analytical estimate (79%, SE = 6.6%), but the enrichment was still highly significant (p = 5.5 × 10⁻¹³), and the overall results were not substantially affected. Because the jackknife makes no assumptions about the underlying distribution of enrichment, this consistency with the analytical estimate supports the use of REML SEs for case-control data (see also simulations below).

Ancestry

We found little population structure in all of the traits except for MS and SP (Figure S1), which have been previously reported as structured. For the MS cohort, we have shown previously²¹ that rigorous ancestry matching did not substantially change the total or partitioned $h_g^2$. For the SP cohort, we relied on the consistently replicated enrichment across the PGC2 and Swedish SP cohorts, which have been rigorously quality controlled for the avoidance of population stratification. Recently, Janss et al.⁷⁷ demonstrated that $h_g^2$ can vary significantly when principal components are also included as fixed effects as a function of the number of included eigenvectors. To assess the presence of this bias in our Swedish SP data, we recomputed the joint variance-component estimates of ${\hat{h}}_g^2$ while including an increasing number of eigenvectors as fixed effects. We observed no significant fluctuation of ${\hat{h}}_g^2$ such that the estimates over 1–20 eigenvector covariates had a SD of 0.002, suggesting a tight estimate unbiased by the fixed effects.

Case-Control Ascertainment

Recent work^37,78,79 has shown that liability-scale estimates of $h_g^2$ from REML can be biased downward in dichotomous traits with strong case-control ascertainment. Golan and Rosset⁷⁸ and Hayeck et al.⁷⁹ propose an alternative estimator based on Haseman-Elston (H-E) regression⁸⁰ and show that it eliminates bias. In brief, this approach regresses the product of normalized phenotypes on the genetic covariance (off-diagonal GRM entries) for all unique pairs of samples; the resulting slope is used as an estimate of the observed-scale $h_g^2$ and is converted to the liability scale. This method can be extended naturally to multiple components, where the product of phenotypes is regressed onto GRM entries from each analyzed component in a multiple linear regression. Here, we compared the method and transformation of Golan and Rosset⁷⁸ to the REML estimator described in the main text. We also evaluated the impact of incorporating principal components as fixed effects to account for genetic ancestry. This is particularly important for the SP and MS cohorts (see below), which were ascertained in a way that induces correlations between ancestry and phenotype. All analyses were performed with the same set of GRMs computed from 1000 Genomes imputed data, and the H-E regression (and H-E regression with fixed effects) was implemented as described in Golan and Rosset.⁷⁸ In all instances, we used analytical error-covariance estimates and rescaled them with the delta method to compute SEs. (We note that the SE for H-E regression makes strongly violated assumptions about independence, and they are therefore only presented for completeness). We observed little difference between variance-component methods and H-E regression methods, and H-E regression yielded an average estimate 1.05× greater than that of REML and an overall r² = 0.95 between the two methods (across 11 traits; Table S32). The relative performance was similar when we considered only the percentage of $h_g^2$ from the DHS component (Table S33) such that H-E regression yielded average estimates 1.04× higher than those of REML and an overall r² = 0.94. When principal components where included as fixed effects, meta-analysis across traits within each method did not yield significant differences (Table S34); H-E regression identified DHS enrichment of 5.8× (SE = 0.45), and REML identified DHS enrichment of 5.1× (SE = 0.42). When we did not include principal components as fixed effects, we observed a large difference between variance components and H-E regression in the SP and MS cohorts, where liability-scale H-E regression estimates of liability-scale $h_g^2$ were 10.00 and 2.91, respectively (Table S32), outside the plausible 0–1 bound and vastly larger than REML estimates without fixed effects. This suggests that H-E-regression-based estimates might be particularly sensitive to the confounding effects of ancestry.

Lastly, we repeated our null simulations by using the merged WTCCC2 cohort of ∼33,000 samples, allowing us to simulate a case-control ascertainment (327 case and 654 control subjects) at a prevalence of 0.01 (see Table S35 for simulation details). When we generated ∼1,000 samples on chromosome 1 only, this simulated cohort had an effective SNP-sample ratio (the key quantity driving the effects of case-control ascertainment³⁷) corresponding to that of ∼10,000 samples genome-wide. We tested a “polygenic” scenario where causal variants were sampled uniformly, as well as a “high-effect” scenario where DHS variants had 10× the effect of other SNPs, and found no significant deviation from the null estimate (Table S35) or the analytical SE (Table S36). Although ascertainment has previously been shown to induce correlation between causal variants, our simulations indicate that this does not bias estimates of enrichment for the prevalence and sample size simulated here.

Detailed Analyses of Rare-Variant $h_g^2$

Having identified no significant rare-variant $h_g^2$ at any coding regions, we were interested in quantifying this phenomenon at the set of loci known to be associated with SP. To do so, we constructed six variance components only from SNPs at the 22 loci identified by the PGC1 in a large meta-analysis⁴⁸ and estimated $h_g^2$ jointly with a component for the remaining noncoding variants genome-wide (to account for tagging). As expected, we found the union of all noncoding GWAS variants at these loci to harbor significant heritability of 0.018 (SE = 0.004) (Table S37). However, we did not see any significant heritability from the coding variants at these classes when they were modeled jointly with the other component. This is consistent with our genome-wide finding that common noncoding variants explained a substantial fraction of trait heritability and tagged nearly half of the common coding variation. We also partitioned $h_g^2$ at the set of 1,796 “composite” genes reported by Purcell et al.⁵⁴ to exhibit enrichment of rare disruptive mutations, modeled jointly with exome-chip variants in the remaining genes and noncoding GWAS-chip variants as separate components. However, no significant $h_g^2$ was observed at either the entire set of composite variants ($h_g^2$ = 0.014, SE = 0.012) or the rare composite variants ($h_g^2$ = 0.008, SE = 0.012).

We observed a significant enrichment in $h_g^2$ at 4,919 (nonsingleton) loss-of-function variants, which collectively accounted for 6.0% of (nonsingleton) exonic SNPs but explained 24.3% of the exonic $h_g^2$ (permuted p = 0.02 after MAF matching). We saw no significant enrichment of $h_g^2$ at coding sites that were predicted to be functionally important by PolyPhen-2.⁵² Comparing likelihoods between the model where variants were split into (1) probably damaging and damaging, (2) benign and other, and (3) noncoding components and the model with only (1) coding and (2) noncoding components yielded no significant difference by a 1-degree-of-freedom likelihood-ratio test (p = 0.13).

Web Resources

The URLs for data presented herein are as follows:

• 1000 Genomes Phase 1 reference panels, https://mathgen.stats.ox.ac.uk/impute/impute_v2.html#reference

• CARDIoGRAM CAD summary statistics, http://www.cardiogramplusc4d.org/downloads/

• DIAGRAM T2D summary statistics, http://diagram-consortium.org/downloads.html

• DNaseI Digital Genomic Footprinting (DGF) annotations, http://hgdownload.cse.ucsc.edu/goldenPath/hg19/encodeDCC/wgEncodeUwDgf/

• Exome Chip Design, http://genome.sph.umich.edu/wiki/Exome_Chip_Design

• fgwas, https://github.com/joepickrell/fgwas

• Functional annotations, http://www.hsph.harvard.edu/alkes-price/software/

• Genome-wide Complex Trait Analysis (GCTA), http://www.complextraitgenomics.com/software/gcta/

• HAPI-UR, http://genetics.med.harvard.edu/reich/Reich_Lab/Software.html

• IMPUTE2, https://mathgen.stats.ox.ac.uk/impute/impute_v2.html

• NHGRI GWAS catalog, http://www.genome.gov/gwastudies/

• Oxford recombination map, http://hapmap.ncbi.nlm.nih.gov/downloads/recombination/

• Psychiatric Genomic Consortium, Sweden+SCZ1 schizophrenia summary statistics, http://www.med.unc.edu/pgc/downloads

• RA summary statistics, http://www.broadinstitute.org/ftp/pub/rheumatoid_arthritis/Stahl_etal_2010NG/

• Segway-chromHMM combined enhancer annotations, ftp://ftp.ebi.ac.uk/pub/databases/ensembl/encode/integration_data_jan2011/byDataType/segmentations/jan2011