Abstract
Motivation: Epistasis analysis is an essential tool of classical genetics for inferring the order of function of genes in a common pathway. Typically, it considers single and double mutant phenotypes and for a pair of genes observes whether a change in the first gene masks the effects of the mutation in the second gene. Despite the recent emergence of biotechnology techniques that can provide gene interaction data on a large, possibly genomic scale, few methods are available for quantitative epistasis analysis and epistasis-based network reconstruction.
Results: We here propose a conceptually new probabilistic approach to gene network inference from quantitative interaction data. The approach is founded on epistasis analysis. Its features are joint treatment of the mutant phenotype data with a factorized model and probabilistic scoring of pairwise gene relationships that are inferred from the latent gene representation. The resulting gene network is assembled from scored pairwise relationships. In an experimental study, we show that the proposed approach can accurately reconstruct several known pathways and that it surpasses the accuracy of current approaches.
Availability and implementation: Source code is available at http://github.com/biolab/red.
Contact: blaz.zupan@fri.uni-lj.si
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Epistasis analysis is a tool of classical genetics for inferring the order of genes in pathways from mutant-based phenotypes (Avery and Wasserman, 1992; Botstein and Maurer, 1982). Epistasis asserts that two genes interact if the mutation in one gene masks the effects of perturbations in the other gene. Then, assuming a common pathway, the first masking gene would be downstream, and the products of the second gene would regulate the expression of the first one (Avery and Wasserman, 1992; Cordell, 2002; Huang and Sternberg, 1995; Roth et al., 2009). Epistasis analysis uncovers the relationship between a pair of genes. Its logic can be further extended to uncover parallelism, where both genes have an effect on the phenotype but where there is no epistasis (Battle et al., 2010; Zupan et al., 2003) (Fig. 1). Uncovered pairwise relationships in a group of genes can give rise to a reconstruction of more complex multi-gene networks. An enlightening demonstration of the power of epistasis for assembly of gene networks is for instance a reconstruction of a four-gene cell death pathway in Caenorhabditis elegans (Metzstein et al., 1998).
Fig. 1.
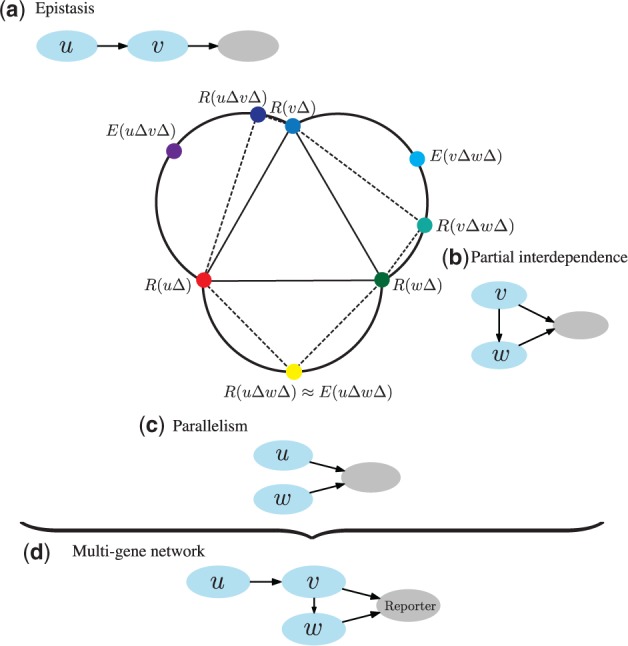
A hypothetical example of epistasis analysis with three genes, u, v and w. Nodes in the central graph represent mutant phenotypes. The phenotypic difference between a double knockout [e.g. ] and a single knockout mutant [e.g. ] is represented with the length of the corresponding dotted edge. Expected double mutant phenotypes, which assume no interaction between genes (see also Section 2.1), are denoted with E [e.g. ]. A double mutant (a) has a phenotype similar to that of a single mutant , which indicates that v is epistatic to u. From the activity of genes v and w (b) we conjecture that gene v partially depends on gene w, i.e. v also acts through a separate pathway because their double mutant has a phenotype that is equally similar to the single knockout and the expected phenotype . The phenotype of double knockout (c) is close to the expected phenotype of which may be explained by u and w acting independently in parallel pathways. Gene ordering from these three relations is preserved in the joint network (d), which is a candidate pathway of genes u, v and w
Emergent technologies from molecular biology that record phenotypes of single and double mutants at a large, possibly genomic scale, prompt for the development of systematic approaches for epistasis analysis and pose the need to devise computational tools that support gene network inference. Approaches of mutagenesis by homologous recombination (Collins et al., 2006; Tong et al., 2004) or RNA interference can yield phenotype observations for thousands or even millions of mutants (Costanzo et al., 2010). Several past studies considered mutant assays with qualitative phenotypes (Zupan et al., 2003), quantitative fitness scores (Battle et al., 2010; Beerenwinkel et al., 2007; Drees et al., 2005; Phenix et al., 2011, 2013; St Onge et al., 2007) or even whole-genome transcriptional profiles (Hughes, 2005; Van Driessche et al., 2005). Majority of these studies present gene networks as collections of directly observed pairwise interactions (e.g. Phenix et al., 2013; St Onge et al., 2007) and do not propose a generally applicable formalism to model the data. Only few general-purpose algorithms for inference of epistatic networks have been proposed. Zupan et al. (2003) introduced formal rules and inference algorithm to infer different types of relationships between genes, but could treat only qualitative phenotypes and could not handle noise. These limitations were elegantly bypassed by a Bayesian approach of Battle et al. (2010) that can handle larger data sets with few hundred genes. This algorithm is to our knowledge also the only modern approach to inference of epistasis networks.
Gene epistasis analysis infers interactions that stem directly from mutant phenotypes. Its causative reasoning is different from other network reconstruction tools that observe correlations between gene profiles (e.g. Ahn et al., 2011; Mohammadi et al., 2012) and infer relationships that are circumstantial (Hughes et al., 2000). Despite the growing body of quantitative genetic interaction data and our ability to collect such data, computational approaches and tools to support epistasis are at best scarce (Battle et al., 2010; Jaimovich and Friedman, 2011; Zhang and Zhao, 2013). Devising methods for inference of gene pathways from mutant-based phenotypes and developing related software tools remains a major challenge of computational systems biology.
We here present a new epistasis analysis-inspired computational approach to infer gene networks from a collection of quantitative mutant phenotypes. We refer to our method as Réd (pronounced as réd, meaning ‘order’ in Slovene). Our work was motivated by the Bayesian learning method of Battle et al. (2010), henceforth denoted by activity pathway network (APN), that starts from a random network and then iteratively refines it to best match data-inferred relationships. The model refinement in APN is carried out through a succession of local structural changes of the evolving network. This procedure may substantially depend on (arbitrary) initialization of network structure, and hence requires ensembling across many runs of the algorithm to raise accuracy of the final network.
Our approach is conceptually different from APN. We first simultaneously infer a probabilistic model for the entire set of pairwise relationships. Relationship probabilities serve as preferences for different types of pairwise relationships (e.g. epistasis, parallelism and partial interdependence) used in a single-step construction of a gene network. In contrast to APN’s local network changes, Réd applies a global procedure to infer the relationships between genes and does not require ensembling. The probabilistic model of Réd uses matrix completion-derived latent data representation to account for noise and sparsity. Inference of factorized model also includes construction of a gene-specific data transformation to account for the differences in single mutant backgrounds, which may affect the phenotype of double mutants. In an experimental study, we show that both components are necessary for inferring gene networks of high accuracy.
2 MATERIALS AND METHODS
Réd, the proposed gene network reconstruction algorithm (Alg. 1), considers quantitative phenotype measurements over a set of single and double mutants, provides preferential order-of-action scores of possible pairwise relationships and assembles them in a joint gene network. The essential steps of the algorithm are overviewed in Figure 2 and are described in detail below.
Fig. 2.
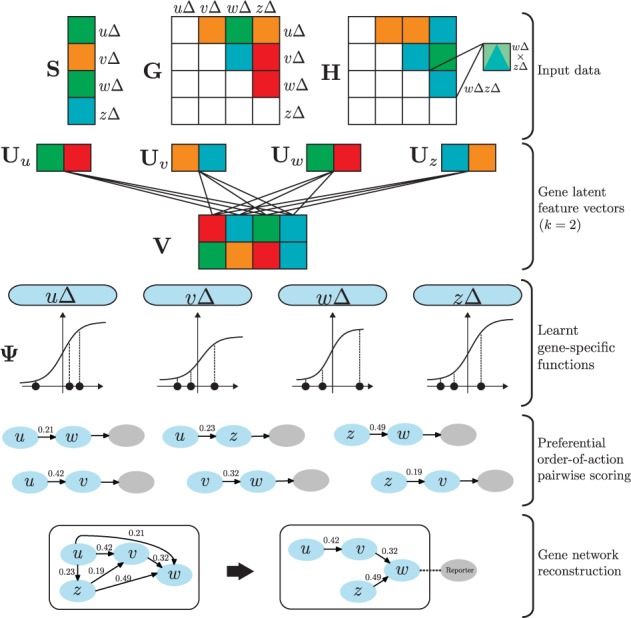
An overview of Réd, a novel approach for automatic gene network inference from mutant data. Inputs to the preferential order-of-action factorized algorithm of Réd include a matrix of double knockout phenotypes (G), a vector of single knockout phenotypes (S) and a matrix of expected phenotypes corresponding to the assumption of absent interactions between genes (H). Réd estimates a factorized model from G, whose gene latent feature vectors capture the global structure of the phenotype landscape, and learns a parametrized logistic map Ψ, which is a gene-dependent non-linear mapping from latent to phenotype space. A scoring scheme is then applied to the inferred model to estimate the probabilities of pairwise gene relationships of different types. Finally, a multi-gene network is reconstructed, which aims to minimize the number of violating and redundant edges
2.1 Problem definition
In quantitative analysis of genetic interactions we typically observe pairwise interactions between n genes and measure mutant phenotypes, such as the fitness of an organism or expression of a reporter gene (Reporter). Measurements over a set of double knockout mutants are given in a sparse matrix and those of single knockout mutants in a vector In these matrices, quantifies a phenotype of double mutant and denotes a phenotype of single mutant The expected mutant phenotypes, which represent phenotypes of double mutants in the absence of genetic interactions, are given by a matrix H.
We aim to reconstruct a gene network that is consistent with pairwise gene relationships inferred from G, H and S. Inputs to network reconstruction are preferential scores for all four modeled gene relationships that include epistasis , epistasis , parallelism and partial interdependence (Table 1). Réd represents the scores as and computes them from the latent gene representation, which is obtained in the inference of a factorized model.
Table 1.
Probabilistic scoring of gene-gene relationships
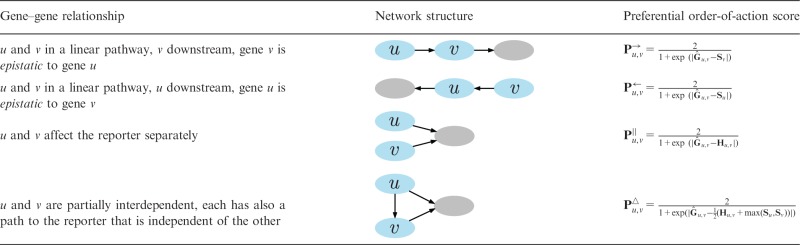 |
Given genes u and v, the table shows all four pairwise relationships and their corresponding network structures. These relationships have already been considered by Battle et al. (2010) but are here studied with probabilistic scoring functions. See main text for explanation of preferential order-of-action scores.
2.2 Factorized model
To deal with noise and address possibly incomplete input data, Réd estimates probabilities of gene relationships through a factorized model. We use a Bayesian inference approach and formulate the conditional probability of observed double mutant phenotype data, given their latent representation, as follows:
where is a normal distribution with mean μ and variance , and indicates whether the phenotypic measurement of is available.
We assume that the observed phenotype of is governed by the latent features associated with both genes u and v. To learn the latent features of u and v, we factorize double mutant phenotype data (G) into a product of two low-dimensional latent matrix factors and . Their column vectors, and , represent k-dimensional u-specific and v-specific gene latent feature vectors, respectively. Instead of using linear latent Gaussian model of gene interactions, we pass the dot product through a parametrized logistic function g. Thus, the model of interaction between genes u and v is represented by the factorized parameter . In the factorization, gene interactions depend on each other, as they overlap and share parameters. For instance, given genes u, v and w, their factorized parameters and share a common gene latent feature vector .
Parametrized logistic function g is given by
and bounds the range of factorized parameters by modeling saturation of the Reporter. Here, parameter represents the limiting value of the output past that cannot grow and represents the number of times that must grow to reach the value of If is positive, g is increasing in x, otherwise g is a decreasing function. Note that corresponds to the well-known sigmoid function. For every double mutant , we represent its logistic function parameters in a triple and define Ψ to hold the parametrized logistic function representation over all possible double mutants: . We reduce the complexity of this factorized model in Section 2.3 by replacing dense parametrization of Ψ (one parameter set for every factorized parameter, with gene-dependent parametrization (one parameter set for every gene, ).
We use a Gaussian prior centered at 1 for logistic function parametrization Ψ over given phenotypic measurements:
For gene latent feature vectors in U and V we assume zero-mean Gaussian priors to avoid overfitting:
Through Bayesian inference we derive the posterior probability of gene latent vectors and logistic function parametrization given the available double mutants phenotypes:
| (1) |
We select the factorized model according to the maximum a posteriori (MAP) estimation by maximizing the log-posterior of Equation (1) over latent feature matrices and logistic function parametrization. The measurement noise variance () and prior variances ( and ) are kept fixed. This is equivalent to minimizing the following objective function (see Supplementary Material for a detailed derivation of a MAP estimator), which is a sum of squared errors with quadratic regularization terms:
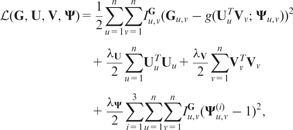 |
(2) |
where and .
Because Ψ, U and V are unknown, the function is not convex. In particular, is convex in either U or V but not in both factors together, which is a known result from matrix factorization studies (Koren et al., 2009; Lee and Seung, 2000). In our study, is further coupled by the parametrization of Ψ. Thus, it is unrealistic to expect an algorithm to solve the optimization problem defined by in the sense of finding global minimum. We thus estimate latent features and logistic function parameters by finding a local minimum of the objective function through application of gradient descent. Derivatives of with respect to gene latent features and logistic parameters are given by the following equations:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where for convenience of notation, is substituted for , penalty term stands for and is logistic function derivative with respect to x. Efficiency in training Réd model comes from finding point estimates of model unknowns instead of inferring the full posterior distribution over them.
2.3 Gene-dependent weighting
We further reduce complexity of the model described in the previous section by combining evidence from multiple phenotypic measurements through their latent representation. We replace entrywise (double-mutant-phenotype-dependent) logistic function parametrization Ψ with gene-dependent parametrization that is given by for i = 1, 2, 3. This reduces the number of parameters in Ψ that have to be learned from to . Intuitively, measurements that involve gene u are not independent from each other but are rather governed by the gene pathways in which u participates. Gene-dependent parametrization of Ψ represents a method of regularization allowing us to remove penalty terms in Equations (5)–(7).
Derivatives of Ψ use only available phenotypic measurements owing to the application of an indicator function [cf. Equations (5)–(7)]. We relax this limitation by considering current estimates of G when computing the derivatives of Ψ. These estimates are given by where U and V are latent matrix factors from the previous iteration of gradient descent (Step 3c in Alg. 1).
2.4 Preferential order-of-action scoring of gene pairs
Probabilities of gene–gene relationships in P are computed from the inferred phenotypes given by , with the rules outlined in Table 1. Estimated probabilities in P approach 1 when inferred phenotypic values in are close to the phenotypes, which would be expected if a certain network structure () existed between genes, and they slowly vanish when the inferred values deviate from the values expected by a certain type of relationship.
For instance, an epistatic genetic interaction is inferred when the trait of the double mutant is similar to the single mutant phenotype and the two single mutant phenotypes are different (). This brings close to 0 and, consequently, close to 1. With different single mutant phenotypes, the expected phenotype of the double mutant that assumes no genetic interaction is different from both single mutant phenotypes (), bringing and close to 0. Likewise, the phenotype of would be different from the phenotype of the double mutant, bringing close to 0.
Cases with less pronounced differences between phenotypes would lead to smaller differences in relationship probabilities. Preferential order-of-action scores generalize the epistasis analysis framework by Avery and Wasserman (1992), wherein the signal and the genes under study were strictly on or off with no intermediate levels of activity. An appealing feature of scores in P is that they have a direct probabilistic interpretation.
2.5 Multi-gene network inference
Given probabilistic scores of gene–gene network structures in P from Section 2.4, we reconstruct a detailed multi-gene network that is consistent with the inferred relationship probabilities and contains a minimum number of violating and redundant edges. Examples of inferred networks are given in Figures 4–7. A network is a weighted directed graph with genes as vertices and directed edges that determine the order of action. A designated vertex represents the observed quantitative trait. A directed edge from u to v is violating (Fig. 3a) if there is evidence in P for both and u ← v (e.g. ). A directed edge from u to v is redundant (Fig. 3b) if there is evidence in P that some intermediate gene exists between u and v. That is, u and v are not adjacent in a genetic network but rather u indirectly affects v, i.e. captures the extent to which strict weak ordering of u and v holds.
Fig. 4.

Gene network of the N-linked glycosylation pathway inferred by Réd. For reference, we show the true ordering of this pathway (Helenius and Aebi, 2004) as adapted from Battle et al. (2010). The inferred gene network reflects many correct gene placements
Fig. 5.
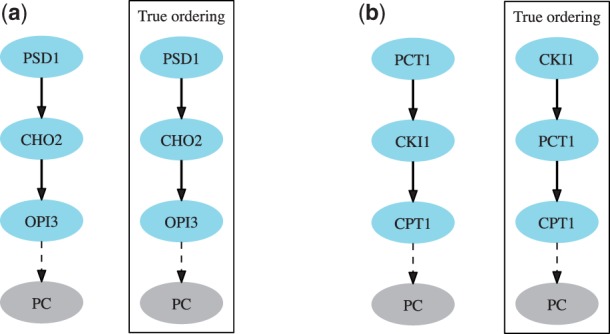
Gene networks of the phosphatidylserine to PC conversion pathway (a) and the Kennedy pathway (b) as inferred by Réd. For reference, we show the true orderings in both pathways adapted from Surma et al. (2013). Réd correctly and with high confidence () inferred all three pairwise gene relationships of the PC conversion pathway. It also correctly predicted two out of three gene relationships of the Kennedy pathway with the wrong prediction (PCT1 → CKI1) being assigned a low confidence ()
Fig. 6.

The ERAD pathway predicted by Réd is shown by solid edges. Placement of genes in the inferred network is consistent with known interdependencies (dotted edges)
Fig. 7.
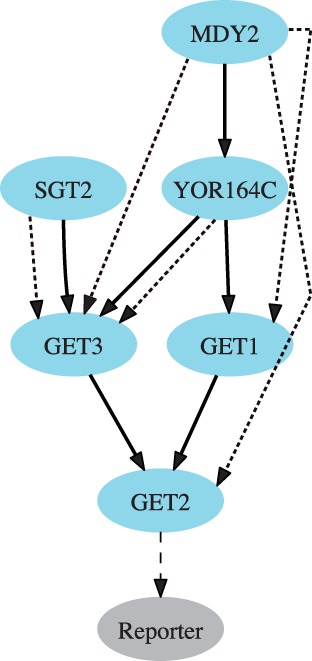
Gene network inferred by Réd that represents the likely ordering of genes belonging to the TA protein biogenesis machinery (solid edges). Known relationships between genes are denoted by dotted edges. Note that the predicted ordering strongly reflects known interdependencies between genes
Fig. 3.
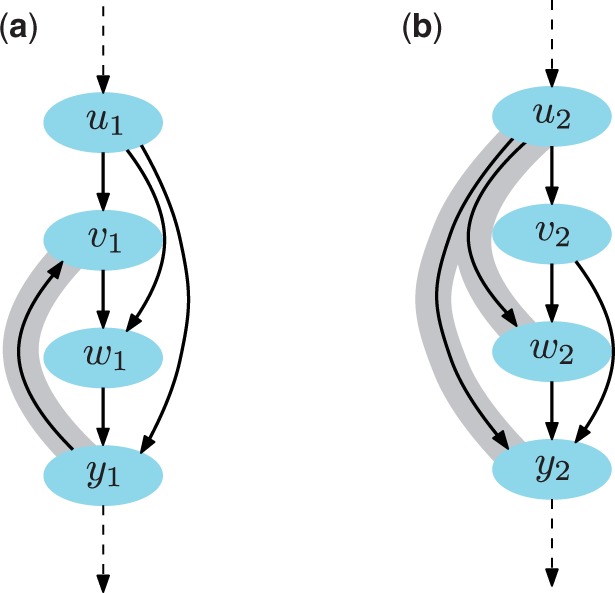
Illustration of violating (a) and redundant (b) edges (in gray) in a pathway with four genes. Edge is violating because there is evidence that v1 is placed upstream of y1 ( and ) but also that y1 is upstream of v1 (). Edge is redundant because there is evidence of an intermediate gene Similarly, edge is redundant because of two intervening genes, v2 and w2
Network inference procedure assigns a level to every gene in a manner that if there is strong evidence in P that gene u is placed upstream of gene v, that is, if v is epistatic to u, then In the case of stronger evidence of parallelism or partial interdependence between u and v the Several genes can be assigned the same level, but a designated vertex corresponding to a phenotype of interest is the only vertex placed on the lowest level.
Inference of a genetic network involves two phases. In the first phase we perform an approximate topological sort through construction of a directed weighted graph. Given genes u and v and the inferred epistasis relationships between them, the direction and weight of a between-level edge are determined by the maximum of the values (edge ) and (edge u ← v). Given a parallelism or partial interdependence relationship between u and v, a within-level edge is determined by the maximum of the values (no edge between u and v) and (edge ). This graph may contain directed cycles, and finding an exact topological ordering of its vertices with the minimal set of violating edges is a known NP-hard problem (Charbit et al., 2007; Eades et al., 1993). Thus, we proceed in the following way. We select a vertex with no incoming between-level edges, assign that vertex to the currently top-most level and recurse on the graph with that vertex removed. We also look for vertices with no outgoing between-level edges and assign them to the currently lowest level. If in some step multiple vertices have no incoming or outgoing between-level edges, they are assigned the same level. It can happen that all vertices have incoming and outgoing between-level edges. In this case, we select the vertex with the highest differential between weighted incoming between-level degree and weighted outgoing between-level degree.
Alg. 1: Réd, the proposed approach for gene network inference by scoring relationships from a factorized model of interactions.
Input:
sparse matrix of double mutant phenotypes ,
typical interaction values ,
measured phenotypes of single mutants ,
parameters , rates α and β, and rank k.
Output:
preferential order-of-action score matrices P,
completed matrix ,
gene-dependent logistic function parametrization Ψ,
inferred gene network for a gene subset of interest.
Initialize and
Initialize as for
- Repeat until convergence:
- Compute and with Equation (3) and (4), respectively.
- Update and
- Compute for i = 1, 2, 3 using Equations (5)–(7), respectively. Substitute therein with , where if and otherwise. Here, is computed using the latent matrix factors from the previous iteration.
- Update for i = 1, 2, 3.
- Set gene-dependent weights for i = 1, 2, 3 and .
Compute preferential order-of-action scores for and using Equations from Table 1.
Normalize for and
Compute
Given a gene subset of interest, infer a network (Section 2.5).
In the second phase of gene network inference we retain within-level edges and those edges that link adjacent levels and are directed downward. The latter procedure eliminates violating edges. As a final step, we remove redundant edges according to their definition above.
3 DATA AND EXPERIMENTAL SETUP
We assess the accuracy of Réd by applying our inference approach to the datasets of Jonikas et al. (2009) and Surma et al. (2013) and compare results to known or partially known networks. Experiments that use data from Jonikas et al. closely follow the setup by Battle et al. and use the same datasets and reference pathways.
3.1 Mutant phenotype data
Jonikas et al. (2009) measured unfolded protein response (UPR) levels in single and double mutants to systematically characterize functional interdependence of yeast genes with roles in endoplasmic reticulum (ER) folding. The dataset contains 444 genes that caused high UPR reporter inductions. The interaction data include phenotypes of 42 240 distinct double mutants (matrix G) corresponding to 43% of all possible double mutants. Jonikas et al. also computed typical (i.e. expected) values of genetic interactions for every double mutant (matrix H). They considered multiplicative neutrality function (Mani et al., 2008) and computed it using reporter levels of pairs of single mutants, modified by a Hill function to account for the saturation of the reporter signal.
Surma et al. (2013) considered 741 genes and observed the growth phenotype (colony size) for all pairs of double mutants. In total, after filtering out unreliable measurements, their dataset comprises 251 383 double mutant fitness scores. We computed single mutant scores by averaging across all scores of double mutants that included mutations of the corresponding genes. We considered multiplicative model to calculate the expected fitness of a double mutant in the absence of a genetic interaction.
3.2 Gene pathways
We compare gene networks inferred by Réd to a number of known or partially known cellular pathways that include genes whose perturbations are measured by Jonikas et al.:
The N-linked glycosylation pathway consisting of 10 genes whose true ordering is known (Helenius and Aebi, 2004),
The ER-associated degradation (ERAD) pathway for which many functional interdependencies between its member genes are known,
Tail-anchored (TA) protein biogenesis machinery consisting of TA proteins important for transmembrane trafficking and the recently discovered GET pathway (Bozkurt et al., 2009; Schuldiner et al., 2008; Stefanovic and Hegde, 2007).
We also compare Réd’s networks to well-characterized cellular pathways of phospholipid biosynthesis whose gene mutants are measured by Surma et al. and that include the following:
The Kennedy pathway involved in the synthesis of phosphatidylethanolamine and phosphatidylcholine (PC), and
The phosphatidylserine to PC conversion pathway.
3.3 Experimental setup
In the first part of the experiments, we use mutant phenotype data to qualitatively evaluate the reconstruction of five gene pathways from Section 3.2. In the second part of the experiments, we evaluate the accuracy of gene ordering through three different setups. In the first two setups, the data-inferred gene ordering was compared with the known pathways. In the third setup, we use cross-validation to estimate the accuracy of prediction of gene interaction scores with the following experiments:
Battle et al. (2010) provided 168 test gene pairs (v, u) from common KEGG pathways (Kanehisa et al., 2008). For 21 gene pairs v is known to be upstream of u, and for 147 gene pairs v is not known to be upstream of u. Given a gene pair, Réd predicted the probability of epistasis as , and the accuracy of predictions on entire set of 168 gene pairs.
Using the setup from Battle et al. we evaluate the accuracy of prediction of direct edges in the N-linked glycosylation pathway (Fig. 4) based on the model-estimated probability of epistasis .
We estimate the accuracy when predicting that two genes are in epistasis, that is, or . Note that in the literature this relationship is also referred to as an alleviating interaction, where the phenotype of a double mutant is less severe than expected from the phenotypes of the corresponding single mutants (Jonikas et al., 2009; Mani et al., 2008). For the data from Jonikas et al. this means that the double-mutant cell responds to ER stress surprisingly better than how the ER stress would typically be mitigated. The data for this experiment were preprocessed according to the procedure described by Battle et al. A positive set included gene pairs (u, v) with significant alleviating genetic interactions, for which the observed phenotype (interaction score) was negative with a magnitude greater than (see St Onge et al., 2007). It was further required that the double-mutant phenotype data contained a sufficient number of observations that included or , such that the geometric mean of such measurements for u and for v was at least 180. There are 2723 gene pairs in the data of Jonikas et al. that match these criteria. In each test run, we form a test set with a random selection of 5% of the positive gene pairs and a negative set of equal size of gene pairs that fail to satisfy the selection criteria. We remove the test data from the interaction score matrix G, and predict whether a test gene pair is alleviating using the probability that u and v occur together in a linear pathway, i.e. . We report an averaged accuracy across 10 different test runs.
We characterize the accuracy of predictions through the area under the receiver-operating characteristic curve (AUC), with a baseline of 0.5 (random networks) and a perfect score of 1.0 (inferred networks that are identical to gold standard—known networks).
We compare Réd, our network inference approach, with a recently published Bayesian approach by Battle et al. They developed preference scoring functions over all possible pairwise gene relationships and applied annealed importance sampling to reconstruct high scoring multi-gene networks. Their method (referred here as APN) was shown to be superior to a number of other approaches that can infer networks from gene interaction data by Jonikas et al. These other approaches include baseline techniques such as Pearson correlation of genetic interaction profiles and raw interaction values as well as more sophisticated techniques such as Gaussian process regression (GP; Williams and Rasmussen, 1996), a method that uses the correlation of observed interaction profiles, the diffusion kernel method (DK; Qi et al., 2008) and GenePath (Zupan et al., 2003). For brevity, we therefore focus on comparing our method with APN, which was run with default parameters as chosen by Battle et al. for the dataset of Jonikas et al., but we also report the accuracies achieved by GP and DK.
Two essential components of Réd are latent representation of gene interactions and their transformation through the logistic function. To test the extent to which the performance of Réd depends on these two components we also run experiments where the algorithm infers probabilities and makes predictions from raw (not factorized) phenotypes, and where the latent representation is used without logistic transformation. We refer to these two approaches as RAW and MF, respectively.
In all experiments with data from Jonikas et al., the parameters of Réd are set as . The same parameters are used on data from Surma et al. with the exception of and k = 50, which were selected to minimize the normalized root mean square error of . This choice of regularization parameters and learning rates is common (cf. Min and Lee, 2005; Pedregosa et al., 2011). We also show (see Supplementary Material; Supplementary Fig. S4) that the performance of Réd does not critically depend on the rank of factorization k. Réd’s optimization by gradient descent is terminated when the Frobenius distance between G and over known values fails to decrease between the two consecutive iterations of optimization.
4 RESULTS AND DISCUSSION
4.1 Reconstruction of a known gene pathway from data by Jonikas et al. (2009)
We analyzed the ability of Réd to reconstruct the known N-linked glycosylation pathway. Figure 4 shows the inferred network next to the known pathway as reported by Helenius and Aebi (2004). Genes CWH41, DIE2 and ALG8 are correctly placed such that they are dependent on the other genes. Also, ALG12 is placed upstream of ALG9, which is also upstream of ALG3. OST3 is correctly placed downstream, but OST5 is incorrectly placed, likely because double-mutant data with the other ALG genes were not available. Surprisingly, Réd correctly placed CWH41, a gene that encodes glucosidase I, an integral membrane protein of the ER involved in sensing ER stress (Romero et al., 1997), at the beginning of the pathway despite mild downstream effects observed in CWH41 mutants. Note that the interaction profile of CWH41 is only moderately correlated with those of ALG genes, and thus, CWH41 was not clustered together with them (Jonikas et al., 2009). We hence conclude that Réd inference of the N-linked glycans synthesis pathway was successful with a network that closely resembles that reported in the literature.
4.2 Reconstruction of known gene pathways from data by Surma et al. (2013)
We applied Réd to mutant data by Surma et al. to reconstruct two thoroughly studied pathways of phospholipid biosynthesis. Réd’s ordering of genes in the phosphatidylserine to PC conversion pathway is fully consistent with the reference pathway (Fig. 5a). In the Kennedy pathway, Réd correctly placed PCT1 upstream of CPT1 and CKI1 upstream of CPT1 with high confidence (Fig. 5b), but it misplaced gene pair PCT1 and CKI1 likely owing to the ambiguity in the data. However, as Réd performs global reasoning by combining evidence from all measurements, it handled the data uncertainty by assigning PCT1 → CKI1 structure the lowest score in the reconstruction of the Kennedy pathway.
4.3 Reconstruction of partially known gene pathways
Jonikas et al. (2009) identified several pathways that are important for ER protein folding. Of these, the pathways for ERAD and TA protein insertion were considered in Battle et al. (2010). Réd-inferred networks for these two pathways are shown in Figures 6 and 7. The solid edges in these figures are those inferred by our algorithm, while the dotted edges indicate gene interactions reported in the literature (Battle et al., 2010; Carvalho et al., 2006; Clerc et al., 2009; Jonikas et al., 2009; Kim et al., 2005; Nakatsukasa and Brodsky, 2008).
The ordering of inferred networks is entirely consistent with the partially known gene pathways. For instance, in the network for the ERAD pathway (Fig. 6), the upstream placement of MNL1 to YOS9 is consistent with existing data showing that MNL1 generates the sugar species recognized by YOS9 (Clerc et al., 2009). Also, MNL1, YOS9, DER1 and USA1 are placed upstream of HRD3 and HRD1, which is compatible with data showing that degradation of certain substrates requires all six components (Carvalho et al., 2006; Kim et al., 2005; Nakatsukasa and Brodsky, 2008). For the TA protein insertion pathway, Réd inferred a network (Fig. 7) that placed the poorly characterized protein SGT2 upstream of the TA protein biogenesis machinery components according to its function in the insertion of TA proteins into membranes (Battle et al., 2010).
Similarly, positive results of network inference are also reported in (Battle et al., 2010). Their method inferred a number of candidate networks of which the best-scored were shown to be partially consistent with known gene interdependencies. In contrast, for each pathway, Réd inferred a single network that is entirely consistent with known gene relationships.
4.4 Quantitative analysis of gene ordering
Table 2 reports the accuracies of gene ordering prediction obtained by four different algorithms, Réd, APN and two simplified variants of Réd. In comparison with APN, Réd performs substantially better in predicting the edges of the KEGG pathways and slightly better in predicting the edges of the N-linked glycosylation pathway (Supplementary Figs S1 and S2).
Table 2.
The predictive accuracy (AUC) of gene ordering by a Bayesian learning method [APN; Battle et al. (2010)], Réd, our proposed approach, and its simplified variants: without factorization (RAW) and with factorization but in the absence of transformation by logistic function (MF)
| Prediction | AUC |
|||
|---|---|---|---|---|
| RAW | MF | APN | Réd | |
| KEGG pathway ordering | 0.563 | 0.583 | 0.648 | 0.728 |
| N-linked glycosylation pathway | 0.591 | 0.638 | 0.731 | 0.749 |
The poor performance of the simplified variants of Réd (RAW and MF) indicates that Réd’s latent representation inferred from the factorized model, the non-linear logistic map and gene-dependent weighting are the essential components of Réd. Without any of these, Réd would not be able to achieve the resulting accuracy.
4.5 Prediction of alleviating genetic interactions
Given the training and separate test datasets, we predict whether an interaction is alleviating (see Section 3.3). Table 3 shows that Réd performs substantially better than APN (P < 0.001). Réd also outperforms standard two-factor matrix factorization (MF) by a large margin, which is an indicator that transformation via a logistic map is essential to the performance of our algorithm. We compare these results with those obtained by GP (Williams and Rasmussen, 1996) using squared exponential autocorrelation model constructed from the genetic interaction profiles, and with the interactions predicted with the DK (Qi et al., 2008). Réd achieves significantly higher accuracy than GP (P < 0.01) and DK (P < 0.001), although the difference with GP is small and may be worthy of further study. Note that RAW, a Réd variant without factorization, is not applicable for this experiment, as it does not generalize across gene interaction scores.
Table 3.
Prediction of unknown alleviating genetic interactions
| Prediction | AUC |
||||
|---|---|---|---|---|---|
| MF | DK | APN | GP | Réd | |
| Alleviating genetic interactions | 0.723 | 0.759 | 0.783 | 0.862 | 0.906 |
We report the accuracy of predicted interactions based on the DK (Qi et al.), predictions based on latent representation obtained with standard two-factor matrix factorization (MF), APNs learned through a Bayesian method by Battle et al., predicted genetic interaction values from GP (Williams and Rasmussen) that uses the correlation of observed interaction profiles, and Réd, our proposed approach.
We have observed that the probabilities of alleviating gene pairs predicted by Réd are well correlated to the strength of alleviating interactions (Spearman ; Supplementary Fig. S3). Réd scores gene pairs with stronger alleviating effects (negative interaction values with greater magnitude) higher than those that interact moderately.
5 CONCLUSION
Réd is a conceptually new approach for inference of gene networks from quantitative genetic interaction data. It implements a probabilistic epistasis analysis and assembles pairwise relationships into gene networks. In our experiments, Réd was able to reconstruct several known and partially known pathways with accuracy above that of the state-of-the-art approaches. Réd outperforms APN, the state-of-the-art method by Battle et al. (2010), both in accuracy and speed, with CPU runtime of only a few minutes compared with APN’s 30 min for an inference of a single full network in an ensemble of 500 networks. We also show that Réd’s power of generalization comes from its two key components, a factorized model with latent representation of gene interactions and a gene-dependent logistic map of interaction scores.
Our evaluation in this article was computational and thus limited to datasets for which several gene pathways or at least partial gene orderings were available (Battle et al., 2010; Jonikas et al., 2009). Réd can efficiently handle similar datasets as well as much larger ones, such as that from the recent yeast experiments by Costanzo et al. (2010). These are also the datasets for which we foresee future applications of Réd and which will require subsequent verification of inferred networks in the wet lab.
Supplementary Material
ACKNOWLEDGEMENTS
We would like to thank Uroš Petrovič for recommending the data set by Surma et al. (2013).
Funding: This work was supported by the grants from the Slovenian Research Agency (P2-0209, J2-5480), EU FP7 (Health-F5-2010-242038), NIH (P01-HD39691) and the Fulbright Scholarship (BZ).
Conflict of Interest: none declared.
References
- Ahn J, et al. Integrative gene network construction for predicting a set of complementary prostate cancer genes. Bioinformatics. 2011;27:1846–1853. doi: 10.1093/bioinformatics/btr283. [DOI] [PubMed] [Google Scholar]
- Avery L, Wasserman S. Ordering gene function: the interpretation of epistasis in regulatory hierarchies. Trends Genet. 1992;8:312–316. doi: 10.1016/0168-9525(92)90263-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battle A, et al. Automated identification of pathways from quantitative genetic interaction data. Mol. Sys. Biol. 2010;6:379. doi: 10.1038/msb.2010.27. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beerenwinkel N, et al. Analysis of epistatic interactions and fitness landscapes using a new geometric approach. BMC Evol. Biol. 2007;7:6. doi: 10.1186/1471-2148-7-60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Botstein D, Maurer R. Genetic approaches to the analysis of microbial development. Annu. Rev. Genet. 1982;16:61–83. doi: 10.1146/annurev.ge.16.120182.000425. [DOI] [PubMed] [Google Scholar]
- Bozkurt G, et al. Structural insights into tail-anchored protein binding and membrane insertion by Get3. Proc. Natl Acad. Sci. USA. 2009;106:21131–21136. doi: 10.1073/pnas.0910223106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carvalho P, et al. Distinct ubiquitin-ligase complexes define convergent pathways for the degradation of ER proteins. Cell. 2006;126:361–373. doi: 10.1016/j.cell.2006.05.043. [DOI] [PubMed] [Google Scholar]
- Charbit P, et al. The minimum feedback arc set problem is NP-hard for tournaments. Comb., Probab. Comput. 2007;16:1–4. [Google Scholar]
- Clerc S, et al. Htm1 protein generates the N-glycan signal for glycoprotein degradation in the endoplasmic reticulum. J. Cell Biol. 2009;184:159–172. doi: 10.1083/jcb.200809198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins SR, et al. A strategy for extracting and analyzing large-scale quantitative epistatic interaction data. Genome Biol. 2006;7:R63. doi: 10.1186/gb-2006-7-7-r63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cordell HJ, et al. Epistasis: what it means, what it doesn’t mean, and statistical methods to detect it in humans. Hum. Mol. Genet. 2002;11:2463–2468. doi: 10.1093/hmg/11.20.2463. [DOI] [PubMed] [Google Scholar]
- Costanzo M, et al. The genetic landscape of a cell. Science. 2010;327:425–431. doi: 10.1126/science.1180823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drees BL, et al. Derivation of genetic interaction networks from quantitative phenotype data. Genome Biol. 2005;6:R38. doi: 10.1186/gb-2005-6-4-r38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eades P, et al. A fast and effective heuristic for the feedback arc set problem. Inf. Process. Lett. 1993;47:319–323. [Google Scholar]
- Helenius A, Aebi M. Roles of N-linked glycans in the endoplasmic reticulum. Annu. Rev. Biochem. 2004;73:1019–1049. doi: 10.1146/annurev.biochem.73.011303.073752. [DOI] [PubMed] [Google Scholar]
- Huang LS, Sternberg PW. Genetic dissection of developmental pathways. Methods Cell Biol. 1995;48:97–122. doi: 10.1016/s0091-679x(08)61385-0. [DOI] [PubMed] [Google Scholar]
- Hughes TR. Universal epistasis analysis. Nat. Genet. 2005;37:457–457. doi: 10.1038/ng0505-457. [DOI] [PubMed] [Google Scholar]
- Hughes TR, et al. Functional discovery via a compendium of expression profiles. Cell. 2000;102:109–126. doi: 10.1016/s0092-8674(00)00015-5. [DOI] [PubMed] [Google Scholar]
- Jaimovich A, Friedman N. From large-scale assays to mechanistic insights: computational analysis of interactions. Curr. Opin. Biotechnol. 2011;22:87–93. doi: 10.1016/j.copbio.2010.10.017. [DOI] [PubMed] [Google Scholar]
- Jonikas MC, et al. Comprehensive characterization of genes required for protein folding in the endoplasmic reticulum. Science. 2009;323:1693–1697. doi: 10.1126/science.1167983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kanehisa M, et al. KEGG for linking genomes to life and the environment. Nucleic Acids Res. 2008;36(Suppl. 1):D480–D484. doi: 10.1093/nar/gkm882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim W, et al. Yos9p detects and targets misfolded glycoproteins for ER-associated degradation. Mol. Cell. 2005;19:753–764. doi: 10.1016/j.molcel.2005.08.010. [DOI] [PubMed] [Google Scholar]
- Koren Y, et al. Matrix factorization techniques for recommender systems. Computer. 2009;42:30–37. [Google Scholar]
- Lee DD, Seung HS. Advances in Neural Information Processing Systems. Denver, Colorado: MIT Press; 2000. Algorithms for non-negative matrix factorization; pp. 556–562. [Google Scholar]
- Mani R, et al. Defining genetic interaction. Proc. Natl Acad. Sci. USA. 2008;105:3461–3466. doi: 10.1073/pnas.0712255105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Metzstein MM, et al. Genetics of programmed cell death in C. elegans: past, present and future. Trends Genet. 1998;14:410–416. doi: 10.1016/s0168-9525(98)01573-x. [DOI] [PubMed] [Google Scholar]
- Min JH, Lee YC. Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters. Expert Syst. Appl. 2005;28:603–614. [Google Scholar]
- Mohammadi S, et al. Role of synthetic genetic interactions in understanding functional interactions among pathways. Pac. Symp. Biocomput. 2012;17:43–54. [PubMed] [Google Scholar]
- Nakatsukasa K, Brodsky JL. The recognition and retrotranslocation of misfolded proteins from the endoplasmic reticulum. Traffic. 2008;9:861–870. doi: 10.1111/j.1600-0854.2008.00729.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F, et al. Scikit-learn: machine learning in Python. J. Mach. Learn. Res. 2011;12:2825–2830. [Google Scholar]
- Phenix H, et al. Quantitative epistasis analysis and pathway inference from genetic interaction data. PLoS Comput. Biol. 2011;7:e1002048. doi: 10.1371/journal.pcbi.1002048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Phenix H, et al. Identifiability and inference of pathway motifs by epistasis analysis. Chaos. 2013;23:025103. doi: 10.1063/1.4807483. [DOI] [PubMed] [Google Scholar]
- Qi Y, et al. Finding friends and enemies in an enemies-only network: a graph diffusion kernel for predicting novel genetic interactions and co-complex membership from yeast genetic interactions. Genome Res. 2008;18:1991–2004. doi: 10.1101/gr.077693.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Romero PA, et al. The yeast CWH41 gene encodes glucosidase I. Glycobiology. 1997;7:997–1004. doi: 10.1093/glycob/7.7.997. [DOI] [PubMed] [Google Scholar]
- Roth FP, et al. Q&A: epistasis. J. Biol. 2009;8:35. doi: 10.1186/jbiol144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schuldiner M, et al. The GET complex mediates insertion of tail-anchored proteins into the ER membrane. Cell. 2008;134:634–645. doi: 10.1016/j.cell.2008.06.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- St Onge RP, et al. Systematic pathway analysis using high-resolution fitness profiling of combinatorial gene deletions. Nat. Genet. 2007;39:199–206. doi: 10.1038/ng1948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stefanovic S, Hegde RS. Identification of a targeting factor for posttranslational membrane protein insertion into the ER. Cell. 2007;128:1147–1159. doi: 10.1016/j.cell.2007.01.036. [DOI] [PubMed] [Google Scholar]
- Surma MA, et al. A lipid E-MAP identifies Ubx2 as a critical regulator of lipid saturation and lipid bilayer stress. Mol. Cell. 2013;51:519–530. doi: 10.1016/j.molcel.2013.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tong AH, et al. Global mapping of the yeast genetic interaction network. Science. 2004;303:808–813. doi: 10.1126/science.1091317. [DOI] [PubMed] [Google Scholar]
- Van Driessche N, et al. Epistasis analysis with global transcriptional phenotypes. Nature Genetics. 2005;37:471–477. doi: 10.1038/ng1545. [DOI] [PubMed] [Google Scholar]
- Williams CK, Rasmussen CE. Advances in Neural Information Processing Systems. Denver, Colorado: MIT Press; 1996. Gaussian processes for regression; pp. 514–520. [Google Scholar]
- Zhang XD, Zhao XM. Computational approaches for identifying signaling pathways from molecular interaction networks. Curr. Bioinform. 2013;8:56–62. [Google Scholar]
- Zupan B, et al. GenePath: a system for automated construction of genetic networks from mutant data. Bioinformatics. 2003;19:383–389. doi: 10.1093/bioinformatics/btf871. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


