COMBINING ISOTONIC REGRESSION AND EM ALGORITHM TO PREDICT GENETIC RISK UNDER MONOTONICITY CONSTRAINT

Abstract

In certain genetic studies, clinicians and genetic counselors are interested in estimating the cumulative risk of a disease for individuals with and without a rare deleterious mutation. Estimating the cumulative risk is difficult, however, when the estimates are based on family history data. Often, the genetic mutation status in many family members is unknown; instead, only estimated probabilities of a patient having a certain mutation status are available. Also, ages of disease-onset are subject to right censoring. Existing methods to estimate the cumulative risk using such family-based data only provide estimation at individual time points, and are not guaranteed to be monotonic, nor non-negative. In this paper, we develop a novel method that combines Expectation-Maximization and isotonic regression to estimate the cumulative risk across the entire support. Our estimator is monotonic, satisfies self-consistent estimating equations, and has high power in detecting differences between the cumulative risks of different populations. Application of our estimator to a Parkinson’s disease (PD) study provides the age-at-onset distribution of PD in PARK2 mutation carriers and non-carriers, and reveals a significant difference between the distribution in compound heterozygous carriers compared to non-carriers, but not between heterozygous carriers and non-carriers.

1. Introduction

In genetic epidemiology studies (Struewing et al., 1997; Marder et al., 2003; Goldwurm et al., 2011), family history data is collected to estimate the cumulative distribution function of disease onset in populations with different risk factors (e.g., genetic mutation carriers and non-carriers). Such estimates provide crucial information to assist clinicians, genetic counselors and patients to make important decisions such as mastectomy (Grady et al., 2013). The family history data, however, raises serious challenges when estimating the cumulative risk. First, a family member’s exact risk factor is unknown; the only available information is the estimated probabilities that a family member has each risk factor. Second, ages of disease onset are subject to censoring due to patient drop-out or loss to follow-up. For such family history data, the cumulative risk of disease is thus a mixture of cumulative distributions for the risk factors with known mixture probabilities. While different parametric and nonparametric estimators have been proposed for estimating these mixture data distribution functions, they are not guaranteed to be monotonic, nor non-negative: two principle features of distribution functions. Most of these estimators also examine the mixture distributions only at individual time points, rather than at a range of time points. To overcome these challenges, we develop a novel, simultaneous estimation method which combines isotone regression (Barlow et al., 1972) with an Expectation-Maximization (EM) algorithm. Our algorithm is based on the binomial likelihood at all observations (Huang et al., 2007; Ma and Wang, 2013), and yields estimated distribution functions that are non-negative, monotone, consistent, efficient and that provide estimates of the cumulative risk over a range of time points.

Family history data is often collected when studying the risk of disease associated with rare mutations (Struewing et al., 1997; Marder et al., 2003; Wang et al., 2008; Goldwurm et al., 2011). For example, estimating the probability that Ashkenazi Jewish women with specific mutations of BRCA1 or BRCA2 will develop breast cancer (Struewing et al., 1997); estimating the survival function from relatives of Huntington’s disease probands with expanded C-A-G repeats in the huntingtin gene (Wang et al., 2012); and, in this paper, estimating age-at-onset of Parkinson’s disease in carriers of PARK2 mutations (Section 1.1).

In all these cases, a sample of (usually diseased) subjects referred to as probands are genotyped. Disease history in the probands’ first-degree relatives, including age-at-onset of the disease, is obtained through validated interviews (Marder et al., 2003). Because of practical considerations including high costs or unwillingness to undergo genetic testing, the relatives’ genotype information is not collected. Instead, the probability that the relative has the mutation or not is computed based on the relative’s relationship to the proband and the proband’s mutation status (Khoury et al., 1993, section 8.4). Thus, the distribution of the relative’s age-at-onset of a disease is a mixture of genotype-specific distributions with known, subject-specific mixing proportions.

A first attempt at estimating the mixture distribution functions was based on assuming parametric or semiparametric forms (Wu et al., 2007) for the underlying mixture densities. To avoid model misspecification, however, nonparametric estimators such as the nonparametric maximum likelihood estimator (NPMLE) were also proposed. While in many situations the NPMLEs are consistent and efficient, they are neither for the mixture model (Wang et al., 2012; Ma and Wang, 2013). As improvements over the NPMLEs, Wang et al. (2012) and Ma and Wang (2013) proposed consistent and efficient nonparametric estimators based on estimating equations. The estimators stem from casting the problem into a semiparametric theory framework and identifying the efficient estimator. The resulting estimator, however, can have computational difficulties when the data is censored as it uses inverse probability weighting (IPW) and augmented IPW to estimate the mixture distribution functions (Wang et al., 2012). The weighting function involves a Kaplan-Meier estimator which can result in unstable estimation because the weighting function can be close to zero in the right tail. There is also no guarantee that the resulting estimator is monotonic or non-negative; thus, a post-estimate adjustment was implemented to ensure monotonicity.

In this paper, we propose a novel nonparametric estimator that is neither complex, nor computationally intensive, and yields a genuine distribution for the mixture data problem under the monotonicity constraint of a distribution function. Providing nonparametric estimators for survival functions under ordered constraints has received considerable attention recently (Park et al., 2012; Barmi and McKeague, 2013), but the emphasis has been on non-mixture data. The method we propose is applicable to mixture data. Our method is motivated from a real world study on genetic epidemiology of Parkinson’s disease (see Section 1.1), and is based on maximizing a binomial likelihood simultaneously at all observations (Huang et al., 2007). Our method involves combining an EM algorithm and isotone regression (Ayer et al., 1955) so that monotonicity is ensured. We demonstrate that our estimator is consistent, satisfies self-consistent estimating equations, and yields large power in detecting differences between the distribution functions in the mixture populations. Our estimator is easy to implement, and for non-mixture data, we show that our method coincides with the NPMLE.

1.1. CORE-PD study to estimate the risk of PARK2 mutations

Parkinson’s disease (PD) is a neurodegenerative disorder of the central nervous system that results in bradykinesia, tremors, and problems with gait. PD mostly affects the elderly 50 and older, but early onset cases do occur and are hypothesized to be a result of genetic risk factors. Mutations in the PARK2 gene (Kitada et al., 1998; Hedrich et al., 2004) are the most common genetic risk factor for early-onset PD (Lücking et al., 2000) and may be a risk factor for late onset (Oliveira et al., 2003). While mutations in the PARK2 gene are rare, genetic or acquired defects in Parkin function may have far-reaching implications for the understanding and treatment of both familial and sporadic PD.

To understand the effects of mutations in the PARK2 gene, the Consortium on Risk for Early Onset PD (CORE-PD) study was begun in 2004 (Marder et al., 2010). Experienced neurologists performed in-depth examinations (i.e., neurological, cognitive, psychiatric assessments) of proband participants, a subset of non-carriers, and some of the first-degree relatives of probands and non-carriers. For relatives who were not examined in person, their PARK2 genotypes were not available, but their age-at-onset of PD was obtained through systematic family history interviews (Marder et al., 2003). Based on this family history data, the objective then is to determine the age-specific cumulative risk of PD in PARK2 mutation carriers and non-carriers. The results will help patients interpret a positive test result both in deciding treatment options and making important life decisions such as family planning.

The remaining sections of this paper are as follows. Section 2 describes our proposed estimator which involves maximizing a binomial log-likelihood with an EM algorithm. We demonstrate that the ensuing estimator solves a self-consistent estimating equation, and is consistent for complete and right censored data. We demonstrate in Section 3 that we can re-formulate the estimator using a different EM algorithm, for which we can apply the pool adjacent violators algorithm (PAVA) from isotone regression to yield a non-negative and monotonic estimator. We demonstrate the advantages of our new estimator over current ones through extensive simulation studies in Section 4. We apply our estimator to the CORE-PD study in Section 5 and conclude the paper in Section 6. Technical details are in the Appendix, and additional numerical results are available in the Supplementary Material.

2. Binomial Likelihood Estimation

To simplify the presentation, we focus on a mixture distribution with two components; the techniques presented can be easily extended to more than two components.

For i = 1, …, n, we observe a quantitative measure S_i known to come from one of p = 2 populations with corresponding distributions F₁, F₂ and densities dF₁, dF₂. For example, in the Parkinson’s disease study, S_i is the age of disease-onset, F₁ is the distribution for the PARK2 mutation carrier group, and F₂ is for the non-carrier group. The exact population to which S_i belongs is unknown (i.e., we do not know whether a family member is a mutation carrier or non-carrier), but one can estimate the probability q_ki that S_i was generated from the kth population, k = 1, 2. We suppose the mixture probability Q_i has a discrete distribution, denoted as p_Q(q_i), with finite support u₁, …, u_m. We also suppose that q_1i + q_2i = 1, and hence, sometimes write q_1i ≡ λ_i and q_2i ≡ 1 − λ_i. In this case, instead of referring to the discrete distribution p_Q(q_i), we simply refer to the distribution of λ_i, denoted as η(λ_i). Furthermore, S_i is subject to right-censoring, so we observe X_i = min(S_i,C_i), where C_i is a random censoring time independent of S_i. We let G(·) denote the survival function of C_i and dG(·) its corresponding density. Lastly, we let Δ_i = I(S_i ≤ C_i) denote the censoring indicator.

Our objective is to use the independent, identically distributed (iid) data (Q_i = q_i, X_i = x_i, Δ_i = δ_i) to form a nonparametric estimator of F(t) = {F₁(t), F₂(t)}^T that is consistent, monotone on the support of S_i, and efficient. Identifiability of F(t) is ensured since the mixture probabilities are assumed known and Q_i are not all the same Wang et al. (2007). In fact if Q_i has at least k distinguished the support points, then the model is identifiable. To estimate F(t), we first consider the nonparametric log-likelihood

$$\sum _{i=1}^n\text{log}(p_{\mathit{Q}}({\mathit{q}}_i){\{{\mathit{q}}_i^T\mathit{d}\mathit{F}(x_i)G(x_i)\}}^{{\delta }_i}{[\{1-{\mathit{q}}_i^T\mathit{F}(x_i)\}dG(x_i)]}^{1-{\delta }_i}).$$

Because p_Q(q_i) is independent of the estimation of F(t), and the censoring times are random, the log-likelihood above simplifies to

$$\sum _{i=1}^n\text{log}[{\{{\mathit{q}}_i^T\mathit{d}\mathit{F}(x_i)\}}^{{\delta }_i}{\{1-{\mathit{q}}_i^T\mathit{F}(x_i)\}}^{1-{\delta }_i}].$$ (1)

Different maximizations of (1) result in the commonly used NPMLEs (see Appendix A.1). Unfortunately, for the mixture data problem, they turn out to be inconsistent or inefficient (Ma and Wang, 2012).

2.1. Motivation for binomial likelihood formulation

As an improvement over the NPMLEs, we consider a binomial likelihood estimator. To motivate this estimator, we first consider a non-mixture model without censoring. That is, we observe independent observations S₁, …, S_n generated from a common distribution F. Without loss of generality, we suppose S₁ ≤ S₂ ≤ ⋯ ≤ S_n (i.e., ties may occur). We demonstrate that, in this setting, the NPMLE and the binomial likelihood estimator of F are the same. Thus, because the NPMLE is most efficient in this setting, the binomial likelihood estimator is as well.

For non-mixture data without censoring, the nonparametric estimator of F maximizes

$$\sum _{i=1}^n\text{log}dF(s_i)$$

with respect to dF(s_i) subject to ${\sum }_{i=1}^{n}dF(s_i)=1$ and dF(s_i) ≥ 0. From first principles, the maximizer is the well-known empirical distribution function, ${\mathrm{F̂}}_n(t)=n^{-1}{\sum }_{i=1}^{n}I(s_i\le t)$.

On the other hand, the empirical distribution function is also the maximizer of the following binomial log-likelihood. For distinctive time points t₁ < t₂ < ⋯ < t_h and each S_i, denote a success if S_i > t_j and a failure if S_i ≤ t_j i = 1, …, n, j = 1, …, h. The probability of a success is F̄ (t_j) ≔ 1 − F(t_j), and the probability of a failure is F(t_j). The times t₁, …, t_h can be arbitrary, but are typically chosen to span the support of the events S_i so as to estimate the cumulative distribution function over the full support.

Accounting for all possible successes and failures, the binomial log-likelihood is

$$\sum _{j=1}^h\sum _{i=1}^n\{I(s_i\le t_j)\text{log}F(t_j)+I(s_i>t_j)\text{log}\mathrm{F̄}(t_j)\}.$$

Maximizing the above with respect to each F(t_j) and subject to the monotonic constraint F(t₁) ≤ F(t₂) ≤ … ≤ F(t_h) gives

$${\mathrm{F̂}}_n(t_j)=n^{-1}\sum _{i=1}^{n}I(s_i\le t_j),j=1,\dots ,h.$$

However, this is exactly the empirical distribution function which, by definition, satisfies the monotonic constraint.

Therefore, in the non-mixture case, maximizing the nonparametric log-likelihood with respect to dF is equivalent to maximizing the binomial log-likelihood with respect to F subject to the monotonic constraint F(t₁) ≤ F(t₂) ≤ … ≤ F(t_h). Because the two estimators are equivalent and the NPMLE is known to be most efficient, the resulting binomial likelihood estimator is fully efficient. Motivated by this result, we anticipate that maximizing the binomial log-likelihood may yield highly efficient estimators in more general mixture models.

2.2. Binomial Likelihood Estimator for Censored Mixture Data

We now construct a binomial likelihood estimator for mixture data with censoring. Again, consider arbitrary time points t₁ < ⋯ < t_h, such that for each event time S_i, a success occurs if S_i > t_j and a failure if S_i ≤ t_j, i = 1, …, n, j = 1, …, h. As in Section 2.1, we allow for ties in the event times S_i, and choose times t₁, …, t_h to span the support of the event times.

Under censoring, we observe X_i = min(S_i, C_i), which means a success, I(S_i > t_j), is unobservable for those subjects who are lost to follow-up before t_j. A natural approach then is to view the unobserved successes as missing data and to use an EM algorithm to maximize the constructed binomial log-likelihood.

Let V_ij = I(S_i > t_j), the unobserved success. For mixture data, when V_ij is observable (i.e., non-censored data), we have that P(V_ij = 1) = λ_iF̄₁(t_j)+(1 − λ_i)F̄₂(t_j), and P(V_ij = 0) = λ_iF₁(t_j) + (1 − λ_i)F₂(t_j), where F̄_k(t_j) = 1 − F_k(t_j), k = 1, 2. Considering all time points t₁, …, t_h, and all possible successes and failures, the complete data binomial log-likelihood of {I(S_i > t_j)}, i = 1, …, n, j = 1, …, h, is

$$\sum _{j=1}^h\sum _{i=1}^n[I(s_i\le t_j)\text{log}\{{\lambda }_i{F}_1(t_j)+(1-{\lambda }_i)F_2(t_j)\}+I(s_i>t_j)\text{log}\{{\lambda }_i{\mathrm{F̄}}_1(t_j)+(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)\}].$$

If V_ij = I(S_i > t_j) were observable, we could estimate F(t_j), j = 1, …, h, by maximizing the binomial log-likelihood with respect to F₁(t_j) and F₂(t_j). However, because V_ij is unobservable, we instead use an EM algorithm for maximization. An EM algorithm at a single t_j was given in Ma and Wang (2013), but, they did not further pursue it. In fact, Efron (1967) did impute this.

The EM algorithm we propose is an iterative procedure where at the bth step, the imputed V_ij is

$$w_{ij}^{(b)}=E\{I(S_i>t_j)|x_i\}=I(x_i>t_j)+(1-{\delta }_i)I(x_i\le t_j)\frac{{\lambda }_i{\mathrm{F̄}}_1^{(b)}(t_j)+(1-{\lambda }_i){\mathrm{F̄}}_2^{(b)}(t_j)}{{\lambda }_i{\mathrm{F̄}}_1^{(b)}(x_i)+(1-{\lambda }_i){\mathrm{F̄}}_2^{(b)}(x_i)},$$ (2)

based on the observed data X_i = x_i. The E-step is then the imputed binomial log-likelihood

$$\sum _{j=1}^h\sum _{i=1}^n[(1-w_{ij}^{(b)})\text{log}\{{\lambda }_i{F}_1(t_j)+(1-{\lambda }_i)F_2(t_j)\}+w_{ij}^{(b)}\text{log}\{{\lambda }_i{\mathrm{F̄}}_1(t_j)+(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)\}].$$ (3)

The M-step then maximizes the above with respect to F₁(t_j) and F₂(t_j); specifically, the M-step involves solving

$$-\sum _{i=1}^n{\lambda }_i\frac{w_{ij}^{(b)}-{\lambda }_i{\mathrm{F̄}}_1(t_j)-(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)}{\{{\lambda }_i{F}_1(t_j)+(1-{\lambda }_i)F_2(t_j)\}\{{\lambda }_i{\mathrm{F̄}}_1(t)+(1-{\lambda }_i){\mathrm{F̄}}_2(t)\}}=0,-\sum _{i=1}^n(1-{\lambda }_i)\frac{w_{ij}^{(b)}-{\lambda }_i{\mathrm{F̄}}_1(t_j)-(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)}{\{{\lambda }_i{F}_1(t_j)+(1-{\lambda }_i)F_2(t_j)\}\{{\lambda }_i{\mathrm{F̄}}_1(t)+(1-{\lambda }_i){\mathrm{F̄}}_2(t)\}}=0,$$ (4)

for j = 1, …, h. The solution to (4) leads to the new estimate $F_1^{(b+1)}(t_j)$ and $F_2^{(b+1)}(t_j)$. Iterating the E- and M-steps until convergence leads to the binomial likelihood estimator F̂(t_j), j = 1, …, h, for censored mixture data. We now make several observations about this proposed estimator.

The estimating equations in (4) are optimally weighted (Godambe, 1960), and are, in fact, self-consistent estimating equations (Efron, 1967). The self-consistency stems from the imputation procedure of the EM algorithm, analogously to the work of Efron (1967). In the special case of right censoring but no mixture, the above approach has a closed form solution, which is the celebrated Kaplan-Meier estimator (Efron, 1967). In the general case, it can be shown that the proposed estimator F̂ is consistent. The proof is trivial if F takes discrete finite many values. On the hand if F is a continuous distribution, one may use the law of large sample and Kullback-Leibler information inequality to prove it. Details are given in the Appendix A.2. Asymptotics of F̂(t_j) are much more involved, however, and require solving a complex integral equation which is impractical. Hence, inference is usually performed using a Bootstrap approach.

Solving for F̂(t) in practice is also a computationally intensive task. No closed form solution to (4) exists, and ensuring monotonicity and non-negativity of F̂(t) would actually require solving (4) subject to the constraints F_k(t₁) ≤ F_k(t₂) ≤ … ≤ F_k(t_h), k = 1, 2, for t₁ ≤ ⋯ ≤ t_h. Such a constraint only further complicates the already demanding estimation procedure. Still, requiring monotonicity is essential when the data is censored. Without monotonicity, the imputed weights $w_{ij}^{(b)}$ may not be in the range (0,1), which could lead to non-convergence when solving (4). Thus, to ensure monotonicity and avoid the complexities of directly solving (4), we now describe another approach for obtaining the binomial likelihood estimator.

3. Genuine Nonparametric Distribution Estimators

To construct a monotone and non-negative estimator F̂(t) at times t₁ < ⋯ < t_h, we maximize a binomial log-likelihood using a combined EM algorithm and pool adjacent violators algorithm (PAVA). Before describing the new method, we first provide a brief overview of PAVA.

3.1. Pool Adjacent Violator Algorithm

Isotone regression (Barlow et al., 1972) is the notion of fitting a monotone function to a set of observed points y₁, …, y_n in a plane. Formally, the problem involves finding a vector a = (a₁, …, a_n)^T that minimizes the weighted least squares

$$\sum _{i=1}^n{r}_i{(y_i-a_i)}^2$$

subject to a₁ ≤ ⋯ ≤ a_n for weights r_i > 0, i = 1, …, n. The solution to this optimization problem is the so-called max-min formula (Barlow et al., 1972):

$${â}_j=\underset{s\le j}{\text{max}}\underset{t\ge j}{\text{min}}\frac{{\sum }_{h=s}^t{y}_h{r}_h}{{\sum }_{h=s}^t{r}_h},j=1,\dots ,n.$$

Rather than solving this max-min formula, the weighted least squares problem is instead solved using PAVA (Ayer et al., 1955; Barlow et al., 1972): a simple procedure that yields the solution in O(n) time (Grotzinger and Witzgall, 1984). The history of PAVA, its computational aspects, and a fast implementation in R are discussed in Leeuw et al. (2009). Variations of PAVA implementation include using up-and-down blocks (Kruskal, 1964) and recursive partitioning (Luss et al., 2010).

Our idea is to apply PAVA to a variant of our binomial loglikehood and yield a monotone estimator F̂(t). It is important to note that we cannot simply apply PAVA to the estimator solving (4). The E-step in (3) is not in the exponential family, which is a requirement of PAVA (Robertson et al., 1988). Furthermore, applying PAVA to maximize a binomial loglikelihood has been used in current status data (Jewell and Kalbfleisch, 2004), but not in the context of mixture data as we do.

3.2. PAVA-based Binomial Likelihood Estimator for Censored Mixture Data

We now modify the construction of the binomial likelihood estimator for censored mixture data (Section 2.2) so that PAVA may be applied. In our earlier construction (Section 2.2), we viewed the event I(S_i > t_j) as the only missing data, i = 1, …, n, j = 1, …, h. Now, we also consider the unobserved population membership as missing. Let L_i denote the unobserved population membership for observation i.

Analogous to the argument in Section 2.2, we first consider the ideal situation when L_i and I(S_i > t_j) are observable. We suppose L_i = 1 when S_i is generated from F₁, and L_i = 0 when S_i is generated from F₂. In this case, P(L_i = 1) = λ_i and P(L_i = 0) = 1 − λ_i. For mixture data, the probability S_i > t_j is λ_iF̄₁(t_j) when L_i = 1, and is (1 − λ_i) F̄₂(t_j) when L_i = 0. Likewise, the probability S_i ≤ t_j is λ_iF₁(t_j) when L_i = 1 and is (1 − λ_i)F₂(t_j) when L_i = 0. Therefore, the complete data log-likelihood of {L_i, I(S_i ≤ t_j)}, i = 1, 2…, n, j = 1, 2, …, h, is the binomial log-likelihood

$${\ell }_c=\sum _{j=1}^h\sum _{i=1}^n[L_{i}I(S_i\le t_j)\text{log}\{{\lambda }_i{F}_1(t_j)\}+L_{i}I(S_i>t_j)\text{log}\{{\lambda }_i{\mathrm{F̄}}_1(t_j)\}+(1-L_i)I(S_i\le t_j)\text{log}\{(1-{\lambda }_i)F_2(t_j)\}+(1-L_i)I(S_i>t_j)\text{log}\{(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)\}].$$

However, neither the population membership L_i, nor the event I(S_i > t_j) are available. Hence, these values must be imputed, and an EM algorithm will be used for maximization.

At the bth step of the EM algorithm, we compute E{L_iI(S_i ≤ t_j)|x_i} = E{L_i|S_i ≤ t_j}E{I(S_i ≤ t_j)|x_i} and E{L_iI(S_i > t_j)|x_i} = E{L_i|S_i > t_j}E{I(S_i > t_j)|x_i} based on observed data X_i = min(S_i, C_i) with X_i = x_i. We found earlier that $E\{I(S_i>t_j)|x_i\}=w_{ij}^{(b)}$ as defined in (2). Using a similar calculation, we obtain

$$u_{ij}^{(b)}\equiv E(L_i|S_i\le t_j)=\frac{{\lambda }_i{F}_1^{(b)}(t_j)}{{\lambda }_i{F}_1^{(b)}(t_j)+(1-{\lambda }_i)F_2^{(b)}(t_j)},{\upsilon }_{ij}^{(b)}\equiv E(L_i|S_i>t_j)=\frac{{\lambda }_i{\mathrm{F̄}}_1^{(b)}(t_j)}{{\lambda }_i{\mathrm{F̄}}_1^{(b)}(t_j)+(1-{\lambda }_i){\mathrm{F̄}}_2^{(b)}(t_j)}.$$

Therefore, at the bth step, with observed data O^(b) = {X_i}, i = 1, …, n, the E-step is

$$E({\ell }_c|{\mathit{O}}^{(b)})=\sum _{j=1}^h\sum _{i=1}^n[u_{ij}^{(b)}(1-w_{ij}^{(b)})\text{log}\{{\lambda }_i{F}_1(t_j)\}+{\upsilon }_{ij}^{(b)}{w}_{ij}^{(b)}\text{log}\{{\lambda }_i{\mathrm{F̄}}_1(t_j)\}+(1-u_{ij}^{(b)})(1-w_{ij}^{(b)})\text{log}\{(1-{\lambda }_i)F_2(t_j)\}+(1-{\upsilon }_{ij}^{(b)})w_{ij}^{(b)}\text{log}\{(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)\}].$$

The M-step then maximizes the above expression with respect to F₁(t_j) and F₂(t_j) at each t_j. To ensure monotonicity, however, the M-step actually involves maximizing E(ℓ_c|O^(b)) subject to the monotonic constraints F_k(t₁) ≤ F_k(t₂) ≤ … ≤ F_k(t_h), k = 1, 2. Though constrained maximization is typically a challenging procedure, the task is simplified because the log-likelihood E(ℓ_c|O^(b)) belongs to the exponential family, in which case PAVA is applicable. From the theory of isotonic regression (Robertson et al., 1988), we have

$$\underset{F_1(t_1)\le \cdots \le F_1(t_h)}{\text{arg max}}E({\ell }_c|{\mathit{O}}^{(b)})=\underset{F_1(t_1)\le \cdots \le F_1(t_h)}{\text{arg min}}\sum _{j=1}^h\sum _{i=1}^n{r}_{1ij}^{(b)}{\{u_{ij}^{(b)}\frac{1-w_{ij}^{(b)}}{r_{1ij}^{(b)}}-F_1(t_j)\}}^2,\underset{F_2(t_1)\le \cdots \le F_2(t_h)}{\text{arg max}}E({\ell }_c|{\mathit{O}}^{(b)})=\underset{F_2(t_1)\le \cdots \le F_2(t_h)}{\text{arg min}}\sum _{j=1}^h\sum _{i=1}^n{r}_{2ij}^{(b)}{\left\{\right(1-u_{ij}^{(b)})\frac{1-w_{ij}^{(b)}}{r_{2ij}^{(b)}}-F_2(t_j)\}}^2,$$

where $r_{1ij}^{(b)}=u_{ij}^{(b)}(1-w_{ij}^{(b)})+{\upsilon }_{ij}^{(b)}{w}_{ij}^{(b)}$ and $r_{2ij}^{(b)}=(1-u_{ij}^{(b)})(1-w_{ij}^{(b)})+(1-{\upsilon }_{ij}^{(b)})w_{ij}^{(b)}$.

These formulations suggest that ${\{F_1(t_j)\}}_{j=1}^h$ is the weighted isotonic regression of $u_{ij}^{(b)}(1-w_{ij}^{(b)})/r_{1ij}^{(b)}$ with weights $r_{1ij}^{(b)}$. Likewise, ${\{F_2(t_j)\}}_{j=1}^h$ is the weighted isotonic regression of $(1-u_{ij}^{(b)})(1-w_{ij}^{(b)})/r_{2ij}^{(b)}$ with weights $r_{2ij}^{(b)}$. Thus, the max-min results of isotone regression apply and yield solutions

$${\mathrm{F̃}}_1^{(b+1)}(t_j)=\underset{s\le j}{\text{max}}\underset{t\ge j}{\text{min}}\frac{{\sum }_{h=s}^t{\sum }_{i=1}^n{u}_{ih}^{(b)}(1-w_{ih}^{(b)})}{{\sum }_{h=s}^t{\sum }_{i=1}^n\left\{u_{ih}^{(b)}\right(1-w_{ih}^{(b)})+{\upsilon }_{ih}^{(b)}{w}_{ih}^{(b)}\}},{\mathrm{F̃}}_2^{(b+1)}(t_j)=\underset{s\le j}{\text{max}}\underset{t\ge j}{\text{min}}\frac{{\sum }_{h=s}^t{\sum }_{i=1}^n(1-u_{ih}^{(b)})(1-w_{ih}^{(b)})}{{\sum }_{h=s}^t{\sum }_{i=1}^n\left\{\right(1-u_{ih}^{(b)}\left)\right(1-w_{ih}^{(b)})+(1-{\upsilon }_{ih}^{(b)}\left)w_{ih}^{(b)}\right\}}.$$

Rather than solving these max-min formulas, we instead use the PAVA algorithm implemented in R (Leeuw et al., 2009). Iterating through the E- and M- steps with PAVA leads to a genuine estimator of the mixture distributions.

For non-censored data (i.e., δ_i = 1, i = 1, …, n), $w_{ij}^{(b)}$ in (2) simplifies to $w_{ij}^{(b)}=I(S_i>t_j)$. In this case, the proposed EM algorithm with PAVA in the M-step remains as stated but with $w_{ij}^{(b)}=I(S_i>t_j)$ throughout.

Finally, the proposed EM-PAVA algorithm converges to the maximum likelihood estimate of the binomial likelihood. This follows because E(ℓ_c|O^(b)) belongs to the exponential family and is convex (Wu, 1983). Thus, the derived estimator is the unique maximizer and satisfies the monotonic property of distribution functions.

3.3. Hypothesis Testing

For a two mixture model, one key interest is testing for differences between the two mixture distributions; i.e., testing H₀ : F₁(t) = F₂(t) vs. H₁ : F₁(t) ≠ F₂(t) for a finite set of t values or over an entire range. To test this difference, we suggest the following permutation strategy (Churchill and Doerge, 1994). For the data set given, obtain the estimate F̃⁽⁰⁾ (t) using the EM-PAVA algorithm, and compute $s^{(0)}={\text{sup}}_t|{\mathrm{F̃}}_1^{(0)}(t)-{\mathrm{F̃}}_2^{(0)}(t)|$. Then, for k = 1, …, K, create a permuted sample of the data by permuting the pairs (X_i, δ_i) and coupling them with the mixture proportions q₁, …, q_n. For the kth permuted data set, compute F̃^(k) (t) and $s^{(k)}={\text{sup}}_t|{\mathrm{F̃}}_1^{(k)}(t)-{\mathrm{F̃}}_2^{(k)}(t)|$. Finally, the p-value associated with testing H₀ is ${\sum }_{k=1}^{K}I(s^{(k)}\ge s^{(0)})/K$. In practice, we recommend using K = 1000 permutation data sets. We compare the power of various tests in Section 4.

4. Simulation Study

4.1. Simulation Design

We performed extensive simulation studies to investigate the performance of the proposed EM-PAVA algorithm. We report here the results of three experiments comparing EM-PAVA to existing estimators in the literature: the type I NPMLE, type II NPMLE (see Appendix A.1 for the forms of the NPMLEs), and the oracle efficient augmented inverse probability weighting estimator (Oracle EFFAIPW) of Wang et al. (2012, sec. 3). “Oracle” here refers to the assumption that the underlying density dF(t) is known exactly and is not estimated using nonparametric methods.

The three experiments were designed as follows:

• Experiment 1: F₁(t) = {1 − exp(−t)}/{1 − exp(−10)} and F₂(t) = {1 − exp(−t/2.8)}/{1 − exp(−10/2.8)} for 0 ≤ t ≤ 10.

• Experiment 2: F₁(t) = 0.8/[1 + exp{−(t − 80)/5}] for 0 ≤ t ≤ 100 and F₁(t) = 0.678 + 0.001t for 100 ≤ t ≤ 300. F₂(t) = 0.2/[1 + exp{−(t − 80)/5}] for 0 ≤ t ≤ 100 and F₂(t) = −0.205 + 0.004t for 100 ≤ t ≤ 300. Data is generated as specified, however, the estimation procedure focuses on estimates of F(t) for 0 ≤ t ≤ 100.

• Experiment 3: F₁(t) = {1−exp(−t/4)}/{1−exp(−2.5)} for 0 ≤ t ≤ 10 and F₂(t) = {1 − exp(−t/2)}/{1 − exp(−2.5)} for 0 ≤ t ≤ 5.

The second experiment is designed to mimic the Parkinson’s disease data in Section 5. In all experiments, we set the random mixture proportion q_i = (λ_i, 1 − λ_i) to be one of m = 4 vector values: (1, 0)^T, (0.6, 0.4)^T, (0.2, 0.8)^T and (0.16, 0.84)^T. The four vector values had an equally likely chance of being selected. Our sample size was 500 and we generated a uniform censoring distribution to achieve 0%, 20%, and 40% censoring rates.

The primary goal of the simulation studies is to compare the bias, efficiency and power of detecting distribution differences. Bias and efficiency were evaluated at different t values. First, we evaluated the pointwise bias, F̂(t) − F₀(t), at different t values, where F₀(t) denotes the truth. Specifically, we ran 500 Monte Carlo simulations and evaluated the pointwise bias at t = 1.3 in Experiment 1 (Table 1); at t = 85 in Experiment 2 (Table 1); and at t = 2 in Experiment 3 (Supplementary Material, Table ??).

Table 1.

Results for Experiment 1 at t = 1.3 and Experiment 2 at t = 85: bias, empirical standard deviation (emp sd), average estimated standard deviation (est sd), and 95% coverage (95% cov) of estimators at different censoring rates. Results based on 500 simulations with sample size n = 500.

		Experiment 1
		F1 (t) = 0.7275				F2 (t) = 0.3822
Estimator	bias	emp sd	est sd	95% cov	bias	emp sd	est sd	95% cov
	Censoring rate = 0%
EM-PAVA	0.0002	0.0471	0.0440	0.9420	−0.0015	0.0438	0.0419	0.9480
Oracle EFFAIPW	0.0004	0.0461	0.0440	0.9520	−0.0014	0.0435	0.0419	0.9480
type I NPMLE	−0.0159	0.1048	0.0579	0.9120	−0.0029	0.0804	0.0627	0.9160
type II NPMLE	−0.0674	0.0588	0.0329	0.5040	0.0824	0.0473	0.0288	0.2980
	Censoring rate = 20%
EM-PAVA	0.0023	0.0491	0.0456	0.9360	−0.0024	0.0445	0.0430	0.9520
Oracle EFFAIPW	0.0019	0.0488	0.0454	0.9420	0.0011	0.0447	0.0432	0.9440
type I NPMLE	−0.0089	0.0921	0.0588	0.9260	−0.0041	0.0835	0.0644	0.9180
type II NPMLE	−0.0846	0.0849	0.0440	0.5720	0.0920	0.0720	0.0393	0.3900
	Censoring rate = 40%
EM-PAVA	0.0022	0.0526	0.0486	0.9420	−0.0025	0.0464	0.0456	0.9500
Oracle EFFAIPW	0.0057	0.0562	0.0486	0.9220	−0.0017	0.0508	0.0460	0.9360
type I NPMLE	−0.0103	0.0981	0.0614	0.9160	−0.0061	0.0868	0.0674	0.9120
type II NPMLE	−0.0954	0.0952	0.0453	0.5580	0.1008	0.0854	0.0395	0.3800
		Experiment 2
		F1 (t) = 0.5848				F2 (t) = 0.1462
Estimator	bias	emp sd	est sd	95% cov	bias	emp sd	est sd	95% cov
	Censoring rate = 0%
EM-PAVA	−0.0009	0.0482	0.0470	0.9540	−0.0037	0.0398	0.0357	0.9280
Oracle EFFAIPW	−0.0015	0.0480	0.0472	0.9600	−0.0036	0.0403	0.0368	0.9480
type I NPMLE	−0.0133	0.0890	0.0597	0.9500	−0.0034	0.0659	0.0521	0.8980
type II NPMLE	−0.0872	0.0697	0.0349	0.4520	0.1035	0.0532	0.0248	0.0520
	Censoring rate = 20%
EM-PAVA	0.0002	0.0548	0.0493	0.9300	−0.0013	0.0391	0.0381	0.9540
Oracle EFFAIPW	0.0006	0.0548	0.0498	0.9340	−0.0015	0.0396	0.0389	0.9640
type I NPMLE	−0.0078	0.0908	0.0623	0.9160	−0.0030	0.0682	0.0544	0.8860
type II NPMLE	−0.0959	0.0792	0.0437	0.4800	0.1086	0.0695	0.0353	0.1160
	Censoring rate = 40%
EM-PAVA	−0.0016	0.0557	0.0525	0.9320	−0.0002	0.0425	0.0401	0.9500
Oracle EFFAIPW	0.0009	0.0578	0.0525	0.9380	−0.0008	0.0434	0.0410	0.9560
type I NPMLE	−0.0111	0.0977	0.0650	0.9100	−0.0043	0.0711	0.0560	0.8760
type II NPMLE	−0.1048	0.0857	0.0454	0.4740	0.1153	0.0846	0.0361	0.1380

Second, we evaluated the estimators over the entire range of t values based on results from 500 Monte Carlo simulations; see Tables 2 and ?? (Supplementary Material). In this case, we evaluated the estimators based on the integrated absolute bias (IAB), average pointwise variance, and average pointwise 95% coverage probabilities. The integrated absolute bias (IAB) is ${\int }_0^{\infty }|{\mathrm{F̄}}_k(t)-F_{k0}(t)|dt$, k = 1, 2, where F̄_k(t) is the average estimate over the 500 data sets, and F_k0 is the truth. In our simulation study, the integral in the IAB was computed using a Riemann sum evaluated at 50 evenly spaced time points across the entire range (i.e., over (0,10) in Experiments 1 and 3, and over (0,100) in Experiment 2). The IAB for F₂(t) in Experiment 3 was computed over (0,5) because it is only defined on this interval. The average pointwise variance and average pointwise 95% coverage probabilities were also computed over 50 time points evenly spaced across the entire range (i.e., over (0,10) in Experiments 1 and 3, and over (0,100) in Experiment 2). Specifically, for each of the 50 time points, we computed the pointwise variance and pointwise 95% coverage probabilities of the 500 data sets. Then, we reported the average of the 50 pointwise values.

Table 2.

Results for Experiment 1 and 2 across a range of time points: integrated absolute bias, average pointwise variance, and average 95% coverage probabilities of estimators at different censoring rates. Results based on 500 simulations with sample size n = 500.

	Censoring rate
	0%		20%		40%
Estimator	F1 (t)	F2 (t)	F1 (t)	F2 (t)	F1 (t)	F2 (t)
		Experiment 1
	Integrated absolute bias*
EM-PAVA	0.0085	0.0065	0.0190	0.0071	0.0327	0.0199
Oracle EFFAIPW	0.0040	0.0055	0.0248	0.0232	0.0967	0.0689
type I NPMLE	0.1409	0.0407	0.2276	0.1063	0.4726	0.5084
type II NPMLE	0.4290	0.2960	0.5656	0.3332	0.7127	0.3814
	Average pointwise variance*
EM-PAVA	0.0009	0.0005	0.0012	0.0006	0.0015	0.0014
Oracle EFFAIPW	0.0009	0.0005	0.0011	0.0007	0.0016	0.0015
type I NPMLE	0.0010	0.0013	0.0013	0.0017	0.0022	0.0038
type II NPMLE	0.0006	0.0003	0.0013	0.0004	0.0024	0.0009
	Average 95% coverage probabilities†
EM-PAVA	0.9512	0.9551	0.9530	0.9518	0.9513	0.9535
Oracle EFFAIPW	0.9498	0.9557	0.9535	0.9514	0.9519	0.9445
type I NPMLE	0.9471	0.9508	0.9378	0.9344	0.9130	0.8458
type II NPMLE	0.3756	0.5838	0.4234	0.5927	0.3890	0.6760
		Experiment 2
	Integrated absolute bias**
EM-PAVA	0.1372	0.0342	0.1140	0.0307	0.1049	0.0261
Oracle EFFAIPW	0.0966	0.0266	0.1282	0.0729	0.2704	0.1215
type I NPMLE	0.1097	0.0467	0.0770	0.0574	0.0791	0.0557
type II NPMLE	3.7021	2.4581	3.9157	2.4937	4.4027	2.5877
	Average pointwise variance**
EM-PAVA	0.0011	0.0003	0.0013	0.0003	0.0014	0.0003
Oracle EFFAIPW	0.0011	0.0003	0.0013	0.0003	0.0015	0.0003
type I NPMLE	0.0013	0.0007	0.0016	0.0007	0.0017	0.0008
type II NPMLE	0.0006	0.0001	0.0006	0.0001	0.0007	0.0002
	Average 95% coverage probabilities††
EM-PAVA	0.9564	0.9495	0.9538	0.9513	0.9552	0.9530
Oracle EFFAIPW	0.9547	0.9436	0.9518	0.9475	0.9507	0.9467
type I NPMLE	0.9556	0.9479	0.9506	0.9492	0.9505	0.9481
type II NPMLE	0.5738	0.4737	0.5781	0.4740	0.5504	0.4805

^*Computed over (0,10) for F₁ (t) and F₂ (t).

^†Computed over (0,4) for F₁(t) and over (0,9) for F₂(t).

^**Computed over (0,100) for F₁ (t) and F₂ (t).

^††Computed over (48,100) for F₁ (t) and F₂ (t).

Third, we evaluated the type I error rate and power in detecting differences between F₁(t) and F₂(t) over the entire range of t values. We investigated the type I error rate under H₀ : F₁(t) = F₂(t) based on 1000 simulations. In this case, we generated data so that F₂(t) was set to the form of F₁(t) in each experiment (see the description of Experiment 1, 2, 3). Everything else was left unchanged. The type I error rate was then computed using the permutation test in Section 3.3 using 1000 permutations. The power was computed based on 200 Monte Carlo simulations. That is, we tested for differences between F₁(t) and F₂(t) when F₁(t), F₂(t) were evaluated at 50 time points evenly spaced across the entire range: over (0,10) in Experiments 1 and 3, and over (0,100) in Experiment 2. To compute the empirical power under H₁ : F₁(t) ≠ F₂(t), we used the permutation test in Section 3.3 with 1000 permutations. Results are in Tables 3 and ?? (Supplementary Material).

Table 3.

Empirical rejection rates for Experiment 1 and 2. Test of F₁ (t) = F₂ (t) over the entire time range was performed using a permutation test with 1000 permutations. Results based on 1000 simulations (for test under H₀) and 200 simulations (for test under H₁), with sample size n = 500 and 40% censoring (under H₁).

	Nominal Levels
Estimator	0.01	0.05	0.10	0.20	0.01	0.05	0.10	0.20
			Experiment 1
	Under H0 : F1 (t) = F2 (t)				Under H1 : F1 (t) ≠ F2 (t)
EM-PAVA	0.0120	0.0560	0.0950	0.1920	0.9000	0.9800	0.9900	1.0000
Oracle EFFAIPW	0.0090	0.0500	0.0900	0.1820	0.6150	0.7950	0.8650	0.9350
type I NPMLE	0.0130	0.0550	0.1020	0.1970	0.6200	0.7650	0.8450	0.9000
type II NPMLE	0.0060	0.0490	0.1020	0.2020	0.4400	0.5150	0.5550	0.5900
			Experiment 2
	Under H0 : F1 (t) = F2 (t)				Under H1 : F1 (t) ≠ F2 (t)
EM-PAVA	0.0170	0.0551	0.1022	0.2094	0.9950	0.9950	0.9950	1.0000
Oracle EFFAIPW	0.0140	0.0600	0.1100	0.2050	0.9950	0.9950	0.9950	1.0000
type I NPMLE	0.0080	0.0550	0.1120	0.2100	0.9200	0.9400	0.9500	0.9600
type II NPMLE	0.0100	0.0550	0.1120	0.2150	0.7000	0.7300	0.7500	0.7700

4.2. Simulation Results

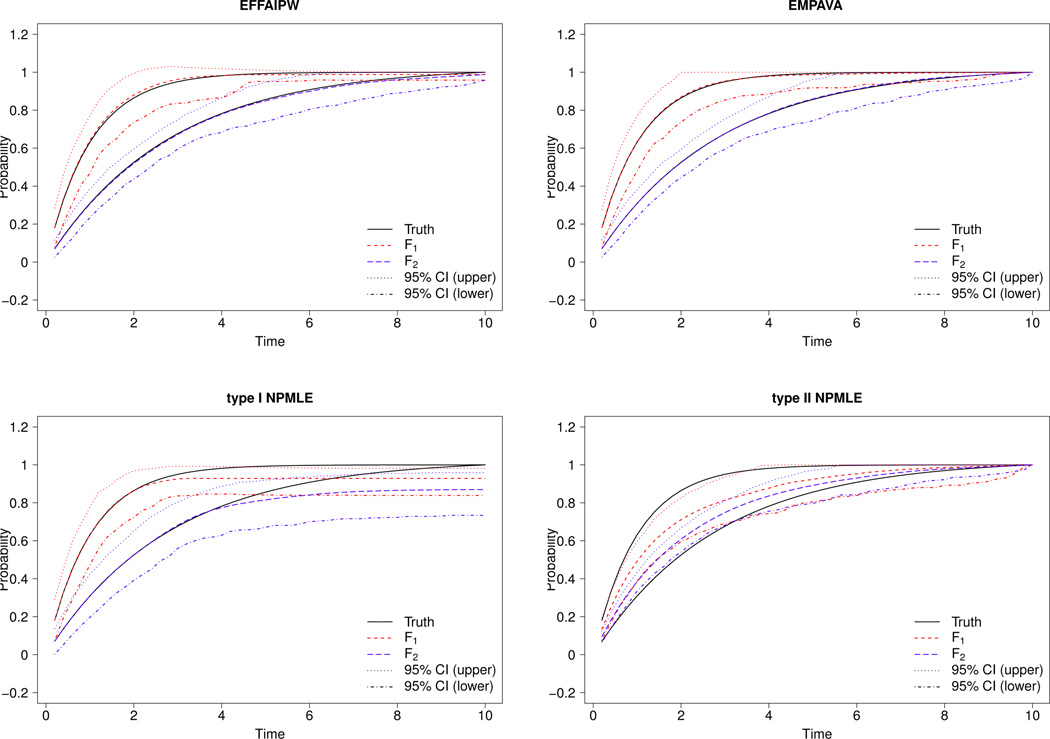
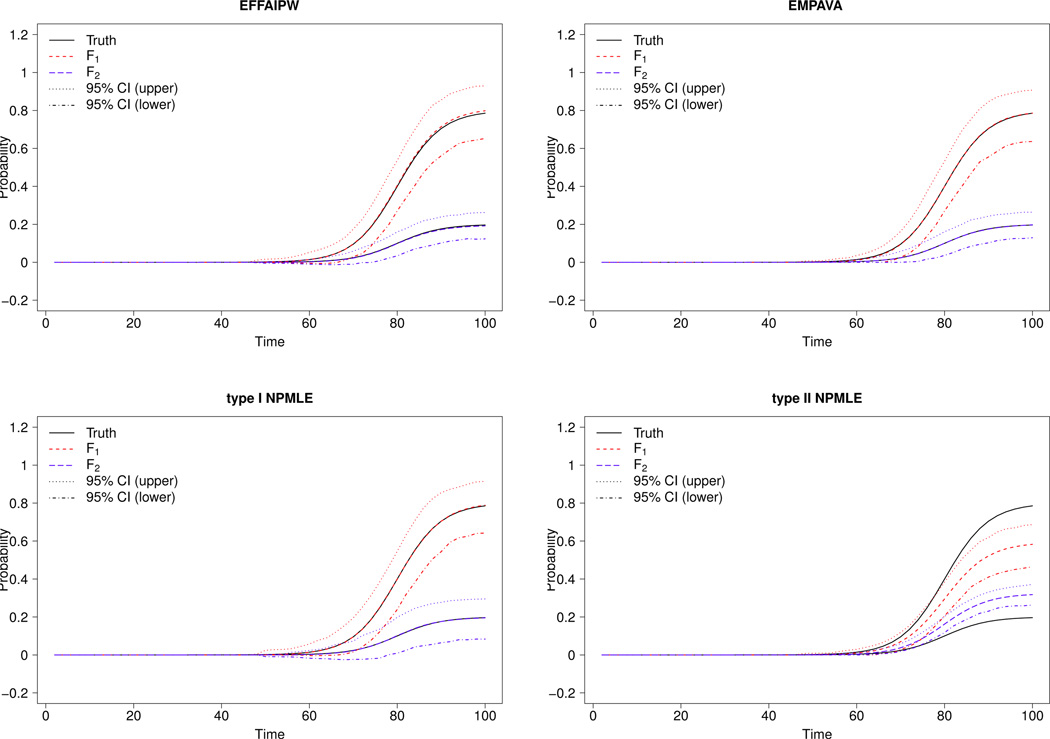
Among all four estimators considered, the type I NPMLE has the largest estimation variability and the type II has the largest estimation bias (see Tables 2 and ?? (Supplementary Material)). In all experiments, as the censoring rate increases from 0% to 40%, the inefficiency for the type I and the bias for the type II worsens. These poor performances alter the 95% coverage probabilities, especially for the type II NPMLE which has coverage probabilities well under the nominal level (see Table 2). The inconsistency of the type II NPMLE is most apparent in Experiments 1 and 2, where the estimated curve and 95% confidence band completely miss the true underlying distributions; see Figures 1 and 2. The type II NPMLE is also not consistent in Experiment 3, but to a lesser extent; see Figure ?? (Supplementary Material).

Fig 1.

Experiment 1. True cumulative distribution function and the mean of 500 simulations along with 95% confidence band (dotted) for the four proposed estimators. Sample size is 500, censoring rate is 40%.

Fig 2.

Experiment 2. True cumulative distribution function and the mean of 500 simulations along with 95% confidence band (dotted) for the four proposed estimators. Sample size is 500, censoring rate is 40%.

In contrast, across all experiments and censoring rates, the EM-PAVA estimator performs satisfactorily throughout the entire range of t (see Figures 1, 2 and ?? (Supplementary Material)). The EM-PAVA estimator is as efficient as the Oracle EFFAIPW, but with much smaller bias especially when censoring is present. The EM-PAVA also performs well in detecting small differences between F₁(t) and F₂(t). In Table 3, the type I error rates for all estimators adhere to their nominal levels. When F₁(t) and F₂(t) are largely different (i.e., Experiment 2), then both EM-PAVA and the Oracle EFFAIPW have similar power in detecting differences. However, when F₁(t) and F₂(t) are different but to a lesser degree (i.e., Experiment 1) then EM-PAVA has larger power in detecting the difference than all other estimators, including the Oracle EFFAIPW. The larger power of the EM-PAVA estimator is not too surprising considering that it estimates F(t) across a range of time points, unlike the point-wise estimation of the Oracle EFFAIPW.

A benefit of EM-PAVA over the Oracle EFFAIPW (and the two NPM-LEs) is that EM-PAVA yields a genuine distribution function (i.e., the estimator is monotone, non-negative and has values in the [0,1] range). The curves shown in Figures 1, 2 and ?? (Supplementary Material) for Oracle EFFAIPW are the result of doing a post-estimation procedure to yield monotonicity. The ingenuity of the Oracle EFFAIPW estimator, however, is evident from its 95% confidence band, which was constructed from the 2.5% and 97.5% pointwise quantiles of the 500 Monte Carlo data sets. Figure ?? (Supplementary Material) shows that the Oracle EFFAIPW estimator can have 95% confidence bands outside of the [0,1]; for large t in Figure ??, the upper confidence bound is larger than 1. In contrast, the EM-PAVA estimator is always guaranteed to be within [0,1], and thus its 95% confidence bands are always within this range.

5. Application to the CORE-PD study

5.1. CORE-PD data and mixture proportions

We applied our estimator to the CORE-PD study introduced in Section 1.1. Data from the CORE-PD study include information from first-degree relatives (i.e., parents, siblings, and children) of PARK2 probands. The probands had age-at-onset (AAO) of Parkinson’s disease (PD) less than or equal to 50 and did not carry mutations in other genes (i.e., neither LRRK2 mutations nor GBA mutations, Marder et al. (2010)). The key interest is estimating the cumulative risk of PD-onset for the first-degree relatives belonging to different populations:

1. PARK2 mutation carrier vs. non-carrier: We compared the estimated cumulative risk in first-degree relatives expected to carrying one or more copies of a mutation in the PARK2 gene (carriers) to relatives expected to carry no mutation (non-carrier).

2. PARK2 compound heterozygous (or homozygous) mutation carrier vs. heterozygous mutation carrier vs. non-carrier: We considered first-degree relatives who have the compound heterozygous genotype (two or more different copies of the mutation) or homozygous genotype (two or more copies of the same mutation). We compared distribution of risk in this population to two different populations: (a) relatives who are expected to have the heterozygous genotype (mutation on a single allele), and (b) relatives who are expected to be non-carriers (no mutation). These comparisons will bring insight into whether heterozygous PARK2 mutations alone increase the risk of PD, or if additional risk alleles play a role.

In the CORE-PD study, the ages-at-onset for the first-degree relatives are at least 90% censored. Information discerning to which population a relative belongs is available through different mixture proportions. The mixture proportions are vectors (p_i, 1 − p_i), where p_i is the probability of the ith first-degree relative carrying at least one copy of a mutation. This probability was computed based on the proband’s genotype, a relative’s relationship to a proband under Mendelian transmission assumption. For example, a child of a heterozygous carrier proband has a probability of 0.5 to inherit the mutated allele, and thus a probability of 0.5 to be a carrier. A child of a homozygous carrier proband has a probability of 1 to be a carrier. More details are given in Wang et al. (2007, 2008). Summary statistics for the populations and the mixture proportions are listed in Table 4.

Table 4.

Summary statistics for CORE-PD study. Total number of first-degree relatives (n), number of parents, siblings, and children, and percentage of first-degree relatives who have the specified mixture-proportion (p; 1 − p), where p is the probability of a relative carrying at least one copy of mutation.

					Mixture proportion (%)
	n	Parents	Siblings	Children	(1,0)	(0,1)	(0.5,0.5)
Carrier vs. Non-Carrier	355	63	182	110	31.5	64.8	3.7
Compound Heterozygous Carrier or Homozygous Carrier*	17	1	15	1	100.0	0	0
Heterozygous Carrier vs. Non-Carrier	338	62	167	109	28.1	68.1	3.8

^*Genotype for subjects in this group are known.

5.2. Results

We estimated the cumulative risk based on the EM-PAVA estimator and compared its results with the type I NPMLE. The Oracle EFFAIPW estimator could not be used because the high censoring led to unstable estimation: the inverse weights in the estimator were close to zero. Estimates for the PARK2 compound heterozygous (or homozygous) mutation carriers were based on a Kaplan-Meier estimator because these subjects were observed to carry two or more mutations and there is no uncertainty about the relatives’ genotype status (i.e., the data is not mixture data). We report the cumulative risk estimates along with 95% confidence intervals based on 100 Bootstrap replicates.

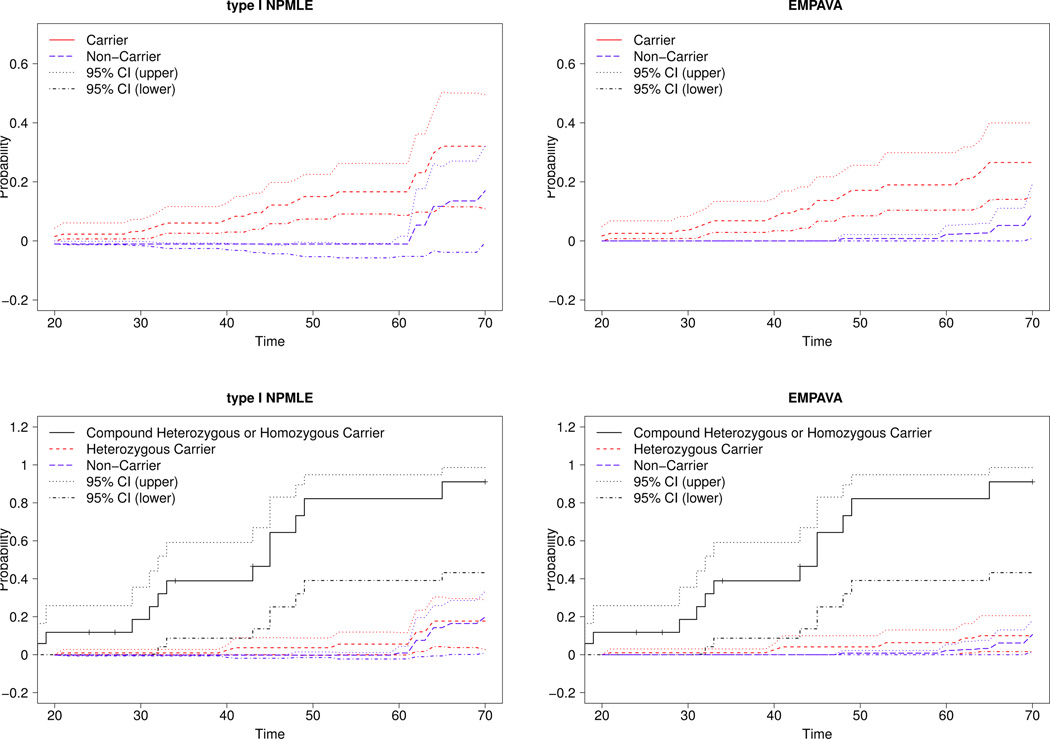
Figure 3 (top-right) shows that by age 50, PARK2 mutation carriers have a large increase in cumulative risk of PD onset compared to non-carriers. Based on EM-PAVA, the cumulative risk (see Table 5) of PD-onset for PARK2 mutation carriers at age 50 is 17.1% (95% CI: 8.5%, 25.6%) whereas the cumulative risk for non-carriers at age 50 is 0.8% (95% CI: 0%, 2.1%). This difference between PARK2 mutation carriers and non-carriers at age 50 was formally tested using the permutation test in Section 3.3. We found that carrying a PARK2 mutation significantly increases the cumulative risk by age 50 (p-value< 0.001, Table 7), suggesting that a mutation in the PARK2 gene substantially increases the chance of early onset PD. The difference is smaller yet still significant at age 70 (p-value=0.04, Table 7). Even across the age range (20,70), the cumulative risk for PARK2 mutation carriers was significantly different than the cumulative risk for non-carriers (p-value=0.010, see Table 7). These findings are consistent with other clinical and biological evidence that PARK2 mutations contribute to early age onset of PD (Hedrich et al., 2004; Lücking et al., 2000).

Fig 3.

CORE-PD study. Estimated cumulative distribution function for age-at-onset of Parkinson’s disease for Parkin mutation carrier vs. non-carrier (top), and Parkin compound heterozygous or homozygous carrier vs. Parkin heterozygous carrier and non-carrier (bottom).

Table 5.

Results for Parkin mutation carriers vs. non-carriers: estimated cumulative distribution function and 95% confidence intervals (in parentheses) based on type I NPMLE and EM-PAVA.

Age	type I NPMLE	EM-PAVA	type I NPMLE	EM-PAVA
	Carrier		Non-Carrier
20	0.015 (0.000, 0.043)	0.017 (0.000, 0.048)	−0.011 (−0.009, 0.000)	0.000 (0.000, 0.000)
25	0.023 (0.007, 0.061)	0.026 (0.008, 0.068)	−0.011 (−0.013, −0.001)	0.000 (0.000, 0.000)
30	0.032 (0.008, 0.073)	0.036 (0.009, 0.083)	−0.011 (−0.016, −0.002)	0.000 (0.000, 0.000)
35	0.061 (0.026, 0.116)	0.068 (0.029, 0.134)	−0.011 (−0.026, −0.007)	0.000 (0.000, 0.000)
40	0.072 (0.030, 0.128)	0.081 (0.034, 0.143)	−0.011 (−0.030, −0.008)	0.000 (0.000, 0.000)
45	0.121 (0.058, 0.198)	0.137 (0.067, 0.217)	−0.011 (−0.044, −0.015)	0.000 (0.000, 0.000)
50	0.150 (0.074, 0.225)	0.171 (0.085, 0.256)	−0.011 (−0.053, −0.005)	0.008 (0.000, 0.021)
55	0.166 (0.091, 0.263)	0.190 (0.104, 0.299)	−0.011 (−0.057, −0.008)	0.008 (0.000, 0.021)
60	0.166 (0.086, 0.262)	0.190 (0.105, 0.299)	−0.011 (−0.053, 0.016)	0.023 (0.000, 0.053)
65	0.321 (0.117, 0.505)	0.266 (0.138, 0.400)	0.117 (−0.039, 0.250)	0.027 (0.000, 0.060)
70	0.321 (0.109, 0.495)	0.266 (0.148, 0.400)	0.170 (−0.005, 0.323)	0.094 (0.009, 0.193)

Table 7.

P-values associated with testing H₀ : F₁ (t) = F₂ (t) at different t-values for CORE-PD study. H₀ was tested using the permutation test with 1000 permutations.

	type I NPMLE	EM-PAVA
	Carrier vs. Non-Carrier
t ∈ [20, 70]	0.013	0.010
t = 50	<0.001	<0.001
t = 70	0.073	0.04
	Het. Carrier vs Non-Carrier
t ∈ [20, 70]	0.790	0.594
t = 50	0.341	0.386
t = 70	0.813	0.969
	Compound Het./Hom. Carrier vs Het. Carrier
t ∈ [20, 70]	0.013	0.006
t = 50	<0.001	<0.001
t = 70	0.013	0.017
	Compound Het/Hom. Carrier vs Non-Carrier
t ∈ [20, 70]	0.011	0.007
t = 50	<0.001	<0.001
t = 70	0.013	0.017

To further distinguish the risk of PD among compound heterozygous or homozygous carriers (with at least two copies of mutations) from heterozygous carriers, we separately estimated the distribution functions in these two groups and compared them to the risk in the non-carrier group. The numerical results in Table 6 and a plot of the cumulative risk in Figure 3 (bottom panel) indicate a highly elevated risk in compound heterozygous or homozygous carriers combined. In contrast, the risk for heterozygous carriers closely resembles the risk in non-carriers. This result that being a heterozygous carrier has essentially similar risk to being a non-carrier was also observed in another study (Wang et al., 2008). Further investigation in a larger study is needed to examine whether risk differs in any subgroup. Using a permutation test, we also formally tested for differences between the distribution functions for each group. Results in Table 7 show that there is a significant difference between compound heterozygous carriers and heterozygous carriers as well as a significant difference between compound heterozygous and the non-carriers over the age range (20,70), and at particular ages 50 and 70. Furthermore, there is no significant difference between heterozygous carriers and non-carriers. These analyses suggest a recessive mode of inheritance for PARK2 gene mutations for early onset PD.

Table 6.

Results for Parkin compound heterozygous or homozygous carrier (Compound Carrier), Parkin heterozygous carrier and non-carrier: estimated cumulative distribution function and 95% confidence intervals (in parentheses).

Age	Kaplan-Meier*	type I NPMLE	EM-PAVA
	Compound Carrier	Heterozygous Carrier
20	0.118 (0.000, 0.258)	0.000 (0.000, 0.000)	0.000 (0.000, 0.000)
25	0.118 (0.000, 0.258)	0.009 (0.000, 0.027)	0.010 (0.000, 0.030)
30	0.186 (0.000, 0.355)	0.009 (0.000, 0.027)	0.010 (0.000, 0.030)
35	0.389 (0.087, 0.591)	0.009 (0.000, 0.027)	0.010 (0.000, 0.030)
40	0.389 (0.087, 0.591)	0.023 (0.000, 0.049)	0.026 (0.000, 0.056)
45	0.644 (0.252, 0.830)	0.037 (0.000, 0.089)	0.041 (0.000, 0.100)
50	0.822 (0.391, 0.948)	0.037 (−0.004, 0.088)	0.041 (0.000, 0.100)
55	0.822 (0.391, 0.948)	0.056 (0.000, 0.119)	0.063 (0.000, 0.130)
60	0.822 (0.391, 0.948)	0.056 (−0.001, 0.116)	0.064 (0.000, 0.131)
65	0.911 (0.432, 0.986)	0.177 (0.042, 0.304)	0.100 (0.016, 0.206)
70	0.911 (0.432, 0.986)	0.177 (0.027, 0.288)	0.100 (0.016, 0.206)
		Non-Carrier
20		−0.002 (0.000, 0.000)	0.000 (0.000, 0.000)
25		−0.002 (−0.007, 0.000)	0.000 (0.000, 0.000)
30		−0.002 (−0.007, 0.000)	0.000 (0.000, 0.000)
35		−0.002 (−0.007, 0.000)	0.000 (0.000, 0.000)
40		−0.002 (−0.014, 0.000)	0.000 (0.000, 0.000)
45		−0.002 (−0.018, 0.000)	0.000 (0.000, 0.000)
50		−0.002 (−0.015, 0.014)	0.008 (0.000, 0.022)
55		−0.002 (−0.023, 0.011)	0.008 (0.000, 0.022)
60		0.009 (−0.022, 0.044)	0.023 (0.000, 0.055)
65		0.142 (−0.006, 0.259)	0.032 (0.000, 0.076)
70		0.199 (0.009, 0.334)	0.106 (0.015, 0.181)

^*Genotype for subjects in this group are known. When there is no mixture, both methods reduce to Kaplan-Meier.

In comparison to the EM-PAVA, the type I NPMLE had wide and non-monotone confidence intervals, which altered the inference conclusions and is undesirable (see Table 7). Moreover, the type I NPMLE provided a higher cumulative risk in non-carriers by age 70 (17%) which appear to be higher than reported in other epidemiological studies (e.g., Wang et al. (2008)). The poor performance of the type I NPMLE can be due to instability and inefficiency of the type I especially at the right tail area. In contrast, EMPAVA always provided monotone distribution function estimates, as well as monotone and narrower confidence bands. The EM-PAVA also gave a lower cumulative risk in non-carriers by age 70 (9.4%) which better reflects the population based estimates. The increased risk in PARK2 carriers at earlier ages compared to population based estimates can also suggest that there are other genetic and environmental causes of PD in early onset cases that are different than late onset.

6. Concluding Remarks

In this work, we provide nonparametric estimation of age-specific cumulative risk for mutation carriers and non-carriers. This topic is an important issue in genetic counseling since clinicians and patients use risk estimates to guide their decisions on choices of preventive treatments and planning for the future. For example, individuals with a family history of Parkinson’s disease generally stated that if they were found to be a carrier and in their mid-thirties, they would most likely elect to not have children (McInerney-Leo et al., 2005). Or, in the instance they did choose to start a family, PARK2 mutation carriers were more inclined to undergo prenatal testing (McInerney-Leo et al., 2005).

It is well known that the NPMLE is the most robust and efficient method when there is no parametric assumption for the underlying distribution functions. Unfortunately, in the mixture model discussed in this paper, the NPMLE (type II) fails to produce consistent estimates. On the other hand, the maximum binomial likelihood method studied in this paper provides an alternative consistent estimation method. Moreover, to implement this method we have used the combination of an EM algorithm and PAVA, which leads to genuine distribution function estimates. For a non-mixture model, the proposed method coincides with the NPMLE. As a result, we expected the proposed method to have high efficiency which was apparent through the various simulation studies. Even though we only considered two-component mixture models, in principle the proposed method can be applied to more than two components mixture models without essential difficulty.

In some applications, it may be desirable to consider parametric or semi-parametric models (e.g., Cox proportional hazards model, proportional odds model) in a future work. However, diagnosing model misspecification has received little attention in the genetics literature. Our maximum binomial likelihood method can be used as a basis to construct numerical goodness-of-fit tests. In this case, we can test whether the distributions conform to a particular parametric or semiparametric model. That is, the interest is in testing H₀ : F₁(t) = F₁(t, β₁), F₂(t) = F₂(t, β₂) for some parametric models F₁(t, β₁) and F₂(t, β₂). To perform this test, we can use the Kolmogorov-Smirov goodness of fit

$$\mathrm{\Delta }=\sqrt{n}\underset{-\infty <t<\infty }{\text{max}}\{|{\mathrm{F̃}}_1(t)-F_1(t,{\mathit{\beta ̂}}_1)|+|{\mathrm{F̃}}_2(t)-F_2(t,{\mathrm{\beta ̂}}_2)|\}$$

where β̂₁, β̂₂ are the parametric maximum likelihood estimates of β₁ and β₂. Moreover if one is interested in estimating other quantities of the underlying distribution functions, for example the densities, one may use the kernel method to smooth the estimated distribution functions.

In our analysis of CORE-PD data, probands were not included due to concerns of potential ascertainment bias that may be difficult to adjust (Begg, 2002). In studies where a clear ascertainment scheme is implemented, adjustment can be made based on a retrospective likelihood. Lastly, the computational procedure of the proposed estimator is simple and efficient. An R function implementing the proposed method is available from the authors.

APPENDIX A

SKETCH OF TECHNICAL ARGUMENTS

A.1. The type I and type II NPMLEs

For the type I NPMLE, let $s_j(x_i)={\mathit{u}}_j^T\mathit{d}\mathit{F}(x_i)$ and $S_j(x_i)=1-{\mathit{u}}_j^T\mathit{F}(x_i)$, i = 1, …, n, j = 1, …, m. The type I NPMLE maximizes

$$\sum _{j=1}^m\sum _{i=1}^n\text{log}\left\{s_j{(x_i)}^{{\delta }_i}{S}_j{(x_i)}^{1-{\delta }_i}\right\}I({\mathit{q}}_i={\mathit{u}}_j)$$

with respect to s_j(x_i)’s and subject to ${\sum }_{i=1}^n{s}_j(x_i)I({\mathit{q}}_i={\mathit{u}}_j)\le 1,s_j(x_i)\ge 0$ for j = 1, …, m. Because this is equivalent to m separate maximization problems, each concerning s_j(·) and S_j(·) only, the maximizers are the classical Kaplan-Meier estimators:

$${Ŝ}_j(t)=\prod _{x_i\le t,{\mathit{q}}_i={\mathit{u}}_j}\{1-\frac{{\delta }_i}{{\sum }_{{\mathit{q}}_k={\mathit{u}}_j}I(x_k\ge x_i)}\},$$

with s_j(t) = S_j(t⁻) − S_j(t) for all t. With Ŝ (t) = {Ŝ₁(t), …, Ŝ_m(t)}^T, and U = (u₁, …, u_m)^T, the type I NPMLE is

$${\mathit{F̃}}_{\text{type}\mathrm{I}}(t)={({\mathit{U}}^T\mathit{U})}^{-1}{\mathit{U}}^T\{{\mathbf{1}}_m-\mathit{Ŝ}(t)\}.$$

Let the variance-covariance matrix of Ŝ (t) be Σ, which is a diagonal matrix because each of the m components of Ŝ (t) is estimated using a distinct subset of the observations. Then, F̃_w(t) = (U^TΣ⁻¹U)⁻¹U^TΣ⁻¹{1_m − Ŝ (t)} is a weighted version of the type I NPMLE and is more efficient than the type I NPMLE.

The type II NPMLE has no closed form solution, and an EM algorithm is typically employed. Specifically, for k = 1, 2, we form at the bth step in the EM algorithm:

$$c_{ik}^{(b)}={\delta }_i\frac{q_{ik}d{F}_k^{(b)}(x_i)}{{\sum }_{k=1}^2{q}_{ik}d{F}_k^{(b)}(x_i)}+(1-{\delta }_i)\frac{q_{ik}\{1-F_k^{(b)}(x_i)\}}{{\sum }_{k=1}^2{q}_{ik}\{1-F_k^{(b)}(x_i)\}},$$

and update the type II NPMLE estimate as

$$1-{\mathrm{F̌}}_{\text{type}\mathrm{I}\mathrm{I},k}^{(b+1)}(t)=\prod _{x_i\le t,{\delta }_i=1}\{1-\frac{{\sum }_{j=1}^{n}I(x_j=x_i,{\delta }_j=1)c_{jk}^{(b)}}{{\sum }_{j=1}^n{c}_{jk}^{(b)}I(x_j\ge x_i)}\}=\prod _{x_i\le t,{\delta }_i=1}\{1-\frac{c_{ik}^{(b)}}{{\sum }_{j=1}^n{c}_{jk}^{(b)}I(x_j\ge x_i)}\}.$$

The procedure is iterated until convergence.

A.2. Consistency of Imputed Log-Likelihood

We first demonstrate consistency for the non-censored data case. When F takes discrete finite many values, the result holds true trivially. If F is a continuous distribution function, then for non-censored data, the binomial log-likelihood is

$$\ell =\sum _{j=1}^h\sum _{i=1}^{n}I(s_i\le t_j)\text{log}[{\lambda }_i{F}_1(t_j)+(1-{\lambda }_i)F_2(t_j)]+I(s_i>t_j)\text{log}[{\lambda }_i{\mathrm{F̄}}_1(t_j)+(1-{\lambda }_i){\mathrm{F̄}}_2(t_j)].$$

This can be written as

$$n^{-2}\ell =\int \int I(s\le t)\text{log}[\lambda F_1(t)+(1-\lambda )F_2(t)]+I(s>t)\text{log}[\lambda {\mathrm{F̄}}_1(t)+(1-\lambda ){\mathrm{F̄}}_2(t)]d{\eta }_n(s,\lambda )d{\xi }_n(t)$$

where

$${\eta }_n(s,\lambda )=n^{-1}\sum _{i=1}^{n}I(s_i\le s,{\lambda }_i\le \lambda ),{\xi }_h(t)=h^{-1}\sum _{i=1}^{h}I(t_i\le t).$$

By the Law of Large Numbers, it can be shown that

$$n^{-2}\ell =\int \{\lambda F_{10}(t)+(1-\lambda )F_{20}(t)\}\text{log}\{\lambda F_1(t)+(1-\lambda )F_2(t)\}d{\eta }_0(\lambda )d{\xi }_0(t)+\{\lambda {\mathrm{F̄}}_{10}(t)+(1-\lambda ){\mathrm{F̄}}_{20}(t)\}\text{log}\{\lambda {\mathrm{F̄}}_1(t)+(1-\lambda ){\mathrm{F̄}}_2(t)\}d{\eta }_0(\lambda )d{\xi }_0(t)≕\mathrm{\Delta }$$

where η₀(λ) is the marginal distribution of λ and

$${\xi }_0(t)=\int \{\lambda F_{10}(t)+(1-\lambda )F_{20}(t)\}d{\eta }_0(\lambda ).$$

Here, the subscript ₀ denotes the truth. By the Kullback-Leibler information inequality, the above limiting value achieves the maximum if and only if F₁ = F₁₀ and F₂ = F₂₀. Therefore, the maximum binomial likelihood estimation is consistent.

For the censored data case, consistency also holds following a similar argument. The only difference in the log-likelihood is that the indicator function I(S_i ≤ t_j) is replaced by w_ij = E{I(S_i ≥ t_j)|S_i ≥ x_j}. If ŵ_i(t_j) is replaced by an initial consistency estimation, then the log censored binomial likelihood will converge to Δ again.