Biophysics of protein-DNA interactions and chromosome organization

Abstract

The function of DNA in cells depends on its interactions with protein molecules, which recognize and act on base sequence patterns along the double helix. These notes aim to introduce basic polymer physics of DNA molecules, biophysics of protein-DNA interactions and their study in single-DNA experiments, and some aspects of large-scale chromosome structure. Mechanisms for control of chromosome topology will also be discussed.

1. Introduction

DNA molecules in cells are found in double helix form, consisting of two long polymer chains wrapped around one another, with complementary chemical structures. The double helix encodes genetic information through the sequence of chemical groups - the “bases” adenine, thymine, guanine and cytosine (A,T,G and C). Corresponding bases on the two chains in a double helix bind one another according to the complementary base-pairing rules A=T and G≡C. These rules follow from the chemical structures of the bases, which permit two hydrogen bonds to form between A and T (indicated by =), versus three that form between G and C (indicated by ≡). Each base pair has a chemical weight of about 600 Daltons (Da).

The presence of the two complementary copies along the two polynucleotide chains in the double helix provides redundant storage of genetic information and also facilitates DNA replication, via the use of each chain as a template for assembly of a new complementary polynucleotide chain.

1.1. Basic physical properties of the DNA double helix

The structure of DNA gives rise to a number of interesting physical properties.

Stiffness

The DNA double helix is a moderately stiff semiflexible polymer, with a persistence length of about 50 nm (containing 150 base pairs or bp; there are approximately 0.34 nm per base pair along the double helix). The thickness of the double helix is about 2 nm, so a persistence length of double helix DNA is long and thin.

Length

Double-helix DNAs in vivo are generally very long polymers: the chromosome of the λ bacteriophage (a virus that infects E. coli bacteria) is 48502 bp or about 16 microns in length; the E. coli bacterial chromosome is 4.6×10⁶ bp (4.6 Mb) or about 1.5 mm long; small E. coli “plasmid” DNA molecules used in genetic engineering are typically 2 kb to 10 kb (0.7 to 3 microns) in length; and the larger chromosomal DNAs in human cell nuclei are roughly 200 Mb or a few cm in length.

Electrical charge

The environment in the cell is essentially aqueous solution, in which DNA molecules are ionized, so as to carry essentially one electron charge per base (2 e⁻/bp≈ 6e⁻/nm, each negative charge coming from an ionized phosphate on the DNA backbone, see Fig. 1(a)). The high electric charge density along the double helix makes it a strong polyelectrolyte, and gives it strong electrostatic interactions with other electrically charged molecules. Notably, in cells, the univalent salt concentration is 100 to 200 mM, making the Debye length shorter than 1 nm λ_D ≈ 0.3 nm/ √M where M is the concentration of 1:1 salt in mol/litre=M): thus electrostatic interactions with DNA, while strong, are essentially short-ranged. Electrostatic repulsions give rise to an effective hard-core diameter of dsDNA of ≈ 3.5 nm under physiological salt conditions [1].

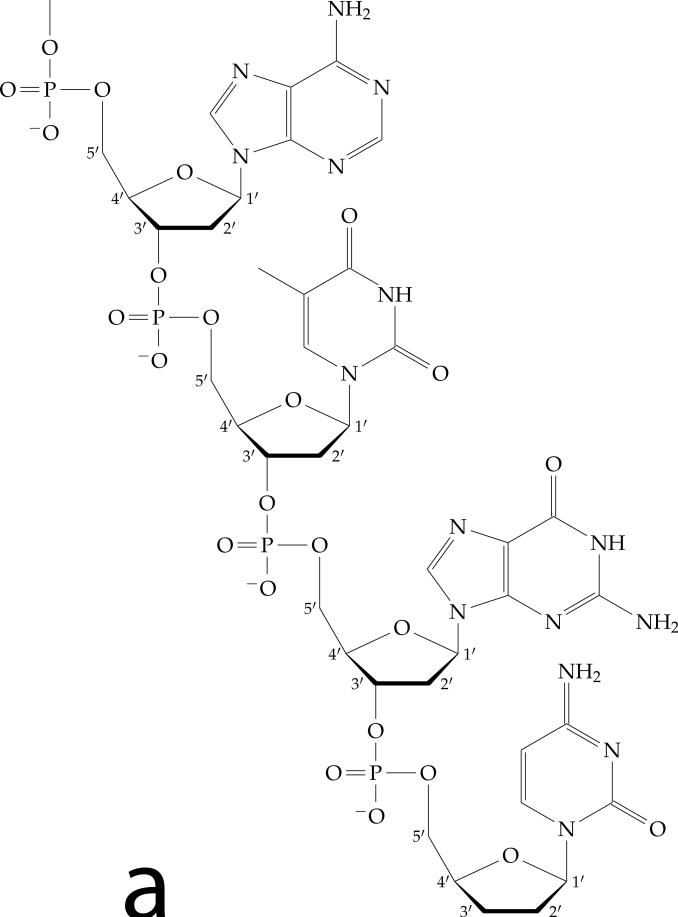
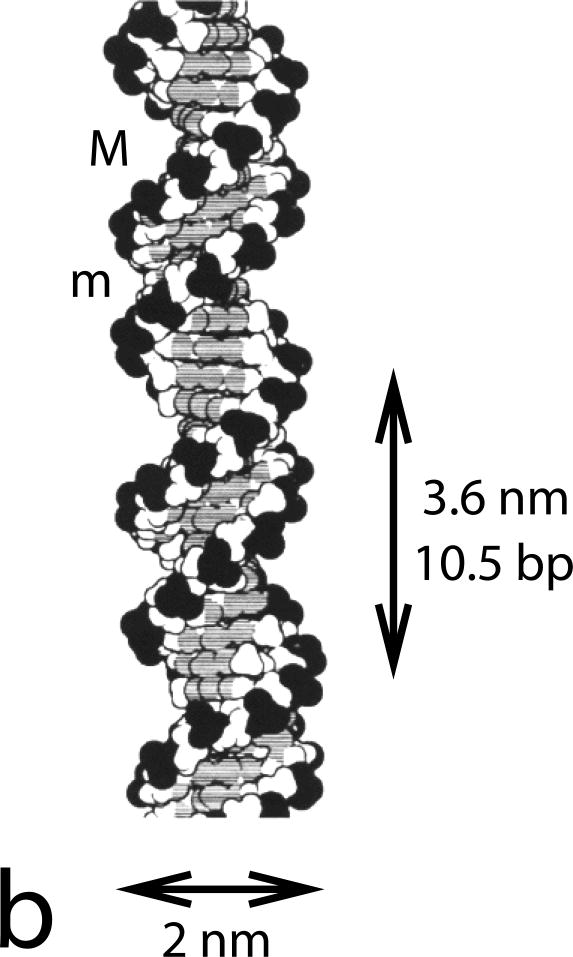
Figure 1.

DNA double helix structure.

(a) Chemical structure of one DNA chain, showing the deoxyribose sugars (note numbered carbons) and charged phosphates along the backbone, and the attached bases (A, T, G and C following the 5′ to 3′ direction from top to bottom).

(b) Space-filling diagram of the double helix. Two complementary-sequence strands as in (a) noncovalently bind together via base-pairing and stacking interactions, and coil around one another to form a regular helix. The two strands can be seen to have directed chemical structures, and are oppositely directed. Note the different sizes of the major (M) and minor (m) grooves, and the negatively charged phosphates along the backbones (dark groups). The helix repeat is 3.6 nm, and the DNA cross-sectional diameter is 2 nm. Image reproduced from Ref. [2].

Helical structure

The DNA double helix is really two polymers wrapped around one another, with one right-handed turn every ≈ 10.5 bp, or about 0.6 radian/bp (Fig. 1(b)). This, combined with the moderate strength of the base-pairing interactions holding the two strands together (about 2.5 k_BT per base pair when averaged over base-pair sequence) gives rise to the possibility of stress-driven structural defects (“bubbles” of locally base-unpaired single-strands) or transitions (stress-driven strand-separation). In addition, the two-strand structure implies the possibility of trapping a fixed linking number of the two strands when a DNA is closed into a loop. Constraint of strand linking number - a topological property of DNA - gives rise to a rich array of phenomena.

1.2. Proteins and DNA

DNA molecules by themselves are already quite interesting objects for biophysical study. However, the functions of DNA in vivo cannot be realized without the action of a huge number of protein molecules. Proteins are the workhorse molecules of the cell, and are themselves polymers of amino acids, folded into specific shapes by the action of relatively complex amino-acid-amino-acid interactions. Most proteins are in the range of 100 to 1000 amino acids in length (since amino acids are ≈ 100 Da on average, this corresponds to masses from 10⁴ to 10⁵ Da), and since each amino acid is about a cubic nanometer in volume, folded proteins are from a few to a few tens of nm in size.

DNAs in cells are covered with proteins, some of which interact rather specifically with short (< 20 bp) specific base-pair sequences, and some of which are less discriminating, interacting with DNA of essentially any sequence. Proteins that bind DNA tend to have positively charged patches on them to allow them to stick to the double helix (many DNA-binding proteins have a net positive charge in solution). Many proteins that bind DNA have hydrophobic amino acids which insert between bases, or hydrogen-bonding groups which link to corresponding hydrogen-bonding groups on the bases.

The functions of proteins which bind the double helix in cells are highly varied (Fig. 2). Some proteins bend the double helix so as to help it to be folded up to fit inside the cell (e.g., HU and Fis from E. coli, and histones from human and other eukaryote cells). Other proteins serve to mark specific sequences, providing platforms for more complicated activities of yet other proteins (e.g., transcription factors which trigger the copying of DNA sequence to RNA sequence, the primary step in the reading of a gene). Still other proteins catalyze cutting and resealing of the DNA backbone, allowing cut-and-paste and topological changes of DNA molecules to occur. More complex “protein machines” burn chemical fuels (including ATP, NTP, dNTP) to replicate, transcribe, and repair the double helix. Proteins thus give DNA its functions - its personality - in cells, turning a DNA molecule from just naked DNA, into a chromosome.

Figure 2.

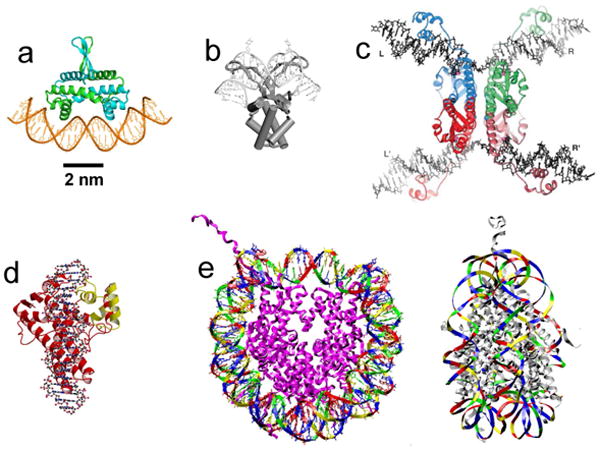
Structural models of protein-DNA complexes based on x-ray crystallography studies, all shown at approximately the same scale.

(a) Fis, a DNA-bending protein from E. coli; the two polypeptide chains are shown in green and blue. Image courtesy of R.C. Johnson.

(b) HU, another DNA-bending protein from E. coli. Image reproduced from data of Ref. [3].

(c) Four resolvase proteins bound to two DNA segments. The proteins mediate cut-and-paste site-specific recombination between the halves of the DNA segments. Exchange of the cut DNAs is thought to occur by rotation of the flat protein-protein interface in the middle of the structure. Image reproduced from Ref. [4].

(d) Topoisomerase V, an archaeal enzyme that cuts one strand of DNA, allowing internal linking number of the double helix to change. Image reproduced from Ref. [5].

(e) Eukaryote nucleosome. The roughly 10-nm-diameter particle contains 147 bp of DNA are wrapped around eight histone proteins (purple chains). Top view is shown on the left, side view is shown on the right. Image reproduced from data of Ref. [6].

Many enzymes (proteins which perform catalytic functions) are used as tools to alter DNA structure in the test tube (“in vitro”): these include restriction enzymes which cut DNA at specific base-pair sequences; DNA ligases which reseal broken covalent backbones along DNA molecules; topoisomerases which change DNA topology. Combined with DNA base-pairing, which allows “hybridization” of different DNA molecules with complementary overhangs, these enzyme tools allow one to cut and paste different DNA segments together. Reinsertion of synthetic DNA segments into cells is the basis of genetic engineering. The same general methods allow DNA molecules to be end-attached to surfaces and particles in a selective, controlled manner, or to be assembled into human-designed nanoscale assemblies.

DNA-binding proteins generally distort and restructure the double helix (Fig. 2), making the mechanics of DNA important in thinking about its functions. The corollary is that DNA mechanics can be used to analyze protein-DNA interactions. This has been widely exploited in the past 15 years, via use of single-molecule DNA pulling and twisting experiments to study proteins acting along DNA. These notes are meant to provide some basic background in DNA statistical mechanics, some discussion of models useful for thinking about protein-DNA interactions from the point of view of single-DNA micromechanics experiments, and some description of biophysical problems associated with entire chromosomes.

1.3. Physical scales relevant to protein-DNA interactions

Length

The basic length scale relevant to molecular biology is the nanometer (nm= 10⁻⁹ m). DNA bases, amino acids, simple sugars, energy-transferring molecules such as ATP, and many of the other basic molecular units used by living things are all roughly 1 nm in size. Therefore, the nm is the scale of modularity of chemical structure, and also the scale of information granularity. It is good to keep in mind that the length of a small bacterial cell or a small fraction of a eukaryote cell is ≈ 10⁻⁶ m or μm, 1000 nm in length.

Concentration

Another scale to remember is the concentration of one molecule per cubic micron, which is 10¹⁵ molecules per litre, or about 1.6 × 10⁻⁹ mol/litre= 1.6 nM (the number of molecules in a mol is N_A ≈ 6 × 10²³). This is very roughly the concentration of a transcription factor protein one might find in a bacterial or eukaryote cell.

Energy

There are two main energy scales of interest to us. First, there is the thermal energy per degree of freedom, k_BT ≈ 4 × 10⁻²¹ J at room temperature (T = 300 K; for biological systems, T is never too far from this so we will regard k_BT as essentially fixed). The binding energies of the noncovalent bonds that hold biological molecules in their folded conformations (folded proteins, double helix structure of DNA) are naturally measured in k_BT units, e.g., base-pair binding energies along the DNA double helix range from ≈ 1 to 4k_BT per base pair under normal physiological solution conditions.

The second energy scale of relevance here is that of a covalent chemical bond, which is much larger, comparable to 1 eV ≈ 40k_BT. This level of energy stabilizes the polymer backbones of protein and nucleic acid chains, and allows biological molecules to have their secondary (folded) structure changed, without breaking their primary (backbone) structure.

Force

The force scale most relevant to molecular biology is k_BT/nm≈ 4 × 10⁻¹² N= 4 piconewtons (pN). The pN force scale appears as the characteristic force scale asssociated with biomolecule conformational change, since it corresponds to the breaking of noncovalent bonds of a few k_BT binding energy, by stretching them a fraction of a nm.

The few pN force scale should be contrasted with the much larger force scale of ≈eV/Å≈ 10⁻⁹ N= 1 nN, the characteristic force one might expect to break a covalent bond [7].

We can quickly estimate the force scale to tear a protein off a DNA molecule (or to tear apart a dimeric protein complex). To do this one can expect to have to do a few k_BT of work over a reaction distance of a nm or so (the size of the binding site), indicating a rupture force of ≈ 10 pN in accord with experimental data, e.g., Ref. [8].

A lower force scale is associated with the force needed to prevent the initial looping of DNA by a protein that binds two sites ℓ apart. In this case, the work done against the applied force f is ≈ fℓ [9]. If looping is to occur by thermal fluctuation against that force, we can expect a strong suppression of the rate of loop formation relative to the zero-force case when fℓ > 10k_BT, or for f > 10k_BT/ℓ (for more detailed calculations including effects of DNA bending see Refs. [10, 11, 12]; note that DNA bending elastic energy controls loop formation rate at zero tension and is an additional free energy cost of loop formation, adding to the force-extension free energy).

For example, for ℓ = 100 nm (300 bp, a rather typical distance for loop formation by site-specific DNA-looping proteins as occurs during gene regulation) we have strong suppression of loop formation when f > 0.1k_BT/nm≈ 0.4 pN. In this situation we expect the loop formation rate to be suppressed relative to the zero-force case by a factor ≈ e⁻¹⁰ < 10⁻⁴. Strong suppression of DNA looping by roughly piconewton forces has been observed [13, 14, 15].

A larger force is associated with the “stalling” of a molecular machine which burns ATP or similar energy-rich molecules, which transfer 10 k_BT into mechanical energy per step of nm dimensions. This stall force scale is roughly ≈ 10k_BT/nm ≈ 40 pN. This is comparable to the stall forces observed for RNA and DNA polymerases [16, 17].

Time

At molecular scales, all dynamics is driven by thermal motion, and is highly overdamped: we don't need to worry about inertia for nm or even μm sized objects. All the motion we will worry about is diffusive, controlled by diffusion constants of the form D = k_BT/(6πηR) where R is the scale size of the object in question (the formula is the Einstein diffusion constant for a sphere of radius R) and where η is the fluid viscosity (η ≈ 10⁻³ Pa·s for water, η ≈ 5 × 10⁻³ Pa·s for cytoplasm). This gives rise to a self-diffusion time τ ≈ 6πηR³/(k_BT) which is on the order of 10⁻⁹ s for R = 1 nm, and about 1 s for R = 1 μm. The very strong R dependence of this diffusive relaxation time makes it change from a molecular timescale for nm-sized small molecules, to human-observable timescales for μm-scale objects.

2. The DNA double helix is a stiff polymer

The starting point for thinking about double helix DNA conformation is the semiflexible polymer, which models the double helix as having bending stiffness [18]. If we consider the double helix to have a fixed length L (not a bad approximation to start with), then we can describe it with a space curve r(s) where s is contour distance along the polymer, running from s = 0 to s = L. The tangent vector is a unit vector, dr/ds = t̂(s); the local curvature is κ = |dt̂/ds|. The polymer conformation is controlled by bending energy:

$$\beta E_{\text{bend}}=\frac{A}{2}{\int }_0^{L}ds{\left(\frac{d\widehat{\mathbf{t}}}{ds}\right)}^2$$ (1)

which is zero for the straight configuration κ = 0 (β ≡ 1/[k_BT]). The bending stiffness is controlled by the constant A, which has dimensions of length, and is called the persistence length. The flexible polymer limit is obtained for L ≫ A; for L ≪ A, the polymer will be essentially unbent by thermal fluctuations. For double helix DNA, A ≈ 50 nm, or about 150 bp.

2.1. Statistical mechanics of the semiflexible polymer

Thermal fluctuations give rise to bending, and are described by the partition function

$$Z=\int \mathcal{D}\widehat{\mathbf{t}}(s)exp(-\beta E_{\text{bend}})$$ (2)

where the notation t̂ indicates a path integral over t̂(s). This “free” polymer model (no applied force or self-interactions) can be solved in closed form [19]. The correlation function for the tangent vector is 〈t̂(s) · t̂(s′)〉 = e^{−|s−s′|/A}. Since the end-to-end vector R can be expressed in terms of the tangent vector via $\mathbf{R}=\mathbf{r}(L)-\mathbf{r}(0)={\int }_0^{L}ds\widehat{\mathbf{t}}(s)$, the mean square end-to-end distance can be computed from the tangent vector correlation function. This approaches the limit, for L ≫ A, of 〈R²〉 = 〈[r(L) − r(0)]²〉 = 2AL, the scaling behavior for the coil size of a Gaussian polymer¹. The correspondence between A and the statistical segment length b for the random flight or Gaussian polymers (for which 〈R²〉 = Nb²) is b = 2A and N = L/(2A) = L/b.

2.1.1. Stretching the semiflexible polymer by weak forces (< k_BT/A)

In the absence of force, since 〈R²〉 = 〈x²〉 + 〈y²〉 + 〈z²〉 where x, y and z are the Cartesian components of the end-to-end vector R, we have 〈R²〉 = 3 〈x²〉. This zero-force fluctuation tells us the spring constant for linear response of a force applied to separate the ends, namely k = k_BT/〈x²〉 = 3k_BT/(2AL). This corresponds to the result for a Gaussian polymer, that the spring constant is inversely proportional to polymer length. The low-force response is f = kx + 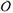(x³), with the linear response regime essentially holding for f < k_BT/A. For double helix DNA, this characteristic force is quite low since A = 50 nm; k_BT/A ≈ 0.1 pN (recall k_BT/(1 nm) ≈ 4 pN).

The linear low-force behavior is eventually replaced by the nonlinear scaling law for a self-avoiding polymer, for sufficiently large L [20]. However, for double-helix DNA, the narrow thickness (≈ 3.5 nm including electrostatic effects[1]) of the double helix compared to its effective segment length b = 2A ≈ 100 nm) leads to quite weak self-avoidance, and makes dsDNA elasticity quite close to that of an ideal polymer for DNA lengths (< 50 kb ≈ 16 μm) routinely studied experimentally [21].

2.1.2. Including external force in polymer models

For any polymer model, to go beyond linear force response, we need to include force in the energy function:

$$E=E_{\text{bend}}-\mathbf{f}·\mathbf{R}$$ (3)

Force is added as a field conjugate to the end-to-end vector, so that expectation values of end-to-end extension appear as force derivatives of the partition function Z, as expected for identification of k_BT ln Z as a free energy in the fluctuating-extension, constant-force ensemble (the ensemble relevant to magnetic tweezers experiments, which apply a constant force to a paramagnetic particle attached to one end of a DNA [22]).

There are a number of general consequences for this form of statistical weight. For nonzero force along the z direction, or f = fẑ, we have an average end-to-end extension 〈z〉 = ∂k_BT ln Z/(∂βf), and an extension fluctuation of 〈z²〉 − 〈z〉² = ∂² ln Z/∂(βf)². Components of R transverse to the force have zero average by symmetry (〈x〉 = 〈y〉 = 0), but their fluctuations are nonzero, and are computed as 〈x²〉 = ∂² ln Z/∂(βf_x)²|_{f = fẑ}.

An important feature of any model of the form of Eq. (3) where there is no preferred orientation other than that of the force f, is that the free energy only depends on the magnitude of force f, ln Z = ln Z(|f|). For nonzero force f along z, if we imagine applying small transverse forces f_x and f_z, we can expand $|\mathbf{f}|=\sqrt{f^2+f_x^2+f_y^2}=f+(f_x^2+f_y^2)/(2f)+\dots$, and expand the partition function as

$$lnZ(|\mathbf{f}|)=lnZ(f)+\frac{f_x^2+f_y^2}{2f}\frac{\partial lnZ(f)}{\partial f}+\dots$$ (4)

A simple relationship between “longitudinal” and “transverse” derivatives of ln Z follows:

$$\frac{{\partial }^{2}InZ}{\partial {(\beta f_x)}^2}=\frac{1}{\beta f}\frac{\partial lnZ}{\partial (\beta f)}$$ (5)

where both sides are evaluated for f_x = f_y = 0. This indicates that extension and transverse fluctuations are related: 〈x²〉 = 〈z〉/(βf). Therefore, if we measure thermally averaged transverse fluctuations and average extension we can infer the applied force:

$$f=\frac{k_{B}T\langle z\rangle }{\langle x^2\rangle }$$ (6)

This exact relationship holds for any polymer model with a roationally symmetric conformational energy (essentially any model without a preferred direction in space other than the applied force, notably including models with polymer self-interactions) and is a powerful tool used for force calibration in magnetic tweezers experiments. Notably this relation is model-independent and not limited to the case of small fluctuations [12].

2.1.3. High-force behavior of the semiflexible polymer

We return to the specific case of the semiflexible polymer. Expressing the end-to-end vector $\mathbf{R}={\int }_0^{L}ds\widehat{\mathbf{t}}(s)$ allows us to rewrite the energy as a local function of t̂(s), with force applied in the z direction (f = fẑ):

$$\beta E={\int }_0^{L}ds[\frac{A}{2}{\left(\frac{d\widehat{\mathbf{t}}}{ds}\right)}^2-\beta f\widehat{\mathbf{z}}·\widehat{\mathbf{t}}]$$ (7)

In terms of t̂(s), the energy is one-dimensional and local, which allows one to solve for the partition function using continuum transfer matrix (Schrodinger-like equation) methods [21].

The asymptotic high-force behavior is readily obtained using small-fluctuation analysis. We split the tangent vector into components longitudinal and transverse to applied force: t̂ = t_zẑ + u, with u in the xy plane. Since $|\widehat{\mathbf{t}}|=1=\sqrt{t_z^2+u^2}$, we have t_z = ẑ · t̂ = 1 − u² + ⋯. For large force, t̂ is aligned with ẑ, so u is small; to Gaussian order we have

$$\beta E=-\beta fL+\frac{1}{2}{\int }_0^{L}ds[A{\left(\frac{d\widehat{\mathbf{u}}}{ds}\right)}^2+\beta f{u}^2+\mathcal{O}(u^4)]$$ (8)

In terms of Fourier components $({\mathbf{u}}_q\equiv {\int }_0^{L}d{\mathit{\text{se}}}^{-iqs}\mathbf{u}(s)$, for q = 2πn/L, n = 0, ±1, ±2, ⋯) we have

$$\beta E=-\beta fL+\frac{1}{2L}\sum _q(A{q}^2+\beta f){|{\mathbf{u}}_q|}^2+\mathcal{O}(u^4)$$ (9)

Using the equipartition theorem,

$$\langle {|{\mathbf{u}}_q|}^2\rangle =\frac{2L}{A{q}^2+\beta f}$$ (10)

where the factor of 2 in the numerator reflects the two (x and y) components of u. The form of this wavenumber-space correlation function indicates that the real-space bending correlations decay exponentially, 〈u_i(s)u_j(s′)〉 ∞ δ_ije^{−|s−s′|/ξ}, with a high-force correlation length $\xi =\sqrt{k_{B}TA/f}$.

Fourier transforming² Eq. (10) gives the fluctuation of u,

$$\langle {|\mathbf{u}(s)|}^2\rangle =2{\int }_{-\infty }^{+\infty }\frac{dq}{2\pi }\frac{1}{A{q}^2+\beta f}=\frac{1}{\sqrt{\beta Af}}$$ (11)

This allows us to compute the average extension

$$\frac{\langle z\rangle }{L}=\langle \widehat{\mathbf{z}}·\widehat{\mathbf{t}}\rangle =1-\frac{1}{2}\langle u^2\rangle +\mathcal{O}(u^4)=1-\sqrt{\frac{k_{B}T}{4Af}}+\dots$$ (12)

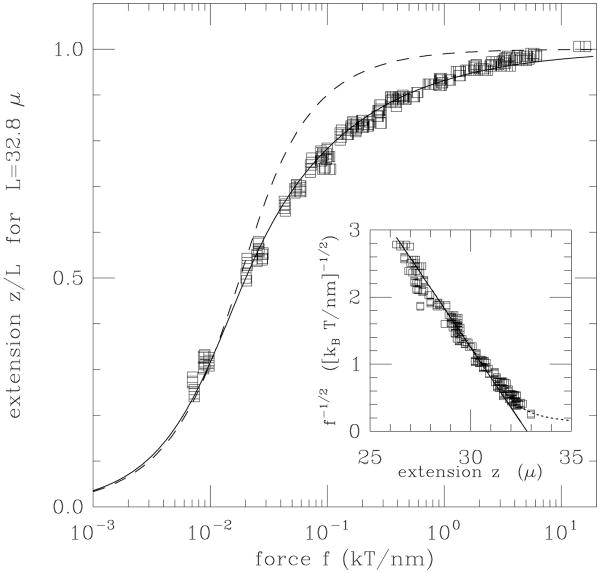
This characteristic reciprocal square-root dependence of extension on force for a semiflexible polymer in the regime f ≫ k_BT/A is observed in single-molecule experiments on double-helix DNA for forces from about 0.1 up to 10 pN (Fig. 3) [21].

Figure 3.

Force versus extension data for 97 kb dsDNA (L ≈ 33 μm) of Smith et al [24] compared to force-extension curve of semiflexible polymer (solid curve) and freely-jointed polymer (dashed curve). Inset is proportional to 1/√f and shows a linear dependence on extension as expected for the semiflexible polymer. Note that 1 k_BT/nm = 4.1 pN. Figure adapted from Ref. [21].

2.2. Denaturation of DNA by stress

From thermal DNA “melting” (strand separation) studies, we know that the cohesive free energy holding the two single-stranded DNAs (ssDNAs) into double helix form is about g = 2.5k_BT per base pair [23].³ For forces in the ≈ 10 pN range, we can expect deformation of the secondary structure of any biological molecule which is stabilized by weak non-covalent chemical bonds of binding energy ≈ k_BT. This has been experimentally observed for double-helix DNA in a few different ways.

Unzipping

If one imagines grabbing the two ssDNAs at one end of a double helix and then forcing them apart, one can imagine “unzipping” of the two strands to occur. This has been done in a number of laboratories, with the result that the resulting ssDNA liberates about ℓ = 1 nm per base pair “unzipped” (this length is shorter than twice the ≈ 1 nm length of the extended ssDNA length per base because of thermal fluctuations). Therefore the work done per base pair as the helix is unzipped should be ΔW ≈ fℓ. Since this work is done directly against the cohesive energy of the double helix, we could expect an unzipping force of f_unzip ≈ g/ℓ ≈ 2.5k_BT/nm≈ 10 pN. This is in fact the approximate force observed for DNA unzipping, which is observed to range from 8 to 15 pN depending on sequence (essentially AT/GC content) [25, 26, 27, 28, 29, 30]. The variations in unzipping force have been proposed to be used to analyze DNA sequence.

Overstretching

If a large force is applied to the two opposite ends of a long dsDNA, one might expect lengthening of the double helix. In this geometry, the length increase is bound to be less since it is in the direction of the double helix (rather than perpendicular to it as for DNA unzipping). In such experiments, the double helix length per base pair increases from 0.34 nm/bp to about 0.6 nm/bp; again using the DNA strand separation free energy as the free energy scale, we obtain an overstretching forces of f_overstretch ≈ 2.5k_BT/(0.2 nm) ≈ 50 pN. In fact such an “overstretching” transition is observed at a well-defined force ≈ 65 pN [31, 32, 33].

Unwinding

One might also imagine a torque acting to unwind the DNA double helix, which would liberate a wrapping angle of about 0.6 rad/bp unwound (2π radians per 10.5 bp). The torque required for this should be, following the same arguments as above, τ_unwind ≈ −2.5k_BT/(0.6 rad) ≈ −4k_BT ≈ −16 pN·nm (the sign reflects the left-handed nature of the unwinding torque. Unwinding actually occurs for torques ≈ −10 pN·nm [34, 35, 36, 29, 37, 38]. (a slightly lower torque than the above estimate occurs since left-handed wrapping is driven after denaturation by a left-handed torque).

Experimental observations and more detailed theoretical work has resulted in development of a force-torque “phase diagram” for the double helix, with a variety of different structural states [36, 38, 39].

3. DNA-protein interactions

In cells, proteins cover the DNA double helix, allowing it to be stored, read, repaired, and replicated. Different proteins have different functions on the double helix:

Architectural: Proteins that help to package DNA, bending and folding it, typically binding to 10 to 20 bp regions and often without a great deal of sequence dependence; examples include histones (eukaryotes) and HU, H-NS and Fis (E. coli);

Regulatory: Proteins that bind to specific DNA sequences from 4 to 20 bp in length, and which act as “landmarks” for starting transcription or other genetic processes; examples include TATA-binding protein (eukaryotes) and Lac repressor (E. coli);

Catalytic: Proteins which cut and paste DNA, accomplishing breaking and resealing of the covalent bonds along the DNA backbone, or inside the bases; examples include topoisomerases, DNA oxoguanine glycosylase (Ogg1, an enzyme that recognizes and repairs oxidative chemical damage to the base guanine);

DNA-sequence-processing: Proteins which burn NTPs or dNTPs and which move processively along the DNA backbone, reading, replicating, unwinding or otherwise performing functions while translocating along DNA; examples include RNA polymerases, DNA polymerase and DNA helicases.

3.1. Classical two-state kinetic/thermodynamic model of protein binding a DNA site

The starting point for thinking about protein-DNA interactions is binary chemical reaction kinetics (P + D ↔ C) where P is a particular protein, D is one of its binding sites, and C is the protein-DNA bound “complex”. Consider just one binding site in a sea of proteins at concentration c. Supposing diffusion-limited binding kinetics, we have to wait for a particular protein to “find” the binding site; the on-rate in this case is the result of Smoluchowski, r_on = 4πDac where D is the diffusion constant for the protein, and a is the “reaction radius”, the distance between reactants at which the reaction occurs, a scale comparable in size to the binding site. Since D ≈ k_BT/(6πηR), where R is the approximate size of the protein, we have r_on = k_onc, where the chemical forward rate constant for the reaction is k_on ≈ (a/R)k_BT/η. Since R > a we can take k_BT/η as a kind of “speed limit” for a binary reaction controlled by three-dimensional diffusion. For T = 300 K and η = 10⁻³ Pa·s (appropriate for water at room temperature),

$$k_{\text{on}}<\frac{k_{B}T}{\eta }=\frac{4\times {10}^{-21}\mathrm{J}}{{10}^{-3}\text{Pa}·\mathrm{s}}=4\times {10}^{-18}{\mathrm{m}}^3/\mathrm{s}\approx {10}^9{\mathrm{M}}^{-1}{\mathrm{s}}^{-1}$$ (13)

where the final units indicate a a rate per unit concentration (M = mol/litre; recall 1 M= 6 × 10²³/litre).

It turns out that this rate can be increased by roughly an order of magnitude if in addition to three-dimensional diffusion, there is also one-dimensional “search” over a restricted region of a long DNA polymer in which a specific binding site is embedded [40, 41]. However, the rate at which initial encounters of protein and DNA occur is still controlled by Eq. (13). There remain many interesting problems having to do with (small) proteins binding to a (long) DNA polymer, for example the dependence of multiple sequential interactions on polymer conformation [42].

Returning to the basic picture of proteins binding to one DNA binding site, once the complex is formed, one usually considers it to have a lifetime, described by a concentration-dependent rate k_off of dissociation of the protein from the DNA (units of k_off measured in s⁻¹).

Once our proteins come to equilibrium with the binding site, the probability that the site will be bound relative to being unbound will be

$$\frac{P_{\text{on}}}{P_{\text{off}}}=\frac{k_{\text{on}}c}{k_{\text{off}}}\equiv \frac{c}{K_d}$$ (14)

where the dissociation constant K_D ≡ k_off/k_on describes the strength of the binding. Since K_D is the concentration at which the site is 50% bound, the smaller K_D is, the tighter the binding.⁴ The site-occupation probability is the familiar Langmuir adsorption isotherm, P_on = c/(K_D + c).

The Boltzmann distribution gives the equilibrium free energy difference between the bound and unbound states,

$$G_{\text{on}}-G_{\text{off}}=-k_{B}Tln\frac{P_{\text{on}}}{P_{\text{off}}}=k_{B}T(ln{K}_d-lnc)$$ (15)

The bound state is reduced in free energy (becomes more probable) as solution concentration of protein is increased. Eq. (15) can be thought of as reflecting the free energy associated with interactions (G_int = k_BT ln K_D; smaller K_D gives a more negative “binding” free energy) in competition with the ideal gas entropy loss associated with localizing the protein to the DNA binding site (G_ent = −k_BT ln c; an ideal-gas entropy model is appropriate since the volume fraction of any particular DNA-binding protein species is usually very small in vivo or in test-tube experiments). This basic type of model is widely used to analyze protein-DNA interactions.

3.2. Salt-concentration-dependence of proteins binding to DNA

Although the two-state model described above is very useful, under many circumstances it is important to keep in mind even one protein binding a DNA is an interaction between macromolecules which are covered with adsorbed water molecules and ions. Even one binding interaction involves changing the positions of many molecules. In general proteins which bind to DNA make an array of non-covalent bonds to the double helix, and usually a number of those are electrostatic in character (say n ≈ 5 to 10); the highly negatively charged phosphates along the DNA backbone are often found in registry with positively charged chemical groups along a bound protein. However, when the protein is dissociated, those same positive (protein) and negative (DNA) interaction sites have associated with them essentially “condensed” counterions. Thus binding of one protein to DNA results in release of 2n counterions. The resulting free energy of the released counterions gives rise to a dependence of the “interaction energy” on solution univalent ion concentration:

$$G_{int}=k_{B}Tln{K}_D+2n{k}_{B}Tln(c_{\text{salt}}/c_0)$$ (16)

where K_D is the dissociation constant at salt concentration c₀. Since n is in the range of 5 to 10 for typical DNA-binding proteins, one can expect a strong dependence of binding free energy (affinity) on bulk salt concentration (lower salt: stronger binding; higher salt: weaker binding).

This behavior has been carefully studied for short basic polypeptides interacting with nucleic acid oligomers [43], but there is plenty of room for more studies of this type on “real” proteins interacting with DNA. There is a similar competition that can occur between a group of proteins binding small adjacent binding sites, and one large protein which binds all of their binding sites, a situation which arises in gene expression in eukaryotes [44].

3.3. Cooperativity

Biochemical cooperativity refers to the synergistic effect associated with two binding events which happen at once. The simplest example of this is the presence of a contact interaction between two proteins which bind adjacent binding sites along a DNA; if that contact interaction is favorable (lowering the net free energy), it is termed cooperative; if unfavorable, it is called anticooperative. If we imagine describing occupation of two adjacent binding sites using occupation variables n₁ and n₂ (n_i = 0 or 1 for empty or bound sites, respectively), then the general energy function describing the interactions of protein and DNA is

$$G_{int}=G_1{n}_1+G_2{n}_2+G_c{n}_1{n}_2$$ (17)

For the four possible states, we have three interaction parameters (the unbound state n₁ = n₂ = 0 is taken as a reference state of zero free energy). If G_c < 0, we have a model of cooperative binding.

The analogy of Eq. (17) with Ising interaction between two spins in a field is useful, and generalization of this type of model to a string of interacting proteins can be used to describe “polymerization” of proteins along DNA, driven by adjacent-protein interactions [45, 46]. A variety of proteins have been observed to be able to form filaments along DNA. A classic example is RecA, which forms a helical filament as it binds along DNA [47]. RecA polymerization along DNA is thought to play a role in its function in searching along DNAs for regions of similar sequence or homology; the RecA filament is thought to act as both a scaffold and as a machine to test for sequence similarity along two juxtaposed DNA strands.

3.4. Force effect on protein-DNA binding

If tension f is present in a DNA molecule during interaction with proteins, that tension can affect the binding. In general there will be some mechanical change in length of the DNA if the protein binds; suppose there is a length contraction ℓ (or lengthening if ℓ < 0) of the DNA molecule when binding occurs. As examples, imagine a protein which bends or loops DNA, cases for which ℓ > 0. Tension plausibly slows down k_on (since now one must get to a transition state by doing work against the applied tension) and plausibly speeds up k_off (the chemical bonds in the complex will be destabilized by any applied tension). By Eq. (14), in equilibrium, the ratio of these rates and therefore the binding/unbinding probability ratio reflect the presence of the additional mechanical work fℓ [9]:

$$\frac{P_{\text{on}}}{P_{\text{off}}}=\frac{c}{K_D}{e}^{-\beta f\ell }$$ (18)

where β = (k_BT)⁻¹, and where K_D indicates the dissociation constant at zero force. Eq. (18) suggests that we identify a force-dependent dissociation constant, K_D(f) = K_D(0) exp(βfℓ) and for ℓ > 0 we see that applied force increases the K_D strongly, since tension is destabilizing the bound complex.

This effect becomes dramatic for DNA looping. Note that even in the absence of force, the stiffness of the double helix essentially constrains thermally-formed loops to be longer than ≈ 50 nm (somewhat shorter loops can form but at a large free energy cost, i.e., slowly). If tension is present, there is an additional force-retraction free energy cost [9]. For example, even a rather small loop with ℓ ≈ 100 nm under moderate tension of f = 0.5 pN will have fℓ ≈ 12.5k_BT, leading to a large perturbation of the K_D. In such a case, the on-rate will be most strongly affected (suppressed) by applied force, since the “transition state” for the looping reaction requires nearly all of the work fℓ to be done by thermal fluctuation, if the protein-mediated looping interaction is of short range [10, 11].

3.5. A model for DNA-bending proteins binding along a long double helix

DNA in most organisms is covered with “architectural” DNA-bending proteins, to help package it compactly. In eukaryotes the “histone” proteins (two each of histones H2A, H2B, H3 and H4) complex together as octamers to form “nucleosomes”, with each histone acting to bend DNA [48]. In addition a variety of small DNA-bending proteins act to further kink DNA between nucleosomes (including HMG proteins such as HMGB1). In bacteria, “nucleoid” proteins (in E. coli, Fis, HU, H-NS and StpA) act independently to generate bends along DNA [49]. These bacterial proteins will bind well to most DNA sequences, although they certainly all have affinities that vary with DNA sequence.

It is of interest to consider the situation where one has a long dsDNA subject to insertion of kinks when proteins bind to it; this situation has been studied in a variety of single-DNA experiments [50, 51, 52, 53, 54] and is a simplified version of the situation occurring in vivo. A simple polymer model that is useful for considering this situation is a discretized semiflexible chain model, where each segment is a potential binding site for a protein, which when present induces a bend [55]:

$$\beta E=\sum _{i=1}^M[\frac{a}{2}{({\widehat{\mathbf{t}}}_{i+1}-{\widehat{\mathbf{t}}}_i)}^2{\delta }_{n_i,0}+\frac{a^{\prime }}{2}{({\widehat{\mathbf{t}}}_{i+1}·{\widehat{\mathbf{t}}}_i-cos\psi )}^2{\delta }_{n_i,1}-\beta f\ell \widehat{\mathbf{z}}·{\widehat{\mathbf{t}}}_i-\beta \mu n_i]$$ (19)

This model divides a DNA molecule up into M segments of length ℓ, so the total length of the DNA is L = Mℓ. At each segment there is a orientation variable t̂_i, and a protein occupation variable n_i which takes on values 0 and 1 for no protein or protein bound, respectively.

The orientations are principally controlled by applied force f. Protein binding is controlled by the chemical potential μ, and for ideal solution (suitable for describing the sub-micromolar protein concentrations used in most experiments) we can use the relation μ = k_BT ln c + ε, taking into account the ideal solution entropy loss and the binding energy gain associated with protein binding. When there are no proteins bound (n_i = 0) the bending stiffness of the chain is a, which is related to the continuum model persistence length via A = aℓ in the continuum limit ℓ → 0. For double-stranded DNA, this model is reasonable since a protein binding site size is a few nm in length; using ℓ < 5 nm defines a model with ℓ ≪ A, and therefore with semiflexible polymer elasticity.

In this model, when a protein is bound to a segment, its local bending stiffness is modified (the a′ term) and a kink is generated with preferred bending angle ψ. This couples the bending and binding degrees of freedom and makes the binding isotherm force-dependent. For the partition function Z = [∏_i∫ d²t_iΣn_i] exp(−βE) we have the simple expectation value relations

$$\langle z\rangle \equiv \langle \sum _{i=1}^M\widehat{\mathbf{z}}·b{\widehat{\mathbf{t}}}_i\rangle =\frac{\partial lnZ}{\partial \beta f}\langle P\rangle =\langle \sum _{i=1}^M{n}_i\rangle =\frac{\partial lnZ}{\partial \beta \mu }$$ (20)

where 〈z〉 and 〈P〉 are the end-to-end extension in the force direction and the total number of proteins bound, respectively. This type of model can be numerically solved using transfer matrix methods [55, 56], and one sees a shift of the force-extension curve to larger forces as protein concentration is increased (Fig. 4), as observed in corresponding experiments [50, 51, 52, 53, 57].

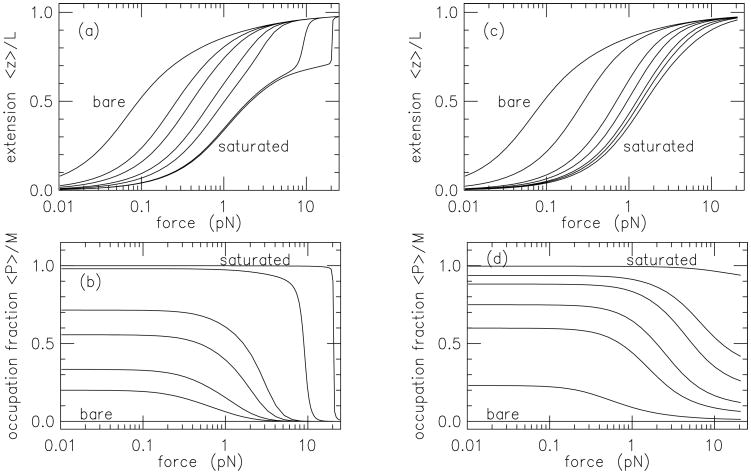
Figure 4.

Non-specificially binding DNA-bending protein; binding induces a ψ = 90° bend. Segment length is ℓ = 5 nm, and bend moduli are a = 10 (corresponding to bare-DNA persistence length of 50 nm). (a) Force-extension curves for stiff protein-DNA complex (a′ = 100) for binding strengths μ = −∞ (bare DNA, leftmost curve), -2.30, -1.61, -0.69, 0, 3.00 and 6.91. The DNA straightens out and the protein unbinds at a characteristic force. (b) Protein binding site occupation corresponding to (a). the same set of binding strengths. At high binding strength the high stiffness of the DNA-protein complex causes an abrupt unbinding transition, corresponding to the abrupt extension increase seen in the corresponding curves of (a). (c) Force-extension curves for flexible protein-DNA complex (a′ = 2) for binding strengths μ = −∞ (bare DNA, leftmost curve), -3.91, -2.30, -1.61, -0.69, 0 and 3.00. At low binding strength the force-extension curves are similar to those of (a), but at high binding strength no abrupt extension is observed due to the capacity of the DNA-protein complex to deform. (d) Protein binding site occupation corresponding to (c). Figure adapted from Ref. [55].

An interesting feature of this type of model (in particular any model where force is coupled to extension and where the binding chemical potential is coupled to occupation) is the “Maxwell relation” arising from the second mixed derivatives of the partition function [58]:

$${\left(\frac{\partial \langle z\rangle }{\partial \mu }\right)}_f={\left(\frac{\partial \langle P\rangle }{\partial f}\right)}_{\mu }$$ (21)

This exact relation is potentially useful since it allows one to estimate changes in binding occupation 〈P〉 from measurements of force-extension curves:

$${\langle P\rangle }_{f,\mu }={\langle P\rangle }_{f_0,\mu }+{\int }_{f_0}^{f}d{f}^{\prime }{\left(\frac{\partial \langle z\rangle }{\partial \mu }\right)}_{f^{\prime }}$$ (22)

Interestingly, this purely thermodynamical relation is able to count changes in absolute numbers of molecules bound to a DNA. This type of model-free relation has been used to estimate protein binding changes with force [59, 57], torque changes in twisted molecules [60] (as proposed in Ref. [58]), and changes in ions bound to stretched nucleic acids[61].

An interesting feature of this type of model is the emergence of interactions, or cooperativity, between nearby proteins along the DNA without any intrinsic interactions (e.g., as in Eq. (17)) [56]. These interactions appear for nonzero force, because of the bends. If two nearby bends are oriented oppositely to one another, then they can compensate for one another, in the sense that the DNA can extend a little more [62]. The result is an attractive interaction between two DNA-bending proteins bound along a DNA, that can be quite strong for forces where the DNA is stretched out (the regime f > k_BT/A) [56]. For large forces the interaction effective energy has an exponential dependence on distance between the proteins ∞ e^{−|i−j|ℓ/λ}. One might expect this since in this regime the free energy of the DNA is determined by small-amplitude bending fluctuations with correlation length $\xi =\sqrt{k_{B}TA/f}$ (Eq. (10)). A surprise is that λ = ξ/2, half of what a naive argument based on Eq. (10) predicts. This factor of two difference arises due to rotational symmetry around the force axis [63]. This is an example of a situation where one has a local degree of freedom (the occupation number for protein occupation n_i) whose correlation function decays with a correlation length differing from that controlling the free energy (i.e., distinct from the correlation length arising from the two largest eigenvalues of the transfer matrix).

Recently, it has been observed that there is another type of cooperativity acting between two nearby DNA-interacting proteins. A protein bound at one specific binding site has been observed to alter the binding properties of a second nearby (up to 15 bp away) binding site, with a DNA helical orientation dependent interaction. This effect is thought to be due to the “allosteric” deformation response of the DNA between the two proteins [64]. A reasonable model for this effect can be based on introduction of an interaction between nearby tangent vectors which introduces correlations in nearby bending angles (i.e., in Eq. (19), correlations in t̂_i · t̂_i+1) in a double-helix-orientation dependent fashion [65].

3.6. Concentration-dependent dissociation

In Sec. 3.1 we discussed the classical picture of the kinetics of protein binding and unbinding, where there is concentration-dependent binding (r_on = k_onc) and concentration-independent unbinding (r_off = k_off, just a constant rate). The concentration-independent off-rate model is generally assumed to describe biomolecule interactions, including protein-DNA binding. Note that this simple model assumes only two states: an “off”, dissociated state, and an “on”, bound state, with single transitions linking them (recall P + D ↔ C from Sec. 3.1).

There is starting to be a fair amount of experimental evidence that this simple type of model with a constant off-rate is often inappropriate; a number of groups have reported solution-concentration-dependent off rates [66, 67, 68, 69, 70], i.e., k_off(c) = k_off,0 + k_off,1c + ⋯. In this kind of power-series expansion of the concentration-dependence of k_off(c), the first term k_off,0 is the classical concentration-independent “decay” rate, or rate at which thermal fluctuations break the bonds holding the protein to the double helix. The second term k_{off, 1} introduces a linear dependence of the off-rate on concentration, and describes the interaction of one protein in solution with a bound protein. If k_{off, 1} > 0, the protein in solution increases the rate at which the bound protein leaves the DNA.

This is possible if the protein in solution, the protein bound to the DNA, and the DNA itself form a ternary complex, i.e., if both proteins simultaneously interact with the DNA. This can happen at a single binding site, since a protein is not held on DNA by just one chemical bond, but instead is bound by an array of chemical interactions. One can imagine partial dissociation of a bound protein which allows a protein in solution to interact with part of its binding site. This second protein could plausibly block complete rebinding of the first protein, allowing it to dissociate and to be replaced by the second protein. The result of this would be an exchange of the first and second protein, at a rate of k_{off, 1}c.⁵

One can write down a simple chemical reaction diagram for this (Fig. 5) based on a two-step dissociation pathway for a “two-bond” binding site. Many proteins that bind DNA have a dimeric structure, with two well-defined DNA-binding domains, see e.g., Fig. 2 A-B, also see Ref. [71]; the two ‘bonds’ can be thought of as the binding of two DNA-binding domains to the two halves of a binding site. We suppose that an initially bound protein can be fully bound (state 1, held on by two bonds) or partially bound (state 1*, held on by only one bond). In the partially bound state, a second protein can also be partially bound (state 1*2*). In this new state, protein 1 is blocked from being fully bound by partial occupation of the binding site by protein 2, and has an appreciable probability of completely dissociating. If protein 1 dissociates, we are left with only protein 2 partially bound (state 2*), which we can take to be a state equivalent to state 1*. Solving the equilibrium for this model we can obtain the rate at which exchanges occur (the rate of transitions from 1*2* to 2*), which is concentration-dependent. For the model sketched in Fig. 5 the number of proteins that occupy the binding site is

Figure 5.

Chemical reaction diagram for exchange of an initially DNA-bound protein (black balls), with a similar protein arriving from solution (gray balls), using a two bond (dimeric) mechanism.

$$n_{\text{bound}}=\frac{2k_{12}^{\prime }(k_1+k_1^{\prime })k_{0}c+2k_1^{\prime }{k}_0{k}_2{c}^2}{k_1{k}_{1\ast }^{\prime }{k}_{12}^{\prime }+2k_{12}^{\prime }(k_1+k_1^{\prime })k_{0}c+k_1^{\prime }{k}_0{k}_2{c}^2}$$ (23)

The binding isotherm ceases to have the ‘hyperbolic’ form of the classical Langmuir-like model (n_bound = c/[K_D + c]). If $k_{1\ast }^{\prime }$ is sufficiently slow compared to k₂c, exchange will dominate as the pathway to dissociation of an initially bound protein. Note that at high solution concentration, the binding saturates at two proteins per binding site. Simulations and more detailed calculations have provided additional information about this exchange-facilitated dissociation mechanism and have been used to quantitatively model experimental data[71, 72].

4. DNA topology

Topology of polymers generally refers to linking or entanglement properties, which are invariant under smooth geometrical deformations, and which can only change when one polymer passes through another. A simple example is the linking of two rings; they can be unlinked, or linked together; one cannot pass from the unlinked to a linked state without breaking one of the rings (Fig. 6).

Figure 6.

Simple links of oriented loops. Lk for each pair is computed by adding up the signs of the crossings and dividing the sum by 2.

(a) unlinked rings; the signs of the crossings cancel, so Lk = 0.

(b) the Hopf link; the signs of the crossings add, so Lk = +1 (Lk would be −1 if the orientation of one of the loops were reversed).

(c) for this link (sometimes called “Solomon's knot”) the signs of the crossings again add, making Lk = +2.

(d) the Whitehead link has canceling signs of its crossings, and has Lk = 0 despite being a nontrivial link.

4.1. Linking number

We can compute the linking number of two oriented closed curves by just counting up all of their mutual signed crossings, according to the rules shown in Fig. 7. Dividing the total crossing number by two gives an integer, the linking number Lk of the two curves (Fig. 6). This quantity can only change when one curve is passed through another. ⁶

Figure 7.

Sign convention for computation of linking number using crossings. Left: left-handed (−1) crossing. Right: right-handed (+1) crossing.

The Gauss invariant computes the same quantity, but determines it from the geometry of the two curves without directly counting their crossings:

$$\text{Lk}=\frac{1}{4\pi }{\oint }_{C_1}{\oint }_{C_2}\frac{d{\mathbf{r}}_1\times d{\mathbf{r}}_2\cdot ({\mathbf{r}}_1-{\mathbf{r}}_2)}{{|{\mathbf{r}}_1-{\mathbf{r}}_2|}^3}$$ (24)

For DNA, we can distinguish between external linking of two double helix molecules together, and the internal linking property of the double helix itself.

4.1.1. Internal double-helix linking number LK

We first consider the internal linking of the two strands inside one double helix. The double helix contains two single-stranded DNAs which are wrapped around one another in a right-handed fashion, with a preferred twist rate of one turn every n_h ≈ 10.5 bp, or every h ≈ 3.6 nm of contour length. For helical wrapping, we can associate a linking number, which is just the number of times one strand crosses over the other ⁷. For a double helix of length L and N_bp base pairs, Lk ≈ Lk₀ = L/h = N_bp/n_h. However, Lk is an integer for a closed double helix, and is not in general equal to Lk₀.

The difference between double helix linking number and the preferred linking number, ΔLk = Lk − Lk₀, is often expressed as a fraction of the preferred linking number (linking number density), σ ≡ ΔLk/Lk₀ (the excess linking number per DNA length is ΔLk/L = σ/h). In E. coli and many other species of bacteria, circular DNA molecules are maintained in a state of appreciably perturbed Lk, with σ ≈ −0.05.

4.1.2. DNA twist stiffness

If Lk is sufficiently different from Lk₀, then there will be a buildup of twist in the DNA, leading to a geometrical response. This response is often a wrapping of the double helix around itself, a phenomenon known as supercoiling. One can observe this by taking a stiff cord and twisting it. This behavior arises from a competition between the bending energy (Eq. (1)) and the elastic twist energy,

$$\beta E_{\text{twist}}=\frac{C}{2L}{\mathrm{\Theta }}^2$$ (25)

where Θ is the net twist angle along the double helix. In the absence of other constraints, thermal fluctuations of twist give rise to a fluctuation

$$\langle {\mathrm{\Theta }}^2\rangle =\frac{L}{C}$$ (26)

suggesting the interpretation of the elastic constant C as a characteristic length for twist fluctuations. For the double helix, this twist persistence length is C ≈ 100 nm. Note that the derivative of E_twist with respect to Θ is the torque or “torsional stress” in the DNA:

$$\tau =\frac{\partial E_{\text{twist}}}{\partial \mathrm{\Theta }}=\frac{k_{B}TC}{L}\mathrm{\Theta }$$ (27)

If there is no bending, then any excess linking number ΔLk goes entirely into twisting the double helix: Θ = 2πΔLk (or σ = Θ/ [2πL/h]). The mechanical torque in DNA will be τ = 2πk_BTCΔLk/L = (2πk_BTC/h)σ. The parameter 2πC/h ≈ 175 sets the scale for when the linking number density will start to appreciably perturb DNA conformation, i.e., when |τ| ≈ k_BT. This level of torque occurs for |σ| ≈ 0.005.

4.1.3. Linking number LK, twist Tw and writhe Wr

The previous computation supposed that there was no bending, in which case all of the ΔLk is put into twisting the double helix. This DNA twisting can be quantified through the twist angle Θ, or equivalently through the twisting number ⁸.

If DNA bending occurs, there may be nonlocal crossings of the double helix over itself. These nonlocal crossings contribute to double helix linking number, and the separation of length scales between DNA thickness and the longer scale of DNA self crossing (controlled by the persistence length A) allows linking number to be decomposed into local (twist) and nonlocal (writhe) crossing contributions:

$$\text{Lk}=\text{Tw}+\text{Wr}$$ (28)

or equivalently, ΔLk = ΔTw + Wr.

One can demonstrate this with a thin strip of paper (30 cm by 1 cm works well). Put one twist into the strip, closing it in a ring. The two edges of the strip are linked together once. Now without opening the ring, let it assume a figure-8 shape; you will see that you can make the twist go away: in this state there is only writhe (Fig. 8)

Figure 8.

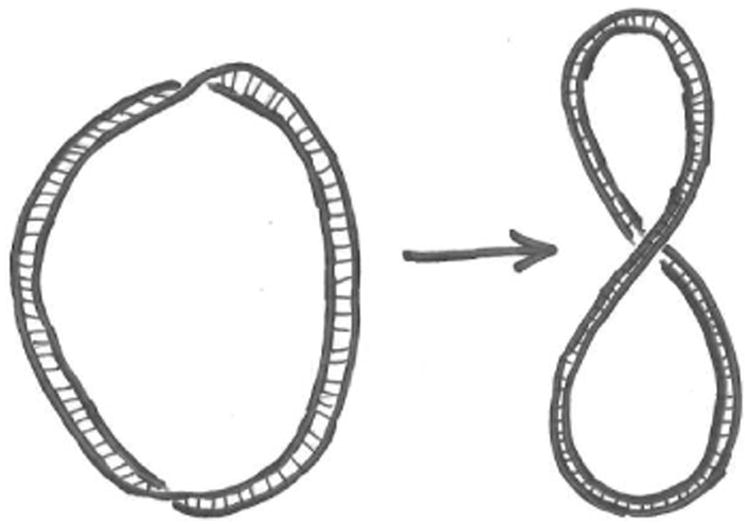
Left: a ribbon with Tw ≈ −1 and Wr ≈ 0. Right: deforming the ribbon allows the twist to be transferred to writhe, so that Tw ≈ 0 and Wr ≈ −1. The linking number is fixed at Lk = −1 as long as the strip is not broken.

For elastic ribbon models of DNA, suitable definition of the twist allows Wr to be expressed by the analytical formula [74, 75]:

$$\text{Wr}=\frac{1}{4\pi }{\oint }_C{\oint }_C\frac{d{\mathbf{r}}_1\times d{\mathbf{r}}_2\cdot ({\mathbf{r}}_1-{\mathbf{r}}_2)}{{|{\mathbf{r}}_1-{\mathbf{r}}_2|}^3}$$ (29)

where r₁ and r₂ are the two edges of the ribbon. The similarity of this equation to the Gauss invariant, Eq. (24), arises from the partitioning of the double integral into contributions from local wrapping of the strands in the double helix (Tw), and from nonlocal contributions (Wr) arising from nonlocal crossings of the centerline of the molecule. Eq. (29) is the sum of the signed nonlocal crossings for one curve (following the rule of Fig. 7), averaged over all orientations [75]. A key point is that while Lk is a topological property, Wr and Tw are geometrical, and change value as the molecule is distorted.

4.1.4. DNA Supercoiling

The ability to transfer Tw to Wr suggests that when there is appreciable torsional stress in a flexible filament, it can be relaxed by wrapping the filament around itself. For DNA we should also include the entropic cost of bringing the filament close to itself. A type of model model widely used to describe the “plectonemic” wrapping of DNA around itself (Fig. 9) is based on treating the wrapping as helical, and by writing down a variational free energy [76, 77, 78, 39]:

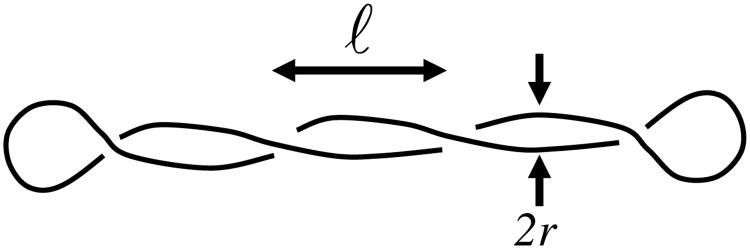
Figure 9.

Geometry of plectonemic supercoil, based on consideration of the shape as two interwound regular helices of radius r and an intercrossing distance ℓ. Note that the helix repeat is 2ℓ and the helix pitch p = ℓ/π.

$$\beta F=\frac{C}{2L}{\mathrm{\Theta }}^2+\frac{AL}{2}{\kappa }^2+\frac{L}{{(A{r}^2)}^{1/3}}+Lv(r)$$ (30)

where Θ = 2πΔTw is the DNA twisting (which costs twist elastic energy), κ is the bending curvature, which is κ = r/[r² + p²] for a regular helix of radius r and pitch p (the intercrossing distance is ℓ = πp, Fig. 9). The final two terms describe the entropic confinement free energy for a semiflexible polymer in a tube [79, 77, 80] and direct electrostatic and hard-core interactions per molecule length, v(r).

The confinement entropy is based on estimation of the correlation length for bending fluctuations for a confined chain, which will have curvature fluctuations ≈ r/ξ². The fluctuations in the bending free energy per length (in k_BT units) will be ≈ Ar²/ξ⁴, and over a correlation length the fluctuation free energy is therefore ≈ Ar²/ξ³. But the fluctuation free energy over a correlation length in k_BT units should be ≈ 1, giving us ξ³ ≈ Ar², and the confinement free energy per length (still k_BT units) of ≈ 1/ξ = 1/(Ar²)^1/3.

The important final ingredient is Eq. (28) which allows the twist to be expressed in terms of linking number and the writhe: Θ = 2πΔTw = 2π(ΔLk − Wr). For a plectoneme based on regular helices, Wr = ∓Lp/(2π [r² + p²]) where the upper/lower signs are for right/left handed plectonemic wrapping [77].

Putting this together gives the free energy per length

$$\frac{\beta F}{L}=2{\pi }^{2}C{(\frac{\mathrm{\Delta }\text{Lk}}{L}-\frac{p}{2\pi (r^2+p^2)})}^2+\frac{A}{2}\frac{r^2}{{(r^2+p^2)}^2}+\frac{1}{{(A{r}^2)}^{1/3}}+v(r)$$ (31)

where the sign of the writhe has been chosen to provide the lower twist energy for positive ΔLk, which is the case of a left-handed superhelix (note that left-handed plectonemes form for ΔLk > 0 while right-handed ones form for ΔLk < 0).

The free energy (31) can be optimized numerically to determine r and p [77, 81, 78, 39]. However, it is instructive to consider an approximate computation for the case of a slender superhelix (r ≪ p), for which the curvature is κ ≈ r/p², and the writhe per length is Wr/L ≈ 1/(2πp), corresponding to one crossing per length 2ℓ of DNA. Dropping the molecular interaction potential v(r) gives

$$\frac{\beta F}{L}\approx 2{\pi }^{2}C{(\frac{\mathrm{\Delta }\text{Lk}}{L}-\frac{1}{2\pi p})}^2+\frac{A}{2}\frac{r^2}{p^4}+\frac{1}{{(A{r}^2)}^{1/3}}$$ (32)

Now, this expression can be minimized to determine optimal values of r and p. Up to numerical constants, minimization over r sets Ar² ∝ p³ (setting the correlation length for bending fluctuations in the plectoneme to ξ ≈ p), and reduces the final two terms of Eq. (32) to k/p where k is a (1) constant. Subsequent minimization with respect to 1/p gives −2π²C(ΔLk/L − 1/[2πp]) + k= 0, or 1/(2πp) = Δ Lk/L − k/(2π²C). There is a threshold ΔLk* = kl/(2π²C) for appearance of a valid minimum (p > 0), introduced by the entropic cost of confinement; in terms of superhelix density σ = ΔLk/(L/h) this is σ^*= k/(2π²C/h), which is small compared to unity due to the ratio of length scales C/h ≈ (100 nm)/(3.6 nm). Beyond this characteristic value of linking number, the plectoneme becomes stable, and has a free energy below the essentially unwrithed, twisted molecule. This provides a rough idea of the behavior of the full plectoneme model Eq. (31) [76, 77, 81, 39]. For sufficient ΔLk, “screening” of the twist energy Eq. (25) by the writhe becomes favorable, which has little bending free energy cost if the superhelix radius r is kept relatively small.

Given that the main result for the free energy of the plectoneme is a free energy that rises from zero and eventually becomes superlinear, a useful approximate form to use for the free energy per length of the plectoneme is βF(σ)/L = (2π²C_p/h²)σ², where C_p ≈ 25 nm, C_p<C reflecting the twist-energy-screening effect [82].

4.1.5. Twisting stretched DNA

In single-molecule DNA stretching experiments, if a force in the pN range is applied the double helix will be nearly straight. If it is then twisted while under ≈ pN forces, the molecule will tend to coil chirally, leading to a slight contraction. For small twisting, a small-fluctuation-amplitude computation can be done [83, 84], expanding the tangent vector fluctuations around the force direction (again t = t_zẑ+u, where u are the components of t perpendicular to ẑ). We begin with the energy for a DNA under tension and twist:

$$\beta E=\frac{2{\pi }^{2}C}{L}{(\mathrm{\Delta }\text{Lk}-\text{Wr})}^2-\beta fL+\frac{1}{2}{\mathit{\int }}_0^{L}ds[\frac{A}{2}{\left(\frac{d\mathbf{u}}{ds}\right)}^2+\frac{\beta f}{2}{\mathbf{u}}^2]+\mathcal{O}(u^4)$$ (33)

just Eq. (8) with the addition of the twist energy. For a single-DNA experiment, ΔLk is just the number of full turns made of the end of the molecule (in a magnetic tweezers experiment, the number of times the magnet and therefore the bead at the end of the DNA is rotated [85]).

The challenge is how to include the linking number constraint in Eq. (33). The solution is to use an alternative representation of the writhe which takes the form of a single integral over contour length s [86]:

$$\text{Wr}{|}_{\text{mod}1}=\frac{1}{2\pi }\oint \frac{\widehat{\mathbf{z}}\cdot \widehat{\mathbf{t}}\times d\widehat{\mathbf{t}}}{1+\widehat{\mathbf{z}}\cdot \widehat{\mathbf{t}}}$$ (34)

The appearance of the “mod 1” in Eq. (34) reflects the fact that this expression for Wr (unlike the double integral Eq. (29)) is not sensitive to antipodal points, essentially nonlocal crossings which contribute ±1 to the total writhe (for a detailed discussion see Ref. [87]). The huge advantage of Eq. (34) over Eq. (29) is the presence of only a single integral, permitting expansion in powers of u for small deformations away from a straight configuration:

$$\text{Wr}=\frac{1}{4\pi }\mathit{\int }ds\widehat{\mathbf{z}}\cdot \mathbf{u}\times \frac{d\mathbf{u}}{ds}+\mathcal{O}(u^4)$$ (35)

This quantity is quadratic in u since the writhe of a straight line configuration is zero.

Using this in the twisting energy Eq. (33) and expanding to quadratic order in u gives:

$$\beta E=\frac{2{\pi }^{2}C}{L}{(\mathrm{\Delta }\text{Lk})}^2-\beta fL+{\mathit{\int }}_0^{L}ds[\frac{A}{2}{\left(\frac{d\mathbf{u}}{ds}\right)}^2+\frac{\beta f}{2}{\mathbf{u}}^2-\frac{\pi C\sigma }{h}\widehat{\mathbf{z}}\cdot \mathbf{u}\times \frac{d\mathbf{u}}{ds}]$$ (36)

which when Fourier transformed is

$$\beta E=\frac{2{\pi }^{2}C}{L}{(\mathrm{\Delta }\text{Lk})}^2-\beta fL+\frac{1}{2L}\sum _q{({\mathbf{u}}_q^{\ast })}^T\left(\begin{array}{cc}A{q}^2+\beta f& -i(2\pi C/h)\sigma q\\ i(2\pi C/h)\sigma q& A{q}^2+\beta f\end{array}\right){\mathbf{u}}_q$$ (37)

For the untwisted case σ = 0 this reduces to the fluctuation free energy of the untwisted chain, Eq. (9).

In terms of Cartesian components of u, nonzero twisting leads to an off-diagonal coupling, which can lead to a zero eigenvalue and an elastic instability. The stability condition is the requirement of a positive determinant (Aq² + βf)² − (2πC/h)²σ²q² > 0. The eigenvalue vanishing condition occurs for σ_c satisfying (2πC/h)²σ_c² = 4βAf. This instability places a hard limit on the maximum value of σ^* for which this type of model can be applied; for f = 0.5 pN, this is σ_c ≈ 0.028. By expressing this in terms of the DNA torque for a straight molecule τ = k_BT(2πC/h)σ we obtain ${\tau }_c^2=4k_{B}TAf$, which is the classical buckling instability of a rod subject to tension and torque [88]. The same instability can be observed in dynamical models of twisted and stretched DNA [89].

Diagonalization ⁹ of Eq. (37) allows computation of 〈u²〉 and the free energy, in a Gaussian approximation. The extension is 〈t̂⋅z〉 = 1 − 〈u²〉/2 + 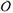(u⁴), or

$$\frac{\langle z\rangle }{L}=1-\sqrt{\frac{k_{B}T}{4Af}}-\frac{1}{2}{\left(\frac{2\pi C}{h}\sigma \right)}^2{\left(\frac{k_{B}T}{4Af}\right)}^{3/2}+\dots$$ (38)

where the neglected terms are of higher order in 1/f. Changing σ from zero leads to additional shrinkage over the untwisted case, due to chiral bending fluctuations.

Either integration of the extension with force, or direct computation of the partition function gives the free energy per length in a similar 1/f expansion:

$$\frac{\beta F}{L}=-\frac{lnZ}{L}=-\beta f+\sqrt{\frac{f}{k_{B}TA}}+\frac{2{\pi }^{2}C}{h^2}[1-\frac{1}{2}\frac{C}{A}{\left(\frac{k_{B}T}{4Af}\right)}^{1/2}]{\sigma }^2$$ (39)

The last term shows that the effect of the chiral fluctuations is to, as for DNA supercoiling, partially screen the twist energy, generating a reduction in the effective twist modulus C→ C_f = C[1 − (C/2A)(k_BT/4Af)^1/2]. This effect was used by Moroz and Nelson [83] to estimate the twist elastic constant C from single-molecule data of Strick et al [85] and led to a substantial revision in the accepted value of C from 75 nm up to the range 100 to 125 nm.

4.1.6. Coexistence of supercoiled and twisted-stretched DNA

For fixed force and sufficient ΔLk, one has “phase coexistence” of domains of plectonemic supercoiling and exended DNA (sketched in Fig. 10) [76, 77, 82, 39]. These “pure” states can be described by free energies per B-DNA length dependent on applied force f and the linking number density σ, say (σ) for stretched and (σ) for plectonemic DNA (the free energies per length discussed in the prior two sections, i.e., up to a factor of k_BT, Eqs. (39) and (31)). For these pure states, the rate that work is done injecting linking number is proportional to torque, for example:

Figure 10.

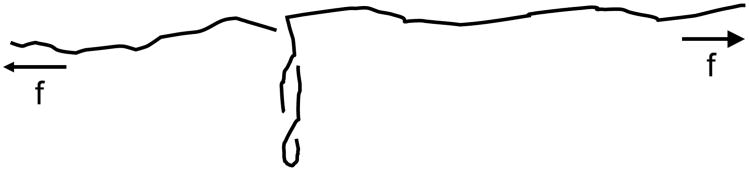
Sketch of a DNA molecule under tension f, and with linking number fixed so as to put the double helix under torsional stress. Over a range of applied tension, the molecule breaks up into “domains” of extended and plectonemically supercoiled DNA. Only a single domain of plectonemic DNA is shown for clarity.

$$\tau =\frac{1}{{\omega }_0}\frac{\partial \mathcal{S}(\sigma )}{\partial \sigma }$$ (40)

The prefactor ω₀ = 2π/h = 2π/(3.6 nm) is the angle of twist per molecule length for relaxed B-DNA, which converts the σ derivatives to ones with respect to angle.

Along a molecule which is a fraction x_s of state S and fraction x_p = 1 − x_s of state , the free energy per base pair of the mixed phase is

$$ℱ(\sigma )=x_{\mathrm{s}}\mathcal{S}({\sigma }_{\mathrm{s}})+x_{\mathrm{p}}\mathcal{P}({\sigma }_{\mathrm{p}})$$ (41)

The equilibrium length fraction x_s and the free energy is determined by minimization of this free energy subject to the constraint σ = x_sσ_s + x_pσ_p: linking number is considered as being partitioned between the two states. In the case of interest here, the plectonemic regions are essentially closed loops (see Fig. 10). By “pinching” of those loops off to form circular plectonemic supercoils separated from the extended DNA, the calculation of writhe can be decoupled into separate writhes for extended and plectonemic regions.

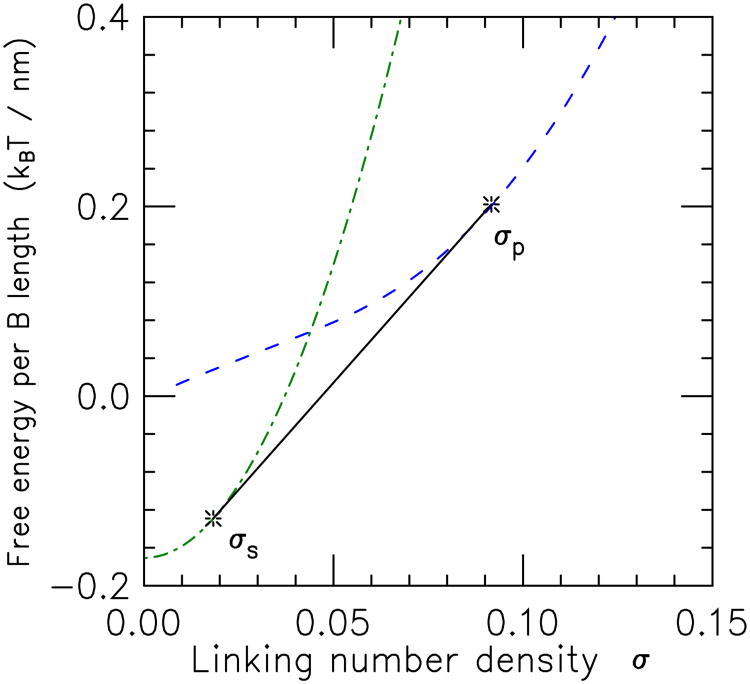
If the pure state free energy densities plotted as a function of linking number density never cross, then one pure state or the other will be the equilibrium state, i.e., one of the two extreme cases x_s = 0 or x_s = 1 will always minimize Eq. (41). If the two free energy densities cross, then there will be a range of σ over which there will be coexisting domains of the two states. Fig. 11 shows this situation, sketched to correspond to the case of main interest here, where at low values of σ the stretched state is stable (lower in free energy) relative to the plectoneme state, but where at large σ the stability reverses due to “screening” of the twist energy by the plectonemic state's writhe [76, 21, 39].

Figure 11.

Illustration of free energies of extended (dot-dashed curve, (σ)) and plectonemic supercoil (dashed curve, (σ)) DNA states as a function of linking number σ. For σ < σ_s, the state is lower in free energy than either or any mixture of the two. Similarly, for σ >σ_p, pure is the lowest-free energy configuration. On the other hand, for σ between σ_s and σ_p the tangent construction shown (solid line segment between tangent points indicated by stars), representing coexisting domains of (σ_s) and (σ_p), is the lowest free energy state. Note that the gap between the two states near σ = 0 is the free energy difference between random coil DNA [ (0)] and stretched unsupercoiled DNA [ (0)]; this difference grows with applied force and is due to the term −βf in the extended state free energy Eq. (39).

Minimization of Eq. (41) leads to a double-tangent construction familiar from other examples of phase coexistence (e.g., liquid-gas); in this case the conserved density is that of linking number (Fig. 11). The two coexisting states of linking number densities σ_s and σ_p satisfy ∂ (σ_s)/∂σ_s = ∂ (σ_s)/∂σ_p, i.e., they have equal torques. They mix in proportions x_s and x_p, so the free energy in the coexistence region is

$$ℱ(\sigma )=\mathcal{S}(\sigma )+\frac{\partial \mathcal{S}({\sigma }_{\mathrm{s}})}{\partial {\sigma }_{\mathrm{s}}}(\sigma -{\sigma }_{\mathrm{s}})=\mathcal{P}(\sigma )+\frac{\partial \mathcal{P}({\sigma }_{\mathrm{p}})}{\partial {\sigma }_{\mathrm{p}}}(\sigma -{\sigma }_{\mathrm{p}})$$ (42)

In the coexistence region, the fractions of the two states in the mixed state depend linearly on σ, as

$$\begin{array}{cc}{x}_{\mathrm{s}}=\frac{{\sigma }_{\mathrm{p}}-\sigma }{{\sigma }_{\mathrm{p}}-{\sigma }_{\mathrm{s}}}& x_{\mathrm{p}}=\frac{\sigma -{\sigma }_{\mathrm{s}}}{{\sigma }_{\mathrm{p}}-{\sigma }_{\mathrm{s}}}\end{array}$$ (43)

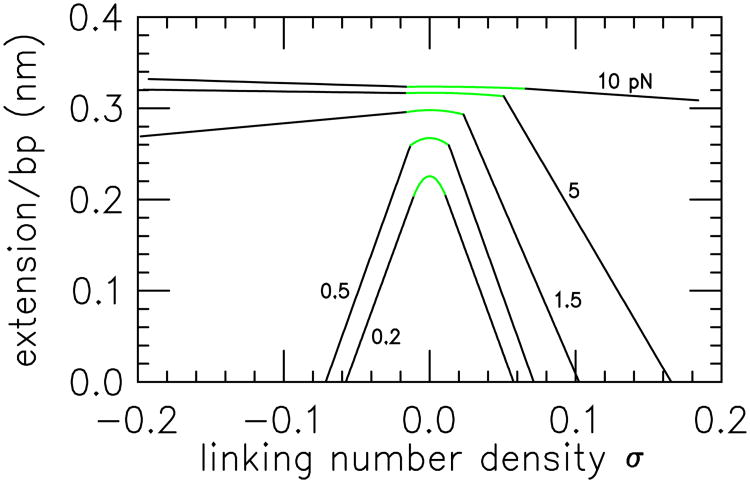
The coexistence construction guarantees that the free energy is a convex function of linking number, and therefore that the torque is a monotonic function of linking number, as required for mechanical stability. In the coexistence region (σ between the limits σ_s and σ_p) the torques in the two types of domains are equal and σ-independent; i.e., the σ-derivative of Eq. (42) is constant. This is quite useful for experiments on topoisomerases, since measurements carried out in the rather broad plectoneme-extended coexistence regions (along the linear portions of the “hat” curves of Fig. 12) are done at fixed torque. The value of torque in the coexistence regions is controlled by the constant force, varying from about 7 pN·nm at 0.5 pN (approximately the torque in a plasmid with physiological supercoiling σ ≈ 0.06 [82, 60], to a little more than 25 pN·nm at 3 pN [82, 90] (note that there is an appreciable torque decrease with increased salt [60], since DNA hard-core diameter drops and therefore plectoneme tightness increases [81] with increased salt concentration).

Figure 12.

Extension versus linking number curves for forces 0.2 pN (lowest curve), 0.5 pN, 1.5 pN, 5 and 10 pN (highest curve) from Ref. [82]. As force is increased, the extension increases, and the contracting effect of torsional stress (linking number) is reduced. The parabolic peak of each extension curve occurs when the DNA is purely in the extended state; extended and plectonemic DNA are in coexistence on the steep linear parts of each extension curve. The beginning of the steep black linear segments for positive supercoiling for 0.2, 0.5 and 1.5 pN, and for negative supercoiling for 0.2 and 0.5 pN indicate σ_s, and their intercepts with the σ axis indicates σ_p. For 10 pN and positive supercoiling, as well as for 2, 5 and 10 pN for negative supercoiling, formation of plectonemic DNA is pre-empted by DNA strand separation (the torque exceeds the critical torque for “melting”) with the result that a much shallower coexistence line is obtained, corresponding to coexistence of the extended state and torque-melted DNA. For details of the entire force-σ and force-torque phase diagrams see Ref. [39].

In the coexistence region Eq. (43) indicates that the rate of change of the length fractions with σ is constant; ∂x_s/∂σ = −1/(σ_p − σ_s). This generates the linear dependence of molecule extension on linking number observed experimentally once the threshold for generating plectonemic DNA is reached, as can be seen by computing the molecule extension (as a fraction of relaxed double helix contour length L):

$$\frac{z}{L}=-\frac{\partial ℱ}{\partial f}=-x_{\mathrm{s}}\frac{\partial \mathcal{S}({\sigma }_{\mathrm{s}})}{\partial f}-x_{\mathrm{p}}\frac{\partial \mathcal{P}({\sigma }_{\mathrm{p}})}{\partial f}$$ (44)

In the coexistence region, the only σ dependence is the linear variation of x_s and x_p, making the dependence of extension on σ linear, a feature seen clearly in single-molecule experiments [60]. A series of extension versus σ curves computed as in Ref. [39] are shown in Fig. 12 to illustrate this. These are computed for the extended-state free energy per length, Eq. (39), and for the result of the plectoneme model of Eq. (31) [77, 81, 78, 39]. One alternately can use an approximate “harmonic” free energy model of the plectonemic phase, β (σ) = (2π²C_p/h²)σ², where C_p ≈ 25 nm which permits analytical computations of the phase diagram, see Ref. [82].

In the main case of interest here where is the plectonemic supercoil state, its zero length eliminates its contribution to Eq. (44) (i.e., ∂ /∂f = 0), yielding

$$\frac{z}{L}=-x_{\mathrm{s}}\frac{\partial \mathcal{S}({\sigma }_{\mathrm{s}})}{\partial f}=\frac{{\sigma }_{\mathrm{p}}-\sigma }{{\sigma }_{\mathrm{p}}-{\sigma }_{\mathrm{s}}}\frac{z({\sigma }_{\mathrm{s}})}{\mathrm{L}}$$ (45)

where the final extension per length factor is the extension per length of the extended DNA state.

Experimentally, σ_s and σ_p may be measured from the beginning and the end of the linear coexistence regime of extension as a function of σ. Likewise, z(σ_s)/L is the extension per length of the molecule at the onset of the linear regime. Thus Eq. (45) can be used to determine the coexisting state linking number values, the extension of the stretched DNA state as a function of force and linking number, and via integration, the free energy of the stretched state. Then through use of the tangent construction (Fig. (11)), the free energy of the plectonemic state can be measured. Note that when the molecule is entirely converted to plectoneme (x_s = 0, x_p = 0) the extension reaches zero. The point σ = σ_p where this occurs can be estimated experimentally from extrapolation of extension data to zero.

As mentioned above, the phase-coexistence model generates torques which are constant along the linear regions of the “hat curves” of Fig. 12. For the model of Refs. [39] the extended-plectoneme coexistence torques are shown as a function of force in Fig. 13, and for a few salt concentrations (the models of Refs. [77, 81, 78] give very nearly the same results). There is a quite strong dependence of the torque on salt, due to electrostatic repulsions limiting the tightness of plectoneme winding for lower salt, which tends to drive the torques higher. Interestingly the torque follows a power law τ ≈ f^0.72 in accord with experiment [60]; theoretically this is due to a f^3/4 dependence plus a logarithmic correction (Eq. 17 of Ref. [81], note g(f) ≈ f for f ≫ k_BT/A).

Figure 13.

Torques for extended-plectonemic supercoiled B DNA coexistence as a function of force, computed from the model of Ref. [39].

(a) As force increases, torque increases, and as univalent salt concentration is increased, the torque decreases. Results are shown for 10 mM (dot-dashed), 50 mM (short dashed), 150 mM (solid) and 500 mM (long dashed) salt.

(b) The torque follows nearly a power law in force, τ ≈ f^{0. 72} (solid straight line), in accord with experimental measurements [60].

An interesting aspect of experiments done on twisted DNA is that now one has an additional control parameter, ΔLk which can be used to construct thermodynamical “Maxwell relations” analogous to Eq. (21), but now involving torque 〈τ〉 = ∂F/∂(2πΔLk) and force (and in principle, also chemical potential of molecules binding to the double helix) [58]. The Maxwell relation involving f and ΔLk has, for example, been used to indirectly measure torque, starting from extension-σ curves at a series of fixed forces [60] in reasonable accord with direct measurements [90].

Further interesting phenomena associated with twisted stretched DNA include the appearance of various structurally modified DNA states for sufficiently large twisting and force [39] (largely associated with torque-driven strand separation), appearance of multiple plectonemic domains for large molecules [78], and the discontinuous (first-order) nature of the onset of the plectonemic state [90].

4.2. Topoisomerases: protein machines that change DNA topology

In single-molecule DNA twisting experiments (as examples Refs. [85, 90, 60]), one changes the topology of the double helix (the value of ΔLk) by directly twisting the DNA molecule. In the cell, specialized enzymes (proteins that catalyze rearrangements of covalent bonds) allow double-helix topology to be changed. These topoisomerases cut and reseal the sugar-phosphate backbones in a double helix; depending on whether one or both backbones are cut, they are classified as type I or type II [91].

Type I topoisomerases do not require ATP for their operation, and just reversibly cut one backbone of the double helix, allowing it to rotate around the uncut strand, thus changing the ΔLk of a double helix. These enzymes therefore allow ΔLk of a DNA to reach mechanical-chemical equilibrium, which can be driven by other proteins acting on the double helix. In the absence of other factors acting on the double helix, type I topoisomerases therefore tend to relax ΔLk → 0. At present there are three subclasses of type I topoisomerases, which differ in details of their structures and their mechanisms [91]. The most important distinction is between type IA and IB, the former accomplishing a change in ΔLk = +1 per backbone cut-reseal catalytic cycle, and the latter changing ΔLk by one or more turns per catalytic cycle. Type I topos also can act on separate DNA molecules, typically in decatenation (disentanglement) of entangled single-stranded DNAs [92].

Type II topoisomerases cut both strands of a double helix, making a gap through which a second double helix is passed. Type II topos do this once per reaction cycle, and require ATP for this (the requirement of ATP appears to ensure that the second molecule is passed through the gap in a specific direction). This type of operation is essential to the removal of entanglements of separate DNA molecules. If a type II topo makes this topology change on two DNA molecules, the result is a change of the sign of a crossing (as in the two crossings shown in Fig. 7). Therefore the total number of crossings changes by ±2, and so the linking number of the two molecules changes by ±1. To avoid confusion with ΔLk, the linking number of two separate double helices is called catenation number Ca. Thus type II topoisomerases are able to change the Ca of two DNAs by ±1. An important example of a type II topoisomerase is Topo IIα, which is the main enzyme acting to remove entanglements between DNAs in eukaryote cells¹⁰.

Type II topoisomerases can also act at two points along a single DNA molecule. When this happens, there are two crossings of single strands inside the double helix which change sign, leading to a total change in ΔLk of the molecule being operated on by ±2. Bacteria contain a type II topoisomerase called DNA gyrase which is specially adapted for this function. This is thought to be accomplished the enzyme binding a +1-crossing loop, which then is changed in sign to −1. By this mechanism DNA gyrase is able to couple the energy stored in ATP into reduction of ΔLk to negative values (towards unwinding the double helix). DNA gyrase can drive σ →≈ −0.05.

4.3. Linking of two double helices: DNA entanglement

Cells need to control the topology of very long DNA molecules. One can ask how DNA topology will change when topoisomerases are allowed to act on them, and how interactions with other proteins might be used to control DNA entanglement topology. The enzymes acting in a cell cannot directly sense entanglement or other nonlocal topological properties of chromosomes, and the mechanisms of DNA entanglement control are only starting to be understood.

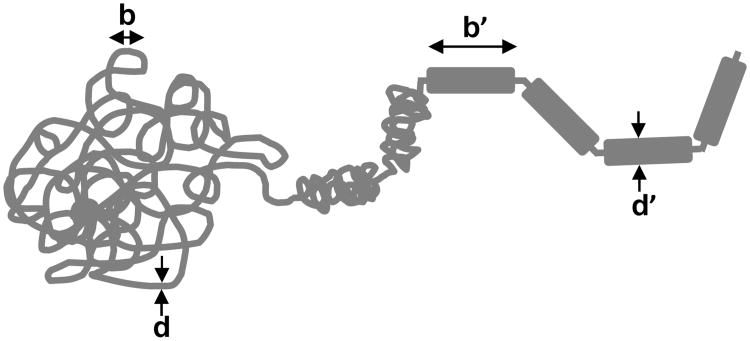
4.3.1. Knots

A single circular molecule is in one of many possible knotted states. We can imagine having an ensemble of circular polymers which are allowed to slowly change their topology, so as to have equilibrated knotting topology (this is possible to achieve using topoisomerases, or using enzymes that alternately linearize and recircularize the molecules). We can ask what the probability P_unknot is that any molecule will be unknotted.

One might ask how P_unknot behaves with the length L of the circles. For small L, (more precisely for L/b < 1 where b is the segment length; recall A = b/2 and N = L/b) there will be a large free energy cost of closing a molecule into a knot, driving P_unknot → 1. One can argue that for large L, P_unknot ≈ exp [−L/(N₀b)], for some constant N₀ as follows. Over some polymer length N₀ segments we suppose that the probability of having no knot drops to 1/e. Applying this probability to each L₀ along a DNA of length L gives P_unknot(L) ≈ (1/e)^L/(N₀b). This rough argument can be made mathematically rigorous[93].

Remarkably, even for an ‘ideal’ polymer which has no self-avoidance interactions, N₀ ≈ 300; for a slightly self-avoiding polymer like dsDNA in physiological buffer, N₀ ≈ 400 [94]. What this means is that to have an appreciable probability (1 − 1/e) to find even one knot along a dsDNA, it has to be 400 × 300 = 120, 000 bp long (the long persistence length of DNA - b contains 300 bp - helps make this number so impressive). The knotting length N₀ depends very strongly on self-avoidance; for a strongly self-avoiding polymer (meaning an excluded volume per statistical segment approaching b³), N₀ ≈ 10⁶. The remarkably low probability of polymer knotting lacks fundamental understanding, being based on numerical simulation results[94].

Experiments on circular DNAs are in good quantitative agreement with statistical mechanical results for the semi-flexible polymer model including DNA self-avoidance interactions. For example, it is found that the probability of finding a knot generated by thermal fluctuations for a 10 kb dsDNA is about 0.05 both experimentally and theoretically [95, 1]. This can be interpreted thermodynamically; the free energy of the knotted states relative to the unknotted state in this case is k_BT ln(0.95/0.05), or about 3k_BT.

A remarkable experimental observation is that type II topoisomerases are by themselves able to push this probability down, by a factor of between 10 and 100[96]. Somehow topo II is able to use energy from ATP hydrolysis to actively suppress entanglements.

4.3.2. Suppressing knotting by lengthwise compaction

Having a formula for the unknot probability, P_unknot(L) = e^−L/(N₀b) gives some insight into a mechanism by which locally acting enzymes could control global DNA topology. Consider a long dsDNA of length L, in the presence of some proteins which act to fold DNA up along its length. Imagine that these proteins cannot ‘cross-link’ DNA segment but that they can only compact the molecule along its length (Fig. 14). As lengthwise-compacting proteins bind, we imagine that they modify the total contour length to be L′ < L, and effective segment length to b′ > b.

Figure 14.

Lengthwise compaction of a polymer. A segment of length b of thickness d is lengthwise-compacted into a new segment of length b′ and thickness d′. Successive segments are connected by short flexible linkers of the original polymer. As the segments become longer and thicker, entanglements are driven out of the polymer.

If these proteins bind slowly in the presence of type-II topoisomerases so that the knotting topology can reach close to equilibrium, then the unknotting probability will have the form P_unknot = exp [−(L′/b′)/N₀]. Therefore, gradually compacting (decreasing L′) while stiffening (increasing b′) DNA can drive knotting out of it. Unknotting (an example of “entanglement resolution”) will occur on progressively larger length scales as this compaction process proceeds [41].

4.3.3. Proteins that lengthwise-compact DNA

Actual chromosomes in cells are substantially lengthwise-compacted by the action of locally-acting DNA-binding proteins. In eukaryotes, histone protein octamers wrap 147 bp of dsDNA into nucleosomes about 10 nm in diameter [48]. Chromosomal DNAs typically have short (15 to 50 bp) “linker” DNA stretches between successive nucleosomes. It is presently thought that a persistence length of this type of “chromatin” fiber contains at least 10 nucleosomes, or about 2 kb of DNA. This means that even with no self avoidance, a knot in an isolated chromatin fiber will only become likely for an 800 kb segment (4000 nucleosomes). In a cell, additional proteins that mediate chromatin-chromatin contacts will keep the statistics of the fibers from being those of simple polymers at very large scales, but there should still be a strong knotting suppression by the folding of DNA by architectural proteins.

At larger scales, chromosomes are folded and compacted by other proteins. One of the most important classes of proteins which accomplish this are “Structural Maintenance of Chromosomes” (SMC) complexes (Fig. 15) [97, 98, 99, 100]. These protein complexes are based on heterodimers of SMC proteins, which are long (≈ 50 nm), stick-like coiled-coil proteins with a dimerization domain at one end and an ATP-binding/hydrolyzing domain at the other end. These SMC “sticks” dimerize at one end, and are thought to be capable of undergoing conformational changes in response to ATP binding and hydrolysis so as to compact DNA molecules that they are interacting with. Via interactions with a third “kleisin” protein, SMC dimers form a tripartite ring structure that can encircle DNA, indicating a topological element to their DNA-organizing functions [101, 102, 103]. Furthermore, eukaryote SMCs appear to favor formation of right-handed DNA loops (loops with positive DNA writhe) [104, 105, 106, 107].

Figure 15.

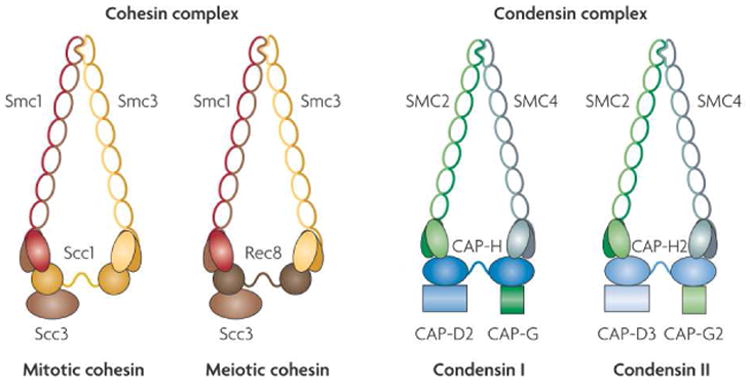
Schematic diagrams of cohesin and condensin eukaryote SMC complexes. SMC complexes are built around stick-like heterodimeric SMC proteins, each of which is approximately 50 nm in length. Reproduced from Ref. [100].

Single-molecule experiments do indicate that SMC complexes can compact DNA molecules by mediating contacts between distant DNA loci [108, 109, 110, 107]. Cell-biological experiments indicate clearly that the lengthwise compaction that occurs during mitosis in eukaryote cells depends crucially on the presence of “condensin” SMCs [98], and that proper regulation of contacts (“cohesion”) between replicated DNAs depends on “cohesin” SMCs [97, 100]. Cohesins also appear to play a critical role in stabilizing gene-regulating loops along chromosomes in eukaryotes. SMC complexes are found in bacteria and archae [111], making SMCs the most universal class of DNA-folding proteins, present in all three domains of life.

4.3.4. Linking of two “tandem” circular DNAs

The simplest topological problem involving more than one circular polymers involves the level of linking between two chain molecules. As a DNA is replicated, one often encounters the situation where the two duplicate molecules are attached together at a point along their contours. This situation suggests the problem of the computation of the catenation number statistics for two long circular polymers each N statistical segments long, attached together at one segment (Fig. 16).

Figure 16.

Two polymers of N segments, joined together at one point along their contours.

The catenation number Ca is just the Gauss invariant, Eq. (24), of the two polymers, and is the sum of signed crossings (Fig. 7). Therefore we expect 〈Ca〉 = 0; right- and left-handed crossings occur with similar probabilities. However, the width of the Ca distribution, 〈Ca²〉 will be nonzero, and at least as large as the number of nearby crossings, since those close crossings will appear with either sign in the conformational ensemble.

We can estimate the number of nearby crossings for ideal random-walk polymers using the segment density of ϕ ≈ 1/N^1/2, which tells us 〈Ca²〉 ≈ Nϕ ≈ N^1/2. This suggests a scaling law of

$$\langle {\text{Ca}}^2\rangle =a_0{N}^{1/2}$$ (46)

or |Ca| ≈ N^1/4. This scaling behavior has been suggested by des Cloixeau[112] and calculated by Tanaka[113]; numerical simulations for ideal random walks suggest a₀ ≈ 0.25 [114].

This fluctuation scaling indicates a free energy cost of catenations of F(Ca) ≈ k_BTCa²/〈Ca²〉, or F(Ca) ≈ k_BTCa²/N^1/2. Since Ca is extensive, the free energy is superextensive; if we scale Ca up with polymer length (L = Nb), we see F ≈ L^3/2. Comparing this to the form of the twist elasticity for an elastic rod Eq. (25), we see that the effective twist persistence length diverges with polymer length, C_eff ≈ L^1/2 (this divergence is due to the large entropy cost of forcing two otherwise conformationally unconstrained polymers to wrap one another).

If one has excluded volume interactions along two polymers that are tethered together, the number of nearby crossings drops to (1) [115], and no longer dominates over the ≈ ln N number of crossings that comes from nonlocal wrapping of the polymers around one another. The ln N arises simply because each successive nonlocal wrap requires an additional increment of chainlength ≈ N, making dCa²/dN ≈ 1/N. ¹¹ Simulations verify this [114], showing that for polymers with excluded volume

$$\langle {\text{Ca}}^2\rangle \approx a_{1}lnN$$ (47)

with a₁ dependent on the excluded volume of the polymer segments.

A consequence of this low fluctuation is a high stiffness; for small Ca, the free energy of catenation will be F(Ca) ≈ k_BTCa²/(a ln N). The higher cost of catenations in the self-avoiding case (relative to the ideal random walk case) gives rise to a more strongly diverging effective elastic constant, C_eff ≈ L/ln L. This large cost of interwindings can be expected to lead to “phase separation” of loose and tight catenations. In simulations one observes a sign of this in a nearly linear dependence of F(Ca) on Ca, with a cost of about 4k_BT per catenation over a wide range of catenation [114]. A key point is that in this nonlocally wrapped structure, most of the catenations will be located where the chains are near one another, i.e., near the tethering point of the two chains.

Catenations between either ideal or self-avoiding polymers have a high free energy cost. This can be argued to give some insight into the origin of the knotting length N₀ since the simplest “trefoil” knot involves the wrapping of a polymer around itself, with at least three crossings [114]. This also indicates that catenations between isolated DNAs will be disfavored; type II topoisomerases can be expected to reduce catenation down to the thermal levels of 〈Ca²〉 discussed above (this ignores any ATP-driven topological simplification effects which type II topos may possess [96].

Lengthwise compaction of polymers as discussed above for knots will drive out catenations. For both ideal and self-avoiding polymers, changing N → N′ < N will increase the free energy cost of Ca, guiding topoisomerases to remove catenations.

The tendency for interwindings to “condense” together will tend to drive the helical catenations resulting from DNA replication to be near one another. Along chromosomes which are attached together at a point, one can expect a domain of tight catenation, on which type II topoisomerases can be expected to act to release the catenations. The 4k_BT per catenation expected in such a structure will strongly bias catenation release.

4.3.5. Linking of confined polymers

The two examples discussed above - knotting of one polymer and catenation of two polymers tethered together at one point - both indicate that entanglements cost a good deal of free energy, but these were cases of isolated polymers. We now consider entanglements between n polymers each of N segments, in a dense melt- or semi-dilute-solutionlike state, confined to a radius-R spherical cavity ¹². The polymers are long enough so that their random-walk size N^1/2 ≫ R, so that each chain fills the confinement volume. This is a crude model of chromosomes confined to a nucleus, or inside a bacterial cell.

We now ask what the degree of catenation will be if the entanglement topology of these confined chains is equilibrated (for example by topoisomerases). For a polymer melt, along a chain of N segments, every segment is nearby other segments (not counting the segments to the left and right along the same chain). Most of these near encounters are with segments from other chains, since the number of collisions of a chain with itself is ≈ N^1/2 for the random-walk statistics in a melt. This means that each chain has N near collisions with other chains, or N/n near collisions with any particular chain. But since these near collisions appear in the ensemble of configurations with either crossing sign, we expect 〈Ca²〉 ≈ N/n. For this problem, the high segment density and the proximity of the polymers to one another forces them to be much more entangled than isolated chains.

In the semi-dilute solution case (volume fraction ϕ = nNb³/R³ ≪ 1 but with overlapping chains), exactly the same argument can be made, but now for semi-dilute solution blobs, which each have g ≈ ϕ^−5/4 segments in them. The result is that 〈Ca²〉 = ϕ ^5/4N/n. Simulations indicate that the two regimes can be described by one scaling formula (Fig. 17) [116]

Figure 17.

Scaling behavior of catenation fluctuations for circular polymers of N unit-length segments confined to a sphere of R. The segments have a diameter 0.2 times their length (d/b = 0.2) and interact via excluded-volume interactions. Catenation 〈Ca²〉/N scales linearly with the segment density ϕ = nN/R³ for x > 1, and faster than linearly for ϕ < 1. Solid curve is a fit function that interpolates between the asymptotic behaviors ϕ^5/4 and ϕ¹ expected for ϕ < 1 and ϕ > 1, respectively. Figure reproduced from Ref. [116].

$$\langle {\text{Ca}}^2\rangle =\frac{N}{n}c(\varphi )$$ (48)

where f is a scaling function with limiting behaviors c(ϕ) ∝ ϕ^5/4 for ϕ ≪ 1, and c(ϕ) → const for ϕ → 1.

Once again one can see that lengthwise compaction so as to reduce N = L/b (by either or both of reduction of chromosome length L or increase of segment length b, while keeping ϕ about the same) will drive down 〈Ca²〉.

An interesting issue is the influence of the shape of the volume on entanglement of confined polymers. For tight cylindrical confinement, chains will tend to separate from one another along the cylinder, to minimize their stretching (and therefore to maximize their entropy). This effect has been proposed to play a role in the segregation of bacterial chromosomes in rod-shaped bacteria[117, 118] although folding and compaction of bacterial chromosomes (Fig. 18) likely play an important role in their separation [119].

Figure 18.

Cell division (A) and chromosome segregation (B) visualized in live E. coli bacterial cells. The chromosomes are visualized using a fluorescent version of the chromosomal protein Fis. The chromosomes have a filamentous, coiled structure, and separate from one another well before the cells themselves divide. Bar is 2 μm. Figure adapted from Ref. [119]; see that paper for three-dimensional deconvolution analysis of the coiled chromosome shape.

4.4. Estimate of equilibrium entanglement for human chromosomes

Given a scaling theory for equilibrium linking for confined polymers, one can estimate the thermal equilibrium entanglement using Eq. (48) that would occur for otherwise unconstrained chromosomes within a cell nucleus, under the assumptions that random strand passages are made by type-II topoisomerases, and that the chromosomes behave as self-avoiding polymers [116].

A statistical segment of chromatin is thought to be roughly b = 60 nm in length[120], and considering it to be a well-packed fiber about 30 nm wide, contains about 35 nucleosomes or 6 kb of DNA. Thus, the larger human chromosomes, approximately 200 Mbp in length, as chromatin correspond to N ≈ 30,000 segment-long polymers. Human chromosomes are confined within a cell nucleus of radius R ≈ 3 μm, or measured in polymer segment units, R/b = 50. The number of chromosomes in a human nucleus is n = 46, thus we can compute the segment density ϕ = nN/(R/b)³ = 10, corresponding to a volume fraction of roughly 10%. Reading off 〈Ca²〉/(N/n) = 0.06 for this ϕ value from Fig. 17 gives the estimate 〈Ca²〉₀ = 40. This is likely an overestimate since chromatin fiber has a segment diameter-to-length ratio larger than the b/d = 0.2 used to compute Fig. 17. In conclusion, if human chromosomes were to fully equilibrate their topology, they would be expected to have 〈Ca²〉 ≈ 40; i.e., they would equilibrate to an entangled state. The value of 〈Ca²〉 is much smaller than N in numerical size.

It is to be stressed that 〈Ca²〉₀ is not necessarily the actual catenation that occurs in the cell, but only that which would occur if topology were equilibrated for uncondensed chromosomes in a nucleus. It has been estimated that the time needed for topological equilibrium may greatly exceed cell-cycle timescales, and that observations of chromosome territories (distinct spatial regions of the nucleus that contain separate chromosomes) may be related to this kinetic constraint [121]. Other factors such as tethering of chromosomes to the nuclear envelope during interphase [121], or formation of condensed heterochromatin domains, likely play a major role in maintaining chromosome territories and limiting chromosome entanglement. Nevertheless, the estimate 〈Ca²〉₀ is useful as it is a thermodynamic upper bound on entanglement of chromosomes confined to a nucleus.

4.5. Lengthwise compaction and control of chromosome entanglements

During cell division, eukaryote chromosomes become completely segregated from one another, despite the fact that following DNA replication, the chromosomes are released from being tethered to the inside of the nuclear envelope, and have an opportunity to entangle with one another [122]. Evidence for inter-chromosome entanglements have been obtained from experiments in fission yeast where the DNA-topology-changing enzyme topo II was disabled during chromosome condensation: different chromosomes were observed to be unable to segregate from one another [123]. Similar effects have been observed in vitro in experiments with Xenopus egg extracts [124], and in vivo for mammalian cells [125, 126]. These observations of inter-chromosome entanglements following suppression of topo II activity imply that chromosomes became entangled with one another at some time prior to the inhibition.

Strikingly, following DNA replication, chromosomes start to condense into string-like structures that become gradually visible in the light microscope (Fig 19, also see Ref. [122]). This process of “chromosome condensation” is thought to be coupled to the process of segregation of chromosomes from one another [127, 128, 129, 122] as well as to separation of sister chromatids from one another inside each chromosome The peculiar type of “condensation” that occurs - “lengthwise compaction”, or folding of chromosomes along their length - ensures separation of different chromosomes, provided that topo II is present during the compaction process This should be contrasted with the manner of condensation discussed in polymer physics (“poor solvent” or “polymer melt” conditions) whereby all segments stick to one another; if this occurred to chromosomes they would become hopelessly entangled with one another, as occurs in a polymer melt [130].

Figure 19.

Cell division (mitosis) in animal cell A: late interphase showing dark nucleoli and still uncondensed chromosomes; B: prophase showing long but condensed prophase chromosomes; C: spindle-aligned and shortened metaphase chromosomes; D: separation of chromatids at anaphase; E: telophase chromosomes beginning to decondense; F: interphase nuclei in daughter cells Bar is 20 μm Images courtesy of M.G. Poirier.

Eq (48) can be used to show how lengthwise compaction can drive segregation of different chromosomes even while confined inside the nucleus. Consider chromosomes which are initially in the form of flexible polymers of N statistical segments each of b and cross-sectional diameter d. Suppose lengthwise compaction occurs: the chromosomes will become locally thicker (d → d′ > d) but in doing so will become stiffer (b → b′ > b) and shorter (L = Nb → L′ = N′b′ < N) A simple and reasonable assumption is that the condensation process will conserve chromatin volume i.e. Ld² = L′d′² or Nbd² = N′b′d′². To simplify the calculation to follow it will be assumed that as condensation occurs b and d will increase by the same factor, i.e., b′= λb and d′ = λd. For this particular model the volume conservation constraint indicates N′ = N/λ ³. This simple model of chromosome condensation describes the degree of condensation by the single parameter λ > 1.

As chromosome condensation occurs λ gradually increases, and by Eq. (48) the equilibrium catenation of chromosomes will be

$${\langle {\text{Ca}}^2\rangle }_{\lambda }=\frac{N^{\prime }}{n}c([n{N}^{\prime }{b}^{\prime 3}]/R^3)=\frac{1}{{\lambda }^3}\frac{N}{n}c([nN{b}^3]/R^3)=\frac{1}{{\lambda }^3}{\langle {\text{Ca}}^2\rangle }_0$$ (49)

where 〈Ca²〉₀ is the catenation that would be achieved in topological equilibrium before chromosome condensation begins (the estimate made above for human chromosomes)

The level of entanglement of chromosomes need not initially be close to 〈Ca²〉₀ for Eq. (49) to apply during chromosome condensation Eq. (49) indicates the equilibrium catenation that can be reached, assuming random strand passages by topoisomerase II, given lengthwise condensation by a factor λ, and shows how lengthwise compaction can generate a strong thermodynamic drive to eliminate catenations between different chromosomes. The interactions that accomplish local condensation of chromosomes by a factor λ suppress the equilibrium level of entanglement 〈Ca²〉 by a factor λ⁻³.

Therefore, the equilibrium catenation expected for uncondensed human chromosomes, 〈Ca²〉 = 40, can be pushed well below 1 by only moderate condensation λ = 6. By locally folding chromatin fiber from its uncondensed level (30 nm thickness) to a lengthwise-compacted 200 nm-thick fiber will ensure complete decatenation of different chromosomes. The increase of b and d by the same factor λ allows the same scaling function c(ϕ) to be used which simplifies this computation, but this condition is not required to obtain the same condensation-driven topological resolution. Finally, it should be noted that the segment density is unchanged by this condensation process, but the total number of segments per chain is reduced by a factor λ³; for the human chromosome case considered above (λ = 6) N′ = N/λ³ ≈ 30,000/200 ≈ 150. Thus, when human chromosomes become separated by this process, they will still be relatively long, flexible polymers.

At the same time that the chromosomes are being separated from one another, the chromatids will separate, via the same general mechanism but now using Eqs. (46) and (47) applied to tandem stretches of chromatin between chromatid cohesion points [129].

To summarize, the mechanism outlined here of lengthwise-compaction-driven entanglement removal requires that there first be enzymes which act to fold chromatin along its length, without introduction of extensive “cross-links” between different chromosomes. Then, this compaction system must act slowly enough that there is time for topology-changing enzymes (topo II) to release entanglements between different chromosomes. Given these two requirements, as lengthwise compaction goes forward, entanglements will be released at successively large length scales by the combined action of the lengthwise compaction mechanism and topo II.

In accord with this, disturbing either the compaction or topology-changing machinery has been observed to disrupt the condensation-resolution process [123, 124, 125, 126, 98, 131]. Finally, fully condensed chromosomes become “individualized” (lengthwise compaction can generate this as well, see Ref. [114]), and following separation of sister chromatids, the two sets of replicated chromosomes then decondense to form nuclei. As emphasized by Rosa and Everaers[121] kinetic effects may delay full re-entanglement, giving time for establishment of chromosome tethering and other nuclear structures factors stabilizing chromosome territories.

5. Conclusion

These lectures have introduced statistical-mechanical models that can be used to describe the polymer elasticity of DNA and other biological polymers. Methods have been discussed for including effects of DNA-binding proteins into these models. Many more problems, particularly concerning the kinetics associated with DNA-binding proteins, remain to be studied. This paper has emphasized the importance of considering the multi-step kinetics associated with the array of chemical bonds between a typical DNA-binding protein and its binding site.

A few problems associated with the topology of DNA molecules have also been described. The simplest of these concerns the supercoiling of DNA, or the response of a single DNA to perturbation of its internal linking number. The more complex problem of entanglement of separate DNA molecules (or chromosomes) has been discussed, mainly in terms of the width of the catenation number distribution, 〈Ca²〉, which is a simple and useful tool for gauging the entanglement in multi-polymer systems.

This approach has been used to rationalize how chromosome condensation - or better put “lengthwise compaction” of chromosomes - can lead to topological simplification and chromosomes separation. The key idea has been to consider topo II as a “topology-changing machine” which needs to be directed by a “lengthwise-compaction machine”. The free energy drive to direct topo II to remove entanglements comes from the free energy associated with chromosome lengthwise compaction. Some preliminary ideas of how specific chromosome-structuring proteins (specifically the “condensin” chromatin-folding complex) might accomplish this are described in Ref. [132]. Single-molecule studies of condensin and other “SMC” (Structural Maintenance of Chromosome) proteins are of obvious interest; single-DNA experiments have demonstrated DNA-folding capabilities of condensin and cohesin complexes [108, 107].

Highlights.

1. Review of mechanical properties of DNA and DNA-protein complexes

2. Pedagogical presentation of statistical-mechanics of DNA response to tension and twist

3. Discussion of DNA topology and topology control in cells