Abstract
Biochemical reaction networks are subjected to large fluctuations attributable to small molecule numbers, yet underlie reliable biological functions. Thus, it is important to understand how regularity can emerge from noise. Here, we study the stochastic dynamics of a self-repressing gene with arbitrarily long or short response time. We find that when the mRNA and protein half-lives are approximately equal to the gene response time, fluctuations can induce relatively regular oscillations in the protein concentration. To gain insight into this phenomenon at the crossroads of determinism and stochasticity, we use an intermediate theoretical approach, based on a moment-closure approximation of the master equation, which allows us to take into account the binary character of gene activity. We thereby obtain differential equations that describe how nonlinearity can feed-back fluctuations into the mean-field equations to trigger oscillations. Finally, our results suggest that the self-repressing Hes1 gene circuit exploits this phenomenon to generate robust oscillations, inasmuch as its time constants satisfy precisely the conditions we have identified.
Introduction
Most cellular functions are controlled by molecular networks involving genes and proteins that regulate each other so as to generate the adequate dynamical behavior. A major goal of systems biology is to understand how sophisticated functional modules emerge from the combination of elementary processes such as transcriptional regulation, complex degradation, active transport,… and how each of these processes influences the collective dynamics (1).
A specificity of regulatory networks viewed as dynamical systems is that they are both strongly nonlinear and inherently stochastic, which considerably complicates the mathematical analysis. In a cell, protein and mRNA molecules are often found in low abundance so that variations of their copy numbers by one unit represent significant fluctuations. Furthermore, there are generally very few copies of a gene-carrying DNA fragment, with only a few possible configurations depending on promoter occupancy. When its transcription is regulated by a single protein, a gene can essentially be in two states: free, or bound to its transcription factor. Gene activity is then described mathematically by a binary variable, which more generally can also account for the transcriptional pulsing that has been observed both in prokaryotes (2) and eukaryotes (3–6). The stochastic dynamics of the gene randomly flipping between the bound and free states with probabilities depending on transcription factor abundance is a major source of intrinsic fluctuations, all the more as it was shown that this flipping can occur at timescales that are comparable to other biochemical processes (2). Although stochasticity in gene networks has been often viewed as an undesirable perturbation blurring deterministic behavior, it is increasingly recognized that noise can in fact be harnessed to become a functional component of a regulatory network and make its dynamics richer (7–11). It is thus important to understand how the deterministic and stochastic aspects of cellular processes interact and contribute to the same global dynamics, all the more because they are intimately coupled in nonlinear systems.
However, even moderately complex regulatory networks resist mathematical analysis and require formidable computational resources. A natural strategy to study such general questions as the interplay of dynamics and noise, is to focus on small genetic networks comprising only a few elementary components, the analysis of which can identify the key mechanisms and parameters and cast light on the dynamics of more complex networks. This approach is all the more valuable because the recent developments of synthetic biology allow experimental tests of the theoretical analyses (12).
Here, we study how stochastic fluctuations in gene activity feed-back into the deterministic dynamics of the smallest genetic network, which consists of a single gene repressed by its own protein product. This system is an ideal workbench to investigate how the dynamics of the network emerges from the properties of its elementary components. In fact, this motif is very common in transcriptional networks and is thus biologically relevant (∼40% of Escherichia coli transcription factors are self-repressing (13–15)). Self-repression is known to be an important ingredient for generating oscillatory behavior (16). For instance, Hirata et al. (17) proposed that the somite clock network is governed by the self-repressing gene Hes1. Accordingly, the dynamics of the self-repressing gene has been actively investigated throughout mathematical biology (18–26).
Most theoretical analyses of the self-repressing gene based on a deterministic description assume that gene-state flipping occurs on much faster timescales than other processes such as transcription, translation, and degradation. The flipping dynamics can then be taken into account through an average activity, which adapts to protein concentration either instantaneously or after a time delay. If intrinsic fluctuations are neglected, the analysis of the rate equations reveals that oscillatory behavior can only be found by one of the following:
-
1.
Introducing an explicit time delay in the equations (e.g., to take into account the transcriptional dynamics (16,23–25,27,28));
-
2.
Inducing an implicit time delay via a reactional step, which can be intrinsic (20) or describe transport between two compartments (22); and
-
3.
Incorporating complex degradation mechanisms (16,26,28,29).
However, experiments have shown that gene activity may display an intrinsic dynamics on timescales comparable to that of other cellular processes (2,4–6). This may be taken into account in a deterministic model by introducing an average gene activity variable, which reacts gradually to protein concentration (30). In particular, how such a transcriptional delay and a nonlinear degradation mechanism conspire to generate oscillations has been studied in detail by Morant et al. (26), who obtained analytical expressions for the instability thresholds.
To take into account the binary nature of the gene state and its stochasticity, the most general approach to study the dynamics of the self-repressing gene is to use the chemical master equation (CME) (31). The steady-state solution of the CME provides the probability distribution of molecular copy numbers, characterizing both the averages and the fluctuations around them. An analytical solution of the CME for the self-repressing gene can be obtained when the mRNA variable is considered to be fast and can be eliminated adiabatically (32,33), but this assumption is unrealistic for the Hes1 feedback network, where mRNA and protein have similar lifetimes (17). A classical strategy for approximating the CME is the system-size expansion also known as van Kampen’s Ω-expansion (31). Assuming that the system size is large but not infinite, the solution is expanded in powers of the inverse system size. The deterministic mean-field equations are obtained at lowest order while next-to-leading order corrections determine finite-size fluctuations in the so-called linear noise approximation (LNA).
This approach can be used to estimate the amplitude of fluctuations (34) but also to determine their spectrum. In particular, the LNA has been useful to characterize the appearance of stochastic oscillations in parameter regions where the mean-field equations predict stable steady behavior (35,36) or to verify that oscillations predicted by a deterministic modeling persist in presence of fluctuations (37)—two problems that have been actively studied (38–41). To overcome the fact that LNA does not allow one to determine precisely when the steady state loses stability, Scott et al. (42) proposed an extension of this method, one that takes into account how fluctuations modify the linearized dynamics around steady state and allows one to study how bifurcation diagrams are modified by noise. However, all these methods based on system size expansion assume that fluctuations vanish in the infinite size limit, without affecting the average values. This assumption clearly does not hold when the gene state is a binary variable, which fluctuates between two discrete values, regardless of system size. A different approach must then be taken.
In this article, we propose a strategy to describe the stochastic dynamics of a basic self-repressing gene circuit, with no cooperativity in the transcriptional regulation and a linear degradation mechanism (Fig. 1 A). The gene switches stochastically between the active and inactive state, so that this circuit can be viewed as a random telegraph signal generator, whose output is sent through a low-pass filter before being fed back to itself (Fig. 1 B). It is well known that a mean-field model of this system is unconditionally stable (see, e.g., Morant et al. (26)). Our main result is that a low-dimensional model taking fluctuations into account predicts oscillatory behavior in a region of parameter space, where we observe relatively regular spiking in protein concentration.
Figure 1.
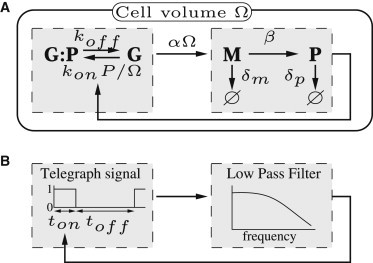
Schematic view of the self-repressing gene network. (A) Biochemical reactions composing the network. P, M, G, and G:P denote protein, mRNA, free gene, and bound gene chemical species, respectively. The kinetic constants of the reactions are indicated, with Ω denoting cell volume. In the limit where Ω is large, the mRNA and protein copy numbers become macroscopic variables, with decreasing fluctuations; this is in comparison to the gene state, which remains microscopic and displays full-scale variations. (B) Block diagram representation of the network, consisting of a random telegraph signal generator representing the gene state-flip dynamics, and of a low-pass filter of cut-off frequency ωc representing proteins and mRNA dynamics. The telegraph signal regulates its frequency and duty cycle through feedback from the low-pass filter.
To derive this model, we use a moment-closure approximation of the master equation (33,43–45), and derive a set of ordinary differential equations (ODEs) that generalize the usual mean-field description while taking into account the binary nature of the gene state variable. These equations describe the combined time evolution of average quantities and of fluctuations around them. They reproduce accurately the stationary state values of the dynamical variables and predict the appearance of oscillations, without any assumption on the gene switch timescale or on the statistical distribution of random variables. We then explain the appearance of stochastic oscillations by a resonance effect between the characteristic timescales of the stochastic network and derive an analytical criterion for their appearance. Finally, the parameter values relevant for the Hes1 network suggest that the mechanism we describe may be exploited to generate robust oscillations in Hes1 expression. Our findings highlight the functional role of intrinsic fluctuations arising from the gene-state flip dynamics as an important ingredient for shaping the dynamics of genetic networks.
Methods
To assess the validity of moment-closure approximations of the CMEs, we performed numerical stochastic simulations of the chemical network of Fig. 1 A for various values of the reduced parameters ρ, Λ, and δ (see Results). The stochastic simulations were performed using an implementation of the next reaction method (Gibson-Bruck algorithm (46)). The integration time used for numerical estimation of moments was chosen to ensure a relative error of the average gene activity estimator smaller than 10−4, by monitoring the convergence of the estimator and its fluctuations. To estimate the Fano factor quantifying the regularity of protein spikes, we recorded 4000 interspike intervals, after a transient whose duration was chosen by monitoring the convergence of the estimator for the gene average activity.
To obtain a one-to-one correspondence between the original parameter space {kon, koff, β, α, δm, δp} and the reduced parameter space {ρ, Λ, η}, three constraints are required. Thus, we fixed the following:
-
1.
The ratio β/δp = 10 to enforce a protein/mRNA concentration ratio of 10, which is a realistic assumption for a biological network;
-
2.
The gene repression threshold Ωkoff/kon = 100, to keep computation time within reasonable limits while being consistent with the assumption of infinite cell volume;
-
3.
δm = 1 to set the timescale to the mRNA half-life; and
-
4.
Because stochastic simulations deal with copy numbers instead of concentration, the cell volume has no influence, and we fixed Ω = 1.
The validity of the truncation schemes investigated can then be assessed by comparing the values of the averages in the stochastic simulation with the fixed point values of the ODE models obtained by truncating the moment expansion.
Results
Corrections to the rate equation
Three stochastic variables characterize the network dynamical state: the gene state g, the mRNA copy number m, and the protein copy number p. The time evolution of the probabilities Pg,m,p of being in a state with given values of g, m, and p is given by the following CME:
| (1) |
which can be read from Fig. 1 A and provides the most general description of the dynamics. The parameters kon and koff characterize the kinetics of protein-DNA binding and unbinding, respectively. The transcription rate and translation rate are α/Ω and β, where Ω represents the cell volume, and δm and δp values are the mRNA and protein degradation rates. The equations are normalized so that in the large volume limit, the average gene activity 〈g〉 and average concentrations 〈m〉/Ω and 〈p〉/Ω become independent of Ω.
Unfortunately, the master equation has generally no analytical solution. Contrary to the mRNA and protein copy numbers, which become much larger than 1 in the large volume limit and have then negligible fluctuations when a single molecule is created or destroyed, the gene state is a binary variable and its relative jump size does not decrease. Therefore, the standard approximation method based on the large-volume expansion of the master equation with the van Kampen ansatz fails (31). Alternatively, the CME can be reformulated as an infinite hierarchy of coupled differential equations whose variables are the moments of the random variables g, m, and p (31). This strategy leads to deterministic differential equations taking the fluctuations into account and having the mean-field rate equations as a limiting case.
To be specific, let us consider the equations describing the time evolution of the averages of gene activity and mRNA and protein concentrations in the infinite volume limit,
| (2a) |
| (2b) |
| (2c) |
where (respectively, ) denotes the mRNA (respectively, protein) concentration m/Ω (respectively, p/Ω),
is the average of the stochastic variable x and cov(x,y) = 〈xy〉 – 〈x〉〈y〉 is the covariance of x and y. These equations are derived by following the approach described in the Supporting Material. Because of the nonlinear term associated with DNA-protein binding in Eq. 2c, this equation can only be reformulated in terms of the average values 〈x〉 by introducing the covariance term cov(g, ). This term does not appear in the usual rate equations describing the kinetics of the self-repressing gene. It describes the feedback from stochastic fluctuations into the dynamics of the average values and plays therefore a key role to model the influence of the gene-state flip dynamics. Equations 2, a–c, also indicate that the dynamics of mRNA and proteins behaves as a low-pass filter whose input is the mean gene state 〈g〉 and output is the mean protein concentration 〈P〉. The cutoff frequency of this low-pass filter depends only on mRNA and protein degradation rates, and is well approximated by
(see the Supporting Material).
Equations 2, a–c, are only the first of an infinite hierarchy of equations where time derivatives of the first raw moments (the averages) are expressed in terms of the first and second raw moments, the time derivatives of second raw moments are expressed in terms of second and third raw moments, and so on (see the Supporting Material). To truncate this infinite hierarchy to a finite set of equations, a closure approximation must be used. For instance, the usual rate equations are obtained when infinite cell volume and vanishing covariances are assumed (i.e., the cov(g, ) term in Eqs. 2, a–c, is set to 0). The approximation neglects all fluctuations and assumes that all variables have precise values, which conflicts with the binary nature of the gene state.
Here, we derive and analyze a higher-order model by using a closure approximation of the moment expansion hierarchy in the limit of an infinite cell volume. In this limit, protein and mRNA copy numbers are also infinite and thus their variation by one unit is negligible, whereas the gene state is a binary variable, whose time evolution is similar to a random telegraph signal. Then the only remaining fluctuations in the models are those induced by the gene-flipping dynamics.
The moment expansion equations up to order 2 are most conveniently expressed in terms of g, p, and of a new variable u = (βm + δmp)/(δp + δm), after suitable rescaling (see the Supporting Material for a detailed derivation). More precisely, the equations read
| (3a) |
| (3b) |
| (3c) |
| (3d) |
| (3e) |
| (3f) |
| (3g) |
| (3h) |
where P, U, and G are rescaled concentrations of the random variables p, u, and g, and T is a rescaled time. The three control parameters η, Λ, and ρ are defined below. The key point is that Eqs. 3, a–h, are not closed, because Eqs. 3, d and e, depend on third-order moments 〈GUP〉 and 〈GP2〉, respectively, whose time evolution is unknown.
The dynamics is controlled by three key parameters
The biochemical reaction network of the self-repressing gene (Fig. 1 A) has six independent kinetic parameters. Three parameter combinations represent scales and thus can be taken out of the equations by rescaling time as well as mRNA and protein concentrations. These are koff/kon, which is the protein concentration at which the gene is half-repressed;
which is the mRNA concentration corresponding to half-repression in steady state; and
which is the response time of the low-pass filter. There remain three reduced parameters, denoted below by ρ, Λ, and η, which control the dynamics, and are discussed below.
The first reduced parameter
corresponds to the maximum possible protein concentration relative to the half-repression protein concentration threshold koff/kon. Dynamically, Λ characterizes the amplification of the gene telegraph signal sent to the low pass-filter. A low value of Λ(Λ << 1) indicates that the gene remains unbound most of the time; the average period of one gene on/off cycle is essentially the on-state duration ton. On the contrary, a high value of Λ(Λ >> 1) indicates that the gene is repressed most of the time; the period of the gene on/off cycle is essentially the off-state duration toff, governed by koff. Thus, Λ can also be viewed as characterizing the strength of the feedback from the gene to itself via its protein product.
The second parameter
measures the gene unbinding rate relative to the cutoff frequency of the low-pass filter. A low value of ρ indicates that the low-pass filter transmits all the fluctuations of the gene state: the protein concentration time profile displays square waveforms enslaved to the gene flip. By contrast, a high value of ρ corresponds to the case where the low-pass filter averages out the gene-flip dynamics: protein concentration evolves with small amplitude fluctuations around its mean value.
The third parameter
characterizes whether the protein and mRNA degradation rates are balanced or not. This indicator reaches a minimum value of 4 for equal degradation rates (δm = δp) and increases to infinity inasmuch as one of the degradation rates becomes negligible compared to the other. It is worth noting that the expressions of all key parameters ρ, Λ, and η are symmetric with respect to exchange of δm and δp. As a consequence, the dynamical properties are unchanged if the mRNA and protein degradation rates are swapped, a fact which was already noted in Morant et al. (26). To distinguish the two regimes that have identical ρ, Λ, and η parameter values but different values of δm and δp, we will later consider the ratio of protein and mRNA degradation rates δ = δp/δm, with η = (1 + δ)2/δ. Obviously, the value of η is unchanged under the transformation δ ↔ 1/δ.
In the fast and slow gene limits, asymptotic expressions of the averages are obtained from the fixed point of Eqs. 3, a–h, regardless of how they are closed. In particular, 〈U〉 = 〈P〉 = Λ〈G〉 in all cases. The value of 〈G〉 depends on the gene response timescale. In the fast gene regime (ρ → ∞), it is determined by equating expression (Eq. 3c) to zero, whose solution satisfies in the limit of strong feedback (large Λ). In the slow gene limit (ρ → 0), one has 〈GP〉 = 〈P〉 (expressing the fact that protein concentration quickly relaxes to 0 when the gene is off), so that equating Eq. 3c to zero now leads to 〈G〉 ∼ 1/Λ for strong feedback. The dramatic decrease in gene average activity is related to the longer memory of the gene, which remains off for longer times after the repressor has disappeared.
Simple considerations also allow us to obtain the asymptotic behavior of the two third-order moments appearing in Eqs. 3, a–h. In the fast gene limit, the protein and mRNA can be considered as constant so that 〈GUP〉 = 〈G〉〈U〉〈P〉 ∼ . In the slow gene limit, 〈U〉 and 〈P〉 quickly relax to their equilibrium value Λ when the gene switches on, so that 〈GUP〉 = 〈UP〉G=1 ∼ Λ2〈G〉 ∼ Λ and thus that 〈GUP〉 ∼ 1/〈G〉 again. Similarly, one finds that 〈GP2〉 ∼ 1/〈G〉 in both limits.
Truncation of the moment equations
A natural closure approximation, which is described in detail in the Supporting Material, would be to assume vanishing third-order central moments 〈(G − 〈G〉)(U − 〈U〉)(P − 〈P〉)〉 and 〈(G − 〈G〉)(P − 〈P〉)2〉. The resulting model is eight-dimensional, incorporating three averages and five covariances as dynamical variables. Note that because not all third-order central moments are constrained to zero, this is a weaker requirement than assuming that variables are Gaussian-distributed. The predictions of this model are exact when the gene is either infinitely fast or slow.
Here, we focus on another closure approximation, which leads to a simpler yet accurate model. It assumes that the two unknown third-order moments are slaved to the gene state according to
| (4) |
This relation is obtained by requiring that, in the limit of strong feedback (large Λ),
-
1.
It matches the slow-gene and fast-gene asymptotic behaviors of the two moments, as obtained in previous section; and
-
2.
The fixed point of the resulting equations agrees with that of the rate equations in the fast gene limit (see the Supporting Material).
Using stochastic numerical simulations, we also checked that it is relatively well satisfied for all intermediate gene response timescales, as will be shown in next section.
When rewritten using Eq. 4, Eqs. 3, a–e, decouple from the others and form a closed system of only five differential equations, named thereafter the truncated moment expansion (TME) model, which read:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
This model predicts the time evolution of the three averages and of the two moments involving the gene state (〈GU〉 and 〈GP〉). This is consistent with the fact that only the gene-state fluctuations survive in the infinite volume limit. The TME model thus provides a minimal extension of the rate equations, allowing us to describe the stochastic dynamics of the network, including the stationary state average values, and thus to study the impact of the gene state fluctuations.
The truncated moment expansion reproduces well the time averages of the stochastic dynamics
To assess the influence of stochastic fluctuations of the gene state on the dynamics of the self-repressing gene, we performed stochastic numerical simulations to determine the values of the time averages and covariances of the rescaled random variables G, M, and P (see Methods) as a function of the control parameters. These time averages were then compared to the fixed point values of two truncations of the moment equation hierarchy: the rate equation model, defined by Eqs. 2, a–c, with the covariance term set to zero; and the TME model defined by Eqs. 5, a–e. These models are defined by sets of ODEs, whose fixed points are specified by the values of the variables such that all time derivatives are zero. These fixed points are usually stable and thus reflect the stationary regime; however, we shall see later that they may become unstable in some conditions, indicating the appearance of spontaneous oscillations.
Let us examine how the average gene activity depends on ρ, which characterizes the gene response timescale, and Λ, which characterizes feedback strength, when protein and mRNA lifetimes are identical (δ = 1). Gene average activity as determined by stochastic simulations is shown in Fig. 2 A. The rate equation model correctly predicts the output of stochastic simulations only when gene dynamics is fast (ρ → ∞) or when the gene repression is small (Λ << 1) (Fig. 2 B). In contrast to this, the TME model predicts quantitatively gene average activity in the entire (ρ, Λ) plane (Fig. 2 C), in particular in regions where the rate equation approximation fails.
Figure 2.
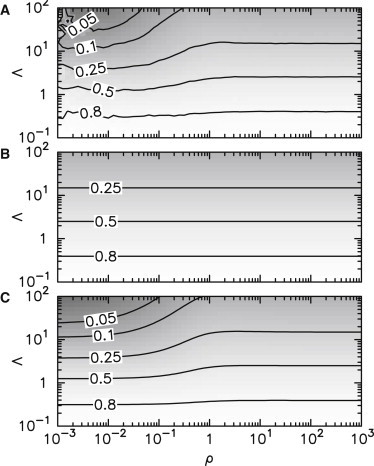
Level sets of average gene activities in the (ρ, λ) parameter plane. (A) Numerical estimation of 〈g〉 using stochastic simulations with parameter values koff/kon = 100, δ = 1, β/δp = 10. (B) Average gene activity predicted by rate equation. (C) Fixed point value of gene activity in the TME model.
A more detailed assessment of the TME model accuracy is provided in Fig. 3, which shows how the time averages of G, U, and P, and their products evolve with ρ and δ, depending on whether they are computed from stochastic simulations (Fig. 3, left column) or from the fixed point values of the TME model (Fig. 3, right column). The computations are carried out in the strong feedback (i.e., high repression) limit (Λ = 100). Note that in the rate equation approximation, all averages would be constant and the covariances would vanish. Fig. 3 displays only a subset of components of the TME model fixed point, from which the other can be obtained using the relations 〈M〉∗ = 〈P〉∗ = Λ〈G〉∗, 〈GP〉∗ = 1 − 〈G〉∗, and 〈P2〉∗ = 〈PU〉∗ = Λ〈GU〉∗. An important finding is that ρ is the main parameter controlling the averages of the stochastic variables G, U, and P, inasmuch as the curves obtained for various values of δ superimpose remarkably well (Fig. 3 A, left column). As expected, using the variable U leads to numerical results which are symmetrical with respect to the δ ↔ 1/δ inversion.
Figure 3.
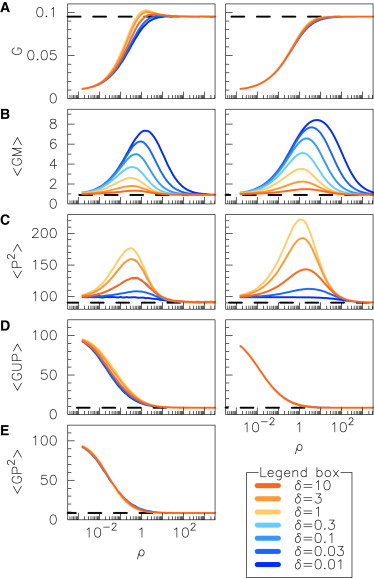
Comparison of raw moments obtained from stochastic simulations (left column) and from the TME model (right column) as functions of parameter ρ, and for various values of δ. (A) Average gene activity 〈G〉. (B and C) Second raw moments 〈GM〉 and 〈P2〉. (D and E) Third raw moments 〈GUP〉 and 〈GP2〉. Curves for different values of δ are color-coded according to legend box. The value of Λ = 100 used in the simulations corresponds to strong feedback (strong gene repression). Stochastic simulations are performed while constraining koff/kon = 100 and β/δp = 10 (see Methods for details). To see this figure in color, go online.
Fig. 3 shows that the fixed point values of the TME model are in very good quantitative agreement with the numerical estimators. However, the stochastic estimators of the averages display an overshoot for ρ close to 1, which is emphasized when η is small (Fig. 3 A). This behavior is not recovered by the TME model, which predicts that averages increase monotonously with ρ. More precisely, the averages in the TME model are specified by
| (6) |
where
Presumably, this discrepancy could be resolved with a better closure approximation. The global evolution of the second raw moments is also well reproduced, even though the TME model overestimates the moments 〈GM〉∗ and 〈P2〉∗ (Fig. 3, B and C) for high values of ρ. The left column of Fig. 3, D and E, displays how 〈GUP〉∗ and 〈GP2〉∗ vary with ρ and δ, in good agreement with the closure assumption (4) (Fig. 3 D, right column). Although discrepancies are slightly more pronounced for 〈GUP〉∗, Fig. 3, D and E, supports the assumption that the two third-order raw moments have equal values. In comparison, the model obtained by assuming vanishing third-order central moments also correctly predicts stationary values and captures more precisely the overshoot of the average near ρ = 1, but displays a stiffer transition for the averages (see the Supporting Material).
Dynamical considerations can explain the variation of averages with ρ observed. If ρ >> 1, the gene-flip dynamics is averaged by the low-pass filter, and the stationary regime is correctly predicted by the fixed point values of the rate equations. In this limit, the gene remains bound or unbound for very short amounts of time, during which mRNA and proteins copy numbers can be considered as constant. RNA and protein levels keep a memory of many previous state switching cycles, and reach a stationary state with a probability distribution that is expected to be Gaussian. The coefficient of variation
tends to zero as ρ increases, indicating that fluctuations in protein concentration become negligible compared to the average concentration in the limit of fast gene dynamics (ρ → ∞).
Conversely, if ρ << 1, the gene reacts infinitely slowly. The dynamics is then driven by the gene jumping between two states according to a Poisson process. During the time where the gene is active (respectively, inactive), protein and mRNA levels quickly converge to their maximum value Λ (respectively, to zero); at the end of a gene switching state cycle, variables are always in the same state with no memory of previous cycles. Protein concentration temporal profiles feature a sequence of squared shape spikes, distributed in time according to a Poisson process, and characterized by a coefficient of variation, , increasing with the overall production rate Λ. Thus, fluctuations are enhanced by a slow gene and a high repression.
Then, a natural question is whether there exists between these two limit cases a dynamical regime that behaves deterministically, as in the fast-gene limit, and also displays strong variations of the protein concentration, as in the slow-gene limit. Such dynamical behavior would feature a sequence of protein concentration spikes, but with a time interval distribution more regular than a Poisson process. This intuition is based on the fact that when the gene-flip frequency and the cut-off frequency of the low-pass filter are resonant (ρ ≈ 1), the random fluctuations of gene flips generated by the Poisson process should be partially buffered by the low-pass filter. This mechanism should prevent spike bunching, generating a more regular dynamical behavior that is the stochastic analog of an oscillatory behavior (which we term thereafter “stochastic oscillations”). To assess the veracity of this idea, we developed a criterion to quantify the regularity of stochastic oscillations, described in the next section.
Negative feedback induces protein spike antibunching
The regularity of a stochastic oscillatory behavior is often quantified using a temporal autocorrelation function (8,37,47). This measure is sensitive to reproducibility in both time and amplitude. However, temporal regularity is certainly more relevant than amplitude regularity for biological protein signals. The highly nonlinear response of many signaling cascades can protect them against fluctuations in amplitude, for example by saturating output above an input threshold. A standard technique for assessing temporal regularity is to divide the state space into two regions I and II and to study the distribution of the times where the system leaves I to enter II. It is often useful to require a minimal excursion in region II to avoid spurious transitions induced by noise. Here, we detect events where the protein level crosses successively the mean protein level 〈P〉∗ and the P′∗ = 〈P〉∗ + 0.25 stdev(P) level before falling back below the mean protein level, where “stdev(P)” denotes the standard deviation of P.
Given the list of times where the system transits from low to high protein levels, we compute the probability of detecting n transitions within a time interval of fixed duration. To be specific, we select a time interval equal to 10 times the average time between two events, and characterize the probability distribution of the number of events by the variance to mean ratio, also known as the Fano factor (48). This method is inspired by how the temporal distribution of photons from a light source is generally characterized, with the event of interest being a photon detection. A Fano factor close to unity is obtained when time intervals between events follow a Poisson distribution. A Fano factor greater (less) than unity indicates super-Poissonian (respectively, sub-Poissonian) behavior corresponding to a bunching (respectively, antibunching) of protein spikes. Spike anti-bunching can be viewed as a stochastic counterpart of deterministic oscillations. Although using the coefficient of variation of the interspike interval would give similar results, the method described above has the advantage to take into account correlations between the successive transitions.
Fig. 4 displays stochastic simulations of the chemical reaction network of Fig. 1 for a slow, an intermediate, and a fast gene, as well as the probability distribution of the number n of transitions within a given time window. As expected, protein spikes in the slow gene case (Fig. 4 A) are slaved to the switching process, leading to a Poisson probability distribution for n (Fig. 4 D) and accordingly a unit Fano factor. In the intermediate gene response time case (Fig. 4 B), protein spikes are mostly antibunched (see solid circles). The probability distribution of spike number is Gaussian-like (Fig. 4 E), the Fano factor being ∼0.25. This antibunching degrades in the case of a fast gene (Fig. 4 C) with the Fano factor rising to 0.9. Thus, we observe a resonance effect, which results from the coincidence of the characteristic time of the gene response to protein variations with the time during which gene state history is remembered, which is controlled by the protein and mRNA decay rates.
Figure 4.
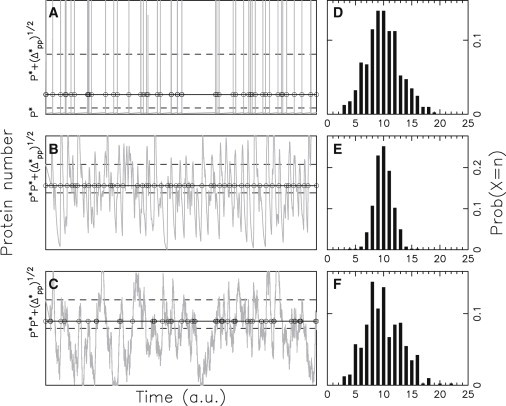
Protein spike antibunching. (A–C). Time evolution of protein copy number for Λ = 100, δ = 1, and ρ = 10−3, 1, 103, respectively. (Dashed lines) Mean protein level and mean protein level plus standard deviation. (Solid lines) High trigger level; (solid circles) spiking events. (D–F) Probabilities of observing n spikes during a time window of 10 average transition times ρ = 10−3, 1, 103, respectively.
We studied systematically how the Fano factor depends on the gene resonance parameter ρ and the relative protein decay rate δ in stochastic simulations (Fig. 5). We found that the regularity of protein spikes is reinforced by 1), similar mRNA and protein decay rates (δ ≈ 1); 2), a resonance parameter close to unity (ρ ≈ 1); and 3), a sufficiently strong feedback (Λ >> 1), as shown in Fig. 5, A and B. Thus, the most regular oscillations are observed when the gene cycling period resonates with the average mRNA/protein lifetime.
Figure 5.
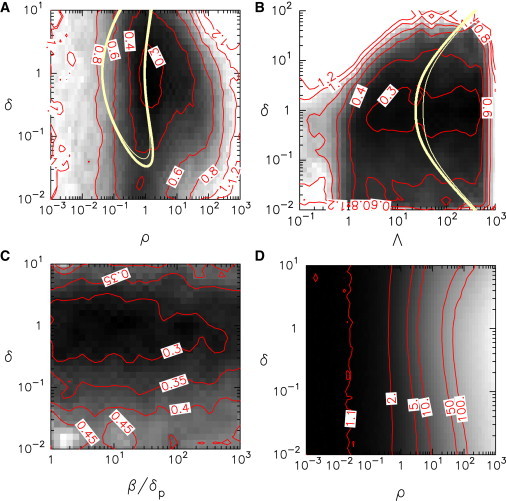
(Color online) Regularity of stochastic oscillations. In panels A–C, the value of the Fano factor F, which quantifies spiking regularity, is shown as a function of two parameters (grayscale color-code; level lines are displayed in red). (Yellow lines in panels A and B) The region where the TME model predicts oscillations based on numerical analysis (thick lines) or analytical criterion Eq. 7 (thin lines). The regularity of stochastic oscillations is favored by balanced protein and mRNA degradation rates (corresponding to δ ≃ 1) as well as (A) a resonance parameter ρ close to 1, and (B) a high value of the overall production rate Λ. (C) The ratio β/δ controlling the relative mRNA to protein concentration has no effect on spike regularity. (D) The oscillation period (or protein average interspike time interval) is controlled by the resonance parameter ρ. The variation of χ, the average number of on/off cycles in an interspike interval, is displayed (grayscale code) as a function of the lifetime ratio δ and of the resonance parameter ρ. (Red) Level lines. Stochastic simulations of the biochemical network have been carried out with koff/kon = 100; β = 10δ (A, B, and D); ρ = 1 (B and C); Λ = 100 (A–C). To see this figure in color, go online.
The lack of symmetry with respect to the transformation δ ↔ 1/δ for low values of Λ (Fig. 5 B) results from numerical difficulties to reach the infinite cell volume limit for small δp (δ << 1). As a control, we checked that the Fano Factor is almost independent of the ratio β/δp (see Fig. 5 C), which determines the protein to mRNA ratio.
In the large Λ-limit, it is expected that the gene spends most of the time in the off-state so that the average duration of one on-/off-cycle is approximately given by τoff = 1/koff in original time units. To study the interplay between the gene state dynamics and the protein spike dynamics, a useful indicator is χ = koff〈Ts〉, where Ts is the average time interval between two spikes. In the slow gene limit (ρ → 0), χ tends to 1, indicating that protein and mRNA are slaved to the gene dynamics in a fire-and-degrade mode. Conversely, the high value of χ in the fast gene limit indicates that the gene dynamics is too fast to be relevant and justifies an adiabatic elimination of the gene state variable. In the parameter region where spikes are more regular, the intermediate values taken by χ (between 1 and 10) reveal that the gene dynamics and the mRNA/protein dynamics influence each other, and together generate the stochastic oscillations observed.
The truncated moment expansion predicts the appearance of stochastic oscillations
If a moment-closure model such as the TME model (Eqs. 5, a–e) is relevant to the dynamics of the self-repressing gene, it should be able to predict the stochastic oscillations evidenced in the previous section. Although such models take fluctuations into account, they are deterministic ODE models, where the natural counterpart of the regular spiking observed in stochastic simulations would be the occurrence of self-sustained oscillations. A linear stability analysis of the TME model should then provide analytical insight into the key parameters controlling the stochastic oscillations.
Indeed, the TME model exhibits oscillatory behavior and the region in the parameter space where oscillation occurs (identified by numerical stability analysis) is consistent with the region of parameter space where regular stochastic oscillations are observed (Fig. 5, A and B), at least for small ρ (slow gene) or ρ ≈ 1. In particular, the TME oscillation region contains the point (ρ = 1, δ = 1), which is the organizing center of the stochastic oscillation region in parameter space. However, the TME model does not capture well the occurrence of regular stochastic oscillations when ρ > 1 (Fig. 5 A). The influence of feedback strength Λ on the appearance of oscillations depending on degradation rate balance is correctly captured (Fig. 5 B), although the TME model overestimates the value of Λ at which regular oscillations are first observed (Fig. 5 B).
It is interesting to note that while the mean-field model of the self-repressing gene is unconditionally stable, the simplest model incorporating the feedback from fluctuations, namely the TME model, predicts oscillations in good agreement with the observed regular stochastic oscillations. This strongly supports the idea that fluctuations play a functional role to promote oscillations. Thus, it is interesting to check whether an analytical criterion for the appearance of oscillations can be derived, so as to identify the role of each parameter in this dynamical behavior. In generally, oscillation criteria for systems with four or more variables are difficult to obtain. In this case, however, an approximation in the stability analysis (see the Supporting Material) leads to a relatively compact Routh-Hurwitz oscillation criterion (49), indicating the parameter space region in which oscillations originating from a Hopf bifurcation occur. In our case, the criterion states that oscillations occur in the TME model when the inequality
| (7) |
is satisfied, the average gene activity 〈G∗〉 being defined by Eq. 6. As Fig. 5, A and B, shows, the criterion (7) delimitates very accurately the parameter space regions where oscillatory behavior is observed in the TME model, as indicated by a numerical stability analysis. Therefore, it is tempting to use it to discuss the influence of the different parameters on the appearance of regular stochastic oscillations, at least for ρ ≤ 1, where the TME model reflects the existence of these stochastic oscillations with oscillating averages and moments.
In particular, it can be seen that the only negative term in Eq. 7 is −ρηΛ, and thus that a sufficiently large value of Λ is required for oscillations. On the other hand, η should not be too large, otherwise the η2 term of Eq. 7 is dominant. Given that η = (1 + δ)2/δ, the lowest possible value for η is 4, which is reached when δ = 1. This implies that the mRNA and protein degradation rates should not be too different, as is observed in the stochastic simulations. More precisely, a necessary condition for the occurrence of oscillatory behavior at ρ = 1 is Λ ≥ 3η + (13η + 6)/(η – 1), which shows that larger values of η require larger values of Λ (i.e., stronger feedback), as indicated by Fig. 5 B.
Let us now consider how the value of ρ influences oscillatory behavior. When ρ → 0 (i.e., the gene cycling period is much longer than average protein/mRNA lifetimes), the criterion is never satisfied because = η2 > 0, and no oscillations occur. When ρ → ∞, the dominant term is obviously positive, and no oscillations occur either. For intermediate values of ρ, the quantity can become negative when Λ is sufficiently large and η is sufficiently close to its minimum value of 4, as discussed above.
The discussion is easier in the limit of large Λ, where the oscillation criterion simplifies considerably (see Section S.H. Linear Stability Analysis of the TME Model in the Supporting Material). Two cases must be considered according to whether ρ is small or close to 1, because the gene average activity scales differently with Λ in these two cases. For ρ = O(1), we find that the leading term of the exact Routh-Hurwitz criterion is
| (8) |
so that oscillations occur when
| (9) |
which describes well the rightmost boundary of the oscillation region in Fig. 5 A (see Fig. S3 in the Supporting Material). The simplicity of the criterion allows us to discuss the relative influences of gene response time (characterized by ρ) and degradation rate balance (characterized by η) on the appearance of oscillations. We see that changes abruptly from large negative to large positive values at
| (10) |
so that oscillations are lost for higher values of η. When ρ is small (ρ = O(1/Λ)), then the oscillation criterion simplifies to
| (11) |
corresponding to the leftmost boundary of the oscillation region in Fig. 5 A (see Fig. S3).
Thus, oscillations are systematically found for ρ ∈[η/Λ,ρc], where ρc is the value of ρ satisfying Eq. 10 for a given value of η, with ρc ≈ 1.07 for δ = 1 (η = 4), and where switches from negative infinity to positive infinity. This confirms unambiguously the existence of a wide region of oscillation in parameter space. The singular behavior observed at ρc is presumably an artifact of the truncation scheme used, and is related to the fact that the choice of the moment-closure function affects the highest-order term in ρ in the criterion (7) (see Section S.H. Linear Stability Analysis of the TME Model in the Supporting Material). It is plausible that the singularity would disappear at a higher truncation order, and that in this case, the oscillation region would extend further toward larger values of ρ, improving the agreement with stochastic simulations. However, the system would then perhaps be too complicated to obtain an analytical oscillation criterion.
Globally, the TME model captures well how the mean-field variables and fluctuations interact through nonlinearities to generate relatively regular stochastic oscillations, at least when the gene response time is not too small (i.e., when ρ ≤ 1). The fact that an analytical criterion for its oscillation threshold, which becomes very simple in the limit of large Λ, can be obtained allows one to understand the role of the different parameters. In particular, it confirms that oscillations are favored when mRNA and protein degradation rates are close to each other (i.e., δ = 1 and η = 4). It is also consistent with the fact that oscillations always occur in the neighborhood of ρ = 1.
Oscillations in Hes1 expression match the criterion for fluctuation-induced oscillations
The main result of this work is that stochastic fluctuations in a self-repressing gene can play a functional role in promoting the appearance of relatively regular oscillations in specific regions of the parameter space. It is then natural to ask whether oscillating self-repressing gene circuits found in biological systems operate in the parameter region we have identified. One such circuit that has been intensively studied is the Hes1 gene, which is believed to be at the core of the somite clock (17). It is well known that a crucial ingredient of oscillations in Hes1 expression is the presence of a time delay, associated to transcription, translation, or transport. This time delay is often modeled as an explicit time delay (23–25,40); however, it can also result from a slow reactional step (21,22,26).
In our system, the time delay is due to the finite gene response time related to the binding/unbinding dynamics. This finite gene response time can also be viewed as taking into account phenomenologically other sources of delay, if they arise from reactional steps and thus are exponentially distributed. More precisely, the gene can persist in the off-state for some time after protein level goes down because of the characteristic time τg = k−1off (in original time units) needed to switch from the off- to the on-state. Therefore, this characteristic time can be viewed as the delay inducing oscillations, and large-scale variations of protein concentration will typically appear when it is not too small compared to protein half-life. We found that these variations are more regular when these two timescales are equal. Of course, the oscillations in our model remain less regular than those observed in Hes1 because 1), the delay is exponentially distributed rather than constant, and 2), there is no cooperativity. Yet, the models are sufficiently similar that if there is a parameter region where fluctuations promote oscillations in our stochastic self-repressing gene model, this should remain true for the Hes1 circuit because oscillations would then be more robust to random variations of the delay. Such random variations could be due, for instance, to the presence of reactional steps. We should then expect this specific parameter region to be selected by evolution.
The initial observation of interest is that in the Hes1 oscillator, the protein and mRNA half-lives are approximately equal, with reported values of 22 and 24 min, respectively (17). This is fully consistent with both our observation that regular oscillations occur preferably for δ = 1 (Fig. 5). Note that this contrasts with what is known for the mean-field model, where making degradation rates unbalanced while keeping their sum constant favors oscillations (26).
A crucial parameter for the regularity of the stochastic oscillations is the resonance parameter ρ, which depends on the time delay and on the mRNA and protein half-lives. However, the time delay in the Hes1 circuit is not known experimentally. In theoretical investigations (see, e.g., Barrio et al. (40) and Bernard et al. (50)), it is generally assumed that the time delay ranges from 10 to 40 min. We assume here a value of 30 min, which is consistent with the fact that for large half-lives, the oscillation period of 120 min is approximately equal to four times the delay (23). With the known values for the mRNA and protein half-lives (which translate to δp ∼ δp 0.03 min−1), this yields ρ ∼ 2. Together with δ = 1, this value corresponds precisely to the region of regular oscillations in Fig. 5 A. Furthermore, note that Fig. 5 D indicates that for ρ = 2, the ratio of the oscillation period to the delay 1/koff is indeed close to 4.
Finally, other theoretical investigations (see, e.g., Barrio et al. (40) and Bernard et al. (50)) assume that Λ >> 1. This, in fact, is a natural condition, which requires that the maximum protein level reached when the gene is fully active must be much larger than the half-repression threshold. This ensures that the protein level can go either below or above this threshold during the course of oscillations, and that the gene is strongly repressed when protein level is high.
Taken together, these facts strongly suggest that the Hes1 mRNA and protein half-lives have been tuned to be close to the time delay to make oscillations in Hes1 expression robust against stochastic fluctuations in delay.
Discussion and Conclusion
In this article, we have studied the stochastic dynamics of a self-repressing gene model, in which the gene switches randomly between the active and inactive state with a characteristic time which can be arbitrarily small or large compared to mRNA and protein lifetimes. The regularity of the protein spikes generated by the dynamics was characterized using a Fano-like indicator. This allowed us to evidence a dynamical resonance phenomenon, namely that a more regular time evolution of protein concentration is observed when the protein and mRNA degradation rates and the gene response time are nearly equal. It should be stressed that fluctuations are here the only factor triggering oscillations, because our model does not incorporate cooperativity or nonlinear degradation. The regularity of the oscillations displayed in Fig. 4 B would be significantly improved by using these two ingredients, as is done in most theoretical investigations, or by considering a fixed time delay in addition to the exponentially distributed gene response time.
To understand the resonance phenomenon, we developed a deterministic ODE model using a moment-closure approximation of the master equation. The TME model describes the combined time evolution of the average gene activity, protein, and mRNA concentrations and of the two raw moments linking gene activity with protein and mRNA concentrations, in accordance with the fact that the gene state remains a binary variable in the infinite volume limit and thus is the most stochastic variable. Such a model naturally describes how nonlinearity injects fluctuations into the average dynamics, which can be substantially modified. The steady state of the TME model predicts well how averages and covariances vary with the gene response time and the ratio of mRNA and protein degradation rates.
In particular, it reproduces the fact that the average gene activity is significantly reduced in the slow gene limit. Unlike rate equations, which are unconditionally stable, the TME model displays a Hopf bifurcation and predicts oscillations in a parameter region where numerical simulations indicate that the protein spikes are indeed more regularly spaced. It remains that the agreement is less good when ρ > 1, presumably because the moment closure approximation affects the ρ3 term in the oscillation criterion, making it sensitive to tiny variations. A direction for future research will thus be to better understand this effect and to derive a more comprehensive description of the self-repressing gene.
Globally, we believe that our results support the idea that deriving deterministic equations through a moment-closure approximation of the master equation is an interesting approach to describe the bifurcation diagram of stochastic dynamical systems, which is generally a difficult problem (see, e.g., Bratsun et al. (51) and Song et al. (52)). This approach is all the more interesting, inasmuch as computer software is available to derive the hierarchy of equations for the moments or cumulants of increasing order (43,53). The approach described here is also well fitted to problems where one variable remains microscopic, such as gene state, and where fluctuations dramatically affect the average values. It thus brings a distinctive advantage compared to other methods based on the linear noise approximation (42).
To check whether the resonance effect discussed here is relevant in real genetic oscillators, we examined the timescales reported for the Hes1 self-repressing gene (17,23,24). In this circuit, the mRNA and protein lifetimes are approximately equal to the time delay. We found that this situation is characterized by the reduced parameters ρ = 2, δ = 1, which are located near the center of the parameter region where regular protein spiking is observed. This strongly suggests that the phenomenon of stochastic resonance we have unveiled plays an important role for generating robust genetic oscillations, independently of other oscillation-enhancing effects such as cooperativity in the transcriptional regulation (54) or nonlinear degradation (26,29), which can be simultaneously harnessed. A possibly related observation by Murugan and Kreiman (55) is that protein response times fluctuate less when mRNA and protein lifetimes are closer. Another interesting fact is that when the sum of half-lives is kept constant, balanced degradation leads to a longer delay in the feedback loop (see Section S.G. Analysis of the Low-Pass Filter: Cut-Off Frequency and Feedback Delay in the Supporting Material). From a mathematical point of view, the fact that several important timescales coincide may favor the appearance of complex conjugate eigenvalues in the Jacobian matrix, a prerequisite for oscillations.
More generally, we believe that our findings provide a remarkable example of how stochastic fluctuations, which are unavoidable in genetic networks, may play a functional role to shape their dynamics (7).
Acknowledgments
The authors thank Benjamin Pfeuty for careful reading of the manuscript.
This work has been supported by Ministry of Higher Education and Research, Nord-Pas de Calais Regional Council, and Le Fonds Européen de Développement Régional through the Contrat de Projets État-Région 2007–2013, as well as by Labex Le Laboratoire d’Excellence Centre Européen pour les Mathématiques, la Physique et Leurs Interactions (grant No. ANR-11-LABX-0007).
Supporting Material
References
- 1.Hartwell L.H., Hopfield J.J., Murray A.W. From molecular to modular cell biology. Nature. 1999;402:C47–C52. doi: 10.1038/35011540. [DOI] [PubMed] [Google Scholar]
- 2.Golding I., Paulsson J., Cox E.C. Real-time kinetics of gene activity in individual bacteria. Cell. 2005;123:1025–1036. doi: 10.1016/j.cell.2005.09.031. [DOI] [PubMed] [Google Scholar]
- 3.Darzacq X., Shav-Tal Y., Singer R.H. In vivo dynamics of RNA polymerase II transcription. Nat. Struct. Mol. Biol. 2007;14:796–806. doi: 10.1038/nsmb1280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Chubb J.R., Trcek T., Singer R.H. Transcriptional pulsing of a developmental gene. Curr. Biol. 2006;16:1018–1025. doi: 10.1016/j.cub.2006.03.092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Suter D.M., Molina N., Naef F. Mammalian genes are transcribed with widely different bursting kinetics. Science. 2011;332:472–474. doi: 10.1126/science.1198817. http://www.sciencemag.org/content/332/6028/472 [DOI] [PubMed] [Google Scholar]
- 6.Harper C.V., Finkenstädt B., White M.R.H. Dynamic analysis of stochastic transcription cycles. PLoS Biol. 2011;9:e1000607. doi: 10.1371/journal.pbio.1000607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Eldar A., Elowitz M.B. Functional roles for noise in genetic circuits. Nature. 2010;467:167–173. doi: 10.1038/nature09326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Simpson M.L., Cox C.D., Sayler G.S. Frequency domain analysis of noise in autoregulated gene circuits. Proc. Natl. Acad. Sci. USA. 2003;100:4551–4556. doi: 10.1073/pnas.0736140100. http://www.pnas.org/content/100/8/4551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Warren P.B., Tănase-Nicola S., ten Wolde P.R. Exact results for noise power spectra in linear biochemical reaction networks. J. Chem. Phys. 2006;125:144904. doi: 10.1063/1.2356472. http://link.aip.org/link/?JCP/125/144904/1 [DOI] [PubMed] [Google Scholar]
- 10.Lestas I., Paulsson J., Vinnicombe G. Noise in gene regulatory networks. IEEE Trans. Auto. Control. 2008;53:189–200. [Google Scholar]
- 11.Aquino T., Abranches E., Nunes A. Stochastic single-gene autoregulation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2012;85:061913. doi: 10.1103/PhysRevE.85.061913. http://link.aps.org/doi/10.1103/PhysRevE.85.061913 [DOI] [PubMed] [Google Scholar]
- 12.Stricker J., Cookson S., Hasty J. A fast, robust and tunable synthetic gene oscillator. Nature. 2008;456:516–519. doi: 10.1038/nature07389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hermsen R., Ursem B., ten Wolde P.R. Combinatorial gene regulation using auto-regulation. PLOS Comput. Biol. 2010;6:e1000813. doi: 10.1371/journal.pcbi.1000813. http://dx.doi.org/10.13712Fjournal.pcbi.1000813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Salgado H., Santos-Zavaleta A., Collado-Vides J. RegulonDB (version 3.2): transcriptional regulation and operon organization in Escherichia coli K-12. Nucleic Acids Res. 2001;29:72–74. doi: 10.1093/nar/29.1.72. http://nar.oxfordjournals.org/content/29/1/72 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keseler I.M., Collado-Vides J., Karp P.D. EcoCyc: a comprehensive database resource for Escherichia coli. Nucleic Acids Res. 2005;33:D334–D337. doi: 10.1093/nar/gki108. http://nar.oxfordjournals.org/content/33/suppl_1/D334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Novák B., Tyson J.J. Design principles of biochemical oscillators. Nat. Rev. Mol. Cell Biol. 2008;9:981–991. doi: 10.1038/nrm2530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hirata H., Yoshiura S., Kageyama R. Oscillatory expression of the bHLH factor Hes1 regulated by a negative feedback loop. Science. 2002;298:840–843. doi: 10.1126/science.1074560. [DOI] [PubMed] [Google Scholar]
- 18.Goodwin B.C. Oscillatory behavior in enzymatic control processes. Adv. Enzyme Regul. 1965;3:425–438. doi: 10.1016/0065-2571(65)90067-1. [DOI] [PubMed] [Google Scholar]
- 19.Griffith J.S. Mathematics of cellular control processes. I. Negative feedback to one gene. J. Theor. Biol. 1968;20:202–208. doi: 10.1016/0022-5193(68)90189-6. [DOI] [PubMed] [Google Scholar]
- 20.Bliss R.D., Painter P.R., Marr A.G. Role of feedback inhibition in stabilizing the classical operon. J. Theor. Biol. 1982;97:177–193. doi: 10.1016/0022-5193(82)90098-4. [DOI] [PubMed] [Google Scholar]
- 21.Goldbeter A. A model for circadian oscillations in the Drosophila period protein (PER) Proc. Biol. Sci. 1995;261:319–324. doi: 10.1098/rspb.1995.0153. [DOI] [PubMed] [Google Scholar]
- 22.Leloup J.-C., Gonze D., Goldbeter A. Limit cycle models for circadian rhythms based on transcriptional regulation in Drosophila and Neurospora. J. Biol. Rhythms. 1999;14:433–448. doi: 10.1177/074873099129000948. [DOI] [PubMed] [Google Scholar]
- 23.Lewis J. Autoinhibition with transcriptional delay: a simple mechanism for the zebrafish somitogenesis oscillator. Curr. Biol. 2003;13:1398–1408. doi: 10.1016/s0960-9822(03)00534-7. [DOI] [PubMed] [Google Scholar]
- 24.Monk N.A.M. Oscillatory expression of Hes1, p53, and NF-κB driven by transcriptional time delays. Curr. Biol. 2003;13:1409–1413. doi: 10.1016/s0960-9822(03)00494-9. [DOI] [PubMed] [Google Scholar]
- 25.Jensen M.H., Sneppen K., Tiana G. Sustained oscillations and time delays in gene expression of protein Hes1. FEBS Lett. 2003;541:176–177. doi: 10.1016/s0014-5793(03)00279-5. [DOI] [PubMed] [Google Scholar]
- 26.Morant P.-E., Thommen Q., Lefranc M. Oscillations in the expression of a self-repressed gene induced by a slow transcriptional dynamics. Phys. Rev. Lett. 2009;102:068104. doi: 10.1103/PhysRevLett.102.068104. http://link.aps.org/doi/10.1103/PhysRevLett.102.068104 [DOI] [PubMed] [Google Scholar]
- 27.Tiana G., Krishna S., Sneppen K. Oscillations and temporal signaling in cells. Phys. Biol. 2007;4:R1–R17. doi: 10.1088/1478-3975/4/2/R01. [DOI] [PubMed] [Google Scholar]
- 28.Mengel B., Hunziker A., Krishna S. Modeling oscillatory control in NF-κB, p53 and Wnt signaling. Curr. Opin. Genet. Dev. 2010;20:656–664. doi: 10.1016/j.gde.2010.08.008. [DOI] [PubMed] [Google Scholar]
- 29.Tyson J.J., Hong C.I., Novak B. A simple model of circadian rhythms based on dimerization and proteolysis of PER and TIM. Biophys. J. 1999;77:2411–2417. doi: 10.1016/S0006-3495(99)77078-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.François P., Hakim V. Core genetic module: the mixed feedback loop. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:031908. doi: 10.1103/PhysRevE.72.031908. [DOI] [PubMed] [Google Scholar]
- 31.van Kampen N.G. Elsevier; New York: 2007. Stochastic Processes in Physics and Chemistry. [Google Scholar]
- 32.Hornos J.E.M., Schultz D., Wolynes P.G. Self-regulating gene: an exact solution. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2005;72:051907. doi: 10.1103/PhysRevE.72.051907. [DOI] [PubMed] [Google Scholar]
- 33.Grima R., Schmidt D.R., Newman T.J. Steady-state fluctuations of a genetic feedback loop: an exact solution. J. Chem. Phys. 2012;137:035104. doi: 10.1063/1.4736721. [DOI] [PubMed] [Google Scholar]
- 34.Elf J., Ehrenberg M. Fast evaluation of fluctuations in biochemical networks with the linear noise approximation. Genome Res. 2003;13:2475–2484. doi: 10.1101/gr.1196503. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.McKane A.J., Newman T.J. Predator-prey cycles from resonant amplification of demographic stochasticity. Phys. Rev. Lett. 2005;94:218102. doi: 10.1103/PhysRevLett.94.218102. [DOI] [PubMed] [Google Scholar]
- 36.McKane A.J., Nagy J.D., Stefanini M.O. Amplified biochemical oscillations in cellular systems. J. Stat. Phys. 2007;128:165–191. [Google Scholar]
- 37.Galla T. Intrinsic fluctuations in stochastic delay systems: theoretical description and application to a simple model of gene regulation. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2009;80:021909. doi: 10.1103/PhysRevE.80.021909. [DOI] [PubMed] [Google Scholar]
- 38.Loinger A., Biham O. Stochastic simulations of the repressilator circuit. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 2007;76:051917. doi: 10.1103/PhysRevE.76.051917. [DOI] [PubMed] [Google Scholar]
- 39.Blossey R., Cardelli L., Phillips A. Compositionality, stochasticity, and cooperativity in dynamic models of gene regulation. HFSP J. 2008;2:17–28. doi: 10.2976/1.2804749. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Barrio M., Burrage K., Tian T. Oscillatory regulation of Hes1: discrete stochastic delay modeling and simulation. PLOS Comput. Biol. 2006;2:e117. doi: 10.1371/journal.pcbi.0020117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lepzelter D., Feng H., Wang J. Oscillation, cooperativity, and intermediates in the self-repressing gene. Chem. Phys. Lett. 2010;490:216. doi: 10.1016/j.cplett.2010.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Scott M., Hwa T., Ingalls B. Deterministic characterization of stochastic genetic circuits. Proc. Natl. Acad. Sci. USA. 2007;104:7402–7407. doi: 10.1073/pnas.0610468104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Gillespie C.S. Moment-closure approximations for mass-action models. IET Syst. Biol. 2009;3:52–58. doi: 10.1049/iet-syb:20070031. [DOI] [PubMed] [Google Scholar]
- 44.Lee C.H., Kim K.-H., Kim P. A moment closure method for stochastic reaction networks. J. Chem. Phys. 2009;130:134107. doi: 10.1063/1.3103264. http://link.aip.org/link/?JCP/130/134107/1 [DOI] [PubMed] [Google Scholar]
- 45.Singh A., Hespanha J.P. Approximate moment dynamics for chemically reacting systems. IEEE Trans Auto. Control. 2011;56:414–418. [Google Scholar]
- 46.Gibson M.A., Bruck J. Efficient exact stochastic simulation of chemical systems with many species and many channels. J. Phys. Chem. A. 2000;104:1876–1889. [Google Scholar]
- 47.Coulon A., Gandrillon O., Beslon G. On the spontaneous stochastic dynamics of a single gene: complexity of the molecular interplay at the promoter. BMC Syst. Biol. 2010;4:2. doi: 10.1186/1752-0509-4-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Fano U. Ionization yield of radiation. 2. The fluctuations of the number of ions. Phys. Rev. 1947;72:26–29. [Google Scholar]
- 49.Gradshteyn I.S., Ryzhik I.M. Academic Press; San Diego, CA: 2000. Tables of Integrals, Series, and Products. [Google Scholar]
- 50.Bernard S., Cajavec B., Herzel H. Modeling transcriptional feedback loops: the role of Gro/TLE1 in Hes1 oscillations. Philos. Trans. A Math. Phys. Eng. Sci. 2006;364:1155–1170. doi: 10.1098/rsta.2006.1761. [DOI] [PubMed] [Google Scholar]
- 51.Bratsun D., Volfson D., Hasty J. Delay-induced stochastic oscillations in gene regulation. Proc. Natl. Acad. Sci. USA. 2005;102:14593–14598. doi: 10.1073/pnas.0503858102. http://www.pnas.org/content/102/41/14593 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Song C., Phenix H., Perkins T.J. Estimating the stochastic bifurcation structure of cellular networks. PLOS Comput. Biol. 2010;6:e1000699. doi: 10.1371/journal.pcbi.1000699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Vidal S., Petitot M., Kuttler C. Models of stochastic gene expression and Weyl algebra. In: Horimoto K., Nakatsui M., Popov N., editors. Algebraic and Numeric Biology, Vol. 6479 of Lecture Notes in Computer Science. Springer; Berlin, Germany: 2012. pp. 76–97. [Google Scholar]
- 54.Purcell O., Savery N.J., di Bernardo M. A comparative analysis of synthetic genetic oscillators. J. R. Soc. Interface. 2010;7:1503–1524. doi: 10.1098/rsif.2010.0183. http://rsif.royalsocietypublishing.org/content/7/52/1503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Murugan R., Kreiman G. On the minimization of fluctuations in the response times of autoregulatory gene networks. Biophys. J. 2011;101:1297–1306. doi: 10.1016/j.bpj.2011.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


